Many human RNA viruses show extraordinarily stringent selective constraints on protein evolution

Significance

The nonsynonymous substitutions (d_N)-to-synonymous substitutions (d_S) ratio in protein-coding genes is commonly used to study the mechanisms of gene evolution. To understand why RNA viruses show large variations in d_N/d_S, we studied the d_N/d_S ratios in 21 human RNA viruses, 8 human DNA viruses, and 17 mammals. Eighteen RNA viruses, but only 2 DNA viruses and no mammals, showed a genome-average d_N/d_S < 0.10. Thus, many human RNA viruses exhibited extraordinarily stringent selective constraints on protein evolution. Our among-gene and among-species comparisons revealed that both positive selection and population size play significant roles in the d_N/d_S variation among genes and species. This study clarified several controversial issues and increased our understanding of the mechanisms of RNA virus evolution.

Abstract

How negative selection, positive selection, and population size contribute to the large variation in nucleotide substitution rates among RNA viruses remains unclear. Here, we studied the ratios of nonsynonymous-to-synonymous substitution rates (d_N/d_S) in protein-coding genes of human RNA and DNA viruses and mammals. Among the 21 RNA viruses studied, 18 showed a genome-average d_N/d_S from 0.01 to 0.10, indicating that over 90% of nonsynonymous mutations are eliminated by negative selection. Only HIV-1 showed a d_N/d_S (0.31) higher than that (0.22) in mammalian genes. By comparing the d_N/d_S values among genes in the same genome and among species or strains, we found that both positive selection and population size play significant roles in the d_N/d_S variation among genes and species. Indeed, even in flaviviruses and picornaviruses, which showed the lowest ratios among the 21 species studied, positive selection appears to have contributed significantly to d_N/d_S. We found the view that positive selection occurs much more frequently in influenza A subtype H3N2 than subtype H1N1 holds only for the hemagglutinin and neuraminidase genes, but not for other genes. Moreover, we found no support for the view that vector-borne RNA viruses have lower d_N/d_S ratios than non–vector-borne viruses. In addition, we found a correlation between d_N and d_S, implying a correlation between d_N and the mutation rate. Interestingly, only 2 of the 8 DNA viruses studied showed a d_N/d_S < 0.10, while 4 showed a d_N/d_S > 0.22. These observations increase our understanding of the mechanisms of RNA virus evolution.

Rates of nucleotide substitution can be up to 1 million-fold higher in RNA viruses than in their cellular hosts (1–3). This rapid evolution is mainly due to high mutation rates (4, 5), while natural selection occurs mostly as purifying selection (5, 6). Selection is usually measured by the d_N/d_S ratio, where d_S (d_N) is the number of synonymous (nonsynonymous) substitutions per synonymous (nonsynonymous) site between 2 sequences. Although d_N/d_S has been studied in many RNA viruses (7), some important issues remain unresolved. One question is the relative contributions of natural selection and effective population size (N_e) to differences in d_N/d_S among viral species. Positive (Darwinian) selection increases, while negative (purifying) selection decreases, d_N/d_S. Unfortunately, it is difficult to determine whether an instance of elevated d_N/d_S is due to positive selection or relaxed negative selection. Positive selection has been found in viruses such as influenza A viruses (8, 9) and HIV-1 (10–12). However, the contribution of positive selection to the genomic mean d_N/d_S has not been evaluated. Because natural selection is more effective in large populations and negative selection predominates (7), an increase in N_e would be expected to reduce the mean d_N/d_S. Unfortunately, N_e is usually unknown.

To address the above questions, we have developed an approach. Specifically, we propose 5 rules to infer the roles of positive selection, negative selection, and N_e in the d_N/d_S variation among genes in the same genome and among species (or strains) (Results and Materials and Methods).

Another issue is whether evolutionary rates are correlated with mutation rates, as previous studies yielded conflicting results (5, 13). One major difficulty is that mutation rate is measured per cell infection cycle, whereas evolutionary rate is measured per year (5). Moreover, previous studies did not separate nonsynonymous and synonymous rates, so the observed correlation could be mainly due to the correlation between synonymous rate and mutation rate. We address these issues by computing the correlation between d_N and d_S, using d_S as a proxy for mutation rate (14).

We focus on human RNA viruses, which are better studied than nonhuman viruses. For comparison, we also include human DNA viruses and mammalian genes.

Results

d_N/d_S Ratios in Mammals.

We first obtained the d_N/d_S ratios of mammalian genes, which are relatively well studied, so that the ratios can serve as a reference for human RNA viruses. Nikolaev et al. (15) estimated the d_N and d_S values for 17 mammalian lineages using 218 protein-coding genes. The d_N/d_S ratios vary from 0.155 to 0.351, with an average of 0.219 (Table 1 and Fig. 1), which is similar to the ratio (0.211) obtained from the pairwise d_N and d_S values between human and mouse genes in table 7.1 of ref. 3. The data in Table 1 suggest an important role of population size in the d_N/d_S variation among species (Discussion).

Table 1.

d_N, d_S, and d_N/d_S values in mammalian genes

Lineage name	Scientific name	dN*	dS*	dN/dS	Population size or density	Body mass,* g
Shrew	Sorex araneus	0.053	0.338	0.155	200 to 1,750 per km2†	10
Mouse	Mus musculus	0.012	0.077	0.159	NA	18
Dog	Canis lupus familiaris	0.023	0.142	0.162	NA	40,000
Rabbit	Oryctolagus cuniculus	0.037	0.229	0.162	NA	1,820
Rat	Rattus norvegicus	0.015	0.092	0.165	>200 million†	340
Galago	Otolemur garnetti	0.027	0.160	0.168	NA	760
Cow	Bos taurus	0.034	0.181	0.187	NA	890,000
Tenrec	Echinops telfairi	0.054	0.281	0.193	NA	126
Gray short-tailed opossum	Monodelphis domestica	0.070	0.346	0.201	NA	71
Bat	Rhinolophus ferrumequinum	0.029	0.142	0.204	∼10,000 to 100,000‡	21
Marmoset	Callithrix jacchus	0.015	0.064	0.226	>10,000§	300
Armadillo	Dasypus novemcinctus	0.042	0.177	0.236	13 per km2†	4,200
Elephant	Loxodonta africana	0.027	0.101	0.268	625,000†	3,980,000
Human	Homo sapiens	0.002	0.006	0.285		70,000
Baboon	Papio anubis	0.003	0.009	0.289	1 to 63 per km2†	21,400
Macaque	Macaca mulatta	0.005	0.017	0.309	5 to 15 or 57 per km2 in high or low forests†	6,000¶
Chimpanzee	Pan troglodytes	0.003	0.008	0.351	192,500†	45,000
Average (SD)		0.026 (0.019)	0.140 (0.107)	0.219 (0.059)

NA, not available.

^*The d_N and d_S values and the body mass (g) data were obtained from Nikolaev et al. (15).

^†From ref. 49 (pp. 207, 1,520, 66, 1,003, 588, 583, and 625).

^‡From https://www.iucnredlist.org/species/19517/21973253#population (accessed 6 December 2018).

^§From https://www.iucnredlist.org/species/41518/17936001 (accessed 6 December 2018).

^¶From Wikipedia.

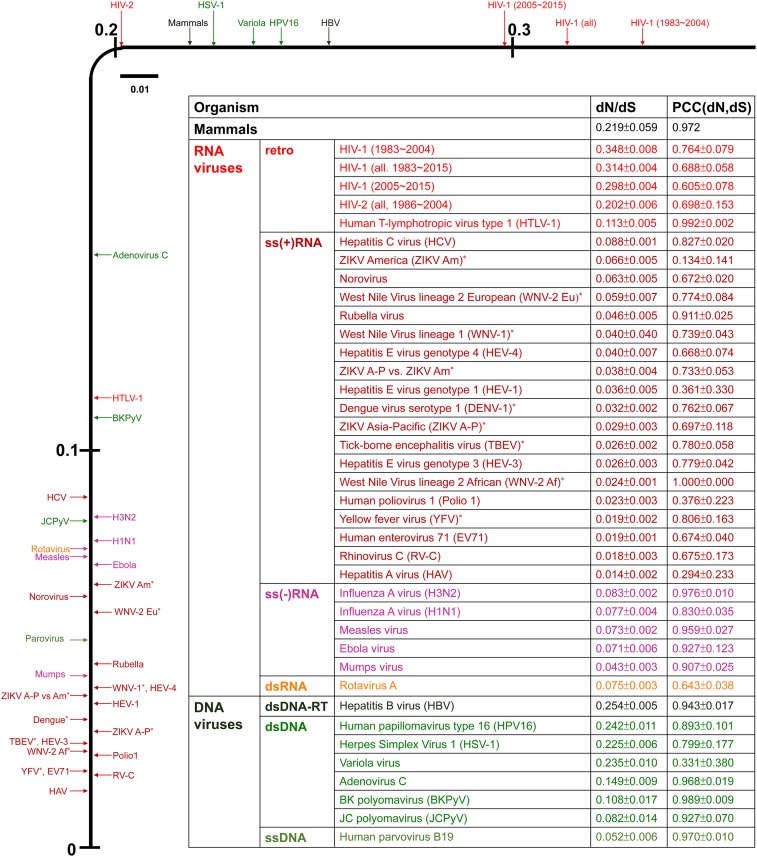
Fig. 1.

The d_N/d_S ratios in viruses and mammals. For each virus, the d_N/d_S ratio was calculated for the entire coding region of the genome. The values for each virus are the mean ratio of whole-genome d_N and d_S values reported in Dataset S3. Each d_N/d_S ratio is shown on the y axis of the figure. The flaviviruses are indicated by an asterisk. RT, retrotranscribing.

Five Rules for Inferring the Mechanisms of RNA Virus Evolution.

We proposed 5 rules for inferring the roles of positive selection, negative selection, and N_e in RNA virus evolution when d_N/d_S values are available for 2 or more species (or strains) from the same viral family. These rules are based on 2 rationales. First, positive selection increases, whereas negative selection decreases, the d_N/d_S ratio. Second, in RNA virus evolution, negative selection is much more prevalent than positive selection (7), so our interpretation of d_N/d_S is largely based on the slightly deleterious mutation hypothesis of Ohta (16). Under this hypothesis, an increase in the N_e tends to decrease the d_N/d_S ratio. Note that the genes in a genome share the same N_e.

The 5 rules are described below:

• Rule 1: If a species shows low d_N/d_S ratios for all or most genes in the genome compared with those in other species, that species likely had a larger N_e than the other species. Alternatively, one may assume that these genes were subject to stronger negative selection in that species than in the other species, but this assumption is unlikely to hold for most genes in the genome.

• Rule 2: If a gene shows a high d_N/d_S ratio in a species compared with both other genes in the same genome and the same gene in other species, it has likely undergone positive selection in that species. Alternatively, one may assume that the elevated d_N/d_S was due to relaxation of negative selection, but relaxed negative selection is less effective than positive selection in increasing the d_N/d_S value.

• Rule 3: If the d_N/d_S ratio for a gene is low both among genes in the same species (genome) and among species, the gene was likely subject to stronger negative selection than other genes. The low d_N/d_S ratio could not be due to a larger N_e; otherwise, the other genes in the same species should also tend to show a low d_N/d_S.

• Rule 4: If a gene shows a high d_N/d_S in all species, it is likely subject to weaker negative selection than other genes. There can be exceptions to this rule; for example, the HA (hemagglutinin) gene can potentially be subject to positive selection and show a high d_N/d_S in different influenza A strains. Therefore, some caution is needed when applying this rule.

• Rule 5: If a strain (or species) shows high d_N/d_S ratios for all or most of the genes in the genome compared with those in other strains, then that strain likely has had a relatively small N_e and/or the effects of negative selection have not yet fully accumulated [e.g., when closely related viral isolates are compared (17)]. In contrast to rule 1, the d_N/d_S ratios are elevated rather than decreased, implying a smaller N_e. An elevated d_N/d_S can occur in a new population (strain) (i.e., the virus has not been found before in that locality) if it has undergone a population bottleneck, so that it has a small N_e, or if the new locality represents a new niche for the virus.

In the above, rule 2 is for inferring positive selection. We did not use any of the standard methods for detecting positive selection, such as that of the PAML program package (18), because most of those tests require d_N/d_S > 1, which is difficult to meet in RNA viruses because of the prevalence of negative selection (deleterious mutations) in RNA viruses.

d_N/d_S Ratios in RNA and DNA Viruses.

We studied 21 human RNA viruses, including 13 positive-sense, single-stranded [ss(+)] RNA viruses; 4 negative sense, single-stranded [ss(−)] RNA viruses; 3 ss RNA retrotranscribing (retro) viruses; and 1 double-stranded (ds) RNA virus (Fig. 1 and Dataset S1). For comparison, we also included 8 DNA viruses: 1 ds retro DNA virus, 6 ds DNA viruses, and 1 ss DNA virus (Fig. 1 and Dataset S1).

A striking observation is that 18 of the 21 RNA viruses studied show a d_N/d_S ratio between 0.01 and 0.10, implying that more than 90% (in some cases, close to 99%) of nonsynonymous mutations are eliminated by negative selection in these species (Fig. 1). The picornaviruses show the lowest d_N/d_S ratios, with 0.014 for hepatitis A virus, 0.018 for rhinovirus, 0.019 for human enterovirus 71, and 0.022 for human poliovirus 1. The flaviviruses, which include the Zika virus (ZIKV), the West Nile virus (WNV), the dengue virus (DENV), the yellow fever virus (YFV), and the tick-borne encephalitis virus (TBEV), also show very low d_N/d_S ratios, ranging from 0.019 to 0.066. HIV-1 is an outstanding exception, with a d_N/d_S ratio (∼0.314) that is much higher than that for mammals (0.219). HIV-2 shows a d_N/d_S ratio (0.202) close to that for mammals. Human T-lymphotropic virus type 1 (HTLV-1) shows a moderate value of 0.113. Among the 21 RNA viruses studied, only HIV-1 and HIV-2 showed a d_N/d_S ratio higher than the observed smallest mammalian d_N/d_S ratio (0.155).

The 8 DNA viruses studied tend to show a higher d_N/d_S ratio than the RNA viruses (Fig. 1), as found by Hughes and Hughes (19). Indeed, 4 species (hepatitis B virus, human papillomavirus type 16, herpes simplex virus type 1, and variola virus) show a d_N/d_S higher than that for mammals. However, 2 (JC polyomavirus and human parvovirus B19) show a d_N/d_S ratio < 0.1.

Flaviviruses.

In this and the next subsections, we examine the d_N/d_S ratios in RNA viruses in detail, trying to understand the roles of positive selection, negative selection, and N_e in the d_N/d_S variation among genes within and among species. For this purpose, each d_S value is computed from the entire coding region of the genome under study to reduce the effect of stochastic variation in d_S on the variation in d_N/d_S among genes (Dataset S3).

Table 2 shows the d_N/d_S ratios for 8 flavivirus strains (or species). In WNV-1, the NS4A gene shows the highest d_N/d_S among the genes in the genome and among the 8 flaviviruses, so it likely has undergone positive selection (rule 2) (20–23). We divide WNV-2 into WNV-2 Africa and WNV-2 Europe. WNV-2 Africa shows the lowest average d_N/d_S among the 8 strains compared; indeed, all genes except NS5 show a lower d_N/d_S in WNV-2 Africa than in WNV-1. Thus, WNV-2 Africa likely has a larger N_e than the other strains (rule 1). The d_N/d_S ratios for all genes in WNV-2 Europe are higher than those in WNV-1 except NS4A and also those in WNV-2 Africa except NS5, suggesting that WNV-2 European has a smaller N_e than WNV-1 and WNV-2 Africa and/or the effect of negative selection has not been fully accumulated (rule 5). Note that WNV-2 Europe is likely a young strain, as it was transmitted to Europe probably in early 21st century (24).

Table 2.

Means (SEs) of d_N/d_S values for genes in flaviviruses

	dN/dS (SE)*
Gene (no. of codons)	WNV-1		WNV-2 Africa		WNV-2 Europe		YFV		TBEV		ZIKV A-P		ZIKV Am		DENV		Average (SE)
Capsid (118)	0.047	(0.016)	0.000	(0.000)	0.057	(0.031)	0.050	(0.009)	0.083	0.012)	0.119	(0.044)	0.104	(0.030)	0.051	(0.010)	0.064 (0.035)
prM (167)	0.036‡	(0.012)	0.008†	(0.006)	0.085‡	(0.033)	0.012†	(0.003)	0.044‡	(0.007)	0.083‡	(0.022)	0.035†	(0.014)	0.030†	(0.005)	0.041 (0.027)
E (498)	0.030	(0.006)	0.013	(0.005)	0.064	(0.014)	0.010	(0.002)	0.018	(0.003)	0.034	(0.012)	0.033	(0.010)	0.035	(0.005)	0.029 (0.016)
NS1 (352)	0.037†	(0.010)	0.015†	(0.008)	0.073	(0.019)	0.014†	(0.002)	0.022†	(0.005)	0.034†	(0.007)	0.137‡	(0.015)	0.037†	(0.005)	0.046 (0.039)
NS2A (226)	0.061	(0.011)	0.023†	(0.005)	0.066	(0.018)	0.041	(0.007)	0.051	(0.009)	0.038†	(0.014)	0.039†	(0.012)	0.080‡	(0.013)	0.050 (0.017)
NS2B (130)	0.049	(0.015)	0.013	(0.009)	0.104	(0.029)	0.034	(0.008)	0.015	(0.005)	0.039	(0.022)	0.066	(0.021)	0.044	(0.007)	0.046 (0.028)
NS3 (620)	0.026	(0.005)	0.016	(0.000)	0.030	(0.010)	0.010	(0.002)	0.020	(0.002)	0.019	(0.005)	0.057	(0.008)	0.024	(0.004)	0.025 (0.013)
NS4A (131)	0.073‡	(0.018)	0.000†	(0.000)	0.037†	(0.025)	0.022†	(0.005)	0.020†	(0.005)	0.012†	(0.008)	0.038‡	(0.021)	0.040‡	(0.007)	0.030 (0.021)
NS4B (251)	0.071	(0.012)	0.013	(0.007)	0.106	(0.031)	0.018	(0.005)	0.022	(0.005)	0.028	(0.013)	0.051	(0.014)	0.028	(0.005)	0.042 (0.030)
NS5 (903)	0.036†	(0.007)	0.052	(0.005)	0.049	(0.012)	0.022†	(0.004)	0.023†	(0.002)	0.019†	(0.005)	0.085‡	(0.008)	0.026†	(0.004)	0.039 (0.021)
Average (SE)	0.046	(0.016)	0.015	(0.014)	0.067	(0.024)	0.023	(0.013)	0.032	(0.021)	0.042	(0.032)	0.064	(0.033)	0.039	(0.016)
Effect of positive selection removed	0.041		0.015		0.061		0.023		0.032		0.036		0.048		0.035

^*Boldface (underlined) indicates a significantly higher (lower) d_N/d_S ratio than those ratios in other genes in the same genome.

^†The gene has a significantly lower d_N/d_S ratio in the strains (or species) indicated than those in some other strains (species).

^‡The gene has a significantly higher d_N/d_S ratio in the strains (species) indicated than those in some other strains (species).

Like WNV-2 Africa, YFV and TBEV show low average d_N/d_S ratios, so these 2 species likely have relatively larger N_es (rule 1).

For ZIKV, we consider ZIKV Asia-Pacific (ZIKV A-P) and ZIKV America (ZIKV Am) separately. In ZIKV A-P, the d_N/d_S ratio for the prM gene is the second highest among the genes in the genome and is significantly higher than those in the other flaviviruses except WNV-2 Europe, suggesting that this gene in ZIKV A-P has undergone positive selection (rule 2). The d_N/d_S ratios, except those for Capsid, prM, and E, are higher in ZIKV Am than in ZIKV A-P, suggesting that ZIKV Am has a smaller N_e than ZIKV A-P and/or the effect of negative selection has not been fully accumulated in ZIKV Am because it is a new population (25) (rule 5). In ZIKV Am, the d_N/d_S ratios for the NS1 and NS5 are high compared with other genes in the genome and higher than those d_N/d_S ratios in the other flaviviruses, suggesting that these 2 genes have undergone positive selection in America (rule 2).

In DENV, the NS2A gene shows strong evidence of positive selection because its d_N/d_S (0.080) is the highest among all genes in the genome and among all of the flaviviruses in Table 2 (rule 2).

Picornaviruses and Hepatitis E Virus.

Table 3 shows the d_N/d_S ratios for 4 picornaviruses. In hepatitis A virus, 6 genes (VP1, VP2, VP3, 3B, 3C, and 3D) show the lowest d_N/d_S ratios among the 11 genes in the genome and 3 genes (VP1, 3C, and 3D) show the lowest d_N/d_S ratios among the 4 species studied, suggesting that hepatitis A virus had a larger N_e than the other 3 species (rule 1) and VP1, VP2, VP3, 3B, 3C, and 3D were subject to stronger selective constraint (negative selection) than the other genes in the genome (rule 3). In rhinovirus C, 4 genes (2B, 2C, 3A, and 3B) show the lowest d_N/d_S ratios among the 4 species, suggesting it likely had a larger N_e than poliovirus 1 and enterovirus 71. On the other hand, rhinovirus C VP1 likely has undergone positive selection because it shows the highest d_N/d_S ratio among the 4 species and the second highest d_N/d_S among the genes in the same genome (rule 2). In poliovirus 1, 3C and 3D show relatively higher d_N/d_S values among the genes in the genome and the highest d_N/d_S among species, so these 2 genes likely have undergone positive selection in poliovirus 1. The 3C and 3D genes in enterovirus 71 might have undergone positive selection because their values are significantly higher than those in the other species, except poliovirus 1.

Table 3.

Means (SEs) of d_N/d_S values for genes in picornaviruses

	dN/dS (SE)*
Gene (no. of codons)	Hepatitis A virus		Rhinovirus C		Poliovirus 1		Enterovirus 71		Average (SE)
VP1 (293)	0.009†	(0.003)	0.030‡	(0.008)	0.012	(0.002)	0.019‡	(0.001)	0.018 (0.008)
VP2 (252)	0.003	(0.002)	0.017‡	(0.008)	0.002†	(0.001)	0.010‡	(0.003)	0.008 (0.006)
VP3 (240)	0.002	(0.001)	0.013	(0.006)	0.006	(0.002)	0.005	(0.001)	0.007 (0.004)
VP4 (57)	0.024	(0.010)	0.010	(0.004)	0.014	(0.006)	0.011	(0.003)	0.014 (0.006)
2A (158)	0.031	(0.005)	0.037	(0.007)	0.035	(0.012)	0.023	(0.002)	0.032 (0.005)
2B (101)	0.022	(0.008)	0.008	(0.004)	0.017	(0.006)	0.014	(0.002)	0.015 (0.005)
2C (330)	0.020	(0.006)	0.009	(0.003)	0.020	(0.006)	0.011	(0.001)	0.015 (0.005)
3A (81)	0.050	(0.008)	0.015	(0.007)	0.030	(0.008)	0.036	(0.004)	0.033 (0.013)
3B (22)	0.009	(0.008)	0.008	(0.009)	0.043	(0.017)	0.051	(0.008)	0.028 (0.019)
3C (192)	0.007†	(0.003)	0.021‡	(0.004)	0.031‡	(0.005)	0.027‡	(0.002)	0.022 (0.009)
3D (468)	0.013†	(0.002)	0.016	(0.005)	0.044‡	(0.008)	0.028‡	(0.001)	0.025 (0.012)
Average over genes (SE)	0.017	(0.014)	0.017	(0.009)	0.023	(0.014)	0.021	(0.013)

^*Boldface (underlined) indicates a significantly higher (lower) d_N/d_S ratio than those ratios in other genes in the same genome.

^†The gene has a significantly lower d_N/d_S ratio in the species indicated than those in some other species.

^‡The gene has a significantly higher d_N/d_S ratio in the species indicated than those in the other species.

Table 4 shows the d_N/d_S ratios for 3 genotypes of hepatitis E virus (HEV-1, HEV-3, and HEV-4). In HEV-4, 2 of the 3 genes have higher d_N/d_S ratios than those in the other 2 strains (e.g., 0.047 and 0.031 in HEV-4 vs. 0.028 and 0.024 in HEV-3). We propose that HEV-4 had a substantially smaller N_e than HEV-1 and HEV-3 (rule 5); indeed, a study suggested that the population size of HEV-4 started to decline in the 1990s (26).

Table 4.

Means (SEs) of d_N/d_S values for genes in HEVs

	dN/dS (SE)*
Gene (no. of codons)	HEV-1	HEV-3	HEV-4	Average (SE)
ORF1 (1,693)	0.043 (0.006)	0.028 (0.002)	0.047 (0.009)	0.039 (0.008)
ORF3 (114)	0.052 (0.014)	0.040 (0.006)	0.045 (0.016)	0.046 (0.005)
C (660)	0.016 (0.004)	0.024 (0.008)	0.031 (0.006)	0.024 (0.006)
Average over genes (SE)	0.037 (0.015)	0.031 (0.007)	0.041 (0.007)

^*Boldface (underlined) indicates a significantly higher (low) d_N/d_S ratio than those ratios in other genes in the same genome.

Influenza A, Mumps, and Measles Viruses.

Table 5 shows the d_N/d_S ratios for influenza A virus subtypes H1N1 and H3N2. It is well known that the HA and NA (neuraminidase) genes often undergo positive selection, and Table 5 shows that the d_N/d_S ratios for their encoding genes are indeed high, especially in H3N2. The M2 (matrix protein 2) and NS1 (nonstructural protein 1) genes also have higher d_N/d_S ratios. The d_N/d_S ratio for the M2 gene is significantly higher in H1N1 than in H3N2, suggesting that this gene in H1N1 has undergone positive selection. The NS1 and NEP (nuclear export protein) genes also show substantially higher d_N/d_S ratios in H1N1 than in H3N2. Thus, the average d_N/d_S for all genes is virtually the same for H1N1 (0.092) and H3N2 (0.088) and is substantially higher for H1N1 (0.076) than for H3N2 (0.062) if the HA and NA genes are excluded from comparison (Table 5). Therefore, positive selection in H1N1 might have been as frequent as in H3N2. The N_e has been suggested to be both larger [Volz et al. (27)] and smaller [Rambaut et al. (28)] in H1N1 than in H3N2. The data in Table 5, however, give no evidence for a substantial difference in N_e between H1N1 and H3N2 because the d_N/d_S ratios for the PB2, PA, and M1 genes are similar for H1N1 and H3N2 (i.e., 0.041 vs. 0.033, 0.039 vs. 0.047, 0.041 vs. 0.046). The low d_N/d_S ratios for these 3 genes suggest that they are subject to strong negative selection. Therefore, a significantly smaller N_e should lead to weaker negative selection and a higher d_N/d_S ratio (rule 4), but no such difference is observed between H1N1 and H3N2.

Table 5.

Means (SEs) of d_N/d_S values for genes in influenza A viruses

	dN/dS (SE)*
Gene (no. of codons)	H1N1		H3N2
PB2 (759)	0.041	(0.004)	0.033	(0.002)
PB1 (758)	0.041‡	(0.003)	0.028†	(0.002)
PA (716)	0.039	(0.003)	0.047	(0.005)
HA (563)	0.147†	(0.017)	0.202‡	(0.009)
NP (498)	0.055	(0.006)	0.072	(0.006)
NA (468)	0.169	(0.015)	0.180	(0.008)
M2 (97)	0.159‡	(0.018)	0.097†	(0.016)
M1 (252)	0.041	(0.008)	0.046	(0.006)
NS1 (230)	0.152	(0.017)	0.131	(0.019)
NEP (121)	0.078	(0.010)	0.046	(0.009)
Average (SE)	0.092	(0.054)	0.088	(0.060)
Average (SE) (excluding HA and NA)	0.076	(0.048)	0.062	(0.033)

^*Boldface (underlined) indicates a significantly higher (lower) d_N/d_S ratio than those ratios in other genes in the same genome.

^†The gene has a significantly lower d_N/d_S ratio in the strain indicated than that in the other strain.

^‡The gene has a significantly higher d_N/d_S ratio in the strain indicated than that in the other strain.

Although the measles and mumps viruses (Paramyxoviridae) are not related to influenza A virus, we include them here so that their estimated N_es (29) may be compared (Discussion). Table 6 shows the d_N/d_S ratios for the mumps and measles viruses. As the d_N/d_S ratios tend to be higher in the measles virus than in the mumps virus, the N_e is likely smaller in the measles virus (rule 5). For the N, P/V, and L genes, the d_N/d_S ratios are considerably higher in the measles virus, suggesting that these genes have undergone positive selection in the measles virus (rule 2). Thus, in this virus, positive selection may have occurred rather frequently, although it is not known for frequent positive selection.

Table 6.

Means (SEs) of d_N/d_S values for genes in mumps and measles viruses

	dN/dS (SE)
Gene (no. of codons)	Mumps		Measles§
N (537)	0.030†	(0.008)	0.076‡	(0.008)
P/V (449)	0.097†	(0.008)	0.169‡	(0.011)
M (355)	0.022	(0.005)	0.025	(0.006)
F (550)	0.072	(0.006)	0.047	(0.005)
H/HN (600)	0.074	(0.005)	0.097	(0.006)
L (2,222)	0.019†	(0.002)	0.058‡	(0.003)
Average (SE)	0.052	(0.030)	0.079	(0.046)

*Boldface (underlined) indicates a significantly higher (lower) d_N/d_S ratio than those ratios in other genes in the same genome.

^†The gene has a significantly lower d_N/d_S ratio in the species indicated than that in the other species.

^‡The gene has a significantly higher d_N/d_S ratio in the species indicated than that in the other species.

^§The SH gene in mumps was excluded because it is absent in measles.

Retroviruses.

Table 7 shows the d_N/d_S ratios for HIV-1 and HIV-2. For HIV-1, we separated the isolates into 2 groups, one from 1983 to 2004 and the other from 2005 to 2015, because AIDS drugs have become increasingly effective. We note that for all genes, the d_N/d_S ratios are higher in the first group than in the second group of HIV-1 isolates. This difference could be because more effective drug treatments after 2004 have put a stronger negative selection pressure on the virus. Note that the difference is larger for the ENV (envelope), TAT (transactivator), and REV (regulator of expression of virion proteins) genes; TAT and REV both partially overlap ENV. Our result is in agreement with the proposal that positive selection on the ENV gene was stronger in the 1980s than in the 2000s (30). Compared with HIV-1, HIV-2 shows a lower d_N/d_S ratio for all genes except the VPR gene. In particular, the ratio for the ENV gene is almost 2-fold higher in HIV-1 (1983 to 2004) than in HIV-2. This is consistent with the observation that in intrapatient viral evolution, the ENV C2V3 regions evolved faster in patients infected with HIV-1 than in those infected with HIV-2 (31, 32). The POL and GAG genes show the lowest and the second lowest d_N/d_S among the genes in the genome in both HIV-1 and HIV-2, so they are likely subjected to stronger negative selection than the other genes (rule 3).

Table 7.

Means (SEs) of d_N/d_S values for genes in retroviruses

	dN/dS (SE)*
	HIVs									HTLV-1
Genes (no. of codons)	HIV-1 (1983 to 2015)§		HIV-1 (1983 to 2004)§		HIV-1 (2005 to 2015)§		HIV-2 (1985 to 2004)¶		Average (SE)
GAG (510, 429)	0.204	(0.004)	0.216‡	(0.009)	0.199‡	(0.005)	0.121†	(0.006)	0.185 (0.037)	0.081 (0.009)
POL (1,057, 864)	0.141	(0.003)	0.142‡	(0.005)	0.140‡	(0.003)	0.110†	(0.004)	0.133 (0.014)	0.086 (0.007)
VIF (204)	0.329	(0.007)	0.355‡	(0.011)	0.312‡	(0.009)	0.185†	(0.009)	0.295 (0.066)	NA
VPR (92)	0.266	(0.009)	0.279	(0.018)	0.260	(0.010)	0.308	(0.028)	0.278 (0.019)	NA
TAT (108)	0.466	(0.013)	0.524‡	(0.024)	0.432	(0.014)	0.358†	(0.020)	0.445 (0.060)	NA
REV (110)	0.479	(0.013)	0.557‡	(0.023)	0.437‡	(0.013)	0.312†	(0.030)	0.446 (0.089)	NA
ENV (858, 488)	0.561	(0.010)	0.643‡	(0.023)	0.523‡	(0.009)	0.315†	(0.013)	0.511 (0.121)	0.149 (0.012)
NEF (232)	0.452	(0.010)	0.501‡	(0.021)	0.426	(0.010)	0.385†	(0.019)	0.441 (0.042)	NA
REX (372)#	NA		NA		NA		NA		NA	0.131 (0.011)
TAX (353)#	NA		NA		NA		NA		NA	0.134 (0.011)
PRO (229)	NA		NA		NA		NA		NA	0.201 (0.019)
Average (SE)	0.362	(0.140)	0.402	(0.168)	0.341	(0.126)	0.262	(0.100)		0.130 (0.040)

^*Boldface (underlined) indicates a significantly higher (lower) d_N/d_S ratio in this (or these) gene(s) than those ratios in other genes in the same genome. NA indicates the gene is absent in the genome.

^†The gene has a significantly lower d_N/d_S ratio in HIV-2 than those in HIV-1 (1983 to 2004) and HIV-1 (2005 to 2015).

^‡The gene has a significantly higher d_N/d_S ratio in the strain(s) indicated than that (or those) in the other strain(s). HIV-1 (1983 to 2015) was not included in the tests.

^§The extra gene in HIV-1, viral protein U (VPU), is not included.

^¶The extra gene in HIV-2, viral protein X (VPX), is not included. After 2004, only 2 isolates for HIV-2 were available.

^#The TAX coding region is contained in the coding region of REX.

Table 7 also shows the d_N/d_S ratios for HTLV-1, also a retrovirus. This virus shares 3 genes (GAG, POL, and ENV) with HIV-1 and HIV-2, and all of them show a much lower d_N/d_S in HTLV-1, suggesting a larger N_e for HTLV-1 (rule 1). The much lower d_N/d_S values in HTLV-1 suggest that it undergoes much less frequent adaptive evolution than HIV-1 and HIV-2, as proposed previously (33). However, in HTLV-1, the d_N/d_S ratios for PRO and ENV (0.201 and 0.149, respectively) are considerably higher than those for the other genes in HTLV-1. This observation suggests that PRO and ENV have undergone positive selection or have been subjected to weaker selective constraint than the other genes.

Correlation between d_N and d_S.

As the d_N and d_S values were computed from each isolate pair within a species/strain and no isolate was used more than once (Materials and Methods), pairwise comparisons between isolates could be used to compute the Pearson correlation coefficient (PCC) between d_N and d_S for each species/strain. Among the 30 PCC values for the RNA viruses studied, PCC ≥ 0.70 for 20 cases, 0.64 < PCC < 0.70 for 6 cases, and PCC < 0.036 for 4 cases (Fig. 1). The evolutionary implications of these data will be discussed in Discussion.

Discussion

In this study, the d_N/d_S ratios for the viruses were computed using the Li–Wu–Luo method (34), while those for the mammals in Table 1 were cited from a study by Nikolaev et al. (15), which used the method of Goldman and Yang (35). In table 2 of ref. 35, it is indicated that the method of Nei and Gojobori (36) gave higher d_N/d_S ratios for mammalian α- and β-globin genes than the method of Goldman and Yang (35). This is because the method of Nei and Gojobori (36) assumes equal likelihoods for d_N and d_S, so that it tends to overestimate d_N and underestimate d_S. The Li–Wu–Luo method (34) would not have this problem because it gives higher weights for d_S than d_N. Note that as mentioned in the first subsection of Results, the mean d_N/d_S (0.211) between human and mouse genes computed by the Li–Wu–Luo method (34) was very close to the mean d_N/d_S (0.219) for mammalian lineages shown in Table 1, which was computed by the method of Goldman and Yang (35). Thus, the mean ratio of 0.219 seems to be a reasonable mean value for mammalian genes.

The d_N/d_S ratios in mammals showed a large variation, ranging from 0.155 to 0.351 (Table 1). Small mammals such as the shrew, mouse, rat, and rabbit, which are 4 of the most common mammals, tend to have large population sizes and also have the lowest d_N/d_S ratios. The galago, which is a small lower primate and likely has a large population size, has a lower d_N/d_S than the other primates (human, chimpanzee, baboon, macaque, and marmoset). Although the African elephant is much larger than the chimpanzee, the estimated census population size (625,000) is much larger than that of the chimpanzee (192,500), probably because the elephant has a larger territory. Again, this may explain why it has a lower d_N/d_S (0.269) than the chimpanzee (0.351). Thus, it seems that the difference in population size is an important factor for the variation in d_N/d_S among mammals, and these comparisons suggest that the d_N/d_S ratios in Table 1 may be used to infer the relative long-term values of N_e in these mammals. Note that although mammals show a large variation in d_N/d_S, their d_N/d_S ratios are far less variable than those of viruses (2-fold vs. 20-fold) and that only HIV-1 and HIV-2 showed a ratio higher than the lowest ratio (0.155) in mammals. We speculate that one reason for the much larger d_N/d_S ratios in mammals is that they have a smaller N_e than RNA viruses.

Among the 21 human RNA viruses studied, 18 showed a d_N/d_S ratio <0.10. This observation supports the view that natural selection plays mostly a negative role in RNA virus evolution (4, 5). However, it does not imply that positive selection plays an insignificant role. Indeed, we found that positive selection plays a significant role even in the evolution of picornaviruses and flaviviruses, which showed the lowest d_N/d_S ratios among the RNA viruses studied.

Estimating the contribution of positive selection to genome-wide d_N/d_S is a complex problem and does not seem to have been attempted before. However, it may be roughly evaluated as follows, using the flaviviruses as an example. In Table 2, the d_N/d_S for NS4A in WNV-1 is 0.073, while the mean for the 7 other strains is (0.012 + 0.038 + 0.000 + 0.037 + 0.040 + 0.022 + 0.020)/7 = 0.024. Thus, we might predict that the d_N/d_S ratio for NS4A in WNV-1 would be 0.024 instead of 0.073 in the absence of positive selection. Under this assumption, the average d_N/d_S for WNV-1 becomes 0.041 instead of 0.046, resulting in a >10% reduction. WNV-1 NS2A also shows a relatively high d_N/d_S, but it is lower than those in WNV-2 and DENV NS2A; thus, whether WNV-1 NS2A has undergone positive selection is uncertain. In a similar manner, we obtain the new ratios for the other strains in Table 2. Note that we have made no change in the average d_N/d_S ratios in WNV-1 Africa, YFV, and TBEV because no gene in these 3 species shows clear evidence of positive selection. However, on average, positive selection has contributed ∼10% to the d_N/d_S ratios in flaviviruses (Table 2). Thus, when several species from a virus family or several strains from a species are available, one may be able to make a crude estimate of the contribution of positive contribution to the d_N/d_S ratio. This approach likely tends to give an underestimate if only clear cases of positive selection are used to estimate the contribution. A more rigorous method is needed to estimate the contribution of positive selection to d_N/d_S.

The 5 rules we proposed have facilitated data interpretation. In particular, using these rules, we have inferred the significant roles of both positive selection and N_e in RNA virus evolution. Moreover, we found that although the HA and NA genes are more often subject to positive selection in influenza A subtype H3N2 than subtype H1N1, the opposite is true for the M2 and PB1 genes (Table 5) and that there seems to be no substantial difference in N_e between H3N2 and H1N1.

It is interesting to note that RNA viruses from the same family tend to have similar d_N/d_S ratios (Tables 2–4). This might be because they experience similar transmission dynamics, live in similar intrahost environments, and may have similar genome structures and N_es. However, the ratio tends to be higher for a new population or strain (as discussed above). That might be because the virus has recently experienced a population bottleneck, it may have a selective advantage in a new niche and/or the effect of negative selection has not been fully accumulated (7, 17).

It has been suggested that vector-borne RNA viruses have lower d_N/d_S ratios than non–vector-borne RNA viruses (7). However, the majority of the strains used to draw this conclusion were flaviviruses (figure 3.8 of ref. 7), and, as mentioned above, these viruses belong the same family, so they would tend to have similar d_N/d_S ratios. Moreover, many non–vector-borne RNA viruses showed lower or similar ratios as vector-borne RNA viruses (figure 3.8 of ref. 7). Among the RNA viruses examined in this study, the 4 picornaviruses, which are non–vector-borne, showed the lowest d_N/d_S ratios and the 3 HEV strains showed similar ratios as the flaviviruses studied (Fig. 1). Vector-borne RNA viruses indeed tend to have low d_N/d_S ratios, and the proposed hypothesis that there are inherent difficulties for a virus to cyclically infect hosts that are phylogenetically divergent (e.g., from mosquitoes to humans) is attractive. However, there are other determinants of d_N/d_S. For example, a very large N_e would likely lead to a low d_N/d_S.

Bedford et al. (29) estimated N_e = 526 for influenza A H3N2 and N_e = 4,135 for the measles virus, a 7.86-fold difference. If N_e in H3N2 is indeed only 526, both negative and positive selection would be ineffective for those mutations with a fitness effect of <(1/526) = 0.0019, much higher than the selection threshold (1/4,135 = 0.0002) for the measles virus. However, despite this implied relaxed negative selection and frequent positive selection in H3N2, it has an average d_N/d_S ratio for all genes similar to that for the measles virus (0.088 vs. 0.079). Thus, if H3N2 has an 8-fold smaller N_e than the measles virus, this observation implies much more stringent functional constraints on influenza A virus genes except HA and NA. Note, however, that the estimate of N_e = 526 for influenza A H3N2 was based on HA gene sequences. The other genes are unlinked to HA (37), so their N_e would be larger. However, because a substantial number of mutations have small fitness effects in RNA viruses (38), the question remains how to explain the low average d_N/d_S over genes (0.062, when HA and NA are excluded; Table 5) if N_e is not considerably larger than 526. On the other hand, although it is not certain if the N_e values of H3N2 and measles viruses really differ by 8-fold, the study by Bedford et al. (29) did suggest a considerably smaller N_e in H3N2 than in the measles virus. Therefore, the similar d_N/d_S ratios for the PB1 and PB2 genes in H3N2 (0.28 and 0.33, respectively) and for the M gene in the measles virus (0.22) suggest much more stringent selective constraints on the PB1 and PB2 genes than on the M gene.

One intriguing question is why only 1 (HIV-1) of the 21 RNA viruses studied, but 4 of the 8 DNA viruses studied, showed a ratio higher than that (0.22) for mammals. It is possible that most RNA viruses have a larger N_e than DNA viruses and mammals, so that negative selection is more effective. As an RNA virus replicates rapidly, it can quickly recover from a bottleneck, so that its effect on N_e would be much less severe than that in mammals. HIV-1 shows an exceptionally high d_N/d_S, probably because positive selection is prevalent. Indeed, evidence for positive selection in HIV-1 has been found for the ENV, NEF, and GAG genes (12, 39–41).

ZIKV Am is a new strain and shows a ratio (0.066) considerably higher than that (0.029) for the ZIKV A-P strain, which is older. It is unlikely that this is due entirely to small d_S values for the ZIKV Am isolates, because a higher average d_N/d_S was also seen when the d_N and d_S values were computed between ZIKV A-P vs. ZIKV Am (Fig. 1). Note also that almost all genes in WNV-2 Europe, a new population, showed a higher d_N/d_S ratio than the corresponding ratio in WNV-2 Africa, an old population. When a new virus emerges or when a virus enters a new territory, it may enjoy some selective advantages, which increases the d_N/d_S ratio. Also, a new strain may have recently gone through a severe bottleneck in population size, so that slightly deleterious mutations may become fixed in the population, which might later be subject to reverse and/or compensatory mutation. Additionally, the effect of purifying selection may not have fully accumulated in an emerging strain (population), so that the d_N/d_S ratio would tend to be higher than that of a well-established strain (17).

As RNA viruses have been found to evolve rapidly despite being subject to strong negative selection, the question arose as to whether the rapid evolution is almost completely due to high mutation rates and whether there exists a positive correlation between the rate of evolution and the rate of mutation. A weak or no correlation would mean that the rate of evolution has been strongly distorted by positive selection. Some previous studies found a correlation (5), while others did not (13, 17). However, as mentioned in the Introduction, while mutation rate is measured in terms of per cell generation, evolutionary rate is measured in terms of per year, making it difficult to compute their correlation. Moreover, previous studies did not separate synonymous and nonsynonymous rates, so it was not clear if an observed correlation was largely due to the correlation between synonymous rate and mutation rate. We therefore studied the correlation between d_N and d_S, because d_S can be used as a proxy of mutation rate. Since d_N is more strongly affected by positive selection than d_S, a weak correlation between d_N and d_S would imply a strong effect of positive selection. We did find a positive correlation between d_N and d_S in the majority of the species studied, but it varied considerably among species (Fig. 1). There are 3 possible reasons for the large variation: statistical fluctuations, estimation errors, and variation in the intensity of positive selection among species. The first 2 factors can be important when d_N and d_S are small. To see this, let us consider the case of ZIKV Am, which has a very small PCC, only 0.13. The d_N and d_S values were very small (d_S ranging from 0.010 to 0.025, with first, second, and third quartiles of 0.013, 0.015, and 0.017, respectively), so they were subject to strong statistical fluctuations, and even a small estimation error in d_S or d_N can have a strong effect on PCC. In comparison, the PCC values for ZIKV A-P and ZIKV A-P vs. ZIKV Am were 0.70 and 0.73, respectively, much higher than that (0.13) for ZIKV Am, suggesting that a positive PCC indeed exists for long-term evolution of ZIKV. For HEV genotype 1, d_S ranged from 0.101 to 0.412, which is a suitable range for computing d_S, so it is not clear why the PCC was only 0.36. It is also not clear why the PCC was low for human poliovirus 1 and hepatitis A virus (PCC = 0.38 and 0.29, respectively), because the ranges of d_S used for these 2 cases were [0.102, 0.489] and [0.102, 0.330], respectively. Thus, although a positive correlation generally exists between d_N and d_S, a substantial fraction of cases show low or no correlation and the reason is unknown, although one may speculate it is, in part, due to positive selection. In conclusion, the relationship between d_N and d_S (or mutation rate) in RNA viruses is more complex than that in mammals (Fig. 1). Further research is required to have a good understanding of this relationship and the factors that affect this relationship.

The d_N/d_S values of ss(−)RNA, ss(+)RNA, and dsRNA viruses are intermingled (Fig. 1). The d_N/d_S values of ss(−)RNA viruses are similar to those of the rotavirus (a dsRNA virus). The retrovirus HTLV-1 has an intermediate d_N/d_S, whereas the retrovirus HIV-1 has the highest d_N/d_S. Thus, there seems to be no strong relationship between the type of replication mechanism and d_N/d_S, although this conclusion is difficult to assess for retroviruses, for which our sample size was small.

Materials and Methods

Data Collection and Preprocessing.

We first collected the data for the 21 RNA viruses that infect humans and have at least 10 distinct genome sequences curated by the National Center for Biotechnology Information (NCBI) Viral Genomes browser (https://www.ncbi.nlm.nih.gov/genomes/GenomesGroup.cgi?taxid=10239, accessed 13 September 2018) (Dataset S1). For DENV, we selected serotype 1 because it has more genomes available than the other serotypes. For the same reason, rotavirus A was selected to represent rotaviruses, HIV-1 group M subtype B was selected to represent HIV-1, and HIV-2 group A was selected to represent HIV-2. For influenza viruses, we selected influenza A H1N1 and H3N2 because their data were most abundant and there were disagreements about which of them had a larger population size (28, 42). For comparison, we also included 8 DNA viruses. The genome annotation and genome sizes of the viruses under study were obtained from RefSeq (43).

For each virus, we first collected the available genome sequences for isolates with a clearly labeled collection year and location (country). For HIV-1 and HIV-2, we first downloaded the codon-based multiple sequence alignments (MSAs) of the protein-coding genes of HIV-1 and HIV-2 from the HIV Sequence Database (https://www.hiv.lanl.gov/content/index) (44). An HIV-1 or HIV-2 genome was selected if the sequences of all its genes could be found in the downloaded alignments. For the viruses that were specifically curated by the NCBI Virus Variation Resource, we excluded Middle East respiratory syndrome-related coronavirus because more than half of the isolate pairs showed d_S < 0.01; when d_S < 0.01, the d_N/d_S ratio can be overestimated because an underestimation of d_S can substantially inflate d_N/d_S. For each of the remaining viruses (ZIKV, DENV, WNV, rotavirus A, Ebola virus, and influenza A virus H1N1 and H3N2) (https://www.ncbi.nlm.nih.gov/genome/viruses/variation/), we first collected a set of genomes in which all of the genomes had distinct protein sequences in at least 1 protein-coding gene. For the case where more than 1 strain had the same protein sequences for all protein-coding genes, we chose that with the earliest isolation date according to the NCBI Virus Variation Resource. For ZIKV, we excluded the strains isolated in Africa because almost all African strains were not isolated from humans. For the viruses that were not specifically curated by the HIV sequence database and/or the NCBI Virus Variation Resource, we collected all available genomes from GenBank.

After the data collection, we first tried to eliminate closely related sequences to reduce statistical correlations. For a virus with >1,000 available genomes, we randomly selected only 1 genome per year in 1 country. For a virus with ≤1,000 genomes, we selected the genomes that had the complete set of protein-coding genes. A genome was considered to have a complete protein-coding gene if we could identify at least 90% of its coding region in the reference genome of the virus. We discarded a genome if not all of the genes were found. The genomes chosen for our analysis are indicated in red in Dataset S2.

MSA.

For HIV-1 and HIV-2, we used the codon-based MSAs we obtained in our preprocessing steps. For each of the other viruses, we first constructed the codon-based MSA for each of its protein-coding genes from the selected genomes using MUSCLE (45). Then, we constructed a codon-based MSA of the entire coding region of each virus by concatenating the codon-based MSAs of its protein-coding genes. In the case of 2 overlapping genes, we kept the overlapping region if it was <10% of both genes; otherwise, the overlapped region on the shorter gene was cleaved.

Calculation of d_N/d_S Ratios.

The d_N and d_S values between each isolate pair were computed for each gene by the Li–Wu–Luo method (34), using MEGA6.0 (46). These values were then used to compute the d_N/d_S ratios (Dataset S3). However, the d_N and d_S values in Fig. 1 were computed for the entire (concatenated) coding region of each genome because the d_S value fluctuates among genes and because if the d_S value for a gene is small, the estimate may have a large SE relative to the mean. Also, we avoided using any isolate more than once to reduce the correlation between isolate pairs.

For the ZIKV, the WNV, and the HEV, we classified the isolates in a species into subgroups by constructing a neighbor-joining (NJ) tree of the isolates in the species using the d_S values for the entire genome. For the ZIKV, our NJ tree (SI Appendix, Fig. S1) exhibited a clear separation of the American isolates from the non-American isolates similar to that of Metsky et al. (25). For the WNV, our NJ tree exhibited a clear separation between lineage 1 and lineage 2 (SI Appendix, Fig. S2), similar to the tree of Lanciotti et al. (47). For the HEV, the genotypes of the isolates we selected were determined by comparing our NJ tree (SI Appendix, Fig. S3) with the phylogenies of the HEVs reported by Smith et al. (48).

Virus isolates are often collected from the same patients or from the same local area. Such closely related isolates usually have very small d_S values, which are not suitable for computing the d_N/d_S ratio because the ratio can be overestimated. We therefore tried to select isolate pairs with suitable d_S values. We first studied the d_S distribution of all isolate pairs in a species. We then focused on the species whose median of the d_S values was ≥0.1 (rhinovirus C, human poliovirus 1, human enterovirus 71, hepatitis A virus, HEV, rubella virus, norovirus, hepatitis C virus, YFV, DENV, TBEV, influenza virus A H1N1 and H3N2, measles virus, rotavirus A, HIV-1, HIV-2, and hepatitis B virus). For each of these species, we first selected a set of isolates with the criterion that all selected genome pairs have a d_S ≥ 0.05. This step is performed to reduce the chance that 2 selected isolates are very closely related to each other. Then, we started the set construction by first randomly picking up 1 genome from the species under study. Additional genomes were added 1 at a time into the set only if its d_S to all of the genomes already in the set was ≥0.05. After we finished constructing the set, we selected genome pairs for estimating d_S and d_N values. For this purpose, we required the d_S value for each pair to be in the range [0.1, 0.5] because the estimation of d_N/d_S could be inflated if d_S < 0.1 and might not be accurate if d_S > 0.5. In this way, we collected a set of isolate pairs to be used for computing the d_S, d_N, and d_N/d_S values as follows. First, we randomly chose 1 pair from the set of collected pairs and removed all pairs in the set that contained either of the 2 isolates, so that no isolate was selected more than once. We continued this process until no pair remained in the set. Second, we computed the d_S and d_N and recorded the number of pairs that satisfied the criterion of 0.1 ≤ d_S ≤ 0.5. This procedure was repeated 5,000 times to obtain an empirical distribution of the number of nonoverlapping pairs we could select. Let M be the median of the numbers of nonoverlapping pairs in the 5,000 rounds. Third, we repeated 1,000 rounds of selecting M random pairs from the collected pairs; in each round, we estimated the d_N, d_S, and d_N/d_S for each protein-coding gene and the entire genome, and also the PCC between d_N and d_S [PCC(d_N, d_S)] for the entire genome. Finally, we computed the averages and the SEs of d_N, d_S, d_N/d_S, and PCC(d_N, d_S) from the 1,000 rounds.

For the viruses whose median of the d_S values was <0.1 (WNV, ZIKV, mumps virus, HTLV-1, and all of the dsDNA and ssDNA viruses), we followed the above procedure, but we defined the threshold for set construction as 0.005 and the d_S range for collecting a set of genome pairs as [0.01, 0.5].

There were 3 cases whose M value was <4. Therefore, we relaxed the selection conditions, so that we could choose more pairs. For the WNV-2 African strains, we skipped the step for selecting the subset of strains and instead used all strains available because there are only 4 strains available. For rhinovirus C, we skipped the step for selecting the subset of strains and instead used all strains available because its d_S values were generally high (median d_S ≈ 2.33), and we used the range [0.1, 0.5]. For the variola virus, we defined the threshold for set construction as 0.001 and the d_S range for collecting genome pairs as [0.005, 0.5] because its median d_S was only ∼0.002. As the genome size of the variola virus is ∼185 kilobases, lowering the threshold to 0.005 would not severely compromise the d_N/d_S calculation, for the following reason. For the variola virus genome, the length of the coding region was 164,451 nucleotide sites and the number of synonymous sites is ∼32,000 according to the Li–Wu–Luo method (34). Therefore, for d_S = 0.005, the SD of d_S is ∼0.0004, which is much smaller than the mean.

Statistical Tests.

To compare the d_N/d_S ratios of a gene with the other genes in the same genome or its orthologs in the other species (strains), we first collected the 1,000 sets of d_N/d_S ratios of random pairs of the genes, which were generated in the preceding subsection when we calculated the averages and the SEs of d_N, d_S, and d_N/d_S.

We first compare the d_N/d_S ratios of the genes in the same genome. Let G be the set of n genes g₁, . . ., g_n in a genome that are sorted in the increasing order of the d_N/d_S ratio. When there are only 2 genes in G, we use the Wilcoxon rank-sum test to assess whether the distribution of the d_N/d_S ratios is significantly different between the 2 genes using the 1,000 sets of random pairs. The null hypothesis is that the d_N/d_S ratios for the 2 genes are equal, while the alternative hypothesis is that the 2 genes have different d_N/d_S ratios. We say that the 2 genes differ significantly in d_N/d_S if ≥950 tests with a P value <0.05 are observed among the 1,000 tests.

When there are more than 2 genes in G, we use the Kruskal–Wallis H test, a nonparametric and rank-based variant of ANOVA. If the null hypothesis that all genes in G have the same d_N/d_S ratio is rejected (i.e., ≥950 tests with a P value <0.05 among the 1,000 tests), we identify the smallest j such that the null hypothesis of equal d_N/d_S ratios for all genes in G_1,j = (g₁, . . ., g_j) is rejected. Then, G_j,n = (g_j, . . ., g_n) represents the set of genes with relatively high d_N/d_S ratios. Similarly, we obtain the gene set G_1,i = (g₁, . . ., g_i) with relatively low d_N/d_S ratios. If G_1,i and G_j,n overlap, we remove the genes in G_1,i (G_j,n) with a d_N/d_S ratio higher (lower) than the average d_N/d_S for all genes. In this way, we obtain 2 nonoverlapping gene sets, one with relatively low d_N/d_S ratios and the other with relatively high d_N/d_S ratios.

In a similar manner, we compare the d_N/d_S ratios of a gene among different strains or species.

The results of our analysis are given in Dataset S4.

Explanations for the 5 Rules.

We now provide some arguments for the 5 rules proposed in Results. Rule 1 says, “If a species shows low d_N/d_S ratios for all or most of the genes in the genome compared with those in other species, then that species likely had a larger N_e than the other species.” This rule is based on the reasoning that in RNA viruses, negative selection is much more prevalent than positive selection, implying that a larger N_e will increase the effectiveness of negative selection, and thus reduce the d_N/d_S ratio. Note that we do not require a low d_N/d_S for all genes because a gene could have undergone positive selection and show a relatively high d_N/d_S. Rule 2 says, “If a gene shows a high d_N/d_S ratio in a species compared with both the ratios for the other genes in the same genome and the ratios for the same gene in other species, it likely had undergone positive selection in that species.” This rule is based on the following reasoning. If a gene shows a higher d_N/d_S than some other genes in the genome, it can be because the gene is subject to weaker negative selection or it had undergone positive selection. However, weaker negative selection is not a good explanation if a higher d_N/d_S is not observed in other species. Rule 3 says, “If the d_N/d_S ratio for a gene tends to be low both among genes and among species, the gene is likely subject to stronger negative selection than other genes.” The logic for this rule is that it obviously cannot be due to positive selection or to a larger N_e, which should reduce the d_N/d_S for all genes, except for genes that had undergone positive selection. Rule 4 says, “If a gene shows a high d_N/d_S in all species, it is likely subject to weaker negative selection than other genes in the genome.” An alternative explanation for the observed high d_N/d_S in all species is that the gene was subject to positive selection in all species, but this possibility is low if several species (strains) have been studied. Rule 5 says, “If a strain (or species) shows high d_N/d_S ratios for all or most of the genes in the genome compared with those in other strains (species), then that strain likely had a smaller N_e than the other strains and/or the effect of negative selection in that strain has not been fully accumulated yet if closely related viral isolates are compared.” A smaller N_e is a better explanation for this observation than positive selection because positive selection is unlikely to occur for all or most genes in a genome at the same time. Note that if a gene shows high d_N/d_S ratios both within the genome and among the species compared, it is not simple to infer if the high d_N/d_S ratios are due to positive selection, weak negative selection, or both. The 2A gene in picornaviruses (Table 3) is such an example. The d_N/d_S ratios (0.031, 0.037, 0.035, and 0.023) of this gene in the 4 species studied are not significantly different. In such a case, data from more species can be helpful because if the new data again show no significant difference in d_N/d_S among species, the higher d_N/d_S ratios are likely due to weaker negative selection. On the other hand, if the new data reveal significantly lower d_N/d_S ratios in some species, which would imply strong negative selection (selective constraint), then the higher d_N/d_S ratios in other species would likely be due to positive selection.