Regression to the Mean in Pre–Post Testing: Using Simulations and Permutations to Develop Null Expectations

To the Editor:

In a recent analysis, Blumer and Beck (2019) argue that guided-inquiry modules in laboratory courses may help less-prepared undergraduates improve in scientific reasoning and experimental design. In one study, they use a test of scientific reasoning (modified from Lawson, 1978), and in another they use the Experimental Design Ability Test (EDAT; Sirum and Humburg, 2011). Both studies collect paired data: pretest scores at the start of the semester and posttest scores at the end. Part of the analysis explores the relationship between initial score and change in score (posttest minus pretest). The authors bin the responses into quartiles by pretest score, then analyze each quartile separately. However, this analysis does not control for regression to the mean (RTM), a statistical phenomenon that creates patterns of change by chance alone (Galton, 1886; Marsden and Torgerson, 2012). I outline here how RTM appears in paired testing data, what this suggests for Blumer and Beck’s conclusions, and how numerical statistical methods can help disentangle RTM from real effects.

RTM occurs whenever you compare paired numerical or ordinal measurements that are not perfectly correlated; the most extreme measurements in one data set will tend to be closer to the middle of the other. In educational research, RTM can occur in pre–post testing, as some students with high or low test scores will score closer to the mean upon retesting (Smith and Smith, 2005). This produces a negative relationship between initial score and change in score. For a reader curious to learn more about RTM, Kahneman (2011, pp. 175–184) presents wide-ranging examples, and Barnett and colleagues (2005) outline the problem of RTM in epidemiological studies.

Experimental design can prevent this issue altogether. With randomization or matching between a control group and an intervention group, one can observe whether an effect is larger for the intervention group. Alternatively, binning or ranking by a separate variable (e.g., students’ entering grade point average) also avoids RTM.

When one is not able to avoid RTM, how can one identify it? Consider a model in which variation in test scores stems from among-student variation (e.g., relevant skill level, constant across testing instances) and independent within-student variation (random error across testing instances). In this case, the correlation ρ between pretest and posttest scores tells you the proportion of all variation that is explained by among-student variation, and the coefficient for a regression of change in score on pretest score is ρ – 1 (see Section S1 in the Supplemental Material). This coefficient is one way to measure the strength of RTM and is more negative for weaker pre–post correlations. The mean and the variance should be similar for both pretest and posttest scores in this null model. However, if the lowest-scoring students truly do improve the most across testing instances, then the overall variance in posttest scores may decrease. This could occur because some of students with the lowest pretest scores will have improved, and will be likely to score closer to the mean. See Section S3B of the Supplemental Material for a simulated example. Blumer and Beck (2019) do not observe this; they report similar standard errors of the mean for both pretest and posttest EDAT scores (0.16 and 0.17, respectively).

For normally distributed data, the RTM effect is well quantified (Davis, 1976), but educational assessment data are often discrete, ordinal, or otherwise poorly approximated by a normal distribution. In these cases, numerical simulations of a null model can show the expected strength of RTM. To analyze the expected effect of RTM on EDAT data binned by pretest quartile, we simulate a bivariate binomial random variable with expected mean of 3.75 and expected pre–post correlation of 0.6. For each simulation, we then calculate the per-quartile mean change. Figure 1 summarizes the distributions of the mean changes across 10,000 simulations. The differences in the distributions among quartiles are solely due to RTM. By chance alone, a large increase in score is expected in the lowest quartile, while a large decrease is expected in the highest quartile. The t tests by quartile performed by Blumer and Beck (2019) are based on the assumption that each quartile should have zero expected mean change, which neglects the impact of RTM. Consequently, their comparisons are likely to exaggerate the magnitude and significance of any real effect mediated by student preparation level. Section S2 in the Supplemental Material presents the statistical model and code using the programming language R (R Core Team, 2018) with package dplyr (Wickham et al., 2019).

FIGURE 1.

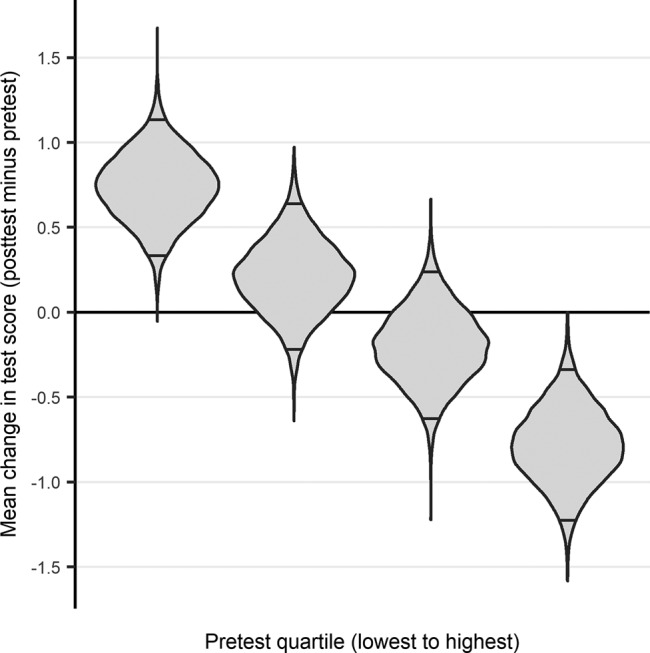
Distributions of mean change in test score (posttest minus pretest) by pretest quartile for bivariate binomial simulated EDAT data. The model simulates 145 students, with expected mean of 3.75 points and expected pre–post correlation of 0.6. The distributions summarize mean change by quantile calculated for each of 10,000 simulations. The differences in mean change between quartile represent regression to mean, and appear solely due to chance. Of the calculated simulation means, 95% lie between the upper and lower horizontal lines within each distribution, with 2.5% at each extreme.

One can also use permutations of the original data to generate a null distribution (Edgington and Onghena, 2007; Huo et al., 2014). The objective is to permute scores while preserving key relationships in the data, then to calculate relevant statistics for each permutation. In practice, permutation testing may be easier to apply than simulation-based approaches, as one does not need to choose an appropriate null model to simulate. Instead, permutation testing makes the null hypothesis that the values being permuted are “exchangeable” (Edgington and Onghena, 2007). When pretest and posttest scores are permuted, this hypothesis is that the distribution of scores is the same in either testing instance. It is usually not computationally feasible to examine every permutation, so one instead looks at a random subset of all possible permutations (this is called randomization testing). Considering again Blumer and Beck’s (2019) EDAT data, one can randomly permute which score is “pre” and which score is “post” across the pairs. This negates any effect of test order in the permuted sample while maintaining similar means, variances, correlation, and strength of RTM. Permuting many times and calculating per-quartile means for each permutation allow the comparison of the original per-quartile means with these generated null distributions. Section S3 and Supplemental Figure S1 in the Supplemental Material demonstrate randomization testing applied to two simulated EDAT data sets: one with random bivariate binomial data and one in which the least- and most-prepared students truly experienced stronger than expected shifts toward intermediate scores. Although the code presented uses base functions in R for the permutations, readers can use the R package permute for flexible permutation-testing tools (Simpson, 2016).

Some interventions may create real disproportionate gains for the least-prepared students. However, researchers must carefully define their null expectations when looking at biased subsets of paired data. Simulations or permutations can approximate the expected distribution of RTM effects for paired test data under a null hypothesis in which an educational intervention does not have any effect. These null distributions offer context for the original statistics calculated from the data, helping to disentangle real effects from statistical artifacts. Although the choice of model or permutation approach affects the exact conclusions to be drawn, these numerical methods offer valuable intuition about what to expect by chance alone.