Influence of probe pressure on the pulsatile diffuse correlation spectroscopy blood flow signal on the forearm and forehead regions

Abstract.

In a pilot study of 11 healthy adults (24 to 39 years, all male), we characterize the influence of external probe pressure on optical diffuse correlation spectroscopy (DCS) measurements of pulsatile blood flow obtained on the forearm and forehead. For external probe pressure control, a hand inflatable air balloon is inserted between the tissue and an elastic strap. The air balloon is sequentially inflated to achieve a wide range of external probe pressures between 20 and 250 mmHg on the forearm and forehead, which are measured with a flexible pressure sensor underneath the probe. At each probe pressure, the pulsatility index (PI) of arteriole blood flow on the forehead and forearm is measured with DCS (2.1-cm source-detector separation). We observe a strong correlation between probe pressure and PI on the forearm ($R=0.66$, $p<0.001$), but not on the forehead ($R=-0.11$, $p=0.4$). The forearm measurements demonstrate the sensitivity of the DCS PI to skeletal muscle tissue pressure, whereas the forehead measurements indicate that DCS PI measurements are not sensitive to scalp tissue pressure. Note, in contrast to pulsatility, the time-averaged DCS blood flow index on the forehead was significantly correlated with probe pressure ($R=-0.55$, $p<0.001$). This pilot data appears to support the initiation of more comprehensive clinical studies on DCS to detect trends in internal pressure in brain and skeletal muscle.

1. Introduction

Diffuse correlation spectroscopy (DCS) utilizes photon correlation techniques to noninvasively measure blood flow in deep tissues continuously and at the bedside.^1–6 It has been used in a variety of clinical applications, including stroke and muscle disease. Recently, improvements in DCS measurement speed have been exploited to resolve the pulsatile heartbeat fluctuations of arterial blood flow.^7–11 DCS measurement of blood flow pulsatility has generated considerable interest in new clinical applications for the optical technology, which include assessment of intracranial pressure (ICP)^10,12,13 and arterial stiffness.^10,11

To date, Doppler ultrasound techniques have been dominantly used for noninvasive assessment of flow pulsatility in the clinic. Doppler ultrasound measures blood velocity in major feeder arteries of the brain and peripheral tissues. Among numerous applications, the relation of Doppler waveforms to ICP and arterial stenosis has been investigated, and encouraging preliminary results were observed.^14–16 In traumatic brain-injured adults, for example, a transcranial Doppler ultrasound (TCD) derived pulsatility index (PI) was proportionally correlated with intrasubject trends in invasively measured ICP ($R=0.61$).¹⁷ This TCD PI was defined as the difference of systolic flow velocity (${\mathrm{FV}}_{\mathrm{sys}}$) and diastolic flow velocity (${\mathrm{FV}}_{\mathrm{dia}}$) divided by mean flow velocity ($⟨\mathrm{FV}⟩$), i.e., $({\mathrm{FV}}_{\mathrm{sys}}-{\mathrm{FV}}_{\mathrm{dia}})/⟨\mathrm{FV}⟩$.

Although Doppler ultrasound is routinely used in the clinic, it has limitations. For instance, Doppler ultrasound measurements are sensitive to probe orientation, which makes stable fixation of the probe for continuous monitoring challenging.^18,19 Further, because Doppler ultrasound interrogates large proximal arteries, measurements may be relatively insensitive to localized diseases/injuries. DCS measurement of blood flow pulsatility in the microvasculature is a potential complementary and alternative approach to Doppler ultrasound. DCS is well-suited for continuous monitoring and sensitive to localized microvasculature.^3,19–22 To realize the full clinical potential of DCS pulsatility monitoring, however, a better understanding of confounding influences on the DCS pulsatility measurement is needed.

Previous work has shown that time-averaged steady-state DCS measurements of blood flow can be influenced by factors such as external probe pressure against the tissue, superficial tissue layers, and tissue optical properties.^20,23–26 This pilot study examines the influence of external probe pressure on DCS measurements of blood flow pulsatility on the forearm and the forehead. The influence on pulsatility is further compared to the influence on steady-state blood flow measurements.

2. Materials and Methods

2.1. Pressure Sensor Calibration

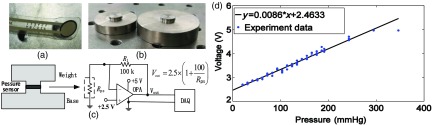
We used a thin and flexible resistive pressure sensor (1 lb, 9.5-mm diameter, A201, FlexiForce, Tekscan) for probe pressure measurement [Fig. 1(a)]. To calibrate the sensor for absolute pressure measurement, we used a series of custom built metal weights with a contact surface area equivalent to effective area of the pressure sensor (i.e., $0.71{\mathrm{cm}}^2$), as shown in Fig. 1(b). During calibration, the pressure sensor was sandwiched between metal weights to ensure exact overlap of the sensor area with the weights’ contact surface area [Fig. 1(c)]. The output voltage of the sensor (stabilized with a voltage follower circuit²⁷) was recorded with a DAQ board (USB-6356, NI). Different weights (between 20 and 335 g) were employed to apply 21 pressures against the sensor, which ranged from 20.7 to 346.3 mmHg. Note three repetitions of the calibration measurement were made at each applied pressure, and the mean of the sensor’s output voltage across the three repetitions was computed. This mean output voltage from the sensor was plotted against the exact probe pressure exerted by the weights, and a linear best-fit line was computed [Fig. 1(d)]. This linear best-fit line was then used to convert voltage from the sensor to absolute probe pressure on tissue.

Fig. 1.

Pictures of: (a) the pressure sensor and (b) exemplar custom metal weights with raised platforms that have a contact surface area equivalent to the effective area of the pressure sensor ($0.71{\mathrm{cm}}^2$, 9.5-mm diameter). (c) The output voltage from the pressure sensor (stabilized with a voltage follower circuit) sandwiched between two weights was recorded with a DAQ board. (d) Voltage from the pressure sensor plotted against the known pressures applied to the sensor by weights. The linear best-fit line of the data was used to convert voltage to probe pressure on tissue.

2.2. DCS Instrumentation, Probe, and Measurement of Blood Flow

DCS uses rapid speckle intensity fluctuations of multiply scattered light that has traversed tissue to estimate blood flow. Specifically, these intensity fluctuations, which are induced by red blood cell motion, are quantified through measurement of the normalized intensity autocorrelation function, $g_2(\tau )=⟨I(t)I(t+\tau )⟩/{⟨I(t)⟩}^2$ at multiple delay-times $\tau$.^28,29 Here $I(t)$ is the detected light intensity at time $t$, and the angular brackets $⟨⟩$ denote time averages. A semi-infinite tissue model was employed to derive a DCS blood flow index (BFI) from the decay of $g_2(\tau )$.¹ Note that assumed tissue optical absorption and reduced scattering coefficients of 0.12 and $7.38{\mathrm{cm}}^{-1}$ for the forehead, and 0.16 and $4.32{\mathrm{cm}}^{-1}$ for the forearm were used for deriving BFI.⁸ Note further, only values for which $g_2(\tau )>1.05$ were used in the semi-infinite fit, and a DCS coherence parameter (i.e., $\beta$ coefficient)¹ was fitted with the BFI for every frame.

Our DCS instrument consists of a long coherence-length, continuous-wave laser (785 nm, 90 mW, DL785-100-3O, Crysta Laser Inc.), two single photon avalanche photodiodes (APDs) (SPCM-AQRH, Excelitas, Canada), and a custom-built software autocorrelator that is described elsewhere.^8,30,31 Briefly, the single-photon APDs convert the detected photons to digital TTL pulses, which are sent to pulse counters in a PCIe-6612 board (National Instruments). The counters continuously accumulate photon counts, and the computation of $g_2(\tau )$ is performed by software implementing a multi-tau scheme.^32,33 Specifically, $g_2(\tau )$ is computed at 87 delay-times ranging from $0.2\mu \mathrm{s}$ to 1.5 ms. The first seven delay-times are given by ${\tau }_N=\sum _{n=1}^{N}n·\mathrm{\Delta }t$ $(N=1,2,\cdots ,7)$, and the last 80 delay-times are given by ${\tau }_{8M+N}=\sum _{m=0}^M\sum _{n=0}^N(8+n)·2^m·\mathrm{\Delta }t$ ($M=0,1,\dots 9$; $N=0,1,\dots 7$), where $\mathrm{\Delta }t=0.2\mu \mathrm{s}$. Note, at the $i$’th delay-time, $g_2({\tau }_i)$ is computed as $N(i)·N(1)/(N(1)·N(1))$, where $N(i)$ is the photon count in the $i$’th correlator bin, and $N(1)$ is the photon count in the first correlator bin (here, the first bin is defined to have the same bin width as the $i$’th bin³³). The temporal width of the $i$’th delay-time bin, i.e., $w(i)$, is given by $w(i+1)={\tau }_{i+1}-{\tau }_i$ for $1\le i\le 86$, and $w(1)=\mathrm{\Delta }t$. For each delay-time, $g_2({\tau }_i)$ is averaged for 50 ms to obtain normalized autocorrelation values at 20 Hz (the average photon count in the 50-ms interval is also recorded).

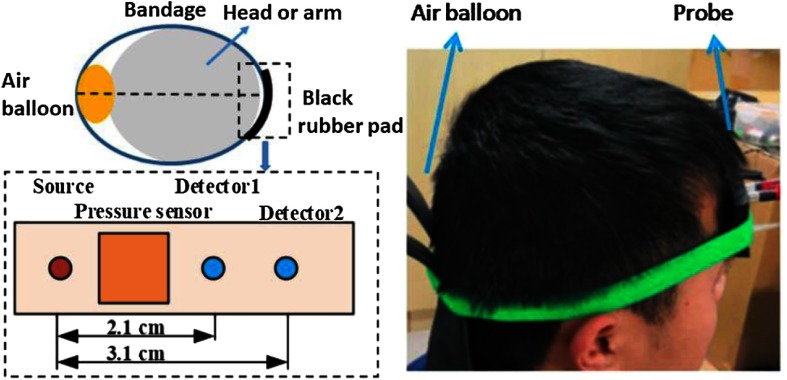
The DCS tissue probe acquired data at two source-detector separations (i.e., 2.1 and 3.1 cm) via one multimode source optical fiber ($200\mu \mathrm{m}/0.22\mathrm{NA}$, Nufern) and two single-mode detector fibers ($4.4\mu \mathrm{m}/0.13\mathrm{NA}$, 780-HP, Nufern) embedded in a $100\mathrm{mm}\times 40\mathrm{mm}\times 10\mathrm{mm}$ black urethane rubber pad (Fig. 2). Note a glass diffuser with a length of 5 mm was attached to the source fiber to increase the beam diameter to 2.2 mm. Given the output power emerging from the fiber of 70 mW, the irradiant power on the skin was $18{\mathrm{mW}/\mathrm{mm}}^2$, which is less than the maximum permissible exposure ($20{\mathrm{mW}/\mathrm{mm}}^2$) allowed by Chinese standard at the 785-nm wavelength (GB/T 7247.9-2016). We found the DCS signal at 3.1 cm was too low to resolve flow pulsatility during the cardiac cycle (discussed further in Sec. 4.4). Accordingly, only steady-state BFI data for the 3.1-cm separation are reported.

Fig. 2.

For each subject, continuous DCS blood flow index measurements (20-Hz sampling rate) were sequentially acquired across a wide range of external probe pressures on the forehead and forearm flexor. An elastic strap secured the optical probe and an air balloon to opposite sides of the right forearm flexor or right forehead. The optical probe has two DCS source-detector separations (2.1 and 3.1 cm), and a pressure sensor between the probe and skin measured the external probe pressure against the skin. Gradual inflation of the air balloon achieved $\sim 6$ discrete probe pressures between 20 and 250 mmHg (1 min of DCS data acquired at each probe pressure).

2.3. Subjects and Experimental Protocol

Eleven healthy adults (11 males and 0 females) were enrolled in this study. The average age across subjects was 31.4 years old (range 24 to 39), distributed per decade as reported in Table 1. All subjects were Chinese. All subjects provided written consent, and all protocols/procedures were approved by the Institutional Review Board at the Army Medical University. Throughout the experiment, subjects sat comfortably upright.

Table 1.

Demographic data of the enrolled subjects

Age (year)	$\text{Mean age}\pm \mathrm{SD}$	No. males	No. females
20 to 29	$26.3\pm 1.7$	3	0
30 to 39	$34.3\pm 2.1$	8	0

For each subject, DCS measurements were sequentially obtained across a wide range of increasing probe pressures on the right forearm flexor and the right forehead. The probe was secured on the forearm or forehead by an elastic strap, with the resistive pressure sensor sandwiched between the probe and the skin. A hand-inflatable air balloon (XL-10, Xintian Liming Medical Device, China) inserted between the strap and the tissue on the opposite side of the probe was used for pressure control (see Fig. 2). Via gradual inflation of the air balloon, DCS measurements were acquired at $\sim 6$ discrete probe pressures between 20 and 250 mmHg for both the forearm and forehead. Approximately 1 min of continuous DCS data was obtained for each probe pressure.

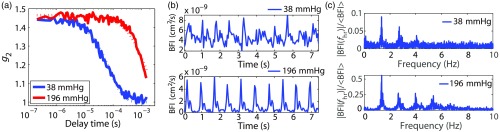
The means of the BFI measurements acquired at 2.1- and 3.1-cm separations were calculated for each probe pressure and are denoted as ${⟨\mathrm{BFI}⟩}_{2.1}$ and ${⟨\mathrm{BFI}⟩}_{3.1}$ (note probe pressure dependence is implicit). The DCS PI of BFI measurements acquired at 2.1 cm was further determined for each probe pressure. The DCS PI is defined as the Fourier spectral amplitude of BFI at the heart rate frequency divided by the mean BFI, i.e., $\mathrm{PI}\equiv |\mathrm{BFI}(f_{\mathrm{hr}})|/⟨\mathrm{BFI}⟩$. The $|\mathrm{BFI}(f_{\mathrm{hr}})|$ amplitude (also known as the first harmonic) of the 1-min time-domain signal acquired at each pressure was computed with a discrete Fourier transform method implemented in MATLAB R2014a (FFT, Mathworks). Note that $|\mathrm{BFI}(f_{\mathrm{hr}})|$ is considerably less than the difference between systolic and diastolic BFI, since the latter difference also reflects higher order harmonics in the signal. We chose to use first harmonic Fourier filtering to calculate PI because this approach is less affected by measurement noise than the difference between systolic and diastolic BFI.^10,34 Exemplar mean intensity autocorrelation curves at two discrete probe pressures obtained on the forearm, along with their respective temporal BFI traces in the time domain and Fourier spectral amplitudes in the frequency-domain, are shown in Fig. 3.

Fig. 3.

(a) Exemplar DCS $g_2(\tau )$ measurements obtained at two distinct probe pressures on the right forearm of a healthy adult at a source-detector separation of 2.1 cm and a sampling rate of 20 Hz (solid lines are data and dotted lines are semi-infinite fits). The mean photon count rates for the 38- and 196-mmHg probe pressures were 220 and 623 kcps, respectively. (b) Exemplar temporal measurements of DCS BFI at each probe pressure and (c) Fourier spectral amplitudes of the 1-min data intervals acquired at each probe pressure plotted against frequency.

2.4. Statistical Analysis

We assembled data sets of external probe pressure ($P$), ${⟨\mathrm{BFI}⟩}_{2.1}$, ${⟨\mathrm{BFI}⟩}_{3.1}$, and PI across all 11 subjects on the forearm flexor and on the forehead. In addition to these two absolute data sets, we also assembled corresponding intrasubject normalized relative data sets of $\mathrm{\Delta }P\equiv P-P_o$, ${\mathrm{rBFI}}_{2.1}\equiv {⟨\mathrm{BFI}⟩}_{2.1}/{⟨\mathrm{BFI}⟩}_{2.1,o}$, ${\mathrm{rBFI}}_{3.1}\equiv {⟨\mathrm{BFI}⟩}_{3.1}/{⟨\mathrm{BFI}⟩}_{3.1,o}$, and $\mathrm{rPI}\equiv \mathrm{PI}/{\mathrm{PI}}_o$ on the forearm flexor and on the forehead. Here the subscript $o$ indicates the subject’s mean values during the baseline (initial) pressure of the probe against the tissue (also recall that the subscripts “2.1” and “3.1” refer to the two source-detector separations, and that PI is only obtained at the 2.1-cm separation). For the two absolute data sets (i.e., on forearm and on forehead), we computed the Pearson correlation between: (1) $P$ and ${⟨\mathrm{BFI}⟩}_{2.1}$; (2) $P$ and ${⟨\mathrm{BFI}⟩}_{3.1}$; and (3) $P$ and PI. Similarly, for the two relative data sets, we computed the Pearson correlation between: (1) $\mathrm{\Delta }P$ and ${\mathrm{rBFI}}_{2.1}$; (2) $\mathrm{\Delta }P$ and ${\mathrm{rBFI}}_{3.1}$; and (3) $\mathrm{\Delta }P$ and rPI. Finally, we used individual linear mixed effects models to model ${⟨\mathrm{BFI}⟩}_{2.1}$, ${⟨\mathrm{BFI}⟩}_{3.1}$, and PI as a function of $P$, as well as ${\mathrm{rBFI}}_{2.1}$, ${\mathrm{rBFI}}_{3.1}$, and rPI as function of $\mathrm{\Delta }P$, for both the forearm and the forehead. The mixed effects models, which were implemented in MATLAB (fitlme), account for each subject contributing multiple data points. In these models, 95% confidence intervals for the slopes are reported, and a type 1 error rate of 0.05 was used.

3. Results

3.1. DCS Measurements on Forearm

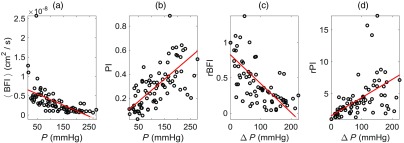
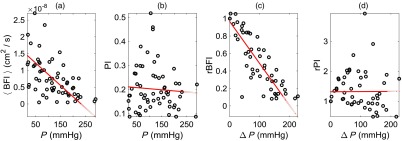
For the 11 subjects measured (all male), the average ($\mathrm{mean}\pm \mathrm{SD}$) heart rate, DCS BFI (at 2.1-cm separation), DCS PI, probe pressure, and DCS intensity (at 2.1-cm separation) obtained at baseline on the forearm were ($74\pm 14$) beats per min, $(8.4\pm 6.5)\times {10}^{-9}{\mathrm{cm}}^2/\mathrm{s}$, $0.09\pm 0.03$, $35\pm 13\mathrm{mmHg}$, and $260\pm 119$ kilo counts per second (kcps), respectively. Across all subjects, we observed strong correlations between $⟨\mathrm{BFI}⟩$ and $P$ ($R=-0.57$) and between PI and $P$ ($R=0.66$) (Fig. 4). We also observed strong correlations between rBFI and $\mathrm{\Delta }P$ ($R=-0.74$) and between rPI and $\mathrm{\Delta }P$ ($R=0.56$) (Fig. 4). In linear mixed effects regression analysis, the slopes of the best-fit lines were further significantly different from zero ($p<0.001$; see Table 2). The interquartile ranges of the fractional deviation of the measured data from the best-fit lines are reported in Table 2.

Fig. 4.

Plots of: (a) steady-state (mean) DCS blood flow index ($⟨\mathrm{BFI}⟩$) versus external probe pressure ($P$), (b) DCS PI versus $P$, (c) intrasubject normalized relative change in mean DCS blood flow index $(\mathrm{rBFI}\equiv ⟨\mathrm{BFI}⟩/{⟨\mathrm{BFI}⟩}_o)$ versus change in probe pressure $(\mathrm{\Delta }P\equiv P-P_o)$, and (d) intrasubject normalized relative change in DCS PI $(\mathrm{rPI}\equiv \mathrm{PI}/{\mathrm{PI}}_o)$ versus $\mathrm{\Delta }P$. These data were obtained on the right forearms of 11 healthy adult volunteers at multiple probe pressures for each subject (i.e., $N=79$ probe pressures total; 1-min of DCS data acquired for each pressure, 2.1-cm source-detector separation). ${⟨\mathrm{BFI}⟩}_o$, $P_o$, and ${\mathrm{PI}}_o$ denote the subject’s mean steady-state blood flow index, probe pressure, and PI measured at the baseline (initial) probe pressure. The solid red lines are the best fits to the data from linear mixed effects regression analysis. The Pearson’s correlations, as well as the slopes of the best-fit lines, were all significantly different from zero (see main text and Table 2).

Table 2.

Summary of linear mixed effects regression models and Pearson correlations on forearm and forehead

Location	Relationship	$m$ (95 CI)	$b$ (95 CI)	IQR of (data/fit − 1)	$R$
Forearm	${⟨\mathrm{BFI}⟩}_{2.1}=mP+b$	$-2.9(-3.9,-2.0)\times {10}^{-11}({\mathrm{cm}}^2/\mathrm{s})/\mathrm{mmHg}$	$6.9(5.6,8.2)\times {10}^{-9}{\mathrm{cm}}^2/\mathrm{s}$	0.62	$-0.57$*
	${⟨\mathrm{BFI}⟩}_{3.1}=mP+b$	$-2.6(-3.4,-1.8)\times {10}^{-11}({\mathrm{cm}}^2/\mathrm{s})/\mathrm{mmHg}$	$5.8(4.6,6.8)\times {10}^{-9}{\mathrm{cm}}^2/\mathrm{s}$	0.61	$-0.60$*
	$\mathrm{PI}=mP+b$	$1.8(1.4,2.2)\times {10}^{-3}1/\mathrm{mmHg}$	0.08 (0.01, 0.15)	0.64	0.66*
	${\mathrm{rBFI}}_{2.1}=m\mathrm{\Delta }P+b$	$-4.1(-4.8,-3.4)\times {10}^{-3}1/\mathrm{mmHg}$	0.83 (0.72, 0.94)	1.08	$-0.74$*
	${\mathrm{rBFI}}_{3.1}=m\mathrm{\Delta }P+b$	$-4.0(-4.7,-3.4)\times {10}^{-3}1/\mathrm{mmHg}$	0.78 (0.67, 0.89)	0.77	$-0.75$*
	$\mathrm{rPI}=m\mathrm{\Delta }P+b$	$0.03(0.02,0.04)1/\mathrm{mmHg}$	$1.55(0.36,2.73)$	0.46	0.56*
Forehead	${⟨\mathrm{BFI}⟩}_{2.1}=mP+b$	$-6.7(-7.6,-5.7)\times {10}^{-11}({\mathrm{cm}}^2/\mathrm{s})/\mathrm{mmHg}$	$1.6(1.2,1.9)\times {10}^{-8}{\mathrm{cm}}^2/\mathrm{s}$	0.99	$-0.55$*
	${⟨\mathrm{BFI}⟩}_{3.1}=mP+b$	$-4.7(-5.7,-3.7)\times {10}^{-11}({\mathrm{cm}}^2/\mathrm{s})/\mathrm{mmHg}$	$1.6(1.3,2.0)\times {10}^{-8}{\mathrm{cm}}^2/\mathrm{s}$	0.66	$-0.37$*
	$\mathrm{PI}=mP+b$	$-9.2(-43,24)\times {10}^{-5}1/\mathrm{mmHg}$	0.21 (0.16,0.27)	0.58	$-0.11$
	${\mathrm{rBFI}}_{2.1}=m\mathrm{\Delta }P+b$	$-4.8(-5.4,-4.3)\times {10}^{-3}1/\mathrm{mmHg}$	0.97 (0.88,1.05)	0.79	$-0.88$*
	${\mathrm{rBFI}}_{3.1}=m\mathrm{\Delta }P+b$	$-3.2(-4.0,-2.4)\times {10}^{-3}1/\mathrm{mmHg}$	1.04 (0.93, 1.14)	0.26	$-0.71$*
	$\mathrm{rPI}=m\mathrm{\Delta }P+b$	$6(-239,252)\times {10}^{-5}1/\mathrm{mmHg}$	1.31 (1.06,1.57)	0.59	0.01

Note: $⟨\mathrm{BFI}⟩$, mean blood flow index; PI, blood flow pulsatility index;$\mathrm{rBFI}\equiv ⟨\mathrm{BFI}⟩/{⟨\mathrm{BFI}⟩}_o$; $\mathrm{rPI}\equiv \mathrm{PI}/{\mathrm{PI}}_o$; $P$, probe pressure; subscript “o” indicates initial baseline probe pressure; subscripts “2.1” and “3.1” refer to data acquired at 2.1- and 3.1-cm source-detector separations (PI only computed at 2.1 cm); IQR is interquartile range of the fractional difference (measured data)/(estimate from best-fit line) − 1; $R$ is Pearson’s correlation. *$p<0.001$; $p>0.05$ for other two comparisons.

Note the DCS data shown in Fig. 4 were acquired at the 2.1-cm source-detector separation. DCS measurements were also made at 3.1 cm, but the signal-to-noise was too low to resolve flow pulsatility. Plots of the steady-state data (i.e., $⟨\mathrm{BFI}⟩$ versus $P$ and rBFI versus $P$) acquired at the 3.1-cm separation for the forearm are shown in Figs. 5(a) and 5(b). The correlations between $⟨\mathrm{BFI}⟩$ versus $P$ and rBFI versus $P$ were $R=-0.60$ and $R=-0.75$, respectively. In addition, the corresponding slopes of the best-fit lines were not significantly different from the slopes of the best-fit lines at the 2.1-cm separation (Table 2). Finally, the average DCS BFI and DCS intensity across subjects obtained at baseline with the 3.1-cm separation were $(7.4\pm 5.1)\times {10}^{-9}{\mathrm{cm}}^2/\mathrm{s}$ and $29\pm 13\mathrm{kcps}$, respectively, and the average difference between the blood flow indices acquired at 3.1- and 2.1-cm separations at baseline (i.e., ${⟨\mathrm{BFI}⟩}_{3.1,o}-{⟨\mathrm{BFI}⟩}_{2.1,o}$) was $(-1.0\pm 4.4)\times {10}^{-9}{\mathrm{cm}}^2/\mathrm{s}$. Thus the steady-state blood flow indices acquired at 3.1- and 2.1-cm separations on the forearm were not significantly different.

Fig. 5.

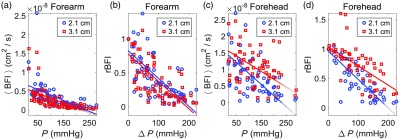
(a) Steady-state (mean) DCS blood flow index ($⟨\mathrm{BFI}⟩$) measurements obtained at 2.1 cm (blue circles) and 3.1 cm (red squares) separations on the forearm plotted against external probe pressure ($P$) ($N=79$ pressures total divided across 11 healthy adults; 1 min of DCS data per pressure). (b) Corresponding intrasubject normalized relative changes in the mean DCS blood flow index $(\mathrm{rBFI}\equiv ⟨\mathrm{BFI}⟩/{⟨\mathrm{BFI}⟩}_o)$ plotted against changes in probe pressure $(\mathrm{\Delta }P\equiv P-P_o)$ on the forearm. (c) $⟨\mathrm{BFI}⟩$ measurements obtained at 2.1- and 3.1-cm separations on the forehead plotted against $P$ ($N=60$ pressures total). (d) Corresponding rBFI data plotted against $\mathrm{\Delta }P$ on the forehead. The solid lines are the best fits to the data from linear mixed effects regression analysis (the slopes and intercepts, as well as Pearson’s correlations, are reported in Table 2). ${⟨\mathrm{BFI}⟩}_o$ and $P_o$ denote the subject’s mean steady-state blood flow index and probe pressure measured at the baseline (initial) probe pressure. The slopes of the lines on the forearm at 2.1 cm are not significantly different from those at 3.1 cm. On the forehead, in contrast, the magnitudes of the slopes at 3.1 cm are significantly smaller than those at 2.1 cm.

3.2. DCS Measurements on Forehead

For the 11 subjects measured, the average ($\text{mean}\pm \mathrm{SD}$) heart rate, DCS BFI (at 2.1-cm separation), DCS PI, probe pressure, and DCS intensity (at 2.1-cm separation) obtained at baseline on the forehead were ($72\pm 12$) beats per min, $(1.3\pm 0.7)\times {10}^{-8}{\mathrm{cm}}^{-2}/\mathrm{s}$, $0.16\pm 0.06$, $41\pm 19\mathrm{mmHg}$, and $140\pm 55\mathrm{kcps}$, respectively. Across all subjects, we observed strong correlations between $⟨\mathrm{BFI}⟩$ and $P$ ($R=-0.55$, $p<0.001$) and between rBFI and $\mathrm{\Delta }P$ ($R=-0.88$, $p<0.001$) (Fig. 6). Interestingly, the correlations between PI and $P$ ($R=-0.11$, $p=0.4$) and between rPI and $\mathrm{\Delta }P$ ($R=0.01$, $p=1.0$) were not significant (Fig. 6). The slopes and intercepts of the linear best-fit lines obtained from linear mixed effects regression analysis, as well as the interquartile range of the fractional deviations from the best fit, are reported in Table 2. The slopes are significantly different from zero ($p<0.001$) for the $⟨\mathrm{BFI}⟩$ versus $P$ and rBFI versus $\mathrm{\Delta }P$ comparisons, but not for the PI versus $P$ ($p=0.4$) and rPI versus $\mathrm{\Delta }P$ ($p=1.0$) comparisons.

Fig. 6.

Plots of: (a) steady-state (mean) DCS BFI ($⟨\mathrm{BFI}⟩$) versus external probe pressure ($P$), (b) DCS PI versus $P$, (c) intrasubject normalized relative change in mean DCS BFI $(\mathrm{rBFI}\equiv ⟨\mathrm{BFI}⟩/{⟨\mathrm{BFI}⟩}_{\mathrm{o}})$ versus change in probe pressure $(\mathrm{\Delta }P\equiv P-P_o)$, and (d) intrasubject normalized relative change in DCS PI $(\mathrm{rPI}\equiv \mathrm{PI}/{\mathrm{PI}}_o)$ versus $\mathrm{\Delta }P$. These data were obtained on the right foreheads of 11 healthy adult volunteers at multiple probe pressures for each subject (i.e., $N=60$ probe pressures total; 1-min of DCS data acquired for each pressure, 2.1-cm source-detector separation). ${⟨\mathrm{BFI}⟩}_o$, $P_o$, and ${\mathrm{PI}}_o$ denote the subject’s mean steady-state BFI, probe pressure, and PI measured at the baseline (initial) probe pressure. The solid red lines are the best fits to the data from linear mixed effects regression analysis. The Pearson’s correlations and the slopes of the best-fit lines were significantly different from zero for only the $⟨\mathrm{BFI}⟩$ versus $P$ and rBFI versus $\mathrm{\Delta }P$ comparisons (see main text and Table 2).

Plots of the steady-state data (i.e., $⟨\mathrm{BFI}⟩$ versus $P$ and rBFI versus $P$) acquired at the 3.1-cm separation on the forehead are shown in Figs. 5(c) and 5(d). The correlations between $⟨\mathrm{BFI}⟩$ versus $P$ and rBFI versus $\mathrm{\Delta }P$ were $R=-0.37$ and $R=-0.71$, respectively, and the slopes of the corresponding best-fit lines were significantly smaller in magnitude than the analogous slopes at 2.1-cm separation (see Table 2). Contrastingly, the average DCS BFI across subjects obtained at baseline with the 3.1-cm separation, i.e., $(1.4\pm 0.7)\times {10}^{-8}{\mathrm{cm}}^2/\mathrm{s}$, was not significantly different from the corresponding average BFI obtained at 2.1-cm separation. Similarly, the average ${⟨\mathrm{BFI}⟩}_{3.1,o}-{⟨\mathrm{BFI}⟩}_{2.1,o}$ difference at baseline of $(1.4\pm 2.1)\times {10}^{-9}{\mathrm{cm}}^2/\mathrm{s}$ was not significantly different from zero. The average DCS signal intensity across subjects at baseline for the 3.1-cm separation was $12\pm 3\mathrm{kcps}$.

Finally, we consider the sensitivity of the steady-state measured BFI to scalp flow. We assume that cerebral blood flow remains constant during our measurements at different scalp pressures. Accordingly, we define the sensitivity of BFI to scalp flow (i.e., $S$) as the fractional change in the measured steady-state BFI divided by the fractional change in scalp flow caused by increased pressure on the scalp: $S\equiv [(⟨\mathrm{BFI}⟩-{⟨\mathrm{BFI}⟩}_o)/{⟨\mathrm{BFI}⟩}_o]/[(\mathrm{SBF}-{\mathrm{SBF}}_o)/{\mathrm{SBF}}_o]$. Analogously to $⟨\mathrm{BFI}⟩$ and ${⟨\mathrm{BFI}⟩}_o$, SBF and ${\mathrm{SBF}}_o$ denote the scalp blood flow levels at the scalp pressures $P$ and $P_o$, respectively. The ratio of the scalp sensitivities of BFI data acquired at 2.1- and 3.1-cm source-detector separations is thus $rS=S_{2.1}/S_{3.1}=({\mathrm{rBFI}}_{2.1}-1)/({\mathrm{rBFI}}_{3.1}-1)$. For each subject, we computed $rS$ for the highest scalp tissue pressure. The average ($\text{mean}\pm \mathrm{SD}$) across subjects of $rS$ was $2.3\pm 2.0$ [note the median (25th percentile, 75th percentile) of $rS$ was 1.5 (1.2, 2.6)]. Thus the steady-state BFI at 2.1 cm is substantially more sensitive to the scalp than the steady-state BFI at 3.1 cm.

4. Discussion

Elevated ICP on brain tissue, which may compromise cerebral blood flow and lead to ischemia and secondary brain injury, is a major complication of traumatic brain injury and hydrocephalus.^35–37 Accordingly, invasive ICP monitoring is widely employed in neurocritical care to detect dangerous elevations in ICP, which in turn trigger therapeutic interventions. Invasive ICP monitors, however, carry risks, including intracranial hemorrhage and infection, and these risks may be too great in some brain injured patients. Consequently, noninvasively measured biomarkers of ICP would be greatly beneficial in clinical care.

Previous research based on TCD measurements has shown that the shape of pulsatile arterial blood flow waveforms during the cardiac cycle is influenced by the tissue pressure (e.g., ICP) compressing the arteries.^14,17,38,39 Specifically, the waveform shape was characterized by a PI, which is defined as the systolic minus diastolic blood flow difference divided by the mean blood flow. Numerous comparisons of TCD measurements of PI in the middle cerebral artery with invasive measurements of ICP in brain-injured patients have been performed.^{17,36,39–42} These comparisons, which are documented in useful reviews,^{14,36,40–42} have investigated the ability of PI to monitor trends in ICP, as well as the ability of PI to detect absolute tissue pressure values. Modest to strong Pearson’s correlations between PI and ICP were observed for both types of comparisons, depending on the study (e.g., from 0.31 to 0.94 for the absolute comparisons^39,40 and from 0.61 to 0.83 for trend comparisons^17,43,44). Overall, the PI reflected trends in ICP more reliably.^14,17,41 The equivocal findings have hindered clinical translation of TCD-measured PI as a tool for noninvasive assessment of ICP. The variation in reported correlations may arise, in part, from intra- and interobserver variations in TCD PI measurements,⁴² which are in part a consequence of the sensitivity of the TCD technique to probe orientation and motion artifacts.^18,19,42

Recently, DCS measurement of blood flow pulsatility in the microvasculature has emerged as a potential complementary and alternative approach to Doppler ultrasound.^7–11 The DCS measurement is robust to the particular placement and orientation of its sensors, which can be held on the head with clinical tape or an elastic strap.^11,19 Accordingly, DCS is well-suited for continuous prolonged monitoring.^20–22,45 Herein, we investigated the effects of pressure on the DCS blood flow pulsatility signal acquired at the 2.1-cm source-detector separation on both the forehead and forearm. The measured external probe pressures on the forehead and forearm are the scalp and muscle tissue pressures, respectively.

4.1. DCS PI Measurements on Forearm Are Sensitive to Muscle Tissue Pressure

The strong correlation between DCS-measured PI and muscle tissue pressure ($R=0.66$; Fig. 4, Table 2) shows the sensitivity of PI to pressure, which is consistent with TCD-measured PI. As with TCD, caution is warranted in the use of PI as a one-to-one measure of pressure. The interquartile range of the fractional deviation of the DCS PI measurements from the linear mixed effects regression of PI versus pressure is 64% (Table 2, Fig. 4). A similar interquartile range of the fractional deviation (i.e., 46%) was observed in the comparison of relative changes in PI to relative changes in pressure (Table 2, Fig. 4). In future work, arterial blood pressure measurements and DCS PI measurements utilized in combination with a model of the arterial vascular tree may be more predictive of tissue pressure.¹⁰

Steady-state BFI was modestly less correlated with muscle tissue pressure than the PI (i.e., $R=-0.57$). Thus the BFI can also potentially be used as a biomarker of tissue pressure. Previous work has shown that errors in the absolute tissue optical properties substantially influence the BFI measurement.^23,25,26 In clinical patient populations wherein optical properties can be substantially different from healthy controls, this source of error may be important. The DCS PI measurements, however, are based on relative changes in BFI, which are more robust to errors in absolute optical properties.⁴⁶

These results suggest the promise of using DCS PI measurements in the future, potentially in conjunction with absolute BFI, to aid noninvasive diagnosis of compartment syndrome. Compartment syndrome is a condition wherein increased tissue pressure within a localized space in the limbs compromises blood supply to, and ultimately the function of, tissues (especially nerve and muscle) within that space.^47–49 It is presently diagnosed with invasive pressure monitors.

4.2. DCS PI Measurements on Forehead Are not Sensitive to Scalp Tissue Pressure

Interestingly, on the forehead, we found that DCS PI measurements were not correlated with scalp tissue pressure ($R=-0.11$, $p=0.4$; Fig. 6, Table 2). Relative changes in PI were also not sensitive to relative changes in scalp tissue pressure ($R=0.01$, $p=1.0$; Fig. 6, Table 2). Contrastingly, the absolute steady-state BFI, as well as relative changes in the BFI, were correlated with scalp tissue pressure (i.e., $R=-0.55$ and $R=-0.88$, respectively; Table 2). The observed sensitivity of the DCS steady-state BFI measurement to scalp pressure is consistent with previous work and is indicative of scalp contamination in the DCS BFI measurement.^24,50

The insensitivity of the DCS PI measurement to scalp pressure, however, shows that scalp contamination is substantially less severe in the PI measurement. Future work is needed to better understand the theoretical explanation of this finding. The result is likely in part a consequence of the brain tissue being less compliant than peripheral tissues (e.g., scalp).³⁸ The lower compliance in the brain translates to less attenuation of the pulsatility in the microvasculature of the brain tissue compared to that of the scalp tissue.

It is important to note that for some of the subjects, PI changed considerably with changes in probe pressure (Fig. 6). In the comparison of relative changes in PI to relative changes in probe pressure across all subjects, the slope of the best-fit line was nearly zero, but the interquartile range of fractional deviation in the rPI measurements from the best-fit line was 39% (Table 2). Some of this heterogeneity likely arose from confounds that can be addressed in future work, such as low signal-to-noise, our assumption of constant tissue optical properties, and intersubject variations in scalp/skull thickness (see Sec. 4.4).

Overall, the low sensitivity of the DCS PI to scalp contamination has exciting implications for the ability of DCS to accurately monitor PI in the brain. Future work is needed to compare prolonged DCS PI monitoring to invasive ICP monitoring.

4.3. Steady-State BFI Measurements at 3.1-cm Source-Detector Separation

Although signal-to-noise was too low to resolve flow pulsatility at 3.1-cm source-detector separation, measurement of steady-state BFI was still feasible. For the forearm, the slopes of BFI versus muscle tissue pressure for the data obtained at 3.1- and 2.1-cm separations were the same (Fig. 5, Table 2), as well as the absolute BFI measurements at baseline. This result is reasonable since the forearm is, to a good approximation, homogenous tissue. For the forehead, the attenuation in BFI with increasing scalp pressure was less severe in the 3.1-cm separation data than the 2.1-cm separation data (Fig. 5, Table 2). At a probe pressure of 200 mmHg, on average, the attenuation in the BFI at 2.1-cm separation was $\sim 70\%$ lower than the initial baseline pressure, whereas the attenuation in the BFI at 3.1-cm separation was $\sim 35\%$ lower (Fig. 5). Accordingly, the steady-state BFI at 2.1-cm source-detector separation was substantially more sensitive to scalp changes than the BFI at 3.1-cm separation (i.e., the median scalp sensitivity at 2.1-cm was roughly 1.5 times higher than the scalp sensitivity at 3.1 cm, see Sec. 3.2). Our latter finding on scalp sensitivity is roughly consistent with a previously published simulation of healthy adults, wherein scalp sensitivity at 2 cm was reported to be $\sim 1.3$ times higher than scalp sensitivity at 3 cm.⁵¹

The absolute BFI at baseline acquired at 3.1-cm separation, however, was not significantly different from the absolute BFI acquired at 2.1-cm separation (Sec. 3.2). This last result is unexpected, since in healthy adults, cerebral blood flow is roughly a factor of 6 higher than scalp flow.^51,52 Consequently, if the 3.1-cm separation was substantially more sensitive to the brain, a higher BFI at 3.1-cm separation is expected. Indeed, the BFI at 3.1-cm trended higher than 2.1, but the trend was not significant because of high variability across subjects. We note the high variability in absolute BFI across subjects could in part be an artifact from our assumption of equal optical properties for all subjects.

Finally, our experimental results provide direct evidence only about scalp sensitivity, not brain sensitivity. Specifically, the variation in scalp tissue pressure will influence scalp blood flow, but it would not influence the skull.

4.4. Limitations

A well-known limitation of DCS is low signal-to-noise ratio, which prevented accurate PI measurements at 3.1-cm source-detector separation. Specifically, in the Fourier transform of the temporal BFI data acquired at 3.1-cm separation, there was not a clear peak at the heart rate frequency above the noise floor. In our previous work, we found that for a single-detection channel, DCS signal intensities of $>50\mathrm{kcps}$ were optimal for fast DCS measurement of blood flow pulsatility at the heart rate.⁸ The DCS signal intensities were less than this on both the forearm (i.e., $29\pm 13\mathrm{kcps}$) and forehead (i.e., $12\pm 3\mathrm{kcps}$) at 3.1-cm separation. It will be important future work to implement strategies to boost signal-to-noise in DCS to achieve greater depth sensitivity to the brain.^4,53–57 Notably, in this study, there was only one single mode DCS detection fiber at each separation. With instrumentation that has more DCS detection channels, it is possible to measure PI at longer separations beyond 2.1 cm to increase sensitivity to the brain.

Increased brain sensitivity will in turn mitigate confounds in DCS PI measurements. For instance, though our measurements at 2.1 cm provide clear evidence of DCS sensing arterial flow beyond the scalp on the forehead, variations in brain sensitivity arising from variations in skull thickness (and potentially skull vascularization) may confound comparisons across subjects. DCS measurements acquired at longer separations are less sensitive to this source of error.

This study also assumed constant tissue optical properties in deriving BFI. The DCS PI calculation, which is based on relative changes in BFI, is expected to be relatively robust to errors in the assumed tissue optical properties,⁴⁶ though in the future, accurate measurement of absolute optical properties is desirable. Errors in the optical properties will be more pronounced in the steady-state BFI measurements.^23,25,26 For this reason, caution is warranted for quantitative interpretation of the absolute BFI versus pressure slopes reported.

5. Conclusion

We investigated the influence of pressure on the DCS PI measurements on the forearm and forehead acquired at 2.1-cm source-detector separation on eleven healthy adults. The strong correlation between DCS PI and muscle tissue pressure demonstrates the sensitivity of PI to the tissue pressure compressing the arterial microvasculature. The lack of correlation between DCS PI measurements on the forehead and scalp tissue pressure indicates that DCS senses arterial flow beyond the scalp on the forehead. Together, these results suggest the promise of using DCS PI measurements to aid timely noninvasive detection of trends in ICP in the clinic.

Biographies

Detian Wang received his PhD in physics from the Institute of Fluid Physics in 2017. He is a postdoctoral researcher in the Department of Neurosurgery of Southwest Hospital at Army Medical University (also called the Third Military Medical University) and is an assistant professor at the Institute of Fluid Physics of the China Academy of Engineering Physics (CAEP). He had been a visiting student at the University of Pennsylvania to study biomedical optics from 2013 to 2015. His research interests include noninvasive brain disease diagnosis with diffuse optical methods and fiber sensing technology for shock physics.

Wesley B. Baker received his PhD in physics from the University of Pennsylvania in 2015. He is a research associate in the Division of Neurology at the Children’s Hospital of Philadelphia. His research interests include cerebral blood flow and oxygen metabolism monitoring with optical spectroscopy/imaging techniques.

Hui He received his MS degree from the University of Chongqing in 2012. He is a research engineer in electronics at the Institute of Fluid Physics.

Peng Gao is an assistant engineer at the Institute of Fluid Physics. His major is mechanics.

Liguo Zhu received his PhD from Tsinghua University, Beijing, China, in 2011. From 2009 to 2011, he worked as a joint-PhD student at Case Western Reserve University, Ohio, USA. He is a professor of optics at CAEP. Now, he is a group leader of terahertz spectroscopy and imaging at CAEP. His current research majors are ultrafast terahertz spectroscopy and imaging, material dynamic response studied by terahertz spectroscopy, and terahertz techniques for biomedical applications. He was awarded with “Double-Hundred Talents” Project of CAEP, President’s Scholarship of CAEP, and two prizes for scientific innovation.

Qixian Peng is a professor at the Institute of Fluid Physics. His research interests include developing the ultrafast optoelectronics techniques for shock physics.

Zeren Li is a professor at the Institute of Fluid Physics. His research interests include ultrafast photography and optical interferometric techniques for shock physics.

Fei Li received his MD and PhD degrees in medicine from the Third Military Medical University in 2003 and 2011, respectively. He is an associate professor of neurosurgery at Chongqing Southwest Hospital of Army Medical University. From 2014 to 2016, he worked as a postdoctoral fellow at the Cold Spring Harbor Laboratory in the United States. At present, he is mainly engaged in the interdisciplinary research of new physical technology in the diagnosis and treatment of nervous system diseases.

Tunan Chen received his PhD in neurosurgery from the Third Military Medical University, Chongqing, China, in 2012. He is a lecturer in the Department of Neurosurgery of Southwest Hospital at the Army Medical University. His research interests include terahertz biomedical application, interdisciplinary research, and clinical transformation of physical and biomedical sciences.

Hua Feng received his BS degree in medicine and his PhD in neurosurgery from the Fourth Military Medical University, Xi’an, China, in 1984 and 1997, respectively. He is a director and a full professor in the Department of Neurosurgery of the Southwest Hospital at the Army Medical University. His research interests include research of brain science, transformation of physics and biomedicine, treatment for nervous system trauma, and reconstruction of neurological function.

Disclosures

No conflicts of interest, financial or otherwise, are declared by the authors.