A Method to Determine the Coincidence of MRI-Guided Linac Radiation and Magnetic Isocenters

Abstract

To assure accurate treatment delivery on any image-guided radiotherapy system, the relative positions and walkout of the imaging and radiation isocenters must be periodically verified and kept within specified tolerances. In this work, we first validated the multiaxis ion chamber array as a tool for finding the radiation isocenter position of a magnetic resonance–guided linear accelerator. The treatment couch with the array on it was shifted in 0.2-mm increments and the reported beam center position was plotted against that shift and fitted to a straight line, in both X and Y directions. From the goodness-of-fit and intercepts of the regression lines, the accuracy and precision were conservatively estimated at 0.2 and 0.1 mm, respectively. This holds true whether the array is irradiated from the front or from the back, which allows efficient collecting the data from the 4 cardinal gantry angles with just 2 array positions. The average isocenter position agreed to within at most 0.4 mm along any cardinal axis with the linac vendor’s film-based procedure, and the maximum walkout radii were 0.32 mm and 0.53 mm, respectively. The magnetic resonance imaging isocenter walkout as a function of gantry angle was studied with 2 different phantoms, one employing a single fiducial at the center and another extracting the rigid displacement values from the distortion map fit of 523 fiducials dispersed over a large volume. The results were close between the 2 phantoms and demonstrated variation in the magnetic resonance imaging isocenter location as high as 1.3 mm along a single axis in the transverse plane. Verification of the magnetic resonance imaging isocenter location versus the gantry angle should be a part of quality assurance for magnetic resonance-guided linear accelerators.

Introduction

Magnetic resonance imaging (MRI)–guided radiation therapy is gaining clinical acceptance around the world. We have recently installed an MR-guided linear accelerator (MRIdian, ViewRay Inc, Cleveland, Ohio). It consists of a 6 MV flattening filter free (FFF) linac coupled with a 0.35T (MRI scanner, ViewRay Inc, Cleveland, Ohio). As any image-guided radiotherapy device, it requires initial and periodic verification of coincidence between the imaging and radiation isocenters.¹ The manufacturer-recommended procedure relies on radiochromic film and is somewhat cumbersome. We report here on the validation of a multiaxis ion chamber array as an on-line tool for radiation isocenter localization. In the process of verifying the coincidence between the radiation and MRI isocenters, we have discovered a previously unreported dependency of the latter one on the gantry angle, which we have also quantified in this article.

Methods

Isocenter Definition and Alignment

There are 3 points in space that are important to the MRIdian isocenter alignment. First is the radiation isocenter, its walkout is attributed only to the gantry rotation, as the collimator and couch angles are fixed. The second one is the MRI isocenter. In theory, it is defined by the fixed geometry of the MRI gradient coils and should not wobble. And finally, since the radiation and MRI isocenters are located within the bore and are not readily accessible, a virtual isocenter is defined 155 cm along the International Electrotechnical Commission Protocol 61217 Y axis from the radiation isocenter and is marked by the laser cross-hairs. The isocenter localization and alignment is currently a 3-step process. First, the radiation isocenter is localized. The vendor’s procedure calls for 2 pieces of radiochromic film and a proprietary cylindrical daily quality assurance (DQA) Acrylic phantom. The phantom can accommodate a precision-cut circular piece of film in transverse orientation (for the IEC X and Z positions measurements). Another piece (for the Y position) is wrapped around the phantom. Both films are marked at the laser cross-hairs and the phantom is translated 155 cm to the center of the bore. A star shot (typically 5 beams) is delivered to the phantom. The films are scanned and analyzed with standard software, such as RIT (Radiological Imaging Technologies, Colorado Springs, Colorado). In the transverse plane (X and Z directions), the minimum radius and the center of the circle touching the center lines of all beams are determined. On the wrap-around film, the full width at half-maximum (FWHM) of the entrance- and exit-exposed areas of each beam is localized in the Y direction (along the couch). The center of the circle on the transverse film (X and Z) and the center of the FWHM line (Y) on the wrap-around film are related back to the lasers. If necessary, those are adjusted to minimize displacement from the radiation isocenter. After that, the DQA phantom is aligned on the lasers and an MR image is taken. It is registered to the planned reference image. To obtain the reference plan, a virtual simulation is performed with a phantom MR image as a primary data set. Using the fiducials, the plan isocenter is placed at a point where the virtual isocenter would be when the lasers are aligned to the phantom cross-hairs. The shifts established during the registration process indicate the displacement between the virtual (lasers) and MRI isocenters and by transitivity between the MRI and radiation isocenters. The user must enter the MRI isocenter shift in relation to the radiation one in the MRIdian software configuration tool, to obtain properly aligned clinical images thereafter. Any pair of the 3 isocenters should be no more than 1 mm apart by a 3-dimensional (3D) Euclidean distance.

Chamber Array Sensitivity to Beam Center Shift

An MR-safe planar multiaxis ion chamber array (IC Profiler-MR [ICP-MR], Sun Nuclear Corp, Melbourne, Florida) is a convenient tool for measuring the cross-beam profiles in the MR-linac bore, especially since MR-compatible water tanks are not readily available yet. The ICP-MR has modified parallel-plate ion chambers along the cardinal axes and 2 diagonals. The primary (X and Y) axes are of interest here, and the chambers are ∼2 mm in size along their respective axes and are spaced 5 mm apart. The ICP-MR cross-beam profiles were previously demonstrated to agree well with the ion chamber in water on a conventional linac² and also with film in the presence of 1.5 T static magnetic field.³ The ICP-MR software (Profiler v. 3.4.3) also reports the radiation beam center position along the X and Y axes. It is determined by fitting an analytical function in the penumbra region to the ion chamber readings and extracting the beam edge location. For the conventional beams, it is customary to define the beam edge as a 50% profile intensity point (defined in this case on the sum-of-arctangents penumbra-fitting curve). For the FFF beams, it is more appropriate to find the derivative and the inflection point of the descending slope⁴ fitted to a Gaussian. The inflection point is considered to be the beam edge. However, the difference between the 2 methods is significant only for the absolute beam width determination. For the beam center position, the method-dependent differences are symmetrical and cancel out between the opposite edges of the beam, and the 2 approaches in our case agreed to within 0.1 mm or better. In this study, we evaluated the precision of the ICP-MR beam center position reporting against a direct mechanical translation with high resolution. Moreover, since unlike on a conventional accelerator,⁵ on the MRIdian the array cannot be gantry-mounted, for efficiency it is preferable to irradiate the array from the front and back without having to flip it for opposing beams. Since the device is calibrated in the normal position only, it had to be verified if irradiating from the back, and particularly through the treatment couch, would alter the results.

The ICP-MR was sandwiched between 2 pieces of solid water so that the total buildup (inherent plus added) from both directions was 5 cm water equivalent. The multi leaf collimator-defined field size was 19.92 × 19.92 cm². The ICP-MR was first centered on the lasers in the normal position (horizontal, face plate up). The MRIdian couch can be moved with 0.1 mm resolution. The couch was moved in 0.2 mm increments from −1 to +1 mm relative to the isocenter first in the X and then Y directions. Care was taken to always move the couch in the same direction to avoid hysteresis. A series of beams with the couch shifts between them was delivered, with 100 MU each. The ICP-MR was irradiated first with the gantry at 0° and then at 180°. The gantry angle was set with an electronic protractor. The ICP-MR beam center readouts were correlated to the known couch position shifts.

To ascertain the effect of the allowed gantry angle errors, the gantry was rotated ±0.5° from vertical in both up and down positions, and the beam center readouts were compared. To evaluate the absolute isocenter localization accuracy, the measured radiation isocenter positions relative to the virtual isocenter were compared between the ICP-MR and film.

Radiation Isocenter Position

For the isocenter position determination, 4 cardinal gantry angles were used with the same ICP-MR buildup as above. The ICP-MR was set up in one of the 2 positions: horizontal or vertical, so for example with the gantry at 0°, the beam entered from the front of the device, while at 180° from the back. The beam center coordinates were converted into the radiation isocenter displacements from the lasers in the room coordinate system, depending on the ICP-MR orientation. The displacement along the room y-axis was averaged between the vertical and horizontal ICP-MR orientations. The ICP-MR-based isocenter position and walkout radius were compared to film.

Magnetic Resonance Imaging Isocenter Position

Only one MRI pulse sequence is currently available for patient setup and monitoring during radiation treatment: a Siemens “true fast imaging with a steady state precession” (TrueFisp).⁶ The unique characteristics of this fast sequence are a very high signal-to-noise ratio and a T2/T1-weighted image contrast.⁷ The isotropic 1.5-mm voxels were used for all scans in this work. At the time, there was no specific manufacturer’s provision for the investigation of the MRI isocenter walkout (wobble) as it was assumed to be stationary and determined by the fixed locations of the MR gradient coils. However, during routine measurements, it was discovered that the MRI isocenter position was gantry angle-dependent. We investigated this phenomenon with 2 MR imaging phantoms. One was the cylindrical DQA phantom. Water provided the signal background and the ion chamber cavity in the center served as a dark fiducial. The cross-hairs on the phantom have a known relationship to the fiducial. They were aligned with the lasers and axial images were acquired with 1.5 mm resolution in all directions. The images were manually rigidly registered on the fiducial to the reference images of the phantom, and the resulting shifts in 3 dimensions were recorded. Images were taken at 4 cardinal gantry angles. This procedure was repeated 3 times with complete disassembly of the phantom in between. The displacement values were averaged between the 3 runs for each gantry angle.

The second phantom was MagPhan RT (The Phantom Laboratory, Salem, New York). We used the 2-module configuration (Model 820, 35 × 27 × 21 cm³). Relevant to this discussion, the phantom includes 513 one-cm diameter Acrylic fiducials immersed in the water-based solution containing sodium chloride, copper sulfate, and some other additives. The same imaging sequence was used and the series were uploaded to the cloud-based Total QA software (Image Owl Inc, Greenwich, New York) for analysis. In this case, comparison is performed not with the reference image of the phantom but with the ideal design geometry. To that end, the geometrical center point of the phantom is marked externally by the manufacturer, and the lasers are aligned to those cross-hairs. The positions of the fiducials relative to this point are known from the design specifications. Typically, not all 513 fiducials are recognized because of the banding artifacts, but no less than 98% were recognized in each experiment, which was sufficient for analysis. The software reports the phantom image displacement from the geometrical center marked by the cross-hairs. This rigid transformation is determined as the best-fit uniform offset during the distortion analysis. Images were again taken 3 times at each cardinal gantry angle, with the phantom removal from the table in between. The displacements were averaged for the 3 runs at a given gantry angle.

The maximum differences between the MRI isocenter positions at different gantry angles were found for both phantoms and compared. Also, the average MRI isocenter position was compared between the 2 MR phantoms and to the radiation isocenter.

Results

Chamber Array Sensitivity to Beam Center Shift

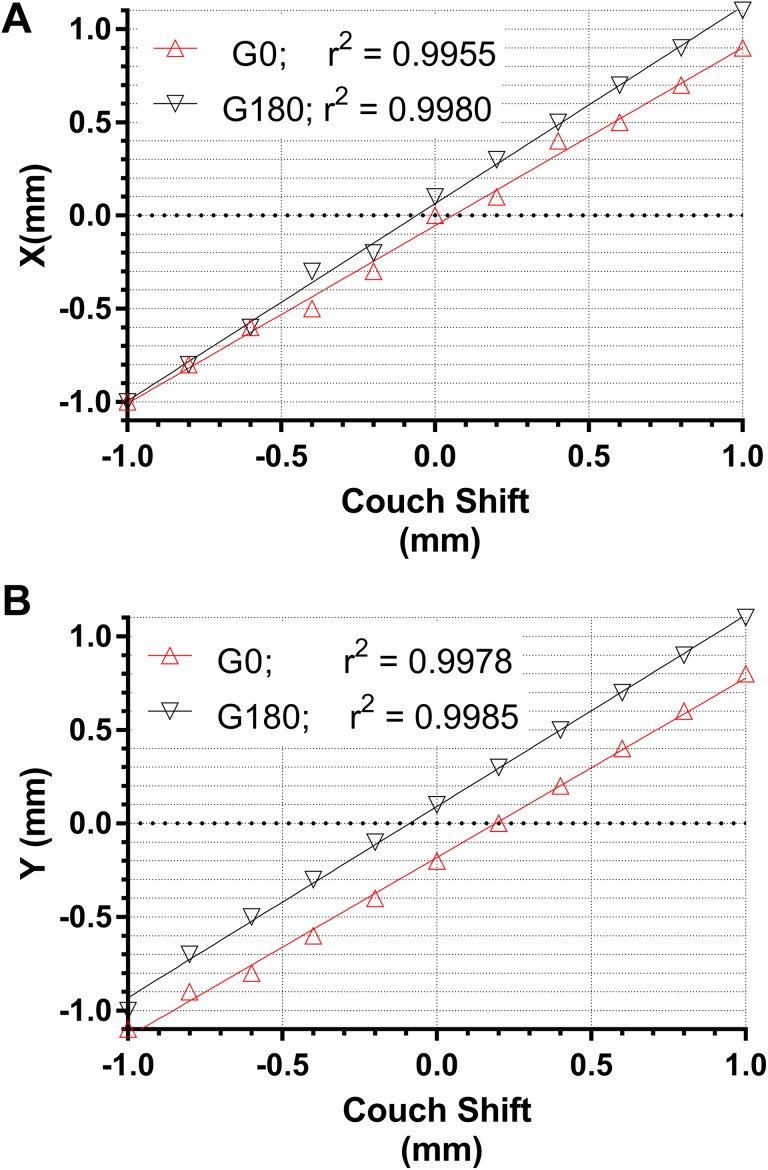
Figure 1 demonstrates the linear relationship between the couch position and the corresponding ICP-MR-reported beam center shift. In the worst-case scenario, the goodness-of-fit parameter r2 = 0.9955 and root-mean-square deviation (RMSD) is <0.05 mm. The linearity of the reported shifts is maintained with the ICP-MR irradiated from the front or from the back. There appears to be a slight difference in the linear regression lines slopes between the gantry at 0° and 180°. However, it leads to no more than 0.2 mm difference over the 2 mm range of motion (Figure 1). The largest intercept value for the 4 linear regression lines in Figure 1 was 0.17 mm. Rotating the gantry by ±0.5° did not cause any change in the reported center position for either the Y or X axes. The gantry angle accuracy should be routinely maintained within 0.5°, so this test range was sufficient.

Figure 1.

Plots of the ICP-MR-reported beam center shifts against the couch shift digital readout in the X (A) and Y (B) directions. Gantry angles 0° and 180°. ICP-MR indicates ion chamber profiler (MR-safe).

Radiation Isocenter Position

The average ICP-MR beam center (isocenter) displacements from the virtual isocenter defined by the lasers are presented in Table 1 as compared to the film measurements.

Table 1.

Average Displacements (Ranges) of the Radiation Isocenter From the Virtual Isocenter (Lasers).

	ΔX (mm)	ΔY (mm)	ΔZ (mm)	3D (mm)
ICP-MR	−0.40 (−0.3 to −05)	0.18 (−0.1 to 04)	0.20	0.48
Film	−0.04	0.16	−0.20	0.26
Difference	−0.36	0.02	0.40	0.54

Abbreviations: 3D, 3-dimensional; ICP-MR, ion chamber profiler (MR-safe).

Overall, the agreement was within 0.40 mm along any cardinal axis and 0.54 mm for the 3D Euclidean distance. The radius of the sphere encompassing all radiation isocenter positions with gantry rotation was estimated at 0.53 mm for film and 0.32 mm for the ICP-MR.

Magnetic Resonance Imaging Isocenter Walkout

The detailed results of the MRI isocenter displacement from the virtual one are presented in Table 2. The 2 phantoms produced close results: the range of the isocenter movement with gantry angle was within 0.1 mm between the 2 phantoms along all axes, and the absolute displacement from the lasers differed by no more than 0.33 mm.

Table 2.

Magnetic Resonance Imaging Isocenter Displacement From the Virtual Isocenter Measured With the DQA and MagPhan.^a

Gantry Angle	DQA			MagPhan
	Ave. ΔX± 1SD (mm)	Ave. ΔY± 1SD (mm)	Ave. ΔZ± 1SD (mm)	Ave. ΔX± 1SD (mm)	Ave. ΔY± 1SD (mm)	Ave. ΔZ± 1SD (mm)
0°	0.57 ± 0.12	0.63 ± 0.12	−0.20 ± 0.0	0.57 ± 0.06	0.50 ± 0.0	−0.37 ± 0.06
270°	0.43 ± 0.12	0.50 ± 0.0	0.87 ± 0.06	0.37 ± 0.06	0.50 ± 0.0	0.53 ± 0.06
180°	−0.70 ± 0.0	0.50 ± 0.0	0.70 ± 0.10	−0.80 ± 0.0	0.57 ± 0.06	0.30 ± 0.0
90°	−0.57 ± 0.12	0.47 ± 0.06	−0.27 ± 0.06	−0.50 ± 0.0	0.50 ± 0.0	−0.70 ± 0.0
Ave	−0.07	0.53	0.28	−0.09	0.52	−0.06
Max-Min	1.27	0.17	1.13	1.37	0.07	1.23

Abbreviations: Ave, average; DQA, daily quality assurance; Max, maximum; Min, minimum; MRI, magnetic resonance imaging.

^a The standard deviation is for the 3 experimental runs, while the average and range in the bottom 2 rows are for the 4 cardinal gantry angles.

In addition, Table 3 shows the displacement of the MRI isocenter form the radiation isocenter as a function of gantry angle, combining the results from Tables 1 and 2.

Table 3.

Magnetic Resonance Imaging Isocenter (MagPhan) Displacement From the Radiation Isocenter for the Cardinal Gantry Angles.

	ΔX (mm)	ΔY (mm)	ΔZ (mm)	3D (mm)
0°	−0.30	0.03	0.30	0.43
270°	−0.10	0.03	−0.60	0.61
180°	1.10	0.03	−0.40	1.17
90°	0.80	0.03	0.50	0.94

Abbreviation: MRI, magnetic resonance imaging.

Discussion

Since we need to prove the isocenters’ coincidence within 1 mm, the measurement tool resolution should ideally be an order of magnitude less. The ICP-MR precision of the beam center measurement was not previously studied in detail, particularly in the FFF beams, although Barnes et al ⁸ reported a maximum 0.1-mm error between the ICP and EPID-based measurements of the accelerator focal spot position during translational beam steering. The quantitative evaluation of the ICP-MR precision and accuracy in finding the beam center is confounded by the fact that the couch movement has 0.1-mm display resolution, and its positional precision can be estimated at 0.2 mm. Thus, the independent variable in the regression has about the same error as the one we are trying to evaluate. The ICP-MR precision can be estimated conservatively from the goodness-of-fit at 2 × RMSD = 0.1 mm. From the largest linear regression intercept in Figure 1 (0.17 mm), the accuracy (bias) could be, again conservatively, estimated at 0.2 mm. These are not necessarily intuitive results. The ICP-MR ion chambers are approximately 2-mm wide along the cardinal axes and the detector pitch is 5 mm. While the chamber in this context can be considered approaching a point detector along the axes,^9,10 a 5-mm sampling step is not sufficient to faithfully reconstruct an arbitrary profile from the Nyquist theorem point of view.⁹ However, if a robust analytical function describing the shape of the penumbra is known, and the noise is low, fitting the function to the sparse measurement points should lead to a sufficiently accurate representation of the profile. This in turn results in a precise extraction of the beam edge position, in agreement with the experimental data. The absolute ICP-MR-measured isocenter position deviations from the film data, which were used by the linac manufacturer to establish the radiation isocenter position, were between 0.02 and 0.40 mm along the cardinal axes. Wen et al ⁶ used a yet different test (modified film-based Winston-Lutz test in a prototype phantom), and their average radiation isocenter location deviated from the virtual isocenter by 0.84 mm in 3D, compared to our result of 0.48 mm. It is worth noting that both film and ICP-MR measurements rely on the manual positioning on the room lasers, with the line width ∼1 mm at the isocenter. Both methods have other sources of uncertainty as well, making it overall hard to ascertain whether one is inherently more accurate than the other. We concluded that the absolute isocenter position agrees reasonably well between the ICP-MR and film and the ICP-MR is a valid and efficient tool for recommended routine isocenter localization tests.¹

In theory, the MRI isocenter is fixed in space as defined by the position of the gradient coils, corresponding to the point where the gradient magnetic fields change directions. However, we have shown with 2 different phantoms that the MRI isocenter shifts with gantry rotation by as much as 1.3 mm along a single axis in the transverse plane. The reason for this isocenter walkout is likely the eddy current calibration that was performed at 0° gantry angle. The MRI isocenter did not wobble with gantry rotation in the previous version of the device, where the gantry supported essentially only the 3 equally spaced ⁶⁰Co heads.¹¹ The gantry in the linac-based machine is inherently less symmetric in the transverse plan. The gantry rotation does not change the conducting mass distribution along the Y axis; hence the isocenter Y position change with rotation is nominal (0.1-0.2 mm, as shown in Table 2). The reported MagPhan 3D rotations did not depend on the gantry angle, and the maximum 3D distortion within 10 cm of the isocenter did not deviate from the average by more than 0.1 mm, which can be considered negligible. Thus the phantom image undergoes only translational shifts with gantry rotation, which is consistent with the uniform central frequency change due to the uncompensated eddy currents.

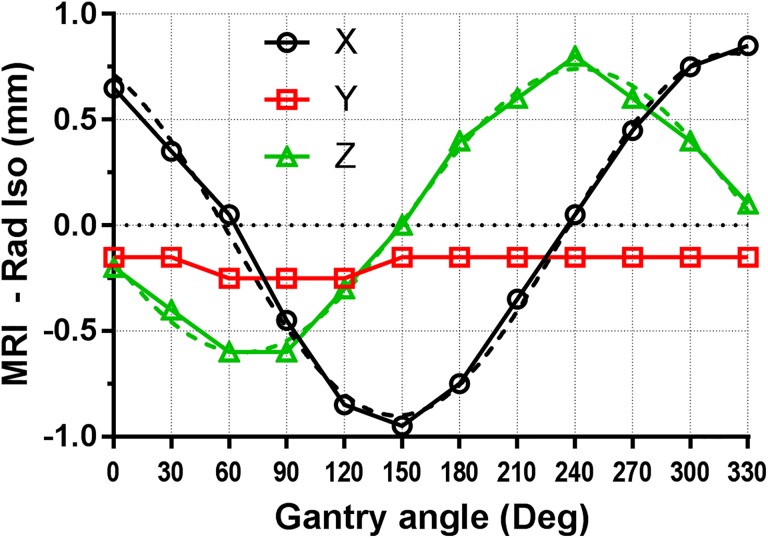
It is important that the wobble of the MRI isocenter is accounted for when setting its location. One solution is to simply set the isocenter position in the middle of the range for each axis. As indicated in Table 3, if the MRI isocenter is set at any given gantry angle, there will be another angle where the wobble reaches its maximum amplitude, and the 3D displacement exceeds 1 mm. However, setting the MRI isocenter at the centroid of the walkout envelope effectively cuts the displacements in half, and the 3D error would not exceed 0.7 mm, within the machine specifications. This averaging solution is quick and fairly simple but not the most accurate. It can only compensate for so much of the MRI isocenter wobble. A smaller effective walkout can be likely achieved by mapping the isocenter displacement as a function of the gantry angle and applying these shifts in the software, instead of the single offset used currently for all gantry angles. That would be conceptually similar to the mapping of the flat-panel imager arms flex in the modern C-arm linacs.¹² To illustrate this possibility, we have collected the MRI isocenter location data as a function of gantry angle with a finer, 30°, angular increment (Figure 2). The figure provides a greater insight into the behavior of the MRI isocenter displacements (X and Z), which appear to be relatively smooth periodic functions, reasonably represented by simple sinusoids (dashed lines), shifted in phase by 90° between the X and Z directions. This set of data was taken after repairs and adjustments were performed on the couch and the lasers, so the exact values of the isocenter displacements vary somewhat from the original data set. In this set of measurements, the maximum 3D distance between the magnetic isocenter and the radiation isocenter did not exceed 0.96 mm. It is also important to put these MRI isocenter shifts in a broader perspective of MRIdian MR imaging. For the setup of 3D imaging, aside from the esoteric 12-minute 0.8 mm × 0.8 mm × 0.8 mm voxel protocol, the best available resolution is 1.5 mm × 1.5 mm × 1.5 mm, while realistically 1.5 mm × 1.5 mm × 3 mm is used clinically because the scan time is compatible with breathhold. Even a 1-mm error is just slightly above the expected image registration accuracy of 1/2 pixel size in the best case scenario.¹³ For the real-time planar tracking, the best available resolution is 3 mm × 3 mm ×5 mm, which puts the isocenter wobble amplitude below the 1/2 pixel size.

Figure 2.

X, Y, Z displacements of the MRI isocenter from the radiation isocenter as a function of gantry angle. Dashed lines represent sinusoidal fits to the X and Z data. MRI indicates magnetic resonance imaging.

Conclusions

Routine radiation isocenter localization/walkout test on MR-guided linear accelerators can be conveniently performed with an electronic chamber array positioned in 2 orientations to collect the data from 4 cardinal beam angles. To confidently maintain submillimeter coincidence with the radiation isocenter, the MRI isocenter localization procedure must take into account possible variations with gantry angle.

Abbreviations

3D

3-dimensional

DQA phantom

daily quality assurance phantom

EPID

electronic portal imaging device

FFF

flattening filter free

FWHM

full width at half-maximum

ICP-MR

ion chamber profiler (MR-safe)

MRI

magnetic resonance imaging

MU

monitor unit

RMSD

root-mean-square deviation