Rapid Compressed Sensing Reconstruction of 3D Non-Cartesian MRI

Abstract

Purpose

Conventional non-Cartesian compressed sensing requires multiple nonuniform Fourier transforms (NUFFTs) every iteration, which is computationally expensive. Accordingly, time-consuming reconstructions have slowed the adoption of undersampled 3D non-Cartesian acquisitions into clinical protocols. In this work we investigate several approaches to minimize reconstruction times without sacrificing accuracy.

Methods

The reconstruction problem can be reformatted to exploit the Toeplitz structure of matrices that are evaluated every iteration, but it requires larger oversampling than what is strictly required by NUFFT. Accordingly, we investigate relative speeds of the two approaches for various NUFFT kernel sizes and oversampling for both GPU and CPU implementations. Second, we introduce a method to minimize matrix sizes by estimating the image support. Finally, density compensation weights have been used as a preconditioning matrix to improve convergence, but this increases noise. We propose a more general approach to preconditioning that allows a trade-off between accuracy and convergence speed.

Results

When using a GPU, the Toeplitz approach was faster for all practical parameters. Second, it was found that properly accounting for image support can prevent aliasing errors with minimal impact on reconstruction time. Third, the proposed preconditioning scheme improved convergence rates by an order of magnitude with negligible impact on noise.

Conclusion

With the proposed methods, 3D non-Cartesian compressed sensing with clinically relevant reconstruction times (< 2 min) is feasible using practical computer resources.

Introduction

Non-Cartesian trajectories offer greater flexibility compared to Cartesian sampling in MRI acquisitions, which may be used to increase efficiency, reduce TE, or improve robustness to motion. To accelerate non-Cartesian acquisitions, data can be undersampled and re-constructed using an iterative model-based reconstruction (1, 2). Many undersampled non-Cartesian trajectories are inherently well-suited to reconstructions with compressed sensing (3) because they often exhibit incoherent aliasing artifacts.

During iterative compressed sensing or other regularized SENSE reconstructions of non-Cartesian acquisitions, nonuniform Fourier transforms (NUFFTs) into the non-Cartesian sampling domain and back to the object-domain are required in every iteration to enforce consistency with the acquired data (4, 5). Compared to Cartesian FFTs, these nonuniform Fourier transforms are time consuming, which detracts from the overall utility of 3D non-Cartesian undersampled trajectories. In this work we investigate several approaches to minimize reconstruction times of non-Cartesian compressed sensing with practical computational resources.

First, it has been shown that non-Cartesian iterative reconstructions can be reformatted to exploit the Toeplitz structure of matrices that are evaluated every iteration and avoid NUFFT convolutions (6, 7). While others have proposed approximate methods that preinterpolate onto a Cartesian grid before iterations (8), the Toeplitz approach involves no simplifying assumptions and results in identical solutions to NUFFT-based methods. However, it is not necessarily faster than NUFFT because it may need larger oversampling (9). Further, the parallelizability of Toeplitz and NUFFT approaches differ, which may have consequences on run-times. Interestingly, while the Toeplitz method was first reported more than a decade ago, many recent studies still report using NUFFT during iterations (10–12). Here we investigate the speed of the two approaches for various NUFFT kernel sizes and oversampling ratios for both GPU and CPU implementations.

Second, non-Cartesian iterative SENSE and/or compressed sensing requires solving over a large enough field-of-view (FOV) to avoid aliasing, but computation times increase rapidly for 3D acquisitions as the image matrix size (i.e., FOV) is increased. Therefore, we introduce a method to determine the optimal FOV by estimating the image support from the calibration data used to estimate receiver sensitivities.

Finally, density compensation weights have been suggested as a preconditioning matrix to improve convergence (1), but this increases noise in least-square solutions (13). It has been argued that the reduction in convergence rate when omitting density compensation weights is not prohibitive (13,14). However, these studies were performed on 2D acquisitions (small amount of data) with fully sampled (well-conditioned) spiral trajectories (relatively uniformly sampled). In this paper, we investigate the effects of density compensation on 3D highly undersampled non-uniform trajectories. Additionally, we introduce a more general choice of weights that permits a trade-off between accuracy and convergence rate. We find that including the density compensation function improves the convergence rate by up to a factor of 75, but increases reconstruction error. However, the weights we propose improve the convergence rate by an order of magnitude with negligible impact on accuracy compared to when no weights are used.

Using these approaches, accurate reconstructions of 8 channel 3D non-Cartesian acquisitions with a matrix size of 234 × 234 × 118 were achievable in clinically relevant reconstruction times (< 2 min) with only a single NVidia GTX 1080 GPU.

Theory

The general approach for non-Cartesian compressed sensing will be described here, followed by descriptions of the three proposed approaches for improving reconstruction speed. Model-based reconstructions of non-Cartesian data are performed by considering the MRI sampling equation:

$$Em=y$$ [1]

where m is the 2D or 3D image (vectorized), the system matrix E models the MRI physics, and y is the measured data. For non-Cartesian trajectories, the system matrix can be estimated using E = F_NS, where F_N is a nonuniform Fourier transform from Cartesian object space with N voxels along each dimension to non-Cartesian k-space (i.e., type 1 NUFFT (15)), and S is a tall block matrix with diagonal blocks that represents multiplication by receiver sensitivity profiles. Image sizes do not need to be symmetric, but symmetry is assumed in the notation F_N for simplicity. The normal equation for a weighted least-squares solution is given by

$$S^H{F}_N^{H}W{F}_{N}Sm=S^H{F}_N^{H}Wy$$ [2]

where H signifies a Hermitian transpose and W is a diagonal matrix of weights. Assuming uncorrelated receivers, setting W = I (the identity matrix) minimizes noise according to the Gauss-Markov theorem. It has been shown that setting W to the density compensation weights used for gridding (16) improves the condition number of $S^H{F}_N^{H}W{F}_{N}S$, which hastens convergence for gradient-based iterative solutions (1); however, this increases noise (13). With regularization, the image is found via

$$\underset{m}{\arg \min }{\Vert \sqrt{W}\left(F_{N}Sm-y\right)\Vert }_2^2+\mathrm{\Phi }(m)$$ [3]

where Φ is the regularization function. For compressed sensing, typically Φ(m) = μ||Ψ(m)||₁, where Ψ is a sparsifying transform (e.g., wavelet transform) and μ > 0 is a constant that controls the strength of regularization.

For the evaluation of Eq. [3] with gradient-based optimization methods, such as FISTA that is commonly used for compressed sensing (17), $S^H{F}_N^{H}W{F}_{N}Sm$ must be evaluated every iteration. Nonuniform Fourier transforms are computationally expensive, rendering non-Cartesian regularized SENSE reconstructions time-consuming.

Exploiting Toeplitz Structure

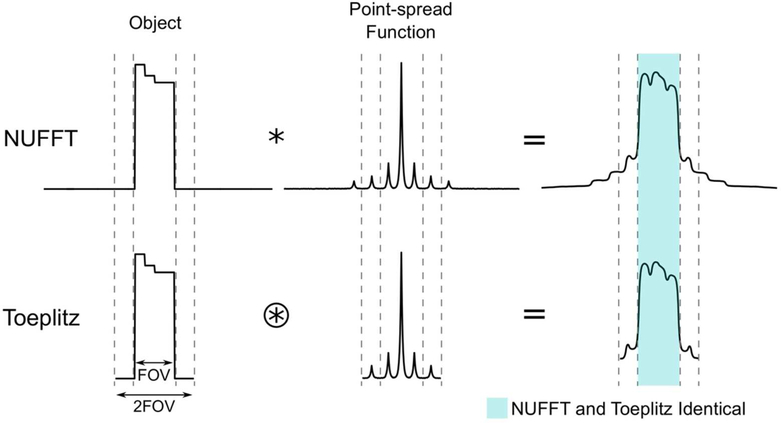
The matrix $F_N^{H}W{F}_N$ in Eq. [2] is Toeplitz, and can be efficiently evaluated using FFTs zero-padded by a factor of two (18). This property can be understood using a point-spread-function formalism. $F_N^{H}W{F}_N$ is equivalent to a convolution of the object with the Fourier transform of W (i.e., the point-spread-function), followed by cropping to the FOV with matrix size N (Fig. 1). The point-spread-function has infinite support because W (i.e., a weighted non-Cartesian sampling function) is finite in k-space. However, the object is understood to have finite support within the FOV, and knowledge of the point-spread-function to only 2N is required to obtain an accurate result within N using a circular convolution via FFTs (Fig. 1). This point-spread-function can be explicitly estimated in Cartesian coordinates via

$$P=F_{2N}^{H}W{F}_{2N}\delta$$ [4]

where δ is a Kronecker delta function. The corresponding transfer function is the Cartesian FFT, $\mathcal{F}$, of the point-spread-function,

$$M=\mathcal{F}{F}_{2N}^{H}W1$$ [5]

where recognizing that the discrete Fourier transform of a delta function is a constant allows replacing F_2Nδ with a vector of ones. Similar determination of the transfer function using NUFFT has been described previously (19). Accordingly, the transfer function can be applied using

$$F_N^{H}W{F}_N=Z^H{\mathcal{F}}^{-1}\mathrm{diag}(M)\mathcal{F}Z$$ [6]

where Z is zero-padding to twice the image size (i.e., (2N)^D, where D is the number of dimensions), and Z^H is cropping. Notably, zero-padding and cropping are required to maintain accuracy within N^D because of the circular convolution implicitly applied by the FFT (Fig. 1). Then, $F_N^{H}W{F}_N$ can be interchanged with $Z^H{\mathcal{F}}^{-1}\mathrm{diag}(M)\mathcal{F}Z$ during iterations when solving Eq. [3].

Figure 1:

Traditional algorithms for non-Cartesian regularized SENSE implicitly estimate a convolution with the sampling point spread function every iteration using nonuniform Fourier transforms (NUFFTs) (top row). The Toeplitz-based method computes a circular convolution over twice the image size using a transfer function represented in Cartesian coordinates (Eq. [6]), which produces an identical result within the original image size provided that the object is bounded. Cropping after circular convolution eliminates the erroneous result outside the original image size (Eq. [6]).

Using this Toeplitz method, NUFFTs in each iteration (one type-1 and one type-2) are replaced by Cartesian FFTs with 2× zero-padding and point-wise multiplication by M. Accordingly, over the entire iterative reconstruction, $F_N^H$ is only evaluated once to determine $F_N^{H}Wy$ (Eq. [2]) and F_N is never evaluated. Since Cartesian FFTs are rapid and efficiently multithreaded, this method has the potential to improve computation times compared to NUFFT. Importantly, M can be precomputed since it depends only on the k-space trajectory.

Minimal Image Matrix Size

In the iterative reconstructions described above, it is important for the image size N (i.e., the FOV) to be large enough to capture the object-domain support of the data to avoid aliasing errors. In many cases, some signal may lie outside the desired FOV. A simple solution to properly account for all signal could be to use an image matrix size twice as large as the nominal matrix size (e.g., twice the FOV); however, this drastically increases computation times for 3D acquisitions because it increases the number of points by a factor of 8. This is especially problematic for the Toeplitz method, which requires a further factor of 2 oversampling (8 times more points for 3D).

Here, we estimated the receiver sensitivity profiles using ESPIRiT (20). Eigenvalues computed during the ESPIRiT calibration process are close to 1 in only regions with signal; accordingly, we defined the support by choosing all positions with eigenvalues above a threshold. Typically, the support is not centered, which increases the minimum reconstructed matrix size. This was addressed by applying a phase-ramp to the raw non-Cartesian data before reconstruction. Finally, N was chosen as the smallest image size that both included the region of support and had small prime factors (e.g., <= 7) for more efficient FFTs.

Generalized Density Weighting

Setting W as density compensation weights for gridding has been suggested to accelerate convergence of unregularized iterations (1), but this increases noise in least-square solutions compared to using an identity matrix (13). To allow a trade-off between convergence rate and noise, we propose setting

$$W=\mathrm{diag}{(d)}^{\kappa }$$ [7]

where d is the gridding density compensation function and 0 ≤ κ ≤ 1. Thus, κ = 0 (i.e., W = I) minimizes noise while κ = 1 (i.e., W = d) maximizes convergence rate.

Methods

All tests were performed using MATLAB on an Intel Xeon E5–2650 v4 2.20 GHz workstation with 100 GB RAM. GPU computations were performed an a NVidia GTX 1080 with 8 GB RAM. The Michigan Image Reconstruction Toolbox was used for the CPU tests (21) and only a single computational thread was permitted. The gpuNUFFT library was used for the GPU tests (22).

Benchmarking Tests

The purpose of the benchmarking tests was to determine the relative performance of NUFFT and Toeplitz methods for several practical NUFFT kernel sizes, NUFFT oversampling ratios, and FOVs. The time-per-iteration required for NUFFT (i.e., $F_N^{H}W{F}_N$) and Toeplitz (i.e., $Z^H{\mathcal{F}}^{-1}\mathrm{diag}(M)\mathcal{F}Z$) to operate on random complex data was measured. The gpuNUFFT library used a Matlab MEX implementation, while built-in Matlab functions were used for the Toeplitz approach. The NUFFT implementation required more memory transfer between the CPU and GPU compared to the Toeplitz implementation; however, with an ideal implementation both should have similar memory transfer requirements and, to enable a more fair comparison, timings were corrected to exclude time for memory transfer between the CPU and GPU. Both 3D cones (23) and 3D radial (24) trajectories were tested, and timings from the two trajectories were averaged. Trajectories were designed for a 1.2 mm isotropic resolution and nominal image matrix size of 128×128×64 with one receiver, with undersampling rates ranging from 1 to 16. Reconstruction image matrix sizes ranging from 128 × 128 × 64 to 256 × 256 × 128 were tested. For the computation of $F_N^{H}W{F}_N$, NUFFT kernel sizes of 4, 6, 8 and oversampling ratios of 1.125, 1.25, 1.5, 2 were tested. In all cases, M was estimated using NUFFT with a kernel size of 6 and oversampling of 1.25.

In Vivo Tests

The purpose of the in vivo tests was to investigate the impact of the choice of image matrix size and κ on accuracy and reconstruction speed. Fully sampled data was acquired using a spoiled gradient echo 3D cones trajectory in the brain of a volunteer on a 1.5 T GE Signa Excite with TR = 5.5 ms, TE = 0.6 ms, flip 30°, BW = 250 kHz, FOV = 28 × 28 × 14 cm³, matrix size 234 × 234 × 118, 9137 readouts, readout duration = 2.8 ms, and 8 receiver channels. Receiver sensitivity profiles were estimated from the fully sampled data using ESPIRiT (20). Notably, ESPIRiT estimation of the profiles could also be performed on a fully sampled central region of k-space for prospectively undersampled data (25, 26). The extent of image support was estimated using an ESPIRiT eigenvalue threshold of 0.7. The fully sampled data was gridded and denoised using a stationary wavelet transform, and undersampled non-Cartesian data was generated using a type-1 NUFFT. Gaussian white noise was added to the non-Cartesian data before reconstructions. This procedure allowed control of undersampling with a known ground-truth.

Reconstructions were performed using the GPU Toeplitz method and bFISTA (27) with random shifting (28). A 3D Daubechies 4 wavelet transform with one level was used, and several values of κ were tested. For all cases, the optimal regularization weighting parameter was determined via a multi-resolution search that resulted in the lowest mean squared error relative to the fully sampled image from which the non-Cartesian data was synthesized from. Undersampled data was synthesized from the fully sampled data for both 3D cones and 3D radial trajectories with net undersampling rates of 6.8 and 7.1, respectively.

Results

Benchmarking Tests

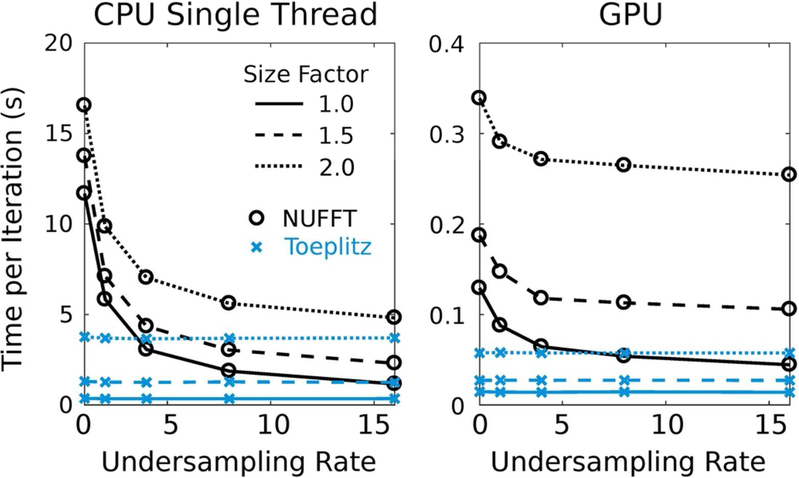
The times per gradient computation for the benchmarking tests with NUFFT oversampling of 1.5 and kernel width 4 are shown in Fig. 2 for a trajectory designed for a nominal image matrix size of 128×128×64. For all the undersampling rates and image matrix sizes shown in Fig. 2, the Toeplitz method was faster than NUFFT. However, the advantage of Toeplitz diminished as undersampling rate increased because the number of samples in the NUFFT convolution decreased. Notably, considerable time savings occur for both cases as the matrix size is decreased, especially for the Toeplitz method, which gives motivation for estimating the minimum required size to capture the support.

Figure 2:

The reconstruction times for the gradient computation (i.e., $F_N^{H}W{F}_N$ for NUFFT and $Z^H{\mathcal{F}}^{-1}\mathrm{diag}(M)\mathcal{F}Z$ for Toeplitz) for both CPU and GPU implementations for various undersampling rates and image matrix size factors compared to the nominal matrix size of 128 × 128 × 64. NUFFT oversampling was 1.5 and the kernel width was 4.

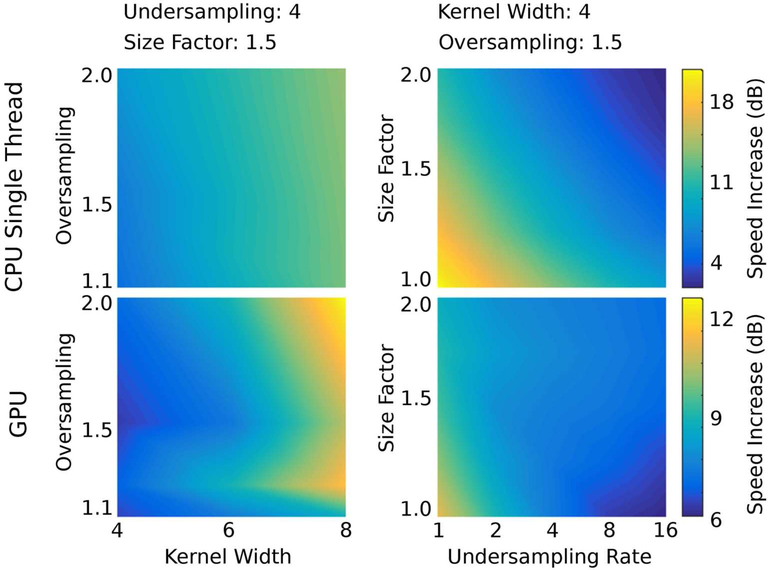
The factor of speed increase for Toeplitz compared to NUFFT over the range of testing parameters is shown in Fig. 3. Individual results for the 3D radial and 3D cones trajectories are shown in Supporting Figure S1. For CPU processing with large trajectory undersampling, small kernel width, small NUFFT oversampling, and/or large image matrix sizes, the NUFFT approach can potentially outperform the Toeplitz method. This occurred for 3D cones with low-accuracy NUFFT parameters (i.e., oversampling near 1.125 and a kernel size of 4). Notably, the Toeplitz method does not have this trade-off because accuracy is determined by the NUFFT parameters for the one-time computation of M and $F_N^{H}Wy$. With GPU processing, the Toeplitz method was at least a factor of 2 faster for all testing parameters. Notably, the time required for wavelet transforms also decreases with smaller matrix size, which gives further incentive to minimize matrix sizes via an estimate of image support.

Figure 3:

Rates of speed increase for Toeplitz compared to NUFFT for the gradient computation (i.e., $F_N^{H}W{F}_N$ for NUFFT and $Z^H{\mathcal{F}}^{-1}\mathrm{diag}(M)\mathcal{F}Z$ for Toeplitz) for both CPU and GPU implementations. The left panels show trends as the kernel width and oversampling ratio are varied, while the undersampling rate is fixed at 4 and the FOV size factor relative to the nominal FOV of 128×128×64 is fixed at 1.5. The right panel shows trends as the undersampling rate and size factor are varied, while the NUFFT oversampling and kernel width are fixed to 1.5 and 6, respectively. Timings for 3D cones and radial trajectories were averaged with each other before computing the speed increases (individual trends were similar). The speed increase rates in decibels (dB) were computed using 10log₁₀(time_NUFFT/time_Toeplitz).

In Vivo Tests

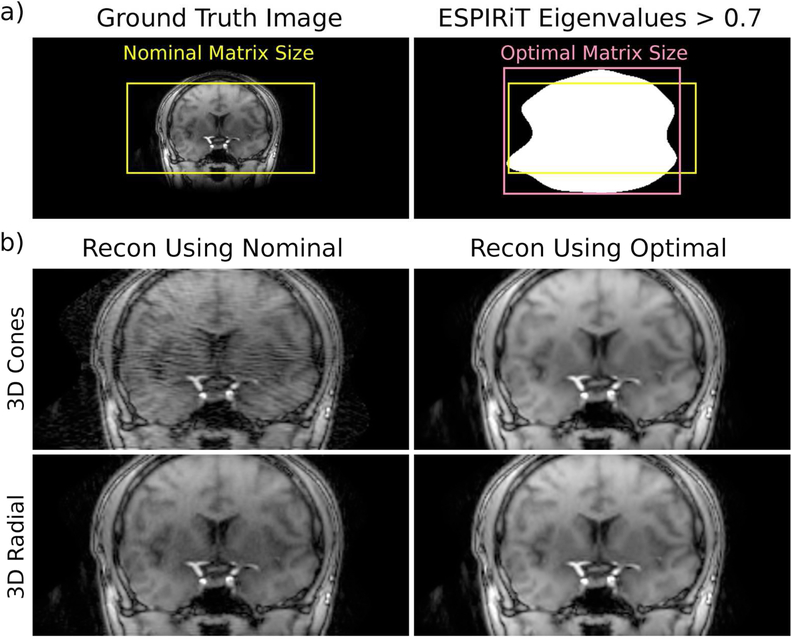
While the nominal matrix size for the in vivo scans was 224 × 224 × 108, the matrix size determined from the ESPIRiT eigenvalue maps (i.e., optimal matrix size) was 216 × 270 × 160 (Fig. 4a). Notably, attempting to reconstruct at the nominal matrix size resulted in considerable error, especially for 3D cones, that was eliminated upon using the optimal matrix size (Fig. 4b).

Figure 4:

(a) In some non-Cartesian acquisitions, signal may lie outside the FOV the trajectory was designed for, which can be assessed from calibration data using an ESPIRiT eigenvalue threshold. (b) Compressed sensing reconstructions that ignored the signal outside the nominal matrix size exhibited errors that were eliminated when the optimal size was used.

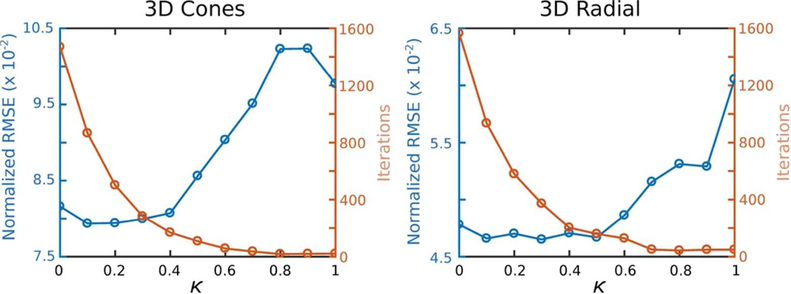
The normalized root-mean-squared-error (RMSE) along with number of iterations required until the RMSE falls within 1% of the converged value are shown in Fig. 5 for both 3D cones and radial trajectories for various κ. As expected, for κ ~ 1 the noise is increased (Fig. 6). For both trajectories, the number of iterations required to converge decreases rapidly as κ is increased from 0, while the net error stays relatively flat. As κ is increased beyond 0.5, the error quickly increases while the number of iterations does not markedly change. For conservative weighting where the error is minimally impacted, κ = 0.3 for cones and κ = 0.5 for radial could be chosen to reduce the time for convergence by 81% and 90%, respectively, compared to when κ = 0. For more aggressive weighting that allows, for example, a 10% increase in RMSE (κ = 0.5 for cones and κ = 0.7 for radial), convergence times are decreased by 93% and 97%, respectively. For κ = 1, only 21 and 49 iterations were required for cones and radial, respectively, compared to ~1500 iterations for both when κ = 0, but RMSE was increased by ~ 50%.

Figure 5:

Normalized root-mean-square-error (RMSE) and number of iterations required to converge as κ is varied from 0 to 1. There is little change in error, but large changes in convergence speed, for κ near 0.

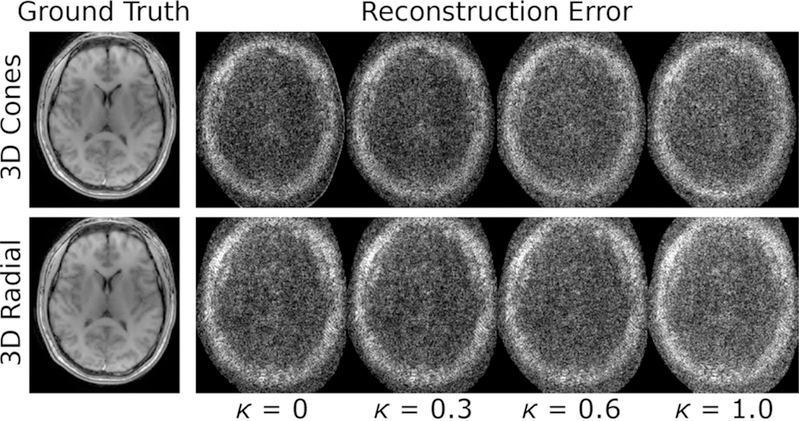
Figure 6:

The difference of reconstructed images from ground truth show increasing amplitude of noise-like error for increasing κ in a sample slice (similar results in other slices). The difference images are scaled by 10 for 3D cones and 20 for 3D radial, relative to the ground truth image.

Discussion

There are three major findings in this study. First, with GPU processing the Toeplitz method outperforms NUFFT for all practical parameters. Second, using minimum image matrix sizes is straightforward and minimizes reconstruction error without unnecessary increases in reconstruction time. Third, a weighting function given by the gridding density compensation function with an exponent less than 1 (i.e., κ) can be used to improve convergence speeds without sacrificing reconstruction accuracy.

For the trajectories used here, choices of κ between 0.3 and 0.7 resulted in convergence speed improvement by an order of magnitude with little to no impact on RMSE. Relative to reconstructing to a 1.5× image matrix size with NUFFT (kernel width = 4, oversampling = 1.5, κ = 0), utilizing all three of the above time-saving approaches (κ = 0.5) reduced the time required for GPU-based reconstruction of the 3D cones example depicted in Fig. 6 from 2.5 hr to 1.8 min. While compressed sensing with ℓ1-wavelet regularization was the focus of this work, similar results would likely be obtained for other choices of regularization. Notably, GPU memory constraints required looping through receiver coils for every FFT/NUFFT. Since these operations could be performed in parallel given enough memory, there is still room for fairly drastic reconstruction time improvements beyond what was observed here as GPU performance improves.

Interestingly, the dependence of RMSE on κ was not monotonic, and in some cases RMSE was slightly lower than when κ = 0. The latter finding is contrary to the Gauss-Markov theorem, and may have stemmed from interaction between the wavelet regularization (which biases the solution, violating the Gauss-Markov theorem) and the choice of weighting function W. Also, the multi-resolution search for optimal μ did not necessarily find the exact optimal value; however, the minimum search spacing was < 3% of the final value of μ in all cases. More study may be warranted to gain a more precise understanding of this phenomenon, and to possibly design W that minimizes the net error or other criteria, such as structural similarity index (29).

This work used an initialization of zero to begin FISTA iterations. When κ = 0, an initialization determined from several regularization-free conjugate gradient iterations with κ = 1 drastically lowers the RMSE for early iterations; however, the number of iterations required to obtain the RMSE threshold used for Fig. 5 was only reduced by 2.5% for both trajectories (Supporting Figure S2). For other choices of κ for the FISTA iterations, the reduction is even smaller (e.g., only 1 total iteration fewer for κ = 0.4 with 3D cones). Notably, using this initialization requires an extra NUFFT to determine $F_N^{H}Wy$ for the conjugate gradient iterations, which detracts from the time savings. An extra transfer function also needs to be computed for Toeplitz implementation of the conjugate gradient iterations, but this could be precomputed.

NUFFT and Toeplitz methods have been compared for both CPU (6, 9) and GPU (30) in several conference proceedings. In the CPU comparisons, undersampling was not considered and no regularization was used (aside from stopping iterations early, which in itself can be considered a form of regularization). In the GPU comparisons, the focus of the work was on speedup relative to CPU. The Toeplitz method has also been suggested for iterative reconstructions of non-Cartesian data with correction of magnetic field inhomogeneity (7), but only a kernel width of 6 and oversampling of 2 was considered in comparisons to NUFFT (CPU only). Finally, speed improvements for GPU determination of the transfer function using NUFFT compared to direct computation on a CPU has been investigated (19), but comparisons of NUFFT to Toeplitz during iterations were not performed. Notably, none of this previous work explored reconstructing to a minimal matrix size dictated by an estimation of the image support.

It should be noted that the Toeplitz method typically requires more memory than NUFFT, which may be a limiting factor in some cases. Also, there have been methods proposed that perform a preinterpolation before iterations to align the data onto a Cartesian grid (8). While these approaches sacrifice some accuracy, a comparison to the Toeplitz approach may be warranted. Finally, it is also notable that the Toeplitz approach forms the foundation for the determination of a circulant preconditioner used in other algorithms (e.g., ADMM (31)).

A potential limitation of the proposed weights may be difficulty in choosing κ for a particular trajectory, especially when ground-truth is unknown. Since the error incurred by increasing κ is manifested as increased noise (Fig. 6), it may be possible to measure the standard deviation in a region with relatively flat contrast for various choices of κ. Investigation of the variation of optimal choice of κ for a more diverse range of trajectory types and anatomy may be warranted, but is beyond the scope of this introductory work.

Conclusion

Compressed sensing is a powerful method for reconstructing images from highly undersampled data. Non-Cartesian trajectories allow further acceleration, but lengthy reconstruction times hamper clinical utility. Here, accurate compressed sensing reconstruction of 3D non-Cartesian data was shown to be feasible in clinically relevant times using practical hardware.

Supplementary Material

Supp info

Supporting Figure S1: Rates of speed increase for Toeplitz compared to NUFFT for the gradient computation (i.e., $F_N^{H}W{F}_N$ for NUFFT and $Z^H{\mathcal{F}}^{-1}\mathrm{diag}(M)\mathcal{F}Z$ for Toeplitz) for both CPU and GPU implementations. Results for both 3D radial and 3D cones trajectories are shown. The left panels show trends as the kernel width and oversampling ratio are varied, while the undersampling rate is fixed at 4 and the FOV size factor relative to the nominal FOV of 128 × 128 × 64 is fixed at 1.5. The right panel shows trends as the undersampling rate and size factor are varied, while the NUFFT oversampling and kernel width are fixed to 1.5 and 6, respectively. The speed increase rates in decibels (dB) were computed using 10log₁₀(time_NUFFT/time_Toeplitz). The 3D radial trajectory has greater speed increases because it has more k-space samples, which increases the duration of NUFFT convolutions.

Supporting Figure S2: Convergence of normalized root-mean-square-error (RMSE) for 3D cones and 3D radial trajectories when κ = 0. When an initialization obtained from two conjugate gradient (CG) iterations is used (dashed), early iterations have a much lower RMSE than when an initialization of zero is used (solid). However, for highly accurate solutions the number of iterations required is similar for both cases. As κ is increased, the differences between these choices of initialization are diminished further.