Abstract
Soft-tissue deformation presents a confounding factor to rigid image registration by introducing image content inconsistent with the underlying motion model, presenting non-correspondent structure with potentially high power, and creating local minima that challenge iterative optimization. In this work, we introduce a model for registration performance that includes deformable soft tissue as a power-law noise distribution within a statistical framework describing the Cramer-Rao lower bound (CRLB) and root-mean-squared error (RMSE) in registration performance. The model incorporates both cross-correlation and gradient-based similarity metrics and was tested in application to 3D-2D (CT-to-radiograph) and 3D-3D (CT-to-CT) image registration. Predictions accurately reflect the trends in registration error as a function of dose (quantum noise) and choice of similarity metric for both registration scenarios. Incorporating soft-tissue deformation as a noise source yields important insight on the limits of registration performance with respect to algorithm design and the clinical application or anatomical context. For example, the model quantifies the advantage of gradient-based similarity metrics in 3D-2D registration, identifies the low-dose limits of registration performance, and reveals the conditions for which registration performance is fundamentally limited by soft-tissue deformation.
Keywords: Image-guided treatment, Image quality assessment, Registration, X-ray imaging and computed tomography
I. Introduction
UNDERSTANDING and modeling the factors that affect image registration performance is of fundamental interest to the medical imaging community as the error in registration directly affects the utility of an image guidance system. Rigid registration performance is typically characterized by studying the accuracy of the geometric transformation (translation and rotation) parameters that relate the two images. While experimentation and analysis involving imaging phantoms or clinical image data provide important characterization of registration performance, a theoretical / statistical model of image registration that includes factors relating to image quality, algorithm parameters, and anatomical context provides valuable insight on the development and application of new registration methods and sheds light on the fundamental limits of registration performance.
Recent work [1] sought to address this gap in theoretical insight by deriving a statistical model for registration error that describes the relationship between (rigid) registration error and image quality characteristics such as spatial resolution (modulation transfer function, MTF), image noise (noise-power spectrum, NPS), and spatial-frequency-dependent signal-to-noise ratio (noise-equivalent quanta, NEQ). The model considered rigid translation between two images (I1, I2):
| (1) |
| (2) |
where the discretely sampled images (denoted [·]) contain the same true underlying continuous image function (g); however, both are contaminated with independent additive noise (ni ), and I2 contains an unknown translation, , which the registration process attempts to estimate.
While the framework in [1] provides insight on the effects of image quality (viz., dose, quantum noise, and spatial resolution), the underlying assumptions are in part broken when structures in g are subject to deformation between I1 and I2, suggesting a disparity in the true underlying signal (g). For example, anatomy presenting in medical images often consists of rigid (bone) and deformable (soft tissue) components. In such a scenario, despite soft-tissue deformation, bone anatomy still provides salient structure suitable to rigid registration. By considering rigid anatomy to be the “true” underlying signal (g), a model can be constructed in which non-rigid structures (soft tissue) are considered as a confounding noise source with respect to the task of rigid registration.
This approach is analogous to approaches drawn from signal detection theory (SDT) in which background anatomical “clutter” is considered as a confounding noise source with respect to the task of detection [2]–[4]. Such SDT frameworks have provided an important basis for imaging system optimization – e.g., in flat-panel detectors [5] and cone-beam CT [6], [7] – and an important aspect of such models is a generalization in which not only quantum noise is considered as a confounding influence on detection, but also any fluctuation in the image that is not associated with the stimulus [8], [9], an insight which provided further guidance for system design. – e.g., background parenchyma of breast or lung tissue. Such generalization of the visual detection process is clearly an abstraction, since background anatomy is not a random process, but it provided guidance on important aspects of imaging system design – e.g., a quantitative basis for detectability in projection, tomosynthesis, and fully 3D tomographic imaging and the point beyond which detection is not improved by increasing dose. In a similar manner, rigid registration of a rigid (bone) structure can be confounded by nearby soft-tissue deformation acting as “noise” in the registration. We therefore present a statistical model that incorporates this deformation as a source of noise in image registration, while also including factors of spatial resolution and quantum noise as in [1].
The work reported below is distinct from preliminary studies reported in [10] as follows. Experiments in [10] treated the image backgrounds as two independent realizations of soft-tissue – an idealization in which soft-tissue clearly acts as a noise source in registration, but does not explicitly treat the question of a deformed soft-tissue background. The work reported below, however, investigates the framework in more realistic scenarios in which the soft-tissue background is deformed (rather than simply re-instantiated). Prior work [10] only examined the performance of the cross-correlation similarity metric in the presence of background anatomical mismatch. In the current work, we extend the statistical framework to model the performance of gradient-based similarity metrics, which are shown to be robust to the confounding influence of soft-tissue deformation. Furthermore, whereas prior work [10] examined 3D-3D registration alone, in this work we also examine 3D-2D registration scenarios, which previous studies [11], [12] showed to have better performance when using gradient-based metrics (cf., cross-correlation metrics). Finally, we present an analytical derivation of the power spectrum associated with 2D and 3D Voronoi images. The derivation may be of general interest beyond this work, and we use the Voronoi power spectrum as a model for piece-wise constant soft-tissue backgrounds (§III.B) analogous to the presentation of anatomy in tomographic imaging (e.g., abdominal CT, which is the subject of experiments below).
The theory and experiments in this paper involve translation-only registration, and the understanding gained regarding the effects of soft-tissue deformation as a confounding noise source is presumably applicable to rigid registration more generally. Furthermore, the work shows how the “noise” imparted by soft-tissue deformation may be minimized by careful choice of similarity metric.
II. Statistical Evaluation of Image Registration
Over the past 15 years, there have been several contributions to understanding the lower bounds in image registration accuracy. Robinson and Milanfar performed early work in statistical evaluation of registration performance by deriving the Cramer-Rao Lower Bound (CRLB) for translation-only image registration in the presence of additive Gaussian white noise (AGWN). Yetik and Nehorai [13] extended this derivation to model both translation and rotation, and Pham et al. [14] extended the model to more general projective transformations. Uss et al. [15], through an alternative approach, derived a translation-only CRLB that assumed AGWN and an underlying image distributed according to a fractal Brownian motion model, showing good agreement with measurements of registration performance in high signal-to-noise (SNR) scenarios. Xu et al. [16] derived Ziv-Zikai Bounds (ZZB) for translation-only registration and was able to model the steep drop in performance in very low SNR conditions due to registration failure. Aguerrebere et al. [17] later explained these works to be associated with the signal-known-exactly scenario (SKE, where a noiseless image is available) and derived the CRLB for registering 2 or more images, each of which contained stationary Gaussian noise (no longer limited to AGWN). Their work also examined various other lower bounds such as the extended ZZB for white noise contaminated images and a Bayesian CRLB when a shift prior was known.
Beyond evaluation of the lower bounds, it is also important to examine the registration method itself, which includes factors such as image preprocessing, similarity metric, and optimization method. Aguerrebere et al. [18] provided a review of general registration frameworks (particularly in the presence of white noise) and distinguished methods that do not rely on prior information (e.g., Maximum Likelihood Estimator) from those that do by incorporating information about the statistical distribution of both the signal and noise (e.g., Bayesian Maximum Likelihood Estimator via the Wiener filter). Robinson and Milanfar [19] and Pham et al. [14] demonstrated the bias present in several registration estimators, fundamentally limiting the registration performance in very high SNR scenarios. The effect of image quality on registration accuracy was investigated by Zhao et al. [20] for translation-only registration under AGWN to understand the influence of spatial resolution (cf., noise) on the sum of squared difference (SSD) similarity metric. Their work indicated that when registering images at different spatial resolutions using SSD, the higher resolution image should be blurred to match the lower resolution. The result is particularly interesting since, by the data-processing inequality, such blur does not improve the CRLB and thus depends on the similarity metric itself (whereas the CRLB is independent of similarity metric). Such work demonstrates the necessity for a statistical registration framework to examine both the theoretical limits of registration accuracy and the influence of the similarity metric to more fully describe the relationship between image quality and registration performance. Such consideration prompted Ketcha et al. [1] to investigate the effects of image quality on both the CRLB and the registration error for the cross-correlation similarity metric.
For the scenario of (1–2), the CRLB for translation-only image registration sets a lower-bound on the root-mean-square error (RMSE) of the translation estimate . For an unbiased estimator it was shown that where the Fisher information matrix (FIM) is defined as:
| (3) |
where G (fx, fy) is the power spectrum of g (x, y), Ni (fx, fy) is the NPS of image Ii (x, y), A is the image area, and fNyq is the Nyquist frequency. The f j, fk terms are the frequency components of the power spectra, with j, k substituted for x, y depending on which γjk term in the FIM is being computed.
As shown in [1], a Taylor series expansion shows the RMSE for the cross-correlation (CC) estimator in translation-only registration to be:
| (4) |
where H (fx, fy) is the frequency weighting provided by any post-processing blur or filtering and should therefore be constructed to minimize RMSE in (4). For example, in the case where both images contain equal-magnitude white noise, (4) is minimized via the Weiner filter (described in [18]). However, when considering the common method of CC with Gaussian blurred images (of characteristic width σb) H is expressed as:
| (5) |
Combining HCC with (4) then allows optimal selection of σb. In this work, we extend (4) to other similarity metrics such as gradient correlation (GC), defined as:
| (6) |
where ⊗ is the cross correlation function defined by:
| (7) |
Equation (6) shows that GC is the sum of the cross-correlation of the partial derivative images . These partial derivative images are typically computed by convolving the images with spatial derivative filters hx (x, y), hy (x, y) (e.g., Sobel, derivative of a Gaussian, etc.), thus we rewrite (6) as:
| (8) |
where the Fourier transform (, with the bar in indicating complex conjugation) in the last line shows that GC can be computed by filtering the CC function (I1 ⊗ I2) with the function HGC (fx, fy). When hx (x, y), hy (x, y) are the derivative of Gaussian spatial derivative filters, we have:
| (9) |
which can be used with (4) to model registration performance for the GC similarity metric. A more general form for the n-th derivative of a Gaussian spatial filter is:
| (10) |
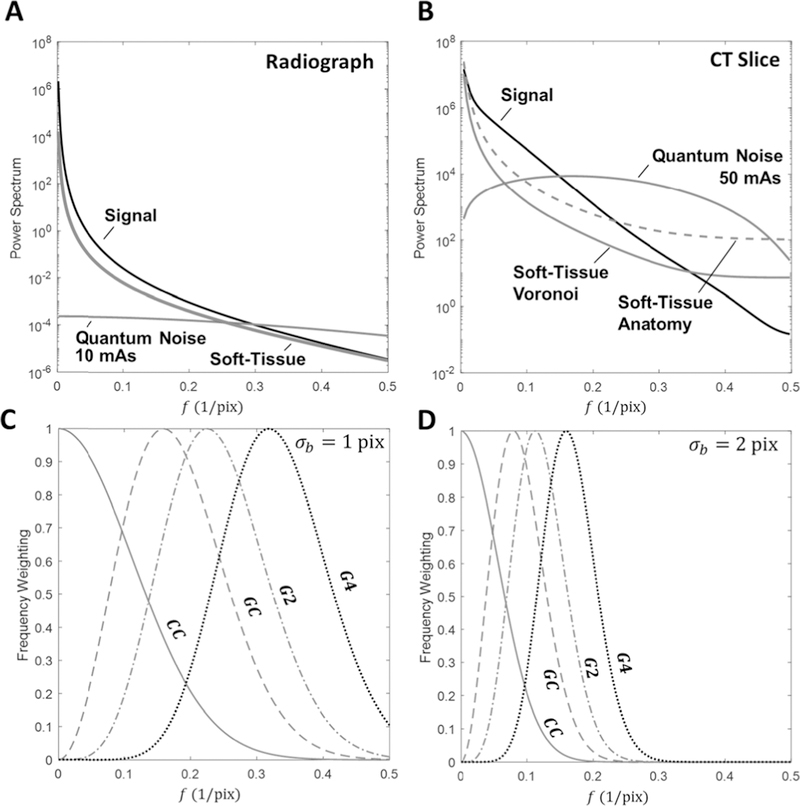
allowing one to model the performance of higher-order gradient similarity metrics (referred to as Gn, e.g., G2, G4, etc.). As shown below, the generalized form is useful in selecting specific spatial-frequency bands to weight in the registration process, with peak weighting about:
| (11) |
and with frequency band width proportional to 1/σb.
III. Model for Soft-Tissue Deformation
A. Soft-Tissue Deformation as a Noise Source
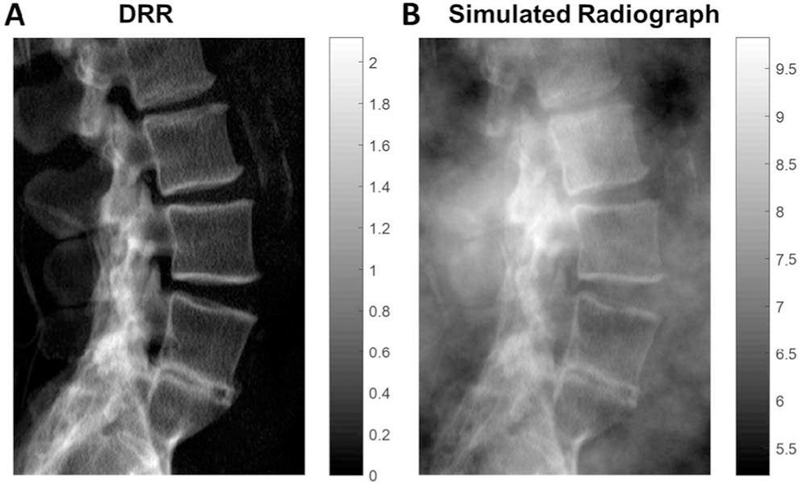
We consider two cases of soft-tissue deformation, the first being 3D-2D registration [11], [21] in which a 2D digitally reconstructed radiograph (DRR) is computed from a 3D CT volume and aligned to a radiograph as illustrated in Fig. 1. (Note that this process corresponds to projection-based 3D-2D registration, not slice-to-volume registration). Throughout this work, projection images – radiographs or DRRs – are referred to as 2D, and volumetric images – namely CT – are termed 3D, even with respect to a single slice of a CT volume. In 3D-2D registration scenarios, the impact of soft-tissue deformation on registration of bone anatomy can be large, since thick regions of soft tissue carry a high degree of power in the image (obscuring even bone), and deformations can be large (since the patient moves between 2D and 3D imaging systems). To compensate for this, soft tissue is often thresholded out of the CT image (by intensity threshold) before generating the DRR, presenting an “absence” of soft-tissue compared to the radiograph. Since the soft-tissue is present in only one image, it acts as an independent additive noise source described by (1–2) and can be easily incorporated in the model by modifying the noise-term (n2, taking the radiograph to be I2) to contain both quantum noise (q2) and soft-tissue anatomical noise (s2), giving . A statistical model for s2 is described in §II.B. With n2(x, y) defined in this manner, g(x, y) represents just the bone anatomy, and n1(x, y) represents the quantum noise projected in the DRR.
Fig. 1.
3D-2D registration. (A) Lateral DRR computed from a CT image thresholded to remove soft tissue. (B) Lateral radiograph (in this case, simulated from the DRR in (A) plus power-law soft-tissue anatomical noise).
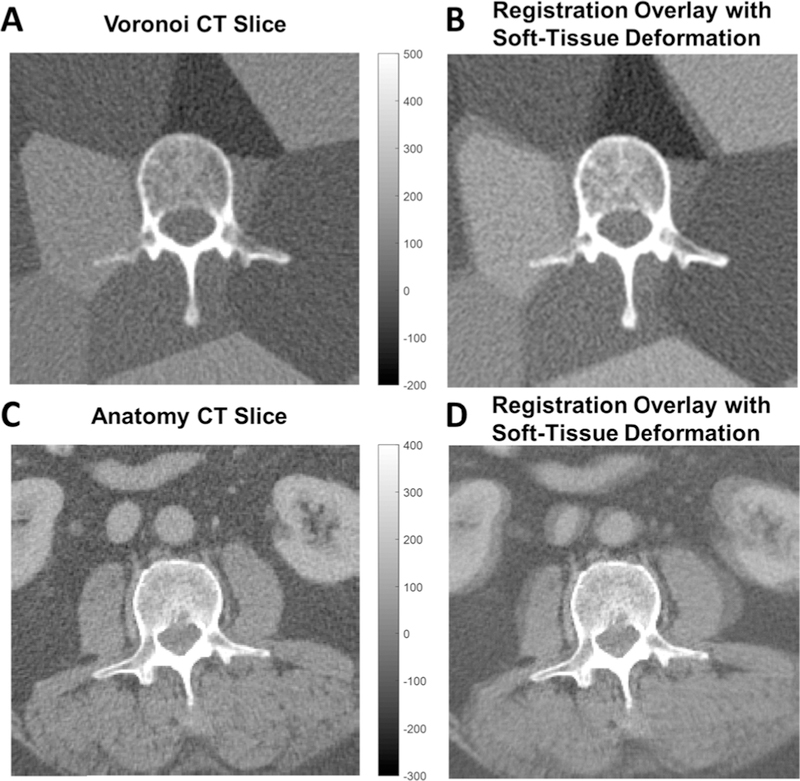
The second case considers soft-tissue deformation in 3D-3D image registration, starting with the example of registering two axial CT slices, as illustrated in Fig. 2. Rigid registration in the presence of soft-tissue deformation still can accurately align bone anatomy (g(x, y)), leaving residual misalignment of the deformed soft-tissue. From an optimization standpoint, this misalignment of soft-tissue structures (depicted in the colorwash of Fig. 2B,D) diminishes the similarity metric and reduces the quality of the search space, including introduction of false local minima. A problem introduced in modeling deformed soft-tissue as noise is that the noise terms in (1–2) are assumed independent, which is not the case in this scenario, since soft-tissue presenting in one image is just a deformed version of its manifestation in the other. However, if the deformation is large compared to the correlation length of the gradient image (i.e., high-gradient regions are no longer overlapping), then s1 (x, y) and s2 (x, y) can be treated as independent. Therefore, both images carry a noise term: . Note that in the case of no deformation, the soft-tissue function is rightly incorporated in the true signal as it contributes positively to the similarity metric.
Fig. 2.
3D-3D registration. (A) Axial CT with a rigid bone (vertebra) and simulated soft-tissue background approximated by a deformable Voronoi distribution of piece-wise constant regions. (B) Colorwash depicting misalignment (green/magenta) of soft tissues following rigid registration. (C) Axial CT image showing real anatomy (abdominal CT). (D) Colorwash depicting misalignment (green/magenta) of soft tissues following rigid registration.
B. The Soft-Tissue Power Spectrum
To incorporate the soft-tissue noise into the error models of (3–4), we need a model for the power spectrum of ni (x, y). We first note that under the assumption that the quantum noise and soft-tissue signals are independent, then the power spectrum of is the sum of the two power spectra, giving , where Qi is the quantum NPS and Si is the soft-tissue power spectrum. Quantum noise in radiographs and CT images have been well described by models of the quantum NPS, including factors determined by the acquisition technique (e.g., energy and exposure) and imaging system characteristics (e.g., blur, pixel size, and electronic noise) [22]–[24]. Furthermore, the power spectrum associated with cluttered scenes (e.g., soft-tissue anatomy overlying structures of interest) has been described from the standpoint of statistical decision theory in terms of a power-law distribution:
| (12) |
where and Sobj refers to the power spectrum of the object (cf., the image of the object, which is further attenuated by the MTF squared). The parameter αS is a scaling term proportional to the tissue contrast, βS governs the low-frequency extent, and f0 removes the discontinuity at f = 0 as discussed in [4], nominally set to be the inverse of the image width.
Depending on the type of anatomy and imaging modality, βS has been shown to be typically in the range of 2–4 [25]–[28], where larger values describe increasingly clumpier background texture. For example, the power-law distribution with βS = 3.6 yields the clumpy texture shown in Fig. 1B, which is similar in structure to anatomy presenting in a thoracic radiograph [26]. Further, studies comparing breast tissue background in projection and 3D imaging (typically shown to have βs = 3 in mammograms [25], [29]) revealed important general properties: 1) that a slice of a βs power-law image follows a power law of βs − 1; and 2) a projection of the image follows a power law of βs (note that both have dimensionality that is one less than the original image) [29], [30].
While previous work [10] modeling axial CT registration considered direct sampling from the power-law distribution yielding clumpy and cloudy texture appropriate for radiographic (Fig. 1B) and breast anatomy, the background texture associated with axial CT, however, tends to follow a piece-wise constant background. Therefore, we use simulated axial CT soft-tissue images that follow Voronoi distributions, with randomly placed seed points and piece-wise constant background defined by intensity values drawn from a uniform distribution over the range of soft-tissue Hounsfield unit values (shown in the background of Fig. 2A). While the Voronoi diagram is not a perfect model for solid-organ tissues in tomography (which do contain some level of heterogenous structure) it does provide a reasonable first-order approximation. To gain analytical insight on the power spectrum of the piece-wise constant Voronoi image, we begin by considering an analogous 1D case constructed by summing randomly scaled and shifted rect functions:
| (13) |
where T ~ Uniform(Tmin, Tmax ) and E{A2} is finite. By utilizing the Fourier pair relating the rect function to the sinc:
| (14) |
the expected power spectrum of is:
| (15) |
The first equality assumes independence of the summed rect functions, leaving only the summation of the expectations, and the multiplication of complex conjugates cancels the exponential terms. By writing out the sinc, we need only to compute the expectation of the sin2(·) term over T, giving:
| (16) |
which for large (Tmax − Tmin ), yields the result:
| (17) |
In 1D, therefore, this piece-wise constant function follows a power-law distribution with βs = 2.
We extend this derivation to 2D by approximating the Voronoi image as a sum of 2D rects with random rotation (θ):
| (18) |
Where X ~ Uniform(Xmin, Xmax ), Y ~ Uniform (Ymin, Ymax ), θ ~ Uniform (0, 2π). As shown in Appendix A, supported by numerical simulations, the resulting 2D power spectrum can be approximated by:
With
| (19) |
where the terms in µXY are the uniform distribution parameters on the rect widths. We see that (19) again follows a power law distribution, this time with βs = 3. In this way, the Voronoi image yields a random image model that is visually similar to the piece-wise constant background of soft-tissues presenting in axial CT and has a power spectrum in line with the models derived previously for detection of a signal against a lumpy background with βs = 3. Note that βs is independent of the number of rect functions (n) and widths, implying that a Voronoi image of any density of seed points follows a power law distribution with βs = 3. This point is confirmed by the power spectra measured for randomly generated Voronoi images described in §V.
Extension of the derivation to 3D Voronoi images is shown in the Appendix, yielding an approximate power spectrum:
| (20) |
where , and µXYZ is the mean over the 6 uniform distribution width parameters [similar to µXY in (19)], yielding βs = 4.
IV. Test Images
A. 3D-2D: DRR and Radiograph Images
We consider 3D-2D registration (translation-only) of a radiograph to a CT image via DRR. The DRR was generated from an abdominal CT volume (Somatom Definition, Siemens) with a 250 HU soft-tissue threshold and forward projection by trilinear interpolation as illustrated in Fig. 1A. Simulated radiographs (Fig. 1B) were generated by computing separate forward projections and adding a power-law-distributed random image sample to simulate overlying soft-tissue and injecting quantum noise correlated by the system MTF. Two CT noise realizations were generated (as described in IV.B) to ensure that the CT-derived quantum noise was independent between DRRs and simulated radiographs. This method allows generation of many images for performing registration (each having different realizations of soft-tissue content) while maintaining a known ground-truth transformation.
The soft-tissue background was generated from the power law distribution with βs = 3.6 (as in Fig.1B), yielding a distribution that is visually similar and, more importantly, statistically matches that observed in tomographic images of real anatomy [26]. This background image was scaled and re-centered so that the mean approximated attenuation by 30 cm of water with a standard deviation equal to 5% of the mean. The power-law soft-tissue image was added to the DRR, and quantum noise was simulated using the SPEKTR toolkit [31] to determine the x-ray fluence at the detector for a specified dose, determined by the x-ray tube output (current – time product, mAs) and beam energy. The transmitted fluence was sampled according to a Poisson distribution to simulate quantum noise, and the image was filtered according to a Lorentzian MTF to simulate scintillator blur [32], yielding simulated radiographs as shown in Fig. 1B. The resulting images were 768 × 512 pixels with 0.279 mm pixel size. This process was repeated for 100 instances of power-law soft tissue realizations and 11 dose levels (ranging 0.005–500 mAs).
B. 3D-3D: Voronoi CT-CT Slice Images
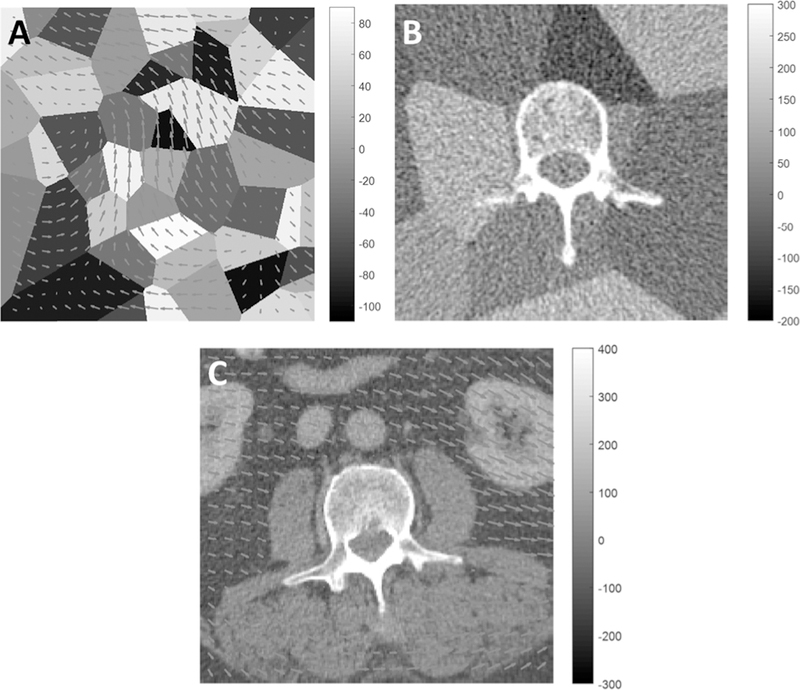
CT slices featuring rigid bone and deformable soft tissue were simulated as illustrated in Fig. 2B. Soft tissue was represented by Voronoi distributions from 50 randomly placed seed points in the 512 × 512 image, each assigned HU values in the range −110 HU to +90 HU in a uniform random distribution. A rigid bone region was inserted using a segmented CT image of a human lumbar vertebra, and the image was cropped to a 32 cm diameter cylinder (typical scale for body CT). Prior work [10] examined registration of images containing independently generated soft-tissue backgrounds, and the work reported below examines the effect of deformation at different degrees of deformation magnitude. To obtain a realization of the same image with soft-tissue deformation, the Voronoi image (prior to inserting the bone segmentation) was subjected to a smooth, random displacement field (Fig. 3A) also defined by a low-frequency power-law distribution (β = 4.5) in displacement vectors in the x and y directions, with α scaled to achieve various magnitudes of deformation.
Fig. 3.
Images depicting rigid bone (vertebra) and deformable soft-tissue background. (A) Displacement field overlaid on a Voronoi soft-tissue model. (The example shows a mean displacement of 7 pixels). (B) Example vertebra + Voronoi image showing a realistic level of correlated noise in CT. (C) Anatomical image (abdominal CT) overlaid with an example deformation field (mean displacement 7 pixels). A mask was applied to ensure rigid motion within the bone region.
Quantum noise in the CT image was simulated by injection of Poisson noise proportional to (with nominal scatter-to-primary ratio SPR = 2). The SPEKTR toolkit [31] was used as in §IV.A to determine the fluence for a specified dose for mAs levels ranging 5–1500 mAs (for a 120 kV beam). Projection images (720 images over 360°) were generated from the attenuation values in the CT image and used to compute the expected number of detected photons for each pixel, which was taken as the mean (i.e., lambda) parameter for Poisson sampling at each pixel. Noisy projection images were then reconstructed by filtered backprojection using a Hann apodization filter with a cutoff frequency of 0.8 × fnyq. An example image is shown in Fig. 3B.
C. 3D-3D: Anatomy CT-CT Slice Images
Realistic anatomy depicted in abdominal CT (Fig. 2C, a patient image from an IRB-approved study) was regenerated at various dose and deformation levels to test the statistical model on real soft-tissue anatomy. The deformation and noise injection process described in §IV.B was repeated for this CT image, and the region corresponding to the vertebra was masked to ensure zero motion within the bone and smooth reduction of the motion vector field magnitude near the bone boundary (Fig. 3C).
V. Power Spectral Estimates
The power spectrum estimates for signal (G) and noise (Si, and Qi ) entering the model of (3–4) are described below for both 3D-2D and 3D-3D registration scenarios. For a given signal- and noise-only image [g(x, y) and s (x, y) + q (x, y), respectively], the power spectrum was estimated by 2D Welch periodogram estimation (3 windows in each direction with 50% overlap) [33] with Hann tapering windows. Models for the power spectra of anatomy [both G (fx, fy) and S (fx, fy)] were based on the estimated periodograms and the well-studied power-law properties of soft-tissue described in §III.B. Models for quantum NPS were based on physical models that describe quantum noise propagation in radiographic [32] and CT [22], [24] imaging systems. In radiographic systems, dominant contributors to the NPS are scintillator blur and the detector aperture, the MTF of which may be modeled as a Lorentzian times a sinc [32]. In CT, dominant contributors to the NPS further comprise the ramp filter, apodization filter, and aliasing. The NPS therefore included a ramp multiplied by the square of the MTF (Hann apodization filter) and an additive constant. The models and parameters are summarized in Tables I and II. Parameters for G and Si were assumed independent of dose, whereas quantum noise parameters were computed at each dose level.
TABLE I.
Power Spectrum Models for DRRs and Radiographs
| 3D-2D: DRR (I1) to Radiograph(I2) | |
|---|---|
| Signal (Bone) Spectrum | |
| Soft-Tissue Spectrum | |
| Quantum Noise | |
| MTF |
TABLE II.
Power Spectrum Models for CT Slice
| 3D-3D: CT-to-CT Slice | |
|---|---|
| Signal (Bone) Spectrum | |
| Soft-Tissue Spectrum | |
| Quantum Noise | |
| MTF |
A. DRR (I1) and Radiograph (I2)
For the 3D-2D case, the true signal image g(x, y) was given by the DRR, and its estimated periodogram was fit via the model in Table I. The DRR carries a small amount of CT-derived quantum noise which was assumed negligible in fitting G (fx, fy) but should still be accounted in Q1 (fx, fy). Based on the projection-slice theorem, Q1 is related to a slice of the CT NPS; however, this CT-derived quantum noise was small in magnitude compared to the signal, and the model simply approximated Q1 as a constant (cQ). To determine this constant, two DRRs from two CT instances (§IV.A) were subtracted to yield a noise-only image. A periodogram of the difference image (corrected by a factor ) was estimated and the constant was set to the mean over this periodogram.
The soft-tissue βS was taken from the radiograph simulations (§IV.A) leaving the power-law scaling parameter (αS) and the quantum noise parameters (αQ) to be fit. Periodograms from 100 radiographs (with DRR subtracted to yield soft-tissue + quantum noise only images) were averaged to obtain power spectrum estimates at each dose level. Fits for αS and αQ were performed jointly for the highest dose power spectrum, and the resulting αS was fixed in fitting αQ at other dose levels.
B. CT Slice
The bone-only g(x, y) images for the Voronoi 3D-3D case were formed from the mean of 100 CT images (10 quantum noise realizations for 10 different Voronoi backgrounds) at each dose level. The g(x, y) from the highest dose level was used to compute the periodogram for G(x, y) which was fit to a power-law + exponential function as shown in Table II. This step was repeated to obtain G(x, y) for the bone in the anatomy 3D-3D case using 50 images (each with new noise and deformation).
Based on power spectrum analysis in Appendix A, βS = 3 was used for the soft-tissue parameter value for both the Voronoi and anatomy images. The remaining noise parameters were determined by fits to estimated Si + Qi spectra at each dose. Power spectra for each dose level were estimated by averaging the periodograms of 100 CT slices (50 in the anatomical case) with g(x, y) subtracted (leaving s (x, y) + q (x, y)). Again, αS was determined in a joint fit with the quantum noise parameters at the highest dose level, and the value was fixed when fitting the quantum noise parameters for lower dose levels.
VI. Experimental Methods
A. Registration Experiments
For each image pair in the following registration scenarios, an initial translation of τ = [1.2 pix, 1.2 pix] (registration was observed to be insensitive to small changes in initial shift value) was imparted in the moving image prior to registration using cubic B-spline interpolation. Following the shift, translation-only rigid registration was performed in SimpleITK [34] using each of the similarity metrics (CC, GC, G2, or G4 as described in §II) at σb levels ranging from 1 to 4 pixels in 0.5 increments. As gradient-based similarity metrics were not implemented in SimpleITK, an analytical equivalent was implemented by noting from (8) that these metrics can be achieved by prefiltering the images to achieve the frequency weighting in (10) (by filtering both images according to the square root of HGn) and using the built-in normalized cross-correlation metric (NCC) in SimpleITK. NCC differs slightly from CC (7) in that the images are renormalized at each spatial shift according to the values in the overlapping regions; however, the normalization primarily serves to reduce the influence of local optima rather than improve accuracy at the true solution (which is reflected in (3–4) as both are unaffected by DC shifts and scaling).
For each similarity metric (i.e., n in ), the optimal blur was determined by minimizing (4) with respect to σb, and the observed RMSE at that blur level was compared to both the RMSE predicted by (4) and the CRLB in (3) (which is independent of σb). Computation of (3–4) was achieved using the power spectrum model fits discussed in §V. Cases of registration failure were observed to occur for σb < 1 pix or in cases for which fpeak [described in (11)] was larger than approximately half the Nyquist frequency; therefore, optimization of σb was constrained to satisfy these requirements. Image edge effects introduced by prefiltering were avoided by excluding image boundary regions during registration.
1). 3D-2D Registration (Effect of Dose):
DRR-to-radiograph registration error was examined as a function of radiograph dose, ranging 0.005–500 mAs. For each dose level, 100 simulated radiographs (§IV.A), each with different quantum and soft-tissue realization, was registered to the bone-only DRR using CC, GC, G2, and G4. RMSE was computed for each dose level and compared to the predicted RMSE and the CRLB.
2). Voronoi 3D-3D Registration (Effect of Dose):
Voronoi CT-CT slice registration error was examined as a function of dose over the range 5–1500 mAs. For each of 10 Voronoi images, 10 displacement fields (mean displacement magnitude of ~7 pix) were applied to generate 110 CT slices (100 deformed, 10 with original Voronoi) at each dose level. Each of the deformed images was registered to the undeformed slice at the matching dose level using CC, GC, and G4. RMSE at each dose level was compared to the predicted RMSE and CRLB.
3). Anatomy 3D-3D Registration (Effect of Dose):
Anatomy CT-CT slice registration error was examined as a function of dose over the range 5–1500 mAs. At each dose level, 10 non-deformed noisy images were generated and registered to 10 deformed images generated at the same dose level, yielding 100 registrations for each dose level. The RMSE for CC, GC, and G4 was compared to the predicted RMSE and CRLB. The experiment was performed for two conditions of deformation magnitude with mean displacement magnitude of ~7 pix and 22 pix.
4). Voronoi 3D-3D Registration (Effect of Deformation Magnitude):
Voronoi CT-CT slice registration error was examined as a function of the soft-tissue deformation magnitude. The experiment of §VI.A.2 was repeated (at 250 mAs dose level) for 12 levels of displacement field magnitude by varying α in the power-law derived displacement fields to yield mean pixel displacement magnitude ranging from ~0.01 to 22 pix.
Registration results were compared to RMSE predictions and RMSE measurements in registered images containing different Voronoi backgrounds (such that the soft-tissue noise terms were truly independent) to check the extent of deformation necessary to justify the assumption of independence. Registrations were performed for each of the 10 no-deformation CT slices (each with a different Voronoi background), yielding 45 (i.e., 10-choose-2) registrations to examine RMSE for CC, GC, and G4.
5). Anatomy 3D-3D Registration (Effect of Deformation Magnitude):
Anatomy CT-CT slice registration error was examined as a function of the soft-tissue deformation magnitude. The experiment of §VI.A.3 was repeated (at the 250 mAs dose level) for 14 levels of displacement field magnitude by varying α in the power-law displacement fields to yield mean pixel displacement magnitude ranging from ~0.01 to 22 pix. Registration results were compared to RMSE predictions for each similarity metric (CC, GC, and G4).
B. Effect of Soft-Tissue Characterization (αS and βS)
The soft-tissue power-law parameters (αS and βS) can vary as a function of both the contrast and texture of the soft-tissue. Increasing αS leads to a greater soft-tissue intensity range. Increasing βS leads to cloudier, more smoothly varying texture, whereas reducing βS yields higher-frequency content (and βS = 0 giving white noise). Such texture changes may be associated with changes in anatomical region (e.g., abdominal anatomy vs. breast tissue) or the use of a different imaging modality (e.g., radiography vs. CT or ultrasound). To understand the role of these parameters on registration performance, we used (4) to predict the registration error for CC, GC, and G4 (at optimal σb) as a function of these soft-tissue power-law parameters. For both 3D-2D and 3D-3D scenarios, we fixed the model parameters described by Tables I–II at several dose levels and separately varied αS and βS. As αS values are not comparable for different values of βS, the αS value was scaled to achieve the same area under the curve (energy) of the original power-law distribution.
VII. Results
A. Registration Results: Comparison of Theory and Measurement
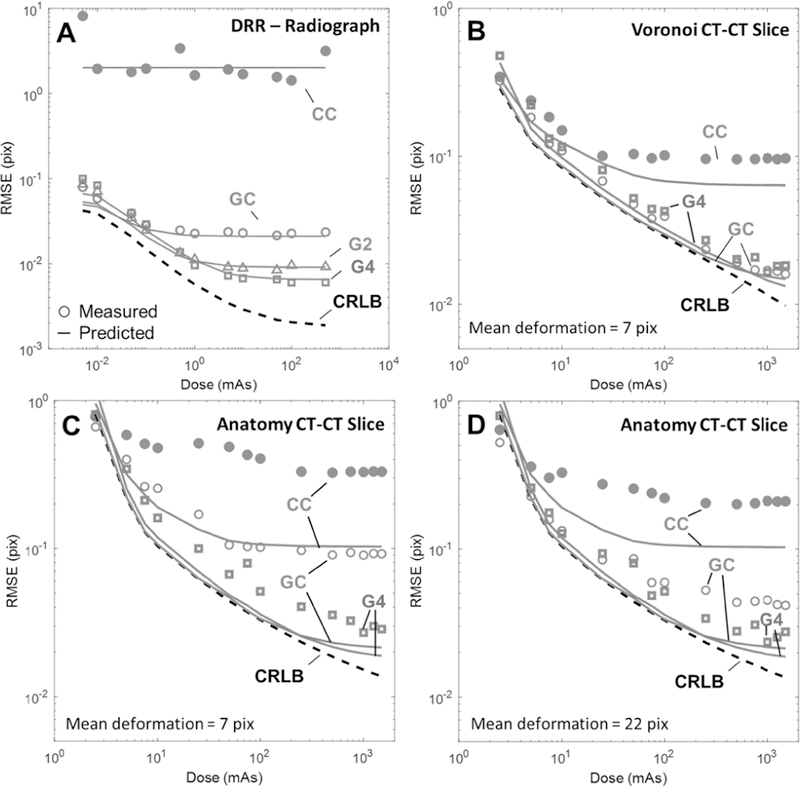
Fig. 4A shows 3D-2D registration error as a function of dose for 4 similarity metrics. Solid lines depict the predicted RMSE via (4) for each metric at optimal σb (computed for each dose level and metric), and the markers represent the experimental error using that σb. Immediately apparent is the large performance gap between CC and gradient-based metrics, with CC showing more than an order-of-magnitude greater error than the other metrics. Further, CC performance appears to be soft-tissue limited in that increased dose (and thus reduced quantum noise) does not yield improved registration accuracy. For the gradient-based metrics, however, RMSE decreases as a function of dose over the range ~0.005–1 mAs and follows the trend set by the CRLB (dashed line). For higher dose, a plateau in RMSE is exhibited for all metrics (and the CRLB), again indicating that the registration is limited by soft-tissue noise rather than quantum noise. The best registration error was obtained using the G4 metric, giving RMSE = 0.006 pix, (compared to the CRLB = 0.003 pix) at the 500 mAs dose level.
Fig. 4.
Effect of dose on registration performance for (A) 3D-2D registration and (B) Voronoi 3D-3D registration with 7 pix mean deformation, and anatomy 3D-3D registration with (C) 7 pix mean deformation and (D) 22 pix mean deformation. Each plot shows the predicted error for each metric at optimal σb (solid lines), the measured error for each metric at that σb (markers), and the CRLB (dashed line). Similarity metrics examined included CC (red), GC (blue), G2 (magenta), and G4 (green).
Fig. 4B shows Voronoi 3D-3D registration error as a function of dose for CC, GC, and G4 similarity metrics in the presence of soft-tissue deformation. Each metric exhibits a similar plateau as seen above; however, CC plateaus at a much lower dose level than GC, G4 (~25 mAs vs. ~1000 mAs). Interestingly, GC (only slightly outperforming G4) nearly achieves the CRLB over all dose ranges tested, indicating near optimality as a metric for the soft-tissue deformation scenario.
Fig. 4C,D shows anatomy 3D-3D registration error in the presence of soft-tissue deformation with mean deformation magnitude of 7 mm and 22 mm, respectively. RMSE is shown as a function of dose for CC, GC, and G4 similarity metrics. Interestingly, the agreement between theory and measurement improve with the magnitude of displacement – with predictions underestimating the measurements at 7 pix displacement and agreeing well for larger displacement (e.g., 22 pix deformation). It is important to note that the predicted RMSE is identical for the two plots in Fig. 4C,D, showing that the measured RMSE for CC and GC improves greatly in the presence of increased soft-tissue deformation. Meanwhile, the G4 metric shows good agreement between measurement and prediction for both the small and large deformation scenarios. Together, this indicates that small deformations in the case of real anatomy (c.f., the sharp edge scenario of the Voronoi images) do not sufficiently decorrelate the soft-tissue background for the CC and GC metrics, and the lack of non-correspondence in soft-tissue backgrounds degrades the search space. The G4 metric, however, emphasizes finer gradient features, and a smaller magnitude of deformation is sufficient for corresponding background structures to become uncorrelated, thereby improving the search space quality and improving registration accuracy.
It is important to keep in mind that for both scenarios of soft-tissue noise (i.e., soft-tissue absence in 3D-2D and soft-tissue deformation in 3D-3D), the model predictions were achieved by simply incorporating soft-tissue as a power-law noise distribution in (3–4). Further, in both scenarios the predictions and experiments showed improved performance when using the gradient-based similarity metrics. This is particularly interesting when compared to results in the following section which show that CC outperforms GC when no deformation is present. To understand this change in the preferred metric, it is important to examine the power spectra of both the signal and noise terms as seen in Fig. 5 and to compare these spectra with the frequency weighting that each metric provides. In the presence of quantum noise alone, it is clear from Fig. 5A–B that there is a large signal-to-noise ratio near the zero-frequency region; therefore, it is intuitive that CC (which weights the low-frequency band) is the preferred metric. However, in the presence of soft-tissue deformation (modeled as low-frequency noise), the low-pass nature of the power-law soft-tissue spectrum leads to a sharp reduction in signal-to-noise ratio near zero frequency. Therefore, using gradient-based metrics, which down-weight the near-zero frequency regions, is preferred.
Fig. 5.
Power-spectrum profiles for the signal (black), soft-tissue (red), and quantum noise (blue) terms fit to (A) Radiograph (10 mAs) and (B) Voronoi CT slice (50 mAs) image data (with an additional dashed line profile of the soft tissue anatomy spectrum) using the models in Tables I–II. Registration frequency weighting profiles using Eq. 10 for CC (red), GC (blue), G2 (magenta), and G4 (black) at (C) σb = 1 pix and (D) σb = 2 pix.
B. Effect of Deformation Magnitude
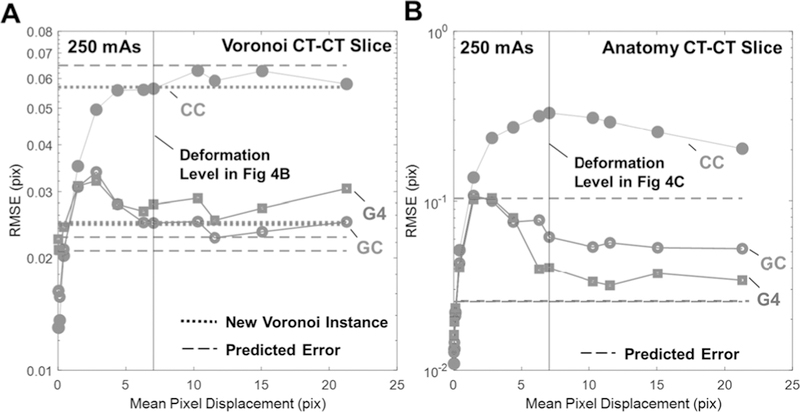
Fig. 6A shows Voronoi CT-CT slice registration error as a function of the mean magnitude of pixel displacement in deforming soft tissue. The results are compared with the dashed lines that show predicted RMSE and dotted lines showing experimental registration performance for images with different realizations of Voronoi background (i.e., independent soft-tissue noise terms). The lowest registration error was observed for cases of minimal deformation, since soft tissue anatomy contributes to accurate alignment in such cases. Furthermore, in the absence of deformation (in which case the underlying images differ only by quantum noise), CC is found to be the optimal metric. However, as deformation magnitude increases, registration error increases up to a plateau near 5–6 mean pixel displacement, showing that beyond a certain level of deformation, when the soft-tissue backgrounds are sufficiently decorrelated, the magnitude of deformation has little effect on the registration error. For both metrics, the plateau occurs at the error level observed when registering newly-generated independent Voronoi backgrounds, supporting the assumption that, under large deformations, the soft-tissue can be treated as an independent noise term. It is also interesting to note the hump in RMSE for GC, which is attributable to local optima created when gradient-based metrics are used with small deformation.
Fig. 6.
3D-3D registration error as a function soft-tissue deformation magnitude for CC (red, solid circle), GC (blue, open circle), and G4 (green square) for (A) Voronoi and (B) anatomy CT-CT slice registration. Dashed lines show the predicted registration performance of Eq. 4 for each metric. Dotted lines in (A) depict the registration performance for each metric when registering CT slices that contain different (independent) instances of Voronoi soft-tissue background.
Fig. 6B similarly examines the impact of deformation magnitude for anatomy CT-CT slice registration. A similar behavior to the Voronoi results is observed for deformation <5 pix, and the measured RMSE values plateau at much higher levels of deformation than in Fig. 6A, particularly for the CC and GC metrics. Interestingly, it appears that the speed of convergence is related to the metric order, with G4 plateauing faster than GC, which in turn converges faster than CC. We observe this effect also in Figs. 4 C–D, where smaller deformation magnitude was needed for the soft-tissue background to be sufficiently decorrelated when using higher-order gradient metrics.
C. Effect of Soft-Tissue Characteristics (αS and βS) on Registration Performance
Figure 7A shows the predicted 3D-2D RMSE at optimal σb for CC (red), GC (blue), and G4 (green) as a function of soft-tissue magnitude (αS) for 2 dose levels. At small αS (thus dominated by quantum noise) CC slightly outperforms the others and registration performance is quantum limited, with changes in αS having little or no effect on registration. As αS increases, however, (yielding stronger contrast from soft-tissue) GC becomes the preferred metric due to its effective down-weighting of low frequency noise content. As αS becomes large, G4 becomes the preferred metric and the RMSE converges for all dose levels, indicating that the performance is limited by soft-tissue deformation. Similar behavior is observed in Fig. 7B for 3D-3D registration.
Fig. 7.
The effect of the deformed soft-tissue contrast term, αS, on registration performance. Predicted RMSE at optimal σb shown for CC (red), GC (blue), and G4 (green) at various dose levels for (A) DRR-radiograph and (B) voronoi CT-CT slice registration.
Figure 8A shows the effect of βS (at fixed total power) on the performance of CC, GC, and G4 similarity metrics for 3D-2D registration. At βS = 0 (i.e., white noise) CC is the preferred metric, since the NPS does not peak near zero frequency. As βS increases, however, soft-tissue noise occupies the same frequency region as the signal term, leading to increased error for all metrics. For further increase in βS (and the soft-tissue power spectrum is concentrated near the zero frequency) we see that error decreases for the GC and G4 metrics, since they effectively attenuate the increasingly low-frequency soft-tissue noise. The performance of CC, however, plateaus at a much higher RMSE and has no dose dependence, illustrating that soft-tissue deformation dominates CC registration performance. Figure 8B shows a similar non-monotonic trend for the GC and G4 case in 3D-3D registration. Interestingly in both scenarios, the highest CRLB error is seen for βS in the range of 1–2. This can be understood by comparison of (3) with signal power spectra of Fig. 5A–B, where we see from the term in (3) that higher frequencies provide quadratically more information in registration (with the DC component providing no information). However, in Fig. 5A–B we see that the signal power spectrum is concentrated in the low frequency range, which combined with the weighting, implies that the mid-to-low frequencies effectively provide the most information for registration. Therefore, soft-tissue noise with βS ~ 1–2 presents the most confounding influence in the mid-to-low frequency range. Higher values of βS concentrate the noise in the low-frequency region, and lower values of βS pushes the noise to the higher frequency range, where there is little signal power.
Fig. 8.
The effect of the deformed soft-tissue texture term, βS, on registration performance. Predicted RMSE at optimal σb shown for CC (red), GC (blue), and G4 (green) at various dose levels for (A) DRR-radiograph and (B) voronoi CT-CT slice registration.
VIII. Conclusion
This work demonstrates a model for rigid registration performance including soft-tissue deformation as a noise source. By adopting concepts from signal detection theory in modeling soft tissue by a power-law spatial-frequency distribution and incorporating it in a statistical framework for registration error, we quantify the influence of factors such as dose, noise, and choice of similarity metric on registration performance. In particular, CC-based and gradient-based metrics were shown to differ according to their frequency domain weighting of the signal, quantum noise and soft-tissue power spectra.
This work investigates the extent to which large magnitude soft-tissue deformation can be treated as “noise” in the model for rigid registration performance. Of course, soft-tissue deformation is not a random process, but the abstraction was shown to hold reasonably well for large deformations giving rise to large regions of non-corresponding tissue overlap. This in turn was shown to be modeled well as noise in the RMSE for various similarity metrics. We further showed (Fig. 6A) that large deformations yield the same RMSE as that for registering images with independent realizations of soft-tissue background (which closely follows the assumption of an independent noise source), supporting the notion that soft-tissue deformation may be incorporated as a confounding influence (viz., noise) in rigid registration. It is important to note that deformation magnitude should be much larger than the correlation length of the soft-tissue gradient image (such that high-gradient regions are no longer overlapping). The study shown above (§VII.B) investigated the magnitude of deformation required to justify this claim for Voronoi images in the 3D-3D case, where mean deformation magnitudes >5 pix yielded the same error as the independent background case. However, the Voronoi images contain sharp gradients which have small correlation length (on the level of system blur, ~2 pix) due to the step-function nature of the model. For the anatomy CT-CT registration case (which exhibited somewhat longer-range correlations in the gradient images compared to the Voronoi case) larger deformations were necessary to support the assumption of independence. Interestingly, however, the long-range gradient correlations in such images were suppressed by gradient-based similarity metrics (especially G4), thereby greatly reducing the magnitude of deformation that was necessary for the independence assumption. Finally, it is important to note that this assumption is not necessary in the 3D-2D registration case, since soft tissue is only present in one of the images.
The experiments in this work examined x-ray projection (3D-2D) and CT images (3D-3D). The framework, however, is certainly generalizable in the 3D-3D case to other same-modality registration scenarios (e.g., magnetic resonance, MR-MR, or ultrasound, US-US), as long as the underlying image content is consistent, and the noise is properly characterized. While the projection-based 3D-2D registration is unique to x-ray/CT, the model may generalize to other 3D-2D scenarios (e.g., US slice-to-volume). Multi-modality registration is not considered in the current work, as significant modification to the statistical model would be required to capture the mismatch in the image content.
The method for simulating soft-tissue deformation in this work (§IV.B) involved a random displacement that was not physically / biomechanically motivated and may imply somewhat unrealistic deformation characteristics. For example, since the displacement fields were randomly generated from a power-law distribution, there is no guarantee that the transformations are Sdiffeomorphic; despite this, we observed that the method did indeed exhibit diffeomorphic properties (positive Jacobian determinant) over the range of deformation magnitude considered. (Non-diffeomorphic fields were observed for mean pixel displacement greater than 23 pix). Another potential limitation in the simulation is the lack of a biomechanical model to constrain deformation magnitude – for example, constraining deformation to be small near bone-tissue interfaces (attachment). Doing so would suggest that some soft-tissue (i.e., that near bone) should not be treated as noise and should be included as salient features for registration. A simple method to accomplish this would be to split the soft-tissue power spectrum across N and G, with and , where a ϵ [0, 1] represents the portion of non-deformed soft tissue. However, such a model is outside of the scope of this work.
The equations in Tables 1–2 represent anatomy, soft-tissue clutter, and quantum noise described by circularly symmetric power spectra for purposes of simplicity. The isotropic assumption is not central to the methods described above, and while such models provided reasonable fits to the experiments conducted in this work, anisotropic power spectra can straightforwardly be incorporated in the framework. Scenarios that may warrant such models include anatomy presenting strong directionality (e.g., 3D ductal breast tissue [35]) or CT quantum noise that can be strongly correlated in non-circular objects and/or with x-ray tube mA modulation techniques.
In the current work, the statistical framework describes the translation-only case in order to gain basic insight into more general scenarios. Extension to the rigid translation + rotation scenario adds a degree of freedom and should follow the framework described above in principle, but with considerably more complex error terms associated with rotation. While the effect of soft-tissue deformation on rigid registration was examined in this work, it is important to note that the current framework does not apply to deformable registration. Future work aims to extend the analysis to scenarios of deformable registration in which both bone and soft tissue present salient information in the registration process.
Acknowledgments
The research was supported by NIH grant R01-EB-017226 and research collaboration with Siemens Healthineers (XP and AT groups, Forcheim Germany).
Appendix A
A. Voronoi Power Spectrum in 2D
Consider the distributions X ~ Uniform(Xmin, Xmax ), Y ~ Uniform (Ymin, Ymax ), θ ~ Uniform(0, 2π), and E{A2} to be finite. As the Fourier transform of a rotated function is simply the rotation of the Fourier transform, we begin by computing the power spectrum of unrotated rect functions and then compute the expectation over θ in Fourier space:
| (A1) |
Rewriting in polar coordinates and simplifying, we have:
| (A2) |
where the expectation of the inner function is computed over X, Y, and θ. Numerical simulation showed this expectation to closely follow:
| (A3) |
for large values of (Xmax − Xmin) and (Ymax − Ymin), where we simplify notation by using µXY to refer the mean over the uniform random variable parameters for the rect widths, giving:
| (A4) |
B. Voronoi Power Spectrum in 3D
Extending the analysis to 3D rect functions begins by incorporating spherical rotations so that:
| (A5) |
The distributions of the random variables are identical to the 2D case, where now Z ~ Uniform (Zmin, Zmax ) and φ ranges from 0 to 2π and follows a distribution with a cumulative distribution function F (φ) = (1 − cos (φ))/2 so that the spherical rotations uniformly sample the sphere. Similarly:
| (A6) |
By converting to spherical coordinates, numerical simulation shows the expectation to closely follow the form:
| (A7) |
where f is now the 3D Euclidian distance and µXYZ is mean over the 6 uniform distribution width parameters.
Contributor Information
Michael D. Ketcha, Department of Biomedical Engineering, Johns Hopkins University, Baltimore, MD 21205 USA.
Tharindu De Silva, Department of Biomedical Engineering, Johns Hopkins University, Baltimore, MD, 21205 USA..
Runze Han, Department of Biomedical Engineering, Johns Hopkins University, Baltimore, MD, 21205 USA..
Ali Uneri, Department of Biomedical Engineering, Johns Hopkins University, Baltimore, MD 21205 USA..
Sebastian Vogt, Siemens Healthcare XP, Erlangen 91052, Germany..
Gerhard Kleinszig, Siemens Healthcare XP, Erlangen 91052, Germany..
Jeffrey H. Siewerdsen, Department of Biomedical Engineering, Johns Hopkins University, Baltimore, MD 21205 USA.
References
- [1].Ketcha MD, De Silva T, Han R, Uneri A, Goerres J, Jacobson MW, Vogt S, Kleinszig G, and Siewerdsen JH, “Effects of Image Quality on the Fundamental Limits of Image Registration Accuracy,” IEEE Trans. Med. Imaging, vol. 36, no. 10, pp. 1997–2009, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Burgess AE and Judy PF, “Signal detection in power-law noise: effect of spectrum exponents,” JOSA A, vol. 24, no. 12, pp. B52–B60, 2007. [DOI] [PubMed] [Google Scholar]
- [3].Eckstein MP, Abbey CK, and Bochud FO, “Visual signal detection in structured backgrounds. IV. Figures of merit for model performance in multiple-alternative forced-choice detection tasks with correlated responses,” JOSA A, vol. 17, no. 2, pp. 206–217, 2000. [DOI] [PubMed] [Google Scholar]
- [4].Burgess AE, “Visual signal detection with two-component noise: low-pass spectrum effects,” JOSA A, vol. 16, no. 3, pp. 694–704, 1999. [DOI] [PubMed] [Google Scholar]
- [5].Richard S and Siewerdsen JH, “Optimization of dual-energy imaging systems using generalized NEQ and imaging task,” Med. Phys, vol. 34, no. 1, pp. 127–139, 2007. [DOI] [PubMed] [Google Scholar]
- [6].Siewerdsen JH and Jaffray DA, “Optimization of x-ray imaging geometry (with specific application to flat-panel cone-beam computed tomography),” Med. Phys, vol. 27, no. 8, p. 1903, 2000. [DOI] [PubMed] [Google Scholar]
- [7].Gang GJ, Siewerdsen JH, and Stayman JW, “Task-Driven Optimization of Fluence Field and Regularization for Model-Based Iterative Reconstruction in Computed Tomography,” IEEE Trans. Med. Imaging, vol. 36, no. 12, pp. 2424–2435, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Burgess AE, “Statistically defined backgrounds: performance of a modified nonprewhitening observer model,” JOSA A, vol. 11, no. 4, pp. 1237–1242, 1994. [DOI] [PubMed] [Google Scholar]
- [9].Rolland JP and Barrett HH, “Effect of random background inhomogeneity on observer detection performance,” JOSA A, vol. 9, no. 5, pp. 649–658, 1992. [DOI] [PubMed] [Google Scholar]
- [10].Ketcha MD, De Silva T, Han R, Uneri A, Jacobson MW, Vogt S, Kleinszig G, and Siewerdsen JH, “A statistical model for image registration performance: effect of tissue deformation,” Proc. SPIE, vol. 10574, 2018. [Google Scholar]
- [11].Penney GP, Weese J, Little JA, Desmedt P, Hill DLG, and others, “A comparison of similarity measures for use in 2-D-3-D medical image registration,” IEEE Trans. Med. Imaging, vol. 17, no. 4, pp. 586–595, 1998. [DOI] [PubMed] [Google Scholar]
- [12].De Silva T, Uneri A, Ketcha MD, Reaungamornrat S, Kleinszig G, Vogt S, Aygun N, Lo SF, Wolinsky JP, and Siewerdsen JH, “3D-2D image registration for target localization in spine surgery: investigation of similarity metrics providing robustness to content mismatch,” Phys. Med. Biol, vol. 61, no. 8, p. 3009, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Yetik IS and Nehorai A, “Performance bounds on image registration,” IEEE Trans. Signal Process, vol. 54, no. 5, pp. 1737–1749, 2006. [Google Scholar]
- [14].Pham TQ, Bezuijen M, Van Vliet LJ, Schutte K, and Hendriks CLL, “Performance of optimal registration estimators,” in Visual Information Processing XIV, vol. 5817, pp. 133–145, 2005. [Google Scholar]
- [15].Uss ML, Vozel B, Dushepa VA, Komjak VA, and Chehdi K, “A precise lower bound on image subpixel registration accuracy,” IEEE Trans. Geosci. Remote Sens, vol. 52, no. 6, pp. 3333–3345, 2014. [Google Scholar]
- [16].Xu M, Chen H, and Varshney PK, “Ziv-Zakai bounds on image registration,” IEEE Trans. Signal Process, vol. 57, no. 5, pp. 1745–1755, 2009. [Google Scholar]
- [17].Aguerrebere C, Delbracio M, Bartesaghi A, and Sapiro G, “Fundamental limits in multi-image alignment,” IEEE Trans. Signal Process, vol. 64, no. 21, pp. 5707–5722, 2016. [Google Scholar]
- [18].Aguerrebere C, Delbracio M, Bartesaghi A, and Sapiro G, “A Practical Guide to Multi-image Alignment,” arXiv Prepr. arXiv1802.03280, 2018.
- [19].Robinson D and Milanfar P, “Fundamental Perfromance Limits in Image Registration,” IEEE Trans. Image Process, vol. 13, no. 9, pp. 1185–1199, 2004. [DOI] [PubMed] [Google Scholar]
- [20].Zhao C, Carass A, Jog A, and Prince JL, “Effects of spatial resolution on image registration,” Proc. SPIE, vol. 9784 97840Y–97840Y–9, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Otake Y, Schafer S, Stayman JW, Zbijewski W, Kleinszig G, Graumann R, Khanna a J., and Siewerdsen JH, “Automatic localization of vertebral levels in x-ray fluoroscopy using 3D-2D registration: a tool to reduce wrong-site surgery.,” Phys. Med. Biol, vol. 57, no. 17, pp. 5485–5508, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Tward DJ and Siewerdsen JH, “Cascaded systems analysis of the 3D noise transfer characteristics of flat-panel cone-beam CT,” Med. Phys, vol. 35, no. 12, p. 5510, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Siewerdsen JH, Antonuk LE, El-Mohri Y, Yorkston J, Huang W, Boudry JM, and Cunningham IA, “Empirical and theoretical investigation of the noise performance of indirect detection, active matrix flat-panel imagers (AMFPIs) for diagnostic radiology,” Med. Phys, vol. 24, no. 1, pp. 71–89, 1997. [DOI] [PubMed] [Google Scholar]
- [24].Kijewski MF and Judy PF, “The noise power spectrum of CT images.,” Phys. Med. Biol, vol. 32, no. 5, pp. 565–575, 1987. [DOI] [PubMed] [Google Scholar]
- [25].Burgess AE, “Mammographic structure: data preparation and spatial statistics analysis,” Proc. SPIE, vol. 3661 pp. 642–653, 1999. [Google Scholar]
- [26].Richard S, Siewerdsen JH, Jaffray DA, Moseley DJ, and Bakhtiar B, “Generalized DQE analysis of radiographic and dual-energy imaging using flat-panel detectors,” Med. Phys, vol. 32, no. 5, pp. 1397–1413, 2005. [DOI] [PubMed] [Google Scholar]
- [27].Cockmartin L, Bosmans H, and Marshall NW, “Comparative power law analysis of structured breast phantom and patient images in digital mammography and breast tomosynthesis,” Med. Phys, vol. 40, no. 8, p. 81920, 2013. [DOI] [PubMed] [Google Scholar]
- [28].Chen L, Abbey CK, and Boone JM, “Association between power law coefficients of the anatomical noise power spectrum and lesion detectability in breast imaging modalities,” Phys. Med. Biol, vol. 58, no. 6, p. 1663, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Metheany KG, Abbey CK, Packard N, and Boone JM, “Characterizing anatomical variability in breast CT images,” Med. Phys, vol. 35, no. 10, pp. 4685–4694, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Gang GJ, Tward DJ, Lee J, and Siewerdsen JH, “Anatomical background and generalized detectability in tomosynthesis and cone-beam CT,” Med. Phys, vol. 37, no. 5, pp. 1948–1965, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Punnoose JJ, Xu J, Sisniega A, Zbijewski W, and Siewerdsen JH, “SPEKTR 3.0—A computational tool for x-ray spectrum modeling and analysis,” Med. Phys, vol. 43, no. 8Part1, pp. 4711–4717, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Siewerdsen JH, “Signal, noise, and detective quantum efficiency of amorphous-silicon:hydrogen flat-panel imagers,” Ph.D. dissertation, Dept. Phys., University of Michigan, 1998. [Google Scholar]
- [33].Welch PD, “The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging Over Short, Modified Periodograms,” IEEE Trans. Audio and electroacoustic, vol. 15 pp. 70–73, 1967. [Google Scholar]
- [34].Lowekamp BC, Chen DT, Ibáñez L, and Blezek D, “The Design of SimpleITK.,” Front. Neuroinform, vol. 7, p. 45, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Reiser I, Lee S, and Nishikawa RM, “On the orientation of mammographic structure,” Med. Phys, vol. 38, no. 10, pp. 5303–5306, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]