Abstract
Assessment of permeability is a critical step in the drug development process for selection of drug candidates with favorable ADME properties. We have developed a novel physics-based method for fast computational modeling of passive permeation of diverse classes of molecules across lipid membranes. The method is based on heterogeneous solubility−diffusion theory and operates with all-atom 3D structures of solutes and the anisotropic solvent model of the lipid bilayer characterized by transbilayer profiles of dielectric and hydrogen bonding capacity parameters. The optimal translocation pathway of a solute is determined by moving an ensemble of representative conformations of the molecule through the dioleoyl-phosphatidylcholine (DOPC) bilayer and optimizing their rotational orientations in every point of the transmembrane trajectory. The method calculates (1) the membrane-bound state of the solute molecule; (2) free energy profile of the solute along the permeation pathway; and (3) the permeability coefficient obtained by integration over the transbilayer energy profile and assuming a constant size-dependent diffusivity along the membrane normal. The accuracy of the predictions was evaluated against experimental permeability coefficients measured in pure lipid membranes (for 78 compounds, R2 was 0.88 and rmse was 1.15 log units), PAMPA-DS (for 280 compounds, R2 was 0.75 and rmse was 1.59 log units), BBB (for 182 compounds, R2 was 0.69 and rmse was 0.87 log units), and Caco-2/MDCK assays (for 165 compounds, R2 was 0.52 and rmse was 0.89 log units).
Graphical Abstract
INTRODUCTION
A variety of organic molecules, including metabolites, drugs, and xenobiotics, interact with cellular membranes and modulate their properties. Many of them translocate across the lipid bilayer using diverse mechanisms of active and passive membrane transport.1 The quantification and analysis of direct physical interactions of organic molecules with the lipid bilayer is required to understand, model, and predict many of these processes.
There is strong experimental evidence that small lipophilic molecules, including many marketed drugs, are able to traverse artificial lipid bilayers by passive diffusion driven by the concentration gradient between the solutions on the opposite sides of the bilayer.1 Spontaneous membrane permeation is often described in terms of a solubility−diffusion model or the so-called “Overton’s rule” stating that the permeability coefficient is proportional to the solute partition in water−oil systems.2 Indeed, fair correlations were obtained between measured permeability coefficients of organic molecules and their partition coefficients in water/organic solvent systems (e.g., octanol, hexadecane, etc.).3,4 To rationalize permeation of solutes through the lipid bilayer, solubility−diffusion models were applied, where permeability coefficients were assessed using solute diffusion coefficients in the membrane, their partitioning between water and the nonpolar solvent, and the width of the barrier domain.4–6
In natural membranes, mechanisms of selective permeability are more complex: in addition to passive transbilayer diffusion and diffusion through aqueous boundary layer, there are compound-specific transporter- and carrier-mediated influx and efflux, adsorptive transcytosis of cationic compounds, receptor-mediated endocytosis, micropinocytosis, and other mechanisms.2,7–9 The relevance of the passive diffusion and transport-mediated influx and efflux of drug-related compounds has been extensively discussed,1,8,10–13 and it was concluded that both mechanisms coexist and contribute to translocation across biological membranes.1,10 However, rigorous evaluation of the contribution of passive diffusion in vivo is a challenging task, as the measurable permeation of drugs across biological membranes depends on many factors, such as physicochemical properties of drugs (molecular weight, polarity, lipophilicity, hydrogen bonding capacity, charge, etc.) and specific properties of biological membranes, including the presence of particular transporters.
The prediction of membrane permeability is also required for the development and optimization of new drugs. The primary goal of drug development is to enhance drug efficiency, bioavailability, and delivery to the intended target while reducing its toxicity and side effects. During the design of promising drug candidates, optimization of their pharmaco logical efficiency is usually performed in parallel with selection of leads with favorable pharmacokinetics, i.e. absorption, distribution, metabolism, and excretion (ADME). Properties that influence drug delivery and distribution, include water solubility, metabolic stability, absorption, and the permeability coefficient. The latter determines the rate at which drugs cross permeability barriers, such as epithelial cell membranes from the intestinal mucosal barrier or endothelial cell membranes of the blood−brain barrier (BBB). Several in vitro experimental systems have been developed to predict drug permeation across the BBB or the intestinal barrier: black lipid membranes (BLM), liposomes, parallel artificial membrane permeability assay (PAMPA), cell-based Caco-2 (colon adenocarcinoma cell line), or MDCK (Madin−Darby canine kidney cell line) assays, as well as in situ rodent brain perfusion experiments.14–17
As an alternative, diverse computational methods have been proposed. These methods have an advantage over experimental approaches for conducting high-throughput permeability analysis. At the early stages of drug discovery, the filtering of candidates that more likely exhibit poor permeation is routinely based on the violation of two or more physicochemical criteria of drug-likeness, known as Lipinski’s “rule-of-five” (MW < 500, calculated octanol−water partition coefficient < 5, number of H-bond donors ≤ 5; number of H-bond acceptors ≤ 10).18 However, this rule is not quantitative; it focuses mainly on the oral drug space and does not apply to natural products (NP) or substrates of transporters. Besides, up to 6% of FDA-approved oral drugs that are not NPs violate two or more of these criteria.19 To refine this rule, quantitative estimates of drug-likeness were proposed.19
Quantitative structure−activity relationship (QSAR) and structure−permeability relationship (QSPR) models are regarded as primary quantitative tools for ADME optimiza tion.20–23 Statistically based QSPR models of drug absorption use correlations between the experimental cell permeability and physicochemical descriptors related to experimentally derived molecular properties. Improved multidimensional QSAR models have been developed that use addition levels of chemical structure representation, including molecular topology (2D-QSAR), information from 3D-structures (3D QSAR), combination of 3D-coordinates and sampling of conformations (4D-QSAR), or mutual orientation and dynamics (4D-6D QSAR).20–24 Some models, such as the MI-QSAR models developed by Hopfinger, complement properties of solutes by descriptors for membrane interactions calculated by MD simulations.25 More general QSPR models26–28 predict partition and permeability coefficients of solutes using a set of five Abraham solvation parameters.
The QSPR models are usually trained on limited sets of compounds and show good performance for classes of similar molecules but have poor transferability to compounds with different molecular skeletons.21 The statistical relationships derived from limited training sets of chemicals do not encompass numerous newly approved drugs, including orally available NP-inspired compounds which lay outside the traditional drug property space but can passively penetrate through membranes.18,29,30 Importantly, the QSPR models for drug transport do not allow deriving a physically accurate picture of the permeation process through the lipid bilayers.
Optimization of permeability coefficients of structurally diverse and complex leads, including large permeants violating Lipinski’s rules, requires a theoretical model that adequately describes different aspects of drug−membrane interactions, such as the anisotropic lipid environment, membrane binding and dissociation, rotational and translational diffusion, and conformational changes.31 For relatively large and structurally flexible molecules, it is important to address the existence of multiple conformations32,33 and their spatial positioning in membranes that may influence calculated partitioning and permeability coefficients.5
Several general physics-based computational methods have been applied to overcome these problems. All-atom molecular dynamics (MD) simulations,31,34–41 multiscale (CG/MD) simulations,42,43 Monte Carlo simulations,44 and simulations with milestoning algorithms45,46 were used to obtain detailed information on the dynamics of small molecules in phospholipid bilayers. MD simulations in explicit lipid bilayers were used to calculate free-energy profiles of small molecules in membranes and their permeability coefficients,35–43 evaluate their optimal orientations in the bilayer,47 and predict BBB-permeable drugs.48,49 However, high computational cost hampers application of MD simulations with explicit solvent models for high-throughput drug screening.
Simulations of molecules in the membrane treated as a low-dielectric continuum50–53 are less computationally extensive. Such an approach was applied in the SMx-based54,55 and COSMO-based methods.56–61 The anisotropic complexity of the lipid bilayer was approximated by a low-dielectric slab with either isotropic or anisotropic properties along the normal.62,63 Implicit solvent models have been successfully applied for prediction of transfer free energies and partition coefficients of neutral and ionic solutes from water to organic solvents, micelles, and lipid bilayers.57,60,62–65 More recently, physical models of passive membrane permeation based on solubility−diffusion and barrier domain approaches were developed by Leung et al.,32,33 Swift and Amaro,66,67 and Brocke et al.68 These models assume that the passive membrane permeability primarily depends on the free energy change of barrier crossing, ΔG. The value of ΔG can be calculated as the solvation energy difference between global minimum con formations evaluated in water and in implicit nonpolar organic solvent32,33 or by integration of transbilayer profiles of the free energy of membrane insertion using heterogeneous dielectric generalized Born (HDGB) or dynamic HDGB (DHGDB) implicit membrane models.68 An extended solubility-diffusion model was proposed by Ferrarini et al.69 to describe translocation across membrane using complex free energy landscapes, multiple permeation paths, and the mechanical properties of membranes, such as lateral pressure and acyl chain ordering. Despite rigorous treatment of conformational distributions of permeants32 or advanced models for lipid membranes,68 the performance of these methods against PAMPA permeability coefficients for sufficiently large data sets (≥70 compounds) was unremarkable, with correlation coefficients (R2) below 0.60 and highly variable slopes (ranging from 0.5 to 5) and intercepts (from −9 to 15) of correlation plots for different data sets.32,68
Here we present a novel physics-based computational method, PerMM, that calculates the passive transmembrane translocation pathways and permeability coefficients of structurally diverse molecules (first reported as a conference abstract70). It is based on the solubility−diffusion model5 and our computational method PPM (positioning of proteins in membranes) that was developed for analysis of interactions of arbitrary organic molecules with the lipid bilayer.63,71 The PPM method was parametrized to reproduce free energies of transfer for a large set of small molecules from water to various isotropic organic solvents or anisotropic solvent environments, such as the lipid bilayer. Unlike most other implicit solvent models, it accounts not only for the hydrophobic interactions and electrostatic solvation energy, but also for the solute−solvent hydrogen bonding. The corresponding dielectric and hydrogen bonding polarity profiles were derived from the distributions of different lipid groups that were experimentally determined for DOPC and other bilayers by X-ray and neutron scattering. PPM has been successfully applied to predict membrane binding affinities and spatial positions in membranes of small molecules, peptides, and proteins.63,71,72 The PerMM method calculates (1) the spatial arrangement of solutes in membranes, including the selective accumulation of amphiphilic molecules on the membrane/water interface; (2) the solvation free energy changes of compounds as they move along the translocation pathway in the fluid DOPC bilayer; and (3) the permeability coefficient across the artificial (BLM, PAMPA) and natural (Caco-2/MDCK and BBB) lipid membranes. The method was not trained using any data sets but relies on a general approach to calculating the energy of atomic solvation and electrostatic interactions of solutes translocated across the implicit membrane with anisotropic properties. It successfully reproduced the experimental permeability coefficients of large sets of compounds across different membrane systems with R2 ranging from 0.52 (Caco-2/MDCK cells) to 0.88 (BLM) and root-mean-square errors (rmses) ranging from 0.69 (BBB) to 1.59 (PAMPA-DS) log units. The method has been implemented into an open-access PerMM web server (https://permm.phar.umich.edu/server).
METHODS
Calculation of Membrane Permeability Coefficients.
The overall membrane resistance (R), which is inverse to the permeability coefficient (Pm), was calculated based on the inhomogeneous solubility-diffusion model5 as the integral of the local resistance across the membrane:
| (1) |
where K(z) and D(z) are partition and diffusion coefficients, respectively, which depend on the z position of the solute along the bilayer normal and d is the membrane thickness.
The K(z) value was calculated from the Gibbs free energy of a solute in membrane:
| (2) |
where ΔGtransf(z) is the transfer free energy of the molecule from water to the position z along the bilayer normal (the energy was averaged for a set of conformers). The profile ΔGtransf(z) reflects the solute affinity to the different membrane regions and determines the lowest free energy translocation pathway.
Diffusion coefficients of molecules in membranes cannot be measured experimentally but can be approximated by their diffusion coefficients in water or organic solvents73 or assessed from MD simulations.35–43,74 According to MD simulations, the diffusion coefficient profiles, D(z), are relatively flat along the bilayer normal, with values that are several times lower than in water or at the water−lipid interface.35,36,42 A notable exception includes small molecules (e.g., water, ammonia, oxygen) that demonstrate an increased diffusivity at the center of the membrane.74 Hence, we assumed that the diffusion coefficient Di for an organic molecule i can be considered invariable along the lipid bilayer but dependent on the permeant size. The dependence of diffusion coefficient Di on the volume of a permeant molecule, Vi, is frequently described as in the publication by Xiang and Anderson:6
| (3) |
where D0 is a constant for a particular membrane type characterized by its microviscosity η. The parameter n was suggested to be ~2/3 because the diffusion coefficient depends mainly on the cross-sectional area of the permeant.75 However, fitting to experimental permeability data for bilayers suggested a slightly higher value of n ~ 0.8.6
To simplify the calculations, we used the total accessible surface area of the molecule (ASA), instead of molecular volume, as another parameter related to the cross-section area:
| (4) |
Based on eqs 1–4, the log of calculated membrane permeability coefficient for compound i, can be written as
| (5) |
where a = log kD0(η) and
| (6) |
Parameters “a” and “b” can be empirically determined by a linear fit of experimental coefficients for N compounds and the corresponding calculated log PΣi values.
We also tested a simplified version of the model, without molecular size correction, where D(z) was considered constant and independent of molecular size. We found that including the cross-section area-dependent contribution ASAn leads to only a minor improvement of the fit, and the results are not sensitive to the value of n in (4). Hence, we used n = 1.
The calculation of the free energy profiles, ΔGtransf(z), was performed in the interval from −30 to +30 Å distance from the lipid bilayer center. The permeability barriers (positive values of ΔGtransf relative to the aqueous solution) were observed only in the hydrophobic lipid core but not in the headgroup regions for all compounds, hydrophilic and hydrophobic. Therefore, the integral in eq 6 was calculated through the hydrocarbon core of the lipid bilayer, i.e. in the interval from −15 to +15 Å distance relative to the bilayer center with a step of 1 Å. This part of the lipid bilayer includes the acyl chains and lipid carbonyls with some residual water (Figure S1). Extending the integration interval did not lead to significant changes in the calculated permeability coefficients or to a better agreement with experimental data. We did not include the unstirred water layers outside membrane boundaries, also known as aqueous boundary layer (ABL). While calculating the permeability coefficients of highly hydrophobic compounds, we focused on their intrinsic permeability coefficients, omitting ABL-effects.
Free Energy of Transfer from Water to the Lipid Bilayer.
The energy of transfer of a molecule from water to different positions (z) in membrane, ΔGtransf(z), was calculated by the PPM 2.0 method, as previously described.63 Calculations were based on our version of the universal solvation model65 and the anisotropic solvent model of the lipid bilayer,63 which account for contributions of ionizable groups and the dependence of atomic solvation parameters σ and η on the atom position along the bilayer normal (z). The energy was represented as a sum of a short-range ASA-dependent term (hydrogen bonding, van der Waals, and hydrophobic interactions), long-range electrostatic contributions of dipole moments (μ), and energy of deionization of ionizable groups in the nonpolar environment:
| (7) |
where σi(zi) is an atomic solvation parameter describing transfer energy (per squared angstrom) of atom i from water to the point zi along the bilayer normal, ASAi is a solvent-accessible surface area of atom i, η(zj) is an energy penalty of transferring the dipole moment of 1D from water to point zj, μj is a dipole moment of group j, and are energies of ionizable group k in ionized and neutral states, respectively, N is the number of atoms in the molecule, M is the number of group dipoles, L is the number of ionizable groups, and parameters d, φ, and τ define spatial position of the molecule with respect to the lipid bilayer, as previously described.71 Thus, for each ionizable group, the lowest energy ionization state (charged or uncharged one) was automatically selected at the given position in the membrane. The transfer energy of an ionizable group k in neutral state was calculated as a sum of the deionization energy of the group and ASA-dependent transfer energies of the corresponding atoms (Lk is the number of atoms in ionizable group k):
| (8) |
The energy cost of deionization during transfer from water to the nonpolar environment was defined by the Henderson−Hasselbalch equation:
| (9) |
The transfer energy in the ionized state was described by the following equation:
| (10) |
where σl,ion is solvation parameter of O or N atoms in a charged state; eBorn is a weight factor of long-range electrostatic contribution to transfer energy; rk is an ionic radius. The dielectric function for ions was described by the Born equation modified by Abe:76
| (11) |
Dipolar contribution was calculated using the Block−Walker dielectric function of the media, FBW(ε):77
| (12) |
| (13) |
All types of atoms (26 types) with their solvation parameters and atomic radii were chosen as described previously.65 We assumed that all charged and dipolar groups with ASA > 0.1 Å are in contact with the surrounding solvent and, therefore, their electrostatic contributions to solvation energy should be included.
The atomic solvation parameters σi depend on the polarity parameters of the lipid bilayer:
| (14) |
where αbil(z), βbil(z), and εbil(z) are transbilayer profiles of hydrogen bonding donor and acceptor capacities and dielectric constant, respectively, and αwat, βwat, and εwat are the corresponding values in water. The values of coefficients eBorn, σ0, ei, ai, bi, edip,π, and edip,BW (from eqs 10, 12, and 14) were defined previously.63
The profiles of hydrogen bonding donor and acceptor capacities (αbil(z), βbil(z)), dielectric constant (εbil(z)), and dipolarity/polarizability parameter were calculated for several artificial membranes from distributions of groups in lipids and membrane protein structures along the bilayer normal.78 In this work, we used profiles obtained for the fluid DOPC bilayer based on the distributions of lipid segments determined by X-ray and neutron scattering78,79 (Figure S1).
Here, we modified the original PPM method to work with small molecules. The adapted PPM version automatically defines atom types and assigns dipole moments to all polar groups. The program uses a library of dipole moments for different standard functional groups, taken from the previously published tabulations of group dipole moments.80,81 In addition, the pKa values of ionizable groups should be included in the coordinate file. The experimental pKa values were taken from the compilation by Avdeef82 and from the literature.83–85 In a few cases, the values were not experimentally determined and, therefore, they were calculated using Marvin Suite (ChemAxon). All pKa values for compounds used in this work can be found in the PerMM database (https://permm.phar.umich.edu/).
Calculation of Transmembrane Translocation Path way.
To determine the lowest energy pathway of a molecule across the lipid bilayer, we used two options. The first option was the “drag” method for finding saddle points.86 The transfer energy was locally minimized with respect to rotational variables of the molecule in every z + Δz point of the transmembrane pathway, starting from the optimal rotational orientation calculated in the previous point z. Hence, the rotational position of a molecule was gradually changing during its movement along the membrane normal. This method produced an asymmetric energy curve.
As an alternative approach, we tested an option of “global rotational optimization” of transfer energy with respect to rotational variables of the molecule at every point (z) along the membrane normal. Step Δz was taken as 1 Å. To sample different orientations, the permeant was rotated using 2° steps in the intervals [0°, 360°] and [0°, 180°] in the rotational (φ) and tilt (τ) angles relative to the membrane normal, and the solvation energy was locally minimized with respect to the φ and τ variables starting from each rotational position. The lowest energy orientation was selected automatically for each z value. This approach produced a symmetric energy curves, but it nullified the energy barrier for flip-flop of the molecule in the middle of the membrane. Therefore, the “drag” optimization is preferable for calculation of permeability coefficients.
The location of a molecule along membrane normal was defined by the coordinate z of a “reference atom” representing the atom closest to the center of mass of polar groups of the molecule. To simultaneously move an ensemble of multiple conformations through the membrane, we superimposed conformations through four common atoms that are the closest to the “reference atom”. The local rotational optimization was accomplished for each conformer, and the Boltzmann average value of ΔGtransf(z) was calculated for the set of conformers. For local energy minimization, we used the Davidon−Fletcher−Powell method with analytically calculated partial derivatives of the transfer energy (as implemented in the original PPM method63), where each conformer was considered as a rigid body.
The free energy profiles for 506 compounds that were used in this work can be obtained by running the PerMM web server with source coordinate files provided in the PerMM database. The web server and the database are described in more detail in the accompanying paper.97 The PerMM source code will be provided by the authors upon request, after receiving permission from the owners of the program NACCESS used for ASA calculations.
Generating Structures of Molecules.
The 3D structures of compounds used in this study were downloaded from the PubChem databases in the structure data format (sdf), converted into the pdb format using PyMol (https://pymol.org/2/). The PubChem structures were already energetically optimized.87 Only in a few cases, the 3D structures were taken from the Protein Data Bank (PDB)88 or the Cambridge Structural Database (CSD).89 For example, 3D structures of the 11-residue cyclic peptide cyclosporine A were downloaded from PDB (PDB IDs 2mrc, 1ikf) and CSD (CSD ID KERNAU). The coordinates of several molecules not found in public databases were generated using molecular modeling modules of QUANTA software package for molecular mechanics simulations (BIOVIA-Accerlys Inc.).
The analysis of flexible molecules requires conformational sampling.33,90 To increase the speed of calculations, a set of low-energy conformers was precalculated for every conformationally flexible molecule, and each conformer was considered as a rigid body. As described above, the multiple conformers were superimposed and moved through the membrane to calculate their average transfer energy from water. We found that it is sufficient to include only 6 to 15 significantly dissimilar conformers for medium-size flexible molecules. Further increasing the conformational ensemble did not affect the values of calculated permeability coefficients. For compounds used in this study, we selected conformers that were the lowest energy representatives of different structural clusters identified using the Conformational Search module of QUANTA. A grid scan in the space of torsion angles was followed by ABNR local energy minimization was conducted with CHARMm27 (100 steps, ε = 10) and cluster analysis. Multiple conformers of a molecule were included into an input coordinate file (in pdb format) as multiple models, using MODEL records.
Experimental Permeability Coefficients.
Using reliable experimental data from publications is critical for development and testing of a new permeability model. Our work is focused on modeling of passive permeability across the fluid DOPC bilayer. Thus, to verify our method, we compared our calculations with permeability coefficients measured in vitro through artificial lipid bilayers. After collecting available data from publications and a critical assessment of the data quality, we obtained 132 permeability coefficients through BLM and liposomes: 111 intrinsic permeability coefficients ( in Table S1) and 21 membrane permeability coefficients for ionized compounds ( in Table S1). These data originated from many reputable research groups (e.g., those of Xiang and Anderson, Finkelstein, Walter and Gutknecht, Pohl, Antonenko, and others; see the Supporting Information for references). The main data set included 58 values for the un-ionized species and 20 values for the ionized in water species obtained in comparable experimental conditions (eggPC and DOPC, 25 °C). Data obtained in slightly modified experimental conditions were included in the additional data set.
Data for more complex membrane systems were taken from a compilation by Avdeef15–17 who provided the intrinsic permeability, P0, which refers to the membrane permeability of the neutral form of ionized molecules, i.e., the maximum possible value that the membrane permeability can reach. Overall, we used ~700 intrinsic permeability coefficients through PAMPA-DS, BBB, and Caco-2/MDCK cells that Avdeef collected from reliable publications and processed using the pCEL-X computer program (http://www.in-adme.com/pcel_x.html).
Hence the intrinsic permeability data obtained in vivo for BBB (Table S3) were taken from Avdeef’s compilation.16 Most data were obtained from in situ rodent brain perfusion studies and referred to permeation from saline at pH 7.4 and corrected for ionization, while some were based on in vivo intravenous injections (i.v.). The i.v. data were not used for lipophilic compounds that are known to bind plasma proteins. The in situ brain perfusion technique is used for the in vivo measurement of the initial rate of brain penetration at the luminal BBB membrane.16 The permeability−surface area product, PS, is the product of the luminal permeability, Pc (cm s−1), and the endothelial surface area, S (cm2 g−1). PS is the transfer constant for the initial brain transport of a drug corrected for the velocity of the perfusion flow. Data were selected for efflux-minimized conditions, in which PS values were measured during inhibition of carrier- or transporter-mediated permeability or in knockout mouse models.
Intrinsic permeability data for intestinal cellular membranes (Table S4) were taken from Avdeef’s database17 that collects high-quality Papp values measured in Caco-2 and MDCK epithelial cell lines. These data were collected by Avdeef from 55 reliable publications and corrected for all non-trans-cellular effects using the pCEL-X computer program (http://www.in-adme.com/pcel_x.html). To cancel contributions from active or facilitated transport, the average was taken between apical-to-basolateral and basolateral-to-apical measurements for compounds that are known as substrates for efflux/uptake carrier-mediated transport.
The parallel artificial membrane permeability assay (PAMPA) is another experimental assay quantifying the passive diffusive permeability of artificial membrane systems . Here we used values obtained by Avdeef in PAMPA-DS assay using the lecithin-based double sink model (with 0.5% DMSO in donor chamber, surfactant in acceptor chamber), where the membrane retention of hydrophobic compounds is greatly reduced (Table S5).15 These experimentally obtained permeability coefficients were additionally corrected by Avdeef for permeability through the ABL adjacent at both sides of the membrane.
Experimental permeability coefficients for 506 compounds measured in different membrane systems can be found in our PerMM database (https://permm.phar.umich.edu/, see the accompanying paper97).
RESULTS
We assessed the performance of the PerMM method using large sets of organic compounds, FDA-approved drugs, and similar molecules, for which permeability coefficients were experimentally determined in artificial (BLM/liposomes and PAMPA-DS) and natural (BBB and Caco-2/MDCK cells) membrane systems (Tables S1–S9). For each molecule studied, the program calculated a series of its optimized spatial arrangements as a permeant moves along the membrane normal. The free energy profile (ΔGtransf(z)) along the permeation pathways was produced by optimizing the free energy of transfer of the molecule from water to each position within the lipid bilayer combined with the search for its optimal conformer from precalculated variants. Integration of the obtained transfer energy profile along the membrane normal (eqs 5 and 6) allows calculating the permeability coefficient.
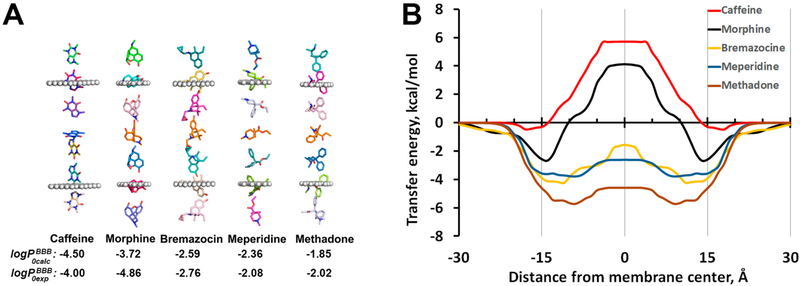
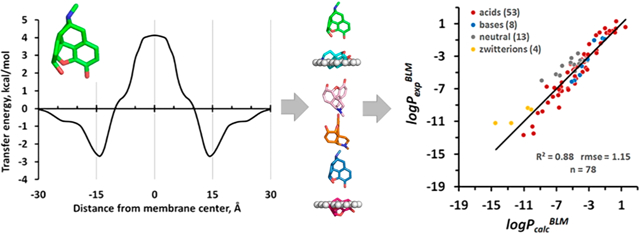
Such energy profiles were calculated for more than 500 permeants, most of which were included in this work. The representative examples of transbilayer energy profiles obtained for five BBB-penetrating drugs, a cyclic peptide, and 17 organic molecules from the initial testing set are shown in the Figures 1, S2, and S3, respectively. For hydrophilic molecules, the free energy profile has a maximum at the bilayer center, which constitutes the main barrier for their permeation (Figure 1B). For hydrophobic molecules, the transbilayer profiles of ΔGtransf are negative at all depths, with a minimum at the membrane center, so that the partition is more favored in the hydrophobic core of the lipid bilayer than at the lipid−water interface. In contrast, all amphiphilic molecules have two minima with negative ΔGtransf values at the water−lipid interfaces and a maximum in the membrane center. Similar free energy profiles for small organic molecules and drugs were obtained in MD simulations,35,41,43,47,48,91 except that small energy barriers were found in the lipid headgroup region for some hydrophobic compounds in a number of studies.35,38,42,92,93 During the movement, the permeant molecule rotates to place its nonpolar groups deeper to the lipid acyl chain region and to orient the most polar atoms toward the membrane boundaries (see Figure 1A). The predicted changes in spatial orientations along the translocation pathway of 506 permeants can be inspected using the interactive GL mol viewer included in the PerMM database.
Figure 1.
Spatial positions, optimized orientations (A), and transfer energy profiles (B) calculated for several drug molecules as they move through the DOPC bilayer. Calculations of transbilayer energy profiles were performed by the publicly available PerMM web server (https://permm.phar.umich.edu/server) using the “global rotational optimization” option. The locations of hydrocarbon core boundaries between the acyl chains and head groups of lipids (at ±15 Å distances from the membrane center) are approximated by planes and shown as dummy atoms (A).
Performance of PerMM for Model Lipid Bilayers.
The current version of PerMM was developed using polarity parameters of the DOPC bilayer. Therefore, the performance of the method was initially assessed using data for similar lipid bilayer systems, such as BLM or liposomes primarily composed of phosphatidylcholine (PC), rather than data for more complex PAMPA, Caco-2/MDCK, and BBB membranes. Hence, we compared the permeability coefficients calculated by PerMM with the corresponding experimental data measured in PC-based BLM or liposomes (Tables S1 and S2). First, we used a main set of the most frequently cited data determined by Anderson and co-workers, Walter and Gutknecht, and several other groups. It included 58 intrinsic permeability coefficients published for uncharged forms of permeants ( for 42 acids, 3 bases, and 13 neutral molecules) and 20 membrane permeability coefficients for molecules ionized in water ( for 11 acids, 5 bases, and 4 zwitterions). The PPM solvation model considers the equilibrium between charged and neutral states of ionizable groups, depending on their pKa and pH values (eqs 7–13),63 thus allowing ionizable groups to diffuse through the membrane in the neutral state. The ionized species can still be present in the membrane region at 10−15 Å distance from the membrane center, where the protonation or deprotonation takes place. The deionization energy cost was estimated using the Henderson−Hasselbalch equation. This energy was not included in calculation of permeability coefficients for the neutral states of acids, bases, and zwitterions.
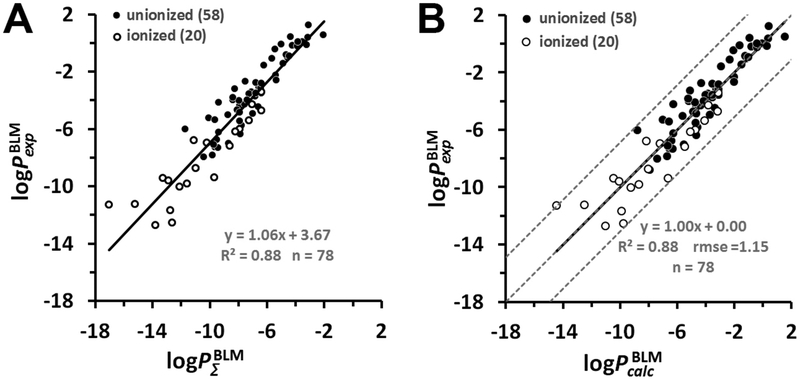
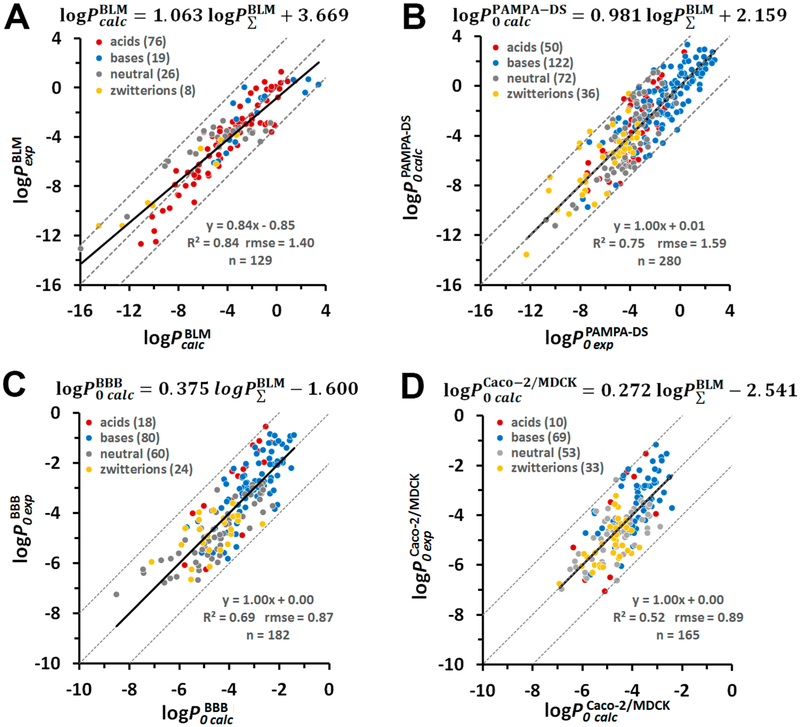
We found a good correlation (R2 = 0.88) between integrals calculated according to eq 6 and experimental permeability coefficients of 58 un-ionized and 20 ionized compounds combined, which covered a wide range of experimental permeability values, from −13 to +1 log units (Figure 2A). The linear fitting of the scatter plot allowed us to find parameters “a” (intercept) and “b” (slope) in eq 5. Importantly, the slope b was found to be close to 1, as expected. The intercept value a represents a constant related to the diffusion coefficient in membrane with the viscosity η that depends on the lipid composition. The following linear regression model (eq 15) was included into the PerMM method for the prediction of permeability coefficients of molecules crossing lecithin-based bilayers (e.g., BLM):
| (15) |
Figure 2.
Prediction of the permeability of artificial lipid bilayers to organic molecules. (A) Comparison of experimental and calculated permeability coefficients across unilamellar lipid bilayers of 58 un-ionized (black circles) and 20 ionized in water (open circles) organic molecules. The corresponding data values are from Tables S1 and S2. (B) Plot of experimental BLM permeability coefficients vs the calculated ones for 78 organic molecules. Dashed lines indicate ideal line and residual line limits (using a cutoff of |3.1| that corresponds to 2.0 rmse for ionized molecules). Predicted permeability coefficients, , in B were calculated using eq 15. The values were calculated using eq 6. For ionized species, the integral accounted for the deionization penalty of ionizable groups at the specified pH. The number of molecules “n” is indicated in parentheses.
Equation 15 was applied for scaling the values to experimental BLM data so that a and b became 0 and 1, respectively. This transformation resulted in rmse value of 1.15 log units between experimental and estimated permeability coefficients (Figure 2B).
We found that it was important to have a sufficiently large set of compounds (>50) to obtain a reliable calibration curve (Figure 2A). For example, two separate linear regression fits for 58 un-ionized and 20 ionized molecules were described by the equations: and log , respectively (Figure S4). The regression function for the first data set of 58 compounds was similar to that for the larger set of 78 compounds (Figure 2A) but different for the data set of 20 molecules. The parameters of regression varied for small data sets from individual publications.
To validate the linear model described by eq 15, we increased the main data set by including 54 additional compounds that were studied in BLM and liposomes under more variable experimental conditions. The linear regression fit for the extended set of 132 compounds was described by equation (Figure S5A). After excluding three outliers (represented using green triangles in Figure S5A), the equation did not change significantly, but the correlation improved: . Thus, after addition of 51 experimental data points obtained in slightly altered experimental conditions, R2 only slightly decreased, but the slope remained close to 1. The estimated rmse for sets of 129 and 132 compounds were of 1.40 and 1.56 log units, respectively. Thus, we defined as outliers three additional compounds (nitric acid, hydrofluoric acid, and lysine), which significantly increased the rmse.
Importantly, our model was able to evaluate the intrinsic permeability coefficients for highly hydrophobic compounds with P0 ≫ PABL, whose measurable permeability coefficients are limited by diffusion through ABL (PABL of 15−30 × 10−6 cm/s).15 For example, PerMM-calculated permeability coefficients through the DOPC bilayer for imipramine, desipramine, and chlorpromazine were 2.70, 2.63, and 1.39, respectively, whereas experimental values through the DOPC bilayer provided by Avdeef (Figures 7.26 and 7.30 in ref 15) were 5.1, 1.74, and 1.62, respectively.
We also tested the influence of the conformational flexibility of molecules with multiple rotating bonds on the results of our calculations. We found that the use of multiple precalculated conformations of compounds slightly changed the permeability coefficients of some conformationally flexible compounds (Figure S2). For example, the optimal membrane-bound conformation of the cyclic peptide cyclosporine A was oval-shaped and stabilized by four intramolecular hydrogen bonds (CSD ID KERNAU), while the optimal conformations in water and at the water−membrane interface were more round-shaped (PDB IDs 2rmc, 1ikf) with one intramolecular hydrogen bond. The application of three dissimilar con formations of cyclosporine A in our PerMM calculation decreased the BLM permeability coefficient by ~0.6 log units as compared to calculations with just one round-shaped conformation. For the whole data set, the use of a conformational ensemble instead of a single conformation did not significantly improve the accuracy of calculations (Figure S4). Nevertheless, we opted to use multiple conformations for flexible compounds in all subsequent calculations.
Comparison of Experimental Permeability Coefficients in Different Membrane Systems.
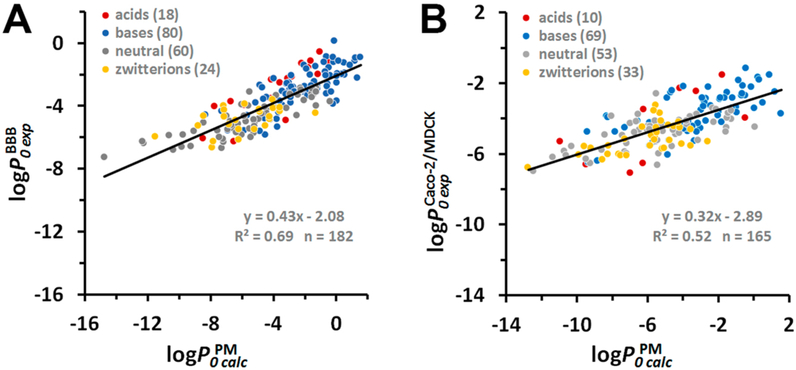
To investigate how permeability data depend on the experimental method applied, we compared experimental permeability coefficients of the same compounds measured in different artificial (BLM and PAMPA-DS) and natural (BBB and Caco-2/MDCK) membranes. To simplify the analysis, we considered only intrinsic permeability coefficients with log P0exp values ranging from −7 to 0 (Tables S7–S9).
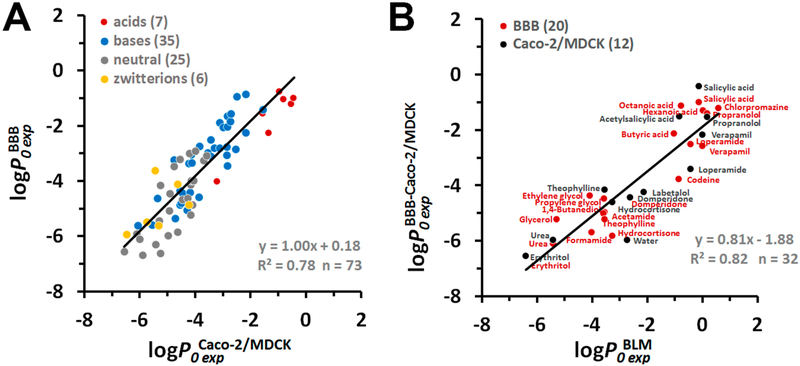
Such comparisons lead to several important conclusions. First, we found a sufficiently good correlation between the intrinsic permeability coefficients obtained using in situ BBB assay and in vitro cell-based Caco-2/MDCK assays (73 compounds, Figure 3A). The linear regression curve had a slope b close to 1, the intercept a close to zero, and R2 of 0.78 This is consistent with the general expectation that Caco-2 or MDCK cell-based assays can be used as models for predicting BBB permeability of drugs.94
Figure 3.
Comparison of experimental permeability data for natural and artificial membrane systems. (A) Correlation between intrinsic permeability coefficients obtained in situ rodent brain perfusion experiments vs Caco-2/MDCK assays . (B) Correlation between intrinsic BBB or Caco-2/MDCK permeability coefficients vs intrinsic permeability coefficients through BLM/liposomes . Colors indicate different types of molecules: red for acids, blue for bases, gray for neutral molecules, and yellow for zwitterions. The number of molecules “n” is indicated in parentheses. Experimental BLM, BBB, and Caco-2/MDCK permeability coefficients are from Tables S7 and S8.
Second, we found a good correlation (R2 of 0.82 and slope b of 0.81) between experimental permeability coefficients measured in BLM and in “efflux minimized” BBB assay or Caco-2/MDCK assays after correction for nontrancellular effects (set of 32 compounds, Figure 3B). The regression function was
| (16) |
The significant intercept value (a = −1.88) in the linear regression line can be explained by the difference in lipid composition between epithelial membranes and BLM. The presence of cholesterol and sphingomyelin in epithelial membranes could be a cause of the much lower permeability (by 1.88 log units) of natural membranes as compared to lecithin-based BLM. Indeed, the addition of cholesterol (CHOL) to BLM formed by PC in experiments performed by Finkelstein95 and Xiang et al.,96 reduced the experimental permeability coefficients by ~0.6 log units, while addition of both cholesterol and sphingomyelin (CHOL+SM) decreased these coefficients by ~1.9 log units, which appeared as a decrease of the intercept values in corresponding plots (Figure S5B). The PM-correction in accordance with eq 16 was included to predict the permeability coefficients through the plasma membranes.
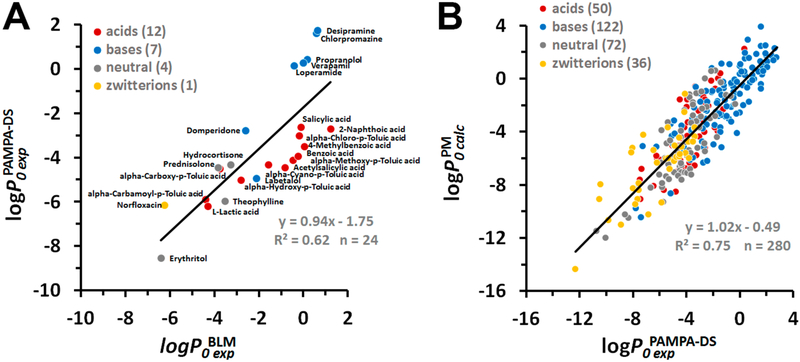
Finally, we compared permeability coefficients measured in PAMPA-DS vs BLM assays for the set of 24 compounds (Figure 4A). We found a slightly lower correlation between experimental data obtained in both assays (R2 = 0.62, slope b of 0.94). The regression function, based on PAMPA-DS data, was
| (17) |
Figure 4.
Experimental and calculated permeability data for PAMPA-DS. (A) Correlation between intrinsic permeability coefficients obtained in PAMPA-DS assays and using BLM or liposomes . Experimental PAMPA-DS and BLM data were taken from Table S9. (B) Correlation between permeability coefficients through the plasma membrane and PAMPA-DS. Intrinsic permeability coefficients of molecules through the plasma membrane were calculated using eq 17. Experimental data for PAMPA-DS were taken from Table S5. Colors indicate different types of molecules: red for acids, blue for bases, gray for neutral molecules, and yellow for zwitterions. The number of molecules “n” is indicated in parentheses.
The value of the intercept a indicated the lower permeability coefficients (by 1.75 log units) through PAMPA-DS membranes as compared to BLM, which is reminiscent of the decreased permeability of cholesterol- and SM-rich epithelial membranes of Caco-2/MDCK cells and the BBB.Such a permeability difference could be attributed to a larger width and different lipid composition (20% lipid mixture of PC, PE, PI, PA, and triglycerides)15 of a hydrophobic barrier in PAMPA-DS relative to that in BLM. Equation 17 was used instead of eq 16 for PM-correction, while calculating data for the PAMPA-DS assay.
Prediction of Permeability Coefficients for BBB, Caco-2/MDCK, and PAMPA-DS Assays.
In this work, we used three sets of experimental intrinsic permeability coefficients (log P0exp) that were compiled by Avdeef for PAMPA-DS, BBB, and Caco-2/MDCK assays.15–17 They included 322, 199, and 185 data points, respectively. The intrinsic permeability coefficients of these compounds ranged from −12 to +2 for PAMPA-DS, from −9 to +1 for BBB, and from −7 to −2 for Caco-2/MDCK assays.
To reproduce these data, values were calculated for all compounds in the neutral form using eq 6. For each of three data sets, we then compared experimental log P0exp values with calculated integrals in three subsets: (1) the whole data set; (2) the core set, excluding outliers; and (3) the reduced set, excluding outliers and zwitterions (Figure S6). We considered data points as outliers if they deviated by more than 2 rmse from the value predicted by the linear regression line(i.e., the cutoff of 2 in absolute value for standardized residuals) and their one-by-one exclusion significantly improved the correlation coefficient and decreased the rmse. Such an approach allowed us to exclude 42 compounds from the PAMPA-DS data set (13% outliers), 17 compounds from the BBB data set (8.5% outliers), and 20 compounds from the Caco-2/MDCK data set (10.8% outliers) (shown as green triangles on Figures S6 and S7). Interestingly, excluding zwitterions from these sets did not significantly improve the R2 for BBB data and even decreased the R2 for PAMPA-DS and Caco-2/MDCK data. Therefore, during subsequent calculations, we used the core sets of 280, 182, and 165 compounds for PAMPA-DS, BBB, and Caco-2/MDCK data, respectively.
As follows from the experimental data (Figures 3B and 4A), the permeability of plasma membranes (PM) of the BBB and Caco-2/MDCK cells and of PAMPA membranes is lower by ~1.8 log units as compared to permeability of the lecithin-based BLM. Therefore, we used corrected values for PM in all subsequent comparisons. The calculation of values can be viewed as a two-step linear transformation. First, the permeability coefficients through BLM were estimated using eq 15. Then, we applied eq 16 to obtain PM-corrected values for BBB and Caco-2/MDCK or eq 17 for PAMPA-DS data.
The scatter plots for experimental permeability coefficients for PAMPA-DS, BBB, and Caco-2/MDCK assays versus are shown in Figures 4B and 5. We found a sufficiently good correlation (R2 = 0.75, b ~ 1, a ~ 0) between experimental intrinsic PAMPA-DS permeability coefficients for 280 diverse molecules (50 acids, 122 base, 72 neutral molecules, and 36 zwitterions) and the corresponding PM-corrected permeability values (Figure 4 B). The linear regression model for PAMPA-DS was
| (18) |
Using this model for scaling calculated data produced the rmse value of 1.59 log units (Figures 6B and S6B).
Figure 5.
Correlation between calculated intrinsic permeability coefficients through the plasma membrane (PM) and experimental intrinsic permeability coefficients through BBB (A) and Caco-2/MDCK cells (B). Intrinsic permeability coefficients of molecules through the plasma membrane were calculated using eq 16. Experimental data were taken from Tables S3 for BBB and Table S4 for Caco-2/MDCK assays . Colors indicate different types of molecules: red for acids, blue for bases, gray for neutral molecules, and yellow for zwitterions. The number of molecules “n” is indicated in parentheses.
Figure 6.
Prediction of intrinsic permeability coefficients through different membrane systems. Plot of experimental vs calculated permeability coefficients through BLM (A), PAMPA-DS (B), BBB (C), and Caco-2/MDCK cells (D). The formula above each panel relates the calculated intrinsic log P0calc values for each systems and the integral values of molecules in the neutral state determined by integration of eq 6. Dashed lines indicate the ideal line and residual line limits with cutoffs of |3.2| (A and B) and |2.0| (C and D). Colored circles indicate different charge classes of molecules: red for acids, blue for bases, gray for neutral molecules, and yellow for zwitterions. The number of molecules “n” is indicated in parentheses.
The relationships between experimental and PM-corrected permeability coefficients of 182 compounds (18 acids, 80 bases, 60 neutral molecules, and 24 zwitterions) studied in the BBB assay and 165 compounds (10 acids, 69 bases, 53 neutral molecules, and 33 zwitterions) studied in Caco-2/MDCK assays can be described by the linear regression lines with R2 of 0.69 and 0.52, respectively, and slopes b of 0.43 and 0.32, respectively (Figure 5A, B). The observed deviation of slopes from 1 can be attributed to the presence of diverse transporters in natural membranes, which, despite experimental efforts to minimize their contribution, may not be completely eliminated. The presence of influx and efflux transporters would increase the uptake of low-permeable polar molecules and decrease the inward translocation (by promoting the outward efflux) of highly permeable hydrophobic molecules. The linear regression models for BBB and Caco-2/MDCK data were the following:
| (19) |
| (20) |
Using eqs 19 and 20 for scaling calculated data to experimental data to get linear regression line with a = 0 and b = 1 produced the rmse values of 0.87 log units for BBB data and 0.89 log units for Caco-2/MCDK data (Figures 6C, D and S6C, D).
Hence, the resulting equations to relate the integrals over transfer energy profiles for the neutral forms and calculated intrinsic permeability coefficients (log P0calc) through PAMPA-DS, BBB, and Caco-2/MDCK membranes were the following (Figures 6 and S6):
| (21) |
| (22) |
| (23) |
Equations 15 and 21 can be also applied to predict membrane permeability coefficients through artificial membranes of compounds ionized in water. In this case, the corresponding integrals of transbilayer energy profiles will account for contribution from deionization penalty for ionizable group(s) with specified pKa at indicated pH. Indeed, membrane permeability coefficients for ionized compounds were satisfactory reproduced for artificial bilayers, BLM and liposomes (Figures 2, S4, and S5), and the PAMPA DS system (Figure S8). In the latter case, a reasonably good prediction of PAMPA-DS log Pmexp values at pH 6.5 and 7.4 (with rmse of 1.77 and 1.69 log units; R2 of 0.58 and 0.69, respectively) was obtained for weak acids and bases from Avdeef’s data set15 (Table S6), excluding zwitterions.
To predict membrane permeability coefficients of ionized compounds through the BBB membranes, the following equation was obtained:
| (24) |
The accuracy of the prediction of BBB membrane permeability coefficients using eq 24 was moderate (rmse of 0.65 log units; R2 of 0.60) for the set of 79 bases and 23 acids from the Avdeef’s database.16
Finally, we assessed the ability of PerMM to distinguish compounds able to cross BBB by passive diffusion (BBB+) from BBB-impermeable molecules (BBB−). We analyzed the range of permeability coefficients for both types of compounds (Figure S9) and found that the predicted intrinsic permeability coefficients of BBB-impermeable compounds were less than −4.35 log units.
Thus, the compounds with higher permeability coefficients are expected to cross the BBB and serve as central nervous system-active agents, unless they are substrates for efflux transporters, such as P-glycoprotein or other ABC transporters.
Equations 7 and 13–15 were included in our PerMM program and the web server for prediction of permeability coefficients of organic chemicals and drug-like molecules through different membrane systems based on integration of transfer energy profiles over the permeation pathway. Using these equations, PerMM reproduced experimental permeability coefficients in different systems well: BLM and liposomes (78 compounds, R2 = 0.88, rmse = 1.15), PAMPA-DS assay (280 compounds, R2 = 0.75, rmse = 1.59), Caco-2/MDCK assays (165 compounds, R2 = 0.52, rmse = 0.89), and in situ brain perfusion experiments (182 compounds, R2 = 0.69, rmse =0.87) (Figure 6).
Comparison of PerMM with Other Computational Methods.
To assess the utility and the predictive power of the PerMM method, we compared it with other computational methods, in particular, with the physics-based methods recently developed by Leung et al.32 and Brocke et al. (implemented in the MemDrugPerm web server).68 These methods were applied for the relatively large and structurally diverse sets of compounds, many of which were also calculated by PerMM. We also compared results of calculations by PerMM, with predictions by the QSPR-based QikProp method (Schrödinger) and by the machine learning algorithm developed by Brocke et al.68 as an alternative approach to MemDrugPerm. Comparison of performances of these methods is shown in Figures S10 and S11. We evaluated the intrinsic permeability coefficients of compounds that were common for our and other data sets against the experimental intrinsic log P0exp values compiled for PAMPA-DS and Caco-2 assays by Avdeef,15,17 rather than against diverse data sets obtained by various authors in dissimilar experimental conditions.
We founds that PerMM outperformed both physics-based methods with respect to R2 and rmse values and demonstrated better accuracy than the statistically based QikProt method and the machine learning algorithm. For the set of 58 common compounds, PerMM predicted PAMPA-DS permeability coefficients with R2 of 0.67 and rmse of 1.51, while the HDGB and DHDGB models of Brocke et al. demonstrated rmse of 1.99 and 1.73 log units and R2 of 0.50 and 0.49, respectively (Figure S10A, C, D). Results of the machine learning algorithm were less impressive with R2 of 0.40 and rmse of 2.28 log units, though rmse decreased to 1.68 log units after scaling the calculated values to the experimental values to get a linear regression line with a = 0, b = 1 (Figure S10B). Importantly, the slopes (b) of the regression lines were rather close to 1 for PerMM and the HDGB model but smaller for the DHDGB model (b = 0.66) and much smaller for the machine learning algorithm (b = 0.23), while intercepts increased from 0 for PerMM to ~0.5 for both HDGB and DHDGB models and to ~4 for the machine learning approach. Scaling the calculated values to experimental values for HDGB and DHGB models did not improve rsme values (Figure S10C and D).
The performance of the method by Leung et al. for the prediction of PAMPA-DS permeability was also moderate. The scatter plot of predicted vs experimental data for 73 compounds was fitted by the regression line with R2 of 0.38,b of 1.31, and a of −9.12. The significant intercept value was likely due to the extremely low permeability coefficients predicted by Leung’s model (in the range from −28 to −4 log units) (Figure S11C). For the same set of compounds, the accuracy of PerMM predictions was much better: the linear regression line had R2 of 0.68, b close to 1, and a close to 0 (Figure S10A). The accuracy of the Leung’s and QikProp methods for prediction of Caco-2 permeability for 44 compounds was also lower than that of PerMM: R2 values were of 0.30, 0.27, and 0.59, respectively (Figure S11B, D, and F).
DISCUSSION
In this study, we developed a novel physics-based computational method PerMM for predicting passive membrane permeation of structurally diverse molecules through the phospholipid bilayer. In addition to estimating the permeability coefficients, this method provides visualization of the transmembrane translocation pathway for a compound of interest. By describing the thermodynamics of membrane-solute interactions, such an approach helps to understand the mechanisms of permeability of drug candidates, which may assist in optimization of their ADME properties.
Our data set included nonpolar and polar nonelectrolytes and weak electrolytes. According to results of our calculations, the ionized species of weak acids and bases become uncharged in the lipid carbonyl region and cross the lipid bilayer in the neutral form. Consistent with experimental studies,4 we found that the permeability barriers are located in the hydrophobic domain of the lipid bilayer but not outside this region.
To verify the method, we compared the results of our calculations for the DOPC bilayer with permeability coefficients measured in unilamellar phospholipid bilayers (Figures 2 and S4). This comparison covered a wide range of log P0 values (from −12 to +2) and produced R2 of 0.88 and the slope b close to 1 (Figure 2 A), as expected. A comparison of experimental and calculated permeability coefficient through BBB and Caco-2/MDCK cells demonstrated a smaller slope (b of 0.43 and 0.32, respectively) and lower R2 values (0.69 and 0.52, respectively) (Figure 5). Although these correlations can be used for evaluation of permeability of BBB and Caco-2/MDCK systems, the prediction accuracy is lower than that for model phospholipid bilayers (Figures 2 and 6C, D).
We assume that the observed permeability differences between artificial and natural membrane systems could be due to the presence of the facilitated molecular transport in biological membranes. To reduce the effect of transporters, a significant effort was made by Avdeef in collecting “efflux-minimized” BBB permeability data16 and including Caco-2/MDCK data that represent the averages of apical-to-basolateral and basolateral-to-apical measurements canceling out some of carrier-mediated contributions.17 Nevertheless, the efflux and influx effects can still be present or not completely eliminated for a number of permeants due to the presence of multiple transporters. In fact, the vast majority of drugs included in our data set can interact with a variety of influx and efflux transporters8 (see pages for individual molecules in the PerMM database). The possible effect of influx transporters is expected to result in a higher permeability of polar permeants than that predicted from passive diffusion. The possible effect of efflux transporters would decrease the measured permeability of highly hydrophobic permeants relative to predictions based on passive diffusion. Thus, both effects would results in the observed slope b < 1 of the linear regression fits for BBB and Caco-2/MDCK data (in addition to possible scattering), as we actually observed (Figure 5).
Similar to other physics-based methods, PerMM operates with atomic structures of molecules moving across the lipid bilayer and uses the solubility-diffusion framework for estimating the molecular permeability. However, our and other methods employ different approaches for calculating the free energy change of barrier crossing and the corresponding permeability coefficients of permeants. For example, Leung et al.32 represent the lipid bilayer as an implicit organic solvent and calculate the solvation energy difference between global minimum conformations evaluated in water and chloroform. Brocke et al.68 describe the implicit membrane by varying dielectric profiles along the membrane normal, based on either standard HDGB or dynamic (D)HDGB models, and calculates membrane insertion energy profiles and their integrals to derive permeability coefficients. The PerMM method uses a general anisotropic solvent representation of the lipid bilayer that has been previously developed and extensively tested to study spatial positioning in membranes of peptides, proteins, and small molecules.63,71,72 Furthermore, similar to Brocke’s method, PerMM calculates permeability coefficients by integration over transfer energy profiles instead of using a simple barrier approximation as in the Leung method.
There are other methodological differences between these methods, including treatment of conformational flexibility of permeants and calculation of their diffusivity in membranes. For better computational efficiency, PerMM utilizes precalculated structures of permeants, similar to that in Brocke’s method.68 To account for the conformational dynamics, we use a limited set of structurally diverse conformations for flexible molecules, instead of performing the more exhaustive conformational sampling proposed by Leung et al.32 We found that including conformational flexibility only slightly improves the permeability coefficients of conformationally flexible molecules but does not significantly affect the overall accuracy of permeability predictions (Figures S2 and S4). Similar to other methods, we consider the size-dependence of permeant diffusion in membranes. However, instead of diffusivity profiles along the membrane normal, we assume a constant diffusivity of a solute throughout the membrane. This is a reasonable approximation, because the exact shape of D(z) was shown not to be important for permeability prediction.68
As described in Results, PerMM demonstrated better performance than two other recently developed physics-based methods, as well as the machine learning algorithm by Brocke et al. and the regression-based QikProp method. We found that PerMM outperformed these methods in terms of R2 and rmse for prediction of PAMPA or Caco-2 permeability coefficients for relatively large data sets (Figures S10 and S11). The MemDrugPerm method68 showed the closest accuracy to PerMM against PAMPA data.
The advantages of our approach are likely due to the better parametrization of atomic solvation (σ) and dipolar (η) parameters for different chemical groups in our universal solvation model, as described in our previous publication65 and to the use of dielectric and hydrogen bonding parameter profiles for the DOPC bilayer in the PPM method.63 The correct evaluation of the solvation energy in the heterogeneous environment is critical, because permeability depends exponentially of this energy.
It is of note that PerMM has broad applicability: it allows quantitative calculation of permeability coefficients in different membrane systems, including BLM, PAMPA, Caco-2/MDCK cells, and the BBB. It demonstrated the best accuracy (R2 =0.88, rmse of 1.15 log units) for pure lecithin-based unilamellar membranes. This was expected because the method implements the dielectric and polarity parameters of the DOPC bilayer. PerMM also showed a reasonably good performance in predicting BBB and Caco-2/MDCK permeability coefficients with accuracy within 1 log unit (rmse of 0.87 and 0.87 log units, respectively), even though the permeability of a number of compounds in such systems could be affected by the active efflux and influx and carrier-facilitated transport, in addition to passive diffusion. Our results suggest that plasma membranes of Caco-2/MDCK and the BBB cellular systems are less permeable than the lecithin-based bilayers or DOPC by ~1.8 log P0 units, probably due to the presence of cholesterol and sphingomyelin.
The PerMM method properly reproduced experimental permeability coefficients for a large set of 506 compounds, which differed in sizes, structural scaffolds, and chemical classes. This demonstrates the transferability of our approach, similar to other physics-based methods. Importantly, the PerMM allows predicting the absolute values of intrinsic permeability coefficients, especially for the phospholipid bilayers, rather than the relative permeability data for a series of compounds, as is customary in other methods. We also found that correlations between calculated and experimental permeability coefficients for molecules from different charge classes (acids, bases, neutral molecules) can be described by the same regression line, as should be expected for calculations with any physics-based model.
In summary, the PerMM method can be useful for prediction of intrinsic permeability coefficients through lipid membranes of a wide spectrum of drug candidates, including natural product-derived compounds with large molecular weight. However, our method is still approximate, as it employs the flat diffusion coefficient profiles across the membrane, does not account for the mechanical properties and the lipid composition of membranes, especially in the headgroup region, and does not include effects of dipole and surface membrane potentials, as well as the influence of permeants on properties of the lipid bilayer. We envision addressing these issues in the future, which may improve the method’s accuracy. To facilitate practical use of our method by the scientific community, we have implemented it as a publicly available web server with a supplementary database, as described in the accompanying paper.97
Supplementary Material
ACKNOWLEDGMENTS
We are grateful to Dr. Avdeef for the provided sets of membrane binding and permeability data of drugs and numerous organic molecules that were experimentally obtained in PAMPA, BBB, and Caco-2/MDCK assays. We are thankful to Dr. Mosberg for helpful discussions and comments.
Funding
NIH R21DA040752 and NSF DBI-1458002 (to A.L.L. and I.D.P.).
ABBREVIATIONS
- ADME
absorption, distribution, metabolism, and excretion
- ABNR
adopted basis Newton−Raphson
- ASA
accessible surface area
- BBB
blood−brain barrier
- BLM
black lipid membranes
- Caco-2
colon adenocarcinoma cell line
- CG/MD
coarse-grained molecular dynamics
- CHARMm
chemistry at Harvard molecular mechanics
- DHDGB
dynamic heterogeneous dielectric generalized Born
- DOPC
dioleoyl phosphatidylcholine
- FDA
Food and Drug Administration
- HDGB
heterogeneous dielectric generalized Born
- MD
molecular dynamics
- MDCK
Madin−Darby canine kidney cell line
- NP
natural product
- PAMPA
parallel artificial membrane permeability assay
- PAMPA-DS
PAMPA double-sink
- PC
phosphatidylcholine
- PDB
Protein Data Bank
- PPM
positioning of proteins in membranes
- QSAR
quantitative structure−activity relationship
- QSPR
quantitative structure−permeability relationship
- rmse
root-mean-square error
Footnotes
Supporting Information
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jcim.9b00224.
Experimental data sets, results of PerMM calculations, illustrations of technical details, Figures S1–S10, and Tables S1–S9 (PDF)
The authors declare no competing financial interest.
REFERENCES
- (1).Smith D; Artursson P; Avdeef A; Di L; Ecker GF; Faller B; Houston JB; Kansy M; Kerns EH; Kramer SD; Lennernas H; van de Waterbeemd H; Sugano K; Testa B Passive Lipoidal Diffusion and Carrier-Mediated Cell Uptake are Both Important Mechanisms of Membrane Permeation in Drug Disposition. Mol. Pharmaceutics 2014, 11, 1727–1738. [DOI] [PubMed] [Google Scholar]
- (2).Al-Awqati Q One Hundred Years of Membrane Permeability: Does Overton Still Rule? Nat. Cell Biol 1999, 1, E201. [DOI] [PubMed] [Google Scholar]
- (3).Missner A; Pohl P 110 Years of the Meyer-Overton Rule: Predicting Membrane Permeability of Gases and Other Small Compounds. ChemPhysChem 2009, 10, 1405–1414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).Xiang TX; Xu YH; Anderson BD The Barrier Domain for Solute Permeation Varies with Lipid Bilayer Phase Structure. J.Membr. Biol 1998, 165, 77–90. [DOI] [PubMed] [Google Scholar]
- (5).Diamond JM; Katz Y Interpretation of Nonelectrolyte Partition Coefficients Between Dimyristoyl Lecithin and Water. J. Membr. Biol 1974, 17, 121–154. [DOI] [PubMed] [Google Scholar]
- (6).Xiang TX; Anderson BD The Relationship Between Permeant Size and Permeability in Lipid Bilayer Membranes. J. Membr. Biol 1994, 140, 111–122. [DOI] [PubMed] [Google Scholar]
- (7).Kramer SD; Aschmann HE; Hatibovic M; Hermann KF; Neuhaus CS; Brunner C; Belli S When Barriers Ignore the ″Rule-of-Five″. Adv. Drug Delivery Rev 2016, 101, 62–74. [DOI] [PubMed] [Google Scholar]
- (8).Kell DB; Oliver SG How Drugs Get Into Cells: Tested and Testable Predictions to Help Discriminate Between Transporter-Mediated Uptake and Lipoidal Bilayer Diffusion. Front. Pharmacol 2014, 5, 231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Mikitsh JL; Chacko A-M Pathways for Small Molecule Delivery to the Central Nervous System Across the Blood-Brain Barrier. Perspect. Medicin. Chem 2014, 6, 11–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Sugano K; Kansy M; Artursson P; Avdeef A; Bendels S; Di L; Ecker GF; Faller B; Fischer H; Gerebtzoff G; Lennernaes H; Senner F Coexistence of Passive and Carrier-Mediated Processes in Drug Transport. Nat. Rev. Drug Discovery 2010, 9, 597–614. [DOI] [PubMed] [Google Scholar]
- (11).Di L; Artursson P; Avdeef A; Ecker GF; Faller B; Fischer H; Houston JB; Kansy M; Kerns EH; Kramer SD; Lennernas H; Sugano K Evidence-Based Approach to Assess Passive Diffusion and Carrier-Mediated Drug Transport. Drug Discovery Today 2012, 17, 905–912. [DOI] [PubMed] [Google Scholar]
- (12).Kell DB; Dobson PD; Oliver SG Pharmaceutical Drug Transport: the Issues and the Implications That It Is Essentially Carrier-Mediated Only. Drug Discovery Today 2011, 16, 704–714. [DOI] [PubMed] [Google Scholar]
- (13).Kell DB What Would Be the Observable Consequences if Phospholipid Bilayer Diffusion of Drugs into Cells is Negligible? Trends Pharmacol. Sci 2015, 36, 15–21. [DOI] [PubMed] [Google Scholar]
- (14).Kramer SD Quantitative Aspects of Drug Permeation Across in Vitro and in Vivo Barriers. Eur. J. Pharm. Sci 2016, 87, 30–46. [DOI] [PubMed] [Google Scholar]
- (15).Avdeef A Permeability—PAMPA In Absorption and Drug Development; John Wiley & Sons, Inc.: Hoboken, NJ, 2012; pp 319–498. [Google Scholar]
- (16).Avdeef A Permeability: Blood−Brain Barrier In Absorption and Drug Development; John Wiley & Sons, Inc.: Hoboken, NJ, 2012; pp 575–680. [Google Scholar]
- (17).Avdeef A Permeability: Caco-2/MDCK In Absorption and Drug Development; John Wiley & Sons, Inc.: Hoboken, NJ, 2012; pp 499–574. [Google Scholar]
- (18).Lipinski CA Rule of Five in 2015 and Beyond: Target and Ligand Structural Limitations, Ligand Chemistry Structure and Drug Discovery Project Decisions. Adv. Drug Delivery Rev 2016, 101, 34–41. [DOI] [PubMed] [Google Scholar]
- (19).Bickerton GR; Paolini GV; Besnard J; Muresan S; Hopkins AL Quantifying the Chemical Beauty of Drugs. Nat. Chem 2012, 4, 90–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Andrade CH; Pasqualoto KF; Ferreira EI; Hopfinger AJ 4D-QSAR: Perspectives in Drug Design. Molecules 2010, 15, 3281–3294 [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Cherkasov A; Muratov EN; Fourches D; Varnek A; Baskin II; Cronin M; Dearden J; Gramatica P; Martin YC; Todeschini R; Consonni V; Kuz’min VE; Cramer R; Benigni R; Yang C; Rathman J; Terfloth L; Gasteiger J; Richard A; Tropsha A QSAR Modeling: Where Have You Been? Where Are You Going To? J. Med. Chem 2014, 57, 4977–5010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Damale MG; Harke SN; Kalam Khan FA; Shinde DB; Sangshetti JN Recent Advances in Multidimensional QSAR (4D–6D): a Critical Review. Mini-Rev. Med. Chem 2014, 14, 35–55. [DOI] [PubMed] [Google Scholar]
- (23).Tropsha A Best Practices for QSAR Model Development, Validation, and Exploitation. Mol. Inf 2010, 29, 476–488. [DOI] [PubMed] [Google Scholar]
- (24).Fujikawa M; Ano R; Nakao K; Shimizu R; Akamatsu M Relationships Between Structure and High-Throughput Screening Permeability of Diverse Drugs with Artificial Membranes: Application to Prediction of Caco-2 Cell Permeability. Bioorg. Med. Chem 2005, 13, 4721–4732. [DOI] [PubMed] [Google Scholar]
- (25).Liu J; Li Y; Pan D; Hopfinger AJ Predicting Permeability Coefficient in ADMET Evaluation by Using Different Membranes-Interaction QSAR. Int. J. Pharm 2005, 304, 115–123. [DOI] [PubMed] [Google Scholar]
- (26).Nitsche JM; Kasting GB A Correlation for 1,9-Decadien/Water Partition Coefficients. J. Pharm. Sci 2013, 102, 136–144. [DOI] [PubMed] [Google Scholar]
- (27).Nitsche JM; Kasting GB Permeability of Fluid-Phase Phospholipid Bilayers: Assessment and Useful Correlations for Permeability Screening and Other Applications. J. Pharm. Sci 2013, 102, 2005–2032. [DOI] [PubMed] [Google Scholar]
- (28).Nitsche JM; Kasting GB A Universal Correlation Predicts Permeability Coefficients of Fluid- and Gel-Phase Phospholipid and Phospholipid-Cholesterol Bilayers for Arbitrary Solutes. J. Pharm. Sci 2016, 105, 1762–1771. [DOI] [PubMed] [Google Scholar]
- (29).Stratton CF; Newman DJ; Tan DS Cheminformatic Comparison of Approved Drugs from Natural Product Versus Synthetic Origins. Bioorg. Med. Chem. Lett 2015, 25, 4802–4807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (30).Faller B; Ottaviani G; Ertl P; Berellini G; Collis A Evolution of the Physicochemical Properties of Marketed Drugs: Can History Foretell the Future? Drug Discovery Today 2011, 16, 976–984. [DOI] [PubMed] [Google Scholar]
- (31).Shinoda W Permeability Across Lipid Membranes. Biochim. Biophys. Acta, Biomembr 2016, 1858, 2254–2265. [DOI] [PubMed] [Google Scholar]
- (32).Leung SS; Mijalkovic J; Borrelli K; Jacobson MP Testing Physical Models of Passive Membrane Permeation. J. Chem. Inf. Model 2012, 52, 1621–1636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (33).Rezai T; Bock JE; Zhou MV; Kalyanaraman C; Lokey RS; Jacobson MP Conformational Flexibility, Internal Hydrogen Bonding, and Passive Membrane Permeability: Successful in Silico Prediction of the Relative Permeabilities of Cyclic Peptides. J. Am. Chem. Soc 2006, 128, 14073–14080. [DOI] [PubMed] [Google Scholar]
- (34).Awoonor-Williams E; Rowley CN Molecular Simulation of Nonfacilitated Membrane Permeation. Biochim. Biophys. Acta, Biomembr 2016, 1858, 1672–1687. [DOI] [PubMed] [Google Scholar]
- (35).Bemporad D; Essex JW; Luttmann C Permeation of Small Molecules Through a Lipid Bilayer: a Computer Simulation Study. J. Phys. Chem. B 2004, 108, 4875–4884. [Google Scholar]
- (36).Xiang TX; Anderson BD Liposomal Drug Transport: a Molecular Perspective from Molecular Dynamics Simulations in Lipid Bilayers. Adv. Drug Delivery Rev 2006, 58, 1357–1378. [DOI] [PubMed] [Google Scholar]
- (37).Lee CT; Comer J; Herndon C; Leung N; Pavlova A; Swift RV; Tung C; Rowley CN; Amaro RE; Chipot C; Wang Y; Gumbart JC Simulation-Based Approaches for Determining Membrane Permeability of Small Compounds. J. Chem. Inf. Model 2016, 56, 721–733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (38).Comer J; Schulten K; Chipot C Permeability of a Fluid Lipid Bilayer to Short-Chain Alcohols from First Principles. J. Chem. Theory Comput 2017, 13, 2523–2532. [DOI] [PubMed] [Google Scholar]
- (39).Zocher F; van der Spoel D; Pohl P; Hub JS Local Partition Coefficients Govern Solute Permeability of Cholesterol-Containing Membranes. Biophys. J 2013, 105, 2760–2770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (40).Sun R; Han Y; Swanson JMJ; Tan JS; Rose JP; Voth GA Molecular Transport Through Membranes: Accurate Perme ability Coefficients from Multidimensional Potentials of Mean Force and Local Diffusion Constants. J. Chem. Phys 2018, 149, 072310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (41).Palaiokostas M; Ding W; Shahane G; Orsi M Effects of Lipid Composition on Membrane Permeation. Soft Matter 2018, 14, 8496–8508. [DOI] [PubMed] [Google Scholar]
- (42).Orsi M; Sanderson WE; Essex JW Permeability of Small Molecules Through a Lipid Bilayer: a Multiscale Simulation Study. J. Phys. Chem. B 2009, 113, 12019–12029. [DOI] [PubMed] [Google Scholar]
- (43).Dickson CJ; Hornak V; Pearlstein RA; Duca JS Structure-Kinetic Relationships of Passive Membrane Permeation from Multiscale Modeling. J. Am. Chem. Soc 2017, 139, 442–452. [DOI] [PubMed] [Google Scholar]
- (44).Ghaemi Z; Minozzi M; Carloni P; Laio A A Novel Approach to the Investigation of Passive Molecular Permeation Through Lipid Bilayers from Atomistic Simulations. J. Phys. Chem. B 2012, 116, 8714–8721. [DOI] [PubMed] [Google Scholar]
- (45).Votapka LW; Lee CT; Amaro RE Two Telations to Estimate Membrane Permeability Using Milestoning. J. Phys. Chem. B 2016, 120, 8606–8616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (46).Cardenas AE; Jas GS; DeLeon KY; Hegefeld WA; Kuczera K; Elber R Unassisted Transport of N-Acetyl-L Tryptophanamide Through Membrane: Experiment and Simulation of Kinetics. J. Phys. Chem. B 2012, 116, 2739–2750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Tejwani RW; Davis ME; Anderson BD; Stouch TR An Atomic and Molecular View of the Depth Dependence of the Free Energies of Solute Transfer from Water into Lipid Bilayers. Mol. Pharmaceutics 2011, 8, 2204–2215. [DOI] [PubMed] [Google Scholar]
- (48).Carpenter TS; Kirshner DA; Lau EY; Wong SE; Nilmeier JP; Lightstone FC A Method to Predict Blood-Brain Barrier Permeability of Drug-Like Compounds Using Molecular Dynamics Simulations. Biophys. J 2014, 107, 630–641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (49).Wang Y; Gallagher E; Jorgensen C; Troendle EP; Hu D; Searson PC; Ulmschneider MB An Experimentally Validated Approach to Calculate the Blood-Brain Barrier Permeability of Small Molecules. Sci. Rep 2019, 9, 6117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (50).Shivakumar D; Deng Y; Roux B Computations of Absolute Solvation Free Energies of Small Molecules Using Explicit and Implicit Solvent Model. J. Chem. Theory Comput 2009, 5, 919–930. [DOI] [PubMed] [Google Scholar]
- (51).Roux B; Simonson T Implicit Solvent Models. Biophys. Chem 1999, 78, 1–20. [DOI] [PubMed] [Google Scholar]
- (52).Feig M; Brooks CL 3rd Recent Advances In the Development and Application of Implicit Solvent Models in Biomolecule Simulations. Curr. Opin. Struct. Biol 2004, 14, 217–224. [DOI] [PubMed] [Google Scholar]
- (53).Oren I; Fleishman SJ; Kessel A; Ben-Tal N Free Diffusion of Steroid Hormones Across Biomembranes: a Simplex Search with Implicit Solvent Model Calculations. Biophys. J 2004, 87, 768–779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (54).Cramer CJ; Truhlar DG Implicit Solvation Models: Equilibria, Structure, Spectra, and Dynamics. Chem. Rev 1999, 99, 2161–2200. [DOI] [PubMed] [Google Scholar]
- (55).Cramer CJ; Truhlar DG A Universal Approach to Solvation Modeling. Acc. Chem. Res 2008, 41, 760–768. [DOI] [PubMed] [Google Scholar]
- (56).Hornig M; Klamt A COSMOfrag: a Novel Tool for High-Throughput ADME Property Prediction and Similarity Screening Based on Quantum Chemistry. J. Chem. Inf. Model 2005, 45, 1169–1177. [DOI] [PubMed] [Google Scholar]
- (57).Klamt A; Huniar U; Spycher S; Keldenich J COSMOmic: a Mechanistic Approach to the Calculation of Membrane-Water Partition Coefficients and Internal Distributions within Membranes and Micelles. J. Phys. Chem. B 2008, 112, 12148–12157. [DOI] [PubMed] [Google Scholar]
- (58).Wittekindt C; Klamt A COSMO-RS as a Predictive Tool for Lipophilicity. QSAR Comb. Sci 2009, 28, 874–877. [Google Scholar]
- (59).Klamt A; Eckert F; Arlt W COSMO-RS: an Alternative to Simulation for Calculating Thermodynamic Properties of Liquid Mixtures. Annu. Rev. Chem. Biomol. Eng 2010, 1, 101–122. [DOI] [PubMed] [Google Scholar]
- (60).Jakobtorweihen S; Zuniga AC; Ingram T; Gerlach T; Keil FJ; Smirnova I Predicting Solute Partitioning in Lipid Bilayers: Free Energies and Partition Coefficients from Molecular Dynamics Simulations and COSMOmic. J. Chem. Phys 2014, 141, 045102. [DOI] [PubMed] [Google Scholar]
- (61).Ebert A; Hannesschlaeger C; Goss KU; Pohl P Passive Permeability of Planar Lipid Bilayers to Organic Anions. Biophys. J 2018, 115, 1931–1941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (62).Parisio G; Ferrarini A Solute Partitioning into Lipid Bilayers: an Implicit Model for Nonuniform and Ordered Environment. J. Chem. Theory Comput 2010, 6, 2267–2280. [DOI] [PubMed] [Google Scholar]
- (63).Lomize AL; Pogozheva ID; Mosberg HI Anisotropic Solvent Model of the Lipid Bilayer. 2. Energetics of Insertion of Small Molecules, Peptides, and Proteins in Membranes. J. Chem. Inf. Model 2011, 51, 930–946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (64).Chambers CC; Giesen DJ; Hawkins GD; Cramer CJ; Truhlar DG; Vaes WH J. Modeling the Effect of Solvation on Structure, Reactivity, and Partitioning of Organic Solutes: Utility in Drug Design In Rational Drug Design; Truhlar DG, Howe WJ, Hopfinger AJ, Blaney J, Dammkoehler RA, Eds.; Springer: New York, NY, 1999; Vol. 108, pp 51–72. [Google Scholar]
- (65).Lomize AL; Pogozheva ID; Mosberg HI Anisotropic Solvent Model of the Lipid Bilayer. 1. Parameterization of Long-Range Electrostatics and First Solvation Shell Effects. J. Chem. Inf. Model 2011, 51, 918–929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (66).Swift RV; Amaro RE Modeling the Pharmacodynamics of Passive Membrane Permeability. J. Comput.-Aided Mol. Des 2011, 25, 1007–1017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (67).Swift RV; Amaro RE Back to the Future: Can Physical Models of Passive Membrane Permeability Help Reduce Drug Candidate Attrition and Move Us Beyond QSPR? Chem. Biol. Drug Des 2013, 81, 61–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (68).Brocke SA; Degen A; MacKerell AD; Dutagaci B; Feig M Prediction of Membrane Permeation of Drug Molecules by Combining an Implicit Membrane Model with Machine Learning. J. Chem. Inf. Model 2019, 59, 1147–1162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (69).Parisio G; Stocchero M; Ferrarini A Passive Membrane Permeability: Beyond the Standard Solubility-Diffusion Model. J. Chem. Theory Comput 2013, 9, 5236–5246. [DOI] [PubMed] [Google Scholar]
- (70).Lomize AL; Pogozheva ID Prediction of Passive Membrane Permeability and Translocation Pathways of Biologically Active Molecules. Biophys. J 2017, 112, 525a. [Google Scholar]
- (71).Lomize AL; Pogozheva ID; Lomize MA; Mosberg HI Positioning of Proteins in Membranes: a Computational Approach. Protein Sci. 2006, 15, 1318–1333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (72).Lomize AL; Pogozheva ID; Lomize MA; Mosberg HI The Role of Hydrophobic Interactions in Positioning of Peripheral Proteins in Membranes. BMC Struct. Biol 2007, 7, 44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (73).Xiang TX; Anderson BD Influence of Chain Ordering on the Selectivity of Dipalmitoylphosphatidylcholine Bilayer Membranes for Permeant Size and Shape. Biophys. J 1998, 75, 2658–2671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (74).Marrink SJ; Berendsen HJC Permeation Process of Small Molecules Across Lipid Membranes Studied by Molecular Dynamics Simulations. J. Phys. Chem 1996, 100, 16729–16738. [Google Scholar]
- (75).Bemporad D; Luttmann C; Essex JW Computer Simulation of Small Molecule Permeation Across a Lipid Bilayer: Dependence on Bilayer Properties and Solute Volume, Size, and Cross-Sectional Area. Biophys. J 2004, 87, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (76).Abe T A Modification of the Born Equation. J. Phys. Chem 1986, 90, 713–715. [Google Scholar]
- (77).Block H; Walker SM Modification of Onsager Theory for a Dielectric. Chem. Phys. Lett 1973, 19, 363–364. [Google Scholar]
- (78).Pogozheva ID; Tristram-Nagle S; Mosberg HI; Lomize AL Structural Adaptations of Proteins to Different Biological Membranes. Biochim. Biophys. Acta, Biomembr 2013, 1828, 2592–2608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (79).Kučerka N; Nagle JF; Sachs JN; Feller SE; Pencer J; Jackson A; Katsaras J Lipid Bilayer Structure Determined by the Simultaneous Analysis of Neutron and X-Ray Scattering Data. Biophys. J 2008, 95, 2356–2367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (80).Lien EJ; Guo ZR; Li RL; Su CT Use of Dipole-Moment as a Parameter in Drug Receptor Interaction and Quantitative Structure Activity Relationship Studies. J. Pharm. Sci 1982, 71, 641–655. [DOI] [PubMed] [Google Scholar]
- (81).Li WY; Guo ZR; Lien EJ Examination of the Interrelationship Between Aliphatic Group Dipole-Moment and Polar Substituent Constants. J. Pharm. Sci 1984, 73, 553–558. [DOI] [PubMed] [Google Scholar]
- (82).Avdeef A pKa Determination In Absorption and Drug Development; John Wiley & Sons, Inc.: Hoboken, NJ., 2012; pp 31–173. [Google Scholar]
- (83).Manchester J; Walkup G; Rivin O; You Z Evaluation of pKa Estimation Methods on 211 Druglike Compounds. J. Chem. Inf. Model 2010, 50, 565–571. [DOI] [PubMed] [Google Scholar]
- (84).Hickey AL; Rowley CN Benchmarking Quantum Chemical Methods for the Calculation of Molecular Dipole Moments and Polarizabilities. J. Phys. Chem. A 2014, 118, 3678–3687. [DOI] [PubMed] [Google Scholar]
- (85).Hermone AR; Gussio R Calculation Methods for the Enhancement of Pharmaceutical Properties in Small Molecules: Estimating the Cationic pKa. Curr. Pharm. Des 2013, 19, 4310–4315. [DOI] [PubMed] [Google Scholar]
- (86).Henkelman G; Jόhannesson G; Jόnsson H Methods for Finding Saddle Points and Minimum Energy Paths In Theoretical Methods in Condensed Phase Chemistry; Schwartz SD, Ed., Springer; Netherlands: Dordrecht, 2002; pp 269–302. [Google Scholar]
- (87).Bolton EE; Chen J; Kim S; Han L; He S; Shi W; Simonyan V; Sun Y; Thiessen PA; Wang J; Yu B; Zhang J; Bryant SH PubChem3D: a New Resource for Scientists. J. Cheminform 2011, 3, 32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (88).Burley SK; Berman HM; Kleywegt GJ; Markley JL; Nakamura H; Velankar S Protein Data Bank (PDB): the Single Global Macromolecular Structure Archive. Methods Mol. Biol 2017, 1607, 627–641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (89).Groom CR; Bruno IJ; Lightfoot MP; Ward SC The Cambridge Structural Database. Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater 2016, 72, 171–179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (90).Kalyanaraman C; Jacobson MP An Atomistic Model of Passive Membrane Permeability: Application to a Series of FDA Approved Drugs. J. Comput.-Aided Mol. Des 2007, 21, 675–679. [DOI] [PubMed] [Google Scholar]
- (91).Cardenas AE; Shrestha R; Webb LJ; Elber R Membrane Permeation of a Peptide: It Is Better to Be Positive. J. Phys. Chem. B 2015, 119, 6412–6420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (92).MacCallum JL; Tieleman DP Computer Simulation of the Distribution of Hexane in a Lipid Bilayer: Spatially Resolved Free Energy, Entropy, and Enthalpy Profiles. J. Am. Chem. Soc 2006, 128, 125–130. [DOI] [PubMed] [Google Scholar]
- (93).Tse CH; Comer J; Wang Y; Chipot C Link between Membrane Composition and Permeability to Drugs. J. Chem. Theory Comput 2018, 14, 2895–2909. [DOI] [PubMed] [Google Scholar]
- (94).Hellinger E; Veszelka S; Toth AE; Walter F; Kittel A; Bakk ML; Tihanyi K; Hada V; Nakagawa S; Duy TD; Niwa M; Deli MA; Vastag M Comparison of Brain Capillary Endothelial Cell-Based and Epithelial (MDCK-MDR1, Caco-2, and VB-Caco-2) Cell-Based Surrogate Blood-Brain Barrier Penetration Models. Eur. J. Pharm. Biopharm 2012, 82, 340–351. [DOI] [PubMed] [Google Scholar]
- (95).Finkelstein A Water and Nonelectrolyte Permeability of Lipid Bilayer Membranes. J. Gen. Physiol 1976, 68, 127–135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (96).Xiang TX; Chen J; Anderson BD A Quantitative Model for the Dependence of Solute Permeability on Peptide and Cholesterol Content in Biomembranes. J. Membr. Biol 2000, 177, 137–148. [DOI] [PubMed] [Google Scholar]
- (97).Lomize A; Hage JM; Schnitzer K; Golobokov K; Lafaive MB; Forsyth AC; Pogozheva ID PerMM: A Web Tool and Database for Analysis of Passive Membrane Permeability and Translocation Pathways of Bioactive Molecules. J. Chem. Inf. Model 2019, DOI: 10.1021/acs.jcim.9b00225. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.