Structured odorant response patterns across a complete olfactory receptor neuron population

Summary

Odor perception allows animals to distinguish odors, recognize the same odor across concentrations, and determine concentration changes. How the activity patterns of primary olfactory receptor neurons (ORNs), at the individual and population levels, facilitate distinguishing these functions remains poorly understood. Here, we interrogate the complete ORN population of the Drosophila larva across a broadly sampled panel of odorants at varying concentrations. We find that the activity of each ORN scales with the concentration of any odorant via a fixed dose-response function with a variable sensitivity. Sensitivities across odorants and ORNs follow a power law distribution. Much of receptor sensitivity to odorants is accounted for by a single geometrical property of molecular structure. Similarity in the shape of temporal response filters across odorants and ORNs extend these relationships to fluctuating environments. These results uncover shared individual and population level patterns that together lend structure to support odor perceptions.

In Brief

The combinatorial olfactory code conveys odor stimulus features in an entangled manner. Si et al. uncover structure and statistical properties in ORN responses, allowing separated representations of odor features and shining light on the molecular recognition mechanism by olfactory receptors.

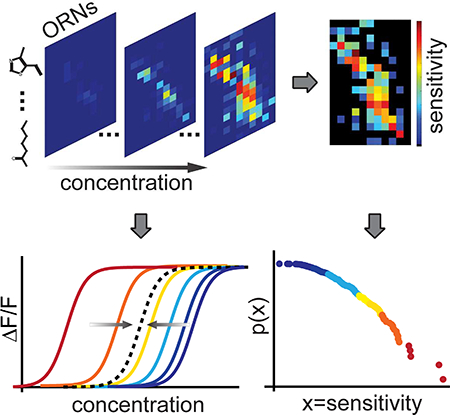
Graphical Abstract

Introduction

The ability to identify odorants across a wide range of concentrations and detect changes in odorant concentration are essential for olfactory perception and behavior. How olfactory representations are organized to support these distinct functions is not yet fully understood. In mammalian and insect olfactory systems, combinatorial receptor codes allow a limited number of olfactory receptor neurons (ORNs) to encode a large number of odorants (Malnic et al., 1999). Each ORN typically expresses one olfactory receptor (Or) type (Buck and Axel, 1991), but a single Or can be activated by many odorants and a single odorant can activate many Ors (Friedrich and Korsching, 1997). Different odorants can be discriminated by distinct activity patterns across a population of olfactory neurons (Hallem and Carlson, 2006; Kreher et al., 2008; Nara et al., 2011). The olfactory receptor code also conveys information about odorant intensity, as odorants at higher concentrations typically activate more ORNs (Kajiya et al., 2001; Wang et al., 2003). Odorants may also evoke different temporal response patterns in ORNs, augmenting information coding using time (De Bruyne et al., 2001; Friedrich and Laurent, 2001; Grillet et al., 2016; Junek et al., 2010; Raman et al., 2010).

Behavioral experiments in mammals and insects indicate that animals can distinguish and learn differences between odor identities and concentrations (Apostolopoulou et al., 2013; Chen et al., 2011; Mishra et al., 2013; Pelz et al., 1997; Uchida, 2008; Wang, 2004). Thus, olfactory perception likely requires the ability to independently represent both odor identity and intensity. Distinct and invariant representations of odor identity and intensity appear in neurons in central olfactory processing regions (Bolding and Franks, 2017; Roland et al., 2017; Sachse and Galizia, 2003; Stopfer et al., 2003; Wang, 2004). However, ORN activity patterns always reflect both odor identity and intensity in a seemingly intertwined manner. Increasing the concentration of any odor typically recruits more ORNs, altering the combinatorial activity pattern in a complex manner. Two previously described properties of ORN responses may help disentangle odor identity and intensity. First, the relative activity of different ORNs largely persists across concentrations of an odor (Cleland et al., 2007; Wachowiak et al., 2002). Second, normalized ORN responses exhibit a stereotyped distribution across odors. The mean population activity, used to normalize ORN responses, scales on average with odor concentration (Stevens, 2016). However, these studies lack the full dynamic range of individual ORN responses, leaving it unclear what and how properties of individual ORNs give rise to the emergent properties characteristic of the population. To assess the underlying mechanisms and further develop a statistical description of population responses requires a comprehensive analysis of ORN population activity, with single cell resolution, over a broad stimulus space that spans many odorants across varying intensities.

Here, we asked whether a complete olfactory receptor population has cellular and systems level properties that structure the responses to help disentangle odorant type and concentration dependent variations. We hypothesized that such properties might be reflected in functional relationships between individual and complete ORN responses to a broad set of odorant concentrations and types. We leveraged the experimental accessibility of the olfactory system of the Drosophila larva to search for quantitative structure in the responses of a complete primary olfactory population as well as in the sensitivity and dynamics of individual ORNs. The numerical simplicity of Drosophila olfactory neurons facilitates such a system-level dissection of a full set of ORNs. Furthermore, the larval ORNs form the first layer of an olfactory circuit that also shares glomerular organization with adult insects and vertebrates (Ramaekers et al., 2005; Su et al., 2009; Vosshall and Stocker, 2007).

To perform our study, we developed an in vivo imaging setup with microfluidics to simultaneously deliver highly controlled stimuli from a panel of 34 odorants while monitoring the responses of all ORNs with cellular resolution. Our odorant panel elicits activity in all 21 ORNs, allowing us to characterize the functional structure of the entire population. We find that all ORN-odorant pairs share the same activation or dose-response function: ORN activity increases with odorant concentration along the same Hill curve for any odorant, but with different sensitivities. Thus, the principal free variable that characterizes the interaction between any odorant molecule and any receptor is the sensitivity. We find that the statistical distribution of these sensitivities follows a power-law. The consequence of this power law is that the relative change of overall ORN activity becomes proportional to the relative change of odorant concentration, potentially simplifying the problem of how downstream neurons process information about odor intensity. In addition, the primary principal component of ORN sensitivities is correlated with a molecular property that describes the geometric and electrotopological states of odorants (Haddad et al., 2008). Finally, ORNs share a stereotyped temporal filter shape such that the observed similarities in odorant response patterns may also extend to fluctuating environments, underscoring the computational significance of these shared features. These structured ORN response patterns may constitute a simple strategy to represent odors.

Results

A microfluidic setup for in vivo calcium imaging of larval ORNs

To record from a population of olfactory neurons with single cell resolution, we developed a microfluidics setup for delivering a large range of odorant inputs while simultaneously imaging neural activity. Small size and optical transparency make the larva’s olfactory system - like that of C. elegans - suitable for in vivo multineuronal calcium imaging with microfluidic control of olfactory inputs (Chronis et al., 2007). Furthermore, fluid delivery of odorants allows for precise control of odorant concentration, stimulus waveform, and timing between stimulus delivery compared to gaseous odorant delivery (Andersson et al., 2012). Our microfluidic device allows for recording from an intact, immobilized, and un-anesthetized larva with as many as 24 fluid delivery channels (Figures 1A–1D and S1A–S1D). Calcium imaging and genetic labeling allow us to record the activity of any individual ORN alone or the activity of all ORNs simultaneously, by expressing the calcium indicator GCaMP6m (Chen et al., 2013) under the control of either a specific ORN Gal4 driver or the Orco-Gal4 driver, respectively (Vosshall et al., 1999). We use this microfluidic setup to perform single cell and population level recordings of olfactory processing in single animals exposed to inputs spanning a broad range of odorant types and concentrations.

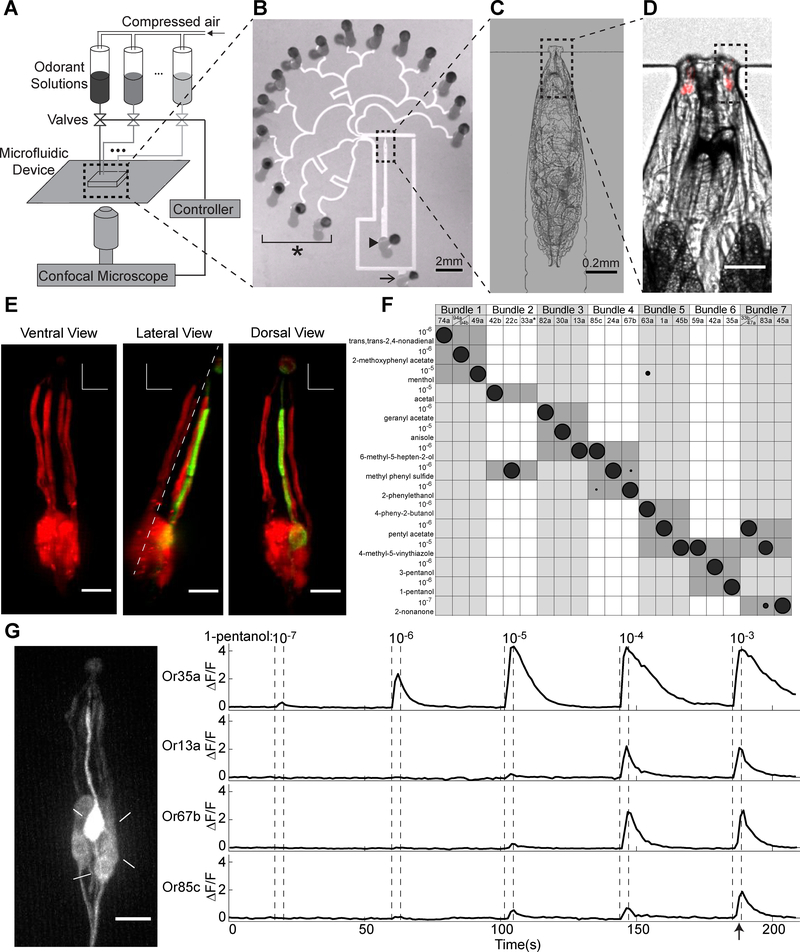
Figure 1. Anatomical and functional identification of individual ORNs within the complete population.

(A) Schematic of the microfluidic setup for odorant delivery and larval ORN calcium imaging.

(B) 16-channel microfluidic chip. Arrowhead marks inlet channel for loading a larva, arrow marks outlet channel for fluid waste, and * marks odorant stimuli delivery channels.

(C-D) Magnified views (10X in C and 40X in D) of an immobilized larva in the inlet channel. Red indicates RFP labeling of all ORN dendrites and cell bodies.

(E) Organization of the seven ORN dendritic bundles (numbered) in the larva. Or35a>GFP; Orco>RFP used to label all ORNs in red and the Or35a-ORN in green. Dashed line in lateral view marks separation between ventral and dorsal bundles.

(F) Functional mapping between each of 15 odorants that primarily activate a single ORN within each dendritic bundle, at low concentrations. Size of shaded circles indicates normalized neural activity level (ΔF/F) of the specified ORN to an odorant. * indicates inferred location of the Or33a-ORN based on dendritic bundle 2 vacancy (Figure S2).

(G) DOG cell body locations and GCaMP6m responses of four ORNs responsive to 1-pentanol (left). Fluorescence intensity changes for each of the four ORN cell bodies during pulsed presentations of increasing 1-pentanol concentrations (right). Arrow indicates time point at which left panel in G was captured. See also Figure S1, Figure S2 and Video S1.

Single ORN identification from population recordings

We sought to efficiently record ORN population responses to many odorant stimuli in the same animal with single cell identification. To do this, we developed a method to unambiguously identify all 21 ORNs during population recordings. First, we assessed the stereotypy of larval ORN anatomical organization. We found that the layout of ORN dendrites aids in segmenting and identifying cells during calcium imaging. The larva has 21 ORNs located in each bilaterally symmetric dorsal organ ganglion (DOG). The 21 ORN dendrites are organized into seven parallel bundles, each containing three dendrites, that project from an ORN cell body to a perforated dome structure on the animal’s head called the dorsal organ (Singh and Singh, 1984). When a larva is immobilized in the microfluidic device, four ventral and three dorsal dendritic bundles are easily distinguished (Figure 1E). We mapped individual ORNs to each bundle by expressing RFP in all ORNs and GFP in a selected ORN using a cell-specific Gal4 driver (Fishilevich et al., 2005; Kreher et al., 2005) ( Figure S2). We found that the three ORN dendrites located in each bundle were stereotyped (confirmed in n ≥ 5 animals for each ORN). Thus, by following the activation of any cell body in the DOG to its corresponding dendritic bundle, we narrowed its possible identity to one of three ORNs.

To complete the identification of individual ORNs, we used a set of odorants that activate single ORNs of known identity at low concentrations (Mathew et al., 2013) (see Methods). We delivered these odorants to larvae expressing GCaMP6m in all ORNs and found that 15 of these odorants are sufficient to identify each ORN when examined in conjunction with dendritic bundle location (Figure 1F). Together, the anatomical map and functional responses to this subset of odorants provides a comprehensive means of identifying and segmenting the ORNs responsive to any olfactory input during multi-neuronal calcium imaging.

Orthogonality of odorant identity and intensity in ORN population activity

We next searched for general patterns in population level olfactory responses that might emerge from a sufficiently broad analysis of odorant types and intensities. We assembled a panel of 34 odorants that broadly samples the full olfactory sensitivity of larval ORNs (see Methods and Figure S3A). This panel primarily contains odorants that are components of fruits or plant leaves, which make up the larva’s natural environment (Dweck et al., 2018), and have been shown to elicit innate attractive or aversive behavior in the larva (Table S1). Furthermore, these odorants have molecular structures that span a variety of functional groups, such as esters, alcohols, aromatics, aldehydes, ketones, pyrazines, thiazoles, and phenyl groups. To characterize the ORN representation of these stimuli, we simultaneously recorded from all ORNs while exposing larvae to all 34 odorants across the concentration range of olfactory sensitivity. Using our anatomical and functional ORN identity mapping method in addition to intensity based registration and segmentation methods (Pnevmatikakis et al., 2016; Thévenaz et al., 1998), we quantified each ORN’s peak response (Figures S3B). The peak response was defined as the highest ORN activity during odorant delivery. We found that all 21 ORNs in each DOG were responsive to at least one odorant in the panel.

We measured the response amplitude of every ORN to step stimuli across five orders of magnitude in concentration, from 10⁻⁸ dilution (where all odorants were at or below the threshold of ORN detection) to 10⁻⁴ dilution (where many ORNs reached saturation). We used five second step pulses interleaved with 20–60 seconds of water, a protocol that allowed for us to measure peak responses and for full recovery of neural activity (Figure S1E–S1F). We measured ORN activity using the calcium indicator GCaMP6m, a sensitive reporter of neural excitation. Previous studies have reported that some odor molecules can inhibit some ORNs in Drosophila and other insects (Cao et al., 2017; Hallem and Carlson, 2006; Tichy et al., 2005). We did not observe odorant induced inhibition across ORNs, although the low background intensity of GCaMP6m makes it much more sensitive to excitatory than inhibitory responses. We note that calcium imaging also limits our temporal resolution to that of the GCaMP6m indicator (Chen et al., 2013).

We found that ORNs that are most sensitive to particular odorant are also more sensitive to molecules with similar chemical structure. For example, the long chain alcohol 1-pentanol slightly evoked activity specifically in the Or35a-ORN at a 10⁻⁷ dilution. Higher concentrations of 1-pentanol gradually saturated the Or35a-ORN, while also activating four other ORNs expressing either Or67b, Or85c, O13a, or Or1a (Figure 1G and Video S1). The additional ORNs recruited by 1-pentanol were also activated at low concentrations by other long chain alcohol odorants (Mathew et al., 2013). We next examined the population-wide dose-response curves for these additional alcohol odorants. Low concentrations of each alcohol specifically activated a distinct ORN. Higher concentrations reliably activated the Or35a, Or13a, Or67b, and Or85c ORNs to varying degrees (Figure S3C). We then collected dose-dependent responses across the entire ORN population for all 34 odorants, with at least five animals per odorant (Figure 2A). Specific activation of single ORNs at low concentrations (10⁻⁷ and 10⁻⁶ dilutions) is in agreement with previous reports (Mathew et al., 2013). We found a similar pattern of overlapping activation for ORNs that were selectively responsive to odorants with similar molecular structures at low concentrations.

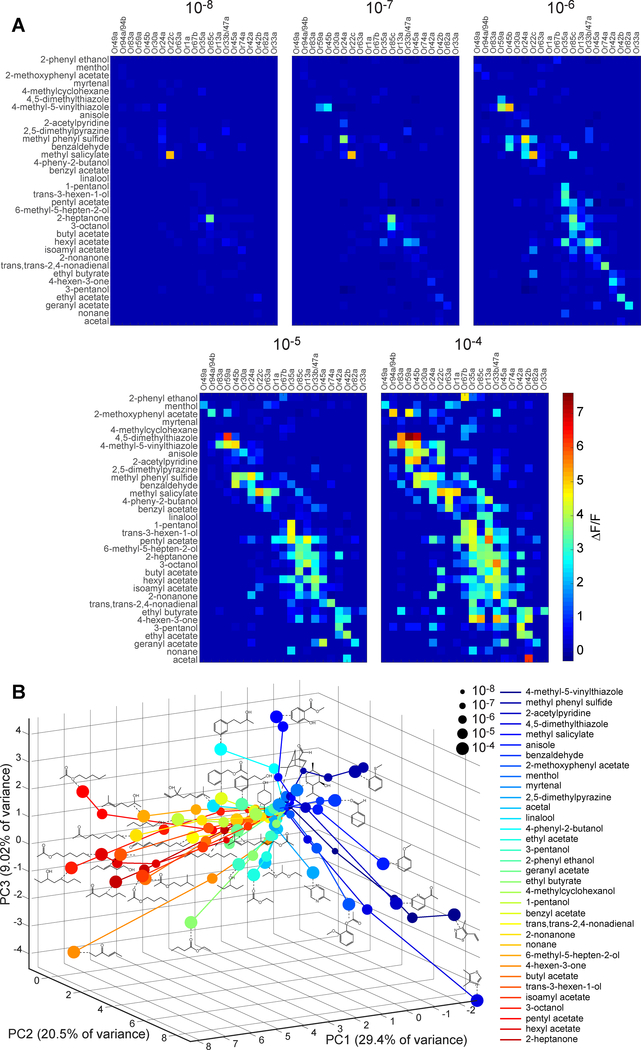
Figure 2. Orthogonality of odorant identity and intensity in ORN population activity.

(A) Averaged peak responses of all 21 ORNs to a panel of 34 odorants, each delivered at five concentrations (n ≥ 5 for each odorant type and concentration; odorant pulse duration = 5 s).

(B) PCA of ORN population responses. Colored dots represent the projection of ORN population activity onto the first three principal components. Size and color of dots correspond to odorant concentration and type, respectively. Dots from the same odorant are linked and the molecular structure of the odorant is shown adjacent to each trajectory. Aromatic versus aliphatic odorants cluster in separate regions of PCA space. See also Figure S3, Table S1 and Data S1.

As in other animals, the combinatorial olfactory activity pattern changes with increasing odorant intensity (Malnic et al., 1999), and with a pattern of ORN recruitment that is correlated with molecular selectivity. To discern this pattern, we performed principal component analysis (PCA) on the ORN population activity responses to all 34 odorants across all five concentrations (i.e., PCA across 170 odorant-concentration pairs). We projected ORN activity responses in the space of the first three principal components, which accounts for 60% of the variance in the data (Figure 2B). At the lowest concentrations, olfactory representations at or below detection thresholds were tightly clustered at a central point in the PCA space. At higher concentrations, olfactory representations diverged, increasing distance monotonically from the central point. Interestingly, the trajectory of each odorant tended to follow its own direction in PCA space. This pattern is particularly clear for aliphatic and aromatic odorants. Aliphatic odorants with long carbon chains form trajectories projecting in a similar direction of PCA space, since higher concentrations of these odorants tend to selectively recruit ORNs that are also sensitive to aliphatic odorants. The same was true for aromatic odorants and their corresponding group of sensitive ORNs. Clustering of ORNs as primarily responsive to aliphatic or aromatic odorant types agrees with previous Drosophila ORN electrophysiology recordings using large panels of odorant and natural odor stimuli (Dweck et al., 2018; Kreher et al., 2008). The trajectories corresponding to structurally similar molecules are separated by small angles (Figure 2B). Visualization of ORN responses in PCA space reveals structure in the population representation of odorant identity over a large range of intensities. The population wide response maintains a fixed direction in the representation of each odorant with rising concentration. This property also holds true for temporal responses of the ORN population over the course of stimulus delivery (see Methods and Figure S3D).

A Hill function with variable sensitivity describes dose-response relationships

We uncovered shared structure in each ORN’s activation function when we compared all odorant-ORN pairs that reached saturation (n=36 pairs). We found that the dose-response curves were well described by a Hill function:

$$y=A_{max}\frac{c^n}{c^n+E{C_{50}}^n},$$

where A_max is the maximum response amplitude measured by the calcium indicator, c is the odorant concentration, n is the Hill coefficient or steepness of the linear portion of the curve, and EC₅₀ is the half-maximal effective concentration. The Hill function canonically describes binding affinities in ligand-receptor interactions such as that between odorants and olfactory receptors. We performed a population fit on the 36 saturated dose-response curves to the Hill function and find that all curves were well fit by a shared Hill coefficient with R² = 0.99 (see Methods, Figure S4A). Each recorded neuron reaches a similar saturated response amplitude (A_max) across different molecules within each experiment (Figure S4B–S4C). The amplitude normalized dose-response curves, aligned by the EC₅₀, collapse onto a single Hill function with n = 1.42 (Figure 3A).

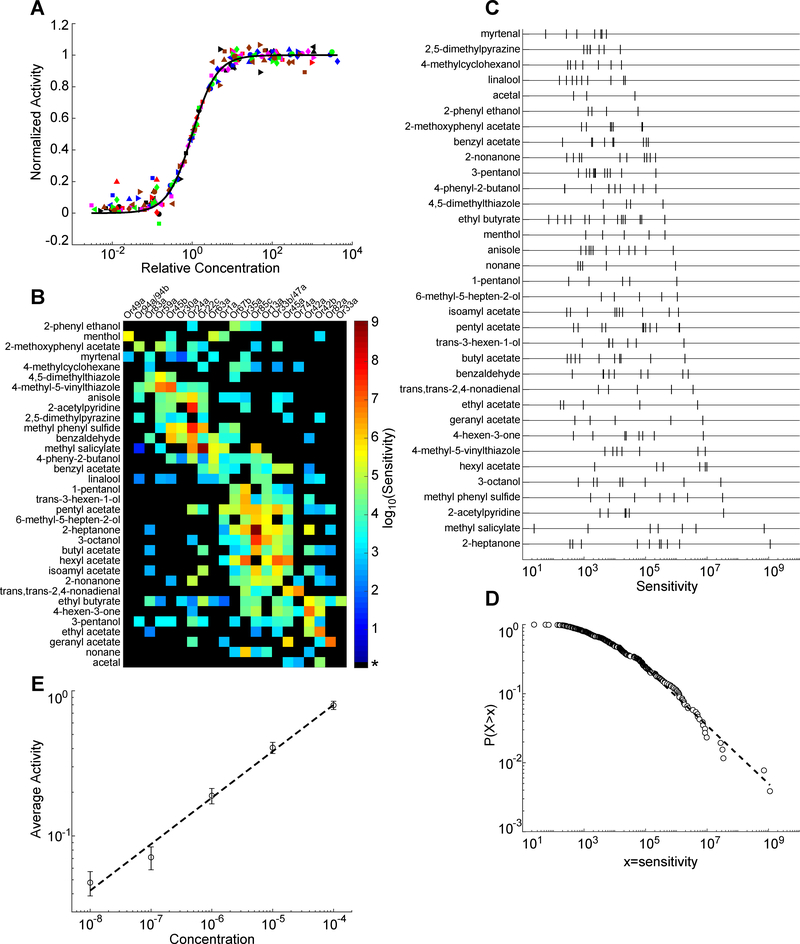
Figure 3. Individual ORNs share a common activation function and population sensitivities follow a power law distribution.

(A) Normalized ORN responses across relative odorant concentration (actual concentration divided by EC₅₀), for odorant-ORN pairs reaching saturation. Individual curves for plotted odorant-ORN pairs collapse onto a single curve described by a Hill equation with a shared Hill coefficient of 1.42. Black line indicates the Hill equation fit. Each distinct colored and shaped point represents data from an unique odorant-ORN pair.

(B) Heatmap of the logarithm of sensitivity values, log₁₀(1/EC₅₀), from each odorant-ORN pair. * for black elements indicates odorant-ORN pairs that had no response within the tested concentration range.

(C) Raster plot of ORN sensitivities (defined as 1/EC₅₀) for each odorant. Each tick mark represents an ORN.

(D) Log-log plot of the cumulative distribution function of ORN sensitivities across all odorants. Dashed line is a linear fit to the data with slope = −0.42.

(E) Log-log plot of average neuron activity (ΔF/F) across all odorant-ORN pairs for each concentration. Error bars = SEM. Slope of least-squares fit line = 0.32 ± 0.06 (R² = 0.99). See also Figure S4 and Table S2.

We further sought to determine the EC₅₀ values for unsaturated odorant-ORN pairs. To this end, we used a maximum-likelihood based method (see Methods) to estimate the mean EC₅₀ value for each odorant-ORN pair. Our only constraint on the estimation was that the amplitude and Hill coefficients had shared mean values across all measurements, an assumption supported by the 36 activity curves that reached saturation. Using this method, we were able to extract EC₅₀ values for the majority of odorant-ORN pairs. EC₅₀ values spanned several orders of magnitude. We assembled a matrix of odorant-ORN sensitivity (the inverse of EC₅₀), which is most easily visualized on a logarithmic scale (Figure 3B). This sensitivity matrix, combined with the activation functions with shared Hill coefficients, was able to account for 99% of the variance in the entire dataset of odorant-ORN interactions across all concentrations (Figure S4D).

We conclude that a common Hill function, with the sensitivity as the principal free parameter, describes the dose-response relationship for any odorant-ORN interaction. For each odorant, the vector of sensitivity (a row in the matrix in Figure 3B) specifies the identity and threshold of each activated ORN with increasing odorant concentration. A corollary of having a unique sensitivity vector for each odorant is having a unique direction for the trajectory of population responses in principal component space across concentrations (Figure 2B).

ORN population sensitivities follow a power law distribution

Next, we examined the probability distribution of ORN sensitivities. For each odorant, responsive ORNs were distributed along a sensitivity axis, with most ORNs in the low sensitivity region (Figure 3C). The density of ORNs diminishes with increasing sensitivities, generating a heavy-tailed probability distribution. To quantify this distribution, we constructed a cumulative density function of ORN sensitivities that is well fit by a line in a log-log plot, indicative of a power law (Figure 3D). The probability density function is described by: P(x) ∝ x^−λ−1, λ = 0.42 for x > 4.2 × 10⁴ (methods from (Clauset et al., 2009)). We compared the fitting of the power law with other heavy-tailed distributions and concluded that the power law is the simplest form with a good fit to the probability density of odorant-ORN sensitivities (see Methods and Table S2).

A power law distribution of ORN sensitivities means that a relative change of concentration of any odorant will trigger, on average, the same relative change in the number of activated ORNs. The power law distribution of ORN sensitivities, together with a common Hill function, should give rise to population-wide activity that follows a power law relationship with respect to concentration, with exponent λ (See Methods). We confirmed this prediction in our experimental data (Figure 3E). The mean activity of the ORN population grows with odorant concentration following a power law with an exponent of 0.32±0.06, which is close to the exponent found from fitting the sensitivity distribution (Figure 3D). The power function in a log scale is a linear relationship, such that log(A) ∝log(c), where A is ORN population activity and c is odorant concentration. Thus, on average, the relative change of the ORN population activity is proportional to the relative change of odorant concentration, $d(\log (A))\propto d(\log (c))=\frac{dA}{A}\propto \frac{dc}{c}$ (as shown in Figure 3E).

Correlations in ORN sensitivities correspond to molecular structure

We used principal component analysis to study the structure of the sensitivity matrix (see Methods). We found that the first principal component in odorant space of the logarithmically scaled matrix explains a significant portion of the variance compared to shuffled data (Figure 4A). The eigenvector of the 1^st principal component indicates the relative weights of different ORNs along its axis. As shown in Figure 4B, neurons that prefer long chain alcohols (e.g., Or35a, Or13a, and Or85c) and neurons that prefer aromatic odorants (e.g., Or45b, Or59a, and Or24a) are at opposite extremes. Arranging all 34 odorants by their projection on the 1^st principal component, a clear trend based on molecular structure emerges, progressing from long carbon chains on one end to aromatic molecules on the other (Figure 4C).

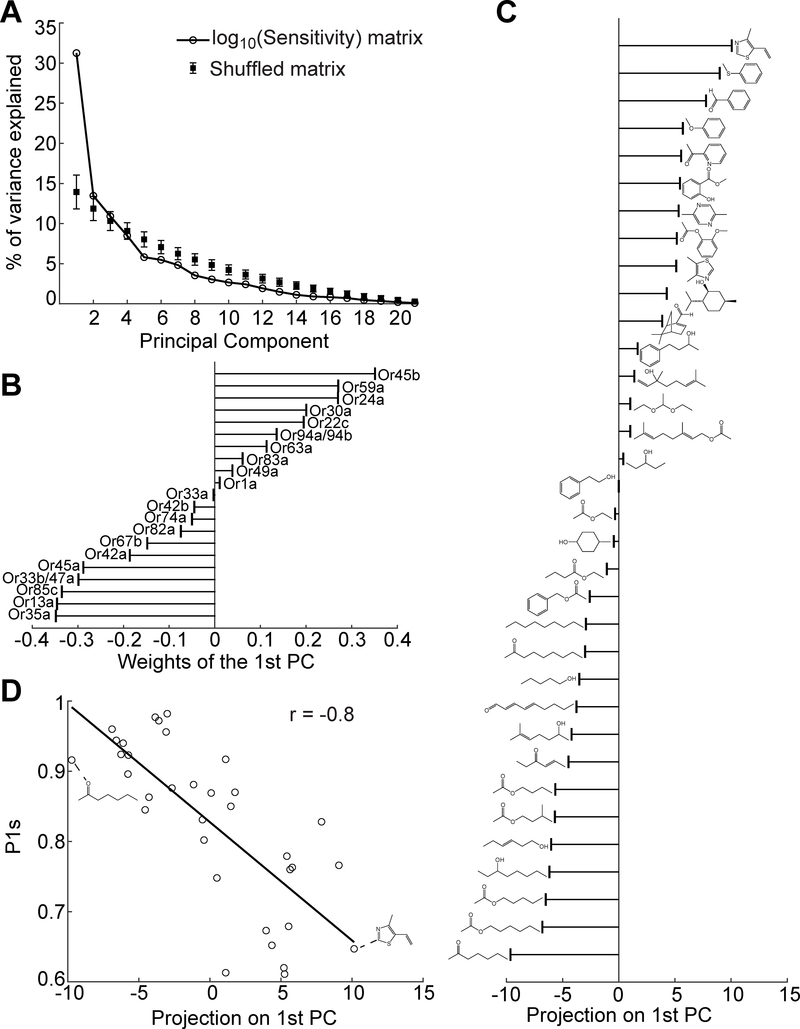
Figure 4. Correlation between ORN-odorant sensitivities and odorant molecular structure.

(A) Percentage of variance explained by each principal component of the ORN sensitivity matrix in Figure 3B. Data compared with the results from 1000 randomly shuffled matrices.

(B) Weights indicating each ORN’s contribution to the 1^st principal component.

(C) Each odorant’s (indicated by molecular structure) projection onto the 1^st principal component.

(D) Correlation between each odorant’s projection on the 1^st principal component and the most correlated molecular descriptor, P1s.

To further examine the correlation with molecular structure, we considered an extensive list of molecular descriptors that were found to be relevant to odor discrimination across animal species (Haddad et al., 2008). We found that one of these molecular descriptors, “P1s”, has the highest correlation to the first principal component (Figure 4D, correlation coefficient(r) = −0.8). “P1s” is a geometric descriptor of molecular structure weighted by atomic electrotopological state. 1D long-chain molecules have large P1s values and 2D ring-like molecules have small values (see examples in Figure 4D) (Todeschini and Lasagni, 1994). The dominance of the “P1s” molecular descriptor is in agreement with the trajectories of aromatic and aliphatic odorant representations pointing in opposite directions in Figure 2B.

ORN-odorant responses share similar temporal characteristics

An additional challenge to olfactory coding of a wide variety of odorant types across concentrations arises from complex temporal dynamics due to physical fluctuations, such as turbulence or convection, in the stimulus itself. To examine how fluctuations affect ORN responses, we compared the conversion of temporal patterns of olfactory input for different odorant-ORN pairs across odorant intensities (Figure 5). To do this, we used reverse-correlation analysis, subjecting larvae to “white noise” olfactory input by stochastically switching between odorant and water delivery and seeking the temporal filter that best maps olfactory inputs into calcium dynamics (Figure 5A) (Geffen et al., 2009; Kato et al., 2014). We found that random olfactory input could evoke fluctuating calcium activity in an ORN, and repeated presentation of the same input pattern would evoke consistent normalized responses from animal to animal (Figure S5A). The systematic conversion of the stimulus to response waveform is well characterized by a linear-nonlinear (LN) model. A linear transfer function estimates the relative weight of each time point in stimulus history to determine the time-varying response amplitude (Figure 5B). The convolution of the linear transfer function with stimulus history is then passed through a static nonlinearity to correct for saturation (Figure S5B). We verified the LN model by predicting the response to a novel random input using a filter calculated from different random inputs (Figure S5C). To make comparisons across odorants, concentrations, and ORNs we used normalized response amplitudes that preserve temporal characteristics encoded in the filter shape.

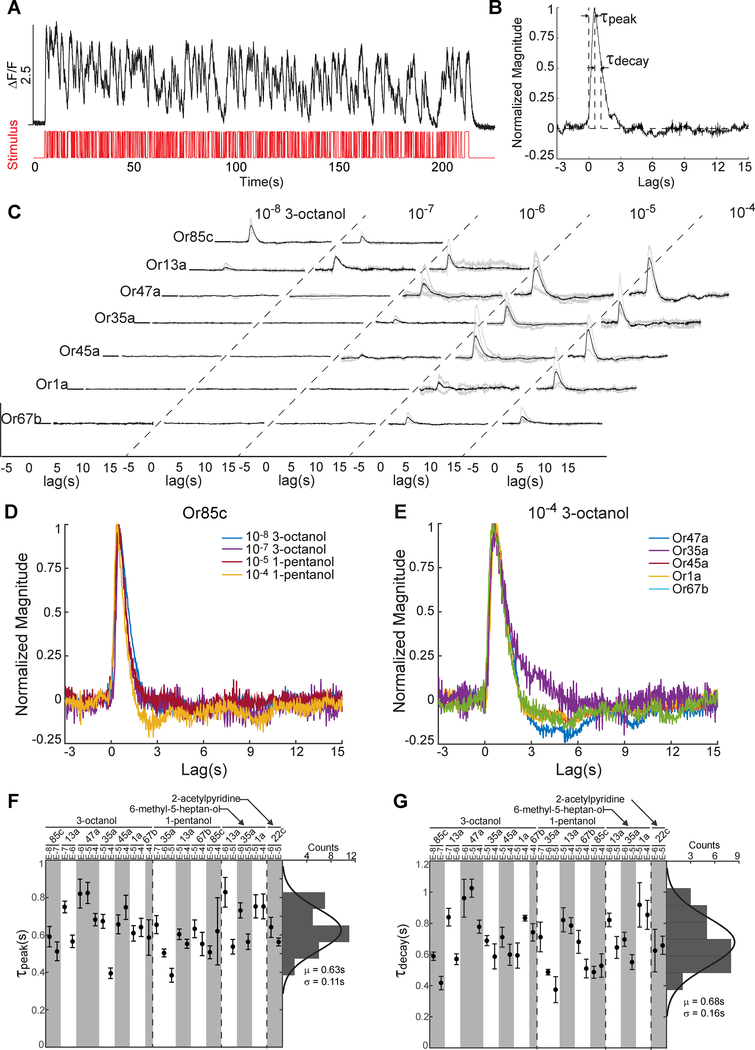
Figure 5. Common temporal signal processing across ORNs.

(A) Or42a-ORN response to an m-sequence delivery of 3-pentanol at 10⁻⁷ dilution. Red indicates on-off stimulus sequence over time and black curve indicates ORN response.

(B) Linear filter calculated via reverse-correlation analysis from the data shown in A.

(C) Linear filters of seven ORNs responding to 3-octanol across five concentrations. Black curve indicates the averaged filter from data across multiple animals (individual filters shown in gray).

(D-E) Comparison of filter waveforms for the same odorant (10⁻⁴ dilution of 3-octanol) activating different ORNs (D), and the same ORN (Or85c) responding to different odorants and concentrations (E). All filters were normalized by their peak amplitude.

(F-G) Distribution of peak time (F) and decay time (G) of 31 averaged filters measured from various ORN and odorant stimuli. Distributions of peak and decay times were fit to Gaussian distributions with mean and variance indicated below each histogram. See also Figure S5 and Video S2.

We measured the linear transfer function for 3-octanol as it has a relatively broad recruitment of ORNs across the concentration range studied. At the lowest concentrations of 3-octanol, a filter describing ORN activity only emerges for the Or85c-ORN (Figure 5C). At higher concentrations, filters begin to emerge for additional ORNs. These filters for each ORN, when normalized for response amplitude, were virtually identical in their temporal response profiles as single lobed functions with similar peak and decay times (Figures 5D–5E and S5D). The shapes of the filters for different odorants activating the same ORN are also virtually indistinguishable, on the order of ~100 ms (Figure 5F–5G). Thus, the rank order of the ORN responses could be preserved in an environment with fluctuating odor intensities.

Discussion

Olfactory receptor neurons have diverse tuning properties to odorant molecules. This diversity forms a combinatorial receptor code that represents a broad range of odorant molecules across concentrations. Changes in concentration lead to changes in the combinatorial pattern of activated ORNs, potentially complicating the ability to separate differences in odor identity and odor intensity. Here, we asked whether olfactory receptor neurons, at the individual and population levels, display structured response patterns that might facilitate in separating such differences. Previous efforts at characterizing Drosophila ORNs necessarily focused analysis on particular ORN types, odorants or odorant concentrations (Asahina et al., 2009; Hallem and Carlson, 2006; Martelli et al., 2013; Mathew et al., 2013; Nagel and Wilson, 2011). Electrophysiological studies of larval olfactory receptors, expressed in “empty olfactory neurons” of the adult fly, revealed the tuning of individual receptors to large numbers of odorant molecules (Kreher et al., 2008; Mathew et al., 2013). Calcium imaging of larval ORNs directly revealed how subsets of larval ORNs are activated by selected odorants and concentrations (Asahina et al., 2009). This study bridges these pioneering efforts with an analysis of population-wide olfactory responses with single cell resolution across a broad olfactory space. The small size of the Drosophila larva, combined with multi-neuronal imaging and new microfluidic tools, has allowed us to characterize the responses of a complete ORN population to a panel of odorant types and concentrations that fully spans the sensitivity of larval ORNs.

Our broad characterization has uncovered features in the response patterns of individual ORNs and of the ORN population that are shared across different ORNs and across odorants. At the level of individual neurons, each ORN response to odorants exhibits the same activation function shape with varying sensitivity levels. At the level of the population, the relative change of ORN activity across all tested odorants is proportional to the relative change of odorant concentration, a consequence of a power law that describes the sensitivity distribution of ORNs. Furthermore, a common temporal filter shape converts different stimulus waveforms into ORN calcium activity patterns. Here, we discuss the functional implications of such shared structure in ORN responses, and we connect our findings to computations thought to occur in the early olfactory system.

Common activation function across ORN-odorant pairs

We confirmed that a shared activation function across ORNs and odorants is consistent with available electrophysiological recordings of Drosophila ORNs, which also reveal activation functions across concentrations that can be fit to Hill curves with shared coefficients (see Methods and Figure S4H–S4I)(Kreher et al., 2008). The exact value of the Hill coefficient for activation functions corresponding to spike rates (~0.7) and calcium dynamics (~1.4) are different, likely reflecting the nonlinear transformation between electrical activity and calcium activity across ORNs. Common activation functions have also been observed for subsets of ORNs responding to molecularly similar odorants in the cockroach antenna and the rat olfactory bulb (Meister and Bonhoeffer, 2001; Sass, 1976).

The underlying molecular basis for shared activation functions across receptor types may be similar stoichiometries in odorant/receptor binding across Ors and/or similar internal signaling pathways for spike generation across ORNs. Nagel and Wilson, 2011 found that dynamics of spike generation were highly stereotyped from ORN to ORN. Common signaling pathways would be consistent with the observation that expressing an Or in different ORNs or the endogenous ORN lead to similar tuning properties and background firing rates (Hallem et al., 2004). Such a property could be analogous to that of photoreceptors in the visual system. Red and green cones share a similar shape in their response profiles across wavelengths. The only difference in their stimulus evoked activity patterns is their spectral sensitivity (Naka and Rushton, 1966).

A common activation function across odorant and receptor types is one component of correlations in ORN response patterns across olfactory space. Shared activation functions and the sensitivity distribution across ORNs likely allow the vector representation of any odorant to maintain a similar direction across concentrations. An uniform intraglomerular transfer function from ORNs to second order projection neurons (PNs) has been described in the adult Drosophila antennal lobe (Olsen et al., 2010). Together, these common functions allow the olfactory system to maintain distinct representations of different odorants that are stable across concentrations as has been demonstrated by (Sachse and Galizia, 2003; Stopfer et al., 2003). Our work suggests that an intensity invariant aspect of odor representation - the direction of the activity vector in principal component space - already emerges at the ORN layer, and this property may be carried forward to the PN layer.

Power law distribution in olfactory sensitivities across ORNs

Different neurons are required to sense odorants in different regimes of odorant concentration needed for long-range chemotaxis, in the Drosophila larva (Asahina et al., 2009). Encoding a broad concentration range requires a distribution of ORNs with varying sensitivities. We find that these olfactory sensitivities are drawn from a power law distribution.

To our knowledge, a power law distribution of olfactory sensitivities has not yet been described in any animal. One possibility for the power law in olfactory sensitivity is to match the distributions of odorant concentrations found in natural olfactory environments. Natural odors are mixed by convection and turbulence, physical processes that are rich in power law dynamics (Celani et al., 2014; Murlis, 1992; Riffell et al., 2008). Power laws appear in the statistics of other natural stimuli as well. Natural visual scenes exhibit a power law relationship between spectral power and spatial frequency (Field, 1987; Simoncelli and Olshausen, 2001). The loudness of natural sounds across frequencies are distributed by power laws (Theunissen and Elie, 2014). Sensory systems, in general, may adapt the statistical distribution of their sensitivities to their natural environments.

The natural environment may drive the selection of a molecular recognition mechanism for olfactory receptors that gives rise to a power law distribution in ORN sensitivities. Lancet et al., 1993 proposed a molecular recognition system in which a receptor has multiple selective binding subsites. Each binding subsite contributes in a combinatorial manner to the binding strength between a receptor and molecule. This simple probabilistic model generates a power law sensitivity distribution for receptors with random sets of binding subsites. The statistics of an olfactory code using such a molecular recognition system would be preserved with expansion of the ORN periphery, as occurs with Drosophila in which the adult has nearly triple the number of receptor types as that found in the larva.

A power law distribution implies a fixed ratio between the relative change in ORN population activity for a relative change in odorant concentration. Detection of relative change in stimulus intensities has been observed in psychophysical studies of diverse sensory modalities. A notable example is Stevens’s Law in human psychophysics, where perceived response magnitudes have been shown as a power function of actual stimulus intensities (F(I)~Iⁿ), across many sensory modalities including olfaction (Stevens, 1957). Our results reveal that a phenomenon analogous to Stevens’s Law can be attributed to the olfactory sensory periphery itself, a direct outcome of the statistical distribution of response sensitivities across the ORN population. Cao et al. (Cao et al., 2016; Gorur-Shandilya et al., 2017) find that at the individual ORN level, adaptation scales ORN gain with respect to odorant concentration according to the Weber-Fechner Law. These findings are complementary to our study, which expands the scaling observation to the entire ORN population and across several orders of magnitude in concentration. Together these results suggest that multiple complementary mechanisms underlie the Weber-Fechner and Steven’s Law.

Common temporal signal processing across ORNs

We observed a common temporal filter shape across ORNs in an environment with fluctuating odorant concentrations. Although calcium imaging limited our ability to resolve possible temporal differences in these filters faster than ~100 ms, we note that Martelli et al. (2013) also reported remarkable similarities in their measurement of temporal filters for LN models that connect odorant dynamics to electrical activity in adult Drosophila ORNs (Martelli et al., 2013). Common temporal filters are also consistent with the observation of a fixed degree and kinetics of adaptation in ORNs (Martelli et al., 2013).

A constant temporal filter in conjunction with uniform ORN activation function over concentrations could allow a population of responsive neurons to maintain the same relative amplitudes of activation in a static or fluctuating odorant environment. Instantaneous olfactory representations would not change simply because each ORN has a different rate of activation or inactivation in response to the same changes in odor concentration. Constant temporal filters across ORNs may arise from stereotyped transduction dynamics among ORNs. Thus, a common temporal filter shape across ORNs could preserve the olfactory code in an environment with fluctuating odor concentrations.

Implications for olfactory processing

Shared patterns in single and population level ORN responses across olfactory space are in agreement with previously described circuit mechanisms in the antennal lobe, the first olfactory processing center in Drosophila. Normalization is thought to occur through a class of local interneurons that receive and pool inputs from all ORNs, thereby normalizing the olfactory representation across concentrations through inhibitory feedback (Olsen and Wilson, 2008; Olsen et al., 2010). Anatomical studies in the larva have revealed the class of local interneurons that could carry out this normalization function (Berck et al., 2016). The shared activation function across ORNs and across odorants could benefit this circuit mechanism by preserving the rank order of ORN activity before and after normalization, helping maintain odorant identification and discrimination across varying intensities. The power law distribution of sensitivities means that most ORNs will be weakly active for most odors at most concentrations. A nonlinear transformation from ORNs to PNs during divisive normalization helps amplify the signal of weakly active ORNs (Olsen et al., 2010), benefitting the population level representation.

For animals that sniff, the change in concentration through inhalation generates a temporal sequence of ORN activity, reflecting the order of olfactory sensitivities for the inhaled odorant molecules. In a primacy code for odorant identification, animals use the first set of activated ORNs to recognize an odor (Wilson et al., 2017). Such a code would benefit from shared activation functions across ORNs by preserving the rank order of ORN activation as odorants are sniffed at different concentrations. Furthermore, high sensitivity ORNs are generally less densely distributed along the sensitivity spectrum, in relation to other ORNs. Thus, the sensitive ORNs would be the most informative for odor identification by the primacy code since they are more separated.

In conclusion, this study highlights properties of individual ORNs (common activation functions with different sensitivities) and of the ORN population (a power law distribution of sensitivities) that may reflect simple strategies for representing odor identity and intensity. In the future, it will be interesting to examine how downstream olfactory neurons ultimately extract and use the described structure in ORN responses.

STAR METHODS

Contact for Reagent and Resource Sharing

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Dr. Aravinthan Samuel (samuel@physics.harvard.edu).

Experimental Model and Subject Details

Drosophila melanogaster flies were reared at 22°C under a 12:12 hour light/dark cycle in vials containing conventional cornmeal-agar based medium. Adult flies were transferred to a larvae collection cage (Genesee Scientific) containing a grape juice agar plate and a dime-sized amount of fresh yeast paste. Flies could lay eggs on the grape juice agar plate for two days and then the plate was removed for collection of first instar larvae. Both female and male larvae were used in all experiments. Transgenic stocks were obtained from the Bloomington Drosophila Stock Center (BDSC). The following fly strains were used in this study: UAS-mCherry.NLS; UAS-GCaMP6m (a combination of UAS-mCherry.NLS:BL38425, and UAS-GCaMP6m:BL42750), UAS-mCD8::GFP; Orco::RFP (BL63045), Orco-Gal4 (BL23292), Or1a-Gal4 (BL9949), Or7a-Gal4 (BL23908 and BL23907), Or13a-Gal4 (BL9945), Or22c-Gal4 (BL9953), Or24a-Gal4 (BL9958), Or30a-Gal4 (BL9960), Or33b-Gal4 (BL9963), Or35a-Gal4 (BL9968), Or42a-Gal4 (BL9970), Or42b-Gal4 (BL9971), Or45a-Gal4 (BL9976), Or45b-Gal4 (BL9977), Or47a-Gal4 (BL9982), Or49a-Gal4/Cyo; Dr/TM3 (gift from John Carlson lab), Or59a-Gal4 (BL9990), Or63a-Gal4 (BL9992), Or67b-Gal4 (BL9995), Or74a-Gal4 (BL23123), Or82a-Gal4 (BL23125), Or83a-Gal4 (BL23128), Or85c-Gal4 (BL23913), and Or94b-Gal4 (BL23916).

Method Details

Microfluidic device design, fabrication, and specifications

The microfluidic device pattern was designed using AutoCAD. Devices were designed to have either 8, 16, or 24 channels, but all devices operate using a similar strategy (Figure S1A). For example, the 16-channel device includes two control channels to direct odorant flow, 13 odorant channels, one water channel to remove odorant residue, a larva loading channel, and a waste channel. The odorant, water, and control channels are of equal length to ensure equal resistance. The device was designed to function using a directed flow strategy similar to that described in (Chronis et al., 2007). Briefly, the device always has three channels open: the water, an odorant and a control channel (Figure S1C). Switching between the two control channels directs either water or an odorant to flow past the larva, as demonstrated in Figure S1D. The loading channel is 70 pm high with a width starting at 300 pm and gradually tapering to 60 pm in order to immobilize a first instar larva. The tapered end of the loading channel is positioned perpendicular to a stimulus delivery channel to allow for odorant flow past larval ORNs (Figure 1D).

The design pattern was sent to a mask-making service (outputcity.com), which provided the photomask. The mask was then transferred onto a silicon wafer using photolithography. The wafer was used to fabricate microfluidic devices using polydimethylsiloxane (PDMS) and the standard soft lithography approach. The resulting PDMS molds were cut and bonded to glass cover slips. Each microfluidic device was used with only a single panel of odorants to prevent odorant contamination.

We used fluorescein dye to measure the switching time between water and odorants as well as to verify the spatial odorant profile in the device during stimulus delivery. Our standard air pressure for stimulus delivery was 6 psi, which led to a flow rate of 0.5 mL/min or 0.2m/s in the microfluidic device. With these conditions, the switching time between water and odorant was ~20 ms (Figure S1B).

Odorant delivery

Odorants were obtained from Sigma-Aldrich, diluted in deionized (DI) water (Millipore) and stored for no more than one week. To prevent contamination, each odorant concentration was stored in a separate glass bottle and delivered through its own syringe and tubing set. Panels of odorants were delivered using a 16-channel pinch valve perfusion system (AutoMate Scientific, Inc.). Each syringe and tubing set contained a 30 mL luer lock glass syringe (VWR) connected to Tygon FEP-lined tubing (Cole-Parmer), which in turn was connected to silicone tubing (AutoMate Scientific. Inc.). The silicone tubing was placed through the pinch valve region of the perfusion system since its flexibility could allow for the passage or blockage of fluid flow to the microfluidics device. The silicone tubing was then connected to PTFE tubing (Cole-Parmer), which was then inserted into the microfluidic device. A microcontroller and custom written Matlab code were used to control the on/off sequence of the valves and to synchronize valve control with the onset of recording in the imaging software (NIS Elements).

The larva experienced continuous fluid flow at a rate of 0.5 mL/min for the entire duration of a recording. In dose-response experiments, the stimulus sequence consisted of five second odorant pulses interleaved by a water washout period. The odorant pulse duration time was chosen such that ORN soma responses reached maximum amplitude (Figure S1E). The water washout duration was adjusted based on stimulus concentration to allow for ORN recovery back to baseline activity levels, and thus ensured that measurements of ORN responses were independent of stimulus sequence (Figure S1F and Video S1). For white noise experiments, a 1024-step m-sequence of odorant and water was delivered with a time step of 0.2 s (Video S2).

Odor selection

We pooled all 690 odorants described on the database for odor responses (DoOR), a repository of odor response measurements from studies on the fruit fly Drosophila melanogaster and the honeybee Apis mellifera (Münch and Galizia, 2016). For each of the 690 odorants, we used the E-Dragon software (http://www.vcclab.org/lab/edragon/) to determine the values corresponding to 32 molecular descriptors of the multidimensional odor metric described in (Haddad et al., 2008). We next performed PCA on all odorants with their descriptors and visualized odorant distribution using the first three PCs. We first picked the 19 odorants described in (Mathew et al., 2013) for our panel. To select the remaining odorants, we picked ones such that our odorant panel closely matched the density profile and distribution of the 690 odorants represented along the first 3 PCs of the PCA space. We found that 35 odorants were sufficient to meet our distribution matching requirements and for the panel to include stimuli that cover a broad range of molecular functional groups, are relevant environmental odorants for the larva, have been previously shown to elicit behavioral responses in the larva (see Figure S3A and Table S1). During our imaging experiments, we found that one odorant, pentanoic acid, did not elicit any ORN responses and thus removed it from the panel.

Calcium imaging

First instar larvae were loaded into a microfluidic device using a 1 mL syringe filled with a 0.1% triton-water solution. Each larva was gently pushed to the end of the loading channel where it was mechanically trapped. The larva was positioned such that its left and right dorsal organs (nose) were exposed to the stimulus delivery channel and its dorsal side (location of ORN cell bodies) was closest to the objective.

Larvae were imaged using an inverted Nikon Ti-e spinning disk confocal microscope with a 60X water immersion objective (NA 1.2). A charged-coupled device (CCD) microscope camera (Andor iXon EMCCD) captured images at 30 frames/sec. ORN cell bodies were recorded by scanning the entire volume (~20 slices with a step size of 1.5 μm) of the dorsal organ ganglion (Video S1), while ORN axon terminals were recorded from a single slice of the antennal lobe (Video S2).

Initial experiments were performed to verify the identity of ORNs activated by each of the 19 odorants that were described in (Mathew et al., 2013) and used in our panel for ORN identification (data not shown). We used single ORN Gal4 drivers expressing GCaMP6m to confirm the ORN(s) responsive to each of the 19 odorants.

Dose-response experiments (data shown in Figures 1–2 and S3B–S3C, Video S1) were performed using larvae of the Orco>GCaMP6m, Orco>mCherry.NLS genotype and recording from ORN cell bodies. White noise experiments (data shown in Figures 5 and S5, Video S2) were performed using larvae expressing GCaMP6m in a single ORN (e.g. Or42a>GCaMP6m used in Figure S5) and recording from ORN axon terminals. For all experiments, both the left and right sides of ORN soma or axon responses were recorded simultaneously and used for analysis. Recordings from at least five larvae were collected for each odorant. All samples were used for analysis unless dendritic varicosities developed over the course of the recording, a sign of unhealthy neurons likely due to mechanical stress.

Quantification and Statistical Analysis

Data were analyzed with custom scripts written in MATLAB, available at https://github.com/samuellab/Larval-ORN. The statistical tests, representations of sample sizes (“n”), what each n value represents, and other related measures are shown in the legend of each relevant figure. No statistical methods were used to determine sample sizes in advance, but sample sizes are similar to those reported in other studies in the field.

Quantification of dose-response recordings

Custom code written in ImageJ and published Matlab code were used to track and identify each ORN as well as its responses to odorant stimuli. Slight movement artifacts were corrected by aligning frames using mCherry NLS labeling of ORN cell bodies and the ImageJ TurboReg plugin (Thévenaz et al., 1998). ROI segmentation was performed using the method of constrained nonnegative matrix factorization (CNMF) (Pnevmatikakis et al., 2016). Each ORN activated in response to an odorant stimulus was visually identified using both the anatomical location of its dendritic bundle and the functional map of cognate odorant to ORN activation (Figures 1 E–G, and S2). ORN identification was performed independently by two experimenters to ensure accuracy. Changes in fluorescence were then quantified as (F_peak − F₀)/F₀, where F₀ was the average ORN intensity sampled from the frames immediately preceding odorant delivery and F_peak was the highest intensity in ORN fluorescence during odorant delivery. Each odorant stimulus was repeated across at least 5 animals. The raw response data is summarized in Data S1.

The heatmap in Figure 2A was generated by directly averaging the peak responses across animals (no normalization was performed). Simulated annealing was used to optimize the order of ORNs and odorants presented in this heatmap, such that it minimized a loss function in which cost increased linearly with the distance that activated odorant-ORN pairs were from the matrix diagonal. Matrices of neural responses at each concentration were concatenated, such that columns corresponded to ORNs and rows corresponded to odorants, for all five concentrations. We then centered the data and performed PCA using the SVD method, along the ORN axis (Figure 2B).

To visualize temporal dynamics of ORN responses over the duration of stimulus delivery, we performed PCA on ORN responses over time to two odorants, benzaldehyde and ethyl butyrate, across five concentrations (Figure S3D). The time period starts from odorant pulse delivery and continues up to 15 seconds after delivery offset. Similar methods and findings have been described in insect olfactory projection neurons (Mazor and Laurent, 2005; Stopfer et al., 2003).

Estimation of EC₅₀ values

Dose-response data were modeled as following a Hill equation, the general form of which is as follows:

$$\mathrm{y}={\mathrm{A}}_{max}\frac{{\mathrm{c}}^{\mathrm{n}}}{{\mathrm{c}}^{\mathrm{n}}+{\mathrm{EC}}_{50}^{\mathrm{n}}}\#$$ (1)

where A_max is the maximum ORN response level across concentrations, c is the odorant concentration, EC₅₀ is the half-maximal effective concentration, and n is the Hill coefficient. There were a total of 259 odorant-ORN pairs in which some odorant response was observed. Saturation of the dose-response curve was observed in 36 of these odorant-ORN pairs. We first performed a least-squares fit on each of the individual 36 curves and found that the curves had similar Hill coefficients. However, with only five data points to describe each curve and three free parameters to fit the Hill function, there was large uncertainty in the fit estimates. We instead perform a population fit on all 36 saturated curves to a Hill function with a common Hill coefficient, by optimizing the following equation:

$$\underset{A_{ma{x}_i},E{C}_{{50}_i},n}{\min }\sum _{i=1}^{36}\left|{\mathit{Y}}_i-f\left(A_{ma{x}_i},E{C}_{{50}_i},n,\mathit{c}\right)\right|$$

where i indicates each of the 36 saturated odorant-ORN pairs, Y_i is the average ORN response for an odorant-ORN pair, f is the Hill equation with parameters $A_{ma{x}_i}$ and $E{C}_{{50}_i}$ for each pair, n is the shared Hill coefficient, and c is the five concentration levels used in this study. The optimization method uses the standard Matlab fminsearch function. We find that this approach yields a R²=0.99, which is comparable to the goodness of fit from 36 independent Hill coefficients (Figure S4A).

For the remaining 223 non-saturated pairs, there were not enough points on the dose-response curve to estimate parameters of the Hill equation using the previous method. To make estimates of the Hill equation parameters for pairs in which saturation was not observed, we modeled a single animal response using the Hill function. For a given odorant-ORN pair, for a single animal, the ORN’s A, n, and k = log_l0(1/EC₅₀) parameters were each drawn from normal distributions. Additionally, we assumed that the distributions for A and n as well as the variance of the EC₅₀ distributions were independent of odorant and ORN. Thus, the distributions for A and n across all odorant-ORN pairs were the same, and the distributions of k across all odorant-ORN pairs differed only in their mean value $\overline{k}$.

The data were modeled in this way because the primary source of variance in the data was from animal-to-animal response variation. This variation was much larger than the trial-to-trial variation in a single animal. For a single odorant-ORN pair across different animals, different values for A, n, and k may be resolved. Further, the mean and variance in A and n across animals for the same odorant-ORN pair appeared comparable to the mean and variance in A and n for different odorant-ORN pairs. Similarly, the variance in k across animals for the same odorant-ORN pair appeared comparable to the variance in k across animals for different odorant-ORN pairs.

We perform maximum likelihood estimation on this model by writing down the probability that the data might be generated by the model with particular values for the moments of the distributions of A, n, and k. For this model, we use the log scale of concentration and EC₅₀: x = log₁₀(c), k = log₁₀(1/EC₅₀), and the logistic function in place of the Hill equation: $y(x)=\frac{A}{1+\exp (-v(x+k))}$, with v = n ln 10. Deviations from the logistic function are modeled as Gaussian noise $\mathcal{N}$ (y_qi(x), σ_N), where σ_N represents experiment noise. Specifically, for a single-animal i of one odorant-ORN pair (indexed by q), the probability of generating responses Y_i given normal distributions for A, v, and k is

$$\begin{gathered} P\left(Y_{qi}|\overline{A};{\sigma }_A;\overline{k_q};{\sigma }_k;\overline{v};{\sigma }_v;{\sigma }_N\right) \\ =\iiint P\left(Y_{qi}|A_j;k_j;v_j;{\sigma }_N\right)P\left(A_j|\overline{A};{\sigma }_A\right)P\left(k_j|\overline{k_q};{\sigma }_k\right)P\left(v_j|\overline{v};{\sigma }_v\right)d{A}_{j}d{k}_{j}d{v}_j. \end{gathered}$$ (2)

Here, the first term P(Y_qi|A_j; k_j; v_j; σ_N) represents the probability of generating the data from a logistic function with parameters A_j, k_j, v_j, given Gaussian noise with variance σ_N². The other three terms on the right side are also Gaussians. Note that the only dependence on the odorant-ORN pair q is in the mean value $\overline{k_q}$. For one odorant-ORN pair, across all animals, the probability is then the product of the individual animals

$$P\left(Y_q|\overline{A};{\sigma }_{\text{A}};\overline{k_q};{\sigma }_k;\overline{v};{\sigma }_{\nu };{\sigma }_N\right)=\prod _i^{M}P\left(Y_{qi}|\overline{A};{\sigma }_{\text{A}};\overline{k_q};{\sigma }_k;\overline{v};{\sigma }_{\nu };{\sigma }_N\right)$$

where M is the number of animals for that odorant-ORN pair. The probability of generating all the data across odorant-ORN pairs from this model is then

$$P\left(Y|\overline{A};{\sigma }_{\mathrm{A}},\overline{\mathbf{k}};{\sigma }_k;\overline{v};{\sigma }_v;{\sigma }_N\right)=\prod _q^{Q}P\left(Y_q|\overline{A};{\sigma }_{\mathrm{A}};\overline{k_q};{\sigma }_k;\overline{\nu };{\sigma }_v;{\sigma }_N\right),$$

where Q is the total number of odorant-ORN pairs and $\overline{\mathbf{k}}=\left(k_1,k_2,\dots k_Q\right)$ is the vector of log₁₀(1/EC₅₀) values for all odorant-ORN pairs. Maximum likelihood estimation amounts to maximization of this expression, or, typically, the logarithm of this expression

$$\underset{\overline{A};{\sigma }_{\mathrm{A}};\overline{\mathbf{k}};{\sigma }_k;\overline{v};{\sigma }_v;{\sigma }_N}{\max }\ln \left[P\left(Y|\overline{A};{\sigma }_{\mathrm{A}};\overline{\mathbf{k}};{\sigma }_k;\overline{v};{\sigma }_v;{\sigma }_N\right)\right]\#$$ (3)

We characterize $\left(\overline{A};{\sigma }_{\text{A}};{\sigma }_k;\overline{v};{\sigma }_{\nu };{\sigma }_N\right)$ as being global (applying to all odorant-ORN pairs) and $\overline{\mathbf{k}}$ as being local (different for every odorant-ORN pair). The moments of the distribution are optimized by alternatively optimizing for the global moments while fixing the local moments and optimizing the local moments while fixing the global moments. This is done to limit the number of optimization parameters for any given optimization step. Function maximization was performed using MATLAB’s fminsearch function, and initial values for the distribution moments were chosen based on a least-squares regression assuming fixed values for v and A across all odorant-ORN pairs. The result of the optimization in equation (3) was found to be robust to choices of initial values.

The estimated $\overline{\mathbf{k}}$ for all odorant-ORN pairs is summarized in Figure 3B. The black elements in the matrix indicate that the corresponding ORN showed no activity within the tested concentration range, i.e., we were unable to fit a $\overline{k}$ value for these odorant-ORN pairs. The standard deviation for the set of k’s was found to be α_k = 0.45. Because the primary source of variance in the data is variation in animal responses, we can treat this as an error bar on a single animal-trial measurement of $\overline{k}$. The moments of the distribution for A were found to be $\overline{A}=4.1$, α_A = 2.3, and the moments for the distribution of n = v/ln 10 were found to be $\overline{n}=1.6$, α_n = 0.6.

Using these estimated distributions, single animal-trial values for the logistic function parameters A_i, k_i, v_i can be estimated using maximum likelihood estimation. Maximization is performed on the probability of single animal data for a given odorant-ORN pair q and animal i, which is similar to equation 2, but without the integrals:

$$P\left(Y_{qi}|\overline{A};{\sigma }_A;\overline{k_q};{\sigma }_k;\overline{v};{\sigma }_v;{\sigma }_N\right)=P\left(Y_{qi}|A_i;k_i;v_i;{\sigma }_N\right)P\left(A_i|\overline{A};{\sigma }_A\right)P\left(k_i|\overline{k_q};{\sigma }_k\right)P\left(v_i|\overline{v};{\sigma }_v\right).$$ (4)

Doing this can help test the self-consistency of the model. It is not guaranteed (or even expected) that the single-trial values of A_i, k_i, v_i should match the distributions of A, k, v, but they should be similar, and they should fit the data well (Figure S4E, S4F and S4G). We find that the values for A_i, k_i, v_i explain the data very well (R² = .989) (Figure S4D).

Analysis of the sensitivity matrix

To perform PCA on the sensitivity matrix, we first transformed the EC₅₀ values to the ln(1/EC₅₀), such that odorant-ORN pairs with a high sensitivity (small EC₅₀) were now represented by large values, those that were less sensitive (large EC₅₀) had small values, and the logarithmic scale allowed for coverage of the broad range of EC₅₀ values spanning several orders of magnitude. The remaining pairs that that did not have an EC₅₀value (the missing data, represented by black squares in Figure 3B), represent pairs with a much lower sensitivity and were set to zero. Figure 4A shows the percentage of variance explained by each PC once PCA was performed on the ln(1/EC₅₀) matrix. In comparison to a shuffled matrix (in which each row is randomly permuted), we found that only the first PC was significantly different (p < 0.0001 for 1000 instances of shuffled data).

We fit the power law distribution using code from (Clauset et al., 2009). The resulting fitting index of 0.17 (large values mean better fit to the power law for this metric) is larger than the threshold (0.1) needed to accept the power law hypothesis. Furthermore, we performed a likelihood ratio comparison with other heavy tailed distributions (Clauset et al., 2009), using parameters best fit to our data, and found that no other distributions are significantly better (need p<0.1) than the power-law (Table S2).

Derivation of power law scaling of ORN population responses from sensitivity distribution

Here, we explain analytically the power law relation between odorant concentration and the population response of ORNs. Under the same Hill equation we used to fit individual dose-response curves (Eq. 1, here we set y_max = 1 for simplicity), assume that (i) sensitivities follow a power law distribution P(1/EC₅₀) ∝ (1/EC₅₀)^−λ−1 (or equivalently an exponential distribution for $k=\ln \left(1/E{C}_{50}\right):P(k)=\lambda {\text{e}}^{-\lambda \left(k-k_0\right)}$, k ≥ k₀) (ii) the Hill coefficient n for all odorant-ORN pairs are the same and greater than λ (satisfied in the data as 1.42 vs. 0.42). If so, the population response follows an approximate power law form r(c) ∝ c^λ for concentrations $c\le e^{-k_0}$ (which means the weakest response pair in the population has not reached the half level). For convenience, we use the log scale of concentration and EC₅₀: x = ln(c), k = ln(1/EC₅₀) and the logistic function in place of the Hill equation: $y(x)=\frac{1}{1+\exp (-n(x+k))}$.

This result can be intuitively obtained by considering the limiting case where the logistic function is infinitely steep (large Hill coefficient) and is thus replaced by a step function. The population response combining a large number of odorant-ORN pairs can be expressed as an integral: $r(x)={\int }_{k_0}^{\infty }y(x,k)\lambda e^{-\lambda \left(k-k_0\right)}dk,y(x,k)=\frac{1}{1+\exp (-n(x+k))}$ is the log-concentration. When y(x, k) is a step function, the integral becomes P(k ≥ −x), which is essentially the cumulative density function for k. Given the distribution of k, this is exactly an exponential function $r(x)=e^{\lambda \left(x+k_0\right)}$ (or a power law function of c) for x ≤ −k₀, and saturates at larger concentrations.

For the general case of logistic activation, the integral does not have a simple form expression but involves hyper-geometric functions. However, we can derive a simple closed form approximation by approximating the logistic function f(x) = 1/(1 + e^−nx) using piecewise exponential functions:

$$f(x)\approx \{\begin{array}{c}{\text{e}}^{nx}-\frac{{\text{e}}^{2nx}}{2},x\le 0\\ 1-{\text{e}}^{-nx}+\frac{e^{-2nx}}{2},x>0\end{array}$$

Such an approximation becomes asymptotically exact when the steepness n goes to infinity, or when the absolute value of x goes to infinity. Substituting y(x, k) with this approximation, the integral splits into segments, over which the integrand are sums of exponential functions, and therefore can be easily integrated. This gives the closed form approximation of r(x):

$$r(x)=\{\begin{array}{c}\left(1+\frac{2{\lambda }^2}{n^2-{\lambda }^2}-\frac{{\lambda }^2}{4n^2-{\lambda }^2}\right)e^{\lambda \left(x+k_0\right)}-\frac{\lambda }{n-\lambda }{e}^{n\left(x+k_0\right)}+\frac{\lambda }{2(2n-\lambda )}{e}^{2n\left(x+k_0\right)},x\le -k_0\\ 1-\frac{\lambda }{n+\lambda }{e}^{-n\left(x+k_0\right)}+\frac{\lambda }{2(2n+\lambda )}{e}^{-2n\left(x+k_0\right)},x>-k_0\end{array}$$

For small concentrations, x ≤ −k₀, the leading term in the above expression is $e^{\lambda \left(x+k_0\right)}$, since λ < n. This explains that the population response is approximated by an exponential function with exponent λ. Furthermore, the theory also predicts the magnitude (vertical shift in the log-log plot of population response as in Figure 3E), that is, $r(x)\approx (1+\frac{7}{4}\frac{{\lambda }^2}{n^2})e^{\lambda \left(x+k_0\right)}$, which explains how the Hill coefficient affect the population response.

Reverse-correlation analysis

White noise experiments were performed in a manner similar to those described in (Kato et al., 2014). Briefly, we used custom code written in MATLAB to control odorant and water switching such that it followed an m-sequence. Calcium imaging was performed on the axon terminal of individual ORNs at ~30 frames per second. Calibration and an example of such a recording is shown in Video S2. We then used a linear-nonlinear model to compare the m-sequence input to ORN responses during a 150 second interval (from 60 – 210 sec). An 18 second time window was used for the linear filter, of which 15 seconds represented stimulus history in order to ensure extraction of the full filter dynamics (Figure 5B). The raw filter amplitudes across individual animals varied, possibly due to variations in GCaMP6m expression levels or imaging quality, but the shape of normalized filters was comparable across animals (Figure S5A). Next, we applied the linear filter to the data and compared this to the output in order to capture the nonlinear function. We found that a sigmoidal function fits the nonlinear function well (Figure S5B). We then applied novel m-sequences on the same animal to validate the linear-nonlinear model (Figure S5C) and found that they fit the data well. Peak and decay times for each filter were found by extracting the time points corresponding to the maximum amplitude and half maximum amplitude of the decay phase, respectively. 454 filters were calculated from the recording of 138 larvae responding to various m-sequence stimuli. Each of the 31 filters quantified in Figures 5F–5G and S10, are averaged across 10 animals.

Analysis of previous electrophysiology studies on odorant-ORN responses

To assess the concordance between electrophysiology and calcium imaging techniques, we applied our analysis to Drosophila ORN electrophysiology data previously described in the literature. We used the following two data sets for comparison, 1) Figure 7B from (Kreher et al., 2008) showing Or42a and Or42b responses to ethyl acetate across seven orders of magnitude in concentration, 2) Figure 1B from (Kreher et al., 2008) showing ORN responses to 26 odorants.

We fit the first data set of ORN dose-response curves to Hill equations in which all parameters were free, as this electrophysiology data was densely sampled across concentration (Figure S4H). The second data set was used to compare correlations in the odorant-ORN response matrices and thus we applied the simulated annealing method described above, to order ORNs and odorants for comparison with our data (Figure S4I).

Data and Software Availability

Data, code and software are available at https://github.com/samuellab/Larval-ORN.

Supplementary Material

1

Data S1. Raw activity data of 21 ORNs responding to 34 odorants at multiple concentration levels collected from 238 recordings. Related to Figure 2.

4

Video S1. Dose-dependent activation of ORNs.

Left: Calcium imaging of 21 pairs of larval ORNs in response to increasing concentrations of the 1-pentanol odorant, from 10⁻⁷ to 10⁻³ dilutions. Video starts by scanning through the imaging volume to identify all ORNs activated by the odorant. Three ORNs are responsive on the left side and five on the right side. ORN identity was confirmed from the dendrite location and response to panel of 15 odorants (not shown in the Video). Right: Fluorescence traces of ORN responses to step pulses of odorant stimuli. Related to Figure 1.

5

Video S2. ORN responses to pseudorandom white noise stimulus.

Top left, stimulus delivery marked by fluorescence. Bottom left, axon terminal of Or45a-ORN responding to the white noise stimulus using 10⁻⁷ dilution of 2-nonanone. Top and bottom right, real time plots of the input stimulus and ORN response during an experiment. Related to Figure 5.

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals
4,5-Dimethylthiazole	Sigma-Aldrich	CAS 3581–91–7
Geranyl acetate	Sigma-Aldrich	CAS 105–87–3
2,5-dimethylpyrazine	Sigma-Aldrich	CAS 123–32–0
2-acetylpyridine	Sigma-Aldrich	CAS 1122–62–9
3-octanol	Sigma-Aldrich	CAS 589–98–0
6-methyl-5-hepten-2-ol	Sigma-Aldrich	CAS 1569–60–4
1-pentanol	Sigma-Aldrich	CAS 71–41–0
Isoamyl acetate	Sigma-Aldrich	CAS 123–92–2
Butyl acetate	Sigma-Aldrich	CAS 123–86–4
Ethyl butyrate	Sigma-Aldrich	CAS 105–54–4
Benzaldehyde	Sigma-Aldrich	CAS 100–52–7
Methyl salicylate	Sigma-Aldrich	CAS 119–36–8
2-heptanone	Sigma-Aldrich	CAS 110–43–0
4-methylcyclohexanol	Sigma-Aldrich	CAS 5899–91–3
Ethyl acetate	Sigma-Aldrich	CAS 141–78–6
2-phenylethanol	Sigma-Aldrich	CAS 60–12–8
Pentyl acetate	Sigma-Aldrich	CAS 628–63–7
3-Pentanol	Sigma-Aldrich	CAS 584–02–1
Anisole	Sigma-Aldrich	CAS 100–66–3
Methyl phenyl sulfide (Thioanisole)	Sigma-Aldrich	CAS 100–68–5
Trans-3-Hexen-1-ol	Sigma-Aldrich	CAS 928–97–2
Acetal	Sigma-Aldrich	CAS 105–57–7
2-Nonanone	Sigma-Aldrich	CAS 821–55–6
4-Hexen-3-one	Sigma-Aldrich	CAS 2497–21–4
4-Methyl-5-vinylthiazole	Sigma-Aldrich	CAS1759–28–0
Trans, trans-2,4-Nonadienal	Sigma-Aldrich	CAS 5910–87–2
2-Methoxyphenyl acetate	Sigma-Aldrich	CAS 613–70–7
Hexyl acetate	Sigma-Aldrich	CAS 142–92–7
Benzyl acetate	Sigma-Aldrich	CAS 140–11–4
Linalool	Sigma-Aldrich	CAS 78–70–6
(1R)-(-)-myrtenal	Sigma-Aldrich	CAS 18484–69–6
4-phenyl-2-butanol	Sigma-Aldrich	CAS 2344–70–9
Pentanoic acid (valeric acid)	Sigma-Aldrich	CAS 109–52–4
Nonane	Sigma-Aldrich	CAS 111–84–2
Menthol	Sigma-Aldrich	CAS 89–78–1
Experimental Models: Organisms/Strains
UAS-mCherry.NLS; UAS-GCaMP6m	This study
UAS-mCD8::GFP; Orco::RFP	Bloomington Drosophila Stock Center (BDSC)	RRID:BDSC_63045
Orco-Gal4	BDSC	RRID:BDSC_23292
Or1a-Gal4	BDSC	RRID:BDSC_9949
Or7a-Gal4	BDSC	RRID:BDSC_23907 RRID:BDSC_23908
Or13a-Gal4	BDSC	RRID:BDSC_9945
Or22c-Gal4	BDSC	RRID:BDSC_9953
Or24a-Gal4	BDSC	RRID:BDSC_9958
Or30a-Gal4	BDSC	RRID:BDSC_9960
Or33b-Gal4	BDSC	RRID:BDSC_9963
Or35a-Gal4	BDSC	RRID:BDSC_9968
Or42a-Gal4	BDSC	RRID:BDSC_9970
Or42b-Gal4	BDSC	RRID:BDSC_9971
Or45a-Gal4	BDSC	RRID:BDSC_9976
Or45b-Gal4	BDSC	RRID:BDSC_9977
Or47a-Gal4	BDSC	RRID:BDSC_9982
Or49a-Gal4/Cyo; Dr/TM3	Gift from John Carlson
Or59a-Gal4	BDSC	RRID:BDSC_9990
Or63a-Gal4	BDSC	RRID:BDSC_9992
Or67b-Gal4	BDSC	RRID:BDSC_9995
Or74a-Gal4	BDSC	RRID:BDSC_23123
Or82a-Gal4	BDSC	RRID:BDSC_23125
Or83a-Gal4	BDSC	RRID:BDSC_23128
Or85c-Gal4	BDSC	RRID:BDSC_23913
Or94b-Gal4	BDSC	RRID:BDSC_23916
Deposited Data
Raw and analyzed ORN dose-response data	This paper	https://github.com/samuellab/Larval-ORN
Raw activity data of 21 ORNs responding to 34 odorants.	This paper	https://data.mendeley.com/datasets/7kbsmx94zm/draft?a=8ad617e6-e9db-4e4f-b1a2-776b00fb4c58
Software and Algorithms
TurboReg	Thévenaz et al., 1998	http://bigwww.epfl.ch/thevenaz/turboreg/
CalmAn-MATLAB	Pnevmatikakis et al., 2016	https://github.com/flatironinstitute/CalmAn-MATLAB
Power-law distribution in empirical data	Clauset et al., 2009	http://tuvalu.santafe.edu/~aaronc/powerlaws/
Algorithms for analyzing ORN ensemble dose-response data	This paper	https://github.com/samuellab/Larval-ORN
Linear-Nonlinear model analysis of ORNs’ response to m-sequence stimuli	This paper	https://github.com/samuellab/Larval-ORN

Highlights.

• All ORNs share a common dose-response function with variable sensitivity across odors

• Sensitivities across odorants and ORNs follow a power law distribution

• Correlation in sensitivities corresponds to a geometric molecular property

• ORN-odorant responses share similar temporal filters