A neural mass model to predict electrical stimulation evoked responses in human and non-human primate brain

Abstract

Objective.

Deep brain stimulation (DBS) is a valuable tool for ameliorating drug resistant pathologies such as movement disorders and epilepsy. DBS is also being considered for complex neuro-psychiatric disorders, which are characterized by high variability in symptoms and slow responses that hinder DBS setting optimization. The objective of this work was to develop an in silico platform to examine the effects of electrical stimulation in regions neighboring a stimulated brain region.

Approach.

We used the Jansen–Rit neural mass model of single and coupled nodes to simulate the response to a train of electrical current pulses at different frequencies (10–160 Hz) of the local field potential recorded in the amygdala and cortical structures in human subjects and a non-human primate.

Results.

We found that using a single node model, the evoked responses could be accurately modeled following a narrow range of stimulation frequencies. Including a second coupled node increased the range of stimulation frequencies whose evoked responses could be efficiently modeled. Furthermore, in a chronic recording from a non-human primate, features of the in vivo evoked response remained consistent for several weeks, suggesting that model re-parameterization for chronic stimulation protocols would be infrequent.

Significance.

Using a model of neural population activity, we reproduced the evoked response to cortical and subcortical stimulation in human and non-human primate. This modeling framework provides an environment to explore, safely and rapidly, a wide range of stimulation settings not possible in human brain stimulation studies. The model can be trained on a limited dataset of stimulation responses to develop an optimal stimulation strategy for an individual patient.

1. Introduction

Deep brain stimulation (DBS) is an established treatment for movement disorders and refractory epilepsy [1–3]. Clinical targeting of the stimulating electrodes is typically done by a combination of imaging and direct electrophysiological recordings with macrostimulation to evoke the desired symptom response. Final selection of stimulation parameters are done by clinical assessment on the effect of symptoms and is largely a trial and error procedure [4]. DBS is emerging as a potential treatment for psychiatric disorders, on the premise that DBS can potentially alter network dynamics between brain structures. Psychiatric disorders are a leading cause of disability, morbidity, and mortality and are often drug resistant and challenging to treat. Disorders such as depression, obsessive-compulsive disorder, and anxiety are believed to arise from dysfunctional communication among brain structures [5–11]. To this point, DBS has had promising open-label results [12–16], although randomized clinical trials have shown inconsistent effects [17]. Part of the difficulty is the lack of a well-established biomarker to assess the effective-ness of DBS. Therefore, the effect of stimulation is typically based upon qualitative assessments, including the patient’s immediate emotional response to stimulation changes and the long-term change in subjective self-reports.

A more quantitative, and potentially more effective approach, would be to design stimulation that changes a specific brain signature (biomarker) that in turn is associated with a disease relevant behavior. This raises a new challenge: finding a set of stimulation settings that could reliably change a given physiological correlate. Existing DBS systems have a complex 4D (frequency, amplitude, pulse width, electrode contact) programming space. Devices currently in development will add more channels, more potential waveforms, and thus even more dimensionality [18–21]. It is not feasible to explore the entire stimulation parameter space with a patient and characterize the behavioral response, given patients’ limited tolerance for extensive programming sessions during which a wide range of parameters could be tested. A better solution would be to develop computational models of the brain’s response to electrical stimulation, such that the ideal sequence to achieve a given electrophysiological change could be predicted in advance. Similar approaches have had good success in modeling the anatomic spread of the DBS electric field in tissue [22, 23]. Optimal closed-loop DBS paradigms for Parkinson’s disease have been designed by modeling the Subthalamic nucleus—Globus Pallidus network using neural field models [24] and conductance based neural models [25].

The local field potential (LFP) is a good target for this modeling, given its success as a biomarker in movement disorders [26–29]. A wide range of models such as data-driven statistical models [30–32], neural mass models [33, 34], oscillator models [35] and detailed conductance based biophysical models [36–39] have been used to simulate aggregate neural activity. Mean field or neural mass models represent a balance between more abstract statistical models and more biophysically detailed single neuron models [40, 41]. While neural mass models incorporate some of the biophysics of neuronal activity, the parameter space of these models is much smaller than conductance-based single neuron models. Both types of models utilize a relatively simple representation of the main features of subpopulations of neurons (typically pyramidal cells and interneurons) and their interactions (mostly synaptic). Neural mass models are used to describe the temporal activity of a local neuronal population (without the notion of space); they can be extended to the class of neural field models (which incorporate both time and space variables) [42].

In this work, we use a Jansen–Rit (JR) neural mass model of coupled cortical columns [43] to simulate the local response evoked by electrical simulation on the LFP. This model has been successfully used in various contexts including simulating visually evoked potentials [33], epileptic activity in the cortex [34] and mechanisms for short term memory and motion perception [36]. We specifically simulate the local evoked response to a train of electrical pulses at varying frequencies (10–160 Hz) in the amygdala and in cortical structures such as orbito-frontal cortex (OFC) and dorsal anterior cingulate cortex (dACC). These regions have been repeatedly implicated as important in a variety of psychiatric disorders, and as such may be viable targets for brain stimulation [5]. Amygdala and cingulate in particular are already under study as targets for psychiatric DBS [45, 46].

The evoked response is the most stereotyped/repeatable brain response to stimulation and modeling it might thus be a pre-requisite for capturing more complex phenomena such as oscillations or inter-regional synchrony. It is theorized that stimulation evoked response (SER) is caused by direct depolarization of the superficial dendritic trees of pyramidal cells and those of inhibitory interneurons that synapse near the soma on adjacent pyramidal cells, leading to an indirect decrease in pyramidal cell firing through the activation of GABAergic synapses. The injected current also depolarizes long-range axons traversing the region of stimulation, generating action potentials propagating orthodromically (to local and distant pyramidal synapses) as well as antidromically (backpropagating to depolarize the pyramidal cell soma and possibly dendrites [44, 45]. It is likely that responses to single pulse stimulation in humans reflect both a major pyramidal cell contribution via orthodromic cortico-cortical and cortico-subcortical-cortical projections as well as a minor antidromic contribution [46]. Evoked responses have, on their own, been sufficient to guide closed-loop stimulation in neurological disorders [29] and are also used for cortical mapping [47, 48]. We are particularly interested in the role of stimulation frequency on the evoked response because frequency has been found to be a determining factor in the efficacy of DBS in movement disorders [49]. We compare the simulation results to matching in vivo stimulation paradigms performed in human and non-human primates (NHPs). In doing so, we identify a subset of the model parameters that produce results consistent with the in vivo responses to stimulation at low and high frequencies. We propose that this simple neural mass model of coupled cortical columns can be used to simulate the local effects of stimulation over a range of frequencies, bringing us one step closer to rational stimulation design.

2. Methods

We recorded LFP data from five patients with medically refractory epilepsy who were monitored for seizure focus localization. Each patient had stereotactically placed depth electrodes. Electrode locations were reconstructed based on post-operative CT scans co-registered with preoperative MRI [50, 51]. In general, the same regions were targeted, but not the same coordinates, since the clinically relevant regions and patient’s brain anatomy were variable. However, by mapping the electrodes to each patients’ MRI using both automatic and visual examination tools (ELA and Dykstra reference), we found that there were close similarities in the electrode locations in terms of the relevant brain structures. Each patient was stimulated across a pair of electrodes spanning either the amygdala or the cingulate/orbitofrontal cortical structures using a 400 ms train of charge-balanced symmetrical biphasic 90 μs pulses, with an inter-phase-interval of 53 μs. Pulse frequencies ranged from 10–160 Hz and currents from 1–8 mA. We employed a standard stimulation protocol used in some clinically relevant stimulation regimes which also allows for delivery of charge balanced stimulation which is expected to be safer [52]. For all patients, this procedure was done while they received normal seizure medication before resective surgery, so as to minimize the risk of evoking a seizure. The LFP recorded from the electrode pair adjacent to the stimulating electrode contact pair was used for modeling. Before analysis and modeling, we converted each such electrode pair to a single bipolar channel to reduce the effects of volume conduction [53]. We chose the neighboring electrode pairs to the stimulating electrode to avoid the effects of amplifier saturation at the stimulating electrodes. In all cases, we confirmed that the adjacent electrodes studied were located in the same brain region as the stimulating electrodes.

One adult male NHP was implanted with two depth electrodes (customized miniaturized DBS leads; NeuMed; Hopkinton NY) and an intracranial grid (AdTech) to mimic the brain regions spanned in some of our human subject implants. Implants had been in place for over a month before stimulation experiments, such that tissue responses such as glial scarring had stabilized and progressed to their chronic state. The depth electrodes were primarily in the medial orbito-frontal cortex (mOFC, cortical area 25), dorsal anterior cingulate (dACC, spanning cortical areas 24c and 9/32), and nucleus accumbens (NAcc) based on three standard macaque brain atlases [54, 55]. The intracranial grid was over the dorsolateral prefrontal cortex (dlPFC). Electrode locations were reconstructed using similar approaches to human localization based on post-operative CT scans co-registered with preoperative MRI. A similar stimulation paradigm to the human experiment was followed with 0.16–4 mA injected current, and a finer frequency sampling (10, 20, 40, 80, 100, 130, 160, 200 Hz). These experiments were done in five sessions over the course of a month as the NHP viewed a blank computer screen for 20 min in between running tasks for other experiments.

Human subject data collection was done following a protocol which was approved by the Partners Healthcare Institutional Review Board and after participants provided informed consent. All animal care and experimentation were overseen and approved by the Institutional Animal and Care Use Committee at the Massachusetts General Hospital and were directed in agreement with the Public Health Services Guide for the Care and Use of Animals.

2.1. Stimulation evoked response (SER)

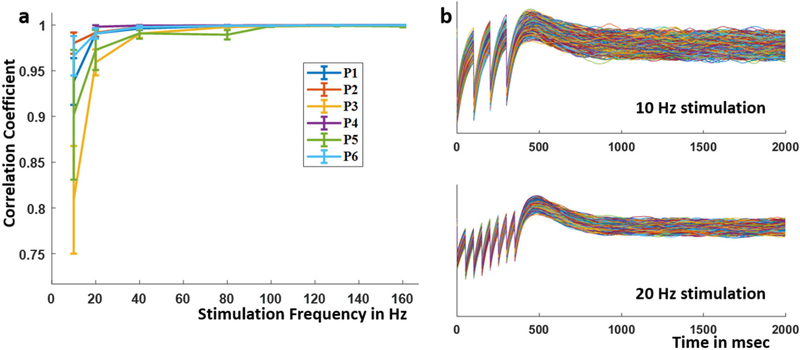
Each subject dataset consisted of five–ten trials at each stimulation frequency and current. Each such trial consisted of a 400 ms train of stimulation followed by an evoked response immediately after the cessation of the stimulation train (figure 1(b)). To characterize this stimulation evoked response (SER) and to determine how it varied over stimulation frequencies and across datasets, the following two quantities were calculated: (i) The normalized peak voltage, calculated as the first positive peak value of the SER divided by the standard deviation of the recorded LFP over a period of 500 ms before stimulation was delivered; (ii) The time of occurrence of the peak SER. Error bounds for both the quantities at a specific stimulation frequency and current were determined using standard deviations of 1000 surrogate SERs. Each such surrogate was constructed by averaging SERs sampled from the recorded five–ten trials with replacement. These quantities were chosen motivated by the classical P300 observed in evoked response potentials (ERP) [56, 57].

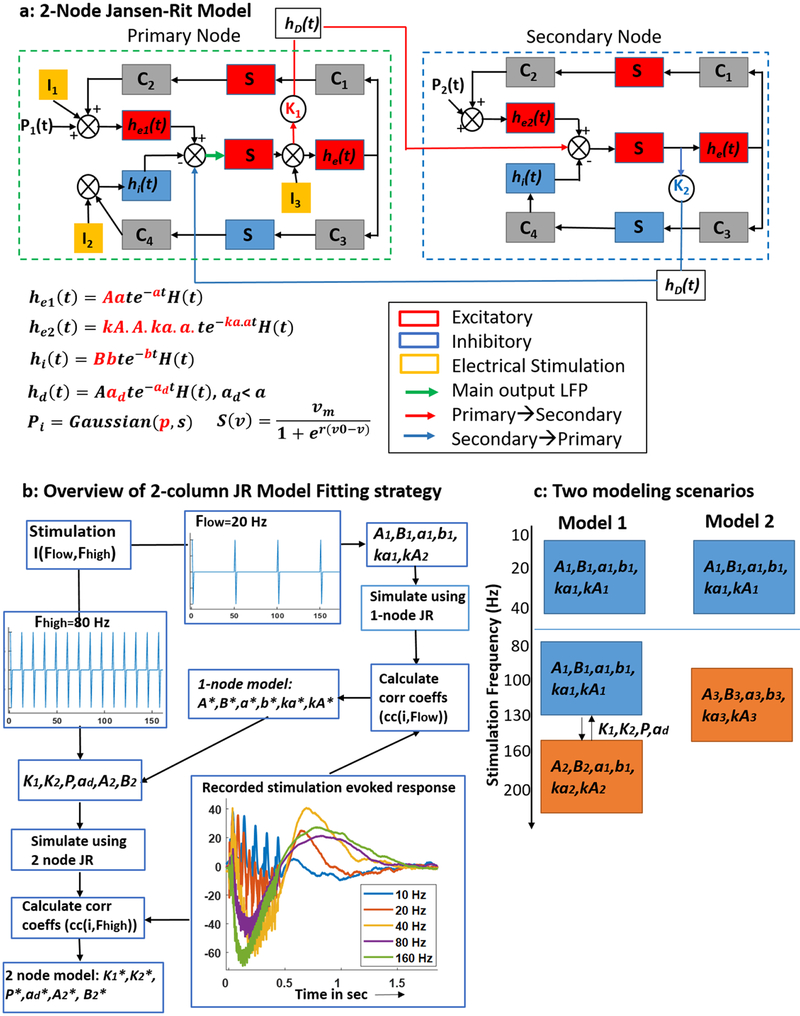
Figure 1.

Model schematic and method for identifying model parameters: (a) schematic of a 2-node JR model. Boxes represent neuronal populations and circles represent intra and inter population couplings. The parameters in red are the ones that were estimated. (b) A flowchart representation of the steps followed for model parameterization. The model parameters are described in table 1. The parameters with asterisks indicate those identified using recorded SER. Example SERs recorded from amygdala is also shown along with a reconstruction of the patient brain and electrode locations. (c) Two possible model paradigms: Model 1: 1-node JR model to simulate low frequency SERs and a second node added onto this to simulate high frequency SERs, Model 2: a combination of two 1-node JR models to simulate SERs in the low and high frequency stimulation regimes.

2.2. JR neural mass model

The JR model is a neural mass model that simulates the aggregate neuronal population activity of a local cortical circuit or cortical column [33]. A single cortical column is modeled as a population of pyramidal cells receiving inhibitory and excitatory feedback from local interneurons and excitatory input from neighboring or distant columns (figure 1(a)). In this representation, each neuronal population is modeled by two blocks:

1. An alpha function block that converts the average input action potential density of a neural population to an average output postsynaptic membrane potential (PSP) which can either be excitatory (h_e (t) = Aate^−at, t > 0) or inhibitory (h_i (t) = Bbte^−bt, t > 0). In these expressions, the parameters A and B determine the maximum amplitude of the excitatory and inhibitory PSP respectively, while the parameters a and b represent the average reciprocal time constant of the passive membrane and other spatially distributed delays in the dendritic network.

2. A sigmoid function block (S (v) = 2E/[1 + e^r(v0−v)]) that transforms the average membrane potential (v) of a neuronal population into the average action potential density fired by the neuronal population. Here, parameter E represents the maximum firing rate of the neural population, parameter v0 is the PSP that produces 50% of the maximum firing rate, and parameter r is the steepness of the sigmoid function.

In this model, a pyramidal population (middle red box in figure 1(a) receives feedback from the inter-neuronal populations via internal connections (C1–C4 in figure 1(a). The original model proposed in (33) possessed one external input (p(t)), that represented local and distant excitatory inputs from other cortical columns. Here we have included additional inputs (symbols I1, I2, I3 in figure 1) to model the tendency of external electrical stimulation to depolarize all neuronal sub-types. Here we used the cortical column model to represent the neuronal population in a brain region (cortical or subcortical). In some simulations, we coupled a second cortical column to the first cortical column via coupling constants (symbols K1 and K2 in figure 1(a) and a delay block (h_D) simulating the neuronal transmission delay. We consider the second column as representing a neighboring region coupled to the primary region of interest. The second cortical column consists of the same neuronal populations and connections and has similar parameters to those used in the first column. The parameters that differ include A (excitatory PSP amplitude), B (inhibitory PSP amplitude), and the mean value of the external input p(t) (does not include DBS input). We assumed that the neuronal population in neighboring brain regions have the same intrinsic properties except slight differences in the excitability (A, B) and the mean value of the external input (P2 in figure 1(a). For the rest of the paper, we will refer to the single and double column models as 1-node and 2-node models respectively.

2.3. Model parameter identification

A 1-node JR model has three parameters associated with the sigmoid function (E, r, v0), two parameters for each alpha function block (and therefore six for the three populations) and four internal connectivity parameters (C1–C4), resulting in a total of 13 parameters (table 1). In our 1-node JR model, we fixed the sigmoid function parameters and the internal connection parameters to those used in (43). These parameters were chosen such that the model operated in a non-oscillatory regime, i.e a free running model without an external perturbation will not produce any oscillations. We also set the external input (p) to a zero mean Gaussian process with a standard deviation of 0.1. The three time constant parameters, namely a, ka * a, and b of the pyramidal, excitatory interneuron and inhibitory interneuron populations, respectively, as well as the corresponding maximum PSP A, kA * A, B were identified from measured data (figure 1(b). We estimated the parameters corresponding to the synaptic time constants from data, as these parameters determine the shape of the response to input stimulation.

Table 1.

Model parameter description.

1-region parameter	Value	Description
Cl	135	Pyramidal to excitatory interneuron connection
C2	108	Excitatory interneuron to pyramidal connection
C3	33.75	Pyramidal to inhibitory interneuron connection
C4	33.75	Inhibitory interneuron to pyramidal connection
e	5	Maximum firing rate of a neuronal population
r	0.3	Steepness of sigmoid function
v0	6	Post-synaptic potential (PSP) for which 50% of e is achieved
A, B, kA * A	Estimated from data	Maximum PSP amplitude for pyramidal (A), inhibitory (B) and excitatory (kA * A) interneurons
a, b, ka * a	Estimated from data	Lumped representation of the sum of reciprocal of the membrane time constant and other spatially distributed delays in the dendritic network for pyramidal (a), inhibitory (b) and excitatory (ka * a) interneurons
2-region parameter
K1	Estimated from data	First to second region coupling strength
K2	Estimated from data	Feedback from 2nd region to the 1st region
Ad	Estimated from data	Inverse of delay time constant
P	Estimated from data	Constant added to external input p
External inputs
P	Gaussian (0,0.1)	Excitatory input from other cortical columns
I1	60 * unit impulse train	Electrical current input to pyramidal population
I2, I3	18 * unit impulse train	Electrical current inputs to interneurons

The following steps were used to identify these six parameters for a 1-node JR model:

1. A stimulation train of unit amplitude biphasic pulses (positive and negative square wave as shown in figure 1(b) at a frequency of F_low = 20 Hz or F_high = 80 Hz was provided as inputs (I1, I2, I3) to a 1-node JR model. A set of SERs was simulated as an output of the JR model, where each SER was simulated for a different combination of the parameters [A, B, a, b, ka, kA] which were varied over a range of [1 5], [16 27], [20 120], [10 80], [0.2 2], [0.2 2], respectively. In total, 950 400 parameter combinations were simulated.

2. The correlation coefficient was calculated between each simulated SER and the recorded SER from each patient at the 6 mA, 20 Hz or 80 Hz stimulation frequencies. Two types of SER were considered; SER1: the entire duration of the stimulation, including both the stimulated period and 1 s after stimulation ceased; SER2: 1s of response following stimulation. This produced two correlation values, cc1 and cc2 for each set of parameters and each recorded SER. We chose to examine the correlation in these two intervals as there are evoked responses both during stimulation and for at least 1 s after (figure 1(b).

3. The parameter sets that produced the top five correlation coefficients (cc1, cc2) were determined and the corresponding simulated SER1 and SER2 were visually inspected to avoid parameter sets that produced an unstable model in the form of oscillations. The final parameter set was chosen based on two criteria: (a) dynamics did not exhibit oscillatory SER, (b) The dynamics produced high correlation values during both SER1 and SER2. For example, if parameters S1 producing max (cc1) also produced a high cc2 (>0.6), while parameters S2 producing max (cc2) showed a poor cc1, then we chose S1.

This three-step procedure was repeated for each patient dataset corresponding to 20 and 80 Hz SERs, and the best-fitting parameter set for the 1-node model determined. This produced, for each patient dataset, two 1-node models corresponding to 20 Hz and 80 Hz stimulation train input. We chose the 20 and 80 Hz stimulation frequencies to create training datasets based on the SER shapes in the low and high frequency ranges, respectively. We chose 80 Hz based on the empirical observation that the SER shape changes around 80 Hz (figure 1(a). Hence 80 Hz is in the 2nd frequency group which we label high frequency. In addition, we note that these stimulation frequencies were applied to and recorded from all patient datasets.

The 2-node JR model was built by coupling a second node to the 1-node JR model parameterized using the 20 Hz SERs. Using the 80 Hz SERs, an additional six parameters were identified for this 2-node JR model: three coupling parameters K1, K2, ad; the input parameter P; and two parameters A, B corresponding to excitatory and inhibitory populations in the second node. Here K1 denotes the connection strength from the primary to the secondary node, while K2 denotes the feedback that the first node receives from the second coupled node. The delay between these nodes is simulated using an alpha function with time constant 1/ad. P is a constant value added to the existing external input to the primary node. The other parameters of the second node matched those of the primary node, except for the values of A and B, which were similar, but not identical to, those of the primary node. These parameters were identified using a similar approach as described above with a set of simulated responses generated from the 2-node JR model with an input stimulation train of frequency F_high = 80 Hz. The correlation coefficients were then calculated between the simulated responses and the recorded 80 Hz SERs for each patient (parameter identification is outlined in figure 1(b). We note that the 2-node model is not a combination of two 1-node models, each of the nodes fit at 20 and 80 Hz SERs. Instead, for the 2-node model, we use the 20 Hz SERs to estimate a 1-node model and then the 80 Hz SERs to estimate a subset of the 2nd node parameters as well as inter node coupling parameters.

This procedure produced two types of models (figure 1(c) to simulate SERs over a range of stimulation frequencies (10–160 Hz):

• Model 1:

  A 1-node JR model to simulate the lower frequency (10–40 Hz) SERs and a 2nd node coupled to this first one (2-node model) to simulate higher frequency (80–160 Hz) SERs;

• Model 2:

  Two independently parameterized 1-node JR models, one for simulating lower frequency SERs and the other one to simulate higher frequency SERs.

The Model 1 framework suggests that the low frequency stimulation response is governed by a local region, while higher frequency stimulation involves connected brain regions. Model 2 on the other hand, suggests that the local effect of stimulation in lower frequencies is different from that in higher frequencies, and that the two ranges of frequencies activate local neuronal masses with different properties.

2.4. Model performance

We implemented the following procedure to compare the in vivo stimulation data and the simulation results. We first calculated a correlation coefficient between the recorded SER and the simulated SER at each stimulation frequency using both Models 1 and 2. We then compared for significant differences between these two correlation coefficients at each frequency by using a resampling procedure. To perform the resampling, we generated 1000 surrogate SERs from the in vivo recordings by resampling with replacement from the individual SER trials, computed the correlation coefficient between each of these surrogate in vivo SERs and the model SERs, then computed the difference in correlation between the two model results. We used the surrogate difference to construct a confidence bound to test the null hypothesis that Models 1 and 2 produce the same correlation coefficient across all stimulation frequencies

To test the robustness of the simulations to changes in the fixed model parameters (E, v0, r, C) of the primary node, we performed a sensitivity analysis. We varied these fixed parameters by +/−1, +/−2, +/−−3, +/−4 and +/−5% of their nominal value to create a set of 14 640 (11⁴−1) combinations of perturbed and nominal parameters. For example, one combination of parameters corresponds to the three parameters E, v0, and r fixed at their nominal values, and the parameter C increased by 2%. For each such combination of fixed parameters (with at least one parameter different from the corresponding nominal value), we simulated responses to electrical stimulation over 10–160 Hz. Each simulated SERs was compared to the SER simulated in the original model by calculating a correlation coefficient between the two SERs. The simulated SERs were also visually inspected to determine if perturbing the model parameters by 5% results in model dynamics that did not relax to rest (i.e. model dynamics consisting of oscillations).

3. Results

We analyzed SER in five human patients and one NHP to determine consistent SER characteristics across these datasets. We then fit JR models [43] using a subset of this data (figure 1). We show that these models can be used to accurately simulate the entire dataset. We also show that this model can predict responses across recording sessions over a month in an NHP.

3.1. SER peak latency is more consistent across patients than SER peak voltage

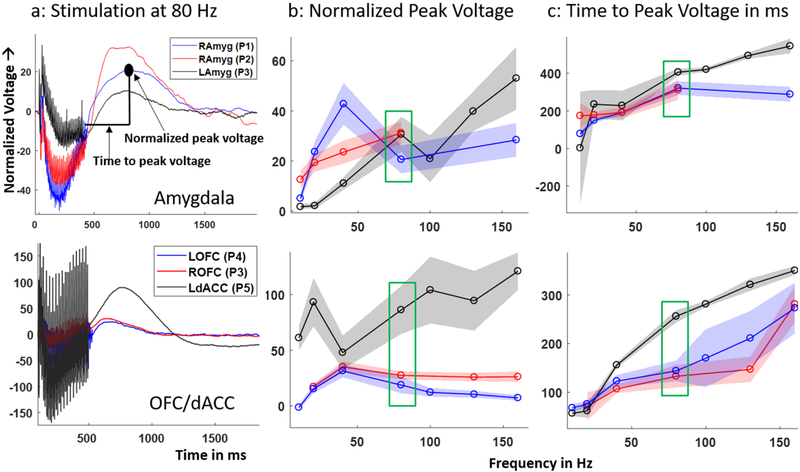
To study the neural dynamics of SERs and determine if there are consistent response characteristics across human participants, we compared local neural responses to amygdala and cortical stimulation across six datasets from five patients (figure 2). In the example 80 Hz SERs recorded in the amygdala and cortex (figure 2(a), the first 400 ms is the duration when the stimulation train was applied at the neighboring electrode pair, the artifacts of which are seen in the recorded LFP. The artifacts are modulated by a slower varying response during this period. After the stimulation train ended, the voltage reached a maximum value (indicated by a black circle) and then returned to resting state. This after-stimulation response (SER) lasted for approximately 0.6–1 s.

Figure 2.

Recorded SER trends across patients: (a) example 80 Hz SER normalized to pre-stimulation baseline in the six datasets recorded from N = 5 patients. Each SER (averaged over trials) was recorded in the amygdala (top) and OFC/dACC (bottom). (b) Variation of normalized peak voltage, (c) time to peak voltage over stimulation frequencies. The shaded error bars indicate 1 standard deviation calculated from 1000 surrogate SERs generated by resampling with replacement 5–10 recorded SER trials at each stimulation frequency and for each dataset. The coloring scheme for b and c are same as in a. The recorded SER corresponding to 80 Hz stimulation for all the datasets (boxed in green) are plotted in a. Note: P2 had SERs from 10–80 Hz.

The general time course of the SER shape is similar across datasets in the cortex and the amygdala (figure 2(a). The normalized peak voltage, calculated as the maximum value of the SER divided by the standard deviation of the pre-stimulation period voltage (figure 2(b), showed a variable relationship with stimulation frequency across patients. The time taken for the voltage to reach this peak value (figure 2(c) increased with stimulation frequency, indicating that the SER peak shifts later as stimulation frequency increases. The shaded error bars in figures 2(b) and (c) represent 1 standard deviation calculated from 1000 surrogates generated by resampling with replacement of the five–ten trials recorded at each stimulation frequency. The normalized peak voltage did not show any consistent trend over stimulation frequency, even within an individual cortical structure or amygdala. The time to peak voltage showed a general increase and saturation with increase in stimulation frequency in both brain structures. Overall, the time to peak voltage showed a more consistent trend across frequencies and patients than the normalized peak voltage.

3.2. A neural mass model of cortical population activity mimics the in vivo SER

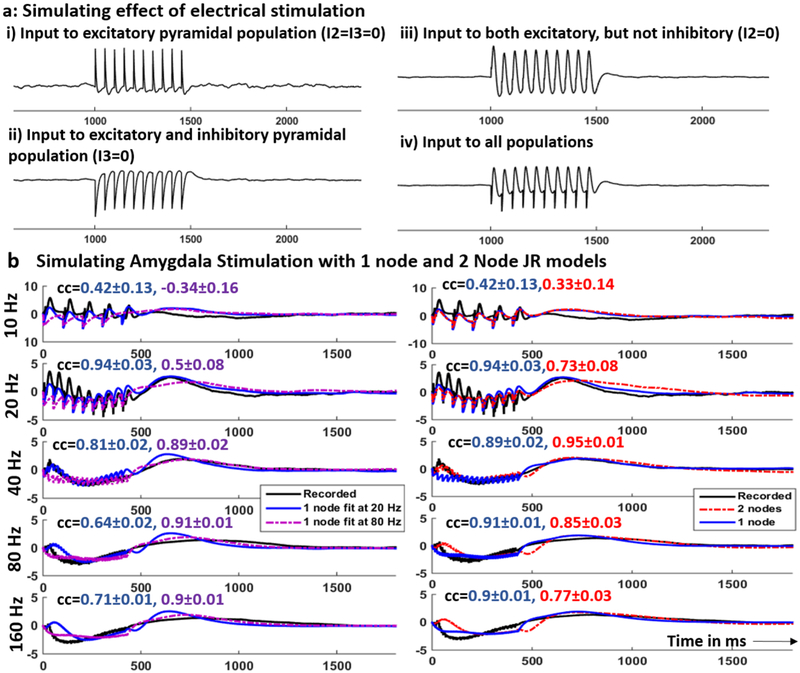
To determine the parameter sets in the 1-node JR model that mimicked in vivo SER, we simulated this model with parameters as in (43) and different combinations of external input chosen to reproduce different stimulation trains. For example, we compared simulated response of the 1-node JR model to a train of 20 Hz stimulation pulses applied as input to different combinations of the model’s three neural populations to the in vivo SER (figure 3(a). Visual inspection suggests that the model produced a SER similar to the in vivo data (figure 3(b) only when the same stimulation input was provided to all three neuronal populations (figure 3(a), subpanel iv). This is biophysically plausible, because electrical stimulation generates a wide electric field affecting all the populations, rather than a single population in the column [58]. We therefore chose to model stimulation as impacting all three neural populations.

Figure 3.

Examples of recorded and simulated SERs in amygdala: (a) simulating the effect of stimulation on a 1-node JR model by adding input stimulation train to one, two or all three populations within a column. (b) Left: Recorded (black) and simulated SER using the 1-node JR models fit to 20 Hz (blue) and 80 Hz (purple) SERs in the amygdala. Right: Recorded (black) and simulated SER using 1-node JR model (blue) and that using the 2-node JR model (red). The blue SER is simulated using the 1-node model that produced a higher correlation coefficient. Each row in b corresponds to a different stimulation frequency as indicated on the y-axis. The correlation coefficients (mean ± 2 std dev) between the recorded and the simulated SER are shown in the same color as the corresponding plot.

The recorded SERs were used to estimate model parameters in a 1-node and 2-node JR model (see methods). All the simulations including model parameter identification, model prediction and model robustness analysis were performed using custom written codes in MATLAB software. The basic code for simulating a 1-node and a 2-node model are in a github repository (https://github.com/tne-lab/Jansen–Rit-model/blob/master/jansen_sim.m). The initial simulations corresponding to 950 400 parameters for the 1-node model took around 6 h for each stimulation frequency. The simulation corresponding to the 2-node model at a particular stimulation frequency took around 7.5 h.

Using the 1-node JR model parameterized using 20 Hz and 80 Hz SERs and the 2-node JR model, we simulated response to stimulation for the entire frequency range (10–160 Hz) and computed the correlation coefficient between the recorded and the simulated SERs. We also calculated correlation coefficients between the simulated SERs and 1000 surrogate SERs generated by resampling with replacement of the recorded SER trials. This procedure generated 1000 correlation coefficients for each stimulation frequency which were then used to generate the confidence bounds (5th and 95th percentiles). An example set of recorded and simulated SERs in the amygdala of patient P1 is shown in figures 3(b) and (c). Comparing the two 1-node JR models (figure 3(b), the 1-node model fit to 20 Hz SERs produced correlation coefficients 0.42 ± 0.13 and 0.94 ± 0.03 (mean ± 2 std) at 10 Hz and 20 Hz stimulation respectively. Thus, the model fit to 20 Hz SER provided a better fit than that fit to 80 Hz both quantitatively and qualitatively (visual inspection) in the lower frequency range. At these two stimulation frequencies, this 1-node model also produced a better fit than the 2-node model (figure 3(c). On the other hand, at 40, 80 and 160 Hz, the 1-node model fit to 80 Hz SERs produced a better fit than the one fit to 20 Hz SERs. Thus, any given 1-node model is only able to capture SER over a limited frequency range. The 2-node model (figure 3(c) improved the fit at 40 Hz (not used for parameter estimation) over both 1-node models with a correlation of 0.95 ± 0.01. At 80 and 160 Hz, the 1-node model fit to 80 Hz SER provided a better fit than the 2-node model as shown by higher correlation coefficients (figure 3(c).

We considered two modeling paradigms (figure 1(c): (i) Model 1 combining a 1-node JR model fit to 20 Hz SER and a 2-node JR model with the 2nd node parameters estimated from 80 Hz SER, (ii) Model 2 combining a 1-node JR model fit to 20 Hz SER and another 1-node JR model fit to 80 Hz SER. In both models 1 and 2, the 1-node JR model fit to 20 Hz SER was used to simulate SERs in the low frequency (10–40 Hz) range while the high frequency (80–160 Hz) SERs were simulated using the 2-node model (Model 1) or the 1-node model fit to 80 Hz SER (Model 2).

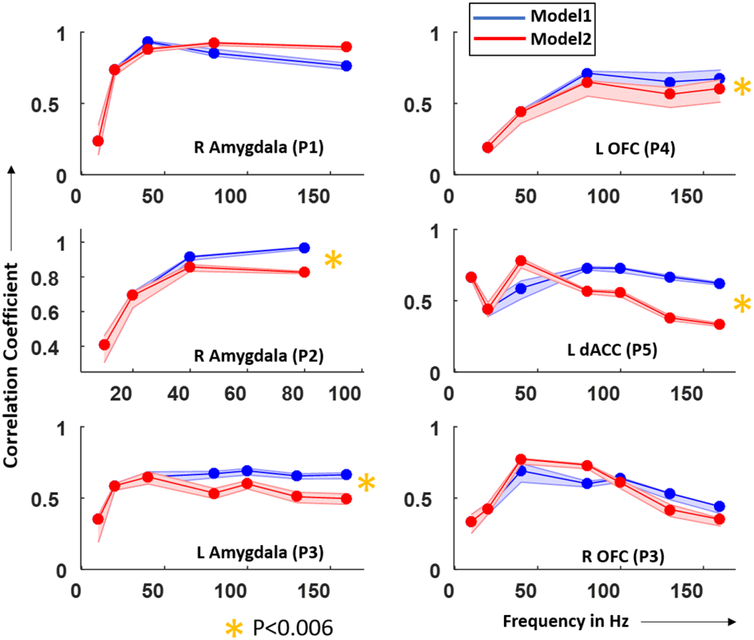
To compare the performances of Models 1 and 2 across stimulation frequencies, we averaged the correlation coefficients over all frequency points greater than 40 Hz and calculated the difference in the average correlation coefficients between Models 1 and 2. We constructed 95% confidence intervals for this difference through a resampling procedure as described in methods section. In both amygdala (left column in figure 4) and OFC/dACC (right column in figure 4), 2/3 datasets had a significantly higher correlation coefficient using models 1 than 2 (p < 0.06). We conclude that, in most cases, Model 1, which included both 1-node and 2-node models, had a better performance across the 40–160 Hz range of stimulation frequencies and hence would be a preferred modeling strategy. We also noted that the correlation coefficient decreases at higher frequencies mostly in Model 2 where a 1-node JR model was used for higher frequencies. This might indicate that a 2-node model is necessary to simulate the SERs at higher frequencies.

Figure 4.

The correlation between the human and model SERs tends to be highest for the 2-node model. Correlation coefficient between recorded and simulated SERs in the amygdala (left) and dACC/OFC (right) across subjects plotted over stimulation frequencies. SERs used to calculate the correlation coefficients were simulated using Model 1 (blue) and Model 2 (red). Yellow stars indicate the datasets for which Model 1 had significantly better fit (higher correlation coefficient) than Model 2 across stimulation frequencies greater than that where Models 1 and 2 were used (same 1-node model for lower frequencies). The p-value was determined based on empirical distributions generated by 1000 correlation coefficients calculated between surrogate SERs and simulated SERs averaged over frequencies. The p-value is corrected for multiple comparisons (N = 6 datasets) using Bonferroni correction. Note: amygdala (P2) did not have stimulation frequencies above 80 Hz as epileptiform activity appeared at 160 Hz.

3.3. Estimated model parameters are more variable in the cortical than subcortical regions

Visual inspection of figure 5 reveals that some the estimated model parameters for the 1 node and 2 node models show some variability across 6 human datasets. This observation is especially strong for the amygdala, where the variability in most parameter estimates is less than for cortex. This difference in variability could be due to the fact that the cortical region sampled across datasets (determined by electrode placements in the cortex) is inherently more variable than the amygdala. To quantify the range of parameter space spanned by each region model, we calculated the ratio of the range of each estimated parameter for a particular region to the range considered for parameter estimation.

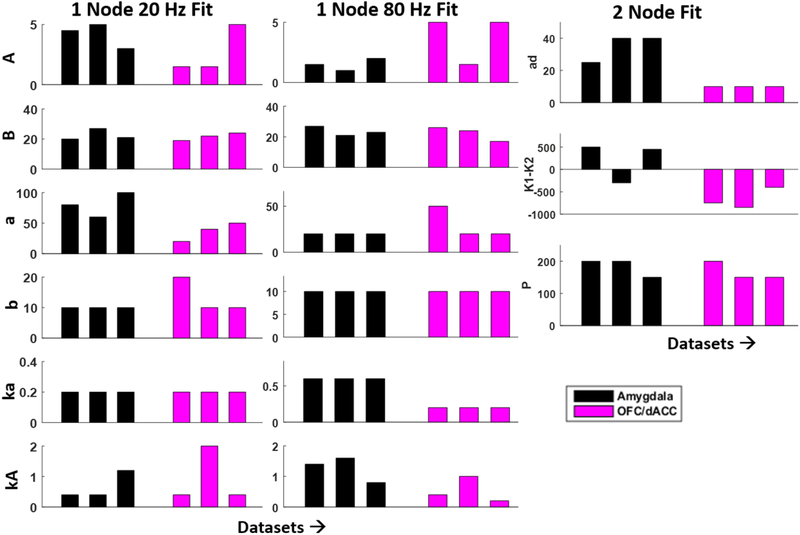
Figure 5.

Estimated model parameters differ between amygdala and cortex. (left, middle): 1-node model parameter estimates using recorded SERs at 80 and 20 Hz stimulation. (right): the 2nd node coupling parameters that were used to improve model fit in higher frequency stimulation (80–160 Hz) regime for amygdala (black) and cortical (magenta) structures.

This ratio can vary between 0 and 1, with 0 indicating an identical parameter value estimated across all patient datasets, and 1 indicating estimated parameters extending across the entire range of values considered. For the 1-node model fits, the cortical regions exhibited ratios between 0 and 0.875 (parameters ka and A, respectively for the 20 Hz fit), and between 0 and 0.89 (b or ka, and kA, respectively, for the 80 Hz fit). In the amygdala, these ratios tended to be smaller; between 0 and 0.64 for the 20 Hz fit, and between 0 and 0.54 for the 80 Hz fit. In general, we note that parameters linked to time constants (a,b,ka,ad) and couplings (K1,K2) showed lesser variability (0–0.5) for both regions.

3.4. Simulated LFP is robust to changes in fixed parameters

When the fixed model parameters of the primary node were varied by +/−5%, the simulated SERs closely followed the ones corresponding to the original parameter values. This correspondence results in high correlation coefficients between the SERs simulated with different parameter configurations (figure 6). These results support the conclusion that the simulations are robust to minor changes in the fixed parameters.

Figure 6.

(a) Mean and standard deviation of the correlation coefficient between simulated SER from the original fixed parameters and those simulated using perturbed fixed parameters across stimulation frequencies. Each fixed parameter was perturbed by 1%–5%. The different datasets are color-coded. (b) Example simulated SER using perturbed parameters for 10 Hz and 20 Hz stimulation.

3.5. Model predictions remain accurate over multiple days of recording in an NHP

The application of chronic stimulation to treat brain disorders requires models that can be accurate for long periods of time. This is important for model development and prediction of how neural tissue responds to electrical stimulation. This is because model parameter estimation is time-consuming, and frequent re-estimations of the model parameters would not be practical. To test whether the present model has the desired long-term accuracy, we recorded SERs to 4mA, 10–200 Hz stimulation over five sessions in the medial orbito-frontal cortex (mOFC) of a non-human primate (NHP, figure 7(a). These five sessions spanned a month and intervals between sessions ranged between 2–15 d. As observed for the human data, the NHP dataset showed an increase and saturation of the time to first peak with increasing stimulation frequency (figure 7(b), top). There is more variability in the time to first peak across recording sessions in the lower frequency range (<100 Hz). The normalized peak voltage did not show any consistent trend across recording sessions with stimulation frequency and had overlapping error ranges except for session 2 (figure 7(b); bottom).

Figure 7.

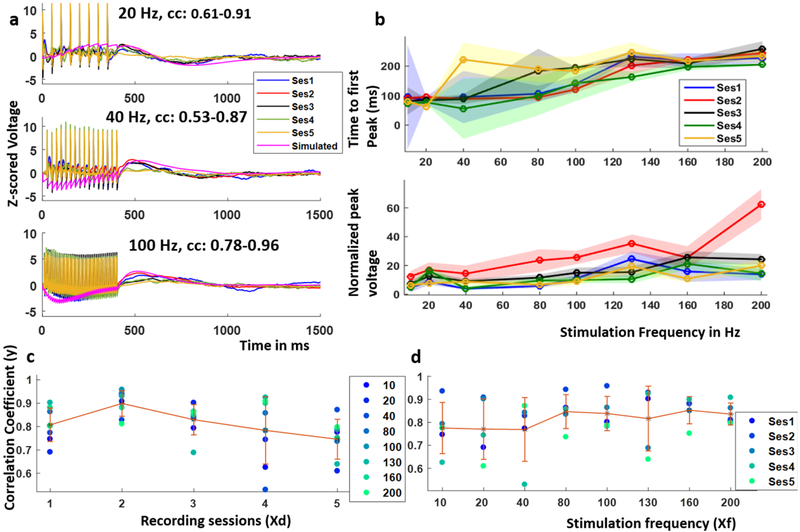
The brain responds consistently to stimulation over one month. (a) Example SERs recorded in the mOFC with local stimulation at 4 mA and 10–200 Hz frequency over a period of 1 month and that simulated using a 2-node JR model which was parameterized using SERs recorded in the first session, the range of correlation coefficients between the recorded and simulated SERs across sessions included, (b) normalized peak voltage and time to peak voltage over the five recording sessions, (c) variation of the correlation coefficient between the recorded and simulated SER over recording sessions and that over stimulation frequencies.

To determine if model parameters from one session could predict subsequent stimulation sessions, the mOFC SERs recorded at 4 mA, 20 Hz and 80 Hz on session 1 were used to parameterize a 2-node JR model using the same procedure as described for human data (examples shown in figure 7(a). Using the optimal parameter sets from the first session, we then simulated the SERs for all stimulation frequencies and compared these simulated SERs to the SERs recorded from the other four sessions. In the examples shown in figure 7(a), the correlation coefficients between the simulated SERs and those recorded across five sessions ranged from 0.61–0.91, 0.53–0.87 and 0.78–0.96 at 20 Hz, 40 Hz and 100 Hz respectively. Over the last two recording sessions, the mean correlation coefficient over all the frequencies decreased, however the correlation tended to remain high (mean correlation = 0.75 in session 5, highest mean correlation of 0.90 in session 2, figure 7(c). We note that the higher stimulation frequencies produced a better overall fit with less variability in the correlation coefficient across the five sessions (figure 7(d).

To determine if the recording session and/or the stimulation frequency had a significant effect on the correlation coefficient, we fit a linear regression model of the form:

$$y~x0+Xf+Xd$$

with the response variable (y) being the correlation coefficients (figures 7(c) and (d)) and the two predictors Xf and Xd being the stimulation frequency and the recording day respectively. x0 is an intercept term. The recording session number had a significant effect in predicting the correlation coefficients (p < 0.05) while the stimulation frequency did not (table 2). This is why we observe a higher variability of the correlation coefficient across recording sessions (figure 7(c) as compared to that across stimulation frequency (figure 7(d).

Table 2.

Coefficients of regression model.

variable	Estimated coefficient	Std error	T-stat	P-value
Xf (frequency)	0.0004	0.0002	1.84	0.074
Xd (day)	−0.0033	0.0015	−2.23	0.032

4. Discussion

Electrical stimulation of cortical and sub-cortical brain structures is a promising treatment paradigm for neurological and neuropsychiatric disorders [16, 59, 60]. Understanding and quantifying how neuronal populations respond to electrical stimulation could help design optimal stimulation paradigms, particularly in biomarker-based treatment. Toward this end, we showed that a neural mass model of cortical columns can successfully simulate electrical SERs in cortical and sub-cortical structures. Such a model, once calibrated using data recorded from a subset of stimulation frequencies, can then be used to predict the effects of electrical stimulation at frequencies not used to train the model. This allows an exploration of the stimulation response over a wide range of stimulation parameter values that would be difficult to test in vivo. Although the model framework is calibrated for local responses, this could be extended to a wider network of two or more brain regions by adding more JR nodes and using appropriate recorded data. This would require more data to estimate the additional parameters introduced. Recordings from each region would be necessary and SERs from each region would be required to estimate network connectivity. Furthermore, we could modify the model parameters to simulate responses in other brain regions using a recorded LFP from the target regions for model calibration.

We chose a neural mass model to simulate the effect of electrical stimulation in local neuronal populations for two main reasons. First, this class of models has a relatively constrainable parameter space when compared to more detailed biophysical models. Second, neural mass models generate biophysically interpretable results and hence provide a balance between data-driven abstract models and detailed biophysical models. Such neural population models have been used in different contexts. They have successfully simulated resting brain rhythms in normal and pathological states as well as event-related responses [38, 61]. There have been relatively few attempts at simulating the effects of external electrical [62] and magnetic [63] stimulation in neural mass models. Here we chose the JR neural mass model originally developed to simulate visual evoked response in EEG signals. We extended this model by (i) adapting it for LFP recorded from both cortical and sub-cortical structures and (ii) introducing external electrical stimulation of varying frequency in this model. This suggests that this model can be used as a general model of neuronal interactions.

We considered two modeling regimes to account for the variability in the SERs caused by variation in stimulation frequency. We showed that the stimulation parameters influence the model’s response characteristics. A model calibrated to match the in vivo response to low frequency stimulation does not predict the in vivo response to high frequency stimulation, and vice versa. This is evident from the change in the shape of the evoked responses with variations in stimulation frequencies, which is not a simple linear effect. This change in response was observed in the 40–80 Hz range. Hence, we chose the two training sets to be 20 Hz and 80 Hz. A similar change in therapeutic regimes has been found in DBS for Parkinson’s disease where low frequency DBS can worsen symptoms while high frequency stimulation ameliorates symptoms [49, 64]. We further demonstrated that variability in the SER could be better captured by a 2-node model than by 1-node models. Biophysically, we interpret this model to indicate that the system enters different network states corresponding to different ranges of stimulation frequency. This could be caused by frequency dependent plasticity [65]. Intuitively, we expect that a higher order model (i.e. a model with more variables) will better reproduce the in vivo responses observed at higher frequencies. Our results indicate that the higher frequency response is better simulated by using a higher order dynamic system than the lower frequency response. Here, we chose to implement these additional variables by developing a 2-node model which has a biophysically realistic interpretation. We note that other model choices may succeed as well.

We observed consistent SERs over a month in an NHP, particularly in the higher frequency range. This was also captured by the model, which was parameterized using data from the first recording session. As expected, due to the consistency of the in vivo SERs, the simulated SERs from the model showed high correlation with the in vivo observations over the remaining 4 recording sessions. These results indicate that, for chronic implants, stimulation effects and model fits are stable and do not require recalibration over a period of at least two–four weeks. However, we note that this stable duration may depend on the frequency of stimulation, because in the current dataset, we observed that the model predictions were more variable in the lower frequency range than the higher frequency. Higher frequencies are more common in present-day clinical applications, a model limitation that would merit exploration in future research. Moreover, the response to stimulation over time will potentially depend on patient comorbidities and stimulation target which could potentially be tested with the next-generation DBS systems such as the PC+S. Here, we did not examine responses to long term stimulation. For long term responses, we expect that we would have to change the coupling parameters as a function of external stimulation with some decay over time after stimulation stops.

In this work, we fit a model to individual patient dataset and did not average across datasets as we envision that such a model fit should be patient specific. We chose to model the time domain evoked response because this feature has been demonstrated as a potential feedback control signal for adjusting DBS parameters for tremor reduction [29]. DBS evoked response in scalp EEG has also been shown to be a good discriminator between primary and secondary dystonia [66]. Evoked compound nerve action potentials have been used to design an autonomous neural control for vagus nerve stimulation for treating epileptic and depressed patients [67]. Although we focused on simulating the electrical SER, and used this feature to calibrate the model, the approach employed here could be extended to model oscillatory features, such as the evoked alpha or theta band power. For parameter identification, we used a grid search method to maximize the correlation coefficient between the in vivo and simulated data. We used correlation coefficient as a distance metric because we were interested in the shape of the SER.

We also identified a subset of the model parameters while fixing the rest of the parameters to previously used values. The fixed parameters corresponded to intrinsic subpopulation connectivity and the nonlinear transfer function from the mean membrane potential to the mean output spiking rate [43]. We chose to fix these parameters, as these are typically time independent and less likely to be affected by external stimulation on a short time window. The values were chosen to produce a non-oscillatory regime. We also showed that the simulations were robust to changes in these fixed parameters by 1%–5% of their nominal values. The estimated parameters from recorded data reflect the linear time varying transfer function that converts the average input action potential density of a neural population to an average output PSP. Although we did employ some visual inspection as part of the model parameter estimation, we then validated the results by testing the models against datasets that were not used for the model fitting. We thus avoided overfitting by using only one or two sets of SERs for training, and then testing on the rest of the dataset. This is evident from the simulated SERS in similar frequency ranges which showed comparable correlation coefficients as the training dataset. Other data assimilation techniques, such as dynamic causal modeling [68] and Monte Carlo methods [69], might be used for identifying all or a subset of the model parameters. In addition, other features from the data—for example, measures of coupling between two brain areas—may help further constrain and validate multi-node, network models. We note that this modeling approach is not meant for online parameter estimation. Instead, this procedure is most compatible with offline model fitting to support an in silico simulation engine. Here we used visual inspection as part of the parameter estimation procedure, as is common in offline signal analysis and modeling.

An important direction of future work would be to use this modeling framework to find the SER correlates of therapeutic outcome [29]. For example, if specific aspects of the SER produce a positive therapeutic outcome, we could attempt to identify stimulation parameters that maximize those physiologic responses. Another application would be to use animal models of psychiatric disorders for testing effects of model-based predicted stimulation parameters on behavior. This would help design model-based stimulation to change behavior in a desired manner.

5. Conclusion

We show that a relatively simple neural mass model of coupled cortical columns predicts the response to electrical stimulation in human and NHP brain. This modeling framework can potentially help overcome an inherent drawback of human brain stimulation studies, where investigators tend to use a narrow subset of stimulation parameters. By using the model to explore a wider range of stimulation settings, an optimal stimulation strategy for a given patient could be proposed and tested. This has applications in designing DBS-based neuro-physiology experiments and in the creation of model-driven closed-loop neuro-stimulation algorithms.