Adaptive optics in the mouse eye: wavefront sensing based vs. image-guided aberration correction

Abstract

Adaptive Optics (AO) is required to achieve diffraction limited resolution in many real-life imaging applications in biology and medicine. AO is essential to guarantee high fidelity visualization of cellular structures for retinal imaging by correcting ocular aberrations. Aberration correction for mouse retinal imaging by direct wavefront measurement has been demonstrated with great success. However, for mouse eyes, the performance of the wavefront sensor (WFS) based AO can be limited by several factors including non-common path errors, wavefront reconstruction errors, and an ill-defined reference plane. Image-based AO can avoid these issues at the cost of algorithmic execution time. Furthermore, image-based approaches can provide improvements to compactness, accessibility, and even the performance of AO systems. Here, we demonstrate the ability of image-based AO to provide comparable aberration correction and image resolution to the conventional Shack-Hartmann WFS-based AO approach. The residual wavefront error of the mouse eye was monitored during a wavefront sensorless optimization to allow comparison with classical AO. This also allowed us to improve the performance of our AO system for small animal retinal imaging.

1. Introduction

Retinal imaging with Adaptive Optics (AO) is necessary to allow reliable visualization and monitoring of single retinal cell morphology in vivo by correcting for ocular aberrations of the eye, which acts as the microscope objective. Animal models are important for studying pathophysiology and treatment of many human diseases. This also includes common eye diseases such as diabetic retinopathy, glaucoma, and age-related macular degeneration, as well as rare genetic diseases such as retinitis pigmentosa. Conventional ex vivo immunohistochemistry often used in these studies provides exquisite cellular contrast and high cellular resolution of the retina, but only at a single point in time. This results in studies with large cohorts of animals multiplied by the number of time points that are needed. Non-invasive imaging of living animals enables the characterization of the progression of pathology and the evaluation of new therapies for eventual use in humans within a single mouse during longitudinal studies, greatly reducing numbers of animals needed for the experiment [1]. Mouse models are widely used in preclinical research partially due to the availability of transgenic strains, which includes mice with the relevant cell classes labeled by fluorescent proteins. Imaging modalities such as Adaptive Optics - Scanning Light Ophthalmoscopy (AO-SLO) employed with fluorescence detection can be used to examine the structural and functional features [2,3] in the retina at cellular resolution. A recent review article [4] further describes the significance of AO for retinal imaging in vision science.

In comparison to primates, mice have eyes with a relatively high numerical aperture that provides the potential for sub-micrometer diffraction limited resolution. There are challenges associated with consistent high-resolution AO imaging for small animal eyes that arise from sensitivity to alignment, and the length of the eye relative to the thickness of the retina. The short focal length creates a large relative optical thickness of the retina, requiring a large dioptric power to optically section through the retinal layers [5], which is often also a source of aberrations.

Accurate measurements with a Shack-Hartmann (SH) Wavefront Sensor (WFS) require a well-defined reference light source or ‘guide star’, with sufficient signal above the background noise photons from other scattering tissue for layer specific aberration correction [6]. The so-called ‘small eye artifact’ [7] means that instead of a single scattering reference for the SH-WFS as in the case in human retinal imaging, the various strongly scattering retinal layers, such as the heavily pigmented Retinal Pigmented Epithelium (RPE), Choroid, and Nerve Fiber Layer (NFL), have the potential to confound wavefront sensor measurements. The difficulty of performing direct wavefront measurements from the small animal eye further increases for albino strains where the backscattered signal from the desired imaging target, such as RPE, is not present due to lack of melanin and the WFS is overwhelmed by background scattering from the sclera.

The conventional method for aberration correction with AO requires closed-loop feedback between residual aberrations measured by SH-WFS in response to changing the shape of wavefront corrector. Multiple groups have demonstrated WFS AO to provide high-resolution retinal images in the mouse eye, including [1,8,9] to list a few. However, a direct measurement of the wavefront from the retinal volume of interest in small animal eyes requires a complex system and may not always be possible due to the multi-layered structure of the sample, in addition to mild cornea or intraocular lens opacities.

Wavefront Sensorless (WFS-less) AO is an alternative approach to the WFS based AO method that uses an image-based optimization method to correct the aberrations. Multiple approaches to WFS-less AO have been reported, including amongst others: stochastic steepest gradient descent, simulated annealing, hill climbing modal optimizations, and pupil segmentation [10–12]. WFS-less AO SLO has been demonstrated for cellular resolution retinal imaging in mice [13–15], and WFS-less AO has also been demonstrated to correct for non-common path errors in combination with WFS AO [16]. WFS-less AO has the potential to alleviate the dependency on the WFS alone and provide an alternative method for aberration correction at multiple depths in the retina as well as simplifying the imaging system [17]. However, WFS-less AO requires an optimization execution time several times longer, which can be disrupted by the motion inherent in a living, breathing animal.

In this work, we demonstrate WFS-less AO for aberration correction that was implemented in a state-of-the-art WFS AO SLO system design for mouse retinal imaging, and present comparisons of the image quality and wavefront measurements during AO correction performed by each method. Confocal SLO back-scattering images of the mouse photoreceptor mosaic are presented, representing a case where the WFS and WFS-less AO are both using the same reference to guide the AO. As an example of a case where the wavefront sensing and the imaging planes are different, images of mouse retinal microglia labeled with fluorescent proteins are presented. We demonstrate that WFS-less AO can correct the same aberrations that are measured by a SH-WFS and that WFS-less AO can perform depth-resolved aberration correction resulting in reliable imaging focal plane shift in a mouse eye.

2. Methods

Mouse retinal imaging was performed using a custom designed AO SLO system that has previously been described [9,18]; please see Section 2.1 for details. The AO SLO design was based on SH-WFS AO, using wavefront measurements from the mouse eye to perform aberration correction. The differences from the previously reported configuration include: the scanning mirrors were changed to galvanometer mounted mirrors, and the optical detection path. For WFS AO, the deformable mirror (DM) control was provided by the WFS measurement software, which allowed for the closed-loop functionality. The SH-WFS sub-system is described in Section 2.2. Only software changes were required to implement the image-based WFS-less AO approach; the WFS-less AO software is described in Section 2.3. The WFS-less AO required the image acquisition software to control the DM. The system recorded wavefront data from the mouse eye as measured by the SH-WFS while performing WFS-less AO.

2.1 AO SLO system description

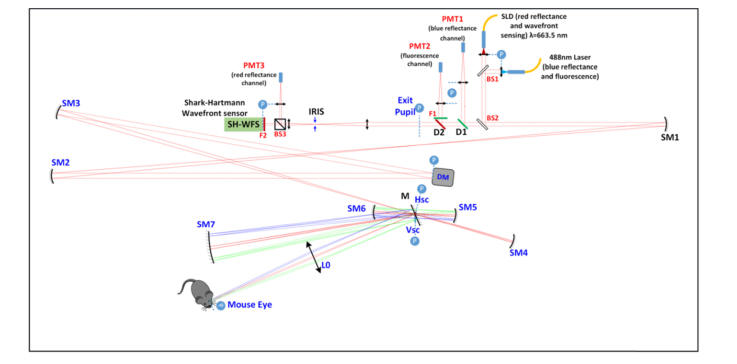
The AO SLO system was custom designed for reflectance and fluorescence imaging of the mouse retina, further described in Zawadzki et al. [9,18]. Light from a superluminescent diode (SLD, Superlum, SLD-26-HP) with a 663 nm center wavelength was used for reflectance imaging, and as a beacon for wavefront sensing. The system also used co-aligned light from a 488 nm laser (Coherent, OBIS 488 nm LX) for fluorescence excitation. The laser power at the mouse eye was limited to 100 μW for each light source. The first pupil plane was defined by the continuous membrane DM (ALPAO, DM97-15). The optical plane was relayed to the horizontal galvanometer scanning mirror and then to the vertical galvanometer scanning mirror (Cambridge, 6215H) using afocal telescopes made from pairs of spherical mirrors. The pupil plane was further relayed with a spherical mirror and a lens to the mouse eye with a final beam diameter of 2 mm to be focused to the retina with the maximum available numerical aperture of ~0.5. The contact lens was mounted at the last pupil plane for alignment of the mouse eye. The optical layout of the system is shown in Appendix A. Figure 8 and Appendix A. Table 1 lists the optical parameters of the important system components.

The back-scattered light from the 488nm laser was split and relayed with pairs of lenses from the DM to the first photo multiplier tube (PMT1, Hamamatsu Photonics, H7422-20). The fluorescence light was separated with a dichroic mirror and relayed to PMT2 (Hamamatsu Photonics, H7422-40). The back-scattered light from the 663nm SLD was split by BS3 (beamsplitter, R:T = 30:70), the reflected portion was acquired by PMT3 (H7422-50), and the other portion went to the SH-WFS, which was created by a lenslet array (Pitch = 150 μm, f = 6.43 mm) and a CMOS camera (UI306xcp-M; IDS Imaging Development Systems GmbH). The back-scattered light created a 6 mm circular aperture on the SH-WFS with a total of 1264 wavefront samples. The WFS-AO control is described in Section 2.3.

The image acquisition program was developed using custom C/C + + for real-time image display and to control the galvanometer mirrors. The current output from each PMT was converted to voltages with transimpedance amplifiers (Femto, HCA-2M-1M-C) and digitized with an analog-to-digital converter (NI PCIe-6363) capable of multi-channel acquisition at 1.00 MSPS (mega samples per second). The frames were sampled at 400 x 200 pixels during acquisition, and the sampling density was reduced to 400 x 100 pixels to increase the frame rate during WFS-less AO optimizations. The galvanometer mirrors were scanned using a bi-directional pattern in a 1 kHz sinusoid that acquired data in the forward and backward scan directions. The images were de-warped for display in real-time.

2.2 WFS AO description

We used a custom control software to perform WFS measurements from the sample and to control the DM for closed-loop AO aberration correction. This software was provided by the University of Verona [19]. The WFS centroids were selected with a circular aperture for wavefront reconstruction and display in Zernike modes. The WFS-AO was activated by closing the control loop between the WFS and DM. In order to image different retinal layers within the eye, the user could enter the desired amount of defocus. Under this condition, the wavefront measurement would be relative to a reference with the defocus value included. The WFS software could release the connection from the DM so that the acquisition software could control the DM for WFS-less AO, yet allow the wavefront measurements to still be recorded for analysis. The exposure time of the WFS was set to capture light as the beacon was scanned across the sample, which accumulated light in the WFS from across an area within the eye. The camera exposure time and wavefront reconstruction time limited the WFS AO system to 100Hz.

The AO control began with calibrated actuator settings or ‘system flat’, which removed the system’s static aberrations measured by the WFS. The calibration procedure is further described in Appendix B.

2.3 WFS-less AO algorithm

We implemented a hill climbing Coordinate Search (CS) algorithm, which was driven by either the reflectance images or the fluorescence images [13]. The CS algorithm searched within the range of Zernike coefficients expected for a mouse eye. Modal control of the DM was calibrated using the procedure further described in Appendix B. The optimization algorithm used a merit function for the highest image sharpness (S_img), which was calculated by the sum of the pixel intensity squared on the entire image, Eq. (1). This metric has been used extensively in implementations of WFS-less AO [20–23], since it is easy to compute with good performance on both reflectance and fluorescence SLO imaging of a variety of features in the retina [17].

$$S_{\mathit{\text{img}}}={\displaystyle \sum _{x,y}{\left[I(x,y)\right]}^2,}$$ (1)

Where I(x,y) is the pixel intensity at the location x,y in the image.

The CS algorithm began with the system flat and then for a given mode (k), a range of coefficients ( ± α) were applied to the DM. The coefficient (a*_n) that corresponded to the best image according to the image metric was applied to the DM and the algorithm moved onto the next mode. Before recording the metric values used for the optimization algorithm, extra imaging frames were included each time the DM returned to the best coefficients to guarantee sufficient settling time between searched modes.

For the first iteration, the CS algorithm began by finding the best initial defocus (k = 4) value, then the astigmatisms, and then continuing in ascending order to include up to the 5th radial order of the Zernike polynomials (18 modes total). The Zernike polynomials were ordered and reported using the mode number according to the OSA/ANSI standard [24]. Further iterations always began with defocus and then the other 17 modes were optimized in a variety of sequences. Typically, we searched 3 to 4 iterations of n = 18 modes with m = 21 coefficients for each mode, which would require 20 seconds per iteration. Note that the optimization speed was limited by the imaging system frame rate. The number of coefficients and the number of iterations could be easily adjusted within the same imaging session if required. We stopped iterating when the image quality metric no longer significantly increased from the previous iteration. The following procedure further explains each step in the CS algorithm.

• 1) Set the DM actuators values to the calibrated system flat and set the Zernike coefficients to be a_k = 0, for k = 1, 2, …, n.
• 2) If this is not the first iteration, then the selected Zernike coefficients from the previous optimization are applied to the DM.
• 3) For each Zernike mode k for k = 1, 2, …, n starting with k = 1.
  • aUpdate DM shape using Zernike mode k with varying amplitude over a range of ± a_k,max by incrementing with m evenly spaced steps: a_k,m = –a_k,m + (2a_k,max(i – 1) / (m – 1)), for i = 1, 2, …, m.
  • bCalculate the merit function on the image, S_img, for each coefficient i = 1, 2, …, m and select the coefficient with the highest value from the search, a*_k,m.
  • cApply the selected coefficient a*_k,m.
  • dMove optimization search to the next Zernike mode, k = k + 1.
• 4) After each iteration through the Zernike modes, the algorithm can repeat and search around the chosen coefficient values from the previous iteration, a*_k,m. The Zernike modes can also be searched in a different sequence in further iterations.

The WFS-less could also be performed after the SH-WFS optimization. In this case, the best-corrected wavefront as determined using the SH-WFS software could be applied as a starting point for the WFS-less algorithm to perform additional image improvement.

2.4 Animal handling and image processing

The animal handling in this work was performed in accordance with guidelines of the animal study protocol approved by the University of California Animal Care and Use Committee (IACUC). The three strains of adult animals, pigmented (C57Bl/6), albino (BALB/cJ), and Cx3cr1GFP/+ mice from Jackson Labs (2-6 months old, female, 5 for each strain) were used in the experiments, including Cx3cr1GFP/+ mice strain had retinal microglia cells labeled with Enhanced Green Fluorescent Protein (EGFP). During imaging, the mice were anesthetized with isoflurane (2% in O2), and the eye was dilated with tropicamide (1%) and phenylephrine (2.5%). The anesthetized mouse was aligned to a zero Diopter contact lens (Unicon Corporation, Osaka, Japan) with a gel (GenTeal, Alcon, Fort Worth, United States) placed between the lens and the cornea to prevent dehydration and the development of cataract.

Motion within and between imaging frames was mostly caused by the respiration of the anesthetized mouse [25]. Registering and aligning frames in post-acquisition processing was required for averaging of frames to improve the image quality. Typically, frames were recorded at 10 fps for 5 to 10 seconds for a total of 50 to 100 frames for averaging. The methods used for image registration are further described in Appendix C.

3. Results

3.1 WFS and WFS-less AO for phantom imaging, comparison of performance

We constructed an imaging phantom (a ‘model eye’) prior to in vivo mouse retinal imaging in order to evaluate the AO performance in an ideal case. The model eye was composed of a 100 mm focal length achromatic doublet and 30 µm diameter fluorescent particles (Cat. No. 36-6, Ex/Em Max: 542/612 nm, Dry Fluorescent Particles, Thermo Scientific, Waltham, US) on white paper. This enabled good WFS measurements for the WFS-based AO and the fluorescence images provided well-defined features for the WFS-less optimization using the fluorescent channel. Aberrations were loaded onto the DM using a prior wavefront measurement from a mouse eye [18], which decreased the fluorescence image quality as shown in Fig. 1(a). First, we used WFS AO to correct the aberrations; then we used WFS-less AO to correct the same aberrations. As described in the Methods, the WFS-less AO correction proceeded for 4 iterations and increased the sharpness metric during the optimization, as shown in Fig. 1(b). The image quality metric after WFS-less AO was 16% better than the image produced by the WFS-based AO.

Fig. 1.

Phantom imaging of fluorescent beads and wavefront measurements during Wavefront Sensor Adaptive Optics (WFS AO) and Wavefront Sensorless Adaptive Optics (WFS-less AO). (a) Fluorescence images of 30 µm beads on white paper with a 100 mm focal length model eye before AO, after WFS AO, and after WFS-less AO. For the inset image before AO, the pixel intensity values were multiplied by 8, so the beads could be visualized. (b) The increase in the fluorescence image quality during the WFS-less AO optimization. (c) The wavefront RMS excluding defocus, tip and tilt during WFS AO correction. (d) The wavefront RMS excluding defocus, tip and tilt during WFS-less AO optimization. (e) The Zernike decomposition of the wavefront measured before and after each method of AO correction.

The residual ocular wavefront was recorded before, during, and after aberration correction using the slopes from the 1264 wavefront centroids, which was used to reconstruct the first 300 Zernike modes and to calculate the RMS of the wavefront. The WFS AO-corrected aberrations typically within the first 0.25 seconds, as shown in the recorded wavefront in Fig. 1(c). The WFS-less AO total execution time depended on the optimization parameters selected for the CS algorithm, which could be modified in the software user interface. In this optimization, we densely sampled 18 modes with 21 coefficients. This required about 80 seconds to decrease the WFS measurement to below the diffraction limit according to the Maréchal criterion (λ/14), as shown in Fig. 1(d). The optimization proceeded for 4 iterations, but it only took 2 iterations to get to 70% of the final image metric value. Figure 1(e) compares the wavefront measurements in Zernike modes before and after each method of AO to show that both methods effectively remove aberrations.

The measured RMS of the residual wavefront after WFS AO was 0.023 ± 0.003 µm and after WFS-less AO was 0.047 ± 0.002 µm over 100 measurements (1 s of wavefront data) including defocus. The RMS after WFS-less AO was 0.029 ± 0.002 µm when defocus was removed from the calculation. The defocus term could explain the image quality improvement of the WFS-less image over the WFS image, which would be a result from the WFS-less AO having an imaging plane at the middle of the fluorescent beads and the WFS AO having an imaging plane on the paper. Tip/tilt aberrations caused by scanning across the sample were removed from all RMS calculations.

3.2 WFS and WFS-less AO comparison on mouse photoreceptor mosaic

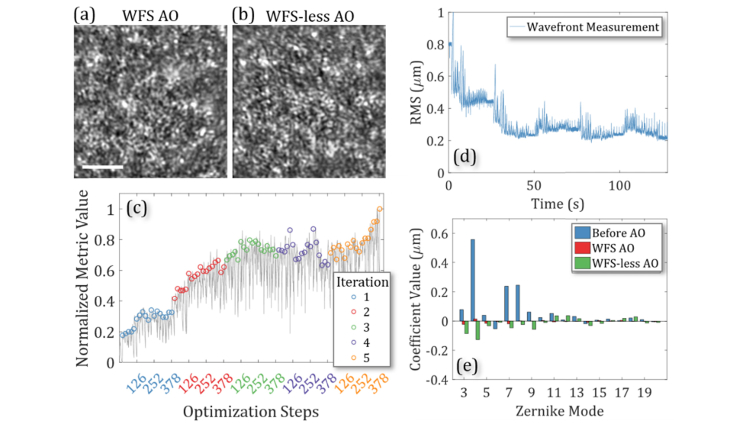
To perform in vivo imaging experiments, we first we used pigmented mouse strain (C57BL/6J) and targeted the strongly scattering RPE/choroid layer for good WFS measurements. The SLD source was used for imaging and wavefront measurements with a Field of View (FOV) of ~70 µm. First, we corrected and recorded the aberrations from the mouse eye with WFS AO and acquired reflectance images of the rod photoreceptor mosaic after the aberration correction, shown in Fig. 2(a). After WFS AO correction, the RMS was calculated to be 0.07 ± 0.02 µm over 100 measurements. The system flat was applied to the DM and aberration correction was performed with the reflectance images to drive the WFS-less AO. The images after optimization are shown in Fig. 2(b). The optimization is shown Fig. 2(c) used 5 iterations; however, the image quality was 75% of the final quality after only 3 iterations. Figure 2(d) shows the aberrations removed from the wavefront as the RMS of the wavefront decreased during the optimization from 0.80 ± 0.01 µm to 0.22 ± 0.01 µm over 100 measurements, which included defocus in the calculation. Note, we did not separately correct non-common path aberrations although based on Fig. 1 results, correcting them would have a negligible impact on the remaining results presented this paper. In this optimization, the Zernike modes were searched in the same order for each iteration. During iteration 4, the motion of the mouse disrupted the optimization but the algorithm recovered in the final iteration. Figure 2(a,b) shows that the image quality is similar after both methods of AO finish correcting residual waterfront error and the image quality metric after WFS-less AO was 9% better than the image produced by the WFS-based AO before post-processing. Figure 2(e) shows the wavefront represented by Zernike modes before and after each correction method. We repeated this imaging experiment and measurements with different mouse eyes with a variety of optimization parameters with similar imaging performance, presented in Appendix D, Fig. 9.

Fig. 2.

Imaging the mouse photoreceptor mosaic with Wavefront Sensor based Adaptive Optics (WFS AO) and Wavefront Sensorless Adaptive Optics (WFS-less AO). (a,b) Images after WFS AO and WFS-less AO. Scale bar: 10 µm. (c) The image quality improvement during WFS-less AO optimization. (d) The wavefront RMS during WFS-less AO optimization. (e) The Zernike decomposition of the wavefront measured before and after each method of AO.

3.3 AO SLO reflectance imaging of an albino mouse strain

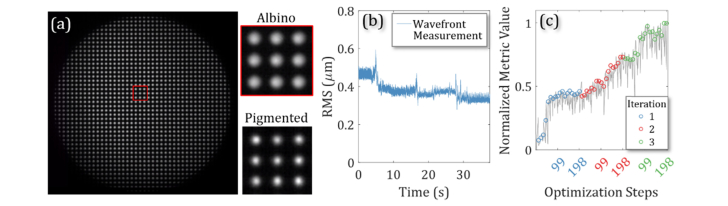
To demonstrate the potential advantage of WFS-less AO over classical AO, we performed imaging of an albino mouse strain (BALB/cJ). Since these mice lack melanin, which highly scatters light in the RPE and choroid, we expect the WFS measurements to be greatly degraded due to lack of well-defined reference plane. The SLD source was also used for imaging as well as wavefront measurements. The WFS centroids shown in Fig. 3(a) show the scattered light used for the WFS measurements in an albino mouse for inner retinal imaging compared to the ideal case in a pigmented mouse and the centroids from the albino mouse are larger and less sharp than the centroids from a pigmented mouse. Figure 3(b) shows the RMS excluding tip, tilt, and defocus of the measured wavefront and Fig. 3(c) shows the improvement in the image quality metric during the 3-iteration WFS-less AO optimization on the NFL layer in an albino mouse. Defocus was excluded from the RMS calculation since the imaging light was manually focused on the inner retina. The optimization that had a 52% increase in the image quality metric. However, the WFS could not measure the wavefront properly in albino. The attempted WFS measurements reported an RMS change during the optimization from 0.47 ± 0.02 µm to 0.33 ± 0.01 µm with little response to the changes to the wavefront during the optimization, especially in the high-order Zernike modes.

Fig. 3.

SH-WFS measurements from an Albino mouse strain (BALB/cJ) retina. (a) The SH-WFS centroids of an albino mouse compared to a pigmented mouse. (b) The RMS of the wavefront measurement without defocus. (c) The image quality metric during WFS-less AO optimization.

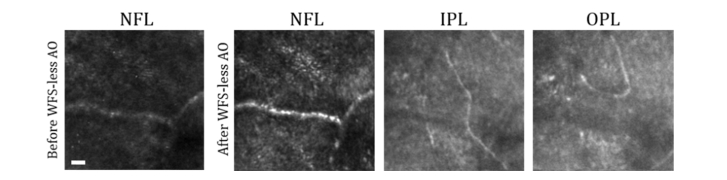
Figure 4 shows WFS-less AO images of the blood vessels of the retina. The optimization was performed on the NFL layer, and then the focus was incremented through the other vascular layers of the inner retina to image the Nerve Fiber Layer (NFL), Inner Plexiform Layer (IPL), and Outer Plexiform Layer (OPL). The WFS data was not acquired during this optimization; however, the optimization results demonstrated a 2.2-fold increase in the image quality after WFS-less AO. The image brightness increased for NFL, and the image pattern differed among layers, which indicates that the WFS-less AO-corrected the aberrations to some extent. In contrast, WFS AO was not effective due to its inability to perform wavefront measurement on the albino fundus.

Fig. 4.

Imaging the inner retina of an Albino mouse (BALB/cJ) with Wavefront Sensorless Adaptive Optics (WFS-less AO). Images of the retina vasculature before and after WFS-less AO in the Nerve Fiber Layer (NFL), and after WFS-less AO in the Plexiform Layer (IPL), and Outer Plexiform Layer (OPL). Scale bar: 10 µm.

3.4 AO SLO fluorescence imaging of EGFP microglia cells

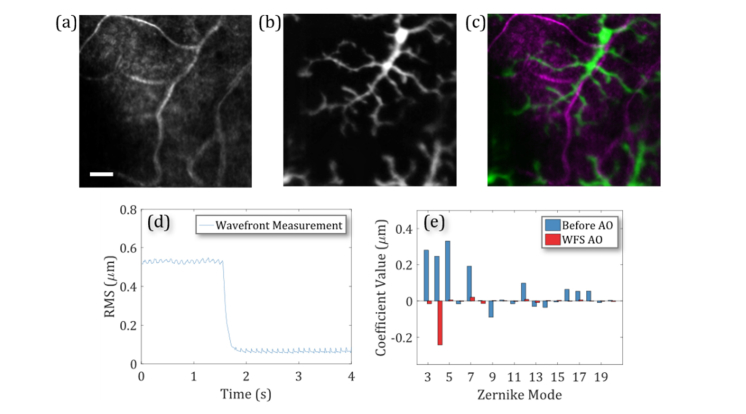
Fluorescence SLO imaging was demonstrated with both WFS and WFS-less AO on EGFP labeled microglia cells (Cx3cr1^GFP/+), which were typically found at varying depths throughout the inner retina. Figure 5(a) shows the WFS AO SLO reflectance image of the 488 nm excitation light and the simultaneous fluorescence image of a microglia cell in Fig. 5(b). The fluorescence image was superimposed in green on the reflectance image in magenta in Fig. 5(c). Figure 5(d) shows the RMS of the wavefront during the WFS AO correction calculated with the defocus value excluded since the imaging system was focused at the inner retina. Figure 5(e) presents the Zernike decomposition of the wavefront before and after WFS AO to show that measured aberrations are removed.

Fig. 5.

Imaging EGFP labeled microglia with Wavefront Sensor Adaptive Optics (WFS AO). (a) Reflectance imaging in the inner retinal blood vessels. (b) Fluorescence imaging of EGFP labeled microglia. (c) The fluorescence image superimposed in green on the reflectance image in magenta. Scale bar: 20 µm. (d) The measured wavefront RMS during WFS AO without defocus. (e) The wavefront measurements in Zernike decomposition before and after the WFS AO aberration correction.

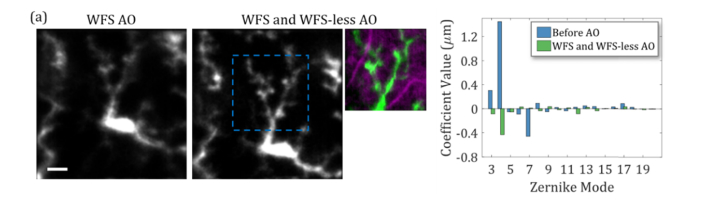
In the next example, the aberration correction was performed at the same region of the retina twice, first by the SH-WFS AO, followed by WFS-less AO for comparison as shown in Fig. 6. The WFS-less AO was optimized using the fluorescence images of microglia and started from a system flat. The optimization was performed with a small FOV (~40 µm across) and had a 3.5-fold improvement in the image quality after two iterations, as shown in the before and after WFS-less images. Both methods of aberration correction show a similar AO imaging performance in the over all image quality in Fig. 6(a). The intensity line plot across the WFS and WFS-less AO images in Fig. 6(b) show small differences in sharpness and brightness at the top and the bottom of the images, which could be due to a small shift in the focal plane due to the WFS-less AO. However, the overall resolution is similar.

Fig. 6.

(a) Imaging EGFP labeled microglia within the inner retina of a mouse with Wavefront Sensor based Adaptive Optics (WFS AO) and Wavefront Sensorless Adaptive Optics (WFS-less AO). Fluorescence image with WFS AO aberration correction (left). Fluorescence image with WFS-less AO aberration correction (middle). Fluorescence images before and after WFS-less AO with a ~40 µm FOV (right). Scale bar: 20 µm. (b) The intensity line plot between the red arrows on the WFS AO image and between the blue arrows on the WFS-less AO image.

In some cases, during mouse retinal imaging, the wavefront aberrations are not reliably measured for WFS AO as presented in Fig. 5, so we used WFS-less AO to provide additional aberration correction. In a representative case, we first used WFS AO to measure and correct aberrations, which resulted in the left image in Fig. 7(a) where the residual aberrations are apparent by the blurred image. The wavefront measured before WFS AO as shown in Fig. 7(b), then WFS AO decreased the wavefront RMS from 1.60 ± 0.01 µm to 0.06 ± 0.01 µm before manually shifting the imaging plane to the microglia in the inner retina. The DM actuator values for the AO correction were loaded as the starting point for the WFS-less AO to provide further improvements to the image quality, with the results of the correction shown in the images (middle, right) of Fig. 7(a). The measured wavefront RMS (excluding defocus) increased to 0.18 ± 0.01 µm after shifting the imaging plane and WFS-less AO optimization. However, the aberrations in the inner retina were not correctly measured, as indicated by improvement in the image quality despite the measured increase in aberrations. This optimization was performed with two iterations on a smaller FOV (~80 µm across) and demonstrated that WFS-less AO can correct for residual aberrations and improve upon WFS AO images during in vivo retinal imaging sessions.

Fig. 7.

(a) Imaging EGFP labeled microglia within the inner retina of a mouse with Wavefront Sensor based Adaptive Optics (WFS AO) and Wavefront Sensorless Adaptive Optics (WFS-less AO). Fluorescence image after WFS AO (left). Fluorescence image after WFS AO and WFS-less AO aberration correction of residual aberration (middle). Fluorescence image with a smaller FOV of microglia dendrites superimposed in green on the reflectance image of the retinal blood vessels in magenta (right). (b) The Zernike decomposition of the wavefront measured before WFS AO and after both methods of AO. Scale bar: 20 µm.

4. Discussion

Aberration correction in the living mouse eye presents challenges that include the relatively thick retina, multiple scattering surfaces, the motion of the sample, and light-sensitive tissue. This requires a WFS AO system with a fast and densely sampled WFS and additional system complexity to make wavefront measurements that are suitable for aberration correction. Alternatively, WFS-less AO can provide image-based aberration correction at the cost of wavefront optimization time. In this work, we presented a comparison between the imaging performance between the two AO techniques and demonstrated their trade-offs. Our results include depth-resolved AO-SLO images at multiple layers of the mouse retina, including reflectance imaging of the photoreceptor layer of a pigmented mouse and vascular layers of an albino mouse, and fluorescence imaging of various layers in the inner retina where microglia cells were located. The wavefront was measured during the WFS-less optimizations to verify that the measured aberrations from the mouse eye were removed. We also demonstrated that the WFS-less AO could provide similar image resolution as WFS AO for imaging the rod photoreceptors in the outer retina and fluorescently labeled microglia cells found in the inner retina of a living mouse.

The WFS AO was operated at 100 Hz and, unlike the WFS-less AO, was not limited by the imaging frame rate and the aberrations were typically corrected within ~0.25 seconds. The WFS-less approach implemented in this paper used a coordinate search (CS) algorithm, requiring ~20 seconds per iteration through 18 Zernike modes. This makes WFS AO advantageous in the presence of varying aberrations from the sample (in our case, mostly due to eye movements) as the speed of WFS AO enables continuous correction. However, WFS-less AO, as a method of correcting static aberrations, is valid for in vivo mouse retinal imaging since the aberration correction can converge and data can be acquired before the aberrations change (e.g. 5 minutes). The WFS AO was also less affected by the amplitudes of the aberrations from the sample, as long as the aberrations were within the dynamic range of the WFS. In contrast, the sample aberrations in each case can affect the length and search space required for WFS-less AO. The results presented in this report showed that WFS-less AO was able to provide similar or slightly better imaging performance to the WFS-based AO. However, it may be required to search higher-order Zernike modes to guarantee diffraction-limited performance in all cases [7] or, alternatively, a more compact search space could be used [26].

The CS approach was used because it is straight forward to understand and reproduce. Our optimization time could be reduced by calculating the best Zernike mode amplitude based on fewer measurements [27]. Theoretically, as few as 2n + 1 measurements for n Zernike modes could be used [10], but practically the convergence of our algorithm would be limited by the image noise and motion artifact. Real-time image registration and tracking on a region of interest could also be used to reduce erroneous measurements due to the motion of the sample [28]. Other algorithms have also been demonstrated such as Steepest gradient descent, and simulated annealing [29–31]. Alternatively, model-based approaches can theoretically converge even faster such as ‘sphere packing’ described by Booth et al. [32], and the DONE algorithm described by Verstraete et al. [33]. Also, so-called pupil segmentation approaches have been demonstrated [11,15]. Several reviews are available on the topic such as [10,34] just to name a few. However, all of these methods will experience the same challenges to enable rapid convergence in vivo.

Exclusively using WFS-less AO allows for more flexibility and simplicity when designing the imaging system, such as our recent report on a compact WFSless AO system [17]. The lens-based system with WFS-less AO allowed for a larger FOV and could potentially have better peripheral retinal imaging [35]. WFS-less AO also provides flexibility with the imaging sample since often retinal feature in other layers such as the large blood vessels can cause strong reflection that confounds the WFS measurement. Although for both WFS and WFS-less AO, we must also consider the size of the isoplanatic patch. If our FOV is too large when performing AO, we may only partially correct for the aberrations.

A comparison can be made between AO for human retinal imaging versus other applications, such as microscopy of small animal brain imaging in vivo. In the first case, with a relatively long eye length and thin retina, the focal planes of the WFS beacon and the imaging plane are nearly the same. In the latter case, backscatter from multiple depths of the thick tissue layers impedes conventional WFS. The case of mouse retina AO is an intermediate case between these extremes. Under ideal circumstances for mouse retinal imaging, WFS works extremely well. When alignment to the mouse eye is near perfect, and when the beacon and image focal planes are coincident, the convergence is rapid, and diffraction limited imaging is quickly attained. For the more general case of mouse retinal imaging, when the region of interest is outside of the mouse eye optical axis, or when there are features (like blood vessels) that impede WFS measurement, the WFS-less provides a solution.

The accuracy of WFS-less AO has been investigated by others including Facomprez et al. [36] for microscopy and demonstrates that WFS-less approaches are capable of diffraction limited imaging. WFS-less AO has been compared to WFS AO in microscopy by Bourgenot et al. [37] demonstrating a benefit of an image-based approach to AO. A comparison of imaging quality between WFS and WFS-less AO has also been performed for human retinal imaging by Hofer et al. [29]. Although our results demonstrate a similar image quality between each method in Fig. 2 (photoreceptor imaging), the residual wavefront RMS values are different. This may be due to small differences between the focal planes of the beacon used for the WFS and the imaging plane, or imaging an area larger than the isoplanatic patch where the aberrations are not uniform across the entire FOV. Non-common path errors could also be a suspected source of measurement errors; however, in this system, the phantom imaging in Fig. 1 indicates the amount of non-common path aberrations in the system. The phantom images revealed a 16% improvement in the image quality in favor of the WFS-less AO but, the difference in wavefront measurements between the WFS AO and WFS-less AO had an RMS of only ~0.029 µm (excluding defocus). In the mouse eye, the difference between the wavefront measurements after each method of AO was typically much larger. For example, the case presented in Fig. 2 had a measurement difference of ~0.15 µm imaging the photoreceptor layer and the case presented in Fig. 7 had a measurement difference of ~0.17 µm imaging the inner retina. So, it is likely that the non-common path aberrations as a source of discrepancy could be neglectable here.

WFS-less AO is advantageous in the optically thick small animal eyes where aberration correction can be performed at the specific depths where the features of interest are located, such as the microglia cells that are found at many layers throughout the inner retina. The outer retinal layers typically provide the strongest scattering plane for the WFS, and a large defocus is required to image the inner retinal layers. When the WFS beacon and the imaging light share the same focal position at the inner retina, and the scattering from the outer retina dominates and thus reduces the WFS spot quality. This is the case represented in Fig. 7, where the WFS-less further improved the imaging quality after the WFS AO. Another solution is to defocus the beacon relative to the imaging beam, but this difference could also adversely affect the performance of the WFS.

Albinism in mice and other small animals is a common background phenotype for transgenic strains. In the retina, the reflectivity characteristics are different in the albino specimen due to the different amounts of pigments in the retina layers [38,39]. Performing retinal AO on albino mice would be more similar to the case of brain imaging since there is no good intrinsic guide star for the WFS AO, and alternatives such as WFS-less need to be considered.We have previously demonstrated that albinism does not affect the ability of WFS-less OCT [40]. In this work, we have demonstrated that WFS-less AO for SLO also provides the flexibility to include albino mice as samples using depth-resolved back reflectance. Albino images were not presented with the SH-WFS mode of operation since a good wavefront measurement is difficult due to enhanced scattering from the choroid and sclera (due to the lack of pigment in the RPE and choroid).

The imaging applications presented in this report span the scenarios of having the wavefront sensing plane and the imaging plane coincident and separated. For the case where the WFS-less approach used the fluorescently labeled cells of interest as guide stars, it is reasonable that the aberration correction would be better based on reports in the Literature using guide stars, for example [6,41]. Alternatively, in cases where fluorescence guide stars are not available, methods such as coherence-gated wavefront sensing [42,43] have been shown to provide depth-resolved measurements, but at the expense of imaging system complexity.

5. Conclusions

In this report, we confirm previous reported WFS-less AO aberration correction for imaging the eye using direct measurements. For retinal imaging in anesthetized and stable small animals, our results indicate that exclusively using WFS-less methods is reliable given enough time for the optimization method to find the best correction. However, when imaging time is limited, WFS-based methods have a large advantage in achieving the optimal aberration correction, especially for the correction of time-varying aberrations. The ideal AO imaging for small animal imaging should use both methods in order to find the best aberration correction across different mouse strains, different retinal layers and eccentricities, and for different levels of sedation. Finally, our results also suggest that AO without a well-defined guide star requires the use of WFS-less methods for the optimal aberration correction.

Appendix

A. System schematic and parameters

Fig. 8.

Adaptive Optics Scanning Laser Ophthalmoscopy (AO-SLO) system schematic. The layout is presented in a scale drawing. Abbreviations: L#, lens; F#, filter; BS#, beamsplitter; M, mirror; SM, spherical mirror; DM, deformable mirror; D#, dichroic mirror; Hsc, horizontal resonant scanner; Vsc, vertical scanner; PMT, photomultiplier tube; P (circled in blue) optical planes conjugate with the pupil; SLD, superluminescent diode. Collimated beams are marked as dashed lines and focusing beams are marked as solid lines. The on-axis beams are represented by red lines and scanned beams by green and blue.

Table 1. Key optical parameters of the AO-SLO system components.

Item	BS1	BS2	BS3	D1	D2	F1	F2	DM
Type	R:T = 50:50	R:T = 10:90	R:T = 30:70	T635lpxr-UF, Chroma	ZT488rdc-UF, Chroma	FF01-660/13, Semrock	FF01-525/45, Semrock	DM97-15, Alpao
Item	SM1	SM2	SM3	SM4	SM5	SM6	SM7	L0
Focal length	900mm	1350mm	1350mm	375mm	150mm	150mm	762mm	400mm

B. WFS and WFS-less AO system calibration

The system was calibrated for WFS AO by placing a model eye and using the imaging light source for measurements. The model eye was constructed from a 100 mm focal length achromatic doublet (AC254-100-A) that focused light onto a scattering sample such a paper. Wavefront measurements were extracted from the SH-WFS camera image feed. The incoming light passed through the Shack-Hartmann lenslet array, where each lenslet focuses the incoming beam over a portion of the CMOS pixel array. The distance from the measured position of the focused spot to the position of the ideal, non-aberrated spot is related to the local wavefront gradient and is called slope [44]. The spot position relative to each lenslet was determined with a Thresholded Weighted Center of Gravity (TWCoG) algorithm. Then, using Zernike polynomial derivatives as modal reconstructor, the extracted slopes are projected into Zernike coefficients.

The influence of each actuator on the wavefront was measured by poking the actuators and collecting the slope responses. Hadamard pattern was used to reduce calibration time and maximize SNR [45]: Each poke pattern was a vector of half 0’s and half 1’s, with an orthogonal column space generated from all the patterns. The slopes are then measured after the actuators reach steady state. To account for stroke hysteresis, the actuators are poked with the same patterns but with an inverted sign, and the average between the two slopes responses is kept. The slopes are projected into actuator control value space, obtained with the SVD of the calibrated influence matrix. The control values are processed in an integrator array which asymptotically steers to remove the difference between the aberrated wavefront and the DM shape compensating for it. With the model eye in place, the actuator control values to remove the system’s static aberrations were characterized by closing the WFS AO control loop using the calibrated control matrix. Those values, called system flat, are saved for the WFS-less AO mouse imaging.

For the WFS-less AO algorithm, the system was calibrated for modal control with the Zernike polynomials. This was performed by stopping the scanning and illuminating the DM and WFS in the reverse direction, starting at the sample pupil plane, illuminating the sample with a ‘single pass’ of the DM. This was necessary in order to include the Zernike modes tip and tilt in the actuator measurements. The wavefront influence of each actuator was measured in Zernike modes, and each measurement was used as a column in an influence matrix (A). Then, the pseudo-inverse was calculated so that the actuator control values (c) for any Zernike vector (z) could be calculated by Eq. (2).

$$\mathbf{c}\mathbf{=}{\mathbf{A}}^{†}\mathbf{z}.$$ (2)

C. Image registration

The registration process began by manually selecting a single frame, ideally free of motion artifact, as the template to align the other frames. The rigid registration process included a global frame translation followed by the translation of image slices created in the horizontal fast-scan direction. The global frame translation was determined by maximizing the cross-correlation between the target frame and the template frame using the fast Fourier transform. Frames that had a much lower cross-correlation value than most other frames due to large amplitude of motion were discarded. The remaining frames were broken up into horizontal strips of 3 vertical pixels. Each strip was translated horizontally and then vertically with subpixel resolution to maximize the cross-correlation with equivalently sized strips on the template. Finally, the translated strips were averaged together and down-sampled to the original frame size. This method was effective on low SNR images [46]. However, it would not be capable of correcting motion within the 1.5 ms required to acquire 3 lines as well as rotational and torsional distortions.

D. WFS and WFS-less AO comparison on mouse photoreceptor mosaic

Figure 9

Fig. 9.

(a, b) Further mouse photoreceptor imaging with Wavefront Sensor Adaptive Optics (WFS AO) and Wavefront Sensorless Adaptive Optics (WFS-less AO). Images mouse photoreceptor mosaic after WFS AO and WFS-less AO. Scale bar 10 µm. The Zernike decomposition of the wavefront measured before and after each method of AO. The wavefront RMS during WFS-less AO optimization. The image quality improvement during WFS-less AO optimization.

represent additional measurements for imaging the mouse retina photoreceptors. In both of these cases, the WFS AO and the WFS-less AO demonstrated similar image quality and measured aberrations were removed. In Fig. 9(a), after WFS AO correction, the RMS was calculated to be 0.06 ± 0.02 µm. For the WFS-less optimization after the first iteration, the search order of the Zernike modes was shuffled for each of the following two iterations. The wavefront RMS decreased during the optimization from 0.93 ± 0.04 µm to 0.20 ± 0.01 µm. In Fig. 9(b), after WFS correction, the RMS was calculated to be 0.08 ± 0.03 µm. For the WFS-less optimization, the number of coefficients searched for each Zernike mode was decreased from 21 to 11 and further iterations were included instead. The wavefront RMS decreased during the optimization from 1.16 ± 0.02 µm to 0.24 ± 0.01 µm. (Note: The Zernike decomposition coefficient values of the measured wavefront after WFS AO were too small to be well visualized on the same plot as the measured wavefront before AO.)

Funding

T Canadian Institutes of Health Research (CIHR), Natural Sciences and Engineering Research Council of Canada (NSERC), the Michael Smith Foundation for Health Research (MSFHR), Brain Canada Foundation, Genome British Columbia, Pacific Alzheimer Research Foundation (PARF), and Innovate BC. Zawadzki was supported by the National Eye Institute UC Davis Vision Center Core Grant (P30 EY012576) and R01 EY026556, UC Davis Research Investments in Science and Engineering (RISE) Grant, and NSF I/UCRC CBSS Grant.

Disclosures

YJ: Seymour Vision (I), MVS: Seymour Vision (I), SB: Dynamic Optics (I).