FullMonteCUDA: a fast, flexible, and accurate GPU-accelerated Monte Carlo simulator for light propagation in turbid media

Abstract

Optimizing light delivery for photodynamic therapy, quantifying tissue optical properties or reconstructing 3D distributions of sources in bioluminescence imaging and absorbers in diffuse optical imaging all involve solving an inverse problem. This can require thousands of forward light propagation simulations to determine the parameters to optimize treatment, image tissue or quantify tissue optical properties, which is time-consuming and computationally expensive. Addressing this problem requires a light propagation simulator that produces results quickly given modelling parameters. In previous work, we developed FullMonteSW: currently the fastest, tetrahedral-mesh, Monte Carlo light propagation simulator written in software. Additional software optimizations showed diminishing performance improvements, so we investigated hardware acceleration methods. This work focuses on FullMonteCUDA: a GPU-accelerated version of FullMonteSW which targets NVIDIA GPUs. FullMonteCUDA has been validated across several benchmark models and, through various GPU-specific optimizations, achieves a 288-936x speedup over the single-threaded, non-vectorized version of FullMonteSW and a 4-13x speedup over the highly optimized, hand-vectorized and multi-threaded version. The increase in performance allows inverse problems to be solved more efficiently and effectively.

1. Introduction

Using light in medical procedures is generally low cost, safe for patients and has simple monitoring options. Here, we consider two medical use-cases for light: photodynamic therapy (PDT) and bioluminescent imaging (BLI). In PDT, the patient receives a photosensitizer (PS) orally, topically or by injection. The PS accumulates preferentially in highly proliferating tissues, like malignancies, and absorbs a specific wavelength of light provided by external or internal light sources chosen by the physician. Both the light and the inactive PS are safe on their own, but when photons interact with the PS, they activate it causing oxygen at the PS location to become reactive. Reactive oxygen species damage the PS containing cells and, after sufficient damage is accumulated, cause tissue necrosis. The overall goal of PDT is to cause enough damage at a specific target, typically a tumour, while minimizing the damage to healthy tissue [1]. The location, orientation and intensity of the light sources; the concentration of the PS; the oxygenation of the surrounding tissue and the optical properties of the patient’s body all influence the effectiveness of the PDT treatment. In BLI, some of the subject’s cells are transfected with viruses causing them to emit light [2]. The light emitted at the subject’s exterior surface can be quantified, but simulations are required to find the location and size of the collection of light-emitting cells based on the detected BLI photon distribution. This method is currently being used in a laboratory setting to track the size and location of cancerous tissues in pre-clinical treatment studies [2].

To develop viable PDT treatment plans and track the location of tumours with BLI, it is vital to simulate the propagation of light through tissues or tissue-like media. The radiative transport equation (RTE) can be solved to achieve this. Solving the RTE analytically in homogeneous materials is possible, but the analytical methods are difficult at the interfaces of materials, the boundaries of a model and at the sources and sinks of light [3,4]. For these reasons, numerical approximations such as the Monte Carlo (MC) method have been adopted as the gold standard for the field [5,6]. Given a sufficiently high number of random samples, the light propagation simulator will converge to a statistically correct result. However, for both PDT and BLI, it is necessary to solve the inverse problem. In BLI, this means determining the location and size of the light-emitting cells given a certain distribution of light [2]. In PDT, it means determining the optimal number, position, orientation, type and intensity of the light sources to inflict sufficiently high damage on the target volume and minimize damage to healthy tissue [1]. Solving an inverse problem empirically can require performing thousands of individual simulations for the various modelling parameters [7,8]. Therefore, it is vital to have a forward simulator which, given a set of parameters, can quickly and accurately solve for the light distribution in the geometry under consideration.

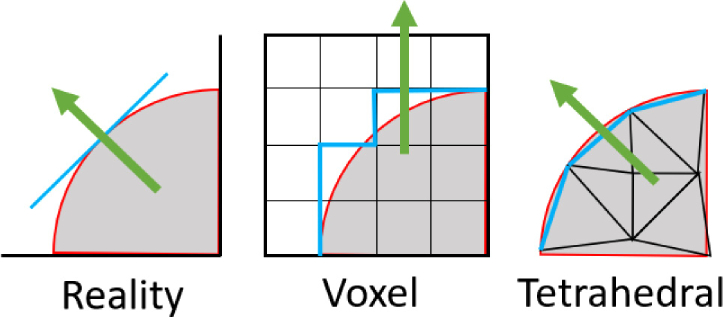
The primary trade-off when performing MC simulations is between accuracy and computational cost. Increasing the accuracy by simulating more photons increases computation time proportionally. We developed the FullMonte project to address this problem. First, we created FullMonteSW: the fastest, tetrahedral-mesh, MC light propagation simulator written in software [9]. Like other high-performance implementations [10,11], FullMonteSW uses multi-threading to exploit multiple CPU cores. Unlike other implementations, it has been further optimized by manually coding the use of vector instructions (each of which performs several computations in parallel using special compute units in the CPU) for key computations to achieve still higher performance. The hand-vectorized instructions can provide additional optimizations at the cost of potentially decreasing the readability and portability of the code. Compared to voxel-based models, tetrahedral-based models require more complex intersection calculations, but they are able to more accurately represent region boundaries and curved surface normals as illustrated in Fig. 1 . FullMonteSW can track any combination of volume absorption, internal surface fluence and exterior surface fluence. The combination of light events can be chosen at runtime without degrading the performance of the simulator. Further software optimizations show diminishing performance gains so various forms of acceleration, including FPGAs [12] and GPUs, need to be explored.

Fig. 1.

A curved surface (left) modelled using voxels (middle) and tetrahedrons (right) - the arrows represent the estimated surface normal.

Recent progressions in GPU technology make them an attractive choice for accelerating the FullMonte algorithm. These progressions include increased memory size and bandwidth, increased floating point performance, support for double precision floating point operations, increased number of streaming multiprocessors and an easier-to-use programming model. The photon packets are independent from one another, so the problem is parallelizable and therefore fits the multi-threading model well [13]. However, the mesh required to represent a realistic complex geometry uses a large amount of memory that is accessed in an irregular fashion, which makes GPU acceleration more challenging.

This paper implements FullMonteCUDA by modifying the FullMonteSW algorithm to accommodate a GPU architecture and the NVIDIA programming model. FullMonteCUDA has been fully integrated into the FullMonte project and supports every feature of the software implementation. It has been validated and benchmarked against other MC simulators and supports a wide range of modern NVIDIA GPUs. FullMonteCUDA can be downloaded as part of the open-source FullMonte project from www.fullmonte.org.

2. Background

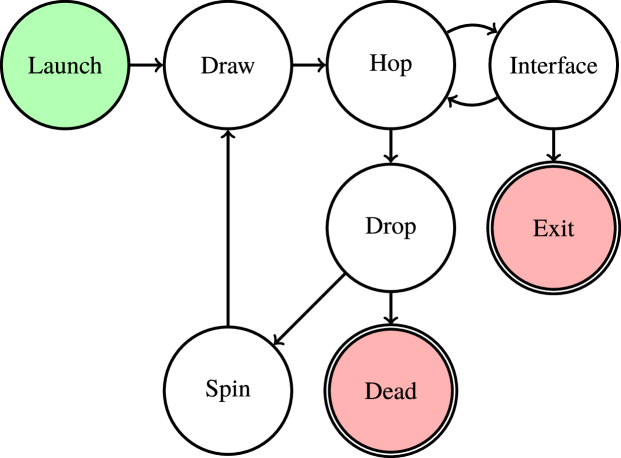
The algorithm used in FullMonte [9] models the propagation of light through a tetrahedral mesh using the hop-drop-spin method first proposed under a different name by Wilson and Adam in 1983 [14]. This method is visualized in Fig. 2 .

Fig. 2.

The core algorithm used in FullMonte.

Light is launched from the sources under consideration in the form of weighted photon packets with an initial position and direction. Once the packet is launched, it enters the draw stage which generates a random step length based on the attenuation coefficient (µ_t) of the material in which it resides. The packet then enters the hop stage where it is moved by this step length along its current direction vector. If the packet remains in the same tetrahedron after the step has finished, the hop stage is complete. If the packet crosses a tetrahedral boundary during the step, it moves to the interface stage where the intersection point on the shared face of the tetrahedrons is calculated. If the refractive indices of the tetrahedrons differ, then the packet crosses a material boundary and calculations are made to account for Fresnel reflections, total internal reflection or refraction based on the incident angle. If the attenuation coefficient of the tetrahedrons differ, then the step length is updated by $s\prime =\frac{{\mu }_t}{{\mu }_t^{\prime }}s$ and the packet moves back to the hop stage with a new step length s’. Once this step has finished, the packet enters the drop stage where it loses a fraction of its weight as absorption into the tetrahedron. If the weight of the packet drops below a certain threshold (wmin), the packet enters the roulette phase of the drop stage where it is given a 1-in-prwin chance of surviving with an increased weight of $\mathit{\text{prwin}}\ast w$ (due to energy conservation). If the packet’s weight is greater than wmin or if it survives roulette, it enters the spin stage where its direction vector is changed based on the Henyey-Greenstein (HG) scattering function. After the spin stage, the packet returns to the draw stage to repeat the process. If the packet loses roulette, then it is marked as dead and computation for it ceases. wmin and prwin are runtime parameters which have computation-accuracy trade-offs as discussed in [15].

3. GPU programming using the NVIDIA CUDA development platform

Efficiently accelerating an algorithm using a GPU requires knowledge of the underlying hardware and development platform. NVIDIA provides a Programming Guide [16] and Best Practices Guide [17] which extensively discuss the GPU architecture, CUDA development platform and best methods for programming their GPUs. Previous works also discuss these concepts in relation to MC light propagation simulation [18–21].

Three significant challenges arise when implementing FullMonte on a GPU. First, the tetrahedral meshes used to represent realistic clinical models require gigabytes of memory. Modern GPUs have sufficient memory to store these large meshes but the access times are slow [16]. Moreover, due to the random nature of MC simulations, the access pattern of the tetrahedrons is irregular, which can make them difficult to cache effectively. Second, MC simulators require many blocks of code that may or may not execute depending on the state of the simulation. This conditional code does not map well to the GPU and can cause significant performance degradation due to thread divergence [22]. Lastly, when many photon packets are being simulated simultaneously, it is possible that multiple packets can drop weight into the same tetrahedron at the same time. Measures must be taken to ensure that simultaneous absorptions into a tetrahedron are handled accurately and efficiently. Section 5.2 describes the optimizations made to FullMonteCUDA to address each of these challenges.

4. Previous work

Examples of previously published MC simulators, chosen for reference because they are the most relevant to FullMonteCUDA, are summarized in Table 1 . CPU implementations exhibit various levels of optimization, which can make comparing relative performance numbers for hardware accelerated versions difficult. We have found that multi-threaded implementations show linear performance scaling with the number of CPU cores as well as significant improvement using simultaneous multi-threading in which one core can run two threads simultaneously by leveraging idle execution units, with somewhat degraded performance [23]. Therefore, multi-threaded implementations using modern CPUs with six cores are inherently ~9x faster than single-threaded implementations. We found that hand-coded vector instructions provided an additional speedup of ~8x [23], which means that unoptimized single-threaded implementations can be ~72x slower than optimized multi-threaded implementations, like FullMonteSW.

Table 1. A subset of existing MC light propagation simulators.

Implementation	Geometry	Acceleration Type
MCML	Planar
CUDAMC	Semi-infinite planar	GPU
CUDAMCML	Planar	GPU
GPU-MCML	Planar	GPU
tMCimg	Voxel
MCX	Voxel	GPU
Dosie	Voxel	GPU
MCxyz	Voxel	GPU
TIM-OS	Tetrahedral	vector (automatic)
MMCM	Tetrahedral	vector (manual)
MOSE	Tetrahedral	GPU
Powell and Leung	Tetrahedral	GPU
MCtet	Tetrahedral	GPU
FullMonteSW	Tetrahedral	vector (manual)
FullMonteCUDA	Tetrahedral	GPU

4.1. MCML, CUDAMC, CUDAMCML and GPU-MCML

The MCML algorithm, originally developed by Wang et al. [24], remains a widely-used MC simulator for turbid media. It uses a planar geometry with a normally-incident pencil beam light source. The main drawbacks of this approach are the limited number of light sources and the restrictions of the planar geometry which is not capable of representing the 3D curved surfaces of general biological tissues. CUDAMC was an initial attempt at accelerating the MCML algorithm using a GPU [18]. It uses a single, semi-infinite, planar slab that does not absorb photons. The reported 1000x speedup over the single-threaded CPU code likely reflects the absence of absorption events and limiting the geometry to a single planar slab. CUDAMCML [18] was a more complete implementation of the MCML algorithm. The authors report a 100x speedup over the original single-threaded CPU code. The 10x difference relative to CUDAMC likely resulted from the increased complexity of multiple absorbing layers. More recent work, by Lo [19] and Alerstam and Lo [20] called GPU-MCML, achieved a 600x speedup over the original MCML code. This incremental improvement on CUDAMCML was achieved by caching absorption around the pencil beam source and by using a modern GPU architecture. However, CUDAMC, CUDAMCML and GPU-MCML are all still restricted by the original MCML limitations.

4.2. tMCimg and MCX

tMCimg [25] was one of the first open-source, voxelized MC simulators. Unlike the FullMonte project, which aims to provide a general MC solution for various light sources and geometries, tMCimg was developed to specifically model the human head and brain for Diffuse Optical Tomography (DOT). tMCimg is single-threaded because it was developed at a time when multi-core machines were scarce. MCX [26] is a GPU implementation of tMCimg and therefore has the same geometrical and use-case limitations. MCX reports a 75-300x speedup over the single-threaded tMCimg software implementation depending on the simulation options. Yu et al. [27] extended and improved the implementation of MCX using OpenCL which, compared to the CUDA implementation, allowed them to more easily target a heterogeneous computing platform. Their optimizations allowed them to achieve up to a 56% improvement on AMD GPUs, 20% on Intel CPUs/GPUs and 10% on NVIDIA GPUs [27].

4.3. Dosie

The Dosie software developed by Beeson et al. [28] calculates light transport and photokinetics for PDT in mouse models. Dosie uses a voxel-based geometry and internal or external light sources. The authors report a 21 second runtime for $2\times {10}^6$ packets in a cube model with ${10}^6$ voxels. The developers of Dosie acknowledge that tetrahedral models can fit curved surfaces better than voxel models [29].

4.4. MCxyz

MCxyz [30] is an open-source, single-threaded, voxel-based MC simulator . It uses the same hop-drop-spin method as FullMonte but only supports emission from one light source. MCmatlab [31] extended the MCxyz algorithm to include a finite-element heat diffusion and Arrhenius-based thermal tissue damage simulator with a MATLAB interface. MCmatlab is roughly 17x faster than the single-threaded unoptimized baseline [31]. Dupont et al. [32] extended MCxyz to specifically simulate the cylindrical diffusers used in interstitial PDT (iPDT). They accelerated MCxyz using an NVIDIA GPU but only provide performance results for a simple homogeneous cube model. They report a 745x improvement over the unoptimized, single-threaded MCxyz code for this model [32].

4.5. TIM-OS

Before the FullMonte project, TIM-OS [10] was the fastest tetrahedral-mesh MC simulator. TIM-OS is highly optimized software that uses automatic compiler vectorization whereby the software compiler attempts to automatically replace conventional instructions with vector instructions where possible. TIM-OS exceeds the performance of MCML on simple layered models and MMCM on more complex tetrahedral models [9]. TIM-OS does not support tracking fluence through surfaces which makes it unsuitable for BLI. FullMonteSW has also been validated against TIM-OS and achieves an average speedup of 1.5x [9].

4.6. MMCM

MMCM is a widely used, multi-threaded, tetrahedral-mesh, MC simulator written in C [11]. It can use meshing shapes other than tetrahedrons, but the authors do not present any significant benefit of that feature. FullMonteSW has been validated against MMCM and achieves a speedup of 2.42x over it. Fang and Kaeli [33] extended MMCM to use manual vector instructions (SSE) with support for multiple ray tracing algorithms. They report an overall speedup of up to 26%.

4.7. MOSE

The Mouse Optical Simulation Environment (MOSE) [34] was developed for optical imaging techniques, such as fluorescence molecular tomography and bioluminescence tomography. Ren et al. [35] created gpu-MOSE, a GPU-accelerated version of the software targeting an NVIDIA GPU. Both MOSE and gpu-MOSE were validated against MCML and gpu-MOSE achieved a speedup of up to 10x over the single-threaded MOSE code.

4.8. Powell and Leung

Powell and Leung [36] developed a GPU-accelerated MC simulator to model the acousto-optic effect in heterogeneous turbid media for imaging and optical property measurement. The simulator was validated against MCML for various models and benchmarked against MMCM. Their GPU-accelerated simulator achieved a 2x speedup over the multi-threaded MMCM code.

4.9. MCtet

MCtet [21] is a GPU-accelerated, tetrahedral-mesh MC simulator. It does not claim to support fluence tracking through surfaces making it unsuitable for BLI. It was validated against three benchmark models: two MCML layered models and a TIM-OS cube model similar to cube_5med in Section 7. However, MCtet’s performance was only benchmarked using the two MCML layered models; the authors do not provide performance comparisons against TIM-OS for any of the three models.

5. FullMonteCUDA implementation

This section provides a high-level overview of how the FullMonte algorithm was accelerated using an NVIDIA GPU. It highlights the algorithmic changes needed to better suit the GPU architecture and discusses some GPU specific optimizations.

5.1. Overview

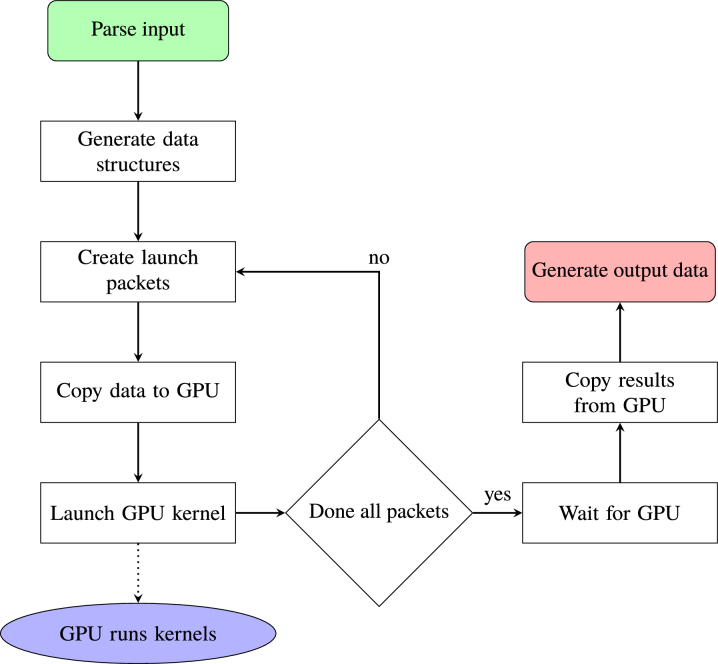
The interaction between the CPU host and GPU device in FullMonteCUDA is shown in Fig. 3 . The host parses the inputs (mesh, material properties and light sources), creates the data structures for the GPU, copies the data to the GPU and signals for it to start the computation. Launching all photon packets may require multiple invocations of the kernel based on the maximum number of threads and global memory size of the GPU. The accelerator determines the number of packets to launch and makes multiple asynchronous kernel invocations until all of the packets have been launched. This is illustrated in the feedback loop in Fig. 3.

Fig. 3.

The CPU host logic of FullMonteCUDA.

After the GPU launches all of the kernels, the host can either wait for them to finish or continue executing other work. Once all the kernels have finished executing in the GPU, the CPU host copies the output data from the memory of the GPU into its own memory and generates the output files.

5.2. Optimizations

A naive implementation of the code, nearly identical to the software version, achieved a speedup of 2x but performed sub-optimally on the GPU. We implemented a series of optimizations which better tailor the algorithm to the GPU architecture. Table 2 summarizes the performance results for some of these optimizations and the following sections discuss them in more detail.

Table 2. Performance increase for each FullMonteCUDA optimization over FullMonteSW.

Optimization	Incremental Speedup
Naive	2x
CUDA vector datatypes and math operations	2.5x
Materials constant cache	1.6x
Thread local accumulation cache	1.3x

In the ideal scenario all GPU threads are constantly performing computations and therefore the device is running at maximum capacity. However, this ideal case is almost never attained as threads are sometimes stalled waiting for data to be ready. For FullMonteCUDA, the most significant reasons for stalls are memory dependencies and execution dependencies. A memory dependency occurs when accessing memory, causing the GPU to stall until the request is complete. An execution dependency occurs when an instruction depends on the result of a previous instruction, causing the GPU to stall until the first instruction is finished.

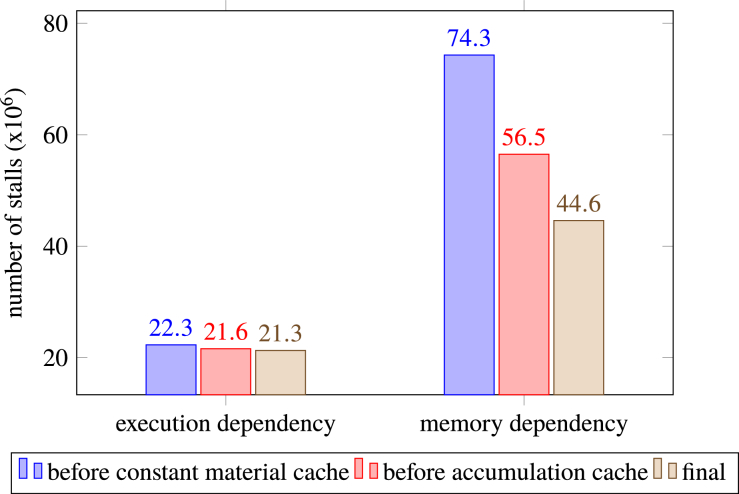
We used the NVIDIA Visual Profiler (NVVP) to identify bottlenecks in the code and more accurately measure the impact of optimizations. Figure 4 shows profiling results for the final implementation of the algorithm on the HeadNeck mesh from Table 4 using ${10}^6$ packets. The chart represents the distribution of reasons for stalling the kernel and helps pinpoint latency bottlenecks [37]. It shows that the largest number of stalls in the fully optimized implementation are due to memory dependencies. This is typical for applications like ours that have large datasets and somewhat unpredictable memory access patterns.

Fig. 4.

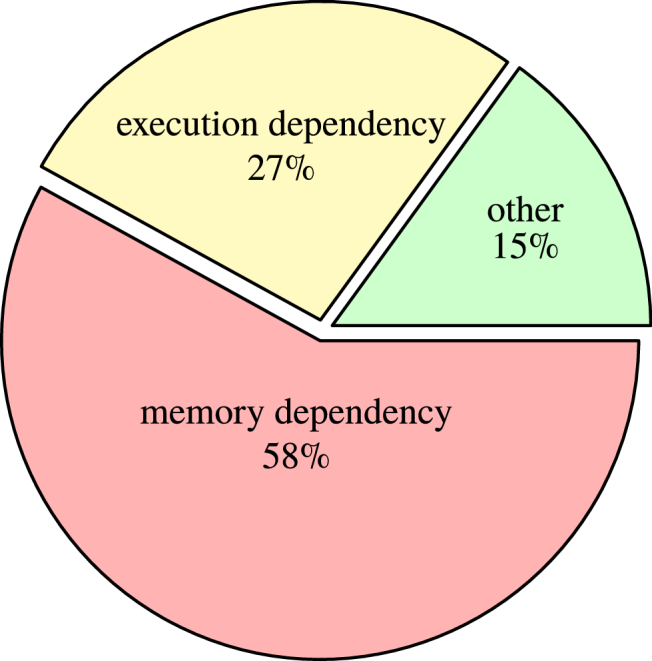
NVVP PC Sampling data for the final implementation.

Table 4. Models used for the validation and benchmarking of FullMonteCUDA.

Model	Tetrahedrons	GPU memory (MB)	Light Sources	Materials (µs [mm-1], µa [mm-1], g, n) 2
HeadNeck1	1088680	139	Isotropic Point,	tongue (83.3, 0.95, 0.93, 1.37)
			Pencil Beam,	tumour (9.35, 0.12, 0.92, 1.39)
			Fiber Cone	larynx (15, 0.55, 0.9, 1.36)
				teeth (60, 0.99, 0.95, 1.48)
				bone (100, 0.3, 0.9, 1.56)
				tissues (10, 1.49, 0.9, 1.35)
				fat (30, 0.2, 0.78, 1.32)
Bladder1	1706958	218	Isotropic Point,	air (0, 0, 0, 1.37)
			Pencil Beam,	urine (0.1, 0.01, 0.9 1.37)
			Volume,	surround (100, 0.5, 0.9, 1.39)
			Ball,
			Line,
			Fibre Cone
cube_5med [10]	48000	6.14	Isotropic Point	mat1 (20, 0.05, 0.9, 1.3)
				mat2 (10, 0.1, 0.7, 1.1)
				mat3 (20, 0.2, 0.8, 1.2)
				mat4 (10, 0.1, 0.9, 1.4)
				mat5 (20, 0.2, 0.9, 1.5)
FourLayer [10]	9600	1.22	Pencil Beam	layer1 (10, 0.05, 0.9, 1.3)
				layer2 (30, 0.1, 0.95, 1.5)
				layer3 (10, 0.05, 0.9, 1.3)
				layer4 (30, 0.1, 0.95, 1.5)

¹Material optical properties extracted from literature [39–47]

²Material properties: scattering coefficient (µ_s), absorption coefficient (µ_s), anistropy (g) and refractive index (n).

5.2.1. Launching packets in the host

FullMonteSW supports a wide range of light sources which requires many conditional statements. Since the packet launch happens exactly once (see Fig. 2), we compute packet launches in the CPU host and send the data to the GPU kernel before starting the simulation. This decision was made for two reasons. First, it allows the same complicated light emitter code to be used whether GPU-acceleration is being used or not. This reduces the development time and effort required to add new sources or modify existing ones. Second, the code that launches packets is highly divergent, which does not map well to GPUs [22]. The worst-case scenario would be if all 32 threads of a warp launched packets from different sources. This would result in increased thread divergence and decreased performance.

5.2.2. Vector datatypes and math operations

CUDA provides native vector datatypes (e.g. float2, float4, uint4) [16]. These datatypes are C-style structs with a specific memory alignment requirement. For example, a float4 must be aligned to 16 bytes. These vector datatypes are particularly efficient when accessing the entire array at once. Therefore, we group logical sets of data, like position and direction vectors, into vector datatypes to improve memory performance. The simulator relies heavily on floating-point mathematical operations (e.g. recip, cos, sin, dot, cross) so we investigate the use of various CUDA compiler flags to improve their performance. When modifying these flags, we monitor the change in performance and ensure the accuracy of the result (discussed later in Section 6) remains sufficient. We determine that it is safe to use the use_fast_math flag to turn on all of the CUDA fast-math approximations without sacrificing accuracy. Together, these two optimizations result in a 2.5x speed improvement, as shown in Table 2.

5.2.3. Constant materials caching

Since the properties of the materials do not change during the simulation, we chose to store them in the constant memory of the GPU to improve read latency. Each set of material properties requires 72 bytes of storage, which are padded to be aligned on a 128 byte boundary to further improve memory performance. The maximum number of materials supported by FullMonteCUDA is bounded by the size of the GPU’s constant cache. All of the currently supported NVIDIA GPUs have a 64kB constant cache which allows for up to 500 materials, which is sufficient for most clinical models. Table 2 shows that caching the materials improves the performance almost twofold. The performance improvement is due to a significant reduction in the number of memory and execution dependency stalls, as shown in Fig. 5 .

Fig. 5.

The number of execution and memory dependency stalls reported by NVVP before the constant material cache, before the accumulation cache and the final implementation.

5.2.4. Local accumulation buffers

When a packet drops some of its weight into a tetrahedron (the drop stage in Fig. 2), a read-accumulate-write operation is performed for that tetrahedron entry to model absorption. For data consistency, this accumulation uses an atomic operation to read the current energy in the tetrahedron, add to it and then write it back. However, atomic operations can be computationally expensive as they will stall other threads trying to update the same tetrahedron, which stalls the entire warp the thread belongs to. Depending on the ratio between the mesh dimension and the inverse of the attenuation coefficient, packets can take several steps within a single tetrahedron before moving to the next. This means that a packet may drop weight multiple times in the same tetrahedron before moving to the next. We use this information to create a custom cache for each thread to store accumulations locally and avoid excessive atomic read-accumulate-write operations to global memory. To implement this, we use the local memory of the GPU to store an array of tetrahedron IDs and accumulated energy for each thread. When a packet drops energy into a tetrahedron, the local accumulation array is checked for the current tetrahedron ID. If the value is currently cached, then the accumulation happens in local memory, otherwise the least recently used entry in the cache is written back to global memory and the current accumulation replaces it in the array. We tested caches of size 1-32 entries and found that all configurations improved performance but a single-entry is optimal, resulting in an approximately 30% speed improvement as shown in Table 2. This was caused by a significant reduction in the number of memory dependency stalls, as shown in Fig. 5.

5.3. Features

The FullMonte project can read and write mesh formats from other MC simulators (like MCML, TIM-OS and MMCM), the COMSOL multiphysics package and the open-source Visualization Toolkit (VTK). It has been developed for use by medical professionals. It is written in highly optimized C++ and CUDA code which could make it difficult for non-developers to use and extend. To remedy this, both FullMonteSW and FullMonteCUDA have been fully integrated with the TCL scripting language. We provide sample TCL scripts that can be used as-is or extended to meet the user’s specific needs - including using the GPU accelerator. Through this TCL interface, users can enable or disable any combination of tracking volume absorption, internal surface fluence and exterior surface fluence. FullMonteCUDA has been designed such that the choice of outputs to track can be made at runtime without degrading the performance. The TCL integration is crucial as it enables medical professionals to easily target different hardware accelerators, perform customized simulations and create TCL programs that use the simulator to solve larger problems without the challenge of modifying complex C++ code. We also produce a FullMonte Docker image (www.docker.com). Docker is a lightweight virtual machine that runs on Linux, Mac and Windows which allows applications to run in a consistent environment called a container. Both the CPU vector instruction and GPU acceleration can be used from within the Docker container. This allows users to easily setup the simulator without installing the prerequisite libraries or compiling code - the container starts within seconds and the simulator is ready.

6. Validation

FullMonteCUDA uses the TinyMT random number generator (RNG) [38]. TinyMT is a pseudorandom RNG which means that, given the same parameters, consecutive runs of the simulation will produce identical results. However, differences in the simulation can arise. For example, different initial RNG seeds and a different number of threads can cause discrepancies between simulations with the same modelling parameters.

To validate FullMonteCUDA, we used our existing software implementation, FullMonteSW, which has been validated against MCML, TIM-OS and MMCM [9]. We use the benchmark models in Table 4 with packet counts ranging from ${10}^6$ to ${10}^8$. To compare the results of two simulations A and B, we compute the normalized L1-norm value (${|\hat{x}|}_1$) for the tetrahedral volume fluences ($\mathrm{\Phi }$) using the formula in Eq. 1. Table 3 shows that the normalized L1-norm value for a FullMonteCUDA and FullMonteSW simulation is comparable to two differently seeded FullMonteSW simulations across the benchmarks. We also observed no qualitative differences between FullMonteCUDA and FullMonteSW simulations, as shown in Fig. 6 .

$${|\hat{x}|}_1={\displaystyle \frac{\sum _i|{\mathrm{\Phi }}_A(i)-{\mathrm{\Phi }}_B(i)|}{\sum _i|{\mathrm{\Phi }}_A(i)|}}$$ (1)

Table 3. Normalized L1-norm values for the models from Table 4 using ${10}^8$ packets for two differently seeded CPU simulations (row 1) and a GPU and CPU simulation (row 2).

	HeadNeck	Bladder	cube_5med	FourLayer
FullMonteSW-FullMonteSW	0.0027	0.0322	0.0028	0.0012
FullMonteCUDA-FullMonteSW	0.0026	0.0342	0.0031	0.0020

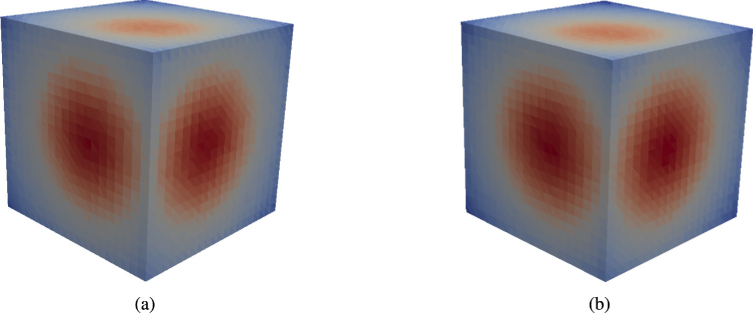
Fig. 6.

Output tetrahedral fluence plots of the cube_5med model (Table 4) for FullMonteSW (a) and FullMonteCUDA (b) using ${10}^8$ packets.

7. Results

To obtain performance results, we used an Intel Core i7-6850 3.8GHz CPU with 6 physical cores (12 virtual cores with hyperthreading) and 32GB of RAM. For FullMonteCUDA, we evaluated compute times on both an NVIDIA Quadro P5000 and Titan Xp GPU.

To benchmark FullMonteCUDA against MCtet, we used the same layered MCML models described in [21]. These are the only models for which the MCtet authors provide performance data. The results, summarized in Table 5 , show that FullMonteCUDA achieves a speedup of 11x over MCtet and 2x over CUDAMCML, even though FullMonteCUDA was designed for much more complex geometries than these layered models.

Table 5. Performance results for CUDAMCML, MCtet and FullMonteCUDA using the MCML layered models from [21].

Model	CUDAMCML (s)	MCtet (s)	FullMonteCUDA (s)
			Quadro P5000	Titan Xp
1-layer	27.1	103.4	23.7	16.8
3-layer	83.8	433.8	75.8	40.9

We also benchmarked FullMonteCUDA with more complex tetrahedral models for which it was designed. We extended the performance analysis from [9] using the same compiler, compiler settings and models to compare FullMonteCUDA against: TIM-OS, MMCM and FullMonteSW. We cross-validated the output tetrahedral volume fluences for ${10}^6$ packets and found that in each case FullMonteCUDA showed agreement with the other simulators. The results are summarized in Table 6 and show that FullMonteCUDA achieves a 12x speedup over MMCM, up to 19x over TIM-OS and up to 11x over FullMonteSW. As discussed in Section 2.4 of [9], we were unable to reproduce the MMCM results for the Colin27 mesh due to a reported bug in MMCM for the combination of simulation options necessary to accurately compare MMCM and FullMonte.

Table 6. Performance results for TIM-OS, MMCM, FullMonteSW and FullMonteCUDA.

Model	TIM-OS (s)	MMCM (s)	FullMonteSW (s)	FullMonteCUDA (s)
				Quadro P5000	Titan Xp
Colin27 [11]	34.1	—	19.8	2.7	1.8
Digimouse [10]	4.7	9.4	3.8	0.9	0.8

To further benchmark FullMonteCUDA against FullMonteSW, we used the complex geometry models in Table 4 with packet counts ranging from ${10}^6$ to ${10}^8$. The results are summarized in Tables 7 and 8 and show that FullMonteCUDA acheives a performance gain of up to 13x over FullMonteSW. The output accuracy of FullMonteCUDA was confirmed using the method discussed in Section 6.

Table 7. Performance comparison against FullMonteSW using ${10}^8$ packets.

Model	FullMonteSW (s)	FullMonteCUDA (s)		Speedup
		Quadro P5000	Titan Xp	Quadro P5000	Titan Xp
HeadNeck	412.4	66.4	31.8	6x	13x
Bladder	1838.3	357.8	215.8	5x	9x
cube_5med	486.5	121.6	69.1	4x	7x
FourLayer	187.9	46.3	24.7	4x	8x

Table 8. Performance comparison against FullMonteSW using ${10}^6$ packets.

Model	FullMonteSW (s)	FullMonteCUDA (s)		Speedup
		Quadro P5000	Titan Xp	Quadro P5000	Titan Xp
HeadNeck	5.1	1.5	1.2	3x	4x
Bladder	18.3	10.0	3.7	2x	5x
cube_5med	5.0	1.3	0.9	4x	6x
FourLayer	2.0	0.5	0.4	4x	5x

FullMonteCUDA performs better when simulating more packets. As illustrated in Fig. 3, FullMonteCUDA has the additional overhead of transferring data to-and-from the GPU. For example, in the case of the HeadNeck model, the total runtime for ${10}^6$ packets is 1.2 seconds. We measure the CPU-GPU memory transfer time to be 0.1 seconds - around 8% of the total runtime. When the number of packets is increased to ${10}^8$, the runtime jumps to 31.8 seconds while the CPU-GPU memory transfer time increases to only 0.15 seconds - 0.5% of the total runtime. When solving inverse problems, this overhead can be amortized since the mesh, which constitutes nearly all of the memory being transferred, often remains constant across the many forward simulation iterations and therefore only needs to be transferred to the GPU memory once.

Our results show that the GPU is capable of handling the large and realistic tetrahedral-meshes required for general clinical models. Moreover, as shown by the model descriptions in Table 4 and performance results in Tables 7 and 8, the GPU achieves equal or greater speedups for the large mesh sizes compared to the smaller ones. This shows that FullMonteCUDA is able to scale to large and realistic clinical models and highlights the value of the GPU memory optimizations from Section 5.2.

8. GPU profiling

The NVVP provides a source level PC sampling option which helped us find performance bottlenecks in the FullMonteCUDA kernel. We found that the tetrahedron intersection calculation was a major bottleneck consisting of mostly memory dependencies from reading the tetrahedron data and execution dependencies when performing the actual calculation. We also found a memory dependency bottleneck when determining whether a packet is crossing a region boundary caused by the memory lookup for the current and neighbouring tetrahedral material ID.

Overall, the profiling data indicates that most stalls are caused by memory and execution dependencies, as shown in Fig. 4. All of the memory dependency bottlenecks occur when accessing the tetrahedron data, so future work may include creating a custom tetrahedron cache in shared or constant memory. For example, a subset of the total packets could be run pre-emptively to determine the tetrahedrons with the highest access rates. These tetrahedrons could then be stored in a hash table in constant memory for the remainder of the simulation to reduce the read latency at these bottlenecks.

9. Conclusion

This paper described FullMonteCUDA, which has been validated and benchmarked against various existing MC light propagation simulators. For layered geometry models, FullMonteCUDA achieves a speedup of 11x over MCtet and 2x over CUDAMCML. For various tetrahedral benchmark models, FullMonteCUDA achieves a speedup of 12x over MMCM, up to 19x over TIM-OS, 288-936x over the single-threaded, non-vectorized version of FullMonteSW and 4-13x over the multi-threaded, vectorized version of FullMonteSW. FullMonteCUDA demonstrates efficient CUDA code with optimizations specific to both the light propagation algorithm and GPU architecture. The optimizations in this work highlight the importance of understanding the underlying GPU architecture when attempting to accelerate MC simulations.

FullMonteCUDA’s performance improvement over the highly optimized software code significantly improves its ability to be used in solving the inverse problem for biophotonic procedures like PDT and BLI. It facilitates this by allowing inverse solvers to finish in minutes rather than hours or improve their accuracy by running significantly more simulations in an allocated time. FullMonte could be extended to applications outside of biophotonics where objects need to be located in turbid media, such as autonomous vehicles navigating through light scattering fog or aquatic navigation when diving close to the seabed. Medical professionals may not have the time or software training to program complex C++ and CUDA code. This is why we have developed the entire FullMonte project with the intention of making it simple to use and extend. FullMonteCUDA has been integrated into the overarching FullMonte project which allows for use of the CPU or GPU acceleration with minimal programming effort. The entire FullMonte project, including FullMonteCUDA, is open-source and can be accessed from: www.fullmonte.org.

Funding

Ontario Research Foundation10.13039/100012171 (RE-08-022); Natural Sciences and Engineering Research Council of Canada10.13039/501100000038; International Business Machines Corporation10.13039/100004316; Intel Corporation10.13039/100002418; Theralase Technologies Inc..

Disclosures

The authors declare that there are no conflicts of interest related to this article.