Picometer scale vibrometry in the human middle ear using a surgical microscope based optical coherence tomography and vibrometry system

Abstract

We have developed a highly phase stable optical coherence tomography and vibrometry system that attaches directly to the accessory area of a surgical microscope common to both the otology clinic and operating room. Careful attention to minimizing sources of phase noise has enabled a system capable of measuring vibrations of the middle ear with a sensitivity of < 5 pm in an awake human patient. The system is shown to be capable of collecting a wide range of information on the morphology and function of the ear in live subjects, including frequency tuning curves below the hearing threshold, maps of tympanic membrane vibrational modes and thickness, and measures of distortion products due to the nonlinearities in the cochlear amplifier.

1. Introduction

A principal tool for the visual inspection of the middle ear is the surgical stereo-microscope. Free-standing and ceiling/wall mounted versions of these are found in every otology (ear) clinic and operating room (OR). They provide high-fidelity imaging for visual assessment of ear pathologies and provide visual guidance during ear surgery. Nevertheless, they can only relay superficial morphological information to the ear surgeon (otologist). The ability to visualize subsurface structures, such as the layers and thickness of the tympanic membrane and position and dimensions of the ossicles would be beneficial both in the clinic and OR.

Here we address that need by developing an Optical Coherence Tomography (OCT) system that can be attached as an accessory to a typical ENT surgical microscope. OCT is well suited to imaging the subsurface microscale features in the middle ear while at the same time imaging over the entire depth of the middle ear space. This is possible because the axial resolution is independent of the numerical aperture of the objective, thus enabling an axial resolution of ∼10 µm with a depth of focus of several millimeters. Functional vibratory imaging of the middle ear components is also possible by measuring the interferometric phase as a function of time, but requires special care to minimize sources of phase noise. As we will show, our system is capable of achieving a sensitivity to vibration of under 5 pm during live human imaging. This is sensitive enough to measure vibrational motion below the threshold for hearing as well as distortions arising from non-linearities within the inner ear, hence it is well suited for clinical measurements of functional change due to ear pathologies.

The use of OCT in the human middle ear has also been investigated for a variety of applications, see for instance [1–4] and a recent review article by Tan et al [5]. The most closely related work to that presented here is by Adamson and coworkers [6]. They developed a device with similar goals to our own, i.e. measuring the function and morphology of the middle ear with attention to functional vibrometry. Their system is supported by a large boom stand similar to a surgical microscope, but it is not integrated into a surgical microscope. In other words, it is a stand-alone instrument rather than an accessory to an instrument that is already part of the workflow in the OR and clinic. We take different approaches to phase stabilization and measuring vibratory responses that have allowed us to improve on their reported sensitivity to vibration by several orders of magnitude.

We should also note that while there has also been a substantial effort to integrate OCT into surgical microscopes for ophthalmic surgery (see for instance [7]), this work is not directly translatable to the microscopes used in an ENT clinic. The integrated OCT systems for the retina also generally operate either in the 800 nm or 1 µm wavelength bands whereas we are working at 1.3 µm for improved penetration depth.

2. Methods

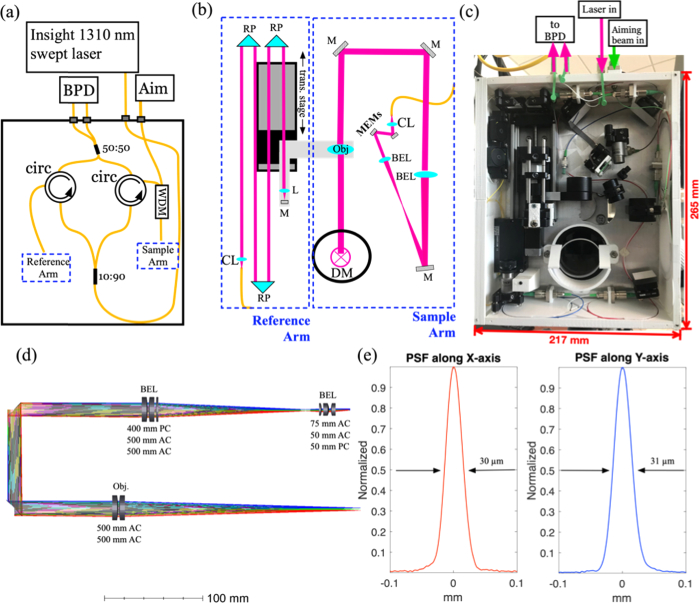
The layout for the ORscope optical system is shown in Fig. 1a-c . The 3-D printed ABS walls (see Fig. 1c) have embedded structures that house the optical fibers (e.g. circulators and couplers) which form the Mach-Zehnder interferometer (Fig. 1a). The reference arm (left side of Fig. 1b) light exits a reflective collimator (CL) passing through three right-angle folding prisms (RP) before entering an achromat (L) and reflecting off of a mirror (M) placed at its focal plane. The achromat and mirror are housed in a custom designed fixture that attaches to a high-speed translation stage (trans. stage) with 5 cm travel. The sample arm (right side of Fig. 1b) light exits a reflective collimator and is directed to a 2.6 mm diameter 2-axis MEMs scan mirror. The scanned beam then passes through a beam expander (BEL) with M = 9.3 before entering the objective lens (Obj.). The objective lens is attached to the same high-speed translation stage as the reference mirror. In this arrangement, the working distance of the OCT system can be changed without altering the optical pathlength difference of the interferometer. In other words, the focal plane of the objective is always at the same depth in the OCT image. A dichroic mirror (DM) merges the optical path of the OCT system and microscope system. The combined optical path would be directed out of the page in Fig. 1(b,c). The microscope’s objective sits in the circular hole just behind the dichroic mirror where it is attached to the microscope. As seen in Fig. 1(c), the sample and reference arm optics are attached to an aluminum plate. The sample arm imaging system was designed using the OpticsStudio (Zemax) optical design suite. The 3-D layout of the sample arm is shown in Fig. 1d. With the exception of the reflective collimator (not shown, Thorlabs, RC02APC-P01) all of the lenses are combinations of commercially available (Thorlabs) lenses. The focal lengths of the lenses are specified below each combination in Fig. 1d, where AC stands for achromatic lens and PC stands for plano-convex. The measured lateral point spread function along X and Y is shown in Fig. 1e. The measured lateral resolution varied from 30-38 µm over a square field of view of 5 × 5 mm², in good agreement with the Optics Studio prediction. The axial resolution is a function of the source bandwidth and any window function used. In our case the source was centered at 1309.5 nm with a spectral bandwidth of 93.3 nm. We used a Hann window to shape the spectrum which resulted in an axial resolution of 18.4 µm in air.

Fig. 1.

(a) Schematic of fiber optic Mach-Zehnder OCT interferometer. Abbreviations: BPD, balanced photodiode, Aim, green aiming beam, circ, circulator, WDM, wavelength division multiplexor. (b) Schematic of bulk optics in reference and sample arm. Abbreviations: CL. Collimating lens, RP, right angle prism, M, mirror, trans. Stage, translation stage, DM, dichroic mirror, Obj., objective lens, MEMs, MEMs scan mirror, BEL, beam expander lens. (c) Photo of optical system shown schematically in (a) and (b). (d) 3-D rendering of sample arm optics from OpticStudio simulation. The focal lengths of the lens are given below each compound lens, where AC is achromat and PC is plano-convex. (c) Measured lateral point-spread function (PSF) along the X and Y-axes.

An important objective of the optical system design described above was to minimize mechanical and thermal instabilities in the system. These accumulate to produce phase-noise in the OCT interferometer. There are number of features in the system that were meant to mitigate these sources of phase noise. The entire interferometer was built on an aluminum plate so that the reference and sample arm are mechanically and thermally coupled. The optical fibers for the interferometer were embedded in the 3-D printed walls to the extent possible for the same reason. Since the entire interferometer is on the microscope head, when the microscope position is adjusted by the clinician, none of the fibers of the interferometer undergo mechanical stress, except the fibers from the light source and to the detector. These fibers run down the length of the boom arm where the mechanical stress will lead to changes in the polarization state of the propagating light. However, since the polarization changes are common to both the reference and sample arm, they do not introduce additional phase-noise. Finally, the MEMs mirror used for beam steering is substantially more stable than the galvo mirrors commonly used for beam steering in OCT systems.

If we hope to enable routine use in the OR and clinic, the ease of attachment of the system to the scope and the scope’s maneuverability once attached are important. We developed a custom circular dovetail connection to the surgical microscope. It bolts directly to the accessory area at the base of the microscope head directly behind the objective. The dovetail enables quick and easy attachment of the OCT system to the scope, requiring only a single thumb screw to secure the system to the dovetail connector. Figure 2(a) shows the system attached to a Leica M400E. The system dimensions are 265 × 217 × 65 mm and weighs 2.3 kg. The weight and dimensions were sufficiently small to allow easy adjustment of the brakes on the microscope such that it could be maneuvered and positioned with similar ease as without the OCT system attached. So far, we have only tested this with the Leica M400E. However, since it is typical of the models used in otology clinics and operating rooms, we expect similar performance on other relevant brands/models.

Fig. 2.

(a) Leica M400E surgical microscope with OCT accessory attachment and ENT examination chair. (b) Close-up showing the OCT accessory mounted to the bottom side of the microscope. (c) Bottom view of OCT accessory. The bottom cover is threaded to match the sterile drapes (SD) commonly used to cover the microscope when used in surgery. (d) Close-up of ENT chair head rest showing the bite bar on the left used for high-phase sensitivity measurements. The speculum fixture is on the right. Both are attached to the chair with lockable articulating arms. (e) Close-up of speculum fixture showing the two earbuds used for introducing sound to the ear canal, the microphone for recording the stimulus sound, and a disposable speculum. (f) Mobile tower, housing the CPU, monitor, all electronics, laser system, and detector.

In the OR, the microscope must also be covered by a sterile drape. We customized the opening of the bottom cover of the system (Fig. 1(c), above DM and Fig. 2(c)) to accept the same threaded window typically used in sterile drapes for Leica scopes. The entire system can be easily draped along with the microscope head.

Figure 2(a) shows the whole system including the ENT examination chair. A close-up of the system attached to the microscope head is shown in Fig. 2(b). The USB video camera (red) to the right allowed us to stream video to a PC (Fig. 2(f)) while collecting OCT images of the patient’s middle ear. The electrical control cables and optical fibers (Fig. 2(c)) were attached to the right and back sides, respectively, with bulkhead connections through the ABS walls. Both were fed along the length of the articulating arm with sufficient slack to avoid tension on any of the connections. The ENT chair was modified to accept a pair of articulating arms at the back of the headrest. A speculum fixture, shown in Fig. 2(c), was designed to be placed in the articulating arm in order to improve visual access to the middle ear. It has a wedge nearIR window tilted at a relatively steep angle to avoid glare due to back reflection of the microscopes white-light illumination. It also has two ports to attach earbud type speakers. We included two speakers because we wanted to be able to introduce two pure tones simultaneously without the possibility of distortion products arising from the speakers themselves. This was important for making measurements of Distortion Product Otoacoustic Emissions (DPOAEs, described below), which is a form of nonlinear feedback from the inner ear. We initially used a single set of stereo ear buds, however we found that there was a small but measureable cross-talk between the two. In order to avoid this, we used a pair of mono ear buds (Far End Gear/XDU stereo-to-mono noise isolating earphone). Using these we could not measure any cross-talk. A third port housed an electret microphone that could be used for calibration if necessary. In practice we used a higher quality microphone for speaker calibration (Brüel & Kjær/4939-A-011), using the method described below. This was done because the results from the electret microphone in the fixture were unreliable when placed in the human ear canal. Nevertheless, we left the microphone port in place for potential future use. Finally, opposite from the nearIR window was a connection designed to fit the Welch-Allyn disposable otoscope speculum. For imaging, the speculum was attached to one of the articulating arms and locked into place via the single knob once positioned by the physician. This provided stability for vibrometry measurements. Optionally, a bite-bar could be attached to the second articulating arm on the opposite side of the ENT chair to provide improved patient stability. This was used when high phase-stability was needed. Currently the bite-bar is 3-D printed, but disposable versions could be deployed for use in the clinic.

In order to mimic the sound field that would be present at the tympanic membrane we used a section of ∼6 mm diameter tubing to approximate the ear canal. The calibrating microphone was fit tightly into one end of the tube while the speculum was placed loosely at the other. The distance between the tip of the speculum (Ø = 4 mm) and the microphone was ∼7 mm. Pure tones were played from each speaker at the desired frequencies and recorded by the microphone. From these recordings calibration files were generated for later use. These were used for single tone and two tone (one from each speaker) stimulus. While we have made our best effort to generate a reliable speaker calibration, undoubtably the geometry of a patient’s ear canal as well as the fit of the speculum into the ear canal will impact the pressure at the tympanic membrane producing systematic error.

All of the system electronics were place on a tower cart, shown in Fig. 2(d). This included a custom designed acoustic attenuator, acoustic amplifier, Insight balanced detector, 1310 nm Insight swept laser, breakout boxes for analog in/out, MEMs mirror driver, desktop computer, and monitor. The output of the laser passed through a fiber polarizer mounted to the base of the tower before entering the long patch cable that traveled along the boom arm of the microscope and inserted into the port labeled in Fig. 1(c). The system software was written largely in Python with subroutines for signal processing written in CUDA and run on a high-end GPU. The software and processing have been reported elsewhere [8,9]. For vibrometry, spectral interferograms are collected as a function of time, i.e. M-mode scanning. After typical OCT processing, the time-dependent interferometric phase is extracted. The phase is converted from radians to displacement by multiplying by the constant, λ/(4nπ), where λ is the source center wavelength and n is the refractive index. A Fourier transform along time is then computed. The magnitude of this Fourier transform is interpreted as the magnitude of the vibratory response. The phase noise in the magnitude of the Fourier transform defines the noise floor for measuring vibrations. The phase of the Fourier transform is interpreted as the phase relative to the acoustic stimulation. More detail on processing of the time-domain phase is provided below in the context of the results. Generally, postprocessing was done using MATLAB (Mathworks, Inc.) and volume rendering using Amira (ThermoFisher Scientific, Inc.).

3. Results and discussion

A primary design motivation was to develop a system that could achieve high phase stability for vibrometry. In addition to controlling for mechanical vibrations in the optical system, we have to deal with motion artifact, which creates sharp changes in the time-domain phase. Just as a delta function in the time-domain contains all frequencies, a noise spike in the time-domain phase contributes to phase noise across a wide frequency band. In order to achieve phase noise levels sufficiently low to observe middle ear motion at the hearing threshold and below, we anticipated the need to acquire data over a defined period of time. Initially, it was not clear how we should partition the time-domain phase data before computing the Fourier transform. In principle, the signal to noise of the vibrational response should be equally improved by computing a long time duration Fourier transform or short time Fourier transform of signals averaged in the time-domain, with equivalent total time duration. In other words the signal to noise for a 200 ms acquisition should be the same if we compute the Fourier transform using the entire time-duration or break it up into 4 × 50 ms time segments, average in the time-domain and then compute the Fourier transform of the 50 ms averaged signal. In both cases it should improve by a factor of 2 over a single 50 ms time acquisition, i.e. by the √n where n is the multiplicative increase in total time duration of the signal. In spite of the signal to noise equivalence, we would prefer to use the longer duration because that leads to the best frequency resolution, hence we would be more robust to noise spikes near the frequency of the signal.

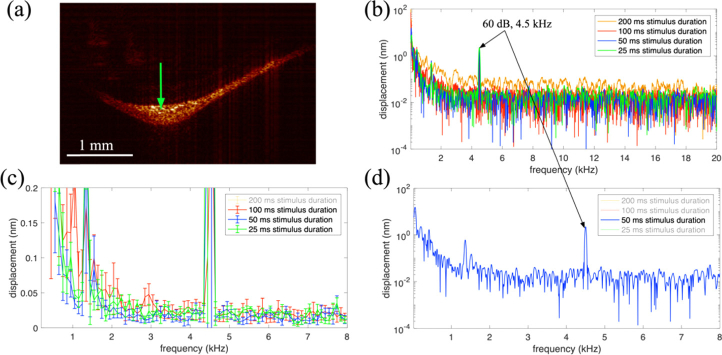
In order to find the best compromise between the length of time-segments and the amount of time domain averaging, we conducted the following experiment. A healthy volunteer was placed in the examination chair. Using the bite-bar and speculum the patient’s left ear canal was oriented to provide a view of the middle ear through the microscope. An OCT cross-sectional image (B-scan) of the patient’s tympanic membrane (TM) is shown in Fig. 3(a) . A green arrow indicates the position where M-scans were acquired. A series of 400 × 200 ms acquisitions were acquired while a 60 dB SPL pure tone at 4.5 kHz was played from one of the ear buds in the speculum. The time-domain phase at the indicated position was processed in the following way. The time-domain phase from the 400 trials was averaged. Before computing the Fourier transform a 3^rd order polynomial was fit to the signal and subtracted from the time-domain phase to remove the low frequency drift. We tried using higher order polynomials however they did not show any significant improvement. This approach substantially reduced the large noise peak near 0 Hz. A Fourier transform was then computed after applying a Hann window over the first 25 ms, 50 ms, 100 ms, and finally the entire 200 ms time segment. In principle a √2 reduction in noise should be observed at each factor of 2 increase in time duration. The frequency domain signal for each with the displacement on a log₁₀ scale is shown in Fig. 3(b) over a range including the entire range of human hearing. The 4.5 kHz vibration of the TM due to the 60 dB SPL 4.5 kHz tonal stimulation is apparent in all traces with comparable amplitude. The noise in the 200 ms trace is clearly much worse than all of the others. Figure 3(c) shows the mean and standard deviation (error bars) of the 100 ms, 50 ms, and 25 ms traces on a linear displacement scale after binning over 100 Hz intervals. Clearly, the 100 ms trace has the largest noise floor of the 3. The 50 ms trace shows the lowest noise floor, but upon closer inspection is approximately √2 better than the 25 ms trace. This is the relationship we would expect based on the factor of 2 increase in time duration. The 50 ms trace is shown by itself in Fig. 3(d) over the 0-8 kHz range. The noise drops to 1 nm by 100 Hz and levels out at ∼10 pm above 2 kHz. For experiments requiring high phase-sensitivity we chose to collect 50 ms time segments (trials), averaging multiple trials in the time-domain before taking the Fourier transform. We felt this approach offered a good compromise between frequency resolution and noise floor as supported by the experiments noted above. While our objective was to determine optimal imaging parameters, we note that this result is consistent with phase noise due to patient movement as suggested above. In other words, longer time series are more likely to suffer from sharp changes in phase due to motion which leads to broadband phase noise.

Fig. 3.

(a) Cross-sectional image (B-scan) of the tympanic membrane in the left ear of a healthy volunteer, near the umbo. The green cross indicates the spatial position of the vibratory response in (b-d). (b) Vibratory response after 200 averages with the stimulus duration indicated in the legend. A 60 dB 4.5 kHz sound was presented to the ear canal using a custom speculum. (c) Mean and standard deviation over 100 Hz bins for the three shortest stimulus durations. (d) 50 ms stimulus showed the best performance considering motion artifact. Above 100 Hz the noise mean drops to less than 1 nm, leveling out at ∼10 pm above 2 kHz.

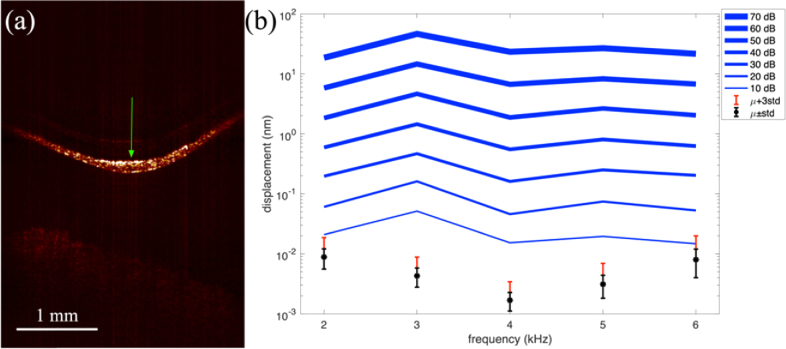
Next we recorded tuning curves on the TM from the same healthy volunteer. A cross-sectional image of the TM taken just prior to the tuning curve data is shown in Fig. 4(a) with a green arrow indicating where tuning curves were measured. They were recorded over the range of 2-6 kHz at 1 kHz intervals and a range of sound pressure levels of 10-70 dB at 10 dB intervals. The data points plotted in Fig. 4(b) were taken from the brightest point in the A-line corresponding approximately to the surface of the TM. The log₁₀ scale plot shows an approximately linear increase in displacement with increasing sound pressure level as would be expected in the middle ear. We chose 10 dB as the lowest sound pressure level because it is near the threshold for human hearing used as a reference for the hearing level (HL) scale commonly used in audiometry. At 2, 3, 4, and 6 kHz, 0 dB HL corresponds to 9.0, 10, 9.5, and 15.5 dB SPL [10]. The noise mean and standard deviation (µ±std) are shown in black on Fig. 4(b) for each stimulus frequency. The red error bar indicates the noise mean plus 3 standard deviations (µ+3std). This is the cutoff we typically use for measuring vibratory response, i.e. our sensitivity to vibration. Signals below this level are considered part of the noise. We can see that for these data all of the signals plotted exceed this threshold except 10 dB SPL stimulus at 6 kHz. Nevertheless, since the hearing threshold at 6 kHz is 15.5 dB SPL, the noise floor is still below the expected vibratory response at the hearing threshold.

Fig. 4.

(a) Cross-sectional image of the tympanic membrane. Green arrow indicates where the vibratory response was recorded. (b) Tuning curves over the 2-6 kHz, 10-70 dB SPL range. The * is the noise mean (µ) with error bars at ± standard deviation (std). The red error bar is µ+3std, i.e. the sensitivity to vibration. Any signals below this level are generally disregarded as too weak to consider.

For these data we recorded 100 trials of 50 ms duration, averaging in the time-domain as described above. The large number of trials was necessary to drive the noise floor low enough to record signals at the lowest sound pressure levels. This resulted in an acquisition time of approximately 3 minutes. We observe variation in the noise floor across the frequency range recorded, unlike Fig. 3(d) which shows an essentially constant noise mean and standard deviation above 2 kHz. The variation in noise is likely due to patient motion during data acquisition. In addition to the noise source noted above, which we have mitigated by limiting the time duration of the trial to 50 ms, there is the chance that the patient moves so that the intensity of the signal becomes diminished. In other words, over the time period of data acquisition the patient can move so that the light impinges on a slightly different area of the TM with lower reflectivity. Since the phase noise is inversely proportional to the signal to noise, the noise floor gets larger. The best approach to mitigating this issue would be imaging faster. We could obviously reduce the acquisition time by only collecting the large number or trials for the low sound pressure levels. If we only collected 50 trials at 20 dB SPL and 100 trials at 10 dB SPL, then we could reduce the acquisition time to approximately 40 seconds. While our current software will not allow this, it is a fairly straightforward coding problem to solve which we will undertake in subsequent updates.

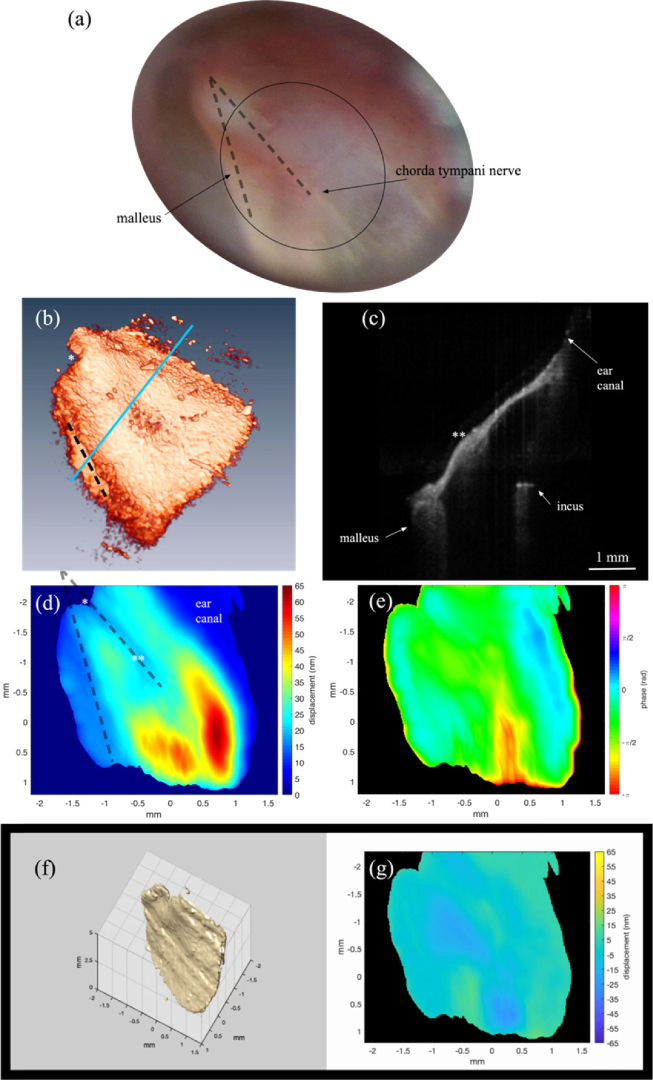
The middle ear vibratory response can also be characterized by spatial variations in amplitude and phase when presented with different tone frequencies. This has been shown before [11]. These are expected to change with different TM pathologies, including perforations, thinning, and scarring. As an example we recorded the vibratory response in the left ear of a healthy volunteer with 65 dB SPL tonal stimulation at 3.3 kHz. Just prior to acquiring the vibratory response a volume image was captured with lateral sampling of Δx=Δy = 12 µm. Figure 5(a) is the first frame of a movie showing that volume image rendered in Amira, looking down on the TM. The full movie (Visualization 1 ^{(7.4MB, mp4)} ) shows the volume as it rotates horizontally. The malleus is located along the left edge as indicated by the black dashed line. The relative position of the malleus is clearly visible in the cross-section shown in Fig. 5(b). This cross-section was taken at approximately the position indicated by the blue line in Fig. 5(a). The image spans approximately 1/3 of the area of the TM from the malleus to the wall of the ear canal and also includes a portion of the incus. The * marks corresponding points in (a) and (c) for visual registration. The ** in (b) indicates a thicker area of the TM, which is indicated in Visualization 1 ^{(7.4MB, mp4)} as a yellow line that appears half way through the movie. Given the relative position of this structure in the images it appears to be a segment of the chorda tympani nerve which passes through the middle ear.

Fig. 5.

All images collected in vivo on the left ear of a healthy patient. (a) Photograph taken through the surgical microscope. The malleus and chorda tympani nerve are labeled and marked with dashed lines. The approximate field of view of the OCT images is indicated by the ellipse. (b) First frame from a movie (Visualization 1 ^{(7.4MB, mp4)} ) of the OCT volume image recorded just prior to the vibrational measurements. The black dashed line indicates the relative position of the malleus. A yellow line in the visualization labels the chorda tympani nerve. The * and ** in (b), (c), and (d), mark corresponding points in the respective images. (c) Cross-sectional image from the volume showing the malleus, incus and wall of the ear canal (d) Vibrational amplitude map at the stimulus frequency (3.3 kHz) following 50 ms 65 dB SPL stimulus. (d) Dashed lines label the malleus and chorda tympani nerve as in (a). (e) Corresponding phase. (f,g) First frame of a movie (Visualization 2 ^{(6.5MB, mp4)} ) showing a volume rendering of the TM vibration in (e) and the corresponding time dependent amplitude map in (f). The vibration was scaled by a factor of 6600 in (e) so that the vibrational pattern would be visible in the image.

The volume acquisition was followed by a volume M-scan with spatial sampling of  Δx=Δy = 99 µm. The lower spatial sampling was done in order to reduce the acquisition time and with the belief that the vibratory response likely does not change rapidly as a function of the lateral dimensions. At each x,y position a tone was played for 50 ms while spectral interferograms were collected for a total acquisition time of ∼95 s. The measured vibratory amplitude and phase for the tympanic membrane are shown in Figs. 5(a,b). These images were prepared by masking out the areas of low signal in the 3-D image, represented by dark blue and black in the amplitude and phase images, respectively. They were then smoothed by convolution with a 3-D Gaussian kernel that had a standard deviation of 1 pixel in x,y and 10 in z, which corresponds approximately to 100 µm in all dimensions. The smoothed data was then resampled in x,y using a 2-D spline interpolation so that the sampling matched that of the volume image in Fig. 5(a). The 2-D images, Figs. 5(c,d) were generated by finding the index of the maximum displacement along z through the TM and plotting the magnitude and phase at that z-index.

As we would expect, the lowest magnitude motion is measured at the wall of the ear canal (upper right). This is followed by the area near the malleus (left). A third region of lower amplitude motion corresponds to a thicker portion of the TM, marked by a ** in Fig. 5(b,c). In total the displacement varies over a range of ∼50 nm with a maximum displacement of 63 nm. The amplitude and phase, which varies by > π, constitute the vibrational mode at the stimulus intensity and frequency. In order to get a better visual understanding of the spatial variation of the vibratory response we created a time series of the TM vibration by assuming a sinusoidal motion at the measured amplitude and phase, i.e. the change in the z-position was Δz(i,j)=scale*M(i,j)cos(2πf_stim+ø(i,j)), where (i,j) are the pixel indices, M is the vibration amplitude and ø is the vibration phase. The scale factor of 6600, was necessary to make the nanometer size vibrations visible in the movie generated from the time series (Visualization 2 ^{(6.5MB, mp4)} ). The sinusoidal motion was calculated in MATLAB and used to create the vibrating 3-D rendering of the TM. The first frame of this movie is shown in Fig. 5(e). We also generated a corresponding map of the time dependent displacement (Fig. 5(f)), also included in the movie.

So far, we have only probed middle ear function, however it is also possible to glean information about the inner ear. The measurement of otoacoustic emissions (OAEs) is a noninvasive method to diagnose the functional state of the cochlear amplifier. It is commonly used as a screening tool for hearing loss in infants using very sensitive microphones to measure the sounds emitted from the cochlea. Similar measurements of a particular form of OAE, distortion product otoacoustic emissions (DPOAEs) can be made using OCT vibrometry by measuring the distortion products as vibrations on the constituents of the middle ear.

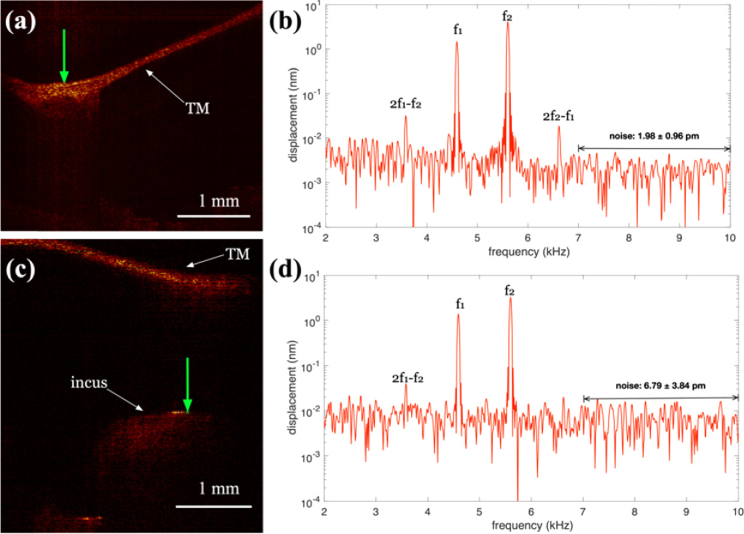
In order to demonstrate this, we used an experimental setup similar to above, except two tones were played simultaneously, one each from the two earbud speakers. Figure 6a shows a cross-sectional image of the tympanic membrane at the umbo. The green arrow indicates the vertical line along which the vibratory response was measured. The stimulus was f₁ = 4.59 kHz, f₂ = 5.60 kHz, and 65 dB SPL. In order to drive the noise floor down we time averaged 400 trials of 50 ms duration for a total acquisition time of ∼ 20 s. The resulting vibratory amplitude response is shown in Fig. 6(b) for the brightest location on the tympanic membrane. The noise floor in the 7-10 kHz range was 1.98 ± 0.96 pm, dictating a sensitivity of 4.86 pm (µ+3std). With the low noise floor, the two fundamental frequencies are readily visible along with the 2f₁-f₂ and the 2f₂-f₁ distortion products at 3.58 kHz and 6.62 kHz, respectively. We can also take advantage of the depth resolved properties of OCT vibrometry to measure the response along the ossicular chain. Figure 6(c) shows a cross-sectional image including the incus. The green arrow indicates the line along which the vibratory response was measured. Figure 6(d) is the vibratory response at the brightest location on the incus. The noise floor in the 7-10 kHz range was 6.79 ± 3.84 pm, dictating a sensitivity of 18.31 pm (µ+3std). The two fundamental frequencies are readily visible along with the 2f₁-f₂ distortion product at 3.58 kHz. With the higher noise floor, the 2f₂-f₁ peak is no longer visible. For comparison, Adamson and coworkers [6] report a 5 nm noise floor (with spatial averaging) over a 5 s acquisition time for imaging the middle ear ossicles. Hence, with roughly the same experimental conditions, we observe a >700x lower noise floor.

Fig. 6.

(a) Cross-sectional OCT images of the tympanic membrane (TM) at the umbo region of the malleus (a) and long process of the incus (c). The green arrow indicates where the displacement was measured in b) and d). b,d) Displacement (log₁₀ scale) vs. frequency. The stimulus was 65 dB SPL pure tones at f₁=4.59 kHz and f₂=5.60 kHz. The stimulus duration was 50 ms with 400 trials. The average response is plotted. Noise floor was calculated in the 7-10 kHz range.

Recent work [12] using a sensitive laser Doppler vibrometer showed that it was possible to measure these distortion products at the umbo with high sensitivity. The authors focused on the 2f₁-f₂ cubic distortion product, observing it in 20 patients. In order to get a strong enough reflection, they typically (17 of 20) placed a strong reflector on the umbo. In our case, we imaged the umbo region and found the area with the highest natural reflectivity to take vibrational measurements. Using this approach, we achieved comparable sensitivity as the laser Doppler vibrometer, clearly resolving the 2f₁-f₂ peak. The OCT vibrometry approach has a clear advantage in that it can also generate images of the middle ear and allows for vibrometry at subsurface locations, e.g. the incus.

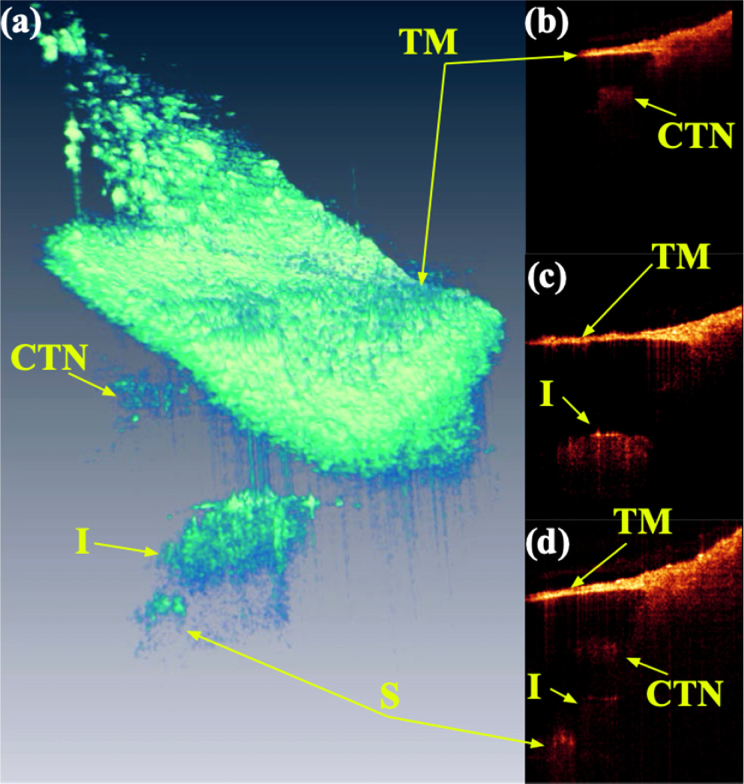
While the central design motivation for this system was to achieve high phase-stability for vibrometry, it is clearly also important to be able to image the structures of the middle ear. Figure 7 shows a volume image in panel (a), accompanied by cross-sections extracted from the volume set in panels (b-d). The tympanic membrane (TM) is a prominent feature in all images. A movie (Visualization 3 ^{(7.3MB, mp4)} ) included in supplementary material of the rendered volume rotating in space is useful to get a sense of perspective. The three cross-sections were chosen because they bisect morphological features of interest. Figure 7(b) shows the tympanic membrane giving way to the wall of the ear canal to the right. Below the TM is a cross-section through what we believe to be the chorda tympani nerve (CTN). Fib. 7(c) shows a cross-section through the incus. The bone shows a strong reflection at the surface with heavy shadowing below. The final panel (d) shows a cross-section that bisects the stapes (S). These images are comparable with recent reports in the literature [1,6].

Fig. 7.

(a) Volume rendering of middle ear in a healthy volunteer showing the tympanic membrane (TM), Chorda tympani nerve (CTN), incus (I), and stapes (S). This is the last frame of movie of the structures (Visualization 3 ^{(7.3MB, mp4)} ). (b-d) Cross-sectional images from volume set showing the same.

Generally, it was a relatively simple task to get good images of the TM, malleus head (umbo area), and incus. However, considerably more effort was required to get images of the stapes. That is in part due to its relatively small size and the fact that it is deep in the middle ear and can be shadowed by the other ossicles. All of the images in Fig. 7 were rendered in Amira. The angle in the x,y plane (where z is depth) of the cross-sectional images was optimized to bisect the features of interest, in other words they do not correspond to the individual B-scans that make up the volume. In our experience, it is especially difficult to identify the stapes from B-scans. Only when we took volumes and later rendered the volume could we be certain we had an image with the stapes. For this to become routine in the clinic, real-time volume rendering may be necessary to give the clinician enough visual cues to reliably position the microscope. This system can sustain a volume rate of ∼1 Hz, however we need to upgrade our software to enable real-time rendering of the volume to make this a reality.

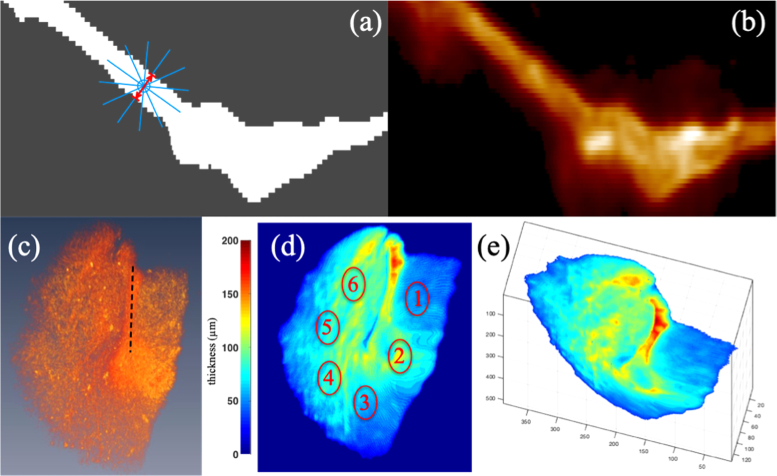
The thickness of the TM is potentially an important metric for wound healing in the case of persistent holes or thinning of the TM, tympanoplasty, and ossiculoplasty. Since the TM is cone-shaped, extracting the thickness requires some effort to determine at what angle to measure the thickness. We used an algorithm developed by Angaj, et al. [13] which allows us to find the thickness measured along the direction normal to the 3D TM structure. Specifically, the thickness at any point (voxel) is defined as the minimum of the line integral on the line segments passing through the voxel on a binary map of the TM. Figure 8(a) illustrates this in 2-D. The binary map is derived from thresholding the cross-section through the TM shown in Fig. 8(b) where gray takes on a value of 0 and white, 1. The blue circle represents the voxel and the blue lines the line segments. The lines segments are all the same length and chosen to be larger than the expected thickness. Obviously the line integral along the line with the least number of white pixels will have the minimum integral value. The distance along this line between gray areas is taken as the thickness at that voxel, represented by the red arrow in the figure.

Fig. 8.

(a) Cartoon illustrating algorithm for finding TM thickness. (b) OCT cross-sectional image used to create the binary mask in (a). (c) Snapshot from a volume rendering of the OCT data oriented to match the orientation of the thickness map in (d). The black dashed line highlights the malleus. This placement is obvious from viewing the associated movie (Visualization 4 ^{(3.6MB, mpg)} ). (d) Thickness map projected on the x,y plane. The thickness at the six labeled regions of interest are provided in table 1. (e) The true 3-D thickness map, rotated out of the x,y plane. See associated movie for various viewing angles (Visualization 5 ^{(3.5MB, mp4)} ).

Before applying this algorithm, the 3D OCT images were preprocessed to remove background noise and saturated A-lines. A 3D Gaussian filter was then applied to the dataset before image segmentation. The processed data was segmented using MATLAB into a binary image mask by automatic thresholding. Specifically, each image frame was first segmented using a locally adaptive threshold method [14]. Segmented regions with area lower than 60% of the largest region were discarded. A binary 2D mask of the TM was then generated for the image frame. A 3D mask for the entire TM was subsequently constructed from each 2D mask. The final 3D mask was further refined by running the mask through imaging volume from the other two orthogonal views using the active contour model [15] in MATLAB.

Shown in Fig. 8(e) is a representatively 3-D TM thickness map that is viewed from an angle rotated out of the (x, y)-plane. The true 3-D nature of the thickness map allows the user or clinician to simultaneously examine the anatomical and thickness changes due to pathology from different viewing angles (Visualization 5 ^{(3.5MB, mp4)} ). The thickness of the TM can be further quantified using the thickness map projected on the (x, y)-plane, which corresponds to the TM viewed through the ear canal (Fig. 8(d)). Listed in Table 1 are the thickness of the TM measured in six different regions from two normal subjects. The thickness in the six regions of TM are different. This indicates a normal occurrence of thickness variation in the TM. The mean thickness of the TM for the two subjects is 75 µm, which is consistent with results from previous OCT studies [16,17]. As mentioned earlier, these maps can not only be used to quantify scarring, thinning, and perforations of the TM, but also allows the visualization of the location and anatomical changes associated with these pathologies. In conjunction with the vibratory response (Fig. 5), a robust measure of the morphological, pathological, and functional changes due to different diseases could be obtained for diagnosis as well as for follow-up examination due to the non-invasive nature of OCT.

(µm)	ROI 1	ROI 2	ROI 3	ROI 4	ROI 5	ROI 6	mean
P1	52.62	93.56	58.74	85.6	77.86	88.56	80.04
P2	60.26	57.62	48.56	58.08	71.61	74.42	70.32

Finally, we recorded a series of B-scan images of the TM and the cochlear promontory in order to use variance analysis [18] to look for vasculature in both. We recorded a total of 495 B-scans and then calculated the median image and the variance. The median image is shown in Fig. 9(a) . The bright TM is at the top of the image. At the bottom of the image is the cochlear promontory and what appears to be the inner wall of the cochlea. We were somewhat surprised to be see the inner wall. While we routinely image through this bone in animal models, we assumed the bone would be too thick in a human. This result inspired us to focus deeper to try to resolve the cochlear partition, including the organ of Corti. In spite of our best efforts we were not able to see anything more. Nevertheless, it may be possible in a patient with a TM perforation or during surgery when the TM is pulled up providing a clear line of sight to the cochlear promontory to see through to the organ of Corti and Reissner’s membrane.

Fig. 9.

(a) Median amplitude image generated from 495 sequentially acquired B-scans. The tympanic membrane is the bright structure at the top of the image. The cochlear promontory along with what appears to be the inner wall of the cochlea are at the bottom of the image. The scale bar is 1 mm. (c) Phase image highlighting the vasculature of the middle ear. (b) Overlay of the variance and median images showing how the large variance on the tympanic membrane aligns with the cutaneous (top) and mucosal (bottom) layers of the membrane. The variance is much lower in the central fibrous layer.

The variance image, Fig. 9(c), shows what appear to be blood vessels in the cochlear promontory with the obvious larger vessel near the surface. Somewhat surprisingly, the cutaneous layer (top) and mucosal layer (bottom) of the TM show up brightly in the variance image. The presumably less vascular fibrous middle layer is much dimmer. This provides for a simple approach for segmenting the three layers as illustrated by the overlay image in Fig. 9(b) which demonstrates that the bright areas in the variance image correspond to the top and bottom of the TM.

Two healthy volunteers were imaged in the course of this work. No special training was done for either. In the clinic, the physician would normally hold the speculum in his/her hand while peering through the microscope. Here we used an articulating arm to hold the speculum more steady and a bite-bar for longer measurements, e.g. the distortion product measurements. Both adaptations are meant to minimize motion artifact. Future speed improvements may make it possible to return to a hand-held speculum, since higher imaging speed helps to mitigate motion artifact. Nevertheless, in practice we would commonly make the same measurement more than once if the phase-noise was poor. It is obvious when you record the data if that is the case. Most measurements are only a few seconds in duration so practically it adds very little time to imaging session.

4. Conclusions

We have developed a highly phase stable OCT imaging system that functions as an accessory to the common surgical microscope, a mainstay in the hearing clinic and OR. It can easily be taken on and off the microscope and sterile draped for use in the OR, while maintaining the free movement of the microscope and its image quality. The phase stability is sufficient to enable vibrational sensitivity under 5 picometers in awake human patients. This sensitivity can be exploited to measure tuning curves in the human middle ear at the threshold for hearing, thus potentially facilitating the identification of middle ear pathologies at their inception, before standard hearing tests could detect them. Measurements of vibratory response across the entire field-of-view produces maps of the vibrational mode structure, which likely change with various pathologies. The vibrational sensitivity can also be purposed to quantify distortion product otoacoustic emissions as a measure of inner ear health. These can be measured at the tympanic membrane and along the ossicular chain. Standard OCT volumetric imaging also provides useful diagnostic information on middle ear structures. From these, thickness maps of the tympanic membrane can be computed which will likely prove valuable for following wound healing in tympanoplasty and ossiculoplasty as well as for monitoring perforations of the tympanic membrane.

In all, a wide variety of diagnostic information on the middle ear can be gleaned in a fairly short amount of time. This along with the fact that the system was designed to fit easily into the workflow of the hearing clinic and OR should ease its integration. The ability to easily conduct 3-D studies of the middle ear morphology and function will provide additional diagnostic information for clinicians, enhancing the current repertoire of diagnostic and monitoring tools.

Funding

National Institute on Deafness and Other Communication Disorders (NIDCD)10.13039/100000055 (1R01DC013774); National Institute of Biomedical Imaging and Bioengineering (NIBIB)10.13039/100000070 (1R01EB027113).

Disclosures

The authors declare that there are no conflicts of interest related to this article.