Depth-resolved assessment of changes in concentration of chromophores using time-resolved near-infrared spectroscopy: estimation of cytochrome-c-oxidase uncertainty by Monte Carlo simulations

Abstract

Time-resolved near-infrared spectroscopy (TR-NIRS) measurements can be used to recover changes in concentrations of tissue constituents ($\Delta C$) by applying the moments method and the Beer-Lambert law. In this work we carried out the error propagation analysis allowing to calculate the standard deviations of uncertainty in estimation of the $\Delta C$. Here, we show the process of choosing wavelengths for the evaluation of hemodynamic (oxy-, deoxyhemoglobin) and metabolic (cytochrome-c-oxidase (CCO)) responses within the brain tissue as measured with an in-house developed TR-NIRS multi-wavelength system, which measures at 16 consecutive wavelengths separated by 12.5 nm and placed between 650 and 950 nm. Data generated with Monte Carlo simulations on three-layered model (scalp, skull, brain) for wavelengths range from 650 to 950 nm were used to carry out the error propagation analysis for varying choices of wavelengths. For a detector with a spectrally uniform responsivity, the minimal standard deviation of the estimated changes in CCO within the brain layer, $\sigma \Delta C_{\text{CCO}}^{\text{brain}}$ = 0.40 µM, was observed for the 16 consecutive wavelengths from 725 to 912.5 nm. For realistic a detector model, i.e. the spectral responsivity characteristic is considered, the minimum, $\sigma \Delta C_{\text{CCO}}^{\text{brain}}$ = 0.47 µM, was observed at the 16 consecutive wavelengths from 688 to 875 nm. We introduce the method of applying the error propagation analysis to data as measured with spectral TR-NIRS systems to calculate uncertainty of recovery of tissue constituents concentrations.

1. Introduction

Functional near-infrared spectroscopy (fNIRS) has showed capability to estimate changes in concentrations of chromophores contained in the brain: oxy-, deoxyhemoglobin and the oxidation state of cytochrome-c-oxidase (CCO) enzyme [1]. Fields of application of near-infrared spectroscopy (NIRS) method have been recently reviewed [1–5] and a common interest on using NIRS to monitor CCO emerges. CCO is present in all mitochondria and is involved in more than 95% of oxygen consumption [6]. Clinical NIRS measurements of cerebral cytochrome-c-oxidase can yield information about energy metabolism on cellular level [7] and have potential to be a metabolic marker of brain injuries [8]. The estimation of CCO is challenging and requires high accuracy in measurements as the CCO has broad spectral absorption peak in NIR region and low cerebral concentration [1]. Hence, the optical signals resulting from changes in cerebral concentration of CCO are much smaller than the signals corresponding to e.g. hemoglobins.

fNIRS relies on changes in the optical properties of tissue to evaluate physiological responses. Optical signals are measured typically in reflectance geometry, where source and detector optodes are positioned on the head surface at a distance of several centimeters (typically 3-4 cm). The changes in the optical signals can originate in the brain, in the overlying scalp or in both tissues. A reliable method to separate signals originating at different depths is required to discriminate between cerebral and systemic physiological changes [9–14] and hence avoid false-positive results in functional studies [15,16]. Number of methods have been suggested and applied to address the problem of contamination by the perfusion of extracerebral tissues when trying to recover brain oxygenation, including with the use of continuous wave sources [17] or the time-resolved NIRS (TR-NIRS) technique [18]. In TR-NIRS, short pulses of light, typically on the order of picoseconds in width, are emitted into the tissue and the arrival times of remitted photons are measured using time-correlated single photon counting electronics. The histogram of the arrival times represents the distribution of time of flight of photons (DTOF). TR data analysis methods calculate the broadening of DTOFs to recover absorption and scattering properties of tissue penetrated by the light pulses. In this study, we analyze DTOFs with the moments method [19], which utilizes statistical moments of the time-resolved distributions and allows to recover changes in the absorption coefficient with depth discrimination [20–22]. The moments method has been validated using Monte Carlo simulations [19], in experiments on phantoms [23] and during functional stimulation experiments [20,21]. The method has been applied during carotid surgery [22], to communicate with patients who are in a functionally locked-in state [24], and for assessment of cerebral perfusion by monitoring the inflow and the washout of an injected optical contrast agent indocyanine green with discrimination between the extra- and intracerebral tissue compartments [25,26]. The estimated depth-resolved changes in absorption coefficient at multiple wavelengths can be converted to depth-resolved changes in concentrations of chromophores using the Beer-Lambert law [20,22]. Literature shows lack of reported uncertainties [22] or the uncertainty is calculated as the standard deviation of block-averaged measurements [20]. Here, we extend the error propagation for the moments method [27] in order to calculate the standard deviations in the estimated changes in concentrations of chromophores within multiple layers applied for TR-NIRS data analyzed using the moments method and the Beer-Lambert law. The error propagation as used in this study accounts for the noise associated with the stochastic nature of the scattered photons, which are assumed to follow the Poisson statistics.

Here we introduce the method of applying the error propagation analysis to data as measured with spectral TR-NIRS systems to minimize uncertainty of recovery of tissue constituents’ concentrations. A recent review [3] summarizes the past studies that found the optimal number and range of wavelengths for different models, number of chromophores and number of wavelengths. The past studies aimed to minimize certain criteria, i.e. the condition number [28] and the residual norms [29] of the absorption extinction coefficients matrix, the levels of separability and cross-talk [30], the signal-to-noise ratio assuming a fixed amount of power [31], sensitivity and resolution [32], sensitivity overlap for different wavelengths [33], and a heuristic search for wavelengths that produce the closest result to the result of using 121 wavelengths [34]. Monte Carlo (MC) simulations are the gold standard for generating TR-NIRS data [35]. As such, we used MC simulated spectral TR-NIRS data for wavelengths from 650 to 950 nm for a three-layered model (scalp, skull and brain). Further, we calculated the standard deviation in estimation of concentration changes ($\sigma \Delta C$) of oxy-, deoxyhemoglobin and CCO in two compartments (scalp, brain) for different choices of wavelengths. The wavelength optimization criteria is to minimize $\sigma \Delta C$ of CCO in the brain layer. The multi-wavelength TR-NIRS system, developed in the author’s group and successfully tested in brain hemodynamic studies [23,25], can measure DTOFs simultaneously at 16 consecutive wavelengths separated by 12.5 nm and placed between 650 nm and 950 nm. We carried out analysis within the instrument wavelength range considering two case studies: 16 consecutive wavelengths separated by 12.5 nm and varying number of evenly spread wavelengths. We included the spectral responsivity [36] of photosensitive element in the analysis. The multialkaline cathode, as used in the TR-NIRS system investigated in this paper, has much higher sensitivity at shorter wavelengths and as such the detector performance can be the dominant factor that affects the optimal wavelengths range.

2. Methodology

2.1. Error propagation in the moments method

The analysis of TR-NIRS measurements based on changes in statistical moments of DTOFs has been presented in [19,20,37]. The DTOF is a histogram of photon counts (N_i) at time channels indexed by i. A time channel in DTOF corresponds to the time of flight of a detected photon. The multi-wavelength TR-NIRS system, as shown in [23,25], records DTOFs typically with 1024 time channels of width t = 13.68 picoseconds. The first three statistical moments of DTOF can be defined as: m₀ = N_tot = ΣN_i (zeroth), m₁ =  <t> = Σt_iN_i/m₀ (first) and $m_2^{\mathrm{c}}$ = V = Σ(t_i – m₁)²N_i/m₀ (second central). These statistical moments of DTOF are known as: total number of photons (N_tot), mean time of flight (<t>) and variance (V). The sensitivity factors relate changes in statistical moments measured for a given source-detector pair to changes in absorption coefficient Δμ_a within sub-volumes (e.g. layers indexed by j): ΔA = -ln(N_tot*/N_tot) = Σ[MPP(j)Δμ_a(j)], ΔT =  <t>*-<t> = Σ[MTSF(j)Δμ_a(j)], ΔV = V^* - V = Σ[VSF(j)Δμ_a(j)]. The star (*) denotes a statistical moment after a change in absorption, MPP is the mean partial pathlength, MTSF is the mean time of flight sensitivity factor and VSF is the variance sensitivity factor. The sensitivity factors can be obtained with a Monte Carlo simulation, or using analytical solutions of the diffusion approximation of light transport for simple geometries, or using the finite element method for heterogeneous models. The recovery method that uses the sensitivity factors relies on the assumptions that changes in statistical moments are linear within corresponding changes in absorption coefficient μ_a±Δμ_a which is true for Δμ_a→0. Additionally, the scattering properties should remain constant (Δμ′_s = 0, where μ′_s is the reduced scattering coefficient). The error propagation analysis proposed in [27] allows to calculate the standard deviation in recovered absorption change (σΔμ_a) within j–th layer for assumed heterogeneous background optical properties. σΔμ_a is calculated from the standard deviations of the three statistical moments, which may be statistically dependent as they are derived from the same DTOF curve. The existing covariances between $\Delta A$, $\Delta T$ and $\Delta V$ are used in the error propagation model to account for a mutual statistical dependence. Assuming the dominant photon noise follows a Poisson distribution, the covariance matrix Z of the first three statistical moments of the DTOF takes the following expression [27]:

$$\mathbf{Z}=\left(\begin{array}{ccc}\text{cov}(\Delta A,\Delta A)& \text{cov}(\Delta A,\Delta T)& \text{cov}(\Delta A,\Delta V)\\ \text{cov}(\Delta T,\Delta A)& \text{cov}(\Delta T,\Delta T)& \text{cov}(\Delta T,\Delta V)\\ \text{cov}(\Delta V,\Delta A)& \text{cov}(\Delta V,\Delta T)& \text{cov}(\Delta V,\Delta V)\end{array}\right)=\left(\begin{array}{ccc}2\frac{1}{N_{\text{tot}}}& 0& 0\\ 0& 2\frac{V}{N_{\text{tot}}}& 2\frac{m_3^{\mathrm{c}}}{N_{\text{tot}}}\\ 0& 2\frac{m_3^{\mathrm{c}}}{N_{\text{tot}}}& 2\frac{m_4^{\mathrm{c}}-V^2}{N_{\text{tot}}}\end{array}\right)$$ (1)

$m_3^{\mathrm{c}}$, and $m_4^{\mathrm{c}}$ represent the third and the fourth centralized moments of DTOF curve. The zeros in the covariance matrix indicate statistically independent measurands and non-zero terms indicate a statistical dependence. We used Monte Carlo simulations to generate data (DTOFs and sensitivity factors) for a three-layered adult human head model (scalp, skull, brain). We assume that a change in chromophores concentration can occur in two layers only: scalp and brain. The matrix X represents the sensitivity factors for the two layers:

$$\mathbf{X}=\left(\begin{array}{cc}{\mathit{\text{MPP}}}_{\text{scalp}}& {\mathit{\text{MPP}}}_{\text{brain}}\\ {\mathit{\text{MTSF}}}_{\text{scalp}}& {\mathit{\text{MTSF}}}_{\text{brain}}\\ {\mathit{\text{VSF}}}_{\text{scalp}}& {\mathit{\text{VSF}}}_{\text{brain}}\end{array}\right)$$ (2)

Square roots of the diagonal elements of the following covariance matrix represent the standard deviations of the estimated absorption changes in the scalp and brain layers ($\sigma \Delta {\mu }_{\mathrm{a}}$) [27]:

$$\sigma \Delta {\mu }_{\mathrm{a}}=\sqrt{\text{diag}(\text{cov}(\Delta {\mu }_{\mathrm{a}},\Delta {\mu }_{\mathrm{a}}))}=\sqrt{\text{diag}({({\mathbf{X}}^{\mathrm{T}}{\mathbf{Z}}^{-1}\mathbf{X})}^{-1})}$$ (3)

The square root operation is carried out element-wise for the diagonal matrix.

2.2. Error propagation for the Beer-Lambert law

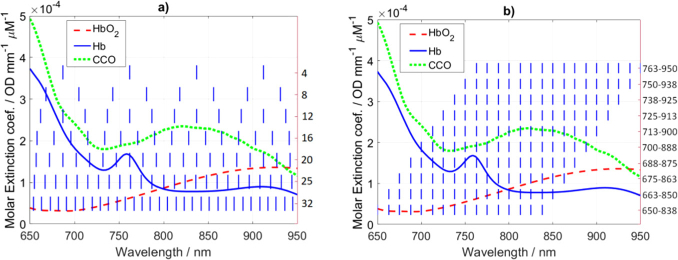
We determined the standard deviations in estimation of the chromophores’ concentrations: oxy- $(\sigma \Delta C_{\text{Hb}{\mathrm{O}}_2})$, deoxyhemoglobin ($\sigma \Delta C_{\text{Hb}})$ and cytochrome-c-oxidase ($\sigma \Delta C_{\text{CCO}}$). The implemented error propagation is similar to the method presented in [28] where authors derived the uncertainties of $\Delta C_{\text{Hb}{\mathrm{O}}_2}$ and $\Delta C_{\text{Hb}}$ for different choices of two wavelengths. The proposed method relies on the known absorption spectra of chromophores (Fig. 1), the calculated $\sigma \Delta {\mu }_{\mathrm{a}}$ in Eq. (3), and the error propagation for the Beer-Lambert law. It was previously shown that CCO occurs in high concentration predominantly in the brain and that it is reasonable to neglect changes in CCO in the scalp for fNIRS studies [6,38,39]. Therefore, in our analysis we included twthe following mannero chromophores (oxy- and deoxyhemoglobin) in the scalp and three chromophores (including CCO) in the brain. Figure 1(a) shows 4, 8, 12, 16, 20, 25 and 32 wavelengths that evenly span the spectral range from 650 to 950 nm. Figure 1(b) shows different choices of 16 consecutive wavelengths separated by 12.5 nm.

Fig. 1.

Specific extinction coefficients of oxy- (HbO₂), deoxyhemoglobin (Hb) and cytochrome-c-oxidase (CCO) [1]. The vertical blue lines show the choices of wavelengths for the analysis of the standard deviations in the estimation of changes in chromophores concentrations for different number of wavelengths (a) and 16 consecutive wavelengths separated by 12.5 nm (b).

2.3. Monte Carlo simulations

Twenty-five sets of DTOFs and sensitivity factor matrices (X) were generated using Monte Carlo simulations for wavelengths from 650 to 950 nm in steps of 12.5 nm. The Monte Carlo code was presented and explained elsewhere [37].

There were simulated $5\cdot {10}^8$ photon packets to generate each DTOF and ${10}^8$ to generate each set of sensitivity factors. The DTOFs were sampled at i_max = 128 time channels 19.5 picoseconds each. Usually, the signal to noise ratio of a DTOF is set within the limit of 1% of the DTOF maximum and the ≥ 1% region is used for the statistical moments calculation [25]. The source-detector separation was set to 3 cm and the detector radius was set to 3 mm. The symmetry of the slab-based layered model (12×12×8 cm) allows positioning many detectors around a centrally-positioned source to significantly increase number of detected photons, hence decreasing the simulations time. Therefore, the detector was modeled as a ring of inner radius of 2.85 cm and outer radius of 3.15 cm with the center positioned at the centrally-located source. The simulations were carried out in reflectance geometry.

We assumed a three-layered model consisting of: scalp (4 mm), skull (7 mm) and brain (‘semi-infinite’). The Monte Carlo simulations generate the sensitivity factors for every layer of the modeled medium [37]. We assumed the optical properties of the skull layer remain constant as in [20,40].

2.4. Spectra of absorption, reduced scattering and extinction coefficients

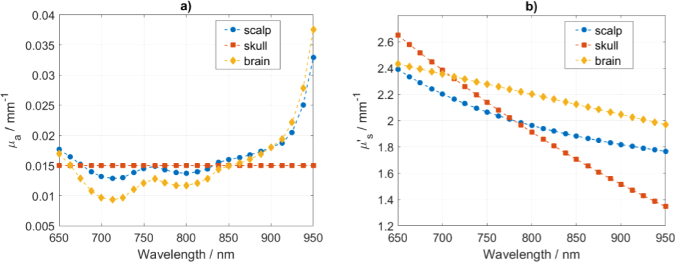
The absorption coefficients for the scalp and the brain layers were estimated assuming tissue constituents concentrations as in [33] and using their known absorption spectra. The constituents that contribute to the absorption spectra are summarized in Table 1. We added a fixed background value of 0.005 mm^-1 to the absorption of scalp making the average absorption around 0.015 mm^-1, which is closer to values reported in [41,42]. The values of absorption assumed for the brain are around 0.013 mm^-1, which is close to the values reported in [43–47]. The absorption of skull depends less on wavelength [48–50] and the reported values of optical properties from different studies cover a wide range [48–54]. Only minor ripples [48] can be observed in the absorption spectra of skull in the range up to 900 nm and it is suggested that these can be neglected when analyzing light penetration [55]. Thus, it was assumed that the absorption coefficient of skull is constant across all wavelengths. Moreover, the extinction coefficients of water and lipids are much smaller than of oxy-, deoxyhemoglobin and CCO in the NIR region [1]. The resulting absorption coefficients, shown in Fig. 2(a), are between 0.01 and 0.02 mm^-1 for wavelengths up to 913 nm and follow values as in [56–62].

Table 1. Tissue constituents assumed for the three layers head model [33].

Layer	Thickness (mm)	${\mathrm{C}}_{\text{Hb}{\mathrm{O}}_2}$ (µM)	${\mathrm{C}}_{\text{Hb}}$ (µM)	$\text{St}{\mathrm{O}}_2$ (%)	Lipid (%)	Water (%)	3 types of Cytochrome (µM)			Constant background ($\mathrm{m}{\mathrm{m}}^{-1}$)	${\mu }_{\mathrm{a}}$ ($\mathrm{m}{\mathrm{m}}^{-1}$)
							Cytochrome c oxidase	Cytochrome b	Cytochrome c		690 nm	830 nm
Scalp	4	46	19	71	13	60	0	0	0	0.005	0.014	0.015
Skull	7	-	-	-	-	-	-	-	-	0.015	0.015	0.015
Brain	87	56	24	70	11.6	80	8	2.37	1.36	0	0.011	0.014

Fig. 2.

Absorption coefficient μ_a (a) and reduced scattering coefficient μ′_s (b) for scalp, skull and brain layers.

A dominant Mie regime scattering within tissues shows a decrease in the reduced scattering coefficient with wavelength (λ) [41–43,45,46,48,50,63]. Mie scattering can be parameterized with scattering amplitude (a) and power (b) in the following manner: μ′_s = aλ^-b. Values of the reduced scattering coefficient in near-infrared (NIR) region are around 2 mm^-1 for scalp [41,48], 1.8 mm^-1 for skull [50,63] and 2.2 mm^-1 for brain [43,47,48,64]. As such, we assumed scatter values as in [33] and in Fig. 2(b). The refractive index was set 1.4 for the media and 1 for the surrounding air.

2.5. Detection system: spectral responsivity (spectral efficiency)

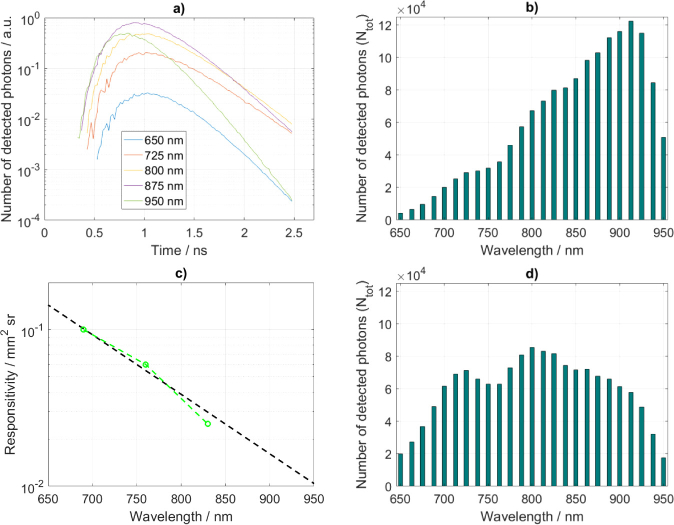
It is necessary to define number of detected photons ($N_{\text{tot}}$) for the calculation of the standard deviation ($\sigma \Delta {\mu }_{\mathrm{a}}$ in Eq. 3). To convert the simulated photon fluence rate expressed in photons per square millimeter per second into number of photons as detected by a measurement system, simulated DTOFs are scaled to set the integral across time and wavelength to 1.5 million detected photons. The simulated DTOFs and the calculated $N_{\text{tot}}$ are shown in Fig. 3(a,b,d). The increase in the number of detected photons at longer wavelengths is in agreement with other studies [65]. A real detector’s sensitivity is wavelength dependent and affects the measurements as shown in [66]. We consider the spectral responsivity based on a multialkali cathode detector, which is commonly used in TR-NIRS systems [23,66]. The responsivity characteristic was interpolated from values reported in [66] and shown in Fig. 3(c). The integrals of simulated DTOFs were scaled to match the spectral responsivity characteristic and, as previously, normalized across time and wavelength to set the total detected photons to 1.5 million (Fig. 3(d)).

Fig. 3.

(a) Examples of the DTOFs generated for the background optical properties that are shown in Fig. 2. Number of detected photons for the case when responsivity is not used (b). The responsivity of a detector based on a multialkali cathode (c) as interpolated using data (green points) reported in [66]. Number of detected photons when the detector’s spectral responsivity is considered (d).

2.6. Wavelength selection analysis

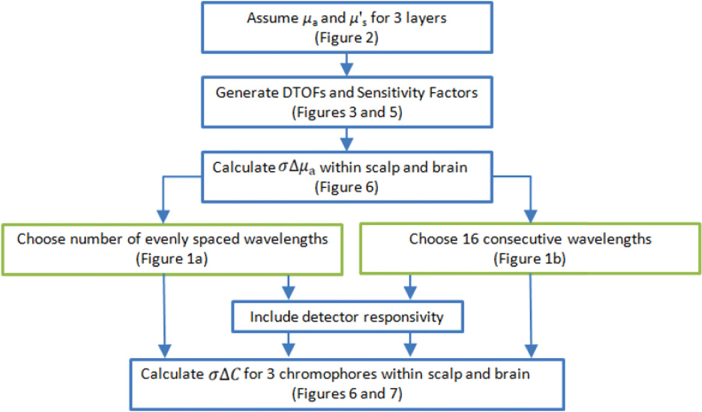
The workflow of the analysis performed in this study and the steps involved are illustrated in Fig. 4.

Fig. 4.

Workflow of the procedure for the calculation of standard deviations of the estimated changes in concentrations of chromophores $(\sigma \Delta C)$ using the error propagation for the moments method [27] and the Beer-Lambert law aiming to optimize wavelength choice.

3. Results

3.1. Sensitivity Factors and the standard deviation of changes in absorption: $\sigma \Delta {\mu }_a$

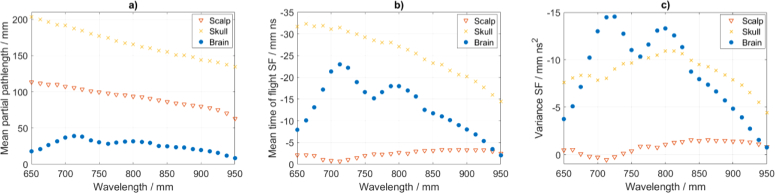
DTOFs generated with the Monte Carlo simulations are shown in Fig. 3(a). MPP is expressed in units of length and represents mean distance travelled by photons passing a layer (volume). The MPP is highest within the skull layer and reduces by about a factor of two going to the scalp layer and by a further factor of two going to the brain layer (Fig. 5(a)). On average, photons travel two times longer distance within scalp than brain. The average travel distance within brain is more than four times shorter as compared to the skull. The MTSF however is the distance travelled (MPP) weighted by the time of travel. Therefore, the maximum of MTSF is shifted to deeper layers as compared to the MPP. The MTSF is low within the scalp as the corresponding time of flight is short and increases significantly within the skull and brain (Fig. 5(b)). The VSF expresses the travelled distance (MPP) weighted by the time of travel squared, where weighting by the square of travel time pushes the maximum sensitivity even deeper. As a result, the sensitivity is further increased within the brain layer (Fig. 5(c)). Therefore, measurements of mean time of flight and variance are better suited for brain activity recovery. Furthermore, differences in the depth profiles of the MPP, MTSF and VSF support depth discrimination in parameters recovery using the moments method.

Fig. 5.

Sensitivity factors for the background optical properties as in Table 1. MPP (a), MTSF (b) and VSF (c) are shown within following layers: scalp, skull and brain.

The MPP, MTSF and VSF as calculated within the scalp, skull and brain layers are shown in Fig. 5(a-c). We find that the MPP decreases with wavelength following the decrease in the values of the reduced scattering coefficient (Fig. 2(b)). The MTSF and VSF for the brain layer reveal stronger relation with the absorption than scatter as they follow the absorption spectra shape. The MPP, MTSF and VSF for the brain layer have peak values in the range between 720 and 800 nm, which follows the regions of lowest absorption coefficient as shown in Fig. 2(a).

The DTOFs and the sensitivity factors were used to calculate the standard deviations of changes in the absorption coefficients within the two layers (scalp and brain) using the method as introduced in section 2.1. Analyses follow methodology as in Fig. 4 and the detector spectral responsivity is considered accordingly. The calculated standard deviations at each wavelength are shown in Fig. 6. The detector responsivity (Fig. 3(c)) introduces increase in standard deviations with wavelength, which strictly follows the detector performance. The standard deviation is always higher in the brain. Photons travel path through the scalp and skull layers is much longer than through the brain (Fig. 5(a)), hence DTOFs are dominated by information originating in the scalp and/or skull layers.

Fig. 6.

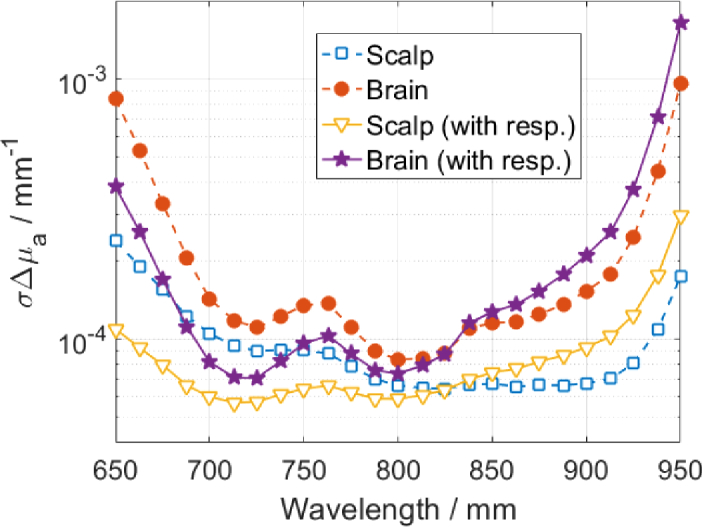
Standard deviation of changes in the absorption coefficients within two layers: scalp and brain, considering the detector responsivity (with resp.) accordingly.

3.2. Varying number of wavelengths

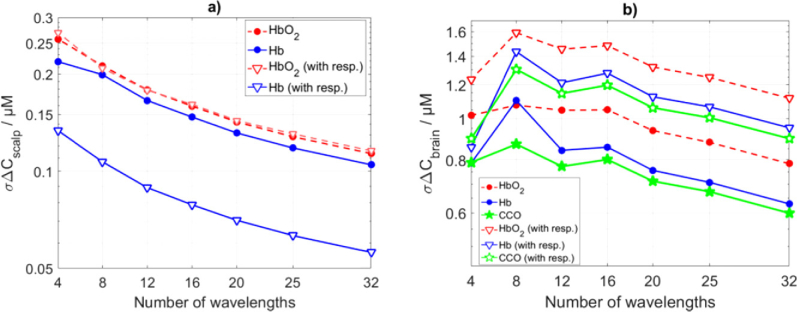
The standard deviations of the estimation of changes in concentrations $(\sigma \Delta C)$ of three chromophores in two layers were calculated using: standard deviations of changes in absorption coefficient $(\sigma \Delta {\mu }_{\mathrm{a}})$ as shown in Fig. 6, extinction coefficients as in Fig. 1 and the Beer-Lambert law. For the varying number of wavelengths analysis, we used MATLAB built-in function (spline) to interpolate $\sigma \Delta {\mu }_{\mathrm{a}}$ in Fig. 6 for missing wavelengths. Results are presented in Fig. 7. The standard deviation of the estimation of CCO in the brain layer $(\sigma \Delta C_{\text{CCO}}^{\text{brain}})$ shows peak at 8 wavelengths which follows from the high values of extinction coefficients (Fig. 1(a)) and low values of $\sigma \Delta {\mu }_{\mathrm{a}}$ (Fig. 6). Responsivity of the detector amplifies the standard deviation in all considered tissue constituents.

Fig. 7.

Standard deviations of estimation of changes in concentrations $(\sigma \Delta C)$ of chromophores within (a) scalp and (b) brain layers using varying number of wavelengths (as shown in Fig. 1(a)).

3.3. Varying range of 16 consecutive wavelengths

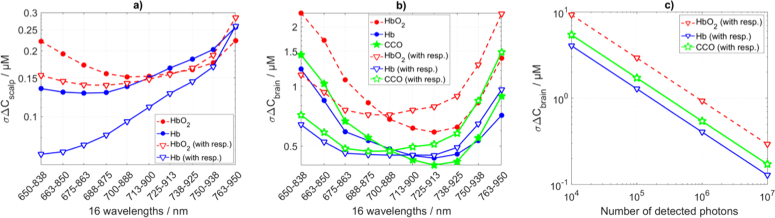
The standard deviations of the estimated changes in concentrations $(\sigma \Delta C)$ of three chromophores in two layers using different range of 16 consecutive wavelengths separated by 12.5 nm are presented in Fig. 8(a-b). Choice of wavelengths region influences the $\sigma \Delta C$ within scalp and brain layers differently following difference in $\sigma \Delta {\mu }_{\mathrm{a}}$ within the scalp and brain (Fig. 6) and presence of two and three chromophores in the scalp and brain respectively. The $\sigma \Delta C$ in the brain is always higher as photons travel shorter distances within the brain. Therefore, $\sigma \Delta C$ in the brain is more sensitive to the choice of wavelengths. We aim to find the wavelengths band that corresponds to minimal $\sigma \Delta C_{\text{CCO}}$ in the brain layer. In case the detector spectral responsivity is not included in the analysis, the minimal $\sigma \Delta C_{\text{CCO}}^{\text{brain}}$ of 0.40 µM is observed in the range from 725 to 913 nm (Fig. 8(b)). This region covers the absorption peak of CCO. When the detector responsivity is considered, the minimal $\sigma \Delta C_{\text{CCO}}^{\text{brain}}$ of 0.47 µM is observed in the range from 688 to 875 nm. Shorter wavelengths benefit more from the high detector responsivity than from the CCO absorption spectra. We repeated the analysis considering varying number of all detected photons $N_{\text{tot}}$. This way we can predict what is the detectable change of CCO concentration for a given number of collected photons. This analysis for the wavelength range of 700 to 888 nm is shown in Fig. 8(c). The maximum expected change in the concentration of CCO during functional brain activation is 4.5-5.5 µM [1]. The typical count rate for a spectral TR-NIRS system [25] is about ${10}^6$ photons per second.

Fig. 8.

Standard deviations of estimation of changes in concentrations $(\sigma \Delta C)$ of chromophores within scalp (a) and brain (b) layers using varying range of 16 consecutive wavelengths (as shown in Fig. 2(b)). The standard deviation in change of CCO concentration in the brain at a given number of collected photons (c) for the 16 wavelengths between 700 and 888 nm. ‘with resp.’ indicates analysis considering the detector spectral responsivity.

4. Discussion

The error propagation analysis for the moments method was used in [27] to study how absorption coefficient recovery within two layers is influenced by the following: varying combination of statistical moments used, combinations of source-detector pairs, thickness of the top layer and source-detector distance. In this study we introduce the error propagation method to calculate the standard deviations in recovery of changes in concentrations of tissue constituents ($\sigma \Delta C$) within head layers. We generated spectral TR-NIRS data and applied the error propagation method to optimize the choice of 16 consecutive wavelengths for the developed TR-NIRS system [25]. The optimization criteria was to minimize the uncertainty of recovery CCO concentration ($\sigma \Delta C_{\text{CCO}}$) within the brain layer. We observed comparable $\sigma \Delta C$ for the three chromophores (HbO₂, Hb, CCO) analyzed. However, monitoring of the CCO is challenging as its low concentration requires high signal to noise ratio in raw data to detect changes in its oxidation state [1]. A recent study shows that monitoring CCO is possible with TR-NIRS [67]. Spectral responsivities vary between systems [34,67,68] and should be included in analyses. Here, we show system-specific methodology of wavelength selection as based on spectrally-resolved TR-NIRS shown in [25]. When the system responsivity was not used, the minimal $\sigma \Delta C_{\text{CCO}}$ of 0.40 µM in the brain was observed for 16 consecutive wavelengths from 725 to 913 nm and separated by 12.5 nm. This region corresponds to the broad absorption peak of CCO in the NIR region. This choice of wavelengths corresponds to systems with flat responsivity spectra, e.g. [66,67]. Inclusion of detection responsivity spectrum shifts the optimal region towards shorter wavelengths from 688 to 875 nm (minimal $\sigma \Delta C_{\text{CCO}}$ of 0.47 µM). This shift follows the detector’s spectral performance that drops with wavelength. It was recently presented that the optimal number of 3, 4, 5 and 8 wavelengths are positioned almost evenly around the peak of the absorption spectra of CCO [34]. Similarly, a broadband NIRS system presented in [69] aiming to monitor changes in CCO was set to utilize the wavelengths range between 770 and 906 nm covering the absorption peak of CCO. Almost identical range (780 to 900 nm) was used in a previous broadband NIRS system for monitoring CCO changes as presented in [14]. The recently presented TR-NIRS system used wavelengths between 780 and 870 nm when demonstrating the system’s ability to estimate changes in oxygenation and oxidate state of CCO [67]. These wavelengths correspond to the region where the performance of our detector is worse and the results of this study suggest that these wavelengths are not optimal for our system.

When changes in concentrations of multiple chromophores are of interest, a cross-talk between recovered chromophores concentrations can be expected [70]. As shown in [30,70], considering the CCO might introduce a noticeable cross-talk. However, as shown in [70] analyzing higher moments of the DTOF (e.g. the time of flight) reduces the cross-talk significantly.

The moments method [19] assumes that the probability of photons being absorbed within a layer is small, i.e. the layer absorption coefficient weighted by the mean pathlength is much smaller than 1: $\mathit{\text{MPP}}\cdot \Delta {\mu }_{\mathrm{a}}\ll 1$. The MPP is derived from diffusion theory with the perturbation approach that linearize the light propagation inverse problem around some base μ_a [71] assuming the Δμ_a→0. As such, if the Δμ_a is expected to be high as related to the base value, an iterative approach can be utilized where the sensitivity factors are iteratively recalculated using previous step recovery as the new base. This approach follows other optical tomography recovery methods [72,73]. It is the suggested next research step.

5. Conclusions

We proposed a method based on the error propagation allowing to calculate uncertainty of estimation of changes in concentrations of chromophores in two layers for a multi-wavelength time-resolved near-infrared spectroscopy system.

The minimal standard deviation of estimated changes in concentration of CCO within the brain layer ($\sigma \Delta C_{\text{CCO}}^{\text{brain}}$ = 0.40 µM) covered by scalp and skull was found for a set of wavelengths that cover the absorption peak of CCO: 725 to 913 nm.

For a realistic responsivitity spectrum of a system the found optimal choice of wavelengths was shifted to direction of better performance: $\sigma \Delta C_{\text{CCO}}^{\text{brain}}$ = 0.47 µM at 688 to 875 nm. The results suggest that the optimal choice of wavelengths is dependent on the specifications of a system.

Funding

Horizon 2020 Framework Programme10.13039/100010661 (675332 (BitMap)); Wellcome Trust10.13039/100010269 (104580/Z/14/Z).

Disclosures

The authors declare that there are no conflicts of interest related to this article.