Abstract
The lateral superior olive (LSO) is one of the most peripheral nuclei in the auditory pathway to receive inputs from both ears, and its cells are sensitive to interaural level disparities (ILDs) when stimulated by sounds presented over earphones. It has, accordingly, long been hypothesized that the functional role of the LSO is to encode a correlate of ILDs, one of the acoustical cues to the spatial location of sound. In the companion paper, we used the virtual space (VS) technique to present over earphones stimuli containing all the acoustical cues to the location of broadband stimuli and measured the spatial receptive fields (SRFs) in azimuth of single LSO cells. The shapes of the SRFs were generally consistent with the ILD sensitivity of the cells (Tollin and Yin, 2002), but because the only variable under our control was azimuth, and not ILD directly, the precise cues responsible for the SRFs could not be unambiguously determined. Here, we test more directly the hypothesis that ILDs are the primary determinants of the SRFs in azimuth of LSO cells by digitally manipulating the head-related transfer functions used to create the VS stimuli by independently varying (or holding constant) in azimuth each of the primary localization cues in isolation while holding constant (or varying) the others. Our results support the classical view of the LSO that the form of the SRFs of the cells in azimuth is determined primarily by the ILDs in a small band of frequencies around the characteristic frequencies of the cells.
Keywords: lateral superior olive, head-related transfer function, sound localization, interaural level difference, interaural time difference, cat
Perception of the location of sounds along the horizontal plane depends on two binaural acoustical cues: interaural time differences (ITDs) and interaural level differences (ILDs). Cells of the lateral superior olive (LSO) are suited to encode ILDs because they receive excitatory input from the ipsilateral cochlear nucleus (CN) (Tolbert et al., 1982; Cant and Casseday 1986;Saint Marie et al., 1989; Glendenning et al., 1991; Smith et al., 1993) and inhibitory input from the contralateral CN via the medial nucleus of the trapezoid body (Elverland 1978; Moore and Caspary, 1983;Glendenning et al., 1985; Spangler et al., 1985; Bledsoe et al., 1990;Smith et al., 1998; Henkel and Gabriele, 1999). The contralateral-inhibitory (I) and ipsilateral-excitatory (E) inputs confer the ability to encode information about differences in sound level at the ears, or ILDs; we call this type of binaural interaction “IE”.
It is commonly hypothesized that the functional role of the LSO is to encode ILDs in free-field sounds because the LSO is one of the earliest sites of convergence of inputs from the two ears and its cells are sensitive to ILDs of stimuli when presented over earphones (Galambos et al., 1959; Boudreau and Tsuchitani, 1968; Caird and Klinke, 1983; Sanes and Rubel, 1988; Joris and Yin, 1995). Recently, using the virtual space (VS) technique we demonstrated that LSO cells are indeed sensitive to variations in source azimuth consistent with IE binaural interaction as determined dichotically (Tollin and Yin, 2002). As expected, responses were greatest for ipsilateral azimuths, where sound levels at the excitatory ear were large, but inhibited for contralateral azimuths where levels at the inhibitory ear were large. When we presented the VS stimuli to the ipsilateral ear in isolation, we found that, relative to these ipsi-ear only responses, the responses to the binaural stimuli were inhibited, particularly for contralateral azimuths confirming that contralateral inhibition led to these responses. Given these and other observations, we concluded that the spatial receptive fields (SRFs) of the cells in azimuth were determined by binaural cues, and most likely by ILDs given the IE binaural interaction of the cells.
However, LSO cells are sensitive to other cues to location, such as ITDs of both the low-frequency envelopes of high-frequency sounds and the onsets of transient sounds (Caird and Klinke, 1983; Joris and Yin, 1995; Park et al., 1996; Batra et al., 1997) and to variations in sound level at the ipsilateral ear (Tsuchitani and Boudreau, 1967). So when presented with the full complement of cues as occurs naturally for free-field sounds, what cues does the LSO actually encode? Here, we test the hypothesis that the SRFs in azimuth of LSO cells are governed predominantly by ILDs. We used the VS technique to not only vary source azimuth but we also manipulated the VS stimuli so that we could independently vary (or hold constant) in azimuth each of the primary cues in isolation while holding constant (or varying) the others, allowing us to identify the determinants of the SRFs of each LSO cell.
MATERIALS AND METHODS
General. Most of the general methods are described in a previous paper (Tollin and Yin, 2002) and will only briefly be outlined here. Adult cats with clean external ears were initially anesthetized with ketamine hydrochloride (20 mg/kg) along with acepromazine (0.1 mg/kg). Atropine sulfate (0.05 mg/kg) was also given to reduce mucous secretions, and a tracheal cannula was inserted. Supplemental doses of sodium pentobarbital (3–5 mg/kg) were administered intravenously as needed to maintain areflexia. The cat's temperature was continuously monitored and maintained with a heating pad at 37°C. Both pinnae were cut transversely, removed, and tight-fitting hollow earpieces were fitted snugly into the external auditory meati. Polyethylene tubing (30 cm, 0.9 mm inner diameter) was glued into a small hole made in each bulla to maintain normal middle ear pressure.
The LSO was approached ventrally by drilling small holes into the basioccipital bone. Parylene-coated tungsten microelectrodes (1–2 MΩ; Microprobe, Clarksburg, MD) were advanced ventromedially to dorsolaterally at an angle of 26–30° into the brainstem by a hydraulic microdrive affixed to a micromanipulator that could be remotely advanced outside the double-walled sound-attenuating recording chamber. Electrical activity was amplified and filtered (300–3000 Hz). Unit responses were discriminated with a BAK Electronics Inc. (Germantown, MD) amplitude-time window discriminator, and spike times were stored at a precision of 1 μsec. After the excitatory ear was determined, the characteristic frequency (CF), spontaneous activity, and threshold were measured using an automated threshold tracking routine. Poststimulus time, interval, and period histograms, and rate and synchronization measures were then obtained for CF tones at different SPLs in 5–10 dB steps and displayed on-line.
Stimuli: general. All stimuli were generated digitally at 16-bit resolution and converted to analog at a rate of 100 kHz. Overall stimulus level was controlled using custom-built programmable attenuators. The conditioned output of the digital-to-analog converter was sent to an acoustic assembly (one for each ear) comprising an electrodynamic speaker (Realistic 40–1377), a calibrated probe-tube microphone (Bruel and Kjaer ½ in), and a hollow earpiece that was fit snugly into the cut end of the auditory meatus and sealed with Audilin. The hollow earpiece accommodated the small probe-tube microphone by which the sound delivery system to each ear was calibrated for tones between 50 Hz and 40 kHz in 50 Hz steps. The calibration data were used to compute digital filters that equalized the responses of the acoustical system and typically yielded flat frequency responses within ±2 dB for frequencies <25 kHz.
Tone bursts of varying frequency were used as search stimuli with the SPL of the tone to the ipsilateral ear being 5–10 dB higher than the tone to the contralateral ear so that the IE cells of the LSO would not be missed. Once a single unit was isolated, its CF and threshold level were estimated. Rate level functions were measured by presenting 200 repetitions of a 50 msec tone pip at CF (3.9 msec rise–fall times) every 100 msec from which the resulting peristimulus time histograms were examined. A tonic response with chopping, or multiple modes unrelated to the frequency of the stimulus, is characteristic of most LSO cells (Tsuchitani, 1982), and the incidence of chopping was measured by computing the coefficient of variation over the first 25 msec of the response (Young et al., 1988). To determine the presence and nature of any binaural interaction, a CF tone or broadband noise (300 msec duration presented every 500 msec with a rise–fall time of 4 msec) was presented to the ipsilateral ear at 10–20 dB above the threshold level, whereas the level of a CF tone or noise presented to the contralateral ear was varied. This procedure reveals whether ipsilaterally evoked neural responses can be inhibited by contralateral stimulation, another hallmark of LSO cells.
Stimuli: virtual space. As in our previous paper (Tollin and Yin, 2002), sound source azimuth was manipulated here using the VS technique. The method of synthesizing the VS stimuli was the same as that used in our companion paper (Delgutte et al., 1999; Tollin and Yin, 2002). A single token of broadband, Gaussian noise of 200 msec in duration (4 msec rise–fall times) was used as the stimulus for all experiments. Before being delivered to one or both ears, the noise token was equalized digitally by the calibration filters appropriate for each ear and preprocessed through digital filters constructed from the head-related transfer function (HRTF) measurements made in one cat from the recordings of Musicant et al. (1990). HRTFs capture the frequency- and direction-dependent filtering by the head and pinna that a broadband sound undergoes as it propagates from the source to the eardrum; a left- and right-ear pair of HRTFs for a given spatial position embodies all the acoustical cues to location available from that particular position (Wightman and Kistler, 1989a,b). Positive azimuths correspond to azimuths contralateral to the recording site. The VS stimuli were also bandpass filtered between 2 and 30 kHz because this is the frequency range where the HRTF recordings of Musicant et al. (1990) were most reliable.
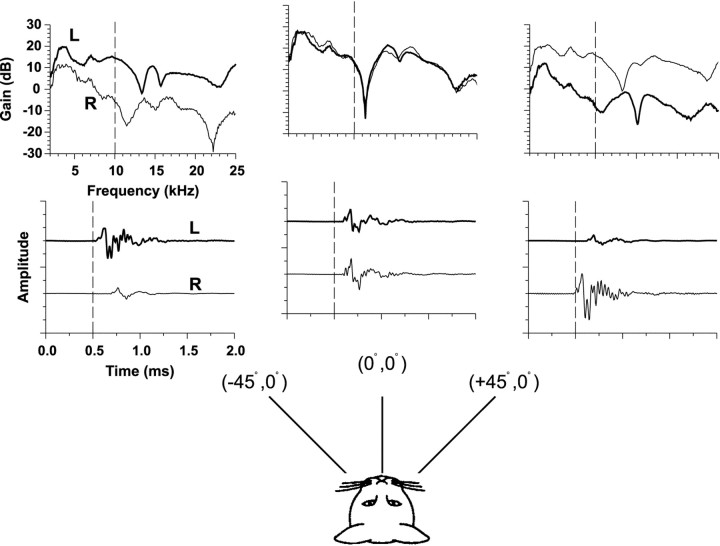
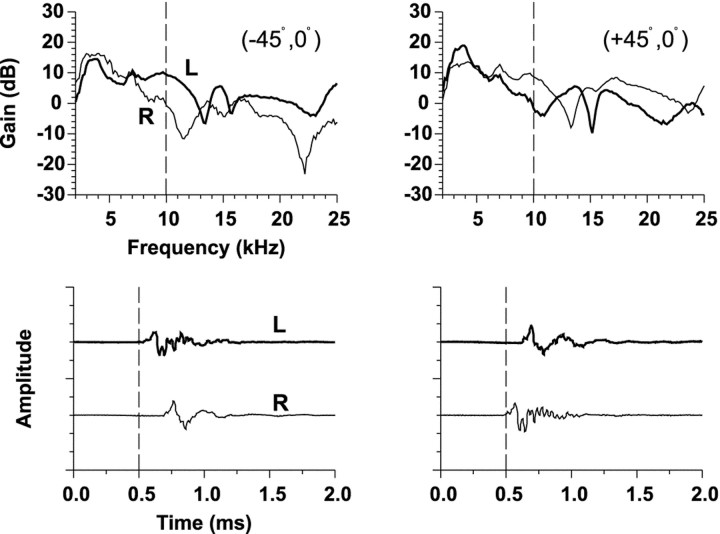
Figure 1 shows for one cat the measurements of HRTFs from three spatial locations on the horizontal plane by Musicant et al. (1990). In Figure 1, each bottom graph shows the impulse response at the left and right ears. The dashed vertical line has been plotted to assist in showing the relative differences in onset times of the clicks arriving at the two ears. The top panels show the gain of the Fourier transform of the impulse responses. The gain represents the frequency-dependent increase or decrease in signal amplitude caused by the cat's head and pinnae relative to the original amplitude of the signal recorded in the absence of the cat.
Fig. 1.
HRTFs (top) and associated time impulse responses (bottom) at the left (L) and right (R) ears of a cat to broadband clicks are shown for three positions on the horizontal plane. The HRTFs are plotted as gain relative to the response to the same click in the absence of the cat versus frequency. ITDs are captured in the relative differences in onset times of the time waveforms and ILDs by the relative differences in gain at the two ears as a function of frequency. The monaural spectral cues can be seen by the changes in spectral shape as a function of azimuth. These HRTF measurements are from one cat from the experiments of Musicant et al. (1990).
The three main acoustical cues to sound location can be easily seen in the HRTF measurements (Fig. 1). The relative difference in onset times of the impulse responses at the two ears indicates the ITD, whereas the relative differences in amplitude of the signals at the two ears indicates the ILD. Note that the sign and magnitude of the ILD cue varies both as a function of azimuth and frequency. The latter component can be seen in the top panels by the difference in the gains of the impulse responses across different frequencies. Both ITD and ILD generally covary as a function of sound source azimuth as can be seen by comparing the binaural cues at each of the three azimuthal locations in the figure; both cues are minimal near the midline and both increase in magnitude for more lateral azimuths. Monaural spectral cues are also apparent by the change in the shape of the spectrum with changes in azimuth; for example, the deep spectral “notches” at the midline azimuth at 11.5 kHz are thought to be important cues for cats localizing sounds particularly in elevation, but azimuth as well (Rice et al., 1992; Huang and May, 1996).
Localization cue manipulations. As shown in Figure 1, as sound source azimuth is changed, the three main localization cues also change and the extent to which the cells in the LSO are sensitive to each cue likely determines how the response of the cell will be modulated with azimuth. But given the full complement of cues, what cue or cues does the LSO really encode? That is, which cues determine the spatial receptive fields of LSO cells in azimuth? To address this question, the HRTFs were digitally manipulated by independently varying (or holding constant) in azimuth each of the three localization cues in isolation while holding constant (or varying) the others. The SRFs measured in the “normal” binaural condition in which all localization cues were allowed to vary naturally with changes in azimuth provides a baseline comparison for the SRFs measured in each of the cue manipulation conditions. When a particular cue was held constant, we fixed the value of the cue for all azimuths at the value occurring at the midline position (0°, 0°). Thus, when ITD or ILD was held constant, they were set to 0 μsec or 0 dB.
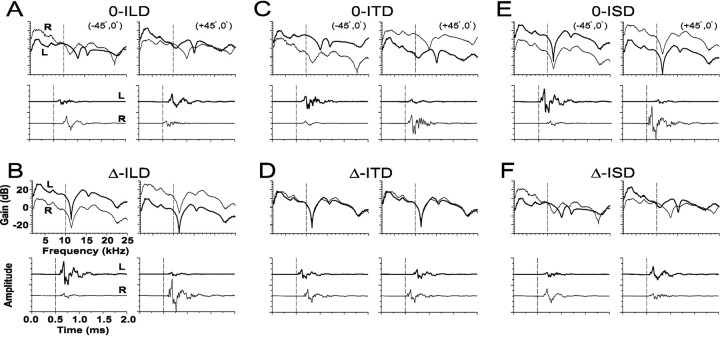
The six panels of Figure 2 demonstrate six of the seven different ways in which the three main sound localization cues were manipulated as a function of azimuth. In the seventh condition, the VS stimuli were presented to the ipsilateral excitatory ear only; we call this the ipsi-only condition. Each of the six panels shows the appropriately manipulated versions of the HRTFs for the left and right ears at two different azimuths, (−45°, 0°) and (+45°, 0°), with the gain on top and the corresponding time impulse responses on the bottom.
Fig. 2.
Examples of the six manipulations of the HRTFs used to independently vary (or hold constant) in azimuth each of the three primary localization cues in isolation while holding constant (or varying) the others. Each of the six panels shows the gains (top) and time waveforms (bottom) at two different azimuths (±45°). For the conditions in which the ITD, ILD, and spectral cues were held constant, they were set to the values corresponding to those at (0°, 0°). For the conditions in which ILD was manipulated, the ILD was calculated through a 1/3-octave Gaussian bandpass filter centered on the CF of the cell under study. A CF of 10 kHz was assumed for illustrative purposes and is indicated by adashed vertical line in each HRTF plot.A, 0-ILD: the amplitudes of the signals at the two ears were adjusted until the ILD was 0 dB for all azimuths, but the ITD and spectral cues varied naturally with azimuth. B, Δ-ILD: the spectra and ITD were held fixed, but the amplitudes of the time waveforms at each ear were adjusted so that the ILD as a function of azimuth was the same as in the natural condition as in Figure 1.C, 0-ITD: the relative onset times of the stimuli presented to the two ears were adjusted so that at each azimuth the ITD was 0 μsec, but the ILD and spectral cues varied naturally.D, Δ-ITD: ILD and spectral cues were held fixed, but onsets of the time waveforms were adjusted so that ITD varied naturally with azimuth. E, 0-ISD: spectral cues were held fixed, but the ILD and ITD cues varied naturally with azimuth.F, Δ-ISD: spectral cues varied naturally with azimuth, whereas ILD and ITD were held fixed.
Manipulations of ILD. Figure 2, A andB, illustrates the two ways that the ILD cues were manipulated. First, for the 0-ILD condition, the amplitudes of the left- and right-ear HRTFs were adjusted so that at each azimuth, the ILD was 0 dB, as computed through a 1/3-octave Gaussian bandpass filter centered on the CF of the cell under study, which for all examples in Figure 2 we chose to be 10 kHz for illustrative purposes (dotted line on gain plots). In all cases, the amplitude of the signal to the ear with the larger signal was reduced, whereas the amplitude of the signal to the other ear was increased by the same amount until an ILD of 0 dB at 10 kHz was achieved for each azimuthal location, which can be seen by inspecting the gains of the HRTFs in Figure 2A. This contrasts with the “natural” ILD present at 10 kHz which can be seen in Figure 1. Note that although ILD around CF is set to 0 dB at all azimuths in the 0-ILD condition, all other aspects of the signals to the two ears as a function of azimuth were not changed; that is, ITD and the monaural spectral cues still changed naturally, as can be seen by comparing the cues shown in Figure 2A to those in Figure 1. In essence, in the 0-ILD condition, we ensure that the ILD that the unit under study “sees” through its frequency selectivity is a constant 0 dB for all azimuths. But even in the 0-ILD condition, there are still large ILDs occurring over frequency regions other than at CF.
In the Δ-ILD condition, ILD was varied naturally with azimuth, whereas the other two cues, ITD and spectra, were held fixed (Fig.2B). The ITD was held constant at 0 μsec by delaying or advancing the impulse responses appropriately (see next section on manipulations of ITDs), and the spectral cues were held constant at those for the location (0°, 0°). The natural ILD was computed for each azimuth as seen through a 1/3-octave filter centered on the CF of the unit under study (again 10 kHz in the example shown in Fig. 2B) for the unmanipulated normal set of HRTFs. The amplitudes of the impulse responses for the left and right ears were appropriately increased and decreased at each azimuth to achieve the natural ILD as seen through the bandpass filter. It is important to point out that our rationale for using a 1/3-octave bandwidth for our filter was to expedite the experiments. We believe that this bandwidth was sufficient to encompass the frequency tuning passbands of virtually all LSO units studied, ensuring that the manipulated cues were present across the bandwidths of the cells. The Q10 of the 1/3-octave Gaussian filter of the form used was equal to ∼2.4, which yields a substantially larger 10 dB bandwidth at any given frequency than that derived from the frequency tuning curves of the units. The mean Q10 of the units was 4.69 (SD, 2.15).
Manipulations of ITD. Figure 2, C andD, illustrates the two ways in which ITD was manipulated. For the 0-ITD case, the HRTFs were manipulated by delaying the leading and advancing the lagging HRTFs in time for each location until the delay corresponding to the maximum in the cross-correlation function between the left- and right-ear HRTFs equaled 0 μsec. Because a pure time delay does not alter the power spectrum of a shifted signal, the time shifting procedure affects neither the monaural spectral nor the ILD cues. ITD was also varied naturally with azimuth in the Δ-ITD condition by taking the HRTFs for the (0°, 0°) position and introducing the normal ITD appropriate for each azimuth, as determined from the unmanipulated HRTFs, by appropriate time delaying or advancing the impulse responses. ILD and spectral cues for the left- and right-ear were held constant at those for the location (0°, 0°) as azimuth was varied.
Manipulations of monaural spectral cues. Finally, Figure 2,E and F, illustrate the ways in which the monaural spectral cues were manipulated. For the 0-ISD (interaural spectral difference) case, spectral cues were held constant by restricting them to those from the (0°, 0°) position. However, ITD and ILD, as computed above, were allowed to vary naturally with changes in azimuth. That is at each azimuth, the value of the ITD and ILD was the same as that in the unmanipulated HRTFs with the ILD computed from the unmanipulated HRTFs as seen through the bandpass filter centered on 10 kHz. For the Δ-ISD condition, the spectral cues at each ear varied naturally with azimuth, but ITD and ILD were held constant at 0 μsec and 0 dB, respectively, as outlined above.
Data analysis methods. If, for example, a single localization cue were to completely determine the SRF of a LSO cell, then the SRF measured under the condition where only that cue is allowed to vary with azimuth should be virtually identical to the normal binaural condition in which all the cues vary naturally with azimuth. Moreover, when that cue is held constant, whereas the remaining two cues vary, not only should there be a large difference between the normal SRF and the SRF measured with the manipulated cues, but the response of the cell should also be relatively constant as azimuth is varied. Evidence of this sort would strongly indicate that the particular cue contributed most to the formation of the SRF of LSO cells under natural free-field conditions in which all cues are varied naturally. Any departures from this hypothesized result would indicate that more than one localization cue played a role in establishing the SRF of the cell.
As a measure of the difference between the normal SRF and the SRFs measured for each of the manipulations shown in Figure 2, we computed for each cell tested the square root of the mean of the squared difference between the discharge rate of the normal SRF and each of the manipulated SRFs across all azimuths. To compare the SRFs of different cells whose maximum discharge rates differed, we normalized the root mean square (RMS) difference error by the mean discharge rate computed across all azimuths for the normal SRF. Consequently, RMS errors larger than the mean rate of the normal SRFs will yield values >1.0, whereas errors smaller than the mean rate will yield values <1.0. The normalization procedure ensures that the RMS error is not inflated by simply having a normal SRF with high discharge rates. That is, all else being equal, the normalized RMS difference error metric yields the same value independent of the overall discharge rate of the cell.
Response consistency. Because we chose the point at 0° azimuth as the reference for all of our manipulations in localization cues, then the stimuli for all of the different cue manipulations are identical at that point. Therefore, the responses of the cell at that point over the different cue manipulations can be used as a measure of its response consistency. This is a potentially important consideration because the time required to do all of the required manipulations was ∼1 hr. Any nonstationarity in the responses over this time period would invalidate our conclusions. Inspection of the responses in Figures 3, 4, 6, and 8 reveals the consistency of the responses of the cells.
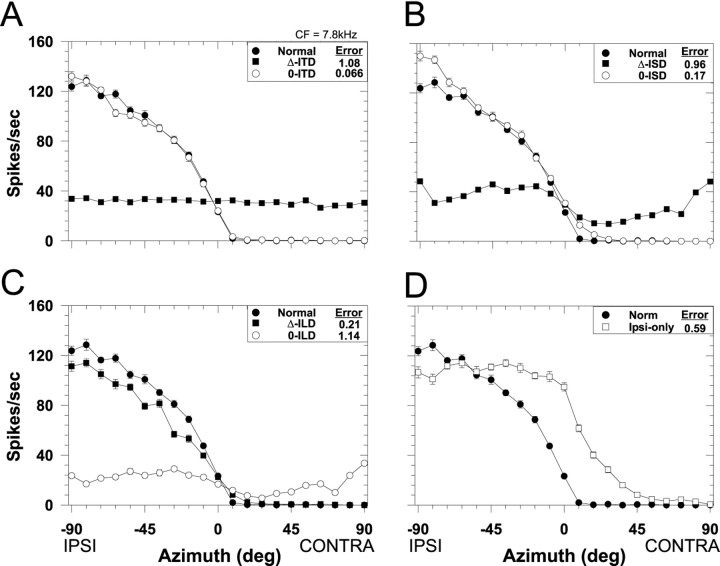
Fig. 3.
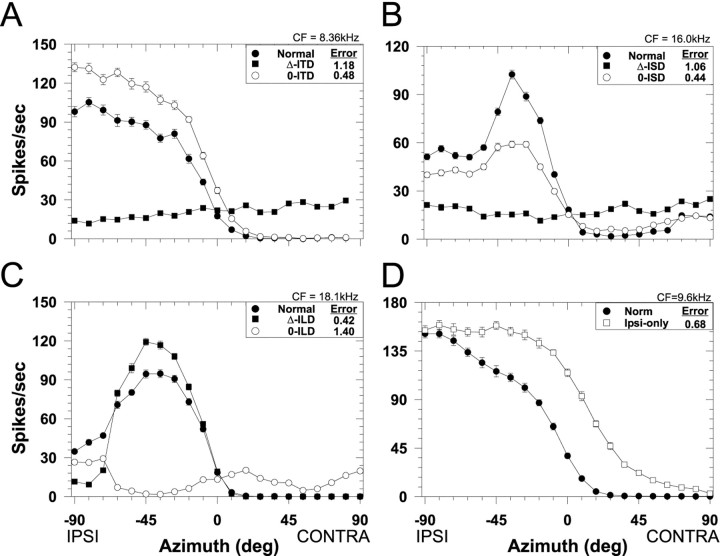
Spatial receptive fields in azimuth for one LSO cell (CF, 7.8 kHz) for both the normal stimulus condition in which all localization cues varied naturally with azimuth (filled circles) and for each of the seven cue manipulation conditions. Each data point plots the mean discharge rate of the cell averaged over the 200 msec duration of the noise stimuli and 20 presentations. Negative azimuths correspond to sounds in the ipsilateral field. Error bars plot ± SEM and when not present, the SEM is smaller than the height of the symbol. The RMS difference error (see Materials and Methods) for each cue manipulation is shown in the caption.A, ITD cue manipulations. B, Spectral cue (ISD) manipulations. C, ILD cue manipulations.D, Monaural ipsilateral-ear only spatial receptive field.
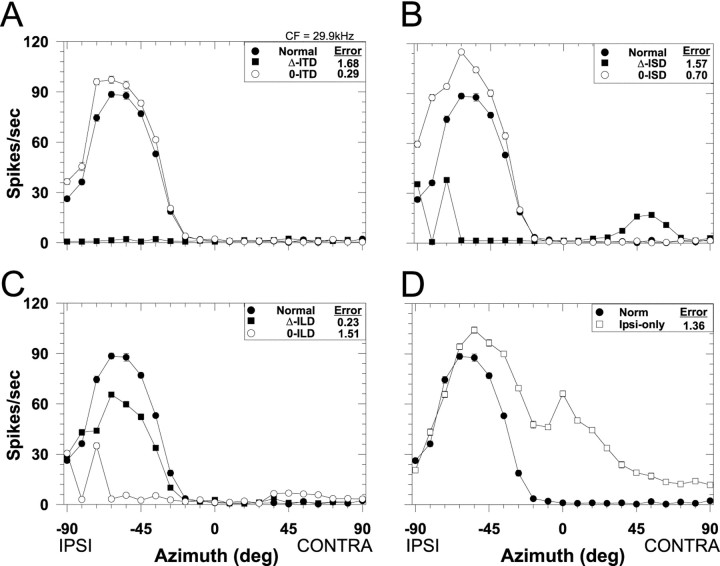
Fig. 4.
Spatial receptive fields in azimuth for another LSO cell (CF, 29.9 kHz). Same format as Figure 3.
Fig. 6.
SRFs in azimuth for the normal condition and each of the cue manipulation conditions. Same format as Figure 3. Each panel plots the SRFs from a different cell whose CF is indicated at the top right of each figure. These examples were chosen because their RMS-difference errors were near the median error across the population of cells for which the particular cue manipulation condition was performed. A, ITD cue manipulations. B,Spectral cue (ISD) manipulations. C, ILD cue manipulations. D, Monaural ipsilateral-ear only SRF.
Fig. 8.
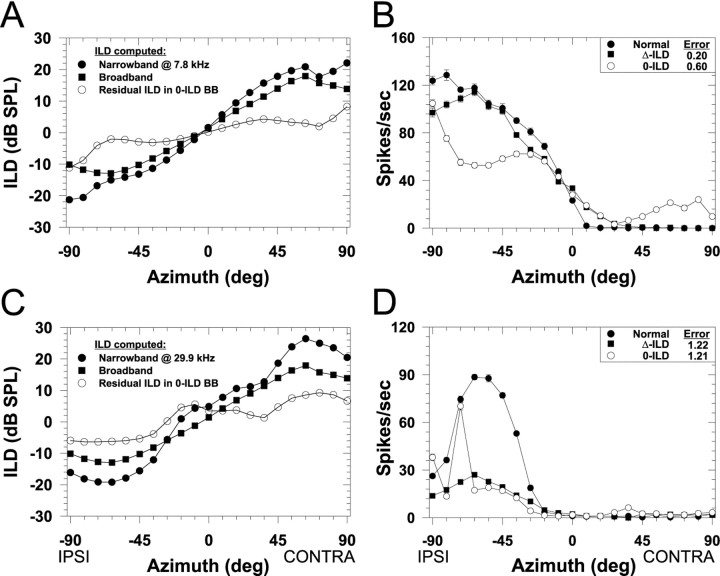
ILDs as a function of azimuth computed under three different conditions and associated spatial receptive fields for two LSO cells. In A and C, the filled circles indicate the ILD as seen through a 1/3-octave Gaussian narrowband filter centered on the CFs of the cells whose spatial receptive fields are shown in Figures 3 (CF, 7.8 kHz) and 4 (CF, 29.9 kHz), respectively. Negative ILDs indicate that sounds at the ipsilateral ear exceed the level at the contralateral ear. Thefilled squares show the broadband ILD computed across the entire spectrum and is thus the same in both A andC. The open circles show the “residual” ILD as a function of azimuth through the 1/3-octave filter at CF in the broadband 0-ILD condition. Note that although the broadband ILD is 0 dB at all azimuths (data not shown), there are nonzero ILDs occurring in narrow bands of frequencies around these and other CFs. B,D, Spatial receptive fields in azimuth for the normal condition and the broadband ILD cue manipulation conditions for the cells shown in Figures 3 and 4. Same format as in Figure 3.
RESULTS
Sufficient cue manipulation data were obtained from 24 of the 28 high-CF (>3 kHz) single units from our companion study (Tollin and Yin, 2002). All units exhibited physiological signatures consistent with previous recordings from LSO, i.e., sensitivity to ILDs of pure tones and IE binaural interaction (Boudreau and Tsuchitani, 1968; Joris and Yin, 1995).
Normal binaural spatial receptive fields in azimuth
The baseline condition in these experiments is the SRF obtained under the natural condition where all binaural and monaural cues were present in the VS stimulus. This normal SRF establishes the spatial location sensitivity of each LSO cell to natural variations of all localization cues brought about by changes in sound source azimuth; the normal SRF approximates that which would be measured under traditional free-field stimulation. We have previously shown that the normal SRFs of LSO cells have characteristics consonant with their IE binaural nature (Tollin and Yin, 2002). That is, the SRFs are generally sigmoidal in shape with discharge rate being greatest for sound sources in the ipsilateral field where the sound level at the excitatory ipsilateral ear exceeds the level at the contralateral-inhibitory ear, a region of sharply declining rate near the midline, and an inhibition of the discharge rate in the contralateral field where the level at the inhibitory contralateral ear exceeds the level at the ipsilateral ear.
Because the binaural and monaural cues to sound location covary with changes in the spatial location of the source and previous studies have shown that LSO cells can be sensitive to each of these localization cues when presented in isolation, it would be nearly impossible to determine which cue (or cues) contributed to the spatial selectivity based only on the response of the cells when stimulated binaurally by free-field sounds (Semple et al., 1983). This is because in traditional free-field experiments the only variable under experimental control is the location of the source and the localization cues for any one location are determined jointly by the direction-dependent acoustical effects of the head and pinnae, the spatial location of the sound source and the spectral characteristics of the sound itself.
Effects of localization cue manipulations on the spatial receptive fields
The four panels of Figure 3 show for one LSO cell (CF, 7.8 kHz) examples of the effects of manipulating each of the localization cues on the SRF. Each figure plots the normal SRF for this cell along with the SRFs measured with the two types of manipulations for each of the three localization cues. To quantify the effect of the various cue manipulations on the SRFs, we used the normalized RMS error of the difference (as shown in each figure legend) between the normal and the manipulated-cue SRF. Small errors indicate a close correspondence between the two SRFs, suggesting that the cues being varied naturally contribute greatly to the normal SRFs.
Figure 3A shows the effect on the spatial sensitivity of this cell of manipulating the ITD cue: the Δ-ITD and the 0-ITD conditions. When ITD was varied naturally with changes in azimuth (Δ-ITD), the response of the cell remained essentially constant and unaffected with changes in azimuth, suggesting that the SRF of this cell was not determined by ITDs. Relative to the normal SRFs, the large differences in discharge rate at most azimuths resulted in a large RMS error. Confirming this, the SRF measured in the 0-ITD condition where ITD was held fixed at 0 μsec for all azimuths was nearly identical to the normal SRF both in shape and magnitude and resulted in a small RMS error. Hence, nulling out the ITD cue by holding it constant in the 0-ITD condition had only a minor effect on the SRF, indicating that one or both of the other two cues that were varying naturally with azimuth contributed greatly to the SRF measured under the normal conditions.
Figure 3B shows for the same cell the effects of manipulating the monaural spectral cues: the Δ-ISD and the 0-ISD conditions. When the monaural spectral cues varied naturally with azimuth (Δ-ISD), whereas the ITD and ILD cues were held fixed at 0 μsec and 0 dB, respectively, there was only minor modulation of the response as a function of azimuth, suggesting that for this cell the monaural spectral cues had little influence on the SRF. Confirming this observation, when the spectral cues were held fixed (0-ISD), but ITD and ILD varied naturally with azimuth, the resulting SRF closely approximated the normal SRF. That is, nulling out the monaural spectral cue had only a small effect on the shape of the SRF.
Figure 3C shows the effects of manipulating ILD: the Δ-ILD and the 0-ILD conditions. Note that, unlike the SRFs measured in the other “Δ-cue” conditions (Fig. 3A,B) where there was no modulation of the response with changes in azimuth, in the Δ-ILD condition the responses were greatly modulated by natural changes in only ILD and the resulting SRF was nearly identical to the normal SRF. The close correspondence between the normal and the Δ-ILD condition yielded a small RMS error, suggesting that for this cell the ILD cues played a large role in determining the SRF. The SRF measured in the 0-ILD condition confirms this hypothesis: holding ILD constant at 0 dB but varying ITD and spectral cues naturally with azimuth had a large detrimental effect on the SRF with effectively no modulation of the response with azimuth. That is, when ILD did not vary with azimuth, the response of the cell did not vary either.
Finally, Figure 3D shows the effects of stimulating just the ipsilateral excitatory ear/the ipsi-only condition. These data indicate that, at the sound levels used in these experiments, this LSO cell retains at least some sensitivity to azimuth when stimulated monaurally.
In our previous study of the SRFs in azimuth of LSO cells, we found that cells with CFs of less than ∼10 kHz tended to have more sigmoidally shaped SRFs, whereas those cells with CFs >10 kHz tended to have more “peaky” and complex-shaped SRFs. Figure4A–D shows the effects on the spatial sensitivity of each of the localization cue manipulations for a different cell with a higher CF (29.9 kHz). Although the shapes of the normal SRFs differ for the cells shown in Figures 3 and 4, the results obtained with the cue manipulations for both cells are similar: they suggest that ILDs are the predominant localization cues shaping the SRFs of these representative LSO cells. The SRFs measured for the cue manipulation conditions for which the ILD cue varied naturally with changes in azimuth, the 0-ITD, 0-ISD, and the Δ-ILD conditions, closely approximated the SRFs measured in the normal condition, leading to small RMS errors. In contrast, the SRFs for the conditions where ILD was held fixed at 0 dB for all azimuths, the Δ-ITD, Δ-ISD, and 0-ILD conditions, there was relatively little modulation of the response as azimuth was changed, leading to large RMS errors. On the other hand the SRFs resulting from the various cue manipulations involving ITD and ISD (Figs. 3A,B,4A,B) that led to small RMS errors were rarely identical to the normal SRF, suggesting at least some minor role for these cues in shaping the SRFs in the presence of all cues. Finally, the SRF measured in the ipsi-only condition confirms the predominant role of the contralateral inhibition in shaping the SRF under the normal binaural condition, yielding moderate RMS errors.
ILD is the primary acoustical determinant of the spatial receptive fields in azimuth
The examples shown in Figures 3 and 4 indicate that ILDs make a large contribution to the SRFs measured under the normal condition. Here we compare the RMS difference errors across all cue manipulation conditions and across our population of LSO cells. We were unable to perform all cue manipulations in all 24 cells tested. And in some cells, we measured responses to the cue manipulations under more than one sound level. The latter data were included in the following analyses.
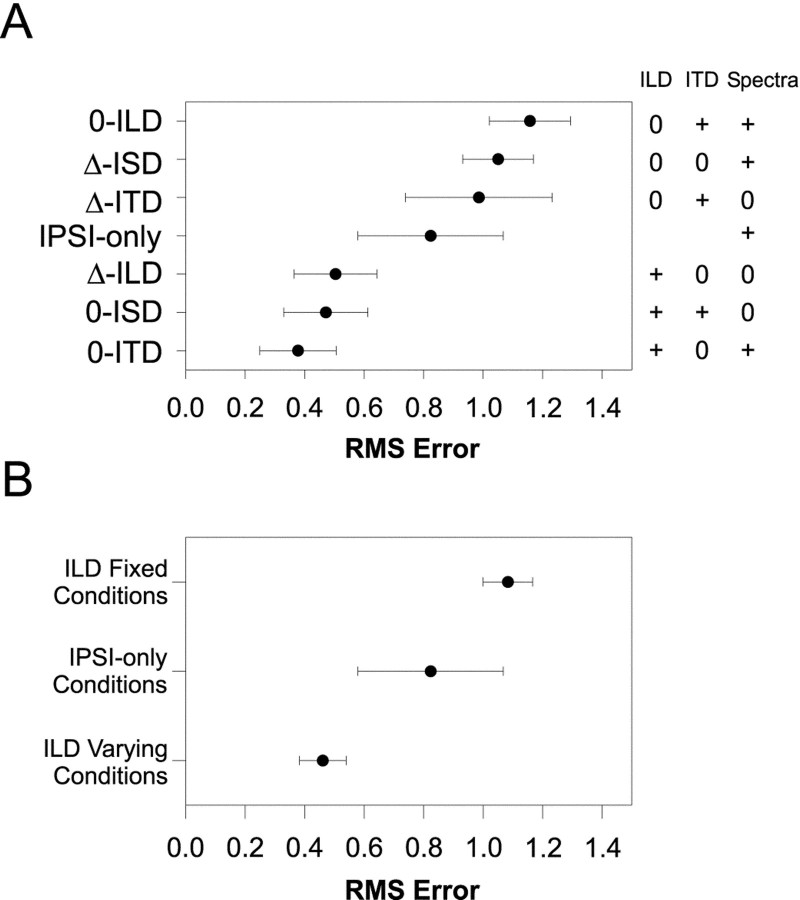
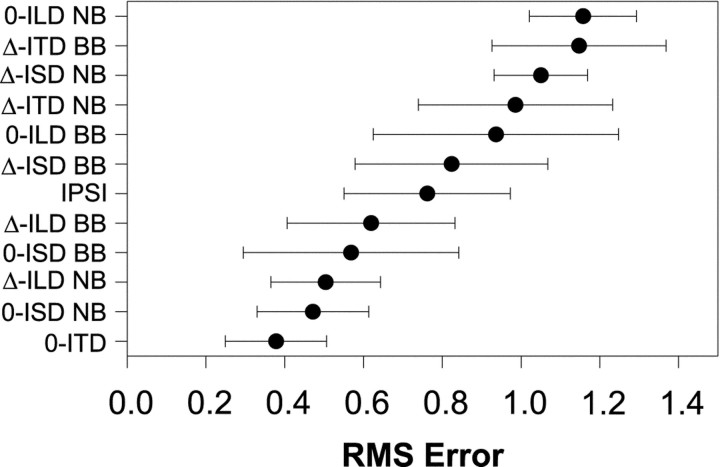
Figure 5A shows the population means and 95% confidence intervals for RMS error computed for each of the localization cue manipulations. Each data point represents the mean RMS errors from 11–28 comparisons of the normal to the respective cue-manipulated SRFs. Recall that small errors suggest that the cues that are being varied contribute greatly to the normal SRFs. In contrast, large errors indicate that the cues being held constant contribute greatly. The data are ordered along the ordinate with the smallest errors at the bottom and the largest at the top. To the right of the figure is a table indicating for each condition which cues were varied naturally (+) with changes in azimuth, and which were held fixed (0). (Note that in the ipsi-only condition, the binaural cues are undefined and left blank).
Fig. 5.
A, Mean RMS-difference errors ± 95% confidence intervals computed for each cue manipulation condition across the population of LSO cells for which each condition was run (N = 149). Small errors indicate that the SRF measured in the cue-manipulation condition closely approximated the SRF measured in the normal condition. The table to the right indicates for each condition whether the cue was held fixed (0) or allowed to vary naturally (+) with changes in the azimuth of the sound source. In the ipsi-only condition, ITD and ILD are undefined, and the corresponding spots are left blank in the table. B, Mean RMS-difference errors ± 95% confidence intervals for the ILD varying conditions (0-ITD, 0-ISD, and Δ-ILD), the ipsi-only condition, and the ILD fixed conditions (Δ-ITD, Δ-ISD, and 0-ILD). Smallest errors across the population of cells occurred for those conditions where ILD varied naturally with azimuth, whereas the largest errors occurred when ILD was held fixed.
Figure 5A shows that when ITD was held constant in the 0-ITD condition, the smallest errors arose, indicating that across the population of cells ITD cues by themselves play little role in shaping the spatial location sensitivity of LSO neurons. This notion is supported in the Δ-ITD condition where large errors were observed. Figure 6A shows the SRFs in the ITD manipulation conditions from an example cell whose RMS-difference errors were near the median errors across the population of LSO cells for which the ITD cue manipulations were performed. Holding the spectral cues constant with azimuth, the 0-ISD case, also led to small errors across the population whereas varying spectral cues alone, the Δ-ISD case, yielded large errors (Fig. 5A), suggesting that spectral cues alone do not contribute greatly to the receptive fields. Figure 6B shows the SRFs for a different cell in the ISD manipulation conditions that resulted in RMS errors near the median error across the population of cells tested in the ISD conditions.
Unlike the SRFs measured in the Δ-ITD and Δ-ISD conditions, when ILD in a 1/3-octave band centered on the CFs of each cell tested was varied in the Δ-ILD condition, relatively small errors were present, indicating that across our population of LSO cells ILD cues alone play a substantial role in determining the binaural SRFs (Fig.5A). Likewise, the data in Figure 5A show that the 0-ILD condition gave the largest errors across the entire population. Figure 6C shows the SRFs in the ILD conditions in another cell whose errors were near the median error.
Finally, as indicated in Figure 4 the ipsi-only condition generally yielded moderately large errors, indicating that at least some azimuthal sensitivity is retained by monaural stimulation, and Figure6D shows an example of the ipsi-only SRF yielding an error near the median error across cells tested in the ipsi-only condition. In fact, all cells tested were modulated by changes in azimuth in the ipsi-only condition.
Together, the population data strongly implicate the ILD cue as the main acoustical determinant of the SRFs of LSO cells when measured in the normal condition. In support of this, note that the population data for the seven cue manipulation conditions fall neatly into three broad categories: (1) the three conditions with the smallest population errors; (2) the ipsi-only condition; and (3) the three conditions with the largest population errors. And by observing the ILD column on the right-hand side of Figure 5A these three groups appear to be determined by whether or not the ILD cue was varying naturally, held constant, or not defined. The ILD cues were allowed to vary in each of the three conditions yielding the smallest errors, whereas the ILD cues were fixed at 0 dB in each of the three conditions yielding the largest errors. Figure 5B shows the mean RMS difference errors and the 95% confidence intervals for these three groups. The analysis of variance revealed a significant effect of ILD cue manipulation (F(2,146) = 39.68;p < 0.0001), and the Scheffe post hoc test indicated significant differences among all three groups (p < 0.05). These data together support the long-standing but hitherto untested hypothesis that ILDs in a small band of frequencies around the CF of LSO cells are the main acoustical cue shaping their SRFs under simulated free-field conditions.
The role of ITD and monaural spectral cues
Note that the smallest errors occurred in the 0-ITD condition, although slightly, but not significantly, larger population errors occurred in the remaining two conditions where ILD was varied naturally, the 0-ISD and Δ-ILD conditions. This difference is expected based on the way that the ILD cues were manipulated in the 0-ISD and Δ-ILD conditions relative to the 0-ITD condition. Note that in the 0-ITD condition, both the ILD and spectral cues varied naturally with azimuth because only the relative onset times of the stimuli presented to the two ears were adjusted. Hence, there were also natural changes in the sound level at the excitatory ipsilateral ear as azimuth was changed (Musicant et al., 1990). There were also natural changes in the overall binaural level of the stimuli as a function of azimuth (Irvine, 1987). On the other hand, in the 0-ISD and Δ-ILD conditions, the spectral cues were held fixed at those corresponding to the (0°, 0°) location, whereas the ILD as seen through the 1/3-octave filter at CF appropriate for each azimuth was imposed on the stimuli by symmetrically incrementing and decrementing the left and right ear signals. As a consequence, the overall binaural level of the stimuli as a function of azimuth in these two conditions was fixed.
The differences in RMS error between the 0-ITD condition and the 0-ISD and Δ-ILD conditions might be attributable to the fact that the ILD sensitivity of LSO cells depends jointly on both the ILD present in the stimulus and the overall sound level of the stimuli present at both ears (Tsuchitani and Boudreau, 1969), and as we pointed out in our previous paper, the changes in overall binaural level of the stimulus with changes in azimuth also appear to be important components in shaping the SRF under natural conditions (Tollin and Yin, 2002). The 0-ITD condition most closely approximates the normal condition because only the relative onset times of the stimuli to the two ears was manipulated, whereas all other aspects of the HRTFs were left unchanged. Hence, slight differences between the normal SRFs and the 0-ISD and Δ-ILD manipulation conditions were expected to the extent that ILD selectivity depends on overall level. Also, to the degree to which the frequency passbands of the units differed from the 1/3-octave bandwidth we used to manipulate the ILD cues, we also expected small differences between the SRFs measured in the 0-ITD conditions and the SRFs measured in the 0-ISD and Δ-ILD conditions.
Supplementary experiment: broadband manipulations of ILD cues
As an additional test, we investigated the effect of manipulating the ILD cues over a broader bandwidth than the 1/3-octave bandwidth used in the previous experiments. Here, instead of manipulating the ILD cues through the 1/3-octave Gaussian filter centered on the CFs of the cells, we adjusted the energy integrated over the entire spectrum of the HRTFs. For example, in the 0-ILD condition, we set the ILD computed across the entire spectrum of the signal to 0 dB at all azimuths while allowing ITD and monaural spectral cues to vary naturally. And in the Δ-ILD condition, the broadband ILD was varied naturally while ITD and spectral cues were held constant at values appropriate for (0°, 0°). But, the direction- and frequency-dependent filtering effects of the pinnae and head result in ILDs that vary not only as a function of azimuth but, at each azimuth, also vary as a function of frequency (Fig. 1). So in these broadband ILD manipulation conditions, there is likely still to be nonzero ILDs seen through the passbands of the cells; thus, the sign and magnitude of the ILD as a function of azimuth will be frequency dependent.
Following the layout of Figure 2, Figure7 shows the left and right ear impulse responses and corresponding gains at two different azimuths, ±45°, resulting from the broadband 0-ILD manipulation. In comparison with the stimuli for the narrowband 0-ILD condition shown in Figure2A, the residual ILD at 10 kHz in the broadband 0-ILD condition shown in Figure 7 is rather large (11 dB) and has a sign consistent with the normal ILD at 10 kHz but smaller in magnitude (Fig.1). Hence, as azimuth is varied in the broadband 0-ILD condition, a cell with a CF of ∼10 kHz would be expected to be modulated with changes in azimuth in a similar manner, but not necessarily the same magnitude, as the normal SRF.
Fig. 7.
Examples of the manipulations of the HRTFs in the broadband 0-ILD cue manipulation condition. Same format as Figure 2. In the broadband cue manipulation conditions, ILD was measured across the entire spectrum of the HRTFs in contrast to the 1/3-octave narrowband measurements shown in Figure 2. Note that although the broadband ILD is 0 dB at the two azimuths in this example, there are nonzero ILDs at many frequencies.
To illustrate this point more clearly, we used the CFs of the cells whose SRFs are shown in Figures 3 and 4 to compute the ILD as a function of azimuth as seen through both the narrowband and broadband conditions. We also computed the residual ILD as seen through the narrowband filter at that CF under the broadband 0-ILD condition, which is essentially the difference between the narrowband and broadband ILDs. Figure 8A shows the ILD computed in these three different ways as a function of azimuth for the cell with a CF of 7.8 kHz and Figure 8C for the cell with a CF of 29.9 kHz.
For the cell with the CF of 7.8 kHz in Figure 8A, the ILD as seen through the bandpass filter corresponds closely both in shape and magnitude to the broadband ILD, except for a deviation at large lateral angles. But in the broadband 0-ILD condition, there are still nonzero ILDs at this CF whose signs are consistent with the natural ILDs as a function of azimuth (Fig. 8A, open circles). Hence, if the SRF of this cell were determined predominantly by ILDs as expected in light of the narrowband manipulations shown in Figure 3, then in the broadband 0-ILD condition we expected some modulation of the response with changes in azimuth. For example, given the large increase in magnitude of the ILD in the broadband 0-ILD condition from −63° to −90°, we expected a large increase in the response of the cell over this same range. The same argument holds for the broadband Δ-ILD condition because as shown in Figure 8A under natural conditions, the ILD computed across the spectrum covaries positively with the ILD as seen through the filter at CF. However, we would expect there to be differences in the response of the cell between the normal and the broadband Δ-ILD condition particularly between −63° to −90° where the magnitude of the broadband ILD begins to become smaller than the narrowband ILD under the normal condition.
Figure 8C shows the same ILD computations but this time for the cell shown in Figure 4 whose CF was 29.9 kHz. In this case, there is less correspondence between the broadband and narrowband ILD. But like the previous example, the sign, but not the magnitude, of the ILD as seen through the filter at CF is consistent with the natural ILD, so we expect some modulation of the response even in the broadband 0-ILD condition. Note that cells at other CFs, however, might have ILDs whose signs are opposite the broadband ILD, particularly if their CF lies in a spectral notch of the HRTF, so they would be expected to be modulated with azimuth opposite to the normal SRFs. So altogether we expected to observe a wide range of RMS errors in the broadband 0-ILD condition because some cells will have small errors, whereas other cells will have large errors depending on how the broadband ILD correlates with the narrowband ILD. A similar analysis applies for the broadband Δ-ILD condition, but in general the ILD at any one frequency covaries positively with the broadband ILD computed across the entire spectrum.
Figure 8, B and D, shows examples of the effects of the broadband ILD cue manipulations on the spatial sensitivity of the two cells shown in Figures 3 and 4 and whose ILD-azimuth functions are shown in Figure 8, A and C, respectively. For both cells, in the broadband 0-ILD condition there was modulation of the responses consistent with the normal SRFs confirming our predictions made above. Although there were also modulations of the responses in the Δ-ILD condition consistent with the normal SRFs, there was a much closer correspondence for the cell shown in Figure8B caused by the similarity in the broadband ILD and the ILD seen through the filter at this CF. Figure 8Balso shows that the increase in response in the broadband 0-ILD condition and a decrease in the broadband Δ-ILD condition for azimuths from −63° to −90° confirms our predictions based on the ILDs in Figure 8A. For the cell shown in Figure8D, the modulation in response in both the broadband 0-ILD and Δ-ILD conditions correlated less well with the normal SRF and yielded much smaller responses, consistent with the much smaller ILDs for this cell under these conditions (Fig. 8C).
Like the narrowband cue manipulation conditions, the data from the broadband manipulations also support the hypothesis that the spatial sensitivity of LSO cells is determined by ILDs. Figure9 shows the mean RMS difference errors across the population of cells for all the cue manipulations both for the broadband and the 1/3-octave narrowband conditions as shown in Figure 5. Each data point in Figure 9 for the broadband conditions is based on 7–19 comparisons of the normal and the respective broadband cue-manipulated SRFs. Two points are apparent. First, the three conditions with the smallest errors are the narrowband conditions for which ILD was varied naturally. The next two conditions with the smallest errors were simply the broadband versions of the narrowband conditions for which ILD was varied. As pointed out in Figure 8, this is to be expected because the narrowband ILD at any CF usually covaries directly with the broadband ILD so that the cell will be modulated in the same direction as the normal SRF, albeit not to the same magnitude as the 1/3-octave narrowband condition, leading to relatively larger errors. Much larger errors occurred in those broadband cue manipulation conditions for which ILD was held constant at 0 dB, but not the largest errors. However, as predicted above, the broadband 0-ILD condition had the largest variability in the error. This is because, even though the ILD computed across the entire spectrum was 0 dB, the ILD as seen by any one cell through its passband either covaried positively or negatively with the natural ILD depending on the CF. Hence, some cells yielded small errors, whereas others yielded large errors resulting in large variability. The largest errors across the population still occurred in the narrowband 0-ILD condition. The broadband cue manipulation data along with those of the narrowband support the hypothesis that the main determinant shaping the SRFs in azimuth of LSO cells is the ILD as seen through the passbands of the cells.
Fig. 9.
Mean RMS-difference errors ± 95% confidence intervals computed for each localization cue manipulation condition, including the broadband ILD manipulations, across the population of LSO cells for which each condition was run (N = 212). Same format as in Figure 5.
Validity of the localization cue manipulations
As pointed out in Materials and Methods, the 1/3-octave bandwidth may have actually been too wide for many units leading to ILDs different from those actually “seen” as a function of azimuth by the units in the normal binaural baseline condition. Such differences in ILD as a function of azimuth might account for the finding that there were appreciable RMS errors even in the conditions in which ILD was allowed to vary naturally with azimuth.
An additional source of error between the SRFs obtained in the Δ-ILD condition and that of the normal SRFs might also have arisen from the method by which we manipulated the sound levels at the two ears to achieve the desired ILD. Recall that in the Δ-ILD condition, the spectral cues were fixed for all azimuths at those corresponding to the (0°, 0°) location, and ITD was also fixed at 0 μsec. The narrowband ILD was then determined for each azimuth, and this ILD was then imposed on the HRTFs corresponding to (0°, 0°) by symmetrically incrementing and decrementing the left- and right-ear HRTFs. The result is that, whereas the narrowband ILD was identical in the normal binaural condition and in the Δ-ILD condition, the overall binaural SPL of the signals to the two ears was not necessarily always the same. This is because under natural free-field conditions, which the normal HRTFs capture and that were present in the normal binaural condition, the mean overall binaural SPL (measured across the entire spectrum of the VS stimuli) varies as a function of azimuth by ∼7 dB (Musicant et al., 1990), and the sensitivity of LSO cells to ILDs has been shown to be a function of not only the magnitude of the ILD itself, but also the overall sound level (Tsuchitani and Boudreau, 1969).
Finally, Brownell et al. (1979) and Caird and Klinke (1983) have reported the existence of ipsilateral inhibitory sidebands in LSO cells. Because the 1/3-octave bandwidth we used was on average larger than the 10 dB passbands of the cells, it might be possible that the action of the inhibitory sidebands led to larger errors in those conditions where ILD was varied. Although we did not routinely assess the presence of ipsilateral inhibitory sidebands, we believe that the effect of such influences was generally small in our barbiturate-anesthetized preparation; Brownell et al. (1979) used a decerebrate-unanesthetized preparation and found in both cells tested that when a barbiturate anesthetic was introduced, the inhibitory sidebands disappeared.
DISCUSSION
An ubiquitous characteristic of neurons in all sensory systems is their sensitivity to a wide range of stimulus parameters. LSO cells, for example, have been shown to be sensitive to each of the three primary cues to location: LSO cells respond to monaural variations in SPL which are important for encoding the monaural spectral cues, to onset ITDs of transient sounds and ITDs of sounds containing low-frequency envelope information, and, of course, to ILDs. However, it has long been hypothesized that the functional role LSO cells is to compute from free-field sounds a correlate of only one cue to location, ILDs. Here, we manipulated directly the acoustical cues to location provided by the VS stimuli to determine which cues contributed to the spatial selectivity of LSO cells. By systematically setting each of the three cues to a constant while letting the others vary naturally in azimuth, we could compare the relative contribution to the SRFs of each cue in isolation and in combination with each other cue. The results were clear: in all cases, the ILD cue in a narrow band of frequencies around the CFs of the units was the major determinant shaping the SRFs in azimuth, thereby supporting the long-held, but hitherto untested, hypothesis that under natural free-field conditions, cells of the LSO compute a correlate of ILD. Moreover, despite the demonstrated sensitivity of high-CF (more than ∼3 kHz) LSO cells to ITDs of the envelope of amplitude-modulated (AM) signals (Caird and Klinke, 1983;Joris and Yin, 1995; Batra et al., 1997) and to transient onset ITDs (Caird and Klinke, 1983; Sanes, 1990; Wu and Kelly, 1992; Joris and Yin, 1995; Park et al., 1996), the ITD information carried in the long duration noise stimuli used here generally had a weak effect in all cells, and to a lesser degree the spectral cues were also largely ineffective in shaping the SRFs.
Comparison of localization cue manipulation conditions to other studies
Several studies of the encoding of localization cues by LSO cells have examined the influence on discharge rate of one cue in the presence of another, but the relationships between the cues were often unnatural with respect to the cues expected under free-field conditions. For example, Caird and Klinke (1983) and Joris and Yin (1995) found that changes in ILD had a much larger effect on discharge rate than changes in ITD. Over the range of ITDs and ILDs that are acoustically plausible for adult cats (Musicant et al., 1990), Joris and Yin (1995) estimated that changes in ILD were ∼4 times more potent than changes in ITD when the stimuli were AM tones whose carriers were at the CF of each unit. Caird and Klinke (1983) also reported that ILDs were generally much more effective at modulating LSO responses than ITDs. Our data are largely in accordance with these findings but extend them by demonstrating that the sensitivity of high-frequency LSO cells to the spatial location of long-duration broadband noise is determined almost completely by the ILD present in a small band of frequencies around the CF of the units. Consistent with previous reports from our laboratory, the data presented here demonstrate that these LSO cells exhibit virtually no sensitivity to ongoing ITDs of long-duration broadband stimuli (Joris and Yin, 1995;Tollin and Yin, 2002). However, with short-duration stimuli, ITDs can have a larger influence on the sensitivity of LSO cells to ILDs by changing the relative timing of the arrival of the contralateral inhibition (Caird and Klinke, 1983; Sanes, 1990; Wu and Kelly, 1992;Park et al., 1996; Irvine et al., 1998).
Previous studies have used the VS method to investigate the encoding of localization cues at virtually all levels of the auditory system including the auditory nerve (Poon and Brugge, 1993; Rice et al., 1995), CN (Yu and Young, 2000), LSO (Tollin and Yin, 2002), inferior colliculus (IC) (Hartung and Sterbing, 1997; Keller et al., 1998;Delgutte et al., 1999), and auditory cortical areas (Brugge et al., 1994; Nelken et al., 1998; Mrsic-Flogel et al., 2001). Fewer studies, however, have exploited the VS stimuli to manipulate the cues independently to assess the determinants of the SRFs. In a previous report from our laboratory, Delgutte et al. (1995) manipulated the cues provided by the HRTFs in a manner similar to that here and found that the main determinant of the azimuthal SRFs of the majority of IC cells was ILD with ITD and monaural spectral cues contributing only little.Nelken et al. (1998) also used the VS method to manipulate the cues and found that the SRFs in azimuth of the cells in the anterior ectosylvian cortex were determined primarily by ILDs. Together with our previous measurements of the SRFs (Tollin and Yin, 2002) and the findings presented in this paper, the results are in agreement with the notion that the LSO can provide much of the sensitivity to ILD seen at levels above the superior olivary complex (Park, 1998; Tollin and Yin, 2002).
An important caveat to these conclusions regarding the prominence of ILD cues is the limitation on the frequency bandwidths of the HRTF measurements. Recall that the HRTFs were bandpass filtered between 2 and 30 kHz because of the poor signal levels outside this range. Furthermore, our conclusions pertain only to cells with CFs >3 kHz. Because sensitivity of auditory neurons to the ongoing ITDs of the fine structure of sounds is primarily restricted to frequencies of <2 kHz (Rose et al., 1966; Goldberg and Brown, 1969; Yin and Chan, 1990), it is clear that we cannot make strong statements regarding the weakness of ITDs as a cue for all cells. In fact, in the course of these studies we have found low-CF cells located in the lateral limb of the LSO that are sensitive to both ILDs and the ongoing ITDs of the fine structure of both tone and broadband noise stimuli (Tollin et al., 2000). But because the CFs of the cells studied in the present work were all >3 kHz, we do not think our results would be affected by wider bandwidth HRTFs. At these CFs, LSO cells are sensitive only to ITDs of the envelopes of the stimuli, not the fine structure (Caird and Klinke, 1983; Joris and Yin, 1995).
Implications for coding spatial location
The data presented here provide physiological evidence supporting the psychophysical “duplex theory” of sound localization, which posits that low-frequency sounds are localized based on ITDs, whereas high-frequency sounds are localized based on ILDs and monaural spectral cues (Rayleigh, 1907; Stevens and Newman, 1936). The sound localization performance of cats is also in agreement with the duplex theory (Casseday and Neff, 1973). Physiologically, the cells of the LSO are biased toward higher frequencies (Tsuchitani and Boudreau, 1966; Guinan et al., 1972b) and are sensitive to only a restricted region of the auditory spectrum as evidenced by their narrow frequency tuning curves (Tsuchitani and Boudreau, 1966; Guinan et al., 1972a; Tsuchitani, 1997;Tollin and Yin, 2001). Both physiological and anatomical studies have shown that the CFs of the inhibitory inputs to the LSO from the ipsilateral medial nucleus of the trapezoid body are well matched to the excitatory inputs from the ipsilateral CN (Boudreau and Tsuchitani, 1968; Glendenning et al., 1985, 1991; Tsuchitani, 1997; Smith et al., 1998). The cells of the LSO then, appear to be suited to collectively encoding ILDs across virtually the entire spectrum, but in piecemeal manner; that is, each cell only encodes the ILD over the restricted portion of the spectrum to which they are sensitive. To date, no systematic mapping of ILD sensitivity has been found in the LSO. This is in contrast to the medial superior olive (MSO), which is traditionally associated with the encoding of low-frequency ITDs because MSO cells are sensitive to ongoing ITDs in the fine structure of low-frequency sounds (Goldberg and Brown, 1969; Moushegian et al., 1975; Caird and Klinke, 1983; Yin and Chan, 1990). Moreover, the cells of the MSO are biased toward lower frequencies than are LSO cells (Guinan et al., 1972b). Hence, at the level of the brainstem there appears to be a anatomical division of labor consistent with the psychophysical duplex theory where the MSO and LSO encode separately, but in parallel, neural correlates of the two binaural cues to sound location, ITDs and ILDs, respectively.
Footnotes
This work was supported by National Institute on Deafness and Other Communication Disorders Grants DC00116 and DC02840 (T.C.T.Y.) and DC00376 (D.J.T.). It is a pleasure to acknowledge the support of R. Kochhar for software and I. Siggelkow for histology.
Correspondence should be addressed to Daniel J. Tollin, Department of Physiology, Room 290, Medical Sciences Building, University of Wisconsin-Madison, 1300 University Avenue, Madison, WI 53706. E-mail:tollin@physiology.wisc.edu.
REFERENCES
- 1.Batra R, Kuwada S, Fitzpatrick DC. Sensitivity to interaural temporal disparities of low- and high-frequency neurons in the superior olivary complex. I. Heterogeneity of responses. J Neurophysiol. 1997;78:1222–1236. doi: 10.1152/jn.1997.78.3.1222. [DOI] [PubMed] [Google Scholar]
- 2.Bledsoe SC, Jr, Snead CR, Helfert RH, Prasad V, Wenthold RJ, Altschuler RA. Immunocytochemical and lesion studies support the hypothesis that the projection from the medial nucleus of the trapezoid body to the lateral superior olive is glycinergic. Brain Res. 1990;517:189–194. doi: 10.1016/0006-8993(90)91025-c. [DOI] [PubMed] [Google Scholar]
- 3.Boudreau JC, Tsuchitani C. Binaural interaction in the cat superior olive S segment. J Neurophysiol. 1968;31:442–454. doi: 10.1152/jn.1968.31.3.442. [DOI] [PubMed] [Google Scholar]
- 4.Brownell WE, Manis PB, Ritz LA. Ipsilateral inhibitory responses in the cat lateral superior olive. Brain Res. 1979;177:189–193. doi: 10.1016/0006-8993(79)90930-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Brugge JF, Reale RA, Hind JE, Chan JC, Musicant AD, Poon PW. Simulation of free-field sound sources and its application to studies of cortical mechanisms of sound localization in the cat. Hear Res. 1994;73:67–84. doi: 10.1016/0378-5955(94)90284-4. [DOI] [PubMed] [Google Scholar]
- 6.Caird D, Klinke R. Processing of binaural stimuli by cat superior olivary complex neurons. Exp Brain Res. 1983;52:385–399. doi: 10.1007/BF00238032. [DOI] [PubMed] [Google Scholar]
- 7.Cant NB, Casseday JH. Projections from the anteroventral cochlear nucleus to the lateral and medial superior olivary nuclei. J Comp Neurol. 1986;247:457–476. doi: 10.1002/cne.902470406. [DOI] [PubMed] [Google Scholar]
- 8.Casseday JH, Neff WD. Localization of pure tones. J Acoust Soc Am. 1973;54:365–372. doi: 10.1121/1.1913586. [DOI] [PubMed] [Google Scholar]
- 9.Delgutte B, Joris PX, Litovsky RY, Yin TCT. Relative importance of different acoustic cues to the directional sensitivity of inferior-colliculus neurons. In: Manley GA, Klump GM, Koppl C, Fastl H, Oeckinghaus H, editors. Advances in hearing research. World Scientific; Singapore: 1995. pp. 288–299. [Google Scholar]
- 10.Delgutte B, Joris PX, Litovsky RY, Yin TCT. Receptive fields and binaural interactions for virtual-space stimuli in the cat inferior colliculus. J Neurophysiol. 1999;81:2833–2851. doi: 10.1152/jn.1999.81.6.2833. [DOI] [PubMed] [Google Scholar]
- 11.Elverland HH. Ascending and intrinsic projections of the superior olivary complex in the cat. Exp Brain Res. 1978;32:117–134. doi: 10.1007/BF00237396. [DOI] [PubMed] [Google Scholar]
- 12.Galambos R, Schwartzkopf J, Rupert A. Microelectrode study of superior olivary nuclei. Am J Physiol. 1959;197:527–536. doi: 10.1152/ajplegacy.1959.197.3.527. [DOI] [PubMed] [Google Scholar]
- 13.Glendenning KK, Hutson KA, Nudo RJ, Masterton RB. Acoustic chiasm. II: Anatomical basis of binaurality in lateral superior olive of cat. J Comp Neurol. 1985;232:261–285. doi: 10.1002/cne.902320210. [DOI] [PubMed] [Google Scholar]
- 14.Glendenning KK, Masterton RB, Baker BN, Wenthold RJ. Acoustic chiasm. III: Nature, distribution, and sources of afferents to the lateral superior olive in the cat. J Comp Neurol. 1991;310:377–400. doi: 10.1002/cne.903100308. [DOI] [PubMed] [Google Scholar]
- 15.Goldberg JM, Brown PB. Response of binaural neurons of dog superior olivary complex to dichotic tonal stimuli: some physiological mechanisms of sound localization. J Neurophysiol. 1969;32:613–636. doi: 10.1152/jn.1969.32.4.613. [DOI] [PubMed] [Google Scholar]
- 16.Guinan JJ, Jr, Guinan SS, Norris BE. Single auditory units in the superior olivary complex. I: Responses to sounds and classifications based on physiological properties. Int J Neurosci. 1972a;4:101–120. [Google Scholar]
- 17.Guinan JJ, Jr, Norris BE, Guinan SS. Single auditory units in the superior olivary complex. II: Location of unit categories and tonotopic organization. Int J Neurosci. 1972b;4:147–166. [Google Scholar]
- 18.Hartung K, Sterbing SJ. Generation of virtual sound sources for electrophysiological characterization of auditory spatial tuning in the guinea pig. In: Syka J, editor. Acoustical signal processing in the central auditory system. Plenum; New York: 1997. pp. 407–412. [Google Scholar]
- 19.Henkel CK, Gabriele ML. Organization of the disynaptic pathway from the anteroventral cochlear nucleus to the lateral superior olivary nucleus in the ferret. Anat Embryol (Berl) 1999;199:149–160. doi: 10.1007/s004290050216. [DOI] [PubMed] [Google Scholar]
- 20.Huang AY, May BJ. Sound orientation behavior in cats. II. Mid-frequency spectral cues for sound localization. J Acoust Soc Am. 1996;100:1070–1080. doi: 10.1121/1.416293. [DOI] [PubMed] [Google Scholar]
- 21.Irvine DR. Interaural intensity differences in the cat: changes in sound pressure level at the two ears associated with azimuthal displacements in the frontal horizontal plane. Hear Res. 1987;26:267–286. doi: 10.1016/0378-5955(87)90063-3. [DOI] [PubMed] [Google Scholar]
- 22.Irvine DRF, Park VN, McCormick L. Contributions of changes in the timing and amplitude of synaptic inputs to neural sensitivity to interaural intensity differences. In: Palmer AR, Rees A, Summerfield AQ, Meddis R, editors. Psychophysical and physiological advances in hearing. Whurr; London: 1998. pp. 359–365. [Google Scholar]
- 23.Joris PX, Yin TCT. Envelope coding in the lateral superior olive. I. Sensitivity to interaural time differences. J Neurophysiol. 1995;73:1043–1062. doi: 10.1152/jn.1995.73.3.1043. [DOI] [PubMed] [Google Scholar]
- 24.Keller CH, Hartung K, Takahashi TT. Head-related transfer functions of the barn owl: measurement and neural responses. Hear Res. 1998;118:13–34. doi: 10.1016/s0378-5955(98)00014-8. [DOI] [PubMed] [Google Scholar]
- 25.Moore MJ, Caspary DM. Strychnine blocks binaural inhibition in lateral superior olivary neurons. J Neurosci. 1983;3:237–242. doi: 10.1523/JNEUROSCI.03-01-00237.1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Moushegian G, Rupert AL, Gidda JS. Functional characteristics of superior olivary neurons to binaural stimuli. J Neurophysiol. 1975;38:1037–1048. doi: 10.1152/jn.1975.38.5.1037. [DOI] [PubMed] [Google Scholar]
- 27.Mrsic-Flogel TD, King AJ, Jenison RL, Schnupp JW. Listening through different ears alters spatial response fields in ferret primary auditory cortex. J Neurophysiol. 2001;86:1043–1046. doi: 10.1152/jn.2001.86.2.1043. [DOI] [PubMed] [Google Scholar]
- 28.Musicant AD, Chan JCK, Hind JE. Direction-dependent spectral properties of cat external ear: new data and cross-species comparisons. J Acoust Soc Am. 1990;87:757–781. doi: 10.1121/1.399545. [DOI] [PubMed] [Google Scholar]
- 29.Nelken I, Bar Yosef O, Young ED. Responses of field AES neurones to virtual space stimuli. In: Palmer AR, Rees A, Summerfield AQ, Meddis R, editors. Psychophysical and physiological advances in hearing. Whurr; London: 1998. pp. 504–510. [Google Scholar]
- 30.Park TJ. IID sensitivity differs between two principal centers in the interaural intensity difference pathway: the LSO and the IC. J Neurophysiol. 1998;79:2416–2431. doi: 10.1152/jn.1998.79.5.2416. [DOI] [PubMed] [Google Scholar]
- 31.Park TJ, Grothe B, Pollak GD, Schuller G, Koch U. Neural delays shape selectivity to interaural intensity differences in the lateral superior olive. J Neurosci. 1996;16:6554–6566. doi: 10.1523/JNEUROSCI.16-20-06554.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Poon PW, Brugge JF. Virtual-space receptive fields of single auditory nerve fibers. J Neurophysiol. 1993;70:667–676. doi: 10.1152/jn.1993.70.2.667. [DOI] [PubMed] [Google Scholar]
- 33.Rayleigh L. On our perception of sound direction. Philos Mag. 1907;13:214–232. [Google Scholar]
- 34.Rice JJ, May BJ, Spirou GA, Young ED. Pinna-based spectral cues for sound localization in cat. Hear Res. 1992;58:132–152. doi: 10.1016/0378-5955(92)90123-5. [DOI] [PubMed] [Google Scholar]
- 35.Rice JJ, Young ED, Spirou GA. Auditory-nerve encoding of pinna-based spectral cues: rate representation of high-frequency stimuli. J Acoust Soc Am. 1995;97:1764–1776. doi: 10.1121/1.412053. [DOI] [PubMed] [Google Scholar]
- 36.Rose JE, Gross NB, Geisler CD, Hind JE. Some neural mechanisms in the inferior colliculus of the cat which may be relevant to localization of a sound source. J Neurophysiol. 1966;29:288–314. doi: 10.1152/jn.1966.29.2.288. [DOI] [PubMed] [Google Scholar]
- 37.Saint Marie RL, Ostapoff E-M, Morest DK, Wenthold RJ. Glycine immunoreactive projection of the cat lateral superior olive: possible role in midbrain ear dominance. J Comp Neurol. 1989;279:382–396. doi: 10.1002/cne.902790305. [DOI] [PubMed] [Google Scholar]
- 38.Sanes DH. An in vitro analysis of sound localization mechanisms in the gerbil lateral superior olive. J Neurosci. 1990;10:3494–3506. doi: 10.1523/JNEUROSCI.10-11-03494.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Sanes DH, Rubel EW. The ontogeny of inhibition and excitation in the gerbil lateral superior olive. J Neurosci. 1988;8:682–700. doi: 10.1523/JNEUROSCI.08-02-00682.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Semple MN, Aitkin LM, Calford MB, Pettigrew JD, Phillips DP. Spatial receptive fields in the cat inferior colliculus. Hear Res. 1983;10:203–215. doi: 10.1016/0378-5955(83)90054-0. [DOI] [PubMed] [Google Scholar]
- 41.Smith PH, Joris PX, Yin TCT. Projections of physiologically characterized spherical bushy cell axons from the cochlear nucleus of the cat: evidence for delay lines to the medial superior olive. J Comp Neurol. 1993;331:245–260. doi: 10.1002/cne.903310208. [DOI] [PubMed] [Google Scholar]
- 42.Smith PH, Joris PX, Yin TCT. Anatomy and physiology of principal cells of the medial nucleus of the trapezoid body (MNTB) of the cat. J Neurophysiol. 1998;79:3127–3142. doi: 10.1152/jn.1998.79.6.3127. [DOI] [PubMed] [Google Scholar]
- 43.Spangler KM, Warr WB, Henkel CK. The projections of principal cells of the medial nucleus of the trapezoid body in the cat. J Comp Neurol. 1985;238:249–262. doi: 10.1002/cne.902380302. [DOI] [PubMed] [Google Scholar]
- 44.Stevens SS, Newman E. The localization of actual sources of sound. Am J Psychol. 1936;48:297–306. [Google Scholar]
- 45.Tolbert L, Morest D, Yurgelun-Todd D. The neuronal architecture of the anteroventral cochlear nucleus of the cat in the region of the cochlear nerve root: horseradish peroxidase labelling of identified cell types. Neuroscience. 1982;7:3031–3052. doi: 10.1016/0306-4522(82)90228-7. [DOI] [PubMed] [Google Scholar]
- 46.Tollin DJ, Yin TCT. Comparison of the response properties of the principal cells of the lateral superior olive and the medial nucleus of the trapezoid body. Assoc Res Otolaryngol. 2001;24:57. [Google Scholar]
- 47.Tollin DJ, Yin TCT. The coding of spatial location by single units in the lateral superior olive of the cat. I. Spatial receptive fields in azimuth. J Neurosci. 2002;22:1454–1467. doi: 10.1523/JNEUROSCI.22-04-01454.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Tollin DJ, Joris PX, Yin TCT. Coding of interaural phase differences in low-frequency cells in the lateral superior olive of the cat. Assoc Res Otolaryngol. 2000;23:113. [Google Scholar]
- 49.Tsuchitani C. Discharge patterns of cat lateral superior olivary units to ipsilateral tone-burst stimuli. J Neurophysiol. 1982;47:479–500. doi: 10.1152/jn.1982.47.3.479. [DOI] [PubMed] [Google Scholar]
- 50.Tsuchitani C. Input from the medial nucleus of trapezoid body to an interaural level detector. Hear Res. 1997;105:211–224. doi: 10.1016/s0378-5955(96)00212-2. [DOI] [PubMed] [Google Scholar]
- 51.Tsuchitani C, Boudreau JC. Single unit analysis of cat superior olive S segment with tonal stimuli. J Neurophysiol. 1966;29:684–697. doi: 10.1152/jn.1966.29.4.684. [DOI] [PubMed] [Google Scholar]
- 52.Tsuchitani C, Boudreau JC. Encoding of stimulus frequency and intensity by cat superior olive S-segment cells. J Acoust Soc Am. 1967;42:794–805. doi: 10.1121/1.1910651. [DOI] [PubMed] [Google Scholar]
- 53.Tsuchitani C, Boudreau JC. Stimulus level of dichotically presented tones and cat superior olive S-segment cell dcharge. J Acoust Soc Am. 1969;46:979–988. doi: 10.1121/1.1911818. [DOI] [PubMed] [Google Scholar]
- 54.Wightman FL, Kistler DJ. Headphone simulation of free-field listening. I: Stimulus synthesis. J Acoust Soc Am. 1989a;85:858–867. doi: 10.1121/1.397557. [DOI] [PubMed] [Google Scholar]
- 55.Wightman FL, Kistler DJ. Headphone simulation of free-field listening. II: Psychophysical validation. J Acoust Soc Am. 1989b;85:868–878. doi: 10.1121/1.397558. [DOI] [PubMed] [Google Scholar]
- 56.Wu SH, Kelly JB. Binaural interaction in the lateral superior olive: time difference sensitivity studied in mouse brain slice. J Neurophysiol. 1992;68:1151–1159. doi: 10.1152/jn.1992.68.4.1151. [DOI] [PubMed] [Google Scholar]
- 57.Yin TCT, Chan JCK. Interaural time sensitivity in medial superior olive of cat. J Neurophysiol. 1990;64:465–488. doi: 10.1152/jn.1990.64.2.465. [DOI] [PubMed] [Google Scholar]
- 58.Young ED, Robert JM, Shofner WP. Regularity and latency of units in ventral cochlear nucleus: implications for unit classification and generation of response properties. J Neurophysiol. 1988;60:1–29. doi: 10.1152/jn.1988.60.1.1. [DOI] [PubMed] [Google Scholar]
- 59.Yu JJ, Young ED. Linear and nonlinear pathways of spectral information transmission in the cochlear nucleus. Proc Natl Acad Sci USA. 2000;97:11780–11786. doi: 10.1073/pnas.97.22.11780. [DOI] [PMC free article] [PubMed] [Google Scholar]