Mechanisms of Active Hair Bundle Motion in Auditory Hair Cells

Abstract

Sound stimuli vibrate the hair bundles on auditory hair cells, but the resulting motion attributable to the mechanical stimulus may be modified by forces intrinsic to the bundle, which drive it actively. One category of active hair bundle motion has properties similar to fast adaptation of the mechanotransducer channels and is explicable if gating of the channels contributes significantly to the mechanics of the hair bundle. To explore this mechanism, we measured hair bundle compliance in turtle auditory hair cells under different conditions that alter the activation range of the channel. Force–displacement relationships were nonlinear, possessing a maximum slope compliance when approximately one-half of the transducer channels were open. When the external calcium concentration was reduced from 2.8 to 0.25 mm, the position of maximum compliance was shifted negative, reflecting a comparable shift in the transducer channel activation curve. Assuming that the nonlinearity represents the compliance attributable to channel gating, a single-channel gating force of 0.25 pN was calculated. By comparing bundle displacements with depolarization with and without an attached flexible fiber, the force contributed by each channel was independently estimated as 0.47 pN. These results are consistent with fast active bundle movements resulting from changes in mechanotransducer channel gating. However, several observations revealed additional components of hair bundle motion, with slower kinetics and opposite polarity to the fast movement but also linked to transducer adaptation. This finding argues for multiple mechanisms for controlling hair bundle position in auditory hair cells.

In the vertebrate inner ear, sound stimuli are detected by auditory hair cells through submicrometer displacements of their mechanically sensitive hair bundles. Evidence has accumulated that motion of the hair bundle driven by the external acoustic stimulus can be modified and augmented by energy supplied by the hair cell (Hudspeth, 1997; Fettiplace et al., 2001). Such action might serve to increase auditory sensitivity by amplifying the hair bundle vibrations to incoming sounds, especially those near threshold. Spontaneous oscillations of the bundle are one manifestation of the active process (Crawford and Fettiplace, 1985; Rüsch and Thurm, 1990; Denk and Webb, 1992; Martin and Hudspeth, 1999; Martin et al., 2000). Another is force generation by the bundle in response to stimulation with a flexible glass fiber (Crawford and Fettiplace, 1985;Howard and Hudspeth, 1987, 1988; Benser et al., 1996; Ricci et al., 2000). The cellular reactions subserving the active process are not fully understood, but multiple mechanisms will probably be needed to explain all results, which display a wide range of kinetics.

We observed recently active bundle movements in turtle hair cells on a millisecond time course synchronous with fast adaptation of the mechanotransducer channels. We proposed that these bundle movements, like adaptation, result from calcium directly closing the mechanotransducer channels (Ricci et al., 2000). The movements can be explained (Howard and Hudspeth, 1988) if a significant portion of the hair bundle stiffness depends on channel gating: as the channels open or close in response to changes in intracellular calcium, they exert force on the bundle, causing it to move. The contribution of channel gating to hair bundle mechanics, known as the “gating compliance,” may comprise as much as 50% of the total compliance of the bundle in frog hair bundles (Howard and Hudspeth, 1988). The remaining compliance, the nongating compliance, is partly attributable to flexure of the actin filaments in the ankles of the stereocilia (Crawford and Fettiplace, 1985; Howard and Ashmore, 1986). An aim of the present experiments was to determine whether the gating compliance in turtle hair cells is sufficient to account for the active bundle movements.

Active hair bundle movements have also been reported in response to changes in membrane potential (Crawford and Fettiplace, 1985; Assad et al., 1989; Rüsch and Thurm, 1990; Denk and Webb, 1992). Such movements may be secondary to a reduction in calcium influx as the membrane potential approaches the calcium equilibrium potential. Depolarizations positive to 0 mV evoke a sustained deflection of the bundle accompanied by an outward current thought to represent the opening of mechanotransducer channels by reduced intracellular calcium. However, the evoked movements differ in both time scale and polarity between preparations. Fast millisecond responses are associated with motion of the hair bundle toward the kinocilium (Ricci et al., 2000), whereas slower displacements lasting tens or hundreds of milliseconds have the opposite polarity (Assad and Corey, 1992). The different polarities imply the operation of two independent mechanisms. Here we show that both processes can be observed in a single hair cell.

MATERIALS AND METHODS

Preparation and recording. The method of recording from hair cells in the auditory papilla of the red-eared turtle was identical to that described previously (Ricci and Fettiplace, 1997). Turtles (Trachemys scripta elegans; carapace length, 75–125 mm) were decapitated, and the cochlea was dissected out, opened, and incubated in saline (in mm: 125 NaCl, 4 KCl, 2.8 CaCl₂, 2.2 MgCl₂, 2 Na pyruvate, 8 glucose, and 10 Na-HEPES, pH 7.6) containing up to 0.06 mg/ml protease (type XXIV; Sigma, St. Louis, MO). The tectorial membrane was then removed to expose the hair bundles. The preparation was mounted in a Perspex chamber on the stage of a Zeiss (Oberkochen, Germany) Axioskop FS microscope and viewed through a 63× water-immersion objective (0.9 numerical aperture). The recording chamber was perfused with standard saline containing (in mm): 130 NaCl, 0.5 KCl, 2.8 CaCl₂, 2.2 MgCl₂, 2 Na pyruvate, 8 glucose, and 10 Na-HEPES, pH 7.6. The upper surface of the hair cell epithelium and the hair bundles were independently perfused with a solution similar in composition to standard saline with Na⁺ as the major monovalent ion and with either normal (2.8 mm) or reduced (0.25 mm) Ca²⁺concentration. Perfusion of the hair cell apical surface with a K⁺-rich saline to fully mimic endolymph was not attempted in the present experiments. However, it is worth noting that exposure of the hair bundle to such a K⁺-based solution may result in a more pronounced gating compliance and active bundle movements closer to those occurring in vivo (Martin and Hudspeth, 1999). Whole-cell currents were measured with an Axopatch 200A amplifier (Axon Instruments, Foster City, CA) connected to a patch pipette filled with an intracellular solution containing (in mm): 125 CsCl, 3 Na₂ATP, 2 MgCl₂, 1 EGTA, and 10 Cs-HEPES, pH 7.2. After applying up to 70% series resistance compensation, electrode access resistances were 1–5 MΩ, and recording time constants were 10–100 μsec. All measurements were begun at a holding potential of −80 mV. Unless otherwise indicated, measurements are quoted as the mean ± 1 SD, and the responses shown are averages of from 5–25 presentations. Cells studied were located between 0.5 and 0.7 of the distance along the basilar papilla from the low-frequency end. Experiments were performed at 19–23°C.

Hair bundle displacement. Hair bundles were stimulated with a flexible glass fiber cemented to a piezoelectric bimorph (Crawford and Fettiplace, 1985). The bimorph was driven differentially with voltage steps, filtered with an eight-pole Bessel filter at 2 kHz to produce a 10–90% voltage rise time of ∼0.2 msec. Fibers were constructed and calibrated as described previously (Ricci et al., 2000) and had a mechanical stiffness between 0.7 and 3.3 mN/m. Before an experiment, the flexible fiber was acid-cleaned to help it stick to the hair bundle membrane, ensuring that the bundle followed motion of the fiber.

The apparatus for measuring hair bundle motion was similar to that described previously (Crawford and Fettiplace, 1985; Ricci et al., 2000). The secondary image of the bundle was projected through the camera port of the Axioskop onto a pair of photodiodes (Centronics LD 2–5) at a magnification of ∼700×. The photodiodes were themselves mounted on a piezoelectric bimorph, sinusoidal deflections of which were used to calibrate the photodiode signals (Art et al., 1986). The bundle image was centered on the photodiode junction, and its lateral motion was always less than the total width of one photodiode (0.5 mm). The difference between the signals from the two diodes should therefore be proportional to the displacement of the image (Crawford and Fettiplace, 1985). The proportionality constant was determined for each hair bundle by measuring the photocurrent produced by small sinusoidal vibrations, 60 nm peak-to-peak, of the photodiodes across the image of the bundle.

For stimulating a hair bundle, the flexible glass fiber was attached to the neural face of the bundle between 0.3 and 0.5 of the distance up the bundle from the epithelial surface. At this position, the fiber was several times more compliant than the hair bundle, and so the stimulus delivered on deflecting the fiber was approximately a force step. The magnitude of the force was calculated from the compliance of the fiber and the difference between the displacements of the end of the fiber fixed to the piezoelectric bar and the free end of the fiber that was attached to the bundle (Crawford and Fettiplace, 1985). The displacement of the tip of the fiber at which it touches the bundle was calculated from the motion of the top of the bundle, deduced from the photodiode signal. Assuming that the hair bundles pivot about their base (Flock et al., 1977; Crawford and Fettiplace, 1985), motion of the end of the fiber will be λ times the motion of the top of the bundle, where λ is the fractional distance up the bundle of the point of attachment of the fiber. The value of λ, which fell between 0.3 and 0.5, was measured at the end of each experiment. If the displacement of the piezoelectric bimorph wasy, the deflection of the top of the hair bundle wasx, and the stiffness of the fiber wasK_F, then the forceF_λ delivered at the point of contact of the fiber with the bundle was calculated as follows:F_λ =K_F · (y − λx). To estimate the stiffness of the bundle, the effective force at the tip of the bundle,F_B, was then approximated as follows:F_B = λF_λ. From recording the unhindered motion of the flexible fiber in solution, it was estimated that the combined stimulation and imaging systems had a time constant of 0.2–0.3 msec. The bundle displacement, x, and hence force,F_B, was taken at a time coinciding with the peak of the current for a small stimulus producing an adapting response. This was between 0.5 and 1 msec after deflecting the fixed end of the fiber.

Hair bundle motion was analyzed in terms of the gating spring model of mechanotransduction (Howard and Hudspeth, 1988; Markin and Hudspeth, 1995; van Netten and Kros, 2000). In this model, gating of the mechanotransducer channels contributes to the mechanical stiffness of the bundle, which declines over the range of displacements at which the channels are opening. The model predicts a relationship between the force, F_B, applied to the bundle and bundle displacement x given as follows:

$$F_B=F_{\text{o}}+x·K_S-\text{Nz}·p_{\text{o}}$$ Equation 1

where K_S is the combined stiffness of the stereociliary pivot, and the gating spring,p_o, is the probability of opening of the mechanotransducer channels, N is the number of mechanotransducer channels in the bundle, and z is the gating force per channel (the decrease in the gating spring force that occurs when the channel opens). F_o is a constant chosen to make F_B zero at the resting position of the bundle. In a two-state channel scheme in which the mechanotransducer channels can occupy either a single closed or open state, p_o is described as follows:

$$p_{\text{o}}=1/(1+exp\{-[z(x-x_{\text{o}})/\text{kT}]\},$$ Equation 2

and the slope stiffness of the hair bundle,K_B, is given as follows:

$$K_B=K_S-K_{\text{c}}/\{\text{cosh}[(x-x_{\text{o}})/\kappa ]{\}}^2$$ Equation 3

where K_c isNz²/4kT and κ = 2kT/z. κ is a space constant reflecting the broadness of the stiffness minimum. Equation 3 was used to fit the hair bundle stiffness measurements and to determine the space constant κ to evaluate z, the gating force per channel. It should be noted that the value of z calculated by this method is the force expressed at the tip of the bundle and therefore depends on the geometry of the bundle. This analysis assumes that gating of the mechanotransducer channel can be described by a scheme with single open and closed states. As noted previously (Corey and Hudspeth, 1983;Crawford et al., 1989), a two-state channel scheme poorly describes the current–displacement relationship in some hair cells, and a three-state scheme, two closed states and one open state, provides a better fit. However, it was not felt that this deviation was sufficient to warrant a more complex analysis of the gating compliance, which requires extra assumptions about channel gating (Markin and Hudspeth, 1995; van Netten and Kros, 2000).

RESULTS

Gating compliance

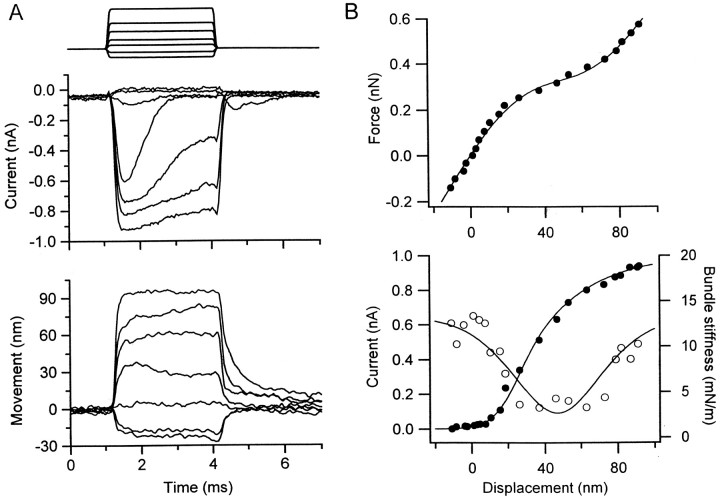
A principal aim of the experiments was to determine whether hair cells displaying active bundle movements also possessed a prominent gating compliance, such that gating of the mechanotransducer channel made a significant contribution to the compliance of the hair bundle. One indication of the active bundle movements was the presence of a recoil in the displacement response to a force step with a time course similar to adaptation of the transducer current (Ricci et al., 2000). The force–displacement relationship in such cells was nonlinear and possessed a point of inflection, corresponding to the minimum stiffness, when approximately one-half of the transducer channels were open. Figure 1 shows an example in which there was an approximately fourfold reduction in stiffness from 12 mN/m for large positive or negative displacements to a minimum of 3 mN/m over the region in which the open probability changed most. In 10 cells, the limiting stiffness for large positive and negative displacements was 3.3 ± 1.7 mN/m (mean ± SD), and this stiffness declined over the gating range to a minimum of 1.4 ± 0.4 mN/m. These values are more than three times the bundle stiffnesses reported for frog saccular hair cells (Howard and Hudspeth, 1988), which probably reflects more intact gating springs. However, the fractional reduction is similar and indicates that, in turtle auditory hair cells, as in frog hair cells, 50–60% of the compliance of the bundle may be contributed by the gating process. The reduction in stiffness varied between 0.6 and 9 mN/m across cells and was proportional to the maximum size of the transducer current, which ranged from 0.2 to 1.1 nA. This correlation is expected if the reduction in stiffness is a consequence of gating of the mechanotransducer channels.

Fig. 1.

Nonlinear compliance of the hair bundle.A, The stereociliary bundle of a hair cell was stimulated with a flexible fiber, delivering a family of force steps (top) that generated mechanotransducer currents (middle) and associated bundle displacements (bottom). The largest force step was 175 pN.B, The force–displacement relationship (top) and the current–displacement relationship (bottom, filled circles) were derived from the records in A, measurements of both mechanotransducer current and bundle displacement being taken 0.5 msec after commencing the force step (see Materials and Methods). Hair bundle stiffness was calculated by differentiating the force–displacement results and is plotted against displacement (bottom, open circles). The force–displacement results are fitted with Equation 1, and the bundle stiffness–displacement results are fitted with Equation 3, withK_s = 13.5 mN/m,K_c = 10.8 mN/m,x_o = 47 nm, and z = 0.27 pN.

The force–displacement relationships were used to obtain the slope stiffness of the bundle, which, when plotted against displacement, could be fitted by Equation 3 (Figs. 1,2). From these fits, the gating force per channel, z, was calculated as described in Materials and Methods. Measurements on 10 cells gave a mean z of 0.25 ± 0.03 pN, which is similar to values reported for other preparations (Markin and Hudspeth, 1995; van Netten and Kros, 2000). The mechanical sensitivity of the hair cells in these experiments was inferred from the plot of the mechanotransducer current divided by its maximum value (I/I_max) against bundle displacement. The plot was fit over its steepest region with a straight line that had a mean inverse slope of 44 ± 19 nm. The slope provides a measure of the operating range of the mechanotransducer channels. It was used to obtain an independent estimate forz, the gating force per channel (Markin and Hudspeth, 1995) of 0.37 ± 0.16 pN, which is similar to the value inferred from the stiffness–displacement relationship.

Fig. 2.

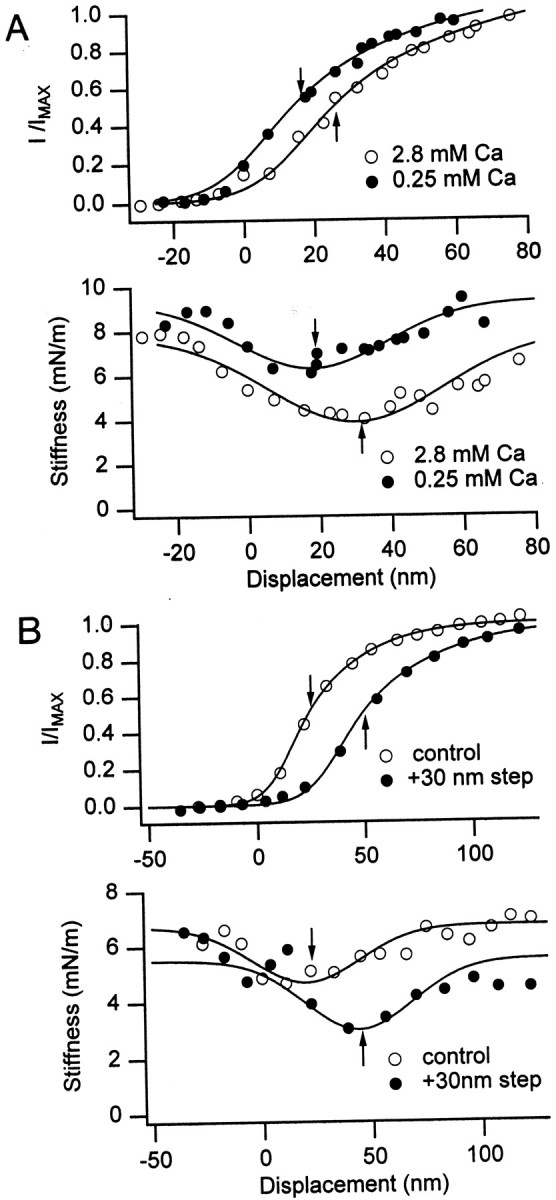
Simultaneous shifts in the mechanotransducer channel activation and gating compliance. A, Reducing the extracellular calcium concentration from 2.8 to 0.25 mmcaused leftward shifts in the channel activation (top) and in the bundle stiffness–displacement relationship (bottom). The channel activation relationship is plotted as the mechanotransducer current, I, normalized to its maximum value, I_max, whereI_max = 0.95 nA (2.8 mmcalcium; open circles) and 1.014 nA (0.25 mmcalcium; filled circles). The bundle stiffness–displacement relationships were fitted with Equation 3, withK_s = 8.0 mN/m,K_c = 4.0 mN/m,x_o = 30 nm, and z = 0.23 pN (2.8 mm calcium) and withK_s = 9.3 mN/m,K_c = 3.0 mN/m, x_o = 18 nm, and z = 0.31 pN. B, A 30 nm sustained displacement of the hair bundle toward the kinocilium caused rightward shifts in the channel activation (top) and in the bundle stiffness–displacement relationship (bottom). The channel activation curve and hair bundle mechanics were assayed with a test stimulus 3 msec in duration starting 5 msec after the onset of the adapting step. Mechanotransducer currents, I, normalized to an I_max of 0.85 nA in both conditions. The bundle stiffness–displacement relationships were fitted with Equation 3, with K_s = 6.7 mN/m,K_c = 2.0 mN/m,x_o = 20 nm, and z = 0.23 pN (control; open circles) and withK_s = 5.5 mN/m,K_c = 2.5 mN/m,x_o = 44 nm, and z = 0.23 pN. In both A and B, thearrows indicate the bundle position for half-activation of the channels (top) and for minimum stiffness of the bundle (bottom).

Effects of calcium on hair bundle mechanics

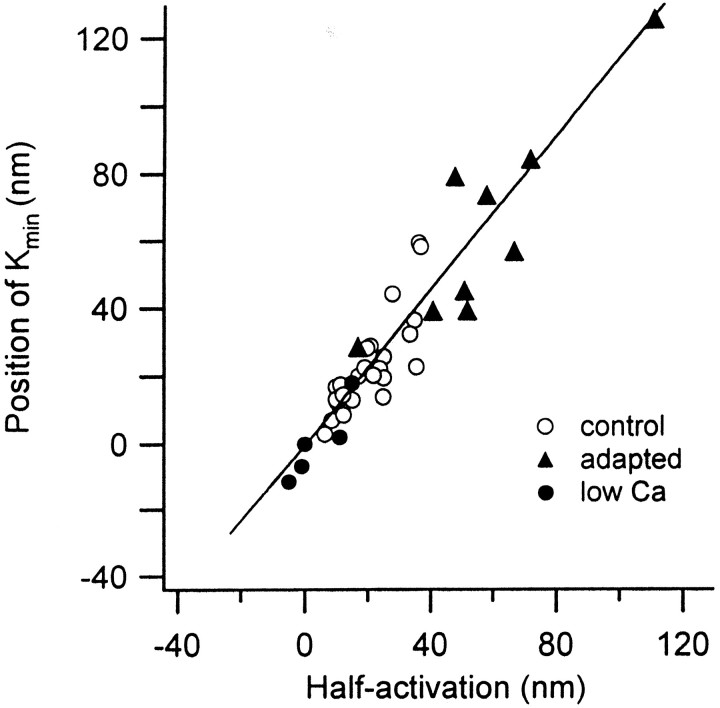
The active bundle movements are thought to be driven by a rise or fall in intracellular calcium acting via a change in the probability of opening of the mechanotransducer channels. A key test of this mechanism for the active movements is to alter the gating compliance by manipulating calcium within the stereocilia. Lowering extracellular calcium should reduce stereociliary calcium, whereas sustained bundle deflection toward the kinocilium should increase stereociliary calcium. Figure 2 shows the results of these procedures, each of which altered the range of bundle positions over which the mechanotransducer channels were activated. Lowering external calcium translated the activation curve to the left, corresponding to a displacement away from the kinocilium, whereas an excitatory adaptive step shifted the activation curve to the right, toward the kinocilium. These shifts in the activation curve along the displacement axis were accompanied by equivalent shifts in the stiffness–displacement relationship, assayed from the bundle position at which the stiffness was a minimum. The bundle position for minimum stiffness is indicated by thearrows in Figure 2. Reducing the external calcium from 2.8 to 0.25 mm translated the position of minimum stiffness by 40 ± 15 nm (n = 5). For both cells in Figure 2, the shift in the bundle position for the stiffness minimum was similar to that for half-activation of the mechanotransducer channels. The correlation between the electrical and mechanical parameters is shown in Figure 3. These results demonstrate that the nonlinear behavior of turtle auditory hair bundle attributable to gating compliance can be changed by procedures that might be expected to alter intracellular calcium. A similar effect on the gating compliance of frog saccular hair cells has been reported previously (Howard and Hudspeth, 1988).

Fig. 3.

Correlation between mechanotransducer channel activation and hair bundle mechanics. The bundle position for minimum stiffness, K_min, is plotted against that for half-activation of the channels (see arrows in Fig. 2). control are measurements in 2.8 mmextracellular calcium (open circles; eachsymbol is a different hair cell); adaptedare in similar conditions to controls, except with a sustained bundle displacement of between 30 and 150 nm toward the kinocilium (filled triangles); low Ca are in 0.25 mm extracellular calcium (filled circles). Line is a least-squares fit with slope 1.15, intercept −0.6 nm, and regression coefficient 0.95.

The effects of reducing extracellular calcium took several minutes to stabilize because of the speed of the perfusion system, and we therefore had no information about how fast these changes occurred. However, for small bundle displacements, adaptation was rapid, and the decline in the mechanotransducer current and the shift in the activation curve of the channel were complete in, at most, 5 msec. There were suggestions that manipulating intracellular calcium had other effects besides those attributable to shifts in channel gating. Thus, in all cells studied, lowering extracellular calcium produced a small increase in the nongating stiffness, and adaptation caused a small decrease in the nongating stiffness. In five cells, the limiting stiffness (the stiffness for displacements in which the probability of channel opening was ∼0 or 1) was 3.0 ± 0.5 mN/m (mean ± 1 SEM) in 2.8 mm external calcium, and it increased to 4.8 ± 1.3 mN/m in 0.25 mm external calcium. In nine other cells, a limiting stiffness of 3.5 ± 0.5 mN/m was reduced to 2.8 ± 0.6 mN/m by a positive adapting step. These changes, although small, were significant at the 0.05 level in a two-tailedt test. An increase in bundle stiffness on reducing extracellular calcium has been reported previously for frog saccular hair cells (Marquis and Hudspeth, 1997). The origin of these effects is unknown, but, because they occur with adaptation, they are likely to be a consequence of changes in intracellular calcium.

Estimate of force generated by the active process

Depolarization of the hair cell positive to 0 mV, which opens transducer channels probably by lowering bundle calcium, also elicits active bundle movements. Such movements are accompanied by the simultaneous development of an outward current flowing through newly opened channels (Ricci et al., 2000). This behavior provided a means of determining the magnitude of force generated by the active process. Figure 4 shows that a depolarizing voltage step to +60 mV from the holding potential of −80 mV caused a sustained displacement of the free-standing bundle toward the kinocilium. When the flexible fiber was placed against the tip of the bundle, on its kinocilial side, the amplitude of the active movement was reduced because the bundle now had to perform work against the stiffness of the fiber. The evoked displacement was restored to its original size on detaching the fiber. The force produced by the active process was then inferred from the reduction in movement caused by the fiber multiplied by the stiffness of the fiber. In Figure4A, a fiber with a stiffness of 3.3 mN/m reduced the bundle movement by 8 nm, so the bundle produced a force of 26 pN.

Fig. 4.

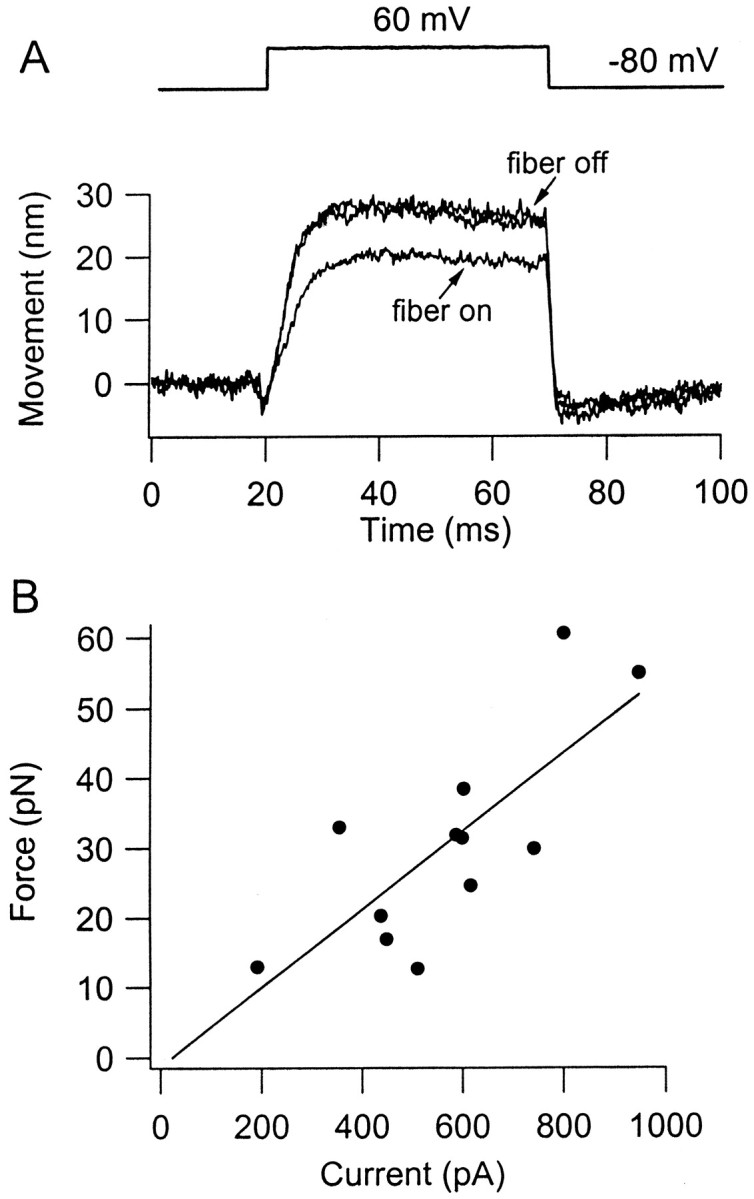
Force generated by active movement of the hair bundle. A, Three averaged bundle displacements produced by depolarizing voltage steps from −80 to +60 mV, in the presence (fiber on) or absence (fiber off) of a flexible fiber attached to the tip of the bundle. Positive displacements are toward the kinocilium. Superimposed movements of the free bundle (fiber off) are measurements before attachment of the fiber and after its removal. The force generated is 26.4 pN, the product of the difference is peak motion with and without the fiber (8 nm) and the stiffness of the fiber (3.3 mN/m). B, Collected results in 12 cells of the force generated by active bundle motion plotted against the mechanotransducer current activated during a depolarization to +60 or +80 mV (for method of measurement, see Ricci et al., 2000, their Fig. 7). All currents have been corrected to a holding potential of +80 mV, assuming a reversal potential for the transducer current of 0 mV. Straight line is a least-squares fit, with slope 0.056 pN/pA and regression coefficient 0.84.

We showed previously that the displacement of the free-standing bundle attributable to depolarization was proportional to the amount of outward current activated and, hence, number of channels opened (Ricci et al., 2000, their Fig. 7). In the present experiments, the force attributable to the active process also increased with the size of transducer current activated (Fig. 4B). The results have been fitted with a straight line, the slope of which can be used directly to determine the gating force per channel. The linear relationship depicted assumes that the bundles assayed all have the same height and stereociliary complement. There are likely to be small differences in both parameters with hair cell location (Hackney et al., 1993), but, because recordings were made at a restricted range of locations (see Materials and Methods), the variations would be within the scatter of the results. After correcting for differences in membrane potential between experiments, the current should be proportional to the number of mechanotransducer channels opened. Assuming that these channels have a unitary conductance of 106 pS (Crawford et al., 1991) and a linear current–voltage relationship, the slope of the fitted line in Figure4B can be expressed as a force of 0.47 pN per transducer channel. This value is comparable with the gating force per channel deduced from the force–displacement relationships (0.25 pN; see above). Such agreement would be expected if the active bundle motion stems from gating of the mechanotransducer channel.

Two components of the active response

The hair bundle movement caused by depolarization (Fig. 4) (Ricci et al., 2000) was of the opposite polarity to that reported for frog saccular hair cells under comparable stimulus conditions (Assad et al., 1989). Thus, depolarization to +80 mV produced a sustained bundle displacement toward the kinocilium in turtle but away from the kinocilium in the frog, the amplitude of the motion being similar in the two cases. The simplest explanation for this discrepancy is that different mechanisms underlie the active movements in turtle and frog. A frequently observed aspect of our measurements was that the displacement would reach a peak and then decline slightly or sag during the depolarization. If the sag was present, at the end of the voltage step, the bundle would overshoot its original position before returning slowly to rest (Figs. 4A,5A). This behavior occurred in free-standing bundles and was more prominent at larger depolarizations, suggesting the recruitment of a second component in the movement of reverse polarity. The reduction in displacement with time was most obvious if the voltage step was lengthened, and sometimes the reversed component would bring the bundle back to its original position. The time course of the second component was slow, and, when fitted with a single exponential, it had a time constant ranging between 100 and 300 msec (mean of 163 ± 95 msec;n = 4). These time constants are 100 times slower than that of the initial movement, which was simultaneous to fast adaptation. The relaxation in bundle position was not accompanied by a decline in the current, signifying channel closure, but was associated with a small slow growth of the outward current. It must therefore reflect a secondary increase in the opening of the mechanotransducer channels. These results indicate that two components of active bundle movement arise in turtle auditory hair cells.

Fig. 5.

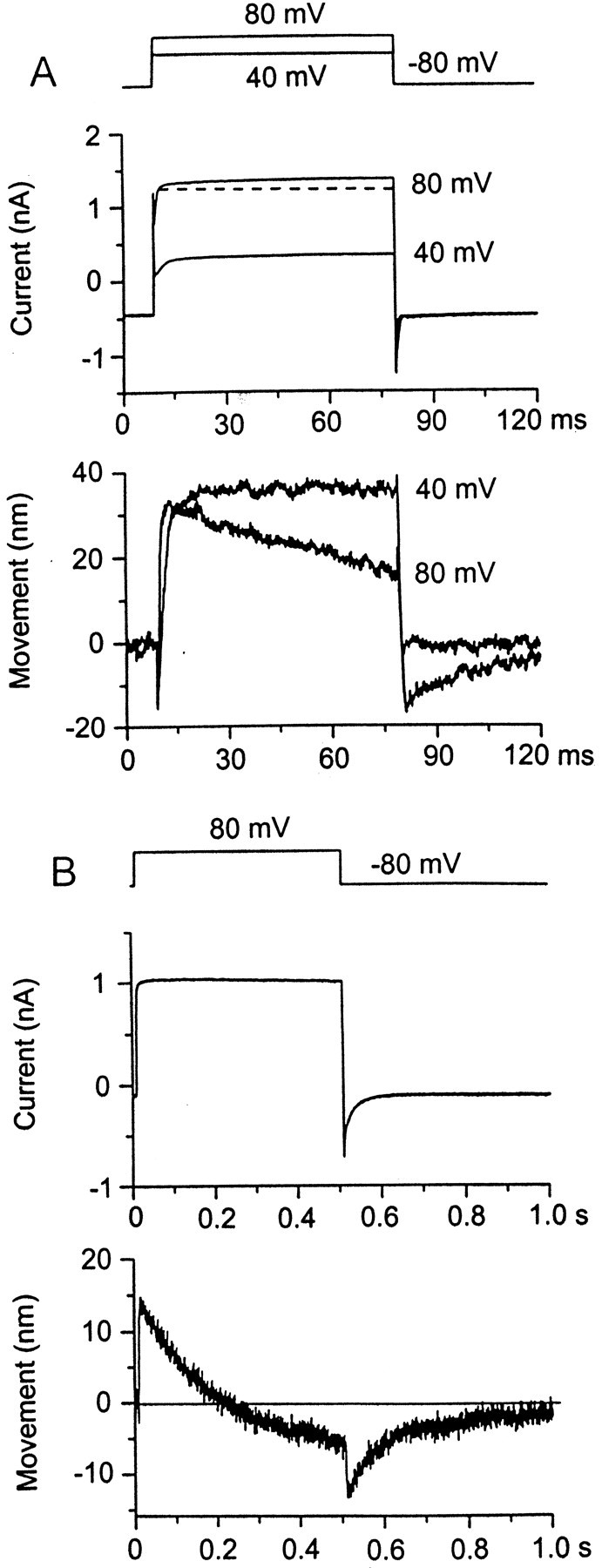
Sags in the bundle displacement produced by depolarization. A, A depolarizing step to +40 mV caused an increase in outward current as a result of opening of mechanotransducer channels (middle) and a sustained displacement of the bundle toward the kinocilium (bottom). When the depolarization was increased to +80 mV, the bundle displacement was not maintained but sagged back toward the resting position, and, on return to the holding potential, the bundle overshot its original position before slowly returning to rest. Despite the sag in the bundle displacement at +80 mV, the current increased slightly. The very fast transient at the onset of the depolarization is unrelated to transducer channel gating (Ricci et al., 2000). B, A pronounced sag in the movement for a longer, 500 msec, depolarizing step in which the bundle went past its resting position during the depolarization. Note that the sag in the bundle movement was not accompanied by a decline in the current.

Polarity of active bundle motion depends on bundle position

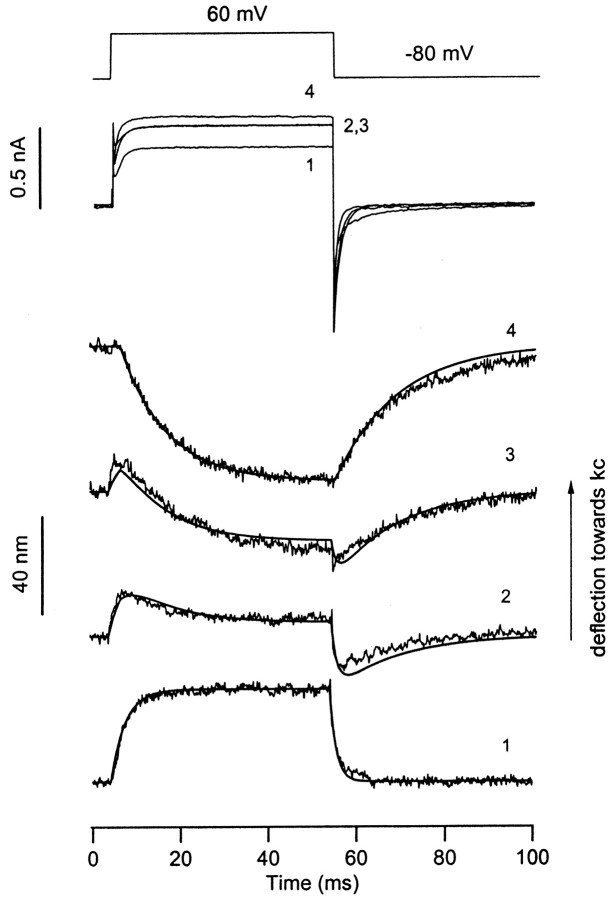
Reversal of the polarity of response to a depolarizing voltage step could also be achieved by a sustained deflection of the hair bundle toward the kinocilium (Fig. 6). In a free-standing bundle, or one in which the flexible fiber had been brought into contact with the bundle without perturbing its position, a depolarization from −80 to +60 or +80 mV caused an initial movement toward the kinocilium, as described above. This will be referred to as the normal response. However, if the fiber was then displaced in the direction of the kinocilium, the response to the depolarization diminished, and, for sustained movements of 90 nm of more, it was reversed. The mean bundle displacement needed to reverse the response in seven cells was 167 ± 67 nm. When the fiber was pulled back, restoring the hair bundle to its original position, the polarity of the displacement response was returned to normal. The reversal is unlikely to be an artifact of a change in position of the image of the bundle on the photodiode because the small transient at the onset of the response did not reverse. The origin of this early instantaneous component is unknown, but it is unlikely to be related to gating of the mechanotransducer channels because it is insensitive to streptomycin (Ricci et al. al., 2000). In many of the experiments, the offset in bundle position slightly increased the steady inward current, presumably because of an increase inp_o for the mechanotransducer channels. Furthermore, the outward current during the step was larger, implying that more mechanotransducer channels opened. A possible explanation for the increase in the number of channels opened by depolarization with a positive bundle deflection is shown in Figure 6B. This explanation requires that the mechanotransducer channels are significantly adapted by the imposed bundle displacement, implying that the resting calcium concentration within the stereocilia was elevated.

Fig. 6.

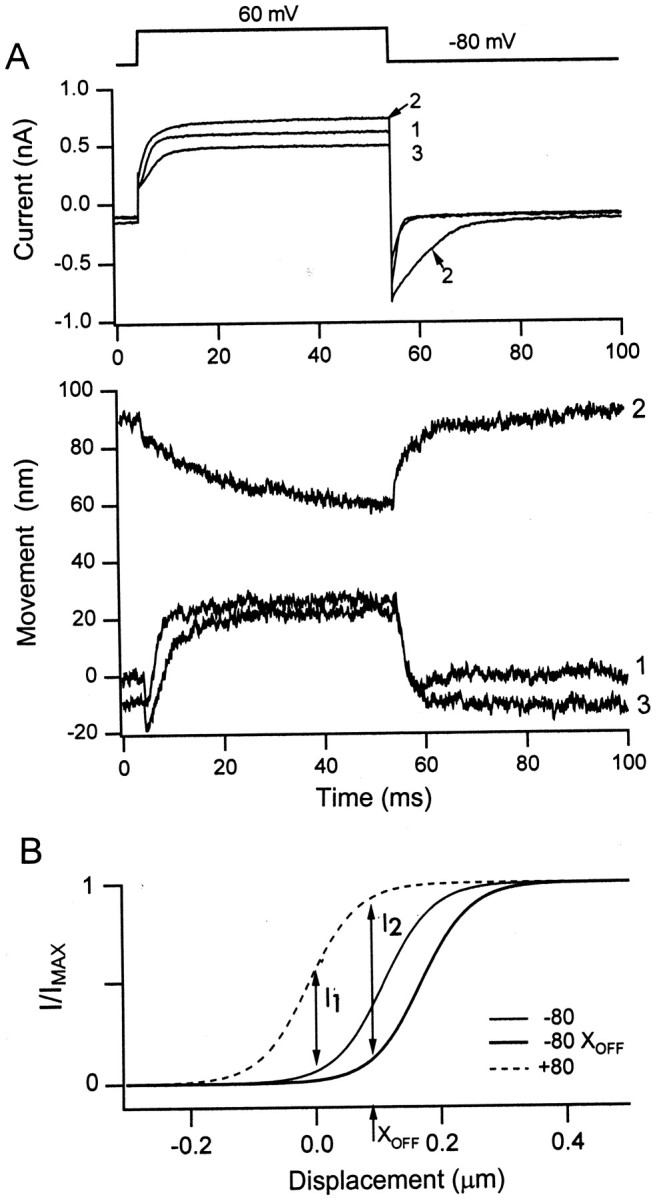
Polarity of active bundle motion depends on bundle position. A, Depolarization to +60 mV produced an outward current and a displacement toward the kinocilium when delivered at the resting position of the bundle (trace 1). With a sustained displacement of the bundle toward the kinocilium by the attached flexible fiber, an outward current still occurred, but the polarity of the bundle motion was reversed and slowed (trace 2). When the bundle was restored to its original position, the polarity of bundle motion for the depolarizing step returned to normal (trace 3). Note that the outward current was larger when the bundle was displaced toward the kinocilium (trace2) than when in its unperturbed position (traces1, 3).B, Theoretical activation curves for the mechanotransducer channels at −80, +80, and −80 mV with a sustained bundle offset, X_OFF. In response to depolarization from −80 to +80 mV, there is an increase in the probability of opening of the transducer channels (I₁), causing an outward current. If the bundle is displaced toward the kinocilium byX_OFF, then the activation curve shifts to the right because of channel adaptation. In response to the same depolarization, there is now a larger increase in the probability of opening of the transducer channels (I₂), causing a greater outward current. The activation curve at +80 mV is the same for the two conditions because the channels do not adapt at positive holding potentials.

The reversed displacement response had a slower time course than the normal response at both the onset and offset of the voltage step. The onset of the displacement could be fit with a single exponential, which, in seven cells, had a time constant of 3.8 ± 1.7 msec for the normal polarity and 17.8 ± 7.4 msec for reversed polarity. This slowing was also evident in the current response, which showed a particularly slow return to the baseline at the end of the voltage step. It has been argued previously that the decline in current at the end of the voltage step is a manifestation of adaptation of the mechanotransducer channels (Assad and Corey 1992; Ricci et al., 2000). Thus, as the membrane potential is stepped back to −80 mV, the electrochemical gradient driving calcium into the stereocilia is increased, so calcium enters the stereocilium to promote adaptation. The slowing of adaptation during sustained bundle deflection may be attributable to a rise in resting stereociliary calcium or may reflect a displacement sensitivity to the process. The phenomenon is probably related to the slowing of adaptation seen with larger displacement steps in a family of mechanotransducer currents, such as those in Figure 1A (see also Wu et al., 1999, their Fig. 1).

It is unclear whether the slower reversed response to depolarization reflects the recruitment of a separate mechanism or whether it is attributable to modification of the normal response by the elevated intracellular calcium. The reversed response showed the same dependence on membrane potential as the normal response, growing for depolarizations positive to 0 mV and then eventually saturating (Ricci et al., 2000). This suggests that the reversed response, like the normal response, is also controlled by changes in intracellular calcium. When the bundle was deflected incrementally during presentation of depolarizing voltage steps, it was possible to observe at intermediate bundle positions a biphasic movement that may represent the transition from the normal to reversed response (Fig.7). To demonstrate that the intermediate responses (Fig. 7, traces 2, 3) were a mixture of the normal (N) and reversed (R) responses (Fig. 7, traces 1,4), N and R were each fit with single time constants for their onset and offset. The onset and offset time constants were 3.3 and 1.5 msec, respectively, for the normal response and 10.3 and 14 msec for the reversed response. The intermediate responses could then be described by a linear sum of N and R. For example, trace 2 was well described by adding 0.63 N and 0.37 R, whereastrace 3 was obtained by adding 0.31 N and 0.69 R. The results imply the mixing of two distinct processes, the normal response diminishing and the reversed response growing, as the bundle is biased toward the kinocilium.

Fig. 7.

Depolarization produces two components of bundle motion. Depolarization to +60 mV produced an outward current and a displacement toward the kinocilium when delivered at the resting position of the bundle (trace 1). When the bundle was displaced incrementally toward the kinocilium by the attached flexible fiber (traces 2–4), the bundle motion became biphasic and then reversed polarity. Superimposed current records are shown for the four positions, with the corresponding bundle motions shown below. The normal response (trace 1; N) and the reversed response (trace 4; R) were fitted with single-exponential onsets and decays. The onset and offset time constants were 3.3 and 1.5 msec, respectively, for N, and 10.3 and 14 msec, respectively, for R. Linear combinations of N and R [aN + (1 − a)R] were calculated to best describe the intermediate responses: a = 0.63 for trace 2, and a = 0.31 fortrace 3. This suggests the mixing of two distinct processes. For all responses, the smooth theoretical lines are superimposed on the noisy experimental records. A negative step corresponding to a small fast component unrelated to gating of the mechanotransducer channels has been subtracted from each averaged displacement record.

DISCUSSION

The mechanotransducer channel as the source of the active movement

Motion of the stereociliary bundle of the hair cell to a force stimulus is governed by its mechanical compliance. This compliance has a passive component attributable to the flexibility of the stereociliary ankles and the stiffness of the gating springs, and an active component, the gating compliance, linked to the opening and closing of the mechanotransducer channels (Howard and Hudspeth, 1988). The relative importance of the gating compliance may differ in different end organs (Russell et al., 1992; van Netten and Khanna, 1994; Géléoc et al., 1997). We described previously for turtle auditory hair cells a fast active bundle motion associated with the gating of the transducer channels, which is most simply explained if the gating compliance makes a substantial contribution to bundle mechanics (Ricci et al., 2000, their Fig. 12). Here we presented several lines of evidence supporting this mechanism. (1) The force–displacement relationship of the hair bundle was nonlinear and possessed a point of inflection, corresponding to the maximum compliance, when approximately one-half of the transducer channels were open. This analysis is consistent with a gating compliance that contributes a significant proportion (50–60%) of the total compliance of the bundle. (2) The nonlinearity in the force–displacement relationship of the bundle occurred over a similar range of open probabilities to the active motion; both the fast recoil in bundle displacement to a force step and the bundle compliance were largest for open probabilities of 0.4–0.6. (3) The nonlinearity in the force–displacement relationship of the bundle, like the active bundle motion, was sensitive to changing intracellular calcium by lowering extracellular calcium concentration or superimposing stimuli on an adapting step. (4) A single-channel gating force of 0.25 pN, derived on the gating spring hypothesis (Howard and Hudspeth, 1988), was comparable with that of 0.47 pN obtained by independent measurements on the force produced by the bundle for a depolarizing voltage step. To account for the fast active bundle movements, the nonlinearity in the force–displacement relationship should shift rapidly with channel gating. In support of this notion, the shifts in open probability and bundle stiffness for an adapting step occurred as quickly as they could be monitored, which was within 5 msec. Together, these pieces of evidence support the idea that the nonlinearity in the force–displacement relationship is attributable to the gating compliance and that its fast translation along the displacement axis as the channel opens and closes can account for the fast active bundle motion.

Because force generation by the bundle is linked to gating of the mechanotransducer channels, it operates at frequencies within the auditory range. For example, the fast recoil that follows adaptation in turtle hair cells has a time constant between 0.3 and 3 msec, corresponding to a frequency range of 50–500 Hz (Ricci et al., 2000). Such speed would enable it to amplify hair bundle movements, thereby increasing auditory sensitivity. The amount of force produced by the hair bundle will be primarily determined by two factors: the number of mechanotransducer channels and the bundle geometry. The gating force per channel exerted at the tip of the bundle will be smaller than at the channel by a geometrical gain, γ, equal to the ratio of the inter-stereociliary spacing divided by the average stereociliary height in the bundle (Howard et al., 1988). For turtle auditory hair cells in the mid-frequency range, γ = 0.06 (Hackney et al., 1993), and the average value for gating force at the tip of the bundle from the two methods is 0.36 pN per channel. Therefore, the force at the channel itself is on the order of 6 pN. Assuming that the gating force at the channel is similar in all hair cells, the force generated by the bundle will become larger with an increase in the number of mechanotransducer channels per bundle and a decrease in bundle height (increasing γ). In turtle hair cells, both parameters vary with the characteristic frequency of the cell (Hackney et al., 1993; Ricci and Fettiplace, 1997), in a manner that makes the force larger in cells tuned to higher frequencies. The increase in active force generation by hair bundles of cells at higher frequency may be needed to offset the viscous load on the bundles, which will also become more prominent at higher frequencies.

Multiple components of force generation

Our experiments demonstrate that other types of active bundle movement can also be observed in turtle auditory hair cells, and these movements are slower and of opposite polarity to the fast movements that were the main focus of the previous study (Ricci et al., 2000). Whereas these fast movements have time constants of ∼1 msec, slower movements with time constants of 10–20 msec (Figs. 6, 7) and 150 msec (Fig. 5) are seen under certain conditions. The time course of the slow movements was variable across cells, but it is unclear whether such intrinsic variability can explain the 10-fold difference in mean values observed under the two experimental circumstances in Figures 5-7, and more than one slower process may be involved. The slow movements are of the same polarity and amplitude as those reported for frog saccular hair cells, in which motion of free-standing bundles could also be produced by depolarizing voltage steps (Assad and Corey, 1992). Those movements had a mean time constant of 193 msec for depolarization to +80 mV and 56 msec for repolarization to −80 mV. Faster displacements may have been missed in their experiments because of the limited sampling imposed by the 30 Hz frame rate of the camera used for imaging the bundle. Indeed, other methods of stimulation have demonstrated both fast and slow active movements in frog hair bundles (Howard and Hudspeth, 1987; Denk and Webb, 1992; Benser et al., 1996). For example, analysis of spontaneous hair bundle motion revealed two temporal distributions with time constants of ∼1.5 and 15 msec, respectively (Denk and Webb, 1992). These values are similar to two of the kinetic components for turtle hair bundles. Thus, it seems likely that multiple mechanisms of active bundle motion and adaptation are a general feature of mechanotransduction in all hair cells.

In both the present results and those of Assad and Corey (1992), the slow bundle displacement produced by depolarization was directed away from the kinocilium. However, a decline of the inward transducer current denoting adaptation always occurred at the end of depolarizing step (Figs. 5, 6A, 7A) despite the polarity of the bundle movement. The underlying mechanisms of the fast and slow processes must therefore differ, although both lead to closure of the mechanotransducer channels. However, why, as is clear from Figure 7, does the fast movement disappear if the bundle is pushed toward the kinocilium? One idea (Wu et al., 1999) sees the state of the mechanotransducer channels as determined by a balance between the tension in the gating springs that favors opening and the binding of intracellular calcium to an intracellular site that causes channel closure. When all of the calcium sites are occupied, the likelihood of channel closure is maximal and constant. At this point, increasing tension in the gating springs will still promote channel opening, and large enough displacements must eventually overcome any action of intracellular calcium to close the channels: hence, the disappearance of fast movements when the bundle is biased toward the kinocilium. This explanation might also account for the disappearance of the fast component of current adaptation with large stimuli (Wu et al., 1999, their Fig. 1).

The results in Figures 6 and 7 indicate that the slower component possesses a displacement sensitivity that would make it most important for large bundle deflections toward the kinocilium. In line with this observation, adaptation in turtle hair cells in response to stepping the bundle becomes slower for larger stimuli, which has been interpreted as being attributable to the recruitment of a second component of adaptation (Wu et al., 1999). This additional component had a time constant in the same range of 10–20 msec as the reversed-polarity bundle movements. Moreover, it depended on the concentration of internal calcium buffer, implying that it, too, was controlled by intracellular calcium. Thus, two calcium-controlled processes both result in closure of the mechanotransducer channels but cause bundle motions of opposite polarity.

It has been argued that the slow adaptation in the mechanotransducer currents of frog hair cells reflects the operation of a motor, powered by an unconventional myosin, which tensions the tip links (Assad and Corey, 1992; Hudspeth and Gillespie, 1994). This motor is also regulated by intracellular calcium. Thus, a fall in intracellular calcium occurring during depolarization will have two effects on bundle position. On a millisecond time scale, the drop in calcium directly opens mechanotransducer channels, causing a movement of the bundle toward the kinocilium (Ricci et al., 2000). Over tens or hundreds of milliseconds, the reduced intracellular calcium will activate the myosin motor applying tension to the tip links to pull the bundle away from the kinocilium (Assad and Corey, 1992). More experiments are needed to show that the slower reversal in polarity of the bundle movement reported here involves the myosin motor.