From Spectrum to Space: The Contribution of Level Difference Cues to Spatial Receptive Fields in the Barn Owl Inferior Colliculus

Abstract

Space-specific neurons in the owl's inferior colliculus have spatial receptive fields (RFs) computed from interaural time (ITD) and level (ILD) differences. Because of the shape of the owl's head, these cues vary with frequency in a manner specific for each location. We sought to determine the contribution of ILD to spatial selectivity. We measured the normal spatial receptive fields of space-specific neurons using virtual sound sources (i.e., noises filtered to simulate external sound sources, presented using headphones). The virtual-source filters were then altered so that ITD was fixed while frequency-specific ILDs varied according to location in the usual manner. The resulting “ILD-alone” RF typically revealed a horizontal band of excitation that included the normal RF. Above and below, the neurons were inhibited. Interestingly, the maxima of ILD-alone RFs were generally outside the normal RF, suggesting that space-specific neurons are not optimally tuned to the ILD spectrum occurring at the normal RF location. Congruously, frequency-specific ILD tuning, assessed with tones, better matched the ILDs at the peak of the ILD-alone RF than those at the peak of the normal RF. The firing evoked from the normal RF may thus reflect the balance of excitatory and inhibitory inputs needed to appropriately restrict the receptive field.

Frequency-specific ILD tuning curves were combined with measured head-filtering characteristics to predict responses to the frequency-specific ILDs at each location. The predicted ILD-alone RFs, which are based on a simple sum of frequency-specific inputs, accounted for 56% of the variance in our measured ILD-alone RFs.

The barn owl (Tyto alba) is a nocturnal predator specialized for sound localization. Its inferior colliculus (IC) contains auditory cells with tightly restricted spatial receptive fields (RFs), topographically arranged into a map (Knudsen and Konishi, 1978b). Despite such specializations, the owl uses the same binaural cues that humans and other mammals rely on, namely, interaural time difference (ITD) and interaural level difference (ILD). In both owls and mammals, the auditory periphery also fractionates sounds into frequency bands. Consequently, the spatial selectivity observed in the owl's IC depends crucially on the integration of information across frequency (Wagner et al., 1987;Brainard et al., 1992; Gold and Knudsen, 2000). Thus, the space-specific neurons provide us with a model with which to uncover general principles of binaural processing and frequency integration.

The filtering characteristics of the ears and face, called the head-related transfer functions (HRTFs), generate a unique combination of frequency-specific ILD and ITD values for each location in space (Moiseff, 1989a; Brainard et al., 1992; Keller et al., 1998). ITD varies primarily with azimuth, and the ITD at any given location is fairly constant across frequencies. In contrast, the spatial distribution of ILD is highly frequency dependent. Below 4000 Hz, ILD varies monotonically with azimuth, whereas at higher frequencies, it varies in a complex manner with both elevation and azimuth. Spatial selectivity is thus derived from a set of frequency-specific ILDs (i.e., an ILD spectrum).

Whereas ITD processing has been well investigated, the contribution of ILD spectra to the spatial selectivity of an IC neuron is less well understood. Brainard et al. (1992) measured RFs using tones emitted from a free-field speaker and, from the RF shapes, inferred the contribution of ILD via modeling. Because they measured the RFs using an external loudspeaker, the contribution of ILD could not be measured independently of ITD. We isolated the contribution of ILD spectra to the spatial RF of a cell by using virtual sound sources, i.e., external sources simulated using headphones. Specifically, we held ITD constant while measuring the response to ILD spectra from different locations. In so doing, we were able to visualize the spatial RF a cell would have were it tuned solely to ILD, referred to as an “ILD-alone” RF.

The ILD selectivity manifest in our measured ILD-alone RFs derives from a frequency integration process (Brainard et al., 1992; Gold and Knudsen, 2000), but exactly how frequencies are combined remains unclear. We examined the hypothesis that the response of a space-specific neuron to broadband ILD spectra can be predicted by a linear sum of its responses to tones at different ILDs. Frequency-specific ILD responses were measured at a constant ITD, and the responses were combined linearly using the HRTFs to predict the ILD-alone RF of the cell. The predicted RF was compared with the ILD-alone RFs measured with noise.

We also examined the hypothesis that the frequency-specific ILD tuning of a space-specific neuron should match the ILD values occurring at the center its spatial RF (Knudsen, 1999). Although Gold and Knudsen (2000)have argued recently that this is in fact the case for space-specific neurons in the owl's optic tectum, the variance in their measurements was large relative to the range of ILDs studied. Our measurements allowed us to evaluate this prediction in more detail.

MATERIALS AND METHODS

Stimulus presentation in virtual auditory space

Stimuli were presented in virtual auditory space using a system developed for the owl in our laboratory. Details of the measurement and use of HRTFs required for this process have been given previously (Keller et al., 1998) and are only summarized below.

For each of the three owls used in this experiment, miniature microphones were used to digitally record the waveform evoked in each ear by an external speaker emitting broadband noise (sampling rate, 30 kHz). As described previously, HRTFs were computed from these waveforms, bandpass filtered between 2000 and 11,000 Hz, and stored as 255-point finite impulse response filters (Keller et al., 1998). Each HRTF filter was capable of reproducing the location-specific filtering imposed on a sound by the ears and facial features. HRTFs were obtained for 684 different locations covering the entire frontal hemifield, spaced every 5° in azimuth and elevation using “double-polar” coordinates (Knudsen, 1982). (In double-polar coordinates, azimuth specifies the angular separation, from the owl's perspective, between a given location and the median plane, whereas elevation specifies the angular separation between a location and the horizontal plane passing through the center of the owl's head.)

Each bird was tested using its own HRTFs. During electrophysiological recording sessions, stimuli were presented via earphones (model ER-1, Etymotic Research, Elk Grove Village, IL; model HB6 amplifier, Tucker Davis Technologies, Gainsville, FL). To simulate a localized external sound source, a signal was convolved with two binaural filters, one that imposed the spectral profile appropriate for the specified location and the other that compensated for the response characteristics of the earphone–ear canal system. Using these filters, we were able to duplicate the waveform that would have been induced at the eardrum by an external sound source at a specified location. The inverse filters used to compensate for the earphone–ear canal system were also used when assessing neuronal responses to ILDs using pure tones. This ensured that ILD values measured with tones and those present in the broadband stimuli were directly comparable. Convolution was handled by dedicated hardware (model AP2 array processor and model PD1 Power DAC programmable digital signal processor/digital-to-analog converter; Tucker Davis Technologies).

To isolate the contribution of ILD spectra to the spatial RF of a cell, we first created a set of filters, called “ILD-alone filters,” that preserved the monaural amplitude spectra of each location but fixed the ITD at the optimal value of a cell. ILD spectra were preserved by virtue of the fact that both left and right monaural spectra remained unchanged. The details of this process are as follows. Using the fast Fourier transform, we first computed the amplitude and phase spectra of the finite impulse response filters described above. The phase spectrum from each ear was then replaced with a linear phase spectrum corresponding to a fixed delay, so that the phase difference between the left and right filters was zero at all frequencies. The original amplitude spectra and the new phase spectra were then transformed back into the time domain using an algorithm that minimized the difference between the spectrum of the filter and the desired spectrum (invfreqz function in the Matlab Signal Processing Toolbox, version 5.2; MathWorks Inc., Natick, MA). The resulting ILD-alone filters had an ITD of zero (i.e., the same delay for left and right ears at all frequencies). We then convolved our zero-ITD filters with a second pair of filters that created the ITD appropriate for the cell under study. These ITD-shifting filters were made by taking a discretely sampled unit impulse function, up-sampling it from 30 kHz to 1 MHz, shifting it by an integer number of samples, and then down-sampling it to 30 kHz. (Shifting the 1 MHz filter by nsamples created a time shift of n microseconds.) A low-pass filter was used to avoid aliasing during resampling (see the resample function in the Matlab Signal Processing Toolbox, version 5.2; MathWorks Inc.).

The ILD-alone filters were also adjusted so that, at each location, the average sound pressure level in the ears, or average binaural level (ABL), was equivalent. This ensured that ILD selectivity could be measured at peripheral locations (i.e., greater than ∼70° away from the center), at which ABLs are generally lower. To this end, the ILD-alone filters were scaled so that the average of the left and right peak amplitudes was identical for every spatial location. Although it is possible to scale the root mean squared amplitudes, the use of peak amplitudes ensured that the full range of the digital-to-analog converters was used while preventing clipping of the signal. The range of these adjustments was from 0 to 19 dB, with a mean of 9.5 dB. ABL adjustments of this magnitude would not be expected to alter the ILD selectivity of space-tuned cells. The ABL tolerance of ILD tuning curves in the IC has not been documented; however, it is known that spatial receptive fields, which depend on both ILD and ITD, do not shift with ABL changes of 20 dB (Knudsen and Konishi, 1978a).

Stimuli consisted of 100 msec bursts of tones or broadband noise with 5 msec onset and offset ramps. Broadband noises were generated by filling a sequence buffer with randomly generated numbers uniformly distributed between −n and +n, in which n was a magnitude value appropriate for our stimulus presentation hardware. Noises were bandpass filtered between 2 and 11 kHz before any other filtering and deviated <1 dB from the mean amplitude across this frequency range.

Neurophysiology

All procedures were approved by the Institutional Animal Care and Use Committee of the University of Oregon.

Our data are based on single-cell recordings from the IC of three owls. Techniques for neural recording were similar to those used previously in our laboratory and reported previously (Takahashi and Keller, 1992), with the exception that the present results were obtained using bilaterally implanted recording wells. The wells, made of stainless steel, were cylindrical and had a 7 mm inner diameter. Wells were implanted bilaterally over the owl's telencephalon under isoflurane anesthesia (Iso-Flo; 0.75%, oxygen flow rate of 1.0 l/min; Abbott Laboratories, North Chicago, IL) and held in place with dental cement. Between recording sessions, the wells were filled with an antibiotic ointment (Vedco Triple Antibiotic Ointment, containing neomycin, polymixin-B, and bacitracin; Vedco Inc., St. Joseph, MO) and covered by fitted delrin caps. During recording sessions, owls were sedated with valium (1.25 mg/kg) and anesthetized with ketamine (2.5 mg/kg) delivered intramuscularly approximately once every 4 hr.

Single cells in the IC were isolated using tungsten microelectrodes (12 MΩ; Fredrick Haer Co., Bowdoinham, ME). Action potentials were recorded using the DataWave Technologies (Longmont, CO) Discovery data acquisition package, which stored the time of occurrence of each spike, as well as a 32-point representation of the waveform. The waveforms were sorted off-line according to shape using a commercial software product (Autocut; DataWave Technologies), allowing us to verify that all data came from the same cell over the course of several tests, and, in a few cases, allowing us to extract data from more than one cell at a single recording site.

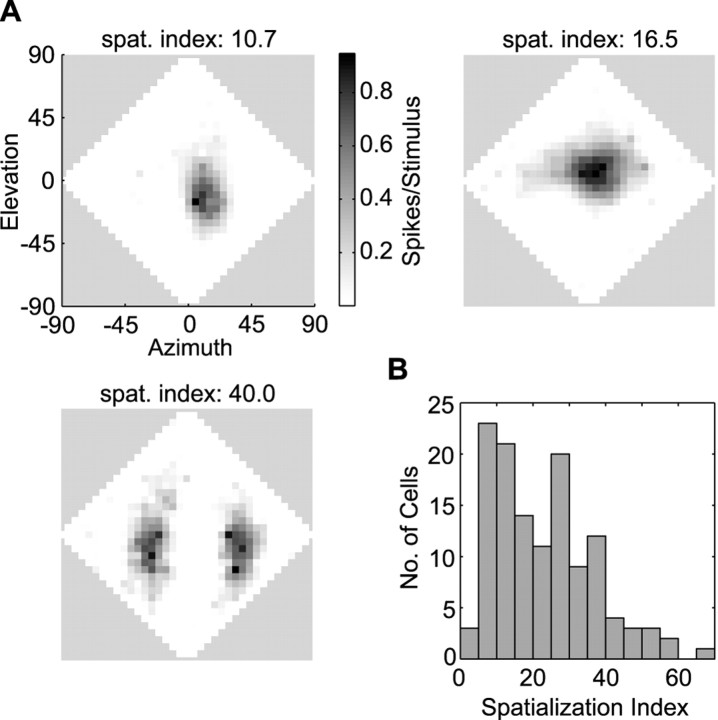
Space-specific neurons were selected based on the compactness of their spatial RFs. To quantify compactness, we developed a metric which we refer to as the “spatialization index:” for each measured RF, all locations that elicited spike rates below spontaneous rate were set to zero, and the entire set of responses was then scaled between zero and one. We then determined the location that elicited maximum firing (i.e., the RF peak). The spatialization index was defined as the sum of the responses at each location times the angular separation of that location from the peak. Angles were measured in double-polar coordinates (see above), and responses were taken every 5° in azimuth and elevation over the entire frontal hemifield. As illustrated in Figure 1A, this quantity was inversely correlated with the spatial specificity of a cell and accorded well with more traditional metrics for selecting space-specific neurons, including degree of ITD side-peak suppression (Takahashi and Konishi, 1986) and width of the frequency tuning curve. We included in our sample only cells whose spatialization index was <15, which gave us a total of 47 cells (Fig.1B).

Fig. 1.

Spatialization indices used in screening cells.A, Examples of normal RFs from three cells and their associated spatialization index values (for definition, see Materials and Methods). Scale bar indicates firing rate scaled between 0 and 1. The diamond-shaped plots represent loci in the frontal hemisphere, from the owl's perspective, expressed in double-polar coordinates (Knudsen, 1982). B, Distribution of spatialization indices for all cells.

The locations of recording sites were verified histologically, using an electrode coated with DiI (Molecular Probes, Eugene, OR) to provide a reference mark. The electrode was prepared by applying several coats of a saturated solution of DiI dissolved in ethyl alcohol. Only a single DiI penetration was made for each side of the brain, and all other penetrations were determined relative to the reference mark. Penetrations for recording sites were clustered in the external nucleus of the IC (ICx) and on the boundary between the ICx and its medial neighbor, the lateral shell of the central inferior collicular nucleus (ICc-ls).

For every cell encountered, a series of three or four tests were run. We first measured the normal and ILD-alone spatial RFs of the cell, using evenly spaced (10° resolution in azimuth and elevation) virtual stimuli presented from 360 locations in the frontal hemisphere. (For the purposes of display, RFs were converted to 5° spacing using linear interpolation.) The term “normal” is used to denote an RF measured with ILD, ITD, and ABL varying as they do under free-field conditions. This differentiates it from an ILD-alone RF, in which only ILD varies.

ITD tuning curves were also measured, using a broadband noise. ITDs typically covered the range of −240 to +240 μsec in 10 μsec steps. Positive values indicate that the sound arrived first in the right ear. The ITD that elicited the maximum response (i.e., the best ITD of the cell) was used in all subsequent tests that required a fixed ITD.

Finally, we measured the response of a cell to pure tones presented at all combinations of evenly spaced ILD and frequency values. Preliminary screening was used to determine the range of frequency values to test. The range of ILDs, on the other hand, was typically set to cover the normal range occurring in the HRTFs: −30 to + 30 dB. Positive ILD values mean that the stimulus was louder in the right ear than the left. All ILD values were generated using programmable attenuators (model PA4; Tucker Davis Technologies). ILD and frequency values were typically spaced by 4 dB and 200 Hz, respectively. The response to these stimuli, plotted as a function of ILD and frequency, is referred to as an “ILD-frequency response surface”.

For all tests, stimuli were presented in blocks, in which a block contained one presentation of each condition. Within a block, the conditions were tested in random order. Blocks were repeated 5–20 times, i.e., each stimulus condition was repeated 5–20 times over the course of the test.

Tones and noises were presented at 15–20 dB above the average tone or noise threshold of IC cells. Average tone and noise thresholds were estimated via ABL response curves measured from IC cells, using either tones (n = 34) or noises (n = 32). If a cell failed to respond well to our stimuli, the sound pressure level was typically increased by 5 dB.

Data analyses

Prediction of ILD-alone receptive fields. The ILD-frequency response surfaces, which demonstrate the tuning of a cell for ILD at different frequencies, were transformed into the spatial domain by combining responses linearly according to the HRTFs. The resulting “predicted ILD-alone RFs” could be compared directly with the measured ILD-alone RFs that were obtained with broadband noise.

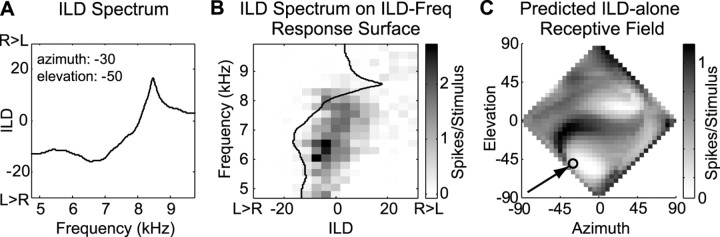
An overview of this process is presented here and is illustrated in Figure 2. Additional details are presented in the next paragraph. Figure 2A shows the ILD spectrum from a particular location (−30° azimuth, −50° elevation; indicated by the arrow in Fig. 2C). This ILD spectrum is superimposed on an ILD-frequency response surface (Fig. 2B). If the ILD spectrum passes through regions of high response, one might expect that the cell would respond strongly to that particular ILD spectrum. If, on the other hand, the ILD spectrum passes only through regions of low response, it is expected that the cell will respond poorly to that spectrum. Therefore, to predict the response at the location of interest, we summed the spike counts elicited by each ILD-frequency combination that was traversed by the ILD spectrum line and divided this sum by the frequency range over which the responses were sampled (Fig. 2C). In other words, the activity along an ILD spectrum line was averaged over the frequencies tested. This process was repeated with the ILD spectra of all loci. Because both ITD and ABL were held constant for all ILD-frequency measurements, the sum of these responses must yield the response to ILD spectra independent of ITD and ABL (i.e., it yields the predicted ILD-alone RF).

Fig. 2.

Transformation of ILD-frequency response surfaces into predicted ILD-alone receptive fields.A, ILD spectrum for a single location (−30° azimuth; −50° elevation). Negative ILDs are louder in the left ear (L>R), whereas positive ILDs are louder in the right ear (R>L). B, ILD spectrum inA superimposed on the ILD-frequency response surface of a cell. The scale bar indicates firing rate in spikes per 100 msec stimulus, less the spontaneous rate. C, ILD-alone RF predicted from the ILD-frequency response surface of a cell. Thearrow points to the location whose spectrum is shown inA and B. The scale bar indicates the averaged sum of pure-tone responses, as described in Materials and Methods.

Before summing, the data were conditioned as follows. ILD-frequency surfaces were transformed so that the frequency axis values matched those of the HRTFs (14.65 Hz spacing) and the ILD axis had spacing of 0.5 dB. Linear interpolation was used to generate the missing spike-rate values. The HRTF-derived ILD spectra associated with each location were also rounded to the nearest 0.5 dB. In addition, the spontaneous rate of the cell was subtracted from the ILD-frequency response surface, thus allowing for negative activity levels in both the ILD-frequency response surface and the predicted ILD-alone RF. For each location, these manipulations yielded an ILD spectrum that corresponded to a string of values on the ILD-frequency response surface. As described above (and in Fig. 2), the predicted response at a particular location was the average of this string of values.

Although it is more consistent with known physiological mechanisms to assume that a linear neuron sums rather than averages the contribution of frequency-tuned inputs, we averaged the response across frequency because the range of frequencies tested varied from cell to cell. For example, a cell whose ILD-frequency surface was measured between 4000 and 8000 Hz would have a total of 273 values along the frequency axis after interpolation, given the 14.6 Hz frequency spacing dictated by the HRTFs (see above). A different cell might have been tested at frequencies between 3000 and 10,000 Hz and would have 477 values along the frequency axis. Averaging therefore ensured that the predicting firing rates are comparable across cells.

One of the important controls in this experiment was that the same ILD spectra were used to measure ILD-alone RFs and to transform pure-tone tuning into a predicted ILD-alone RF. This eliminates the possibility that errors in the measurement of the HRTFs could account for any discrepancies between predicted and measured ILD-alone RFs.

The match between predicted and measured ILD-alone RFs was quantified by a correlation analysis. It should be noted that this analysis is insensitive to differences in overall responsiveness that may exist between the neuron and a linear predictive model. For instance, if the predicted responses were exactly twice as large as measured responses at all locations, the correlation coefficient would still be 1. Therefore, this method is sensitive only to differences in the shapes of the measured and predicted ILD-alone RFs.

ILD curves. Pure-tone ILD tuning curves amount to cross-sections of ILD-frequency surfaces perpendicular to the frequency axis. We determined the best ILD for each such curve (i.e., the ILD that elicited maximum response), using cubic splines to interpolate missing data. Our interpolated curves covered ILD values ranging from −30 to +30 dB in integer steps.

We estimated the variance in our identification of the best ILD by transforming the variance in the neuronal responses to each ILD into the variance in the location of the peak of the ILD tuning curve. For each curve, we took the variance in the neural firing rate at each ILD value as an estimate of the true neural noise. We simulated 2000 measurements of each ILD tuning curve, incorporating Gaussian random noise with the aforementioned variance. Simulated responses below zero were set to zero. We then estimated the best ILD for each of these simulated curves. The variance of this distribution was taken to be the variance in our estimate of the best ILD.

Pure-tone ILD tuning curves were compared against the ILD spectra occurring at the peak of the normal and ILD-alone RFs. For this analysis, the peak of a normal spatial RF was determined via a response-weighted mean of those locations encircled by the half-height contour line. For ILD-alone RFs, the peak location was taken to be the location that elicited maximum response.

RESULTS

Measured ILD-alone receptive fields

For 34 of the 47 cells in our sample, we measured both normal spatial RFs (i.e., with ITD, ABL, and ILD varying as they do with real external sound sources) and ILD-alone RFs (i.e., with ITD and ABL held fixed). The normal spatial RFs of six representative cells are shown incolumn 1 of Figure 3. These RFs, measured with noise sources in virtual auditory space, were similar in shape and size to those observed using free-field stimuli (Knudsen and Konishi, 1978a), confirming the effectiveness of the virtual space technique (Keller et al., 1998).

Fig. 3.

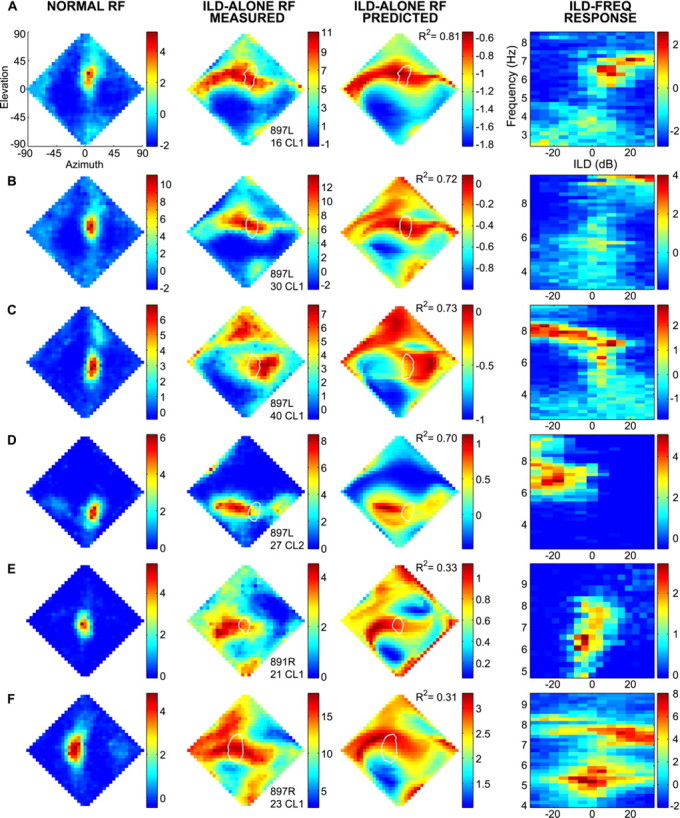
Contribution of ILD to spatial RFs. Rows A–F show the data from six single cells. Thediamond-shaped plots represent loci in the frontal hemisphere, from the owl's perspective, expressed in double-polar coordinates (Knudsen, 1982). Firing rates are represented in pseudocolor. Columns 1 and 2 show the normal RF and the ILD-alone RF, respectively. Column 3represents the ILD-alone RF predicted from the ILD-frequency response surface of that cell (column 4). The white loop on the diamond-shaped plots incolumns 2 and 3 depict the half-height contour line surrounding the normal RF of each cell. The scale bars forcolumns 1, 2, and 4indicate firing rate, in spikes per 100 msec stimulus, less the spontaneous rate. The scale bars for column 3 indicate the averaged sum of pure-tone responses, as described in Materials and Methods.

ILD-alone RFs are provided for each of our six representative cells incolumn 2 of Figure 3. Whereas normal spatial RFs were tightly restricted in both elevation and azimuth, ILD-alone RFs were amorphous and typically showed islands of response separate from the main excitatory region (Fig. 3F, column 2). Compared with normal RFs, ILD-alone RFs showed much greater firing at peripheral locations. This effect is attributable in part to ABL equalization. Under free-field conditions, the frequency-specific ABL at the eardrum falls off by as much as 40 dB as a stimulus of a constant amplitude is moved from the region directly in front of the bird toward the periphery (Keller et al., 1998). This contributes to the lack of firing seen at peripheral locations in normal spatial RFs, which were measured with ABL varying as it does in the free field. In ILD-alone tests, however, ABL was set everywhere equal, thus increasing firing rates at the periphery.

The ILD-alone RFs consistently showed a prominent horizontal band of activity that intersected the normal spatial RF. Based on the known role of ITD in restricting RFs in azimuth (Moiseff and Konishi, 1981;Gold and Knudsen, 2000), it can be inferred that “ITD-alone” RFs (i.e., spatial RFs in which only ITD varies while ILD spectrum and ABL remain fixed) would trace out a narrow, vertically oriented band of locations. Like the ILD band, the ITD band would also intersect the normal RF. The normal RF is thus located at the intersection of the mainly vertical ITD band and the mainly horizontal ILD band.

Although ILD generally appears to restrict firing in elevation, in some cases, it may also provide some degree of azimuthal restriction. For example, the ILD-alone RF shown in Figure 3C clearly shows that ILD limits firing for locations to the left of the normal RF.

The horizontal band seen in the ILD-alone RFs was usually flanked above and/or below by regions of minimal response. In 28 of 34 cells that had significant spontaneous firing rates, 24 had minimal responses significantly below spontaneous rate (p < 0.05). This evidence of active inhibition is remarkable in light of the fact that ITD was set to the preferred value of a cell at all locations. Nonoptimal ILD spectra are thus sufficient to completely inhibit a cell, even when that cell is driven at its best ITD.

For the majority of cells, the peak of the ILD-alone and normal RFs were not the same (Fig. 3D). This effect cannot be accounted for by the fact that ABL was equalized in ILD-alone tests. We estimated the reduction in firing that would have been seen in the ILD-alone RF had ABL varied as it does in normal space tests. This compensation was possible because we knew both the typical ABL response curve of our cells and how much ABL needed to be reduced at each location in the ILD-alone test. Even after this adjustment, the separation between maxima of ILD-alone and normal spatial RFs differed by as much as 53° (mean separation ± SD, 16 ± 12°).

ILD tuning characteristics of space-tuned IC cells

We measured the responses of our 47 space-specific IC cells to all combinations of equally spaced ILD and frequency values, creating an ILD-frequency response surface. A slice parallel to the ILD axis of this surface is an ILD tuning curve at a single frequency. The ILD-frequency response surfaces are shown in column 4 of Figure 3.

We observed that ILD tuning curves for a single cell often changed with frequency. Frequency-dependent ILD changes were sometimes dramatic. For example, in Figure 3C, the best ILD changed from −20 dB at 8000 Hz to +10 dB at 7200 Hz. However, the changes were smaller in most cells. In some cases, ILD tuning curves spaced apart by a mere 200–300 Hz showed clearly different best ILDs. For example, the cell in Figure3A is tuned to +5 dB at 6700 Hz, +15 dB at 6900 Hz, and +20 dB at 7100 Hz.

In cells with spontaneous activity >20% of maximum firing rate, which accounted for 42% of our sample, inhibitory zones were prominent in the ILD-frequency response surfaces. As exemplified by the three cells in Figure 3A–C, it was common to see inhibition on both sides of the ridge defined by the best ILD at each frequency.

Mapping pure-tone ILD-response surfaces to ILD-alone RFs

We used ILD spectra derived from the HRTFs to transform pure-tone, ILD-frequency response surfaces into predicted ILD-alone spatial RFs. As detailed in Materials and Methods and Figure 2, the predicted response to the ILD spectrum from a particular location was taken to be the mean of the pure-tone responses to each of the frequency-specific ILDs occurring in that spectrum. It should be emphasized that this method of transforming pure-tone responses into ILD-alone RFs is based on the assumption that the contributions of each frequency band are independent and are combined linearly by the cell.

ILD-alone RFs predicted from pure-tone responses are shown incolumn 3 of Figure 3. Comparison of columns 2 and3 shows that the predicted ILD-alone RFs were similar in overall shape to those measured directly, although, in some cases, predicted ILD-alone RFs were noticeably misaligned relative to the measured ILD-alone RFs. However, even in the worst cases of misalignment, such as the one shown in Figure 3F, the same general shape was recognizable. In many cases, RFs predicted from pure tones captured idiosyncratic auxiliary zones seen in the measured RF. In Figure 3C, for example, the predicted and measured ILD-alone RFs share a zone of excitation at higher elevations. However, in other cases, predicted ILD-alone RFs were much more extended (Fig.3E).

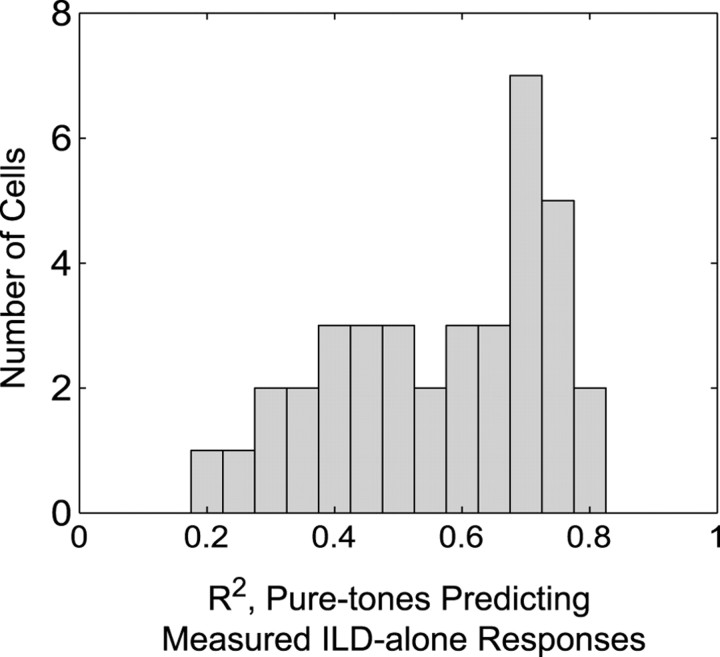
The similarity between predicted and measured ILD-alone RFs was quantified by a correlation analysis. In all cases,R² differed significantly from zero (p < 0.01). As shown in Figure4,R² values ranged from 0.20 to 0.83, with many cells having R²values in the 0.7–0.8 range. The meanR² was 0.56, i.e., the linear sum of pure-tone responses accounted for ∼56% of the variance in the measured ILD-alone responses.

Fig. 4.

Distribution of allR² values for predicting broadband ILD-alone RF values from a linear sum of pure-tone responses.

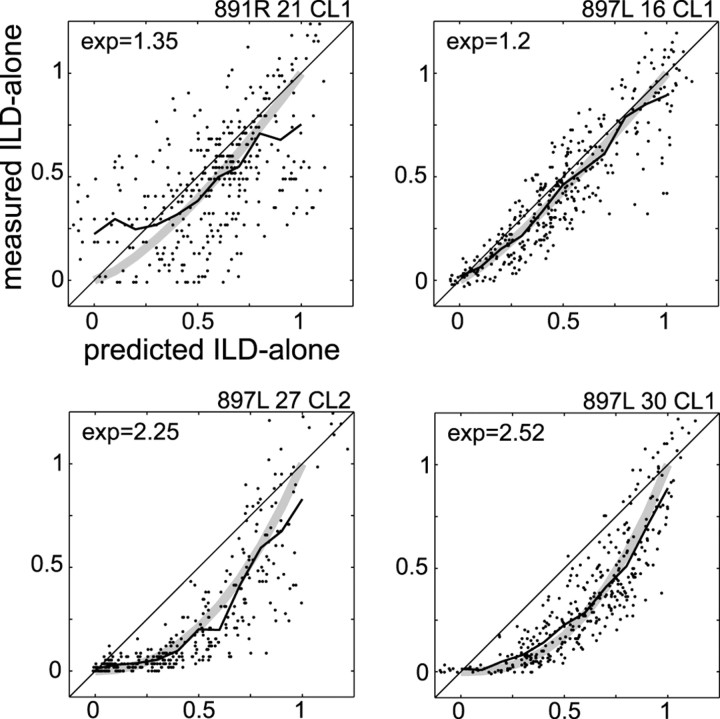
Figure 5 plots the normalized predicted and measured responses for four of the cells shown in Figure 3. In some cells, such as those shown in the bottom half of Figure 5, we observed a downward bowing, which suggests that the predicted responses often overestimated firing rates at intermediate values. The effect is also apparent in plots of predicted ILD-alone RFs, which often were less restricted than measured ILD-alone RFs (Fig. 3, comparecolumns 2, 3). To quantify the degree of bowing, we fit a curve of the form y =xⁿ individually to the predicted versus measured ILD-alone plot of each cell. For the group of cells whose variance about this line was in the lower quartile (n = 9 cells), the mean coefficient, n, was 1.85. This suggests that the normalized broadband response might be better approximated by the square of the normalized pure-tone responses.

Fig. 5.

Normalized, measured ILD-alone firing rate plotted against the normalized predicted ILD-alone firing rate for four cells. The jagged black line shows the running average of the distribution, and the broad gray line shows the best-fitting curve of the form y =xⁿ. The value of n(exp) is shown at the top left of each plot.

Are neurons tuned to ILD values at the normal RF peak?

The ILD-frequency response surfaces allow us to determine the best ILD of a cell at a given frequency. The set of all such preferred ILDs defines a ridge along the ILD-frequency surface. We compared this ridge with the ILD spectra occurring at the peak of the normal RF and at the peak of the measured ILD-alone RF. Comparisons were made only at frequencies at which the maximum firing rate of a given ILD curve was at least 20% of the maximum firing rate of the entire ILD-frequency surface and the SD in the estimate of the ILD peak (i.e., best ILD) was <10 dB (for details, see Materials and Methods).

Figure 6 shows, for six representative cells, the ILD values occurring at the peaks of the ILD-alone and normal RFs superimposed on the ILD-frequency response surface of that cell. We begin by describing the comparison between the ILD spectrum occurring at the peak of the normal RF (solid green lines) with the best ILD values (filled circles). As is apparent in Figure 6, A and B, the best ILD ridge often followed the ILD spectrum from the peak of the normal RF reasonably well below 7000 Hz, although there were noticeable misalignments in some cells (Fig. 6C). At higher frequencies, the best ILD ridge often followed the general trend of the peak-location ILD spectrum but not the details. For example, if the peak-location ILD was right-louder, the ILD tuning of the cell also favored right-louder ILDs. When the ILD tuning and the peak-location ILD of a cell disagreed, the cell was usually tuned to larger absolute values (Fig. 6E,F). For example, in the cell shown in Figure 6F, the 7000 Hz ILD at the peak location was +5 dB, whereas the preferred ILD of the cell at that frequency was approximately +20 dB. When the peak-location ILD was negative, the best ILD ridge was shifted toward more extreme negative values. In a minority of cases (6 of 46), there was no apparent relationship between the best ILD ridge and the peak-location ILD values (Fig. 6D).

Fig. 6.

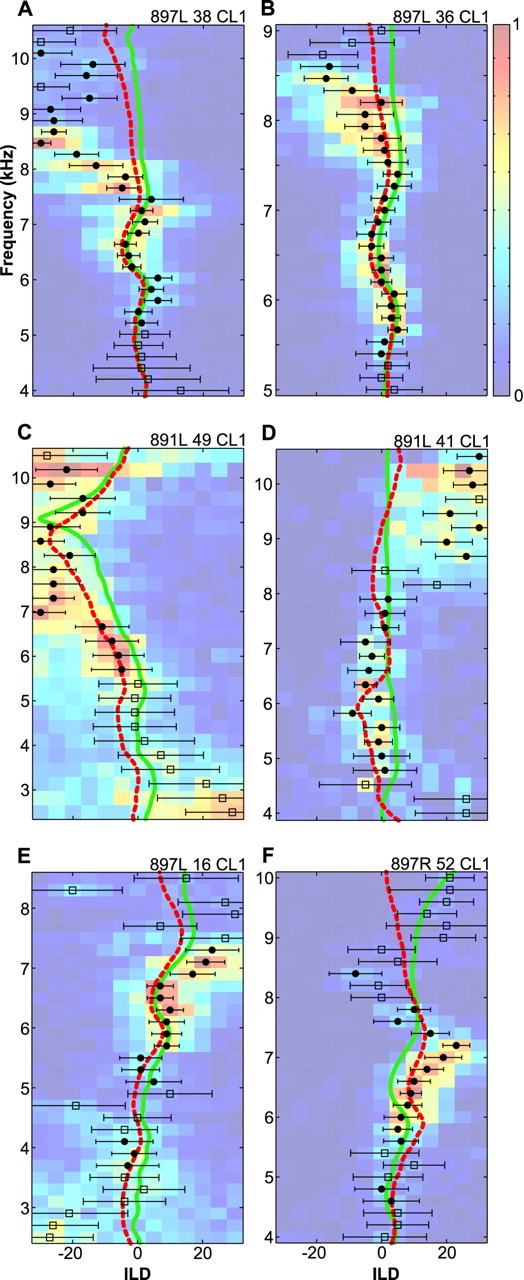
Correspondence between pure-tone ILD tuning curves and ILD spectra. ILD-frequency response surfaces from six cells are shown as colored surface plots. Scale bars indicate firing rate, scaled between 0 and 1 for all cells. The peaks of the ILD tuning curves are indicated by filled circles or open squares, in which circles indicate estimates of peak location with low variance and high overall firing, andsquares indicate less reliable estimates (for details, see Results). The horizontal bars show the SD of the location of the ILD peak. The solid green line indicates the ILD spectrum occurring at the peak of the normal RF, and the dashed red line traces the ILD spectrum occurring at the peak of the ILD-alone RF.

The differences between the frequency-specific best ILDs and the ILD spectra from the peak of the normal RF were generally >5 dB. This discrepancy is unlikely to be attributable to the use of virtual space techniques. First, the same earphones and earphone-equalizing filters were used to present both the spatial and nonspatial stimuli. Any factor that shifted ILD values in the spatial ILD spectra would have shifted pure-tone ILD values by the same amount. Second, the virtual space technique is quite reliable. The largest source of errors arises from the placement of the earphones on each experiment. In an exploratory study, we measured the earphone–ear canal transfer function for 20 repeated insertions of the earphones. The SD of these measurements, averaged across all frequencies, was 1.2 dB. Therefore, even if earphone-placement errors played a role in the mismatch between neuronal tuning and acoustical cues, they could not account for it exclusively.

The patterns illustrated in Figure 6 were even more apparent in the population data shown in Figure7A. For frequencies between 5000 and 7000 Hz, the ILD tuning tended to correspond with the ILD values at the peak of the normal RF, although there was a fair amount of scatter in the data. At lower frequencies, the data are inconclusive because the scatter in the data are large relative to the range of peak-location ILDs. The failure of the pure-tone tuning to track ILD spectra above 7000 Hz is also apparent. As shown in Table1, the slopes of the regression lines in both the 5000–7000 and 7000–9000 Hz ranges are slightly greater than one, showing that the ILD tuning of a cell tended to be more extreme than the peak-location ILD values. This trend is especially apparent in the outlying data points in the 5000–7000 Hz plot.

Fig. 7.

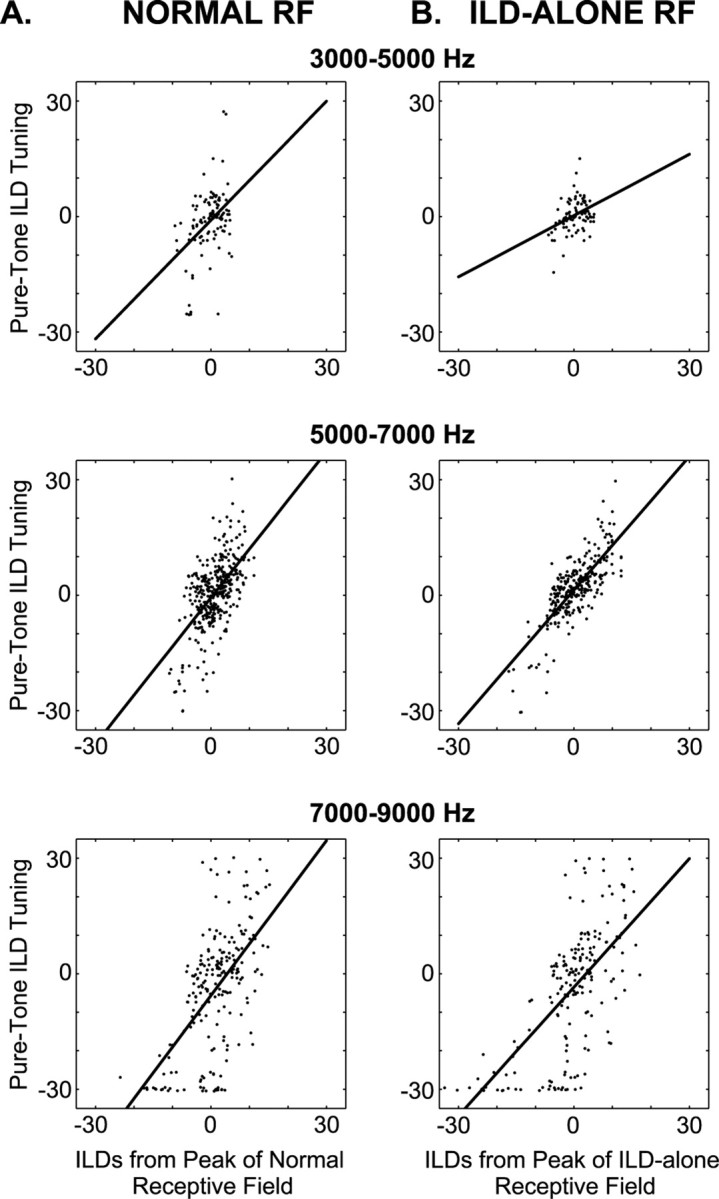
Best ILD plotted against peak-location ILD for all cells. A, Pure-tone ILD tuning plotted against those ILDs occurring at the peak of the normal RF. B, Pure-tone ILD tuning plotted against those ILDs occurring at the peak of the ILD-alone RF. In both A and B, data have been broken down by frequency ranges as indicated by the title of each plot. The black line shows the best-fitting regression line. Regression coefficients are given in Table 1.

Table 1.

Results (broken down by frequency range) of a regression of pure-tone best ILDs against acoustic ILDs occurring at the peak of the normal and ILD-alone RFs (Fig. 7)

	Frequency range	Slope	Intercept	t	df	p
Peak of normal	3000–5000 Hz	1.03	−0.91	4.8	113	<0.0001
RF	5000–7000 Hz	1.26	−0.65	13.6	353	<0.0001
	7000–9000 Hz	1.34	−5.63	10.5	211	<0.0001
Peak of ILD-alone	3000–5000 Hz	0.53	0.25	3.5	83	<0.0001
RF	5000–7000 Hz	1.16	1.35	20.8	286	<0.0001
	7000–9000 Hz	1.11	−3.49	11.8	188	<0.0001

As explained above, the peak of the measured ILD-alone RF was not always the same as the peak of the normal RF. In other words, cells were sometimes driven more strongly by the ILD spectrum from a location other than their normal RF peak. In light of this finding, we compared our pure-tone ILD tuning with the ILD spectra occurring at the peak of the measured ILD-alone RF (Fig. 6, dashed red lines). As exemplified by Figure 6, B and C, the ILD tuning of the cell often matched better with the ILD spectrum occurring at the peak of the ILD-alone RF than it did with the spectrum from the peak of the normal RF. As we found when comparing ILD tuning against the ILD values from the peak of the normal RF, the ILD tuning and peak ILD spectra corresponded below 7000 Hz and diverged at higher frequencies. The population data show clearly that the ILD spectrum at the ILD-alone RF peak was a better predictor of the best ILD of the cell than was the spectrum from the normal RF peak. This can be seen by comparing the 5000–7000 Hz plots of Figure 7, A and B. This difference is also apparent in the values of the Student'st test statistic shown in Table 1.

DISCUSSION

Virtual auditory stimuli have been developed for a variety of species, including humans (Wightman and Kistler, 1989a,b), monkeys (Spezio et al., 2000), cats (Poon and Brugge, 1993; Brugge et al., 1994; Delgutte et al., 1995, 1999; Rice et al., 1995; Nelken et al., 1997; Reale and Brugge, 2000), guinea pigs (Hartung and Sterbing, 1997), and owls (Keller et al., 1998). Recently, this technique has been used to dissociate the various auditory-localization cues and thereby study their effects in isolation (Wightman and Kistler, 1997;Delgutte et al., 1999; Egnor, 2000). Using virtual sources, we separated the influence of ILD and ITD, the primary cues in the owl's auditory system. Our measured ILD-alone RFs uncover the contribution of ILD to the normal spatial RF of each IC cell and, when combined with pure-tone ILD measurements, allowed us to assess the degree to which the response of a cell to ILD at each frequency predicted its response to naturalistic ILD spectra.

The contribution of ILD to spatial tuning

The ILD-alone RFs, measured with ITD fixed, had complex shapes, often with multiple islands of response. However, they consistently had a horizontal band of excitation that traversed the normal RF. Above and/or below this horizontal band, we observed areas with no discharge, which, in cells with an appreciable spontaneous rate, could be shown to be inhibitory.

Because the ILD gradient at frequencies below 4000 Hz has a strong horizontal component, these lower frequencies might allow a cell to restrict its RF in azimuth. As a result, we might have found that ILD-alone RFs were as restricted in elevation and azimuth as the normal RFs are. Instead, our results indicate that restriction of the normal RF requires both ILD and ITD.

The role of ITD as an azimuthal cue is well established (Moiseff and Konishi, 1981; Moiseff, 1989a; Olsen et al., 1989; Keller et al., 1998), and it can be inferred that a cell tuned only to ITD would fire solely along a narrow, vertically oriented strip of locations. The primary role of ILD is thus to restrict an RF perpendicular to this vertical strip. The normal RF center, then, is the location at which both ILD and ITD cues are permissive (Pena and Konishi, 2001). Our findings are completely consistent with previous research that has shown that ILD plays a key role in the computation of elevation (Moiseff, 1989a,b; Olsen et al., 1989).

One of the key hypotheses that we set out to examine held that a space-specific neuron is tuned optimally to the ILD spectrum that occurs at the peak of its normal RF (Knudsen, 1999). It follows that a neuron would respond maximally to a stimulus filtered by this spectrum. We frequently observed, however, that the peaks of the measured ILD-alone and normal RF did not coincide, meaning that the cell could be equally responsive, or in fact, more responsive to ILD spectra that occur outside the normal RF. Because both the ILD-alone and normal RFs were measured using the same set of HRTFs, this phenomenon is unlikely to be an artifact of the use of virtual-space stimuli.

That the ILD tuning of a cell is actually optimal for a location other than the normal RF peak is plausibly explained within a developmental framework. It has been suggested that auditory spatial RFs in the IC develop via a form of “supervised learning” wherein visual signals guide the establishment of the inputs to the space map that are appropriate for an auditory RF at a particular location (Knudsen and Brainard, 1991, 1995; Brainard and Knudsen, 1993, 1995, 1998; Knudsen, 1994, 1999). These inputs are thought to arrive from the ICc-ls, in which the neurons are selective for the ITD and ILD of a particular frequency band (Wagner et al., 1987). Were the developmental process based solely on the modification of excitatory connections, one would expect the cell to establish connections with those ICc-ls neurons tuned to the ILDs occurring at the peak of its normal RF. In fact, this does appear to be the case for ITD (Takahashi and Konishi, 1986; Wagner et al., 1987; Gold and Knudsen, 2000). However, it is clear that inhibition plays a role in the formation of an RF (Fujita and Konishi, 1991; Mori, 1997) and that plasticity also affects inhibitory connections (Zheng and Knudsen, 1999). A cell may therefore form its RF subject to two constraints: it must be excited by sounds occurring at its future RF location and inhibited by sounds arising from other locations, typically, above and below. These two constraints can conflict when a segment of the ILD spectra at the normal RF peak contains the same frequency-specific ILD values as another location in which the firing of the cell is to be prevented. Under these circumstances, a cell may develop connections such that the cell is inhibited by some ILD values occurring at the normal RF peak. Consequently, a location that does not contain these inhibitory ILD values (i.e., the peak of the ILD-alone RF) may actually elicit a stronger response than the normal RF peak. Under ordinary circumstances, the response to the ILD spectrum occurring at the peak of the ILD-alone RF would be suppressed by unfavorable ITD values and is therefore of little functional consequence.

Correspondence between ILD tuning and spatial tuning

Whether an IC neuron fires more at the peak of the normal or ILD-alone RF, the mechanisms of this selectivity have not been established definitively. It has been generally assumed that space-specific neurons are tuned, on a frequency-by-frequency basis, for the ILD values occurring at their optimal location (usually assumed to be the normal RF peak). Brainard et al. (1992) delineated the spatial RFs of cells in the owl's optic tectum using tones broadcast from an external speaker. These pure-tone RFs, although amorphous and spatially ambiguous, tended to overlap at the normal RF of a cell. They concluded that the cell must be excited by the frequency-specific ILD and ITD values occurring at the center of its normal RF. These data, however, reflect the influence of both ILD and ITD. The specific contribution of ILD, although inferred by modeling, could not be directly measured. A more recent study by Gold and Knudsen (2000), which isolated ILD tuning using narrowband stimuli presented over headphones, reported a correspondence between the frequency-specific ILD tuning and ILD values at the normal RF peak of a cell. However, the range of deviations between ILD tuning and ILD cue values (approximately −8 to +13 dB) was almost as large as the range of best ILDs encountered in their study (approximately −6 to +20 dB).

We therefore examined frequency-specific ILD tuning in greater detail. We compared ILD tuning with the ILD values occurring at both the ILD-alone and normal RFs peaks. Although the pure-tone ILD tuning of a cell was coarsely related to the ILD values occurring at the normal RF peak, the match was better for the ILD spectrum associated with the ILD-alone RF peak.

Even when compared with the spectrum at the ILD-alone RF peak, however, the pure-tone ILD tuning of a cell often deviated from the HRTF-derived ILD values: best ILDs measured with noise tended to have larger absolute values than those ILD values at the ILD-alone RF peak. Interestingly, a similar trend is apparent in the data of Gold and Knudsen (2000, their Fig. 13), although the authors did not address it. A possible explanation for these findings is considered below.

Frequency integration by space-specific neurons

To assess the nature of the frequency integration process occurring in the IC, we compared the ILD-alone RF of a cell, charted using broadband stimuli, with the ILD-alone RF predicted from frequency-specific ILD tuning curves, measured with tones. By probing with pure tones, we were, in essence, inferring the ILD tuning of each frequency-specific input to the neuron. If the cell summed these inputs, its responses to broadband ILD spectra (i.e., the ILD-alone stimuli) should be completely predicted by summing its responses to tones at various ILDs. This linear model, in fact, accounts for ∼56% of the variance in the measured ILD-alone RFs.

Why does the linear model fail to do better? A possibility is that tones do not provide a complete picture of the inputs to a space-specific neuron. Space-specific neurons often respond phasically to tones, while their response to broadband stimuli is tonic and more robust (Knudsen and Konishi, 1978a). Space-specific neurons may therefore prefer spectral energy to be spread over a wide band of frequencies. If this were even partly true, narrowband stimuli might not reveal the full frequency sensitivity of a cell.

Differences between tone and noise responses may also account, indirectly, for the shift in ILD tuning curves to greater absolute values when measured with tones. The poor response of space-specific neurons to tones necessitated that the power spectral density of tones be greater than that of noises. In our study, noises and tones were played at approximately equal overall amplitude. However, because tones have all of their spectral energy concentrated in a narrow band, neurons in earlier processing stages, which are narrowly tuned to frequency, might have been pushed near the limits of their dynamic range by the tonal stimuli. Consequently, the processing of ILD might have been affected. It is known that ILD response curves in the nucleus ventralis laterale, pars posterior (VLVp), the first site of binaural convergence in the ILD pathway, shift with increasing ABL (Manley et al., 1988). Based on the generally accepted model that ILD tuning in the ICc-ls is derived via bilateral inhibitory inputs from the VLVp (Adolphs, 1993), these shifts are in the correct direction to account for amplitude-sensitive shifts of best ILD that we observed using tones and Gold and Knudsen (2000, their Fig. 13) observed using narrowband noises.

The limitations above are intrinsic to any study that uses narrowband stimuli to probe the frequency-specific responses of broadband neurons. Additional progress may require the development of techniques, akin to reverse correlation (deBoer and Kuyper, 1968; Eggermont et al., 1983), for inferring selectivity for frequency-specific binaural cues from responses to broadband stimuli.