Circuits for Local and Global Signal Integration in Primary Visual Cortex

Abstract

Contrast-dependent changes in spatial summation and contextual modulation of primary visual cortex (V1) neuron responses to stimulation of their receptive field reveal long-distance integration of visual signals within V1, well beyond the classical receptive field (cRF) of single neurons. To identify the cortical circuits mediating these long-distance computations, we have used a combination of anatomical and physiological recording methods to determine the spatial scale and retinotopic logic of intra-areal V1 horizontal connections and inter-areal feedback connections to V1. We have then compared the spatial scales of these connectional systems to the spatial dimensions of the cRF, spatial summation field (SF), and modulatory surround field of macaque V1 neurons. We find that monosynaptic horizontal connections within area V1 are of an appropriate spatial scale to mediate interactions within the SF of V1 neurons and to underlie contrast-dependent changes in SF size. Contrary to common beliefs, these connections cannot fully account for the dimensions of the surround field. The spatial scale of feedback circuits from extrastriate cortex to V1 is, instead, commensurate with the full spatial range of center–surround interactions. Thus these connections could represent an anatomical substrate for contextual modulation and global-to-local integration of visual signals. Feedback projections connect corresponding and equal-sized regions of the visual field in striate and extrastriate cortices and cover anisotropic parts of visual space, unlike V1 horizontal connections that are isotropic in the macaque. V1 isotropic connectivity demonstrates that anisotropic horizontal connections are not necessary to generate orientation selectivity. Anisotropic feedback connections may play a role in contour completion.

A central question in visual cortical processing is how local signals are integrated across space to generate global percepts. Traditionally, visual information has been seen as ascending through a hierarchy of cortical areas, with cells at each successive stage processing inputs from increasingly larger regions of space. However, long-distance integration of visual signals can occur at very early stages of processing. The response of cells in the primary visual cortex (V1) to stimulation of their receptive field (RF) can be modulated in a selective way by contextual stimuli lying far outside the RF in the RF surround (Blakemore and Tobin 1972; Nelson and Frost, 1978; Allman et al., 1985; Gilbert and Wiesel, 1990; Levitt and Lund, 1997; Walker et al., 1999). Furthermore, V1 RFs show dynamic spatial properties, changing in size depending on stimulus contrast (Kapadia et al., 1999; Sceniak et al., 1999). These neurophysiological responses require integration of visual signals beyond the RF of single V1 neurons and thus cannot be easily explained by classical RF concepts. Identifying the neural circuitry underlying these long-distance computations is crucial, because they may represent the neural substrates for feature grouping (Kapadia et al., 1995; Mizobe et al., 2001) and figure–ground segregation (Knierim and Van Essen, 1992;Nothdurft et al., 1999).

Currently, most models of center–surround interaction in V1 are based on intrinsic horizontal (or lateral) connections (Gilbert et al., 1996;Somers et al., 2002). These are long-range, reciprocal, intralaminar projections made by excitatory neurons in layers 2/3, 4B/upper 4Cα, and 5/6 of macaque area V1 (Rockland and Lund, 1983). These connections show a periodic, patchy pattern of termination and preferentially link cortical domains of similar functional properties (Malach et al., 1993;Yoshioka et al., 1996). On the basis of laminar origin and termination, connections between visual cortical areas have been classified as feedforward (FF) or feedback (FB), and a hierarchical organization of cortical areas has been proposed previously (Rockland and Pandya, 1979;Felleman and Van Essen, 1991). V1, at the bottom of the hierarchy, receives its main FF inputs from the thalamus and sends partially segregated FF projections to several extrastriate cortical areas, which, in turn, send FB projections to V1. It has been suggested that FB connections have a less precise retinotopic organization than FF projections (Perkel et al., 1986; Salin and Bullier, 1995), and that only FF inputs can drive V1 neurons, whereas FB connections would have a modulatory influence (Crick and Koch, 1998). FB connections may therefore represent an additional or alternative substrate for contextual modulation in V1.

The aim of this study was to provide a basis for disentangling the relative roles of inter-areal FB and intra-areal horizontal connections in integrating signals within and beyond the RF of V1 neurons. We reasoned that to mediate interactions within or beyond the RF, a given connectional system must be commensurate with the spatial extent of the RF or modulatory surround field of the neuron. Thus, we have compared the visuotopic scale of each connectional system with the spatial extent of the classical RF, spatial summation field (SF), and modulatory surround field of macaque V1 neurons. Our results demonstrate that monosynaptic V1 horizontal connections are of an appropriate scale to mediate interactions within the SF and could represent an anatomical substrate for dynamic changes in SF size such as induced by stimulus contrast or scotomata (Das and Gilbert, 1995). FB circuits from extrastriate cortex to V1, on the other hand, are of an appropriate scale to play an important role in global integration of visual signals and modulation of responses far beyond the SF of V1 cells.

Parts of this work have been published previously in abstract form (Angelucci et al., 1998, 2000).

MATERIALS AND METHODS

Electrophysiological recording. In a first set of animals, quantitative electrophysiological recording terminal experiments were performed on seven adult macaque monkeys (Macaca fascicularis or M. mulatta). All procedures conformed to British Home Office and United States National Institute of Health guidelines. Animals were premedicated with atropine sulfate (0.02–0.04 mg/kg) and acepromazine maleate (0.05 mg/kg) and preanesthetized with ketamine (10–30 mg/kg, i.m.). The trachea and saphenous veins were cannulated; the animal was artificially ventilated with room air or with a 50:50 mixture of O₂ and N₂O; and anesthesia was maintained by continuous intravenous infusion of sufentanil citrate (4–8 μg · kg⁻¹ · hr⁻¹). The animal's head was fixed to a stereotaxic apparatus; a small craniotomy and durotomy were made over the occipital cortex; and a tungsten-in-glass microelectrode (Merril and Ainsworth, 1972) was positioned over the exposed cortex, which was then covered with warm agar. To minimize eye movements, on completion of surgery, the animal was paralyzed by continuous intravenous infusion of vecuronium bromide (0.1 mg · kg⁻¹ · hr⁻¹) in lactated Ringer's solution with glucose (5.4 ml/hr). Electroencephalogram and electrocardiogram were monitored continuously. Peak expired CO₂ was maintained near 4.0%, rectal temperature near 37°C, and blood oxygenation near 100%.

The pupils were dilated and accommodation paralyzed with topical atropine; the corneas were protected with zero power rigid gas-permeable contact lenses; and the eyes were refracted. The location of the foveas was plotted (and checked periodically throughout the experiment) on a tangent screen using a reversible ophthalmoscope. Extracellular recordings were made in the opercular region of area V1 between 2 and 8° retinal eccentricity in the lower visual field. Spikes were conventionally amplified and displayed and stored on a personal computer (resolution, 250 μsec). Small electrolytic lesions (1–2 μA for 2–5 sec) were made along the electrode track and later reconstructed on Nissl- and cytochrome oxidase (CO)-stained tissue sections. For quantitative studies, visual stimuli were displayed on a Barco ICD 451B color TV monitor driven by an AT Truevision Vista Graphics board. At a viewing distance of 114 cm, the screen subtended 13 × 13° of visual angle. Stimuli consisted of square patches of drifting achromatic sinusoidal gratings of average luminance of 37.5 cd/m². Contrast was held fixed at 75% (i.e., below response saturation for most cells).

The location and size of the classical RF or minimum response field (mrf; Barlow et al., 1967) of the neuron were initially hand-mapped through the dominant eye; this was then confirmed by computer mapping. All subsequent quantitative experiments proceeded under computer control. The preferred orientation, direction of motion, spatial and temporal frequency, and size of stimuli of the neuron were determined. The optimal parameters for the recorded cell were then used to measure RF and surround sizes. Stimuli were presented for 2–4 sec within each block of trials in a randomized order, and results of four to eight repeated blocks were averaged. To measure the spontaneous firing rate of the cell, interleaved blanks of the same mean luminance as the stimuli were presented. To spatial summation data we fit functions representing a difference of the integrals of excitatory and inhibitory Gaussian mechanisms (Sceniak et al., 2001) as described in detail byLevitt and Lund (2002). From these functions we determined the stimulus diameter at which responses peaked and asymptoted. Population values are expressed as mean ± SEM. Statistical significance of laminar variation was tested with the Kruskal–Wallis test.

Combined tracer injections and physiological recording. In a separate set of animals, combined anatomical and electrophysiological recording survival experiments were performed on nine adult macaque monkeys (M. fascicularis or M. mulatta). Tracer injections (n = 17, all clearly confined to the cortical gray matter) were made in electrophysiologically characterized cortical loci between 2.2 and 7.5° eccentricity in the lower visual field representation of areas V1, V2, or V3. The animals were prepared as described above, intubated, and anesthetized with 0.5–2% isoflurane in a 70:30 mixture of N₂O and O₂ (three animals were anesthetized with Sufentanil as described above). Fluids (lactated Ringer's solution at 1–2 ml · kg⁻¹ · hr⁻¹) were continuously infused intravenously to support cardiovascular function. Monitoring of vital signs, surgery, recordings, and hand plotting of RFs were performed as described above. A short-duration topical mydriatic agent (cyclopentolate) was applied to the corneas, and the eyes were fitted with contact lenses.

Areas V2 and V3 were identified electrophysiologically using the known sequence of gray–white matter transitions as described previously (Gegenfurtner et al., 1997). Corresponding retinotopic loci in V1 and V2 were identified in three animals as described by Hupé et al. (2001b). Once the appropriate cortical sites were found, the position of the microelectrode was recorded, the electrode was withdrawn, and the animal was paralyzed by intravenous infusion of vecuronium bromide (0.1 mg · kg⁻¹ · hr⁻¹, with a loading dose of 1 hr). The foveas were plotted, and a foveal mrf was mapped in V1 (and periodically throughout the experiment) to monitor eye movements. A recording electrode glued to a glass micropipette (intertip distance, <50 μm; Hupé et al., 1999) filled with a tracer solution was lowered into the same striate or extrastriate locus where the initial recordings were performed. RF size and eccentricity of cells through the depth of the penetration were first remapped, and then the tracer was injected through the attached pipette (inner tip diameter, 13–17 μm). The tracers used were cholera toxin subunit B [CTB, low salt; List Biologic, Campbell, CA; 1% in 0.1 m phosphate buffer (PB), pH 6.0] or biotinylated dextran amine (BDA, MW 3000; Molecular Probes, Eugene, OR; 10% in 0.01 m PB, pH 7.25). The tracers were delivered iontophoretically using 2 μA for CTB and 6 μA for BDA of positive current in 7 sec on–off cycles for 10–30 min. CTB was preferred for these studies, because its sensitive anterograde and retrograde transport reveals reciprocal connections to an injected point (Angelucci et al., 1996). However, in some cases BDA was used to compare the extent of the label with CTB. At the end of the injection, to avoid leakage of tracer along the pipette track, the pipette was left in place for at least 30 min and then withdrawn while reversing the current to negative. In five V1 and three V2 injection cases (n = 4 animals), after the tracer injection in physiologically characterized loci, additional recordings were made of RF size and location along a few electrode penetrations made at 1 mm intervals around the injection site; recording sites were marked by electrolytic lesions. In all remaining cases (n = 5 V1 and 4 V3 injections) recordings were made only at the injection site; retinotopic maps in these cases could not be recorded because of lack of time and need to recover the animal. The animal was recovered from paralysis and anesthesia, allowed to survive for 10–20 d, and finally killed with an overdose of sodium pentobarbital (100 mg/kg, i.v.) and perfused transcardially with saline followed by 4% paraformaldehyde in 0.1 m PB, pH 7.4, for 30 min.

Areas V1 and V2 were dissected free, flattened between glass slides, postfixed overnight, cryoprotected by sinking in 30% phosphate-buffered sucrose, and finally sectioned on a freezing microtome at 40 μm tangentially to the pial surface. The block containing areas V3 and MT was similarly postfixed and cryoprotected, and then cut parasagittally. CTB was revealed immunohistochemically using the protocol of Angelucci et al. (1996); BDA was revealed using standard Vector Laboratories (Burlingame, CA) ABC VIP-based reactions. Some (n = 3) animals received an injection of CTB and one of BDA in corresponding retinotopic loci in areas V1 and V2. In these brains, CTB was revealed using a standard peroxidase–antiperoxidase method (Lanciego et al., 1998). To reveal areal and layer boundaries, interleaved sections were stained for CO (one in three sections of tissue containing areas V1 and V2) or for myelin (Gallyas, 1979) or Nissl substance (one in five sections, for each method, of tissue containing V3 and MT).

Data analysis. CTB and BDA anterograde and retrograde labels were mapped in each available section using a camera lucida. Layer boundaries were identified and drawn by overlaying the maps of the label to adjacent CO- or Nissl-stained sections. Areal boundaries were identified using the pattern of CO staining (for V1 and V2) or Gallyas staining (for V3 and MT) as well as the specific pattern of anterograde and retrograde label. Surface-view two-dimensional (2D) composite reconstructions of the label were made separately for each V1 and V2 layer by overlaying maps of serial tangential sections using vascular landmarks as alignment points. Surface-view reconstructions of the label in V3 and MT were made from serial sagittal sections as described in detail previously (Johnson et al., 1989). Briefly, the mapped label in each section was projected onto a line running through midlayer 4, using a radial segmentation scheme, and serial sections were aligned using a combination of sulcal and vascular landmarks. Cells were counted, and plots of label density were computer-generated. Typically, label density showed a Gaussian-like distribution. Our definition of a labeled field included all bins with label density within 95% of the peak density (see Fig. 4). For eight injections (five in V1 and three in V2), the density maps of the V1 and V2 label were overlaid to physiological maps obtained from the same animal in these two cortical areas, using the location of electrolytic lesions as alignment points; the visuotopic extent of the labeled fields was measured directly on the retinotopic maps as well as estimated as described below.

Fig. 4.

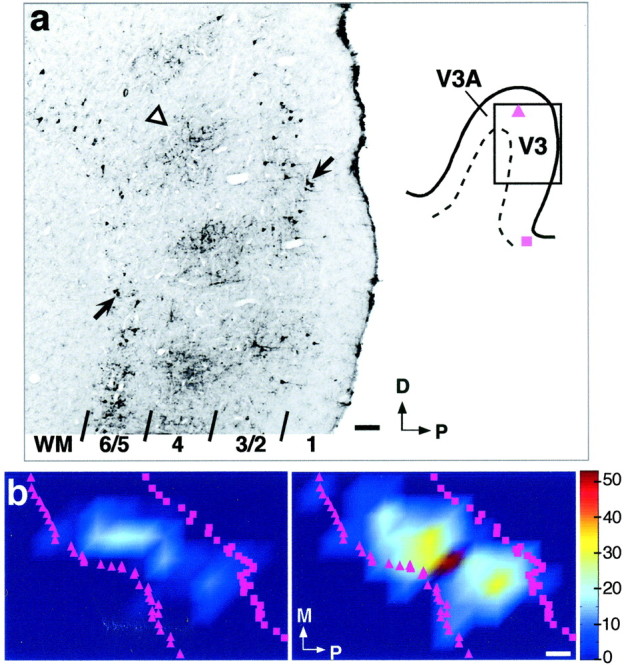
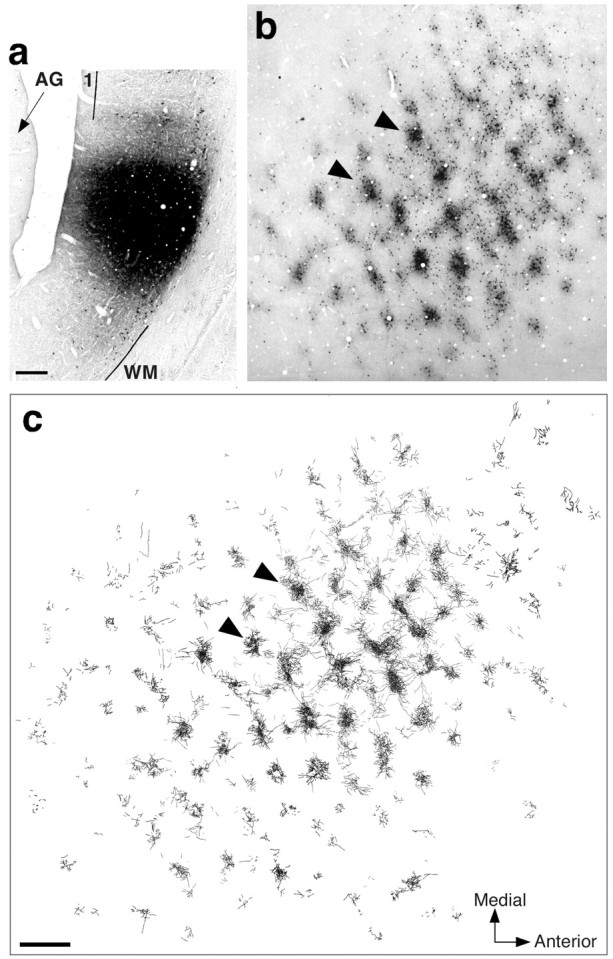
Cells of origin in area V3 of feedback connections to V1. a, Micrograph (left) of a sagittal section through dorsal V3 (shaded box on theright shows location of the photographed region on the annectant gyrus), showing CTB-labeled cell bodies (arrows) in layers 2/3A and 5/6. Cortical layers are indicated at the bottom; WM, White matter; arrowhead, labeled fibers in layers 4 and 3B (terminals of feedforward connections from V1). The composite surface map for this case is shown in b. The injection site involved V1 layers 1–4C and was made at 6.5° eccentricity in the lower visual field (same injection case as in Figs. 6a, 7a). D, Dorsal; P, posterior. Scale bar, 100 μm. b, Surface view plots of cell label density in the upper (left) and lower (right) layers of dorsal V3, generated using custom software written in Matlab. Color scale represents cell density (numbers are cells per 500 μm²). Bins containing <5% of peak cell density were removed from the image. Label anterior to the crown of the annectant gyrus (purple triangles in a,b) is in area V3A. Purple squares (ina, b), Location of the fundus of the lunate sulcus. The long axis of these feedback fields measured 7.8 mm in the upper layers and 9.8 mm in the lower layers. The visual field map of the lower-layer feedback field is shown in Figure 7a. M, Medial (away from the fovea); P, posterior (toward the V1–V2 border). Scale bar, 1 mm (corrected for 30 and 12% shrinkage in the anteroposterior and mediolateral axis, respectively).

In all remaining cases (n = 5 V1 and 4 V3 injection cases) in which retinotopic maps were not recorded, the visuotopic extent of labeled connectional fields was estimated as follows. All labeled fields in striate and extrastriate cortex were anisotropic in cortical space their long axis corresponding to the cortical area elevation axis, and to the axis of anisotropy of the magnification factor (MF), demonstrated at least for V1 (where it runs parallel to the vertical meridian; Van Essen et al., 1984; Tootell et al., 1988;Blasdel and Campbell, 2001) and V2 (where it runs orthogonal to the CO stripes; Roe and Ts'o, 1995). We measured the density map of each labeled field along (elevation axis) and across (azimuth axis) the representation of the isopolar lines of the visual field, using as a reference published retinotopic maps of striate cortex (Van Essen et al., 1984; Dow et al., 1985; Tootell et al., 1988) and extrastriate cortex [V2 (Gattas et al., 1981; Roe and Ts'o, 1995), V3 (Burkhalter et al., 1986; Gattas et al., 1988), and MT (Albright and Desimone, 1987; Maunsell and Van Essen, 1987)]. Cortical measurements were corrected for tissue shrinkage caused by histological processing. This was estimated on a case-by-case basis for 12 of 17 injections using the measured in vivo distance between electrolytic lesions, between injection sites, or both. In our hands, shrinkage caused by CTB and BDA processing ranged in different cases between 30–33 and 8–13%, respectively. We also estimated shrinkage caused by perfusion and cryoprotection (∼12%) and applied this correction factor to the intersection distance, i.e., to the anteroposterior dimension of the 2D maps obtained from serial sagittal section reconstructions (see Fig.4). For five injections in which shrinkage could not be estimated directly, we applied a 30% shrinkage correction for CTB and 10% for BDA (a possible 2–3% error in shrinkage correction in these cases would not have affected our results). Knowing the cortical extent of labeled fields and the eccentricity of injection sites (recorded in all cases), to estimate the visuotopic extent of the two axes of label, we used published equations relating MF and scatter (S) in RF center position to retinal eccentricity in areas V1–V5. For labeled fields within V1, we used equations from Van Essen et al. (1984) and Tootell et al. (1988), because these authors measured MF separately along and across the isopolar axis of V1. Because MF and S are constant along isoeccentricity contours, the linear visuotopic extent (designatedD°) (Fig. 1a) of the axis of the labeled field along these contours was estimated as:

$$D_{(\text{deg})}^{°}=D_{(\text{mm})}/{MF}_{(\text{mm}/\text{deg})}+S_{(\text{deg})},$$ Equation 1

where D_(mm) (Fig.1b) is the measured length (in millimeters) of the labeled field along the isoeccentricity axis, and S was estimated at the injection eccentricity using the equation from Dow et al. (1981). Because retinal eccentricity (E), and thusMF and S, vary along the isopolar axis, we determined the retinotopic location of the end points of this axis of label, denoted as E₊ andE₋, respectively (Fig. 1a; with E₊ > E₋) by integrating the equations (Van Essen et al., 1984; Tootell et al., 1988) relating MF to E along the isopolar axis of V1. Thus, for example, integrating equationMF(E) =aE^−b mm/°, from Van Essen et al. (1984), it follows that:

$$E_{+}={\left[\frac{a}{{\text{aE}}_c^{1-b}-(b-1)\mathrm{\Delta }{X}_{+}}\right]}^{\frac{1}{b-1}},E_{-}={\left[\frac{a}{{\text{aE}}_c^{1-b}+(b-1)\mathrm{\Delta }{X}_{-}}\right]}^{\frac{1}{b-1}},$$ Equation 2

where a and b are constants,E_c is the physiologically recorded eccentricity (in degrees) of the injection site or of the center of the long axis of the label (Fig. 1a), and ΔX₊ and ΔX₋ are the measured cortical separation (in millimeters) of the two end points (X₊ andX₋) from the center,X_c (Fig. 1b).

Fig. 1.

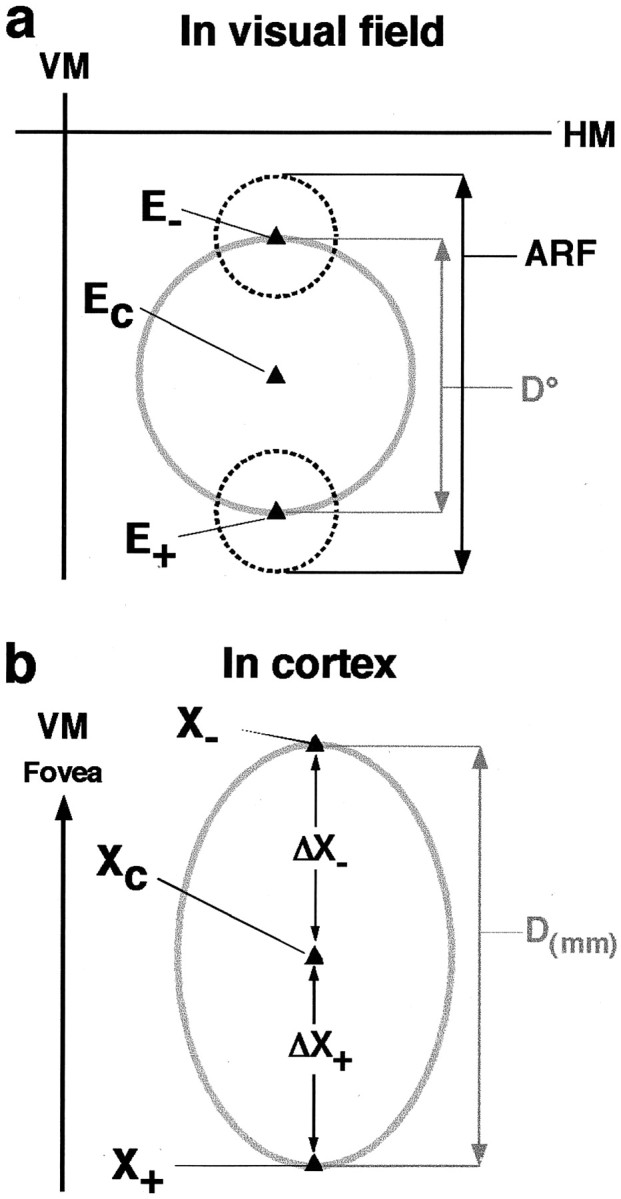
Estimated extent of corticocortical connectional fields in visual field coordinates. a, Visual field measurements. VM, HM, Vertical and horizontal meridian, respectively. E_c, Retinal eccentricity of the center of the injection site or of the labeled field determined experimentally for all cases by electrophysiological recording.E₊, E₋, estimated retinal eccentricity of RF center of cells at the end points of the axis of the labeled field (see Eq. 2). Dashed circles, Mean RF size of neurons at the eccentricity of the end points of the labeled field, measured experimentally in the same or different animals. D°, estimated linear visuotopic extent of the axis of the labeled field (gray circle diameter). ARF, Aggregate receptive field size of the labeled field's axis, calculated as D° + mean RF size of cells at the end points of the labeled field.b, Cortical measurements.X_c, Cortical location of the injection site or of the center of the labeled field.X₊, X₋, Cortical location of cells at the end points of the labeled field's axis. ΔX₊,ΔX₋, Measured cortical distance of the end points of the labeled field from the center.D_(mm), Measured cortical extent of the axis of the labeled field (gray oval diameter).

The linear visuotopic extent (D°) for the long axis of label is then given by:

$$D_{(\text{deg})}^{°}=(E_{+}-E_{-}{)}_{(\text{deg})}+S_{(\text{deg})}.$$ Equation 3

The aggregate receptive field size (ARF) (Fig. 1a) was calculated as:

$${ARF}_{(\text{deg})}=D_{(\text{deg})}^{°}+{\text{mRF}}_{(\text{deg})},$$ Equation 4

where mRF is the mean RF size of cells at the end points of the axis of label, and can reflect the mrf or summation field of the neurons (see Results). We used our own physiological measures of RF sizes appropriate for the end points eccentricity and cortical layer location. These were measured either in the same animal in which the tracer injection was made or in a separate set of quantitative physiological experiments performed in different animals (see above).

Below we provide a detailed example of our estimates of the visuotopic extent of the injection site and resulting labeled horizontal connections for the case in Figure 6a. The V1 injection was made at 6.5° eccentricity in the lower visual field, 4° from the vertical meridian. D° along the anteroposterior (AP; i.e., isoeccentricity) axis of V1 was estimated substituting in Equation 1the following values: D_(mm) = 1.13 mm (measured cortical extent of injection site AP axis) or 4.34 mm (measured cortical extent of horizontal connections AP axis);MF (at E = 6.5°) = 1.3 mm/° (using equation MF = 13E^−1.22 mm/°; Van Essen et al., 1984); and S (at E = 6.5°) = 0.16° (using equation S = 0.314 ×mrf size −0.86 min; Dow et al., 1981).

Fig. 6.

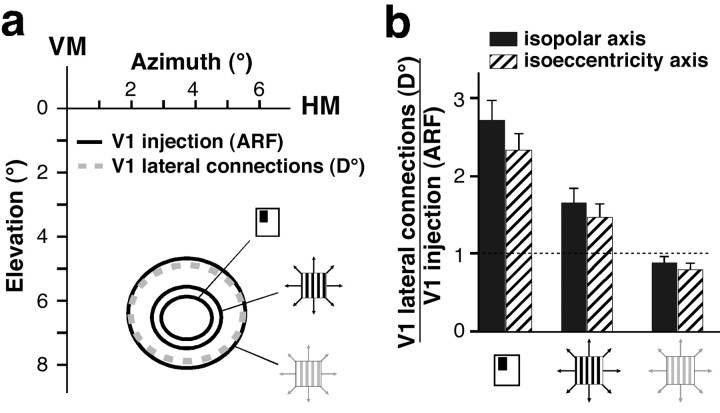
Visuotopic extent of V1 lateral connections.a, Visual field map of a representative CTB injection site and resulting labeled lateral connections in V1 layers 2/3. The injection site was in the lower visual field representation of V1 at 6.5° eccentricity, 4° from the vertical meridian (VM). HM, Horizontal meridian.D° of the V1 connectional field (dashed gray oval, 3 × 3.5°) and ARF size of the V1 injection site (black ovals) were estimated as detailed in Materials and Methods. The black ovals represent ARF sizes computed using three different measures of RF size, each indicated bysymbols as in Figure 2c (aggregate mrf, 1.3 × 1.6°; aggregate high-contrast SF, 1.9 × 2.2°; aggregate low-contrast SF, 3.4 × 3.7°). b, Histogram of the population means (n = 21) of the relative visuotopic extent of labeled V1 lateral connections along the isopolar (black bars) and isoeccentricity (hatched bars) axes of the labeled fields. Data from all layers are pooled together. The visuotopic extent is expressed as the ratio of D° of V1 connections to the ARF size of neurons at the V1 injection site and is shown for each of three different methods of measuring RF (and thus ARF) size (symbols on x-axis, as in Fig.2c). The trend for ratios to be smaller along the isoeccentricity axis of the field was not statistically significant. Error bars indicate SEM. The dashed horizontal linemarks a ratio of 1.

D° of the injection site and resulting horizontal connections along the mediolateral (ML; i.e., isopolar) axis of V1 was estimated substituting in Equations 2 and 3 the following values:a and b = 11.7 and 1.01 (constants from equation MF = 11.7E^−1.01 mm/°; Van Essen et al., 1984); E_c = 6.5° (physiologically recorded E of injection site); ΔX₊ and ΔX₋ (for injection site) = 0.55 mm (measured cortical extent of injection site ML radius); ΔX₊ and ΔX₋ (for horizontal connections) = 2.1 and 3.1 mm (measured cortical separation of furthest medial and lateral labeled points, respectively, from the injection center); and S (at E = 6.5°) = 0.16°.

From Equation 2 we obtained E₊ andE₋ (for injection site) = 6.8 and 6.2°, and E₊ andE₋ (for horizontal connections) = 7.8 and 4.97°. From Equations 1 and 3 we obtained D° (for injection site) = 1.03° (AP axis) × 0.78° (ML axis), and D° (for horizontal connections) = 3.5° (AP axis) × 3° (ML axis).

The ARF size of the V1 injection site in Figure 6a was calculated as follows: ARF of AP axis = D° of injection (1.03°) + mean RF size in V1 layer 2/3 at 6.5° eccentricity [mrf = 0.55°; high- and low-contrast summation field (SF) = 1.15 and 2.65°, respectively]. ARF of ML axis = D° of injection (0.78°) + mean RF size/2 in V1 layers 2/3 atE₊ (6.8°) eccentricity (mrf = 0.56°; high- and low-contrastSF = 1.18 and 2.7°, respectively) + mean RF size/2 in V1 layers 2/3 at E₋ (6.2°) eccentricity (mrf = 0.54°; high and low contrast SF = 1.13° and 2.6°, respectively). RF sizes in this case were obtained from our own equations relating RF size to eccentricity in the different layers of V1 and derived from a separate set of quantitative physiological experiments (see above).

The above estimates were obtained using MF values from Van Essen et al. (1984). Although MF values reported by Tootell et al. (1988) andBlasdel and Campbell (2001) tend to be slightly larger than those ofVan Essen et al (1984), applying MF values from these other authors to the above estimates yielded only slightly smaller values ofD° and ARF size. Thus, for example, the aggregate high-contrast SF size of the V1 injection (along the ML axis) in Figure6a measured 1.9° using the MF of Van Essen et al. (1984)but was 1.8° using the MF of Tootell et al. (1988). The ratio ofD° of lateral connections to the aggregate high-contrast SF size of the V1 injection was 1.6 (for the ML axis) using the MF fromVan Essen et al. (1984) and 1.3 using the MF from Tootell et al. (1988). Thus, using MFs in the literature from different authors, we observed minimal differences in our estimates.

For labeled fields within the central 5° of V2, we used MF and S values from Roe and Ts'o (1995), because they reported separate measures of MF along and across CO stripes. Published measurements of MF in more peripheral V2 (Gattas et al., 1981) and in V3 (Gattas et al., 1988) and MT (Albright and Desimone, 1987; Maunsell and Van Essen, 1987) are averaged across isopolar and isoeccentricity axes, thus not taking into account possible anisotropies in MF. Similar to V1 and V2, anatomical anisotropies of labeled connectional fields in areas V3 and MT likely reflect anisotropies in MF within these areas. Thus, for the label in more peripheral (>5°) V2 and for all labeled fields in V3 and MT, we estimated D° only for the long axis of the label field, substituting in Equation 1 the largest published values of MF (Gattas et al., 1981; Albright and Desimone, 1987; Gattas et al., 1988) at the retinal eccentricity of the injection site. The rationale for this choice was that the largest values of MF at a given retinal eccentricity most likely reflect MF values along the anisotropy axis. Using the largest values of MF might have caused us to underestimate the extent of retrogradely labeled FB fields in visual field coordinates. This error would not have altered our conclusions that the visuotopic extent of FB fields is larger than that of V1 intrinsic horizontal connections. To avoid introducing additional errors, we did not attempt to estimate the visuotopic extent of FB fields along their shorter axis or their visual field anisotropy; thus, the retrogradely labeled fields of cells of origin of FB connections in extrastriate cortex are represented in visual space as circles (see Fig.7a) rather than ovals (as are the fields of V1 horizontal connections, or of terminal FB connections inV1) (see Figs.6a, 7a, 8a,b). To estimate ARFs in V2 and V3, we used our own measures of mrf and summation field sizes (Levitt et al., 1994; Gegenfurtner et al., 1997; this study). MT RF sizes were taken from studies by Albright and Desimone (1987) andMaunsell and Van Essen (1987). Estimated sizes of D° and ARF were consistent with those determined physiologically (see Fig.8a).

Fig. 7.

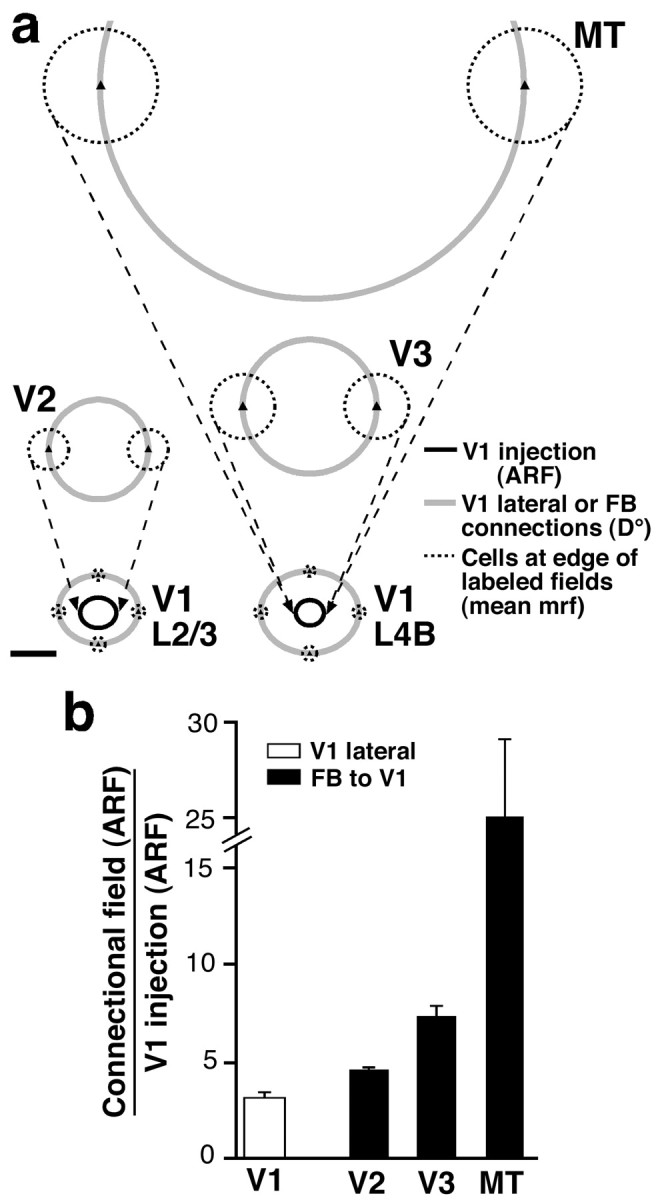
Visuotopic extent of retrogradely labeled fields of cells of origin of FB connections in extrastriate cortex.a, Visual field map of FB fields of neurons in layers 5/6 of areas V2 (top left), V3 (middle right), and MT (top right) labeled by a CTB injection through V1 layers 1–4C at 6.5° eccentricity (same injection case as in Fig. 6a). Visual field maps of V1 lateral connections in layers 2/3 (bottom left) and 4B (bottom right) labeled by the same V1 injection are also shown. Gray circles, D° of the connectional fields. Black ovals, aggregate mrf size of neurons at the V1 injection site (1.3 × 1.6° in layers 2/3; 1.1 × 1.2° in layer 4B). Dashed black circles, mean mrf size of cells at the edge of labeled fields. The aggregate mrf size of each connectional field is the sum of the diameter of thegray circle plus the diameter of one dashed black circle. This was estimated as described in Materials and Methods and measured 3.5 × 4.1° (V1 layers 2/3 horizontal connections), 4.1 × 4.8° (V1 layer 4B horizontal connections), 6.1° (V2 FB), 8.7° (V3 FB), and 23.6° (MT FB). The aggregate mrf of retrogradely labeled neuronal FB fields in the upper layers of extrastriate cortex (data not shown) measured 5.4° (V2), 7.6° (V3), and 15.3° (MT). Scale bar, 2°. b, Histogram of the population means of the relative visuotopic extent of labeled layer 5/6 FB fields (black bars) in areas V2 (n = 6), V3 (n = 5), and MT (n = 2), arising from the same V1 tracer injections. The visuotopic extent is expressed as the ratio of the aggregate mrf size of the FB field along its long axis to the aggregate mrf size of neurons at the V1 injection site. White bar, Mean aggregate mrf ratio (3.3 ± 0.24) for V1 lateral connections (n = 21). Note cut on they-axis scale.

Fig. 8.

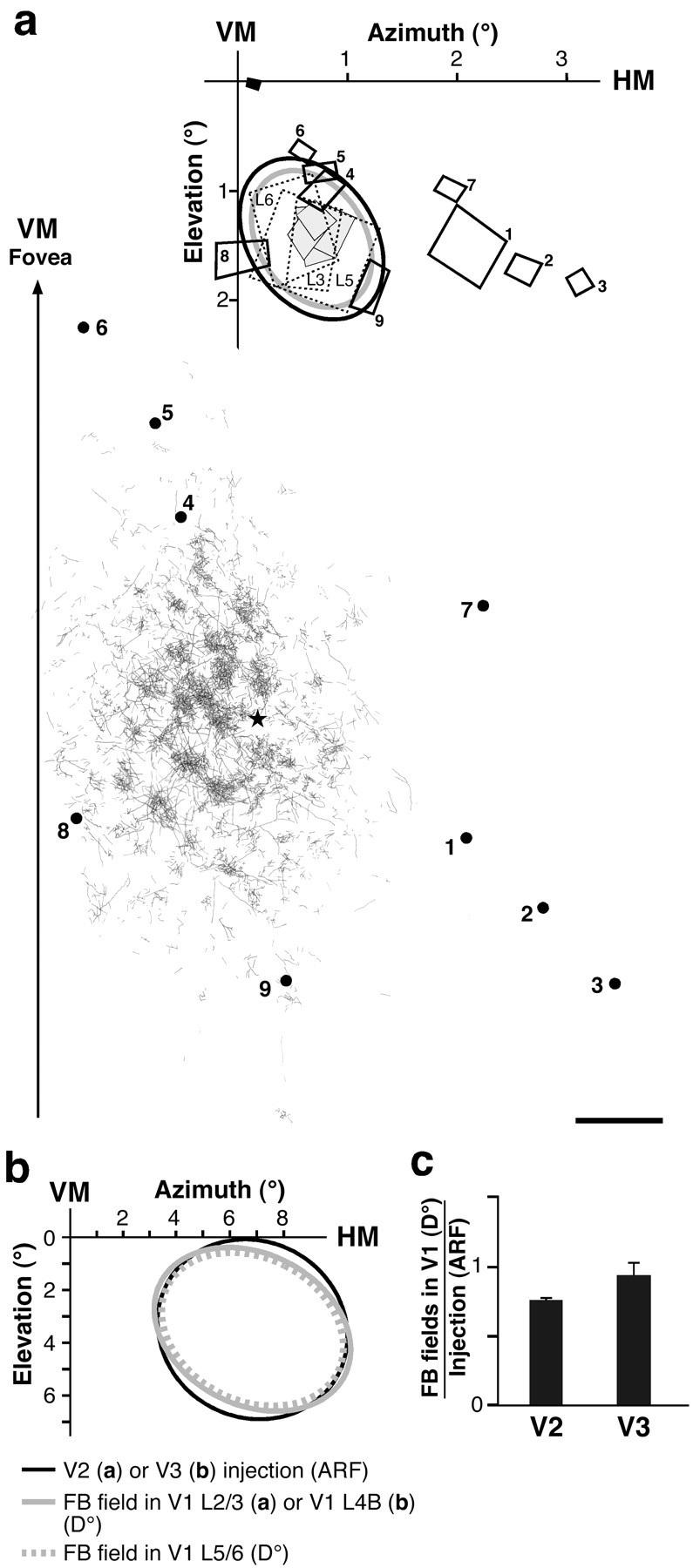
Visuotopic extent of feedback terminal fields anterogradely labeled in V1 by tracer injections in V2 or V3.a, FB field in V1 arising from a V2 injection.Bottom, Surface-view 2D serial tangential section reconstruction of the FB terminal field in layers 2/3 of V1 labeled by a BDA injection through V2 layers 1–6 at ∼2° eccentricity in the lower visual field. The arrow shows the approximate location of the V1–V2 border [vertical meridian (VM)] and points toward the fovea. Dots 1–9, V1 recording sites; numbers correspond to RFs mapped at the top. Star, Center of CTB V1 injection made at the same retinal eccentricity as the V2 injection. The labeled field axes measured 7.6 × 4 mm. Scale bar, 1 mm (corrected for 8% shrinkage). Top, Visual field map of the BDA-labeled FB terminal field shown at thebottom. Black oval, Estimated aggregate mrf of neurons at the V2 injection site (1.6 × 1.15°); gray oval, estimatedD° of resulting labeled FB terminal field in V1 (1.35°x1°). Dashed rectangles, Three RFs (mrf) at V2 injection site recorded in the same vertical penetration at different cortical depths (L3, L5, L6, V2 cortical layers 3, 5, 6, respectively). Gray rectangles, Four RFs (mrf) at V1 injection site (star at the bottom) recorded in the same vertical penetration in different layers (most superficial in layer 2, deepest in layer 6). Note good overlap of RFs at V1 and V2 injected points, and their location at the center of the FB terminal field. Rectangles 1–9, mrf sizes of neurons at V1 recording sites 1–9 shown at the bottom.Filled black rectangle, Foveal RF mapped to monitor eye movements. Note good agreement between estimated and empirically measured visuotopic extents of connections and injection sites.b, Estimated visuotopic extent of labeled FB terminal fields in V1 layers 4B (gray oval, 7.7 × 5.6°) and 5/6 (dashed gray oval, 7.1 × 5.3°) arising from a CTB injection (black oval, 7.2 × 6.6°) through V3 layers 1–6 at 6.4° eccentricity in the lower visual field. c, Histogram of the population means of the relative visuotopic extent of labeled FB terminal fields in V1 (isopolar axis) arising from V2 or V3 injections. The visuotopic extent is expressed as the ratio of D° of the FB fields to the aggregate mrf size of neurons at the extrastriate injection site. Data from all V1 layers are pooled together.

RESULTS

In a first set of single-unit recording experiments, we determined quantitatively the spatial dimension of the RF and modulatory surround field of V1 cells. In a second set of combined anatomical and physiological experiments, we determined the visuotopic extent of V1 horizontal connections and of feedback connections from extrastriate cortex to V1 and compared them with V1 cells' receptive field and surround field sizes measured in the previous set of experiments. The two sets of experiments were performed in different animals but in the same region of visual space (2–8° retinal eccentricity in the lower visual field representation of V1).

Spatial extent of V1 neuron receptive field and modulatory surround field

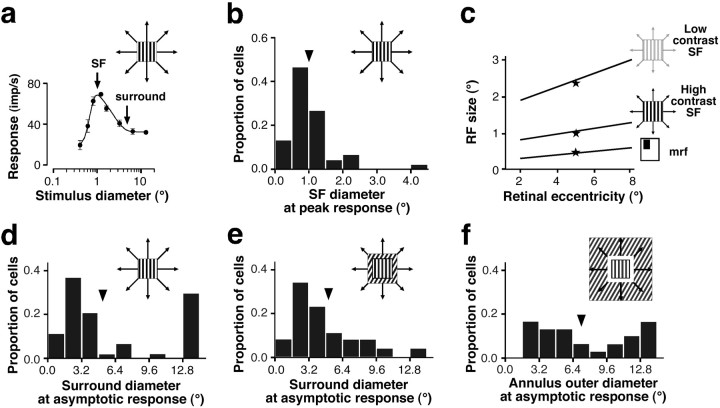
Area summation curves were measured for 59 neurons sampled from all layers of macaque V1 (n = 18 in layers 2/3;n = 24 in layer 4; and n = 17 in layers 5/6) between 2 and 8° eccentricity. Of these cells, 69% had complex RFs; the rest were simple cells (for a detailed report of these data, see Levitt and Lund, 2002). A high-contrast (75%) drifting grating patch of optimal stimulus parameters for the recorded neuron was centered over the computer-mapped RF of the cell, and its diameter was systematically increased. We measured response amplitude as a function of stimulus diameter. Typically, responses increased with patch size to a peak and either asymptoted at the peak or showed response suppression as stimulus size was further increased (i.e., surround suppression) (Fig. 2a). We took as a measure of RF size the smallest stimulus diameter at peak response (Fig. 2a; we included in this analysis only cells that showed surround suppression). We refer to this measure of RF size as the high-contrast SF. SFs for our sample of V1 cells averaged 1.0 ± 0.1° (Fig. 2b), increased with retinal eccentricity (Fig. 2c, middle function), and showed no statistically significant variation across cortical layers despite a trend for the largest SFs to be found in deeper layers. These results on layer differences in SF sizes are consistent with those from other studies (Sceniak et al., 2001; Cavanaugh et al., 2002; Levitt and Lund, 2002). RF size has been shown to vary depending on the method and the stimulus contrast used to measure it. Figure 2c compares RF size as a function of eccentricity using three different test conditions. Figure 2c, middle function, shows our measure of high-contrast SF size as a function of retinal eccentricity. Figure 2c, bottom function, shows data from Dow et al. (1981), who measured RF size by moving a high-contrast bar of light and hand drawing the contours of the area of visual space that elicited spikes from the neuron. This measure of RF size is commonly known as mrf or “classical” RF (Barlow et al., 1967). Our mean high-contrast SFs were 2.2-fold greater than the mean mrf sizes of Dow et al. (1981). Furthermore, RF size depends on stimulus contrast (Kapadia et al., 1999; Sceniak et al., 1999). Sceniak et al. (1999)found that, for the same V1 cells, SFs were on average 2.3-fold greater when measured using low-contrast rather than high-contrast gratings (Fig. 2c, top function).

Fig. 2.

Extent of RF and surround field for a population of macaque V1 cells. a, Response of a representative V1 neuron to an optimal high-contrast grating patch of increasing diameter (top right symbol). Patch diameter at peak response (left arrow) was taken to be the size of the SF of the cell in b and c (middle function). Patch diameter at asymptotic response (right arrow) was taken to be the size of the surround field of the cell ind and e. b, Distribution of SF diameters for a population of V1 neurons (n = 59), measured as in a. Arrowhead, Mean.c, RF size as a function of retinal eccentricity measured under three different test conditions, each one indicated bysymbols to the right of eachline. Straight lines are regression lines. Middle function, SFs measured using expanding high-contrast (75%) gratings; data from this study (n = 59 cells).Bottom function, Hand-mapped mrf; based on data from Dow et al. (1981). Top function, SFs measured using expanding low-contrast gratings; based on data from Sceniak et al. (1999) and obtained by multiplying our high-contrast SF function (middle function) by 2.3. Stars, Means.d–f, Distributions of surround field diameters for a population of V1 cells measured under three different test conditions, each one indicated by top right symbols.d, Expanding high-contrast optimal grating stimulus, including only cells with suppressive surrounds (n= 59, same cells as in b; note different scale onx-axis in b and d).e, Optimal center grating stimulus surrounded by expanding most suppressive grating stimulus (n = 30, subset of cells in b and d).f, Optimal center grating and most suppressive surround grating stimuli plus blank annulus expanding in the surround (n = 30 cells, same cells as in e).Arrowheads in d–f, Means.

For the same V1 cells, we also measured the extent of the modulatory surround field using three different methods (Fig.2d–f). Figure 2d shows the distribution of surround sizes measured for 59 neurons using expanding high-contrast gratings. As stimulus size increased beyond the high-contrast SF of the cells, responses decreased. Surround size was defined as the smallest stimulus diameter at which the response of the neuron asymptoted (Fig.2a). Surround sizes ranged between 1.2 and >13° (13° was the largest stimulus diameter we could produce on our monitor), averaging 5.1 ± 0.6°. For a subset (n = 30) of these cells, surround sizes were measured using two additional methods. A center optimal grating stimulus was confined to a central region the size of the high-contrast SF of the cell and was surrounded by the most suppressive grating stimulus configuration (usually, but not always, a grating at the same orientation as in the center). We then systematically varied either the outer diameter of the surround stimulus from 0° (i.e., central stimulus alone) to 13° (diameter of the display screen) (Fig. 2e) or of a blank annulus introduced between the central stimulus and a full-field (13°) surround stimulus (Fig. 2f). Because the strength of surround suppression has been shown to be highest in the region abutting the RF center (Walker et al., 1999), by blanking out the region of maximal surround strength (as in Fig. 2f), we aimed at revealing the most remote surround influences. As surround outer diameter increased, responses decreased; as annulus outer diameter increased, responses increased. Surround and annulus outer diameters at which responses asymptoted were taken as measures of surround sizes (Fig. 2a,f, respectively). Under all test conditions, surround diameters were found to extend up to and >13°. However, different distributions and mean values [mean, 5.0 ± 0.6° (Fig. 2e) and 7.1 ± 0.2° (Fig.2f)] were obtained with the different test methods, reflecting the fact that the surround region is most suppressive close to the RF. Thus, masking out the most suppressive near surround, as in Figure 2f, revealed more distant influences, whereas the latter were masked by optimally stimulating the most suppressive near-surround region, as in Figure 2e. Surround sizes did not vary significantly with retinal eccentricity or cortical layer. For each neuron, we calculated a “relative” surround extent as the ratio of surround field diameter (measured as in Fig. 2d) to the high-contrast SF diameter; the population average was 4.6 ± 0.7.

To summarize, in V1 at 2–8° eccentricity, surround field sizes were on average 4.6 (up to >13) times larger than high-contrast SF sizes and at least 10 (up to >27) times larger than the mean mrf size of V1 cells.

Several other recent studies have examined the spatial summation properties of macaque V1 neurons (Sceniak et al., 2001; Cavanaugh et al., 2002). In these studies, center and surround responses were modeled as independent, spatially overlapped excitatory and inhibitory mechanisms, each with a Gaussian spatial sensitivity profile and with the inhibitory mechanism being broader than the excitatory one (also see DeAngelis et al., 1994). Cavanaugh et al. (2002) found that a ratio of Gaussian model was the best fit to their data, whereas Sceniak et al. (2001) favored a difference of Gaussian (DOG) model. The spatial spread of the center and surround mechanisms in these studies was estimated directly, and in one study (Sceniak et al., 2001) exclusively, from the fitted curves. In the present study, we fit our spatial summation data to a DOG model and used the fits mainly to derive robust estimates of SF and surround field sizes. Because the parameters derived from the Gaussian sensitivity functions depend strongly on assumptions about the mechanisms underlying center-surround interactions that may not be valid, we chose to report empirical measurements of SF and surround sizes. However, because the DOG model is a good descriptor of our summation data, and to allow for comparison with previous studies, we also derived from the fitted curves the Gaussian spread (radius) of the excitatory and inhibitory components (Sceniak et al., 2001) (for details, see Levitt and Lund, 2002). The population means were 1.2° for the excitatory radius and 2.7° for the inhibitory radius, revealing a somewhat larger mean RF center mechanism than our empirical measurements of high-contrast SF size. The width of the surround inhibitory mechanism instead agreed well with our empirical measurements of surround size as described in Figure 2,d and e. These results are consistent with data from Sceniak et al. (2001), although our model parameters are somewhat larger than those reported by Cavanaugh et al. (2002).

Cortical extent and patterns of horizontal and feedback connections

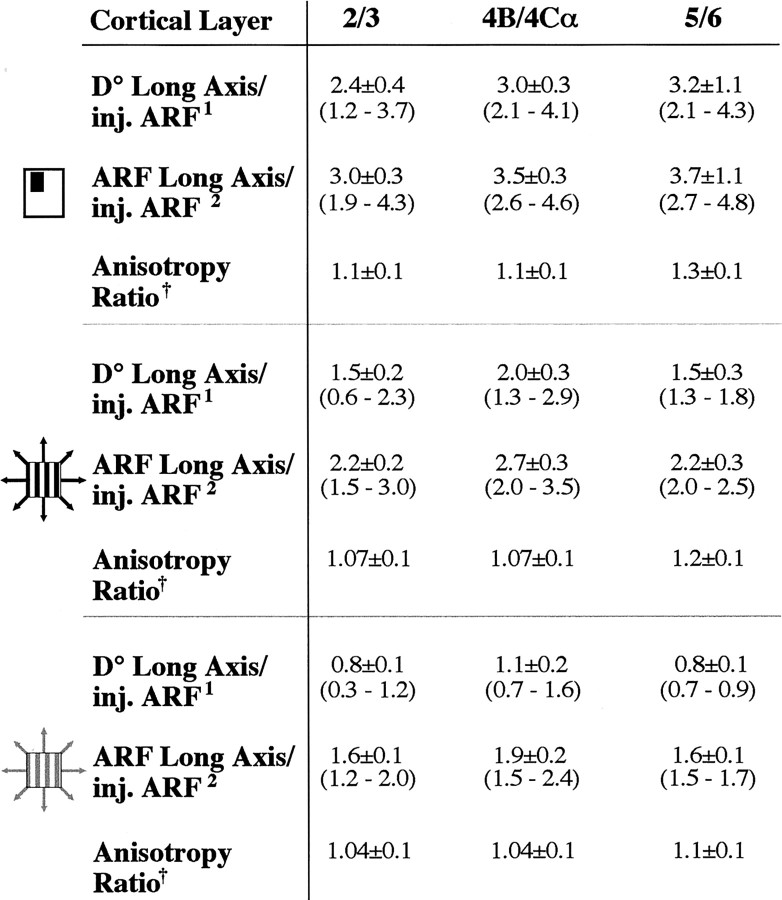
CTB (n = 8) or BDA (n = 2) injections (uptake zone diameters, 0.27–1.2 mm) were made in physiologically characterized V1 loci at different cortical depths (n = 2 in layers 1–3, 5 in layers 1–4C, 1 in layers 1–5, and 2 in layers 1–6) between 2.5 and 7.5° eccentricity in the lower visual field representation. Consistent with previous results obtained with different anatomical tracers (Rockland and Lund, 1983;Yoshioka et al., 1996), CTB or BDA injections in macaque V1 layers 2/3 produced patches of terminal label surrounding the injected V1 column (Fig. 3). CTB additionally retrogradely labeled cell bodies (but not fibers) within each patch, indicating the reciprocal nature of these connections (Fig. 3, inset). Reciprocal lateral connections were also labeled in layers 4B/upper 4Cα and 5/6, when the tracer injection involved these V1 laminas. Both tracers revealed different patterns of label in these layers: bar-shaped fields in 4B/upper 4Cα (Asi et al., 1996; Angelucci et al., 2002) and a less patchy, more diffuse label in 5/6 (Rockland and Knutson, 2001). The labeled fields of lateral connections in all V1 layers were anisotropic in cortical space (Fig. 3). In layers 2/3, the longer axis of label (D_(mm)) (Fig.1b), known to extend orthogonal to the ocular dominance domains (Yoshioka et al., 1996), measured on average 6 ± 0.7 mm (extending up to 9 mm). The distance from the edge of the tracer uptake zone to the farthest labeled cell averaged 2.9 ± 0.4 mm. The most distant labeled cells were consistently located laterally to the injection site, i.e., toward the foveal representation of V1 (Fig. 3). Furthermore, the mean anisotropy ratio (extent of long/short axis) of CTB-labeled layer 2/3 lateral connection fields was 1.56 ± 0.1, closely matching the anisotropy ratio (1.6) of the V1 magnification factor in these layers due to the ocular dominance domains (Blasdel and Campbell, 2001). The latter two observations suggest that lateral connections follow the overall anisotropy of visual field representation in V1. CTB and BDA injections produced similar results. We found no statistically significant difference in the extent or anisotropy ratio between lateral connections in different V1 layers, despite a trend for connections to be more extensive and more anisotropic in the deeper layers. The extent and anisotropy ratio for lateral connections in different V1 laminas are reported in Table1, top.

Fig. 3.

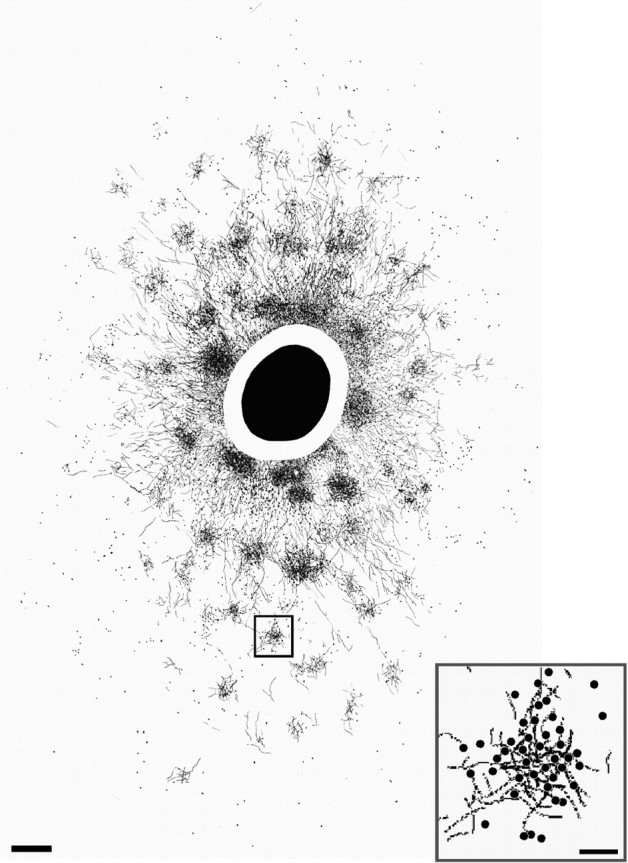
Patchy lateral (or horizontal) connections in layers 2/3 of macaque area V1. A surface view 2D composite reconstruction of CTB-labeled connections is shown. The labeled field axes measured 9 × 6 mm. Black oval, CTB uptake zone; blank annulus, region of heavy label. Note anisotropic distribution of overall label. The foveal representation is toward the bottom (lateral V1); the V1–V2 border is to the right (anterior V1). Small square, Labeled patch shown at higher power in the inset. Scale bar, 500 μm (corrected for 30% shrinkage). Inset,High-power drawing of patch in the small square, showing labeled fibers and somata (dots), indicating reciprocity of connections. Scale bar, 100 μm.

Table 1.

Cortical extent and anisotropy of V1 lateral connections and of feedback connections to V1

Connections	Cortical layer	Long axis1-a	Anisotropy ratio1-b
V1 lateral	2/3 (n = 10)	6  ± 0.7 (3–9)	1.56  ± 0.12
	4B/4Cα (n = 8)	6.7  ± 0.7 (4.7–10)	1.5  ± 0.1
	5/6 (n = 3)	7.9  ± 1.6 (6.3–9.5)	1.76  ± 0.2
FB in V2	2/3A (n = 5)	6.1  ± 0.6 (4.6–8.3)	3.4  ± 0.8
	5/6 (n = 6)	6.4  ± 1.2 (4–9.4)	3.9  ± 1.0
FB in V3	2/3A (n = 5)	5.2  ± 1.2 (2.7–8.1)	3.3  ± 0.6
	5/6 (n = 5)	7.9  ± 1.2 (4.5–9.8)	3.2  ± 0.2
FB in MT	2/3A (n = 1)	4.5	2.8
	5/6 (n = 2)	8.9  ± 2.1 (6.8–10.9)	2  ± 0.4
FB in V1 from V2	all (n = 3)	6.8  ± 0.4 (6.4–7.6)	2  ± 0.1
FB in V1 from V3	all (n = 3)	13.4  ± 0.5 (12.9–13.9)	2  ± 0.2

All values are mean ± SEM. Values in parenthesis are minimum and maximum; n, number of labeled connectional fields in the layer.

^F1-aExtent (D_(mm); see Fig. 1b) of labeled field long axis (i.e., along the cortical area's elevation axis).

^F1-bExtent of long axis/extent of short axis of labeled field.

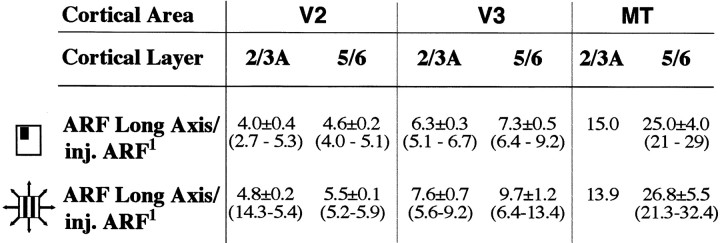
The same V1 injections (n = 10) used to determine the extent of intra-areal V1 lateral connections labeled retrogradely the cells of origin of FB connections to V1 in extrastriate cortex (Fig.4a). We confined our analysis to FB from areas V2, V3, and MT. Small (∼300-μm-diameter) tracer injections confined to V1 layers 1–3 retrogradely labeled extensive fields of somata in the superficial (2/3A) and deeper (at the 5/6 border) layers of area V2; injections involving layers 1–4B or 1–6 additionally labeled cells in the upper and lower layers of areas V3 and MT. Within each extrastriate area, the retrograde label in the upper layers was less dense (Barone et al., 2000) and significantly (p < 0.01) less extensive than in layers 5/6 (Fig. 4b), and decreased in density and spatial extent with distance from V1, whereas the label in the lower layers increased in spatial extent (Table 1, middle). The density of labeled cells within the FB fields gradually declined with distance from a denser center core region. The retrograde label appeared clustered in the upper layers and showed fluctuations in cell density in the lower layers. Labeled FB fields in extrastriate cortex were anisotropic in cortical space (Fig. 4b; Table 1, middle), their long axis following the overall anisotropy of visual field representation of the cortical area. Thus, in V2, the longer axis of the label extended orthogonal to the CO bands, and in all areas was approximately parallel to the longer (i.e., elevation) axis of the cortical area itself. Extent and anisotropy ratios for retrogradely labeled FB connections in the upper and lower layers of extrastriate cortex are reported in Table1, middle.

Our V1 injections were either confined to the CO interblob columns (n = 2 injections through layers 1–3, andn = 1 injection through layers 1–4B) or involved both CO blob and interblob compartments (n = 7). Resulting retrograde FB label involved all V2 stripe compartments, even in cases in which the V1 injection was clearly confined to an interblob column. The anterograde label in V2 (terminals of feedforward axons from V1) arising from these same V1 injections in the interblob columns (n = 3) was more focused than the retrograde (FB) label and was either confined to the pale CO stripes (n = 1; V1 injection in layers 1–3) or involved both the thick and pale stripes (n = 2). There was no obvious difference in extent between FB fields in extrastriate cortex labeled by V1 injections involving CO blob or interblob columns.

We also determined the extent of the divergence region of FB connections to V1. This is the V1 region containing terminals of FB axons, anterogradely labeled by small tracer injections in extrastriate cortex. CTB or BDA injections (uptake zone diameter, 300–1500 μm) were made in physiologically characterized loci in areas V2 (n = 2 CTB and 1 BDA injections) or dorsal V3 (n = 4 CTB injections) (Fig.5a) between 2.2 and 6.5° eccentricity in the lower visual field. To investigate the retinotopic organization of FB connections to V1, all the V2 injected cases (n = 3) received a second injection of a different tracer (BDA or CTB) in V1 at the same retinal eccentricity as the V2 injection. Upper-layer injections in V2 or V3 produced large fields of patchy terminal and cell body label in V1 layers 2/3 and 4B (Fig.5b). Injections involving all V2 or V3 cortical laminas resulted in even larger labeled fields within V1 and additionally produced terminal and sparse cell body label at the layer 5/6 border of V1. The layer 5/6 label appeared less clearly patchy than in the layers above. Labeled patches in different V1 layers arising from the same extrastriate injection were vertically aligned. Anterograde and retrograde labels overlapped in the V1 patches, indicating the reciprocal nature of feedforward and feedback connections to and from V1. FB fields within V1 arising from tracer injections in V2 or V3 greatly exceeded the size of the intra-areal V1 fields produced by similarly sized V1 injections, the V3 injections labeling larger fields in V1 than the V2 injections (Table 1, bottom). The FB fields in V1 were anisotropic in cortical space (Fig. 5c), their longer axis extending parallel to the V1–V2 border when near that border; their mean anisotropy ratio was greater than that of V1 intra-areal lateral connections (Table 1,bottom).

Fig. 5.

Patchy terminal label of feedback connections in layer 4B of V1 arising from a tracer injection in area V3.a, Micrograph of a sagittal section through dorsal area V3, showing a CTB injection site involving all cortical layers (layer 1 is involved in the injection but not in this specific section). The injection was made at 6.4° eccentricity in the lower visual field.1, Layer 1; WM, white matter;AG, annectant gyrus. Scale bar, 200 μm (corrected for 30% shrinkage). b, Micrograph showing a surface view of CTB-labeled terminals and cell bodies (arising from the injection site in a) in a single tissue section cut tangentially through V1 layer 4B. c, 2D composite serial tangential section reconstruction of anterograde (i.e., feedback) terminal label through the whole thickness of layer 4B. Arrowheads inb and c point to the same two patches. Note anisotropic distribution of overall label. The axes of the labeled field measured 13.8 × 8.1 mm. The visual field extent of this layer 4B-labeled field is represented as a gray oval in Figure 8b. Scale bar, 1 mm, for b andc (corrected for 30% shrinkage). Medial, Away from the fovea; Anterior: toward the V1–V2 border.

Our V2 injections (one confined to a pale CO stripe and two involving both thick and pale stripes) produced terminal and cell body labels in the interblob columns of V1 (consistent with results of Sincich and Horton, 2002). Terminal (FB) label in V1 arising from V3 injections was confined either to the CO blob or to the interblob columns; larger injections (∼1.5 mm in diameter) labeled both V1 compartments. These observations suggest that, similarly to corticocortical projections between V1 and V2 (Sincich and Horton, 2002), the connections between V1 and V3 form two parallel, segregated pathways, one related to the CO blob columns of V1 and the other one related to the interblobs (Angelucci and Levitt, 2002). We observed no obvious difference in extent between FB fields terminating in different CO compartments of V1.

Visuotopic extent of horizontal and feedback connections

Cortical measurements of intrinsic V1 and inter-areal FB fields were converted into visual field coordinates and related to the spatial extent of the receptive and surround fields of V1 cells.

Here we use two visuotopic measures: (1) D° is the extent, in degrees of visual angle, of the axis of the connectional field, derived from the cortical retinotopic map (see Eqs. 1, 3) (Fig.1a); its extent is independent of RF size; and (2) ARF is the cumulative RF size of all labeled neurons in a given labeled region; thus its extent is dependent on the method and stimulus contrast used to measure RF size (see Eq. 4) (Fig. 1a). The visuotopic extent (D°) of lateral connections is shown for a representative case in Figure6a. D° of CTB-labeled layer 2/3 lateral connections (dashed gray oval) is shown centered onto three different estimates of the ARF size of the V1 injection (the three black ovalsindicate aggregate mrf and aggregate high- and low-contrast SF, respectively). D° of V1 lateral connections in this case was 2.2-fold greater than the aggregate mrf of the connections cells of origin and closely matched the aggregate low-contrast SF size of the cells of origin. Across the population, the monosynaptic spread (D°) of V1 horizontal connections averaged 2.47 ± 0.3° in extent. V1 injection sites ranged in size between 0.2° and 0.8° (D°) or 0.5° and 1.3° (aggregate mrf). Because our interest lay in determining whether lateral connections extend beyond the limits of V1 cells RFs, we calculated a “relative” visuotopic extent for these connections as the ratio of the visuotopic extent of the connectional field (either D° or ARF size) to the ARF size of its cells of origin. Figure 6b shows population means of the relative visuotopic extent of V1 connectional fields across all cortical layers (n = 21 connectional fields). Mean population values for the different V1 layers are shown in Table 2. Ratios in Figure6b and Table 2 are additionally shown for each of three different methods of measuring RF size (mrf and high- and low-contrast SF). On average, across the population, the monosynaptic spread (D°) of V1 lateral connections was approximately three times larger than the mrf and approximately two times larger than the high-contrast SF of their cells of origin but was commensurate with the low-contrast SF of the cells. Therefore, these connections could account monosynaptically for the apparent expansion of the SF at low contrast (Kapadia et al., 1999; Sceniak et al., 1999). However, because V1 neuron surround fields were on average approximately five (up to >13) times larger than the high-contrast SF of the neurons (see above), V1 horizontal connections are significantly less extensive than the mean surround size of V1 cells. Comparison of the mean visuotopic extent of these connections (2.47°) with the mean Gaussian spread (diameter) of the excitatory center (2.4°) and inhibitory surround (5.4°) mechanisms also revealed that the monosynaptic spread of horizontal connections is too small to account for mean surround size and is instead commensurate with the size of the RF center mechanism.

Table 2.

Visual field extent and anisotropy of V1 lateral connections

Ratios are shown for ARFs computed using three different measures of RF size (symbols on the left; as in Fig.2c). All values are mean ± SEM. Values in parenthesis are minimum and maximum; n, same as in Table 1, V1 lateral.

^F2-1D° along the labeled field's long axis/ARF size of the injection site.

^F2-2ARF size along the labeled field's long axis/ARF size of the injection site.

^†ARF size along long axis/ARF size along short axis of labeled field.

Despite being anisotropic in cortical space (Fig. 3; Table 1, top), V1 lateral connections covered isotropic regions of visual space (Fig.6a; Table 2). The ratio of D° of the foveal half of the connections to D° of their peripheral half averaged 0.94 ± 0.5, indicating that visual space is represented symmetrically along the elevation axis of the connections. In addition, the mean anisotropy ratio of their visual field extent (ARF size along the long axis/ARF size along the short axis of the labeled field) approached 1. There was no statistically significant difference in anisotropy ratio across cortical layers, despite a tendency for connections to be more anisotropic in layers 5/6 (Table 2).

We then asked whether the dimensions of feedback connections from extrastriate cortex to V1 are commensurate with the scale of V1 neuron modulatory surround fields. Because the cells of origin of FB connections in extrastriate cortex and of lateral connections in V1 were labeled by the same V1 tracer injections (n = 10), we were able to directly compare the extent of the visual field region that these two different connectional systems convey to the same V1 column. Figure 7a shows an example of the visuotopic extent of retrogradely labeled fields of cells of origin of FB connections in layers 5/6 of extrastriate cortex. The visuotopic extent of V1 horizontal connections to the same injection site is also shown for comparison. The aggregate mrf sizes of the FB fields in V2, V3, and MT were 4.6-, 7.7-, and 21-fold larger, respectively, than the aggregate mrf size of neurons at the V1 injection sites. In comparison, the aggregate mrf sizes of V1 intra-areal lateral connections in layers 2/3 and 4B were only 2.7 and 3.7 times larger than the aggregate mrf size of the same V1 injection. Across the population, aggregate mrf sizes of retrogradely labeled FB fields in the lower layers of extrastriate cortex averaged 3.8 ± 0.6° (in V2), 6.7 ± 0.7° (in V3), and 26.6 ± 3° (in MT); those of V1 horizontal connections across all layers instead averaged 2.9 ± 0.4. Figure 7b shows population means of the relative visuotopic extent of retrogradely labeled FB fields in the lower layers of areas V2, V3, and MT and, for comparison, of V1 lateral connections. Relative visuotopic extent values are shown in Table 3 for each of two different methods of measuring RF size. These results indicate that the region of visual space conveyed by FB connections from extrastriate cortex to V1 is larger than that conveyed by horizontal connections to the same V1 column. Furthermore, such visual space region increases with cortical distance from V1, relating to the magnification factor and RF size of neurons in the extrastriate region giving rise to the FB projections. This was the case for both upper and lower layer FB fields, but within each extrastriate area, the lower layer fields were always more extensive than the upper layer fields (Table 3).

Table 3.

Visual field extent of feedback neuron fields in extrastriate cortex

Ratios are shown for ARFs computed using two different measures of RF size (mrf and high contrast SF; symbols on the left). Other conventions as in Table 2; n, same as in Table1, FB in V2, V3, and MT.

^F4-1ARF size along the labeled field's long axis/ARF size of the injection site.

We then compared the scale of FB fields with the scale of physiologically measured surround field sizes of V1 neurons. Specifically, we compared the relative visuotopic extent of FB fields (Table 3) with the relative extent of surround fields of V1 neurons (see above). On average, depending on the cortical area of origin, FB connections from the lower layers of extrastriate cortex conveyed information to a V1 column from regions of visual space 5–25 (up to 29) times the aggregate mrf of the V1 column, and 6–27 (up to 32) times the aggregate high-contrast SF of the V1 injection (Table 3). Surround field sizes of V1 cells were on average 10 (up to >27) times larger than the mrf of the cells and 5 (up to >13) times larger than their high-contrast SF (see above). Thus, the spatial scale of FB connections from extrastriate cortex to V1 is commensurate with the full spatial range of empirically measured modulatory surround fields of single V1 cells. Similarly, comparison of the mean visuotopic extent of FB fields with the mean Gaussian spread (diameter) of the inhibitory surround mechanism (5.4°) revealed the mean visuotopic extent of FB from V3 (5.6° in layers 2/3 and 6.7° in layers 5/6) to be commensurate with the mean size of the RF surround mechanism, and FB from V2 (3.4° in layers 2/3 and 3.8° in layers 5/6) and MT (15.3° and 26.6° in the upper and lower layers) with shorter- and longer-range surround sizes, respectively.

Figure 8, a and b, shows the visuotopic extent of anterogradely labeled fields of terminals of FB connections within V1 arising from a BDA injection in V2 (Fig. 8a) or a CTB injection in V3 (Fig. 8b). The relative visuotopic extent (D° of FB field/aggregate mrf of neurons at the injection site) of the FB terminal field in layers 2/3 of V1 labeled by the V2 injection was 0.85 (Fig.8a); those of the terminal FB fields in V1 layers 4B and 5/6 labeled by the V3 injection were 1.1 and 1, respectively. Across the population, the visuotopic extent (D°) of FB terminal fields in V1 labeled by V2 or V3 injections averaged 3.42 ± 1.2° (D° of the injection sites ranging between 0.3 and 2.7° and the aggregate mrf between 1.5 and 7.2°). Figure8c and Table 4 show population means of the relative visuotopic extent (D° or aggregate mrf of FB field in V1/aggregate mrf of extrastriate injection site) of anterogradely labeled FB fields across all layers of V1. These results indicate that the aggregate mrf of FB terminal fields within V1 arising from V2 or V3 injections is commensurate with the aggregate mrf of FB neurons at the injected site; i.e., FB connections link equal regions of visual field in striate and extrastriate cortices. Injections in overlapping retinotopic locations in V1 and V2 further emphasized the orderly topographic organization of these connections, demonstrating that FB neurons project symmetrically to V1 around a central point at the same retinotopic location as the injected V2 column (Fig.8a, bottom). Unlike V1 intra-areal lateral connections, FB connectional fields in V1 were anisotropic in visual space (Fig. 8a, top, b; Table 4).

Table 4.

Visual field extent and anisotropy of feedback terminal fields in V1

Ratios are shown for only one method of measuring RF size (mrf; symbol on the left). n, Same as in Table 1, FB in V1.

^1,2,†As in Table 2.

DISCUSSION

Our results show that the monosynaptic spread of horizontal connections in macaque V1 is commensurate with the low-contrast summation field of V1 neurons. These connections are not sufficiently extensive to account for the mean size of V1 cells' surround fields or longer-range center–surround interactions. Feedback connections from extrastriate cortex to V1, instead, are commensurate with the full range of V1 cells' center and surround field sizes; they show an orderly topographic organization and terminate in a patch-like manner within V1 (Fig. 9). These results strongly suggest that V1 horizontal connections integrate signals within the SF, whereas feedback connections underlie interactions within and beyond the SF of V1 neurons.

Fig. 9.

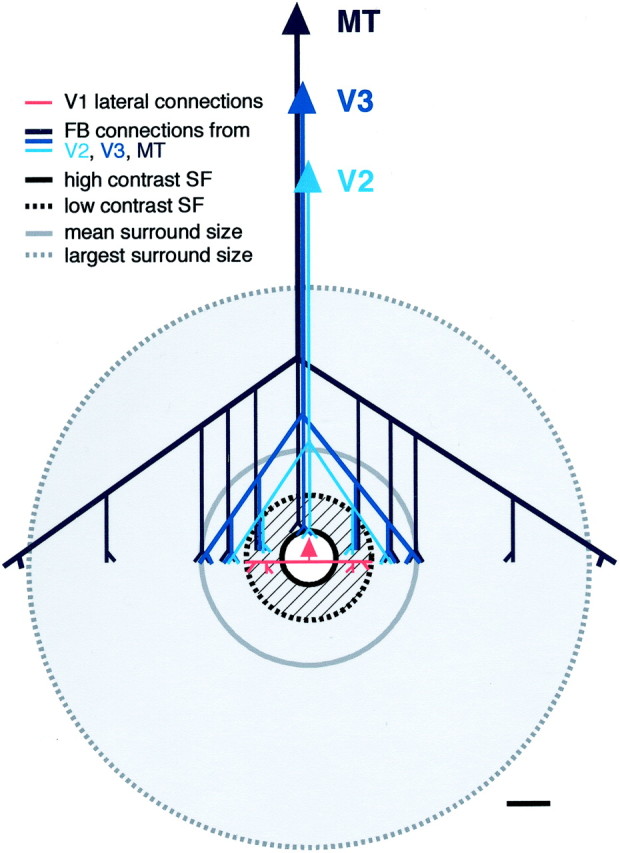
Summary diagram showing the spatial scales of V1 lateral and feedback connections relative to the spatial scales of empirically measured summation receptive field and modulatory surround field of V1 neurons. Gray area, Region over which presentation of stimuli at the same orientation as the center stimulus can suppress the center response to an optimally oriented high contrast stimulus. White area, Region over which presentation of optimally oriented high-contrast stimuli evokes or facilitates a response from the neuron (high-contrast SF). Hatched gray annulus, Region over which presentation of stimuli at the same orientation as the center stimulus can suppress or facilitate the center response to an optimally oriented stimulus depending on the center stimulus contrast. Lateral connections within V1 (red) extend beyond the high-contrast summation field (black circle) and are commensurate with the low-contrast SF (dashed black circle) of the V1 neurons from which they arise. Feedback connections (FB; blue) from extrastriate cortex to V1 are commensurate with the full spatial scale of the SF and surround field. FB from “higher” cortical areas is more extensive than FB from “lower” areas. Both connectional systems (lateral and FB) are patchy in V1. Scale bar, 1°. We have previously proposed a model of how FB and lateral connections might mediate modulation of RF responses (Angelucci et al., 2002). In this model, the output of each excitatory pyramidal neuron (e.g., the center recorded neuron) in V1 is controlled by a local inhibitory neuron having higher response gain and contrast threshold than the pyramid (Lund et al., 1995; Somers et al., 2002). FB and lateral inputs contact directly both neuron types, whereas feedforward inputs are only to the pyramid. The divergent–convergent organization of FB and lateral axons is such that these two systems overlap in space and are active for any stimulus diameter, even for stimuli confined to the RF center. At low contrast, RF excitation predominates; lateral and FB input to the pyramid can be summed from more distant cortical (and visual space) locations before inhibition begins to rise. Suppression of the center neuron response would result from increasing the weight of excitation onto the pyramid and its local inhibitory neuron, either via high-contrast feedforward drive or via lateral and FB inputs, such as by increasing stimulus diameter.

The size of the RF depends on the method used to measure it. The mrf is the low-threshold, spiking region, which can be mapped using moving small stimuli. This region is surrounded by a higher-threshold, depolarizing field, incapable of driving the cell when stimulated in isolation but capable of increasing the response of the cell to stimulation of its mrf (Bringuier et al., 1999). The size of this subthreshold field surrounding the mrf has been measured intracellularly in cat V1 neurons and was found to be coextensive with the monosynaptic spread of V1 horizontal connections in this species (Bringuier et al., 1999). This larger subthreshold region can be revealed extracellularly in areal summation experiments, using expanding gratings, and has been shown to be larger when measured at low stimulus contrast (Kapadia et al., 1999; Sceniak et al., 1999). In the present study, we found the monosynaptic spread of horizontal connections in monkey V1 to be coextensive with the empirically measured low-contrast SF of V1 cells and with the mean Gaussian spread of the excitatory center mechanism. Thus, the subthreshold depolarizing synaptic integration field of V1 neurons, measured intracellularly byBringuier et al. (1999), most likely represents the low-contrast summation field of the neurons measured extracellularly. In macaque, feedforward thalamic afferents to single layer 4C V1 neurons are of appropriate scale to underlie the mrf and, possibly, the high contrast SF of these cells (Angelucci et al., 2002) but are not sufficiently extensive to mediate longer-range interactions. Thus, we suggest that intra-areal V1 horizontal connections play an important role in shaping the spatial summation properties of V1 neurons at low contrast. Somehow, the inputs from laterally offset neurons are more effective in driving the center neuron in a low-contrast regimen, when feedforward (lateral geniculate nucleus) inputs are only moderately driving the response of the center neuron (for a model, see Angelucci et al., 2002) (Fig. 9).

We were surprised to find that horizontal connections in macaque V1 are isotropic in visual space. This contrasts with results in other species, in which these connections are anisotropic along an axis colinear to the optimal orientation in the visual field map [tree shrew (Bosking et al., 1997), cat (Schmidt et al., 1997), and owl monkey (Sincich and Blasdel, 2001)]. Anisotropic lateral connections in visual field have been suggested to serve as an anatomical substrate for intracortical generation of orientation selectivity or for contour completion in V1 (Bosking et al., 1997; Li, 1999; Sincich and Blasdel, 2001). The visual space anisotropy of V1 lateral connections seen in other species might, instead, reflect the longer-length summation receptive fields of V1 cells, which have been demonstrated at least in the tree shrew (Bosking and Fitzpatrick, 1995). Consistent with this hypothesis are the observations that summation fields in macaque V1 are generally isotropic (Sceniak et al., 2001; Levitt and Lund, 2002), and that both horizontal connections (this study) and summation fields (Sceniak et al., 2001) are more anisotropic in layer 6 than in more superficial layers of macaque V1. Our results suggest that visual field anisotropy is not required to generate orientation-selective RFs. Our finding that feedback terminal fields in V1 show visual field anisotropy suggests that contour completion in macaque V1 might instead be mediated by feedback connections.

The monosynaptic spread of horizontal connections is not sufficiently extensive to account for the scale of the modulatory surround region beyond the low-contrast SF of V1 neurons. However, the region between the high- and low-contrast SF (Fig. 9, hatched annulus) can suppress or facilitate the center response depending on the contrast of the center stimulus (Levitt and Lund, 1997; Polat et al., 1998; Sceniak et al., 1999, 2001; Mizobe et al., 2001) (for discussion, see Angelucci and Bullier 2002). Thus, monosynaptic horizontal connections could mediate surround modulation within this region of space. One example of such “short-range” surround modulation is colinear facilitation, i.e., enhancement of the mrf center response to an optimally oriented low-contrast stimulus by flanking co-oriented and coaxial high-contrast stimuli; a phenomenon thought to underlie perceptual grouping of contour elements (Hess and Field, 2000). One interpretation of colinear facilitation is that it simply reflects placement of flank stimuli within the low-contrast SF of the same cell, and could thus be explained by the same mechanism underlying the expansion of the RF at low contrast (for “long-range” colinear facilitation, see Mizobe et al., 2001). Recent evidence that GABA inactivation of laterally displaced V1 sites reduces colinear facilitation suggests that horizontal connections may be the underlying anatomical substrate (Crook et al., 2002). Short-range surround suppression can also be observed for high-contrast center stimuli. The same connectional system, and thus a similar inhibitory mechanism, could account for “shrinkage” of the RF and short-range surround suppression at high contrast (Angelucci et al., 2002) (Fig. 9) [see Sceniak et al. (1999)for an alternative model]. Whether short-range surround suppression is generated via lateral (Hupé et al., 2001b) or feedback connections, it is clear that lateral connections are less extensive than even the empirically measured mean SF size of V1 neurons or the mean Gaussian spread of the inhibitory surround mechanism. Several lines of evidence suggest that polysynaptic circuits of horizontal connections within V1 are unlikely to underlie long-range center–surround interactions. First, the strong inhibitory nature of most surround effects would preclude propagation of signals through a cascade of lateral connections. Because lateral axons are known to target the same population of neurons at every synaptic location (∼80% excitatory and 20% inhibitory neurons; McGuire et al., 1991), inhibition would occur at each relay step. Second, the slow conduction velocity of horizontal axons (Bringuier et al., 1999; Girard et al., 2001) would preclude them from processing fast information across long distances, at least in V1 and V2 where, because of the large magnification factor and small RF sizes, these connections connect relatively small regions of space.

Inter-areal feedback projections provide information to a small column of V1 neurons from larger regions of space than V1 lateral connections, the size of the visual field region conveyed to V1 increasing with cortical distance from V1. The visuotopic size of the feedback projection field within V1 arising from a small column of extrastriate cortical neurons matches the aggregate RF size of the extrastriate neurons of origin, demonstrating an orderly topographic arrangement of these connections. Our results show that feedback connections are of appropriate scale to underlie long-range modulatory effects within and beyond the low-contrast SF of V1 neurons (Fig. 9). The influence of feedback connections on the RF center response of recipient neurons has long been known. Specifically, inactivation of areas V2 and MT reduces the response of neurons in lower-order areas to visual stimulation of their RF center (Sandell and Schiller, 1982; Mignard and Malpeli, 1991; Hupé et al., 1998, 2001a), suggesting that at least part of the FB input normally sums with FF inputs. A role for feedback connections in mediating center-surround interactions is supported by recent evidence that inactivation of area MT reduces the suppressive effect of surround motion stimulation in V3, V2, and V1 neurons (Hupé et al., 1998). Furthermore, feedback from MT has been shown to act on the early part of the response, suggesting that it may act on V1 neurons at the same time as feedforward signals from the thalamus (Hupé et al., 2001a). Feedback connections' conduction velocities are as rapid as those of feedforward connections and 10 times faster than those of horizontal connections (Girard et al., 2001). Because of these spatial and temporal properties, feedback connections are well suited to convey fast visual signals across distant parts of space. Contrary to previous reports that feedback connections are more diffuse and nonspecific than feedforward connections (Rockland and Virga, 1989; Shipp and Zeki, 1989), we show here that feedback projections are parcellated into discrete patches in V1 and overlap with patches of V1 feedforward projecting neurons. The precise alignment of labeled feedback terminal clusters in V1 with clusters of feedforward efferent cells (Salin et al., 1995; Johnson and Burkhalter, 1997), is well suited to fast transfer of specific functional information to and from V1, and it may also explain the orientation specificity of interactions between surround and RF stimulus configuration. The periodicity of feedback connections, much like that of intra-areal connections, matches the periodic distribution of specific functional properties in V1, such as orientation preference. Similarly to V1 lateral connections (Malach et al., 1993), feedback connections appear to link points of like-orientation preference (Gilbert and Wiesel, 1989; Shmuel et al., 1998). Previously we have proposed a detailed model of how feedback connections might mediate orientation specific modulation of RF responses (Angelucci et al., 2002) (Fig. 9). Although patchy feedback connections in V1 appear to reflect linking of similar stimulus attributes in striate and extrastriate cortex, the relationship of the feedback terminal patches to the CO columns in V1 suggests also the existence of specific compartments within V2 and V3, each compartment having a segregated terminal territory in V1 (Angelucci and Levitt, 2002).

Although we are proposing that feedback connections may mediate center–surround interactions in V1, a more general role for this connectional system, consistent with their spatial scale, would be to mediate global-to-local, top-down integration of visual information. Global-to-local signal integration might represent an essential step in visual processing and has been shown to occur in the responses of V1 and V2 cells to illusory contours (Lee and Nguyen, 2001) or to occluded contours defined by contextual depth cues (Sugita, 1999; Bakin et al., 2000).