A Synaptic Explanation of Suppression in Visual Cortex

Abstract

The responses of neurons in the primary visual cortex (V1) are suppressed by mask stimuli that do not elicit responses if presented alone. This suppression is widely believed to be mediated by intracortical inhibition. As an alternative, we propose that it can be explained by thalamocortical synaptic depression. This explanation correctly predicts that suppression is monocular, immune to cortical adaptation, and occurs for mask stimuli that elicit responses in the thalamus but not in the cortex. Depression also explains other phenomena previously ascribed to intracortical inhibition. It explains why responses saturate at high stimulus contrast, whereas selectivity for orientation and spatial frequency is invariant with contrast. It explains why transient responses to flashed stimuli are nonlinear, whereas spatial summation is primarily linear. These results suggest that the very first synapses into the cortex, and not the cortical network, may account for important response properties of V1 neurons.

Neurons in the primary visual cortex (V1) rapidly adjust their gain, or responsiveness, to changes in visual stimulus contrast (for review, see Carandini et al., 1997). This gain control is weaker in the lateral geniculate nucleus (LGN) and is the object of a number of computational models (Albrecht and Geisler, 1991;Heeger, 1991; Heeger, 1992a; Carandini and Heeger, 1994; Carandini et al., 1999; Kayser et al., 2001). Its effects can be summarized by describing two phenomena.

The first phenomenon is contrast saturation. Although responses of lateral geniculate neurons increase with stimulus contrast over the full range of contrasts, at high contrast, responses of V1 neurons reach a plateau (Albrecht and Hamilton, 1982; Li and Creutzfeldt, 1984). Saturation depends on stimulus contrast but is independent of attributes such as orientation. Critically, saturation does not depend on evoked firing rate; responses to different orientations saturate at the same contrast (Sclar and Freeman, 1982).

The second phenomenon is cross-orientation suppression. Responses to a test with optimal orientation are partially suppressed by superposition of a mask with orthogonal orientation (Bishop et al., 1973; Morrone et al., 1982; Bonds, 1989; DeAngelis et al., 1992; Carandini et al., 1997). Arithmetically, suppression corresponds to division; superimposing the mask has the same effect as dividing test contrast (Bonds, 1989; Heeger, 1992a).

Suppression is generally interpreted as evidence for intracortical inhibition (Blakemore and Tobin, 1972; Morrone et al., 1982; Bonds, 1989; DeAngelis et al., 1992). According to this explanation, a V1 neuron receives inhibition from V1 neurons selective for other orientations, which causes suppression. This interpretation had a strong influence on quantitative models developed in the last decade (Albrecht and Geisler, 1991; Ben-Yishai et al., 1995; Somers et al., 1995; Carandini and Ringach, 1997; Kayser et al., 2001; Lauritzen et al., 2001), including our own “normalization model” (Heeger, 1992a;Carandini and Heeger, 1994; Carandini et al., 1997).

However, recent results cast doubt on these views and suggest that suppression cannot come from cortical cells. First, cross-orientation inhibition is supported by some studies (Morrone et al., 1987; Eysel et al., 1990; Borg-Graham et al., 1998; Crook et al., 1998; Martinez et al., 2002) but not by others (Douglas et al., 1988; Anderson et al., 2000a; Carandini and Ferster, 2000). Second, suppression is strongest when test and mask are delivered to the same eye (DeAngelis et al., 1992; Walker et al., 1998), whereas most neurons in the cat V1 are binocular (Hubel and Wiesel, 1962). Third, suppression is also observed with masks that barely evoke cortical responses, such as gratings drifting rapidly (Freeman et al., 2002). Fourth, unlike responses of cortical neurons, signals responsible for suppression are immune to the contrast adaptation typical of V1 neurons (Freeman et al., 2002).

We propose an alternative, feedforward mechanism for gain control in the visual cortex, where the relevant signals originate in the LGN. In particular, we suggest that gain control operates through synaptic depression at thalamocortical synapses. Depression at these synapses has been observed in vitro (Stratford et al., 1996) and is consistent with observations made in vivo (Ferster and Lindström, 1985; Sanchez-Vives et al., 1998; Chung et al., 2002). Depression might be a general mechanism of cortical gain control (Abbott et al., 1997). In V1, it might underlie a number of temporal response characteristics (Chance et al., 1998; Müller et al., 2001). Indeed, depression has been included as a component of detailed V1 models, where it contributed to a variety of behaviors (Kayser et al., 2001; Lauritzen et al., 2001). Here we ask to what degree suppression, saturation, and other properties of V1 neurons can be explained by thalamocortical synaptic depression alone.

Portions of this work appeared in a conference abstract (Carandini et al., 2001) and in a paper reporting experimental results (Freeman et al., 2002).

MATERIALS AND METHODS

We considered a basic model of V1 simple cell summing appropriate LGN inputs, and we endowed thalamocortical synapses with a depression mechanism. To concentrate on the effects of synaptic depression, we kept our model extremely simple and did not include detailed aspects of neuronal biophysics (Koch, 1999) and cortical anatomy (Douglas and Martin, 1998). We believe that our model explains properties of V1 both in the cat and in the monkey, but all of our simulations refer to experiments performed in cats.

Here we briefly describe the model, details of which are given in the.

Receptive fields. Our model V1 simple cell is based on the original proposal by Hubel and Wiesel (1962), in which orientation selectivity arises because of the arrangement of excitatory inputs from the LGN (Reid and Alonso, 1995; Alonso et al., 2001). Thalamocortical synaptic excitation determines the receptive field of the cell, whose ON and OFF subregions are driven by excitation from ON-center and OFF-center LGN neurons.

This pattern of excitation is complemented by subtractive inhibition arranged in “push–pull” manner, whereby excitation by ON-center neurons is matched by inhibition by OFF-center neurons and vice versa (Palmer and Davis, 1981; Glezer et al., 1982; Tolhurst and Dean, 1987;Ferster, 1988; Tolhurst and Dean, 1990; Hirsch et al., 1998). Although for simplicity we have modeled it as coming directly from the LGN, in reality, inhibition would be provided by cortical interneurons (Palmer and Davis, 1981; Troyer et al., 1998). Inhibition in our model contributes to orientation selectivity by silencing responses to orientations orthogonal to the preferred. However, it does not play any role in the divisive gain control effects that are the focus of this study.

With the exception of a threshold for spike generation, we model LGN neurons as responding linearly (Enroth-Cugell and Robson, 1966). This simplified model does not capture the portion of saturation and suppression exhibited by LGN neurons (Ohzawa et al., 1985; Freeman et al., 2002), so any saturation and suppression shown by our model V1 neuron will be ascribable exclusively to synaptic depression.

Synaptic depression. In addition to this classic arrangement of synaptic inputs, we postulate that thalamocortical connections exhibit synaptic depression. Depression can be described by the following equation (Senn et al., 2001):

$$\frac{\text{dp}}{\text{dt}}=\frac{u-p}{{\tau }_R}-\text{upf},$$ Equation 1

where p is the probability of synaptic transmission,f is the presynaptic firing rate, and u is a utilization parameter. This expression is simplified from a more detailed model involving the arrival times of individual presynaptic spikes (Abbott et al., 1997; Tsodyks and Markram, 1997; Varela et al., 1997). Terms on the right side govern recovery and depression. Depression (second term) is proportional to the presynaptic firing ratef and to the utilization parameter u. An increase in f depletes a synaptic resource, and thus reduces the probability of synaptic transmission p. Recovery (first term) makes p return to the value u (iff is zero) over a period determined by the time constant τ_R. If the depression term were absent,p would be constant, and the synapse would operate linearly. Incidentally, the expression above is identical to one describing photopigment depletion in the retina (Rushton and Henry, 1968).

In our simulations, the utilization parameter was u = 0.75, at the high end of the range (0.1–0.95) found in vitro (Tsodyks and Markram, 1997). The time constant of recovery was τ_R = 200 msec, intermediate between those reported for rapid depression in young animals (200–800 msec) (Abbott et al., 1997; Varela et al., 1997) and in adult animals (60–70 msec) (Thomson and Deuchars, 1997). Choosing different recovery time constants (between 50 and 500 msec) did not alter the results considerably: The crucial feature of depression is that it occurs right after an increase in presynaptic firing rate, not the time it requires to recover.

RESULTS

We start by describing the effects of depression in a single synapse and then go on to illustrate a variety of properties of our model V1 neuron.

Suppression in a single synapse

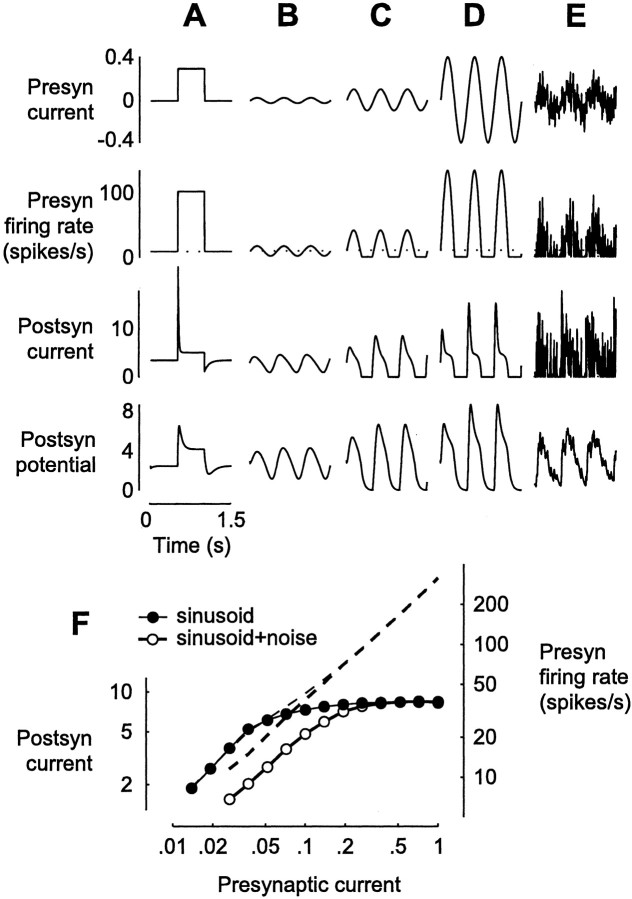
Synaptic depression causes the response to a presynaptic step of current to be transient (Fig.1A). As presynaptic firing rate steps up (Fig. 1A, second row), postsynaptic current increases rapidly but is cut short by synaptic depression, resulting in a sharp transient followed by a plateau and then by recovery at the end of the step (Fig.1A, third row). Although attenuated by the filtering properties of the membrane, this transient is still present in the membrane potential responses (Fig. 1A,bottom).

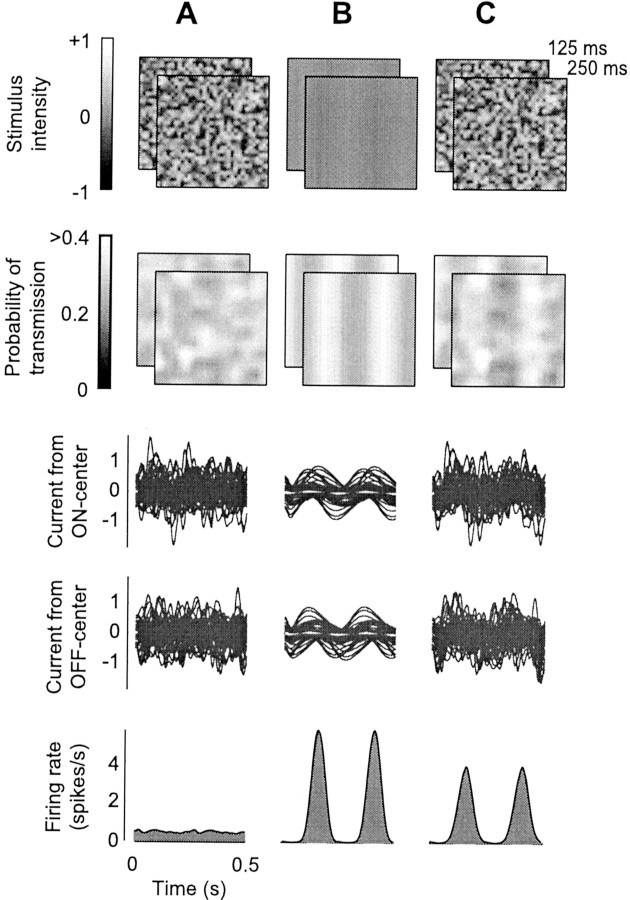
Fig. 1.

Input–output properties of a depressing synapse.A–E, Effects of injection of various waveforms into the presynaptic (Presyn) neuron. Top row, Injected current I_pre (A, step; B–D, 2 Hz sinusoids with amplitudes 0.025, 0.1, and 0.4; E, sinusoid with amplitude 0.1 plus white noise with amplitude 0.25). Second row, The resulting presynaptic firing rate f. Third row, The output of the depressing synapse; postsynaptic (Postsyn) current I_post = p u f.Bottom row, Postsynaptic potential V, which is I_post after filtering by the passive properties of the neuron. To avoid unnecessary free parameters, we have used the same units, spikes per second, for currents, potentials, and firing rates. F, The 2 Hz component of presynaptic firing rate f (right axis,dashed lines) and of postsynaptic currentI_post (left axis,symbols) as a function of the amplitude of presynaptic sinusoidal current I_pre.

Synaptic depression is much more rapid than the subsequent recovery. As explained in the , the effective time constant τ_eff of a depressing synapse is equal to the time constant of recovery τ_R = 200 msec only when the presynaptic firing rate f is zero. As fgrows, τ_eff tends to zero. For example, whenf = 10 spikes/sec, τ_eff is 80 msec, and when f = 100 spikes/sec, τ_eff is 12.5 msec. As a result, at the onset of the step stimulus of Figure 1A (second row), the drop in postsynaptic current is sharp (third row). In contrast, when at the end of the step freturns to zero (second row), the increase in postsynaptic current is slow (third row).

A depressing synapse exhibits saturation. Consider first the presynaptic firing rate responses to sinusoidal injected currents (Fig.1B–D, second row). Because the presynaptic neuron has a resting firing rate of 10 spikes/sec, small current injections result in a sinusoidal firing rate, but larger ones are clipped where firing rates would be negative. The relationship between presynaptic current and firing rate is nonetheless primarily linear (Fig. 1F, right axis). The effects of synaptic depression can be observed in the postsynaptic current (Fig. 1B–D, third row). Depression distorts the postsynaptic current, which is not sinusoidal but exhibits transient increases followed by more tonic responses. Distortion increases with presynaptic firing rate, causing a substantial saturation in response amplitude (Fig. 1F, left axis). This saturation is a well known property of synaptic depression (Abbott et al., 1997; Tsodyks and Markram, 1997; Kayser et al., 2001); it is a simple consequence of Equation 1 (see).

In addition to saturation, a depressing synapse exhibits divisive suppression. Adding noise to the injected current (Fig.1E) increases synaptic depression. This effect is best appreciated in the membrane potential response (Fig. 1,bottom), where high-frequency components of the postsynaptic current have been filtered out by the passive properties of the membrane. The noise current partially suppresses the responses to the sinusoidal current (compare Fig. 1C,E,bottom). This suppression is divisive (Fig.1F, rightward shift of curves on a logarithmic scale), as if the noise had divided the amplitudes of the injected sinusoidal test currents by a fixed scale factor.

Thanks to saturation and suppression exhibited by depressing synapses, our model simple cell displays many properties of real simple cells.

Contrast saturation

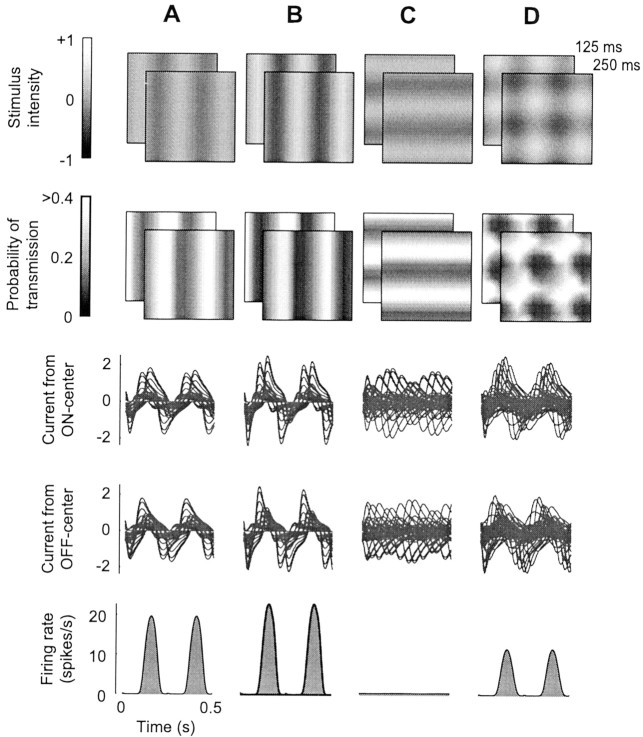
Our model simple cell exhibits contrast saturation; responses to an optimally oriented drifting grating level off at high stimulus contrasts (Figs. 2,3). The firing rate of an ON-center LGN cell increases when the bright bars of the grating pass over its receptive field (and likewise for dark bars for an OFF-center LGN cell). When the firing rate of an LGN cell increases, probability of transmission at its synapses decreases. The pattern of synaptic depression across the spatial array of LGN receptive fields is itself a grating, which closely trails the leftward moving stimulus (Fig.2A, second row) (Senn et al., 2001). The probability of synaptic transmission is lowest (Fig.2A, second row, dark stripes) where presynaptic firing rates are highest; for the ON-center LGN cells, this corresponds to the locations of the bright bars of the grating (Fig. 2A, top, light stripes).

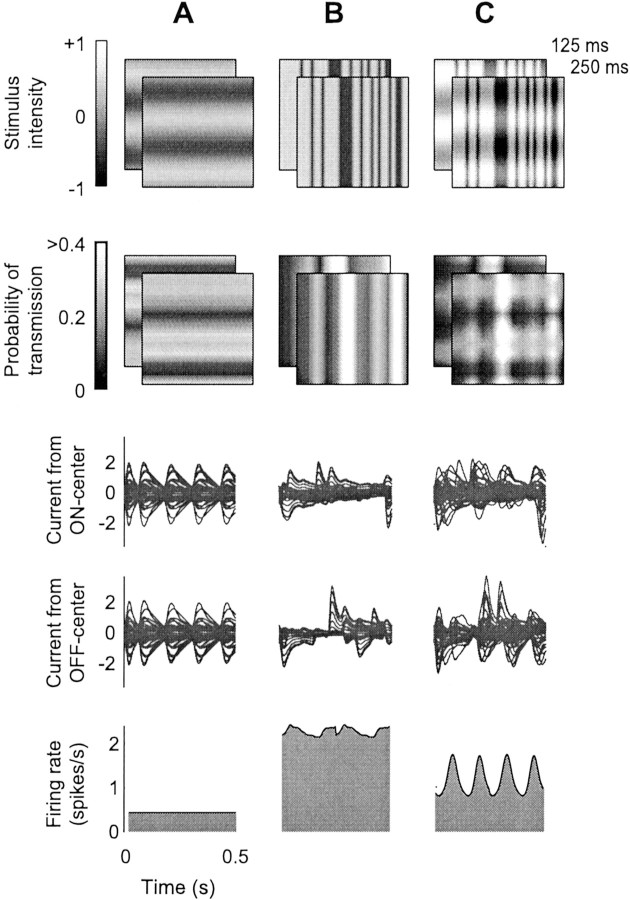
Fig. 2.

Responses to gratings and plaids.A, Vertical grating at 25% contrast drifting to the left at 4 Hz. Top row, Two stimulus frames, att = 125 and 250 msec. Second row, Corresponding spatial maps of synaptic depression, with intensity proportional to probability of transmission for synapses from LGN ON-center neurons. Third row, Postsynaptic currents in the V1 neuron, from ON-center LGN neurons, for the first two stimulus cycles. Fourth row, Same for OFF-center LGN inputs.Bottom row, Average firing rate responses to two stimulus cycles. B, Same grating as in A, at 50% contrast. Saturation is evident; firing rates are less than twice those in A. C, Same grating as inA but oriented horizontal and drifting upward.D, Plaid obtained by summing the gratings fromA and C. Suppression is visible because firing rates are less than those in A.

Fig. 3.

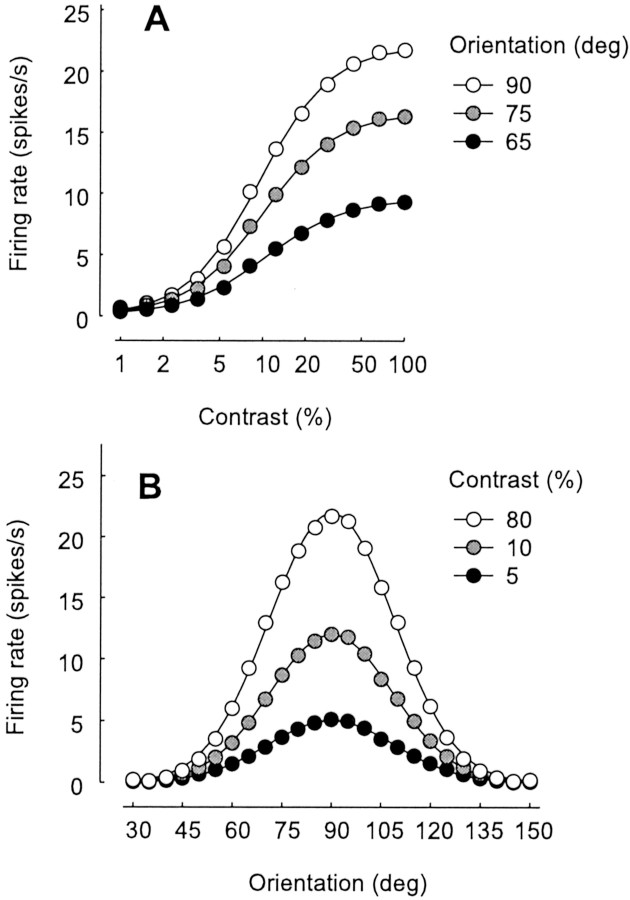
Dependence of response on grating contrast and orientation. A, Response versus stimulus contrast for three stimulus orientations. Curves fitted to data are hyperbolic ratios (Albrecht and Hamilton, 1982) and are vertically scaled versions of each other. B, Response versus stimulus orientation for three stimulus contrasts. Curves fitted to data are Gaussians and are vertically scaled versions of each other. Stimuli were drifting sinusoidal gratings as in Figure 2A–C. Firing rates are first harmonic amplitudes, the component of the responses at the stimulus temporal frequency, obtained by fitting responses with sinusoids.

When stimulus contrast is increased by a factor of two (Fig.2B), firing rates of LGN neurons also increase by a factor of two, causing the probability of synaptic transmission to drop (compare Fig. 2A,B, second row). The increase in synaptic depression causes a greater reduction in individual synaptic currents, so that synaptic currents increase only slightly (compare Fig.2A,B, third andfourth rows). The firing rate response of the neuron barely increases at all (Fig. 2A,B,bottom). Without depression, currents in Figure2B would be twice as large as those in Figure2A. Instead, as contrast increases, responses saturate and reach a plateau (Fig. 3A).

Our model correctly predicts that responses plateau at a given contrast level regardless of firing rate and regardless of stimulus orientation and spatial frequency (Albrecht and Hamilton, 1982; Sclar and Freeman, 1982; Carandini et al., 1997). In the model, saturation is entirely caused by depression at thalamocortical synapses, and these synapses signal all orientations equally. As a result, saturation does not depend on stimulus orientation (Fig.3A).

As a consequence, our model correctly predicts that even in the face of contrast saturation, the selectivity of a neuron for stimulus attributes such as orientation or spatial frequency is invariant with stimulus contrast (Albrecht and Hamilton, 1982; Sclar and Freeman, 1982). For example, changes in contrast scale the curve-relating response to orientation without affecting its width (Fig.3B). As in the original proposal by Hubel and Wiesel (1962), orientation selectivity in our model results from the arrangement of synaptic inputs. When the stimulus has optimal orientation, excitatory inputs arrive at the same time and summate to elicit a response (Fig.2A). When the stimulus has the orthogonal orientation, they arrive at different times and cancel with inhibitory inputs (Fig. 2C). This mechanism for orientation selectivity is contrast invariant (for review, see Troyer et al., 1998 and references therein). Contrast invariance is preserved in the face of synaptic depression; because LGN neurons are not selective for orientation, their synapses are depressed equally by stimuli of all orientations.

Cross-orientation suppression

Our model predicts suppression because two superimposed stimuli cause more synaptic depression than either stimulus alone. This behavior is illustrated by simulating responses to a plaid, the sum of an optimally oriented test grating, and an orthogonal mask grating (Fig. 2D). Responses to this plaid are clearly smaller than to test alone, although the mask did not elicit any response on its own. The reason for this suppression can be observed in the maps of stimulus and of probability of synaptic transmission (Fig.2). As the plaid moves up and to the left, those parts of it that excite ON-center cells (Fig. 2D, top,white blobs) encounter regions that have stronger depression (Fig. 2D, second row, dark blobs) than in the case of individual gratings (Fig.2A, second row). A similar argument could be made for the probability of transmission for synapses from OFF-center cells (data not shown). Therefore, as the vertical component of the plaid moves laterally, it encounters regions where the probability of transmission has been lowered by the passage of the horizontal component. Without depression, the firing rate in Figure2D would be close to that in Figure2A.

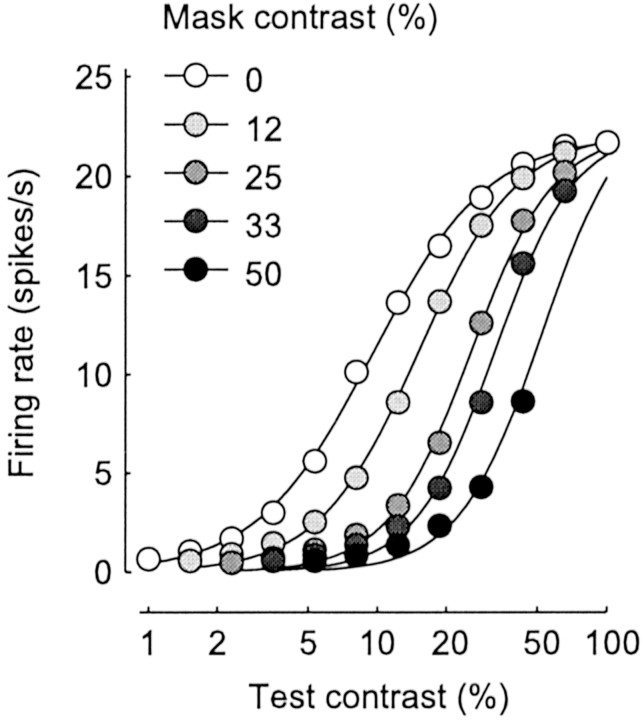
Because the effects of synaptic depression are divisive, the model correctly predicts that the effects of suppression are divisive (Bonds, 1989; Heeger, 1992a; Carandini et al., 1997; Freeman et al., 2002). This property can be observed in the curves relating response to test contrast (Fig. 4). In addition to a slight change in slope, the main effect of increasing mask contrast is to shift the curves to the right. Because of the logarithmic contrast scale, this shift corresponds to division; it is as if the mask had divided the test contrast that is “seen” by the neuron.

Fig. 4.

Cross-orientation suppression. Responses for plaids composed of an optimally oriented test grating and an orthogonal mask grating (as in Fig. 2D). Gray levels correspond to different mask contrasts. Curves are hyperbolic ratios (Albrecht and Hamilton, 1982) fitted to each set of data points independently. The curves shift rightward (and become slightly steeper) with increasing mask contrast.

Moreover, the model easily explains the spatial extent of cross-orientation suppression. Orthogonal gratings cause suppression only when they are presented in a region well within the receptive field (DeAngelis et al., 1992). The model predicts this behavior, because only depression at those thalamocortical synapses that drive the V1 neuron can affect the responses of the neuron.

Time course of suppression

Our model correctly predicts that cross-orientation suppression is very fast. In fact, suppression from within the receptive field appears to have the same latency as the responses themselves, indicating that its mechanism requires less than a few milliseconds (Smith et al., 2001; Albrecht et al., 2002). The behavior of the model is similar (Figure 5). Starting from a blank screen, suppression is already evident at response onset; responses to plaid are immediately smaller than to test alone (Fig. 5A). Suppression caused by the appearance of the mask on top of an already existing test is similarly fast (Fig. 5B), even more so than in real cells, where it is ∼20 msec slower than the reduction in response after test removal (Smith et al., 2001). The model predicts that suppression is fast because depression is fast; we have seen that an increase in presynaptic firing rate causes a sharp depression within a few milliseconds (Fig. 1A, third row).

Fig. 5.

Time course of cross-orientation suppression; simulation of an experiment similar to that of Smith et al. (2001). Stimuli were a blank screen, a test grating with optimal orientation, and the plaid obtained by summing the test and an orthogonal mask grating (for each grating, spatial frequency = 1 cycle/°, drift rate = 5 Hz, contrast = 20%). A, Response to test and to plaid, starting from blank. B, Response to plaid and to blank, starting from test. Responses are mean firing rates, averaged for 12 spatial phases of test grating; for each phase, responses resembled the rectified sinusoid in Figure2A.

Orientation tuning of suppression

Up to now, we have only considered suppression from orthogonal masks. When measured with drifting gratings, however, suppression can be obtained with masks of any orientation (Morrone et al., 1982; Bonds, 1989; DeAngelis et al., 1992). Our model predicts this behavior. For all mask orientations (not only ±90°), responses to the test in the presence of the mask (Fig.6A, ●) are smaller than when the mask is absent (Fig. 6A, straight dashed line). Without depression, the two would be identical. In this simulation of an experiment by Bonds (1989), responses were measured using a test grating drifting at 4 Hz and a mask grating drifting at 3 Hz. These frequencies “tag” the responses to test and mask. Indeed, when its orientation is close to vertical (0°), the mask itself elicits a response. Because this response oscillates at 3 Hz, it can be distinguished from the response to the test, which oscillates at 4 Hz. In the model, suppression by a drifting grating mask is largely independent of mask orientation because thalamic synapses are not selective for orientation, so masks of all orientations cause the same amount of depression. As the mask drifts, the wave of depression drifts behind it and affects all synapses signaling the test.

Fig. 6.

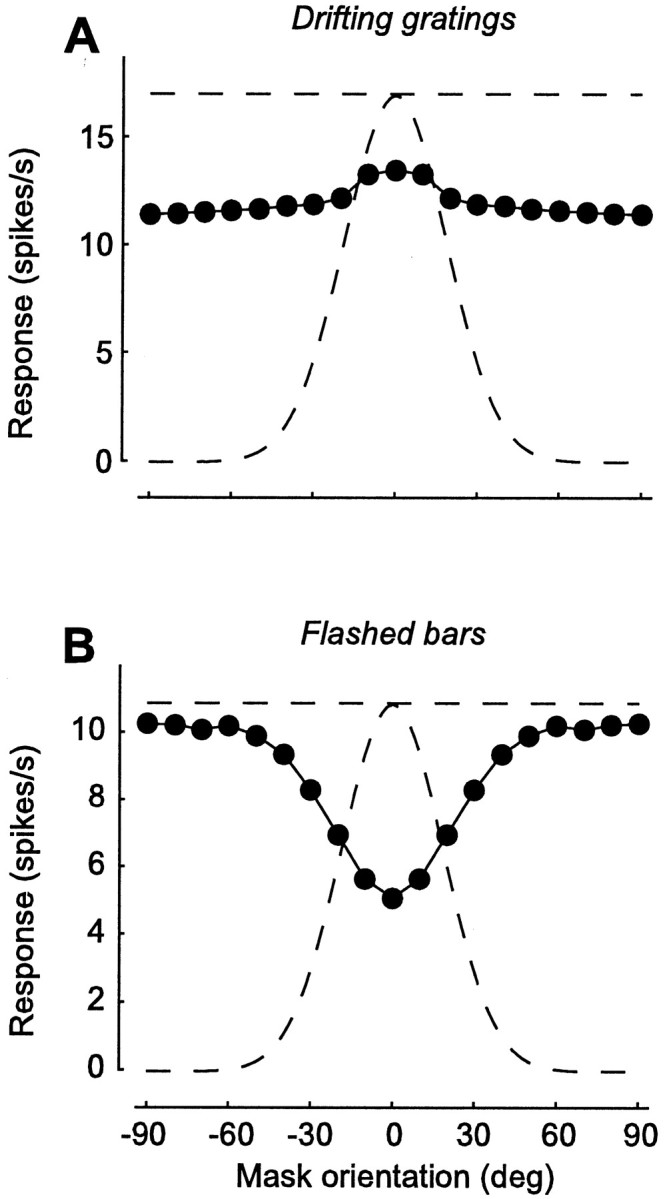
Orientation dependence of suppression by drifting and flashed masks. Responses to an optimally oriented test as a function of mask orientation. For comparison, the curved dashed line shows responses to tests of different orientations, in the absence of a mask. The straight dashed line is the response to optimal orientation. A, Suppression by superimposed drifting gratings. This is a simulation of an experiment by Bonds (1989). Responses are computed by fitting to the firing rate a sinusoid with the temporal frequency of the test grating (4 Hz). Gratings (20% contrast) were presented for 1 sec. Mask grating drifted at 3 Hz and was superimposed to the test. B, Suppression by a mask flashed bar preceding a test flashed bar. This is a simulation of an experiment by Nelson (1991a). Responses are computed by taking the mean firing rate during presentation of a test bar. Bars had maximal intensity on a mean gray background and were flashed for 100 msec; mask preceded test by 50 msec.

The results of the above experiment are different if instead of drifting gratings, one uses briefly flashed bars. If the interval between the two is short (tens to hundreds of milliseconds), the response to a test flashed bar is substantially reduced by a previous presentation of a mask flashed bar (Nelson, 1991a). However, this suppression is strong only when orientation and position of the test and mask are similar (Nelson, 1991a). Our model predicts this behavior (Fig. 6B). Masks parallel to the test (0°) cause strong suppression. As mask orientation is changed from parallel to orthogonal to the test, however, suppression decreases, and responses approach those elicited by test alone (Fig. 6B,straight dashed line). This behavior is easily explained. The mask causes suppression by depressing synapses that shortly afterward will signal the test. If the mask is identical to the test, it depresses the very same synapses that signal the test, and suppression is maximal. If the mask has a different orientation (or a different position), it depresses only some of the synapses signaling the test, and suppression is weaker. The model thus explains orientation selectivity of suppression by flashed stimuli. This explanation requires that the time constant of recovery from depression (200 msec in our simulations) be longer than the interval between mask and test (50 msec in our simulations). If recovery is substantially faster, the model will exhibit little or no suppression to flashed stimuli.

In summary, our model explains a discrepancy in the literature regarding the orientation selectivity of suppression. Suppression has been reported to be present with a broad range of mask orientations, often equally strong when mask and test are parallel as when they are orthogonal (Morrone et al., 1982; Bonds, 1989). Suppression has also been reported to be selective for mask orientation, which is often completely absent when test and mask are orthogonal (Nelson, 1991a). The model ascribes this discrepancy to the type of mask used; drifting grating masks cause equal suppression at all orientations (Fig.6A), whereas flashed bar masks cause the least suppression when they are orthogonal to the test (Fig.6B). The cell is equally selective for the orientation of flashed bar and drifting grating stimuli (Fig. 6,curved dashed lines). Yet responses to these stimuli involve different numbers of thalamocortical synapses. A spatially compact flashed bar depresses only a limited set of synapses, whereas a drifting stimulus causes a wave of depression that affects all synapses in its path.

Suppression with fast stimuli

Because our model explains suppression without recourse to intracortical inhibition, it correctly predicts that stimuli do not have to elicit spikes in V1 to cause suppression. An example of this behavior has been observed with stimuli drifting very fast. The temporal frequency tuning of suppression is broad (Morrone et al., 1982; Bonds, 1989; Allison et al., 2001), so broad that suppression can be observed with masks drifting too fast to elicit much of a response in V1 (Freeman et al., 2002). For reasons that are not entirely understood, neurons in cat V1 do not respond to gratings drifting at rates of >10 Hz or so (Movshon et al., 1978b; Saul and Humphrey, 1992;DeAngelis et al., 1993a), although LGN neurons commonly respond to much higher drift rates (Saul and Humphrey, 1990). Nonetheless, mask gratings drifting at these rates give powerful suppression (Freeman et al., 2002).

These results would be hard to explain with intracortical mechanisms but are easily explained by our model (Fig.7). We have designed our model LGN neurons to respond maximally to gratings drifting at ∼10 Hz and still give a good response to gratings drifting twice as fast (Fig.7A). In contrast, we have designed our model V1 neuron to respond maximally to gratings drifting at ∼2 Hz and to give barely any response to gratings drifting at 20 Hz (Fig. 7B). Although our V1 neuron does not respond to them, mask gratings drifting as fast as 25 Hz give strong suppression (Fig. 7C). Indeed, because suppression is driven by LGN responses, the dependence of suppression on mask drift rate (Fig. 7C) is very similar to that of LGN responses (Fig. 7A). As illustrated by Freeman et al. (2002), a very similar behavior is observed in real V1 neurons.

Fig. 7.

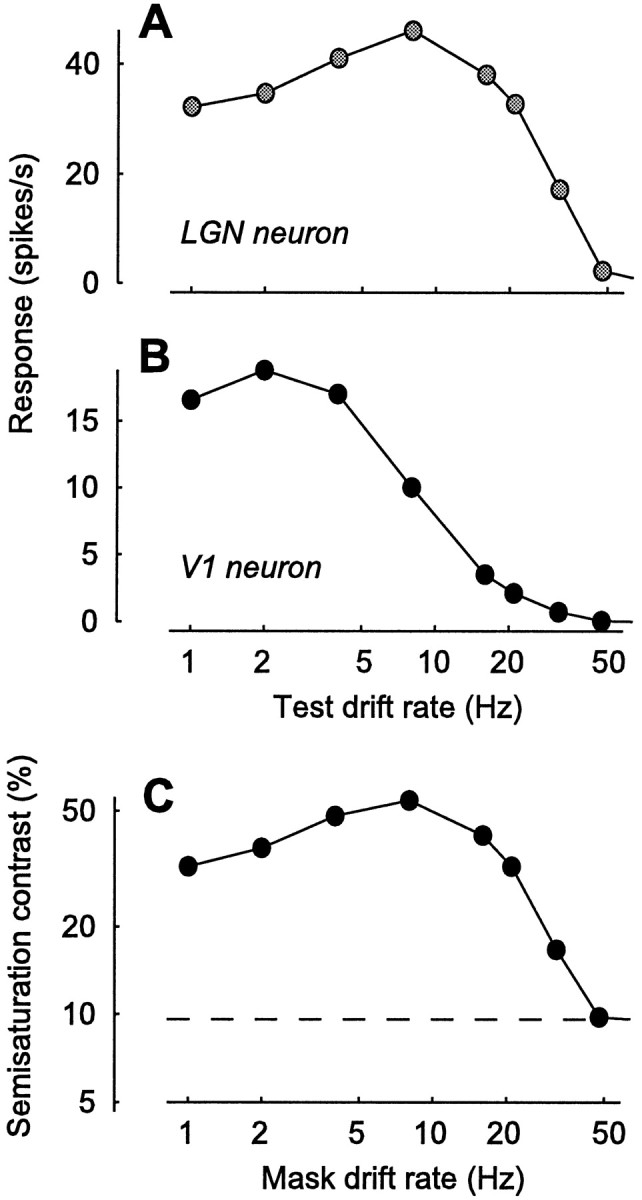
Suppression by masks drifting at different rates. This is a simulation of an experiment by Freeman et al. (2002).A, B, Selectivity for drift rate in our model LGN neurons (A) and in our model V1 neuron (B), measured with drifting gratings.C, Dependence of semisaturation contrast on mask drift rate. The semisaturation contrast, the test contrast needed to reach half the maximal response, is a measure of strength of suppression.Dashed line, Semisaturation contrast for test grating presented alone. In the presence of a mask grating, the semisaturation is larger, corresponding to a rightward shift of the curves in Figure4.

Moreover, our model explains why suppression is immune to visual adaptation effects that follow prolonged stimulation (Freeman et al., 2002). A prolonged mask stimulus (4–30 sec) does depress model synapses, but its effects disappear a few hundred milliseconds after its offset. The responses to test, mask, and plaid that are shown ∼1 sec later are thus unaffected. In contrast, the intracortical inhibition model would predict that adaptation to the mask reduces suppression, because it reduces the activity of cortical neurons responding to the mask.

Suppression with white noise

Dynamic white noise stimuli (which look like “snow” in an untuned television) give powerful suppression, although they do not elicit much of a response in V1 neurons (Morrone et al., 1982;Carandini et al., 1997). There has been much debate as to the degree to which V1 neurons respond to flickering or moving noise patterns (seeHammond, 1991; Skottun et al., 1991, and references therein). One of the key variables appears to be grain size; if pixels composing the noise are small, summation by receptive fields of V1 neurons averages out their contributions, leading to small responses. Although it might be a weak test stimulus, however, dynamic white noise is a powerful mask, one that causes strong suppression. The model predicts this behavior (Fig. 8). Stimulation with spatiotemporal white noise (Fig. 8A) elicits responses in model LGN neurons and thus depression at their synapses (Fig. 8A, second row). It causes minimal responses in the V1 neuron (Fig. 8A,bottom), because synaptic currents cancel one another (Fig.8A, third and fourth row). Therefore, when the noise is superimposed on a test grating (Fig.8C), it increases depression, leading to smaller responses than when the test grating is alone (Fig. 8B).

Fig. 8.

Suppression with dynamic noise (same format as Fig. 2). A, White noise stimulus. B, Grating with 10% contrast, drifting at 4 Hz with optimal orientation and spatial frequency for the model V1 neuron. C, Superposition of white noise and drifting grating. Although it elicits minimal responses in the V1 neuron, the white noise stimulus is a powerful mask.

A similar argument can be made for gratings of low spatial frequency. Although cat V1 neurons are typically bandpass in spatial frequency, the spatial frequency tuning of suppression is often low-pass, similar to that of LGN neurons (Morrone et al., 1982; Bauman and Bonds, 1991;DeAngelis et al., 1992). Our model would explain this effect and correctly predict that gratings of very low spatial frequency can be powerful masks while eliciting poor responses in V1.

Suppression with contrast-reversing stimuli

In an elegant experiment to probe the source of suppression,Morrone et al. (1982) investigated the effects of a contrast-reversing mask. The authors observed that suppression operated at twice the frequency of contrast reversal. Our model provides a simple explanation of this effect (Fig. 9). In this experiment, the test is a pattern of drifting one-dimensional noise with the preferred orientation of the neuron (Fig. 9B,top), which elevates mean firing rate (Fig. 9B,bottom). The mask is a stationary grating with orthogonal orientation, with contrast reversing sinusoidally with a frequency of 4 Hz (Fig. 9A, top). When it reverses polarity (grating bars switching from bright to dark or vice versa), it elicits responses in ON-center LGN cells in some locations and in OFF-center LGN cells in other locations. Because there are two polarity switches for each period, there are two volleys of LGN activity (Fig.9A, third and fourth rows). These volleys do not result in any spike responses in our model V1 neuron; volleys cancel one another because the mask grating has the orthogonal orientation (Fig. 9A, bottom). However, they do cause synaptic depression, twice for each temporal period of contrast reversal. As in the cells of Morrone et al. (1982), the mask suppresses responses to the test, and this suppression operates at twice the temporal frequency of the mask (Fig. 9C,bottom).

Fig. 9.

Suppression from a contrast-reversing mask grating (same format as Fig. 2), simulating the experiment of Morrone et al. (1982). A, Mask stimulus, a contrast-reversing (4 Hz) grating with orientation orthogonal to that preferred by the model V1 neuron. B, Test stimulus, a drifting one-dimensional noise pattern with optimal orientation and speed for the model V1 neuron. C, Superposition of test and mask.

Linear properties

The effects that we have described are major failures of linearity. Contrast saturation is a nonlinearity because doubling stimulus contrast does not double response amplitude. Suppression is a nonlinearity because response to the sum of test and mask is not equal to the sum of responses to those stimuli when presented alone. Synaptic depression explains these phenomena because it is a nonlinear mechanism.

Nonetheless, V1 simple cells also exhibit behaviors that appear linear (for review, see De Valois and De Valois, 1988; Carandini et al., 1999), and although synaptic depression is nonlinear, our model predicts these behaviors. Indeed, Miller et al. (2002) have demonstrated that fundamentally nonlinear models of V1 physiology can exhibit appropriate linear behaviors (Troyer et al., 1998; Kayser et al., 2001; Lauritzen et al., 2001).

First, simple cell responses to sinusoidal temporal modulation are approximately sinusoidal, as would be predicted by a linear model (Maffei and Fiorentini, 1973; Movshon et al., 1978a). Our model predicts this behavior, although depression distorts the synaptic currents contributed by each LGN neuron, making them far from sinusoidal (Figs. 1B–D, 2B,third and fourth rows). In fact, distortion cancels when currents are summed from a large number of synapses. Because the bars of the grating pass through the spatial array of LGN receptive fields in sequence, individual currents are offset in time. Thanks to these offsets, distortions cancel each other in the response of the V1 neuron, which appears much more sinusoidal than individual currents (Fig. 2B, bottom). The smoothness of this response is attributable to the temporal offsets of LGN signals being summed and not to temporal filtering operated by the membrane. Indeed, similar results are obtained with time constants as short as 1 msec.

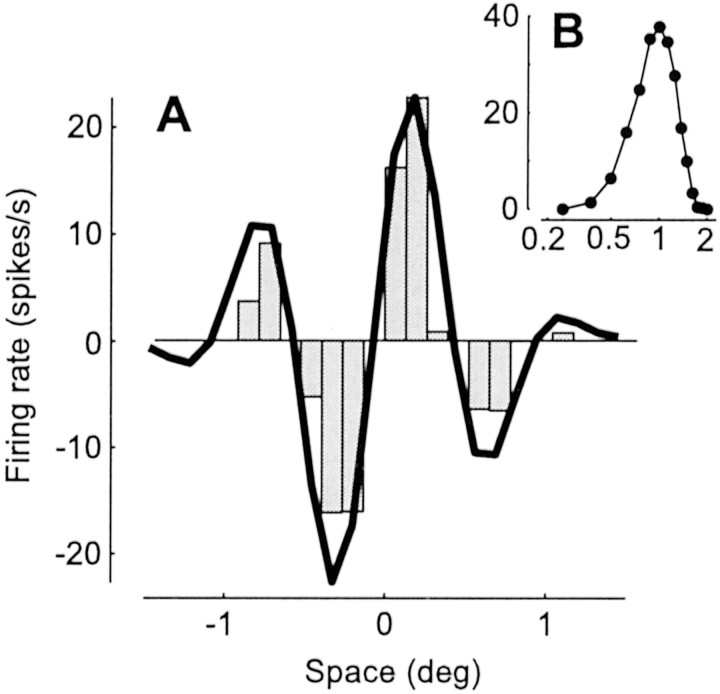
Second, selectivity of simple cells for spatial stimulus attributes such as orientation or spatial frequency can be derived from the shape of the receptive field, as would be predicted by a linear model (Hubel and Wiesel, 1962; Movshon et al., 1978a; DeAngelis et al., 1993b;Volgushev et al., 1996; Gardner et al., 1999; Lampl et al., 2001). Our model predicts this behavior. For example, in Fig.10, we have simulated the classic experiment by Movshon et al. (1978a), who demonstrated that simple cell responses to flashing bars (Fig. 10A) can be used to explain selectivity for spatial frequency (Fig. 10B) and vice versa.

Fig. 10.

Linearity of spatial summation; simulation of the experiment by Movshon et al. (1978a). A, One-dimensional receptive field profile of the model neuron. The histogram shows responses to a stationary full-contrast vertical bar (width, 0.25°; duration, 100 msec); positive (negative) values are responses to a bright (dark) bar, as a function of bar position. A curve indicates a prediction of receptive field profile based on responses to drifting gratings under the assumption of linearity.B, Spatial frequency selectivity of the neuron measured with 4 Hz drifting gratings. The abscissa indicates spatial frequency in cycles per degree, and the ordinate indicates mean firing rate in spikes per second. The curve in Awas derived from these data and arbitrarily rescaled, as by Movshon et al. (1978a).

Recent studies have pointed out that synaptic depression might also explain a large class of nonlinearities of temporal summation (Chance et al., 1998; Kayser et al., 2001; Müller et al., 2001). In our model, these temporal nonlinearities are present but do not overall appear as strong as in real neurons. Our model successfully predicts the effects of superimposing two gratings drifting at different frequencies (simulations not shown). Comparing the frequency components of the response with those evoked by individual gratings presented separately indicates the effect that one frequency has on the other. In particular, a low-frequency component of the response is significantly reduced by superposition of a high-frequency grating (Dean et al., 1982). However, our model does not fully explain other nonlinear temporal effects that have been described. First, increasing the contrast of a grating causes the temporal phase of a response to advance (Dean and Tolhurst, 1986; Albrecht, 1995) and causes the integration time of responses to shorten (Reid et al., 1992). This behavior can be explained by a form of intracortical inhibition that shortens the time constant of the neuron (Carandini and Heeger, 1994;Carandini et al., 1997). Although synaptic depression does exhibit a similar behavior (Chance et al., 1998), it is not clear that it can fully account for these effects (Kayser et al., 2001). Second, unlike for orientation or spatial frequency, selectivity of V1 neurons for stimulus temporal frequency does depend on contrast (Holub and Morton-Gibson, 1981; Albrecht, 1995; Carandini et al., 1997). Again, synaptic depression can exhibit this behavior, but it is not clear that it can account for the full effect (Kayser et al., 2001). Third, real V1 cells exhibit dramatic transient responses after stimulus onset, which rapidly decrease over a period of a few hundred milliseconds (Tolhurst et al., 1980; Müller et al., 1999, 2001). In our model, these transient responses are present in synaptic currents (Fig.1A, third and fourth rows) but are reduced in membrane potential responses (Fig. 1A,bottom) and absent in firing rate responses to visual stimulation (Fig. 5). The transients would be present in the firing rate if we made some minor modifications. We could choose a shorter membrane time constant, one that does not introduce much smoothing in the conversion of postsynaptic current into membrane potential. We could also use a more detailed model of spike generation, because in real cells, the transformation of membrane potential into firing rate accentuates transient responses (Carandini et al., 1996).

To summarize, our proposed mechanism to control neuronal responsiveness, thalamocortical synaptic depression, spares the linearity of spatial summation of the neuron. Spatial averaging of temporally nonlinear inputs allows our model neuron to exhibit some well known linear properties of simple cells.

DISCUSSION

We have proposed a biophysical foundation for the control of cortical responsiveness, thalamocortical synaptic depression, which is alternative to the common view based on intracortical inhibition. The model that we propose successfully explains saturation, suppression, and other phenomena ascribed previously to intracortical inhibition.

Our model can also account for properties that would be hard to explain with intracortical inhibition. First, the model explains how suppression can operate within a few milliseconds (Fig. 5); the intracortical inhibition model would predict longer latencies. Second, our model explains how suppression from drifting gratings is equally strong for all orientations, whereas suppression from flashed bars is strong only at the preferred orientation (Fig. 6); the intracortical inhibition model would predict equal orientation tuning for both types of suppression. Third, our model explains why stimuli that elicit good responses in the LGN but poor responses in the V1, such as gratings with fast drift rates (Fig. 7) and white noise (Fig. 8), can give rise to powerful suppression; the intracortical inhibition model would predict weak suppression. Fourth, our model explains why suppression is immune to visual adaptation effects that follow prolonged stimulation (Freeman et al., 2002); the intracortical inhibition model would predict that suppression would be reduced after adaptation to the mask. Finally, because thalamic neurons are monocular, our model explains why suppression is strongest when both test and mask are delivered to the same eye (Ferster, 1981; DeAngelis et al., 1992; Walker et al., 1998); the intracortical inhibition model would have to rely on responses of other V1 neurons, which (in the cat) are primarily binocular (Hubel and Wiesel, 1962).

Nonetheless, there is a result that is predicted by intracortical inhibition but not by thalamocortical synaptic depression; it has been reported that blocking GABA_A receptors removes cross-orientation suppression (Morrone et al., 1987). Blocking GABA_A would not affect synaptic depression. However, this result is difficult to interpret. First, it primarily concerns local field potentials rather than the activity of single neurons. Second, it does not agree with the results of Nelson (1991b), who blocked GABA_A and did not observe a reduction in the suppression caused by flashed bars. Third, GABA blockers alter the normal function of the local cortical circuit, with effects that range from a loss of selectivity (Sillito, 1975) to epileptogenesis (Chagnac-Amitai and Connors, 1989). Indeed, early conclusions drawn by similar experiments (Sillito, 1975) have later been challenged (Nelson et al., 1994).

Mechanisms controlling cortical responsiveness

In addition to cross-orientation suppression, there are two classes of phenomena considered to be primarily cortical and to control the responsiveness of V1 neurons: surround suppression and visual adaptation. Both are likely to be explained by mechanisms different from synaptic depression.

Surround suppression is the phenomenon whereby mask stimuli located somewhat outside the classical receptive field of a neuron can reduce responses of V1 neurons to test stimuli located in the receptive field (for review, see Fitzpatrick, 2000). Thalamocortical synaptic depression does not predict this surround suppression, because a distant mask would cause depression in different synapses from those that relay signals from the test. In fact, surround suppression is likely to originate from a different mechanism than cross-orientation suppression (DeAngelis et al., 1992, 1994; Sengpiel et al., 1998) and to be caused by intracortical inhibition (Hubel and Wiesel, 1965). Unlike cross-orientation suppression, surround suppression is: (1) strongest when test and mask have the same orientation (Blakemore and Tobin, 1972; DeAngelis et al., 1994), (2) dichoptic (i.e., can be obtained with test in one eye and mask in the other eye) (DeAngelis et al., 1994), (3) slower than that of visual responses to stimuli in receptive field (Smith et al., 2001), and (4) absent in a sizeable portion of V1 neurons (DeAngelis et al., 1994). Measurements of membrane conductance (Anderson et al., 2001) and experiments involving inactivation of layer 6 with GABA (Bolz and Gilbert, 1986; Grieve and Sillito, 1991) further support the intracortical explanation of surround suppression.

Visual adaptation is the phenomenon whereby prolonged stimulation of a V1 neuron reduces the subsequent responses of a neuron (Maffei et al., 1973). Adaptation controls the amount of contrast needed to obtain a given firing rate (Ohzawa et al., 1985) and the maximal firing rate itself (Albrecht et al., 1984); it is dichoptic and can be mediated across the corpus callosum (Maffei et al., 1986). It acts by hyperpolarizing cells by ≤10–15 mV (Carandini and Ferster, 1997;Sanchez-Vives et al., 2000a). This hyperpolarization lasts 10–20 sec, determines the observed reduction in firing rate (Carandini and Ferster, 2000), follows stimulation with optimal orientations but not orthogonal ones (Carandini et al., 1998), and is likely to result from intrinsic cellular mechanisms (Sanchez-Vives et al., 2000a,b). Adaptation is unlikely to result from synaptic depression, because in many cells, the size of the membrane potential modulations evoked by the bars of a drifting grating is the same before and during adaptation (Carandini and Ferster, 1997; Sanchez-Vives et al., 2000a).

We can then begin to assign different physiological mechanisms to different phenomena affecting responsiveness in the primary visual cortex. There are three main physiological mechanisms: (1) synaptic depression, (2) intracortical inhibition, and (3) intrinsic cellular mechanisms. We propose that each of these mechanisms is principally responsible for one type of gain control phenomenon:

1. Synaptic depression is principally responsible for cross-orientation suppression. This type of suppression is fast (a few milliseconds), monocular, present only within the receptive field, obtained with drifting stimuli of all orientations, and even obtained with stimuli that do not evoke V1 responses. A consequence of this type of suppression is contrast saturation.

2. Intracortical inhibition is principally responsible for surround suppression. This type of suppression is slow (tens of milliseconds), binocular, present well outside the receptive field, and strongest with stimuli with preferred orientation.

3. Intrinsic cellular mechanisms are principally responsible for visual adaptation. Adaptation is very slow (seconds), long lasting, binocular, and induced only by stimuli that drive the V1 neuron being adapted.

This schematic picture captures the results of a large body of literature, but it is surely not complete. Although it might take hundreds of milliseconds to reach its peak strength (F. Sengpiel, personal communication), dichoptic cross-orientation suppression has been observed (Sengpiel et al., 1998). This effect might be attributable to intracortical (not thalamocortical) synaptic depression or perhaps more simply to intracortical inhibition. Indeed, some inhibition between neurons selective for different orientations would be consistent with the results of Eysel et al. (1990) and Crook et al. (1998). However, surround suppression is also present in some cells after GABA_A blockage with bicuculline (Grieve and Sillito, 1991), so it might be attributable to additional factors other than intracortical inhibition. Visual adaptation, in turn, reduces responses to some stimuli more than responses to others (Movshon and Lennie, 1979; Albrecht et al., 1984), so it cannot be attributable entirely to intrinsic cellular mechanisms, because these mechanisms do not know to which stimulus they are responding. It might be partially attributable to synaptic depression (Chance et al., 1998; Chance and Abbott, 2001), or may result from prolonged inhibition, which activates extrasynaptic GABA_B receptors (Scanziani, 2000). Finally, our schematic picture does not include mechanisms that could have powerful effects on the responsiveness of V1 neurons, such as recurrent intracortical excitation (Martin, 1988; Douglas et al., 1995) and corticothalamic loops (Murphy and Sillito, 1987; Murphy et al., 1999).

Conclusions

The broad range of phenomena predicted by our model leads us to propose that synaptic depression, and not intracortical inhibition, is the primary mechanism by which V1 neurons adjust their responsiveness to spatially superimposed stimuli. Thus, we suggest a biophysical substrate that is alternative to our previous models, which were based on intracortical inhibition (Heeger, 1992a; Carandini and Heeger, 1994;Carandini et al., 1997).

Future work will be aimed at using our model to fit neuronal responses quantitatively. Indeed, although the responses of the model are the result of simulations, for grating and plaid stimuli, we have derived a closed-form mathematical equation that approximates the model responses (see ). This equation is similar to the one that we derived previously for a model based on intracortical inhibition (Carandini et al., 1997). We have shown previously that these equations closely predict V1 responses to grating and plaid stimuli (Carandini et al., 1997; Freeman et al., 2002).

In conclusion, intracortical inhibition is still a candidate for a gain control mechanism (Carandini et al., 1999) (e.g., for surround suppression), but synaptic depression at thalamocortical synapses appears to be a more plausible explanation for phenomena observed within the receptive field.

In our model, physiological values such as currents, potentials, and firing rates are given units of spikes per second. This simplification reduces the number of model parameters. We held parameters fixed for all of our simulations, rather than individually tailoring them to yield the best match with published results.

LGN neurons

We define visual stimuli in terms of local contrastS(x, y, t) (i.e., with values between −1 and 1). The underlying linear responseC(X, Y, T) of model LGN cells depends on the receptive field location X,Y, and on time T. This linear response is the convolution of a receptive field L with the stimulusS,

$$C(X,Y,T)=\int \int \int \text{dxdydtL}(x,y,t)S(x-X,y-Y,t-T).$$ Equation 2

The output of ON-center cells and OFF-center cells is the rectified version of the positive and negative linear responses,

$$f_{ON}(X,Y,T)=\lfloor f_{\text{rest}}+f_{max} C(X,Y,T)\rfloor$$ Equation 3

$$f_{OFF}(X,Y,T)=\lfloor f_{\text{rest}}-f_{max} C(X,Y,T)\rfloor ,$$

where ⌊X⌋ = X for (X ≥ 0) and 0 otherwise, and where we choosef_max = 100 spikes/sec andf_rest = 10 spikes/sec.

We model LGN receptive fields as the product of a function of time and a function of space.

$$L(x,y,t)=L_{\text{r}}\left(\sqrt{x^2+y^2}\right)L_{\text{t}}(t),$$

where the function of space is a difference of Gaussians (Enroth-Cugell and Robson, 1966),

$$L_{\text{r}}(r)=k_{\text{c}}{e}^{-r^2/(2{\varsigma }_{\text{c}}^2)}-k_{\text{r}}{e}^{-r^2/(2{\varsigma }_{\text{s}}^2)},$$

with ς_c = 0.1°, ς_s = 0.3°,k_c = 1^deg−2,k_r = 0.6^deg−2, and the function of time is a simple bimodal function

$$L_{\text{t}}(t)=k_{\text{f}}{e}^{-(t-1.4{\tau }_{\text{t}}^2/(2{\tau }_{\text{t}}^2)}-k_{\text{s}}{e}^{-r^2/(2{\tau }_{\text{s}}^2)},$$

with τ_f = 10 msec, τ_s = 50 msec,k_f = 1 sec⁻¹, andk_s = 0.6 sec⁻¹.

V1 neuron

The firing rate of our model V1 neuron is a rectified version of the membrane potential with thresholdV_thresh = 5 spikes/sec (Carandini and Ferster, 2000). We take the membrane potential to be noisy, distributed as a Gaussian G[V,V_ς] with mean V and variance V_ς = 10 spikes/sec (Anderson et al., 2000b). The firing rate R is then the weighted average of the portion of Gaussian that is above threshold,

$$R(V)=\int \lfloor v-V_{\text{thresh}}\rfloor G[V,V_{\varsigma }](v)\text{dv}.$$ Equation 4

Contrast invariance of orientation selectivity is preserved in the transformation of membrane potential into firing rate, because this transformation behaves like a power function around spike threshold, and a power function retains contrast invariance (Heeger, 1992b;Anderson et al., 2000b; Hansel and van Vreeswijk, 2002; Miller and Troyer, 2002).

Other than the spike threshold, the neuron is a passive membrane whose potential V is given by

$$\tau \frac{\text{dV}}{\text{dt}}+V=I,$$ Equation 5

where I is the synaptic current, and τ is the membrane time constant.

We chose a relatively long time constant, τ = 50 msec, longer than those measured in vivo (Anderson et al., 2000a). We chose it to attenuate responses of our model V1 neuron to high temporal frequencies. As is common for cat V1 neurons (Saul and Humphrey, 1992), our model V1 neuron has a preferred frequency <4 Hz and gives little or no response to frequencies >15–20 Hz.

The synaptic current is a weighted sum of the currents contributed by LGN neurons, with weights given by the receptive field strength,

$$I(t)=\sum _{\text{i},\text{j}}F(x_{\text{i}},y_{\text{j}})[I_{ON}(x_{\text{i}},y_{\text{j}},t)-I_{OFF}(x_{\text{i}},y_{\text{j}},t)],$$ Equation 6

where the sum is over a 12 × 12 grid of LGN cells covering 3° × 3°, centered on the origin. In our simple model of a synapse, synaptic activity results in current injection rather than in a conductance increase, as would be the case for a more realistic model. The postsynaptic current is thus simply I = p f, the product of the probability of synaptic transmissionp and the presynaptic firing rate f. To distinguish synapses from ON-center and OFF-center cells, we writeI_ON =p_ONf_ON andI_OFF =p_OFFf_OFF. This expression is a simplification; in a more realistic model, synaptic excitation and inhibition would open conductances with appropriate reversal potentials. Here instead they result directly in the injection of positive and negative currents. This current injection behavior of synapses can, in fact, be accomplished thanks to the push–pull arrangement of excitation and inhibition (Carandini and Heeger, 1994).

The spatial receptive field of our V1 neuron is given by a Gabor function (Hawken and Parker, 1987; Jones and Palmer, 1987),

$$F(x,y)\propto e^{-(x^2+v^2)/(2{\varsigma }^2)}sin(2\pi \omega x+\varphi ),$$

where the proportionality factor is 10 over the volume under the Gaussian, and parameters are ς = 0.5°, ϕ= π/8, and ω = 1 cycles/°. For many of the 144 LGN cells in the grid, synaptic weights assigned by the above expression are quite small. For example, for 60 LGN inputs, synaptic weights are <10% of maximum weight. As a result, although the number of LGN afferents to our model V1 neuron is high compared with current physiological estimates (Alonso et al., 2001), the model would behave similarly if approximately half of the synapses were culled.

Synaptic depression

Thalamocortical synapses in the model are subject to synaptic depression. This effect occurs independently at each synapse. Synaptic depression follows presynaptic spikes instantaneously and recovers with a single time constant τ_R. Synaptic transmission depends on a resource (such as vesicles) that is spent and needs time to recover, so that the probability of synaptic transmissionp is the product of the probability u of release of the recovered resource (the utilization parameter u) and the probability that the resource has been recovered. The latter is the expected value of the synaptic resource s described in the following equation:

$$\frac{\text{ds}}{\text{dt}}=\frac{1-s}{{\tau }_R}-\text{us}\delta (t-t_{\text{spike}}).$$

After a presynaptic spike at timet_spike, this resource is reduced by a factor u and then recovers to s = 1 with a single time constant τ_R. If one assumes that the presynaptic spike train is Poisson distributed with mean ratef (Senn et al., 2001), one obtains the expression for the probability of synaptic transmission p given in Equation 1of Results. See Kayser et al. (2001) for a similar rate-based model of synaptic depression.

Time course of depression and recovery

To make the dynamics of depression evident, one can rewrite Equation 1 of Results as

$$\frac{\text{dp}}{\text{dt}}+\frac{p}{{\tau }_{\text{ef\hspace{0.5em}f}}}=\frac{u}{{\tau }_R},$$

where τ_eff is the effective time constant (Senn and Buchs, 2002):

$${\tau }_{\text{ef\hspace{0.5em}f}}=\frac{{\tau }_R}{1+\text{uf}{\tau }_R}.$$

The latter is equal to τ_R only when the presynaptic firing rate f is 0. As f grows, τ_eff tends to zero, leading to faster and faster dynamics.

Saturation in a depressing synapse

The saturation in Figure 1F is a well known property of synaptic depression (Abbott et al., 1997; Tsodyks and Markram, 1997), and (at steady state) it is a simple consequence of Equation 1. Solving Equation 1 for constant presynaptic firing rate gives

$$p=\frac{u}{1+u{\tau }_{R}f}.$$

Because the postsynaptic current isI_post = p f and the presynaptic firing rate is f = k I_pre, where k is the gain of the presynaptic neuron (300 spikes per second per unit current), one can write

$$I_{\text{post}}=I_{max} \frac{I_{\text{pre}}}{\varsigma +I_{\text{pre}}},$$

where I_max = 1/τ_R and ς = 1/(τ_Ru k). AsI_pre grows, this function saturates at I_max and achieves half of its maximal value at I_pre = ς.

Because the injected currents in Figure 1 vary slowly compared with the time constant of recovery τ_R = 0.2 sec, we can use the steady-state solution above to obtainI_max = 1/0.2 = 5 and ς = 1/(0.2 × 0.75 × 300) = 0.02. These approximated values seem reasonable when compared with the data in Figure1F. There the stimuli varied in time asf(t) = ⌊kcsin(2πωt) + f_rest⌋ for different values of c. The approximate solution above would be exact if the stimulus frequency ω had been zero.

Predicted responses to plaids

The responses to plaids illustrated in Figure 4 can be approximated by a family of sigmoidal functions. This family of functions is more easily described for the membrane potentialV than for the firing rate R, which is the output of a nonlinear mechanism. For the membrane potential V, the family of functions is given by

$$V^1=V_{max}\frac{c_{\text{test}}}{c_{50}+\sqrt{c_{\text{test}}^2+c_{\text{mask}}^2}},$$

where V¹ is the component of the membrane potential at the test frequency,c_test andc_mask are test and mask contrasts, andV_max andc₅₀ are fixed parameters. To understand this expression intuitively, consider that without synaptic depression one would have only the term in the numerator; the response would grow linearly to the test contrastc_test regardless of the mask contrastc_mask. The mask does not affect the responses, because the postsynaptic currents that it contributes sum to zero. Consider now synaptic depression in the absence of a mask (c_mask = 0). We know from Figure 1that responses will saturate with increasing contrasts; indeed, the expression above contains c_test both in the numerator and in the denominator. Finally, consider the effect of the mask. Because the mask depresses excitatory and inhibitory synapses equally, the postsynaptic currents that it contributes again sum to zero. Mask contrast c_mask thus does not appear in the numerator. It appears in the denominator because the mask depresses the synapses as much as the test does. The above expression is simple and resembles that obtained in our previous model based on shunting inhibition (Carandini et al., 1997). Its derivation, however, is quite involved and rests on approximations based on simplifying assumptions. It is available at:http://e-collection.ethbib.ethz.ch/show?type=bericht&nr=194