Firing Properties of Identified Interneuron Populations in the Mammalian Hindlimb Central Pattern Generator

Abstract

Little is known about the network structure of the central pattern generator (CPG) controlling locomotor movements in mammals. The present experiments aim at providing such knowledge by focusing on commissural interneurons (CINs) involved in left–right coordination. During NMDA and 5-HT-initiated locomotor-like activity, we recorded intracellularly from caudally or descending projecting L2 and L3 CINs (dCINs) located in the ventromedial area of the lumbar spinal cord in newborn rats. This region is crucial for rhythmic motor output and left–right coordination. The overall sample of dCINs represented a heterogenous population with neurons that fired in all phases of the locomotor cycle and exhibited varying degrees of rhythmicity, from strongly rhythmic to nonrhythmic. Among the rhythmic, putative CPG dCINs were populations that fired in-phase with the ipsilateral or with the contralateral L2 locomotor-like activity. There was a high degree of organization in the dorsoventral location of rhythmic dCINs, with neurons in-phase with the ipsilateral L2 activity located more ventrally. Spikes of rhythmically active dCINs were superimposed on membrane oscillations that were generated predominantly by synaptic input, with little direct contribution from the intrinsic pacemaker hyperpolarization-activated inward current. For both ipsilaterally and contralaterally firing dCINs the dominant synaptic drive was in-phase with the ipsilateral L2 motor activity. This study provides the first characterization of putative CPG interneurons in the mammalian spinal cord. Our results suggest an anatomical and physiological separation of CPG commissural interneurons in the ventral horn and demonstrate that it is possible to target specific interneuron subpopulations in the mammalian locomotor network.

Vertebrate locomotor movements are organized by local neuronal networks, known as central pattern generators (CPGs), situated within the spinal cord. In swimming vertebrates such as the Xenopus tadpole and the lamprey, these CPG circuits have been characterized in some detail (Grillner et al., 1995; Roberts, 2000). In these animals, swimming is mediated by alternating left–right contraction of the segmental muscles, propagated along the body with a rostrocaudal phase delay, resulting in an undulating sinusoidal movement. The timing of the activity in the bilateral motor pools is determined to a large extent by reciprocal inhibition mediated by glycinergic commissural interneurons (CINs), neurons whose axon crosses the midline. These CINs fire one or few spikes per locomotor cycle in-phase with the ipsilateral motor root discharge and so ensure that when CPG neurons on one side of the cord are active, CPG neurons on the other side are inhibited (Buchanan 1982;Soffe et al., 1984; Dale, 1985; Soffe, 1987; Buchanan and Kasicki, 1995). At least part of the reciprocal inhibition is mediated by caudally projecting CINs (Buchanan 1982; Dale, 1985; Buchanan and Kasicki, 1995; Soffe et al., 2001).

Although the basic principles of CPG structure might be phylogenetically preserved, it is evident that a layer of complexity must be added in limbed animals where the CPG is required to coordinate not only alternating movements between the left and right sides but also flexors and extensors in each limb. Relatively little is known about the network structure of the mammalian CPG, which to a large extent is regarded as a “black box.” Our present experiments in the neonatal rat spinal cord aim to explore this black box by focusing on the CINs involved in coordination of the left and right hemicords. The fact that CINs have crossed projections makes them readily identifiable by electrical stimulation. Initial experiments with neonatal rats have shown that the ventromedial region of the lumbar spinal cord is crucial for rhythm generation and left–right coordination (Kjaerulff and Kiehn, 1996; Kiehn and Kjaerulff, 1998). This region contains four anatomically defined populations of CINs: three populations have axons that project intersegmentally over >1.5 segments, ascending (rostral) CINs, descending (caudal) CINs (dCINs), or bifurcating CINs (adCINs), whereas a fourth population projects intrasegmentally over short ranges (Eide et al., 1999; Stokke et al., 2002).

In this study, whole-cell patch recordings were performed from CINs located in the L2–L3 segments with descending axons to the contralateral L4–L5 region. These CINs were monitored during NMDA- and 5-HT-induced locomotor-like activity to provide an insight into the functional role of interneurons in the mammalian hindlimb CPG.

Parts of this paper have been presented previously in abstract form (Butt et al., 2001).

MATERIALS AND METHODS

Dissection. Neonatal (postnatal day 0–4) Wistar rats were used for all experiments, and the dissection was performed as described previously (Kjaerulff and Kiehn, 1996). Briefly, neonatal rats were deeply anesthetized with either ether or isofluran (in accordance with the stipulations of the local Animal Care Committee and National Institutes of Health guidelines), decapitated, and eviscerated. The isolated spinal cord extending from at least C1 to S2 was pinned ventral side-up in a recording chamber superfused with oxygenated (5% CO₂ in O₂) Ringer's solution composed of (mm): 111 NaCl, 3.08 KCl, 25 NaHCO₃, 1.18 KH₂PO₄, 1.25 MgSO₄, 2.52 CaCl₂, and 11 glucose. All experiments were performed at room temperature (20–23°C). In preparation for stimulating CINs with axons projecting caudally, the L4 and L5 segments were sectioned midsagitally up to the level of the most rostral L4 rootlet. The left L4–L5 hemicord was then cut caudally at the L5–L6 boundary and, after trimming away ventral and dorsal roots, placed in a large-diameter stimulating suction electrode (Fig. 1A). Although CINs with axons projecting caudally include both a population of puredCINs and a population of adCINs (Stokke et al., 2002), we will for simplicity call this group dCINs in this paper. A smaller-diameter suction electrode was placed on the L2 root ipsilateral to the L4–L5 stimulating electrode and contralateral (cL2) to the site of intracellular recording.

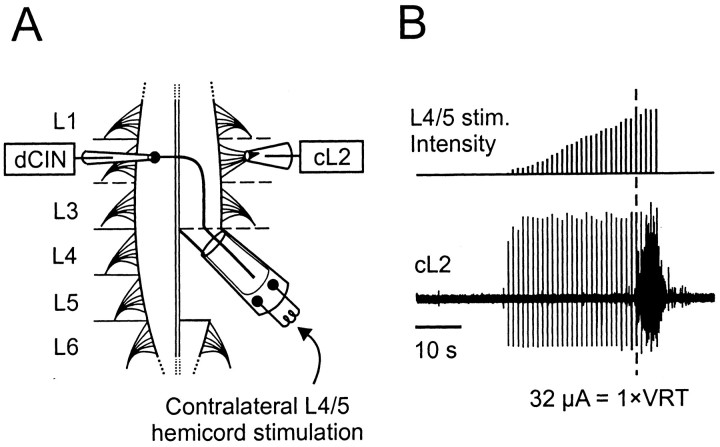
Fig. 1.

Experimental setup. A, Schematic of the lumbar region of the neonatal rat spinal cord and the setup used to investigate the locomotor properties of dCINs. Suction electrodes were placed on the contralateral L4–L5 hemicord for electrical stimulation of caudally projecting axons, and on the cL2 to record ventral root activity. The patch electrode (dCIN) was lowered into a slit made in the ventral surface of L2–L3. B, The intensity of L4–L5 stimulation was increased manually (top trace). At higher levels, the stimulation (stim.) caused sustained activity in the cL2 ventral root (lower trace). The threshold for such activity, as indicated by the dashed line, was termed the VRT.

Electrical stimulation of the contralateral hemicord. dCINs were identified by stimulating the contralateral L4–L5 hemicord at 1 Hz with 2 msec pulses up to 300 μA in amplitude (Isolator-11 stimulator; Axon Instruments). Strong stimulation of the L4–L5 hemicord resulted in sustained activity in the L2 ventral root (Fig.1B). The threshold for such bursting (range, 30–267 μA) was termed the ventral root threshold (VRT) and provided a measure of the relative intensity of stimulation between preparations.

Whole-cell tight-seal recording of ventromedial interneurons. A small slit was cut into the pial surface of segments L2–L3 (opposite to the side of L4–L5 stimulation), into which the patch electrode (resistance, 5–8 MΩ, borosilicate glass; Clark Electromedical Instruments, Pangbourne, UK) was lowered. Blind whole-cell tight-seal intracellular recordings of interneurons were performed in current-clamp mode (Axoclamp 2B; Axon Instruments). Locomotor-like activity was evoked by perfusion with Ringer's solution containing a combination of NMDA (6–8 μm) and 5-HT (6–10 μm). Rhythmic burst activity in the cL2 ventral root was recorded with a suction electrode and bandpass-filtered (100 Hz to 1 kHz). The following drugs were obtained from Sigma (St. Louis, MO): d(−)-2-amino-5-phosphonopentanoic acid (AP-5), 6-cyano-7-nitroquinoxaline-2,3-dione disodium salt (CNQX), and tetrodotoxin (TTX). 4-Ethylphenylamino-1,2-dimethyl-6-methylaminopyrimidinium chloride (ZD 7288) was obtained from Tocris.

Calibration of recording locations. A counter on the microdrive was used to determine the ventral-dorsal depth of the recorded dCIN. The counter was zeroed on contact with the surface of the slit. Once recording was completed, the electrode was retracted and then lowered to the point of contact on either side of the slit. The average of these two values provided a measure of the depth to the initial point of contact within the slit. The distance to the midline was measured using the x–y scale on the micromanipulator stand. Both ventral depth and distance to midline were corrected for the angle of the micromanipulator with respect to the surface of the cord, which was kept constant throughout all the experiments.

To provide an indication of the error involved in such calculations, seven interneurons were labeled with 0.2% Lucifer yellow, and the spinal cords were sectioned transversely. Measurement of these filled neurons revealed that the initial measurement of the distance from the midline was incorrect laterally on average by 88 ± 13 μm (SEM), and the depth from the surface of the cord was incorrect in either direction by on average 61 ± 27 μm. Where recognizable in the transverse slices, the depth of the slit in the spinal cord was 98 ± 8 μm (n = 6). The interneuron positions in Figure2C were not corrected for these values.

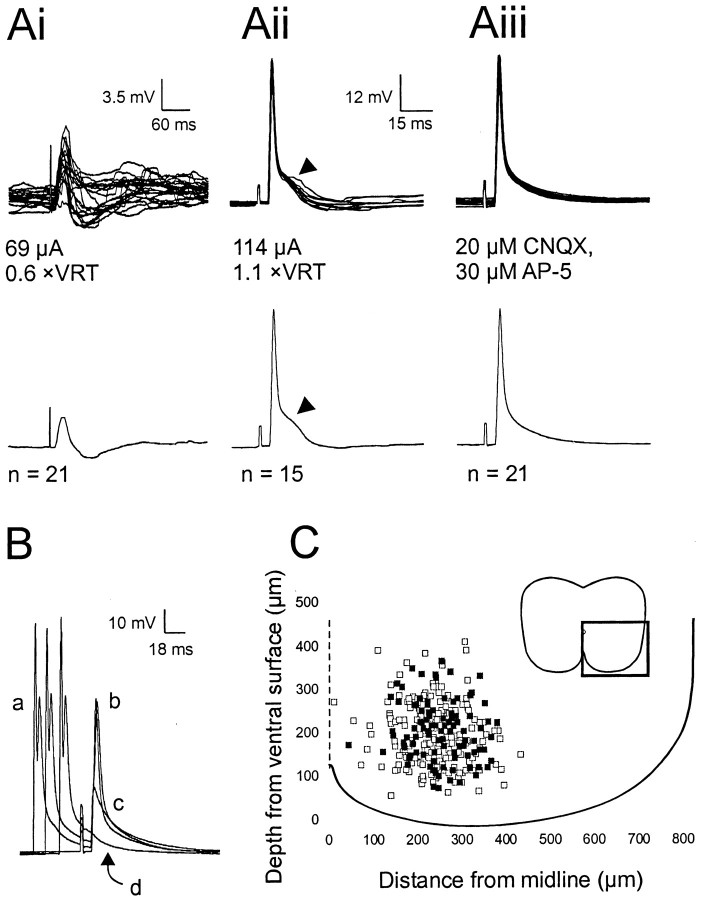
Fig. 2.

Identification of dCINs in the lumbar region by the presence of an antidromic action potential.Ai–Aiii, The top traces show the raw data superimposed, and the bottom traces show the averaged trace. Ai, EPSP–IPSP evoked at low stimulus levels (<1 × VRT) in a neuron subsequently identified as a dCIN by the presence of an antidromic spike (Aii,Aiii). Antidromic spikes were elicited at a short, constant latency (Aii). The hump in the spike, as indicated by the arrowheads in Aii, is the subthreshold EPSP that was abolished on incubation with 20 μm AP-5 and 30 μm CNQX (Aiii). B, Collision test to verify the antidromic nature of the spike. a, Orthodromic spike elicited by a 2 msec suprathreshold depolarizing current pulse;b, antidromic spike; c, initial segment spikelet; d, complete abolition of the antidromic action potential. C, Location of neurons recorded from in the ventromedial area (as indicated by the box,inset) of L2–L3. Black squares, Caudally projecting dCINs; white squares, non-dCINs.

Protocols for identifying the hyperpolarization-activated inward current. Under control current-clamp conditions, 58 dCINs were stimulated at 0.25 Hz with 800 msec hyperpolarizing and depolarizing current pulses. The effect of the hyperpolarization-activated inward current (I_h) was detected in the slow depolarizing voltage sag during steady-state hyperpolarizing current injection at membrane potentials typically more negative than −70 mV. More detailed analysis of the biophysical properties ofI_h was performed under voltage-clamp conditions (see below). However, for initial comparison between dCINs under current-clamp conditions, the voltage sag (from the most hyperpolarized point to the end of the current step) was determined at the maximal potential closest to −110 mV. The current amplitude was adjusted during ZD 7288 application to correct for the increased input resistance observed with this drug (Kiehn et al., 2000).

Voltage-clamp analysis of I_h. For voltage-clamp analysis, neurons were typically maintained in normal Ringer's solution. Neurons were held at –50 mV and given a series of 1.5 sec steps from –60 to –130 mV in 5 mV increments. In general, the series access resistance was within 20–40 MΩ. The currents measured were typically small (200–300 pA at peak; see Fig.6D), so the estimated error attributable to uncorrected series access resistance was <10 mV (with the cell less hyperpolarized than the pipette voltage) and was not corrected. The liquid junction potential was within the range of 6–8 mV (with the cell more hyperpolarized than the pipette voltage) using the intracellular and extracellular solutions (Kjaerulff and Kiehn, 2001). This was also not corrected because of the uncertainty of complete replacement of the contents of the cell by the intracellular solution of the electrode.

Fig. 6.

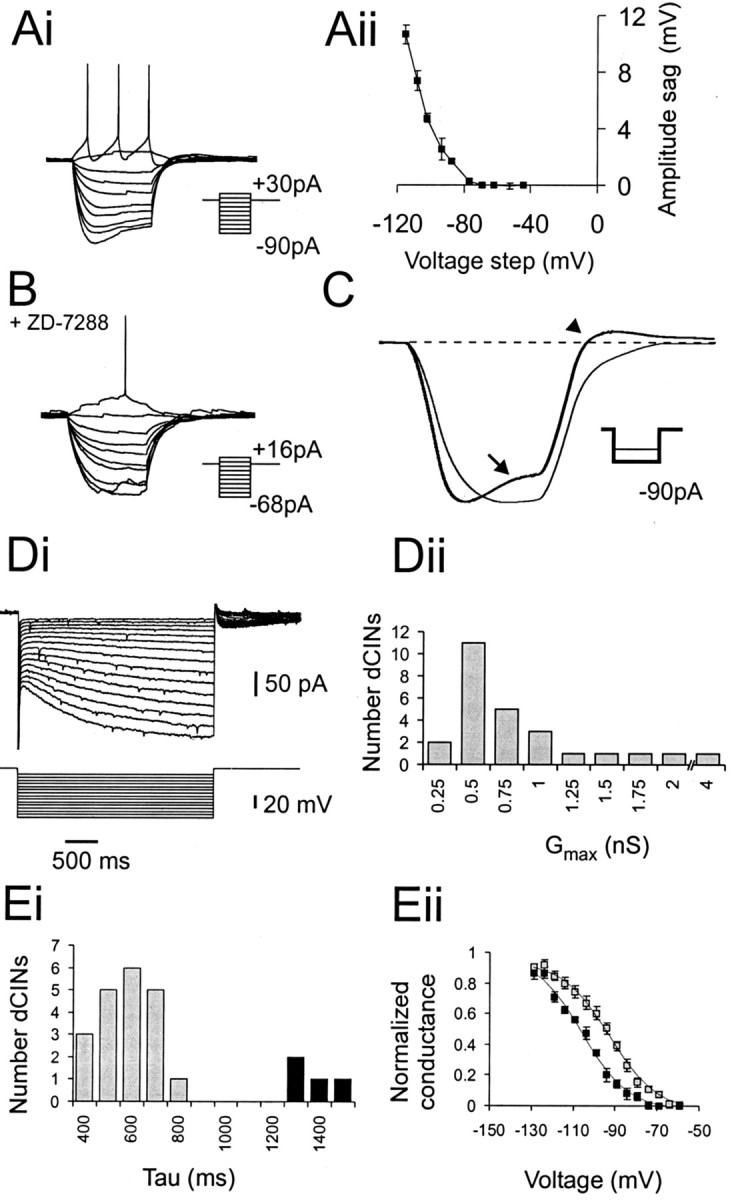
Characteristics of the dCINI_h. A, Intracellular recording from S-dCINs showing a voltage sag (Ai) in response to current injection and a depolarizing rebound after termination of the current pulse. Data of the averageI_h-induced sag amplitude ± SE from three control I–V trials are shown inAii. B, Effect of 20 min incubation with 50 μm ZD 7288. Note the decrease in size of the injected current steps. C, Effect of ZD 7288 shown by comparison of averaged data for three runs at the most hyperpolarized step (control, bold line; ZD 7288,thin line). The control sag is indicated by thearrow, and the rebound depolarization is indicated by the arrowhead. Di, Activation ofI_h measured under voltage-clamp conditions. Five millivolt steps were applied between −60 and −130 mV from a holding potential of −50 mV. Dii, Distribution of G_max (maximal conductance) for 24 dCINs.Ei, Analysis of τ _Act revealed two discrete populations in the sample: short τ _Act(gray) and longer (black) τ_Act dCINs. The plot shows voltage versus normalized conductance for the both populations of τ_Act, same color code as forEi. Note that the dCINs with longer τ_Acthave their activation curves shifted to a more hyperpolarized level than those with short τ_Act.

Data analysis. The locomotor pattern was analyzed off-line using DATAPAC 2000 version 2.41 (RUN technologies Co., Laguna Hills, CA) with the exception of the circular plots, which were calculated as described by Kjaerulff and Kiehn (1996) and plotted in Excel (Microsoft, Redmond, WA). Summary statistics report the mean ± SEM unless otherwise specified. p values with the exception of those for circular statistics (see below) were calculated using Student's t test.

Datapac analysis. For histograms of instantaneous spike frequency, the boundaries of each locomotor cycle were defined as being from the onset of a cL2 ventral root burst to the onset of the following burst. The threshold for spike events was normally set at 0 mV. To average intracellular dCIN membrane oscillations during locomotion, cL2 ventral root recordings were rectified, filtered (Butterworth filter, 100 Hz; rolloff, 5) and linear-smoothed with a time constant of 100–200 msec. dCIN intracellular recordings were filtered (Butterworth filter, 10 Hz; rolloff, 5) to remove fast transients such as spikes. The signals were averaged with respect to cL2 activity (for a minimum of 20 cycles) using the dual normalized function (1% increment, 50% break point).

Circular plots. Circular statistics were performed to ascertain the significance of the coupling between dCIN firing and the locomotor-like activity in the cL2. The latency (Kjaerulff and Kiehn, 1996) to each spike was measured relative to the duration of the contralateral ventral root burst to give the phase value Φ. The mean of 25 Φ was calculated using the formula outlined by Kjaerulff and Kiehn (1996) to give a vector, the direction of which represents the preferred phase of firing of the neuron and the length of which,r, represents the tuning of the spikes around their mean. The onset of the cL2 burst was set as 0.0. Because Φ was calculated relative to cL2 activity, vectors with a direction in the range of 0.0–0.5 corresponded approximately to cells firing in-phase with the cL2 and out-of-phase with the iL2. The cessation of cL2 bursting occurred approximately halfway through the cycle (0.5 on the circular plots), although there was a degree of variability in the duty cycle. For the presentation of individual results the mean and SD of the end of the cL2 burst are shown; however, for pooled vector data, it was assumed to approximate 50% of the cycle. p values for the significance of r were taken from Zar (1974).

Analysis of I_h. Current amplitudes were measured from single exponential fits of the data performed in Clampfit version 8.1 (Axon Instruments), extrapolated back to the beginning of the hyperpolarizing step and forward to approximate the steady state at 2 sec. Currents were converted to conductance using a reversal potential for I_h(V_Rev) of –33 mV, which has been measured previously in neonatal rat spinal neurons (Takahashi, 1990;Kjaerulff and Kiehn, 2001). The conductance–voltage data were fit to a first-order Boltzmann relationship of the form:

$$g/g_{max}=1/(1+e^{-(V-V_{\text{Act}})/s}),$$

where g is the conductance,g_max is the maximal conductance,V_Act is the voltage of half-activation, and s is the slope factor. The kinetics of activation were measured at −125 mV, at which the current was well developed in all cells. The current was fit to a single-exponential relationship of the form:

$$I=I_{\text{Act}}{e}^{-t/{\tau }_{\text{Act}}}+C,$$

where I_Act is the amplitude of the current, τ_Act is the time constant of activation, and C is an offset constant. Attempts were made to fit the data with a double-exponential relationship, but this did not improve the fit.

RESULTS

Identification and initial characterization of dCINs

Ninety-nine dCINs were identified by stimulation of antidromic action potentials from the contralateral L4–L5 hemicord (Fig.1A). All-or-nothing antidromic potentials were elicited in dCINs at constant latencies (range, 4.4–15.2 msec) by stimuli over the range of 21–312 μA (mean ± SEM, 103 ± 6.2 μA), corresponding to a mean VRT of 1.4 × VRT. Subthreshold stimulation (typically <1 × VRT) of the contralateral L4–L5 evoked short-latency PSPs in 72% of dCINs. A significant amount of these neurons received low-threshold, short-latency EPSPs or a mix of a short-latency EPSP followed by an IPSP (Fig. 2Ai). To confirm the antidromic nature of the spike and to prove that the spikes were not driven indirectly by EPSPs, supramaximal concentrations of the excitatory transmitter antagonists CNQX (30 μm) and AP-5 (20 μm) were coapplied. After 5–6 min, evoked EPSPs and polysynaptic IPSPs (see EPSP “hump”; Fig.2Aii, arrowhead) were completely abolished (Fig. 2Aiii). In some instances, a voltage-independent, CNQX- and AP-5-resistant potential was observed at subspike thresholds, indicative of electrical coupling between dCINs (Kiehn and Tresch, 2002). Spikes that persisted in the presence of these antagonists were deemed to be attributable to direct stimulation of the commissural axon. We further confirmed this by measuring the ability of an orthodromic spike (generated by a 2 msec current pulse, 1 Hz frequency applied 15–40 msec before antidromic stimulation) to collide with and abolish the antidromic spike (Fig.2B). Reducing the latency between the orthodromic spike (Fig. 2B, a) and the control antidromic spike (b) first resulted in an initial segmental spike (c) and then a complete elimination of the antidromic spike (d).

Using these tests, we found that 34% (99 of 294) of the neurons recorded were dCINs with axons projecting at least to the contralateral L4–L5 segment. These dCINs were located throughout the ventromedial area sampled (Fig. 2C). Before addition of locomotor-inducing drugs, they had a mean resting potential of −49.3 ± 0.8 mV (n = 99), and 36% of them spontaneously fired action potentials. The conduction velocity of these neonatal dCINs, calculated for the direct distance from the recording site to the edge of the L4–L5 stimulating electrode, had an average value of 0.22 ± 0.01 m/sec (n = 99; range, 0.10–0.59 m/sec). This is probably an underestimate of the normal conduction velocity in vivo, because the axons do not project diagonally to the cL4–cL5 but travel over a longer distance (Eide et al., 1999; Stokke et al., 2002), and all experiments were performed at room temperature instead of 37°C (Oro and Haghighi, 1992; Andersen and Moser, 1995). In addition, the neonatal rat preparation is immature relative to adults.

Activity of dCINs during NMDA- and 5-HT-induced locomotion

To determine whether the dCINs were potential components of the hindlimb CPG, we measured their firing patterns during locomotor-like activity. Previous work has shown that locomotor-like activity can be induced by perfusion with a combination of 5-HT and NMDA (Cazalets et al., 1992; Kiehn et al., 1996; Iizuka et al., 1997), expressed as coordinated rhythmic bursting activity between the two sides of the cord and along the cord. In the present experiments, locomotor-like activity was observed as rhythmic bursting in the L2 ventral root contralateral (cL2) to the site of the intracellular recording (iL2).

Application of locomotor drugs typically resulted in a significant depolarization of the dCIN membrane potential (by 6.5 ± 0.6 mV;n = 84) and an increase in spike firing or modulation of spontaneous firing (Fig.3A). We found that dCINs exhibit a broad range of activities during locomotion. We have divided this continuous spectrum into three broad classes of dCINs on the basis of their firing pattern during NMDA and 5-HT: (1) highly rhythmic firing, often driven by pronounced oscillations in membrane potential, which were phase-related to cL2 ventral root bursting (Fig.3Bi); (2) broadly tuned but rhythmically firing neurons with less distinct oscillations in membrane potential (Fig. 3Ci); and (3) dCINs that appeared to fire randomly with respect to cL2 bursting and that exhibited little or no underlying rhythmic oscillations in membrane potential (Fig. 3Di). Individual dCINs were monitored for a period of at least 10 min during locomotor-like activity. To determine the phase relationship of dCIN firing, we normalized the phasing of spike activity for 50 cycles of stable cL2 activity with respect to the onset of the cL2 burst. To provide a measure of instantaneous spike frequency, the normalized cycle periods were subdivided into 10 equal bins, the first five representing approximately the phase of cL2 bursting and the last five approximately equivalent to the iL2 phase (see Materials and Methods). Examples for the three categories of dCIN as represented in histogram form are shown in Figure 3Bii–Dii. The graphs give an indication of the spike tuning for a sustained period of ∼2–3 min. The variability in the cL2 duty cycles within this time is represented by the error bar (±SD) below the x-axis; the end point of the cL2 burst was within one bin (10%) of the 50% duty cycle.

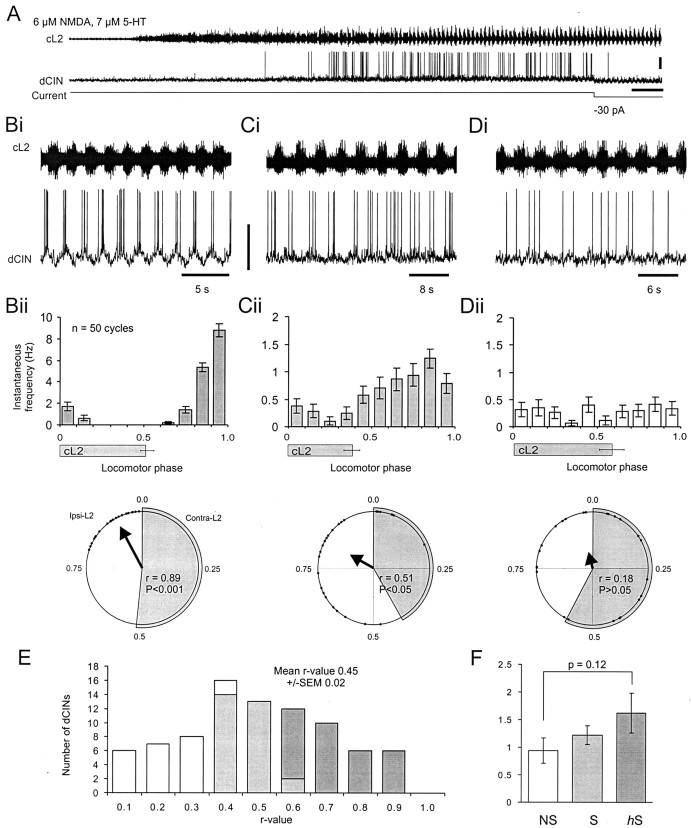
Fig. 3.

Most dCINs are rhythmic during NMDA- and 5-HT-induced locomotor-like activity. A, Application of NMDA and 5-HT to the isolated spinal cord resulted in rhythmic locomotor-like activity in the cL2 (top trace) and a depolarization and rhythmic firing observed in the dCIN (bottom trace). Calibration: 20 mV, 24 sec. B–D, Analysis of the activity of the three types of dCIN during locomotor-like activity. Highly rhythmic hS-dCINs (B) were characterized first, on the basis that they exhibited pronounced oscillations in membrane potential (bottom trace, Bi; calibration, 40 mV) during locomotor activity (top trace,Bi). Second, their spikes were also locked to a specific phase as revealed by the spike frequency histogram of 50 locomotor cycles (Bii, top trace). Third, the circular plot vector for 25 spikes as shown by the bold arrow in the bottom trace of Biiwas highly significant (p < 0.001). The duration of cL2 bursting is indicated in Bii–Dii by thegray bars (±SD; n = 50) under thehistogram and the gray segment in thecircular plot. C, Rhythmic S-dCIN that preferentially fires out-of-phase with cL2 activity.p values for S-dCINs were in the range of 0.001 <p < 0.05 (Cii, bottom trace). D, Nonrhythmic NS-dCIN with spikes not locked to any particular phase of the locomotor cycle and withp > 0.05 (Dii, bottom trace). In all subsequent plots, hS-dCIN data are shown in dark gray; S-dCIN data are light gray; and NS-dCIN data are white.E, Distribution of dCIN r values (n = 84). F, Analysis of the instantaneous firing frequency exhibited by the three classes of dCIN.

To provide a statistical measure of the spike tuning, spikes from every 10th cycle were analyzed using circular statistics (Kjaerulff and Kiehn, 1996). The preferred phase of firing is indicated by the direction of the vector, and the length describes the sharpness of the spike tuning around that point. The three broadly defined classes of dCIN described above could now be defined quantitatively as follows: (1) highly significantly (p < 0.001) tuned firing corresponding to highly rhythmic cells (n = 32) (Fig. 3Bii, bottom); (2) significant (0.001 <p < 0.05) tuning similar to category 2 of the rhythmic dCINs (n = 29), with spikes throughout the cycle but a clearly preferred phase of firing (Fig. 3Cii, bottom); and (3) nonsignificant tuning with cells firing throughout the cycle and no significant preferred phase of firing (p > 0.05), corresponding to nonrhythmic dCINs (n = 23) (Fig. 3Dii, bottom). Henceforth, we will refer to the categories of dCIN as highly significant (hS), significant (S), and nonsignificantly (NS) rhythmic cells.

A plot of r values with respect to number of dCINs (Fig.3E) revealed a broad distribution similar to that previously published for unidentified L2 neurons (Tresch and Kiehn, 1999) and illustrates that although we have divided the dCINs into hS, S, and NS categories, the overall sample represents a continuum of rhythmicity. Interestingly the overall percentage of rhythmic dCINs (73% hS- and S-dCINs) is similar to the value reported previously for unidentified interneuron populations in the ventromedial area (Kiehn et al., 1996; Tresch and Kiehn, 1999; Raastad and Kiehn, 2000). Additionally, the average instantaneous firing frequencies of the three classes of dCIN during locomotor-like activity (Fig.3F) are comparable with those reported previously for unidentified L2 and L5 neonatal rat interneurons (Tresch and Kiehn, 1999, 2000; Raastad and Kiehn, 2000). Although there was a trend for increased firing frequencies in hS and S neurons over NS neurons, this was not statistically significant (p = 0.12).

These results demonstrate that the set of CINs defined anatomically on the basis of axonal projections is heterogeneous with respect to firing properties during locomotor-like activity. The next section will show that rhythmically active cells can be further subclassified on the basis of their preferred phase of firing in the locomotor cycle.

Preferred phase of firing of rhythmically active dCINs

During locomotion, the iL2 alternates with the iL5 and with the cL2, and the iL2 and cL5 burst in-phase (Kiehn and Kjaerulff, 1996;Iizuka et al., 1997). The L2 burst reflects predominantly flexor activity, whereas the L5 burst mainly corresponds to extensor activity (Kiehn and Kjaerulff, 1996). It is therefore of interest to determine whether the L2 dCINs fire mostly in-phase with the ipsilateral, predominantly flexor L2 root or are active throughout the locomotor cycle and, hence, important for the transmission of information to the contralateral L4–L5 on both flexor and extensor phases. Furthermore, we wished to determine whether both broadly tuned S-dCINs and more finely tuned hS-dCINs shared similar distributions of firing phase. This analysis will give us further insights into the possible function of the dCINs in the CPG.

The two rhythmic cells shown in Figure 3, B andC, have their preferred peak of firing in-phase with the iL2 (bins 6–10) and out-of-phase with the cL2 bursts (bins 1–5). This phasing was defined as ipsilateral firing. However, a number of dCINs fired in-phase with the cL2 activity, defined as contralateral firing. Within the total sample of dCINs recorded during locomotor-like activity, 61 significantly rhythmic (hS and S) neurons had their preferred phases of firing distributed throughout the locomotor cycle, but not equally so (Fig.4A). Sixty-four percent of them fired with their peak of activity in-phase with the ipsilateral L2 bursts, whereas only 36% showed predominantly contralateral firing. A plot of the preferred phase of firing of dCINs by type revealed that >50% of the hS-dCINs fired in the final third of the ipsilateral L2 burst just at the peak of the iL2 burst (bin 8) and before the transition to the cL2 burst (bin 9) (Fig.4Ai). This subset of hS neurons may be described as “transition neurons.” The other hS interneurons fired at all other phases but predominantly just before or during the iL2 burst. In contrast, within the S-dCINs, most (62%) fire just before onset (bin 5) or at the midpoint (bins 7–8) of iL2 activity. For the contralaterally firing neurons, there was a less distinct pattern in preferred firing phase.

Fig. 4.

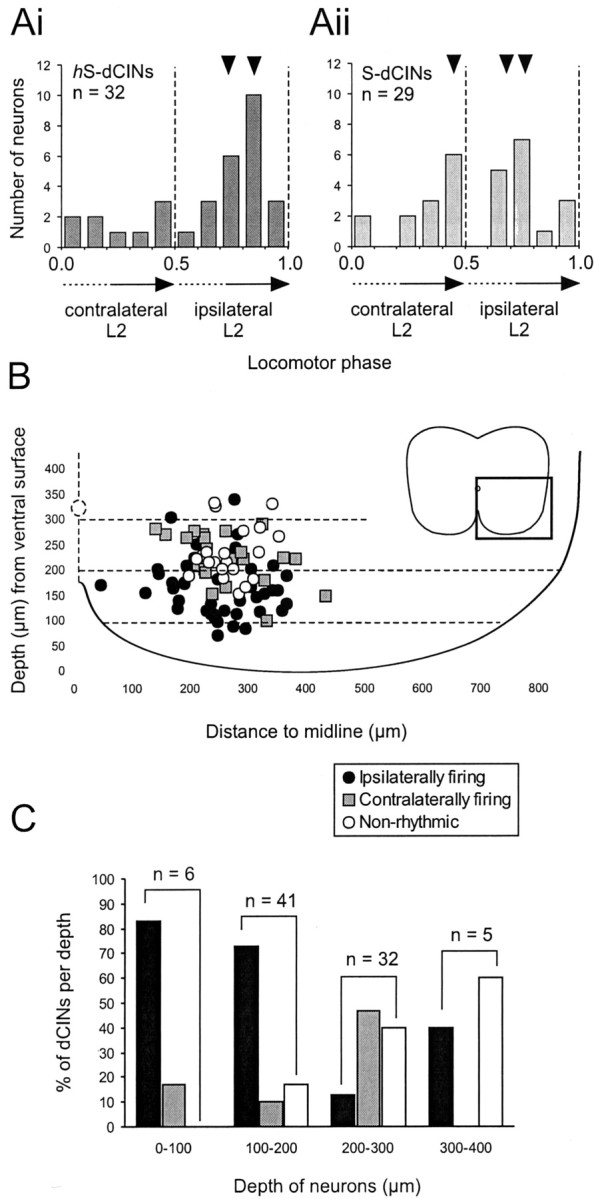
Rhythmic dCIN populations with distinct ventral-dorsal locations exhibit differing phase relationships.A, Plot of dCIN circular statistic vectors over a locomotor cycle showing the distribution preferred phases of firing in rhythmic dCINs (hS-dCINs, Ai; S-dCINs,Aii). The small black arrowheads above the histograms indicate the bins containing most dCINs for each group. The dashed lines indicate the approximate transition points from contralateral bursts (cL2) to ipsilateral burst (iL2) (0.5) and from iL2 to cL2 (1.0).B, distribution of contralaterally firing (gray squares), ipsilaterally firing (black circles), and nonrhythmic (white circles) dCINs in the transverse plane of the lumbar spinal cord (the area magnified as shown in the inset).C, Histogram of the percentage of each cell type at a given depth (color coding as for B).Numbers shown above the bar graphsindicate the size of the sample at each depth. Memb., Membrane.

Because we did not use dual reference in our analysis (Berkowitz and Stein, 1994) the cL2–iL2 and iL2–cL2 transitions are only accurately determined if the duty cycle is 50%. The variability in the duty cycle is therefore an important factor when considering the timing. To test how much variability of the duty cycle affected our classification, cL2 duty cycles were calculated during the locomotor runs for 10 hS-dCINs (five ipsilaterally and five contralaterally firing). The average duty cycle was 57 ± 7% (SD), and in all cases analyzed, the r vector derived from the circular statistics accurately reflected the phase of the dCINs. Our data show that most rhythmic (hS and S) dCINs fire at the midpoint and toward the end of the ipsilateral L2 dominating flexor burst, which occurs synchronously with the contralateral dominating extensor L5 burst.

dCIN subpopulations show a distinct ventral-dorsal distribution

It became apparent during our experiments, as more dCINs were identified, that we could preferentially target either ipsilaterally firing or contralaterally firing dCINs by selecting cells at either shallow or deep locations below the ventral surface, respectively. A plot of the locations of all dCINs based on their preferred phase of firing confirmed that cells firing rhythmically in-phase with their own ipsilateral side are preferentially located closer to the ventral surface than those that fire contralaterally (Fig.4B). Nonrhythmic cells tended to occur in greater numbers at more dorsal locations. This overall distribution became even more apparent when plotted as a histogram of the percentage of the three types of dCINs at each depth: ipsilaterally firing dCINs were primarily found <200 μm below the surface, whereas contralaterally firing dCINs peaked at 200–300 μm. NS-dCINs increase in proportion the more dorsal the location (Fig. 4C). Thus, it appears that there is an anatomical separation of rhythmically active dCINs that may subserve different functional roles in the locomotor network.

Synaptic drive contributes to the rhythmicity of dCIN firing

As mentioned previously, hS-dCINs often displayed pronounced oscillations in membrane potential during the locomotor cycle, similar in nature to the locomotor drive potentials described previously in neonatal rat motor neurons (MNs) (Hochman and Schmidt, 1998; Kiehn et al., 2000). To characterize these oscillations further, the underlying membrane potential of dCINs was normalized and averaged with respect to cL2 bursting, the raw data having been filtered to remove spikes. Figure 5Aishows examples of the normalized voltage oscillations for anhS-dCIN (bold line) and an NS-dCIN (thin line) at similar average membrane potentials. Even NS-dCINs often exhibited a distinct oscillation in membrane potential, although of low amplitude compared with the hS and S-dCINs. Figure5Aii shows the relationship between the action potential rhythmicity of the cell (reflected in r values from circular plots) and the amplitude of the membrane potential oscillations in 77 dCINs analyzed at 0 bias. There was a clear positive correlation between rhythmicity and membrane oscillation amplitude, suggesting that intrinsic properties, the rhythmic pattern of synaptic drive onto dCINs, or both are the principle determinants of rhythmic output rather than spikes being driven by a few precisely timed EPSPs (Beierholm et al., 2001).

Fig. 5.

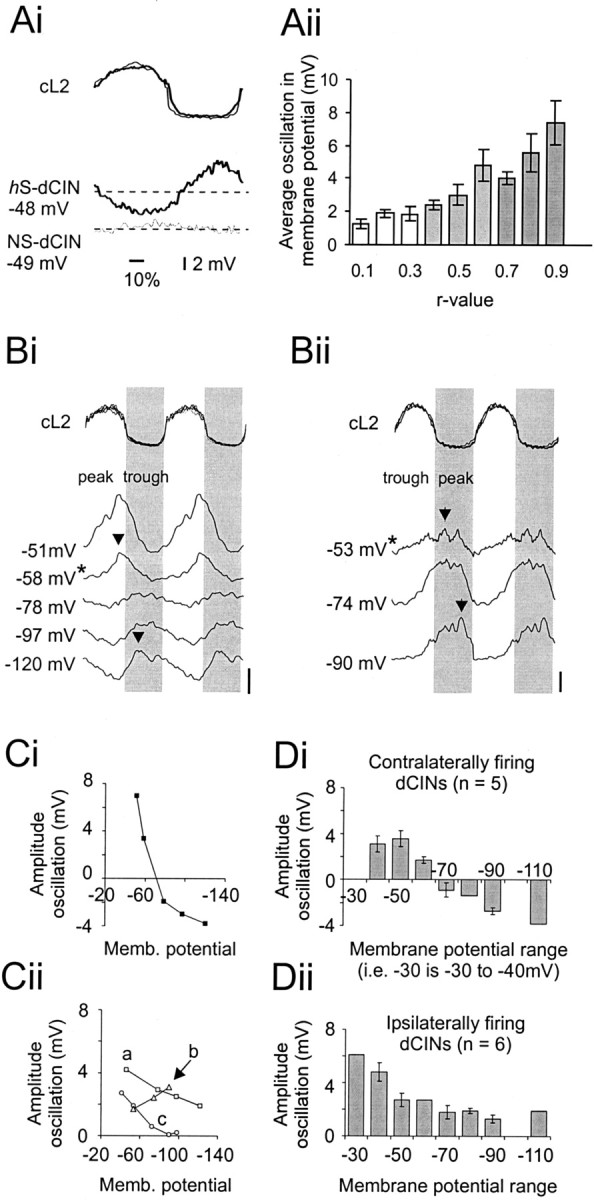
Locomotor-related membrane oscillations of dCINs reflect synaptic input. Ai, Averaged membrane oscillation of an hS-dCIN (bold line,bottom traces) and NS-dCIN (thin line,bottom traces) with respect to the normalized and rectified cL2 cycle (top panel).Aii, Relationship between r value and average membrane oscillation (at 0 bias for a minimum of 20 cL2 cycles;n = 77). B, Membrane oscillations at different holding potentials for two different dCINs (Bi,Bii). Top traces show the normalized cL2 cycle, with the gray areacorresponding to the ipsilateral L2 phase. Lower tracesshow the averaged, 10 Hz filtered intracellular recordings for 2 dCINs. Zero bias is indicated by the asterisk next to the membrane potential. The peak is indicated by the arrows.Bi, Neuron in which the phase of the peak reverses when hyperpolarized beyond the reversal potential for Cl⁻. Bii, Cell with increased oscillation amplitudes at more hyperpolarized levels.Ci, Plot (black squares) of relative amplitude of the peak–trough oscillation at varying membrane potentials for the example shown in Bi. Note the sign reversal when the cell is hyperpolarized. Cii, Example of three dCINs driven predominantly by excitation: a, mixed AMPA and NMDA components (squares);b, mainly AMPA-driven (triangles); c,mainly NMDA-driven (circles). D, Distribution of average membrane oscillation for different membrane potential (in bins of 10 mV) ranges in neurons that are driven predominantly by inhibition and firing in-phase with the contralateral root (Di) and dCINs that receive phasic excitatory input and are firing in-phase with the ipsilateral root (Dii).

It has been shown previously that lumbar motor neurons and unidentified interneurons can be driven by phasic excitation alternating with inhibition during locomotion (Raastad et al., 1997; Hochman and Schmidt, 1998). However, motor neuronal and interneuronal voltage oscillations can also be shaped by rhythmic inhibition acting on a background of tonic excitation or by rhythmic excitation alone. To determine to what extent both inhibitory and excitatory inputs are responsible for the rhythmic voltage oscillations of these interneurons, 14 dCINs (eight out-of-phase with the cL2 burst and six in-phase) were stepped to varying membrane potentials beyond the calculated reversal potential for chloride (−71 mV). Fifty percent of the dCINs tested showed clear reversal of the peak phase when hyperpolarized beyond approximately −71 mV and an increase in amplitude of oscillation when depolarized from resting potential (Fig.5Bi,Ci). This is consistent with the membrane oscillation being driven to a significant extent by rhythmic inhibitory input riding on a tonic excitatory (synaptic or intrinsic) drive. The oscillations in the remaining seven neurons did not reverse, suggesting that this population of cells received less rhythmic inhibitory drive relative to the rhythmic excitatory input (Fig. 5Bii,Cii). Two of these dCINs showed an increase in amplitude of the oscillations at more hyperpolarized levels, suggesting that the rhythmic drive is dominated by AMPA-type receptor-mediated EPSPs whose driving force is increased with hyperpolarization. Three cells showed flat membrane potentials at voltages more hyperpolarized than −70 mV, suggesting that these cells might be driven primarily by an NMDA receptor-mediated EPSP, which is inactive at these hyperpolarized voltages. The remaining two cells showed a slower decrease in amplitude with hyperpolarization, which never disappeared, suggestive of a mixed NMDA–AMPA excitatory profile (Fig. 5Cii).

We then studied whether the sign of the predominant synaptic drive onto dCINs was related to either the ipsilateral or contralateral L2 ventral root phase. This analysis (Fig. 5D) revealed that the oscillations of five of the six cells that fired in the contralateral phase (i.e., with cL2) were shaped primarily by inhibitory rhythmic inputs (Fig. 5Di). These dCINs thus receive rhythmic inhibitory input during the ipsilateral motor neuron burst. In contrast, six of eight dCINs that fired ipsilaterally received predominantly rhythmic excitatory input (Fig. 5Dii), again during the ipsilateral motor neuron burst. Thus, in both cases, the predominant synaptic input onto the dCINs occurred in-phase with the ipsilateral L2 motor pool activity.

Characterization of I_h in dCINs

Intrinsic pacemaker currents can regulate rhythmic firing in both vertebrate and invertebrate preparations (Marder and Calabrese, 1996;Kiehn et al., 1997) and could play an important role in driving the underlying membrane potential oscillations observed in rhythmic dCINs.I_h is one such pacemaker current and has been characterized previously in lumbar motor neurons of the neonatal rat spinal cord (Takahashi, 1990; Kiehn et al., 2000;Kjaerulff and Kiehn, 2001). Of 58 dCINs tested under current-clamp conditions, all but one exhibited a discernible slow depolarizing sag in voltage during square hyperpolarizing current steps and a slowly decaying rebound depolarization after the termination of the pulse (Fig. 6Ai,C). These phenomena are indicative of I_h slow activation and deactivation. The threshold for detection of the voltage sag was at potentials more negative than −70 mV (Fig.6Aii). Application of ZD 7288 (50 μm for 20 min; n = 3), a known and selective blocker of the motor neuronI_h (Kiehn et al., 2000; Kjaerulff and Kiehn, 2001) completely abolished the sag (Fig. 6B,C,arrow) and the rebound depolarization at the end of the current step (Fig. 6C, arrowhead). It also caused an increase in resting input resistance and a slight hyperpolarization of the membrane potential.

These current-clamp data were confirmed by voltage-clamp measurements of I_h in 24 dCINs. As was seen in the current-clamp data, all 24 dCINs had a detectableI_h. Figure 6Di shows typical currents activated from a holding potential of –50 mV with 1.5 sec steps between –60 and –130 mV. In parallel with the depolarizing sag voltage seen in current clamp, a very slowing activating inward current is detected at voltages below −70 mV. With increasing hyperpolarizations, the current grew in amplitude and was activated more rapidly. The maximal conductance was estimated from first-order Boltzmann fits to the current data after conversion to conductance, using V_Rev of −33 mV (Kjaerulff and Kiehn, 2001). The average maximal conductance for the 24 neurons was 0.79 ± 0.05 nS, but the distribution was not normal (Fig.6Dii); most neurons had maximal amplitudes of 0.5–0.75 nS, but a few neurons had much largerI_h amplitudes. To verify that there was no inward rectifying current in dCINs, which could complicate the analysis of our data (Kjaerulff and Kiehn, 2001),I_h in eight neurons was measured in normal Ringer's solution and then in Ringer's solution with 300 μm BaCl₂ (to block inward rectifying potassium channel currents) and 0.25 μm TTX (to block sodium currents and greatly reduce synaptic inputs). There was no significant difference in the parameters of I_h measured in these ways, and subsequent measurements were made in normal Ringer's solution.

The kinetics of activation were measured at –125 mV, at whichI_h was well developed. The curves were well fit by a single-exponential relationship and were not improved by a double-exponential fit. Analysis of the time constant, τ_Act, gave evidence for heterogeneity in theI_h between the cells (Fig.6Ei). Twenty of the 24 cells had shorter τ_Act values, ranging from 394 to 759 msec (mean value, 568 ± 24 msec; gray graph bars). However, four neurons had significantly longer τ_Act values, ranging from 1262 to 1572 msec (mean value, 1377 ± 83 msec; black graph bars;p < 0.001 when compared with the main group). At more depolarized, physiological potentials, τ_Actkinetics become considerably slower (Kjaerulff and Kiehn, 2001).

Boltzmann analysis of the voltage dependence ofI_h activation supported the hypothesis of heterogeneity of I_h in different dCINs (Fig. 6Eii). The 20 neurons with short τ_Act displayed a broad range of voltages for half-activation (V_Act), with a mean of −95.3 ± 2.3 mV. However, the four neurons with slow τ_Act were all activated at significantly more hyperpolarized voltages, with a mean V_Act of –105.3 ± 1.6 mV (range, –102 to –109 mV). This difference was again highly significant (p < 0.005). The populations of cells with fast and slow τ_Actdid not differ in the slope of the Boltzmann relationship (11.9 ± 0.75 vs 11.9 ± 1.50 mV, respectively; p > 0.99) or in the maximal conductance of the currents (0.75 ± 0.18 nS in the rapid τ_Act group vs 1.03 ± 0.39 nS in the slow τ_Act group; p > 0.5).

In conclusion, all dCINs displayed anI_h. Furthermore, voltage-clamp experiments suggested that at least two classes ofI_h are found in different dCINs. In the next analysis, we tested whetherI_h plays a role in shaping the rhythmic spike output in individual dCINs.

I_h does not contribute significantly to dCIN rhythmicity

Comparison of the I_h-evoked voltage sag recorded under current-clamp conditions betweenhS-dCINs (n = 18), S-dCINs (n = 25), and NS-dCINs (n = 15) revealed that there was no significant difference in the amplitude of sag at a holding potential of −110 mV (Fig.7Ai). In fact, theI_h-evoked voltage sag of rhythmic cells is less than that of NS-dCINs, suggesting that this current might play a different role than actively generating the underlying voltage oscillations in these neurons.

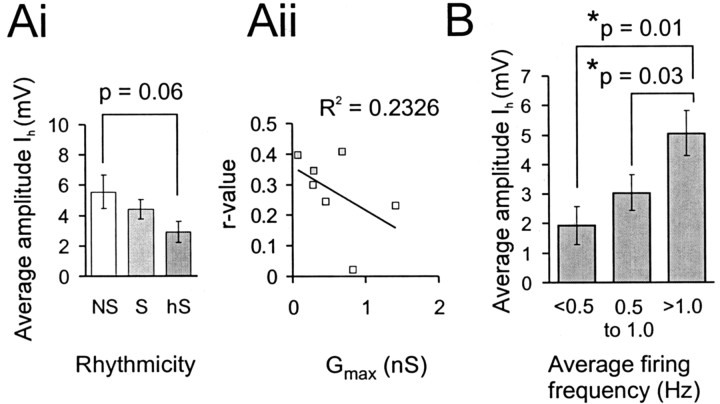
Fig. 7.

Amplitude of I_h is not related to rhythmicity but to firing frequency. Ai, Plot of the average I_h-induced sag amplitude for the three different classes of dCIN as measured under current-clamp conditions (hyperpolarizing step to −110 mV). Aii, Scatterplot showing the insignificant relationship between G_max and rhythmicity (r) in seven neurons recorded under voltage-clamp conditions. B, Distribution of the I_h-induced sag amplitude measured under current-clamp conditions for different ranges of firing frequencies in rhythmic dCINs.

To test this idea, seven neurons whoseI_h had been measured under voltage-clamp conditions were analyzed for rhythmicity in NMDA and 5HT, as described previously. Three of these neurons were significantly rhythmic in-phase with the contralateral L2 root activity (p < 0.05; S-dCINs), whereas four were not (NS-dCINs). None of these cells had a slow τ_Act, so the sample only represents the fast τ_Act group. As seen in Figure 7Aii, there was no significant relationship between the degree of rhythmicity and the maximal conductance of I_h for these cells (R² for linear fit = 0.23; p > 0.5), and the S-dCINs tended to have smaller maximal conductance than the NS-dCINs. These data are consistent with the larger series from the current-clamp data and suggest that I_h does not play a major role in determining the rhythmic firing pattern of dCINs.

I_h amplitude does not relate to rhythmicity as determined by circular statistics; however, it was of interest to determine whether this current shows any relationship to firing frequency. As demonstrated for motor neurons in this preparation (Kiehn et al., 2000), I_h has extremely slow kinetics near the resting potential and can contribute a relatively tonic depolarizing current to enhance spike activity. To test this, the I_h induced sag voltage of rhythmic dCINs was compared with their firing frequency at 0 bias during locomotion. Three arbitrary frequency ranges were defined: low (0.0–0.5 Hz; n = 7), medium (0.5–1.0 Hz;n = 18), and high firing frequency (≥1.0 Hz;n = 21). There was a significant increase in the size of the I_h-evoked sag between low- and high-frequency-firing and also between medium- and high-frequency-firing dCINs (p < 0.05) (Fig.7B). This suggests that I_h, as previously suggested, contributes a tonic depolarizing conductance at membrane potentials at which dCINs are rhythmically modulated during locomotion.

DISCUSSION

Our investigation is the first comprehensive intracellular study of putative CPG interneurons in the developing mammalian spinal cord. The caudally projecting dCINs recorded in this study are located in the rhythm-generating areas of the neonatal rat spinal cord. Within this group, most of the cells exhibited significant rhythmicity, whereas fewer were nonrhythmic. The significantly rhythmic dCINs could be additionally divided into subpopulations on the basis of whether their preferred phase of firing was with the ipsilateral or contralateral motor pools. An important finding from this classification was that the division of rhythmic dCINs based on their phase relationship is reflected in their location in the transverse ventral-dorsal plane; cells in-phase with the cL2 occupy a more dorsal location than those in-phase with iL2. An additional finding is that rhythmicity of dCINs is generated to a significant extent by synaptic input, with little or no contribution to the rhythmicity per se from the endogenous pacemaker current, I_h. Furthermore, the rhythmic activity of the two distinct phase-related subpopulations is driven by different sources of synaptic input that appear to be temporally correlated to the synaptic input driving the ipsilateral motor neurons.

The ventromedial area: a kernel for left–right coordination

The neurons presented in this study are located in the ventromedial area of lumbar segments 2 and 3, an area known from both activity-dependent labeling studies and microlesion experiments to be important for rhythmogenesis (for review, see Kiehn and Kjaerulff, 1998). Thirty-four percent of the neurons studied in this area had contralateral axons descending at least to L4–L5. We know from previous labeling studies that pure ascending and descending CINs constitute ∼30% each of the total CINs in the ventromedial region, whereas bifurcating (with both ascending and descending axons) and intrasegmental CINs constitute ∼20% each (Eide et al., 1999; Stokke et al., 2002). Thus, dCINs and adCINs with caudally projecting axons represent ∼50% of the total number of CINs in the ventromedial area. Supposing that we record with equal probability from all neurons in the ventromedial area (Kiehn et al., 1996; Raastad et al., 1998), ∼68% are thus likely to be CINs in this area of the cord. This remarkably high number, and the fact that almost three-quarters of the recorded dCINs were rhythmically active, raises the possibility that the ventromedial area represents a kernel of neurons fundamental for the coordination of rhythmic left–right hindlimb activity in the neonatal rat. In the discussion below, we will focus on the rhythmically active dCINs, because it is not easy to define a role for the 27% of nonrhythmic NS-dCINs.

Comparison with rhythmic CIN populations in other vertebrates

Although there is a wealth of information on the overall structure, our understanding of the mammalian spinal CPGs at the cellular and network levels is still superficial (Kiehn et al., 1997). Using afferent stimulation to characterize CPG neurons, some progress has been made in defining locomotor circuits in the spinal cord of the decerebrated or spinalized cat in vivo (for review, seeHultborn et al., 1998). However, this characterization has proved to be difficult, and so far no CPG neurons have been defined with certainty in the cat. In the present study, we have therefore focused on a readily identifiable group of cells. Using an in vitropreparation, the electrophysiological properties of the neurons could be studied in detail.

The limited understanding of locomotor CPG networks in the mammalian spinal cord stands in contrast to the considerable amount already known about the locomotor CPGs of a number of aquatic vertebrates, notably those of the Xenopus tadpole and lamprey. In particular, in these preparations, the CINs play an important functional role, using reciprocal inhibition to maintain the alternating phase relationship between bilateral motor pools (Soffe et al., 1984; Dale, 1985; Buchanan 1999) (for review, see Buchanan and McPherson, 1995; Buchanan, 1996;Roberts, 2000). In both animals, CINs fire either a single or only a few spikes per locomotor cycle related to very specific phases (Soffe et al., 1984; Dale, 1985; Buchanan and Kasicki, 1995). This is in contrast to mammalian dCINs. Preliminary studies in the cat (Carr et al., 1994; Matsuyama and Mori, 1998; Huang et al., 2000) and the present study clearly show that rhythmic CINs fire multiple spikes during locomotor-like activity. In addition, we have shown here that the dCINs fire over the complete range of phases in the cycle. Clearly the CIN system in mammals is more complex than reported previously in lower vertebrates.

Putative functional role of dCINs

We can begin to speculate on the roles of the rhythmically active dCINs on the basis of their preferred phase of firing. During locomotion, ipsilateral iL2 flexor bursts are in-phase with contralateral cL4–cL5 extensor bursts to promote alternating movement of the limbs (Kiehn and Kjaerulff, 1996). Figure8 shows that dCINs that fire predominantly in-phase with iL2 (bins 6–10; 0.5–1.0 on the circular plot) should excite cL4–L5 extensor MNs, whereas dCINs that fire in-phase with the cL2 (bins 1–5; 0.0–0.5 on the circular plots) should inhibit cL4–L5 extensor MNs. In this way, the iL2 flexor and cL4–L5 extensor activity is bound together into a functional unit by both excitatory and inhibitory activity in the dCINs. It is known that the L2–L3 segment also contains some extensor-related MNs, whereas L4–L5 also contains some flexor-related MNs (Nicolopoulos-Stournaras and Iles, 1983; Kiehn and Kjaerulff, 1996, and references therein). This would mean that some dCINs that fire in-phase with iL2 inhibit cL4–L5 flexor motor neurons (which fire out-of-phase with the iL2 flexor MNs) and that some dCINs that fire in-phase with the cL2 excite L4–L5 flexor MNs. In this way, the iL2 extensor and the cL4–L5 flexor activity will be bound together. Future experiments looking at the actual synaptic effects of the different dCIN classes on L4–L5 motor neurons will test these predictions.

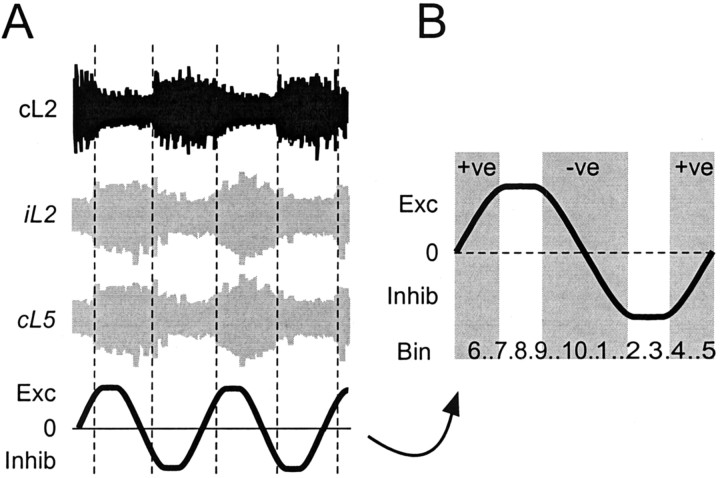
Fig. 8.

Hypothetical model for the role of rhythmic dCINs during locomotor-like activity. A, The phase relationship of dCINs can be related to not only the recorded cL2 activity (black trace) but also to the likely activity of the ipsilateral motor pool (iL2; top gray trace) and target MNs (cL5; bottom gray trace). The expected role of the L2–L5 dCINs is shown in thebottom trace and expanded in B.Exc, Phase of predominantly crossed iL2 to cL5 excitatory information; Inhib, phase of mainly inhibitory information. The gradient of the line, positive (+ve), negative (−ve), or 0, reflects the prevalent drive provided by CINs. Numbers at thebottom reflect the bins for the average firing frequency histograms such as those in Figure 3Bii–Dii.

In this context, the ventral-dorsal distribution of ipsilaterally and contralaterally firing dCINs becomes important, showing that the dCINs can be anatomically separated along the dorsal-ventral plane on the basis of their function. Our arbitrary binning of neurons into depths of 100 μm (Fig. 4B) is unlikely to reflect the true patterns. However, it allows us to specifically record from either ipsilaterally or contralaterally firing dCINs with a reasonable degree of accuracy depending on the depth of the electrode. It remains to be seen whether this organization is true for other commissural interneuron subtypes located in the ventral horn.

The preferred phase of firing of most dCINs was in-phase with the iL2 in bins 7 and 8 (Fig. 4B). One can envisage a role for the broadly tuned but rhythmic firing of these “midphase” cells to stabilize the cL4–L5 extensor MN bursts and to define their burst duration. dCINs firing in the midphase of cL2 could have a similar effect on the bursts in cL4–L5 flexor MNs. Such a stabilizing role is in contrast to that of the “transition” cells firing at the cL2–iL2 and iL2–cL2 transitions (Fig. 3B). These cells might be specialized to determine the exact timing of switching between extensor and flexor phases, as suggested previously (Edgerton et al., 1976; Wheatley et al., 1994; Tresch and Kiehn 1999). Of course this is a simplistic view, and our data show that dCINs are active in all phases of the locomotor cycle. Such a broad distribution of preferred phases of firing has also been found in previous studies of unidentified interneurons in the ventromedial area (Tresch and Kiehn, 1999; Raastad and Kiehn, 2000), suggesting that the locomotion phase is determined by population coding (Tresch and Kiehn, 2000).

Factors influencing rhythmic discharge of CPG interneurons

Evidence from the experiments in which the cells were held at various holding potentials indicates that the rhythmicity is shaped to a significant extent by synaptic input, either predominantly excitation in the case of ipsilaterally firing dCINs or predominantly inhibition in contralaterally firing cells. It is unlikely that these excitatory and inhibitory inputs operate in complete isolation; rather, they are likely to exist in varying proportions (Raastad et al., 1997; Hochman and Schmidt, 1998). The fact that many contralaterally firing dCINs receive a predominantly inhibitory drive during the ipsilateral motor neuron burst suggests a level of complexity in the timing of excitatory and inhibitory inputs that is not seen in the lamprey orXenopus tadpole spinal cords, where inhibitory input is only seen during the contralateral motor neuron bursts.

Because the pacemaker current (I_h) is present in nearly all dCINs, we sought to determine whether this current was involved in generating rhythmic activity. There was heterogeneity in the voltage and kinetic parameters ofI_h in different dCINs. This may represent differential expression, or coexpression, of the four genes (HCN1–4) that encode I_h with somewhat different parameters (Santoro et al., 2000; Chen et al., 2001).I_h in dCINs is activated very slowly compared with neonatal rat spinal motor neurons, which activate in a biexponential manner (Kjaerulff and Kiehn, 2001). The fact that there was no difference between the amplitude ofI_h in rhythmic active and nonrhythmic cells suggests that I_h does not play a major role in shaping membrane oscillations in dCINs. The extremely slow time constant for activation even at very hyperpolarized voltages would also preclude such a role. However, there was a strong positive correlation between I_h amplitude and spike frequency in dCINs. It therefore appears that for rhythmic dCINs,I_h most likely acts as a tonic depolarizing leak conductance to enhance the firing frequency, a role similar to that previously proposed for lumbar neonatal rat motor neurons (Kiehn et al., 2000).

Conclusions

Our results reveal a high degree of organization in the mammalian hindlimb CPG. The ability to target specific interneuronal subpopulations, even at the general level of phasing with ipsilateral or contralateral L2 flexor-related activity, is a considerable step forward in determining the overall function of the locomotor network. Further analysis of synaptic drive and endogenous properties is likely to reveal subtle differences between subpopulations, reflecting their differing inputs and roles in the CPG. Developing such knowledge is fundamental to our understanding of locomotion and neural circuits in general.