Abstract
Two different families of Na+/Ca2+ exchangers, K+-independent NCX and K+-dependent NCKX, are known. Exploiting the outward K+ gradient, NCKX is able to extrude Ca2+ more efficiently than NCX, even when the Na+ gradient is reduced. The NCKX, which was originally thought to be limited to the retinal photoreceptor, was shown recently to be widely distributed in the brain. We investigated the contribution of Na+/Ca2+exchange to Ca2+ clearance mechanisms in neurohypophysial (NHP) axon terminals, using patch-clamp and microfluorometry techniques. In the presence of internal K+, Ca2+ decay was significantly slowed by the removal of external Na+, indicative of the role of Na+/Ca2+ exchange. As internal [K+] was decreased, Ca2+ decay rate and its dependence on Na+ were greatly attenuated. In the absence of internal K+, Ca2+ decay rate was little affected by Na+ removal. Quantitative analysis using Ca2+ decay rate constant indicated that >60% of Ca2+ extrusion is mediated by Na+/Ca2+ exchange when peak [Ca2+] level is higher than 500 nm, and ∼90% of Na+/Ca2+ exchange activity is K+ dependent. In situhybridization confirmed the expression of NCKX2 transcripts in the supraoptic nucleus in which soma of NHP axon terminals are located. To our knowledge, this is the first report to show the significant role of K+-dependent Na+/Ca2+ exchange in neuronal cells other than photoreceptors. Considering that axon terminals are subject to an invasion by high-frequency Na+ spikes, which may lower Na+ gradients, the presence of NCKX may have a functional significance in intracellular Ca2+ regulation.
Keywords: neurohypophysis, axon terminal, Ca2+transient, Na+/Ca2+ exchange, calcium clearance, NCKX
Calcium is an essential mediator that couples an invasion of action potentials (APs) with secretory event in nerve terminals (Lim et al., 1990). Ca2+ clearance mechanisms in combination with Ca2+ influx and cytosolic Ca2+ buffers are key factors in the shaping of Ca2+ transients (Lee et al., 2000). Although Na+/Ca2+exchange and Ca2+-ATPase are thought to be the two major Ca2+ clearance mechanisms in axon terminals (Gill et al., 1981), our knowledge of this is mainly based on flux studies in synaptosomes derived from the whole brain (Fontana et al., 1995). Because synaptosomes are a mixture of axon terminals in which different kinds of Ca2+clearance mechanisms are expressed, studies in single axon terminals are required to understand the role of an individual mechanism in Ca2+ dynamics. Isolated neurohypophysial (NHP) axon terminals, which were first prepared by Cazalis et al. (1987), can provide a useful model system for this purpose.
Despite the suggestion that Na+/Ca2+exchange is important as a Ca2+ clearance mechanism in synaptosomal preparation, similar study on single axon terminals is very limited (Stuenkel, 1994). The role of Na+/Ca2+exchange in Ca2+ clearance mechanism was best understood in heart and in rod cells. The rod type exchanger is distinguished from the cardiac type by its K+ dependence. Exploiting the outward K+ gradient, K+-dependent exchanger was thought to be able to extrude Ca2+ with relatively smaller Na+ gradients (Lagnado and McNaughton, 1989).
Molecular cloning studies have showed that the two types of exchangers are encoded by different genes: cardiac type by NCX and rod cell type by NCKX. Although NCX was known to be distributed abundantly in almost every tissue, NCKX was originally thought to be limited to the retinal photoreceptor. Recently, however, a second and a third type of K+-dependent exchanger (NCKX2 and NCKX3) were identified in many brain regions (Tsoi et al., 1998; Kraev et al., 2001). In contrast to the recent progress made in the understanding of K+-dependent Na+/Ca2+exchangers at the molecular level, little is known about their actual function as a Ca2+ clearance mechanism in real physiological systems other than the photoreceptor.
Here, we present clear evidence that shows the presence and the functional significance of intracellular K+-dependent Na+/Ca2+exchangers in the axon terminals of the neurohypophysis: >60% of Ca2+ extrusion is mediated by Na+/Ca2+exchangers, and ∼90% of Na+/Ca2+exchanger activity is K+ dependent.
MATERIALS AND METHODS
Preparation of isolated nerve endings from the neurohypophysis. Axon terminals were isolated from the neurohypophyses of adult male rats using previously described methods with small modification (Cazalis et al., 1987). Pituitary glands were isolated from male Sprague Dawley rats (11–12 weeks old; 325 ± 25 gm) after killing the animals by CO2asphyxiation and decapitation. Under the stereomicroscope, neural lobes were carefully dissected free of the anterior lobe and the pars intermedia, in bicarbonate buffered solution that had been well aerated with 95% O2–5% CO2 mixed gas. A dissected neural lobe was cut into 9 or 12 pieces with a razor blade in solution containing the following (in mm): 290 sucrose, 10 HEPES, 10 glucose, and 0.01 K-EGTA. Small pieces of the neural lobe were washed twice with HEPES-buffered F-10 culture media (Invitrogen, Carlsbad, CA) and kept in this solution at room temperature until next use. Just before electrophysiological recording, a piece of neural lobe was transferred to a small recording chamber on the stage of an inverted microscope, in which the neural lobe piece was triturated in 50–60 μl of culture medium with fire-polished pipettes (300–500 μm in diameter).
After the isolated nerve endings had settled down on the bottom of the recording chamber, they appeared rounder and more homogenous than pars intermedia cells. They were variable in diameters from 5 to 20 μm. Nerve endings whose diameters are between 12 and 18 μm were chosen for study.
In early experiments, homogenates were incubated in culture medium containing Hoechst 33342 (10 μg/ml) for 30 min at room temperature to differentiate between nerve terminals and melanotrophs and other nuclei-containing cells. Fluorescence microscopy showed that nerve endings were not stained with the Hoechst dye, whereas nuclei of melanotrophs were strongly stained (Fig.1). After becoming accustomed to the morphological characteristics of the nerve endings, staining was not routinely performed. Moreover, we also verified that (1) the nerve endings had neuronal-like rapidly inactivating TTX-sensitive sodium currents, and (2) they were capable of exocytosis, as determined by observing capacitance increments during depolarizing pulses from −80 to 0 mV, using an EPC-9 lock-in module (Lambrecht/Pfalz, Germany; data not shown).
Fig. 1.
Photomicrographs of a putative axon terminal (A) and melanotrophs (B) stained with Hoechst 33342. A-1 and B-1were taken while the cells were simultaneously illuminated by transmitted light from the halogen lamp and by UV excitation light (370 ± 10 nm) for epifluorescence. A-2 andB-2 are corresponding epifluorescence images. Scale bar, 10 μm.
Electrophysiological recordings. Conventional whole-cell patch-clamp technique was used to evoke calcium current from single axon terminals. Patch pipettes with a resistance of 5–6 MΩ were constructed from capillary glass, fire polished, and filled with pipette solutions of the following compositions. The K-pipette solution contained the following (in mm): 110 K-gluconate, 30 KCl, 15 HEPES, 4 MgATP, and 4 Na-ascorbate with the pH adjusted to 7.3 with KOH. To make theN-methyl-d-glucamine chloride (NMG) pipette solution, K+ in the K pipette solution was replaced with equimolar NMG+. The bath solution for the control experiments contained the following (in mm): 143 NaCl, 5.4 KCl, 0.5 MgCl2, 1.8 CaCl2, 5 HEPES, and 10 glucose, pH 7.4 (298 ± 2 mOsm). In those experiments in which the effect of external Na+ was investigated, the [NaCl] was reduced to 20 mmby substituting 120 mm NaCl with LiCl or NMG-Cl.
Currents were recorded using an EPC-9 amplifier. The maintenance of stable and low basal [Ca2+]i values in the patch-clamped nerve terminals required high resistance seals (>10 GΩ) and very low steady leakage current. Recordings were terminated when the leakage current exceeded 20 pA. Experiments were performed at 35 ± 1°C.
Cytosolic Ca2+ measurement.Before cytosolic Ca2+ measurements were made, the cells were either loaded with fura-2 (pentapotassium salt; Molecular Probes, Eugene, OR) via patch electrodes or preincubated in culture medium containing 1 μmfura-2 AM for 10 min. For fluorescence excitation, we used a monochromator (xenon lamp based; Polychrome-IV; T.I.L.L. Photonics, Martinsried, Germany), which provided a band (±10 nm) of monochromatic light. The light source was coupled to the epi-illumination port of an inverted microscope (Olympus IX70; Olympus Optical, Tokyo, Japan) via a quartz light guide and a UV condenser. Microfluorometry was performed with a 40× water immersion objective (numerical aperture of 1.15; UAPO 40×W/340; Olympus Optical) and a photodiode (T.I.L.L. Photonics). The monochromator was controlled by a CED1401 (Cambridge Electronics Design, Cambridge UK) and a personal computer running a custom-made software. A dichroic mirror (DC400LP; AHF Analysentechnik, Tubingen, Germany) and a long-pass emission filter (515LP; AHF Analysentechnik) were used for separating emission light from residual scattered excitation light.
Calibration parameters were determined using the in vivocalibration method (Neher, 1989). Briefly,Rmin was determined by loading nerve terminals with the standard internal solutions plus 10 mm K-EGTA. Axon terminals could not endure internal dialysis with high CaCl2 (5 mm). Therefore, we measured theRmax value from the pipette solution containing 5 mm CaCl2 in vitro. The intermediate fluorescence ratio (Rint) was measured using cells loaded with an intracellular solution containing 2.2 mmK5-BAPTA and 2.8 mmCa-BAPTA. The effective dissociation constant (Keff) of fura was calculated using the following equation:
| Equation 1 |
where [Ca2+] was entered as 288 nm (assuming a dissociation constant (Kd) of BAPTA of 222 nm at pH 7.2). EstimatedRmin,Rmax, andKeff (in μm) values were typically 0.27, 3.95, and 0.93, respectively.
We restricted the fluorescence detection area by adjusting the rectangular aperture stop of the ViewFinder (T.I.L.L Photonics) to the nerve terminal chosen for patch-clamp recording. The background fluorescence at 340 nm (Fb,340) and 380 nm (Fb,340) was measured in cell-attached mode, and Fb values were subtracted from the fluorescence at each corresponding wavelength measured in whole-cell mode. Fluorescence values after subtraction were regarded to be the relevant cellular fura-2 fluorescence values.
Fluorescence at the isosbestic wavelength (Fiso) started to increase and reached a steady state typically 3–5 min after the establishment of the whole-cell mode. When Fiso values became steady, Ca2+ transients were recorded by detecting fluorescence in response to alternative illumination of the cell with 340 and 380 nm at 10 Hz. During off-line analysis, ratios (r =F340/F380) were converted to [Ca2+] values using Equation 1.
Calculation of Ca2+ decay rate constant from a bi-exponential Ca2+decay. When a Ca2+ extrusion process follows the Michaelis–Menten equation, the extrusion rate (dCa(t)/dt) is described as follows:
| Equation 2 |
where ΔCa(t) is the magnitude of Ca2+ excursion from the resting level. When ΔCa(t) is far less thanKm,dCa(t)/dt could be linearized as follows:
| Equation 3 |
The similar linear Ca2+ extrusion mechanism was assumed in the “single compartment model” (Helmchen et al., 1996; Lee et al., 2000). Solving Equation 3 for Ca(t) under the initial condition of the resting [Ca2+] level (A0) and the peak amplitude of Ca2+ transient (A1) yields the following:
| Equation 4 |
or
| Equation 5 |
Here, the Ca2+ decay rate constant, γ, represents the efficiency of the Ca2+extrusion process, independent of the magnitude of Ca2+ excursion level (Δ[Ca2+]). From the decay phase of a Ca2+ transient recorded experimentally, γ could also be extracted by dividing its time derivative by ΔCa(t) according to Equation 3. In other words,
| Equation 6 |
Most of Ca2+ transients in NHP axon terminals were better described with a bi-exponential curve rather than a mono-exponential curve (see Fig. 2Aa) as follows:
| Equation 7 |
The single compartment model with linear approximation of Ca2+ extrusion mechanism is not directly applicable to a bi-exponential Ca2+transient, because the “Ca2+ decay rate constant” is not a constant over its decay phase. Nevertheless, Ca2+ decay rate constant (γ) at a given Δ[Ca2+]i level can be obtained using Equation 6, assuming that γ is constant within a narrow range of Δ[Ca2+]i. The γ estimated in this way can be regarded as an “instantaneous Ca2+ decay rate constant.” The γ at the start of a bi-exponential Ca2+ decay (γt=0) can be calculated as follows:
Fig. 2.
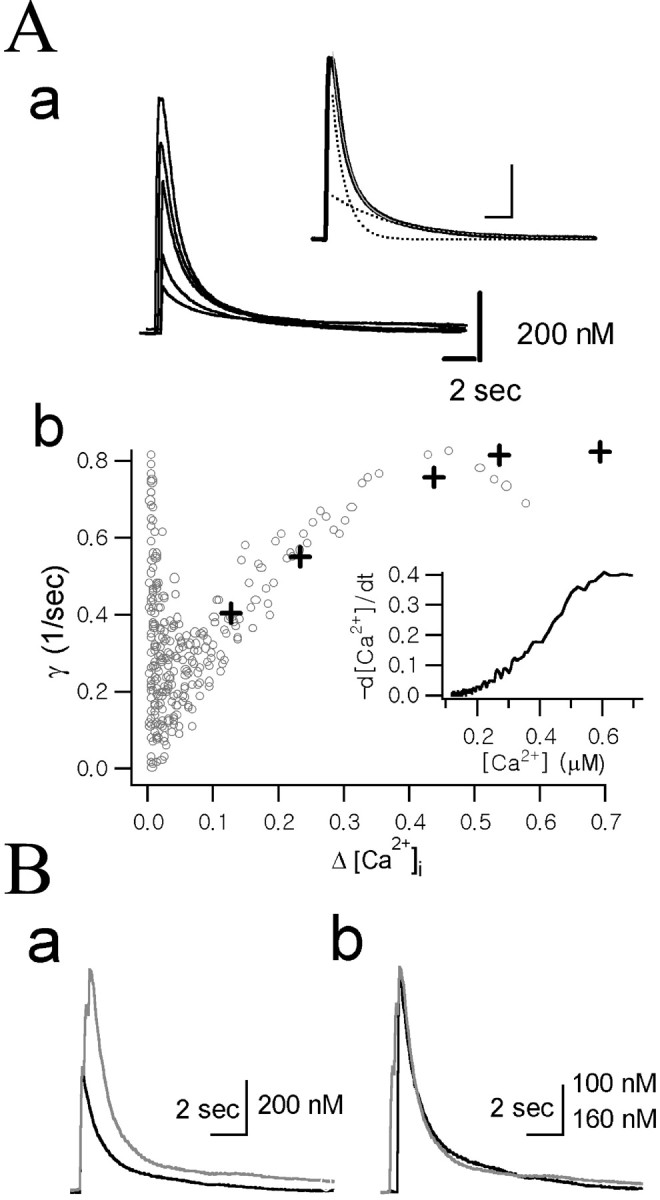
Dependence of the Ca2+ decay rate constants (γ) on Δ[Ca2+].Aa, A set of Ca2+ transients evoked by depolarization pulses of various durations (10, 20, 50, 100, and 200 msec) recorded in the same axon terminal. Inset, The decay phase of the Ca2+ transient evoked by 200 msec depolarization pulse was fitted with the following bi-exponential equation (thin gray line, inset): 0.17 μm · exp (−0.20t) + 0.56 μm · exp (−1.01t). Fast and slow components of the bi-exponential fit are shown (dotted lines, inset). Calibration: 2 sec, 200 nm. Ab, The time derivative (−d[Ca2+]/dt) of the decay phase of the Ca2+ transient evoked by 200 msec depolarization (inset) was divided by Δ[Ca2+](t) to obtain γ (according to Eq. 6) and plotted as a function of Δ[Ca2+] (gray open circles). The γt=0 values were calculated according to Equation 10 from bi-exponential fits to the five Ca2+ transients shown in Aa. The following values for fitting parameters (A1, γ1,A2, and γ2 in Eq. 7) were used: 0.034, 0.043, 0.087, and 0.547 for 10 msec pulse; 0.094, 0.149, 0.131, and 0.839 for 20 msec pulse; 0.154, 0.211, 0.275, and 1.063 for 50 msec pulse; 0.149, 0.226, 0.404, and 1.032 for 100 msec pulse; and 0.169, 0.200, 0.556, and 1.013 for 200 msec pulse. The γt=0 values obtained from these fitting parameters were plotted as a function of the peak Δ[Ca2+] (crosses).B, Comparison of the Ca2+ decay rate between two Ca2+ transients with different amplitudes. Ba, Two Ca2+ transients recorded from the same cell were superimposed. One trace was evoked by a single depolarizing pulse of 100 msec duration (black) and the other one by three depolarizing pulses of the same duration, 200 msec apart (gray). Bb, The two [Ca2+] traces fromBa were scaled to the same maximum, and the black trace was right-shifted along the time axis to superimpose the two decay phases for direct comparison of the kinetics of the decay phases. Vertical calibration bar: black trace, 100 nm;gray trace, 160 nm.
Combining Equation 6 with the following two equations
| Equation 8 |
| Equation 9 |
yields
| Equation 10 |
When γ1 and γ2represent the fast and slow rate constants, respectively, the instantaneous rate constant would start from γt=0, decrease as the [Ca2+]i level decays, and finally converge to γ2 (see Fig.2Ab).
Data analysis and statistics. The decay phases of the Ca2+ transients evoked by single or dual depolarizing pulses were fitted with exponential equations using IgorPro (version 4.1; WaveMetrics, Lake Oswego, OR). Ca2+ decay rate constants obtained from Ca2+ transients in response to a single pulse were not statistically different from those in response to dual pulses protocol, when other conditions were constant. Thus, data obtained from a single pulse protocol and those from a dual pulse protocol were pooled for statistical analysis. Ca2+ decay rate constants were compared statistically using the Student's t test. Statistical data are presented as means ± SD, and n indicates the number of axon terminals studied. Statistical significance was accepted for p values < 0.01.
Reverse transcription-PCR for mRNA of NCKX isoforms. The supraoptic nucleus (SON) region of the brain slice (300 μm thick) was punched out under the stereomicroscope using a custom-made needle (600 μm in diameter). Total RNA was prepared from the tissue homogenate using RNeasy Mini Kit (Quiagen, Mississauga, Ontario, Canada) according to the protocol of the supplier. cDNA was synthesized with a Superscript One-Step RT-PCR System (Invitrogen), following the protocol of the supplier. A programmable thermal cycler (Techene, Mancioux, France) was used for PCR reactions. The primers were used as follows: sense primer, 5′-CACCT CTGAG GAGCA AGTGAC-3′ and antisense primer, 5′-GAAGT AGGTG CCTCT GGGAC-3′ for NCKX1; sense primer, 5′-CTCCA CAAGA TTGCC AAGAA G-3′ and antisense primer, 5′-TCCTC ACTAA TGCCG ATTGTC-3′ for NCKX2; sense primer, 5′-GGCAT ATACC AATGG GGAATC-3′ and antisense primer, 3′-GGAAG CAAAC GTCAC CATAAA-3′ for NCKX3. The primer set for NCKX2 and that for NCKX3 are expected to give PCR products with the size of 466 and 360 bp, respectively. PCR consisted of an initial denaturation cycle at 95°C for 5 min, and it was followed by 40 cycles consisting of annealing at 55°C for 1 min, elongation at 72°C for 1 min, and denaturation at 95°C for 1 min. An additional cycle at 72°C for 10 min finished the amplification process. Amplified PCR products were separated by 1.8% agarose gel electrophoresis and visualized by ethidium bromide staining. The labeled bands were sequenced, and their nucleotide homology with known sequences were identified.
Synthesis of riboprobes for NCKX2 and NCKX3. The PCR product of NCKX synthesized with the primers mentioned above was used as a cDNA template for NCKX3. To make the size of riboprobes for NCKX2 similar to that for NCKX3, reverse transcription (RT)-PCR for NCKX2 transcripts were performed with the following primers: sense, 5′-CTCCA CAAGA TTGCC AAGAAG-3′; antisense, 5′-GGGTA AGGTG ATCCA GAGAGG-3′. The size of PCR products from this primer set is expected to be 332 bp. The PCR products were inserted into a TA cloning site in a pCR2.1-TOPO vector containing the reverse sequence of T7 promoter at the 3′-flank region of the cloning site (Invitrogen, Carlsbad, CA). The orientation of inserted cDNAs was identified by PCR using the specific primers of the NCKXs and the T7 promoter. The plasmids containing the cDNAs of the NCKXs were purified and then linearized with BamHI. Riboprobes were synthesized from linearized NCKX2 and NCXK3 cDNA templates by using T7 RNA polymerase (Promega, Madison, WI) and digoxigenin-11-UTP (Boehringer Mannheim, Mannheim, Germany).
In situ hybridization. Adult male Sprague Dawley rats (10–12 weeks old; 300–350 gm) were perfused transcardially with 4% paraformaldehyde in PBS, and their brains were removed and embedded in paraffin. Sections of 10 μm cut in the coronal plane were collected onto slides. In situ hybridizations for NCKX2 and NCKX3 were performed essentially according to published accounts (Tsoi et al., 1998; Kraev et al., 2001), using digoxigenin-labeled antisense and sense riboprobes. Hybridized probe was detected using alkaline phosphatase-coupled anti-digoxigenin antibody (Boehringer Mannheim) diluted at the ratio of 1:1000, followed by incubation with 4-nitroblue tetrazolium chloride/5-bromo-4-chloro-3-indolyl-phophate substrate solution (Boehringer Mannheim).
RESULTS
We combined a patch-clamp technique and fura-2 fluorescence microfluorometry to measure the Ca2+ decay rate in response to a short depolarizing pulse in isolated NHP nerve endings. Because Ca2+ transients are affected by the cytosolic concentration of Ca2+ indicator dye (Lee et al., 2000), we waited until fluorescence at the isosbestic wavelength reached a steady state after establishing the whole-cell mode with a pipette solution containing 50 μm fura-2. Resting [Ca2+]i levels were typically ∼100 nm.
Dependence of Ca2+ decay rate constant on Δ[Ca2+]i
The transient rise in Ca2+ induced by a depolarizing pulse underwent a spontaneous decay that is considered to be contributed by Ca2+ clearance mechanisms. To test whether the Ca2+extrusion power of the cell, which is represented by γ, is dependent on Ca2+ excursion level (Δ[Ca2+]), a set of Ca2+ transients were evoked by depolarization pulses of various durations (10, 20, 50, 100, and 200 msec) (Fig.2Aa) in the same axon terminal. The instantaneous Ca2+ decay rate (γ) at a given Δ[Ca2+] level was obtained in two different ways. First, values of γt=0 at various peak Δ[Ca2+] levels were obtained from bi-exponential fits to these five Ca2+ transients using Equation 10 and were plotted in Figure 2Ab (crosses) as a function of the peak Δ[Ca2+]. Second, instantaneous γ values at various Δ[Ca2+] were calculated according to Equation 6 from a decay phase of a single Ca2+ transient. For this calculation, the time derivatives (−dCa(t)/dt) of the decay phase of the Ca2+ transient evoked by 200 msec depolarization were used (Fig. 2Ab,inset). Instantaneous γ values were calculated from the −dCa(t)/dt divided by ΔCa(t) and plotted against Δ[Ca2+] in Figure2Ab (open circles). Figure2Ab shows that the γ values estimated in the two different ways are well superimposed on each other, indicating that γt=0 at each peak of Ca2+ transients is equal to the instantaneous γ at the corresponding Δ[Ca2+] levels. The instantaneous γ values, however, were deviated from the γt=0 values near the peak of the Ca2+ transient. Spatial non-uniformity might be one of the cause of the deviation. Imaging of [Ca2+]i change in a single chromaffin cell (diameter of 15 μm) revealed that it took ∼200 msec to achieve spatial uniformity (Neher and Augustine, 1992). Before spatial uniformity is achieved, the global [Ca2+] measured with photodiode might be lower than submembrane [Ca2+], resulting in underestimation of dCa(t)/dt. From these results, it can be suggested that γt=0 is the best parameter for the estimation of the Ca2+ extrusion power near the peak of the Ca2+ transient, whereas instantaneous γ values obtained from a single Ca2+ transient is useful for analyzing the Δ[Ca2+] dependence of a Ca2+ extrusion system.
As shown in Figure 2Ab, γ increased steeply as Δ[Ca2+] increased at the lower range, but at the range of [Ca2+] higher than 500 nm, γ remains relatively constant. The increase in γ could be interpreted as a transition of the major Ca2+ clearance mechanism from a low-capacity and high-affinity mechanism to a high-capacity and low-affinity mechanism. The relative independence of γ in a higher Δ[Ca2+] range was further tested in Figure 2B. The smaller Ca2+ trace (black trace) in Figure 2Ba was evoked by a single depolarizing pulse of 100 msec duration and the other one (gray trace) by triple depolarizing pulses of the same duration, 200 msec apart (Fig. 2Bb). Despite the big difference between the initial amplitudes, the initial decay phases of the two Ca2+ transients were almost completely superimposed when each Ca2+ transient was scaled to the same peak amplitude (Fig. 2B). This result indicates that γt=0 is constant over a wide range of peak Δ[Ca2+]i in which the high-capacity and low-affinity Ca2+ extrusion mechanism plays a dominant role in the Ca2+ clearance. Therefore, in the subsequent experiments, we regarded γt=0 as an estimate for the maximum Ca2+ extrusion power of the cell when the peak amplitude of a Ca2+ transient is higher than 500 nm.
To induce a Ca2+ transient whose peak amplitude is higher than 500 nm, a depolarizing pulse of 100 msec duration from −60 to 0 mV were applied to axon terminals. The mean value for peak Δ[Ca2+]i was 1.03 ± 0.41 μm (n = 39). When the amplitude of the Ca2+ transient induced by a single pulse was not within this range, two depolarizing pulses of 100 msec duration were applied 200 msec apart. To minimize variance in Ca2+ decay rate attributable to surface-to-volume ratio (Eilers et al., 1995), we selected nerve endings with diameters between 12 and 18 μm for the study. No correlation was found between Ca2+ decay rates and the diameters of axon terminals that were used in this study.
Na+/Ca2+ exchange is a major Ca2+ extrusion mechanism in NHP nerve terminals
The effect of Na+ removal on the Ca2+ decay phase was examined in Figure3A. With a K+-rich pipette solution and control bath solution, most of the Ca2+ decays were well fitted with bi-exponential curves. The fast and slow time constants were 0.65 ± 0.12 sec (n = 6) and 9.8 ± 6.2 sec (n = 6), respectively. When external [Na+] was reduced to 20 mm by the iso-osmotic replacement of Na+ with Li+, the decay phase was greatly slowed down. The fast and slow time constants were 1.88 ± 0.23 sec (n = 5) and 9.08 ± 2.23 sec (n = 5), respectively. Similar results were obtained when NMG+ was used instead of Li+ for the replacement of external Na+ (Fig.4B). These results indicate that the Ca2+ removal process in neurohypophysis axon terminals is dependent on external Na+. Considering that neither Li+ nor NMG+can substitute for Na+ in the Na+/Ca2+exchange reaction, Na+/Ca2+exchange is the most plausible mechanism. To test whether the contribution of Na+/Ca2+exchange to the Ca2+ decay rate is dependent on the cytosolic [Ca2+] level, time derivatives (−d[Ca2+]i/dt) of the decay phases of the two Ca2+ traces shown in Figure 3A were plotted as a function of Δ[Ca2+] levels (Fig. 3A,inset). From this plot, instantaneous γ were calculated using Equation 6 and plotted as a function of Δ[Ca2+] in Figure 3B. The difference between the polynomial fit (fNa) to the γ values under control conditions and that (fLi) under low Na+ conditions was considered to be the contribution made by Na+/Ca2+exchange. The relative contribution made by Na+/Ca2+exchange (REXC) to the entire Ca2+ removal mechanism was calculated according to (fNa −fLi)/fNaand plotted as a function of Δ[Ca2+]i (Fig.3B, gray open circles). At low Δ[Ca2+], theREXC was almost linearly proportional to Δ[Ca2+], but at higher Δ[Ca2+], it became much less dependent on Δ[Ca2+], approaching its maximal value (66.2%). Analysis of five axon terminals revealed thatREXC values were fairly constant over the range in which Δ[Ca2+] was higher than 500 nm. The mean values of maximalREXC and the Δ[Ca2+] at half-maximal value ofREXC were 63.3 ± 7.5% and 102.2 ± 44 nm, respectively. The dependence of REXC on Δ[Ca2+] is consistent with the present knowledge that the Na+/Ca2+exchange contributes to the low-affinity and high-capacity Ca2+ extrusion mechanisms, whereas plasmalemma Ca2+-ATPase contributes to a subtle control around resting Ca2+ level. Alternatively, the contribution of Na+/Ca2+exchange at the peak Δ[Ca2+] could be calculated from the difference between γt=0 values in the control and in the low [Na+]o condition. The estimate for γNa(γt=0 at [Na+] of 145 mm) and that for γLi(γt=0 at [Na+] of 20 mm) obtained from the two Ca2+ transients in Figure 3A were 1.23/sec and 0.43/sec, respectively. The relative contribution calculated according to the equation (γNa − γLi)/γNa was 65%. The mean value of the relative contribution of Na+/Ca2+exchange to the total Ca2+ clearance mechanism, averaged from five cells, was 64.3 ± 3.7%, which is fairly close to the mean value of the maximalREXC.
Fig. 3.
Effect of external Na+reduction on the decay phase of Ca2+ transients.A, Two Ca2+ transients from the same cell were superimposed. The traces indicated with NaCl and LiCl were obtained in normal Tyrode's solution (145 mm[Na+]o) and in low Na+ condition (20 mm[Na+]o and 125 mm[Li+]o), respectively. The K pipette solution (for its composition, see Materials and Methods) containing 50 μm fura-2 was used for the internal solution. Calibration: 2 sec, 200 nm. The decay phases of the traces indicated with NaCl and LiCl were fitted with the following bi-exponential equations: 0.20 μm · exp (−0.19t) + 1.18 μm · exp (−1.42t) and 0.19 μm · exp(−0.13t) + 1.02 μm · exp(−0.48t), respectively. Inset, The plot of the time derivatives (−d[Ca2+]/dt) of the decay phases of the two Ca2+ transients as a function of Δ[Ca2+]i (white dots, NaCl; black dots, LiCl). B, The instantaneous γ values at various Δ[Ca2+] were calculated by dividing the time derivatives (insetin A) by Δ[Ca2+](t) and were fitted with fourth-order polynomial functions (fNa, a fit to γ in the normal condition; fLi, a fit to γ in the low [Na+]o condition). The difference between the two polynomial fits was plotted as asolid line (marked byfNa −fLi). The fraction of γ inhibited by the reduction of [Na+]o, (fNa −fLi)/fNa, was plotted as gray open circles (the right ordinate).
Fig. 4.
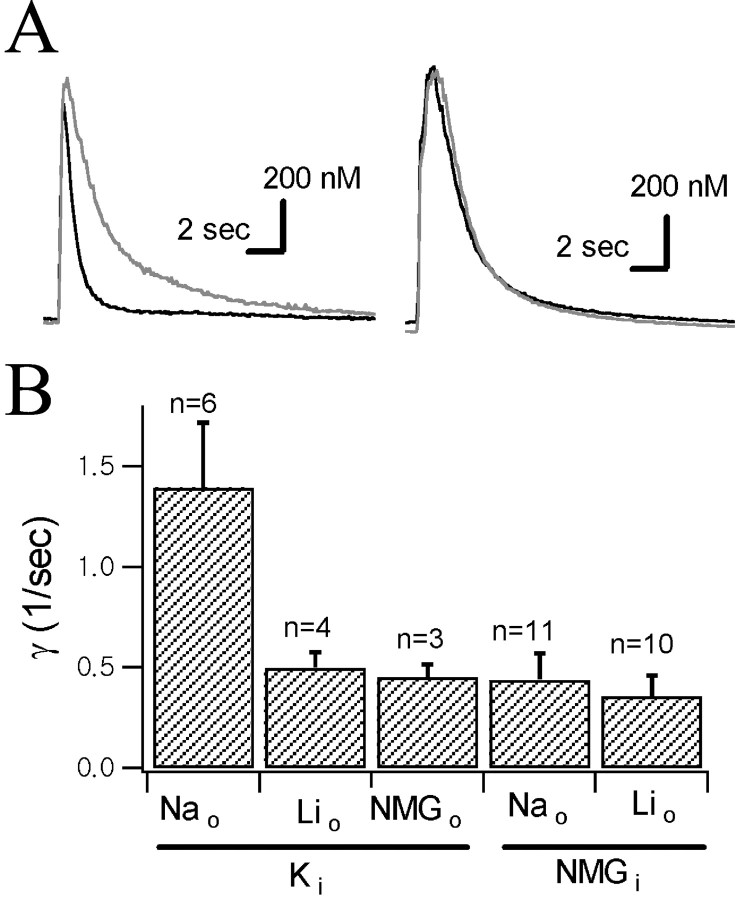
[K+]i dependence of Ca2+ decay rate. A, Representative Ca2+ transients recorded with a K+ pipette (left) and with an NMG+ pipette (right). A Ca2+ transient recorded at 145 mm[Na+]o (black traces) and that recorded at 20 mm[Na+]o (gray traces; Na+ was replaced by Li+) were superimposed. B, Mean Ca2+ decay rate constants (γt=0) of Ca2+transients under conditions indicated below theabscissa. Subscripto andi represent external and internal major cations, respectively.
Na+/Ca2+ exchange is dependent on internal K+
The expression of NCKX in various regions of the brain other than photoreceptor cells was reported recently (Tsoi et al., 1998; Kraev et al., 2001), but functional studies in native tissues have not yet been reported. To test the possible involvement of K+-dependent Na+/Ca2+exchanger in Ca2+ decay in axon terminals, we recorded the Ca2+ transient using a K+-free pipette solution. When internal K+ was replaced with NMG+, the decay rate of the Ca2+ transient was significantly slower (γNa = 0.44 ± 0.13/sec; p< 0.01) than that obtained with a K+pipette and was not statistically different from γLi obtained with a K+ pipette (0.49 ± 0.08/sec;p > 0.05). Furthermore, the inhibitory effect of lowering [Na+]o on Ca2+ decay, which was clearly observed with the K+ pipette, was negligible or markedly reduced under NMG+ pipette conditions (Fig. 4). These results show that the Na+/Ca2+exchange reaction hardly functions in the absence of intracellular K+, which suggests the function of K+-dependent Na+/Ca2+exchanger in NHP axon terminals.
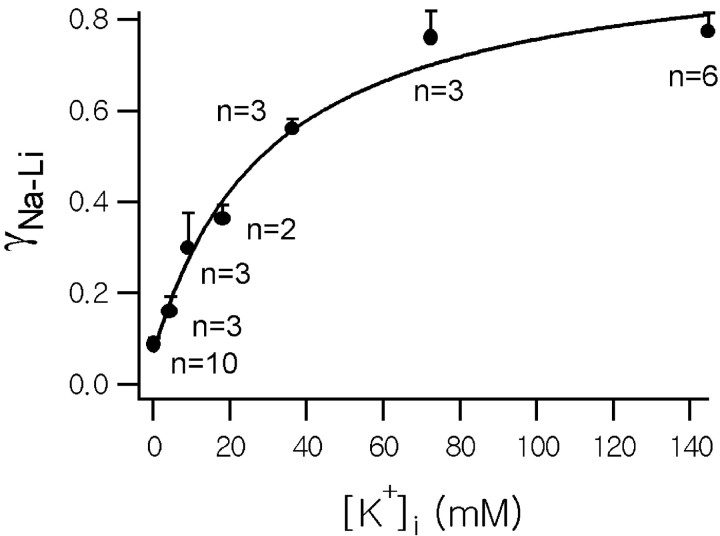
To quantify the dependence of the Na+/Ca2+exchange reaction on cytosolic [K+], we measured the Ca2+ decay rate exerted by Na+/Ca2+exchanger at various [K+]i, which were attained by intracellular dialysis using pipette solutions in which K+ were replaced iso-osmotically with various concentration of NMG+. The Ca2+ decay rate constant exerted by Na+/Ca2+exchanger was calculated from the difference between γNa and γLi. Mean values of the difference between γNa and γLi (denoted by γNa−Lihereafter) were plotted as a function of cytosolic [K+] in Figure5. The relationship between γNa−Li and cytosolic [K+] was hyperbolic. The solid line represents the best fit to the Michaelis–Menten equation, which revealed that a Km value is 30.3 mm.
Fig. 5.
Dependence of Na+/Ca2+ exchange on intracellular [K+]. Activity of Na+/Ca2+ exchange was estimated from the difference (γNa−Li) between the Ca2+ decay rate at 145 mm[Na+]o (γNa) and the decay rate (γLi) at 20 mm[Na+]o (Na+ was replaced with iso-osmolar Li+). Mean values of γNa−Li obtained from n axon terminals were plotted as a function of [K+]i(error bars indicate SEM). The internal K+dependence of γNa−Li was fitted using the following Michaelis–Menten equation (solid line): 0.07/sec + (0.90/sec · [K+]i)/([K+]i+ 30.3 mm).
Although the Na+-dependent Ca2+ extrusion was significantly attenuated under the condition of internal NMG+, the effect of Na+ removal on the Ca2+ decay rate was not completely abolished in some cells. On average, γNa−Liestimated using the NMG+ pipette ([K+]i of 0.25 mm, because 50 μmK5-fura-2 was included in the pipette solutions) was 0.088/sec, which is 11.3% of that estimated with K+ pipette (0.773/sec), indicating that ∼90% of the Na/Ca exchange mechanism is dependent on cytosolic K+.
External K+ dependence of reverse Na+/Ca2+ exchange
In previous studies on the K+dependence of NCKX expressed in cultured cells (Tsoi et al., 1998;Kraev et al., 2001), they observed the dependence of the reverse-mode Na+/Ca2+exchange on external [K+]. In Figure6, we investigated whether Ca2+ influx can be induced through the reverse mode of Na+/Ca2+exchange in NHP axon terminals and its dependence on [K+]o.
Fig. 6.
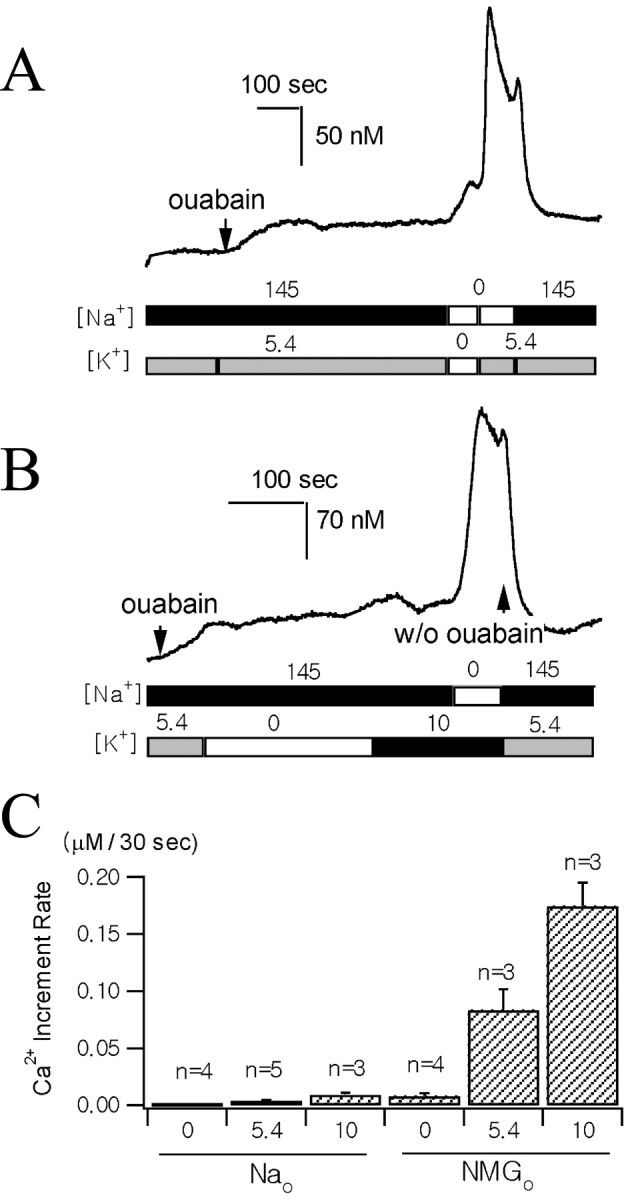
The effect of external K+ on reverse-mode Na+/Ca2+ exchange.A, B, The Ca2+traces were recorded from two different axon terminals preloaded with fura-2 AM. The times when 0.5 mm ouabain was applied are indicated by arrows. The two bars underneath the Ca2+traces illustrate the sequence of changes in [Na+] and [K+] of the external bathing solutions. External Na+ was replaced with equimolar NMG+ in zero Na+ solutions. K+ was added or omitted to the normal Tyrode's solution to make 10 mm[K+]o or zero [K+]o. C, Average [Ca2+]i increases during initial 30 sec after the solution change under various ionic conditions (n, number of individual nerve endings; error bars indicate SEMs). Numbers below theabscissa indicate external concentrations of K+. The major external cation was Na+ (left three bars, 145 mm Na+) or NMG+(right three bars, zero Na+).
Accordingly, we monitored [Ca2+]i of axon terminals preincubated in 1 μm fura-2 AM and used low [Ca2+]o (0.1 mm) in all of the external solutions to prevent [Ca2+]i from increasing to the toxic level. To evoke Ca2+ influx via the reverse-mode Na+/Ca2+exchange, we loaded axon terminals with Na+ by superfusing them with normal Tyrode's solution containing 0.5 mm ouabain (Figs.5A,B). While superfusing them with 0.5 mm ouabain, [Ca2+]i increased slowly. Initial rates of [Ca2+] increase were highly variable, ranging from 3 to 40 nm/min, but, in most cells, [Ca2+]i reached a steady state in 5 min. This result implies that increase in [Na+]iattributable to a blockade of the Na+ pump induces the accumulation of intracellular Ca2+ via an Na+/Ca2+exchange mechanism. Additional increase in [Ca2+]i was expected on the removal of external Na+, which leads to an increase in the driving force for the reverse mode of Na+/Ca2+exchange. In the absence of external K+, however, replacement of external Na+ with equimolar NMG+ resulted in a slight or no [Ca2+]i increase. In contrast, external Na+ replacement invariably caused a rapid Ca2+ increase in the presence of 5.4 mmK+ or 10 mmK+ in the bath solution (Fig.6A). To exclude the possibility that the [Ca2+]i increase during the addition of K+ to the Na+-free solution was caused by Ca2+ channel activation attributable to depolarization, we tested whether [Ca2+]i increases during the addition of 10 mmK+ to the bath solution while [Na+]o was kept normal (Fig. 6B). The increase in [Ca2+]i during the addition of 10 mm K+in normal [Na+]ocondition was far less than in the Na+-free condition (p < 0.01), and, in the same cell, a remarkable increase in [Ca2+]i was induced by the subsequent removal of external Na+ (Fig. 6B). This result further supports that the external K+-dependent [Ca2+]i increase was attributable to the reverse mode of Na+/Ca2+exchange. To compare [Ca2+]i increase rates in various ionic compositions, we measured the mean increase in [Ca2+]i during the initial 30 sec after the solution change and plotted it in Figure6C. It shows that [Ca2+]i increase rates are more greatly affected by external K+ in the Na+-free condition than in the normal [Na+] condition.
Expression of mRNA of NCKX isoforms in the supraoptic nucleus and paraventricular nucleus
Soma of axon terminals of NHP are located in the SON and the paraventricular nucleus (PVN). The expression of NCKX isoforms in those brain regions was determined at the mRNA level.
Total RNAs of supraoptic nucleus were extracted, and RT-PCR amplification was performed using specific sets of primers for NCKX1, NCKX2, and NCKX3 (see Materials and Methods). Each set of oligonucleotides used for RT-PCR amplification of NCKX2 and NCKX3 transcripts yielded the PCR products of the expected size (466 bp for NCKX2 and 360 bp for NCKX3) (Fig.7A), whereas no PCR product was detected for NCKX1 (data not shown).
Fig. 7.
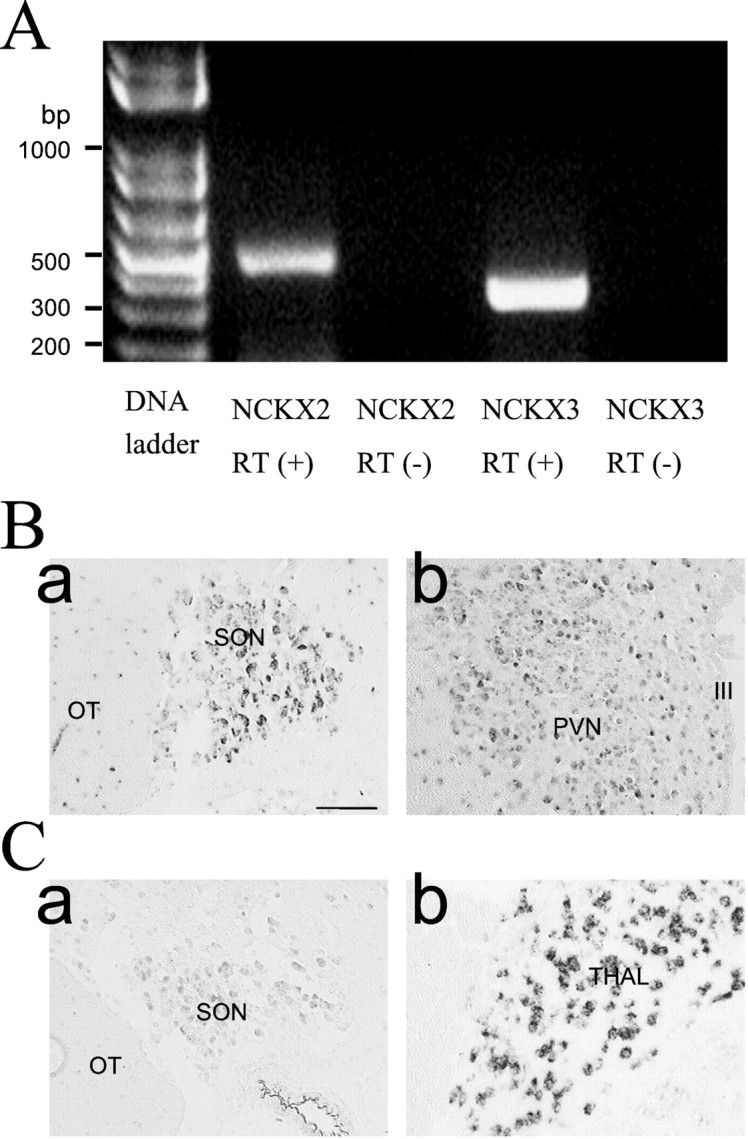
The expression of NCKX transcripts revealed by RT-PCR (A) and in situhybridization (B). A, Total RNAs were extracted from rat brain SON and reverse-transcribed [RT(+)] using reverse transcriptase plus taq polymerase PCR amplification of cDNAs was performed using a specific set of primers for NCKX2 and NCKX3. RT-PCR demonstrates expression of mRNA for NCKX2 and NCKX3 in SON. DNA contamination was tested from the absence of PCR product without reverse transcriptase [RT(−)]. B, C,In situ hybridization using digoxigenin-labeled NCKX2 (B) and NCKX3 (C) antisense riboprobes was performed on the coronal sections of the rat brain. In all cases, the sense control resulted in no increase in contrast above the general background observed in the panels of this figure.Ba, SON; Bb, PVN; Ca, SON;Cb, thalamus (Thal). The regions corresponding to the optic tract (OT) and the third ventricle (III) are marked inBa and Bb, respectively. Scale bar, 100 μm.
Tissue distribution of NCKX2 and NCKX3 transcripts was determined usingin situ hybridization. NCKX2 expression was evident in both the supraoptic nucleus and paraventricular nucleus (Fig.7B), whereas NCKX3 was scarcely detected in the SON (Fig.7Ca) and not detected at all in the PVN (data not shown). NCKX3 transcripts, however, were abundant in thalamus (Fig.7Cb) and in layer IV of neocortex (data not shown). Distribution patterns of NCKX2 and NCKX3 transcripts in other brain regions were essentially the same as previous reports (Tsoi et al., 1998; Kraev et al., 2001).
DISCUSSION
Plasma membrane Na+/Ca2+exchangers have been extensively studied in various cell systems. Two families of Na+/Ca2+exchanger proteins have been described in mammalian tissues: cardiac type Na+/Ca2+exchanger and the K+-dependent Na+/Ca2+exchanger, which is principally expressed in retinal rod outer segments. Three different genes for cardiac type exchanger (NCX1, NCX2, and NCX3) have been described, and it is now known that they are also found in various tissues other than the heart, such as the brain, kidney, and smooth and skeletal muscles. In contrast, the tissue distribution of the K+-dependent exchanger NCKX1 was originally thought to be limited to the retinal photoreceptor. Subsequently, however, a second type of K+-dependent exchanger (NCKX2) was cloned from rat brain and shown to be expressed in many other brain regions (Tsoi et al., 1998). Moreover, a third type of K+-dependent exchanger (NCKX3), which was cloned recently, shows a wide tissue distribution. It is most abundant in the brain and at a lower level in the aorta, uterus, and intestine, which are rich in smooth muscle (Kraev et al., 2001). Accordingly, it is now believed that this class of Ca2+transporter is widely distributed over the brain.
The present study demonstrates that (1) Na+/Ca2+exchange is the most important mechanism of Ca2+ clearance in the rat NHP axon terminals when Δ[Ca2+] is higher than 500 nm, and (2) ∼90% of the extrusion of intracellular Ca2+ via Na+/Ca2+exchanger is dependent on intracellular [K+]. To our knowledge, this is the first report to show that K+-dependent Na+/Ca2+exchanger plays a physiologically significant role in the Ca2+ dynamics of native neuronal cells other than in the cones and rods of the retina. Considering that Ca2+ handling mechanisms in a specific neuron are not uniform but different in soma, dendrite, and axon (Mironov et al., 1993), it remains to be elucidated whether the distribution of NCKX is polarized in a neuron.
Relative contribution of Na+/Ca2+ exchange to Ca2+ clearance
Quantitative studies on Ca2+clearance mechanisms in neuronal cells are very limited. The contribution of Na+/Ca2+exchanger reported in the present study in NHP axon terminals is far greater than that any previous study in the brain, and it is strikingly different from a previous study in the same preparation by Stuenkel (1994). He observed that a reduction of [Na+]o has little effect on the Ca2+ transient and concluded that Na+/Ca2+exchange has no contribution to Ca2+clearance. Stuenkel, however, used NMG+ in the pipette solution instead of K+, and we now understand, based on the results of the present study, the reason why the contribution of Na+/Ca2+exchange was very small in his experimental condition. Our estimate for the contribution of Na+/Ca2+exchanger is also greater than that of Fierro et al. (1998), who used a similar approach to ours in rat cerebellar Purkinje cell soma and reported that Na+/Ca2+exchange account for 26% at 0.5 μmCa2+ and 18% at 2 μmCa2+ of total Ca2+ clearance. It should be noted, however, that their estimates were obtained from experiments performed with Cs+ pipettes. In light of the results of the present study together with other evidence showing that NCKX2 is expressed in cerebellar Purkinje neurons as well as other brain regions (Tsoi et al., 1998), it might be necessary to reevaluate the contribution of Na+/Ca2+exchange to Ca2+ clearance when K+ is present in the pipette solution.
Mechanism of the K+ dependence of Na+/Ca2+ exchange
There are two ways in which K+affects Na+ gradient-dependent Ca2+ efflux: (1) K+ is cotransported with Ca2+, as suggested for rod-type NCKX and NCKX2 (Cervetto et al., 1989; Dong et al., 2001), or 2) K+ modulates the activity of the exchange protein without being transported (Blaustein, 1977; Slaughter et al., 1983; DiPolo and Rojas, 1984). The latter mechanism has been documented in the squid axon but not in mammalian NCX. The involvement of monovalent cations in Na+/Ca2+exchange in the squid axon is not fully understood and thus remains controversial. When internal K+ is replaced with TMA+ in the squid axon, Ca2+/Ca2+exchange is markedly reduced, but Na+o-dependent Ca2+i efflux is inhibited only slightly (Blaustein, 1977). On the contrary, a subsequent study reported that Tris+ substitute for internal K+ causes marked inhibition in Na+o-dependent Ca2+ efflux in the squid axon (DiPolo and Rojas, 1984). Recently squid Na+/Ca2+exchanger (NCX-SQ1) was cloned, but it is not clear whether a similar molecular entity exists in mammalian (He et al., 1998). In cardiac sarcolemmal vesicles, in which existence of NCX1 has been firmly established, monovalent cations stimulated Ca2+/Ca2+exchange, but they did not stimulate Na+/Ca2+exchange when they were present on the same side of the membrane as Ca2+ (Slaughter et al., 1983). Comparable data for brain-type NCX (NCX2 and NCX3) are not available, and, thus, at present, we cannot entirely exclude the possibility that they may have a dependence on K+ or other monovalent cations. However, considering the functional similarities within the mammalian NCX family (Linck et al., 1998), this possibility is not considered very likely. More importantly, the K+ dependence shown in the present study has features that are similar to the known characteristics of NCKX (for details, see the section below). Therefore, we think that NCKX is a more plausible candidate Na+/Ca2+exchanger molecule in NHP axon terminals, although we were not able to directly clarify whether K+ is cotransported with Ca2+ during the Ca2+ extrusion process via Na+/Ca2+exchange in NHP axon terminals.
Comparison of the K+ dependence of Na+/Ca2+ exchange with other studies
In the present study, the apparent dissociation constant (Km) for intracellular K+ was measured in Ca2+ efflux mode, which is more physiologically relevant to the shaping of the Ca2+ transient. In the majority of the previous studies providing quantitative information, theKm value for extracellular K+ was determined using the reverse Ca2+ entry mode. Furthermore, theKm value is known to be affected by other cations present on the side of K+-binding site (Prinsen et al., 2000;Dong et al., 2001). Figure 6 shows that the Ca2+ influx mode requires extracellular K+(K+o), but we were not able to measure Km for extracellular K+ attributable to the limitation in the range of [K+]othat could be changed experimentally without imposing other effects on the cells. Thus, direct comparison ofKm values (K+ dependence) in this study with those in other studies might be misleading. Nevertheless, it may be worthwhile comparing the Km value with those in other studies, if we can assume that internal K+ dependence is not substantially different from external K+ dependence.
Km for the external K+ of the outward NCKX1 current in rod cells was 150 μm (Perry and McNaughton, 1993). In platelets in which rod-type NCKX1 is thought to be present, it was ∼1 mm (Kimura et al., 1999). Previous studies on Na+/Ca2+exchange in the synaptic plasma membrane vesicles of rat brain reported that K+ stimulates Na+ gradient-dependent Ca2+ influx and that the K+ effect is saturated at 2 mm (Dahan et al., 1991). These values are considerably different from the value observed in the present study (Km of 30 mm). Recently, it was reported that Km for the external K+ of the outward NCKX2 current is substantially higher than that of the rod-type NCKX1. Dong et al. (2001) reported that the Kmvalue estimated from NCKX2 expressed in human embryonic kidney cells was reported to be 12 mm when choline was a major cationic component of the extracellular side and thatKm value of NCKX2 was even larger (36 mm) when Li+ instead of choline was used. Based on the proximities of theKm value in this study to the values reported by Dong et al. (2001), we think that NCKX2 is the most plausible Na+/Ca2+exchanger candidate in the NHP axon terminal among the NCKX family cloned so far. This conclusion is further supported by the results ofin situ hybridization that indicate that the expression of NCKX2 transcripts was clearly more abundant than that of NCKX3 (Fig.7B).
Physiological implication
The results of the present study indicate that Na+/Ca2+exchange is a dominant Ca2+ extrusion mechanism when Δ[Ca2+] level is higher than 500 nm. The mean amplitude of Ca2+ transient evoked by a single action potential in current-clamp mode was ∼30 nm (data not shown). The results shown in Figures 2 and 3 imply that, at this level, high-capacity Ca2+ extrusion system is not yet operating and thus Na+/Ca2+exchanger plays little role in Ca2+clearance. It is generally accepted, however, that secretion of oxytocin and vasopressin from neurohypophysis nerve terminals is evoked most effectively by bursts of APs rather than by a single AP (Cazalis et al., 1985). The mean intraburst AP frequency observedin vivo is known as 13 Hz for vasopressin-containing neurons and 24 Hz for oxytocin-containing neurons (Cazalis et al., 1985). When we mimicked the burst spikes by applying a train of 70 short depolarization pulses (3 msec duration) at the frequency of 10 Hz to the axon terminals in voltage-clamp mode, we observed that [Ca2+]i gradually increased and reached a steady value of ∼800 nm. This level is not substantially different from the amplitude of Ca2+ transient evoked by a 100 msec depolarization pulse used in the present study. Thus, Na+/Ca2+exchanger might play a dominant role in Ca2+ clearance when an NHP axon terminal is invaded by a train of APs, which is physiologically more relevant to the secretion.
The results of Km value for internal K+ and those of in situhybridization suggest that NCKX2 (more likely) and/or NCKX3 might be responsible for the K+-dependent Na+/Ca2+exchange in NHP axon terminals. It seems to be clear that K+ is cotransported via NCKX2, because ionic current via NCKX2 is proportional to the transmembrane electrochemical gradient of K+, which was demonstrated in the cells in which NCKX was artificially expressed (Dong et al., 2001). The stoichiometry of NCKX, 4 Na+:1 Ca2+,1 K+, enables the exchanger to attain a much lower level of [Ca2+]i than NCX whose exchange ratio is 3 Na+:1 Ca2+ (Cervetto et al., 1989). Thus, the presence of NCKX reflects a need to extrude Ca2+ rapidly with relatively smaller sodium gradients. Both rod cells and platelets, in which role of NCKX in Ca2+ extrusion was demonstrated, are considered to have such needs (Lagnado and McNaughton, 1989; Kimura et al., 1993). In rod cells, opening of the cGMP-gated channels in the dark results in membrane depolarization and increase in both [Na+]i and [Ca2+]i. Under these unusual ionic conditions, NCKX can extrude Ca2+ by coupling Ca2+ movements to both Na+ and K+gradients. It remains to be elucidated whether there is such demand in NHP axon terminals. It is expected that intracellular [Na+] might increase during AP bursts and that smaller axon terminals would be more vulnerable to [Na+]i increase attributable to high surface-to-volume ratio. Harnessing of K+ gradient in Na+/Ca2+exchange would prevent Na+/Ca2+exchange from attenuation of its Ca2+extrusion activity, when Na+ gradient is reduced. Moreover, the [Ca2+] level at which the flux through NCKX is reversed is supposed to be much lower than NCX. In other words, NCKX would provide a cell with a high-capacity Ca2+ extrusion mechanism that is able to operate in the relatively lower Ca2+ range than NCX. Information about relative contributions of neuron-type NCX to Ca2+ clearance at various Δ[Ca2+] is not available in neuronal cells. The dependence of relative contribution of NCX on Δ[Ca2+] needs to be investigated in future studies.
S.H.L. and M.H.K. contributed equally to this work
This work was supported by Ministry of Health and Welfare Grant 01-PJ1-PG1-10CH06-003. M.H.K. is a postgraduate student supported by Program BK21 from the Ministry of Education. We thank Dr. Y. S. Chun and Dr. J. W. Park for the synthesis of cDNA templates forin vitro transcription.
Correspondence should be addressed to Won-Kyung Ho, Department of Physiology and National Research Laboratory for Cellular Signaling, Seoul National University College of Medicine, 28 Yongon-Dong, Chongno-Ku, Seoul, 110-799, Korea. E-mail: wonkyung@snu.ac.kr.
REFERENCES
- 1.Blaustein MP. Effects of internal and external cations and of ATP on sodium-calcium and calcium-calcium exchange in squid axons. Biophys J. 1977;20:79–111. doi: 10.1016/S0006-3495(77)85538-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Cazalis M, Dayanithi G, Nordmann JJ. The role of patterned burst and interburst interval on the excitation-coupling mechanism in the isolated rat neural lobe. J Physiol (Lond) 1985;369:45–60. doi: 10.1113/jphysiol.1985.sp015887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Cazalis M, Dayanithi G, Nordmann JJ. Hormone release from isolated nerve endings of the rat neurohypophysis. J Physiol (Lond) 1987;390:55–70. doi: 10.1113/jphysiol.1987.sp016686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Cervetto L, Lagnado L, Perry RJ, Robinson DW, McNaughton PA. Extrusion of calcium from rod outer segments is driven by both sodium and potassium gradients. Nature. 1989;337:740–743. doi: 10.1038/337740a0. [DOI] [PubMed] [Google Scholar]
- 5.Dahan D, Spanier R, Rahamimoff H. The modulation of rat brain Na+-Ca2+ exchange by K+. J Biol Chem. 1991;266:2067–2075. [PubMed] [Google Scholar]
- 6.DiPolo R, Rojas H. Effect of internal and external K+ on Na+-Ca2+ exchange in dialyzed squid axons under voltage clamp conditions. Biochim Biophys Acta. 1984;776:313–316. doi: 10.1016/0005-2736(84)90220-7. [DOI] [PubMed] [Google Scholar]
- 7.Dong H, Lights PE, French RJ, Lytton J. Electrophysiological characterization and ionic stoichiometry of the rat brain K+-dependent Na+/Ca2+ exchanger, NCKX2. J Biol Chem. 2001;276:25919–25928. doi: 10.1074/jbc.M103401200. [DOI] [PubMed] [Google Scholar]
- 8.Eilers J, Callewaert G, Armstrong C, Konnerth A. Calcium signaling in a narrow somatic submembrane shell during synaptic activity in cerebellar Purkinje neurons. Proc Natl Acad Sci USA. 1995;22:10272–10276. doi: 10.1073/pnas.92.22.10272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fierro L, DiPolo R, Llano I. Intracellular calcium clearance in Purkinje cell somata from rat cerebellar slices. J Physiol (Lond) 1998;510:499–512. doi: 10.1111/j.1469-7793.1998.499bk.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Fontana G, Rogowski R, Blaustein M. Kinetic properties of the sodium-calcium exchanger in rat brain synaptosomes. J Physiol (Lond) 1995;485:349–364. doi: 10.1113/jphysiol.1995.sp020734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gill DL, Grollman EF, Kohn LD. Calcium transport mechanisms in membrane vesicles from guinea pig brain synaptosomes. J Biol Chem. 1981;256:184–192. [PubMed] [Google Scholar]
- 12.He Z, Tong Q, Quednau BD, Philipson KD, Hilgemann DW. Cloning, expression, and characterization of the squid Na+-Ca2+ exchanger (NCX-SQ1). J Gen Physiol. 1998;111:857–873. doi: 10.1085/jgp.111.6.857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Helmchen F, Imoto K, Sakmann B. Ca2+ buffering and action potential-evoked Ca2+ signaling in dendrites of pyramidal neurons. Biophys J. 1996;70:1069–1081. doi: 10.1016/S0006-3495(96)79653-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kimura M, Aviv A, Reeves JP. K+-dependent Na+/Ca2+ exchange in human platelets. J Biol Chem. 1993;268:6874–6877. [PubMed] [Google Scholar]
- 15.Kimura M, Jeanclos EM, Donnelly RJ, Lytton J, Reeves JP, Aviv A. Physiological and molecular characterization of the Na+/Ca2+ exchanger in human platelets. Am J Physiol. 1999;277:H911–H917. doi: 10.1152/ajpheart.1999.277.3.H911. [DOI] [PubMed] [Google Scholar]
- 16.Kraev A, Quednau BD, Leach S, Li XF, Dong H, Winkfein R, Perizzolo M, Cai X, Yang R, Philipson KD, Lytton J. Molecular cloning of a third member of the potassium-dependent sodium-calcium exchanger gene family, NCKX3. J Biol Chem. 2001;276:23161–23172. doi: 10.1074/jbc.M102314200. [DOI] [PubMed] [Google Scholar]
- 17.Lagnado L, McNaughton PA. The sodium-calcium exchange in photoreceptors. In: Allen TJA, Noble D, Reuter H, editors. Sodium-calcium exchange. Oxford UP; Oxford: 1989. pp. 261–297. [Google Scholar]
- 18.Lee SH, Rosenmund C, Schwaller B, Neher E. Differences in Ca2+ buffering properties between excitatory and inhibitory hippocampal neurons from the rat. J Physiol (Lond) 2000;525:405–418. doi: 10.1111/j.1469-7793.2000.t01-3-00405.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lim NF, Nowycky MC, Bookman RJ. Direct measurement of exocytosis and calcium currents in single vertebrate nerve terminals. Nature. 1990;344:449–451. doi: 10.1038/344449a0. [DOI] [PubMed] [Google Scholar]
- 20.Linck B, Qiu Z, He Z, Tong Q, Hilgemann DW, Philipson KD. Functional comparison of the three isoforms of the Na+/Ca2+ exchanger (NCX1, NCX2, NCX3). Am J Physiol. 1998;274:C415–C423. doi: 10.1152/ajpcell.1998.274.2.C415. [DOI] [PubMed] [Google Scholar]
- 21.Mironov SL, Usachev YM, Lux HD. Spatial and temporal control of intracellular free Ca2+ in chick sensory neurons. Pflügers Arch. 1993;424:183–191. doi: 10.1007/BF00374610. [DOI] [PubMed] [Google Scholar]
- 22.Neher E. Combined fura-2 and patch clamp measurements in rat peritoneal mast cells. In: Sellin LR, Thesleff S, editors. Neuromuscular junction. Elsevier Science; Amsterdam: 1989. pp. 65–76. [Google Scholar]
- 23.Neher E, Augustine GJ. Calcium gradients and buffers in bovine chromaffin cells. J Physiol (Lond) 1992;450:273–301. doi: 10.1113/jphysiol.1992.sp019127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Perry RJ, McNaughton PA. The mechanism of ion transport by the Na+-Ca2+, K+ exchange in rods isolated from the salamander retina. J Physiol (Lond) 1993;466:443–480. [PMC free article] [PubMed] [Google Scholar]
- 25.Prinsen CFM, Szerencsei RT, Schnetkamp PPM. Molecular cloning and functional expression of the potassium-dependent sodium-calcium exchanger from human and chicken retinal cone photoreceptors. J Neurosci. 2000;20:1424–1434. doi: 10.1523/JNEUROSCI.20-04-01424.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Slaughter RS, Sutko JL, Reeves JP. Equilibrium calcium-calcium exchange in cardiac sarcolemmal vesicles. J Biol Chem. 1983;258:3183–3190. [PubMed] [Google Scholar]
- 27.Stuenkel EL. Regulation of intracellular calcium and calcium buffering properties of rat isolated neurohypophysial nerve endings. J Physiol (Lond) 1994;481:251–271. doi: 10.1113/jphysiol.1994.sp020436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Tsoi M, Rhee KH, Bungard D, Li XF, Lee SL, Auer RN, Lytton J. Molecular cloning of a novel potassium-dependent sodium-calcium exchanger from rat brain. J Biol Chem. 1998;273:4155–4162. doi: 10.1074/jbc.273.7.4155. [DOI] [PubMed] [Google Scholar]