Dynamic Interactions between Local Surface Cues, Distal Landmarks, and Intrinsic Circuitry in Hippocampal Place Cells

Abstract

A number of computational models of hippocampal place cells incorporate attractor neural network architecture to simulate key findings in the place cell literature, including the properties of pattern completion, firing in the absence of visual input, and nonlinear responses to environmental manipulations. To test for evidence of attractor dynamics, ensembles of place cells were recorded using multiple-tetrode techniques. After many days of experience in an environment with salient local surface cues on a circular track and salient distal landmarks on the wall, the local surface cues were rotated as a set in opposition to the distal landmarks. The amount of mismatch between the local and distal sets of cues varied from 45 to 180°. If place cells were parts of strong attractors, then their place fields should follow either the local cues or the distal cues as an integrated ensemble. Instead, in single recording sessions, some place cells were controlled by the distal landmarks, other cells were controlled by the local cues, and other cells became silent or gained new fields. In some cases, individual place fields split in half, following both the local and distal cues. If place cells are indeed parts of attractor networks in the hippocampus, then the attractors may be weak relative to the inputs from external sources, such as representations of the sensory environment and representations of heading direction, in a familiar, well explored environment.

Principal neurons of the rat hippocampus fire selectively in restricted locations of an environment (O'Keefe and Dostrovsky, 1971; Muller et al., 1987). Debate continues over whether these place cells are best described as the neural substrate of a cognitive map of the environment (O'Keefe and Nadel, 1978) or as the components of a more general relational learning system (Cohen and Eichenbaum, 1993). One reason for the continued debate is that few rules have been defined that describe precisely the nature of the interactions between the myriad sources of input onto place cells. Although place cells can be controlled by visual landmarks (O'Keefe and Conway, 1978; Muller and Kubie, 1987), this control is not absolute, and idiothetic cues and local surface cues can exert control over the cells in nonlinear ways (Young et al., 1994; Sharp et al., 1995; Shapiro et al., 1997; Knierim et al., 1998; Save et al., 2000;Zinyuk et al., 2000; Knierim, 2001; Knierim and McNaughton, 2001).

A number of models have been proposed to explain the nonlinear responses of place cells to environmental cue manipulations. Some of these models simulate the hippocampus as a set of continuously coupled attractors (Samsonovich and McNaughton, 1997; Doboli et al., 2000; Kali and Dayan, 2000). This network architecture allows the models to simulate such phenomena as the continued firing of place cells in the absence of visual input and the pattern completion properties of place cells when a subset of the landmarks is removed (O'Keefe and Conway, 1978; Quirk et al., 1990). A challenge to these models comes from a set of studies by Tanila and colleagues (Shapiro et al., 1997; Tanila et al., 1997). When they rotated salient distal cues in opposition to salient local cues, place fields that followed the distal cues were recorded simultaneously with place fields that followed the local cues. If place cells form strong attractors, this type of network would tend to prevent such split control of place fields. The limited number of simultaneously recorded cells, however, made the demonstration of split control open to question. Because a number of cells changed their firing properties unpredictably (“remapped”), it was possible that the examples of split control were actually chance results of remapping. In support of this interpretation, a preliminary study byBrown and Skaggs (1999) did not find any examples of split control by the distal and local cues beyond that expected by chance. Similarly, a study by Knierim and McNaughton (2001) showed that all cells in a simultaneously recorded data set either remapped or were controlled by a single set of cues; no examples of split control were observed greater than expected by chance.

The present study adapted the experimental design of Shapiro et al. (1997) to investigate this issue further by incrementally introducing greater degrees of mismatch between local and distal cues and determining whether cells were controlled by only one set of cues or by both sets of cues. The results show unequivocally that when the two sets of cues were placed in conflict with each other, some place cells were controlled by local cues, whereas others were controlled by distal cues.

MATERIALS AND METHODS

Subjects

Eight male rats (five Long–Evans and three Fischer-344), obtained from Harlan Laboratories at 5–9 months old, were maintained at 80–90% of their ad libitum weights, had ad libitum access to water, and were handled and weighed daily. The rats were housed individually on a reversed light/dark cycle (lights off from 12 noon to 12 midnight). Experiments were performed during the dark portion of the cycle. Animal care, surgical procedures, and euthanasia were performed according to National Institutes of Health guidelines and were approved by the University of Texas–Houston Health Science Center Institutional Animal Care and Use Committee.

Surgery

Rats were anesthetized with pentobarbital sodium (Nembutal, 40 mg/kg, i.p.) supplemented with subsequent small doses of Nembutal or by methoxyflurane (Metofane) inhalation as necessary. A recording device (Neuro-hyperdrive; Kopf Instruments, Tujunga, CA) that allowed the independent manipulation of 14 recording probes was implanted over the right dorsal hippocampus of five rats. Twelve of the probes were tetrodes made of four lengths of fine nichrome wire (Rediohm-800, 0.0005 inches; Kanthal, Palm Coast, FL) twisted together (McNaughton et al., 1983; Recce and O'Keefe, 1989; Wilson and McNaughton, 1993). The other two were single-channel probes for recording EEG and reference signals. For two rats, a modified Neuro-hyperdrive was implanted in which the tetrodes were in a fixed position and not adjustable after surgery. For one rat, a custom-built, 18-tetrode drive was constructed using dental acrylic and stainless steel cannulas, according to methods used by Wilson and McNaughton (1993). After surgery, rats were administered 26 mg of acetaminophen (Children's Tylenol) orally for analgesia. They also received 2.7 mg/ml acetaminophen in their drinking water for 1–3 d after surgery.

Training

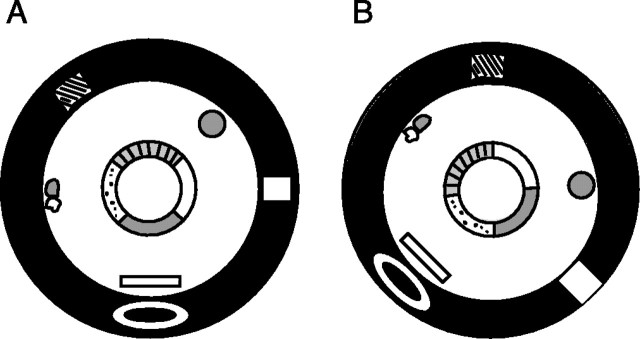
The rats were trained to run clockwise (CW) on a circular ring (56 cm inner diameter, 76 cm outer diameter) for food reward (chocolate sprinkles) placed at arbitrary locations on the track (one to two rewards per lap), such that no specific reward zones were defined on the track. All training and recording sessions were performed in a light-tight, sound-attenuating room. The rats underwent 6–21 training sessions over 2–11 d before the beginning of the experiment. The circular track was composed of four different textured surfaces, each covering one-quarter of the ring: a gray rubber mat with a pebbled surface, brown medium-grit sand paper, beige carpet pad material, and gray duct tape with white tape stripes (Fig.1). The ring was centered inside a 9-foot-diameter black circular curtain, which reached from the ceiling to the floor. Hanging on the curtain or standing on the floor at the perimeter of the curtain were six objects: a brown cardboard circle, a white box, an intravenous stand with a lab coat and a blue cloth, a black and white striped card, a roll of brown wrapping paper, and a white card. For all training sessions, the ring and the array of distal cues were kept at a constant configuration. Lighting was provided by a single 25 W bulb on the ceiling centered over the ring. An intercom speaker, by which the experimenter inside the behavior room could communicate with the experimenter in the adjacent computer room, was mounted 14 cm offset from the light. The light bulb was surrounded by a 13-cm-diameter, 10-cm-high black cylinder, which prevented the video camera (mounted 11 cm offset from the light) and the intercom speaker from being illuminated. As a result, these pieces of equipment were invisible to the human observer. The ceiling was covered with an annulus of black curtains that extended from a 61-cm-diameter hoop centered in the room to the black curtains at the perimeter of the room. The ceiling panel on which the light, camera, intercom, and recording cables were mounted was also painted black. White noise emanated from a small speaker below the behavioral apparatus.

Fig. 1.

Diagram of behavioral apparatus in standard (A) and 90° mismatch (B) configurations. The circular track was composed of four different textured surfaces, each covering one-quarter of the ring: a gray rubber mat with a pebbled surface, brown medium-grit sand paper, beige carpet pad material, and gray duct tape with white tape stripes. The ring was centered inside a 9-foot-diameter black circular curtain. Hanging on the curtain or standing on the floor at the perimeter of the curtain were six objects (see Materials and Methods). Lighting was provided by a single 25 W bulb on the ceiling centered over the ring. In between recording sessions, the track was rotated CCW and the cues on the floor and curtains were rotated CW, as inB.

Recording electronics

After 2–7 d of recovery from surgery, the electrodes were advanced gradually over the course of many days. Neuronal signals were passed through a headstage of complementary metal oxide semiconductor (CMOS) operational amplifiers (Neuralynx, Tucson, AZ). The signals were amplified between 2,500 and 10,000 times and filtered between 600 Hz and 6 kHz, before being digitized at 32 kHz and stored on a Sun Microsystems Ultra2 computer, using the Cheetah data acquisition system (Neuralynx). Also mounted on the front of the headstage was an array of light-emitting diodes to track the animal's position at 60 Hz.

Experimental protocol

On experiment days, baseline data were collected for ∼30 min while the rat slept or sat quietly in a towel-lined bowl in the data acquisition computer room. These data were collected to determine the number of cells that were present and to compare with a subsequent baseline session at the end of the day to assess recording stability. The rat was then placed in a covered box and after 30 sec was walked briefly around the computer room before entering the adjacent behavior room. After closing the door and curtains, the experimenter walked around the ring two to three times. The rat was placed on a pedestal, the headstage and recording cable were attached, and the rat was placed on the ring at an arbitrarily chosen location. The recording cable, which hung from the ceiling offset by 14 cm from the centered light, was pre-twisted seven to eight twists in a counterclockwise (CCW) direction to relieve the amount of tension and twist on the cable when the rat competed the 15 clockwise laps on the track. After ∼15 laps, the rat was placed back in the box and carried around the ring and into the computer room, taking a slightly circuitous route as before. In between sessions, the ring was rotated CCW 22.5, 45, 67.5, or 90°, and the cues along the curtains were rotated CW by an equal amount. Thus, in these mismatch sessions, the total amount of mismatch between the local and distal cues was 45, 90, 135, or 180°. Sleep-baseline sessions were run before the first track session and after the last. The rats experienced two complete sets of each mismatch amount over 4 d, with each mismatch being run in pseudorandom order.

Data analysis

Off-line unit isolation. The tetrode allows the isolation of single units based primarily on the relative amplitudes of signals recorded simultaneously at four slightly different locations. Additional waveform characteristics, such as spike width, are also used. Waveform characteristics were plotted as a scatter plot of one of the electrodes versus another. Individual units formed clusters of points on such scatter plots, and the boundaries of these plots were defined with the use of a custom interactive program (Xclust; M. Wilson, Massachusetts Institute of Technology) running on a Sun Ultra2 workstation. The isolation quality of the cell was rated on a subjective scale of 1 (very well isolated) to 4 (marginally isolated), based on the size of the waveforms relative to background and the closeness and degree of potential overlap between neighboring clusters. These ratings were made completely independent of the place-field quality of the cell or of its response to the cue manipulations. All cells rated “marginally isolated” were excluded from analysis.

Place-field analysis. The specificity of spatial tuning for each cell was calculated as the amount of information about the rat's position conveyed by the firing of a single spike from the cell (Skaggs et al., 1993, 1996). This measure correlated well with the investigator's subjective judgment of the quality of a place field. Only cells that had a statistically significant (p < 0.01) information score >0.99 and that fired >50 spikes in at least one of the sessions on a given day were included in the analysis.

Rotation correlation analysis. To quantify the rotation of place fields between different sessions, a rotation correlation score was measured for each cell. The track was divided into 144 bins (2.5° per bin), and a firing rate for each bin was calculated by dividing the number of spikes fired while the rat occupied that bin by the amount of time spent in the bin. The bins were smoothed by recalculating the firing rate of each bin as the average of itself and its two adjacent bins. For each cell, the Pearson product-moment correlation between its firing rate arrays in each session was measured, and then the firing rate bins of the second session were shifted by one bin, corresponding to a 2.5° rotation of the second session. The firing rate array of the first session was correlated with the 2.5°-shifted array of the second session, and then the second session was shifted again. This was repeated 143 times, and the rotation angle that produced the highest correlation was taken as the amount that the place field had rotated between the two sessions. Correlations between a particular pair of sessions for each cell were calculated only if the cell met the inclusion criteria for at least one session of the pair and if the peak correlation was >0.75. Circular statistical tests were performed on the distributions produced by the rotation analyses (Zar, 1999).

Histology

After recordings, small marker lesions were made on a subset of the tetrode tips (10 μA, 10 sec) 1 d before perfusion. The animal was perfused transcardially with 4% formalin, after which the brain was extracted and placed in a 30% sucrose formalin solution. After the brain sank, it was cut at 40 μm sections on a microtome, mounted, and stained with cresyl violet. Electrode tracks were identified and plotted on a representation of the brain surface to identify which track corresponded to each tetrode. The tetrodes were then assigned to hippocampal subfields based on the histology and EEG signals recorded during the experimental sessions.

RESULTS

These results are based on 31 recording days from eight rats (4 d per rat, with 1 d lost because of technical problems). In most cases, five sessions were run each day, with three standard sessions interleaved with two mismatch sessions. On average, 11 principal cells that had stable waveforms and a place field in at least one of the sessions were recorded each day (range 2–25). (Because multiple sessions were recorded each day and at least some of the cells recorded between days were presumed to be identical, it is difficult to ascertain the total number of cells recorded over time.) This average number does not include interneurons or the many principal cells that were active during a sleep-baseline session but were relatively quiet or silent during the behavioral sessions. Most of the cells (72%) were from the CA1 layer. Other cells were recorded from histologically confirmed sites in the CA3 layer (6%) and the dentate gyrus (DG) granule cell layer (7%). Finally, a number of tetrodes were positioned in the DG or CA3 layers near the region where CA3 inserts into the hilus (15%). There were no statistically significant differences in the cell properties analyzed among these groups, although the small number of CA3 and DG recordings render this negative result inconclusive. Hence, the data are grouped together in all analyses.

Local versus distal cue control

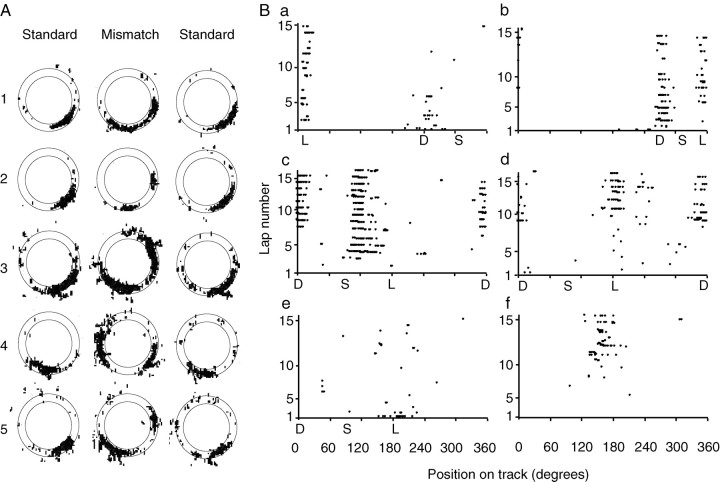
Figure 2 illustrates representative examples from a single data set of the different responses of place cells to the mismatch sessions. On this day, three standard sessions (sessions 1, 3, and 5) were interleaved with a 180° mismatch session (session 2) and a 135° mismatch session (session 4). Ten of the 21 cells that had place fields in at least one of the five sessions are illustrated. The cells are grouped according to their responses to the 180° mismatch. Cells 1, 2, and 3 rotated their place fields CW to follow the distal cue set; cells 4, 5, and 6 rotated their place fields CCW to follow the local cue set; cell 7 split its place field in two, with one subfield following each set of cues; and cells 8, 9, and 10 either gained a field in the mismatch session (cell 8) or lost a field (cells 9 and 10). Responses to the 135° mismatch were slightly different: cell 7 rotated with the distal cues rather than splitting its field, and cell 9 rotated with the distal cues rather than losing its field.

Fig. 2.

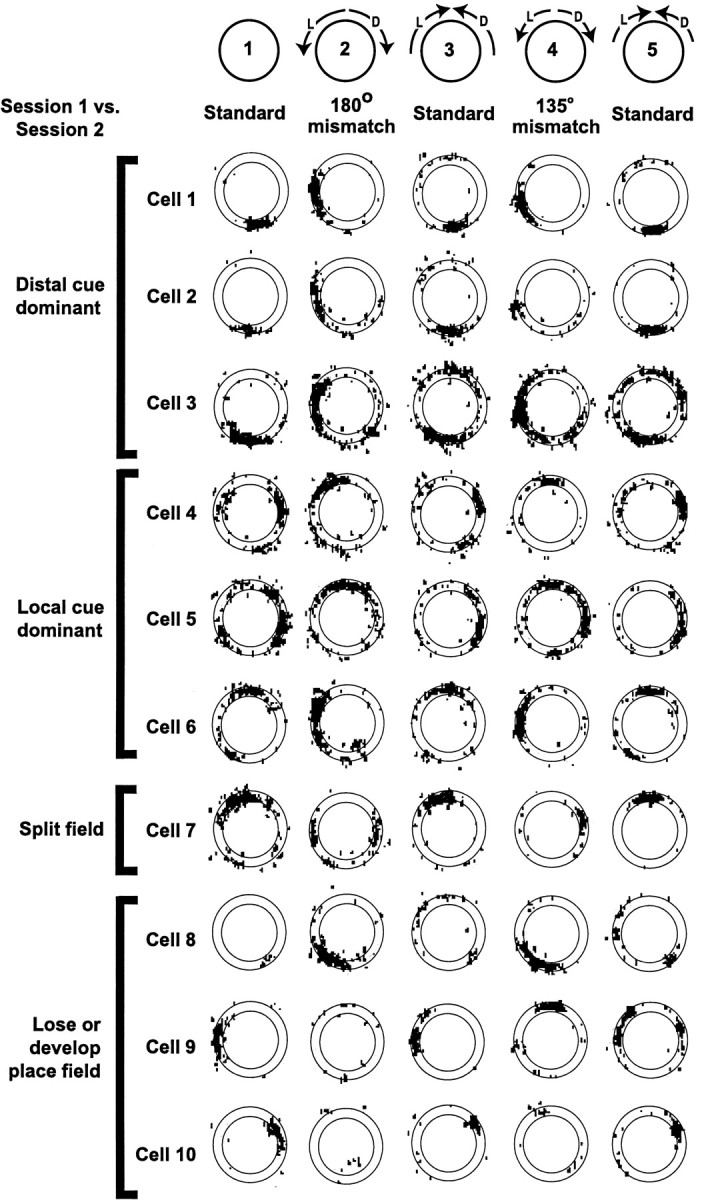
Representative examples of place cells from a single recording session. The black dots indicate the location of the rat when each spike was fired. Because the rat ran the track in a unidirectional manner, each part of the track was visited in approximately equal proportions. Spikes that occur outside the outlines of the circular track result from instances in which the rat extended its head off the track; these spikes were excluded from the quantitative analyses, because the sampling locations were not consistently reproducible between sessions. In Session 2 (180° mismatch), Cells 1–3 rotated their place fields ∼90° CW to follow the distal cues. Cells 4–6 rotated their place fields ∼90° CCW to follow the local cues. Cell 7 split its place field in two, with one subfield rotating CW and the other CCW.Cell 8 developed a field, whereas Cells 9and 10 lost their fields. Most cells behaved similarly in session 4 (135° mismatch), except that Cell 7 rotated CW rather than spitting its field and Cell 9 rotated CW instead of losing its field.

Partial remapping was a prevalent, although not ubiquitous, result of the double rotations. Some cells, such as cells 8–10 of Figure 2, lost or gained fields in the mismatch sessions; other cells changed their firing rates dramatically while still maintaining a place field tied to one set of cues; and other cells rotated their place fields to locations that were not tied to either set of cues. Thus, the ensemble recordings reproduced many phenomena that are characteristic of partial remapping (Tanila et al., 1997; Skaggs and McNaughton, 1998; Knierim and McNaughton, 2001); however, it is beyond the scope of the present paper to analyze these remapping effects fully. Because it is difficult to classify place fields that either changed their firing rates or rotated to unpredicted locations without the use of arbitrary criteria, it was decided to analyze quantitatively all cells that met the criteria for a place field (see Materials and Methods) in both the standard and mismatch sessions, regardless of the rotation angle and change in firing rate. Cells that met the criteria for having a place field in only one of the two sessions were dropped from further analysis. Thus, of the 585 data points in which the cell had a place field in at least one of a pair of sessions, 332 units (57%) had fields in both the standard and mismatch sessions, whereas 160 units (27%) lost the field during the mismatch session, and 93 (16%) had a field in the mismatch session but not in the standard session. There were no significant differences among the four mismatch sessions in this classification scheme (Table1). The rest of this report will be limited to those place cells that had firing fields in both the standard and mismatch sessions.

Table 1.

Proportions of cells that maintain fields for each mismatch session type

	45°	90°	135°	180°
Maintain field	90 (65%)	82 (52%)	81 (52%)	79 (59%)
Lose field	31 (22%)	51 (32%)	42 (27%)	36 (27%)
Gain field	17 (12%)	24 (15%)	34 (22%)	18 (14%)

Population analyses

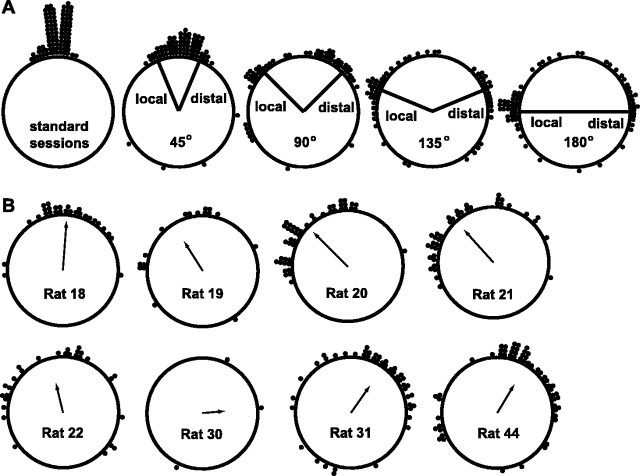
Figure 3A illustrates the relative degree of local versus distal control for each of the four mismatch session types. Each data point represents the amount that a given place field had rotated between the standard session and the rotation session. For comparison, the amount that place fields rotated between standard sessions is shown at left (mean = 1.1 ± 5.9° SE). The radial lines indicate the amount of rotation that corresponds to precise local cue control or precise distal cue control over the place fields. The 45° mismatch sessions produced a unimodal distribution centered around 0° (mean = 3.8 ± 8.0° SE). Although this would appear to indicate that the cells were unaffected by the cue rotations in these sessions, the deviations from the mean were greater in the 45° mismatch session than in the standard sessions (Mann–Whitney U; p < 0.001). Thus, the cells shifted their firing fields CW or CCW to some extent in the 45° mismatch sessions but were not completely controlled by the cue sets. This lack of control may reflect the influence of uncontrolled static background cues in the laboratory. Although great effort was made to eliminate the influence of such cues (see Materials and Methods), there were some subtle cues that were unavoidable (e.g., the slight offset of the recording cable from the centrally located light source on the ceiling). Alternatively, the lack of control may be the result of intrinsic circuitry between place cells (see Discussion). The remaining mismatch sessions (90, 135, and 180°) produced bimodal distributions, with each mode centered near the local and distal control bins. In all cases, some place fields rotated to angles scattered around the ring, which did not correspond clearly to either set of cues. As mentioned above, it is likely that these points represent place fields that remapped the track as the result of the cue rotations, changing to an arbitrary location rather than shutting off.

Fig. 3.

Summary of place field rotations. Eachdot on the diagram represents the amount of rotation of a single place field between the standard and mismatch sessions.A, Degree of rotation for each place field between two standard sessions (left) and between the standard and mismatch sessions (45, 90,135, and 180°). The distribution of rotation angles for the 45° mismatch sessions was centered around 0°, although a comparison with the standard sessions (left) shows that the variance was greater for the 45° mismatch session. For the 90, 135, and 180° mismatch sessions, the distributions were bimodal, with subsets of cells rotating with the distal cue set and with the local cue set. B, Degree of rotation for each place field broken down by subject. All mismatch session types (45, 90, 135, and 180°) are combined. Thearrow represents the mean angle for that rat, and thelength of the arrow signifies the angular dispersion around the mean (Zar, 1999). Some rats were controlled more strongly by the local cue set (e.g., Rats 20 and21), whereas other rats were controlled more strongly by the distal cue set (e.g., Rats 31 and44).

Figure 3B shows the variability in local versus distal control demonstrated between subjects. The data from all four rotation types (45, 90, 135, and 180° mismatch sessions) were combined for each rat. The place fields of some rats were clearly controlled more strongly by the local cue set (e.g., rats 20 and 21), whereas the fields of other rats were controlled more strongly by the distal cue set (e.g., rats 31 and 44). There were no differences throughout the experiment in the local or distal cues used, and the differences between rats did not correlate with strain differences. This variability between rats in the degree of local versus distal control emphasizes the degree to which the response properties of place cells are controlled as much by internal, state-related variables, such as previous experience, as they are by external sensory inputs.

Are simultaneously recorded cells controlled by different sets of cues?

Because of the variability in local–distal control displayed by different rats, and the variability seen in different sessions within rats, the bimodal distributions of Figure 3A can result from two possibilities. Individual data sets might contain a subset of cells that followed the distal cues while another subset simultaneously followed the local cues. Alternatively, these distributions might be an artifact of the pooling of individual data sets in which all cells followed either one set of cues or the other, and the dominant set of cues changed between sessions. This is an important issue, for if the hippocampus contains strong attractor circuitry, this circuitry would tend to suppress the split control of the place cell ensemble. The data from Figure 2 suggest that such split control can occur, but the occurrence of partial remapping in the session makes this interpretation ambiguous (Knierim and McNaughton, 2001). The cells that were bound apparently to the local cues might be cells that actually remapped, and the new fields happened to fall 60–90° from the original field. It is necessary to evaluate statistically whether simultaneous split control of place fields occurs to a degree greater than expected by random remapping.

Because most of the rats in the present experiment did not have enough place fields in a given data set to address this question with sufficient statistical power, an overall population analysis was undertaken for the combined data from all rats. For each simultaneous recording, the dominant set of cues (local or distal) was determined (as described below), and each cell that was controlled by this dominant set was eliminated. It was reasoned that if the remaining cells remapped to arbitrary angles, then the locations of their place fields should be distributed randomly. In contrast, if the remaining cells were controlled by the nondominant set of cues, then their place fields should cluster within the 45° range centered on the rotation of that cue set. To perform this analysis, for each ensemble data set, the number of cells that rotated their field CW was compared with the number that rotated CCW to determine which set of cues was dominant. The cells that followed the dominant set of cues were then dropped from the analysis. (If the number of CCW cells equaled the number of CW cells, both sets of cells were dropped, because neither cue set dominated.) The remaining 29 cells thus formed the group that did not follow the dominant set of cues for each data set. The number of these cells that fell in a 45° range centered on the rotation of the nondominant cues was counted and compared with the number of cells that fell outside this range. On the null hypothesis that these cells remapped to random locations from 0 to 180°, the expected number of cells in the 45° cue-control range would be 7.25 (29 cells × 45°/180°), and the expected number of cells outside this range would be 21.75 (29 cells × 135°/180°). Instead, 14 (48%) fell within the 45° range of nondominant cue control, and 15 (52%) fell outside this range. This proportion is different from expected by the assumption of uniform distribution (χ² = 7.18; p < 0.01), thus indicating that split control of the cells indeed occurs at the level of individual data sets.

Split control of individual place fields

Some individual place cells were controlled by both sets of cues independently. Of the 332 data points in which the cells maintained place fields in the standard and mismatch sessions, 24 (7%) of the cells split their place fields as a result of the double rotation, because one subfield rotated CW and the other rotated CCW (Fig.4A). In some cases one subfield was stronger than the other. The existence of these split fields reinforces the conclusion that the cells can be controlled simultaneously by both local and distal cues when they are placed in conflict with each other (O'Keefe and Burgess, 1996; Fenton et al., 2000).

Fig. 4.

Split place fields. A, Examples of five cells that split their place fields in the mismatch session.B, Examples of six cells that displayed dynamic changes in their place fields over the time course of a mismatch session.S indicates the location of the place field in the previous standard session, L indicates the location corresponding to precise control by local cues, and Dindicates the location corresponding to precise control by distal cues. Note that because the circular track is plotted along the abscissa, there is a wraparound effect for cells c andd. Cell a initially fired at theD location for the first two laps and then fired at both the D and L locations for the next few laps, and eventually fired almost exclusively at the Llocation for the remainder of the session. Cell b (same cell as cell a in a later session) fired initially at the D location and then developed a split field at both the D and L locations. Cellc initially was silent and then after two laps began to fire in between the S and Llocations. Midway through the session, it developed a split field, firing at the D location as well. (In the subsequent standard and mismatch sessions, this cell lost its strong spatial tuning.) Cell d was fairly quiet for the first eight laps and then began to fire at both the L andD locations. (In the second mismatch session of the day, the place field of cell d was controlled only by the distal cues, but the strength of the field changed over time; it started out weak, became strong for 5–6 laps, and then became weaker again.) Cell e had a strong field at theL location on the first lap only and then became relatively quiet. Cell f was quiet for the first 10 laps and then developed a completely new field near the end of the session. (A shift in the recording electrode after the subsequent standard session made it impossible to determine what cells e andf did on the second mismatch session of the day.)

The split place fields in the mismatch sessions were often not statically related to the local or distal sets of cues, but rather they sometimes changed their firing properties within the course of the session. Figure 4B plots the lap-by-lap firing of six representative cells in different mismatch sessions. The position along the track is plotted in degrees on the abscissa, and the lap number is on the ordinate. In Figure 4Ba, the cell initially fired on the first lap in a location consistent with the distal cues and then split its field for the next few laps and finally fired almost exclusively with the local cues. Figure 4Bb shows the same cell recorded during the second mismatch session of that day, in which the cell initially followed the distal cues and then split its field and maintained a split field for the rest of the session. Figure4Bc shows a cell that initially rotated slightly CCW, under-rotating the local cues, but after a few laps developed a new subfield consistent with the distal cues. Figure 4Bdshows the same cell as in Figure 2 (cell 7), in which the cell initially fired sparsely during the first half of the mismatch session and then developed a split field at both the local and distal locations. Figure 4Be shows a cell that followed the local cues for the first lap before losing its place field. Finally, Figure 4Bf shows a cell that did not have a place field in the standard session, but in the mismatch session it developed a field that increased in strength over time. Such dynamic changes in the firing locations occurred in 27 cells, judged by visual inspection of the firing positions over time; it is possible that quantitative changes occurred in a number of other cells that were not large enough to be discerned through inspection of the place fields. Examples of dynamic changes were observed in the first mismatch sessions experienced by some rats (e.g., Fig. 4Bc), as well as in subsequent mismatch sessions on later days.

Cells with overlapping place fields

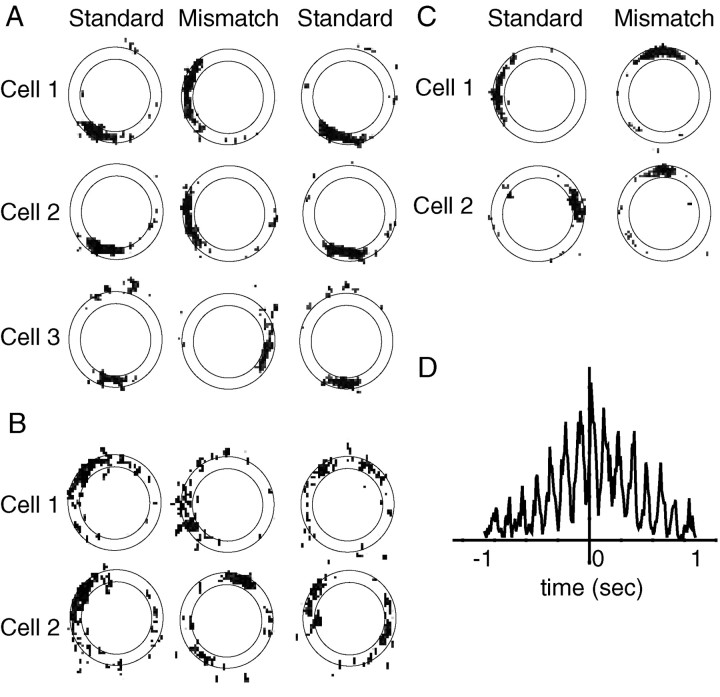
In continuous attractor models of place cells, cells with overlapping place fields are hypothesized to be bound together in a strong attractor basin. It is possible that place cells form strong attractors, but the place fields that rotate in opposite directions are located on different parts of the track. That is, it could be that all of the cells that represent the 12 o'clock location form a stable attractor that follows the distal cues, and all of the cells that fire at 3 o'clock form a stable attractor that follows the local cues. To address this issue, 25 cell pairs were identified in which the place fields overlapped in the standard session (defined as the peak correlation between the two cells occurring when the place fields were rotated ±10° from each other, and the peak correlation being >0.75; see Materials and Methods) and in which both cells rotated their fields in the rotation session (i.e., neither lost its field). The 45° mismatch sessions were excluded from this analysis. Of these cell pairs, 8 rotated in opposite directions, and 17 rotated in the same direction (Fig.5A,B). In comparison, 17 cell pairs (different from the previously mentioned cells) were identified in which the place fields occurred 170–190° apart; of these pairs, 4 rotated in opposite directions, and 13 rotated in the same direction. The proportions of cells rotating together and opposite did not differ between the 25 pairs of overlapping fields and the 17 pairs of nonoverlapping fields (χ² = 0.36; NS), thus showing that cells that fired on the same location on the track were no more strongly coupled than cells that fired on opposite locations on the track.

Fig. 5.

Place fields that overlap in standard or mismatch sessions. A, Of these three simultaneously recorded cells that had overlapping place fields in the standard session,Cells 1 and 2 rotated CW to follow the distal cues and Cell 3 rotated CCW to follow the local cues. B, Two simultaneously recorded cells that had overlapping place fields in the standard session. Cell 1rotated CCW, and Cell 2 rotated CW in the mismatch session (with a slight subfield rotating CCW). Cell 2retained the subfield in the subsequent standard session. Thus, the subfield initially followed the local cues in the mismatch session but then followed the distal cues when they were rotated back to the standard configuration. C, Two simultaneously recorded cells that had place fields originally ∼180° apart. During the mismatch session, the place fields followed different sets of cues and now overlapped. D, A cross-correlogram demonstrates that the two cells in C fired many spikes within 10 msec of each other. The strong rhythmicity in the correlogram is caused by the strong modulation of the cells by the theta rhythm.

A converse test is to look at the place fields that overlap in the mismatch sessions as a result of the cue rotations. Figure5C shows an example of two cells that fired ∼180° apart during the standard session. During the 180° mismatch session, cell 1 rotated with the distal landmarks and cell 2 rotated with the local landmarks, such that the place fields now overlapped. There were 11 examples in which cells that initially had nonoverlapping place fields in the standard session rotated in opposite directions, such that their fields overlapped in the mismatch session. It is possible that although the fields overlapped spatially, they may have been temporally independent (e.g., each cell firing on alternate laps or, within a lap, a rapid alternation between the firing of each cell). If this temporal independence were observed, it would suggest that these two cells were still components of different attractor states (Gothard et al., 1996b;Skaggs and McNaughton, 1998). A cross-correlation analysis (Fig.5D) shows, however, that these two cells fired many spikes within 10 msec of each other, and there is no discernible gap in the cross-correlogram, thus indicating that these cells fired simultaneously (within a resolution of 10 msec). None of the 11 examples showed any indication of a gap in the cross-correlogram.

Precision of cue control

For each cell of the 90, 135, and 180° mismatch sessions, the deviation from absolute cue control was calculated by subtracting the amount that the place field had rotated from the amount that the cues had rotated. The cells that followed the distal cues tended to under-rotate by an average of 7.1° (p < 0.01; sign test), whereas the cells that followed the local cues under-rotated by an average of 1.6°, which was not significantly different from 0 (sign test) but was significantly different from the distal cells (p < 0.05; Mann–WhitneyU). This would suggest that the cells that rotated CCW were more strongly bound to the local cues than the cells that rotated CW were bound to the distal cues. This interpretation is confounded, however, by a recently demonstrated phenomenon by Mehta and colleagues (Mehta et al., 1997, 2000; Ekstrom et al., 2001) that place fields tend to expand and shift in the direction opposite to the rat's movement in stereotyped, unidirectional trajectories such as in the task here. If this CCW shift were greater in the mismatch sessions than in the standard sessions, it might produce an artificial difference in the precision of control by the two sets of cues. To test for such an influence, we calculated the center of mass of each place field on a lap-by-lap basis and subtracted it from the center of mass of the place fields averaged over all laps, according to methods described in Mehta et al. (1997) (Fig.6A). For the first standard session, the place fields clearly shifted back over the course of the session. In the first mismatch session, the place fields appeared to shift by a greater extent. Similarly, the amount of shift in the second standard session was less than that in the second mismatch session (Fig. 6B). A two-factor ANOVA showed a significant main effect of lap number (F_(14,14337) = 11.06;p < 0.001), no significant main effect of session number (F_(4,14337 = 2.84; NS), but a significant lap number × session interaction (F_(56,14337) = 5.09; p< 0.001). These results are consistent with the interpretation that the apparent difference in local versus distal control may be an artifact of the backward-shift effect. To test this interpretation further, the firing of the place cells during the first two laps of each session were analyzed to determine the initial locations of the place fields. There were no differences between the local- and distal-controlled cells during the first two laps, as both of them rotated precisely, on average, with their respective sets of cues (deviation from local cues 2.17 ± 2.74°; distal cues −1.25 ± 3.52° deviation).

Fig. 6.

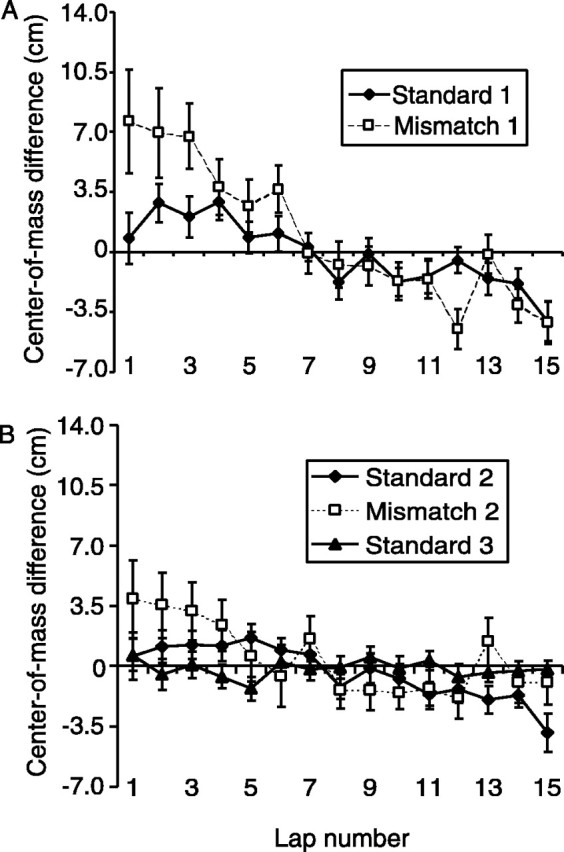
The experience-dependent, backward-shift effect ofMehta et al. (1997).  A, The center of mass of each place field was calculated on each lap that the rat ran, and this lap-specific center of mass was subtracted from the center of mass of the place field calculated from the average of all laps in the session. In the standard session (black dots), the center of mass of place fields shifted in a direction opposite to the trajectory of the rat. In the first mismatch session (open squares), this backward shift was greater than in the standard session. B, The magnitude of the effect decreased in subsequent sessions (Standard 2 and Mismatch 2), although the shift was still greater for theMismatch 2 session compared with Standard 2. The effect was absent by the last standard session (Standard 3).

Interneurons

According to some theorists, a decrease in interneuron firing rate may be associated with the ability to perform pattern completion on a degraded input (Marr, 1971; McNaughton and Morris, 1987). It is possible that the mismatch sessions induced such a reduction in interneuron firing rates, thereby reducing the overall inhibition in the system, which may have led to the disruption of the stable attractors. The mean firing rates of 24 interneurons were calculated for the standard and mismatch sessions. There was a small increase in the mean firing rate between the first standard and the first mismatch sessions (0.74 Hz increase; p < 0.002; pairedt test) and between the second standard and second mismatch session (0.39 Hz increase; p < 0.05; pairedt test). These small increases are most likely the result of the increased running speed of the animals over the course of the day (Czurko et al., 1999). Thus, it is unlikely that the instances of dual control were the result of a decrease in inhibition causing the weakening of the attractor basins in the network.

DISCUSSION

This study demonstrated that, under certain conditions, the ensemble representation of space in the hippocampus can split into two independent representations. When salient local cues were rotated in opposition to salient distal landmarks, a subset of place fields followed the local cues while a simultaneously recorded subset followed the distal landmarks (and other cells changed their place fields unpredictably). In addition to lending support to recent studies that demonstrate a hitherto under-appreciated influence of local cues on place cells (Young et al., 1994; Gothard et al., 1996a; Shapiro et al., 1997; Save et al., 2000; Zinyuk et al., 2000; Knierim and McNaughton, 2001), these results have important consequences for attractor network models of place fields.

Continuous attractor models propose that the place cell representation is stabilized by place cells with similarly located place fields having excitatory connections between them, and the strength of excitation decreases as the distance between place fields increases (Samsonovich and McNaughton, 1997; Doboli et al., 2000; Kali and Dayan, 2000). Furthermore, to increase the stability of the attractors, inhibitory connections limit the number of simultaneously active neurons. As a result of this architecture, random input into the system quickly coalesces into a coherent local energy well in which a single “bump” of activity is present that forms the representation of a single location in an environment (Wang, 2001). If these attractors are sufficiently strong, then these models would predict (1) in a single data set, place cells would either follow the local set of cues or the distal set of cues, but not both; (2) overlapping place fields in the standard session would all follow the local cues or distal cues; (3) place cells that fired at different locations on the track in the standard session, as part of different attractor states, would not fire simultaneously when they overlapped during a mismatch session; and (4) individual place fields would follow one set of cues or the other and not split their firing fields in two. All of these predictions were disproved in this experiment. The interpretation and implications of these results must be considered in light of the other evidence and theoretical arguments in favor of attractor networks in the hippocampus (Gothard et al., 1996a; McNaughton et al., 1996; Tsodyks et al., 1996;Samsonovich and McNaughton, 1997; Battaglia and Treves, 1998).

The simplest model to explain the main results is shown in Figure7A. In this model, individual place cells are controlled by distinct sets of external landmarks, with negligible interactions between them (Fig. 7A,left). Thus, when the cue sets are rotated in opposite directions (Fig. 7A, right), the local fields follow the local cues and the distal fields follow the distal cues. Although this simple model would explain some of the data presented here, it does not explain why the place fields mostly under-rotated in the 45° mismatch sessions, nor does it account for the dynamic properties illustrated in Figures 4 and 6. The model is also not compatible with numerous results in the literature of place cells, including the known presence of extensive connections between hippocampal pyramidal cells, both within CA3 and between CA3 and CA1; theoretical arguments on the utility of attractor networks in generating the properties of associative memories; and experimental results that support the predictions of attractor networks (Gothard et al., 1996b; McNaughton et al., 1996; Brown and Skaggs, 1999; Knierim and McNaughton, 2001). It thus appears necessary to incorporate this type of circuitry into the model, in a way consistent with the present data.

Fig. 7.

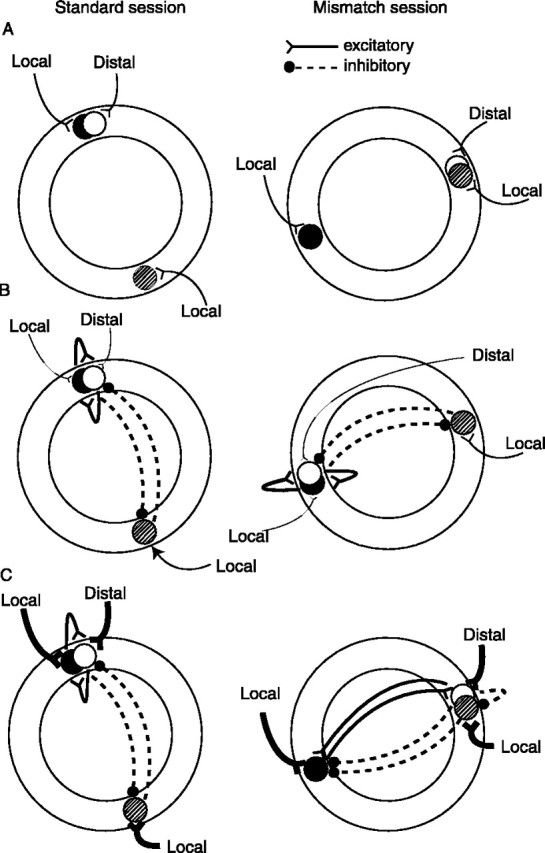
Extrinsic versus intrinsic inputs onto place cells. Distal is shorthand for distal-dominated inputs;local is shorthand for local-dominated inputs.A, A model in which only extrinsic inputs from external cues drive place cells can explain the main effects, but it fails to account for the subtle nonlinear effects of place cells. In this model, remapping might result from cells that are controlled by exact configurations of local and distal cells and become silent or active when presented with new configurations in the mismatch session (AND-gated cells). Split place fields might result from cells that are controlled by either the local or the distal cues (OR-gated cells). B, In a network in which the input from external cues is weak compared with the intrinsic circuitry, the responses of place cells will be dominated by the attractor dynamics of the intrinsic circuitry. Although in this example the local cues dominate over the distal cues, in another session or in another rat, the cells might follow the distal cue set, but they will do so as an integrated ensemble. The differential sensitivity to local versus distal cues does not imply that the black cell is sensitive only to local cues and the white cellsensitive only to distal cues. More likely, each cell gets input from both sets, but because of stochastic differences in input strengths, the black cell has somewhat greater input from local cues, and the white cell has somewhat greater input from distal cues. The differential sensitivity also does not imply that the inputs onto these cells are directly from pure sensory representations of these cues. It is probable that the direct inputs onto place cells are from an intermediary set of cells that are themselves controlled by the cues in complex ways (e.g., head direction cells and entorhinal cortex cells). C, In a network in which the inputs from external cues are much stronger than the intrinsic circuitry, the external cues can dominate over the attractor dynamics, leading to the range of dynamic effects seen when the cues are rearranged. As a result, the white and stippled cells are allowed to fire together because they are being driven by their respective cue sets more strongly than they are being controlled by the intrinsic attractor dynamics. Similarly, the white cellbecomes decoupled from the black cell because the input from the external cues is stronger than the excitatory connections between the two cells. One way in which split place fields might emerge is if certain individual cells are controlled equally by one set of external cues and by other place cells that are controlled by the other set of cues. Cells that gain or lose fields or rotate to arbitrary orientations might result from subsequent alterations in the attractor basins of the network.

Figure 7B (left) shows a situation in which the white and black place cells, overlapping in space, mutually excite each other and also take part in a global inhibitory network with other place cells. In addition, the cells maintain their differential sensitivity to the local and distal cue sets. In this example, the inputs from the external cues are weak compared with the intrinsic circuitry within the hippocampus—a situation likely to be encountered in a novel environment or in an environment with unstable landmarks if the system has to “learn” to incorporate the landmarks into the representation (Knierim et al., 1995; McNaughton et al., 1996;Samsonovich and McNaughton, 1997; Jeffery and O'Keefe, 1999)—and the network response is thus dominated by the internal attractor circuitry when the cues are counter-rotated (Fig. 7B,right). In this example, the local cues are slightly more dominant overall than the distal cues, and the attractor circuitry causes the entire representation to follow the local cues.

Figure 7C shows the results of a situation in which the environment is familiar and well explored, such as in the present experiment. In this situation, the local cues and the distal cues are equivalent in salience and perceived stability, and because of a long period of previous experience in a stable environment, the inputs from these external cues are very powerful (McNaughton et al., 1996). In this situation, during the mismatch session (Fig. 7C,right) the response of the cells is dominated by the extrinsic connections rather than by the intrinsic circuitry, thus allowing the cells that are dominated by distal cue inputs to rotate CW and the cells dominated by local cue inputs to rotate CCW. Depending on the exact patterns of connectivity strengths on each place cell and on nonlinear integration mechanisms, different patterns may arise. In some cases, the excitatory connections may cause a cell to be controlled by both sets of cues; that is, the white cell may follow the distal cue set as it is driven by these cues, but the connections between it and the black cell may cause it to also follow the black cell and be controlled by the local cues, thus resulting in a split place field. Another result of the new arrangement of place fields is that the white and stippled fields now overlap spatially and temporally, such that the strength of excitatory connections between these two cells can begin to increase, leading to the greater backward shift of place fields (Mehta et al., 1997, 2000; Ekstrom et al., 2001) demonstrated in Figure 6. The new configurations of place fields may begin to alter the attractor basins in the network, which may result in remapping over time (Sharp et al., 1995; Lever et al., 2002), as well as in the formation of new subfields. That is, when the cues are rotated back to their standard configurations, the strengthened intrinsic connections between the white and stippled cells may cause the white cell to develop a new subfield 180° away in the standard session (e.g., Fig. 2, cell 3, and Fig. 4B, cell 2).

The attractor circuitry may be critical in the initial formation and stabilization of a representation of an environment. As external landmarks and other locations of behavioral significance become incorporated into the map over time, the strengths of these inputs may begin to predominate over the attractor circuitry. In certain conditions, however, the attractor circuitry may still play important roles in hippocampal function. For example, in situations in which only modest changes occur in an environment, the attractor circuits may allow the hippocampus to maintain a coherent, stable representation of the environment (O'Keefe and Conway, 1978; O'Keefe and Speakman, 1987). When external inputs are eliminated or reduced, such as in the dark, the attractor circuitry allows the animal to maintain its representation of location with the use of purely internal navigation mechanisms (Samsonovich and McNaughton, 1997; Whishaw et al., 1997). Finally, during sleep, when the input from external sources is minimal or absent, the system again becomes dominated by the internal attractor circuitry, perhaps allowing the reactivation of learned experiences that may play a role in memory consolidation in the neocortex (Buzsaki, 1989; Pavlides and Winson, 1989; Wilson and McNaughton, 1994).

It remains for future work to determine whether different results might apply if the present experiment were repeated in a novel environment, before the formation of strong associations with external landmarks is possible. It is also possible that the external inputs initially dominate the firing of place cells and that the attractors form over time as the result of synaptic modifications of the recurrent circuitry in the hippocampus. If this is true, it suggests that the 6–21 previous training sessions were inadequate to promote the formation of strong attractors in this experiment. In addition, the schematic model presented in Figure 7 needs to be tested in a computational simulation to determine whether the results obtained in this experiment can be simulated with an interaction between strong external cue inputs and relatively weaker internal attractor circuitry. Finally, these results are dominated by CA1 recordings. Although DG and CA3 cells displayed effects such as split place fields, the small number of cells recorded from these areas makes it impossible to test whether either one of them displays much stronger attractor dynamics than CA1. Considering that the CA3 and DG regions have the recurrent collateral circuitry critical for the formation of potential attractors, it is imperative to compare the areas more quantitatively than that allowed with the present data. It is conceivable that the hypothesized strong attractor circuitry may reside in these areas and that the results reported here reflect the inputs in CA1 not only from the CA3 Schaffer collaterals but also from the direct pathway from the entorhinal cortex to CA1. If future recordings of CA3 and dentate gyrus fail to support the predictions from attractor models, then that would provide a more compelling case against the validity of these models. In any event, further experiments that probe the experience dependence of these effects in CA1, CA3, dentate gyrus, and entorhinal cortex may provide valuable insight into the different functional roles of these areas and into the changes in hippocampal representations as an animal gains familiarity with an environment.