Neural Coding of the Location and Direction of a Moving Object by a Spatially Distributed Population of Mechanoreceptors

Abstract

A neural code for the location and direction of an object moving over the fingerpad was constructed from the responses of a population of rapidly adapting type I (RAs) and slowly adapting type I (SAs) mechanoreceptive nerve fibers. The object was either a sphere with a radius of 5 mm or a toroid with radii of 5 mm on the major axis and either 1 or 3 mm on the minor axis. The object was stroked under constant velocity and contact force along eight different linear trajectories. The spatial locations of the centers of activity of the population responses (PLs) were determined from nonsimultaneously recorded responses of 99 RAs and 97 SAs with receptive fields spatially distributed over the fingerpad of the anesthetized monkey. The PL at each moment during each stroke was used as a neural code of object location. The angle between the direction of the trajectory of the PL and mediolateral axis was used to represent the direction of motion of the object. The location of contact between the object and skin was better represented in SA than in RA PLs, regardless of stroke direction or object curvature. The PL representation of stroke direction was linearly related to the actual direction of the object for both RAs and SAs but was less variable for SAs than for RAs. Both the SA and RA populations coded spatial position and direction of motion at acuities similar to those obtained in psychophysical studies in humans.

Humans can readily perceive, by tactile cues alone, the location and direction of an object moving over the skin (Bender et al., 1982). Such cues are used, for example, to maintain appropriate contact with an object during manual exploration and manipulation. The location and direction of a moving object are not represented by the responses of single mechanoreceptive afferent fibers or which fibers are active at a given instance. The effects of location and direction on the discharges of an individual fiber are easily confounded by variations in the velocity of the object, contact force, and spatial features to which the fiber also responds (Johnson, 1974; LaMotte and Srinivasan, 1987a,b; Cohen and Vierck, 1993; Essick and Edin, 1995; Goodwin et al., 1995). Therefore, only a spatially distributed population of mechanoreceptors would have the ability to unambiguously code the spatial location and direction of a moving object.

The “spatial event plot” (SEP) (cf. Johnson and Lamb, 1981) has been used to estimate the response of a spatially distributed population of mechanoreceptive afferents to an object applied to the skin. The SEP plots the location of the object on the skin at each occurrence of an action potential as the object occupies sequential loci within the receptive field of a mechanoreceptor (Johnson, 1974). The SEP is interpreted to represent how a spatially distributed population of afferents having similar properties would respond to an object that is centrally located on the skin. However, there are limitations to the inferences that can be made from SEPs. First, the properties of individual afferents differ widely, particularly in response sensitivity. Second, because SEPs are interpreted as a representation of the population response at only a single instance in time, they have not been used to represent the changing location and direction of a laterally moving object.

A second approach to study population coding in the periphery is to record from a representative population of individual afferent fibers with receptive fields that are spatially distributed over the skin (Ray and Doetsch, 1990a,b; Khalsa et al., 1998; Bisley et al., 2000). An advantage of this approach is that the population response includes variations in fiber sensitivity partially because of the geometry of the fingerpad (i.e., differences in receptive field location). In the present study, we used this approach to determine how populations of spatially distributed slowly adapting type I (SAs) and rapidly adapting type I (RAs) mechanoreceptive afferents code the location and direction of objects of differing shape and orientation stroked in a linear trajectory across the monkey fingerpad.

MATERIALS AND METHODS

Twenty-three experiments were performed on five anesthetized, adult male monkeys. The monkeys were four Macaca mulata and one Macaca fascicularis. Standard teased fiber neurophysiological techniques were used to record from mechanoreceptive afferents (Khalsa et al., 1998; LaMotte et al., 1998). All procedures were approved by the Animal Care and Use Committee of Yale University.

Stimulus objects. The three smooth objects of differing eccentricity were a sphere, with a radius of 5 mm (curvature of 200 m⁻¹), and two toroids with radii of 5 mm on the major axis (curvature of 200 m⁻¹) and 1 or 3 mm on the minor axis (curvatures of 1000 and 333 m⁻¹, respectively).

Tactile stimulator. The apparatus used to stimulate the monkey fingerpad has been described in detail previously (Khalsa et al., 1998; LaMotte et al., 1998). In brief, the toroids and sphere were glued to a platform that was attached through a lever arm to a torque motor (model 301B; Aurora Scientific, Aurora, Ontario, Canada). The torque motor was used to maintain a constant contact force of the object against the skin. The motor was mounted to a rotary platform used to position and rotate the object about its center to a desired orientation within the horizontal plane before applying the object to the skin. The rotary platform was mounted to a three-axis (x, y, and z) translation table (Anorad, Hauppauge, NY) used to move the object along a linear trajectory in the horizontal plane.

The backs of the index, middle, fourth, and fifth fingers were glued to finger holders. The holder of the finger under study was adjusted to an angle of 30°; the other holders were horizontal (0°). Before stimulation, a light coat of hand lotion was applied to the finger to reduce the lateral friction and drag, and, thus, the lateral displacement of the fingerpad as the object was stroked over the skin.

Stroke paradigm. The stimulus object was rotated in the air above the fingerpad to one of four orientations: 0, 45, 90, or 135°, in which 90° was parallel to the long axis of the finger, and 0° was perpendicular to this axis but was parallel to the mediolateral axis of the finger. The torque motor then indented the object into the center of the fingerpad to a force of 147 mN (15 gm weight). Depending on the shape and orientation of an object, the range of indentations of the fingerpad at the center of indentation was 3.3–4.2 mm. The location of the center of indentation was midpoint between the medial and lateral sides of the fingerpad and, along the long axis of the finger, was defined as the point located one-third of the distance from the distal end of the fingerpad or phalanx to the crease over the distal interphalangeal joint. After 4 sec of static indentation, the object was moved across the skin 3.5 mm to the starting point of the stroke trajectory. There were eight starting points differing by increments of 45° in the horizontal plane: 180° (from right to left), 0° (from left to right), 270 and 90° (distal to proximal and proximal to distal), and 225, 45, 315, and 135° (the four diagonals). The object was stroked back and forth across the skin along a given trajectory. From each starting point, the object was stroked six times in a given direction. For each trajectory, the long axis of the toroid was oriented either parallel or orthogonal to the stroke direction. Each stroke trajectory had a length of 7 mm. Each toroid with its major axis oriented orthogonal to the stroke trajectory was stroked six times back and forth in the 180 and 0° directions. Then the toroid, with its major axis oriented parallel to the stroke trajectory, was stroked back and forth in the 270 and 90° directions. Next, this sequence of stroke directions was repeated, except with the orientation of the major axis of the toroid reversed. After presenting, in order, the 1 × 5 and 3 × 5 mm toroids, the sphere was stroked six times back and forth in the 180 and 0° and then 270 and 90° directions. A similar presentation pattern was used for the diagonal stroke directions. Stroke velocity was 10 mm/sec. The peak rate of acceleration and deceleration at the onset and end of the stroke was 100 mm/sec². The compressive force of 147 mN was maintained throughout the stroke.

Characterization of the response of an afferent. Standard procedures were used to classify a mechanoreceptive afferent as either SA or RA mechanoreceptor according to standard methods of classification (Vallbo and Johansson, 1984; Srinivasan and LaMotte, 1987). Calibrated nylon filaments (Stoelting, Chicago, IL) were used to map out the borders of a receptive field of an afferent and to obtain the spatial location of the most sensitive spot (MSS) within the receptive field. The MSS was defined as the location on the fingerpad at which the filament with the lowest bending force evoked an action potential 50% of the time. The MSS was used as the receptive field location of the fiber on the finger in the construction of the population response.

For each fiber and stroke, a profile of discharge rate as a function of object location was constructed by dividing the stroke into bins of 0.2 mm (n = 35 for a 7 mm length stroke). For a stroke velocity of 10 mm/sec, these were 20 msec time bins. The method of fractional interval binning was used to generate a continuous spike rate response profile over time (Richmond et al., 1987; Nawrot et al., 1999). For each afferent, the response profiles were averaged across the six repetitions in a given direction and converted to discharge rates by dividing each bin by the bin width (Fig.1A).

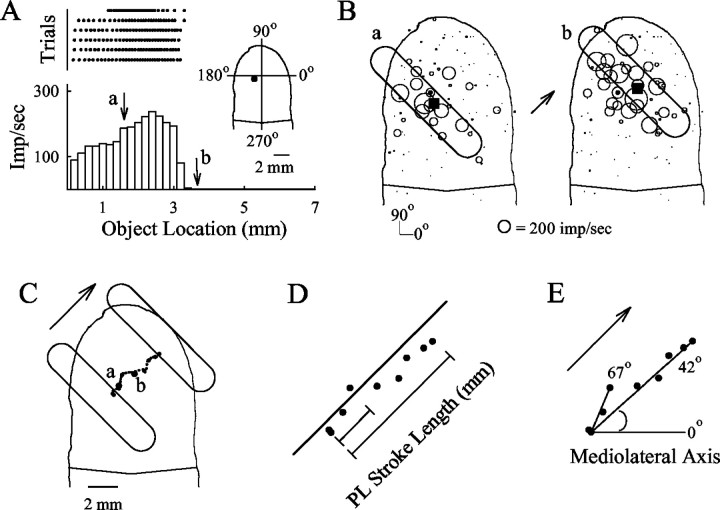
Fig. 1.

Method of determining the locations of the centers of the population responses. An example is given of the responses of a single SA fiber to the 1 × 5 mm toroid stroked in a 45° stroke trajectory. A, In the top panel, each dot in a row marks the location of the center of the toroid at the occurrence of an action potential during a single stroke. The six rasters, fromtop to bottom, show the responses to strokes of the object in the 45° direction (from the bottom left to the top right of thefingerpad). Bottompanel, A histogram of the mean discharge rate of the fiber after fractional interval binning (bin size, 0.2 mm or 20 msec). Arrows a, b, The discharge rates of the afferent during two discrete instances shown in B during the stroke.Inset, Location on the fingerpad of the MSS in the receptive field of the fiber (dot). B, SA populaton response locations (PLs) at discrete instances (a and b in A) during the stroke. Each open circle indicates the location (MSS) and magnitude of the discharge rate of each fiber (1 mm diameter is equal to 100 impulses/sec). The PL (black square) was determined by calculating a center of neural activity in which the contribution of each fiber was made proportional to the discharge rate of the fiber at the indicated object location during the stroke. Thelargerblack circle marks the MSS of the SA fiber shown in A. The location of the object is indicated by the schematic outline of the object (base circumference).Arrow, The direction of motion. C, Succession of PLs determined for the entire stroke. Thearrow and the schematic outlines of the object indicate, respectively, the stroke direction and location of the object at the beginning and end of the stroke. The PLs at instances aand b in B are also shown.D, The position of a PL in the axis parallel to the direction of the stroke direction was taken as the distance in millimeters separating the PL at the beginning of stroking (after 0.2 mm of travel) and a PL at a successive instance (0.2 mm bin) during the stroke, only two of which are shown. Black circles, Nine different PLs during the stroke. E, The direction of the PL trajectory was calculated from the angle between the direction of the PL trajectory and the mediolateral axis. Two directions of the PL trajectory are illustrated, each defined by the angles between the PL at the beginning of the stroke (after 0.2 mm of object movement) and a subsequent PL occurring at given instances during a stroke. These angles were used to evaluate the effects on direction coding of changes in object stroke length and the number of instances used.

Construction of the neural population responses. The neural population response consisted of the average discharge rate of each afferent for a given instance (0.2 msec bin) during the stroke [converted to impulses per second (imp/sec)] mapped to the spatial location of its MSS (Fig. 1B). For each object orientation and curvature and direction of motion, population responses were determined for successive instances during the stroke.

The population responses to stroked objects were reconstructed from electrophysiological recordings obtained in 23 experiments, from 97 SAs and 99 RAs spatially distributed on the glabrous skin of the distal fingerpads of the index, middle, fourth, and fifth finger. The average size of the monkey fingerpads was 8.7 mm wide and 12.6 mm in length from the distal end of the fingerpad to the crease of the distal interphalanegeal joint. The mean density of the 97 SA and 99 RA fibers within this area (∼110 mm²) was 0.88 SAs/mm² and 0.9 RAs/mm². These population densities were comparable with those reported by Darian-Smith and Kenins (1980) for the primate fingerpad.

To construct a population response for a single fingerpad, the absolute location of each MSS (in millimeters in planar X,Y Cartesian coordinates), relative to the center of indentation of the object on the fingerpad (0, 0 mm; coordinate intersection in the inset in Fig. 1A), was mapped onto a two-dimensional schematic drawing of the average size of a monkey fingerpad. Because individual fingerpads varied in size and curvature, the planar map of the MSSs was only an approximation of the absolute locations of the MSSs. For similar reasons, the planar location of the object during the 7 mm stroke only approximated the location of the object on the skin surface. We reconstructed the population response within a planar frame of reference because it was constant across experiments.

Determination of the location of the center of the population response. At each position of the object, in bins of 0.2 mm during the stroke, the location of the center of activity of the population response on the skin or population response center location (PL) was calculated. The contribution of each fiber to the PL was made proportional to the discharge rate of the fiber. Thus, to calculate the PL, for all of the X coordinates and separately for all of the Y coordinates, the product of the discharge rate (r) for each fiber and the coordinate value of its MSS (x or y) was summed from all fibers and divided by the summed total discharge rates of the fibers:

$$x_{\text{center}}=\frac{\mathrm{\Sigma }x\times r}{\mathrm{\Sigma }r} \text{and} y_{\text{center}}=\frac{\mathrm{\Sigma }y\times r}{\mathrm{\Sigma }r}.$$

PLs were determined for each 0.2 mm bin of a stroke of an object across the fingerpad (Fig. 1C), forming a trajectory of PLs.

To be distinguished from a trajectory of PLs, a PL trajectory was defined as a line connecting two PLs, the first at the onset of stroking (after 0.2 mm of travel) and the second at an arbitrary position of the object during or at the end of the stroke. Thus, the PL trajectory represented a neural code of both the direction of motion of the object and the length the object had traveled at a given instance during the stroke (Fig. 1D,E).

Population coding of the object trajectory. The coding of the location of the object by the PL was determined by comparing the location of the object at the beginning, along, and at the end of the stroke and was evaluated for the SAs and RAs as a function of the curvature, orientation, and direction of motion of an object.

Population coding of stroke length. The total length of the trajectory of PLs was defined as the distance separating the PLs at the beginning (after 0.2 mm of travel) and at the end (7 mm of travel) of the stroke (Fig. 1D). The total lengths of the PL trajectories were compared for the SAs and RAs as a function of the curvature, orientation, and direction of motion of an object.

Population coding of the increments in object location. To evaluate how well SAs and RAs coded the increment of travel along the trajectory of the object, for each object, object orientation, and direction of stroking, the locations of the SA and RA PLs in the axis parallel to the stroke direction were obtained for each 0.2 mm of travel. The PLs were plotted as a function of the location of the object during the stroke. To evaluate the linearity in the relationship between the locations of the object during the stroke and the PLs, a regression analysis was used to obtain the Pearson correlation coefficient (r), slope, and sums of square error of the best-fitting line. The slope of the function was used to evaluate the relationship in the increments of travel (in millimeters) between the object location and PL. The sum of square error was used as a measure of the variability in the progression of the PLs along the stroke trajectory.

Population coding of differences in object location. Differences in the positions of the PLs during the stroke were used to determine how well SAs and RAs coded differences in the location of the object. The position of the PL was defined as the distance in millimeters separating the PL at the beginning of stroking (after 0.2 mm of travel) and the PL at a successive instance (0.2 mm bin) during the stroke in the axis parallel to the direction of the stroke direction. This analysis excludes the contribution of the absolute offsets between the PL and object during the stroke. Positions of the SA and RA PLs were obtained for each object and orientation and for all directions of stroking for each increment of 0.2 mm of travel of the object along a trajectory.

The minimal increment in object travel evoking a significantly different PL position was determined statistically (ANOVA, followed by a Bonferroni multiple comparison method). In the case in which we examined the significantly different PL positions along the same trajectory, differences in the PL positions were evaluated by treating the stroke trajectory of the object as a repeated variable in the statistical analysis. In the case in which we examined the significant differences in PL positions across different object trajectories, the object stroke trajectory was treated as a nonrepeated variable. Separate Bonferroni comparison procedures were used to compare the position of a PL for different increments of travel of the object with position of a PL at three standard lengths of travel by the object (0.2, 1, and 3 mm). These distances reflect hyperacuity and two point thresholds for the fingerpad (Loomis and Collins, 1978; Loomis, 1979).

Population coding of the direction of motion. The neural code for the direction of motion of an object was defined as the angle between the PL trajectory and mediolateral axis. This angle describing the direction of each PL trajectory was obtained for the SAs and RAs for each of the eight directions of stroking and each object of a given curvature and orientation. The cumulative mean direction of a trajectory of PLs was defined as the sum of the angles of the PLs for each distance of object travel during the stroke divided by the number of PL angles. The cumulative mean direction was plotted as a function of the location of the object during the stroke. To evaluate the relationship between the locations of the object during the stroke and the angles of the PLs, a regression analysis was used to obtain the Pearson correlation coefficient and slope of the best-fitting line. The cumulative mean direction of a trajectory of PLs was plotted against the angle of the trajectory of the object and was evaluated with a regression analysis.

Two different factors, object stroke length and the number of PLs, contributed to cumulative mean direction of a trajectory of PLs. Subsequently, we examined in isolation the effect of changing the length of travel by the object on the relationship between the direction of the PL trajectory and the direction of the object. The direction of the PL trajectory was determined from the angle of a line connecting the PL at the onset of stroking (after 0.2 mm of travel) and the PL obtained when the object reached 1 of 10 different locations during its stroke trajectory (0.4, 0.6, 0.8, 10, 1.2, 1.4, 1.8, 3.2, 3.6, and 7 mm). For each of the 10 different object locations, a regression of the direction of the PL trajectory onto the direction of the object was used to obtain a 95% confidence interval (CI). The 95% confidence interval was used as a measure of the precision with which the SAs and RAs coded the direction of a moving object as a function of the curvature and orientation of the object and the distance traveled.

We also analyzed how the number of PLs used in calculating the direction of the PL trajectory affected the precision of the direction of motion estimate. Different numbers of PLs were used in calculating the direction of the PL trajectory for the initial 1.6 mm segment of travel by the object and the 95% confidence interval with which SAs and RAs coded the direction of motion. The initial 1.6 mm of the stroke trajectory of the object was used because we expected it would be most sensitive to changes in the number of direction of motion estimates used to calculate a mean direction of motion of the PL trajectory. A mean direction of a PL trajectory was the sum of the angles formed by connecting the PL at the onset of the stroke (after 0.2 mm of travel) with the PLs at successive positions of the object in increments of 0.2 mm up to 1.6 mm (i.e., from one to eight increments) divided by the total number of PL angles. The number of angles used to estimate the mean direction of motion was varied from one to eight. The PL at 1.6 mm of object travel was used in every combination of the object locations to keep the final stroke length of the object constant in the calculations. The directions of the PL trajectories were plotted against the angle of the trajectory of the object. For each number of PL angles, a separate regression analysis of the direction of the PL trajectory onto the direction of object motion was undertaken, and a 95% confidence interval was obtained. The number of PL angles used in the regression analyses increased from 8 to 64 as the number of instances used to estimate the direction of motion increased from one to eight for a given stroke trajectory. The 95% confidence interval obtained from each regression analysis described the precision with which SAs and RAs coded the direction of motion of the object as a function of the curvature and orientation of the object and the number of object locations (number of PLs) used to estimate the direction of the PL trajectory.

Statistical analysis. Significance differences between the SA and RA PLs were assessed with ANOVA procedures (SigmaStat; SPSS, Chicago, IL). The main factors in the analyses included the following: mechanoreceptor afferent type (SA and RA; n= 2) and curvature–orientation pairs (1 × 5 mm toroid–perpendicular orientation, 1 × 5 mm toroid–parallel orientation, 3 × 5 mm toroid–perpendicular orientation, 3 × 5 mm toroid–parallel orientation, sphere; n = 5). For most comparisons, the eight different stroke directions were treated as different population samples. Post hoc analyses were applied with the Bonferroni multiple comparison method. The probability criterion for significance for each statistical test wasp < 0.05.

RESULTS

General characteristics of the afferent responses

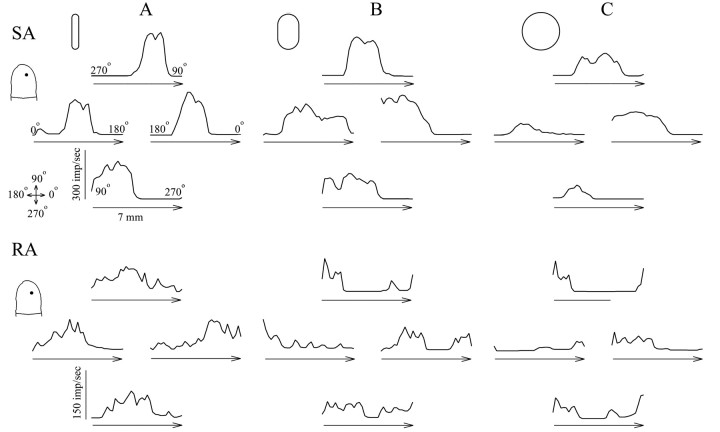
For each fiber and a given object and object orientation, histograms were constructed relating the mean discharge rate (for the six strokes in a given direction) to the position of the object during stroking. The shapes of the histograms (response profiles) differed for the SAs and RAs (Fig. 2). The shapes of the SA response profiles, to these objects, were mound shaped and well fit by Gaussian functions as described previously (cf. Goodwin et al., 1995; Khalsa et al., 1998; LaMotte et al., 1998). The peak discharge rates of the SAs were located over the MSS. The shapes of many of the RA response profiles exhibited two separate areas and peaks in response to the 3 × 5 mm toroid sphere and 1 × 5 mm toroid oriented parallel to the direction of the stroke. The peak discharges in many of the RA response profiles were located lateral to the MSS (Fig.2B,C) (LaMotte et al., 1998).

Fig. 2.

The responses of an SA and RA to objects of differing curvature stroked in four different directions. The histograms show the responses of an SA (top) and RA (bottom) afferent for strokes in directions of 0, 90, 180, and 270° of the 1 × 5 mm (A) and 3 × 5 mm (B) toroidal objects, oriented orthogonal to the direction of motion, and sphere (C), each schematically outlined. Each response profile is a histogram obtained by plotting the mean discharge rate (impulses per second, or imp/sec per 0.2 mm bin), after fractional interval binning, as a function of object position during the stroke for the six strokes of an object in a given direction.Arrow, The direction of the 7 mm stroke of the object. The fingerpad schematics (left) mark the location of the MSS of each fiber (dot). Crossed arrows(left), The coordinate system.

To characterize the response properties of the SAs and RAs, we evaluated the peak discharge rates for each set of experimental conditions (curvature, orientation, and direction). For all conditions, the peak discharge rates were less for the RAs (mean ± SD, 31.9 ± 33.7 imp/sec) than for the SAs (mean ± SD, 92.5 ± 92.1 imp/sec; p < 0.001; two-way ANOVA; fiber type × object curvature orientation). The large SDs were a consequence of a wide range of peak discharge rates elicited by any given fiber for the different stroke trajectories of the object. This occurred because the object entered the receptive field of an afferent during some trajectories but not others.

Peak discharge rates increased significantly with object curvature (p < 0.001). For the SAs, the peak discharge rate evoked by the 1 × 5 mm toroid oriented orthogonal to the direction of stroking (mean of 145.8 imp/sec) was significantly greater than that for 3 × 5 mm toroid oriented orthogonal (97 imp/sec) and any of the other object orientations (sphere, 78.3 imp/sec; 1 × 5 mm toroid stroked parallel, 80.4 imp/sec; 3 × 5 mm stroked parallel, 76.8 imp/sec; Bonferroni post hoc multiple comparison method; all p values < 0.05). For the RAs, only the peak discharge rate evoked by the 1 × 5 mm toroid oriented orthogonal to the direction of stroking (mean of 56.6 imp/sec) was significantly greater than the rate elicited by any other object or object orientation (grand mean of 27.1 imp/sec; all pvalues < 0.05).

The discharge rates of fibers differed in response to opposite directions of stroking of an object along a given trajectory (Fig. 2) (cf. LaMotte and Srinivasan, 1987a,b; Essick and Edin, 1995). To characterize these differences, the percentage of change in the differences in the peak discharge rates evoked by objects stroked in opposite directions along the same stroke trajectory was calculated. The percentage of change in peak discharge rates was greater for the RAs (mean of 54.2%) than the SAs (47.4%; two-way ANOVA;p < 0.001; fiber type × object curvature orientation). For both SA and RAs, greater changes in peak discharge rates were evoked when the toroidal objects were oriented parallel as opposed to orthogonal to the stroke trajectory (57.5 vs 39.6% for the 1 × 5 mm, and 57 vs 48.4% for the 3 × 5 mm toroid; Bonferroni post hoc multiple comparison method; allp values < 0.05). Therefore, the directional sensitivity observed in the response profiles of an afferent was affected by the orientation of the object.

General characteristics of the population responses

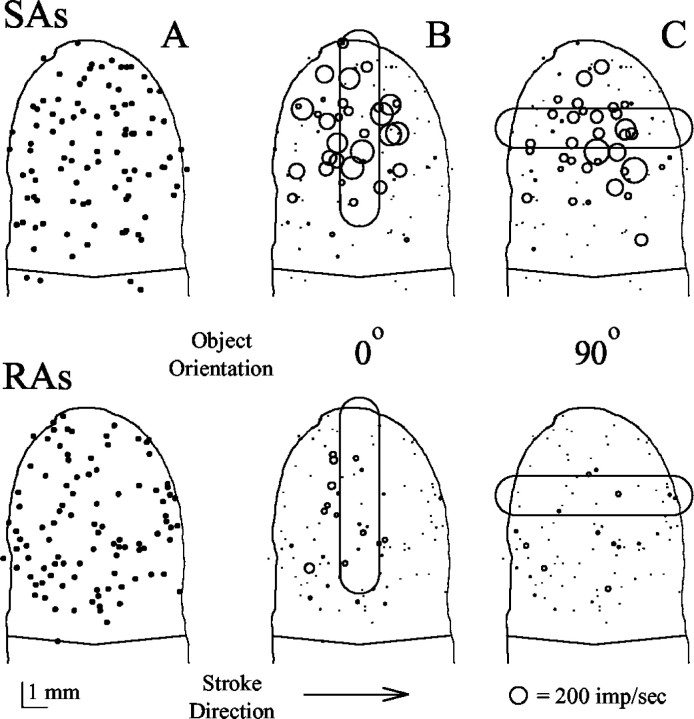
PLs were constructed from the responses of 97 SAs and 99 RAs with MSSs spatially distributed over the fingerpads (Fig.3A). For all three objects, approximately twice as many SA than RA afferent fibers responded with discharges >10 imp/sec to the objects in each bin of a stroke, despite the similar number of fibers in the two populations (Fig.3B,C). The MSSs of responsive SA and RAs included those with locations well beyond the area of contact between the object and skin. The spatial distributions of afferent activity were markedly different in the SA and RA populations. The population of SAs exhibited a gradient of activity with maximal discharge rates centered over the area of contact. A gradient of activity was absent in the response of the RA. The RAs with greater discharge rates were generally located away from the center of contact of the object.

Fig. 3.

The most sensitive spots and the population responses of SAs and RAs at midtrajectory of a toroidal object moving across the fingerpad. A, The location of the MSSs of the 97 SA (top) and 99 RA (bottom) afferent fibers. The absolute locations (in millimeters) of each MSS were mapped onto a representation of a single fingerpad with respect to the center of indentation of the object. The schematic of the monkey fingerpad was based on an average size; therefore, some laterally located MSSs fell outside of the outlines. B, C, Population responses to the 1 × 5 mm toroid stroked from leftto right across the monkey fingerpad. The major axis of the toroid was oriented either perpendicular (0^o) or parallel (90^o) to the direction of stroking (B and C, respectively). Eachcircle indicates the MSS and the magnitude of the discharge rate of each fiber (2 mm diameter is equal to 200 impulses/sec) at the moment the object (outlined schematically) reached the center of its stroke trajectory. Scale bar, 1 mm.

Population coding of the object trajectory

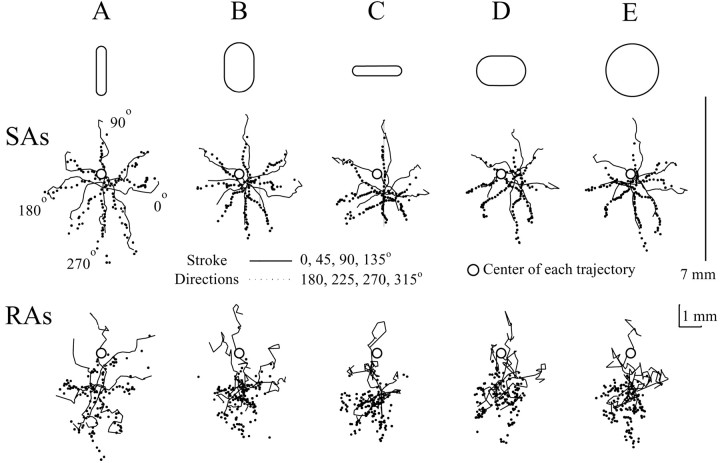
The coding by the SA PLs of successive locations of the object during the stroke and thus the trajectory of the object was evident in the clear star-shaped patterns derived from strokes in the eight directions (Fig. 4). In comparison, the trajectories of the RA PLs were more variable. These results and those described below support the proposition that the SAs coded the location of the object and the direction and length of its trajectory more reliably than the RAs.

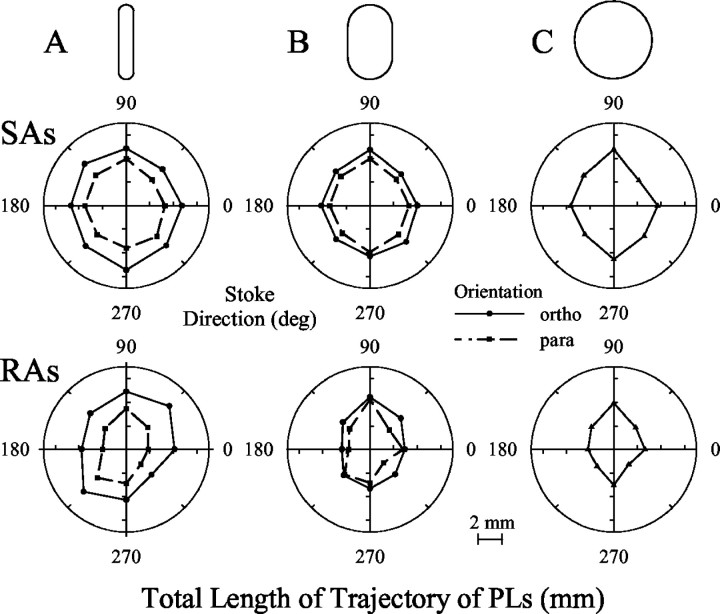
Fig. 4.

The cutaneous locations of the centers of activity of the PLs of SAs and RAs to objects of differing curvature and orientation stroked in different directions over the fingerpad. Thestar-shaped figures show the PLs of the SAs (middle) and RAs (bottom) for strokes in the eight different directions for each object (top, schematically outlined). The 1 × 5 mm (A,C) and 3 × 5 mm (B,D) toroidal objects were stroked either orthogonal (A, B) or parallel (C,D) to the direction of motion. Because a sphere (E) is without a major axis, only one star burst figure is presented. The PLs were calculated after every 0.2 mm of movement of the object during the 7 mm stroke. Solid lines, The PLs for stroke directions of 0, 45, 90, and 135°, in which 90° refers to the tip of the fingerpad (Fig. 1).Dotted lines, The locations of the PLs for stroke directions of 180, 225, 270, and 315°. Open circles, The center of each stroke trajectory. Line, The 7 mm stroke. Scale bar, 1 mm.

The trajectories of the PLs were offset on the skin from the stroke trajectories of the object, and, thus, the centers of the trajectories of PLs were offset from the center of the stroke trajectory of the object (Fig. 4). The center of the trajectory of PLs was calculated by averaging all the X and Y coordinates of the PLs that made up a single trajectory. Instead of being positioned over the trajectories of the object, the center of the trajectory of PLs for the SAs were, on average, offset 0.27 mm to the right (+X) and 0.47 mm proximally on the fingerpad (−Y); the RAs were offset 0.006 mm to the right and 1.6 mm proximally. These offsets seemed to correspond with the average locations of the MSSs of the afferent populations on the fingerpad. The average locations of the MSSs were calculated by determining the mean location of all of the X coordinates and Ycoordinates separately for the SA and RA populations. The average locations of the MSSs were also offset proximally from the center of the stroke trajectories of the objects (SA, X = 0.03 mm, Y = −1.4 mm; RA, X = −0.2 mm,Y = −1.5 mm). Similarly, the weighted center of the trajectory of PLs of the SAs and RAs calculated from the MSSs and the peak discharge rates of afferents recorded during the stroking of an object (as a measure of the sensitivity of a fiber) were also offset proximally. The center of the trajectory of PLs of the RA population (X = −0.18 mm, Y = −1.6 mm) was comparable with the average location of the RA MSSs, suggesting that the sensitivities of the fibers were distributed normally around the fingerpad. The center of the trajectory of PLs of the SA population (X = 0.03 mm, Y = −0.7 mm) was located 0.9 mm more distally on the fingerpad than the average location of the SA MSSs, indicating that there were more SAs with greater sensitivities on the distal part of the fingerpad. Thus, the offsets in the centers of the PL trajectories reflect a positional bias present in the afferent populations.

Population coding of stroke length

For each object and orientation, the PLs of the SAs and RAs led the location of the center of the object at the beginning of the stroke trajectory (SA by 1.6 mm; RA by 1.9 mm) but trailed at the end (SA by 1.4 mm; RA by 2 mm; t tests of the offsets of the PLs vs 0; all p values < 0.001). The total lengths of the PL trajectories (PL at the end of the stroke minus the PL 0.2 mm after the start) were 3.9 and 3.1 mm for SA and RAs, respectively (Figs.5, 6). Therefore, the total lengths of the PL trajectory underestimated the 7 mm of distance traveled by the object.

Fig. 5.

Total lengths of the trajectory of PLs as a function of stroke direction and object orientation. The total lengths of the trajectory of PLs for the SAs (top) and RAs (bottom) are plotted for each stroke direction (n = 8) for objects oriented orthogonal and parallel to the direction of stroking. A, 1 × 5 mm toroid. B, 3 × 5 mm toroid. C, Sphere. The total length of the trajectory of the PLs was less than the object stroke length of 7 mm (outer circle). The total length of the trajectory was greater for SA PLs (top) than RA PLs (bottom) and was greater for objects oriented orthogonal rather than parallel to the stroke direction.

Fig. 6.

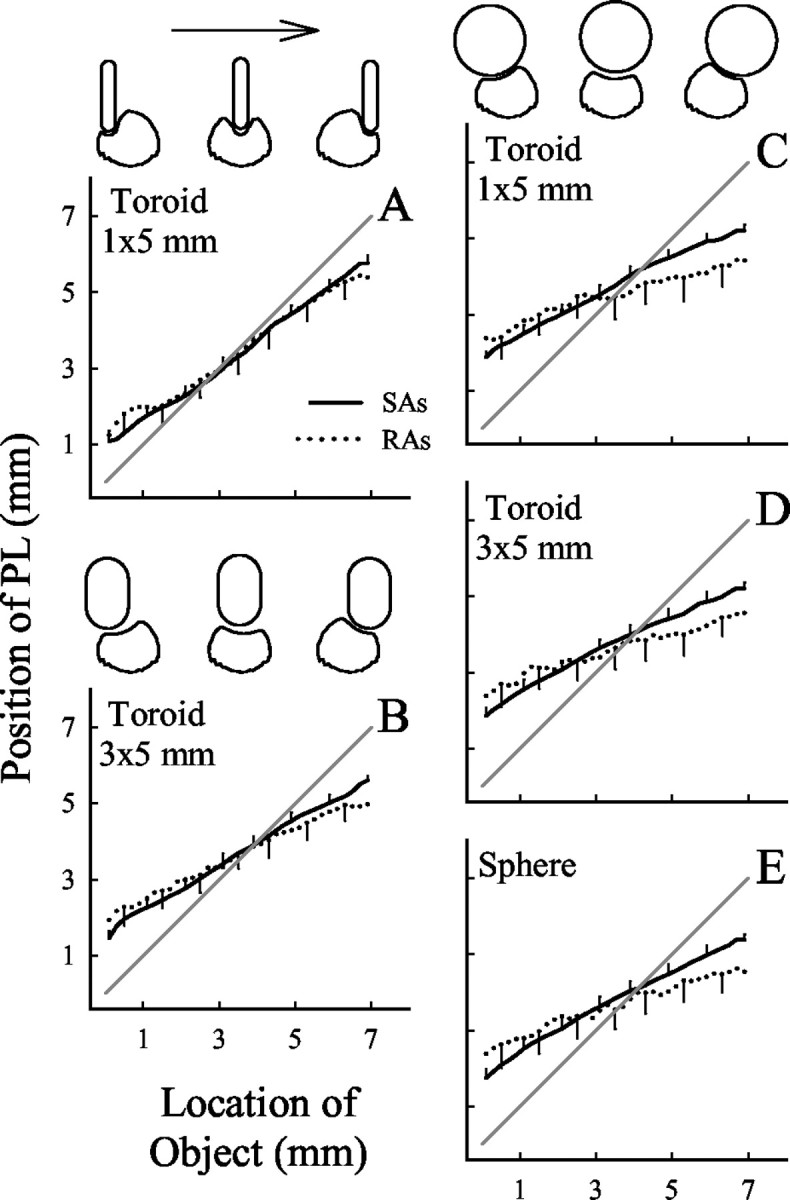
PLs as a function of the location of the object. For each object and orientation, the mean position of the PLs of SAs (solid lines) and RAs (dotted lines) are plotted as a function of the location of the object during a stroke. Each data point is an average of the position of the PLs obtained for all stroke directions. Error bars indicate SEM shown for only a subset of the object locations, each separated by 1 mm. The locations of the toroidal object on the fingerpad are illustrated schematically for the beginning, middle, and end of the stroke.A, B, Toroidal objects oriented orthogonal to the direction of motion. C,D, Toroidal objects oriented parallel to the stroke direction. A, C, 1 × 5 mm toroid.B, D, 3 × 5 mm toroid.E, Sphere.

The total lengths of the trajectories were compared for SAs and RAs for different curvatures and orientations of the object using a two-way ANOVA (fiber type × orientation curvature). The mean total length was significantly longer for SAs than RAs (p < 0.003). Object curvature and orientation influenced the length of the PL trajectory (p < 0.001). For both SA and RAs, when the objects were oriented orthogonal to the stroke direction, the mean total length of the PL trajectories were longer for the 1 × 5 mm than for the 3 × 5 mm toroid or sphere (4.6, 3.7, and 3.2 mm, respectively; Bonferroni post hoc multiple comparison method; p values < 0.05) (Fig.5A,B). On the other hand, when the objects were oriented parallel to the stroke direction, the total lengths were similar for all three objects (mean lengths of 3, 3.1, and 3.2 mm, respectively; all p values > 0.05) (Fig.5A–C). Hence, the total length of the trajectory of both SA and RA PLs was affected by the curvature of the object oriented parallel to the stroke direction.

The total length of the PL trajectory also was compared for SAs and RAs while using the direction of the stroke trajectories of the object as a factor in the statistical analysis (two-way repeated-measures ANOVA; fiber type × stroke trajectory). An interaction was found between the factors (fiber type and stroke trajectory;p < 0.001). For the RAs, the total length of the PL trajectory for object trajectories in the 90° direction was longer than PL trajectory lengths for all other directions (Bonferronipost hoc multiple comparison method; pvalues < 0.05). Additionally, the total length of PL trajectories for object trajectories in the 180 and 315° directions was shorter than PL trajectory lengths for a number of other stroke directions (315°, five of seven; 180°, four of seven; p values < 0.05). For the SAs, the total lengths of the PL trajectories were similar, except for the total length of the PL trajectory for the 45° object trajectory (two of seven; p values < 0.05). Hence, the total lengths of the trajectory of SA PLs coded the 7 mm trajectory of the object more symmetrically than the RA PLs.

Population coding of the increments in object location

Even with the absolute offset between the location of the object and PL, along each stroke trajectory, there was an increment in the position of the PLs corresponding to the location of the object during the stroke across the fingerpad. For both SAs and RAs and for each object and object orientation and eight directions of stroking, the increment in the position of PLs along the stroke trajectory of the object increased linearly with object location (Fig. 6) (SAs, meanr = 0.988; RAs, mean r = 0.910). The slopes of the lines were steeper (closer to one) for the SAs than for the RAs as evaluated with a two-way ANOVA (mean slopes: SAs, 0.562 and RAs, 0.401; p < 0.003; fiber type × object curvature orientation). Bonferroni post hoc multiple comparison tests found that this was true for all object orientations and curvatures (p < 0.05), except for the 1 × 5 mm toroid oriented orthogonal to the direction of stroking (mean slopes: SAs, 0.717 and RAs, 0.696; p = 0.09). The slopes of the lines were steeper (closer to one) for the toroidal objects oriented orthogonal to the direction of stroking (mean of 0.614) (Fig. 6A,B) than they were for the other objects and orientations (mean of 0.429; Bonferronipost hoc multiple comparison method; all pvalues < 0.05) (Fig. 6C–E). Hence, compared with RAs, the change in the position of the SA PLs during a PL trajectory showed a greater one-to-one correspondence with the changing position of the object during a stroke.

The sum of the square error in the linear relationship between the positions of the PL trajectories and the locations of the object during the stroke was significantly greater for the RAs than for the SAs (Fig. 6) (two-way ANOVA; p values < 0.001). There was no effect of the curvature and orientation of the object (p = 0.146). Therefore, regardless of the curvature or orientation of the object, the variability in coding the location of the object during the stroke was greater for the RA PLs than for the SA PLs.

Population coding of differences in object location

The position of PLs, in the axis parallel to the stroke trajectory of the object, was measured for different object locations and used to evaluate the ability of the SA and RA PLs to detect differences in the location of the object during the stroke. The smallest increment of object travel evoking a significantly different position of the PL was determined with a four-way ANOVA: fiber type (SA vs RA) × object curvature orientation × object location × stroke direction, in which each stroke direction was treated as either a repeated or nonrepeated measure. Separate Bonferroni post hoc multiple comparisons were performed for each of the three standard PL positions determined from different distances of travel by the object (0.2, 1, and 3 mm).

The SA PLs were significantly better than the RAs in distinguishing differences in the position of the PL (paired t test;p < 0.001) for the three standard stroke lengths (0.2, 1, and 3 mm) of object movement. When comparisons of PL positions were made within the same object trajectory, significant differences were found for object stroke lengths as short as 0.2 mm for the SA (mean of 0.56 mm; ANOVA performed with stroke direction treated as a repeated measure). For the RA PLs, significant differences were found for object stroke lengths as short as 0.4 mm (mean of 1.5 mm).

The magnitude of the distance between object locations found to be significantly different in positions of the RA PLs depended on the curvature and orientation of the object. Within the same object trajectory, the smallest mean difference in object location coded by the differences in the positions of the RA PLs was obtained in response to the 1 × 5 mm (mean of 0.7 mm) and 3 × 5 mm (mean of 1.0 mm) toroids stroked orthogonal to the direction of stroking. For the other object orientations and curvatures, the magnitudes of the significantly different object locations were larger (sphere, 2.6 mm; 1 × 5 mm toroid stroked parallel, 1.9 mm; 3 × 5 mm toroid stroked parallel, 2.2 mm; Bonferroni post hoc multiple comparisons; all p values < 0.05). In contrast, the smallest significant difference in object location coded by the position of the SA PLs was unaffected by curvature or orientation of the object (1 × 5 mm toroids, mean difference of 0.66 mm; all other objects, mean of 0.53 mm; p = 0.56).

When the comparisons of the positions of the PLs along a stroke trajectory were made across different trajectories (ANOVA performed with stroke direction treated as a nonrepeated measure), statistically different distances in object location as short as 1.4 mm (mean of 2 mm) were found for the SA PLs, whereas for the RA PLs, statistically different distances in object location were found at lengths of ≥3 mm (mean of 3.6 mm). Thus, the SA PLs exhibited an overall superiority to the RA PLs in coding differences in the location of an object during a stroke.

Population coding of the direction of motion

The cumulative mean direction of the SA and RA PL trajectories showed a greater correspondence to the direction of motion of the object as the travel of the object increased during a stroke (Fig.7A–C). During the stroke trajectory (Fig. 7A–C), the cumulative mean direction coded by the PL trajectory attained a relatively constant value (horizontal line) after a short distance of object motion. For the 7 mm stroke length, there was a linear relationship between cumulative mean direction of the PL trajectories and the direction of motion of the object (SA, r = 0.996; slope, 0.997; RA,r = 0.983; slope, 0.999) (Fig. 7D–G). Two different factors, the length of travel of the object and the number of PLs, contribute to the cumulative mean of the direction angles of the PLs. Therefore, we analyzed how fiber type, object shape, and orientation affect the ability of the PLs to code the direction of motion of the object in analyses in which the contributions of changing stroke length of the object and the number of PLs were evaluated separately.

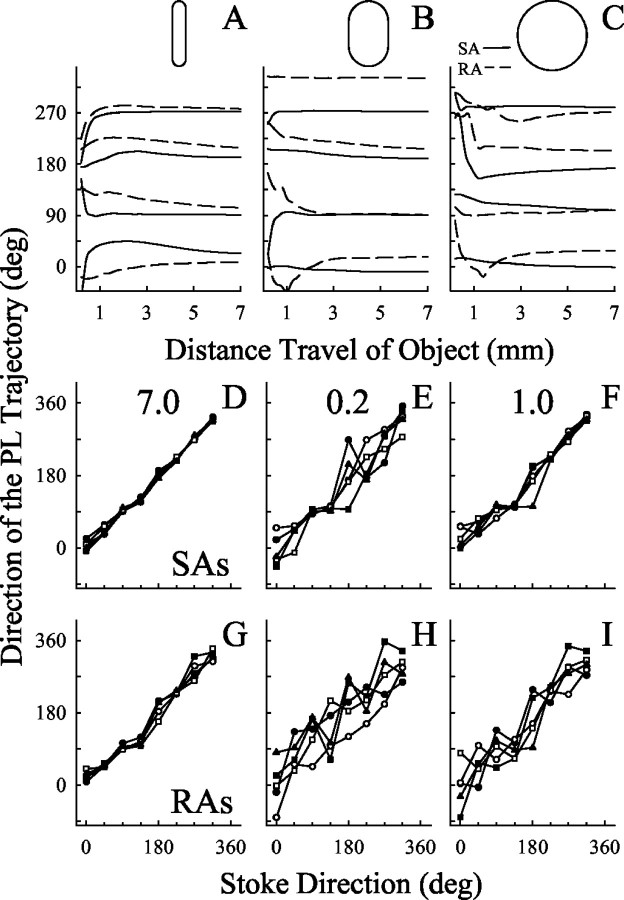
Fig. 7.

The directions of the PL trajectories.A–C, The cumulative mean direction of the PL trajectories as a function of the distance of travel of the object. The cumulative mean direction of a trajectory of PLs was defined as the sum of the direction angles of the PLs for each distance of object travel during the stroke divided by the number of PL angles. A,B, 1 × 5 and 3 × 5 mm toroid, respectively, oriented orthogonal to the direction of stroking. C, Sphere. The cumulative mean direction of the trajectory of the SA (solid line) and RA (dashed lines) PLs were determined for each of the eight different stroke directions of the object; only four are shown (0, 90, 180, and 270°).D–I, The directions of the PL trajectories of SAs (D–F) and RAs (G–I) are shown as a function of the stroke direction and distance of travel of the object. Data in each panel were obtained from the sphere (triangles) and two toroids (1 × 5 mm,circles; 3 × 5 mm, squares). The major axis of each toroid was oriented either orthogonal (filled symbols) or parallel (open symbols) to the direction of motion. The cumulative mean direction of the trajectory of PLs is shown for the entire 7 mm stroke of the object (D, G). The direction of a PL trajectory was defined as the angle between a line extending from the PL at the beginning of the stroke (after 0.2 mm of travel) to the PL at a subsequent length of travel of the object and the mediolateral axis. The direction of the PL trajectory is shown for two of the 10 lengths of object travel: 0.2 mm (E,H) and 1 mm (F,I).

The contribution stroke length had on the coding of stroke direction was examined by determining the direction of motion of the object at different positions during the trajectory. When only the locations of the PL at the beginning (after 0.2 mm of object travel) and at a second location during the stroke were used to determine the direction of the PL trajectory, the relationship between the direction of the object and direction of the PL trajectory was significant for both fiber types, all objects, object orientations, and distances traveled by the object (Fig.7E,F,H,I) (mean slopes: SAs, 0.99; RAs, 0.98; mean, r = 0.964;t tests of slopes; all p values < 0.01). Thus, the direction of the PL trajectories of both the SAs and RAs was linearly related to the direction of motion of the object. However, there was considerable variability in the relationship between the directions of the PL and object. The source of variability decreased and the linearity of the function increased with increases in the distance of travel (Fig. 7).

To evaluate the effects of increasing the length of object travel on the precision with which SAs and RAs coded the stroke direction of the object, a three-way ANOVA was performed. The dependent variable was the 95% confidence interval, and the independent factors were fiber type (SA and RA), object curvature and orientation (n = 5), and the length of object travel (treated as a repeated measure).

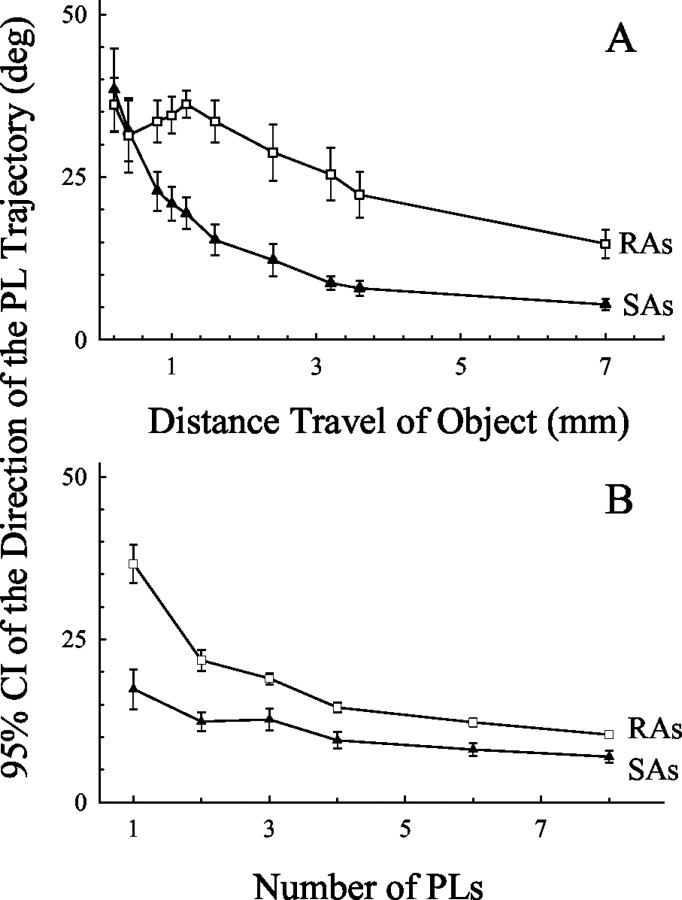
Objects of different curvature or orientation did not alter the 95% confidence intervals in a consistent manner, as shown in Figure 7 in the variability in the relationship between the directions of the PL trajectories and object. The coding of the stroke direction improved with increases in the length of travel along a stroke trajectory when only the PL at the beginning (after 0.2 mm of travel) and at a second object location during a stroke were used to estimate the direction of the object (p < 0.001) (Fig.8A). Overall, the SA PLs were better than RA PLs in coding the direction of motion of the object (p < 0.001) (Figs. 4,8A). For lengths of object travel >0.8 and <6.4 mm, the SAs were better than RA PLs in coding the direction of the object (Bonferroni post hoc multiple comparisons; all pvalues < 0.05) (Figs. 4, 8A). The average 95% confidence intervals for the direction of motion of the SA PLs significantly fell from 38.4 to 32, 22.8, 7.8, and 5.4° as the length of travel of the object increased from 0.2 to 0.4, 0.8, 3.6, and 7.0 mm, respectively. The 95% confidence interval of the SA PLs at 0.2 mm was significantly greater than those at ≥0.8 mm (Bonferroni post hoc multiple comparisons; all p values < 0.05). In contrast, as the length of travel of the object increased from 0.2 to 0.4, 0.8, 3.6, and 70 mm, the 95% confidence intervals for the RA PL fell from 36.1 to 31.4, 33.5, 22.2, and 14.7°, respectively. The 95% confidence interval of the RA PL at 0.2 mm was only significantly greater than those at ≥3.4 mm (Bonferroni post hoc multiple comparisons; all p values < 0.05). Therefore, although the coding of the stroke direction by the SA PLs was present for object displacements as short as 0.2 mm, increasing the length of the stroke, even a short distance, improved the precision with which the SA PLs coded the direction of the object. In contrast, only with large increases in the stroke length of an object did the RA PLs show improvements in coding the direction of an object.

Fig. 8.

Factors affecting the coding of the direction of object motion by the PL trajectory. The variability (95% CI) in the coding of the direction of trajectory of the SA and RA PLs to each object stroked in different directions was studied when the number of PLs and lengths of travel of the object were varied. Data in eachpanel are the overall mean values obtained from the sphere and two toroids oriented parallel and orthogonal to the stroke direction for the SA PLs (filled symbols) and RA PLs (open symbols). A, The mean 95% confidence intervals for 10 different lengths of object travel, in which the direction of motion of a PL trajectory was based on only one angle of motion estimate. The direction of the PLs was the angle between the mediolateral axis and a line extending from the PLs at the beginning of the stroke to the PLs at various distances traveled by the object (≤7 mm). B, The mean 95% confidence intervals when the direction of motion of the first 1.6 mm segment of object travels along a single trajectory were based on a varying number (n = 1–8) of PLs used to determine the direction of the PL trajectory. Error bars indicate SEM.

The precision of coding direction by SAs and RAs was evaluated as a function of the number of PLs used to estimate the direction of the PL trajectory. A three-way ANOVA was performed, in which the dependent variable was the 95% confidence interval, and the independent factors were fiber type (SA and RA), object curvature and orientation (n = 5), and the number of PL instances (n = 6, treated as a repeated measure). Increasing the number of PL instances used to determine the direction of the PL trajectory during the initial 1.6 mm portion of the trajectory of the object improved the precision of coding direction by both RA and SA PLs (Fig. 8B) (p < 0.001). The average 95% confidence interval (across objects) for the direction of motion of the SA PLs fell from 17.3 to 12.4 and 6.9^o as the number of PL instances increased from one to two and eight (Bonferroni post hocmultiple comparisons; n = 1 was significantly different from n ≥ 3; all p values < 0.05). For the RA PL, the 95% confidence interval of the linear regression fell significantly from 36.6 to 21.8 and 10.3° for one, two, and eight numbers of PL instances, respectively (Bonferroni post hocmultiple comparisons; all p values < 0.05). Although the ability of the RA PLs to code the direction of motion showed greater improvement than the SA PLs, with increases in the number of instances used to determine the direction of motion, SA PLs were still better than the RA PLs at discriminating the stroke direction of the object (p < 0.001).

Encoding by the combined SA and RA population

PLs were constructed from the total population of SA and RA afferents combined (PL_T). The ability of the PL_T to code the location and direction of an object were compared with PLs obtained from the SA and RA populations (PL_SA and PL_RA). Measures of the relationship between the PLs and the location of the object revealed that the PL_T exhibited coding properties that were most comparable with the PL_SA. The mean slope, sums of square error, and total stroke lengths of the PL_T trajectories (0.533, 0.234, and 3.8 mm, respectively) fell between those of the PL_SA(0.562, 0.166, and 3.96 mm, respectively) and PL_RA (0.401, 0.264, and 3.1 mm, respectively). Only the slope of the function relating the position of the PL_T to the location of the object was significantly different from the slope of the PL_RA (multiple fiber type of ANOVA × object orientation; all p values < 0.005). Similarly, for different lengths of object travel, the 95% confidence intervals of the PL_T (mean of 13.4°) describing the precision of the direction of PL trajectories coding the direction of the object were comparable with those of the PL_SA(mean of 11.5°) and only significantly different from those of the PL_RA (24.5°; two-way ANOVA; Bonferronit test; p < 0.05). When different numbers of PLs were used to determine the direction of a stroke trajectory, the mean 95% confidence intervals of the PL_T(13.3°) fell between those observed for the PL_SAs (11.2°) and PL_RAs(19.1°). Thus, adding the responses of the RA afferents to those of the SAs only decreased the precision of coding by the PL.

DISCUSSION

By constructing populations of SA and RA mechanoreceptive afferents with spatially distributed receptive fields, we were able to compare the capacities of each fiber population to code the location of a laterally moving object. The calculation of the location of the center of neural activity of a PL allowed us to determine whether the location of the center of activity and the shift in that location provided information the CNS could use to determine the location and direction of a moving object. The calculation of the PL from the population response was used in our analysis because it has predictive value in describing the discriminative performance of humans for tactile stimuli (Goodwin and Wheat, 1999; Schluter et al., 2001).

With the measure of the PL, the location of the contact between the object and skin was better represented in the responses of the SAs than in the RAs, regardless of differences in stroke direction or object curvature. RAs coded poorly the location of the object. The PL representation of stroke direction was linearly related to the actual direction of the object for both RAs and SAs. However, the PL representation of stroke direction was less variable for SAs than for RAs. Modest increases in object stroke length improved the abilities of SAs to code the direction of motion of the object. RAs required longer stroke lengths. Therefore, the SAs have the spatial resolution primates need to locate the position of a laterally moving object.

Constructing the populations from a composite of fibers recorded at different times on different fingers has its disadvantages. One disadvantage is the variability in response measures because of the differences in the compliance and geometry of different fingerpads, possible errors in locating the center of the receptive field of each afferent, and variations (<0.25 mm) in the center alignment of the object. Differences in lateral displacement of the skin produced by the object on different fingerpads add another source of variability. Additionally, the presence of a few highly sensitive afferents and the patchy distribution of the MSSs may have skewed the PLs toward specific locations on the fingerpad. Some of these factors may have lessened the correspondence between the location of the object and the PL. However, they would not alter the differences we observed in capacities of SA and RAs to code the location and direction of a moving object.

Population coding of the location of a moving object

The SA population was superior to the RA in coding the location of an object and in coding differences in object location during a stroke. During lateral motion, the SA PLs statistically discerned the location of an object that differed by only 0.2 mm (mean of 0.5 mm). Similarly, human subjects are capable of discriminating differences as small as 0.1 mm in the length of a stream of air stroked across the fingerpad (De Cillis, 1944). In related studies, Goodwin et al. (Wheat et al., 1995; Goodwin and Wheat, 1999) found that both human subjects and the SA population in the monkey were able to discriminate differences in lateral displacements as small as 0.38 mm for vertically indented objects. This strong correspondence between the abilities of the SA PLs and human subjects to discriminate differences in the location of an object on the fingerpad suggests that the SA population provides the information primates use to locate differences in the location of a laterally moving object.

Similarities also exist between the abilities of the RA PLs and human subjects to discriminate the location of an object on the fingerpad during simulated tactile motion produced by the Optican, consisting of an array of vibrotactile stimulators. The Optican preferentially activates RAs over SAs (Gardner and Palmer, 1989). In a study of simulated motion, subjects were able to discriminate stroke lengths of objects on the fingerpad that differed by 1.2 mm if presented along the same trajectory and 3.6 mm if presented along different trajectories (Schneider et al., 1986). Similarly, the mean differences in the distance between object locations along a stroke trajectory found for the RA PLs were 1.5 mm along the same trajectory and 3.6 mm along different trajectories.

The total length of a trajectory of PLs for a stroke was shorter than the 7 mm stroke length of the object. Because the peripheral representation of the object was derived from the locations of forces exerted by an object against the fingerpad, these findings are not surprising. During the stroke of an object, the region of contact between the fingerpad and the object will move along the curved shape of the object and shift toward the center of the fingerpad because of the cylindrical shape of the finger. Because of the contact mechanics between the fingerpad and the object, the PLs led the absolute location of the object at the beginning of the stroke and trailed at the end of the stroke. Other biomechanical factors also influenced the location of the population response, such as a slight bunching up of the skin and the lateral displacement of the fingerpad because of lateral motion. Consequently, the PLs reflected the location of contact between the object and skin more closely than the location of the object in extrapersonal space.

The different ways in which SAs and RAs code the mechanical states that develop within the skin as an object is stroked across the fingerpad are another reason for the lack of a better correspondence between the locations of the object and the PLs. SA mechanoreceptors encode the rate and magnitude of indentation of the skin (LaMotte and Srinivasan, 1987a; Srinivasan and LaMotte, 1987). Thus, SAs exhibit spatial response profiles that reflect the shape of the stimulus (Goodwin et al., 1995; LaMotte et al., 1998). For our curved objects, the central location of the spatially distributed discharge rates in the SA population would code the location of the center of the contact area because of the sensitivity of SAs to the magnitude of indentation of the skin. However, the center of this response at the beginning of the stroke would be offset toward the center of the fingerpad because of the sensitivity of SAs to the rate of indentation of the skin that is maximal at the leading edge of the object. In contrast, the spatial responses of RAs provide less reliable measures of object location because of their sensitivity to the rate of change in skin curvature as opposed to the magnitude of curvature. Because of the sizes of our objects, relative to the receptive field size of an afferent, RAs would discharge at highest rates as an object entered and exited the receptive field, attributable to their responsiveness to the movement of the skin surrounding the object, and at lowest rates to the location of object when it was directly over the most sensitive spot of the receptive field (LaMotte and Srinivasan, 1987b; Srinivasan and LaMotte, 1987). Without any one aspect of the response profile of an individual RA afferent reflecting the shape of the object, one would predict that the location of the center of the RA population response would be highly variable during a stroke of an object across the fingerpad, as we observed in the present study.

Population coding of the direction of a moving object

The direction of the trajectory of the PL during a stroke of an object was linearly related to the direction of the object for both RAs and SAs. This relationship was found for all objects and object orientations. However, the variability in coding the stroke direction was much greater for the RA than the SA PLs.

The discriminability of different stroke directions is related to the length of the trajectory of an object (Essick, 1998). A very small stroke length of 0.17 mm was sufficient for the discriminations of large differences in object motion of 180°, i.e., left versus right (Loomis and Collins, 1978). Similarly, the SA PLs coded the different directions of object motion at distances as short as 0.2 mm. Human subjects discriminated on the fingerpad differences of 14° in the direction of motion of an 0.8-mm-diameter object when the stroke length was 3.5 mm (Keyson and Houtsma, 1995). When considering the 95% confidence intervals of the PLs as comparable measures of discrimination thresholds of human subjects, the population of SAs in the present study discriminated stroke directions at magnitudes similar to those reported by the human subjects (14°) at stroke lengths of 2 mm or less, depending on the number of PL instances used to determine the direction of a stroke trajectory.

The data in this study suggest that direction discrimination would be poor if only RAs were stimulated and only information at the beginning and ending points of the stroke was available to the nervous system. The ability of the RA population to code direction increased as a function of stroke length but only for lengths >3 mm. Similarly, the ability of humans to discriminate differences in the direction of an apparent trajectory, again generated by an Optican that preferentially stimulated RAs, showed only minimal improvement as the length between the impulses increased from 1.2 to 4.8 mm (Schneider et al., 1986;Gardner and Sklar, 1994).

The reduced capacity of the RA population to code the direction of motion may be caused in part by the relatively lesser number of active RAs than SAs and to their lower rates of discharge. Approximately twice as many SA afferents as RAs were active during the stroke of an object. This was probably caused by the differential sensitivities the SAs and RAs had to the biomechanical states generated by the contact of our objects on the lubricated fingerpad. The RA PLs coded the stroke direction of objects with higher curvature better than those with lower curvature, possibly because of the larger response provoked in RAs by objects with greater curvature (LaMotte and Whitehouse, 1986; Blake et al., 1997). Thus, it is conceivable that the capacities of RAs to code the location and direction of moving objects, particularly those with high curvatures that optimally excite the RAs, may improve if they are recruited in greater number and more vigorously. Alternatively, a more intense activation of the RAs, a less precise system, might only increase the level of noise and interfere with the spatial representation of the object supplied by the SAs.

Gardner and Sklar (1994) found that the number of stimulus pulses used to construct the trajectory was the critical factor in improving subject performance. Therefore, increasing the number of active fibers seemed to improve the ability of the RAs to code the direction of motion of an object. The ability of RA PLs in the present study to discriminate different directions of motion also improved with increases in the number of instances used to determine a stroke direction. However, regardless of the number of instances used to determine a stroke direction, SA PLs were better than RA PLs in coding direction of motion.