Stimulus Encoding and Feature Extraction by Multiple Sensory Neurons

Abstract

Neighboring cells in topographical sensory maps may transmit similar information to the next higher level of processing. How information transmission by groups of nearby neurons compares with the performance of single cells is a very important question for understanding the functioning of the nervous system. To tackle this problem, we quantified stimulus-encoding and feature extraction performance by pairs of simultaneously recorded electrosensory pyramidal cells in the hindbrain of weakly electric fish. These cells constitute the output neurons of the first central nervous stage of electrosensory processing. Using random amplitude modulations (RAMs) of a mimic of the fish's own electric field within behaviorally relevant frequency bands, we found that pyramidal cells with overlapping receptive fields exhibit strong stimulus-induced correlations. To quantify the encoding of the RAM time course, we estimated the stimuli from simultaneously recorded spike trains and found significant improvements over single spike trains. The quality of stimulus reconstruction, however, was still inferior to the one measured for single primary sensory afferents. In an analysis of feature extraction, we found that spikes of pyramidal cell pairs coinciding within a time window of a few milliseconds performed significantly better at detecting upstrokes and downstrokes of the stimulus compared with isolated spikes and even spike bursts of single cells. Coincident spikes can thus be considered “distributed bursts.” Our results suggest that stimulus encoding by primary sensory afferents is transformed into feature extraction at the next processing stage. There, stimulus-induced coincident activity can improve the extraction of behaviorally relevant features from the stimulus.

A defining characteristic of topographic sensory maps is that adjacent neurons process information about neighboring locations in the sensory environment (for review, seeKaas, 1997). Hence, the activity of nearby neurons is often correlated (see for example Usrey and Reid, 1999; Bair et al., 2001). So far, several investigations have addressed the causes and effects of correlated activity on information transmission by studying stimulus encoding by multiple neurons, each of which quite faithfully followed the stimulus time course (Warland et al., 1997; Dan et al., 1998;Stanley et al., 1999; Nirenberg et al., 2001). Using pyramidal cells in the hindbrain of weakly electric fish as a model system, we considered cells that do not precisely follow the stimulus time course but rather appear specialized to extract stimulus features (Gabbiani et al., 1996).

Weakly electric knife fish, Eigenmannia, generate electric fields by periodically discharging their electric organ at rates between 200 and 600 Hz and monitor distortions of the amplitude and phase of the electric field for electrolocation and communication purposes (for review, see Heiligenberg, 1991). The information on amplitude and phase is relayed from electroreceptors embedded in the skin to the electrosensory lateral line lobe (ELL) in the hindbrain, forming three somatotopic maps. A subset of primary sensory fibers, P-receptor afferents, encode changes in the electric field amplitude by firing in a probabilistic manner (Scheich et al., 1973; Hopkins, 1976;Bastian, 1981a). They synapse on E-type pyramidal cells, which respond with excitation to increases in stimulus amplitude. Via interneurons, P-receptor afferents inhibit I-type pyramidal cells, which consequently fire spikes in response to decreases in stimulus amplitude (Bastian, 1981b; Maler et al., 1981; Saunders and Bastian, 1984). E- and I-units are therefore analogous to ON and OFF cells in other sensory systems.

Previous studies of information encoding in the electrosensory system showed that single P-receptor afferent spike trains encode up to 80% of random amplitude modulations (RAMs) of the electric field (Wessel et al., 1996). Single pyramidal cells, however, encode the stimulus time course only poorly. Instead, they reliably indicate the occurrence of upstrokes and downstrokes in stimulus amplitude by bursts of spikes (Gabbiani et al., 1996; Metzner et al., 1998). Extending this line of research to multiple pyramidal cells, we now asked three questions. First, how strongly correlated is the activity of pyramidal cells whose receptive fields overlap, and what is the source of this correlation? Second, is the detailed information on the stimulus time course, which is available from the primary afferent spike trains, indeed transformed at the level of the ELL, or can it still be read from the combined activity of groups of pyramidal cells? Third, can correlations between spike trains of multiple neurons enhance the extraction of behaviorally relevant stimulus features?

To address these questions, we performed dual recordings in vivo from nearby pyramidal cells in the ELL with overlapping receptive fields while presenting RAMs of a mimic of the fish's electric field. We characterized correlations between spike trains of simultaneously recorded neurons by cross-correlation analysis. Stimulus encoding and feature extraction were quantified using reconstruction techniques and methods derived from signal detection theory, respectively (Gabbiani et al., 1996; Rieke et al., 1997; Metzner et al., 1998).

MATERIALS AND METHODS

Preparation. Forty-three specimens of the South American weakly electric knife fish, Eigenmannia sp., ranging in body length from 12 to 22 cm, were used in this study. The animals were obtained from a tropical fish wholesaler (Bailey's, San Diego, CA). Animal handling and all surgical procedures were in accordance with National Institutes of Health guidelines and were approved by the local Institutional Animal Care and Use Committee. Preparation for the electrophysiological recordings has been outlined in detail previously (Metzner et al., 1998). Briefly, after determining a fish's electric organ discharge frequency, the animal was immobilized, and its discharge amplitude was attenuated by intramuscular injection of Flaxedil (gallamine triethiodide; Sigma, St. Louis, MO; <5 μg/gm body wt). The animal was then suspended in the center of the experimental tank (water conductivity, 100–130 μS/cm, pH 7; temperature, 24–26°C) and respirated with aerated aquarium water. Under local anesthesia (2% lidocaine; Western Medical Supply, Arcadia, CA), part of the skull overlying the right caudal cerebellum was removed (∼3 mm²). A Plexiglas rod was glued to the left parietal bone to stabilize the fish.

Electrophysiology. Initially, dual recordings from pyramidal cells were obtained using two separate borosilicate glass micropipettes filled with 3 m KCl. After recordings from 25 cell pairs, we switched to Wood's metal-filled glass micropipettes with platinated tips (Frank and Becker, 1964). These extracellular single-unit recordings proved to be much more stable, thus allowing us to determine whether the receptive fields of the two recorded cells overlapped (see Stimulation).

Recordings for this study were restricted to pyramidal cell bodies within the centromedial segment (CM) of the ELL. The layer of pyramidal cell bodies is easily identified using anatomical and physiological criteria (Metzner et al., 1998). We verified that data collection was from within CM by first physiologically mapping the border between the adjoining medial segment (low-frequency sensitive) and CM and then inserting electrodes only within 500 μm lateral of this border. At this rostrocaudal level, this ensures that penetrations do not reach the laterally adjoining centrolateral segment. Initially, recording sites were also verified histologically by setting small electrolytic lesions at the end of the experiment.

Anatomy. To measure the terminal spread of single P-receptor afferents in CM, we iontophoretically injected Neurobiotin (2% in 1m KCl; Vector Laboratories, Burlingame, CA) into the ganglion of the anterior lateral line nerve. After survival times between 7 and 14 hr, the animals were killed with MS222 (tricaine-methane sulfonate, pH 7; Sigma) and perfused transcardially with saline followed by fixative (4% paraformaldehyde in 0.1m phosphate buffer). The brains were post-fixed overnight, sectioned at 50 μm thickness, and then underwent a standard ABC (Vectastain Elite; Vector Laboratories) and DAB reaction (Metzner and Juranek, 1997a). Terminal spread measurements were not corrected for shrinkage of tissue because of fixation. Axons that did not contact spherical cells were classified as belonging to P-receptor afferents (Maler, 1979; Maler et al., 1981; Carr et al., 1982; Heiligenberg and Dye, 1982; Mathieson et al., 1987). The nomenclature of the brain structures used for the light microscopic analysis follows that ofMaler et al. (1991).

Stimulation. Stimuli were presented as described by Kreiman et al. (2000). Briefly, the mimic of the fish's electric field was presented between an electrode in the mouth of the fish and one close to the tail. The frequency of the sinusoidal carrier signal (f_carrier) was matched to the fish's individual electric organ discharge frequency as measured before its attenuation. The voltage of the electric field mimic followed V(t) =A₀[1 + s(t)] cos(2π f_carrier t), withA₀ being the mean amplitude of the electric field, and s(t) being the RAM that modulated the carrier signal. A₀ took values between 1 and 5 mV/cm (peak to peak) measured at the pectoral fin and perpendicular to the body axis. The mean amplitude was set just above threshold for the spherical cells (located beneath the pyramidal cells recorded from; see above) to fire with one spike per stimulus cycle of the carrier signal (Heiligenberg, 1991). This usually corresponded to a stimulus level 5–10 dB above what was necessary to audiovisually identify a pyramidal cell response as belonging to the E or I type. This assured that the field amplitude in the respective part of the fish's body surface was within the natural range, providing for normal input to the direct and topographic feedback circuits (Bratton and Bastian, 1990; Maler and Mugnaini, 1994; Berman and Maler, 1999), which might affect correlations between nearby pyramidal cells (see Discussion). The stimulus, s(t), had a flat power spectrum up to a fixed cutoff frequency (f_c = 5, 10, or 20 Hz; in some experiments, cutoff frequencies of 40 or 60 Hz were also used). The SD (or contrast), ς, of the stimulus was 25% of the mean amplitude for all f_c. Forf_c = 5 Hz, we additionally presented contrasts of 10, 15, 20, and 27.5% if time permitted. The stimulus was digital-to-analog-converted at a sampling rate of 5 kHz (PCI-MIO16E-4; National Instruments, Austin, TX). After low-pass filtering (2 kHz; Rockland model 452; Wavetek, San Diego, CA), a manual attenuator (839 attenuator; Kay Elemetrics, Lincoln Park, NJ) was used to adjust the final stimulus amplitude. The duration of the stimuli was 15 sec, which is shorter than the duration used in our previous studies on pyramidal cells (Gabbiani et al., 1996; Metzner et al., 1998). We therefore verified by cross-validation that this optimized duration gave reliable results (Press et al., 1996).

To test whether the receptive fields of two simultaneously recorded pyramidal cells were overlapping, we positioned a local electrode (Shumway, 1989a) close to the skin of the animal (distance, <1 mm) and accepted a pair of cells only as having overlapping receptive fields if both units gave robust responses to a sinusoidal amplitude modulation of 5 Hz presented via the local electrode. The mouth electrode served as the reference. We accepted cells only when, for the given stimulation site, they displayed center responses; that is, they showed the same response type (E or I) as for stimulation with the global field. Response strength decreased dramatically within a few millimeters of the strongest center activity, in line with previous measurements of receptive field sizes in Eigenmannia(Shumway, 1989a). Recording time did not permit a detailed mapping of the receptive fields.

Data analysis. Letx^A(n) andx^B(n) represent two simultaneously recorded spike trains after binning, wherex(n) = 1 if and only if there is a spike in bin n (n = 1, . . . , N, whereN is the total number of bins in the spike trains). We computed cross-correlograms:

$$R_{x^A{x}^B}(\tau )=\sum _{n=1}^{N-\tau } x^A(n)x^B(n+\tau ),$$

between pairs of pyramidal cell spike trains. The spike trains as well as τ were binned using bin sizes of 3, 6, and 9 msec. We did not observe any significant differences among these bin size values; our conclusions were therefore robust to changes in the analysis parameters. The statistical significance in departures from random coincident firing was assessed as described by Palm et al. (1988). We also estimated the deviation of the cross-correlograms from the null hypothesis of independent firing by computing the shuffle correctors, that is, the cross-correlograms for successive nonsimultaneous responses to repetitions of the same stimulus (Palm et al., 1988;Brody, 1999). To assess the properties of the correlated firing, each cross-correlogram was fitted by a cubic spline with an upsampling factor of 10 (Dierckx, 1993; Press et al., 1996). The width at half-height, area, and peak values were computed from this interpolated cross-correlogram.

Next, we computed the extent to which the stimulus,s(t), could be linearly reconstructed from the recorded spike trains. A linear estimation of the stimulus,ŝ(t), was obtained by convolving the spike train with a filter h(t):

$$\widehat{s}(t)=\sum _{n=0}^N h(t-n)\tilde{x}(n),$$

where x̃(n) is the spike train after subtraction of the mean value. h(t) was chosen to minimize the mean square error, ε², between the stimulus and estimated stimulus (Bialek et al., 1991; Poor, 1994; Wessel et al., 1996; Rieke et al., 1997; Gabbiani and Koch, 1998). This method was extended to multiple spike trains (Poor, 1994;Warland et al., 1997; Dan et al., 1998). The linear estimatorŝ(t) can be obtained by convolving each spike train with a separate filter:

$$\widehat{s}(t)=\sum _{n=0}^N\mathbf{H}(t-n)\mathbf{X}(n),$$

where the matrix H contains as many filters (i.e., columns) as the number of recorded spike trains, and the matrixX represents the binned spike train of each neuron in a separate row. The filters are again chosen to minimize the mean square error, ε², between the stimulus and its estimate.

The quality of the reconstruction was expressed as the coding fraction, γ, defined by:

$$\gamma =1-\frac{\epsilon }{\varsigma },$$

where ς is the SD of the stimulus (Gabbiani, 1996; Wessel et al., 1996; Gabbiani and Metzner, 1999). This is a normalized measure that ranges from 0 (the estimation is at chance level) to 1 (perfect estimation).

The order of the repetitions of each stimulus was randomized. Assuming independence between different trials and identical neurons, successive responses of the same unit to the same stimulus can be conceived to represent the firing of adjacent neurons of similar firing properties. In this light, we extrapolated our estimation of the stimulus by computing the coding fraction from several repetitions as discussed previously (Kreiman et al., 2000). For this extrapolation, a separate filter was allowed for each repetition, effectively treating each response as a separate “unit.” It should be noted that the firing properties of pyramidal cells are at least in part a function of the depth of their soma within the pyramidal cell layer (Bastian and Courtright, 1991; Berman et al., 1995; Bastian and Nguyenkim, 2001), thus restricting the general validity of our extrapolation. For our set of cell pairs, however, we found no statistically significant difference between the average coding fraction computed for two simultaneously recorded spike trains of same-type cell pairs and the average coding fraction for two successively recorded spike trains of single pyramidal cells.

In previous work, we computed the performance of isolated pyramidal cell spike trains in extracting upstrokes and downstrokes of amplitude modulations (Gabbiani et al., 1996; Metzner et al., 1998). Briefly, for any time interval, [t − Δt;t], let λ_t = 1 if and only if there was a spike in the interval. Furthermore, let us define the stimulus vectors preceding these time bins bys_t = [s(t − 100Δt), . . . , s(t)]. We computed the mean stimulus before bins containing a spike (m₁) and the mean stimulus before bins not containing a spike (m₀). The Euclidian classifier, f = m₁ −m₀, was used to discriminate stimulus vectors preceding spikes against stimulus vectors preceding no spikes. The typical Euclidian feature for an E-unit was a strong upstroke in stimulus amplitude; for an I-unit it was a strong downstroke (Gabbiani et al., 1996; Metzner et al., 1998) (see Fig. 4a). We performed a receiver operating characteristic analysis (Green and Swets, 1966) to quantitatively assess the performance of this classifier in predicting the occurrence of a spike. A spike was detected whenever the projection of the stimulus segment onto the Euclidian feature was larger than a certain threshold, θ. Thus, the projection can be conceived as a measure of the similarity between the feature and the stimulus segment preceding a spike. The probability of correct detection, P_D, and the probability of false alarm, P_FA, were obtained for each threshold by integrating the tails of the probability distributions:

$$P_D=P({\mathbf{f}}^T·{\mathbf{s}}_t>\theta \Vert {\lambda }_t=1)P_{FA}=P({\mathbf{f}}^T·{\mathbf{s}}_t>\theta \Vert \lambda =0),$$

where the superscript T indicates the transpose, and · indicates the dot product. Performance in the feature extraction task was quantified by minimizing P_error = 0.5 P_FA + 0.5 (1 −P_D), yielding the value defined as the probability of error, p_E (Gabbiani et al., 1996; Metzner et al., 1998). Ifp_E = 0, the occurrence of the stimulus feature is perfectly predictable, whereasp_E = 0.5 indicates performance at chance level. Next, we considered the performance of spikes correlated between pairs of pyramidal cells. For that purpose, for a given time window w we separately considered those spikes fired by cell A, which occurred within ±w msec of spikes in cell B,x^Aw. Similarly, we considered those spikes in cell B that occurred within w msec of spikes in cell A, x^Bw. We used the following values of w: 5, 10, 20, 50, and 100 msec. With a coincidence time window of 100 msec, the analysis included almost all spikes produced by the two cells (see Fig. 4c). Time windows of <5 msec were not used, because the number of spikes coinciding within such a time frame was too small to yield reliable results.

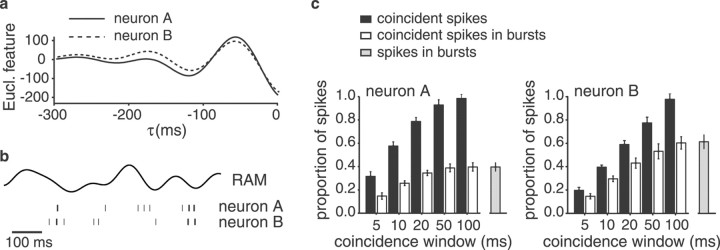
Fig. 4.

Euclidian features and coincident spikes for the pair of I-type pyramidal cells depicted in Figure 1.a, Euclidian (Eucl.) feature for each of the two cells. b, Raster plot example highlighting those spikes that occur synchronously within a time window of ±5 msec asthick bars. c, The proportion of coincident spikes with respect to the total number of spikes for neuron A (top) and neuron B (bottom) is shown asblack bars as a function of the size of the coincidence window. The percentage of spikes that occur in bursts and coincide are shown as white bars. The overall percentage of bursting spikes is indicated as a gray bar at theright.

Let λ ${}_{\text{t}}^{\text{Aw}}$ = 1 if and only if there was a spike inx^Aw (i.e., coincident spike) in the interval [t − Δt;t] and λ ${}_{\text{t}}^{\text{Bw}}$ = 1 if and only if there was a spike inx^Bw in the interval [t − Δt;t]. We then computed the conditional probability distributions for the projections of the stimulus segments preceding such coincident spikes or no spikes within these restricted spike trains onto the original Euclidian feature vectors for each cell: P(f ${}_A^T$· s_t ‖ λ ${}_{\text{t}}^{\text{Aw}}$ = 1) andP(f ${}_B^T$ ·s_t ‖ λ ${}_{\text{t}}^{\text{Bw}}$ = 1). The probabilities of correct detection and false alarm were computed by integration over the tails of these probability distributions (see above). Note that we used the original feature vectorsf_A and f_B. We did not recompute the feature vectors for the coincident spikes to avoid overfitting the data. Following the same procedure described for the one-cell scenario, we computed the minimum probability of error for each cell and for each size of the coincidence window w:p ${}_E^{\text{Aw}}$ andp ${}_E^{\text{Bw}}$.

A typical property of pyramidal cells is their tendency to fire spikes in short bursts (Gabbiani et al., 1996; Metzner et al., 1998; Bastian and Nguyenkim, 2001). The interspike interval distributions generally showed a sharp peak at short intervals and a broader peak at longer intervals. The separation between these two peaks was used to determine the maximum interspike interval for spikes within a burst (Gabbiani et al., 1996; Metzner et al., 1998). Action potentials that were not part of a burst were termed “isolated spikes” (Gabbiani et al., 1996). We separately considered the performance of bursts of spikes and isolated spikes in the extraction of stimulus features.

RESULTS

We performed simultaneous extracellular recordings from 39 pairs of pyramidal cells in the ELL, of which 29 were used for data analysis. Thirteen pairs were composed of opposite types of pyramidal cells (one E- and one I-unit) and 16 pairs were of the same type (seven E–E pairs and nine I–I pairs). For 11 pairs, we confirmed that their receptive fields overlapped (four E–E, three I–I, and four E–I pairs; see Materials and Methods). For the remaining pyramidal cell pairs, we positioned the tips of the two recording electrodes in the same way but did not verify the receptive field overlap. Because cross-correlation analysis (see next paragraph) yielded no differences between the two data sets, they were pooled for all of the following analyses.

Characteristics of correlated activity in ELL pyramidal cells

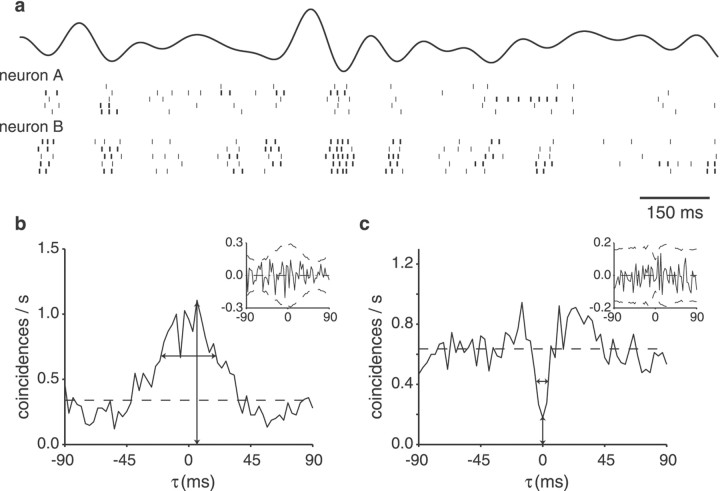
The spiking activity of pairs of pyramidal cells of the same type (E–E or I–I) was clearly correlated when driven by RAMs of the electric field surrounding the fish (Fig.1a). To quantitatively evaluate the degree of coincident firing, we computed the cross-correlograms of the activity of all pairs recorded simultaneously. For pairs of pyramidal cells of the same type, the cross-correlogram showed a strong positive peak (Fig. 1b). In this example >50% of the spikes produced by these two I-units coincided within a time window of ±50 msec. This peak was much stronger than would be expected by random coincidences from homogeneous Poisson processes (Fig. 1b, horizontal dashed line). For pairs of pyramidal cells of opposite type (i.e., one E- and one I-unit), the cross-correlograms displayed a central trough instead of a peak; that is, the probability of one cell firing an action potential was reduced for a short time when the other cell fired (Fig. 1c).

Fig. 1.

Correlated activity of simultaneously recorded pyramidal cells. a, Representative raster plot segments of the spike trains of two simultaneously recorded I-units with overlapping receptive fields. The top trace shows the time course of the random amplitude modulation (cutoff frequency,f_c = 10 Hz; contrast, 25%). Action potentials occurring within a burst of spikes are indicated by thethick bar. The same stimulus was repeated five times, yielding five raster lines for each neuron. b, Cross-correlograms of the responses of the two I-units computed with a bin size of 3 msec. The x-axis indicates the time lag between the coincident spikes. The strong peak centered at 6.3 msec indicates that these two I-units fired coincident spikes within small time windows. The horizontal dashed line gives the expected value for two homogeneous Poisson neurons of the same firing rates as the recorded units firing independently. The peak and width (37 msec) of the responses are marked by vertical andhorizontal arrows, respectively. Inset, Shuffle-corrected cross-correlogram. The horizontal lineat 0 indicates the expected value for independent responses, and the dashed lines show the 2ς confidence limits under this null hypothesis (see Materials and Methods). Because the solid curve fell between these bounds, we conclude that the coincident activity is primarily stimulus induced. The average firing rates for the two units were 9.4 and 15.2 spikes/sec, respectively. c, Cross-correlogram of the responses of one E- and one I-unit. The center trough shows that these cells of opposing response type fired in anticorrelation. The minimum occurred at −0.2 msec; the width at half-height was 10 msec.Inset, Shuffle-corrected cross-correlogram. The average firing rates for the two units were 17.3 and 12.3 spikes/sec, respectively.

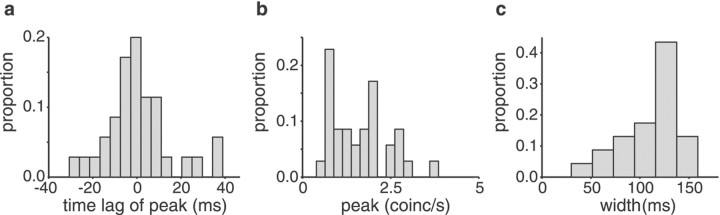
The maximum of the cross-correlogram of the I–I pair occurred at a time lag of 6.3 msec (Fig. 1b, vertical arrow), and the minimum of the opposite-type pair occurred at −0.2 msec (Fig.1c). Both of these values are well within the distribution of time lags found for our population of cell pairs (Fig.2a): the peaks occurred near a lag of 0 msec, ranging from −33 to 55 msec (median, 0.30 msec). We quantified the strength of the correlations for pairs of the same type by measuring the width at half-height and the peak value of the cross-correlograms. The peak and width of the correlograms varied depending on the pair of cells recorded from but also on the stimulus bandwidth and contrast. Overall, the peaks in the raw cross-correlograms ranged from 0.5 to 19 coincidences/sec (Fig.2b); the width varied between 41 and 162 msec (Fig.2c), with no statistically significant differences between E-unit pairs and I-unit pairs (p > 0.1, two-tailed t test). In 11 of the 16 cell pairs of the same type, a strong increase in peak strength correlated with increasing bandwidth (average r² = 0.79 ± 0.17), whereas one cell pair showed a decrease in the correlogram peak with bandwidth (r² = −0.56). For the remaining four pairs, no clear change was observed. Stimulus bandwidth was also clearly correlated with the width of the correlograms. For 10 cells pairs, the width decreased with increasing stimulus bandwidth (mean for r² over the entire sample = −0.85 ± 0.09), indicating that for higher stimulus frequencies, spike timing correlations became more precise. For the remaining six cell pairs, no clear correlation was found between stimulus bandwidth and the width of the cross-correlograms. The time at which the peak occurred did not correlate with bandwidth in any of the 16 cell pairs of the same type.

Fig. 2.

Properties of the cross-correlograms for pairs of units of the same type (n = 16). a, Distribution of the time lags at which the maximum occurred. Bin size, 5 msec.b, Distribution of the maxima of the cross-correlograms. Bin size, 0.25 coincidences (coinc/s). Thex-axis was cut at five coincidences/sec for clarity; there were three values beyond the axis limit (at 7.2, 9.3, and 19.1 coincidences/sec). c, Distribution of the widths at half-height of the peaks. Bin size, 25 msec. a–c,f_c = 5 Hz. For each neuronal pair, values for five stimulus contrasts are included.

To determine whether the correlated activity was stimulus-induced or caused by shared synaptic input to the simultaneously recorded cells, we computed the shuffle corrector, that is, the cross-correlogram for spike trains that had not been recorded simultaneously but successively for consecutive presentations of the same stimulus. After subtraction of the shuffle corrector, the correlograms of most cell pairs studied were virtually flat (98% of cross-correlograms for the 95% confidence limits and 100% of cross-correlograms for 99% confidence limits; see examples in Fig. 1b,c, insets). We also computed the cross-correlograms for spontaneous firing: none of the cell pairs of our study showed correlated activity without being driven by amplitude modulations (data not shown). These findings indicate that the correlations observed in our data set were almost entirely attributable to time locking of spikes to the stimulus.

Encoding of the time course of RAMs

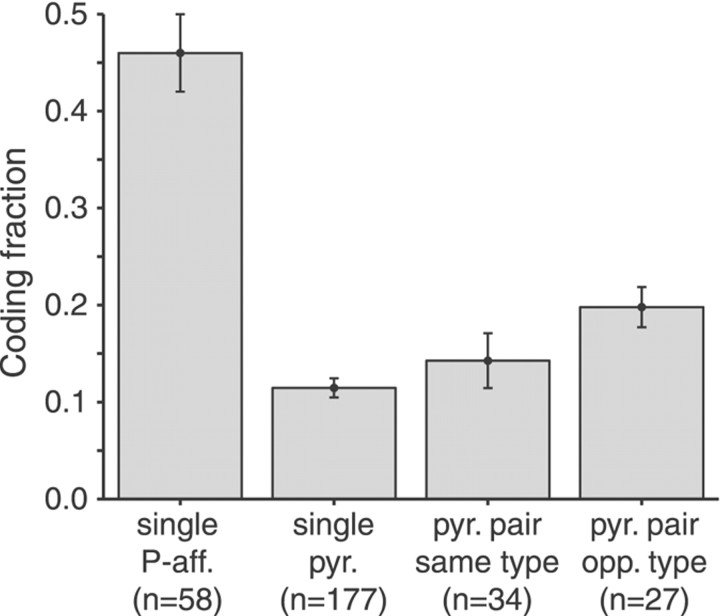
Previous studies using stimulus reconstruction techniques showed that individual P-receptor afferents reliably transmit information on the detailed time course of RAMs of the electric field surrounding the fish (Wessel et al., 1996; Metzner et al., 1998; Kreiman et al., 2000). Single spike trains yielded coding fractions up to 80% depending on the spectral properties and the contrast of the stimulus. For a stimulus with a bandwidth of 5 Hz and a contrast of 25%, the mean coding fraction for P-receptor afferents was 0.46 (Kreiman et al., 2000) (Fig. 3, left bar). In contrast, and confirming previous results, we found that single pyramidal cells performed only poorly at encoding the detailed time course of amplitude modulations, yielding coding fractions of 0.11 ± 0.01 for the same stimulus condition (Fig. 3) (also see Gabbiani et al., 1996; Metzner et al., 1998). We then asked whether the information on the detailed stimulus time course could be represented by the combined activity of groups of pyramidal cells. For this purpose, we applied a simple extension of the stimulus reconstruction algorithm used for single-cell spike trains (Bialek et al., 1991; Rieke et al., 1997; Gabbiani and Koch, 1998) to simultaneously recorded activities of pairs of pyramidal cells (Poor, 1994; Warland et al., 1997; Dan et al., 1998; see Materials and Methods). Indeed, the fraction of the stimulus encoded increased from an average of 0.11 for reconstructions from single-cell spike trains to 0.15 for reconstructions based on the combined activity of E–E or I–I pairs (Fig. 3). Compared with single cells, the coding fraction for cell pairs of opposite type (E–I) almost doubled (Fig. 3).

Fig. 3.

Summarized results of stimulus estimation from spike trains of P-receptor afferents (P-aff.), single pyramidal (pyr.) cells, and pairs of simultaneously recorded pyramidal cells of the same type (E–E and I–I) and of opposite (opp.) type (E–I). The accuracy of the information transmitted about the time course of a stimulus is characterized by the coding fraction. Error bars indicate SD.f_c = 5 Hz. n, Overall number of experimental conditions (contrasts) for all cells or cell pairs analyzed. Data for P-receptor afferents taken from Kreiman et al. (2000).

To determine whether increasing the number of simultaneously decoded spike trains could capture more of the information about the amplitude modulations, we extrapolated our data on pyramidal cell pairs. Hence, we reconstructed the stimulus from up to 10 successive responses of any given pair by effectively treating the successive responses to the same stimulus by a single cell as spike trains simultaneously recorded from different neurons. This assumption seemed justified because the average coding fraction for two successively recorded spike trains of single neurons was statistically indistinguishable from the coding fraction for two simultaneously recorded spike trains of same-type cell pairs (p > 0.1; two-tailed t test). It should be noted that this analysis also assumes that there are no higher-order correlations between spike trains of nearby cells. Increasing the number of spike trains of pyramidal cells of the same type increased the coding fraction on average up to 0.27 ± 0.12. Combining the responses of pyramidal cells of E and I type increased the encoding up to 0.36 ± 0.13. Although these values represent a clear gain over the single-neuron performance, they are, however, still at least 20% lower than those achieved by single P-receptor afferents (Fig. 3).

Feature extraction by multiple pyramidal cells

Single pyramidal cells in the ELL have been shown to reliably transmit information about the occurrence of upstrokes and downstrokes in stimulus amplitude (Gabbiani et al., 1996; Metzner et al., 1998). Here, we studied how well the correlated activity of pairs of pyramidal cells driven by the same stimulus is able to transmit this information.

For each individual unit of a pyramidal cell pair (composed of neurons A and B) we computed a feature vector, f, which predicted the occurrence or nonoccurrence of a spike in this unit (see Materials and Methods). As described previously (Gabbiani et al., 1996; Metzner et al., 1998), the typical feature for an I-unit was a strong downstroke in stimulus amplitude (Fig.4a), whereas for an E-unit it was a strong upstroke in amplitude. We then selected those spikes from neuron A for which there was a coincident spike within a certain coincidence time window in neuron B (Fig. 4b,c). Interestingly, a large proportion of the coincident spikes occurred in bursts of spikes fired by the individual cells (63 ± 15%, mean ± SD for a coincidence window of 5 msec; Fig. 4c,white bars; burst spikes marked in Fig. 1a bythick lines in the raster plot; for the definition of burst spikes, see Materials and Methods).

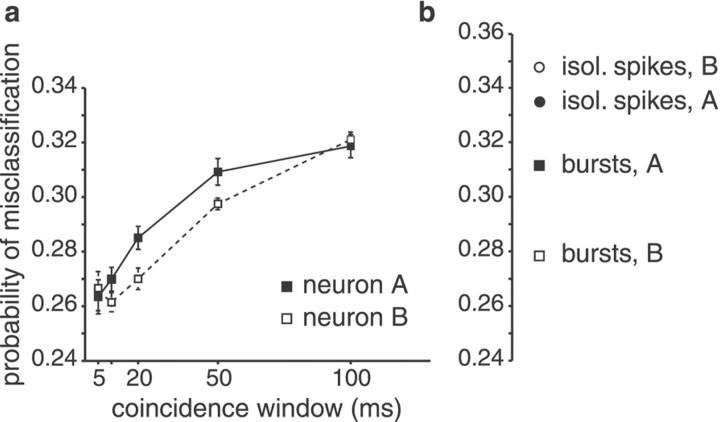
To quantify the reliability of coincident spikes in indicating the occurrence of downstrokes in stimulus amplitude, we computed the probability of misclassification, p_E, for coincident spikes. p_E is the average of the probability that coincident spikes are produced without a downstroke occurring in stimulus amplitude (false alarms) and the probability that a downstroke fails to elicit spikes in both neurons (misses). We found that the probability of misclassification decreased with decreasing size of the coincidence time window (Fig.5a). Restricting the analysis to spikes coinciding within a time window of ±5 msec improved the feature extraction performance with respect to all spikes by 22 and 21% for units A and B, respectively. In general,p_E decreased with the size of the coincidence window. In most cases, the best window size was 5 msec. In a few cases, however, the lowest values ofp_E were found for a window size of 10 msec (for example, see Fig. 5a, unit B).

Fig. 5.

Feature extraction by the same pair of I-type pyramidal cells illustrated in Figure 1. a, Minimum probability of misclassification, p_E, by those spikes of neurons A and B, respectively, which had a coincident spike on the respective other neuron plotted against the size of the coincidence time window. p_E is the average of two error probabilities: in the case of this I-unit pair, these are the probability that coincident spikes are fired even when there is no downstroke in stimulus amplitude (false alarms) and the probability that a downstroke occurs but fails to elicit coincident spikes (misses). p_E decreased with decreasing size of the coincidence time window, indicating that spikes coinciding within a time window of ±5 msec transmit the information on the occurrence of stimulus features more reliably than spikes of single neurons. Filled symbols, Neuron A; open symbols, neuron B. b, Single-neuron performance of units A and B, respectively. isol., Isolated.

As reported previously (Gabbiani et al., 1996; Metzner et al., 1998), the feature extraction for single pyramidal cells improved significantly when only bursts of spikes were considered instead of isolated spikes or all spikes (Fig. 5b). Analyzing the coincident firing of pairs of pyramidal cells, we found that feature extraction improved even more: the minimum misclassification error for coincident spikes was significantly smaller than that achieved by bursts of spikes of either cell alone (p < 0.01, two-tailed t test) (Fig. 5, compare a, b).

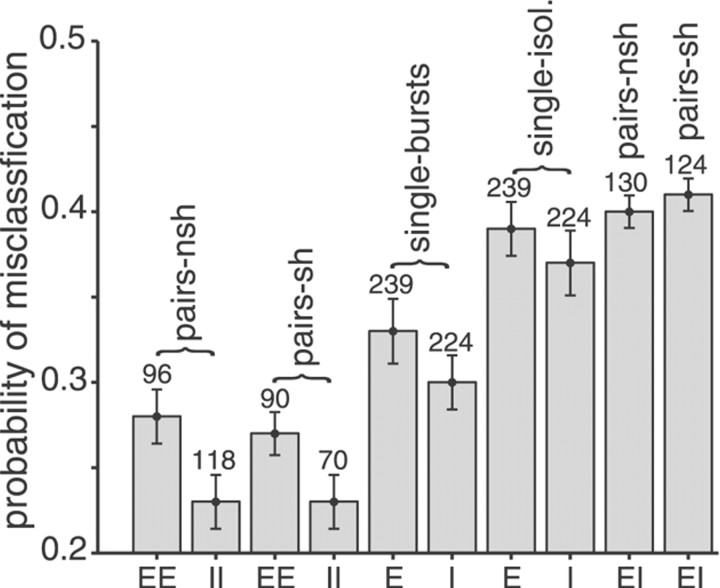
Our findings on feature extraction by single versus pairs of pyramidal cells are summarized in Figure 6 for all cell pairs analyzed. Feature extraction by the coincident activity of pairs of E-units and pairs of I-units was significantly improved compared with spike bursts fired by single cells of the respective cell types (p < 0.01 in both cases, two-tailedt test). The overall gain for coincident spikes versus spike bursts of single neurons reached values up to 54% (mean ± SD, 10 ± 16%). Compared with isolated spikes of single cells, the gain was up to 58% (29 ± 10%). Similar to findings for single pyramidal cells (Gabbiani et al., 1996; Metzner et al., 1998), pairs of I-units performed better than pairs of E-units (p < 0.01). None of the cross-correlation measures yielded any clear indication of the origin of this difference. A possible reason, a difference in connectivity of E- and I-type pyramidal cells, has been discussed previously (Gabbiani et al., 1996;Metzner et al., 1998). For opposite-type pairs, feature extraction was close to chance performance (p_E= 0.5; Fig. 6, rightmost two bars), which is not surprising considering that their responses were virtually anticorrelated (Fig.1c).

Fig. 6.

Summary diagram of feature extraction performance by ELL pyramidal cells. From left toright, bars indicate the averagep_E for coincident spikes of E–E pairs and I–I pairs, for coincident spikes of E–E and I–I pairs after shuffling of trials, for spike bursts of single E- and single I-units, for isolated spikes of single E- and I-units, and for coincident spikes of E-I pairs before and after shuffling of trials. Single I-units and pairs of I-units performed better than single E-units and pairs of E-units, respectively (p < 0.05 andp < 0.01, respectively, two-tailedt test). Pairs of cells of the same type performed better than bursts of spikes of single pyramidal cells (p < 0.01 for both E- and I-type neurons). Bursts, in turn, performed better than isolated spikes fired by the respective units (p < 0.01 for both E- and I-type neurons). Feature extraction by opposite-type pairs was close to chance performance (p_E = 0.5).p_E computed for shuffled spike trains was not significantly different from p_Ecalculated for simultaneously recorded spike trains. The mean values ofp_E were computed from the lowest values ofp_E observed regardless of the size of the best time window. Time windows of <5 msec were not used, because the number of spikes coinciding within such a time frame was too small to yield reliable results (Fig. 4c). Error bars indicate SEM. The numbers above the bars give the overall number of stimulus conditions (cutoff frequencies and contrasts) for all cells or cell pairs analyzed.pairs-nsh, Simultaneously recorded spike trains (trials not shuffled); pairs-sh, pair data with trials shuffled;single-bursts, burst spikes of single pyramidal cells;single-isol., isolated spikes of single cells.

To determine whether shared synaptic input from P-receptor afferents or from feedback connections to both pyramidal cells of a given pair had an effect on feature extraction, we also computedp_E for coincident spikes after shuffling of trials. For same-type as well as opposite-type cell pairs, shuffling did not affect the probability of misclassification (Fig. 6). This supports the results of the cross-correlation analysis and suggests that the gain in feature extraction performance found for coincident spikes of same-type cell pairs was attributable to correlations induced by the stimulus.

Terminal spread of single primary afferents

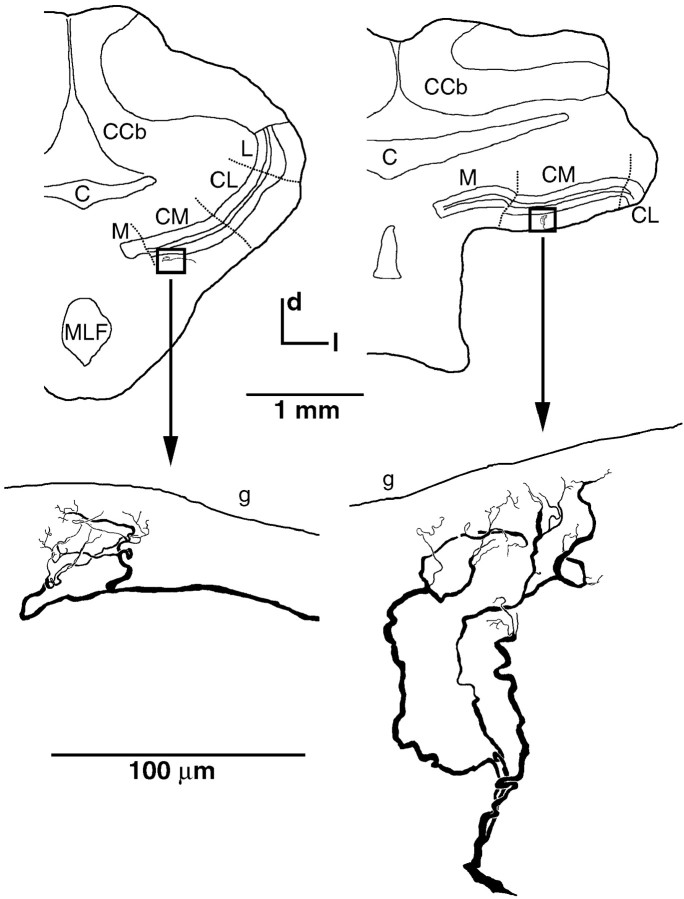
The physiological finding that the correlations between simultaneously recorded pyramidal cell spike trains were primarily stimulus-induced suggests that there is only little shared input from P-receptor afferents to pyramidal cells, i.e., a low degree of afferent divergence. To obtain an anatomical estimate of the level of divergence of P-receptor afferents, we measured the spatial spread of Neurobiotin-labeled single-fiber terminals in CM. We only measured the terminal spread of cells, which clearly did not make contact with the somata of spherical cells, thus excluding T-receptor afferents from the analysis (Maler, 1979; Maler et al., 1981; Carr et al., 1982;Heiligenberg and Dye, 1982; Mathieson et al., 1987). The average spread for five fibers was 76 ± 14 μm along the rostrocaudal axis and 77 ± 34 μm in the mediolateral axis (Fig.7). This is within the range of previous estimates (Shumway, 1989b) of terminal spread for P-receptor afferents (rostrocaudal, 115 μm; mediolateral, 60 μm). When relating this terminal spread to the area covered by the entire CM, the number of pyramidal cells contained in it, and the width of the basilar dendrite of E-units (Maler, 1979; Carr et al., 1982; Shumway, 1989b), we estimate a divergence of one afferent fiber onto three to eight pyramidal cells.

Fig. 7.

Terminal spread of P-receptor afferents.Top, Transverse sections at hindbrain level in two preparations (left, right, respectively). The locations of the terminal fields of two Neurobiotin-filled P-receptor afferent fibers within CM are indicated by the boxes.Bottom, Magnified views of the respective cells. In both cases, the terminal fields were reconstructed from three consecutive transverse sections (thickness, 50 μm) of the ELL. The section at theleft corresponds to level −6, and the section at theright corresponds to level −9 of the brain atlas ofMaler et al. (1991). C, Cerebellomedullary cistern;CCb, corpus cerebelli; CM, centromedial segment of ELL; CL, centrolateral segment of ELL;d, dorsal; g, granular cell layer of ELL;l, lateral; L, lateral segment of ELL;M, medial segment of ELL; MLF, medial longitudinal fasciculus.

DISCUSSION

In the present study, we showed that the noise in the spiking responses of pyramidal cell pairs with overlapping receptive fields is independent and that their stimulus-induced correlated activity can carry important information about behaviorally relevant stimulus features. These upstrokes and downstrokes in electric field amplitude are essential cues, in particular, for eliciting a certain electrolocation behavior, the jamming avoidance response (Heiligenberg, 1991). They can be extracted significantly more reliably from the coincident activity of a neuron pair than even from the best responses of single cells (Fig. 6).

Source of correlated activity

Correlated activity of neuronal ensembles can have several causes (for review, see Usrey and Reid, 1999). First, cells may engage in coherent oscillations of large neuronal ensembles (MacLeod and Laurent, 1996; Singer, 1999). In our sample, we could exclude this possibility, because no oscillations were observed in the cross-correlograms (Figs.1b,c). Second, it can be attributable to intrinsic connections between cells, as found, for example, in the retina of cat (Mastronarde, 1989) and salamander (Brivanlou et al., 1998). In this case, one would expect tight correlations on a millisecond time scale, with the correlogram peaks being shifted away from zero and persisting in the shuffle-corrected cross-correlogram. Neither of these effects was observed in our sample. Third, correlated activity can be caused by divergent feedforward or feedback input. Shared feedback input seemed a likely source of correlated activity in ELL pyramidal cells, considering the strong direct and topographical feedback that the apical dendrites of pyramidal cells receive from the nucleus praeeminentialis (Bratton and Bastian, 1990; Maler and Mugnaini, 1994) (for review, see Berman and Maler, 1999). However, the fact that the shuffle-corrected cross-correlograms did not exhibit significant peaks (Fig. 1b,c) made it unlikely that direct feedback increased the level of correlated activity under the stimulus conditions used in the current study. It also excluded that a large proportion of the feedforward input from P-receptor afferents was shared among the pyramidal cell pairs recorded in our study. This leaves the fourth potential source of correlated activity, the stimulus itself. Indeed, the cross-correlation analysis suggested that the major source of correlated activity in our sample was the stimulus (Fig.1b,c). The notion that nearby pyramidal cells were firing independently was reinforced by the bandwidth dependence of the cross-correlogram peak and width and by the lack of correlations when firing spontaneously.

According to our anatomical estimate for the spread of P-receptor afferents, an individual afferent fiber may diverge onto three to eight pyramidal cells. Therefore, we had expected to find evidence for shared input in the cross-correlation analysis. The lack of significant peaks in the shuffle-corrected cross-correlograms (Fig. 1b,c,insets) could have two causes. First, the cells of our pairs may have been close enough to be driven by the same local stimulus but too distant from each other to share input from the same afferents. Second, the effect of single P-receptor afferent spikes on the joint-firing probability of two target pyramidal cells may be weak considering the multitude of inputs converging onto pyramidal cells; it has been estimated that between 6 and 15 P-receptor afferents converge onto a single pyramidal cell (Bastian, 1981b; Carr et al., 1982;Shumway, 1989b). Apart from that, pyramidal cells receive excitatory and inhibitory input from many other sources (intrinsic and commissural interneurons and extrinsic feedback circuits; for review, see Berman and Maler, 1999).

In conclusion, even for pairs of pyramidal cells with overlapping receptive fields, coincident activity seemed to be attributable to largely separate, but spatially overlapping, primary afferent inputs driven by the same stimulus. Thus, the electrosensory system should be of great interest for comparisons with other systems that display strong circuit-induced synchrony (Dan et al., 1998; Singer, 1999;Nirenberg et al., 2001).

Encoding of stimulus time course

Stimulus reconstruction techniques have been widely used to assess the transmission of information concerning the stimulus time course by spike trains (Bialek et al., 1991; Wessel et al., 1996; Rieke et al., 1997; Stanley et al., 1999; Machens et al., 2001; Nirenberg et al., 2001). In previous work, we showed that single pyramidal cells poorly encode the time course of RAMs compared with the performance of primary afferents (Gabbiani et al., 1996; Wessel et al., 1996; Metzner et al., 1998). We extended this approach to analyze whether the stimulus time course is preserved in the combined activity of groups of pyramidal cells. Indeed, we found a significant gain in the quality of stimulus reconstructions when the stimulus time course was estimated from simultaneous spike trains of pairs of neurons (Fig. 3). This gain was relatively small for pairs of the same type (E–E or I–I) and much larger for pairs of opposite type (E–I). The fact that the coding fraction for opposite-type pairs was almost doubled compared with that for single cells indicates that E- and I-units encode different aspects of the stimulus independently of each other.

The separation of information flow into independent complementary channels is a feature of many sensory and motor systems (Metzner and Juranek, 1997b). So far, a doubling of information transmission has been demonstrated for pairs of sensory interneurons in the cricket cercal system coding for opposite directions of air movements (Theunissen et al., 1996), and for combinations of ON and OFF retinal ganglion cells in salamanders (Warland et al., 1997). To assess whether larger ensembles of pyramidal cells are able to capture more of the stimulus time course, we extrapolated decoding from pairs of same- and of opposite-type cells using spike trains recorded consecutively in response to multiple repetitions of the same stimulus. Although we did not observe a clear saturation of information transmission with increasing ensemble size, coding fractions remained significantly lower than those computed for single primary afferents even when the stimuli were reconstructed from up to 20 spike trains. This contrasts with results from geniculate neurons in the cat visual system, in which ensemble sizes of 12–16 relay cells were sufficient to satisfactorily reconstruct natural-scene movies for a given pixel (Stanley et al., 1999).

Potentially, our linear approach of stimulus reconstruction may have underestimated pyramidal cell performance by missing some nonlinear transformation performed by pyramidal cells. In our previous work on single pyramidal cells, however, we could not find significant gains in the coding fraction when the reconstruction was based on several linear and nonlinear transformations of the stimulus or when we applied a quadratic reconstruction algorithm (Metzner et al., 1998). Thus, it seems unlikely that the information on the detailed stimulus time course is preserved by the pyramidal cells of the ELL.

Extraction of stimulus features by “distributed bursts”

As shown previously, spikes produced by pyramidal cells reliably indicate upstrokes and downstrokes in stimulus amplitude (Gabbiani et al., 1996; Metzner et al., 1998). Action potentials occurring in short bursts perform significantly better than isolated spikes. Here, we showed that the reliability of feature extraction further increased when the analysis was based on spikes from a pair of neurons of the same type coinciding within a time window of 5–10 msec (Figs. 5, 6). If the electrosensory system uses coincidence detection to analyze correlations between pyramidal cell spike trains, this can occur at the next level of electrosensory processing, i.e., the torus semicircularis of the midbrain (Carr et al., 1981; Maler et al., 1982). A series of studies has described the temporal filtering properties of toral neurons (Rose and Call, 1992; Fortune and Rose, 1997, 2000; Rose and Fortune, 1999), but so far none has directly addressed feature extraction or the effect of coincident input from ELL pyramidal cells.

Studies of visual processing have demonstrated that thalamic relay cells can switch between two modes of firing, tonic and burst (for review, see Sherman, 2001). Because bursts as well as spikes generated in tonic mode encode visual information, it was suggested that bursts signal the detection of objects to the cortex, whereas tonic firing may serve in the encoding of object details (Guido et al., 1995; Reinagel et al., 1999; Sherman, 2001). Interestingly, both bursts of single cells and coincident spikes fired by two relay cells with overlapping receptive fields are able to efficiently drive layer IV simple cells (Alonso et al., 1996; Usrey et al., 2000). Both mechanisms are thought to make information transmission to the cortex more reliable. Additionally, coincident activity may contain improved spatial information. Enhanced spatial resolution has been demonstrated for the coincident activity of pairs of visual cortical cells in cat with overlapping receptive fields (Ghose et al., 1994) and has also been suggested for concerted firing patterns among salamander retinal ganglion cells (Meister, 1996). Similarly, correlated activity may improve spatial information in weakly electric fish.

The time scales determined for interspike intervals within bursts of single neurons (7–15 msec; Gabbiani et al., 1996; Metzner et al., 1998) and for the optimal coincidence time window for feature extraction (5–10 msec) (Fig. 5) are remarkably similar. This suggests that integration of both burst-like spike patterns arriving on single neurons and coincident spikes on groups of pyramidal cells may contribute to the detection of stimulus features. Therefore, temporally correlated activity of groups of pyramidal cells may be considered distributed bursts. It has even been suggested that coincident bursts of spikes may constitute the “best neural code” used for synaptic transmission and information coding (Lisman, 1997). Indeed, our data support this notion, because a large percentage of the coincident spikes occurred in bursts (63 ± 15%, mean ± SD for a coincidence window of ±5 msec) (Fig. 4c). Studying postsynaptic effects of pyramidal cell spike patterns on their target neurons in the midbrain torus will help elucidate the physiological significance of such distributed bursts.