Electrotonically Mediated Oscillatory Patterns in Neuronal Ensembles: An In Vitro Voltage-Dependent Dye-Imaging Study in the Inferior Olive

Abstract

Spatiotemporal profiles of ensemble subthreshold neuronal oscillation were studied in brainstem slices using high-speed voltage-sensitive dye imaging. After local electrical stimuli, the overall voltage profile demonstrated coherent oscillatory waves that spread over the inferior olive (IO). These oscillations were also observed in concurrently obtained intracellular recordings from IO neurons. Over the first few seconds after the stimuli, the optically recorded oscillations clustered into coherent groups comprising hundreds of neurons. Statistical analysis of the spatial profiles of these clusters revealed size fluctuation around stable core regions that were surrounded by a rim the diameter of which varied in time during the oscillation period.

The neuronal ensemble oscillations were calcium derived and had an average frequency range of 1–7 Hz. This rhythmic response demonstrated a different spatiotemporal distribution in the presence of picrotoxin, which induced the merging of neuronal clusters into larger areas of coherent activity. The possibility that such clustering is a consequence of intrinsic oscillations in ensembles of coupled neurons was tested using mathematical modeling.

The inferior olive (IO) is a bilateral symmetrical nucleus located in the ventral aspect of the caudal bulbar region of the brainstem. IO neurons project to the contralateral cerebellum and form one of the two major cerebellar afferents known as climbing fibers (Szentagothai and Rajkovits, 1959). Climbing fibers synapse onto the cerebellar Purkinje cells (PCs) in the cerebellar cortex (Ramón y Cajal, 1888) and form one of the largest synaptic junctions in the nervous system (Eccles et al., 1966). Functionally, the IO nucleus is known to be essential in motor coordination (Wilson and Magoun, 1945; Murphy and O'Leary, 1971;Kennedy et al., 1982); its lesions abolish coordinated movements and result in motor disorders similar to those that follow cerebellar damage (Llinás et al., 1975; Soechting et al., 1976). However, the manner in which the olivocerebellar system contributes to cerebellar function is still a subject of extensive debate (for review, see Bloedel and Bracha, 1998; De Zeeuw et al., 1998).

Controversy regarding the function of the olivocerebellar system is attributable partly to its wide responsiveness to peripheral stimuli and its low (1–10 Hz) single-cell firing rate (Eccles et al., 1966). On the basis of its low firing rate, it has been argued that the olivocerebellar system cannot affect cerebellar output directly and its only function is to modify the strength of parallel fiber–Purkinje cell synapses (Keating and Thach, 1995). An alternative view suggests that the olivocerebellar system modifies cerebellar output directly by temporally binding widespread regions of the cerebellar–nuclear system and thereby by specifying combinations of cereberellar outputs in time (Llinás et al., 1975). According to the latter hypothesis, IO activity functions as a timing signal for movement by generating synchronous activation of Purkinje cell outputs (Llinás and Sasaki, 1989; Welsh and Llinás, 1997). Experiments with multiple electrode recordings have further supported this hypothesis. Indeed, rhythmic inhibitory potentials can be recorded at the cerebellar nuclei after olivocerebellar activity (Llinás and Muhlethaler, 1988).

The ability of the olivocerebellar system to generate ensemble synchronous activity has been attributed to the intrinsic properties of the IO neurons (Llinás and Yarom, 1981a,b, 1986; Benardo and Foster, 1986; Bal and McCormick, 1997) and their electrotonic coupling (Llinás et al., 1974; Sotelo et al., 1974; Llinás and Yarom, 1981a; Makarenko and Llinás, 1998). In particular, the interplay between several types of voltage-dependent calcium and potassium conductances enables the IO cells to fire rhythmically at 1–10 Hz. The combination of these intrinsic oscillatory properties with the electrotonic coupling between olivary cells results in the subthreshold membrane potential oscillations (Lampl and Yarom, 1997;Schweighofer et al., 1999). The coherence of such oscillations enables a group of IO neurons to fire in synchrony and simultaneously activate several regions of the cerebellum during movement coordination (Welsh et al., 1995). Therefore, knowledge about the spatiotemporal profiles of the oscillations in the IO nucleus provides additional information regarding the mechanisms responsible for the temporal binding of motoneuron activation and thus of motor coordination.

This question is addressed here by using a voltage-sensitive dye-imaging technique. This technique is presently the methodology of choice in addressing the geometrical distribution of activity in a large neuronal ensemble (Cohen et al., 1978). We report here that ensemble oscillations in the IO emanate from clusters of coherent activity, where each cluster is composed of hundreds of cells. Given the distribution of complex spike (CS) activity in the cerebellar cortex, the clusters are the most likely origin for synchronous activation of Purkinje cells observed in previous in vivomultiple recording experiments. In addition, we compared our experimental results with those obtained by computational modeling of IO neuronal ensembles endowed with oscillatory electrical properties and electrotonic coupling. These modeling results indicate that neuronal oscillatory clustering is a direct consequence of the combined electrotonic/intrinsic properties of coupled IO neurons.

MATERIALS AND METHODS

Inferior olivary slices

Brainstem slices were prepared from postnatal day 13–20 Sprague Dawley rats following protocols from previous in vitrostudies with some modifications (Llinás and Yarom, 1981a; Bleasel and Pettigrew, 1992). Animals were anesthetized with 15–20 mg of ketamine and decapitated. The brainstem was isolated and placed in cold, oxygenated Krebs'–Ringer's solution containing (in mm): 126 NaCl, 5 KCl, 1.25 NaH₂PO₄, 2 MgSO₄, 2 CaCl₂, 10 glucose, and 26 NaHCO₃. Parasagittal slices (300 μm in thickness) were sectioned using a vibratome. The major portion of the IO was contained in one or two slices. In an effort to increase the viability of slices, they were sectioned in sucrose-substituted Krebs'–Ringer's solution in which NaCl was replaced by sucrose while the osmolarity of the solution was kept constant (Aghajanian and Rasmussen, 1989). Slices were then transferred to a chamber containing normal oxygenated Krebs'–Ringer's solution and incubated at room temperature for at least 1 hr. Optical recording was implemented on slices stained with voltage-sensitive dye RH414 (Molecular Probes, Eugene, OR) dissolved in HEPES-based Ringer's solution containing (in mm): 130 NaCl, 6.25 KCl, 2 MgCl₂, 2 CaCl₂, and 25 HEPES, to a final concentration of 2.5 mg/ml. Slices were incubated for 10 min in the dye solution before being transferred to the interface recording chamber. Experiments were conducted at a bath temperature of 33 ± 1°C.

Recordings of optical signals

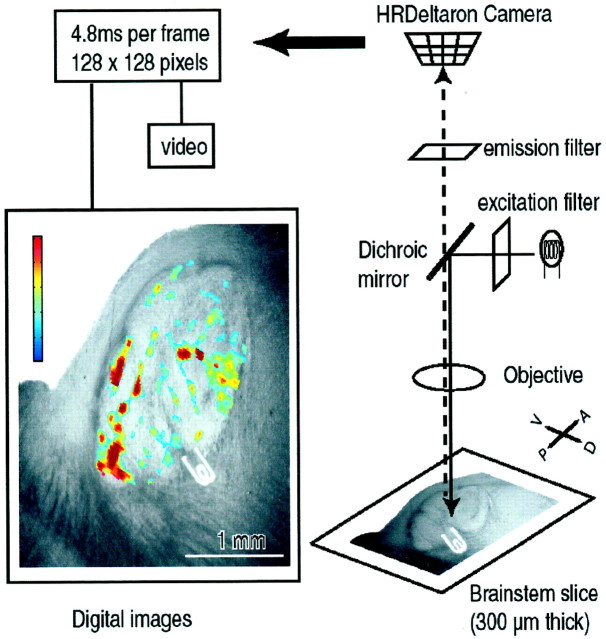
A schematic diagram of the recording setup is shown in Figure1. The recording chamber, attached to an upright microscope (Olympus BX50WI), was illuminated with a halogen lamp (12 W) driven by a stable power supply (Kepco, Inc.). The microscope was mounted onto an air table (Warner Instruments). The excitation light passed to the preparation through a bandpass filter (515 ± 35 nm) via a dichroic mirror. The emitted light returned through a long-pass filter (>590 nm). Optical signals were monitored with a fast CCD camera (HR Deltaron 1700, Fujix) with a 128 × 128 pixel spatial resolution. Images were sampled every 0.6–4.8 msec depending on the experiment. Most of the data presented were taken at 4.8 msec sampling rate. The total area imaged was 2.7 × 2.7 mm, and each pixel collected light from a surface of ∼21 × 21 μm. Optical recordings were averaged over four or eight trials. For each trial, the base fluorescence level (F_o) was initially calculated by averaging 64 frames. Changes in membrane potentials were evaluated as ΔF/F (Grinvald et al., 1982). Bleaching and irregularities of staining and illumination were corrected off-line by using Matlab-based software (The Mathworks, Inc.). In brief, the optical signals were first detrended to compensate for bleaching of the dye and slow responses from glia cells (Lev-Ram and Grinvald, 1986;Konnerth et al., 1987). The signals were then filtered with a three-dimensional moving average (3 × 3 × 3) and with the Gaussian low-pass filter. Finally, the optical signals were displayed using the RGB (red–green–blue) 256 color scale in such a way that their maximum amplitude equaled the maximum red color intensity of the RGB scale. The recordings were analyzed using power-spectrum density and autocorrelation methods written in Matlab.

Fig. 1.

Schematic diagram of the experimental setup. Light from a 12 V halogen source was passed through an excitation filter (515 ± 35 nm), dichoic mirror, and microscope objective (5×) before reaching the slice stained with the voltage-sensitive dye RH-414. Emitted fluorescent light was projected onto a CCD camera after passing through the objective, dichroic mirror, and cutoff filter (>590 nm). The CCD camera (Fujix, HR Deltaron 1700) consisted of 128 × 128 pixels, and each pixel collected light from a surface of ∼21 × 21 μm. Images were sampled every 4.8 msec. The optical data were analyzed off-line using Matlab-based software. An example of analyzed image is shown. Its color calibration bar corresponds to 0.001% change in ΔF/F.

One or two electrical stimuli (0.1–2 mA, 0.2 msec) were applied to the dorsal border of the IO nucleus via bipolar concentric electrodes. In five experiments, intracellular recording and optical recordings were simultaneously acquired to calibrate the optical signals with respect to directly recorded membrane potential. Intracellular recordings were obtained using glass micropipettes filled with 3 mKAcetate (60–100 MΩ). Recordings were amplified with an Axoclamp-2A amplifier (Axon Instruments) and acquired at 10 kHz with an Instrunet board (Omega Engineering, Inc.).

Mathematical modeling of inferior olivary oscillations

The motivation behind modeling of neuronal activity clusters was that of testing the assumption that such clustering, and cluster size, are electrotonic coupling dependent. Indeed, although this assumption may be considered obvious at first glance, it has been demonstrated that activity profiles other than clusters (such as spirals, waves, concentric rings) can occur in coupled neuronal networks (Makarenko, 1994).

The experimental data provided parameters such as membrane potential oscillation (from intracellular recordings) and cluster size and shape and their modulation by pharmacological intervention (from voltage-dependent dye imaging). These parameters stipulated the type of model to be implemented. Picrotoxin effect was modeled as change in electrical coupling, although the drug does not affect coupling between IO neurons directly but rather indirectly by shunting electrotonic current flow at the IO glomerulus (Lang et al., 1996). The single-cell model was developed to mimic the quasi-periodic subthreshold membrane potential oscillation observed electrophysiologically (Velarde et al., 2002). Network properties were modeled by interconnecting a set of these modeled elements into a two-dimensional matrix with isotropic coupling properties. Such a model was more easily implemented and scaled than models that incorporate single-cell cable and ionic conductance properties (Manor et al., 1997; Schweighofer et al., 1999).

Single element model. We represent single neurons as distinct elements (points) in a rectangular connectivity lattice connected to four other elements.

Each element is endowed with quasi-periodic oscillatory properties defined by a set of equations having a periodic and a noise term as follows:

$$z^{\prime }=z({\text{iw}}_0-\gamma )+i\surd 2D\xi (t),$$ Equation 1

where the variable z characterizes neuron dynamics (with x = Re (z), i.e., z = x + iy; prime implies differentiation),i is an imaginary unit, x and y are real numbers, γ is a damping constant,w₀ is angular oscillation frequency in the absence of noise and damping (w₀ = 2π ∗ 10 Hz), D is a parameter determining noise intensity scaling, and ξ(t) is a noise term that has zero mean with a time correlation function given by:

$$\langle {\xi }_{\text{jk}}(t){\xi }_{\text{lm}}(t^{\prime })\rangle ={\delta }_{\text{jk}}{\delta }_{\text{lm}}\delta (t-t^{\prime }),$$ Equation 2

where brackets imply average, and δ denotes a function that is zero when its argument has a non-zero value.

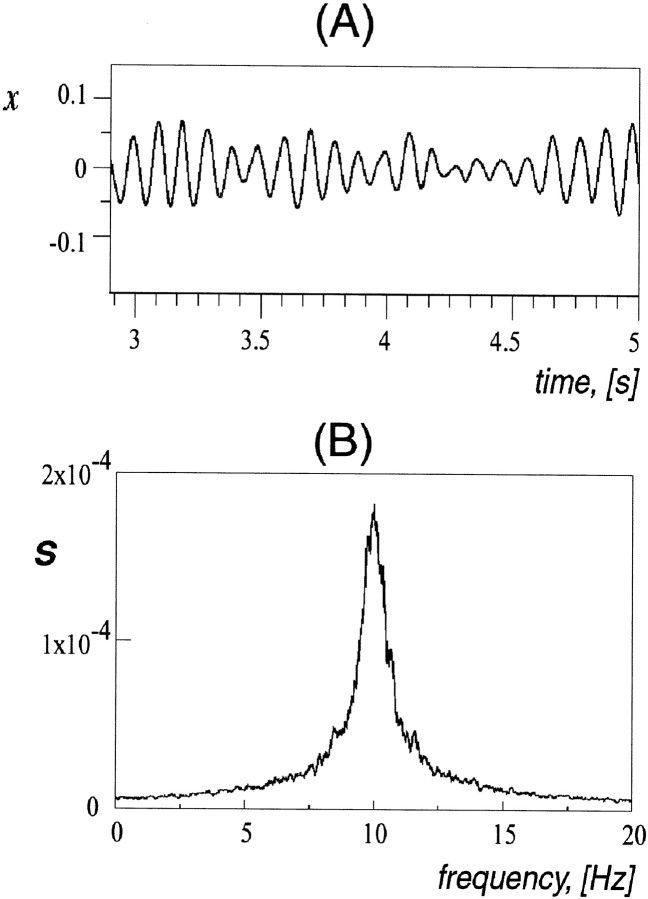
An example of oscillatory behavior of a single element and its power spectrum profile is given in Figure 2. Relatively regular oscillations have variable amplitude with a sharp frequency peak in the region of 10 Hz, which is in good agreement within vivo experimental data (Sasaki et al., 1989).

Fig. 2.

Time series and power spectrum of a model neuron (A). Subthreshold oscillations are almost periodic and have a sharp frequency peak at ∼10 Hz (B). The width of the power spectrum peak and some irregularity in the oscillations are caused by introduction of noise with zero mean.

The network model. The network consisted of a two-dimensional (n × n) lattice of single-modeled neurons, as described above, with their electrotonic coupling properties represented by periodic boundary conditions given by:

$$z_{\text{jk}}^{\prime }=z_{\text{jk}}({\text{iw}}_0-\gamma )+{\sum }_{\text{lm}\in L}{d}_{\text{jk}}^{\text{lm}}(z_{\text{lm}}-z_{\text{jk}})+i\surd 2D{\xi }_{\text{jk}}(t),$$ Equation 3

where the pair (jk) denotes site in the lattice andd^lm_jkaccounts for the electrotonic coupling coefficient (jk) and (lm). Thed^lm_jkis assumed to be the same over the network, i.e., isotropic. The actual value of the coefficient determines the dynamics of the network. The sum in the right part of Equation 3 is taken over neighboring neurons:

$$L:R^2\ge (l-j{)}^2+(m-k{)}^2,$$ Equation 4

where R accounts for the radius of neuronal interaction. For nearest-neighbor coupling r =1. The lattice (Eq. 3) is able to produce oscillations with a well defined frequency band peaked aroundw₀ with relatively slowly varying amplitudes.

Markov random field as an objective pattern descriptor. The introduction of voltage-dependent dye imaging to determine the geometry of the neuronal activity in vitro raised the necessity to qualify ensemble activity patterns in an objective manner. Indeed, in most imaging studies the interpretation of imaging pattern is based on subjective criteria that are open to ambiguous interpretation. In an attempt to alleviate this problem, we used a statistical approach known as the Markov random field (MRF) methodology, originally developed to characterize levels of spatial organization in two-dimensional matrices. This procedure, used often in structural biology (Grundy et al., 1997) and solid-state physics (Besag, 1974), has also proved useful in the analysis of brain imaging (Held et al., 1997; Wang et al., 2001) and multidimensional neuronal ensemble activity (Makarenko et al., 1997).

MRF offers the possibility of quantifying spatial configuration of clustering and stability of a particular spatial configuration with respect to their fluctuations. Thus, if pixel amplitudes are treated as values for the two-dimensional matrix elements, the MRF estimations can be determined unambiguously. The application of MRF estimates two main parameters: α and β. However, in this study only β is relevant, because it presents a quantitative estimation of the level of clustering in the image, whereas α relates to the probability that a particular value may occur in a given element of the matrix. When the matrix is presented as a rectangular lattice with values of elementx_i,j placed at the i,j node of the lattice, then:

$$\beta =\frac{\sum _{i,j\epsilon \mathrm{\Omega }}{x}_{\text{ij}}{y}_{\text{ij}}-1/m\left(\sum _{i,j\epsilon \mathrm{\Omega }}{x}_{\text{ij}}\right)\left(\sum _{i,j\epsilon \mathrm{\Omega }}{y}_{\text{ij}}\right)}{\sum _{i,j\epsilon \mathrm{\Omega }}{y}_{\text{ij}}^2-1/m{\left(\sum _{i,j\epsilon \mathrm{\Omega }}{y}_{\text{ij}}\right)}^2},$$ Equation 5

where y _i,j=x_i−1,j+x_i+1,j+ x_i,j−1+x_i,j+1.

Ω is one of two sublattices that constitutes the original lattice and each of which is distributed as the black and white spaces of a chessboard.

The eventual estimation of the β is taken as an arithmetic mean over the two subsets. The detailed description of the method with an illustration of how β correlates to the spatial organization in an image has been addressed previously (Makarenko et al., 1997). Here we review parameter β: the more the absolute value of β differs from zero, the higher is the level of spatial organization in the image. The “spatial organization” is codependent on the values of the neighboring pixels. The degree of the codependence averaged over the whole matrix reflects the level of spatial organization that exists at a given moment in the total system. Calculating β for a set of consecutive image sequences as a function of time in the course of an experiment we can see how it characterizes the temporal evolution of the spatial organization, bringing together the spatial and temporal features of the network activity. The example illustrated in Figure 7 compares three configurations consisting of zeros and ones with different degree of clustering from absolutely random distribution (no clusters) and how such clusters reflected in the value of β. Values of β for each spatial configuration in Figure7A are given in the figure legend. It must be remembered that the actual values of β are model dependent and only meaningful within a given model, i.e., within a matrix of the same dimension and value ranges. Thus, comparison of modeled and experimental findings must be based on statistics. In the present case, the comparison is based on the variance of β.

Fig. 7.

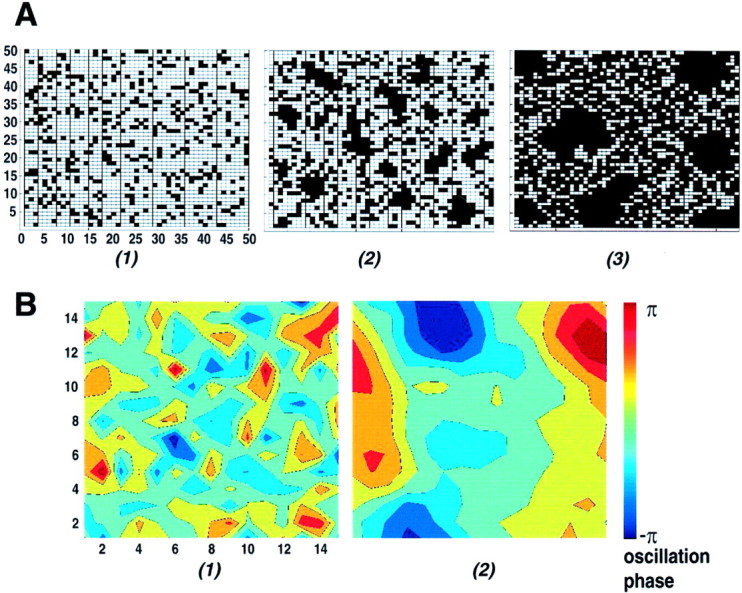
Model results illustrate that β is a measure of clustering and that electrotonic coupling determines the value of β. The different values for β in A andB reflect model differences (A, binary;B, nonbinary). A, Clustering property dependence on the value of the MRF parameter β. Each square takes a binary value of 0 (white square) or 1 (black square). (1), Randomly distributed configuration with no clusters; corresponding β₁∼ 0. (2), Small clusters, β₂ = 2. (3), Big clusters, β₃ = 3.5 > β₂ > 0. B, Clustering in the modeled network as function couplingd^lm_jk degree.(1), In the presence of reduced coupling (inhibition) in the system, β = 1.0. (2), With increased coupling (absence of inhibition), β = 1.5. Values of β differ forA and B because they relate to different models addressing two different issues. A addresses general model properties and B addresses specific IO modeling (for further explanation, see Materials and Methods).

RESULTS

Characteristics of the optical signals

The spatiotemporal characteristics of the ensemble neuronal oscillations in inferior olive slices were studied using optical recordings of voltage-sensitive dye signals. Several steps were taken to increase the signal-to-noise ratio of our imaging responses. First, optical recordings were averaged over four or eight successive trials. Second, the recording sequence was structured in such a way that the electrical stimuli to the IO nucleus were delivered a short time (50 msec) after the beginning of image acquisition. This allowed the electrical stimuli to reset subthreshold oscillation phase and thereby to entrain a large proportion of neurons to in-phase oscillations (Llinás and Yarom, 1986). Because each camera pixel integrates voltage signals over 21 × 21 μm and includes several neurons, only in-phase synchronous activity can be detected readily. Indeed, synchronization of oscillatory activity over the IO network increased the amplitude of the optical signal to the level that can be easily detected.

Because the present experiments were designed to record stimulus-evoked oscillations averaged over several trials, an issue then arises concerning the relation of spontaneous oscillations with stimulus-evoked, averaged oscillations in the IO. This question was addressed directly with intracellular recordings (Fig.3).

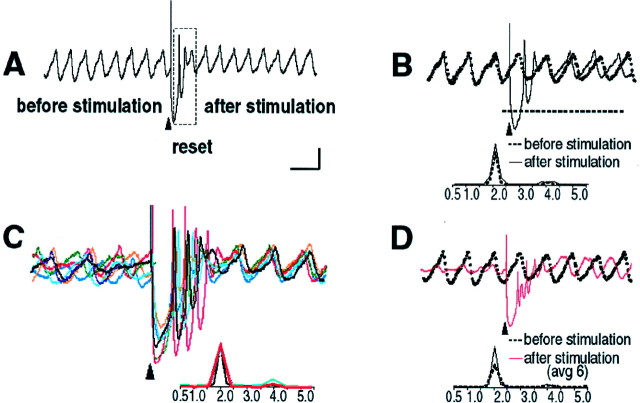
Fig. 3.

Comparison of spontaneous and stimulus-evoked oscillations in the inferior olive. A, Intracellular recording of spontaneous oscillations at 2 Hz interrupted by an extracellular stimulus. After extracellular stimulation (marked with an arrowhead), the oscillations disappeared for 750 msec (boxed area) and then resumed. The membrane potential was −60 mV. B, Intracellular recordings of spontaneous (dashed black line) and stimulus-evoked (solid black line) oscillations from the same cell are superimposed. Their corresponding power spectra are shown below. Note that extracellular stimulation only modified the phase of spontaneous oscillations without affecting their amplitude and frequency.C, Six individual intracellular traces of stimulus-evoked oscillations from the same cell are superimposed on theleft. Each trace is shown in a differentcolor. Their corresponding power spectra are displayed below. In every recording, the frequency of stimulation-evoked oscillation was the same (2.0 Hz). Note that in each trace the stimulation- induced shift in the oscillatory rhythm of the cell is remarkably similar. Oscillations are clearly seen after the stimulus-induced reset but can be barely detected before the stimulation. D, The average of six traces of stimulus-evoked oscillations (red line) and the recording of spontaneous oscillations (dashed black line) are superimposed. The stimulus-evoked oscillations in the average trace have the same frequency and amplitude as the spontaneous oscillations and differ only in the phase shift. Calibration bar: 1 mV;A, 1 sec; B, D, 500 msec;C, 415 msec.

In accordance with previous results (Llinás and Yarom, 1986), an extracellular stimulus delivered at the dorsal border of the IO nucleus generated a full action potential followed by a membrane hyperpolarization in nearby neurons (Fig. 3A, boxed area). The findings also demonstrate that if the cell was oscillating at the time of the stimulus, its rhythmicity was momentarily stopped but then resumed ∼750 msec after the stimulation with a different phase (n = 7). It is important to note that the extracellular stimulation only reset the phase of oscillations, without affecting their frequency or amplitude (Fig. 3B). This electrical behavior could be obtained repeatedly for any given cell, and the stimulation-induced shift in the oscillation phase was remarkably similar (Fig. 3D) (n = 6). Moreover, for a given cell, the average of six individual stimulus-evoked oscillations had the same frequency as that of the spontaneous oscillations (Fig. 3D). When the cell was stimulated by a train of stimuli, the results were similar to those shown for a single stimulus, but the reset time was prolonged (data not shown). Thus, the stimulus-evoked IO oscillations averaged over several trials have the same frequency and amplitude as spontaneous oscillations and differ only in a phase shift. Therefore, characteristics of these oscillations can be used to further understand spontaneous oscillations in the IO.

All the slices used in this imaging study showed oscillatory activity (n = 42, 30 rats). As stated above, the evoked optical response comprised an initial change in background fluorescence near the stimulating electrode (up to 0.027%) followed by several oscillatory cycles (Fig.4A,Control) (n = 14).

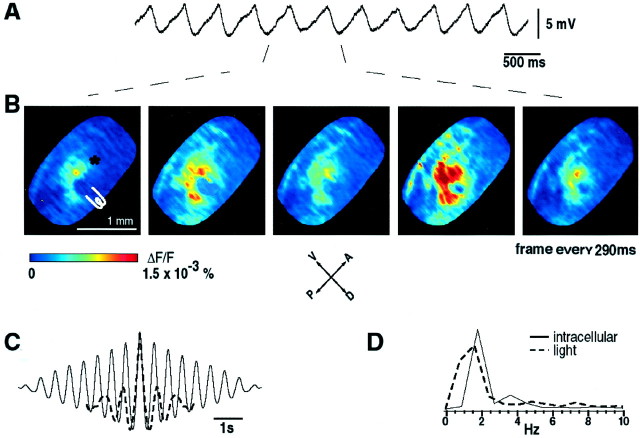
Fig. 4.

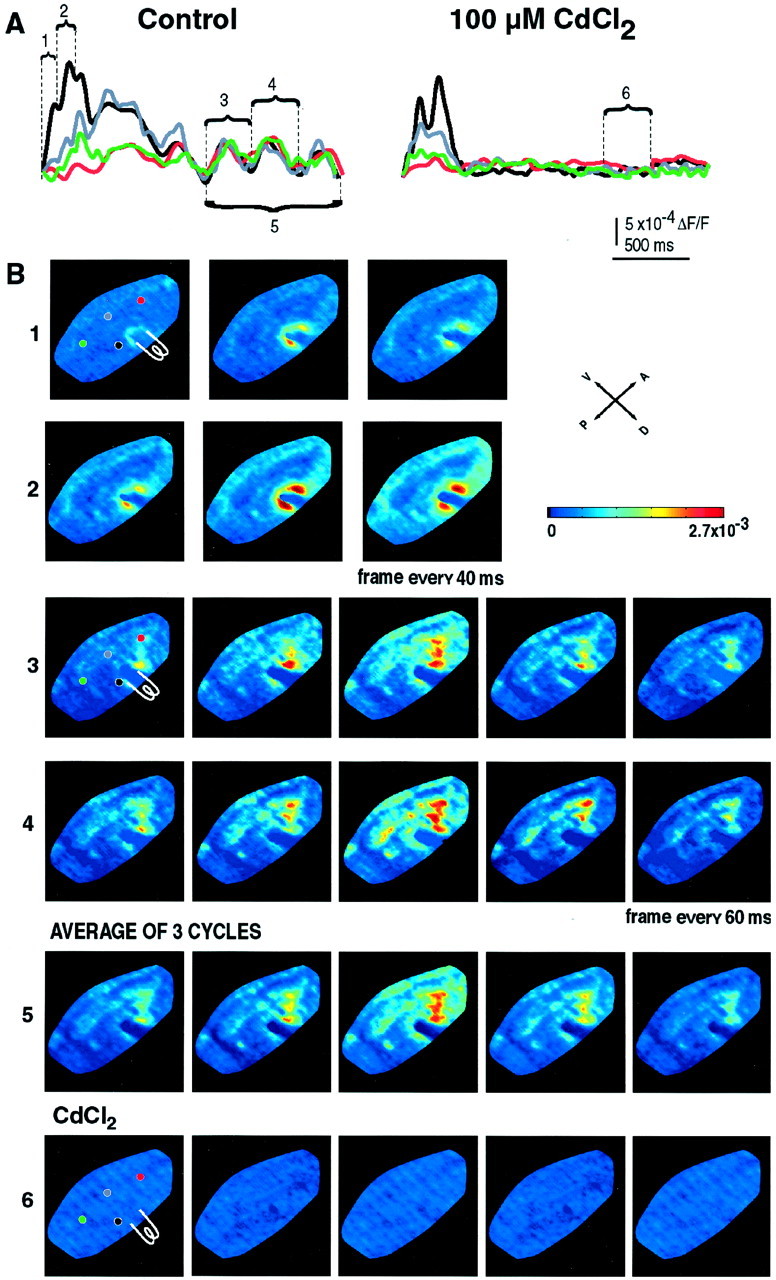
Spatiotemporal patterns of optically recorded inferior olivary oscillations. A, A complete time course of optical responses for four pixels under control conditions (left) and in the presence of 100 μm CdCl₂ (right). Locations of the pixels are marked with circles of differentcolor in B. Under control conditions, the optical response consisted of an initial response to a train of extracellular stimuli (2 stimuli at 10 Hz) followed by three oscillatory cycles. The frequency of the optically recorded oscillations was 4 Hz. Addition of CdCl₂ blocked optically recorded oscillations; only direct depolarization caused by the extracellular stimulation was detected. B, Several multiframe displays for each of the regions marked in A. Only the area of the IO is shown. Position of the stimulating electrode is indicated. The color bar gives the color scale withdark purple corresponding to lowest fluorescence andred corresponding to highest fluorescence. All images were filtered by a low-pass (30 Hz) Gaussion filter. 1, The response of the IO nucleus to the first stimulus. 2, The response of the IO to the second stimulus. Note that the time course and location of the response to the second stimulus are identical to that of the first, but with a larger change in the background fluorescence. 3, 4, The location and spatial spread of two cycles of the ensemble oscillations. The oscillations emanate from several clusters of closely spaced cells throughout the IO (see the change in amplitude with time). These clusters are highly repeatable from cycle to cycle over an oscillation sequence. 5, An average of four oscillatory cycles further underlines the stability of fluorescent clusters.6, Same as in 4, but in the presence of 100 μm CdCl₂.

The initial change in fluorescence indicated the location, amplitude, and time course of the response of the IO neurons to the stimulus (Fig.4A, Control, B1). When a train of two stimuli was applied to the IO, the time course and location of the response to the second stimulus were identical to that to the first stimulus, but the second stimulus induced a larger change in the background fluorescence (Fig. 4, compare B1, B2). These initial responses were followed by several ensemble oscillations that spread throughout the IO nucleus with little spatial or timing variance (Fig.4A,B3,B4). For the most part, the oscillatory sequence repeated itself with a small degree of variability after each stimulus train. The fluorescence clusters emanated from several independent regions of the slice and consisted of closely spaced synchronous neuronal ensemble activity. All regions had the same oscillation frequency and were phase coherent. This phase coherence was most clearly observed after the phase reset triggered by the electrical stimulus. The oscillations were highly repeatable in time and space: the average of three oscillatory cycles had the same spatiotemporal profile as that of the individual oscillations (Fig. 4, compare B3, B4,B5). The average oscillation had the same fluorescent clusters at the same regions of the slice as the individual oscillations.

Within our temporal resolution (4.8 msec between frames), the optical oscillations started synchronously everywhere in the slice (Fig.4A, Control, 1, 2,3, 4), suggesting that the conduction velocity of the oscillation spread was higher than the temporal resolution of the recording camera. In addition, because of temporal resolution, we were low-filtering the neuronal activity and could see only slow subthreshold events.

Ionic mechanisms for cluster oscillation

To determine the ionic mechanism supporting the oscillatory activity of these neuronal clusters, three experiments were conducted in the presence of CdCl₂ (100 μm) in the bathing solution. CdCl₂ is known to block Ca²⁺ ionic conductance subserved by calcium channels and thereby to stop subthreshold oscillations in the IO (Llinás and Yarom, 1986). Addition of cadmium to the bathing solution completely blocked optically recorded oscillations (Fig.4A, right panel, B6). Under this condition, only short-lasting focal activation of the area around the stimulating electrode was detected (Fig.4A, right panel). This result indicates that the optically recorded ensemble oscillations are Ca²⁺ dependent and thus are generated by the same conductances responsible for single-cell subthreshold oscillations recorded intracellularly in the IO neurons (Benardo and Foster, 1986; Llinás and Yarom, 1986; Bleasel and Pettigrew, 1992).

Comparison of optical signals and intracellular recordings

To correlate the time course of our optical signals with intracellular recordings, we compared these two kinds of measurements in five experiments. The subthreshold oscillations were first recorded intracellularly in the presence of the dye (Fig.5A). Location of the recording electrode is marked with an asterisk in Figure5B. The slice was then electrically stimulated with a bipolar electrode at the border of the IO nucleus, and the evoked ensemble IO oscillations were imaged (Fig. 5B). Note that the optically observed oscillations consisted of several clusters that changed its dimensions depending on the oscillation phase. They embraced the largest area during the upward phase of the oscillations (Fig. 5B, second and fourth image fromleft).

Fig. 5.

Comparison between optically recorded and intracellularly recorded IO oscillations. A, Subthreshold oscillations recorded intracellularly from an IO cell in the presence of dye (RH-414). Position of the recording electrode is marked with an asterisk inB. B, Frames from optically recorded oscillations from the same slice as in A. Two cycles of oscillations are shown. The position of the stimulating electrode is indicated. C, Autocorrelograms and power spectra of the optically recorded ensemble oscillations (dashed black line) and intracellular recorded oscillations (solid black line). Note that the clusters, seen as spots of fluorescence in the image panel, have oscillatory voltage profiles at frequencies similar to those observed intracellularly.

The intracellularly and optically recorded signals were analyzed using power-spectrum density and autocorrelation methods written in Matlab. As shown in Figure 5C, the frequencies of the intracellular recorded subthreshold oscillations (dashed black line) and the optically recorded neuronal ensemble oscillations (solid black line) (2.0 and 1.8 Hz, respectively) were closely matched. A slightly slower frequency of the cluster oscillations with respect to the intracellular oscillations was observed. This small difference in oscillatory frequency is probably attributable to the fact that the borders of the clusters oscillated at a slower frequency than the individual cells. Because movement of the cluster borders involves sequential activation of neighboring cells and such activation can occur only during the upward phase of the oscillations, the fluctuation of the borders would be slower than oscillations of the individual cells.

The overall similarity of intracellular and cluster oscillations indicates that the subthreshold IO oscillations observed intracellularly can be studied using voltage-sensitive dyes. Moreover, given the temporal and spatial characteristics of such rhythmic activity and its phase reset properties (Makarenko and Llinás, 1998), such optical measurements most probably reflect the ensemble electrophysiological properties observed previously with multiple simultaneous recordings at the Purkinje cells level (Llinás and Sasaki, 1989; De Zeeuw et al., 1998; Lang et al., 1999; Fukuda et al., 2001; Yamamoto et al., 2001).

The spatial and temporal analysis of the clusters

IO cells are interconnected by gap junctions and can exhibit spontaneous oscillatory activity at a frequency that ranges from 1 to 10 Hz (Llinás et al., 1974; Sotelo et al., 1974, Benardo and Foster, 1986; Llinás and Yarom, 1986; Bleasel and Pettigrew, 1992; De Zeeuw et al., 1996). It has been suggested that the IO nucleus consists of several functionally coupled oscillating clusters of cells (Llinás and Yarom, 1986; Lampl and Yarom, 1993; Devor and Yarom, 2000). In support of this view, in all experiments (n = 14) the recorded optical responses produced oscillating clusters that were time coherent (Figs. 4A,B,5B). Given the possible functional implications of such dynamic structures, the spatial and temporal parameters of the clusters were calculated. In particular, the frequency and average size of a cluster for each experiment were analyzed in detail. Statistical analysis of the properties of a set of clusters from 14 different experiments determined mean size, variances, SE, and oscillatory frequency (Table 1). The oscillation frequency was determined by using power spectrum density analysis (see Materials and Methods). The range of frequencies observed was from 1.6 to 6.5 Hz. These results demonstrate similarities between the optically recorded oscillatory frequency range and those reported for intracellular subthreshold oscillations (Benardo and Foster, 1986;Llinás and Yarom, 1986; Bleasel and Pettigrew, 1992).

Table 1.

Description of dimensions of the optically recorded inferior olivary clusters

Animal no.	Slice no.	Core area of a cluster (×10−3 mm2)	Maximum area of a cluster (×10−3 mm2)	Core volume of a cluster (×10−4mm3)1-a	Maximum volume of a cluster (×10−4mm3)1-a	Cell number in the core area1-b	Maximum cell number in a cluster1-b	Frequency (Hz)
1	1	12	20	36	60	290	480	6.5
1	1	24	35	72	105	580	840	6.5
1	1	11	16	33	48	260	380	6.5
1	2	18	33	54	99	430	790	6.5
2	3	20	31	60	93	480	740	3.3
2	3	18	30	54	90	430	720	3.3
2	3	12	18	36	54	290	430	3.3
3	4	9	27	27	81	220	650	3.3
3	4	10	21	30	63	240	500	3.3
3	4	12	26	36	78	290	620	3.3
3	5	11	29	33	87	260	700	5.0
3	5	8	16	24	48	190	380	5.0
4	6	9	16	27	48	220	380	1.7
4	6	8	17	24	51	190	410	1.7
4	6	22	52	66	156	530	1250	1.7
5	7	5	17	15	51	120	410	4.5
5	7	4	7	12	21	100	170	4.5
5	8	6	10	18	30	140	240	2.0
5	9	5	8	15	24	120	190	2.8
6	10	14	18	42	54	340	430	2.0
6	10	8	12	24	36	190	290	2.0
6	10	7	14	21	42	170	340	3.3
7	11	5	11	15	33	120	260	3.3
7	11	7	17	21	51	170	410	3.3
8	12	21	38	63	114	500	910	3.5
8	12	14	24	42	72	340	580	3.5
8	12	6	11	18	33	140	260	3.5
9	13	5	10	15	30	120	240	3.6
10	14	6	7	18	21	140	170	3.0
10	14	10	17	30	51	240	410	3.0
Mean SD		11  ± 6	20  ± 10	33  ± 17	61  ± 31	260  ± 140	490  ± 250	3.5  ± 1.4

^F1-aVolume of a cluster was determined by multiplying the area of the cluster by the thickness of the response region, which was calculated to be 0.2 mm (see Discussion).

^F1-bNumber of cells in a cluster was estimated by multiplying the volume of the cluster by the density of the IO neurons in rat (80,000 cells/mm³) (see Discussion).

The mean cluster size was determined by choosing a threshold fluorescence level that was 2 SDs above the mean background noise. In every case the chosen threshold level distinguished very adequately areas of optical activity from background noise. A cluster was then defined as an area that showed oscillatory activity with pixel values above the threshold. Each cluster consisted of a core region and the adjoining area (Figs. 4B, 5B). The core region demonstrated a close to constant size, but the extent of the adjoining area was found to be phase dependent. The core area and maximum area (i.e., the core region plus the adjoining area at its uppermost extent) were calculated for several representative clusters in each experiment (Table 1). The mean core area was 11 ± 6 × 10⁻³mm² , and the mean maximum area was 20 ± 10 × 10⁻³mm². Because the size of the cluster is thought to be directly related to the level of functional coupling among IO neurons, the difference in the number of intact gap junctions between slices can account for high SDs in the size of observed clusters.

Because most of the IO neurons are coupled via dendrodendritic gap junctions, which are not located within the same plane (Sotelo et al., 1986; De Zeeuw et al., 1990), we assumed that the optically recorded IO clusters were three-dimensional structures. We then estimated the number of cells in each cluster by multiplying the area of the cluster by the thickness of the response region by the density of the IO cells (Table 1). Both the core area and the maximum area of a cluster consisted of hundreds of cells. On average, there were 260 ± 140 cells in the core region and 490 ± 250 cells in the maximum area of the cluster (Table 1). Although this measurement is only an approximation, it does show statistical consistence across all the experiments.

Thus, our optical data indicate that at the network level, the IO nucleus is organized in functionally coupled activity clusters. Each cluster is composed of several hundreds of cells that may act in unison to simultaneously activate groups of cerebellar Purkinje cells.

Factors affecting cluster dimensions

In the final set of experiments. we attempted to define the mechanisms that determine cluster dimensions. Several possibilities were considered. The first possibility was that the level of functional coupling among the IO neurons defined cluster boarders (Welsh and Llinás, 1997). If this were the case, addition of drugs that modulate electrical coupling among olivary neurons, such as picrotoxin (Lang et al., 1996), would change the area of optically recorded clusters. The second possibility was that a relatively small number of all the cells survived in the slice, and thus, the recorded responses were the product of surviving clusters of neurons.

To distinguish between these two possibilities, several experiments were conducted in the presence of picrotoxin (10 μm). At the single-cell level, addition of picrotoxin reduced the frequency and amplitude of spontaneous subthreshold oscillations without affecting the membrane potential of the cell (Fig.6A,B). The frequency of oscillations was reduced by 15 ± 4%, and the amplitude was decreased by 51 ± 8% (n = 12). At the network level (n = 4), application of picrotoxin increased the size of the clusters by partly merging them into larger areas of activity and by partly activating additional neuronal regions (Fig. 6B–D). In our experiments, application of picrotoxin increased the cluster size by 207 ± 17%. These results demonstrate that clustering was not an artifact resulting from sparcity of neuronal survival, because neurons previously occupying quiescent sites became active after the drug administration.

Fig. 6.

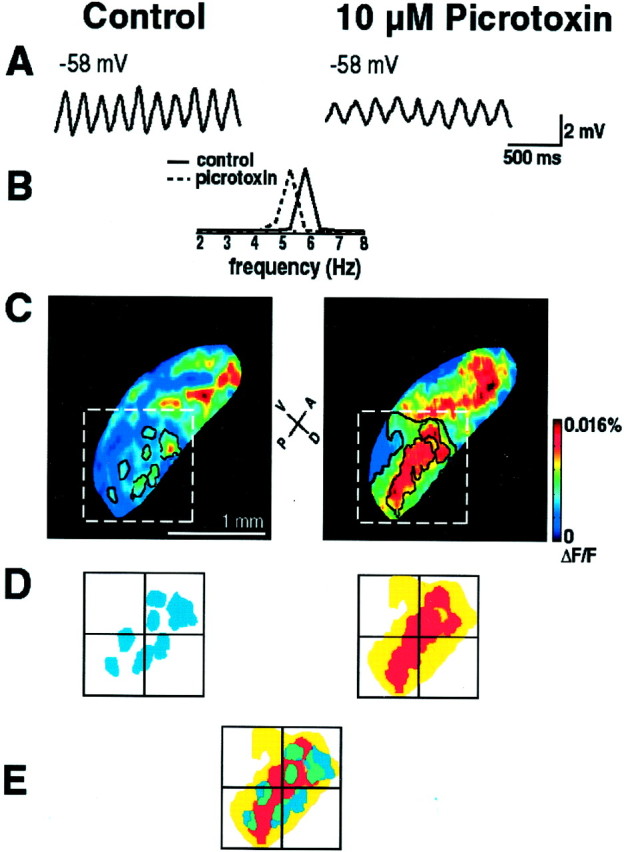
Effects of picrotoxin on intracellularly and optically recorded oscillations in the IO. A, Intracellular recording from an IO neuron showing spontaneous subthreshold oscillations before (left) and after (right) bath application of 20 μmpicrotoxin. B, Power spectra of control (solid black line) and picrotoxin-modulated oscillations (dashed black line) are superimposed. Addition of picrotoxin reduced amplitude and frequency of subthreshold oscillations without changing the resting membrane potential of the cell.C, A frame of imaged ensemble neuronal oscillating clusters in control conditions (left) and after addition of 20 μm of picrotoxin (right). Several representative clusters in the bottom right part of the IO are outlined in black. The clusters were defined as areas with pixel values above the selected threshold level (in this case, 0.007%). After picrotoxin, an additional threshold level was chosen to delineate the highest areas of activity. D, Contours of cluster within the boxed area in A marked withwhite discontinuous lines (1 × 1 mm) are enlarged.E, Areas shown in B are superimposed. Control clusters are shown in blue; picrotoxin clusters of lower threshold are shown in yellow, and those of higher threshold are shaded in red. Overlapping regions of control clusters and picrotoxin clusters of lower threshold are shown in green. Note that picrotoxin significantly increased the size of clusters by merging several small areas into larger activation areas.

Our experiments with picrotoxin showed that the drug that modulated the level of the effective electrotonic coupling among IO cells changed the dimensions of inferior olivary clusters. In accordance with data from previous in vivo studies in which local application of picrotoxin (Llinás and Sasaki, 1989; Lang et al., 1996) or the destruction of cerebellar nuclei resulted in increments of coherent Purkinje cell activity, in our experiments application of picrotoxin significantly increased the size of fluorescent clusters by partly merging several small clusters into larger areas of activation. Thus, our results demonstrate that there is a basal level of inhibition in the IO slices supported by the presence of the presynaptic inhibitory terminals of brainstem and cerebellar origin, which are known to synapse at the IO glomeruli (Sotelo et al., 1986; De Zeeuw et al., 1996, 1998). Indeed, it is now recognized that about half of the cerebellar nuclei cells are GABAergic, and they project directly to the IO. Blocking of such inhibition within the IO glomeruli, where the gap junctions are located, expands the cluster size and increases the electrical load of the network and within the cluster. This increase is the most likely origin for the reduction in amplitude and frequency of spontaneous subthreshold oscillations observed with intracellular recordings.

In conclusion, our results indicate that the cluster size is probably determined by the IO electrical coupling coefficient and thus by the magnitude and distribution of the return inhibition from the cerebellar nuclear feedback as demonstrated in previous in vivoexperiments (Nelson et al., 1989; Ruigrok and Voogd, 1995; Lang et al., 1996).

Model results: IO cluster size is coupling-coefficient dependent

To test the hypothesis that the modulation of electrical coupling is responsible for cluster size modeling, results were obtained by running the simulation protocol described in Materials and Methods. First, as illustrated in Figure 7, variations of the couplingd^lm_jk in the neuronal ensemble model (Eq. 3) were simulated. The results from direct observation of the phase coherence and the calculated value of such statistics as variance for MRF parameter β indicate that clustering of activity among the modeled matrix elements is coupling-coefficient dependent.

The modeling results support the conclusion that modulation of electrotonic coupling in the IO by feedback inhibition from the cerebellar nuclei (Lang et al., 1996) regulates IO cluster distribution and size. That is, increased inhibition results in cluster size reduction and in an increase in the number of independent clusters (Fig. 7A). Conversely, decrease of inhibition results in increased cluster size and a simultaneous decrease in the number of independent clusters (Fig. 7B). Moreover, MRF results indicate that the variance (ς²) of the parameter β increases with reduction of coupling coefficient so that inequality ς_{weak inh} ∼ 0.4 > ς_{strong inh} ∼ 0.25 takes place.

These modeling results are in agreement with the imaging data. We calculated time series for the Markov parameter β and its variance from sets of imaging frames from seven experiments. All frames from complete sequences of optical images were analyzed during oscillatory sequences under normal conditions and after picrotoxin administration. The variance of β reflected cluster size fluctuation probability. Indeed, in the presence of background inhibition, the average β value (n = 7) was 1.7 × 10⁻¹ and its variance (ς²) was ∼1 × 10⁻³, whereas in the presence of picrotoxin (no inhibition) (n = 3) the average β value was 1.4 × 10⁻¹ and its variance (ς²) was twice the control value (∼2 × 10⁻³).

Thus in both modeling and experimental results, blocking of inhibition significantly increased the variance of β, which indicated that although the number of individual clusters was decreased, the probability of cluster size fluctuations was increased.

DISCUSSION

Inferior olivary neurons are characterized by intrinsic rhythmic activity that results from the interplay between the low-threshold calcium spikes, the calcium-dependent potassium, and hyper-polarization-activated cationic conductances (Llinás et al., 1974; Sotelo et al., 1974; Llinás and Yarom, 1981a,b, 1986;Benardo and Foster, 1986; Bleasel and Pettigrew, 1992; Bal and McCormick, 1997). The combination of these intrinsic resonance properties and electrotonic coupling between the olivary cells via gap junctions results in subthreshold membrane potential oscillations (Llinás and Yarom, 1981b, 1986; Benardo and Foster, 1986; Bleasel and Pettigrew, 1992; Bal and McCormick, 1997; Lampl and Yarom, 1997). The olivary gap junctions are mainly located within the structures known as glomeruli (Llinás et al., 1974; Sotelo et al., 1974;King et al., 1975). A high density of gap junctions (De Zeeuw et al., 1996) and their specific location provide an anatomical substrate for generating simultaneous electrical discharges among neighboring IO neurons. Synchronous firing of a group of IO cells, in turn, can result in synchronized climbing fiber activation of Purkinje cells (complex spikes) throughout the cerebellar cortex. The potential for such global synchronization is shown by the fact that concurrent complex spike activity can be detected between the Purkinje cells located in widely separated regions of the cerebellar cortex (De Zeeuw et al., 1996;Yamamoto et al., 2001).

The ability of the olivocerebellar system to generate rhythmic synchronous discharges has been proposed to play a central role in motor coordination for several decades (Llinás et al., 1975;Llinás, 1991). However, although the IO oscillations are a neuronal ensemble event, they have been studied mainly at a single-cell level. In an attempt to understand these ensemble properties, high-speed voltage-sensitive dye imaging was implemented to define the spatiotemporal properties of the IO oscillations at the network level. Our results demonstrate that IO ensemble oscillations result from closely spaced, synchronously oscillating clusters comprising hundreds of neurons. Each cluster is a dissipative functional entity that acts in unison with other clusters and through its connectivity results in a synchronous afferent input volley to the cerebellum.

Description of the IO clusters

On the basis of the anatomical organization of the IO nucleus and widespread synchronicity of the complex spike activity in the cerebellar cortex, it has been proposed that on the functional level, the IO nucleus consists of clusters of electrotonically coupled neurons that can spontaneously generate rhythmic and synchronous outputs to the cerebellum (Welsh and Llinás, 1997). In agreement with that hypothesis, the present study visualizes these clusters and describes their spatial distribution and dynamic behavior in vitro. Extracellular electrical stimuli applied directly to the brainstem slice at the level of the IO were shown to reset the phase of spontaneous subthreshold oscillations and thereby entrain the IO neurons toward coherent in-phase oscillations (Llinás and Yarom, 1986). We showed with intracellular recordings that the IO stimulus-evoked oscillations had the same amplitude and frequency as spontaneous oscillations and differed only in phase shift.

IO oscillations were recently imaged in vitro for the first time (Leznik et al., 1999; Manor et al., 2000). In the study by Manor et al. (2000), the size of their imaging area allowed them to observe only a small number of IO cells. By increasing the number of IO neurons that can be observed simultaneously, we were able to increase the amplitude of the optical signals, improve the signal-to-noise ratio, and observe the entire extent of the IO nucleus.

Our optical responses consisted of initial activation of the area around the stimulating electrode followed by stimulus reset ensemble neuronal oscillations. There was always a close correspondence between the frequency of intracellularly recorded subthreshold oscillations (Benardo and Foster, 1986; Llinás and Yarom, 1986;Bleasel and Pettigrew, 1992) and that of our optical ensemble neuronal oscillations. The optically recorded oscillations emanated from several spatially separated fluorescent clusters. Every cluster had the same oscillation frequency and was phase coherent.

The observed clusters had a core region and the adjoining area that most likely consisted of loosely connected cells. The total area of a cluster, which included the core area and the adjoining area at its uppermost extent, was defined as a maximum area of the cluster. The core of the cluster was constant in size, but its amplitude was modified depending on the phase of the ensemble oscillations. In contrast, the adjoining area of loosely grouped cells changed its dimensions depending on the phase of the oscillations, so that its size was maximal at the peak oscillation amplitude. This phenomenon can be explained by the fact that with relatively few gap junctions that link cells in the adjoining area of the cluster, the amount of current flow needed to entrain these cells in oscillatory activity might be present only during the upward phase of the oscillations (Lang, 2001). As for the tightly coupled cells within the core of the cluster, the high density of the gap junctions may allow them to function in an all-or -one manner throughout the whole oscillatory cycle. Our data are in general agreement with those of Manor et al. (2000), who used a similar optical imaging technique and observed spontaneous oscillatory activity in the IO slices over the area of 80 × 10⁻³mm². These authors, however, did not detect multiple clusters in the IO nucleus, partly because their imaging system had a relatively low spatial resolution and covered only a small area of 600 × 600 μm versus the imaging area of 2700 × 2700 μm used in our study, which was about 20 times larger.

Implications of modeling results

The modeling results support our two main working hypotheses. First, the level of inhibition (i.e., coupling) is a main factor in regulating the average size of a cluster of synchronous activity. Second, with the higher level of inhibition, the number of clusters increases and the variance (ς) of the MRF parameter β decreases. Because the variance of β is proportional to the fluctuations of the average cluster size, our results imply that inhibition decreases and stabilizes the average size of the clusters.

A significant implication of the first finding is that as the degrees of freedom increase with an increased number of clusters, the probability of large fluctuations in cluster size decreases. In fact, although counterintuitive, the system becomes “less liquid” with a larger number of smaller clusters. That is, despite the large number of clusters, the system robustly preserves a particular level of spatial organization. More fundamentally, the results indicate the existence of a maximum number of possible functional states, implying that increased inhibitory feedback does not result in an ever-increasing control ability. Equally interesting, even at high levels of clustering, the IO network demonstrates a short-phase resetting time (∼70 msec) without losing oscillatory robustness, thereby optimizing reset agility without sacrificing control (Makarenko and Llinás, 1998).

Functional significance of IO cluster activity

Taken together, our results demonstrate that the voltage-sensitive dye-imaging technique can be used successfully to study the geometrical distribution of activity in the IO nucleus. We report here that on a functional level, the IO is organized in several coupled clusters of cells with borders that are most likely determined by the level of effective electrotonic coupling and therefore by the state of the IO network.

In an effort to determine the functional significance of the observed clusters, we calculated the maximum number of cells that contributed to each cluster. Because the clusters must be three-dimensional structures, we estimated the volume of each cluster by multiplying the area of the cluster by the thickness of the slice. This can be done because fluorescence is detectable up to 700 μm in depth (Grinvald et al., 1994), and our slices were only 300 μm thick. When multiplying such volume by the density of the IO neurons in rat (80,000 cells/mm³) (Cunningham et al., 1999), the product corresponds to the approximate number of cells in each cluster. We then made the parsimonious assumption that 50 μm of the exterior surfaces of the slice was probably damaged, and the response region was at maximum 200 μm thick and contained at least one cluster. On the basis of the above assumptions, we calculated that the IO clusters consisted of several hundred cells.

Questions then arise concerning the correlation between the size of the IO clusters and the extent of spontaneous synchronous climbing fiber activity in the cerebellum. Results from a number of previous in vivo experiments have shown that synchronized complex spike activity is primarily observed among Purkinje cells located within parasagittally oriented strips of the cerebellar cortex (Bell and Kawasaki, 1972; Llinás and Sasaki, 1989; Sugihara et al., 1995; Lang et al., 1997, 1999; Hanson et al., 2000; Yamamoto et al., 2001). These parasagittal bands are typically narrow structures with a width of only 0.25–0.5 mm. However, in the anterior–posterior direction, they can extend across several successive folia and are at least 4–5 mm long (Yamamoto et al., 2001). Therefore, each parasagittal strip can occupy an area from 1 to 2.5 mm². Because there are ∼1200 PCs per square millimeter (Armstrong and Schild, 1970), the maximum number of PCs per parasagittal band would be 3000. Given that in rat there is an 8:1 ratio of the Purkinje cells to the IO cells, the IO clusters that define the parasagittal bands consist of ∼400 cells. This number is of the same order of magnitude as the calculated number of cells in the core of optically registered IO clusters (260 ± 140 cells). Thus, the optical measurements might reflect the ensemble physiological properties observed previously with multiple recordings at the PC level. We propose that each IO cluster controls the activity of a single parasagittal band in the cerebellar cortex. Simultaneous activation of several IO clusters would result in synchronous CS activity in different parasagittal bands, as observed during coordinated movements.