Functional Stoichiometry of Glutamate Receptor Desensitization

Abstract

Potassium (K⁺) channels and ionotropic glutamate receptors (iGluRs) fulfill divergent roles in vertebrate nervous systems. Despite this, however, recent work suggests that these ion channels are structurally homologous, sharing an ancestral protein, architectural design, and tetrameric subunit stoichiometry. Their gating mechanisms also are speculated to have overlapping features. Here we show that the mechanism of iGluR desensitization is unique. Unlike K⁺ channels, AMPA- and kainate-type iGluR subunits desensitize in several ordered conformational steps. AMPA receptors operate as dimers, whereas the functional stoichiometry of kainate receptor desensitization is dependent on external ions. Contrary to conventional understanding, kinetic models suggest that partially desensitized AMPA and kainate receptors conduct ions and are likely participants in synaptic signaling. Although sharing many structural correlates with K⁺ channels, iGluRs have evolved unique subunit–subunit interactions, tailoring their gating behavior to fulfill distinct roles in neuronal signaling.

Prokaryotes and eukaryotes use a myriad of membrane-bound ion channel proteins to detect and respond to numerous environmental stimuli, from the rapid “trap door” closure of carnivorous plants to the detection of high-frequency auditory signals in songbirds (Hille, 1992). The most striking role of this plethora of ion channel proteins is to establish a complex array of signaling pathways in nervous systems of higher organisms. Although the molecular basis for the complexity of neuronal circuitry is still emerging, it is well established that ion channel proteins are essential components sculpting neuronal behavior via changes in developmental expression patterns, post-translational modification, and subcellular targeting. Two of the most important ion channels are K⁺ channels and ionotropic glutamate receptors (iGluRs). K⁺ channels detect changes in membrane potential and regulate neuronal firing properties (Yi and Jan, 2000). iGluRs respond to the neurotransmitterl-glutamate (l-Glu) and mediate most excitatory information throughout vertebrate brains (Dingledine et al., 1999).

Despite their divergent roles, K⁺ channels and iGluRs share important structural features, including tetrameric subunit stoichiometry (MacKinnon, 1991; Rosenmund et al., 1998) and architectural design of the pore region (Panchenko et al., 2001). The most compelling evidence favoring a homologous design among channels is the identification of a prokaryotic ion channel, GluR0, which is selectively permeable to K⁺ ions and is gated by l-Glu (Chen et al., 1999). GluR0 possesses critical amino acid residues found in iGluRs and K⁺ channels that are responsible for agonist binding and ion permeation, respectively, suggesting that both eukaryotic ion channels may have evolved from a common ancestral protein (Chen et al., 1999). In addition, residues implicated in K⁺ channel gating (Doyle et al., 1998;Perozo et al., 1999) are conserved among prokaryotic and eukaryotic iGluRs (Chen et al., 1999), suggesting that the gating mechanisms of these two important ion channel families may have overlapping features.

Consistent with this, K⁺ channel and iGluR activation pathways exhibit notable similarities. K⁺ channels (Chapman et al., 1997; Zheng and Sigworth, 1997) and iGluRs (Rosenmund et al., 1998; Smith and Howe, 2000; Smith et al., 2000) traverse several intermediate subconductance levels before entering the fully open state. Individual sublevels in each case are proposed to reflect the number of activated subunits per tetramer. A similar comparison between K⁺channel inactivation and iGluR desensitization has not been possible because the molecular basis of iGluR desensitization is not understood fully. K⁺ channels inactivate by two mechanisms, N- and C-type inactivation. N-type inactivation reflects the occlusion of the open channel pore by one of four intracellular blockers tethered to individual subunits (Hoshi et al., 1990; Zagotta et al., 1990), whereas C-type inactivation represents a concerted conformation of all four subunits (Ogielska et al., 1995; Panyi et al., 1995). Currently, the behavior of individual iGluR subunits during desensitization is not well understood. Two recent studies, however, have proposed two opposing mechanisms for AMPA-type iGluRs whereby subunits desensitize in a concerted manner (Partin, 2001) or operate as two dimers (Robert et al., 2001). As yet, the behavior of kainate- or NMDA-subtype iGluR subunits has not been studied in detail.

In this study we have reexamined AMPA receptor desensitization in comparison with kainate receptors. Unlike K⁺ channels, both AMPA and kainate receptors desensitize in a series of sequential conformational steps. Statistical evaluation of different gating schemes suggests that AMPA receptors operate as dimers, whereas kainate receptor desensitization is more consistent with a tetramer arrangement. We also have identified the novel observation that kainate receptor desensitization is regulated strongly by external ions.

MATERIALS AND METHODS

Cell culture and expression of recombinant receptors.Human embryonic kidney 293 (HEK 293) cells (CRL 1573; American Type Culture Collection, Manassas, VA) and tsA201 cells (provided by Dr. R. Horn, Jefferson Medical College, Philadelphia, PA) were maintained at a confluency of 70–80% in MEM with Earle's salts, 2 mm glutamine, and 10% fetal bovine serum. After being plated at low density, the cells were transfected with cDNAs encoding GluR-A and GluR6 receptor subunits (supplied by Drs. M. L. Mayer and K. M. Partin at National Institutes of Health, Bethesda, MD, and Colorado State University, CO, respectively), using the calcium phosphate technique as described previously (Bowie et al., 1998). We routinely cotransfected with the cDNA for green fluorescent protein (GFP S65T mutant) to help identify transfected cells.

Electrophysiological recordings. All recordings were made with an Axopatch 200B amplifier (Axon Instruments, Foster City, CA) that used thin-walled borosilicate glass pipettes (2–5 MΩ) coated with dental wax to reduce electrical noise. Control andl-Glu (10 mm; 50 msec duration) solutions were applied rapidly to outside-out patches excised from HEK 293 or tsA201 cells expressing unedited GluR-A or GluR6 subunits as described previously (Bowie et al., 1998). Solution exchange (10–90% rise time, 25–50 μsec) was determined routinely by measuring a liquid junction current (Bowie et al., 1998). Typical experiments designed to map out recovery from and reentry into desensitization consisted of 33 and 50 paired agonist applications (10 mml-Glu; 50 msec duration each) for kainate and AMPA receptors, respectively, each separated by varying time intervals. The first application, or conditioning response, was used to accumulate receptors into the desensitized state(s). The second application, or test response, provided information on two quantities: (1) the amplitude reported the fraction of the response recovered from desensitization, and (2) the time course of decay indicated the rate at which resensitized channels reenter desensitization.

External solutions contained 55, 150, or 405 mm NaCl, 5 mm HEPES, and 0.1 mm each of CaCl₂ and MgCl₂, pH 7.3. Internal solutions contained (in nm) 10, 115, or 360 NaCl, 10 NaF, 5 HEPES, 5 Na₄BAPTA, 0.5 CaCl₂, 1 MgCl₂, and 10 Na₂ATP, pH 7.3. Osmotic pressure was adjusted to 295 mOsm for 55 and 150 mm NaCl with sucrose and to 750 mOsm for 405 mm NaCl. The osmotic pressure did not influence channel gating. Current records were filtered at 5 kHz and digitized at 25–50 kHz; series resistances (3–10 MΩ) were compensated by 95%. Experiments were performed at ±20 mV potentials to ensure adequate voltage clamp of peak currents (∼1–5 nA). Responses at both potentials were similar, and the data were pooled. Preliminary experiments were recorded in high salt solutions (i.e., 405 mm NaCl) because these conditions increased the amplitude of membrane currents in excised patches, presumably by affecting the unitary current amplitude(s) (see Figs.1-5). In particular, we were able to resolve routinely the amplitude and kinetics of test responses <2% of the peak conditioning response. With careful attention to pipette dimensions and transfection protocols, we also were able to examine the behavior of similar test responses of small amplitude in 55 and 150 mm NaCl solutions (see Figs. 6, 7).

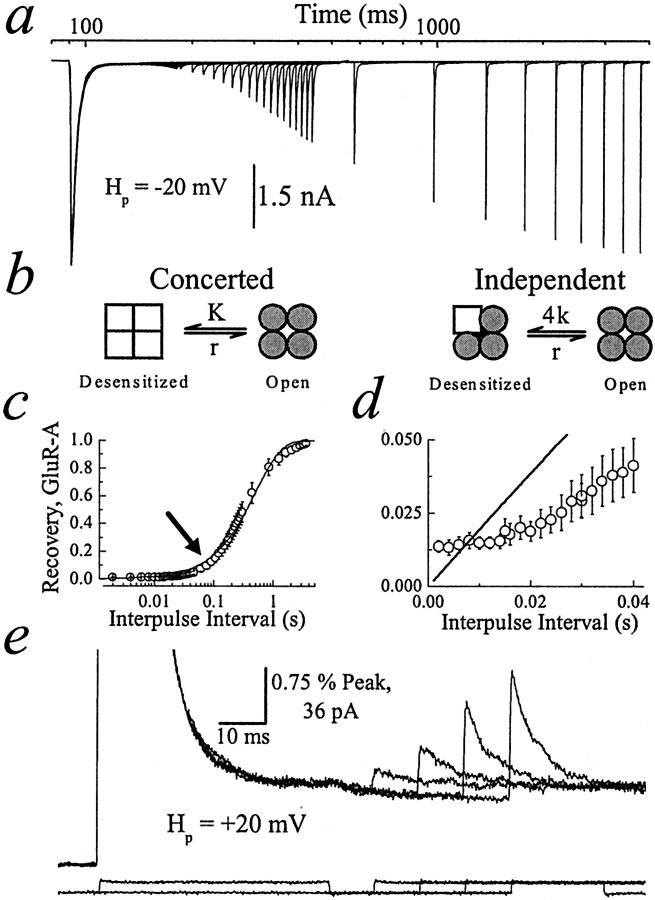
Fig. 1.

Entry into and exit from AMPA receptor desensitization. a, Typical recording showing 50 superimposed conditioning and test pulses (10 mm; 50 msec duration; H_p, −20 mV); patch number 010123p3. b, Schematic of concerted (left) and independent (right) models of desensitization highlights the behavior of individual subunits.c, Summary plot of GluR-A recovery in 405 mmNaCl solution (n = 6; mean ± SEM). Data were fit (solid line) by the expression:I_(t) = I_peak· [1− Exp(−t/τ_rec)], whereI_(t) is the response amplitude at any time,t, I_peak is the peak test response, and τ_rec, the time constant for recovery, is 508 ± 12 msec. The arrow denotes a section of recovery plot not well fit by a single exponential function.d, Concerted/independent models do not fit the data well, particularly during the early recovery phase. e, Same patch as a (H_p, +20 mV) showing four test pulses separated by 10 msec increments.Bottom traces show junction currents to monitor the solution exchange.

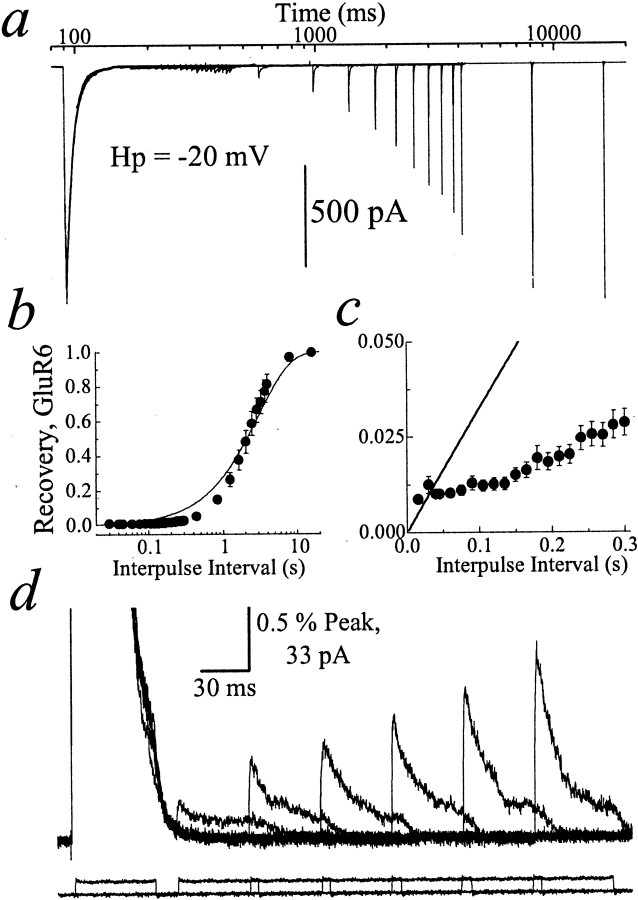
Fig. 2.

Entry into and exit from kainate receptor desensitization. a, Typical recording showing 33 superimposed conditioning and test Glu pulses (10 mm; 50 msec duration; H_p, −20 mV); patch number 000720p2. b, Summary plot of GluR6 recovery in 405 mm NaCl solution (n = 7; mean ± SEM). Data were fit (solid line) by the expression:I_(t) = I_peak· [1 − Exp(−t/τ_rec)], where τ_rec was 3.02 ± 0.14 sec. c, Concerted/independent models do not fit the data adequately, particularly at brief intervals. d, Profile of six test pulses separated by 45 msec increments (patch number 000721p1;H_p, +20 mV). Bottom traces show junction currents recorded with an open electrode tip.

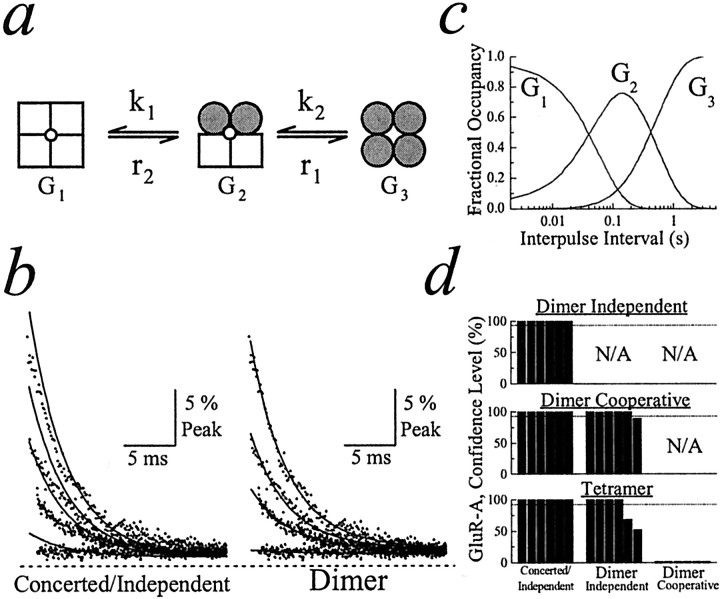
Fig. 3.

Determining the functional stoichiometry of AMPA receptor desensitization. a, Schematic of the cooperative dimer model. b, GluR-A experimental records (dots; patch number 010123p1) fit with the concerted/independent models (left, solid line) and the cooperative dimer model (right,solid line). The first 25 msec of four test responses [time after conditioning response (t_c) was 8, 40, 60, and 105 msec] were superimposed for comparison. The dashedline indicates zero current level. c, Plot profiling the distribution of each state in the cooperative dimer model at a range of interpulse intervals. d, Summary plots showing how fits of experimental data with different models of desensitization were compared. Fits were compared pairwise, using theF ratio test. Top plot shows the independent dimer compared with the concerted/independent models.Middle plot compares the cooperative dimer with concerted/independent models and independent dimer model. Bottom plot compares the tetramer model with all other models of desensitization. Each bar indicates the confidence level distinguishing between two models fit to the same experimental data. For every comparison six bars are shown that represent the results from six separate patch recordings. The dashed line in each plot denotes the 95% confidence level.

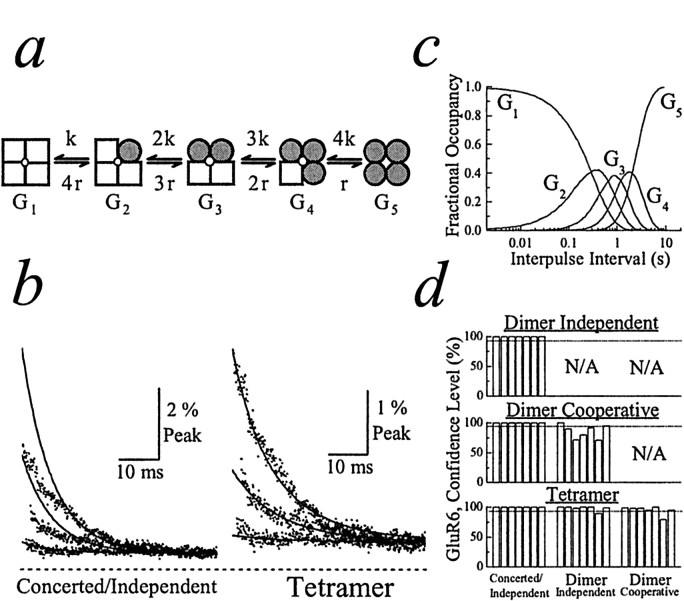
Fig. 4.

Determining the functional stoichiometry of kainate receptor desensitization. a, Schematic of the tetramer model. b, GluR6 experimental records (dots; patch number 000720p2) fit with the concerted/independent (left, solid line) and tetramer (right, solid line) models. Entire 50 msec of three test responses (t_c = 15, 135, and 285 msec) are superimposed for comparison. The dashed line indicates zero current level. c, Plot profiling the distribution of each state in the tetramer model at a range of interpulse intervals.d, Summary plots showing how fits of experimental data with different models of desensitization were compared. Fits were compared pairwise, using the F ratio test. Eachbar indicates the confidence level distinguishing between two models fit to the same experimental data. For every comparison seven bars are shown that represent the results from seven separate patch recordings. The dashed line in each plot denotes the 95% confidence level.

Fig. 5.

Kainate receptor desensitization fit with concerted/independent and tetramer models. a, b, Four superimposed test responses (t_c = 15, 150, 225, and 300 msec; dots; patch number 000720p2) recorded during the early phase of recovery from GluR6 desensitization and fit with the concerted/independent model (a) or tetramer model (b). The dashed line indicates zero current level. Note that the tetramer model fits the data better than the concerted/independent model. c, d, Ten superimposed test responses from the same patch recording (t_c = 0.040, 0.84, 1.24, 1.64, 2.04, 2.44, 2.84, 3.64, 7.95, and 15.95 sec; patch number 000720p2) showing both early and late phases of recovery from GluR6 desensitization and fit with the concerted/independent model (c) or the tetramer model (d). Note that the tetramer model fits the data better than the concerted/independent model. For clarity, the total number of data points on each test response sweep has been reduced (eightfold). The dashed line indicates zero current level.

Fig. 6.

Kainate receptor desensitization is modulated by external ions. a, b, Plots showing typical GluR6 or GluR-A receptor responses in symmetrical solutions of 55, 150, and 405 mm NaCl. Bottom traces show junction currents recorded with an open electrode tip. c, d, Summary plots illustrating the effect of changing the NaCl concentration on the time course of GluR6 and GluR-A receptor desensitization. Data are expressed as mean ± SEM.

Fig. 7.

External ions regulate the functional stoichiometry of kainate receptor desensitization. a, Typical GluR6 test responses recorded in 55 mm NaCl solutions exhibited similar decay kinetics (patch number 000724p2).b, When the first six test responses froma were aligned for comparison, the decay kinetics was revealed to be almost identical. c, Recovery from GluR6 desensitization in 55 (filled circles) and 150 (open circles) mm NaCl solutions. GluR6 recovery in 55 mm NaCl was monoexponential, where τ_rec was 1.88 ± 0.02 sec (n = 5), whereas recovery in 150 mm NaCl was not monoexponential, particularly at brief interpulse intervals (arrow; τ_rec = 3.48 ± 0.09 sec;n = 20). d, A closer examination of the plots in c shows that GluR6 responses in 55 mm NaCl recovered monoexponentially even at brief interpulse intervals, whereas responses in 150 mm NaCl clearly deviated from first-order behavior. e, Summary showing three plots in which the goodness of fit of the experimental data with different models of desensitization was compared. Goodness of fit was compared pairwise, using the F ratio test. Thefilled (n = 5) and open horizontal bars (n = 4) refer to experiments performed in symmetrical solutions of 55 and 150 mm NaCl, respectively. The dashed vertical line in each plot denotes the 95% confidence level.

Modeling AMPA and kainate receptor desensitization. Before performing fits, we normalized the amplitudes of all test responses in a given experiment to the peak conditioning response. Because the total channel number present on excised patches was variable, this normalization step permitted comparison of the fit parameters among different patches and ionic conditions.

Rates into and out of desensitization were estimated from the amplitude and decay kinetics of test GluR6 or GluR-A responses. Code was written that permitted the simultaneous fitting of all test responses with the use of a nonlinear steepest descent algorithm (“NonlinearFit,” Mathematica, Wolfram Research; see ). For each model the rates of entry into and out of desensitization were governed by the rate constants k_i andr_i, respectively.G_i represents the macroscopic conductance(s) in each model expressed in normalized units.G_i reflects the sum of the product of the unitary conductance(s) and open probability. There were no constraints imposed on the various fit parameters, nor was the outcome of the fits sensitive to initial guesses.

The four models we have tested form a hierarchy of functions. With such a hierarchy it is appropriate to measure the improvement in fit achieved by a more complex model compared with a less complex model as the ratio (F) of the relative decrease in error sum of squares over the relative decrease in error degrees of freedom (Horn, 1987; Motulsky, 1999). The error degrees of freedom diminish exactly by the same value as the increase in the number of parameters. With F ratios <1 the more complex model actually has worsened the fit and therefore is rejected. F ratios >1 indicate an improvement in the fit. In this study a given experiment is repeated many times; therefore, pairs of models are compared many times, yielding different F ratio values spread according to the F distribution. The F distribution is used to determine whether the simpler model might by chance cause the same improvement in the fit with another valid set of data. If that probability is sufficiently low, scientific prudence dictates that we adopt the more complex model. A special condition governs comparison between the independent tetramer and the cooperative dimer. Although from a structural point of view the tetramer is the more complex model, the number of parameters, seven, is the same for both. Therefore, the change in degrees of freedom is zero, and the F ratio is infinite. We therefore have adopted a conservative requirement that the independent tetramer will be tested assuming an increase to eight rather than seven parameters. We also have applied Akaike's Information Criterion (AIC) to the fits. AIC is based on maximum likelihood and information theoretical principles. It is another method for choosing the best-fit model (Burnham and Andersen, 1998). Given our very large number of sample points, using AIC is equivalent to choosing the model with the best fit in the sense of smallest error sum of squares. AIC does not assume that the models form a hierarchical set. In every case the F ratio technique and AIC produced the same result. A detailed treatise of the mathematical functions used in fits can be found in the and elsewhere (http://rsb.info.nih.gov/∼gdl/supplement/).

Assumptions of modeling strategy. To estimate the functional stoichiometry of desensitization, we made three assumptions. First, we assumed that AMPA and kainate receptors are tetramers composed of four identical subunits. Several studies suggest that AMPA receptors are tetramers (Rosenmund et al., 1998; Dingledine et al., 1999) in which each subunit provides a clamshell-like binding pocket for a single agonist or antagonist molecule (Armstrong et al., 1998;Armstrong and Gouaux, 2000). Less is known about kainate receptors; however, the behavior of AMPA–kainate receptor chimeras suggests that individual subunits possess a homologous agonist-binding domain (Stern-Bach et al., 1994). Moreover, the structural similarity between pore regions of kainate receptors and potassium channels suggests that kainate receptors probably also assemble as tetramers (Panchenko et al., 2001).

The second assumption is that decay kinetics of test responses reflects entry into desensitization. This assumption remains valid even if the mechanism of desensitization includes coupling to channel opening or closure. Consistent with this, there is some evidence suggesting that deactivation and desensitization of AMPA receptors are coupled (Partin et al., 1996; Trussell and Otis, 1996). In such instances the process of desensitization not only will be governed by entry rates into the desensitized state(s) but will depend additionally on transitions from/into open or closed states. It is not known how channel opening or closure affects entry rates into desensitized states for AMPA or kainate receptors. However, in view of this, it is possible that the rate constants reported in this study describing entry into desensitization reflect the summed contributions of these microscopic gating events.

Third, we have assumed that the agonist concurrently initiates channel activation and the onset of desensitization during each test response. In agreement with this, most studies suggest that AMPA and kainate receptors are not required to traverse the open state to enter desensitized states, because desensitization occurs with low agonist concentrations that fail to gate the channel (Dingledine et al., 1999).

Our modeling of AMPA and kainate receptor desensitization is a simplified approach. An asset of this method is that analysis is more intuitive in nature. Ideally, transitions that are unlikely to impact on the outcome of analysis are neglected. The modeling described in this study does not account for agonist binding or unbinding steps. However, there is justification for this because our fitting strategy relies on fitting the decay of responses elicited by saturating agonist to which binding/unbinding events do not contribute significantly. Finally, the high concentrations of agonist suggest that our models describe mainly the behavior of different states of fully occupied receptors.

RESULTS

Kinetics of AMPA and kainate receptor desensitization

AMPA (Fig. 1) and kainate (Fig.2) receptor desensitization was studied on outside-out patches excised from mammalian cells expressing GluR-A and GluR6 homotetramers, respectively (see Materials and Methods). Entry into and exit from desensitization was determined from the decay kinetics and amplitude of macroscopic responses elicited by paired agonist applications (10 mml-Glu; 50 msec duration each) separated by varying time intervals (Figs.1a, 2a). Agonists were applied to patches by an ultrafast solution exchange (10–90% rise times of 25–50 μsec) two orders of magnitude faster than desensitization kinetics. Our preliminary experiments (see Figs. 1-5) were recorded in 405 mm NaCl salt solutions to increase the amplitude of macroscopic currents in excised patches (see Materials and Methods). In subsequent experiments AMPA and kainate receptor behavior was examined in 55 and 150 mm NaCl solutions (see Figs. 6, 7).

During the first agonist application, or conditioning response, AMPA and kainate receptors were activated rapidly (rise times of 300 μsec) but subsequently were desensitized in the continued presence of agonist to an equilibrium level of 1.4 ± 0.2% (GluR-A, n= 6; Fig. 1a,e) and 0.8 ± 0.05% (GluR6,n = 7; Fig. 2a,d) of the peak response in 405 mm symmetrical NaCl. The rate of onset of AMPA receptor desensitization determined from conditioning responses was fit best by a double-exponential function with fast and slow time constants of 2.49 ± 0.27 and 8.04 ± 1.78 msec (20.7 ± 6.2% of peak; n = 6), respectively. The rate of onset of kainate receptor desensitization estimated from 50 msec conditioning responses to 10 mm Glu decayed with a single time constant of 6.03 ± 0.47 msec (n = 7). Note that for both receptor subtypes the membrane current observed at the end of the conditioning response relaxed to the zero current baseline more slowly than the decay of the peak response described above (Figs. 1e,2d). The difference is more evident for AMPA (Fig.1e) than for kainate receptors (Fig.2d) and suggests that channels with different kinetic behavior mediate peak and equilibrium responses. Consequently, equilibrium desensitization does not reflect the recycling of AMPA or kainate receptors through the main open state as modeled previously (Partin et al., 1993; Heckmann et al., 1996).

Recovery from desensitization was determined from the amplitude of a second agonist application, or test response, that reported the fraction of resensitized channels (Figs. 1a,c,2a,b). AMPA receptors fully recovered from desensitization with interpulse intervals >1 sec (τ_recovery, 508 ± 12 msec;n = 6), whereas kainate receptors recovered almost 10-fold slower (τ_recovery, 3.02 ± 0.14 sec; n = 7) (Figs. 1a,c,2a,b). The time course of recovery for AMPA receptors was slower than reported previously (Partin et al., 1996; Robert et al., 2001) and may reflect the low levels of external divalent ions used in this study on the recovery process (D. Bowie, unpublished observation). To show the amplitude of all test responses and recovery time courses, Figures 1a and 2ahave been plotted on a logarithmic time scale.

The behavior of individual AMPA and kainate receptor subunits during desensitization is still not resolved fully. Most studies have proposed that entry into and exit from kainate receptor desensitization can be described reasonably well as first-order processes (Heckmann et al., 1996; Traynelis and Wahl, 1997; Wilding and Huettner, 1997; Paternain et al., 1998). Assuming this simple kinetic behavior, subunits may operate in two possible arrangements: (1) in a concerted manner involving allosteric cooperation between subunits as postulated for C-type inactivation of K⁺ channels (Fig.1b, left) (Ogielska et al., 1995; Panyi et al., 1995) and (2) independently, in which the transition of only a single subunit is required to enter or exit desensitization (Fig.1b, right) similar to N-type inactivation of K⁺ channels (MacKinnon et al., 1993; Yi and Jan, 2000). For AMPA receptors two opposing mechanisms have been proposed in which subunits operate in a concerted manner (Partin, 2001) as described above (Fig. 1b, left) or as two dimers (Robert et al., 2001). The dimer arrangement would account for the fast and slow components of desensitization described by others (Raman and Trussell, 1992; Patneau et al., 1993; Robert et al., 2001) and in this study supporting the existence of (at least) two kinetically distinct desensitized states (Raman and Trussell, 1992;Patneau et al., 1993). However, one potential caveat with the dimer model is the use of the AMPA receptor mutant GluR-A (L497Y) to determine the functional stoichiometry of desensitization (Robert et al., 2001). The amino acid residue leucine 497, like other residues critical for AMPA receptor desensitization (Lomeli et al., 1994; Partin et al., 1995; Stern-Bach et al., 1998), is grouped at subunit–subunit interfaces (Armstrong and Gouaux, 2000) and, as a result, may be pivotal in orchestrating conformations involving multiple subunits. Consequently, the functional stoichiometry of AMPA receptors containing GluR-A (L497Y) may be distinct from receptors composed exclusively of wild-type subunits.

In view of this, we have reinvestigated the behavior of individual AMPA receptor subunits during desensitization and, for comparison, examined the functional stoichiometry of kainate receptor desensitization also. Initially, we reviewed the concerted/independent models of desensitization that are analogous to K⁺channel inactivation mechanisms (Fig. 1b,right, left). Although subunits behave differently in concerted and independent models, entry and exit rates from desensitization in each case display first-order kinetics. Furthermore, we examined the time course of recovery from desensitization first, because it is more than three orders of magnitude slower than the onset of desensitization. We anticipated that digressions from first-order behavior would be easier, at least initially, to identify experimentally during the recovery step rather than the onset of desensitization.

To study the recovery process carefully, we mapped out the entire time course of GluR6 and GluR-A recovery from the peak amplitudes of 33 and 50 test pulses, respectively, which subsequently were fit with a single-exponential function (Figs. 1c,2b). Contrary to many previous studies (Lomeli et al., 1994; Mosbacher et al., 1994; Heckmann et al., 1996; Partin et al., 1996; Traynelis and Wahl, 1997; Wilding and Huettner, 1997;Paternain et al., 1998), AMPA and kainate receptors did not recover from desensitization in single conformational steps (solid line; see arrow in Figs. 1c,d,2b,c). Moreover, recovery plots show that deviation from the concerted/independent models was noticeably greater for kainate receptors (Fig. 2b,c) than for AMPA receptors (see arrow in Fig. 1c,d). Close inspection reveals that failure in both cases occurred principally during the early phase of recovery when the concerted/independent models predicted more rapid recovery than was observed experimentally (Figs.1d, 2c). The deviation from the concerted/independent models probably does not reflect an initial refractory period as reported for some neuronal AMPA receptors (Smith et al., 1991; Raman and Trussell, 1995) because test responses mapping out the beginning of the recovery process increased in amplitude without delay (Figs. 1d, 2c). It is also unlikely that low levels of circulating agonist molecules distort recovery behavior. First, the fast solution exchange rate (10–90% rise time, 25–50 μsec) in our recordings would replace residual agonist molecules. Second, if low concentrations of agonist did persist, their binding rate would be significantly slower than the solution exchange rate. Finally, the ion dependence of GluR6 recovery described below would be difficult to explain (see Figs. 6, 7).

The concerted/independent models also predict that entry rates into desensitization are independent of the fraction of resensitized channels. To examine this, the decay kinetics of test responses at different interpulse intervals was compared (Figs.1e, 2d). Contrary to the concerted/independent models, decay rates were different between test pulses. For example in Figures 1e and2d, the first GluR-A and GluR6 test responses decayed with time constants of 10.1 ± 1.9 and 20.8 ± 3.2 msec, respectively, whereas the last (fourth or sixth) test responses shown were 5.7 ± 0.4 and 11.6 ± 0.9 msec, respectively. At time intervals >840 msec (11 ± 3% desensitized; τ = 3.2 ± 0.2) and 2.04 sec (55 ± 4% desensitized; τ = 6.5 ± 0.6), respectively, resensitized AMPA and kainate receptors decayed with rates similar to conditioning pulses (see above). Together, these results suggest that the concerted/independent models exemplified by K⁺ channel inactivation do not account for AMPA or kainate receptor desensitization.

Determining the functional stoichiometry of iGluR desensitization

Alternatively, AMPA and kainate receptors may desensitize in several sequential steps. Because individual subunits contain a binding site for a single agonist molecule, desensitization may result from a number of possibilities including combined or independent subunit conformations. To determine the number of conformational steps (or gates) involved, we developed a fitting program to examine four models of desensitization: (1) concerted/independent (one gate; Fig.1b), (2) dimer with independence or cooperativity (two gates; Fig. 3a), and (3) tetramer (four gates; Fig.4a). The program fits experimental records, with each model providing information on transition rates into (k_N) and out of (r_N) desensitization as well as the macroscopic conductance of each state (G_N). In the independent dimer, paired subunits are equivalent and independent; therefore, rate constants are proportional to the number of open or desensitized subunit pairs. In the cooperative dimer, paired subunits are not independent; therefore, their contribution is not proportional to the number of subunit pairs. The F ratio test was used to evaluate statistically the goodness of fit among models with different degrees of freedom. A complete treatise of the statistical methods and mathematical formulae used for fitting is described elsewhere (see Materials and Methods,, and the web address).

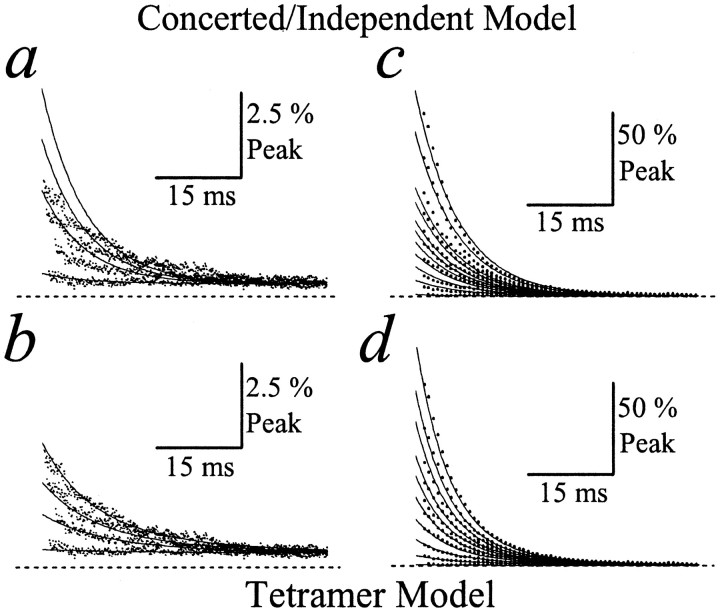
Figure 3 summarizes our results from fits of AMPA receptor data. To provide information on rates into and out of AMPA receptor desensitization, our program simultaneously fit 50 test responses as typified by the patch recording shown in Figure 1a. For convenience, we have not illustrated the fits to all 50 test responses but have selected, instead, several responses that occur at the beginning of the recovery process because they exhibit different decay kinetics (Fig. 3b). Moreover, to compare the goodness of fit of all four models, we have summarized the results of statistical comparisons in a bar graph (Fig. 3d). Figure3b shows several AMPA receptor test responses fit with the concerted/independent models (Fig. 1b) and cooperative dimer model (Fig. 3a). As expected, the concerted/independent models did not account for experimental observations, particularly the test responses observed at brief interpulse intervals (Fig. 3b, left). In contrast, AMPA receptor desensitization was described well by the cooperative dimer model, accounting for the different decay kinetics observed with test responses at the beginning of the recovery process (Fig. 3b, right). Although not shown, the cooperative dimer model fit all 50 test responses well in all patch recordings. The goodness of fit for the cooperative dimer compared with the other models is described below. Because the fitting program provides information on the rate constants governing recovery from desensitization, the fractional occupancy of the various states at different time points during recovery can be calculated. For the cooperative dimer model (Fig. 3a) the distribution of the three states at a range of interpulse intervals is shown in Figure3c.

To evaluate statistically which of the four models of desensitization fit best our experimental data, we have used the F ratio test (see Materials and Methods). The F ratio test examines whether the decrease in the sum of squares, often found when the data are fit to more complicated models, is merited by the loss of degrees of freedom (i.e., additional variables). The results of evaluating the goodness of fit of each model in these pairwise comparisons are summarized in Figure 3d. Figure 3d shows three plots that illustrate paired comparisons between the independent dimer model and concerted/independent models (Fig. 3d, top plot), the cooperative dimer with the independent dimer or concerted/independent models (Fig. 3d, middle plot), and, finally, the tetramer model with all three other models (Fig. 3d, bottom plot). The value denoted by each bar in each of the three plots represents the confidence level observed when two models were compared with data from a single patch recording. For example, the comparison between the tetramer and concerted/independent models (Fig. 3d, bottom plot, left column) shows six bars or six comparisons, which indicates that data from six different patch recordings were used. By noting the position of the bar in a data set (e.g., third bar in a group of six), it is possible to compare how different models fit the data from an individual experiment.

As expected, both dimer (independent and cooperative) and tetramer models fit better the experimental data (>95% confidence level; six of six patches) than the concerted/independent models (Fig.3d, left column). Moreover, five of six and four of six patches favored (>95% confidence level; Fig.3d, dotted line) the cooperative dimer and tetramer models, respectively, over the independent dimer model (Fig. 3d, middle column). However, the goodness of fit of the cooperative dimer model was favored over the tetramer for all patches that were tested (Fig. 3d,bottom, right column; n = 6), suggesting that AMPA receptors assembled from identical subunits operate as dimers of dimers. The rate constants and macroscopic conductances estimated from fits of the dimer model to AMPA receptor data are summarized in Table 1. It is worth noting that the results of our fits suggest that intermediate desensitized conductance states contribute to membrane conductance. As described below, intermediate desensitized states contribute more significantly to the membrane conductance elicited by kainate receptors.

Table 1.

Summary of the rate constants and macroscopic conductance values obtained from model fits

Rate constant/conductance	GluR-A 405 mm NaCl (n = 6)	GluR6 55 mm NaCl (n = 5)	GluR6 150 mm NaCl (n = 4)	GluR6 405 mm NaCl (n = 7)
r	—	—	—	0.77  ± 0.09/sec
r1	1.9  ± 0.6/sec	1.2  ± 0.6/sec	0.25  ± 0.01/sec	—
r2	16.9  ± 5.3/sec	3.4  ± 1.2/sec	2.6  ± 0.3/sec	—
k	—	—	—	55.6  ± 5.8/sec
k1	66.3  ± 19.9/sec	646.2  ± 60.5/sec	72.4  ± 21.3/sec	—
k2	304.6  ± 12.9/sec	782.0  ± 102.8/sec	194.9  ± 7.0/sec	—
G1	0.009  ± 0.002	0.002  ± 0.001	0.003  ± 0.001	0.004  ± 0.0004
G2	0.033  ± 0.010	0.26  ± 0.11	0.015  ± 0.004	0.021  ± 0.006
G3	2.12  ± 0.08	2.32  ± 0.21	1.61  ± 0.12	0.084  ± 0.016
G4	—	—	—	0.42  ± 0.07
G5	—	—	—	1.22  ± 0.03
Model	Cooperative  dimer	Cooperative  dimer	Cooperative  dimer	Tetramer

Data are expressed as the mean ± SD. The conductance of each state is expressed in normalized units that represent the sum of the product of the unitary conductance(s) and open probability.

Figure 4 summarizes our results from fits of kainate receptor data. Consistent with AMPA receptor data, GluR6 test responses also were not fit well by the concerted/independent models. Figure4b shows three test responses observed during the initial phase of recovery and fit with the concerted/independent models (Fig. 4b, left). As expected, the concerted/independent model overestimated the peak amplitude of test responses (Fig. 4b, left). In contrast, the tetramer model fit well the GluR6 responses even at brief interpulse intervals (Fig. 4b, right). The distribution of each state of the tetramer model at different interpulse intervals was calculated and is profiled in Figure4c. As mentioned previously, we have shown only test responses at brief interpulse intervals in Figures 3b and4b for convenience. However, a comparison of fits of different models to the entire range of GluR6 responses, including early and later phases of the recovery process, can be reviewed in Figure 5 (see also the web address in Materials and Methods).

Similar to our analysis of AMPA receptors, we also compared statistically the goodness of fit between pairs of models (Fig.4d). As noted for AMPA receptors, dimer (independent and cooperative) and tetramer models accounted better for the experimental data than the concerted/independent models in all patches that were tested (Fig. 4d, left column; seven of seven; >95% confidence level). However, unlike AMPA receptors, the tetramer model fit the data with GluR6 receptors better than the independent or cooperative dimer models in all cases (Fig.4d, bottom, middle andright columns; six of seven patches; >95% confidence level), suggesting that the functional stoichiometry of kainate receptor desensitization is most consistent with a tetramer arrangement. The rate constants and macroscopic conductances for the tetramer model of GluR6 are summarized in Table 1. It is worth noting that, when compared with AMPA receptors, the intermediate desensitized states (e.g., G₃ andG₄) of the kainate receptor make a significant contribution to the total membrane conductance (see Table1), the physiological significance of which is discussed below. Although fits of GluR6 data consistently favored the tetramer model, the experiments described below revealed that the apparent functional stoichiometry of kainate receptor desensitization was dependent on the external ion concentration.

External ions regulate the gating behavior of kainate, but not AMPA, receptors

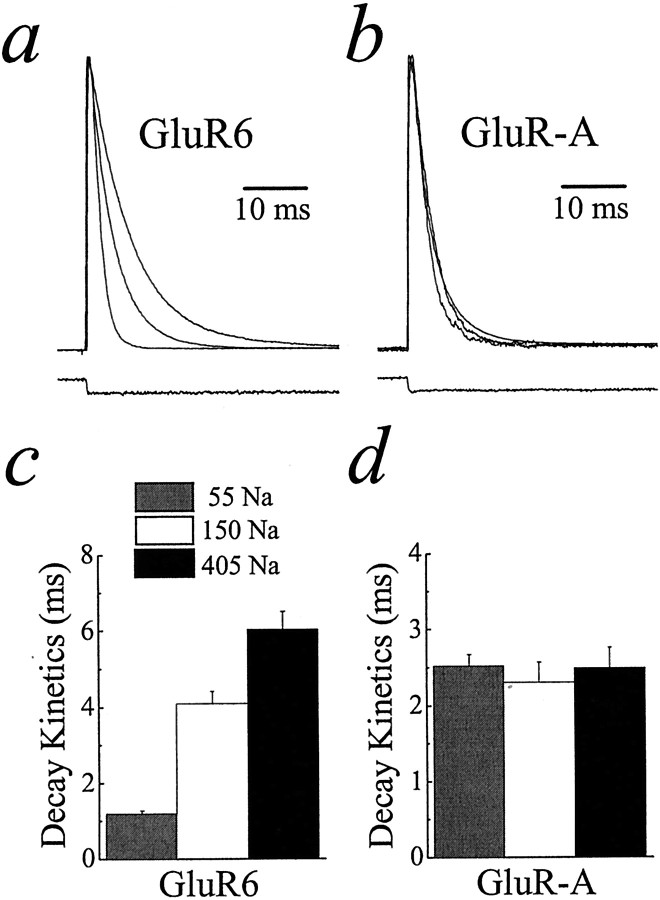
External ions modulate C-type inactivation of K⁺ channels (Baukrowitz and Yellen, 1995;Levy and Deutsch, 1996), and we also wished to test this for iGluRs by comparing responses in 55, 150, and 405 mm symmetrical NaCl. Figure 6 shows typical Glu-evoked currents at kainate (Fig. 6a) and AMPA (Fig.6b) receptors in each ionic condition in which peak responses have been normalized to allow comparison. Unexpectedly, kainate receptor desensitization was strongly dependent on ionic conditions (Fig. 6a,c). The rate of onset of desensitization was approximated by single-exponential time constants of 1.12 ± 0.08 msec (55 mm;n = 9; mean ± SEM), 4.09 ± 0.32 msec (150 mm;n = 6), and 6.03 ± 0.47 msec (405 mm;n = 4). In contrast, AMPA receptor desensitization was similar in all solutions (Fig. 6b,d), with the time constant of the fast (and slow) component in 55, 150, and 405 mm NaCl solutions of 2.52 ± 0.15 msec (τ_slow = 12.2 ± 3.4 msec; 6.7 ± 6.2% of peak; n = 7; mean ± SEM), 2.30 ± 0.12 msec (τ_slow= 11.3 ± 2.9 msec; 10.4 ± 3.2% of peak; n= 10), and 2.49 ± 0.27 msec (τ_slow = 8.04 ± 1.78 msec; 20 ± 6% of peak; n = 6), respectively.

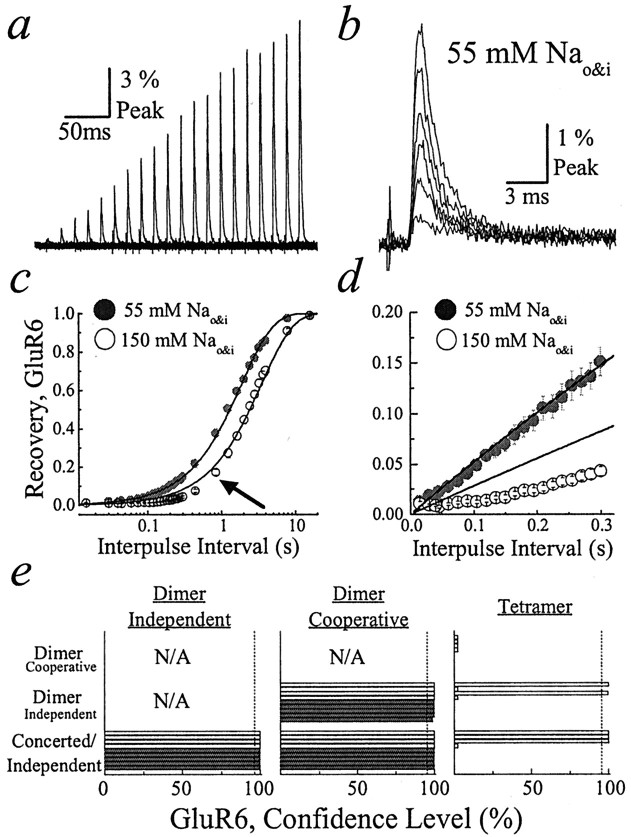
In view of their ion sensitivity, we determined whether kainate receptors still operated as functional tetramers in 55 and 150 mm NaCl. Figure 7ashows the first 20 test responses typically observed in recordings with GluR6 receptors in 55 mm NaCl. In contrast to responses in 405 mm NaCl, the decay kinetics for all test responses was very similar (Fig. 7b). For example, the conditioning response (τ = 1.4 ± 0.8 msec;n = 4) and first test response (τ = 1.5 ± 0.2 msec) that differ in amplitude by 98.7 ± 0.3-fold had similar desensitization kinetics (Fig. 7b). Moreover, the time course of GluR6 recovery in 55 mm NaCl was reasonably well fit by a single-exponential function (τ_rec = 1.88 ± 0.02 sec;n = 4) (Fig. 7c, filled symbols) even during the early phase of this process (Fig. 7d). Despite this, the cooperative dimer model, and not the concerted/independent models, fit the experimental data better. The results of statistical comparisons between different model pairs are summarized in Figure 7e (filled bars for 55 mm NaCl). In five of five patches that were tested, the cooperative dimer model was favored (>95% confidence level) over the concerted/independent and independent dimer models. Fits with the tetramer model provided nonsensical estimates of rate constants and macroscopic conductances and thus were rejected (Horn, 1987; Motulsky, 1999). The rate constants and macroscopic conductances for the dimer model are summarized in Table 1. Note that rate constants describing entry into desensitization (k₁ andk₂; see Table 1) for the cooperative dimer model are similar, accounting for the comparable decay kinetics observed experimentally in 55 mm NaCl solutions (Fig. 7b).

GluR6 responses in 150 mm NaCl exhibited intermediate behavior. Recovery was not monoexponential in nature (Fig.7c, arrow, open symbols), deviating clearly from the concerted/independent models during the early recovery phase (Fig. 7d). However, the monoexponential function fit the data better than GluR6 responses observed in 405 mm NaCl solutions (Fig. 2b). Statistical comparison of the goodness of fit between model pairs revealed that the experimental data were best fit by the cooperative dimer model (Fig. 7e, open bars). In four of four patches that were tested, the dimer cooperative model was favored (>95% confidence level) over the concerted/independent, independent dimer, and tetramer models (Fig. 7e, open bars).

DISCUSSION

Until recently, it was not possible to speculate on the most basic properties of evolutionary precursors to eukaryotic K⁺ channels and iGluRs (Hille, 1992). However, a recent study suggests that K⁺channels and iGluRs may have evolved from a common ancestral ion channel protein, GluR0 (Chen et al., 1999). GluR0 shares many structural and functional features with its proposed progeny (Chen et al., 1999), suggesting that mature ion channel proteins achieve diversity by selecting from an array of modular domains responsible for gating and ion permeation (Hille, 1992; Paas, 1998). Although K⁺ channels and iGluRs share appreciable structural homology, iGluR subunits operate in a manner distinct from the mechanisms described for N-type (Zagotta et al., 1990; Demo and Yellen, 1991) and C-type (Ogielska et al., 1995; Panyi et al., 1995) K⁺ channel inactivation. We show that wild-type AMPA and kainate receptors desensitize in a series of conformational steps. Kainate receptor gating is sensitive to external cations and anions (see below), whereas AMPA receptors are unaffected. During the process of evolution K⁺channels and iGluRs have acquired unique subunit–subunit interactions that have shaped both inactivation and desensitization mechanisms to fulfill distinct roles in vertebrate CNS.

Comparison with previous studies

To our knowledge, a direct comparison between AMPA and kainate receptor desensitization has not been examined previously. Many studies, however, have studied desensitization for each receptor subtype, and, in most cases, the recovery process has been described as first order (Lomeli et al., 1994; Mosbacher et al., 1994; Heckmann et al., 1996; Partin et al., 1996; Traynelis and Wahl, 1997; Wilding and Huettner, 1997; Paternain et al., 1998). Our findings reveal a more complex recovery (and reentry) pathway that probably reflects the greater number of test pulses that were used to map out this process in finer detail.

Some investigations have described more complex recovery behavior (Trussell and Fischbach, 1989; Patneau and Mayer, 1991; Smith et al., 1991; Colquhoun et al., 1992; Raman and Trussell, 1995; Robert et al., 2001). More than a decade ago, several studies noted that AMPA receptor recovery was better fit by a double-exponential function in neuronal preparations (Trussell and Fischbach, 1989; Patneau and Mayer, 1991;Colquhoun et al., 1992). One potential caveat, however, is that the diversity of receptor populations and subunit composition therein is not known. Therefore, it remains to be established whether recovery behavior reflects (at least) two independent channel populations with different kinetic properties or, as we report, the sequential conformations of a homogenous channel population. More recently, Robert et al. (2001), using mixtures of wild-type and nondesensitizing subunits, observed that recovery rates were faster when GluR-A (or GluR1) tetramers contained more nondesensitizing subunits. Our results with wild-type subunits are consistent with this. In our case, tetramers containing fewer desensitized subunits recover more rapidly.

Raman and Trussell (1995) and Smith et al. (1991) reported that native AMPA receptors recover with first-order behavior only after a delay of several milliseconds. The delay duration was apparently agonist-dependent because refractory periods with the high affinity agonist quisqualate (∼10 msec; Smith et al., 1991) were five times longer than with the low affinity agonist glutamate (∼2 msec; Raman and Trussell, 1995). Raman and Trussell accounted for the delay in their gating model of AMPA receptors as a conformational step and slow agonist unbinding (Raman and Trussell, 1995). A similar delay in recovery from sodium channel inactivation reflects a coupling between gating events in which channel closure must occur first before recovery can proceed (Kuo and Bean, 1994). Interestingly, our initial experiments suggested that AMPA and kainate receptors recover with a similar delay of several milliseconds, as reported previously (Smith et al., 1991; Raman and Trussell, 1995). However, we later concluded that this observation reflected our inability to resolve events smaller than a few percentage of peak conditioning responses, because patches of higher channel density exhibited recovery without delay. Nevertheless, the gating behavior of neuronal AMPA receptors may differ where a delay precedes the recovery process (Smith et al., 1991; Raman and Trussell, 1995). However, in our experimental system GluR-A and GluR6 receptors apparently recover from desensitization without delay.

Do AMPA and kainate receptors share common or disparate gating mechanisms?

Although AMPA and kainate receptors have distinct pharmacological profiles (Dingledine et al., 1999), their architectural design and functional behavior are similar. Both receptors possess comparable subunit topologies (Dingledine et al., 1999), bi-lobed agonist-binding domains (Stern-Bach et al., 1994; Armstrong et al., 1998; Paas, 1998;Armstrong and Gouaux, 2000), and similar pore regions (Kuner et al., 2001; Panchenko et al., 2001). However, recent structural analysis of AMPA receptor agonist-binding domains (Armstrong et al., 1998;Armstrong and Gouaux, 2000) suggests that amino acid residues pivotal in orchestrating interactions between subunits are absent from kainate receptors. For example, residues critical in determining AMPA receptor desensitization (Partin et al., 1995; Stern-Bach et al., 1998) and located at subunit–subunit interfaces (Armstrong and Gouaux, 2000) are not conserved among kainate receptors. One possibility supported by findings in this study is that, although AMPA and kainate receptors are constructed from a similar modular design, protein conformations initiated by agonist binding to promote channel openings, closure, or desensitization are different. In agreement with this, single channel analysis of AMPA and kainate receptors suggests that individual subunits may operate in an independent (Rosenmund et al., 1998; Smith et al., 2000) or concerted (Smith and Howe, 2000) manner, respectively, during activation. Taken together with our findings, protein conformations associated with AMPA and kainate receptor activation and desensitization may be fundamentally different.

External ions regulate kainate, but not AMPA, receptor gating behavior

We report that external ions distinguish between AMPA and kainate receptor desensitization mechanisms. Recent experiments suggest that both external anions and cations regulate GluR6 responses via a novel allosteric mechanism (Bowie, 2002). Whether these observations support the existence of distinct gating mechanisms as discussed above requires further study. We propose that AMPA receptors assemble and operate as dimer of dimers in agreement with recent electrophysiological data of wild-type and mutant subunit assemblies (Robert et al., 2001) as well as biochemical studies (Ayalon and Stern-Bach, 2001) and x-ray crystallography (Armstrong and Gouaux, 2000). Because of external ion effects, it is more difficult to identify the functional stoichiometry of kainate receptors. Our method of counting states traversed during desensitization may underestimate the actual number of molecular events involved. In particular, it is likely that each state described in our models represents several subconductance levels, each with comparable open time distributions (see below). In view of this, the most parsimonious interpretation of our results advocates that kainate receptors operate in a tetramer arrangement as observed in solutions of high ionic strength. The apparent dimer behavior in solutions of lower ionic strength (i.e., 55 and 150 NaCl) can be explained by the inability to resolve all of the transition steps from the macroscopic responses fit in this study. Future analysis of single channel behavior may identify more of the microscopic events associated with kainate receptor desensitization. An additional complication is that many native kainate receptors are assembled from more than one subunit. Whether heteromeric receptors operate as tetramers and are similarly sensitive to external ions remains to be established.

The physiological role of intermediate desensitized states

Our modeling suggests that AMPA and particularly kainate receptors containing desensitized subunits contribute to membrane conductance. This result is contrary to previous models of AMPA and kainate receptors in which desensitized states are designated as nonconducting (Raman and Trussell, 1992; Patneau et al., 1993; Heckmann et al., 1996; Partin et al., 1996; Bowie et al., 1998; Smith and Howe, 2000; Smith et al., 2000; Robert et al., 2001). Our conclusion is supported experimentally by the observation that recovering AMPA and kainate receptors reenter desensitization at different rates (see Figs. 1d, 2d). We propose that the number of desensitized subunits per AMPA or kainate receptor tetramer determines macroscopic desensitization. Sequential models described in this study reproduce this observation and require that desensitized states are ion conducting in nature. When desensitized states are designated nonconducting, the models fit the data poorly. We therefore propose that the fraction of desensitized subunits in each tetramer determines three factors: entry into and exit from desensitization as well as conductance. The conductance of each state is defined as the product of the unitary conductance(s) and open probability. As yet, we cannot speculate whether a single or, perhaps more likely, several subconductance levels contribute to the macroscopic conductance of each state in our models. However, because of the saturating agonist concentrations used, each state probably reflects fully occupied receptor populations. One possibility is that fully occupied AMPA and kainate receptors operate like cyclic nucleotide-gated channels in which various subconductance levels are accessed (Ruiz and Karpen, 1999). The relative proportions of sublevels then may be dependent on the number of desensitized subunits per tetramer.

Finally, the possibility that intermediate desensitized states contribute to membrane conductance may provide insight into the paradoxical observation that decay kinetics of recombinant kainate receptors in rapid perfusion systems are two orders of magnitude faster (τ_decay, ∼3–5 msec; Dingledine et al., 1999) than synaptic kainate receptor events (τ_decay, ∼150 msec; Cossart et al., 1998; Frerking et al., 1998; Kidd and Isaac, 1999). A number of mechanisms have been speculated to account for the disparity in kinetic behavior, including the distant location of postsynaptic kainate receptors from presynaptic terminals. One caveat to this proposal is that ultrastructural staining of kainate receptor subunits (GluR6/7 and KA2) indicates that at least some kainate receptors are present at postsynaptic densities and, therefore, in direct apposition to release sites (Petralia et al., 1994). Moreover, a recent study examining the effects of glutamate clearance reports that kainate receptor activity probably does not originate from an extrasynaptic location (Kidd and Isaac, 2001). Our experimental observations provide an explanation to account for the kinetic behavior of synaptic responses as well as the apparently conflicting results identifying kainate receptors at central synapses.

As proposed from anatomical work, neuronal kainate receptors may be juxtaposed to transmitter release sites but would reside mainly in intermediate desensitized states because of their slow recovery from desensitization. For example, if postsynaptic GluR6 receptors were activated at 1 Hz, synaptic responses would be attenuated by >80% (Fig. 7c; 150 mm NaCl), consistent with the small synaptic events observed from in vitro slice recordings (Cossart et al., 1998; Frerking et al., 1998; Kidd and Isaac, 1999). Moreover, because receptors reside in intermediate desensitized states (Fig. 4c), decay kinetics would be slow in agreement with observations in neurons (Kidd and Isaac, 1999). Although scaffolding proteins, such as PSD-95 (Garcia et al., 2001), additionally may regulate the kinetics of kainate receptors, future study may provide the experimental evidence to support this possibility directly. It is interesting, however, that, in contrast, postsynaptic AMPA receptor events would attenuate little at similar stimulation frequencies (i.e., 1 Hz) because recovery is >10-fold faster (Dingledine et al., 1999). Taken together, our results provide the molecular basis by which differences in AMPA and kainate receptor desensitization may be exploited to process information in neuronal circuits.

Deriving a Mathematical Function for Fitting

For each model, two sets of first order linear differential equations are formulated. The first is concerned with recovery from desensitization. The independent variable (x) is the time between agonist pulses. The state functions (P_i) represent the probability of open channels of a given macroscopic conductance current (G_i). The transitions between states are governed by the recovery rate constants (r_i). The second set of rate constants are concerned with entry into desensitization. The independent variable (t) is the time from the beginning of the second agonist pulse. The state functions (p_i) again represent the probability of opening of channels. The transitions between states are governed by the entry rate constants (k_i). The solutions of the first set of equations provide the initial conditions for the second set of equations. Finally, an equation defining the total conductance is achieved by multiplying each state function by its associated conductance (G_i), substituting in the initial conditions and summing over i. The total conductance (G_T) is then a function of both x and t, that is, of both the time between agonist pulses and the time since the beginning of the second pulse.

(a) Concerted Model

Forward differential equations (recovery from desensitization),

$$P_1^{\prime }(x)=-{\text{rP}}_1(x)$$

$$P_2^{\prime }(x)={\text{rP}}_1(x)$$

$$P_1(0)=1$$

$$P_2(0)=0.$$

Solution,

$$P_1(x)=e^{-\text{rx}}$$

$$P_2(x)=1-e^{-\text{rx}}.$$

Reverse differential equations (entry into desensitization),

$$p_1^{\prime }(t)={\text{kp}}_2(t)$$

$$p_2^{\prime }(t)=-{\text{kp}}_2(t)$$

$$p_1(0)=P_1(x)$$

$$p_2(0)=P_2(x).$$

Solution,

$$p_1(x,t)=e^{-\text{rx}}+(1-e^{-\text{kt}})(1-e^{-\text{rx}})$$

$$p_2(x,t)=e^{-\text{kt}}(1-e^{-\text{rx}}).$$

Equation for the total conductance

$$G_T(x,t)=G_1{p}_1(x,t)+G_2{p}_2(x,t).$$

(b) Independent Dimer Model

Forward differential equations (recovery from desensitization),

$$P_1^{\prime }(x)=-2{\text{rP}}_1(x)$$

$$P_2^{\prime }(x)=2{\text{rP}}_1(x)-{\text{rP}}_2(x)$$

$$P_3^{\prime }(x)={\text{rP}}_2(x)$$

$$P_1(0)=1$$

$$P_2(0)=0$$

$$P_3(0)=0.$$

Solution,

$$P_1(x)=e^{-2\text{xr}}$$

$$P_2(x)=2e^{-2\text{rx}}(-1+e^{\text{rx}})$$

$$P_3(x)=e^{-2\text{rx}}(-1+e^{\text{rx}}{)}^2.$$

Reverse differential equations (entry into desensitization),

$$\hspace{1em}{p}_1^{\prime }(t)=k p_2(t)$$

$$\hspace{1em}{p}_2^{\prime }(t)=2k p_3(t)-k p_2(t)$$

$$\hspace{1em}{p}_3^{\prime }(t)=-2k p_3(t)$$

$$\hspace{1em}{p}_1(0)=P_1(x)$$

$$p_2(0)=P_2(x)$$

$$p_3(0)=P_3(x).$$

Solution,

$$p_1(x,t)=e^{-2(\text{kt}+\text{rx})}(1-e^{\text{rx}}+e^{\text{kt}+\text{rx}}{)}^2$$

$$p_2(x,t)=2e^{-2(\text{kt}+\text{rx})}(-1+e^{\text{rx}})(1-e^{\text{rx}}+e^{\text{kt}+\text{rx}})$$

$$p_3(x,t)=e^{-2(\text{kt}+\text{rx})}(-1+e^{\text{rx}}{)}^2.$$

Equation for the total conductance

$$G_T(x,t)=G_1{p}_1(x,t)+G_2{p}_2(x,t)+G_3{p}_3(x,t).$$

(c) Cooperative Dimer Model

Forward differential equations (recovery from desensitization),

$$P_1^{\prime }(x)=-r_1{P}_1(x)$$

$$P_2^{\prime }(x)=r_1{P}_1(x)-r_2{P}_2(x)$$

$$P_3^{\prime }(x)=r_2{P}_2(x)$$

$$P_1(0)=1$$

$$P_2(0)=0$$

$$P_3(0)=0.$$

Solution,

$$\hspace{1em}{P}_1(x)=e^{-{\text{xr}}_1}$$

$$\hspace{1em}{P}_2(x)=\frac{(e^{-{\text{xr}}_1}-e^{-{\text{xr}}_2})r_1}{r_2-r_1}$$

$$\hspace{1em}{P}_3(x)=\frac{(1-e^{-{\text{xr}}_2})r_1+(-1+e^{-{\text{xr}}_1})r_2}{r_1-r_2}.$$

Reverse differential equations (entry into desensitization),

$$p_1^{\prime }(t)=k_1{p}_2(t)$$

$$p_2^{\prime }(t)=k_2{p}_3(t)-k_1{p}_2(t)$$

$$p_3^{\prime }(t)=-k_2{p}_3(t)$$

$$p_1(0)=P_1(x)$$

$$p_2(0)=P_2(x)$$

$$p_3(0)=P_3(x).$$

Solution,

$$p_1(x,t)=e^{-{\text{xr}}_1}+(1-e^{-{\text{tk}}_1})(e^{-{\text{xr}}_1}-e^{-{\text{xr}}_2})\frac{r_1}{r_2-r_1}+$$

$$\frac{((1-e^{-{\text{tk}}_2})k_1+(-1+e^{-{\text{tk}}_1})k_2)}{(k_1-k_2)(r_1-r_2)}$$

$$((1-e^{-{\text{xr}}_2})r_1+(-1+e^{-{\text{xr}}_1})r_2)$$

$$p_2(x,t)=e^{-{\text{tk}}_1}(e^{-{\text{xr}}_1}-e^{-{\text{xr}}_2})\frac{r_1}{r_2-r_1}-\frac{(e^{-{\text{tk}}_1}-e^{-{\text{tk}}_2})k_2}{(k_1-k_2)(r_1-r_2)}$$

$$((1-e^{-{\text{xr}}_2})r_1+(-1+e^{-{\text{xr}}_1})r_2)$$

$$p_3(x,t)=e^{-{\text{tk}}_2}(1-e^{-{\text{xr}}_2})r_1+\frac{(-1+e^{-{\text{xr}}_1})r_2}{r_1-r_2}.$$

Equation for the total conductance

$$G_T(x,t)=G_1{p}_1(x,t)+G_2{p}_2(x,t)+G_3{p}_3(x,t).$$

(d) Independent Tetramer Model

Forward differential equations (recovery from desensitization),

$$P_1^{\prime }(x)=-4{\text{rP}}_1(x)$$

$$P_2^{\prime }(x)=4{\text{rP}}_1(x)-3{\text{rP}}_2(x)$$

$$P_3^{\prime }(x)=3{\text{rP}}_2(x)-2{\text{rP}}_3(x)$$

$$P_4^{\prime }(x)=2{\text{rP}}_3(x)-{\text{rP}}_4(x)$$

$$P_5^{\prime }(x)={\text{rP}}_4(x)$$

$$P_1(0)=1$$

$$P_2(0)=0$$

$$P_3(0)=0$$

$$P_4(0)=0$$

$$P_5(0)=0.$$

Solution,

$$P_1(x)=e^{-4\text{rx}}$$

$$P_2(x)=4e^{-4\text{rx}}(-1+e^{\text{rx}})$$

$$P_3(x)=6e^{-4\text{rx}}(-1+e^{\text{rx}}{)}^2$$

$$P_4(x)=4e^{-4\text{rx}}(-1+e^{\text{rx}}{)}^3$$

$$P_5(x)=e^{-4\text{rx}}(-1+e^{\text{rx}}{)}^4.$$

Reverse differential equations (entry into desensitization),

$$p_1^{\prime }(t)={\text{kp}}_2(t)$$

$$p_2^{\prime }(t)=-{\text{kp}}_2(t)+2{\text{kp}}_3(t)$$

$$p_3^{\prime }(t)=-2{\text{kp}}_3(t)+3{\text{kp}}_4(t)$$

$$p_4^{\prime }(t)=-3{\text{kp}}_4(t)+4{\text{kp}}_5(t)$$

$$p_5^{\prime }(t)=-4{\text{kp}}_5(t)$$

$$p_1(0)=P_1(x)$$

$$p_2(0)=P_2(x)$$

$$p_3(0)=P_3(x)$$

$$p_4(0)=P_4(x)$$

$$p_5(0)=P_5(x).$$

Solution,

$$p_1(x,t)=e^{-4(\text{kt}+\text{rx})}(1+e^{\text{rx}}(-1+e^{\text{kt}}){)}^4$$

$$p_2(x,t)=4e^{-4(\text{kt}+\text{rx})}(-1+e^{\text{rx}})(1+e^{\text{rx}}(-1+e^{\text{kt}}){)}^3$$

$$p_3(x,t)=6e^{-4(\text{kt}+\text{rx})}(-1+e^{\text{rx}}{)}^2(1+e^{\text{rx}}(-1+e^{\text{kt}}){)}^2$$

$$p_4(x,t)=4e^{-4(\text{kt}+\text{rx})}(-1+e^{\text{rx}}{)}^3(1+e^{\text{rx}}(-1+e^{\text{kt}}))$$

$$p_5(x,t)=e^{-4(\text{kt}+\text{rx})}(-1+e^{\text{rx}}{)}^4.$$

Equation for the total conductance

$$G_T(x,t)=G_1{p}_1(x,t)+G_2{p}_2(x,t)+$$

$$G_3{p}_3(x,t)+G_4{p}_4(x,t)+G_5{p}_5(x,t).$$