A Reciprocal Relationship between Reliability and Responsiveness in Developing Visual Cortical Neurons

Abstract

As the visual cortex matures, developmental modifications change the visually evoked firing patterns of single neurons. To explore the relationship between these developmental changes and the fidelity with which neurons transmit information, we measured the reliability of neuronal responses during postnatal development. Infant neurons have lower variability and higher dependence of transmitted information on firing rate than adult cells. Fewer spikes are needed by the infant cortex to convey the same amount of information. The increase in firing rates that occurs during development is largely offset, therefore, by a decrease in the reliability of responses. We propose that these changes are a consequence of the increasing ability of cortical cells to encode rapid changes in the visual environment.

The spatial vision of infant primates is poor; in particular, infant monkeys and humans are 5–10 times less sensitive to contrast than adults (Banks and Salapatek, 1981; Boothe et al., 1988). The visually evoked responses of cortical neurons in infant monkeys are relatively weak, and during development firing rates increase, receptive fields become smaller, and temporal resolution improves (Wiesel and Hubel, 1974; Blakemore, 1990; Chino et al., 1997). It is believed that the postnatal increase in visual sensitivity reflects postnatal maturation of visual cortical response properties.

However, it is not only the absolute firing rate that determines how accurately a neuron can signal the presence or character of a particular stimulus. Information in a neuronal response is limited not only by firing rate but also by variability. Presented with the same stimulus on repeated trials, a neuron responds with a variable number of spikes. If there were a constant relationship between variability and firing rate throughout development, the low firing rates of infant neurons would imply that the information they can transmit increases with age. However, if the variability of responses in infant neurons were lower, this might compensate for their lower spike rates and permit them to transmit more information than their sluggish responses might suggest.

We wanted to determine whether the changes in firing rate and tuning properties observed during development are associated with an increase in the information content of the visual signals carried by cortical neurons. To quantify the efficiency with which neurons signaled information during different stages of development, we calculated two measures: a ratio of the variance-to-mean spike count and an information theory-based measure that relates the amount of information in a response to the number of spikes used to convey that information. Both measures suggested that the responses of infant neurons were more reliable than those of adult neurons, and that the increase in responsiveness during development is paralleled by a decrease in reliability. Therefore, the information that infant cortical neurons transmit need not limit, by itself, the contrast sensitivity of infant vision.

MATERIALS AND METHODS

We made single-unit recordings from the primary visual cortex of 11 anesthetized, paralyzed pigtail macaques (Macaca nemestrina) between 1 and 99 weeks of age, using conventional methods described previously (Carandini et al., 1997). All experiments were performed in compliance with the National Institutes of HealthGuide for the Care and Use of Laboratory Animals and with guidelines of the New York University Animal Welfare Committee.

After isolating each recorded neuron, we tested the more effective eye and optimized the orientation, spatial frequency, temporal frequency, and area of drifting achromatic sinusoidal gratings of 0.5 contrast presented on a gray background. The time- and space-average luminance of the display was 33 cd/m². We then measured the response of each neuron to gratings at six contrasts ranging from 0 to 0.5. Stimuli drifted across the screen at a rate chosen so that an integer (1–8) number of cycles occurred in a 640 msec period (1.6–12.5 Hz). For the neurons reported here, ≥10 640 msec trials were collected for each contrast; stimuli were interleaved and presented in pseudorandom order. The f1/f0 ratio of the response to drifting gratings was used to classify cells as simple or complex (Skottun et al., 1991). A few simple cells with a high spontaneous rate were excluded from the analysis because spike-count-based techniques do not capture correctly the information that these neurons transmit.

A direct method was used to calculate the information about contrast (for review, see Cover and Thomas, 1991) as the difference between the total entropy across all contrasts and the mean noise entropy at each contrast:

$$I=-\sum _r P(r){log}_{2}P(r)+\sum _s P(s)\sum _r P(r\Vert s){log}_2 P(r\Vert s),$$

where r is the number of spikes in a 640 msec trial and s is the contrast level of the grating. This equation was used to calculate both the full mutual information (approximately six contrast levels) and pairwise information (approximately two contrast levels). To compensate for overestimation of information caused by the limited number of available trials (meann = 28.5 cycles), we applied an analytical correction. When the number of trials was less than four times the peak spike count, the responses were quantized into R bins (Panzeri and Treves, 1996) with R chosen such that convergence to the large-N asymptote was observed over the entire data set (this resulted in r = 0.4N in the case of contrast pairs). The effect of this strategy is to exchange a small degree of underestimation caused by quantization loss for overestimation caused by sampling bias to obtain the most accurate results over the entire data set. The analysis also was performed with fixed bin size, and qualitatively identical results were obtained.

We devised a novel metric to compute reliability by relating the pairwise information available in stimulus-evoked responses to differences in spike rates; we will refer to this metric as information density. To calculate information density, mutual information was calculated about all possible pairs of contrasts (six contrasts, 15 pairs) from spike counts in 640 msec bins. Because information was calculated about pairs of contrasts, information could be plotted against the difference in firing rates, which should be related to information, rather than a potentially less correlated measure such as the mean rate. The relationship between mutual information and the difference in spike count was fit with the following curve:

$$I=[1-(1-\alpha {)}^{(\mathrm{\Delta }n{)}^{\beta }}]{log}_2 S,$$

where I is the mutual information, Δn is the difference in spike count, S is the number of stimuli (two), and α and β are free parameters. This curve asymptotes at the theoretical limit of I = 1 bit for large values of Δn. For β = 1, the curve corresponds to an exponential saturation model in which the information provided by each spike has a random overlap with that provided by any other; in this case, α measures the extent of that overlap (Gawne and Richmond, 1993; Rolls et al., 1997b). For β = 2, the curve corresponds to the rate at which information grows as the firing rate distributions for two stimuli are separated if those distributions were Gaussian. Allowing β to vary allows the function to account for a variety of firing rate distributions; the value of β for our sample varied between 1 and 4. The maximum slope of this function represents the peak rate of information growth with difference in spike count; we call this quantity information density to distinguish it from other measures of information. The values of information density obtained by fitting other empirically chosen functions were very similar to those obtained using Equation 2. Neurons were excluded from this and other analyses if the correlation between pairwise mutual information and spike count did not achieve significance on an F test (p < 0.05). The number of neurons so excluded was small (1 week, 1 of 48 neurons; 4 weeks, 7 of 60 neurons; 16 weeks, 2 of 68 neurons; adults, 6 of 72 neurons).

We wanted to know whether the choice of test contrasts had an effect on the full (all stimuli) mutual information values that we computed. In particular, if contrast values were placed too high or too low, most responses would be either small or large, skewing the distribution of responses and reducing the amount of information transmitted. We calculated full mutual information for a Poisson neuron with a conventional contrast–response function and deliberately skewed the chosen contrast values. The full mutual information measure proved quite insensitive to this skewing within the range of skews in our data set, and we used the simulations to estimate the amount by which our full mutual information calculations would have been in error for real neurons. The effect of skewing was modest (<10% underestimate of information for almost all cases), and there was no difference in our estimated errors across the four age groups.

We also measured responses to high contrast gratings of optimal orientation and spatial frequency drifting at frequencies between 0.4 and 25 Hz, and we fit the data with a suitable descriptive function; we took temporal resolution as the frequency at which the response fell to 1/10 of maximum (Foster et al., 1985; Saul and Humphrey, 1992). Response latency also provides a measure of integration time (Maunsell and Gibson, 1992; Gonzalez et al., 2001). We measured response latency by plotting response histograms (in 5 msec bins) over multiple data sets and estimating latency as the first bin in which the response was greater than the mean spontaneous rate measured in response to a gray screen. For simple cells, a latency was recorded only if cycle-triggered averages indicated that at least one stimulus started in the excitatory phase of the cell. For a few cells (19 of 232), we could not determine latency reliably, and those cells were omitted from the latency analysis.

RESULTS

Consider the two cells for which data are shown in Figure1. Figure 1, a andb, shows the mean responses of an infant and an adult neuron, respectively, to an otherwise optimal grating stimulus at six different contrasts; error bars indicate the SD of the firing rate distributions. As is typical of visual cortical neurons, firing rate grew with contrast and saturated at high contrasts for both cells. To discriminate two stimuli perfectly, a neuron with high trial-to-trial variability like the adult cell must signal two different stimuli with very different mean firing rates. Conversely, a neuron with low variability like the infant cell can convey the same amount of information with a smaller dynamic range.

Fig. 1.

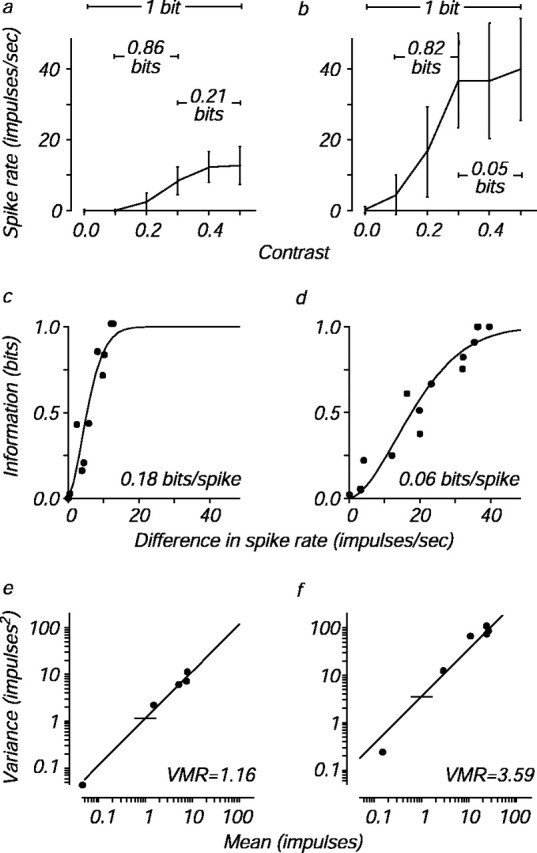
Calculation of information density and variance-to-mean ratio for two cells. a,b, Mean ± SD of the responses of a neuron from a 4-week-old infant (a) and from an adult (b) to an optimized, drifting sinusoidal grating stimulus at six different contrasts evenly spaced between 0 and 0.5. The mutual information about selected contrast pairs is indicated.c, d, Mutual information about every possible pair of the six contrasts (15 pairs) in a andb is plotted against the difference in the mean firing rate between each pair of contrasts. These data are fit with a function, the maximal slope of which is a measure of information density (see Materials and Methods). Information density has units of bits per spike, and the computed information densities for each cell are indicated. This measure, unlike total mutual information, does not depend on the specific contrasts tested, which differed somewhat from cell to cell. e, f, Spike count variance at each contrast is plotted against mean spike count for the example cells in a and b. The variance-to-mean ratio (VMR) is taken from the best fitting line with slope = 1; horizontal ticks mark the ratios for each cell. The counting window was 640 msec and contained an integer number of temporal cycles of the drifting stimulus.

We used Shannon's mutual information to measure how accurately different stimuli can be distinguished based on the number of spikes elicited from a neuron during repeated stimulus presentations (Werner and Mountcastle, 1965; Tolhurst, 1989; Rolls et al., 1997a). The information is related to the distance between the two firing rate distributions and is similar to the d′ measure used in signal detection theory (Parker and Newsome, 1998). To illustrate the relationship between the firing rate and information, Figure 1,a and b, also shows the information transmitted by each neuron about selected pairs of contrasts. Note that both the infant and the adult neuron were capable of perfectly discriminating a zero-contrast stimulus (mean gray background) from the highest stimulus contrast, yielding one bit of information. However, the infant neuron signaled this information with fewer spikes.

To quantify the relationship between information and the number of spikes needed to convey that information, we plotted the information conveyed by a neuron about each of the 15 different contrast pairs against the mean firing rate difference between the members of each pair (Fig. 1c,d). Information about a contrast pair cannot exceed one bit, representing perfect discrimination, and therefore we fit these points with a curve, the form of which accounts for this saturation. The maximum slope of this function captures the shape of the relationship between information and spikes; we call the maximum slope of this curve the information density (see Materials and Methods), with units of bits per spike. This measure differs from the more usual full mutual information in that it depends only on pair comparisons and not on the total number of stimuli used (Tolhurst, 1989; Rolls et al., 1997a). Neurons with larger values of information density use fewer spikes to convey information (Fig. 1c). Neurons with smaller values require a larger dynamic range to discriminate contrast pairs (Fig. 1d).

Another way to capture the change in firing patterns is to analyze the relationship between response mean and variance for the example cells. The variance of cortical neuron spike counts increases in proportion to their mean (Tolhurst et al., 1981, 1983), and the ratio of the two is inversely related to the amount of information transmitted by cortical cells (de Ruyter van Steveninck et al., 1997). Figure 1, eand f, shows the relationship between response variance and mean for the two example cells. As indicated by the reference lines at a spike count of 1, the infant cell had a lower variance-to-mean ratio than the adult cell, as would be expected from its higher information density.

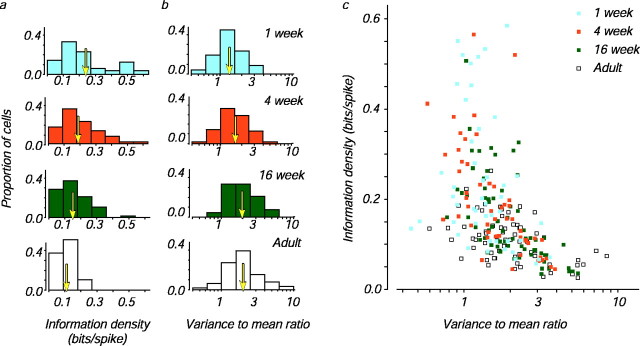
We calculated information density for populations of V1 cells recorded from macaques in four age groups: 1 week, 4 weeks, 16 weeks, and adults (31–99 weeks). Surprisingly, we found that V1 neurons in the youngest animals had the highest information density: mean information density decreased twofold during development (Fig.2a). We also calculated the variance-to-mean ratio for the same populations; as expected from the information density calculation, the variance-to-mean ratio of cortical cells increased during development (Fig. 2b). Adult cells tended to have higher variance-to-mean ratios than infant cells even when cells with similar dynamic range were selected, implying that this developmental difference cannot be attributed to the subpopulation of adult cells with high firing rates (data not shown). It is also interesting to note that simple cells had higher information densities for each age group (mean information densities for simple cells from the 1 week, 4 week, 16 week, and adult animals were 0.33, 0.25, 0.20, and 0.12, respectively; for complex cells, the values were 0.19, 0.15, 0.11, and 0.09, respectively); simple cells had correspondingly lower variance-to-mean ratios than complex cells. A multiple linear regression analysis suggests that these differences cannot be accounted for by differences in spontaneous rate or dynamic range.

Fig. 2.

Changes in information density and the variance-to-mean ratio during development. a, Distributions of information density for neurons from monkeys in the four age groups (see Materials and Methods for calculation).Arrows indicate the means. b, Distributions of the variance-to-mean ratio for each age group (see Materials and Methods for calculation). Arrows indicate the geometric means. c, Scatter plot of the data displayed in a and b for 232 neurons from animals in the four age groups: 1 week (47), 4 weeks (53), 16 weeks (66), and adults (66).

Together, these two measures suggest that the coding properties of neurons change during development. However, how are they related? Figure 2c shows that information density and the variance-to-mean ratio were inversely but imperfectly correlated. This is because the variance-to-mean ratio measures the average variability of the response to a single stimulus, whereas the mutual information quantifies the fraction of the total variability that is attributable to the difference between responses. These two measures are comparable in that each indicates the reliability of neuronal firing, and the regular relationship shown in Figure 2c suggests that during development there was a decrease in the reliability of visual signaling by cortical neurons.

Despite the decrease in reliability during development, total information transmission could be maintained if the range between the lowest and highest firing rates (the dynamic range) also increased. The mean dynamic range did increase twofold during development, and a plot of the mean information density- versus the geometric mean-evoked firing rate for each age reveals the reciprocal relationship between these two measures (Fig. 3a). In the youngest infants, information density was high and firing rate was low, whereas in the adults information density was low and firing rate was high.

Fig. 3.

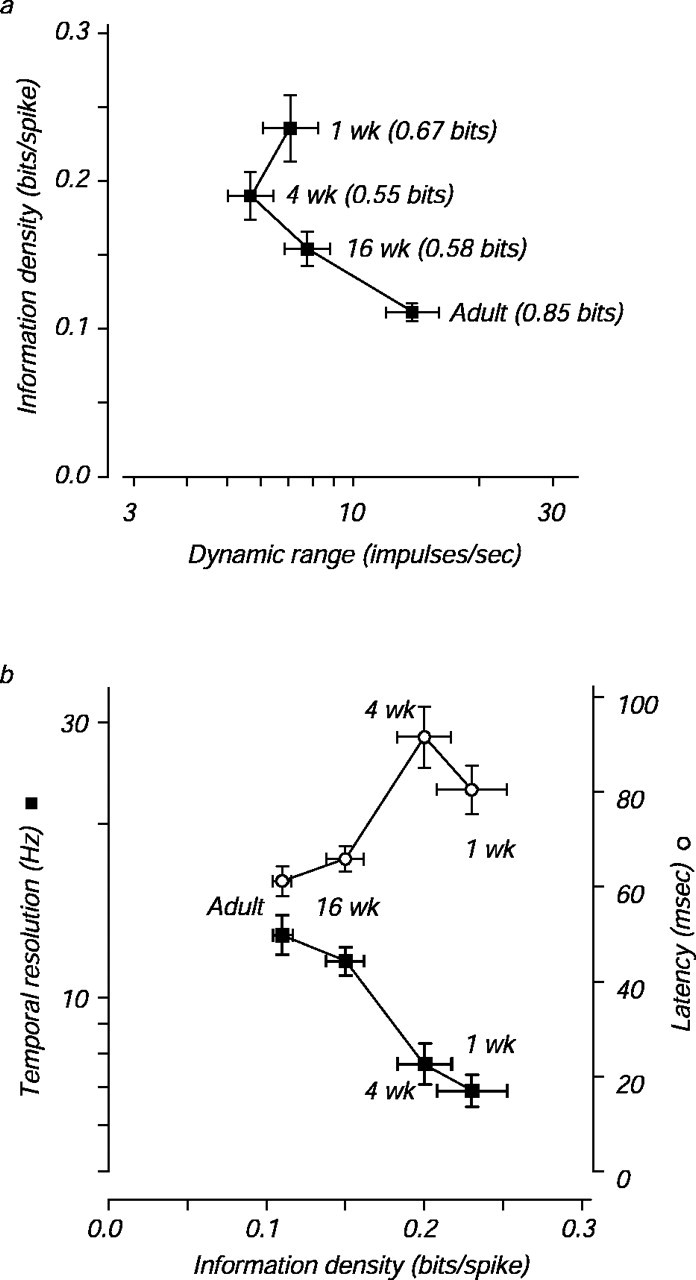
The relationship among information density, dynamic range, and temporal parameters during development.a, Mean information density and geometric mean dynamic range are plotted for each age group. Dynamic range is taken as the largest mean response to a grating target minus the mean baseline response. The mean transmitted full mutual information for all six contrasts is indicated beside each point. b, Mean information density, geometric mean temporal resolution (filled squares), and geometric mean latency (open circles) are plotted for each age group. For each cell, temporal resolution was taken as the drift rate at which the response of the cell fell to $\frac{1}{10}$ of its peak. Latency was taken as the time after stimulus onset at which the firing rate first deviated from baseline. SE are plotted for all axes.

The mutual information about all of the six contrasts presented in an experiment (which we term full mutual information to avoid confusion with the pairwise measure) quantifies the ability of these neurons to distinguish stimuli and depends on both information density and dynamic range. However, unlike information density, full mutual information depends on both the number and the distribution of the contrasts tested. We did not use the same test contrasts every time because we tried to place the contrasts so that they spanned the response range of each cell; however, we verified that the chosen contrasts did not have an important effect on the full mutual information measure for our population (see Materials and Methods). Mean full information values for the four age groups are given next to each point in Figure3a. The modest and inconsistent change in the full mutual information values is attributable to the opposing effects of increasing firing rate and decreasing information density as development progresses. In other words, infant neurons may fire few spikes, but each infant spike carries more information. As a result, 1 week infant neurons can transmit 80% of the total information that adult neurons transmit.

DISCUSSION

Our results suggest that lower firing rates in infant neurons are compensated for partially by lower variability and that infant neurons, therefore, are more efficient at transmitting information about contrast than adult neurons. This leads to an interesting puzzle. If infant neurons can signal 80% of the information that adult neurons signal, why is it that contrast sensitivity in infant primates is 5- to 10-fold lower than in adults (Boothe et al., 1988)? One possibility is that infant neurons have higher contrast thresholds than adult neurons (compare responses in Fig. 1a,b). Our results might have been different had we tested infant neurons with very low contrast targets, but we did not explore systematically the contrast range below 0.1. A second possibility is that the limits to infant contrast sensitivity are not set by V1 neurons and, instead, lie in downstream structures (. The low spike rates of infant neurons might contribute to this by driving downstream neurons less effectively, even if their responses are reliable.

How might the reciprocal relationship between information density and firing rate arise? Many aspects of the visual system change during development, including improvements in the optics of the eye (Kiorpes and Movshon, Williams and Boothe, 1981; Jacobs and Blakemore, 1988), migration of cones in the fovea (Packer et al., 1990), increases in spatial resolution, and decreases in receptive field size (Blakemore, 1990; Movshon and Kiorpes, 1993; Wilson, 1993; Chino et al., 1997; Movshon et al., 2000). Our first thought was that developmental decreases in receptive field size might underlie our observations, but we have shown that these changes are attributable almost entirely to changes in retinal optical magnification and cone distribution (Wilson, 1993; Movshon et al., 2000) and do not reflect neural changes in receptive field organization. However, there are marked changes in the temporal fidelity of responses during development that may drive the change in information density. Figure 3b plots mean information densities for the neurons from each of the four age groups against two temporal measures: the latency of response after stimulus onset and the highest temporal frequency of drift that elicited a response (temporal resolution). A relationship between information density and each of these temporal parameters is clear. The decrease in latency and increase in temporal resolution with age suggest that infant neurons integrate their inputs over longer times than adult neurons. A neuron with a longer integration time would average over more synaptic input events and therefore reduce variability associated with rapid fluctuations in those inputs; such a neuron would carry more information with each spike by sacrificing temporal bandwidth. To improve their resolution of fine temporal structure, developing V1 neurons decrease their integration times, which would increase the variability of spiking. Such an increase would increase variance-to-mean ratios and have a deleterious effect on information transmission, but these effects could be overcome by increasing dynamic range (Fig. 3a).

Developmental changes in temporal integration might arise from changes in either neuronal properties or synaptic properties. Interestingly, in the gerbil lateral superior olive and rat cortex, EPSPs are of longer duration in infant neurons than in adult neurons (Burgard and Hablitz, 1993; Sanes, 1993); this change may be attributable to changes in patterns of glutamate receptor expression (Krukowski and Miller, 2001). Whatever the biological basis, a shift in coding strategy from high information density, low bandwidth, and low firing rate to low information density, high bandwidth, and high firing rate would ensure that information transmission is not sacrificed as temporal resolution grows to adult levels.