Bursting in Leech Heart Interneurons: Cell-Autonomous and Network-Based Mechanisms

Abstract

Rhythmic activity within the heartbeat pattern generator of the medicinal leech is based on the alternating bursting of mutually inhibitory pairs of oscillator heart interneurons (half-center oscillators). Bicuculline methiodide has been shown to block mutual inhibition between these interneurons and to cause them to spike tonically while recorded intracellularly (Schmidt and Calabrese, 1992). Using extracellular recording techniques, we show here that oscillator and premotor heart interneurons continue to burst when pharmacologically isolated with bicuculline, although the bursting is not robust in some preparations. We propose that a nonspecific leak current introduced by the intracellular microelectrode suppresses endogenous bursting activity to account for the discrepancy with results using intracellular recording. A two-parameter bifurcation diagram (E_leak vsg_leak) of a mathematical model of a single heart interneuron shows a narrow stripe of parameter values where bursting occurs, separating large zones of tonic spiking and silence. A similar analysis performed for a half-center oscillator model outlined a much larger area of bursting. Bursting in the half-center oscillator model is also less sensitive to variation in the maximal conductances of voltage-gated currents than in the single-neuron model. Thus, in addition to ensuring appropriate bursting characteristics such as period, phase, and duty cycles, the half-center configuration enhances oscillation robustness, making them less susceptible to random or imposed changes in membrane parameters. Endogenous bursting, in turn, ensures appropriate bursting if the strength of mutual inhibition is weakened and limits the minimum period of the half-center oscillator to a period near that of the single neuron.

Oscillatory patterns of neuronal activity underlie the control of motor functions, information processing, memory formation, and sleep (Cohen et al., 1988; Steriade et al., 1993; Laurent, 1996; Borisyuk et al., 2001; Buzsaki, 2002). The importance of such activity is perhaps most apparent in the control of rhythmic movements by central pattern generators (CPGs) (Dean and Cruse, 1995; Marder and Calabrese, 1996). Two features are commonly observed in CPGs, endogenously bursting neurons and mutually inhibitory connections (Satterlie, 1985; Selverston and Moulins, 1985; Smith et al., 1991; Pearson and Ramirez, 1992; Arshavsky et al., 1993, 1997;Calabrese, 1995; Thoby-Brisson and Ramirez, 2001). The presence of mutual inhibitory connections often organizes neurons into two antagonistic or alternating groups and thus forms a half-center oscillator (Brown, 1911). Mutual inhibition and endogenous bursting are thought to be complementary in the generation of oscillatory activity, but it has been difficult to assess the role of each in the final pattern that is produced, particularly when the mutual inhibition is strong. Under these conditions activity observed in the intact half-center oscillator differs in important characteristics such as cycle period from activity observed in single neurons when the inhibitory synapses are blocked pharmacologically or destroyed by physical isolation (Arshavsky et al., 1986; Bal et al., 1988). To parse out the roles of endogenous bursting and mutual inhibition, it is necessary to quantitatively compare the properties of bursting in the network and in isolated cells and to use modeling to generate testable hypotheses for how these differences arise.

We have analyzed the CPG that generates a heartbeat in the leech (Calabrese et al., 1995; Hill et al., 2001). Two segmentally repeated pairs of mutually inhibitory oscillator heart interneurons form oscillators that pace the rhythm. Previously, the oscillator heart interneurons were not thought to be capable of autonomous bursting (Schmidt and Calabrese, 1992). Here we reassess this ability using less invasive extracellular recording techniques and demonstrate clear endogenous bursting under pharmacological isolation. We compare the bursting characteristics of the neurons in the intact network and under pharmacological isolation; significant differences in cycle period and duty cycle between isolated cells and those in the intact network indicate strong mutual inhibition in the intact case. We perform a bifurcation analysis of a model of an oscillator heart interneuron using the leak conductance and reversal potential as parameters. This analysis indicates that endogenous bursting in this model is narrowly tuned to leak current parameters. Thus a nonspecific leak introduced by sharp microelectrode penetration may suppress endogenous bursting. A similar analysis of a pair of model heart interneurons in a half-center oscillator configuration demonstrates that the region of bursting is greatly expanded with the introduction of strong mutual inhibition. We discuss how robustness is achieved in this system, how critical variables such as period and duty cycle may be controlled, and how modulation may effect this control.

Parts of this paper have been published previously in abstract form (Cymbalyuk and Calabrese, 2000; Cymbalyuk et al., 2001).

MATERIALS AND METHODS

Leeches (Hirudo medicinalis) were obtained from Leeches USA and maintained in artificial pond water at 15°C. After the animals were anesthetized in ice-cold saline, individual ganglia were dissected and pinned ventral side-up in Petri dishes lined with SYLGARD (Dow Corning, Midland, MI; bath volume, 0.5 ml). The methods for preparing and maintaining leech ganglia and for identifying heart interneurons for electrophysiological recording have been described previously (Olsen and Calabrese, 1996). The ganglionic sheath over the cell bodies was removed with fine microscissors or scalpels. Ganglia were superfused continuously with normal leech saline containing (in mm): 115 NaCl, 4 KCl, 1.8 CaCl₂, 10 glucose, and 10 HEPES buffer, adjusted to pH 7.4. Most experiments were performed on heart interneurons in an isolated ganglion (number 3, 4, 6, or 7). For a simultaneous recording of coordinating interneurons from ganglia 1 or 2 and oscillator interneurons from ganglia 3 or 4, a chain of ganglia from the head brain to the fourth ganglion was used. Heart interneurons were isolated pharmacologically with 1 mm bicuculline methiodide (Sigma, St. Louis, MO) added to the saline.

For intracellular recording, neurons were penetrated with borosilicate microelectrodes (1 mm outer diameter, 0.75 mm inner diameter) filled with 4 m potassium acetate with 20 mm KCl (20–35 MΩ). Currents were injected using a switching single-electrode current clamp (Axoclamp 2A; Axon Instruments, Foster City, CA). Sample rates ranged between 2.5 and 3 kHz. The electrode potential was monitored on an oscilloscope to ensure that it had settled between current injection cycles. At the end of the experiment, microelectrodes were withdrawn from the cell, and only those preparations in which the electrode was within ±5 mV of the bath potential were accepted for further analysis. Extracellular recordings were obtained as described by Masino and Calabrese (2002) with suction electrodes pulled to 20–30 μm tip diameters and filled with normal saline. Weak suction was applied with a syringe, and the cell body was drawn into the electrode so that it fit snugly. Extracellular signals were amplified with a differential AC amplifier (A-M Systems model 1700). Data were digitized and stored using pClamp software (Axon Instruments). Analyses of burst characteristics were performed off-line with scripts written in Matlab (MathWorks, Inc., Natick, MA) as described by Masino and Calabrese, (2002). Statistical tests were done using SigmaStat (SPSS, Chicago, IL).

Integration and bifurcation analysis of the systems of stiff ordinary differential equations describing a single oscillatory heart interneuron and a half-center oscillator (Hill et al., 2001) were performed by using XPP-AUTO software (Ermentrout, 2002), Content (Kuznetsov et al., 1996) (Content is available athttp://www.cwi.nl/ftp/CONTENT/), and Matlab. Primarily, Gear's method and a variable-order method based on the numerical differentiation formulas were used to integrate the systems of equations (Gear, 1971; Shampine and Reichelt, 1997). Absolute and relative tolerances were equal to 10⁻⁸and 10⁻⁹, respectively. Here, the model of a half-center oscillator defined by Hill et al. (2001) is slightly modified so that the conductance of each spike mediated synapse is determined by three equations:

$$\hspace{0.5em}{I}_{\text{SynS}}={\overline{g}}_{\text{SynS}}{Y}_{\text{post}}{M}_{\text{post}}(V_{\text{post}}-E_{\text{Syn}})$$

$$\hspace{1em}\frac{{\text{dX}}_{\text{post}}}{\text{dt}}=\frac{(X_{\infty }(V_{\text{pre}})-X_{\text{post}})}{{\tau }_1}$$

$$\hspace{1em}\frac{{\text{dY}}_{\text{post}}}{\text{dt}}=\frac{(X_{\text{post}}-Y_{\text{post}})}{{\tau }_2}$$

$$\hspace{1em}\frac{{\text{dM}}_{\text{post}}}{\text{dt}}=\frac{M_{\infty }(V_{\text{pre}})-M_{\text{post}}}{0.2},$$

$$X_{\infty }(V_{\text{pre}})=\frac{1}{1+e^{-1000(V_{\text{pre}}+0.01)}};M_{\infty }(V_{\text{pre}})=0.1+\frac{0.9}{1+e^{-1000(V_{\text{pre}}+0.04)}}$$ Equation 1

where τ₁ = 0.002 sec; and τ₂= 0.011 sec. All values in these equations are provided in SI units (volts, amperes, siemens, and seconds), subscripts pre and post refer to presynaptic and postsynaptic cells. We adjusted $\overline{g}$_SynS to 150 × 10⁻⁹ S so that the generated synaptic conductance closely approximates the waveforms in the previous model. A model with parameter values chosen as standard according to Hill et al. (2001) and these parameter values are referred to in the text as canonical.

RESULTS

In the heartbeat pattern generator of the medicinal leech (Fig.1A), two segmentally repeated pairs of reciprocally inhibitory heart interneurons located in ganglia 3 and 4 form half-center oscillators that pace the rhythm. These oscillator interneurons are coupled by coordinating interneurons whose somata are located in ganglia 1 and 2 to form an eight-cell beat-timing network. Other premotor interneurons located in ganglia 6 and 7, along with the oscillator interneurons, inhibit heart motor neurons, sculpting their activity into rhythmic bursts. Switch interneurons located in ganglion 5 interface between oscillator interneurons and premotor interneurons to produce two alternating motor neuron coordination states: peristaltic and synchronous. Bicuculline methiodide (10⁻⁴m) blocks IPSPs produced by oscillator interneurons onto contralateral oscillator interneurons and ipsilateral heart motor neurons (Schmidt and Calabrese, 1992). These IPSPs are chloride-mediated and are mimicked by application of acetylcholine or carbachol but not GABA.

Fig. 1.

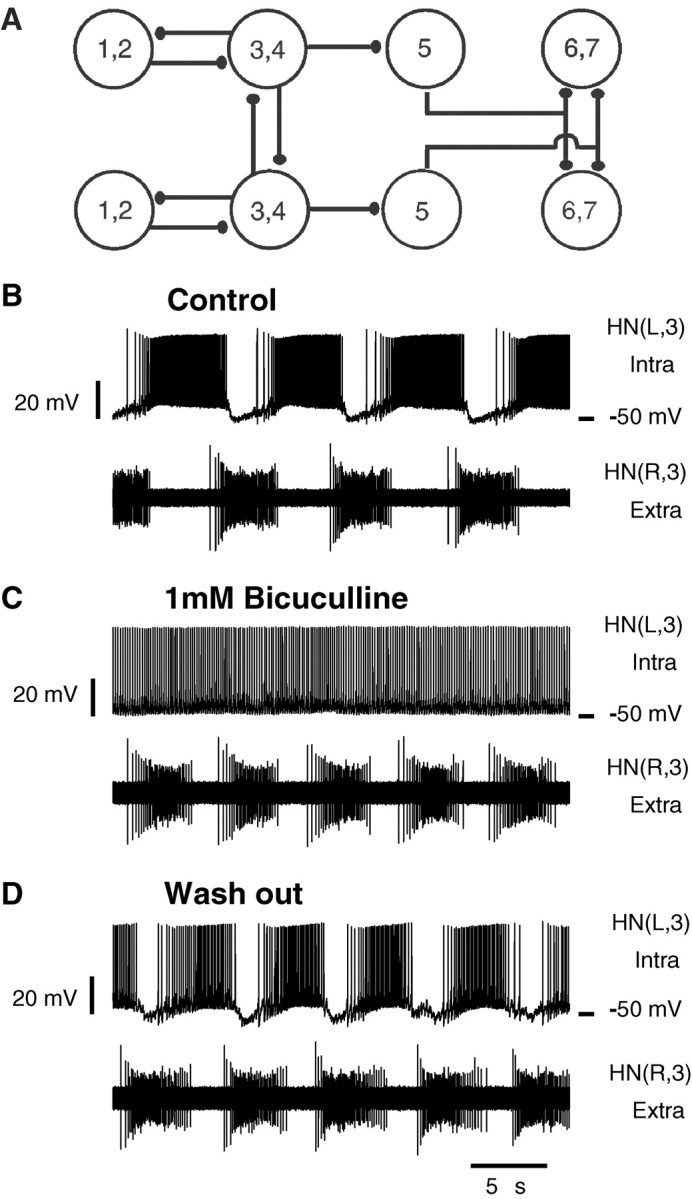
A, Connectivity diagram of the heartbeat neuronal network. Large open circles represent neurons. The neurons playing similar functional roles in the heartbeat network and with similar input and output connections are lumped together. Numbers identify ganglia where somata are located. Small filled ellipses represent inhibitory chemical synapses. Two pairs of reciprocally inhibitory heart interneurons located in ganglia 3 and 4 form half-center oscillators. These oscillators are coupled by coordinating interneurons whose somata are located in ganglia 1 and 2. Other premotor interneurons located in ganglia 6 and 7, along with the oscillator interneurons, inhibit heart motor neurons. Switch interneurons located in ganglion 5 interface between oscillator interneurons and premotor interneurons to produce two alternating coordination states, peristaltic and synchronous, of the motor neurons. B-D, Pharmacologically isolated oscillator heart interneurons fire tonically when recorded with sharp microelectrodes but burst rhythmically when recorded extracellularly. The left oscillator interneuron from a mutually inhibitory pair is recorded intracellularly, and the right one is recorded extracellularly. B, Under control conditions, the two neurons produce rhythmic alternating bursts. C, Addition of bicuculline results in tonic spiking in the intracellularly recorded cell and continued bursting in the other. D, The effects of bicuculline were reversible with washout. In this and all subsequent figures, voltage traces recorded from heart interneurons are labeledHN and indexed by body side (R, L) and ganglion number.

In contrast to intracellular recordings, extracellular recordings from pharmacologically isolated oscillator heart interneurons reveal endogenous bursting

Previous results, using sharp microelectrode recordings, have shown that when mutually inhibitory oscillator heart interneurons are pharmacologically isolated with bicuculline, they spike tonically (Schmidt and Calabrese, 1992). When one oscillator heart interneuron from a mutually inhibitory pair is recorded intracellularly, and the other is recorded extracellularly, they display normal alternate bursting (Fig. 1B). Addition of bicuculline results in tonic spiking in the intracellularly recorded cell and bursting in the extracellularly recorded one (Fig. 1C). The intracellular recording indicates that inhibitory synapses among heart interneurons were indeed blocked in these experiments. The effects of bicuculline were reversible with the short applications (<5 min) used in these experiments (n = 2); inhibitory synaptic potentials are again observed in the intracellular recording, and the two cells resume alternating bursting (Fig. 1D). These results suggest that an additional nonspecific leak current introduced by microelectrode penetration alters the inherent activity of pharmacologically isolated oscillator interneurons preventing them from bursting.

When pharmacologically isolated, oscillator heart interneurons burst independently

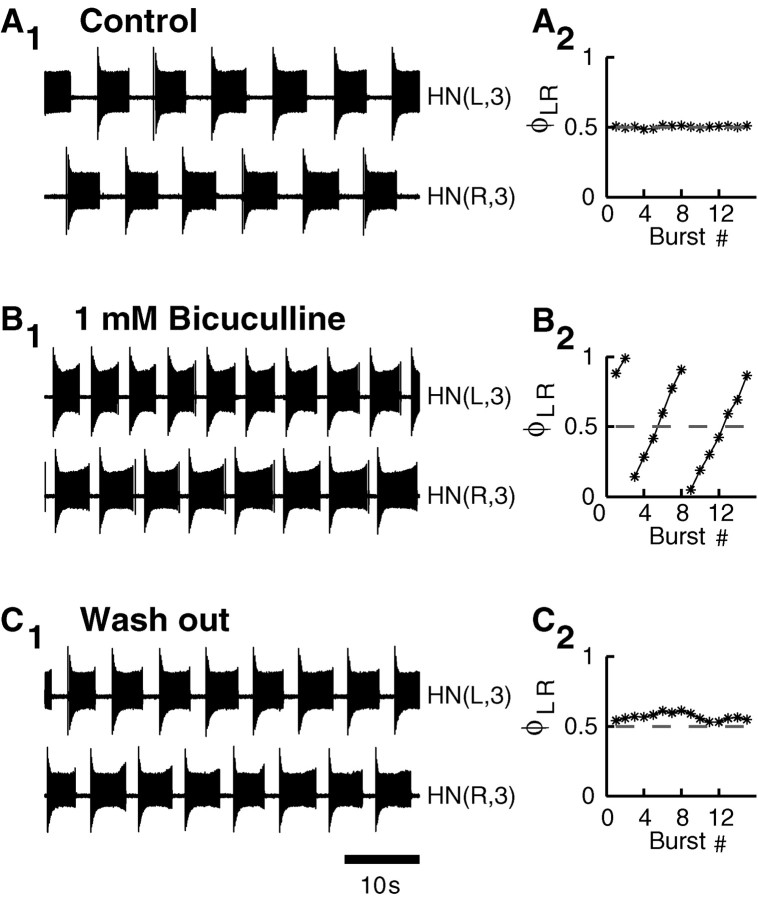
Simultaneous extracellular recordings from both interneurons forming a half-center oscillator in either ganglion 3 or 4 show that these neurons can burst independently when isolated (n= 5 for each of ganglia 3 and 4) (Fig.2). In normal saline, simultaneous extracellular recordings from the two oscillator interneurons show alternating bursting. With the addition of bicuculline methiodide (1 mm), the oscillator interneurons showed bursting that was regular in most preparations (7 of 10). The burst periods of the two isolated oscillator heart interneurons could be slightly different (Fig. 2B), leading to the bursting activity in the two neurons drifting against each other, which indicates that the inhibition between the two neurons is indeed blocked and that the bursting is independent. If bicuculline exposure is limited to <10 min, rhythmic alternating bursting resumes after washout with normal saline (Fig. 2C). In some preparations (3 of 10), we observed less robust activity in which bursting was interspersed with bouts of tonic spiking (Fig. 3). In these preparations, we observed that when one neuron is spiking tonically, its partner may show bursting activity.

Fig. 2.

Oscillator heart interneurons recorded extracellularly burst independently when pharmacologically isolated with bicuculline. A₁, Oscillator interneurons burst rhythmically in alternation in normal saline.A₂, Instantaneous phase between the activity of the neurons plotted against burst number stays close to 0.5.B₁, The oscillator interneurons burst independently in bicuculline methiodide (1 mm).B₂, The instantaneous phase drifts gradually from 0 to 1, demonstrating independent bursting with different cycle periods. C₁, The oscillator interneurons burst in alternation after washout with normal saline.C₂, The instantaneous phase stays near 0.5, although with larger deviations. The instantaneous phase was defined as the delay of the HN(R,3) burst median spike relative to the HN(L,3) burst median spike divided by the currentHN(L,3) cycle period.

Fig. 3.

In some preparations, pharmacologically isolated oscillator interneurons show bursting interspersed with bouts of tonic spiking. A, Normal pattern of alternating bursting in saline. B, In a solution containing bicuculline methiodide (1 mm), bursting is sporadic. Trains of bursts are interrupted by long intervals of tonic spiking. One heart interneuron can be bursting while the other is spiking tonically.C, The normal alternating bursting pattern was restored after washout with normal saline (exposure to bicuculline <10 min).

In bicuculline, bursting activity of premotor heart interneurons in ganglia 6 and 7 is similar to activity of oscillator heart interneurons

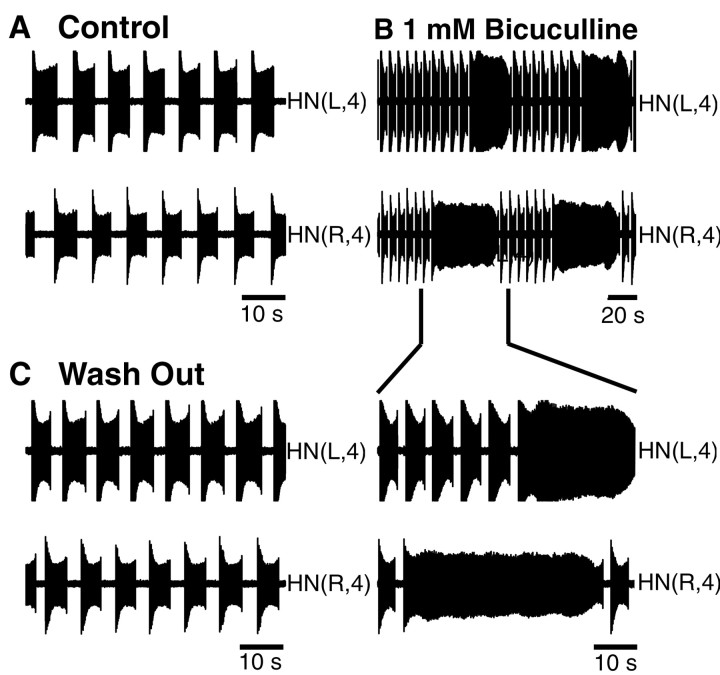
The premotor heart interneurons in ganglia 6 and 7 receive all their inhibitory input from the switch heart interneurons of ganglion 5 (Fig. 1A). Unlike the oscillator interneurons, they do not form mutually inhibitory synapses. When recorded extracellularly (n = 5 for each of ganglia 6 and 7, both heart interneurons recorded in each ganglion) in isolated ganglia, these heart interneurons show rhythmic bursting activity, which can be either independent or in apparent synchrony (data not shown). This bursting can be interrupted by bouts of tonic spiking. When recorded extracellularly and pharmacologically isolated with bicuculline (1 mm), they continue rhythmic bursting, but in most preparations (9 of 10 preparations), the cells start showing long passages of tonic spiking similar to those presented in Figure 3 for the oscillator heart interneurons.

Seizure-like synchronous bursting

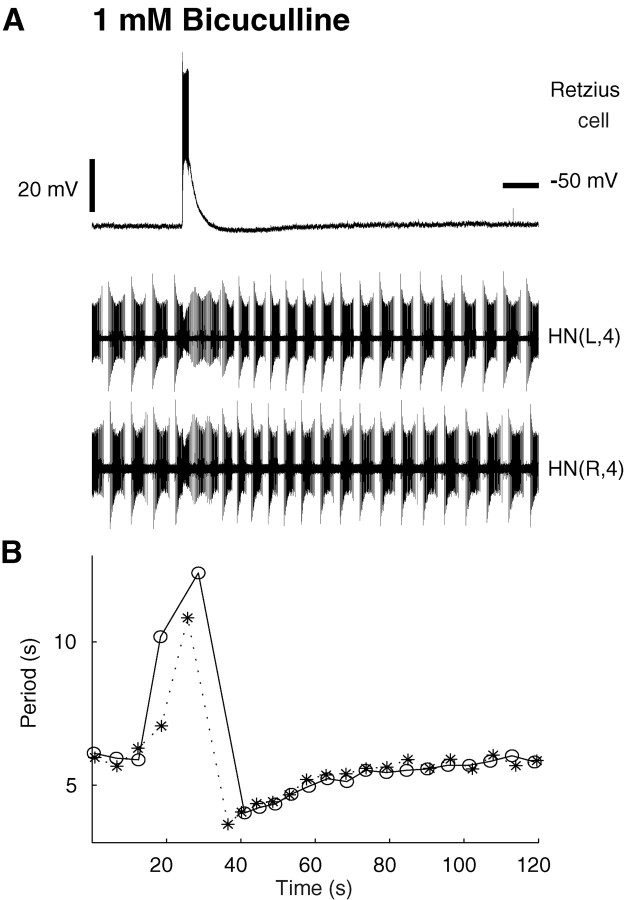
In some preparations (3 of 10 preparations), “seizure-like” synchronous bursting occurred sporadically in pairs of oscillator interneurons recorded extracellularly in bicuculline (1 mm) (Fig. 4A). Simultaneous intracellular recordings from other neurons, e.g., Retzius (Fig.4A) or Leydig (data not shown) neurons, suggest that all cells in a ganglion discharge synchronously during this seizure-like activity. In heart interneurons, these seizures take the form of an extension of ongoing bursts coincident with the seizure discharge so that two or three bursts occur without intervening silent periods. After a “seizure,” both heart interneurons sped up their bursting and then monotonically recovered to a baseline period (Fig.4B). Thus these seizures interrupted regular bursting activity in the oscillator interneurons. Similar seizure-like bursts were observed in heart interneurons from ganglia 6 and 7 (1 of 10 preparations). The seizure-like bursts were qualitatively different from the bouts of tonic spiking observed in heart interneurons in bicuculline in that the seizure bursts were synchronous, perhaps involving the whole ganglion, and were always followed by a transient decrease in the burst period, whereas bouts of tonic spiking were often independent and were not followed by a change in the burst period. The seizure-like bursts occur with very long intervals (hundreds of seconds), and although they reset and modify heart interneuron bursting activity, they do not appear to account for it directly. These seizures may depend on general electrical coupling, whose effects could be potentially enhanced by blockade of inhibitory synapses. Similar synchronized bursts have been observed in all neurons when the nerve cord is exposed to inorganic Ca²⁺ channels blockers such as Co²⁺ and Mn²⁺ (Angstadt and Friesen, 1991).

Fig. 4.

Seizure-like synchronous bursting observed in oscillator interneurons and other neurons in bicuculline (1 mm). A, Electrical activity of a Retzius cell (top trace) and left and right oscillator interneurons from ganglion 4 (bottom 2 traces) showing a synchronous burst two to three times longer than the asynchronous bursts in the oscillator interneurons. The Retzius cell was recorded with a sharp microelectrode. In bicuculline, the Retzius cell was silent most of time. A strong depolarization underlies the seizure-like burst. B, Graph of the cycle period plotted against time for the heart interneurons HN(L,4) and HN(R,4) (open circles, asterisks, respectively) shows that the burst period shortens right after the synchronous burst occurred and returns to baseline after ∼25 sec. The cycle period was defined as the interval between the median spikes of two consecutive bursts.

Activity of coordinating heart interneurons from ganglia 1 and 2 in bicuculline

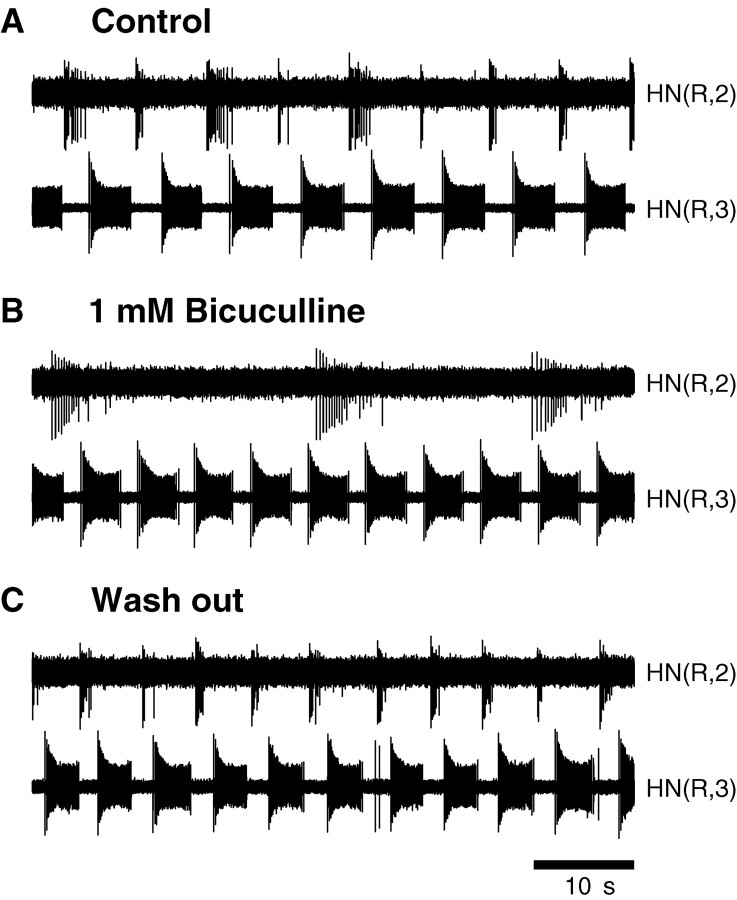
Because axons of coordinating interneurons from ganglia 1 and 2 initiate spikes and make mutual inhibitory synaptic connections with ipsilateral oscillator interneurons in ganglia 3 and 4 (Fig.1A), it is conceivable that despite blockade of the synapses between oscillator interneurons by bicuculline, the synapses between oscillator and coordinating interneurons persist in bicuculline, leading to the observed bursting activity. To eliminate this possibility, we performed experiments in which ipsilateral heart interneurons from ganglia 1, 2, or both and 3 or 4 were simultaneously recorded, and bicuculline was applied in preparations consisting of the head brain through ganglion 4. Coordinating interneurons recorded extracellularly in normal saline generate bursting activity, alternating with ipsilateral oscillator interneuron activity and having a duty cycle and spike frequency smaller than those of the oscillator interneurons (Masino and Calabrese, 2002) (Fig.5A). In initial experiments, bicuculline was applied for 5 min (n = 7). In these preparations, the oscillator interneurons continued to burst during the bicuculline application (1 mm) but the coordinating interneurons were silent; these effects were reversible with washing in normal saline (data not shown). In two experiments, bicuculline application was continued for 15 min. In one of them, we simultaneously recorded from ipsilateral coordinating interneurons in ganglia 1 and 2 and an oscillator heart interneuron in ganglion 3. The coordinating interneurons fired sporadically or underwent bouts of independent bursting with a prolonged period and few (3–20) spikes compared with oscillator interneurons in the same preparation. In the other experiment, in which an ipsilateral coordinating interneuron from ganglion 2 and an oscillator heart interneuron from ganglion 3 were recorded, the coordinating interneuron produced bursts with a period approximately three times slower than the oscillator heart interneuron burst period (Fig. 5A,B). Again the effects of bicuculline were reversible (Fig. 5C). These results support the interpretation that the bursting of oscillator interneurons observed in bicuculline is endogenous.

Fig. 5.

Paired extracellular recordings of a coordinating interneuron (ganglion 2) and an ipsilateral oscillator interneuron (ganglion 3). A, In normal saline (Control), the coordinating interneuron and the oscillator interneuron produced alternating bursts. B, In bicuculline (1 mm, after 8 min of exposure), both interneurons burst independently. C, On washout with normal saline, normal alternating bursting returned.

Characterization of bursting activity in heart interneurons in bicuculline

We quantified bursting activity in oscillator interneurons and in premotor interneurons from ganglia 6 and 7 by measuring burst period, duty cycle, average spike frequency within a burst (spike frequency), and number of spikes per bursts. For this analysis, data were taken only during episodes of regular bursting. In preparations showing bouts of tonic spiking, we did not use stretches of the record containing such bouts, and in preparations showing seizures, after each seizure we waited an interval sufficient for recovery to the baseline period (normally ∼10 bursts). Only burst trains containing at least 20 bursts and having a coefficient of variation of period <20% were considered. We analyzed the bursting characteristics of the heart interneurons in all preparations (n = 5 for each ganglion) and eliminated those that did not meet these criteria. One preparation of ganglion 3, one of ganglion 6, and two of ganglion 7 had no trains of bursts with a sufficiently small coefficient of variation of the period. One preparation of ganglion 4 did not produce sufficiently long burst trains.

The oscillator interneurons (ganglia 3 and 4) form half-center oscillators with their contralateral homologues, but the premotor interneurons (ganglia 6 and 7) do not (Fig. 1A). On the basis of their similarity in connectivity and apparent similarity in intrinsic properties, data obtained from oscillator interneurons and from premotor interneurons were pooled to obtain sufficient sample numbers for statistical comparison of these two groups. These data are summarized in Table 1. Two-way ANOVA was performed on the two neuron groups (oscillator interneurons and premotor interneurons) under the three treatment conditions (control, bicuculline, and washout). Then post hoc pair-wise multiple comparisons were made with a t test using Bonferroni α-level compensation to determine differences. Significant differences, which were found, are described below.

Table 1.

Characteristics of bursting activity recorded extracellularly from heart interneurons in ganglia 3, 4, 6, and 7

Ganglia and neuron group	Treatment condition	Period (sec)	Duty cycle (%)	Spike frequency (Hz)	Spikes/burst (n)	Burst duration (sec)
3 and 4, oscillator interneurons	Control	8.8  ± 2.0	56.5  ± 4.8	13.2  ± 2.7	64  ± 12	4.9  ± 1.0
		(6.4–12.7)	(50.3–66.8)	(10.2–20.0)	(49–91)	(3.6–7.0)
	Bicuculline	6.5  ± 1.0	69.9  ± 2.7	9.3  ± 2.2	42  ± 10	4.5  ± 0.8
		(4.8–8.6)	(65.8–75.5)	(6.6–14.7)	(29–67)	(3.2–6.0)
	Washout	7.1  ± 1.9	63.9  ± 3.2	11.6  ± 3.1	51  ± 13	4.5  ± 1.1
		(4.8–11.0)	(57.5–70.8)	(7.5–18.9)	(31–81)	(3.1–6.9)
6 and 7, premotor interneurons	Control	6.8  ± 1.1	60.9  ± 3.2	11.4  ± 2.2	48  ± 10	4.1  ± 0.7
		(5.2–8.4)	(56.9–68.5)	(8.2–15.9)	(31–68)	(3.1–5.4)
	Bicuculline	6.6  ± 0.8	64.3  ± 2.5	11.1  ± 2.3	48  ± 13	4.2  ± 0.5
		(5.3–7.9)	(59.3–68.2)	(8.4–15.9)	(33–73)	(3.5–5.1)
	Washout	6.4  ± 0.8	63.4  ± 2.5	11.0  ± 2.1	45  ± 8	4.1  ± 0.5
		(4.9–7.9)	(59.8–68.1)	(9.0–16.9)	(35–70)	(3.3–5.0)

Data from ganglia were pooled according to the functional role of the neuron in the network, i.e., oscillator versus premotor interneurons. In a data cell, a mean value ± SD (above) and observed minimal and maximal values (below in parentheses) are presented.

Under control conditions, the two neuron groups differed in period, duty cycle, and spike number per burst (p < 0.05 in each case), possibly reflecting their different connectivity. Bicuculline application produced significant changes in period, duty cycle, spike frequency, and spike number per burst in oscillator heart interneurons (p < 0.05 in each case). In bicuculline, period, spike frequency, and spike number per burst were smaller by ∼25, 30, and 35%, respectively, whereas duty cycle was longer by ∼25% (p < 0.05). In contrast, bicuculline did not produce changes in period, spike frequency, and spike number per burst (p > 0.05 in each case) in premotor interneurons, although duty cycle did lengthen by ∼6% (p < 0.05). In bicuculline, the spike frequency and duty cycle of oscillator interneurons are different from those of premotor interneurons (p < 0.05 in each case). In general, most effects of bicuculline were only partially reversible on washout. The alternation between the bursting activities of the two oscillator heart interneurons was always restored (exposure limited to 10–15 min).

Bursting activity in an oscillator heart interneuron model is sensitive to leak current variation

The results shown in Figure 2 suggest that oscillator interneurons are sensitive to a leak current introduced by sharp microelectrode penetration. We tested this hypothesis with a single-compartment model of an oscillator interneuron. Ionic currents of the oscillator interneurons were determined in voltage-clamp studies, and the kinetic data were incorporated into a thoroughly tested conductance-based model (Nadim et al., 1995; Olsen et al., 1995; Hill et al., 2001). The single-oscillator interneuron model includes nine voltage-dependent currents: a fast Na⁺ current (I_Na), a persistent Na⁺ current (I_P), two low-threshold Ca²⁺ currents, one rapidly (I_CaF) and one slowly (I_CaS) inactivating, a hyperpolarization-activated cation current (I_h), a delayed rectifier-like K⁺ current (I_K1), a persistent K⁺ current (I_K2), a fast transient K⁺ current (I_KA), and FMRFamide (Phe-Met-Arg-Phe-NH₂)-activated K⁺ current (I_KF). This model displays rhythmic bursting for certain values of the leak current parameters (Olsen et al., 1995).

The leak current produced by microelectrode penetration is assumed to be nonselective. Thus penetration modifies original values ofE ${}_{\text{leak}}^{\text{o}}$ and g ${}_{\text{leak}}^{\text{o}}$to the measured values E_leak andg_leak by the addition of a nonspecific leak current component described by E ${}_{\text{leak}}^{\text{el}}$and g ${}_{\text{leak}}^{\text{el}}$:

$$E_{\text{leak}}^{\text{el}}=0\hspace{1em}\text{mV}$$

$$E_{\text{leak}}=\frac{E_{\text{leak}}^{\text{o}} g_{\text{leak}}^{\text{o}}}{g_{\text{leak}}^{\text{o}}+g_{\text{leak}}^{\text{el}}}$$

$$g_{\text{leak}}=g_{\text{leak}}^{\text{o}}+g_{\text{leak}}^{\text{el}}.$$ Equation 2

Thus variation of the parameters,E_leak andg_leak in the model can simulate the additional component of leak current introduced by the intracellular microelectrode. Here we study how changes in the leak current parameters, E_leak, andg_leak, affect activity of a single oscillator interneuron.

To study the effects of this microelectrode-induced change in leak current parameters on model activity, we constructed a two-parameter bifurcation diagram (E_leak vsg_leak) of model activities (Fig.6A). Curves indicating the borders between major dynamic regimes of the model, tonic spiking (pink area), bursting (white area), and silence (yellow area, steady state) are plotted. Figure 6A shows a narrow stripe of parameter values in which bursting occurs (white area) that separates large zones of tonic spiking activity and silence. Plotted points (Fig.6A) correspond to the different examples of the activity of the model illustrated in Figure7A–E. The model oscillator interneuron spikes tonically for parameters covering a relatively large area with relatively depolarized values ofE_leak and small values ofg_leak (Figs. 6A,plus sign, 7A). The transition from tonic spiking to bursting starts at the border marked by the red curve, where a period-doubling bifurcation occurs (Ermentrout, 1984). At theseE_leak andg_leak values, spikes in the model occur with two different alternating intervals (Figs. 6A, open circle, 7B), which can be considered bursting. AsE_leak andg_leak are varied to move farther into the white area in the close vicinity of this border (Fig. 7,filled circle, compare parameter values in B, C), bursting occurs with a larger hyperpolarized membrane potential excursion, longer burst period and duration, and a larger number of spikes per burst (Figs. 6A, filled circle,7C). Qualitatively, these properties of bursting are preserved down to the border between bursting and silence (Figs.6A, open diamond, 7D).

Fig. 6.

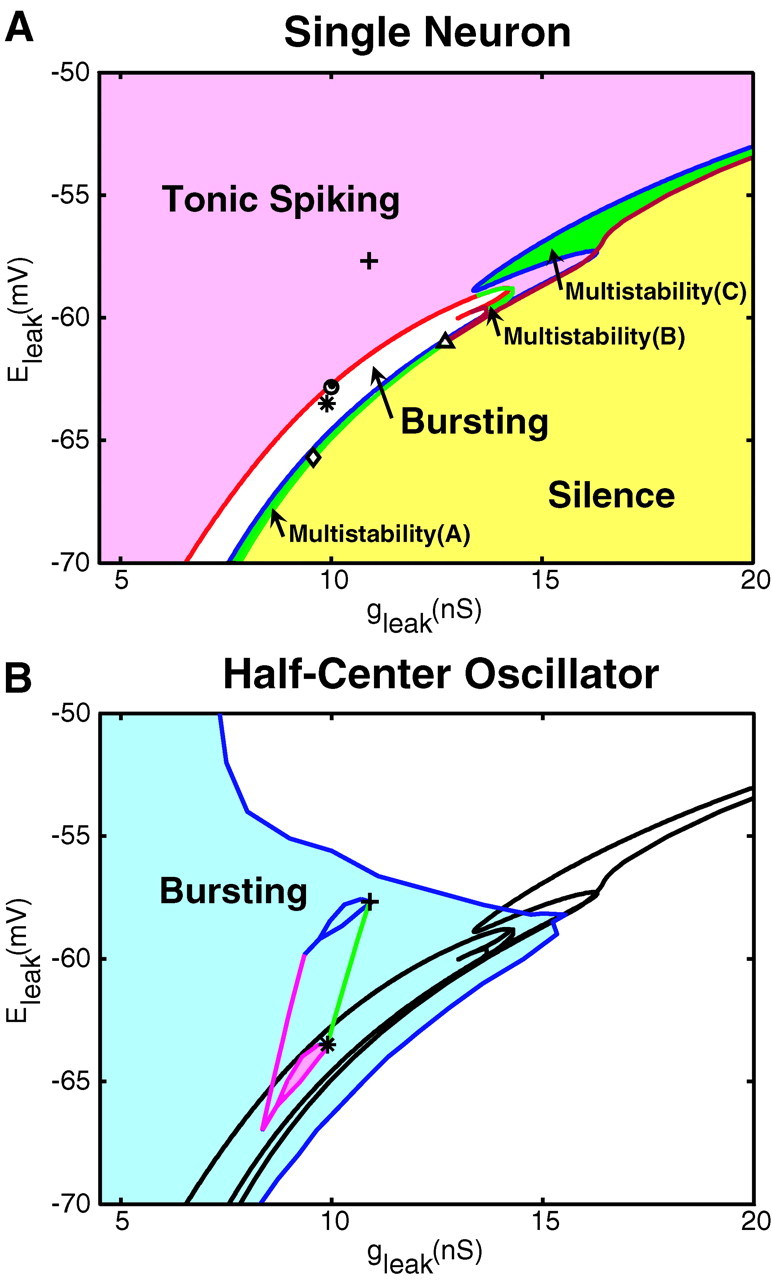
Bifurcation diagram of the single-cell oscillator interneuron model activities (A) and bifurcation diagram of the bursting activity in a half-center oscillator model (B). A, Pink, white, and yellow areas mark the parameter regimes in which tonic spiking, bursting, and silence are stable, respectively. Green areas mark parameter regimes of multistability in which more than one activity is stable.Multistability(A) points to the area where bursting coexists with silence; multistability(B) points to the area where bursting coexists with tonic spiking;multistability(C) points to the area where tonic spiking coexists with silence. The asterisk corresponds to theg_leak and E_leakparameter values (g ${}_{\text{leak}}^{\text{el}}$ = 0) used in the models illustrated in Figure 9. Plus sign, open circle, filled circle, asterisk, and open diamond correspond to the g_leak andE_leak parameter values for oscillator interneuron model activity illustrated in Figure 7 and fall along a line generated when the introducedg ${}_{\text{leak}}^{\text{el}}$ changes from −0.35 to 1 nS about model parameters of E ${}_{\text{leak}}^{\text{o}}$ andg ${}_{\text{leak}}^{\text{o}}$ (asterisk) as used in Figure 9, A and B. Open triangles mark the parameter values corresponding to Figure7E1–E3. B, The blue areacorresponds to the parameter region where stationary bursting activity was observed, and the white area corresponds to the region where stationary bursting was not observed. The borders separating the major activity regimes of the single-cell model taken from A are plotted for comparison. The pink patch delimits the single-cell model parameter values that produced bursting characteristics within the ranges measured experimentally. The green line was generated by varyingg ${}_{\text{leak}}^{\text{el}}$ from 0 to 1 nS about model parameters of E ${}_{\text{leak}}^{\text{o}}$ andg ${}_{\text{leak}}^{\text{o}}$ (asterisk). The marked points in A (except foropen triangles) fall along this line. The pink line was generated similarly by varyingg ${}_{\text{leak}}^{\text{el}}$ from 0 to 1 nS starting withE ${}_{\text{leak}}^{\text{o}}$ andg ${}_{\text{leak}}^{\text{o}}$ at the lowest point of the experimentally constrained patch. A family of such lines originating in the pink patch defines by their end points the upper delimited area.

Fig. 7.

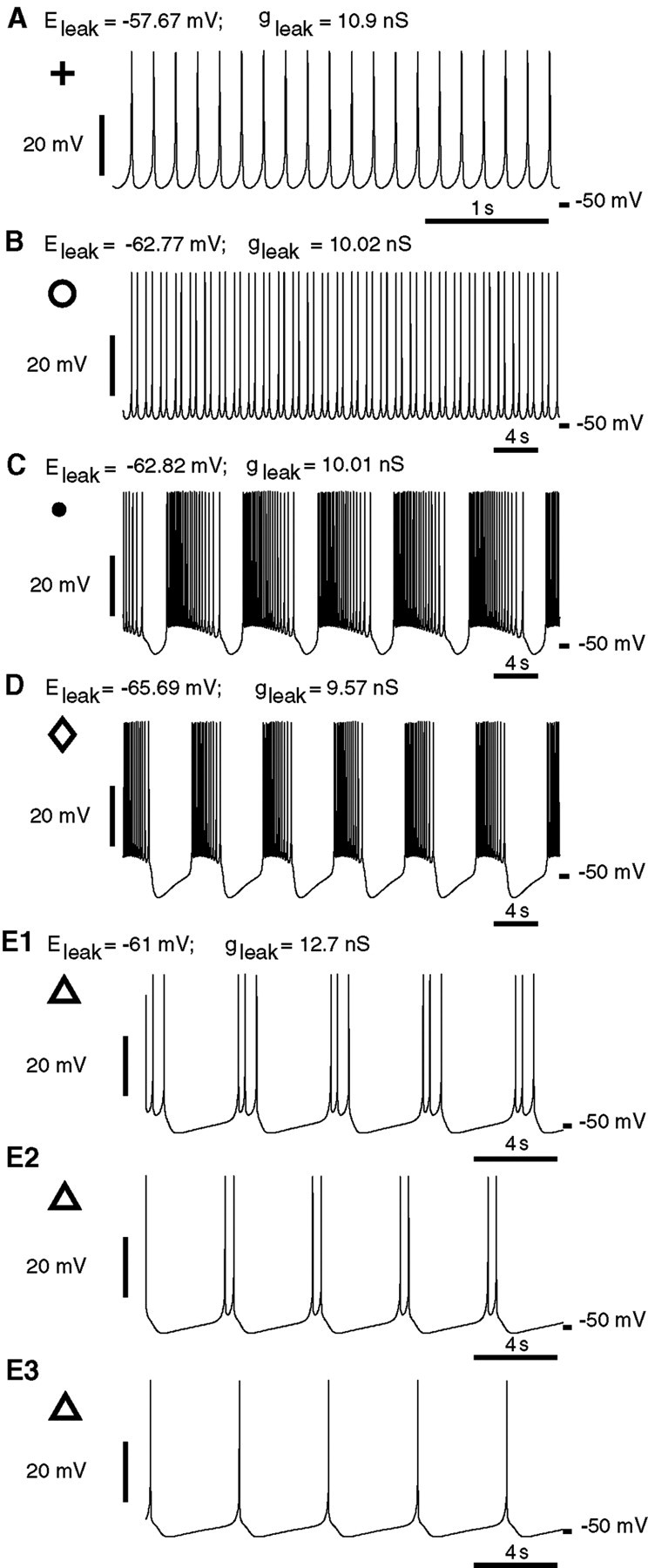
Characteristic activities of the single-oscillator interneuron model. A, Tonic spiking (Fig.6A, plus sign). B, Two-spike bursting (Fig. 6A, open circle). C, Multispike bursting near the border of bursting and tonic spiking (Fig.6A, filled circle). D, Multispike bursting near the border of bursting and silence (Fig.6A, open diamond). E, Three coexisting oscillatory activities of the single oscillator interneuron model at a point (g_leak = 12.703 nS; E_leak = −61 mV) that is marked in Figure 6A by open triangles.E1, Bursting with three spikes. E2, Bursting with two spikes. E3, Tonic spiking. Initial conditions leading to each of these states are as follows:E1, V = −2.1 mV;m_CaF = 0.9940;h_CaF = 0.0123;m_CaS = 0.7722; h_CaS = 0.1255;m_K1 = 0.7880;h_K1 = 0.8775;m_K2 = 0.1947;m_KA = 0.8911;h_KA = 0.0211;m_h = 0.3611;m_P = 0.7529;m_Na = 0.9834;h_Na = 0.2891; E2, V = −7.0 mV; m_CaF = 0.9940;h_CaF = 0.0090;m_CaS = 0.8325;h_CaS = 0.1023;m_K1 = 0.2914;h_K1 = 0.8527;m_K2 = 0.1683;m_KA = 0.8098;h_KA = 0.0216;m_h = 0.3201;m_P = 0.6739;m_Na = 0.9589;h_Na = 0.6024; E3, V = −46.0 mV; m_CaF = 0.5485;h_CaF = 0.0456;m_CaS = 0.5403;h_CaS = 0.1080;m_K1 = 0.0267;h_K1 = 0.9009;m_K2 = 0.0976;m_KA = 0.4296;h_KA = 0.0654;m_h = 0.3667;m_P = 0.2979;m_Na = 0.0726;h_Na = 0.9997.

The area of bursting activity also includes areas of multistability, where different oscillatory regimes and a stable stationary point can coexist with each other. Multistability zones marked in Figure6A (A–C) are areas where the major activities coexist. In area A, bursting activity coexists with silence; in area B, bursting activity coexists with tonic spiking activity; and in area C, tonic spiking activity coexists with silence. A complex example of multistability can be found at the point [g_leak = 12.703 nS; E_leak = −61 mV (Fig.6A, Multistability(B), open triangle)] where three-spike bursting, two-spike bursting, tonic spiking (Fig.7E1–E3), or silence (data not shown) can occur depending on initial conditions. The bifurcation diagram supports the hypothesis that a microelectrode-introduced leak current suppresses bursting because a variation of E_leak org_leak by as little as 2 mV or 1 nS, respectively, can turn a silent model oscillator interneuron into a tonically spiking one, stepping over the area of parameter values where bursting activity manifests itself.

The sensitivity of model endogenous bursting to leak current variation can be reduced

In the single-cell model, there are several parameter variations that can considerably expand the region ofE_leak andg_leak supporting bursting, thus reducing its sensitivity to leak current parameters. Varying maximal conductances of different currents can shift and expand or shrink the region of bursting. Increasing the maximal conductance of inward currents shifts the region of bursting toward largerg_leak and more hyperpolarizedE_leak. For example, forE_leak = −63.5 mV, our canonical model demonstrates bursting activity forg_leak from 9.3 to 10.5 nS. Increasing the maximal conductance of I_hpreserves the peninsula-like form of the area of bursting and expands and shifts it toward larger g_leak and more hyperpolarized E_leak. An increase of $\overline{g}$_h by a factor of 2 ($\overline{g}$_h= 8 nS vs canonical value $\overline{g}$_h = 4 nS) enables the model to support bursting activity forg_leak from 9.5 to 11.8 nS, thus enlarging the range appropriate for bursting activity approximately by a factor of 2. Increasing the maximal conductance of outward currents shifts the region toward smaller g_leakand more depolarized E_leak. As an example of influence of an outward current, we increased the maximal conductance of a FMRFamide-activated potassiumI_KF described by Nadim and Calabrese (1997), which is thought to be responsible for the acceleratory action of this endogenous peptide. In our canonical model,$\overline{g}$_KF = 0. The model with$\overline{g}$_KF = 20 nS demonstrates bursting for g_leak from 7 to 9.42 nS, whereas with $\overline{g}$_KF = 40 nS, it can burst with g_leak from 4.5 to 8.17 nS, thus expanding the bursting range by factors of 2 and 3, respectively. This study indicates that the modulatory action of FMRFamide not only speeds the rhythm, for example, but reduces the sensitivity of endogenous bursting activity to the leak current parameter variation. This hypothesis gains additional plausibility in light of experimental data demonstrating that applied FMRFamide decreases the size of spike-mediated IPSCs between oscillator interneurons (Simon et al., 1994). Reduced mutual inhibition may require more robust endogenous bursting.

The most dramatic expansion of the region of bursting is observed when the half-activation potential of I_CaSis shifted in the negative direction. A shift from V_½mCaS = −47.2 mV (canonical) to V_½mCaS = −53 mV expands the range of bursting activity so that bursting is observed in the range ofg_leak from 10.5 to 18.3 nS. Thus, the model of an oscillator heart interneuron indicates possible mechanisms by which the living neurons could reduce their sensitivity to leak current parameter variation.

Comparison of bursting characteristics in model and experiment

To compare the model and experimental results, the same burst characteristics were measured for model activity as in our experiments. The model shows a variety of bursting activities depending on the values of g_leak andE_leak. Burst period, duty cycle, and spike frequency within a burst versus (g_leak,E_leak) are shown in Figure8A–C, respectively. The burst period (Fig. 8A) and number of spikes per burst (data not shown) grow monotonically asE_leak is hyperpolarized org_leak is decreased; the duty cycle (Fig. 8B) and spike frequency (Fig. 8C) show a more complicated dependence. The minimum and maximum values of corresponding characteristics measured for oscillator heart interneurons recorded extracellularly in bicuculline are marked by pairs of green lines on the axes, except for spike frequency, for which only the lower boundary is marked (Table 1; boundaries were slightly expanded by rounding down the lower boundary and rounding up the upper boundary to the nearest integer). Projection of the surfaces of characteristic values on the plane (g_leak,E_leak) describes the stripe of parameters corresponding to the white area on the bifurcation diagram (Fig. 6A) where bursting occurs. It includes the green area that defines the model values conforming to the experimentally measured boundaries (Fig. 8). Comparison of the plots (Fig. 8) shows that the sets of parameter values (g_leak,E_leak) conforming to each of the experimentally determined bursting characteristic are not identical. Nevertheless, there exists a subset of parameters (g_leak,E_leak) conforming to all the constraints (experimentally constrained patch shown in Fig.6B, pink). Although the model can demonstrate bursting inside the experimentally imposed regimes, it will require additional parameter changes to match average values of the experimentally derived burst characteristics.

Fig. 8.

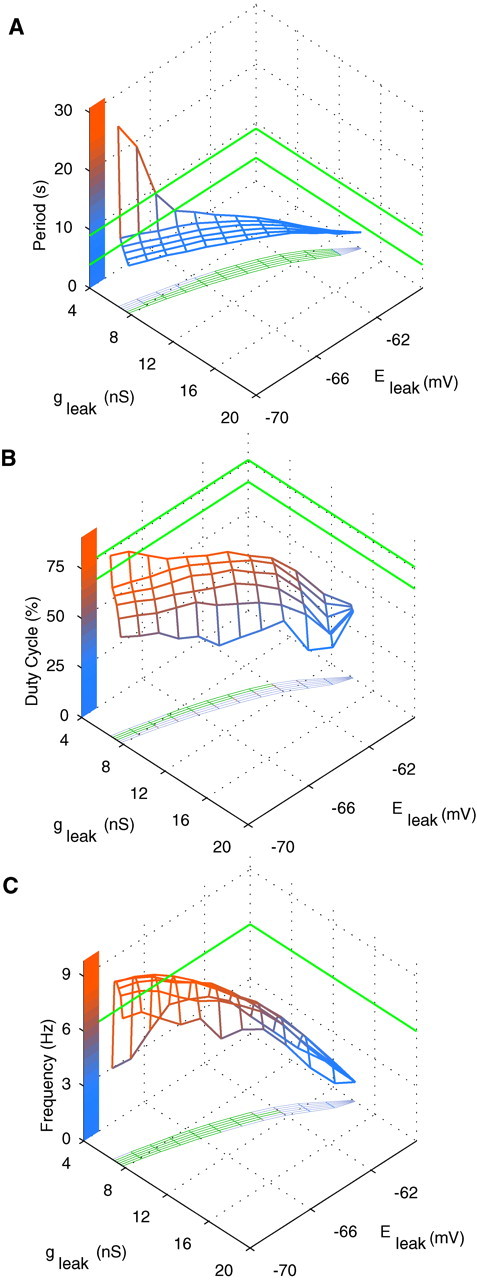
Major bursting characteristics for the single-oscillator interneuron model: the burst period (A), duty cycle (B), and spike frequency (C) observed in the model when the values of (g_leak,E_leak) are varied. The minimal and maximal values experimentally measured for oscillator interneurons are marked by the pairs of green lines on the axes, except for the spike frequency (C), for which the maximum value (upper boundary) was never exceeded by the model; thus only the lower boundary was marked. Projection of the surfaces of characteristics values on the plane (g_leak,E_leak) describes the area where bursting occurs. It includes the green area that defines the model values conforming to the experimentally measured boundaries.

According to Equations 2, microelectrode penetration projects the experimentally constrained patch on the bifurcation diagram (Fig.6B) toward a more depolarized leak reversal potential (E_leak) and larger leak conductance (g_leak), making the model heart interneuron tonically spiking instead of bursting. Projecting a 1 nS addition of g ${}_{\text{leak}}^{\text{el}}$ generates an upper patch, which corresponds to experimentally constrained model neurons penetrated with a sharp microelectrode that adds 1 nS of leak conductance.

Bursting in a half-center oscillator

A mathematical model of two mutually inhibitory oscillator interneurons (a half-center oscillator) has been developed (Nadim et al., 1995; Olsen et al., 1995; Hill et al., 2001). In this paper, we constructed a model half-center oscillator from two oscillator interneurons to determine the borders within which stationary bursting activity occurs in a half-center oscillator (Fig. 6B, blue area). We used a synaptic transfer function (see Materials and Methods) that generated synaptic conductance waveforms corresponding to our previous model (Hill et al., 2001). The bursting region of the diagram is significantly enlarged, primarily because of extension of the upper border into the area of the tonic spiking.

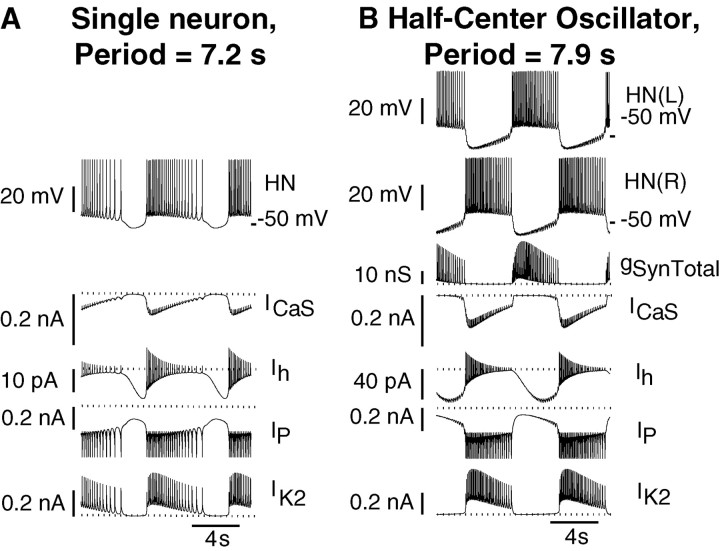
The point marked by an asterisk was chosen for analysis from the experimentally constrained pink patch so that the difference in the burst duration of the single-cell model and the half-center model would be similar to that observed experimentally for oscillator interneurons (Table 1). The periods of the two models are comparable, but that of the half-center model is slightly longer (by 0.7 sec). Such a period difference was also observed experimentally for oscillator heart interneurons, although the corresponding average period difference is larger (by 2.3 sec). This parameter point is also illustrated in Figure6A, asterisk, and falls along the projection line defined by the parameter variations of Figure7A–D. With these g_leak andE_leak parameters, the half-center oscillator model behaves qualitatively very similar to the corresponding model tuned to the intracellularly recordedg_leak andE_leak parameters (Hill et al., 2001). We compared bursting in the single-cell and half-center oscillator models using these experimentally constrainedg_leak andE_leak parameters (Fig.9). In both models, burst duration is determined by endogenous dynamics, namely, the inactivation time constant of I_CaS (Fig.9A,B). Varying this time constant causes significant changes in burst duration (data not shown). In the single-cell model, the interburst interval is controlled by the activation time constant ofI_h (Fig. 9A). Varying this time constant causes significant changes in the duration of the interburst interval (data not shown). In the half-center oscillator model, the burst duration of the opposite cell (hence the time constant of inactivation ofI_CaS) is the major determinant of interburst interval (through synaptic inhibition), and the duty cycle is constrained to ∼50% (for balanced model neurons and synapses) (Fig. 9B). The strength of the spike-mediated synapses exerts a powerful effect on period in the half-center model tuned with leak current parameters so that the single cells are tonically active (Hill et al., 2001); as synaptic strength is decreased, burst duration and interburst interval decrease in a linear manner, so that reduction of the synaptic strength by 50% causes an approximately threefold reduction in the burst period. When the single cells are tuned to be bursters, as here, the period of the half-center oscillator is less sensitive to the synaptic strength. Reducing total synaptic strength even by 87% reduces the period by only 22%. This period is actually 15% faster than the period of the single neuron, but further reductions of synaptic strength increase the period toward that of the single neuron. The duty cycle in the half-center oscillator model with the canonical parameter values was 48%, whereas in the single-cell model, the duty cycle was 66%. The duty cycle in the half-center oscillator model remains at ∼50% as synaptic strength is reduced, only increasing when the synaptic strength is <20% of the canonical value.

Fig. 9.

Voltage and current traces produced by the single-cell (A) and half-center oscillator (B) models. ParametersE_leak = −63.5 mV andg_leak = 9.9 nS (Fig.6A,B, asterisks) were chosen to comply with the experimental data, and all other parameters were canonical. Major inward and outward currents contributing to the slow wave of oscillation in each model are illustrated. Dotted linesmark 0 nA.

Comparison of bursting in the single-cell and half-center configurations

Bursting in the single-cell model appears to be dominated by two time constants. The slow inactivation of the low-threshold Ca²⁺ current,I_CaS, leads to burst termination, thus controlling the duration of the burst phase of the oscillation (Fig.9A). The slow activation of the hyperpolarization-activated inward current, I_h, leads to burst formation, thus controlling the duration of the hyperpolarized phase of the oscillation. Note that I_h is maximal just at the transition to the burst phase (Fig. 9A). Our previous analysis of the half-center model (Hill et al., 2001) demonstrated that bursting in the half-center model is controlled only by the slow inactivation of I_CaS. Because I_h activates more quickly thanI_CaS inactivates (the time constants differ by a factor of >2 in the voltage ranges of interest), the strong inhibition fully activated I_hbut it is insufficient to overcome the inhibition untilI_CaS inactivates sufficiently, reducing the spike frequency and associated inhibition. Thus the maximal conductance, but not the activation time constant, ofI_h controls the burst duration of the opposite cell by determining the level ofI_CaS at which an escape can be effected and the burst of the opposite cell can be terminated by inhibition. Note in Figure 9B thatI_h is maximal well before the transition to the burst phase. During endogenous bursting,I_h is activated and opposed solely by the leak current during the hyperpolarized phase.E_leak must, therefore, be relatively hyperpolarized to near the border where all activity is silenced to provide the hyperpolarization necessary both to activate and opposeI_h (Fig. 6A). In the half-center configuration, strong synaptic inhibition swamps these effects of the leak current during the inhibited phase; therefore,E_leak can be much more positive (Fig.6B).

The half-center oscillator model is considerably less sensitive to the variation of the maximal conductances of the voltage-gated currents as it is with leak current parameters. One maximal conductance was varied at a time, whereas all others were set to their canonical values. Table2 shows the range of maximal conductances of each current that supports bursting activity for both models. The single-neuron model is very sensitive to the variation ofg_leak and$\overline{g}$_p, each of which can only be varied in a range of ∼1 nS. The single-neuron model is a bit less sensitive to the variation of$\overline{g}$_CaS and$\overline{g}$_h; these conductances can be varied over a range of ∼5 and 8 nS, respectively. Other maximal conductances can be varied on the order of tens to hundreds of nanosiemens. In a half-center model, these ranges considerably expand, ranging from factor 1.7 for $\overline{g}$_CaS up to factor of 9.7 for $\overline{g}$_h.

Table 2.

Ranges of the values of the maximal conductances where the bursting state was observed

	Single neuron	Half-center oscillator
$\overline{g}$Na(nS)	63.5–793	72–2416.5
$\overline{g}$P (nS)	6.4–7.2	5.7–9.5
$\overline{g}$CaF (nS)	0–13.2	0–38.5
$\overline{g}$CaS (nS)	0.7–5.8	0.6–9.3
$\overline{g}$h (nS)	1.9–9.6	1.35–46
$\overline{g}$K1 (nS)	30–266	52–760
$\overline{g}$KA (nS)	58.5–135.5	0–185
$\overline{g}$K2 (nS)	64.5–138.8	41.5–172
$\overline{g}$KF (nS)	0–13.2	0–29.8
gleak (nS)	9.5–10.8	2.8–11.5

To determine a range for a parameter, this parameter was varied, whereas all other parameters were the same as in the canonical model (Fig. 6, asterisk).

Leak current subtraction via dynamic clamp

To test our hypothesis concerning the crucial role of a leak current introduced by sharp microelectrode penetration, we performed a series of experiments in which the dynamic clamp (Sharp et al., 1993) was used to attempt to restore endogenous bursting by subtracting the introduced leak current. In almost all experiments (n = 5 of 6), we could easily evoke one to three bursts consisting of two to nine spikes with spike frequency of 1–10 Hz by subtracting the nonspecific leak current with the dynamic clamp; the subtracted current was calculated according to leak current formulas withE ${}_{\text{leak}}^{\text{o}}$ = 0 andg ${}_{\text{leak}}^{\text{o}}$ = −1 to −6 nS (Fig.10A,B). After a few bursts, the neurons went into either sporadic spiking (Fig.10A) or silence (Fig. 10B). The subtracted leak conductances from these experiments (g ${}_{\text{leak}}^{\text{o}}$ = −1 to −6 nS) give us an approximate indirect estimation of the leak conductance introduced by our microelectrodes. These numbers in turn fit well with the range of input conductances that we measured in these experiments (8–16 nS) and the estimate of the minimum leak conductance necessary for bursting to occur in the model neuron (7 nS). Thus in our best sharp microelectrode recordings, we may introduce as little as 1 nS of nonspecific leak conductance into the heart interneurons, an amount that the model predicts should suppress bursting. Our failure to produce longer burst trains with the dynamic clamp leak conductance subtraction may be explained by the narrowness of the bursting region in the plane of theE_leak andg_leak parameters, in which slow fluctuation of the electrode potential as small as ±1 mV could cause a transition from bursting to tonic spiking or silence.

Fig. 10.

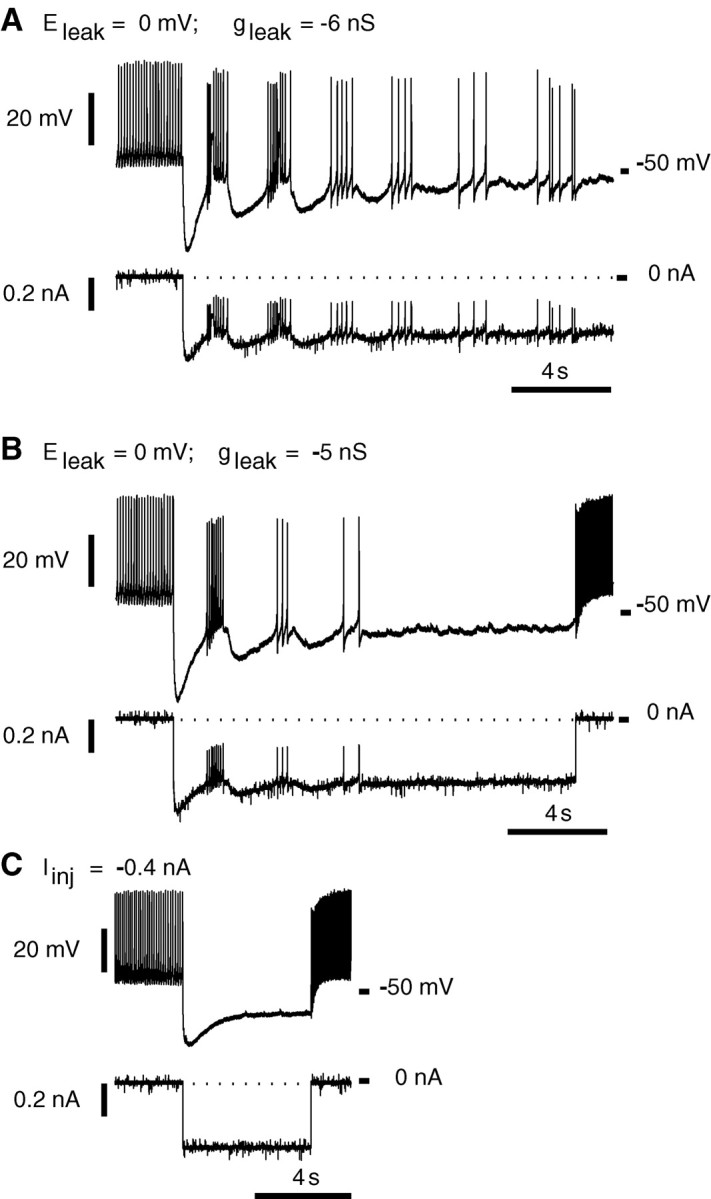
Subtraction of a leak current using a dynamic clamp elicits a few bursts in intracellular recordings (sharp microelectrodes) from oscillator heart interneurons isolated pharmacologically with bicuculline (1 mm).A, Leak current subtraction (E_leak = 0 mV;g_leak = −6 nS) caused five bursts followed by irregular tonic spiking. B, Leak current subtraction (E_leak = 0 mV;g_leak = −5 nS) caused three bursts followed by silence. C, Injection of a steady hyperpolarizing current (−0.4 nA) did not lead to bursting.

Injection of a constant hyperpolarizing current that caused shifts of the membrane potential similar to ones observed in the dynamic clamp experiments did not elicit any bursting (Fig. 10C). Although injection of a hyperpolarizing current is not equivalent to manipulation of leak current parameters, it corresponds approximately to a reduction of E_leak without changing g_leak. Thus in parameter space, it is equivalent to moving the system vertically in the bifurcation diagrams of Figure 6. [Note in Fig. 6Bthat adding nonspecific leak conductance is equivalent to moving the system along steep curves (pink, green lines) up and to the right in the E_leak andg_leak parameter plane and that application of a dynamic clamp to subtract nonspecific leak conductance moves the system along such curves down and to the left.) It should therefore be possible to adjust the hyperpolarizing current so that the neuron demonstrates the bursting mode as long as vertical movement of the system in the parameter plane can enter the bursting zone; i.e.,g_leak is not greater than ∼14 nS. In this case, the value of the hyperpolarizing current should fall within a certain range (approximately, smaller currents support tonic spiking, whereas larger currents cause silence). For example, assuming an introduced nonspecific leak conductance of 1 nS with a starting (single-cell) model leak current parameter (*), the range of injected current that supports bursting is only ∼0.02 nA wide (between –0.04 and –0.06 nA). This range lessens and ultimately vanishes as the introduced nonspecific leak conductance grows.

DISCUSSION

Here we have demonstrated that oscillator heart interneurons, which make mutually inhibitory synapses and pace the leech heartbeat CPG, burst autonomously when isolated with bicuculline. Such bursting had not been observed before (Schmidt and Calabrese, 1992). This discrepancy in results can be attributed to the difference in recording techniques. Instead of intracellular recording with sharp microelectrodes, here we used less invasive extracellular recording. We hypothesize that a nonspecific leak current introduced by microelectrode penetration suppresses bursting in bicuculline.

An oscillator heart interneuron model displays bursting only within a narrow range of leak current parameters (Fig. 6A); thus bursting is very sensitive to perturbations of these parameters. We estimated the introduced leak conductance in our microelectrode recordings to be in the range of 1–9 nS. In the model, a nonspecific leak conductance as small as 0.3 nS can suppress bursting. In some other neurons (e.g., in geniculate local interneurons in the rat), microelectrode-introduced leak conductance appears to suppress bursting (Pape and McCormick, 1995; Zhu et al., 1999a,b). Although our analysis of the model is not exhaustive, we can say that the sensitivity of endogenous bursting to a leak remains over a wide variation of other parameters; therefore, an introduced leak current is at present the most tenable hypothesis. Alternatively, bursting in heart interneuron may be eliminated with microelectrode penetration, because in addition to or as a result of introducing a leak, it alters the intracellular pH or Ca²⁺ concentration.

Any conclusion that heart interneurons are endogenous bursters must be tempered by the observation that bicuculline methiodide may block a small-conductance calcium-activated potassium current and thus support bursting. In rat neostriatal cholinergic (Bennett et al., 2000) and midbrain dopamine (Johnson and Seutin, 1997) neurons, bicuculline converted tonic spiking activity into bursting activity. Nevertheless, the bursting we observed in bicuculline appears to be sensitive to an introduced nonspecific leak current.

Endogenous bursters in a half-center oscillator

The oscillator heart interneurons appear to be endogenous bursters yoked by strong mutual inhibition into a half-center oscillator. This inhibition stabilizes oscillation within the system to variations in intrinsic membrane properties of the oscillator interneurons. In the model of the heart interneuron half-center oscillator, bursting occurs over a wider range of the maximal conductance of intrinsic membrane currents than in a single-cell model (Table 2). Bursting of the single-cell model is especially sensitive to leak current parameters and the maximal conductance of I_P, whereas bursting of the half-center oscillator model is much less sensitive (Table 2; Fig. 6, compare A, B). These predictions of the models are borne out in our experiments. When a nonspecific leak current is introduced by microelectrode penetration, endogenous bursting is suppressed, but the half-center oscillator functions normally. In 30% of preparations, bursting of oscillator heart interneurons isolated in bicuculline was sporadically interrupted by bouts of tonic spiking (Fig. 3). In contrast, in the half-center oscillator configuration, these neurons did not show this intermittency. These results indicate that the half-center oscillator configuration improves the robustness of oscillations in the heartbeat CPG.

Control of burst period, duty cycle, and spike frequency

The burst period, duty cycle, and spike frequency all differ between the half-center and pharmacologically isolated configurations in our extracellular recordings (Table 1). The strong inhibition in the half-center configuration constrains the interburst interval to be approximately equal to the burst duration of the opposite cell, thus lengthening the period (by ∼25%) and reducing the duty cycle to ∼50%. Analysis of the half-center and single-cell models in the constrained region of Figure 6B corroborates these conclusions, although in the particular example illustrated in Figure9, the increase in the period is smaller than experimentally observed.

Role of endogenous bursting

The period of endogenous bursting may set the lower and upper limits on the period of the half-center oscillator. In experiments in which single oscillator interneurons (intracellular recording) were driven with rhythmic current pulses and entrainment throughout the network was observed (extracellular recording), Masino and Calabrese (2002) showed that entrainment broke down when the driven cell period differed by approximately ±15% from the period of the network and was often associated with fissure of the driven half-center oscillator. The endogenous bursting of the opposite oscillator interneuron may limit the ability of the half-center to be thus driven beyond this range.

Endogenous bursting could also ensure oscillation if synaptic inhibition is downregulated by neuromodulators. FMRFamide is an endogenous neuropeptide modulator of the heartbeat CPG. In addition to modulating voltage-gated currents, it also decreases the size and prolongs the duration of spike-mediate IPSCs between oscillator interneurons (Simon et al., 1994). Heart interneurons, being endogenous bursters with weakened mutually inhibitory synapses, would be able to express their faster endogenous period without losing their antiphasic relations, albeit with perhaps an increase in the duty cycle, e.g., in the model, the duty cycle is >50% when the strength of synapses is <20% of the canonical value. With weaker mutual inhibition there is a stronger demand for the robustness of the endogenous bursting, and, interestingly, in the model, the FMRFamide-activated K⁺ current expands the range ofg_leak supporting bursting, thus potentially improving the robustness of endogenous bursting.

In other CPGs, the strength of synapses between neurons can be controlled by neuromodulation and thus regulates the period or phase within the network (Johnson and Harris-Warrick, 1990; Johnson et al., 1991; Mangan et al., 1994; Ayali et al., 1998; McLean et al., 2000). For example, descending brainstem projections modulate tadpole spinal motor networks (McLean et al., 2000). Serotonin decreases IPSPs and speeds up the period of the pattern, and noradrenaline increases IPSPs and slows down the period of the pattern. Our previous analysis of the heart interneuron half-center model tuned with tonically firing model neurons indicates, however, that modulation of synaptic strength can smoothly regulate the period over a considerable range. The synaptic strength can be reduced by 50% without a breakdown in the oscillation, leading to an almost threefold reduction in the burst period, a period much shorter than ever observed in the biological system. On the other hand, the period of a half-center oscillator made of canonical endogenously bursting neurons is less sensitive to the reduction of synaptic strength. Reducing total synaptic strength even by 80% reduces the period by only 21%. Thus it appears that endogenous bursting in oscillator heart interneurons, rather than permitting reduction of the period by a downmodulation of synaptic strength, sets a lower limit for the period in the face of such modulation.

Strong synapses, sensitive bursters

Sensitive endogenous bursters linked into half-center oscillators by strong inhibitory synapses produce the core oscillation of the leech heartbeat CPG. The question arises of the advantage of such an organization for the function of the heartbeat. A heartbeat requires a continuous rhythmic drive. In the leech, which has two hearts driven by motor neurons, these motor neurons must be not only rhythmically driven but also properly coordinated. The oscillator interneurons not only generate this rhythmic drive but also coordinate the heart motor neuron by direct intersegmental inhibitory synaptic connections. The leech heartbeat CPG may not be a system in which flexibility is at a premium; rather, continuous drive with a constant duty cycle and phase may assure continuous and coordinated heartbeat. Only the period appears to be flexible in this system, and several sensory and modulator pathways are known that modulate the period (Arbas and Calabrese, 1984, 1990). Strong reciprocal inhibitory synapses that can harness the inherent rhythmicity of neurons into a half-center oscillator provide the most robust and stable rhythmic output but one that can easily be modulated along a range of periods. The autonomous bursting of the oscillator interneurons supports output generation and provides limits over which the period may be modulated.

One of the few systems that compares with the heartbeat CPG for its continuous and stable activity is the pyloric pattern generator of the crustacean stomatogastric ganglion. It is driven by a strong endogenous burster (AB neuron) that receives only weak inhibitory feedback from the rest of the network, which consists of much less regular, slower bursters interconnected through inhibitory synapses (Harris-Warrick et al., 1992). This pattern generator is phenomenally flexible in terms of period, activity pattern, and duty cycle; a plethora of modulators regulate the inherent membrane properties of the AB neuron, support its bursting by inducing bursting in electrically coupled PD neurons, and modify inherent membrane properties and synaptic connections throughout the network (Nusbaum et al., 2001). A simplified view of this network is that the AB neuron sets the period, whereas flexibility in the activity pattern and duty cycle resides in the flexible network interactions. Rhythmic inhibition provided by the AB neuron can effectively stabilize irregular bursting activity in the rest of the network (Elson et al., 1999).

The half-center oscillator organization described here for the leech heartbeat CPG is suited to ensure antiphasic activity and an equal duty cycle. In other CPGs in which such activity is required, such as in the lamprey swim central pattern generator, strong mutual inhibition may similarly stabilize, augment, and transform the endogenous bursting properties of network neurons.