Cell Type- and Subcellular Position-Dependent Summation of Unitary Postsynaptic Potentials in Neocortical Neurons

Abstract

Theoretical studies predict that the modes of integration of coincident inputs depend on their location and timing. To test these models experimentally, we simultaneously recorded from three neocortical neurons in vitro and investigated the effect of the subcellular position of two convergent inputs on the response summation in the common postsynaptic cell. When scattered over the somatodendritic surface, combination of two coincident excitatory or inhibitory synaptic potentials summed linearly in layer 2/3 pyramidal cells, as well as in GABAergic interneurons. Slightly sublinear summation with connection specific kinetics was observed when convergent inputs targeted closely placed sites on the postsynaptic cell. The degree of linearity of summation also depended on the type of connection, the relative timing of inputs, and the activation state ofI_h. The results suggest that, when few inputs are active, the majority of afferent permutations undergo linear integration, maintaining the importance of individual inputs. However, compartment- and connection-specific nonlinear interactions between synapses located close to each other could increase the computational power of individual neurons in a cell type-specific manner.

The rules of synaptic summation are thought to depend on the dendritic geometry of the postsynaptic cell (Zador et al., 1995; Mainen et al., 1996), on a variety of synaptic- and voltage-dependent conductances distributed heterogeneously over the dendritic tree (Johnston et al., 1996; Hausser et al., 2000), and on the relative position and timing of inputs (Jack et al., 1975; Shepherd and Brayton, 1987; Rall et al., 1992; Segev et al., 1995; Hausser et al., 2000). Theoretical analysis of dendritic integration began by assuming that passive cables serve as reasonable models of dendrites (Jack et al., 1975; Segev et al., 1995). According to cable theory, electrically isolated inputs sum linearly, whereas closely located inputs produce an attenuated response as a consequence of reduction in the ionic driving force or a decrease in dendritic input resistance leading to shunting of synaptic currents (Jack et al., 1975; Segev et al., 1995). However, dendritic membranes are not passive, because they contain voltage-dependent conductances, which could selectively amplify distal inputs or subserve local nonlinear operations (Koch et al., 1983; Mel, 1993). Direct experimental determination of the influence of the location of synaptic inputs on dendritic integration has been relatively sparse. Electrophysiological analysis in vivoshowed sublinear summation in motoneurons (Kuno and Miyahara, 1969) and both linear and nonlinear modes of integration of responses in the visual system (Douglas et al., 1988; Jagadeesh et al., 1993, 1997;Borggraham et al., 1998; Hirsch et al., 1998; Kogo and Ariel, 1999;Anderson et al., 2000). Experiments in brain slices indicated linear input summation in motoneurons (Skydsgaard and Hounsgaard, 1994) and hippocampal pyramidal cells (Langmoen and Andersen, 1983). Physiological tests without the additional information on the subcellular position of inputs leave dendritic integration rules open to several interpretations (Major et al., 1994; Zador et al., 1995;Mainen et al., 1996). Using local glutamate microiontophoresis and extracellular stimulation onto visualized dendrites, Cash and Yuste (1999) reported linear and position-independent summation of EPSPs. Summation of postsynaptic potentials also depends on the ongoing firing rate of neurons because the action potential acts as variable reset of integration (Hausser et al., 2001). Most experiments so far focused on the summation of excitatory inputs; to our knowledge, integration properties of convergent GABAergic synapses have not been reported. To test the effect of synapse location on the integration of inputs, we identified the sources, effect, and subcellular location of local cortical afferents converging onto neurons simultaneously recorded in the neocortex. The integration of two glutamatergic or GABAergic inputs was tested as a function of the relative location of synapses, the relative timing of inputs, and the activation of the voltage-gated conductance,I_h. The results reveal that they all have an influence on the mode of integration of inputs and that different combinations of inputs and postsynaptic cells might express distinct integration kinetics.

MATERIALS AND METHODS

Electrophysiology. Young (postnatal days 17–30) Wistar rats were anesthetized by the intraperitoneal injection of ketamine (30 mg/kg) and xylazine (10 mg/kg), and, after decapitation, coronal slices (350-μm-thick) were prepared from their somatosensory cortex. Slices were incubated at room temperature for 1 hr in a solution composed of (in mm): 130 NaCl, 3.5 KCl, 1 NaH₂PO₄, 24 NaHCO₃, 1 CaCl, 3 MgSO₄, and 10 (+)d-glucose, saturated with 95% O₂ and 5% CO₂. The solution used during recordings differed only in that it contained 3 mm CaCl₂ and 1.5 mm MgSO₄. Micropipettes (5–7 MΩ) were filled with (in mm): 126 K-gluconate, 4 KCl, 4 ATP-Mg, 0.3 GTP-NA₂, 10 HEPES, 10 kreatin-phosphate, and 8 biocytin, pH 7.25 (300 mOsm). Somatic whole-cell recordings were obtained at ∼36°C from concomitantly recorded triplets and quadruplets of interneurons and pyramidal cells visualized in layers 2/3 by infrared differential interference contrast videomicroscopy [Zeiss (Oberkochen, Germany) Axioskop microscope, Hamamatsu (Hamamatsu City, Japan) CCD camera, Luigs & Neumann (Ratingen, Germany) Infrapatch set-up, and two Heka Elektronik (Lambrecht/Pfalz, Germany) EPC 9 double-patch-clamp amplifiers]. Signals were filtered at 8 kHz, digitized at 16 kHz, and analyzed with PULSE software (Heka Elektronik). In all, 237 simultaneous triple and 316 quadruple recordings yielded 258 unitary connections interconnecting fast-spiking (FS), bitufted (BT), and pyramidal cells in the studied directions. In 28 cases, convergent afferents to a common postsynaptic neuron were recorded and are reported here. During stimulation, presynaptic cells were stimulated with brief (2 msec) suprathreshold pulses delivered at ≥5 sec intervals to minimize intertrial variability. Presynaptic cells were stimulated in cycles containing single presynaptic cell activations and synchronous and asynchronous dual presynaptic activation. For synchronous presynaptic activation, action potentials were timed to synchronize maximal unitary postsynaptic current amplitudes measured before the experiments testing convergence. Membrane potentials were corrected for junction potentials. Voltage-clamp recordings were excluded from analysis when series resistance was higher than 25 MΩ. Unless specified, traces shown are averages of 30–60 consecutive episodes. Traces were excluded from the analysis if spontaneous PSPs occurred 20 msec before or 100 msec after the activation of identified responses; this process resulted in the elimination of <10% of events in a particular paradigm. All traces were offset to align their baselines for the period from −20 to 0 msec before the onset of current injections into the presynaptic neuron. The amplitude of postsynaptic event was defined as the difference between the peak amplitude and the baseline value measured 0–20 msec before presynaptic activation. Data for analysis of summation were used only from epochs in which the postsynaptic response remained stationary, i.e., the mean amplitude of 10 consecutive events remained within ±10% of the mean of the first 10 events of the epoch. The difference between the algebraic sums of single input responses and the recorded summed response was calculated during postsynaptic responses and expressed as a percentage of the maximal amplitude of the calculated response at the given time point. The resulting waveform is used as a measure of the degree of linearity over time.

Histology. Visualization of biocytin was performed as described previously (Tamás et al., 2000). Three-dimensional light microscopic reconstructions were performed using Neurolucida(MicroBrightField Inc., Colchester, VT) with a 100× objective; dendrogram constructions and synaptic distance measurements were aided by Neuroexplorer (MicroBrightField Inc.) software. Correlated light and electron microscopy was performed as described previously (Tamás et al., 2000). Distances between dendritic contact sites of different sources were measured along the dendrites, and, when applicable, the somatic distances linking the root of the dendrites were added. Distances between somatic synapses could not be measured as real distances because of the difficulty of following the curvature of the somatic plasma membrane in three dimensions. Therefore, they were measured along the pia–white matter axis of the two-dimensional projected image of the soma. For calculating the mean distance between the identified or light microscopically predicted synaptic sites of two afferents to the same postsynaptic cell, the distances between each synaptic site of one afferent from each synaptic site of the other one were averaged.

Data are presented as mean ± SD; Statistica for Windows software package was used for statistical analysis (StatSoft Inc., Tulsa, OK). The significance for all comparisons was set at p < 0.05.

RESULTS

Of several hundred multiple recordings made, the physiological analysis of 28 triple cell recordings involving convergent inputs onto the same postsynaptic cell in layers 2/3 of somatosensory cortex was performed in detail. Of these, satisfactory intracellular labeling of all three cells permitted the unequivocal tracing of afferents back to the parent somata in 12 cases. Pairs of presynaptic pyramidal or FS cells were activated using a cyclic stimulation paradigm (Fig.1b) (see Fig. 4b) that evoked simultaneous presynaptic action potentials with a relative peak to peak difference of 0.14 ± 0.12 msec. Postsynaptic cells receiving two convergent inputs represented pyramidal neurons, FS and BT cells (McCormick et al., 1985; Reyes et al., 1998) (Fig.1a). In agreement with previous studies (McCormick et al., 1985; Reyes et al., 1998), input resistance and membrane time constant of the postsynaptic cells were, on average, 207 ± 32 MΩ and 23 ± 5 msec in pyramidal cells (n = 15), 127 ± 49 MΩ and 10 ± 3 msec in FS (n = 9) cells, and 405 ± 137 MΩ and 25 ± 6 msec in BT (n= 4) neurons.

Fig. 1.

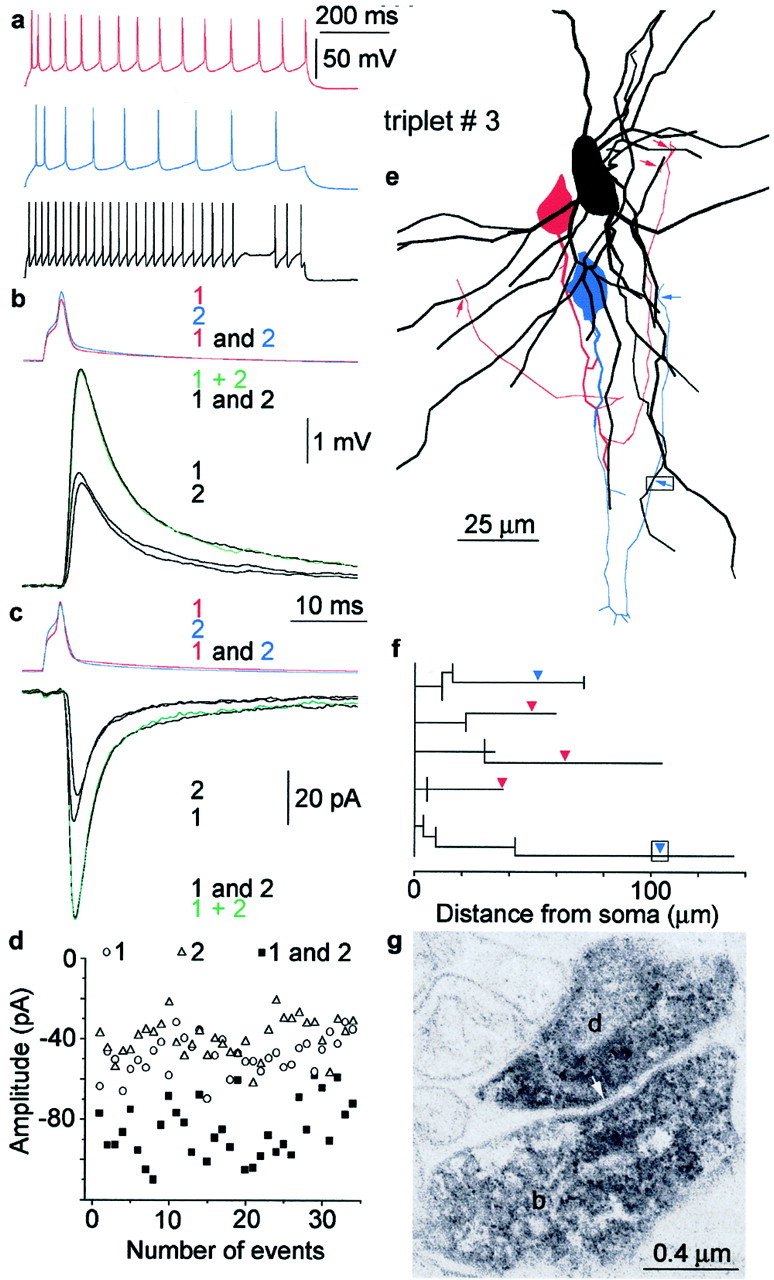
Linear summation of convergent excitatory inputs.a–g, Summation of convergent EPSPs in a layer 3 FS cell. a, Firing pattern of the presynaptic pyramidal cells (red and blue) and the postsynaptic FS cell (black). b, Current-clamp recordings of summation. Repeated and cyclic activation of the presynaptic cells (1, red pyramid alone;2, blue pyramid alone; 1 and 2, both cells together) resulted in unitary EPSPs (black1, black2) and compound responses (black1 and 2) in the postsynaptic interneuron held at −52 mV membrane potential. The calculated algebraic sum of EPSP 1 alone and EPSP 2 alone (green 1 + 2) follows the experimental compound response. c, Repeating the experiment shown inb while holding the postsynaptic cell in voltage clamp at −52 mV resulted in linear summation of EPSCs, as shown by the almost identical recorded (black) and calculated (green) compound traces. d, Stability of recorded EPSCs during the experiment. e, Reconstruction of the postsynaptic dendritic tree (black, partly shown) and presynaptic axons and somata (red, pyramid 1; blue, pyramid 2).Arrows indicate the positions of electron microscopically verified synapses. f, Partial dendrogram representing three-dimensional distances of identified synaptic junctions measured along the postsynaptic dendrites. g, Electron microscopic evidence for the most distal synaptic junction (arrow, boxes in e andf) established by an axonal bouton (b) of pyramidal cell 2 and the dendrite (d) of the postsynaptic FS cell.

Fig. 4.

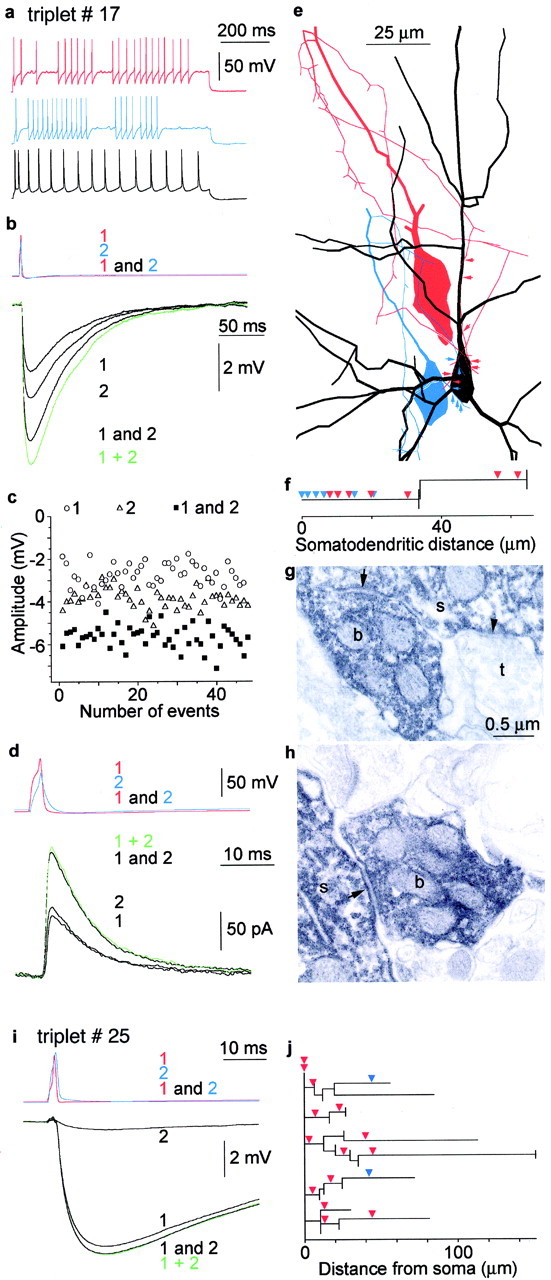
Summation of convergent IPSPs evoked by FS cells in pyramidal cells. a–h, Coaligned GABAergic inputs to a layer 3 pyramidal cell. a, Firing pattern of the presynaptic FS cells (red and blue) and the postsynaptic pyramidal cell (black).b, Current-clamp recordings of the interaction. Activation of the presynaptic cells (1,red FS cell alone; 2, blueFS cell alone; 1 and 2, both cells together) resulted in unitary IPSPs (black 1, black 2) and compound responses (black 1 and 2) in the postsynaptic interneuron held at −50 mV membrane potential. The amplitude of the experimental compound response was 85% of the calculated algebraic sum of IPSP 1 alone and IPSP 2 alone (green 1 + 2).c, Amplitude of recorded IPSPs during recording.d, Repeating the experiment shown inb while holding the postsynaptic cell in voltage clamp at −50 mV resulted in a slightly smaller (94%) compound IPSC (black 1 and 2) than the calculated (green 1 + 2) composite IPSC. e, The course of presynaptic axons (red, FS cell 1;blue, FS cell 2) forming proximal synaptic junctions (arrows) with the postsynaptic cell (black). f, Partial dendrogram representing three-dimensional distances of the electron microscopically identified synapses. The presynaptic cells innervated the postsynaptic soma in neighboring positions. g,h, Electron micrographs of synaptic junctions (arrow) between presynaptic boutons (b) of cell 2 (g) and cell 1 (h) and the postsynaptic somata (s). An unlabeled axon terminal (t) forms a synapse (arrowhead ing) nearby. i, j, Linear summation of relatively distal IPSPs along the postsynaptic dendrites of a layer 3 pyramidal cell. i, Activation of the presynaptic cells (1, red FS cell alone;2, blue FS cell alone; 1 and 2, both cells together) resulted in unitary IPSPs (black 1, black 2) and compound responses (black1 and 2) in the postsynaptic pyramidal cell held at −50 mV membrane potential. The calculated algebraic sum of the two IPSPs alone (green 1 + 2) closely follows the recorded composite response.j, Dendrogram illustrating three-dimensional distances of light microscopically predicted synapses measured along the postsynaptic dendrites.

Summation of convergent EPSPs and EPSCs

Integration of convergent unitary EPSPs evoked by local layer 2/3 pyramidal neurons was tested in nine FS cells, four BT neurons, and two pyramidal cells (Figs.1-3). Based on the linearity of summation between synchronous inputs, pyramid to FS connections could be clearly divided into two groups. Unitary EPSPs summed linearly in five FS cells, but moderately sublinear summation was detected in four postsynaptic FS neurons. In the linearly summating group of cells, amplitudes of the converging smaller and bigger unitary EPSPs were 0.99 ± 0.77 and 2.11 ± 1.84 mV measured at −51 ± 2 mV membrane potential (Fig. 1a–g). Linear summation (100.9 ± 0.4%) was apparent when comparing the peak amplitude of experimentally recorded compound responses (3.12 ± 2.31 mV) with the calculated sums of individual inputs (3.10 ± 2.29 mV). In the group showing sublinear summation characteristics, amplitudes of unitary smaller and bigger EPSPs (1.21 ± 1.06 and 2.31 ± 1.82 mV) were similar to those measured in the linear pyramid to FS connections (Fig. 2). Experimentally recorded maximal amplitudes of compound EPSPs (3.29 ± 2.71 mV) were consistently smaller than those of corresponding algebraic sums of individual EPSPs (3.54 ± 2.85 mV; p < 0.05; Wilcoxon test), indicating moderately sublinear summation (90.8 ± 5.6%;p < 0.04). The time course of the degree of linearity was distinct from the kinetics of EPSPs or EPSCs because decay time constants of unitary EPSPs (10.7 ± 3.0 msec) and EPSCs (2.6 ± 0.7 msec) were, respectively, longer and shorter than that of the degree of linearity (6.7 ± 1.9 msec; p < 0.05; Mann–Whitney U test) (Fig. 2a) (see Fig.5c).

Fig. 2.

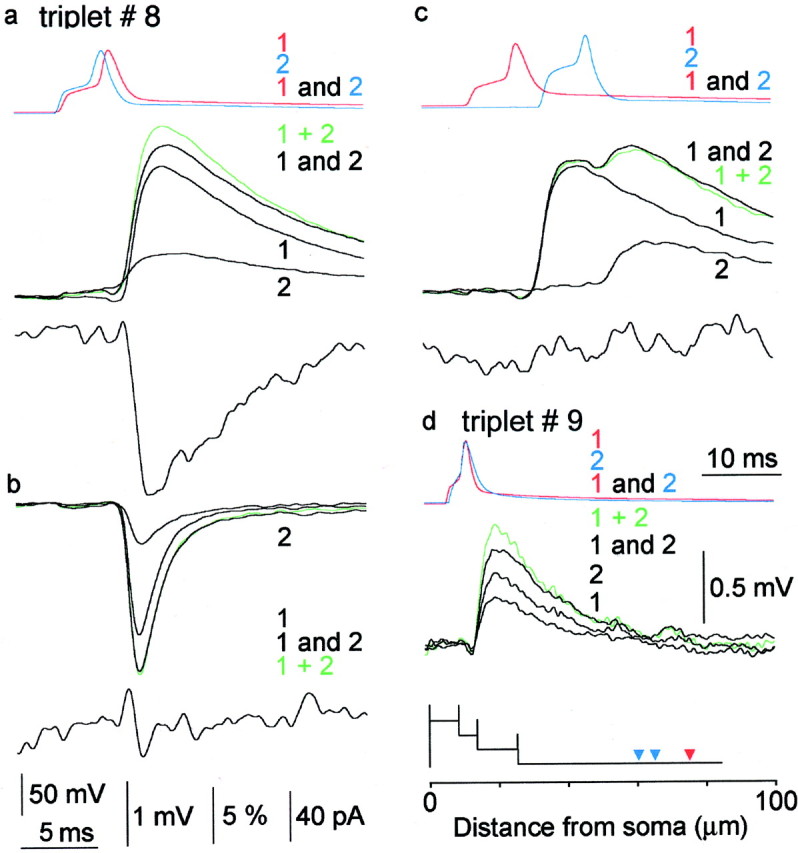
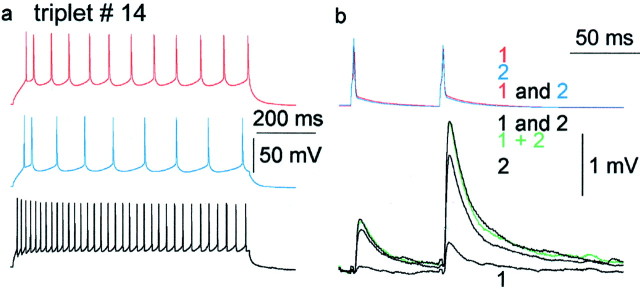
Sublinear summation of convergent EPSPs in FS cells. a, Repeated and cyclic activation of the presynaptic cells (top; 1,red pyramid alone; 2, bluepyramid alone; 1 and 2, both cells together) elicited unitary EPSPs (middle; black1, black2) and compound responses (black1 and 2) in the postsynaptic FS cell held at −50 mV membrane potential. The experimental compound response is smaller than the calculated algebraic sum of EPSP 1 alone and EPSP 2 alone (green 1 + 2), indicating sublinear summation. The time course of linearity is shown in the bottom panel.b, Repeating the experiment shown in awhile holding the postsynaptic cell in voltage clamp at −50 mV resulted in linear summation of EPSCs, as shown by the almost identical recorded (black) and calculated (green) compound traces and the linearity plot (bottom). c, Shifting the activation time of pyramidal cell 2 resulted in linear summation of inputs, as shown by the overlapping recorded (black) and calculated (green) sums and by the linearity trace (bottom). d, Interaction between convergent EPSPs targeting neighboring sites on the same dendrite of a layer 3 FS cell. Repeated activation of the presynaptic pyramidal cells (1, red pyramid alone; 2,blue pyramid alone; 1 and 2, both cells together) resulted in unitary EPSPs (black 1,black 2) and compound responses (black 1 and 2) in the postsynaptic FS cell held at −51 mV membrane potential. The amplitude of the recorded compound response was 83% of the calculated algebraic sum of the two EPSPs (green 1 + 2). The dendrogram on the bottom represents three-dimensional distances of electron microscopically identified synaptic junctions measured along the postsynaptic dendrite.

Fig. 3.

Linear summation of convergent, facilitatory EPSPs in a layer 3 bitufted cell. a, Firing pattern of the presynaptic pyramidal cells (red andblue) and the postsynaptic BT cell (black). b, Repeated activation of the presynaptic pyramidal cells with paired pulses (1,red pyramid alone; 2, bluepyramid alone; 1 and 2, both cells together) resulted in unitary EPSPs (black 1, black 2) and compound responses (black 1 and 2) in the postsynaptic BT cell held at −52 mV membrane potential.

Fig. 5.

Temporal and pharmacological properties of IPSP summation in convergent FS cell to pyramidal cell connections.a, b, Synchronous (a) or asynchronous (b) activation of the presynaptic cells (top; FS cell 1 alone, FS cell 2 alone; 1 and 2, both cells together) elicited unitary IPSPs (middle; black 1,black 2) and compound responses (black 1 and 2′) in the postsynaptic pyramidal cell held at −50 mV membrane potential. Both experimental compound responses are smaller than the calculated algebraic sums of IPSP 1 alone and IPSP 2 alone (gray 1 + 2), indicating sublinear summation. The time course of the degree of linearity is shown in the bottom panels. c, Repeating the experiments in the presence of 40 μm ZD7288 increased the amplitude and decay time of IPSPs and further increased sublinearity of summation.d, Sublinearity was decreased by asynchronous activation of inputs.

In two FS cells, similar experimental paradigms were applied holding the postsynaptic cells in voltage-clamp mode (Figs. 1c,2b). Although measurements in current-clamp mode indicated linear (Fig. 1b) or sublinear (Fig. 2a) integration, summation of postsynaptic currents was close to linear in both cases, because the amplitudes of recorded composite EPSCs were 99.6 and 97.5% of the algebraic sums of individually evoked EPSCs (Figs. 1c, 2b).

To investigate the effect of the relative timing of two EPSPs on their summation characteristics in FS neurons, we tested how asynchronous EPSPs interact by eliciting the smaller unitary responses (0.66 ± 0.38 mV) 5 msec after the bigger EPSPs (1.46 ± 0.52 mV) in two triplets showing linear and in two triplets showing sublinear summation of synchronous inputs. Asynchronous activation produced linear summation (100.7 ± 0.9%) in all four cases, because recorded compound events and calculated sums of unitary PSPs were similar in amplitude (1.41 ± 0.38 and 1.40 ± 0.39 mV), as measured at the peak of the single smaller EPSP (Fig. 2c).

Summation characteristics might depend on the amplitude of inputs. Therefore, we examined the degree of linearity as a function of EPSP amplitude measured as the maximal amplitude of the algebraic sums of individual EPSPs and found no correlation in pyramid to FS cell triplets (n = 9; Spearman correlation;r = 0.13; p > 0.5). Moreover, we tested the summation of EPSPs on BT cells (n = 4), because pyramidal inputs to these cells show relatively strong paired-pulse facilitation (Markram et al., 1998; Reyes et al., 1998) (Fig. 3a,b). Regardless of the amplitude increase from the first to second EPSPs (314 ± 79%), all four triplets showed linear summation for both the first and second events; therefore, we pooled the data. Amplitudes of the smaller and bigger unitary EPSPs were 0.32 ± 0.29 and 0.78 ± 0.79 mV on average (n = 8), as measured at −50 ± 3 mV membrane potential. Simultaneous activation of presynaptic cells produced compound EPSPs with amplitudes of 1.10 ± 1.03 mV, similar to that of algebraic sums of individual EPSPs (1.08 ± 1.07 mV). Linear (101.1 ± 2.1%) summation of EPSPs was apparent when comparing the amplitude of compound recordings with the appropriate calculated sums of individual inputs at the peak of the recorded EPSPs (Fig. 3b). Kinetics of the measured and the corresponding calculated compound events were also similar. The two triplets consisting of convergent pyramidal EPSPs to pyramidal cells also showed linear summation characteristics (data not shown).

Structural analysis of the basis of convergent EPSPs showing linear integration properties was performed in four triplets with two FS cells and two BT cells receiving the pyramidal inputs. On average, unitary innervation was mediated by 2.0 ± 0.8 and 2.8 ± 1.7 predicted contact sites by the axons evoking the smaller and bigger unitary EPSPs, respectively. Measured from the soma, postsynaptic cells were innervated at distances of 79 ± 35 and 76 ± 23 μm by the weaker and stronger inputs, respectively. The two sets of afferents contacted different dendritic segments in all cases, and the contact sites made by the two presynaptic pyramids were relatively distant from each other on the postsynaptic cell (146 ± 42 μm) (Fig.1e,f). Electron microscopic testing of all suspected contact sites confirmed light microscopic predictions as being synaptic junctions in the triplet presented in Figure1a–g. Anatomical analysis of pyramid to FS triplets, which showed sublinear summation, could be performed in two cases. In contrast to distant input sites in triplets producing linear EPSP summation, boutons evoking EPSPs summating sublinearly were relatively close to one another. Light microscopic evaluation of the first triplet indicated five and two contact sites for the two inputs with an average distance of 55 ± 21 μm (n = 10), as measured along the dendrites between all individual predicted synapses of distinct origin. Both presynaptic cells made two contacts on dendritic branches originating from the same stem, and the nearest two synapses made by the two presynaptic axons were 7 μm apart. Analysis of the second triplet revealed that the two inputs targeted the same dendritic segment of the postsynaptic FS cell (Fig. 2d). The average distance of the two inputs was 14 ± 3 μm (n = 2), as proved by electron microscopy.

Summation of convergent IPSPs and IPSCs

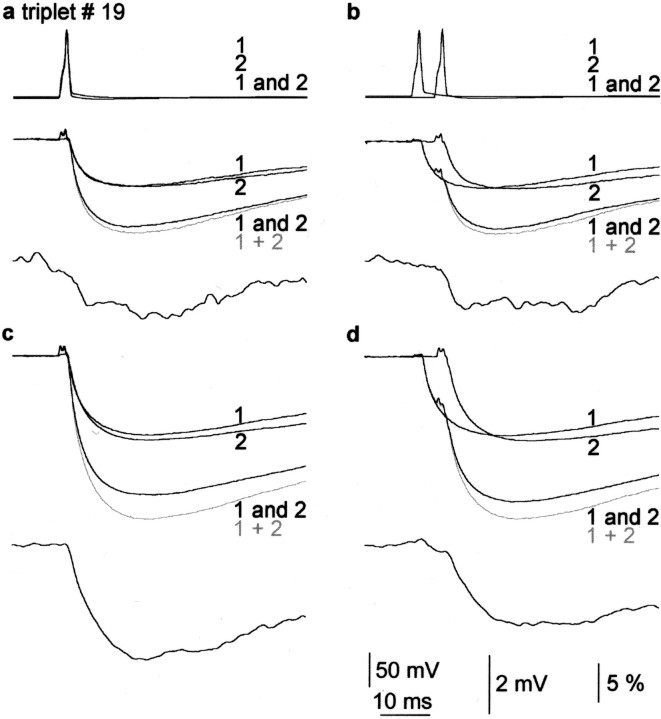
The data derived from EPSP–EPSP interactions indicated that neighboring input positions might result in sublinear summation. Extensive testing of this hypothesis requires input combinations reliably targeting the same postsynaptic domain. Cortical basket cells show FS firing pattern; they selectively target the perisomatic region of postsynaptic cells and frequently innervate pyramidal cells in their vicinity (Somogyi et al., 1998). Therefore, we focused our efforts on recording convergent FS cell inputs onto pyramidal cells (n = 13). The majority of convergent unitary IPSPs synchronously elicited by FS cells in layer 3 pyramidal neurons produced sublinear summation (n = 8), but linear interactions (n = 5) were also apparent (Fig.4). In the sublinearly summating group of cells, smaller unitary IPSPs were 1.49 ± 0.86 mV and greater IPSPs were 2.63 ± 1.42 mV in amplitude, measured at −50 ± 1 mV membrane potential (Fig. 4b,5a). In these triplets, the degree of linearity was correlated with the maximal amplitude of the algebraic sums of convergent IPSPs (n = 8;r = 0.95; p > 0.001). Simultaneously evoked unitary responses produced compound IPSPs with recorded amplitudes of 3.71 ± 1.61 mV, being consistently smaller (91.8 ± 4.0%) than that of corresponding algebraic sums of individual IPSPs (4.11 ± 1.94 mV; p < 0.01; Wilcoxon test). Normalization of composite recorded IPSPs to the amplitude of the calculated IPSPs showed no apparent difference in kinetics. When comparing the kinetics of the degree of linearity with that of unitary IPSPs and IPSCs, the 10–90% rise time (9.8 ± 1.9 msec) was significantly longer than the rise times of IPSPs or IPSCs (5.6 ± 1.2 and 0.92 ± 0.03 msec; p < 0.03; Mann–Whitney U test). Decay time constants of the degree of linearity (55.8 ± 5.7 msec) differed from that of corresponding IPSCs (7.7 ± 0.8 msec; p < 0.01) but were similar to that of IPSPs (60.1 ± 8.4 msec) (Figs.4b,c,6c). In the FS cell to pyramid triplets (n = 5) showing linear summation (Fig.4i), smaller and bigger unitary IPSPs were 0.48 ± 0.14 and 2.77 ± 2.39 mV in amplitude recorded at −50 ± 2 mV membrane potential. These triplets did not show significant correlation between the degree of linearity and the maximal amplitude of the algebraic sums of convergent IPSPs (n = 5;r = 0.60; p > 0.2). Synchronously activated unitary responses produced compound IPSPs with recorded amplitudes of 3.23 ± 2.35 mV, a value similar (99.6 ± 0.4%) to that of the amplitude of calculated composite IPSPs (3.25 ± 2.37 mV).

Fig. 6.

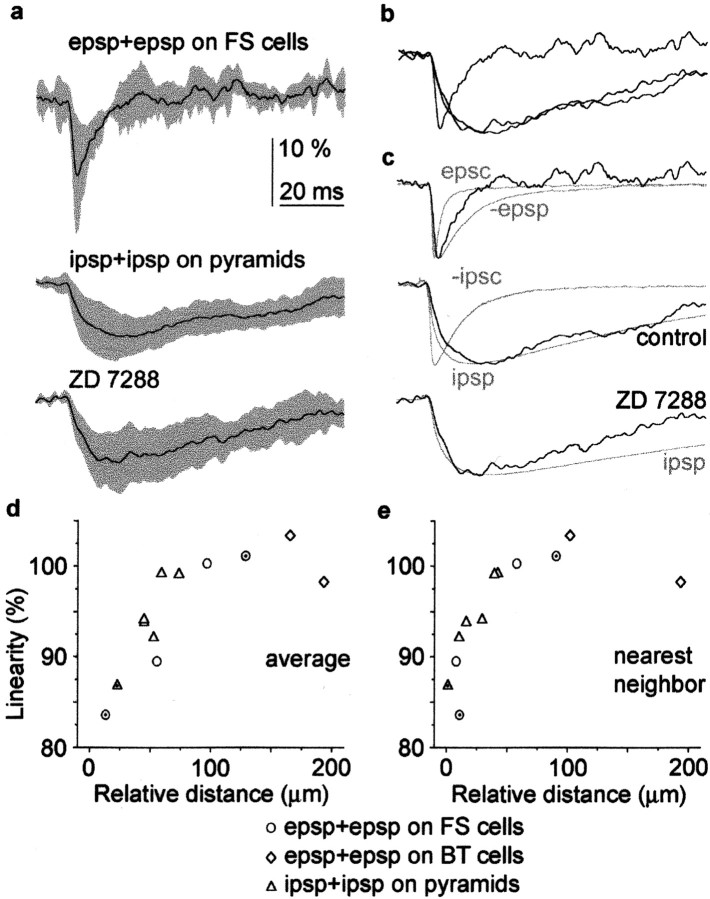
The degree of linearity in the summation of PSPs is connection and subcellular position dependent. a, Average time course of the degree of linearity in the summation of converging unitary EPSP–EPSP (epsp+epsp;n = 4) and IPSP–IPSP (ipsp+ipsp;n = 8; n = 6 in ZD7288) connections, which showed sublinear summation. Gray areas indicate SDs. b, Amplitude normalization of traces shown in a shows that, in EPSP–EPSP in FS cell connections, sublinearity is temporally restricted relative to IPSP–IPSP in pyramid connections.c, Kinetics of linearity relative to corresponding unitary synaptic currents and potentials in sublinearly summating unitary connections (see Results). d, e, Summation of unitary postsynaptic potentials is position dependent. The average distance between two sets of afferent synapses (d) and the distance between nearest neighboring synapses of the two converging axons (e) measured along the postsynaptic soma and dendrites correlates with the degree of linearity in postsynaptic response summation. Dots in the symbols indicate cases in which the site of synaptic junctions was established by electron microscopy; in the remaining cases, distances were mapped by light microscopy.

We tested how asynchronous IPSPs interact by eliciting the smaller unitary responses (0.82 ± 0.48 mV) 5 msec after the bigger IPSPs (2.05 ± 1.64 mV) in two triplets showing linear and in three triplets showing sublinear summation of synchronous inputs (Fig. 5). Asynchronous activation did not change the properties of summation compared with synchronous timing of inputs; the difference in the degree of linearity of the peak response between synchronous and corresponding asynchronous input combinations was 0.6 ± 4.2% (Fig. 5a,b). We also tested synchronous input summation in five pyramidal cells holding the postsynaptic cells in voltage-clamp mode (Fig. 4d). Although, for these connections, the measurements in current-clamp mode indicated either linear (n = 2) or sublinear (n = 3) (Fig. 4b) integration, summation of postsynaptic currents was close to linear in all five cases, because the amplitudes of recorded composite IPSCs were 97.0 ± 2.0% of the algebraic sums of individually evoked IPSCs (Fig. 4d).

Summation properties are likely to depend on voltage-gated conductances, and I_h is thought to be the most prominent current activated by IPSPs in pyramidal cells. Therefore, after completing some of the protocols detailed above in normal extracellular solution, we continued some experiments (n = 6) in the presence of the channel blocker ZD7288 (40 μm) (Fig. 5). The application of ZD7288 increased the input resistance of pyramidal cells by 38 ± 19% and the amplitude and decay time constant of unitary IPSPs to 133 ± 25 and 137 ± 24% of the control, respectively (all three,p < 0.05; Wilcoxon test). When synchronously activating the smaller and bigger IPSPs (1.02 ± 0.84 and 3.19 ± 2.65 mV) in the presence of ZD7288, all six triplets showed sublinear summation, although control measurements indicated three linearly and three sublinearly summating input combinations (99.7 ± 0.5 and 93.6 ± 2.1%, respectively). Overall, ZD7288 significantly increased sublinearity from 96.7 ± 3.5 to 90.4 ± 3.9% (n = 6; p < 0.05; Wilcoxon test). The time course of the degree of linearity and IPSPs were different (Fig. 5c), as shown by the difference in the decay time constants (IPSP, 87.9 ± 9.3 msec vs linearity, 53.5 ± 12.3 msec; p < 0.05; Wilcoxon test). Asynchronous activation of the convergent inputs (n = 6) in the presence of ZD7288 changed the degree of linearity of the peak response from 90.4 ± 3.9 to 95.9 ± 6.2% (p < 0.05; Wilcoxon test) (Fig. 5d), resulting in linearization of three input combinations.

Anatomical analysis of the connections providing convergent IPSPs with sublinear integration properties could be performed in four triplets (Fig. 4e–h). All eight presynaptic FS cells innervated pyramidal cells on or relatively close to the soma. Predicted and/or electron microscopically verified synapses were 20 ± 21 μm from the postsynaptic somata. The average distance between the two sets of contact sites was 41 ± 13 μm, and the closest synapses–contacts originating from two converging presynaptic cells were 12 ± 14 μm apart measured along the postsynaptic dendrites or estimated on the soma. In five measurements of basket cell input to pyramidal cells, light microscopic estimates of somatic synapses cannot account for those that are obscured by the soma; therefore, these estimates are less accurate. Electron microscopic serial section analysis of all suspected contact sites in one triplet showed coalignment of inputs on the soma and proximal dendrites of the postsynaptic cell (Fig. 4e–h). One of the presynaptic FS cells in the somatic cotermination case established synapses (n = 6) exclusively on the cell body, whereas the other presynaptic FS cell targeted the cell body by four synapses and the proximal apical dendrite by three synapses. The distance between the synapses formed by the two presynaptic cells was, on average, 23 ± 22 μm. From the linearly summating triplets, two triplets could be analyzed anatomically. Light microscopic estimates indicated that the postsynaptic pyramidal cells were innervated by two and two contact sites by the cells evoking the smaller IPSPs and 14 and five presumed synapses by the bigger unitary IPSPs, respectively. The four presynaptic cells innervated the postsynaptic cells at an average distance of 32 ± 14 μm from the soma. The mean dendritic distance of the convergent sets of afferents was 59 ± 16 and 73 ± 24 μm from each other, and the nearest neighbors of distinct sources were 42 and 39 μm distant.

Synapse location dependence of the degree of linearity in input summation

Overall, when comparing the time course of the degree of linearity in converging EPSPs on FS cells and converging perisomatic IPSPs on pyramidal cells showing sublinear summation, both the 10–90% rise time and decay time constant are faster in FS cells than in pyramidal neurons (p < 0.01; Mann–Whitney Utest). This indicates that the temporal dynamics of the degree of linearity are connection and/or cell type specific. However, the combined analysis also revealed that EPSP–EPSP and IPSP–IPSP interactions summate similarly, depending on the spatial arrangement of inputs on the postsynaptic neuron (Fig. 6d,e). The average somatodendritic distance of the two sets of afferents and the distance between nearest neighboring synapses made by the two different converging cells correlated with the linearity of input summation (r = 0.81 and r = 0.85;p < 0.001; Spearman correlation).

DISCUSSION

Our results provide direct experimental evidence that the summation of two convergent unitary inputs follows linear or close to linear summation in cortical neurons in vitro. This suggests that, when a small number of afferents are simultaneously active, linear or moderately sublinear summation dominates the integration of inputs as detected at the soma. Taking cortical interneurons, their total dendritic lengths were estimated as between 2500 and 12,000 μm per neuron and synaptic density as between 150 and 500 synapses per 100 μm dendritic length (Gulyas et al., 1999). Based on these ranges, considering a 50 μm relative upper distance limit for significant nonlinear interactions and assuming a uniform input density of one active synaptic junction per presynaptic axon, input through a particular synaptic junction would sum linearly with other inputs, if no more than 1–6% of synapses were simultaneously active. Similar estimates for interactions between unitary inputs providing several active synaptic junctions cannot be made because the number and spatial dispersion of unitary synapses could influence the outcome, and these have been experimentally addressed only for a fraction of cortical connections. Linear operations maintain the impact of individual afferents influencing output at a given time and enable integration of multiple sources of information by an additive interaction of inputs.

Electron microscopic determination of the sites of synaptic junctions provided by the functionally tested converging afferents revealed that the distance between distinct simultaneously active inputs influences the degree of linearity of summation. Supporting predictions made by cable theory (Jack et al., 1975; Rall et al., 1992; Segev et al., 1995), nonlinear interactions were recorded between inputs targeting closely located postsynaptic sites. Compartment-specific interactions between afferents targeting closely situated membrane domains could be detected already between two inputs, as suggested previously (Koch et al., 1983; Shepherd and Brayton, 1987;Bush and Sejnowski, 1994), although sublinearity was moderate. A simultaneous activation of many coaligned inputs might lead to more significant nonlinear interactions. The coalignment of inputs of common origin on neurons is prominent in the hippocampus and neocortex, in which some glutamatergic inputs terminate on distinct dendritic regions and GABAergic interneurons subdivide the surface of postsynaptic cells leading to a pairing of excitatory and inhibitory inputs on particular subcellular regions (Somogyi et al., 1998).

Nonlinear interactions may increase the computational power of neurons (Koch et al., 1983; Segev et al., 1995; Poirazi and Mel, 2001). The degree of linearity of input summation depends on the type of connection, the relative timing of inputs, and the activation state of at least one voltage-gated conductance,I_h. Cellular mechanisms underlying the properties of summation remain to be explored in detail. Part of the sublinearity of interactions between closely located sites might be caused by a larger increase in membrane conductance caused by the opening of synaptic receptor channels when both synapses are active compared with the conductance increase caused by a single active synapse (Kogo and Ariel, 1999). The observation that asynchronous activation of pyramid to FS cell inputs, characterized by rapid synaptic conductances, resulted in the linearization of summation supports that increase in membrane conductance could be a factor in producing sublinearity. In addition, the strong correlation between the amplitude of sublinearly summating IPSPs and the degree of linearity suggests that the local change in the membrane potential and the resulting drop in the relatively small driving force could contribute to the observed sublinearity. The contribution of local changes in driving force to sublinearity might be less in EPSP–EPSP interactions, in which no correlation was found between EPSP amplitudes and linearity, and the EPSPs were of smaller amplitude relative to the driving force than the IPSPs. The uniformly linear summation of currents recorded in voltage-clamp mode suggests the involvement of driving force changes in sublinearity detected in postsynaptic potential recordings; the membrane potential is clamped at the holding potential and cannot approach the reversal potential. Sublinear current summation could result from a lack of diffusible ions on either side of the postsynaptic membrane, and our measurements suggest that changes in driving force are likely to be responsible for nonlinear summation. Active dendritic conductances are involved in sublinear summation (Hoffman et al., 1997; Cash and Yuste, 1999; Kogo and Ariel, 1999), as well as in supralinear boosting (Gillessen and Alzheimer, 1997; Hoffman et al., 1997), of inputs in pyramidal neurons and were proposed to make summation paradoxically linear (Cash and Yuste, 1999). It is likely that the difference in the time course of linearity we found between the summation of EPSPs and IPSPs is to some extent attributable to the distinct passive and/or active membrane properties of the receiving FS and pyramidal cells. In particular, FS neurons were suggested to act as coincidence detectors (Geiger et al., 1997), and, in these cells, nonlinear integration of EPSPs appear to be limited to a narrow time window, thus influencing mainly precisely synchronous EPSPs. In contrast, the degree of linearity of IPSP summation was not influenced by a 5 msec difference between the two inputs. The time course of the degree of linearity for EPSPs and IPSPs duringI_h blockade was shorter than the postsynaptic voltage response, suggesting the involvement of active dendritic properties (Kogo and Ariel, 1999) in unitary input summation in FS as well as in pyramidal cells.

In pyramidal neurons, I_h is likely to be one of the conductances involved in shaping integration properties. Moderate activation of I_h by preceding unitary IPSPs might explain that asynchronous perisomatic IPSPs also showed sublinear summation characteristics. The degree of linearity was correlated with the amplitude of convergent IPSPs; therefore, the increased sublinearity during I_hblockade could result from the greater drop in driving force produced by the larger IPSPs. However, additional experiments are needed to explain the observation that synchronous and asynchronous IPSPs summed similarly in control conditions but desynchronization reduced sublinearity during ZD7288 application. Our results also indicate thatI_h tends to linearize the summation of IPSPs arriving proximally. The scenario for dendritic IPSPs might be different, because I_h and other conductances, which might shape integration properties, are preferentially expressed on distal dendrites (Hoffman et al., 1997;Magee, 1998; Williams and Stuart, 2000; Berger et al., 2001). In addition to I_h examined here, tetrodotoxin-sensitive voltage-gated sodium conductances might also influence the properties of IPSP summation through IPSP amplification at more depolarized membrane potentials (Stuart, 1999). Moreover, voltage-dependent conductances may change integration properties considerably when neurons fire action potentials.

The relative weight of linear and nonlinear interactions of inputs in single neurons could be influenced also by the timing of convergent inputs. Although we have not been able to test the wide range of spatiotemporal parameters of previous simulations examining the time course of nonlinear interactions (Koch et al., 1983), the method applied here was sensitive enough to detect differences between synchronous and asynchronous input summation. Our results suggest that the dependence of summation on the relative activation time of inputs is connection type specific and is influenced by differential activation of I_h. Randomly timed and spatially scattered inputs would favor linear integration, but synchronous activation of coaligned afferents could shift the balance of processing toward nonlinear integration. Orchestrated EPSPs and IPSPs arrive at postsynaptic neurons in experimentally evoked cortical oscillations (Jefferys et al., 1996; Fisahn et al., 1998), suggesting rhythmic alternations in the mode of summation. Postsynaptic potentials arrive at much higher rates in vivo than in the slices studied here; therefore, the ratio of nonlinear interactions might be underrepresented in our study compared with more physiological conditions. The degree of linearity in processing might depend on behavioral states, which are accompanied by a variable synchrony in the firing of GABAergic neurons targeting specific cellular compartments (Csicsvari et al., 1998). At high level of activity, time- and domain-specific nonlinearity of summation in cortical networks might selectively reduce the impact of individual inputs arriving in a synchronous barrage (Destexhe and Pare, 1999). In contrast, at low level of activity, the information content of inputs summating linearly would be maintained.