Abstract
Natural populations display a variety of spatial arrangements, each potentially with a distinctive impact on genetic diversity and genetic differentiation among subpopulations. Although the spatial arrangement of populations can lead to intricate migration networks, theoretical developments have focused mainly on a small subset of such networks, emphasizing the island-migration and stepping-stone models. In this study, we investigate all small network motifs: the set of all possible migration networks among populations subdivided into at most four subpopulations. For each motif, we use coalescent theory to derive expectations for three quantities that describe genetic variation: nucleotide diversity, FST, and half-time to equilibrium diversity. We describe the impact of network properties on these quantities, finding that motifs with a high mean node degree have the largest nucleotide diversity and the longest time to equilibrium, whereas motifs with low density have the largest FST. In addition, we show that the motifs whose pattern of variation is most strongly influenced by loss of a connection or a subpopulation are those that can be split easily into disconnected components. We illustrate our results using two example data sets—sky island birds of genus Sholicola and Indian tigers—identifying disturbance scenarios that produce the greatest reduction in genetic diversity; for tigers, we also compare the benefits of two assisted gene flow scenarios. Our results have consequences for understanding the effect of geography on genetic diversity, and they can assist in designing strategies to alter population migration networks toward maximizing genetic variation in the context of conservation of endangered species.
Keywords: coalescent theory, genetic differentiation, network, population structure
Introduction
Coalescent theory is a powerful tool to predict patterns of genetic variation in models of population structure, and many studies have investigated the predictions of coalescent models about genetic variation under a variety of different assumptions about the genetic structure of populations (Donnelly and Tavaré 1995; Fu and Li 1999; Rosenberg and Nordborg 2002).
Correctly predicting the effect of connectivity patterns on the expected amount of nucleotide diversity and genetic differentiation is important in a range of settings. In population genetics, such predictions enable descriptions of the impact of migration as one of the main evolutionary forces influencing allele frequencies. In molecular ecology, they help evaluate the consequences of abiotic factors such as geographic barriers, and biotic factors such as assortative mating, on levels of genetic diversity and genetic differentiation. In conservation genetics, they can be used to quantify the impact of past and future disturbance, as well as to predict the outcome of management initiatives.
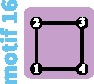
The two most frequently examined models of population structure are the island-migration and stepping-stone models. In the island model, individuals can migrate from any subpopulation to any other subpopulation, all with the same rate (Wright 1951). In the stepping-stone model, individuals can only migrate to neighboring subpopulations (Kimura 1953; Maruyama 1970). Stepping-stone models can represent multiple spatial arrangements. Under the circular stepping-stone model, subpopulations are arranged in a circle, so that all individuals can migrate to exactly two subpopulations. Under the linear stepping-stone model, subpopulations are arranged in a line.
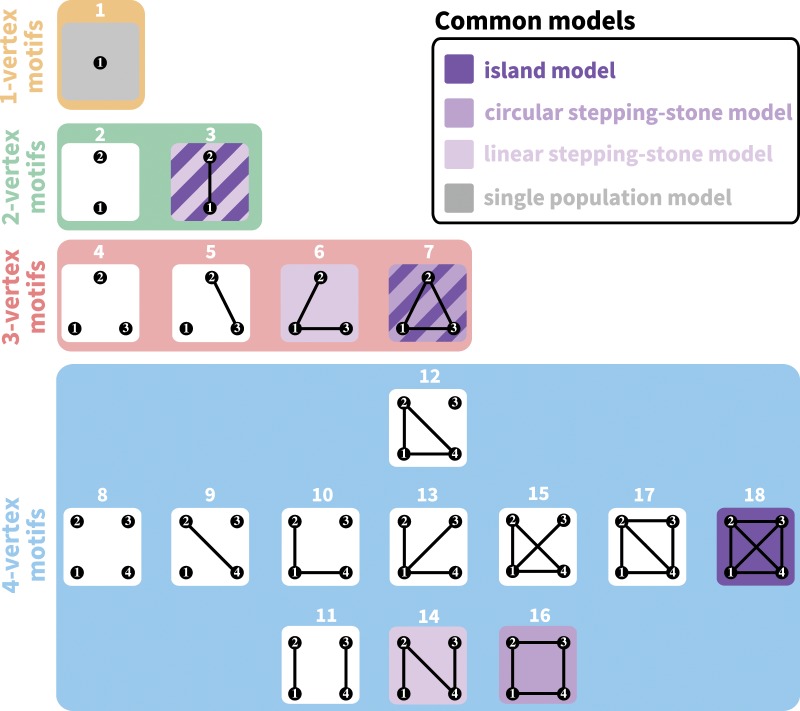
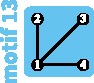
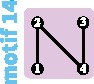
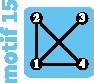
Although the island and stepping-stone models can accommodate a variety of patterns of connectivity among subpopulations, they represent only some of the possible patterns, or network “motifs.” Indeed, these models account for only 7 of 18 motifs possible for sets of 1–4 subpopulations (fig. 1). Numbering motifs by the classification from Read and Wilson (2005, p. 8), motif 1 corresponds to the panmictic population model, motif 18 to the island model, motifs 6 and 14 to linear stepping-stone models, motif 16 to a circular stepping-stone model, motif 3 to island, linear, and circular stepping-stone models, and 7 to both island and circular stepping-stone models. Although tools of coalescent theory to study arbitrary migration models are available (Wilkinson-Herbots 1998), to our knowledge, patterns of variation expected from the remaining 11 motifs have not been described.
Fig. 1.
All possible network motifs for sets of at most four vertices. Purple motif backgrounds highlight motifs that follow standard models, island or stepping-stone (circular or linear) or both. Note that we take the term “motif” to indicate a specific small undirected graph (rather than a small directed or undirected subgraph statistically overrepresented in large empirical networks, as in many applications).
An objective in the study of spatial arrangements of populations is to examine the properties of networks representing arbitrary connectivity patterns. The number of patterns grows rapidly with the number of subpopulations, however, and the comprehensive description of networks of arbitrary size is a combinatorial challenge. Because small network motifs are the “building blocks” of large networks (Milo et al. 2002), understanding the features of small connectivity networks is a useful step in predicting properties of complex networks. We thus characterize coalescent quantities under all possible motifs describing the spatial arrangements of up to four subpopulations.
We first derive the expected coalescence times between pairs of lineages sampled in each of the subpopulations and pairs sampled from different subpopulations. We compute three population-genetic quantities: expected nucleotide diversity in each population, expected FST values between pairs of subpopulations, and half-time to equilibrium after a perturbation. For each motif, we compute four network statistics—number of vertices, number of edges, mean degree, and density—correlating them with the population-genetic quantities. Finally, we investigate the nucleotide diversity lost after a connectivity loss or a subpopulation loss—a transition between motifs. We interpret the results in relation to problems in conservation genetics, considering two case studies, birds of genus Sholicola and Indian tigers. For both examples, we 1) consider genetic data in a network motif framework and 2) evaluate the potential impacts of connectivity change on population-genetic variation.
New Approaches
Population Connectivity
We consider K haploid or diploid subpopulations of equal size N individuals. We denote by Mij the scaled backward migration rate, representing twice the number of lineages per generation from subpopulation i that originate from subpopulation j. Thus, for haploids and for diploids, where mij is the rate at which individual lineages of subpopulation i migrate from subpopulation j. The total scaled migration rate of subpopulation i, or twice the scaled number of lineages that originate elsewhere, is . We further assume that the numbers of incoming migrants (forward in time) in each nonisolated subpopulation are all equal to M, so that for two nonisolated subpopulations i and j, . Time is a continuous variable t, scaled in units of the size of a single subpopulation (N for haploids, 2N for diploids). We focus on cases with , and we consider all possible connectivity patterns between subpopulations, where each pattern represents a distinct graph on at most four vertices (fig. 1).
Coalescence
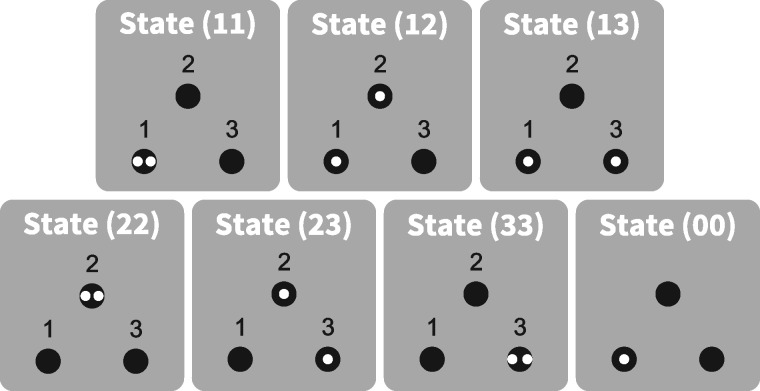
We consider the fate of two gene lineages drawn from a specific pair of subpopulations, either the same or different subpopulations. We denote the state of the two lineages by (ij), where i and j correspond to subpopulations. As the coalescence times between two lineages with initial states (ij) and (ji) are the same, even if populations i and j otherwise have different properties, we consider that state (ij) refers to both (ij) and (ji), and we assume without loss of generality that . Consequently, the number of states for two lineages in K subpopulations is . This quantity includes states where the lineages are in different subpopulations, K where they are in the same subpopulation, and 1 state where they have coalesced.
Assuming that events cannot occur simultaneously, the coalescent process can be described by a continuous-time Markov chain (Kingman 1982; Wilkinson-Herbots 1998). The list of all possible states of the Markov chain in the case where K = 3 is represented in figure 2.
Fig. 2.
Schematic representation of all states for two lineages in a population divided into K = 3 distinguishable subpopulations. Lineages appear in white, and subpopulations appear in black. The two lineages can either be in different subpopulations (states (12), (13), and (23)), in the same subpopulation ((11), (22), and (33)), or they can already have coalesced ((00)).
The instantaneous rate matrix for the Markov chain, where is the instantaneous transition rate from state (ij) to state , is defined in table 1 (Wilkinson-Herbots 1998). It can be seen that the list in table 1 covers all cases for by noting that by assumption, and .
Table 1.
Instantaneous Rates for All State Transitions (ij) to .
| Initial State (ij) | New State | Rate |
|---|---|---|
| (ii) | (ii) | |
| (ij), | (ij) | |
| (ii) | (ki), | Mik |
| (ii) | ||
| (ij), | ||
| (ij), | (ki), | |
| (ij), | (kj), | |
| (ij), | ||
| (ii) | (00) | 1 |
| (ij), | 0 |
The transition probabilities between states after a time interval of length t are given by
| (1) |
The element of P(t) corresponds to the transition probability from state ij to state in time t.
This general model, in which it is not necessarily true that Mij = Mji, embeds known models. Setting for all i and leads to the finite island model (Notohara 1990; Nei and Takahata 1993). Considering subpopulations along a circle and setting for all adjacent subpopulations (, or ) and Mij = 0 for all nonadjacent subpopulations leads to the circular stepping-stone model (Strobeck 1987). Considering subpopulations along a finite line and setting for and or , and Mij = 0 for all nonadjacent subpopulations leads to the linear stepping-stone model (Wilkinson-Herbots 1998).
Results
Expected Coalescence Time
The probability that coalescence has already occurred after time t for two lineages sampled respectively in subpopulations i and j corresponds to the transition probability during time t from initial state (ij) to state (00). This probability is given by element from matrix P(t) (eq. 1). Because is a cumulative probability, the associated density function is
| (2) |
The expected coalescence time for two lineages sampled in subpopulations i and j is thus
| (3) |
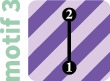
We derive in the Materials and Methods section the system of equations that can be solved to obtain the expected coalescence times in cases with one to four subpopulations. The expected coalescence time for motif 1—one isolated subpopulation—is simply 1. The expected coalescence times for the two-vertex motifs (motifs 2 and 3) appear in table 2, for the three-vertex motifs (4–7) in table 3, and for the four-vertex motifs (8–18) in table 4. Note that owing to complete isolation of certain subpopulations in some motifs, some coalescence times are reported as infinite.
Table 2.
Exact Mean Coalescence Times and FST Values for 2-Vertex Motifs.
| Motif | ||||
|---|---|---|---|---|

|
1 | 1 | 1 | |
|
2 | 2 |
Table 3.
Exact Mean Coalescence Times and FST Values for 3-Vertex Motifs.
| Motif | ||||||
|---|---|---|---|---|---|---|

|
1 | 1 | 1 | 1 | ||
|
1 | 2 | 1 | |||
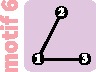
|
||||||
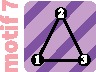
|
3 | 3 |
Note.—Owing to symmetries in migration motifs (fig. 1), and , and thus, .
Table 4.
Exact Mean Coalescence Times for 4-Vertex Motifs.
| Motif | |||||||||
|---|---|---|---|---|---|---|---|---|---|

|
1 | 1 | 1 | ||||||
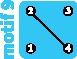
|
1 | 2 | 1 | ||||||
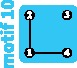
|
1 | ||||||||
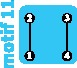
|
2 | 2 | 2 | ||||||
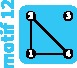
|
3 | 3 | 1 | ||||||
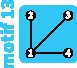
|
3 | 3 | 3 | ||||||
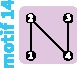
|
|||||||||
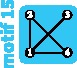
|
|||||||||
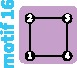
|
4 | 4 | 4 | ||||||
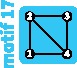
|
|||||||||
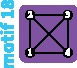
|
4 | 4 | 4 |
Note.—Owing to symmetries in migration motifs (fig. 1), .
The set of all pairwise coalescence times of a motif is informative about another quantity of interest: the total coalescence time, that is, the coalescence time of two lineages randomly sampled in any two K subpopulations, possibly the same one. Indeed, the total coalescence time is simply , the mean coalescence time across all possible subpopulation pairs. The total coalescence times for all motifs presented in figure 1 appear in supplementary table S1, Supplementary Material online.
Expected Within-Subpopulation Nucleotide Diversity
We next calculate the expected within-subpopulation nucleotide diversity, that is, the expected number of differences between two nucleotide sequences sampled from the same subpopulation, assuming an infinitely-many-sites model (Kimura 1969) and a scaled mutation rate θ per site per generation. Here, θ represents twice the number of mutant lineages per generation in a subpopulation ( for haploids, for diploids, where μ is the unscaled per-site per-generation mutation rate). We take the mean across all subpopulations of the pairwise coalescence time within subpopulations:
| (4) |
Note that πS is also informative about total nucleotide diversity when M is large, because from tables 2 to 4 and supplementary table S1, Supplementary Material online, the total coalescence time tends to the mean within-subpopulation coalescence time across all subpopulations as .
We analytically computed the within-subpopulation nucleotide diversities for each motif by substituting the expected coalescence time from tables 2 to 4 into equation (4). Nucleotide diversity appears in supplementary figure S2, Supplementary Material online, as a function of network metrics.
Genetic Differentiation
For each motif, we compute expected values of FST between pairs of distinct subpopulations i and j, denoted by , from pairwise coalescence times. From Slatkin (1991),
| (5) |
where is the expected coalescence time of two lineages sampled in the same subpopulation, and is the expected coalescence time of two lineages sampled in the total population. We compute equation (5) using equation (3).
For a K-vertex motif, FST has mean
| (6) |
across subpopulation pairs. We analytically computed the expected FST from equation (6) for each motif for sets of 3 and 4 subpopulations (fig. 1). The expected pairwise FST values for 2-, 3-, and 4-vertex motifs appear in tables 2, 3, and 5, respectively. FST appears in supplementary figure S2, Supplementary Material online, as a function of network metrics.
Table 5.
Exact FST Values for 4-Vertex Motifs.
| Motif | ||||||
|---|---|---|---|---|---|---|

|
1 | 1 | 1 | 1 | 1 | 1 |
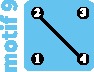
|
1 | 1 | 1 | 1 | 1 | |
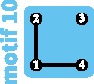
|
1 | 1 | 1 | |||
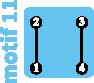
|
1 | 1 | 1 | 1 | ||
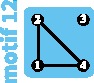
|
1 | 1 | 1 | |||
|
||||||
|
||||||
|
||||||
|
||||||
|
||||||
|
Half-Time to Equilibrium Diversity
Next, we are interested in an approximation of the time needed for population-genetic statistics to reach their expected value for a given migration motif. We therefore investigate the dynamics of πS and FST. These dynamics are governed by the eigenvalues of matrix Q (table 1; e.g., Slatkin 1991). Considering an event that changed the population demography τ time units ago, πS and FST will be at equilibrium in the sense that their values are stable through time if the probability that coalescence occurs at time is small, and thus, if , where is the null vector corresponding to the noncoalesced states and is the vector of ones corresponding to the coalesced state.
Considering the eigendecomposition , where Λ is the diagonal matrix whose elements correspond to the eigenvalues of Q and U is the matrix whose columns are the eigenvectors of Q, . Thus, when . In turn, this condition requires that for all eigenvalues λi except one, for which . The condition holds if the largest eigenvalue of Q is 0 and the second-largest—denoted by λ—satisfies . Because Q is an irreducible instantaneous rate matrix, its largest eigenvalue is 0 and all other eigenvalues are strictly negative (corollary 4.9 in Asmussen [2008]).
We define the half-time to equilibrium τ as a function of λ, the second-largest eigenvalue of matrix Q, by
| (7) |
τ corresponds to the time at which . Thus, when , and πS and FST are approximately at equilibrium. The value of τ gives a sense of the time needed for πS and FST to reach equilibrium values after a perturbation, such as after a loss of a connection or a subpopulation. This value depends on subpopulation connectivity patterns. Note that τ has the same units as t and is measured as a multiple of the number of lineages in a single subpopulation (N for haploids, 2N for diploids).
We computed the half-time to equilibrium from equation (7) for each motif for sets of 1–4 subpopulations (fig. 1), numerically evaluating the second-largest eigenvalue of Q. Results appear in supplementary figure S2, Supplementary Material online, as a function of network metrics.
Network Motifs and Patterns of Genetic Variation
To describe the influence of the properties of network motifs on our genetic variation measures, we computed the correlations between four network metrics and the mean within-subpopulation diversity πS across subpopulations, the mean FST across pairs of subpopulations, , and the half-time to equilibrium diversity τ.
Network Metrics
For a given motif, we denote by V and E its sets of vertices and edges, so that and correspond to the numbers of vertices and edges of the motif.
The first network metric we use is , the motif size, or number of subpopulations K; here, ranges from 1 to 4. The second metric is , which corresponds to the number of pairs of subpopulations between which gene flow occurs; ranges between 0 and . Our third metric is the mean vertex degree , or the number of connections of an average subpopulation; it ranges from 0 to K − 1. The fourth network metric is the density , the number of edges divided by the maximum number of edges possible if the motif were a fully connected graph; it ranges from 0 to 1.
Correlations between Network Metrics and Patterns of Genetic Variation
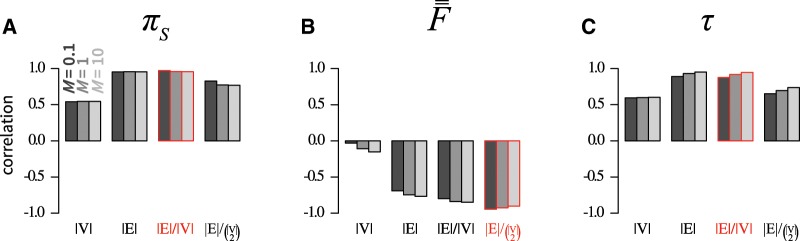
Correlations between network metrics and πS, , and τ for motifs with up to four subpopulations appear in figure 3. Diversity πS is positively correlated with all four metrics, most strongly with the number of edges (r = 0.96 for M = 10; fig. 3A) and the mean degree (r = 0.96 for M = 0.1 and M = 1; fig. 3A). Indeed, the highest values of πS occur for motifs 16, 17, and 18, which have the largest mean degree (2, 2.5, and 3, respectively), whereas the lowest values occur for motifs 1, 2, 4, and 8, which have mean degree 0.
Fig. 3.
Pearson correlations between network metrics and genetic diversity measures. (A) πS, mean within-subpopulation nucleotide diversity (eq. 4). (B) , mean pairwise FST across subpopulations (eq. 6). (C) τ, half-time to equilibrium diversity (eq. 7). Network metrics include number of vertices , number of edges , mean number of edges per vertex , and density of edges . All network motifs in figure 1 are considered. In each panel, the most strongly correlated metric appears in red.
The correlation of πS with can be interpreted in terms of the dependence between πS and the sizes of connected components. From supplementary table S2, Supplementary Material online, the within-subpopulation coalescence time of a subpopulation i generally scales with the size of the component to which it belongs, denoted by : components of size have Tii = 1, components of size have Tii = 2, components of size have , and components of size have . As a result, the mean within-subpopulation diversity πS is expected to be larger for motifs with fewer components. Because the mean component size is expected to be larger when the mean degree is large, we expect to be a proxy for the mean , and thus, to indirectly increase πS.
correlates negatively with the four metrics, especially the density ( for M = 10; fig. 3B). Indeed, for large M (supplementary fig. S2H, Supplementary Material online), the lowest values occur for the densest motifs—3, 7, and 18—which have the maximal number of connections. The largest values occur for the least dense motifs—2, 4, and 8—which have 0 edges. This correlation can be interpreted in terms of isolation by distance (IBD), for which density can be viewed as a proxy. We expect isolation of subpopulations by their network distance to increase . Because IBD is expected to be larger in sparsely connected populations, we expect IBD and to decrease as a function of the mean degree and density .
Finally, τ is positively correlated with the four metrics, and most strongly with the mean degree (r = 0.95 for M = 10; fig. 3C). For large M (supplementary fig. S2I, Supplementary Material online), the largest τ values correspond to the motifs with largest mean degree (16, 17, and 18), whereas the lowest τ values occur for the motifs with the lowest degree (1, 2, 4, and 8). The correlation can be understood in terms of the relationship between τ and the size of the largest connected component of the motif, for which can be seen as a proxy. Because, by construction, transition matrix Q has a block structure when the motif consists of multiple connected components, its eigenvalues can be obtained simply from the smaller submatrices Q corresponding to the components. Thus, τ follows the time to equilibrium in the component that experiences the slowest dynamics, that is, the one with the largest effective population size or total coalescence time. Because we showed in supplementary table S1, Supplementary Material online, that the total coalescence time of a component generally scales with the size of the component, it follows that τ scales with the size of the largest component, a quantity that is expected to increase as the mean degree increases.
Impact of a Disturbance Event
In this section, we focus on the impact of a disturbance event on mean genetic diversity πS. Of the three quantities we emphasize—πS, , and τ—this quantity is perhaps the most central to conservation biology. See also supplementary figure S3, Supplementary Material online, for the impact of a disturbance on mean total genetic diversity πT.
Enumerating Outcomes of Disturbance Events
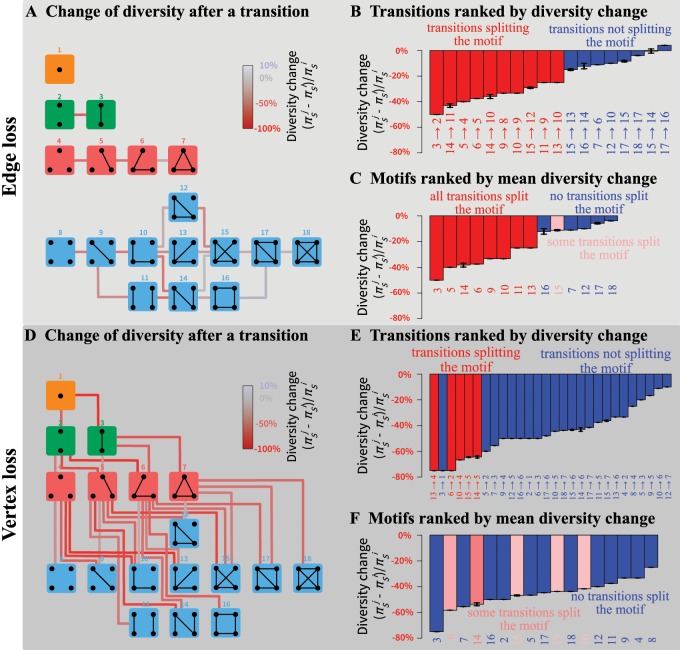
We enumerate all possible outcomes that could follow a disturbance event that removes a connection between two subpopulations or that removes a subpopulation. To do so, we compute a “graph of motifs,” where each vertex represents a motif, and we draw an edge between two motifs if they differ by a single subpopulation or a single connection. We orient edges of this graph from the motif with the larger number of subpopulations or connections toward the motif with the smaller number of subpopulations or connections. We give each edge a weight corresponding to the proportion of within-subpopulation diversity change associated with the transition from motif i to j, , where is the mean within-subpopulation diversity computed from equation (4) applied to motif i. A negative weight indicates that the transition from motif i to motif j induces a loss of mean within-subpopulation diversity, whereas a positive weight indicates that the transition from motif i to motif j induces a gain of mean within-subpopulation diversity. In the case of a vertex loss, we consider that the lost subpopulation has diversity 0; for example, the transition from motif 3, where two subpopulations each have diversity 2 (table 2), to motif 1, where a single subpopulation has diversity 1 and the “other” has diversity 0, leads to a change of , that is, of 75% of the within-subpopulation diversity.
Edge Losses and Vertex Losses
The graph of motifs appears in figure 4A for edge loss and in figure 4D for vertex loss. We focus on the case of M = 1.
Fig. 4.
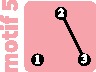
Change of within-subpopulation nucleotide diversity following a transition from motif i to motif j, for all transitions involving the loss of a single edge or a single vertex. (A) Schematic representation of all motif transitions involving an edge loss. (B) Motif transitions involving an edge loss ranked by value. (C) Motifs ranked from largest to smallest diversity loss following edge loss. For each motif, the mean loss or gain is computed across all possible transitions to another motif. For example, for motif 5, three subpopulations can be lost; loss of the isolated subpopulation produces motif 3, leading to , and loss of one of the two other subpopulations produces motif 2 and . The mean diversity loss for motif 5 is thus . (D) Schematic representation of all motif transitions involving a vertex loss; note that in the case of vertex loss, we consider that the lost subpopulation has diversity 0 (see example in the Enumerating Outcomes of Disturbance Events section). (E) Motif transitions involving a vertex loss ranked by value. (F) Motifs ranked from largest to smallest mean diversity loss following vertex loss. In (A) and (D), lines connecting motifs represent transitions and are colored by value. In all panels, values assume M = 1; in (B), (C), (E), and (F), black horizontal bars represent minimum and maximum values for M in . Values of and are computed from equation (4); minima and maxima of are obtained numerically.
Loss of an edge can lead to diversity changes ranging from a loss of 50% to a gain of 4% (fig. 4B). Interestingly, the transitions that lead to the greatest losses all split a motif into disconnected sets of subpopulations (transitions in red, fig. 4B). The greatest diversity loss occurs with the transition from motif 3—which has a single connected pair of subpopulations—to motif 2, which has two isolated subpopulations.
Generally, the change in diversity is negative for the most strongly negative changes in the mean number of edges per vertex (supplementary fig. S4, Supplementary Material online). Transitions that reduce the number of edges without changing the number of vertices—in particular, transitions that lead to linear and circular stepping-stone models (17 to 16, 15 to 14, and 7 to 6)—tend to produce decreases in diversity that are relatively small in magnitude. Surprisingly, one edge-loss transition increases the diversity for all migration rates in : the transition from motif 17 to motif 16. This transition increases the coalescence time for lineages sampled from different subpopulations without isolating any subpopulations.
The impact on diversity of the loss of a vertex ranges from a loss of 75% to a loss of 10% (fig. 4E). Similarly to the edge-loss case, the vertex losses that lead to the greatest losses generally correspond to a split of the motif into disconnected sets of subpopulations (transitions in red, fig. 4E). For instance, the greatest diversity loss is associated with the transition from motif 13—which has a single set of four connected subpopulations—to motif 4, which has three isolated subpopulations.
Similarly to the case of edge losses, we observe a general pattern of greatest diversity loss with the greatest reduction in (supplementary fig. S4, Supplementary Material online). For a similar change in , transitions from the motifs with the most subpopulations and connections (17 to 6 and 18 to 7) tend to lead to lower losses of diversity. By contrast, for a similar reduction in , transitions from the motifs with the fewest subpopulations and connections (3 to 1 and 2 to 1) tend to lead to greater losses of diversity. These cases illustrate that a single subpopulation or connection loss has a lesser impact on larger and more connected populations.
Note that splitting a motif into disconnected components leads to infinite coalescence times between subpopulations, and thus to infinite expected total diversity πT. The transitions that do not split the motif have similar effects on πS (fig. 4B, C, E, and F) and πT (supplementary fig. S3, Supplementary Material online): in particular, the transitions that can lead to an increase in πS (from motif 17 to 16, and from motif 15 to 14) also lead to an increase in πT.
Fragile and Robust Motifs
We can also identify the most “fragile” motifs: the motifs for which disturbance leads to the greatest diversity loss. For each motif, we compute the diversity changes associated with all edge or vertex losses, reporting the mean across the edge or vertex set. Motifs ranked by robustness to an edge loss appear in figure 4C. The most fragile motifs are those split into disconnected components by an edge loss, whereas the most “robust” motifs are those that are not split.
Motifs ranked by robustness to a vertex loss appear in figure 4F. We can see that the most fragile motifs are motifs 3, 6, and 14 (linear stepping-stone models) and motifs 7 and 16 (circular stepping-stone models). The linear stepping-stone motifs are easily split by a vertex loss, producing a disconnection that is expected to reduce diversity. The circular stepping-stone models, however, are not easily split by a vertex loss. Their fragility stems from their high diversity, among the highest of all models, on par with island models (tables 2–4). Any motif transition is thus likely to substantially reduce diversity.
Examples
We use the results from our network-based model to reinterpret spatial genetic structure in two animal examples. Using published spatial and genetic information for each example, we propose a network motif that might represent the structure of the population. We then ask what types of transitions could result in increased or decreased population structure and variation in the context of the conservation biology of the species examined.
Indian Sky Island Birds of Genus Sholicola
First, we consider three species of genus Sholicola, birds endemic to the Western Ghats sky islands of India: S. albiventris, S. major, and S. ashambuensis. Robin et al. (2015) reported microsatellite data from multiple geographically separated subpopulations, sampling 218 individuals at 14 microsatellite loci. These subpopulations have experienced changes in geographic range and gene flow on both evolutionary and anthropogenic time scales, owing to Pleistocene climate change that could have shifted the locations of suitable habitat and recent deforestation. Such changes can influence numbers of populations and gene flow between them and can be interpreted using our network model.
Robin et al. (2015) stated that genetic differentiation in the species was not quite compatible with a simple island-migration model, so that our network approach might provide additional insight. Indeed, consistent with geographic barriers, Robin et al. (2015) observed genetic differentiation between the species, as well as subgroups within each species. The data generally fit motif 11 (fig. 5A), containing two relatively isolated sets of subpopulations, each with two subpopulations that exchange migrants. However, FST values between the two species sets (supplementary table S3 of Robin et al. [2015]) were lower than the high values expected under motif 11 (table 5), potentially as a result of a short time scale of fragmentation.
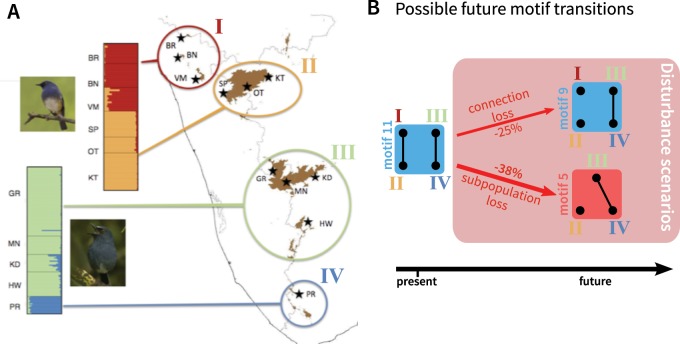
Fig. 5.
Application of the network theory framework to the Indian sky island birds Sholicola albiventris, S. major, and S. ashambuensis. (A) Map of the distribution of S. albiventris, S. major, and S. ashambuensis in the Indian sky islands of the Western Ghats with sampling locations, and STRUCTURE plot. The map and the STRUCTURE plot are adapted from Robin et al. (2015) and informed by Robin et al. (2017). Colors and roman numerals represent the four genetic clusters. Two-letter codes indicate the sampling locations. Sampling locations for S. major include BR, Brahmagiri; BN, Banasura; VM, Vellarimala; SP, Sispara; OT, Ooty; and KT, Kothagiri. Sampling locations for S. albiventris include GR, Grasshills; MN, Munnar; KD, Kodaik-anal; and HW, High Wavys. Sampling locations for S. ashambuensis include PR, Peppara. (B) Possible future motif transitions, based on the transitions from motif 11, which is taken to represent the current state of the population. Numbers on arrows represent predicted losses of mean nucleotide diversity across subpopulations (fig. 4).
Under the network model, supposing that the current motif is 11, we can investigate the future impact of the loss of an edge or vertex, representing events possible for an endangered species (fig. 5B). The transition from motif 11 to motif 9 is seen as a loss of an edge, corresponding to a loss of migration between one of the pairs of subpopulations. This event decreases within-subpopulation nucleotide diversity (−25%; fig. 4C), and leads to increasing FST genetic differentiation between subpopulations, particularly within each species. The loss of a subpopulation, transitioning from motif 11 to motif 5, similarly leads to a loss of within-subpopulation nucleotide diversity (−38%; fig. 4F).
Note that the losses reported are expected losses in the long term. The half-time to equilibrium τ values for motifs 5 and 9 appear in supplementary figure S2C, F, and I, Supplementary Material online. Interestingly, they are equal, and correspond to 7.69 for M = 0.1, 1.81 for M = 1, and 1.42 for M = 10, in units of 2N generations. Thus, depending on the migration rate, the future decrease of genetic diversity substantially changes. The identical τ values for the two motifs result from the fact that τ is determined by the motif component with the lowest half-time to equilibrium, and the two motifs have similar components—a pair of connected subpopulations and either one or two isolated subpopulations.
Comparing the edge-loss and vertex-loss scenarios, a vertex-loss transition from motif 11 to motif 5 has a greater negative effect on nucleotide diversity, because it has the largest long-term effects and the equilibrium is reached as quickly as in the edge-loss transition. In this case, focusing on preserving subpopulations rather than gene flow is predicted to avoid the most detrimental loss of genetic diversity for the subpopulations.
Indian Tigers
Next, we consider genetic variation for tigers in India, representing 60% of the global wild tiger population (Mondol et al. 2009). Natesh et al. (2017) considered the genetic diversity and structure across the Indian subcontinent of tigers, a species that now occupies 7% of its historical range. India’s ∼2,500 tigers are distributed across many small groups, with a median size of 19 across recognized groups. Understanding population structure and connectivity is important to tiger conservation.
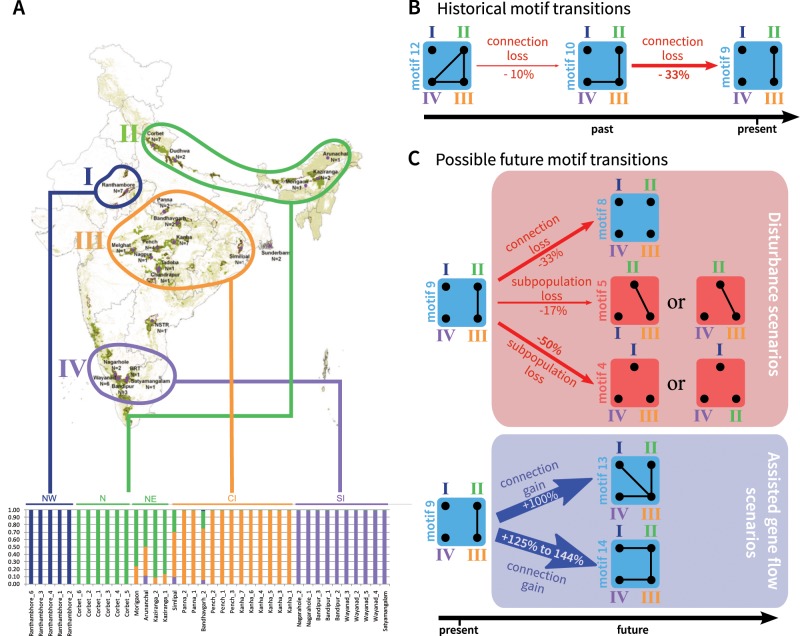
Using 10,184 single nucleotide polymorphisms, Natesh et al. (2017) identified a northwestern subpopulation (dark blue cluster I in fig. 6A), a north/northeastern subpopulation (green cluster II), a central subpopulation (orange cluster III), and a southern subpopulation (purple cluster IV). They reported evidence of gene flow between subpopulations III and IV and between subpopulations II and III. The exact relationship between subpopulations, however was unclear. From the pairwise FST values reported in table 2 of Natesh et al. (2017), levels of divergence between subpopulation I and all other subpopulations were high, suggesting isolation with limited gene flow. fastSTRUCTURE analyses performed by Natesh et al. (2017) suggested connectivity between subpopulations II and III (fig. 6A). Owing to the large FST between the northeastern subpopulation (II) and the southern subpopulation (IV) and between the central subpopulation (III) and the southern subpopulation (IV), we suggest that the motif most clearly fitting the current population structure is motif 9.
Fig. 6.
Application of the network theory framework to Indian tigers. (A) Map of the distribution of tigers with sampling locations, and fastSTRUCTURE plot. The figure is adapted from Natesh et al. (2017). Note that sample sizes for the fastSTRUCTURE plot include only subsets of individuals from Natesh et al. (2017). (B) Hypothetical sequence of past motif transitions proposed by Natesh et al. (2017) on the basis of genetic and historical data, presented in the framework of figure 4. (C) Possible future motif transitions, based on the transitions from motif 9 (fig. 4). For (B) and (C), motif 9 is taken to represent the current state of the population; percentages correspond to the proportion of within-subpopulation diversity change following each motif transition (from fig. 4).
Because of the smaller pairwise FST values between subpopulations II and IV and between subpopulations III and IV than between subpopulations I and IV, we suggest that a recent change in network structure occurred from motif 12 to motif 9 (fig. 6B), involving recent loss of connectivity between subpopulation IV and the other subpopulations, and leading to a loss of 40% of the within-subpopulation diversity (−10% from the transition from motif 12 to motif 10, and then −33% from the transition from motif 10 to motif 9). That connectivity loss might have occurred recently is supported by previous genetic and historical data: an earlier study with ten microsatellite markers suggests an older transition between motif 15 and 12, with connectivity loss between subpopulations I and II (Mondol et al. 2013).
Ongoing perturbations to the network are likely, owing to increasing human pressures and land-use changes that reduce population sizes and increase fragmentation (fig. 6C). The transition from motif 9 to motif 8, involving the loss of an edge, would decrease within-subpopulation nucleotide diversity by 33% (figs. 4C and 6C). The loss of a subpopulation, however, leads to qualitative differences in the genetic structure depending on the subpopulation lost. If the more isolated northwestern subpopulation I or the southern subpopulation IV is lost, then the resulting network is similar to motif 5, with a moderate decrease in within-subpopulation nucleotide diversity (−17%) and a decrease in differentiation overall because an isolated subpopulation is lost (figs. 4D and 6C). By contrast, if one of the connected subpopulations, the central subpopulation III or the northern/northeastern subpopulation II, is lost, then a decrease in diversity is expected (−50%; figs. 4F and 6C).
To maintain or restore some of the recently lost genetic diversity of Indian tigers, Kelly and Phillips (2016) suggested reconnecting isolated subpopulations by assisted migration (fig. 6C). Two such reconnection scenarios can be imagined. The first scenario, which corresponds to restoring lost migration routes (fig. 4B), reconnects the central subpopulation III with all other subpopulations, producing a transition from motif 9 to motif 13. It would lead to an increase of within-subpopulation diversity of 100%. Alternatively, a second scenario in which subpopulations are reconnected along a line, forming a linear stepping-stone, is possible, corresponding to a transition from motif 9 to motif 14. This scenario might seem less intuitive, as it does not correspond to any previous population structure. Interestingly, it leads to a greater increase of diversity (+125% to +144%, depending on the amount of gene flow; supplementary table S2, Supplementary Material online).
Note that the losses and gains of diversity reported are expected losses and gains in the long term. The τ values for motifs 4, 5, 8, 13, and 14—the motifs that are possible as the result of the transitions in figure 6C—appear in supplementary figure S2C, F, and I, Supplementary Material online. τ has the same value of 0.69 for both motifs 4 and 8, because they have only isolated subpopulations. τ for motif 5 is 7.69 for M = 0.1, 1.81 for M = 1, and 1.42 for M = 10, in units of 2N generations. Thus, in addition to being the transition leading to the greatest diversity loss, the transition from motif 9 to motif 4 is also the one that affects diversity the fastest. τ for motif 13 is 17.76 for M = 0.1, 3.34 for M = 1, and 2.19 for M = 10, in units of 2N generations. τ for motif 14 is 29.32 for M = 0.1, 4.72 for M = 1, and 2.68 for M = 10, in units of 2N generations; the time required to restore diversity exceeds the time it takes to lose it. Among assisted gene flow scenarios, the transition to motif 14 that leads to the larger amount of diversity in the long term among the pair of scenarios considered is the one with the slower change of diversity. This result suggests a tradeoff between the magnitude and speed of the transition to long-term effects on diversity.
Discussion
We have presented a novel framework that combines network theory and population genetics to study the impact of population structure on patterns of genetic variation under diverse assumptions about population connectivity. Treating a structured population as a network containing vertices that represent subpopulations and edges that represent gene flow, considering all possible population network motifs for sets of one to four subpopulations, we have determined motif features that correlate with patterns of genetic variation. Among four motif statistics, we found that the mean node degree is the most strongly correlated with within-subpopulation diversity, and that motif density is the most strongly correlated with genetic differentiation among subpopulations.
Our framework makes it possible to predict the impact on genetic diversity of disturbances such as loss of a subpopulation or a connection between subpopulations. The effect of the loss of a vertex or edge depends on the context of the disturbance in the population network. Whereas some disturbances that split the network, including edge losses in transitions from motif 3 to 2 and from 14 to 11 and the vertex loss in the transition from motif 13 to 4, substantially reduce genetic diversity, others such as the transition from motif 17 to 16 instead increase mean diversity across subpopulations (fig. 4).
Theoretical Advances
Our results extend classical coalescent theory results concerning migration models. Among the 18 network motifs we studied, 11 correspond to migration models that differ from the standard models.
As has been seen previously (Slatkin 1987; Strobeck 1987; Wilkinson-Herbots 2003), for connected motifs all of whose subpopulations are exchangeable and none of whose subpopulations are isolated (i.e., motifs 3, 7, 16, and 18), we find that the within-subpopulation pairwise coalescence times are independent of the migration rate, as long as the migration rate is nonzero (supplementary table S2, Supplementary Material online). Interestingly, we observe that this result on migration rate independence also holds for motifs with disconnected components (motifs 2, 4, 5, and 8–12), even though disconnection leads to violation of the assumption of migration matrix irreducibility used by Slatkin (1987). This result can be explained by the fact that such motifs all involve juxtaposition of smaller motifs, each of which has exchangeable subpopulations, none of which are isolated. Consequently, even though motifs 2, 4, 5, and 8–12 do not satisfy the assumptions used by Slatkin (1987), that each component of the motif satisfies them suffices to ensure the result on migration-rate independence.
Motifs 14, 15, and 17, for example, do not have exchangeable vertices, nor can these motifs be decomposed into disconnected components that each have exchangeable vertices. Their within-subpopulation coalescence times do depend on the migration rate (supplementary table S2, Supplementary Material online). Nevertheless, within-subpopulation coalescence times of all motifs vary relatively little with the migration rate: the difference between the maximum and minimum values is less than 15% of the minimum (supplementary table S2, Supplementary Material online). Migration rates have only a small effect on within-subpopulation diversity in many spatial configurations.
We find that total coalescent times for specific connected components of the motifs follow formulas of the form , where a is a scaling factor and f(M) is a rational function of M (supplementary table S1, Supplementary Material online). When a = 1, these formulas resemble the classical formula from the island model (Wakeley 1998), where time is scaled in units of N for haploids and 2N for diploids and the factor in brackets is small for large M. Interestingly, we find cases for which a < 1 (motifs 6, 10, 13, 14, 15, and 17), meaning that for large M, the total coalescence time is less than K, the sum of the local subpopulation sizes (in units of the size of a single subpopulation).
Our results also extend classical theoretical results about genetic differentiation. Under the island model, FST follows a formula , for a constant (Wright 1951; Nei and Takahata 1993). Because FST is by definition a ratio of within-subpopulation pairwise coalescence time to total pairwise coalescence time, FST is governed by the relative waiting time for two lineages to reach the same subpopulation and the waiting time for two lineages in the same subpopulation to coalesce. The constant α determines the relative impact of drift and migration on the values of these waiting times, with small α corresponding to a greater effect of drift and a consequent increase for FST. FST also approximately follows under the linear and circular stepping-stone models (Cox and Durrett 2002). For a fixed number of subpopulations K, among networks with all nodes connected, α is smallest under the island model and largest under the stepping-stone model (Cox and Durrett 2002).
We exhibit additional models under which pairwise FST follows , where α is intermediate between that expected under the island and linear and circular stepping-stone models (supplementary table S3, Supplementary Material online). All models that have exchangeable vertices or that are decomposable into components each with exchangeable vertices (motifs 2–5, 7–9, 11, 12, 16, and 18) have FST values that follow this formula. Interestingly, motif 13, which does not have exchangeable vertices and is not decomposable in this manner, also has an FST that follows such a formula, with α = 2 or 3. Its α values lie near those of the island-migration motif 18, with , and the linear stepping-stone motif 14, with α ranging from 1.129 to 3.2 across population pairs and across migration rates, and they are also similar to that of the circular stepping-stone motif 16 (α = 2 or 8/3), although motif 16 has more connections.
Motifs 15 and 17 also have nonexchangeable vertices and are not decomposable, and they have FST values whose expressions involve rational functions of M (table 5). We show in supplementary table S3, Supplementary Material online, however, that their FST values approximately follow an expression of the form , with α ranging from 1.747 to 2.989; in addition, their α values are close to that of motif 16, with α = 2 or 8/3. Although motifs 4, 5, and 8–12 have at least two disconnected components and thus their global FST is equal to 1 irrespective of the value of M, their pairwise FST values for connected subpopulations do follow , with α ranging from 2 to 4. Overall, our results highlight that the classical formula is a helpful approximation for all motifs with up to four subpopulations.
For decomposable motifs that can be described using combinations of motifs for smaller numbers of subpopulations, the values of πS can be written as weighted averages of values for their components. The mean pairwise FST can be decomposed into contributions from within-component comparisons and contributions from between-component comparisons, the latter values equaling 1. The τ value of a decomposable motif is related to that of the largest component; τ relates to the amount of genetic drift in the component where genetic drift acts the slowest, generally the largest component. The transitions from a decomposable motif, however, cannot easily be described in terms of transitions from its components. For example, the transition from motif 10 to motif 4, which converts a motif with two components into a motif with three components, is most naturally viewed as a loss of a component and a conversion of a three-vertex component into three one-vertex components, rather than a transition in which both initial components are retained.
Data Applications
Our results provide a framework for interpreting empirical patterns of genetic diversity and differentiation, and for predicting future patterns. We have illustrated how they provide insight into two systems of conservation interest, Indian sky island birds of genus Sholicola and Indian tigers. After suggesting the most appropriate motif for each species and the sequence of transitions that might have led to the current motif, we enumerated future disturbances and highlighted the ones that would have the strongest long-term impact on genetic diversity within subpopulations. For tigers, we enumerated possible assisted gene flow scenarios and highlighted scenarios leading to the greatest long-term genetic diversity increase.
In conservation biology, combating the negative effects of fragmentation can require a combination of gene flow interventions and prioritized management of areas that allow for connectivity in the future. As noninvasive population-genomic data become more feasible to produce (e.g., Natesh et al. 2019), network models based on empirical data, such as presented in the examples here, could assist in ensuring connectivity and long-term sustainability of gene flow. As we demonstrate in our examples, our theoretical results suggest hypotheses about conservation scenarios without the need to fit complex models: theoretical results such as ours can provide a path forward, even with data that are not primarily genetic. In other words, beyond the scenarios we have examined, our results could benefit species of conservation interest for which little or no genetic data are available.
Many studies have focused on deducing population networks from genetic data in population genetics; most such applications have focused on clustering with community detection algorithms, without using a population-genetic model (Dyer and Nason 2004; Garroway et al. 2008; Rozenfeld et al. 2008; Ball et al. 2010; Munwes et al. 2010; Dyer 2015; Greenbaum et al. 2016). Although these statistical approaches are appealing for making sense of complex data sets, the population-genetic models we consider are useful for providing predictions about genetic diversity patterns. We have demonstrated how simple network motifs can be deduced from cluster analyses and pairwise FST values and can then be used to predict the impact of future disturbances.
The network theory framework is promising for the analysis of natural populations whose spatial arrangements do not follow classical migration models. For example, river systems involve subpopulations arranged along a stream, leading to a motif with a linear arrangement such as 3, 6, and 14, or in different streams, leading to a star-shaped motif such as 13 (Morrissey and de Kerckhove 2009). Geographic barriers owing to mountains, valleys, and human occupation can isolate one (motifs 2, 5, 11, and 12) or several subpopulations (motifs 4, 8, and 9). Moreover, many landscapes present a specific zone with high resistance, for example owing to low habitat quality, leading to partial isolation of a subpopulation from a strongly connected set of subpopulations (motif 15).
Our exhaustive enumeration of motifs ensures that we can confront empirical data with expected patterns of genetic variation under any spatial arrangement. This enumeration can improve our ability to interpret genetic data, especially for threatened species, which typically present high fragmentation and are likely to undergo future disturbances resulting from further human-induced habitat loss or from conservation efforts such as assisted gene flow. The framework is also promising for conservation planning, because it suggests which connections or subpopulations are more important in contributing to genetic variation. Historical human impacts, ongoing urbanization, and habitat fragmentation are leading to species range collapse and population decline (e.g., carnivores; Ripple et al. 2014). Some species, such as the sky island birds of genus Sholicola, are specialized to habitats that are naturally patchy and isolated (Robin et al. 2015). Understanding the consequences of such patchiness from a network perspective can provide insights on mitigation for ongoing habitat fragmentation.
In species such as the Indian tiger, conservation might require management strategies that include assisted migration (Kelly and Phillips 2016). In such contexts, strategies can be designed for maximizing genetic variation, by giving the existing set of subpopulations the most favorable connections possible. For designing such strategies, our approach provides an alternative to spatially explicit landscape-genetic models focused on effects in physical space, enabling assessment of the potential genetic consequences of alternative network motifs.
Extensions and Limitations
Several assumptions of our model could be relaxed to make it more closely match natural systems. We only considered homogeneous subpopulations, with equal sizes and equal migration rates outward back in time in all nonisolated subpopulations, and equilibrium genetic variation. Heterogeneous sizes are common in environments with varying habitat quality (Dias 1996), and migration-rate differences are common in species that disperse passively, such as by currents or wind (Vuilleumier and Possingham 2006). Permitting heterogeneity would increase the number of motifs possible for fixed numbers of subpopulations, potentially introducing source-sink dynamics (Dias 1996). These dynamics are expected to influence robustness to loss of a connection or subpopulation: we expect nucleotide diversity to be robust to loss of a connection to a sink subpopulation or loss of a sink subpopulation itself, because such subpopulations might be small with relatively low nucleotide diversity. Conversely, we expect nucleotide diversity to be less robust to the loss of a source subpopulation, as these subpopulations are typically larger and more diverse.
Nonequilibrium genetic diversity is common in species that face frequent environmental changes, and it can result in transient levels of genetic variation that strongly differ from the equilibrium and that persist for many generations (Alcala et al. 2013; Alcala and Vuilleumier 2014). The expected diversities in tables 2–5 correspond to long-term expectations, and they give a sense of the potential of a given spatial configuration to permit large levels of genetic diversity. To assess the impact of a perturbation, long-term expectations must be contrasted with the time to reach them. We thus advocate computation of the half-time to equilibrium τ, which gives a sense of the time needed for nucleotide diversity and FST to approach their equilibrium values. Interestingly, we find that τ is strongly correlated with the mean vertex degree; it would be worthwhile to assess the potential of as a predictor of τ in larger networks.
We caution that with the current assumptions and even with extensions implemented, the network model is not expected to apply perfectly to natural systems. The network motifs give a small set of models that can provide a framework for understanding dynamics among small numbers of populations in a conservation setting. Investigators might be aware of deviations from the assumptions constraining the various migration rates or of other deviations from the model, and such deviations could have substantial impact on predictions about optimal conservation strategies. Our view is that the model is valuable for considering when such deviations are known to be relevant, but it is then most usefully applied alongside other theoretical frameworks.
Conclusion
This work is a step toward developing a general theory that links network topology and patterns of genetic variation. Small motifs are the building blocks of complex networks (Milo et al. 2002); thus, our results on small motifs can assist in formulating hypotheses about the behavior of larger networks. For example, because we have seen that within-subpopulation diversity generally increases with the mean degree of the network and relies on a general relationship of diversity πS to the sizes of connected components, we expect this relationship to hold for larger network sizes. For large networks, counting the number of appearances of each 3- or 4-vertex motif can give an initial idea of the fine-scale structure of the population. Because we have observed that FST decreases with network density , we can hypothesize that for a fixed large network size, if the network contains many instances of motifs 17 or 18, then it is dense and thus is likely to have low FST. On the other hand, if we find many instances of lower-density motifs 9, 10, and 14, then we can predict an opposite pattern.
The detection of motifs that are overrepresented in certain types of network (e.g., ecological, neural, protein-interaction) has been used to identify network classes that share common properties despite describing different data types (Milo et al. 2002; Alon 2007). Further work could consider motifs that are overrepresented in population networks, to assess whether population networks have a shared “motif signature” or if certain networks are more common in certain habitats (e.g., marine, river, and terrestrial). Such an approach could help identify similarities between population networks and other types of biological networks. Our results can potentially be extended to larger networks, and it could be assessed how global patterns in genetic diversity and FST can be predicted from information on the occurrence of small motifs. Such an extension will become increasingly valuable as more empirical studies sample genomic data sets from broad geographical scales with fine-grained sampling resolution.
Materials and Methods
Deriving Expected Coalescence Times
Expected coalescence times can be obtained by first-step analysis. The expected coalescence time of all states (ij) (eq. 3), where i ranges in and j ranges in , can be decomposed into a sum of expected coalescence times (Notohara 1990; Wakeley 1998):
| (8) |
where is the expected time before a change of state, and
where q terms are taken from table 1. Equation (8) describes a system of equations. In the next sections, we describe this system of equations in the cases of K = 1 to K = 4. We provide the spreadsheet (Software Maxima 2014) used for all calculations in supplementary file S1, Supplementary Material online.
1-Vertex Motif
The case of one subpopulation has a single possible initial state, which is given by classical coalescent results (Kingman 1982):
| (9) |
This quantity directly gives the expected pairwise coalescence time of motif 1.
2-Vertex Motifs
In the case of two subpopulations, . Equation (8) then simplifies to
| (10) |
This system and its solution were derived by Nath and Griffiths (1993). Setting M = 0 and solving the system for , and gives the expected pairwise coalescence times of motif 2 (table 2). Considering M > 0 and solving the system gives the expected pairwise coalescence times of motif 3 (table 2).
3-Vertex Motifs
In the case of three subpopulations (supplementary fig. S1, Supplementary Material online), equation (8) becomes
| (11) |
We set the values Mij to reflect the network motifs of figure 1, solve the linear system of equations, and report the corresponding expected times in table 3. For example, for motif 5, and in all equations, and we obtain the system of equations:
| (12) |
Note that this system is equivalent to considering that the isolated subpopulation 1 follows equation (9), that subpopulations 2 and 3 follow equation (10) with labels 2 and 3 in place of 1 and 2, and that coalescence times between subpopulations without migration (1 and 2 or 1 and 3) are infinite.
We can solve this system using substitution, by first noting that , and by then substituting the expression for into the equation of . We obtain as reported in table 3.
4-Vertex Motifs
For four subpopulations, equation (8) simplifies to
| (13) |
Similarly to the case of 3-vertex motifs, we set the values Mij to reflect the network motifs of figure 1, solve the system of equations using substitution or matrix inversion, and report the corresponding expected coalescence times in table 4.
Supplementary Material
Supplementary data are available at Molecular Biology and Evolution online.
Supplementary Material
Acknowledgments
We thank Gili Greenbaum, Ben Peter, an anonymous reviewer, and the editor for their helpful comments. Part of this work was completed when U.R. was a visitor at the Stanford Center for Computational, Evolutionary, and Human Genomics (CEHG). This work was supported by National Science Foundation grant DBI-1458059, a Stanford Center for Computational, Evolutionary and Human Genomics postdoctoral fellowship, and Swiss National Science Foundation Early Postdoc.Mobility fellowship P2LAP3_161869.
References
- Alcala N, Streit D, Goudet J, Vuilleumier S.. 2013. Peak and persistent excess of genetic diversity following an abrupt migration increase. Genetics 1933:953–971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alcala N, Vuilleumier S.. 2014. Turnover and accumulation of genetic diversity across large time-scale cycles of isolation and connection of populations. Proc R Soc Lond B Biol Sci. 2811794:20141369.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alon U. 2007. Network motifs: theory and experimental approaches. Nat Rev Genet. 86:450–461. [DOI] [PubMed] [Google Scholar]
- Asmussen S. 2008. Applied probability and queues. New York: Springer-Verlag. [Google Scholar]
- Ball MC, Finnegan L, Manseau M, Wilson P.. 2010. Integrating multiple analytical approaches to spatially delineate and characterize genetic population structure: an application to boreal caribou (Rangifer tarandus caribou) in central Canada. Conserv Genet. 116:2131–2143. [Google Scholar]
- Cox JT, Durrett R.. 2002. The stepping stone model: new formulas expose old myths. Ann Appl Probab. 12:1348–1377. [Google Scholar]
- Dias PC. 1996. Sources and sinks in population biology. Trends Ecol Evol. 118:326–330. [DOI] [PubMed] [Google Scholar]
- Donnelly P, Tavaré S.. 1995. Coalescents and genealogical structure under neutrality. Annu Rev Genet. 291:401–421. [DOI] [PubMed] [Google Scholar]
- Dyer RJ. 2015. Population graphs and landscape genetics. Annu Rev Ecol Evol Syst. 461:327–342. [Google Scholar]
- Dyer RJ, Nason JD.. 2004. Population graphs: the graph theoretic shape of genetic structure. Mol Ecol. 137:1713–1727. [DOI] [PubMed] [Google Scholar]
- Fu Y-X, Li W-H.. 1999. Coalescing into the 21st century: an overview and prospects of coalescent theory. Theor Popul Biol. 561:1–10. [DOI] [PubMed] [Google Scholar]
- Garroway CJ, Bowman J, Carr D, Wilson PJ.. 2008. Applications of graph theory to landscape genetics. Evol Appl. 1:620–630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenbaum G, Templeton AR, Bar-David S.. 2016. Inference and analysis of population structure using genetic data and network theory. Genetics 2024:1299–1312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly E, Phillips BL.. 2016. Targeted gene flow for conservation. Conserv Biol. 302:259–267. [DOI] [PubMed] [Google Scholar]
- Kimura M. 1953. “ Stepping Stone” model of population. Annu Rep Natl Inst Genet Jpn. 3:62–63. [Google Scholar]
- Kimura M. 1969. The number of heterozygous nucleotide sites maintained in a finite population due to steady flux of mutations. Genetics 61:893–903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kingman JFC. 1982. On the genealogy of large populations. J Appl Probab. 19A:27–43. [Google Scholar]
- Maruyama T. 1970. Effective number of alleles in a subdivided population. Theor Popul Biol. 13:273–306. [DOI] [PubMed] [Google Scholar]
- Maxima. 2014. Maxima, a computer algebra system, version 5.34.1. http://maxima.sourceforge.net/ Last accessed on March 2017.
- Milo R, Shen-Orr S, Itzkovitz S, Kashtan N, Chklovskii D, Alon U.. 2002. Network motifs: simple building blocks of complex networks. Science 2985594:824–827. [DOI] [PubMed] [Google Scholar]
- Mondol S, Bruford MW, Ramakrishnan U.. 2013. Demographic loss, genetic structure and the conservation implications for Indian tigers. Proc R Soc Lond B Biol Sci. 2801762:20130496.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mondol S, Karanth KU, Ramakrishnan U.. 2009. Why the Indian subcontinent holds the key to global tiger recovery. PLoS Genet. 58:e1000585.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrissey MB, de Kerckhove DT.. 2009. The maintenance of genetic variation due to asymmetric gene flow in dendritic metapopulations. Am Nat. 1746:875–889. [DOI] [PubMed] [Google Scholar]
- Munwes I, Geffen E, Roll U, Friedmann A, Daya A, Tikochinski Y, Gafny S.. 2010. The change in genetic diversity down the core-edge gradient in the eastern spadefoot toad (Pelobates syriacus). Mol Ecol. 1913:2675–2689. [DOI] [PubMed] [Google Scholar]
- Natesh M, Atla G, Nigam P, Jhala YV, Zachariah A, Borthakur U, Ramakrishnan U.. 2017. Conservation priorities for endangered Indian tigers through a genomic lens. Sci Rep. 7:9614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Natesh M, Taylor RW, Truelove NK, Hadly EA, Palumbi SR, Petrov DA, Ramakrishnan U.. 2019. Empowering conservation practice with efficient and economical genotyping from poor quality samples. Methods Ecol Evol. 106:853–859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nath HB, Griffiths RC.. 1993. The coalescent in two colonies with symmetric migration. J Math Biol. 318:841–852. [DOI] [PubMed] [Google Scholar]
- Nei M, Takahata N.. 1993. Effective population size, genetic diversity, and coalescence time in subdivided populations. J Mol Evol. 37:240–244. [DOI] [PubMed] [Google Scholar]
- Notohara M. 1990. The coalescent and the genealogical process in geographically structured population. J Math Biol. 29:59–75. [DOI] [PubMed] [Google Scholar]
- Read RC, Wilson RJ.. 2005. An atlas of graphs (mathematics). New York, NY, USA: Oxford University Press. [Google Scholar]
- Ripple WJ, Estes JA, Beschta RL, Wilmers CC, Ritchie EG, Hebblewhite M, Berger J, Elmhagen B, Letnic M, Nelson MP, et al. 2014. Status and ecological effects of the world’s largest carnivores. Science 3436167:1241484. [DOI] [PubMed] [Google Scholar]
- Robin VV, Gupta P, Thatte P, Ramakrishnan U.. 2015. Islands within islands: two montane palaeo-endemic birds impacted by recent anthropogenic fragmentation. Mol Ecol. 2414:3572–3584. [DOI] [PubMed] [Google Scholar]
- Robin VV, Vishnudas C, Gupta P, Rheindt FE, Hooper DM, Ramakrishnan U, Reddy S.. 2017. Two new genera of songbirds represent endemic radiations from the shola sky islands of the Western Ghats, India. BMC Evol Biol. 17:31.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg NA, Nordborg M.. 2002. Genealogical trees, coalescent theory and the analysis of genetic polymorphisms. Nat Rev Genet. 35:380–390. [DOI] [PubMed] [Google Scholar]
- Rozenfeld AF, Arnaud-Haond S, Hernández-García E, Eguíluz VM, Serrão EA, Duarte CM.. 2008. Network analysis identifies weak and strong links in a metapopulation system. Proc Natl Acad Sci U S A. 10548:18824–18829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slatkin M. 1987. The average number of sites separating DNA sequences drawn from a subdivided population. Theor Popul Biol. 321:42–49. [DOI] [PubMed] [Google Scholar]
- Slatkin M. 1991. Inbreeding coefficients and coalescence times. Genet Res. 582:167–175. [DOI] [PubMed] [Google Scholar]
- Strobeck C. 1987. Average number of nucleotide differences in a sample from a single subpopulation: a test for population subdivision. Genetics 117:149–153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vuilleumier S, Possingham HP.. 2006. Does colonization asymmetry matter in metapopulations? Proc R Soc Lond B Biol Sci. 2731594:1637–1642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wakeley J. 1998. Segregating sites in Wright’s island model. Theor Popul Biol. 532:166–174. [DOI] [PubMed] [Google Scholar]
- Wilkinson-Herbots HM. 1998. Genealogy and subpopulation differentiation under various models of population structure. J Math Biol. 376:535–585. [Google Scholar]
- Wilkinson-Herbots HM. 2003. Coalescence times and FST values in subdivided populations with symmetric structure. Adv Appl Probab. 35:665–690. [Google Scholar]
- Wright S. 1951. The genetical structure of populations. Ann Eugen. 154:323–354. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.