Composite-scattering plasmonic nanoprobes for label-free, quantitative biomolecular sensing

Abstract

Biosensing based on localized surface plasmon resonance (LSPR) relies on concentrating light to a nanometeric spot and leads to a highly enhanced electromagnetic field near a metal nanostructure. Here, we present a design of plasmonic nanostructures based on rationally structured metal-dielectric combinations, which we call composite scattering probes (CSP), to generate an integrated multi-modal biosensing platform featuring LSPR and surface-enhanced Raman scattering (SERS) measurements. Specifically, we propose CSP configurations that have several prominent resonance peaks enabling higher tunability and sensitivity for self-referenced multiplexed analyte sensing. Using electron-beam evaporation and thermal de-wetting, we have fabricated large area, uniform, and tunable CSP, which are suitable for label-free LSPR and SERS measurements. The CSP prototypes were used to demonstrate refractive index sensing and molecular analysis using albumin as a model analyte. By using partial least squares on recorded absorption profiles, differentiation of subtle changes in refractive index (as low as 0.001) in the CSP milieu was demonstrated. Additionally, CSP facilitates complementary untargeted plasmon-enhanced Raman measurements from the sample’s compositional contributors. With further refinement, we envision that our method may lead to a sensitive, versatile and tunable platform for quantitative concentration determination and molecular fingerprinting, particularly where limited a priori information of the sample is available.

Introduction

Biosensors offering fast and accurate detection of biomarkers can serve as important tools for point-of-care medical diagnostics^[1,2]. Tagging the biomarkers with fluorescent species and detecting them using fluorescence microscopy or assay-based techniques are common approaches^[3–5]. However, addition of exogenous contrast agents may perturb the native environment in cellular or biomarker sensing and intrinsic contrast imaging remains a highly desired commodity. In this milieu, nanoplasmonic sensors provide a highly sensitive and label-free method for detection of target molecules^[6–9]. For instance, ligand-receptor binding events are regularly monitored by detecting variations in surface plasmon resonance (SPR)^[10,11], which involves the collective oscillation of conduction electrons that propagates along a metal-dielectric interface. The excitation of such waves is highly sensitive to the variation of refractive index (RI) at the metal surface due to the generation of strong evanescent waves^[10]. The decay length of these evanescent waves is typically hundreds of nanometers, and biomolecular binding events in this range can be detected in real time by tracking the variation in SPR signal^[12]. Sensors based on SPR are therefore suitable for tracking bulk RI change. Localized surface plasmon resonance (LSPR), on the other hand, confines the plasmon resonance within metallic nanostructures as the near field decays rapidly near the nanostructures^[10]. Thus, this technique operates with low sensing volume and is sensitive to local RI change, making it suitable for integration with lab-on-a-chip devices^[13–15].

There have been a range of LSPR-based RI sensors reported in the past^[6]. Various plasmonic nanostructures have been fabricated by both chemical^[16] and physical^[16,17] methods for LSPR-based sensing. For example, a gold mushroom array was fabricated by interference lithography for detection of cytochrome c and alpha-fetoprotein^[16–18], gold nanoholes and discs were fabricated by nanosphere lithography^[16–19], and gold-coated silica nanospheres were realized by a chemical method^[16–20]. There are also reports in the literature of various shapes of nanoparticles like gold^[21] and silver^[21–23] nanospeheres, gold stars^[24,25], silver cubes^[26], gold pyramids^[27], gold rods^[27,28] and gold nanorice^[29], which have been used for LSPR sensing with varying degrees of success. Theoretical predictions of dielectric sensing based on asymmetric resonances (i.e., Fano resonance^[8] and quadrupolar resonance^[30]) also indicated the capability for ultrasensitive transduction of biomolecular species.

Classically, most of the reported LSPR sensors have used gold nanoparticles/nanostructures with a single resonance peak around 500 nm for tracking the change in surrounding RI. Here, we report an alternate nanostructure design for generating plasmonic hotspots by using a combination of gold, silver and a suitable dielectric for sensing the RI of bioanalytes. In particular, the thin dielectric layer is used for separating the two metallic layers, which helps to prevent any kind of charge transfer between the latter and, crucially, gives rise to two distinct resonance peaks. This allows for more robust detection of RI changes in the media by concomitant computation of the shift in the two resonance peaks that facilitates ratiometric determination. Such a sensing technique enables a self-referenced platform^[31,32] for robust detection of analytes, effectively dealing with a situation for which changes in a single peak may be influenced by non-analyte-specific variations^[33]. Moreover, our design has the added advantage of not being subject to fouling, as the reference feature (stemming from the gold nanosphere) is isolated from the environmentally-sensitive feature (that arises from the silver nanoparticles) by the physical presence of the dielectric layer. Additionally, as reported earlier^[34–36], the advantage of having two distinct peaks is that it increases the dynamic range for sensing, since the sensitivities to the surrounding environment demonstrated by the two peaks are distinct in the two RI ranges. Moreover, the sensitivity and the dynamic range can be tailored by changing the metal or dielectric thicknesses as well as by simply heating the substrate.

Despite its sensitivity to the analyte-induced changes in RI, label-free LSPR sensing does not provide any information on the molecular composition. Raman spectroscopy, however, provides a unique molecular fingerprint by interrogating the vibrational transitions, offering multiplexed detection of biomolecules without necessitating the addition of any contrast agents^[37,38]. The presence of plasmonic nanostructures near the analyte provides an electromagnetic enhancement of the Raman signal, thus, enabling detection at low concentrations – a technique commonly known as surface-enhanced Raman spectroscopy (SERS)^[38]. Indeed, plasmon-enhanced assays have, in recent years, surpassed the detection limits of conventional fluorescence-based techniques^[39,40].

We reason that a combination of LSPR and SERS measurements, which has only been recently explored in the literature^[41–43] for molecular diagnostics, can be readily obtained by leveraging the unique properties of our gold-silver-dielectric nanostructures. The ability to use the same platform with no modifications for acquiring complementary pieces of information is particularly attractive. SERS and LSPR measurements offer distinct insights into the biomolecular environment. SERS, which relies on inelastic scattering of light, provides molecular fingerprinting capabilities, owing to the wealth of information encoded in the vibrational modes of the Raman spectra. On the other hand, LSPR measurements inform on the elastic scattering and absorption events that is manifested in the refractive index of the surrounding. Coupled with its label-free nature, we envision that the molecular specificity and multiplexing capability of this dual-modal sensing construct, which we term as composite scattering probes (CSP), will facilitate the screening of biomarkers in body fluids for diagnosis and monitoring of therapy response. In this report, we demonstrate both detection capabilities by using bovine serum albumin (BSA) as a model analyte for understanding the performance metrics of our nanostructured platform. BSA is a widely used analogue of human albumin, an important circulating protein in the blood of vertebrates, whose detection represents an diagnostic challenge in itself^[44].

Results and Discussion

Fabrication of composite scattering probes (CSP)

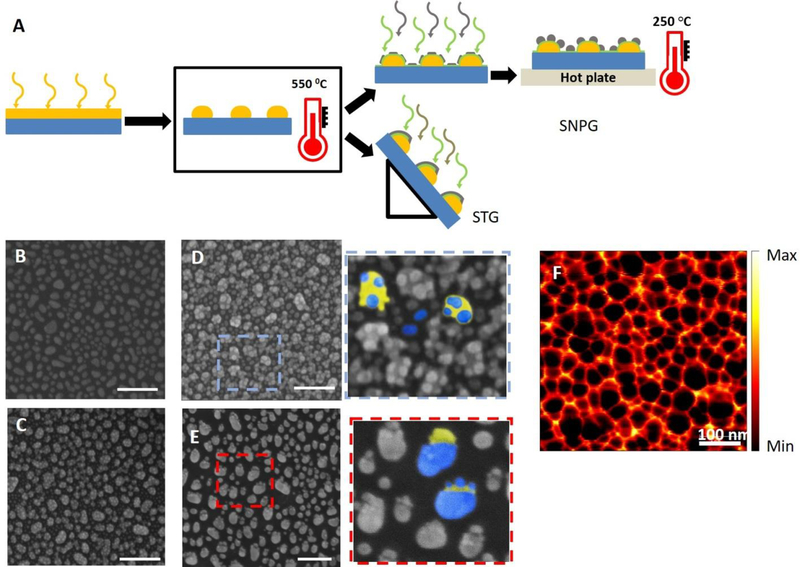
To fabricate the large-area tailored nanostructures (Figure 1), we combined physical vapor deposition with thermal annealing. Specifically, we designed and fabricated different configurations of metal-dielectric combinations to generate a sensitive and robust composite scattering probe; two such designs are shown and analyzed here to assess their relative merits for sensing. The details of the fabrication steps and their corresponding SEM images are shown in Figure 1.

Figure 1:

Fabrication steps: (A) Scheme of fabrication, process flow from left to right. Deposition of a gold thin film (yellow) on a glass coverslip/Si wafer using electron-beam evaporation. Thermal annealing led to de-wetting of Au film and rendered the Au islands to a near-spherical shape. For SNPG configuration, 10 nm of silica (green) and 4 nm of Ag (gray) were subsequently deposited. This was followed by annealing on a hotplate to convert the Ag islands into Ag nanoparticles. For the STG samples, OAD of 10 nm of silica and 10 nm of Ag on the Au nanoparticles by placing the substrates at an oblique angle relative to the evaporant flux (87° to the horizontal). (B) Scanning Electron Micrograph (SEM) image of the Au spheres after deposition and thermal annealing. (C) SEM image of the SNPG sample with 10 nm silica and 4 nm Ag. Since the thickness of Ag film is less, the thin film is not continuous. (D) SEM image of the SNPG sample after 20 min of annealing on a hotplate. The inset shows the zoomed-in version marked by the blue dashed box. The gold (yellow) and the silver (blue) regions of the SNPG structure are highlighted in false color. (E) SEM image of the STG sample. The inset shows the zoomed-in version marked by the red dashed box. The gold (yellow) and the silver (blue) regions of the STG structure are indicated by the false color representation. The scale bars for all the SEM images marked in white are 200 nm. (F) s-SNOM image of the annealed SNPG sample; although the silver nanoparticles cannot be resolved, the gold nanoparticles are readily identified (s-SNOM image courtesy: Bruker Nano Surfaces Division).

As a first step, a thin film of gold (5.5 nm) was deposited on a clean glass coverslip and a silicon wafer by electron-beam evaporation. The thin film was annealed in a muffle furnace for 6 hours at a temperature of 550°C. Thermal de-wetting of the gold film led to the formation of near-spherical nanoparticles of size 40 nm (±10 nm). This provided a quick and simple method of achieving near-spherical nanoparticles over a large area. Figure 1B shows the scanning electron micrograph (SEM) of gold nanoparticles formed on silicon over a large area using the thermal de-wetting process. By changing the thickness of the deposited film as well as varying the annealing temperature and time, the particle size can be altered allowing the plasmon resonance of the gold spheres to be tuned in the visible range^[45].

In order to decorate the gold nanoparticles with silver nanoparticles, we adopted two different techniques. In the first case, we deposited a silica layer of 10 nm on the gold nanoparticle-followed by a thin film of silver (4 nm) in a vacuum chamber with an electron-beam evaporator. The substrates were, then, annealed on a hot plate at 250°C for 20 minutes to modify the silver islands into near-spherical shape. Figure 1C and D show the SEM of silver nanoparticles decorated gold nanoparticles (SNPG) before and after annealing on the hotplate, respectively. Due to low thickness, the silver film was discontinuous before annealing as seen in the SEM image in Figure 1C. Annealing allows these irregular silver islands to transform into more regular near-spherical shapes.

In the second case, we mounted the substrate with the gold nanoparticles at an oblique angle with respect to the evaporant flux (87° to the horizontal) in an electron-beam evaporator for subsequent deposition of 10 nm of silica and 10 nm of silver. Deposition at an extreme angle, known as oblique angle deposition (OAD)^[46], ensured that the evaporant was deposited preferentially on the gold nanoparticles, and no deposition took place in the geometric shadow region of the nanoparticles. While rarely used in this context of generating biosensors^[47], this technique has been shown to be suitable for fabricating various 3D porous hybrid nanostructures with options for easy tunability of the plasmon resonance by variation of shape, size, material etc. of the nanostructures^[48–50]. The SEM image of silica and silver thin film-decorated gold nanoparticles (STG) is shown in Figure 1E. The zoomed-in versions (Figure 1D and 1E insets) serves to highlight the structural differences between SNPG and STG. In case of SNPG, the blue dots (false color) highlight the several silver nanoparticles on top of the gold nanoparticle (represented by the yellow false color). Some of the silver nanoparticles get deposited directly on the glass/silicon substrate as well. In contrast, the STG has a blob of silver (and silica - not visible here) on the gold nanoparticle and almost no depositions on the glass/silicon substrate, indicating a perfect shadowing during deposition. The scattering-type scanning near-field optical microscopy (s-SNOM) image of one of the nanostructures on silicon wafer (SNPG) with high spatial resolution is shown in Figure 1F. A 5 μm laser wavelength, which is far from the plasmon resonance, was used for the scan to record the relative reflected image of the nanostructures.

Optical characterization of CSP

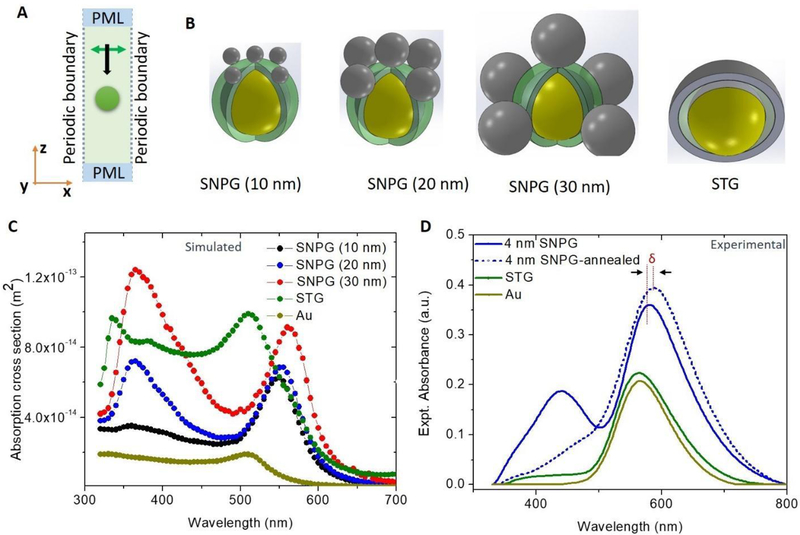
We simulated optical characteristics of the silver-decorated gold nanoparticles using a finite element method (FEM) to predict the resonance wavelengths for the different configurations (simulation details are provided in the Materials & Methods section). Briefly, the FEM calculation was done using commercial software (COMSOL, Inc., Burlington, MA). A periodic boundary condition was considered with infinite periodicity in the X and Y direction. The perfectly matched layer (PML) boundary condition was considered in the Z direction to simulate an infinite space. A schematic diagram of the numerical model is shown in Figure 2A with the direction of propagation and polarization marked in the figure. The nanostructures were arranged in a square lattice with an edge-to-edge spacing of 50 nm. The various structures used in the numerical model are shown in Figure 2B. A gold sphere of 40 nm diameter was considered to be coated with a 10 nm silica layer. Three different sizes of silver nanoparticles of diameter 10 nm, 20 nm and 30 nm were considered to simulate different conditions of experimentally deposited silver, as can be noted in the SEM images (Figure 1C, D). The STG was simulated by considering a silica and silver thin film covering half the gold sphere mimicking the actual structures produced.

Figure 2:

Optical characterization of the fabricated structures, numerical and experimental: (A) FEM 3D model with periodic boundary in the X and Y direction implying the nanostructure (represented by the orange sphere) repeats periodically in the X and Y direction infinitely. The electromagnetic field propagates along the Z direction and is linearly polarized along the X direction represented by the black and the green arrow, respectively. (B) Schematic showing various nanostructure configurations along with their respective labels (which have been used throughout this report). The yellow sphere represents the gold sphere, which is coated with silica (represented by semi-transparent green). The silver nanostructures are in gray color. (C) Simulated absorption spectra for different numerical configurations are plotted along with absorption spectra of a gold sphere. (D) Experimental absorption spectra of various fabricated samples – 4nm SNPG, 4 nm SNPG after annealing, STG and gold islands. δ signifies the shift in peak position of the SNPG sample due to annealing.

The simulated absorption spectra for the different configurations are plotted in Figure 2C. In the case of SNPG, for the silver nanoparticle of size 10 nm, the absorption cross section peak in the lower wavelength region is barely distinguishable in the spectra. For the bigger sizes of silver nanoparticles, there are two distinct peaks visible. The silica layer aids in separating the two metals to prevent hot-electron/charge transfer^[51,52] between the two metals, and two distinct resonance peaks are therefore available for sensing. Due to the presence of silica and silver, the absorption peak around 560 nm is red shifted from the resonance of the gold spheres at 510 nm. The peak due to silver nanoparticles occurs around 380 nm. In the case of the STG configuration, the overall absorption cross section increased due to the presence of the Ag thin film - with no distinct peak appearing for the silver thin film in the visible region of the electromagnetic spectrum.

For experimental optical characterization of the fabricated nanostructures, the optical absorption spectra for the different nanostructure configurations was measured using a UV-Visible spectrometer and results are plotted in Figure 2D. For the SNPG substrate with 4 nm silver coating, two distinct resonance peaks are visible, one around 580 nm, which corresponds to the plasmon resonance of the gold nanoparticle modified with silica and silver nanoparticles/islands, and the other one around 440 nm corresponding to the resonance of silver nanoparticles. Once annealed at a temperature of 250°C, which is below the melting temperature of gold, the silver film/islands get modified into silver nanoparticles. The modification in their shape is reflected in the optical absorption spectra in Figure 2D, where the LSPR peak corresponding to silver around 440 nm diminishes for 4 nm SNPG samples. This is because on heating, the smaller silver islands become larger particles, leading to broadening and red shift of the plasmon peak^[53]. Thus, the peak merges (by red-shifting) with the resonance peak of the gold and appears as a smaller shoulder near the 580 nm feature in the optical absorption spectra. The deviation from our numerical results indicates that the thermal annealing of silver in our structures is not dominated by change in size alone but can be attributed to a combination of other processes including but not limited to film oxidation and increased interparticle distance. The broadening of this silver peak due to such factors has been demonstrated previously ^[54], though the precise mechanism of such deviation in our case needs further investigation. Moreover, due to heating, the peak around 580 nm for the 4 nm-SNPG sample gets red shifted by about 8 nm, which is related to the further change in the dielectric environment of the silica-coated gold spheres due to modification of the silver nanoparticles. Furthermore, the SNPG substrate shows excellent tunability. Both the resonance peaks of the SNPG sample can be easily tuned (to match the excitation for maximum enhancement) by changing the thickness of the silica layer/silver thin film or by varying the annealing time. The shift in resonance peak due to change in thickness of silver layer and annealing time is available in the Supplementary Information (Figure S1 & S2).

The STG sample, however, has a single resonance peak in its absorption spectra at 564 nm. This may be attributed to the dimension of the silver film being too thin to sustain a localized plasmon resonance. Moreover, in the case of the STG sample, the silver does not coat the gold nanoparticle entirely and forms an island on the gold nanoparticle. As expected, the simulated SNPG models are consistent with the pre-annealed 4 nm-SNPG samples, in part, because the size ranges considered in the simulation are similar to the pre-annealed silver islands on the gold nanostructures. The slight discrepancy in the peak position may result from the variability of particle size because the fabrication process involves physical vapor deposition.

CSP-based refractive index sensing

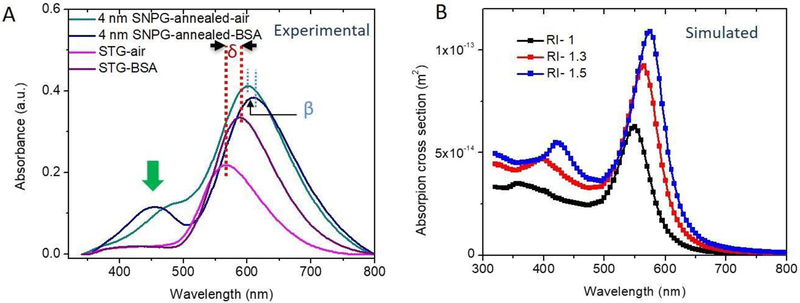
As is well-known, LSPR peaks are sensitive to the dielectric constant of the surrounding medium^[55]. For checking the sensitivity of our substrates to the local environment, we measured the LSPR peaks of the substrates in the presence of 0.1 mmol/L, 1 mmol/L and 2 mmol/L of BSA in aqueous media. The RI of 0.1 mmol/L BSA was measured to be 1.336 as compared to 1.335 for water (measured at a temperature of 4°C; measurement details are discussed in the Supplementary Information and plot of BSA concentration vs. RI is provided in Figure S3A). Using a UV-Visible spectrometer, we first measured the absorption spectra in air by placing the glass substrates in quartz cuvettes. Next, absorption spectra were measured by filling the cuvette serially with, water, 0.1 mmol/L, 1 mmol/L and 2 mmol/L BSA. Figure 3A plots the absorption spectra of the annealed SNPG sample and the STG sample for air and 0.1 mmol/L BSA. In the case of the SNPG sample, it is notable that, with 0.1 mmol/L BSA, a distinct peak appears near 450 nm. The latter is the approximate position of the pre-annealed feature in ambient media, which had diminished when the substrate was annealed. The peak around 580 nm shifts by 10 nm for the SNPG sample with higher RI. For the STG sample, the shift in the resonance peak due to the higher RI is 23 nm. Thus, the dominant LSPR peak is more sensitive to the surrounding media in the case of the STG sample. Nevertheless, the SNPG sample gives rise to a new spectral feature, which may be more effective in monitoring the change in RI.

Figure 3:

Effect of dielectric medium on the resonance position (experiment and simulation): (A) Experimental absorption spectra of the annealed 4 nm SNPG and the STG samples in the presence of air and 0.1 mmol/L BSA. Green arrow indicates the new peak that appears when the SNPG sample was placed in a higher RI. δ and β indicate the shift in dominant peak positions for the STG and SNPG samples, respectively, when placed in a higher RI media. (B) (Simulated) Effect of change in dielectric medium on the absorption spectra for the model SNPG (10 nm) showing the appearance of a second peak with higher RI.

To gain a better understanding of the change in absorption spectra with RI, we employed a FEM similar to the one used for the SNPG sample. A 40 nm gold sphere coated with 10 nm silica is decorated with silver nanoparticles of size 10 nm. The surrounding RI is changed from 1 to 1.3 and 1.5. Figure 3B plots the absorption spectra for these different cases. Similar to our experimental observation, at higher RI a peak appears at ca. 450 nm and becomes more distinct with further increase in RI. Apart from the redshift of the resonance peak, the larger size of the nanoparticle relative to the effective wavelength in presence of a higher RI media results in an increase in absorption cross-section of the silver nanoparticles.

It is worth noting that our observations for the peak corresponding to the silver nanoparticle deviate from the simulation results. While our simulations predict a red-shift in this feature with increasing bulk RI, repeated measurements establish a contrasting behavior. While it is challenging to home in on a specific mechanism for this discrepancy between experimental and numerical findings, literature reports hint at two possible explanations that focus on the effect of molecular adsorption on the nanoparticle surfaces, and alteration of the surface electronic structure of the plasmonic nanoprobes induced by the media, respectively. van Duyne and co-workers’ studies detail differential blue-/red-shifting of LSPR peaks based on how analytes adsorb on nanoparticle surfaces^[56], while Muri et al. have postulated that the latter could explain the non-linear blue-shifting with increasing bulk RI, as they observed for gold nanorods in glycerol and sucrose solutions^[57]. As these mechanisms have not been accounted for in our simulation model, uncovering the basis of this unexpected observation will be a major focus of our ongoing investigations.

In order to establish the sensitivity of capturing small variations in RI with our CSP sensor, we leveraged chemometric analysis of the recorded spectral profiles. Elucidating subtle RI-induced changes in these profiles (as shown in Figure S4, S5) is challenging by gross visual inspection alone but can be realized through application of multivariate analytics algorithms that harness the full spectral information^[58,59].

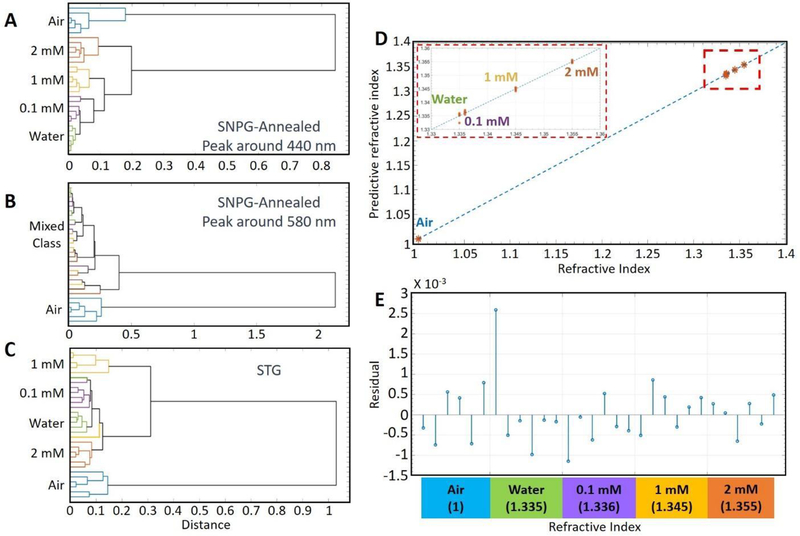
Figure 4A and 4B shows the results of hierarchical cluster analysis (HCA)^[60–62] for the shorter and the longer wavelength resonance peaks of SNPG, respectively. The dendrograms demonstrate that the shorter wavelength peak for SNPG around 440 nm is extremely sensitive to the surrounding conditions and can be used to clearly distinguish between various dielectric media, notably water and 0.1 mmol/L BSA, which vary only by 0.001 in their RI. On the other hand, the peak around 580 nm is markedly less sensitive to the surrounding dielectric media and has difficulty in distinguishing between any of the aqueous solutions considered in our study. We attribute this to the differential near-field intensities experienced by the surrounding dielectric. Specifically, the surrounding media perceives a more pronounced near-field intensity for the silver nanoparticles, which is directly exposed to the media itself, as opposed to the gold nanoparticles that are covered by a 10 nm silica layer. A direct consequence of the differential sensitivities of the two peaks is that it enables the SNPG sample to be suitable for self-referenced measurements. The experimental finding is consistent with the results of our simulation study (further details are provided in the Supplementary Information, Figure S6 & S7). Figure 4C plots the dendrograms showing the performance of STG samples in classifying the various concentrations. The STG sample, which has a single dominant resonant peak around 564 nm, is able to differentiate between the various concentrations although the accuracy is less than the SNPG sample. Thus, the SNPG sample is better suited for sensitive and self-referenced measurement of RI.

Figure 4:

(A) Hierarchical cluster analysis of absorption spectra between 320–500 nm (surrounding the shorter wavelength resonance peak of SNPG) at various concentrations of BSA, air and water. The dendrogram indicates that the different solutions can be accurately identified. (B) Hierarchical cluster analysis of absorption spectra of longer wavelength resonance peak (500–800 nm) of SNPG at various concentrations of BSA, air and water. None of the solutions could be suitably classified. (C) Hierarchical cluster analysis of absorption spectra of resonance peak of STG at various concentrations of BSA, air and water. Different solutions could be identified although the accuracy is less compared to that obtained with the SNPG sample. (D) PLS prediction results of BSA solutions, water and air in the wavelength range of 320–500 nm (around the 440 nm peak region) in case of the SNPG-annealed substrate. The solid line denotes y = x and the red dashed box is an enlarged version of a part of the graph as shown in the subfigure. (E) PLS prediction residuals for absorption spectra of SNPG-annealed sample (around the 440 nm peak) belonging to the different RI.

Figure 4D shows the results of partial least squares (PLS) leave-one-out prediction for the absorption spectra based on analysis of the SNPG-annealed 440 nm peak region. The reference and PLS-predicted RI are given along the X and Y-axis, respectively. The dashed line is plotted to illustrate y = x to explicitly understand the linearity of the response (or the lack thereof). From the figure, it is evident that the predicted values show excellent agreement with the reference concentrations and the corresponding root-mean-square error (RMSE) is calculated to be 0.0007. Figure 4E shows the prediction residual for spectra from various samples. It indicates that the SNPG substrate was able to accurately determine the RI down to the third decimal level, thereby underscoring its utility in monitoring subtle changes in analyte concentration in the surrounding milieu. To evaluate the linearity range of our measurement, we calculate the R-square value (coefficient of determination) between the predicted concentration and actual concentration, which is ca. 0.99. From Figure S3 in the Supplementary Information, it can be concluded that within the range of our measurement, i.e. 0–2 mmol/L, the predicted BSA concentration shows a linear relationship with the refractive index. Using the calibration plot method discussed in the Materials & Methods, the LOD for BSA was computed to be 0.013 mmol/L.

CSP-based biomolecular detection with surface-enhanced Raman spectroscopy

The ability to design and fabricate nanostructures with a high degree of precision has transformed SERS from an esoteric method to a potent analytical tool over the last decade^[38]. The surface properties directly impact the electromagnetic (and chemical) enhancement experienced by the molecules adsorbed on or in the vicinity of the nanostructured surface. Here, through proof-of-concept measurements in BSA solutions, we explored the utility of the CSP structures in recording SERS spectra of biomolecules.

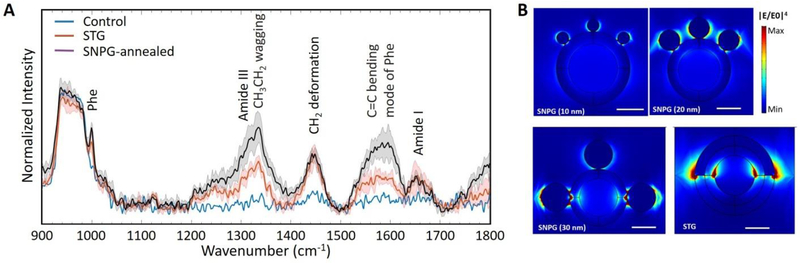
We chose water as a representative solvent to mimic a normal biofluid measurement situation. In our investigation, we pipetted 10 μl of 10 μmol/L BSA solution on the nanostructures fabricated on silicon wafers and allowed it to dry under normal ambient condition. These silicon substrates have the same nanostructure arrangement as the glass substrates used in our RI sensing experiments but contribute lower fluorescence backgrounds to the recorded SERS spectra. SERS signals were collected from the dried spot by focusing on the substrate surface. As a control experiment, Raman spectra were collected with the same concentration on a silicon wafer without any nanostructure. Figure 5A shows the spectra recorded from various kinds of substrates after baseline removal. The Raman spectra were normalized with the silicon background peak at 520 cm^{−1 [63]}. Several vibrational peaks in the range of 900–1800 cm⁻¹ are identified in the spectrum, 1001 cm⁻¹ (phenylalanine), 1321 cm⁻¹ (amide III), 1335 cm⁻¹ (CH₃CH₂ wagging), 1446 cm⁻¹ (CH₂ deformation), 1583 cm⁻¹ (C=C bending mode of phenylalanine) and 1652 cm⁻¹ (amide I)^[63]. The experimental enhancement factor, as defined elsewhere in the literature^[64] at 1335 cm⁻¹ (CH₃CH₂ wagging) for the SNPG-annealed sample is about 22 whereas for STG is about 14. Thus, both the CSPs provide enhancement to the weak Raman signal of BSA, with the SNPG sample expectedly giving better enhancement. The enhancement factor obtained here is competitive with those obtained in the literature for similar measurement protocols^[65] and, while substantially lower than those recorded from unstructured colloids, is more reproducible and has a well-defined spatial distribution. The latter is a key driver for future translation of such SERS platforms to the clinic or field setting. Furthermore, by comparing the intensities between signals from BSA solution on SNPG-annealed substrate and on (blank) silicon substrate, we determined the LOD value for our SERS measurements to be 0.096 μM. The linearity range of SERS study extends up to 0.5 mmol/L, i.e. the highest measured concentration in our pilot study. Our experimental range of measurements could be readily expanded; however, because our aim was to screen biomarkers in body fluids for diagnosis, higher concentrations are not deemed as biologically significant. To evaluate the reproducibility of the SERS measurements, the coefficient of variation/relative standard deviation(RSD) was calculated at few of the major peaks in the Raman spectra (table provided in the Supplementary Information) and ranged between 11 to 19%.

Figure 5:

SERS measurements of BSA solution and numerical calculation of field enhancement: (A) SERS spectra of 10 μmol/L BSA on different substrates measured with a 2 second integration with a 530 nm laser in a micro-Raman system. Prominent Raman peaks are marked in the figure. The solid lines depict the average spectrum, and the shaded region represents the ± standard deviations (SD). (B) Distribution of |E/E₀|⁴ in the XZ plane at 530 nm excitation. All the panels are plotted with the same range of color scale for comparison. The scale bar is 20 nm. The STG configuration shows significant enhancement at the sharp corners, which is due to the lightning rod effect but is absent in our experimental prototype.

In order to determine the origin of the SERS enhancement, using our previous model as in Figure 2A, we calculated the distribution of near field enhancement (|E/E₀|⁴) in the XZ plane considering the analyte molecule to be most exposed to the enhanced field in this plane. A fourth power of electric field was chosen since SERS signal was proportional to the square of the intensity. Figure 5B plots the spatial variation of |E/E₀|⁴ in the XZ plane for a wavelength of 530 nm, which is closer to the Raman excitation wavelength used in our experiments (532 nm). It can be clearly seen that the field enhancement covers a greater area for the SNPG (30 nm) arrangement, which allows for substantial interaction of analyte with the electromagnetic field leading to stronger SERS signals. The STG configuration shows some enhancement at the corner of silver thin film due to the well-known lightning rod effect^[11,64]. But, such sharp corners are absent in our experimental substrate; thus, enhancement in our experimental STG sample is lower than predicted. With near-IR laser excitation, it is expected that the gold nanoparticle will have more contribution relative to its silver counterpart in enhancing the SERS signal.

Conclusion

Localized surface plasmon resonance (LSPR) and surface-enhanced Raman spectroscopy (SERS) measurements offer important methods for label-free fingerprinting and quantitative biomolecular determination. The current study reports a large-area, versatile and self-referenced sensing platform, using a combination of metal and dielectric nanostructures, to perform composite scattering (i.e., elastic and inelastic scattering) measurements. Our design of CSP does not necessitate the use of lithography and is suitable for wafer scale fabrication. Using the CSP nanostructures, we show that LSPR sensing when combined with SERS offers dual-modality sensing that adds redundancy and encoding features, thus increasing measurement robustness and predictability. As a proof of concept, the SNPG design shows the potential as a means to self-reference. Notably, the inclusion of both the reference and sensing regions within the same physical space allows for a more compact design, and permits the use of a single detector rather than multiple detectors^[32]. Crucially, the CSP does not require any physical or chemical alteration for its use as both a SERS probe and a LSPR sensor thereby underscoring its generalizability. In particular, our findings showcase the promise of the CSP as a sensing tool based on its demonstrated detection limit and the fact that Raman spectroscopy yields molecular-specific information in the native state not readily obtainable from many other detection methods. While the preliminary results are promising, we expect additional improvement in detection limit and photonic throughput with further optimization of the probe design and corresponding sample fabrication procedures. Ultimately, we envision that the molecular specificity and multiplexing capability of the CSP will be leveraged for translating molecular markers into serum assays for accurate disease screening.

Materials & Methods

Absorption spectra measurement and refractive index sensing:

A Lambda 950 UV/VIS/NIR spectrometer (PerkinElmer, Waltham, MA, USA) was used to measure absorption spectra from substrates. The measured wavelengths range from 320 nm to 800 nm, covering the entire visible range. The data is collected at an interval of 2 nm for the optical characterization and 1 nm for the RI sensing experiments. The absorption spectra are measured by considering a glass coverslip as the reference. For the RI sensing experiments, the fabricated substrates, BSA solution and reference coverslip were put into quartz cuvettes that were placed in the measurement and reference light paths.

SERS measurement:

Raman spectra were acquired by using an XploRA PLUS Raman microscope (HORIBA Instruments Inc., Edison, NJ, USA). Sample excitation was achieved by using a 532 nm diode laser. The laser beam was focused on the sample through a 10X objective (MPlan N, Olympus, Center Valley, PA, USA). The backscattered Raman signals were collected by the same objective and through a notch filter to remove Raleigh elastically scattered light, and the scattered spectra were collected using a thermoelectrically cooled CCD camera (1024X256-OE Syncerity, HORIBA Instruments Inc., Edison, NJ, USA). Laser intensity at the sample was kept constant at 35 mW for all the measurements. The exposure time for each measurement was 2 seconds with 5 times accumulation. The average SERS spectra, along with the standard deviations, are plotted.

Data analysis:

The collected absorption and Raman spectra were imported into a MATLAB 2018a (Mathworks, Inc., Natick, MA, USA) environment for further analysis. For RI sensing, in order to illustrate the capability to provide quantitative measurements of our substrates, hierarchical cluster analysis (HCA) and partial least squares (PLS) regression were employed. HCA is an algorithm which could group similar patterns into clusters based on Euclidean distance and average linkage method^[62]. Couple dendrograms were displayed to reveal the hierarchy of clustering among samples with various RI. PLS is a widely used multiple linear regression model in quantitative spectral analyses^[66]. PLS was used to establish the fundamental relations between absorption spectra and surrounding RI. For Raman measurements, spectra were processed to remove interference from cosmic rays. The spectra were restricted to the 200 cm⁻¹ to 1800 cm⁻¹ region and subjected to a fifth order best-fit polynomial-based baseline removal. All spectra were smoothed by using the 7 orders and 15 points Savitzky-Golay function^[66,67] and normalized at the silicon background peak at 520 cm⁻¹. Limit of detection (LOD) of LSPR is calculated, based on the IUPAC definition^[68] from the best fit-line obtained between predicted concentrations and reference concentrations. The corresponding equation is:

$$LOD\mathrm{ }\left(mM\right)=3\frac{S_{y/x}}{slope}\mathrm{ }where\mathrm{ }{S}_{y/x}={\left[\frac{\sum {({\widehat{c}}_i-c_i)}^2}{N-2}\right]}^{1/2}$$

Where S_y/x is the standard deviation of the residuals and is a measure of the average deviation of the predicted values from the regression line. The LOD of SERS sensing was defined as the detectable signals from the lowest analyte concentration with a signal-to-noise ratio greater than 3^[69].

Simulation:

A commercial finite element-based tool (COMSOL Inc., Burlington, MA, USA) was used for the numerical modeling. The nanostructures were in a square lattice and periodic boundary condition was applied in the X and Y directions of the simulation model. Through an input port in the Z direction, the nanostructures were excited. Perfectly matched layer (PML) boundary condition was applied at the input and the output port to simulate an infinite space and prevent reflection at the boundary. A dynamic tetrahedral meshing of maximum element size of 10 nm for the nanostructure and λ/6 for the rest of the space were chosen with a minimum element size of 0.1 nm. The fault tolerance was varied to check the convergence of the code. Frequency-dependent gold and silver dielectric constants from Palik^[70] were employed for the simulation. The relative permittivity of silica was considered to be constant at 3.9 over the entire visible wavelength.