A Healthy Dose of Chaos: Using fractal frameworks for engineering higher-fidelity biomedical systems

Abstract

Optimal levels of chaos and fractality are distinctly associated with physiological health and function in natural systems. Chaos is a type of nonlinear dynamics that tends to exhibit seemingly random structures, whereas fractality is a measure of the extent of organization underlying such structures. Growing bodies of work are demonstrating both the importance of chaotic dynamics for proper function of natural systems, as well as the suitability of fractal mathematics for characterizing these systems. Here, we review how measures of fractality that quantify the dose of chaos may reflect the state of health across various biological systems, including: brain, skeletal muscle, eyes and vision, lungs, kidneys, tumours, cell regulation, wound repair, bone, vasculature, and the heart. We compare how reports of either too little or too much chaos and fractal complexity can be damaging to normal biological function, and suggest that aiming for the healthy dose of chaos may be an effective strategy for various biomedical applications. We also discuss rising examples of the implementation of fractal theory in designing novel materials, biomedical devices, diagnostics, and clinical therapies. Finally, we explain important mathematical concepts of fractals and chaos, such as fractal dimension, criticality, bifurcation, and iteration, and how they are related to biology. Overall, we promote the effectiveness of fractals in characterizing natural systems, and suggest moving towards using fractal frameworks as a basis for the research and development of better tools for the future of biomedical engineering.

1. Introduction

“Clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line.”

– BB Mandelbrot¹

Some degree of chaos is universally present in living systems. The case of biological chaos is especially clear, for example, in cardiac systems. One look at the heart’s electrical activity pattern on an electrocardiogram reveals a time-varying myriad of spikes and dips with beat-to-beat variability. Blood vasculature does not form a perfect grid, but rather a branching network. These are examples of chaotic and fractal structures. Today, underlying chaos in the systems we work with is often overlooked. This paper will review the presence and significance of chaos and fractals in biological systems, its uses in biomedical applications, and suggest incorporating fractal frameworks more broadly in biomedical engineering.

2. What are chaos and fractals?

When large iterations of complex computations were first enabled by computers, strange phenomena were revealed^1,2, such as contradicting results from weather models despite increased computational precision. These sensitive nonlinear dynamical systems have now been explained using chaos theory and fractal geometry^11,2.

Chaos is a behavior of dynamics that appears random, even though it has well-defined underlying order. It tends to be the governing order in systems that are sensitive to small factors and perturbations, and single systems may transition between the appearance of ordered and chaotic dynamics. These are typically systems with collective behaviour, e.g. the weather, or single cells that assemble into a coordinated tissue³.

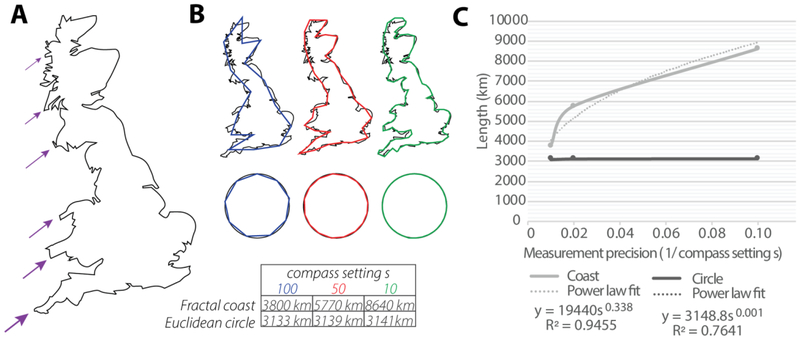
Often, chaotic systems are well approximated by geometries that are fractal. Fractals may be described as structures that have infinitely iterated self-similar patterns. They contain features that are preserved across multiple levels of observation, according to a precise scaling law. This reflects a form of organization in complex structures, that may be quantified with the fractal dimension (D_f) parameter. For instance, the buckled shape of a coastline may be observed on the range of 100 km, again at 50 km, and even at 10 km and so on. The scaling of the buckled feature on a fractal coastline, and more generally the scaling of a feature on any fractal structure, would appear at intervals that follow a characteristic order (Fig. 1A). This results in a phenomenon where if we attempt to measure the length of e.g. the coastline, its length increases by a power law as the scale of measurement decreases, since smaller resolutions of buckles can get measured with each increase in measurement precision (i.e. decrease of measurement scale) (Fig. 1B). By contrast, for non-fractal structures, such as a perfect circle, this power law relationship is absent. By plotting the measured length versus measurement precision of different structures, the power law exponent of the fitted relationship can yield one definition for the fractal dimension, and thus reflects a characteristic value for each structure, which describes that structure’s level of scaling complexity (Fig. 1C). The higher the value, the greater the complexity of the structure. Although several other definitions for fractal dimension have also been developed, such as the more common box-counting dimension and similarity dimension, they all share this same underlying principle.

Fig. 1: The Coastline illustration of the concept of fractal scaling.

(A) Breakdown of Great Britain’s self-similar features in the coastline. (B) Measured length of the fractal coast increases as the scale of measurement, or compass setting, decreases. By contrast, the length of a non-fractal circle’s circumference has a converging value. (C) The scaling of a fractal structure follows a power law from which the fractal dimension may be approximated. Measurement precision is defined as the inverse of the compass setting where for a small setting s the precision 1/s is large. Figure reproduced with permission from [²].

For example, the length of Great Britain’s coast y is related to the scale at which the scale s > 0 which the coast is measured, following the power law:

$$y=b\times {(1/s)}^d$$ (1)

where b > 0 and d ≥ 0 may not be integers. The power d can be estimated by taking the log of this equation and running a regression:

$$\text{log}y=d\times \text{log}(1/s)+\text{log}b$$ (2)

This power d is related to the fractal dimension as we will detail in Section 5. For the coast of Great Britain, d ≈ 0.338. Other coastlines have different values of d; thus d may be considered characteristic².

Further, the mathematical breakdown of fractal structures can be approximated by recursive feedback equations that feature at least some form of similarity transformation function.

$$A_{n+1}=W\left(A_n\right),n=0,1,2\dots ,$$ (3)

where W is one or a set of similarity transformation functions, and A_n, n = 0,1,2…, is a given structure or feature being iterated (such as the buckle of a coastline).

When iterated as a series, this process yields a fractal structure with several unique properties such as invariance, periodicity, and power law scaling. The limiting structure, denoted as A_∞, can be considered an attractor, or limit object, for the system. Further, by relaxing the notion of self-similarity to include functional and statistical self-similarity rather than strictly geometric, it becomes possible to classify a wide variety of fractal structures, such as multifractals and complex fractals. For example, in many cases, when we say a physiological system has a fractal structure, its appearance might not strictly follow the traditional definition of self-similarity in the geometric sense. It also sets some criteria for the exclusion of non-fractals, which may have self-similarity, but lack other properties such as similarity transformations or power law scaling.

In general, it can be considered that fractals describe the geometry of chaos. Thus, it is essential to use chaos and fractals together for modeling complex and non-linear dynamical systems, such as those dominant in nature. There is a large resource of mathematical frameworks and concepts available for describing and elucidating new entities from fractal structures that may be applied to open new doors in biomedical research. For instance, the criticality that leads to specific bifurcations of fractals during scaling, and the determination of system attractors, reflect an entire “fractal dimension” of new, usable information about a system that cannot be captured by standard metrics. In the following section, we will review one way in which fractal frameworks have provided insight in physiology: how fractal dimension and chaotic variability can measure an organ system’s state of health. In Section 5, we will provide a mathematical description of a chaotic system and fractal.

3. Fractality as a metric for health in the body

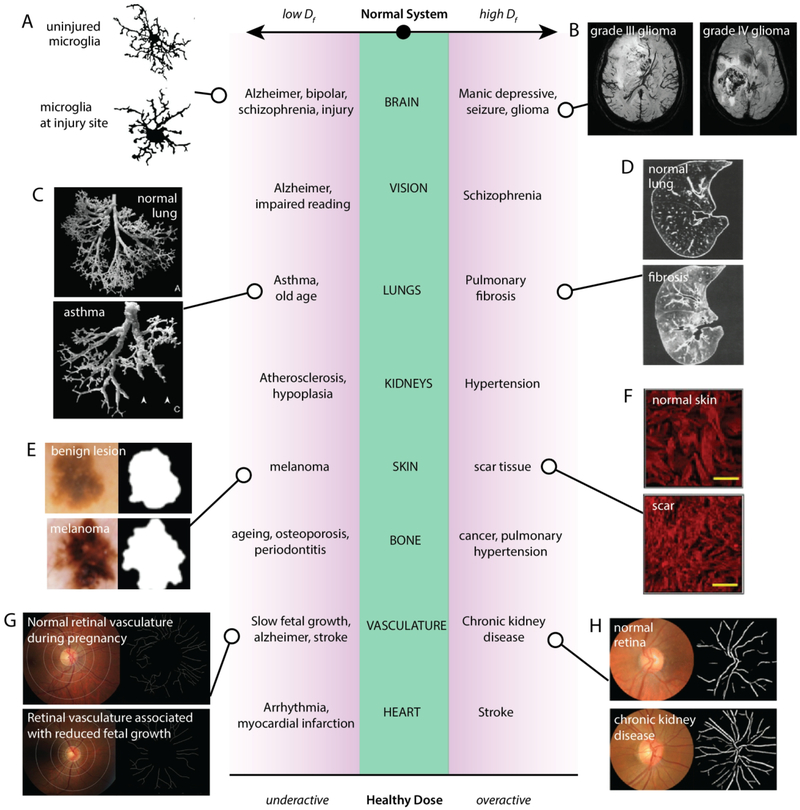
Healthy and stable living systems are generally established as chaotic and fractal in nature. A few of the most accessible examples include neurons and neural networks, heart rate, and the branching vasculature. Although the basis for fractal behaviour in natural systems is still unclear, its relationship to physiological state is much more pronounced. Variability has been analyzed with chaos and fractal theory in many different physiological systems, and the measure of fractality has been demonstrated to be associated with the state of health of the system (Fig. 2).

Fig. 2. A healthy dose of chaos.

Different physiological systems and the phenomena that occur when the fractal dimension characterizing the system becomes too low or too high. (A) Cell outline of microglia in different brain regions following experimental diffuse brain injury [reproduced with permission from⁴]. (B) MRI images of grade III and grade IV gliomas [reproduced with permission from⁵]. (C) Images of silicone rubber casts of normal and asthmatic lungs [reproduced with permission from⁶]. (D) Computed tomography images of normal and idiopathic pulmonary fibrotic lungs [reproduced with permission from⁷]. (E) Skin lesions that are benign or cancerous [reproduced with permission from⁸]. (F) Collagen staining of unwounded or scarred dermis [reproduced with permission from⁹]. (G) Sparser maternal retinal vasculature was associated with reduced fetal growth during pregnancy [reproduced with permission from¹⁰]. (H) Fundus camera images of the retina and skeletonized traces of the retinal vasculature in normal and chronic kidney disease eyes [reproduced with permission from¹¹].

3.1. Brain

The fractal dimension (D_f) has been well suited as a quantitative parameter for describing several brain systems, due to the underlying organization that is hierarchical and topological¹² (Fig. 3A). From the cell scale morphologies of neurons, astrocytes, and microglia^4,13–16; to tissue level neural networks^17,18, gyrification and cortical complexity patterns^19,20; and the temporal recordings of brain signals^21–23; fractal methods have been useful for quantitative studies of brain structure and function. For example, fractal dimension of astrocyte morphology has been demonstrated to be able to differentiate different morphological subtypes, as well as between astrocytes affected by different types of pathologies¹⁵. The fractal dimension of the cortical ribbon has been demonstrated as a significant indicator of Alzheimer’s disease^24,25. Measures of various types of brain scan images also show lower fractal complexity in cases of schizophrenia, bipolar disorder, and brain injury^{4,20,24,26,27} (Fig. 2A), and higher in manic-depression²⁸ and glioma⁵ (Fig. 2B). Fractal measurement of electroencephalogram (EEG) signals has also provided abundant characterization and prognostic value. EEG fractality fluctuates with age²⁹, sleep and wake^30,31, sensitivity to electromagnetic fields³², and circadian rhythm where higher fractal dimensions occur during periods of alertness³³. EEG fractality decreases during stroke, and is negatively correlated with its prognosis³⁴. It may also be able to predict the onset of epileptic seizures³⁵. Thus, fractality has been able provide insight that allows researchers to distinguish different functioning brain states, as well as to speculate on the mechanisms of transitions between states.

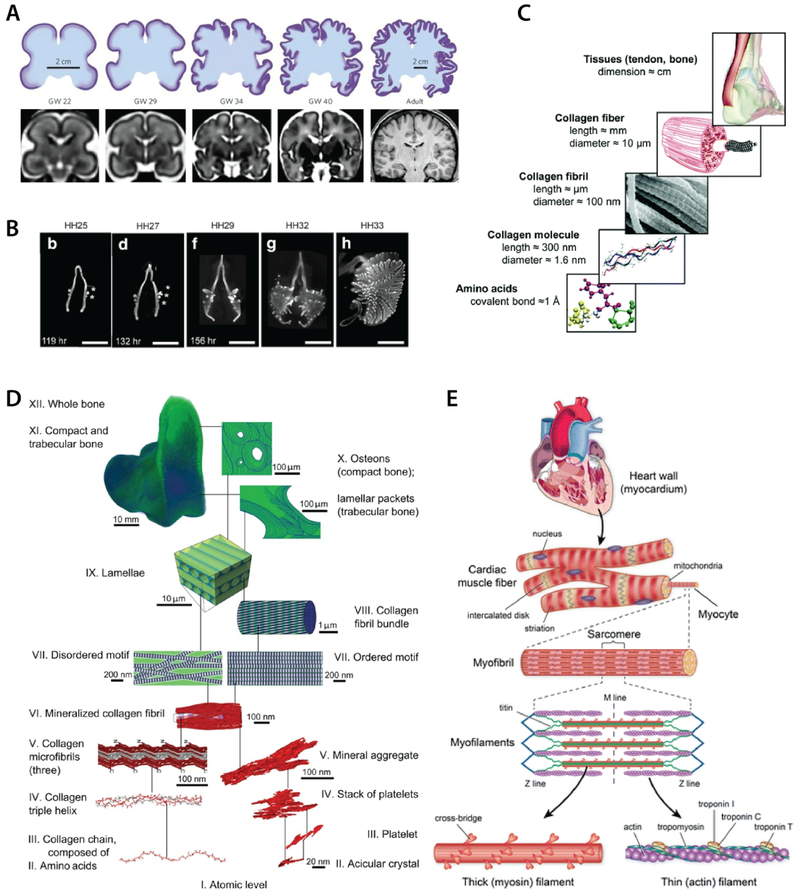
Fig. 3: Hierarchical organization in tissues.

A) self-similar brain convolutions during gestational development [reproduced with permission from³⁶]. B) Lung branching in embryonic chicken forms at precise locations that scale relative to the size of the organ [reproduced with permission from³⁷]. C) Collagen fibrils and bundles follow self-similar fibrous structure across scales [reproduced with permission from³⁸]. D) Bone tissue with up to 12 (I to XII) levels of fractal organization based on collagen fibrils and mineral aggregates [reproduced with permission from³⁹]. E) Hierarchical fibrillar structure of cardiac tissue from actin-myosin filaments, myofilaments, myofibrils, myocytes, and muscle fibers [reproduced with permission from⁴⁰].

3.2. Skeletal muscle

Oscillatory activity in neurons and general spatiotemporal control of the body’s balance can also exhibit chaotic behaviours^41–43. In neurorehabilitation, functional electrical stimulation (FES) therapy is often applied to help correct or repair damage that results from nervous system injury. The therapy applies small electrical shocks similar to the electrical impulses from nerves. This field has begun exploring the benefits of more variable stimulation frequency patterns compared to ordered patterns. Variable patterns of FES are based on native observations⁴⁴ and mainly feature an initial burst of higher-frequency signals followed by regular signals. They have shown better performance results for patients, who experienced less fatigue, reduced spasms, and improved muscle strength after their therapy^45,46. This suggests that increasing variability is more physiologically effective, and perhaps a progression to chaotic dynamics may eventually provide even better results.

3.3. Vision

Eye and vision research has also been facilitated with the use of fractal math. Vision is generated as the eye scans across fixation points⁴⁷. These fixational eye movement time series have been the basis for eye tracking studies. Fixational eye movement is characterized by high-dimensional deterministic chaos in the saccades and other small involuntary eye movements, and has been successfully modelled with nonlinear, fractal, tools⁴⁸. The fractal quantification of these movements has been studied in the cases of Alzheimer’s disease, where data suggest that patient eye movements are less complex than those of healthy subjects⁴⁹, with a similar trend for studies of eye movements versus reading ability⁵⁰. Meanwhile, another study indicates that schizophrenic patients show higher chaos in their eye movements in reading activities⁵¹. Thus, in the example of the eye and visual cognitive function, there may be a sweet spot for how much chaos is best suited for normal vision.

3.4. Lung

The respiratory system follows a self-similar structure from the trachea and lungs (Fig. 3B) down to bronchioles and alveoli,⁵² and its fractality has been used in a number of lung characterization studies^53,54. The fractal design and structure of the lungs is relevant to its functional aspects, where the fractality is a determinant for gas-exchange surface area, and thereby the lung’s function^55,56. For instance, asthmatic patients with difficulties breathing were found to have lower fractal dimensions in their airway walls⁶ (Fig. 2C). Higher-than-normal fractal dimensions were correlated with idiopathic pulmonary fibrosis⁷ (Fig. 2D). Again, there exists a healthy chaotic sweet-spot for lung fractality. Understanding the fractal relationships in the lungs has had clinical consequences. The breathing rate time series considered in breathing rate variability (BRV) is fractal in nature and related to alveolar inflation patterns⁵⁷. It has been linked to aging, disease, and mortality^57–59. Recently, the BRV was applied to predict mechanical ventilator weaning outcome^60–63. This knowledge has led to improvements in the design of ventilation apparatus⁶⁴.

3.5. Kidney

Like the lungs, kidneys are highly branching organs with fractal properties in their overall structure as well as in their functional behaviours. On the organ scale, the renal arterial system is branching with a mean fractal dimension of 1.6, based on image analysis of renal angiograms⁶⁵. This fractal dimension has been shown to decrease with congenital diseases⁶⁵. Kidney podocytes, a cell type essential in glomerular filtration, also appear fractal in structure with at least four degrees of processes branching out from the cell body⁶⁶. During disease, podocytes typically undergo foot process effacement, whereby foot processes retract into broad, flattened protrusions, thereby losing some of the degrees of process formation⁶⁷, consistent theoretically with a decrease in fractal dimension. Although podocyte fractal dimension has not yet been quantified, the specific ratio of podocyte process digitation on a cellular level may suggest the presence of a characteristic scaling law⁶⁸. From the temporal aspect, renal autoregulation also exhibits nonlinear dynamic behaviour, which is paired with the behaviour of arterial blood pressure⁶⁹. However, too much chaos in the tubular pressures over time is indicative of hypertension⁷⁰, again pointing to the notion that there is a healthy dose of chaos to normal biological function.

3.6. Tumours

In cancer and tumour research, fractal dimension on cell or tumour aggregate shape has been studied as a diagnostic parameter. Fractal dimension has been used to classify many types of tumours, by considering the tumor’s cell or tissue morphology: metastatic bone⁷¹; lung carcinoma⁷²; canine circumanal gland tumors⁷³; hyperplasia and endometrial adenocarcinoma⁷⁴; normal mucosa, dysplasia and carcinoma in oral cancers⁷⁵; and bladder cancer⁷⁶. Mitochondrial morphology has also been quantified by fractal dimension and correlated with malignant mesothelioma classification as well as its sensitivity to treatment⁷⁷. In studies of migration modes of a tumour, infiltrative tumours were shown to have higher fractal dimensions than static tumours during growth⁷⁸. By contrast, in a study classifying skin lesions, malignant lesions were found to have lower fractal dimension than benign lesions⁸ (Fig. 2E).

3.7. Cell scale regulatory and growth dynamics

The presence of fractal patterns ranging from gene, to cellular, and tissue-scale structures have also been studied with proposed implications on regulatory mechanisms.

On a molecular scale, it may be appropriate to generalize fractal aspects in terms of clustering patterns. Studies of DNA sequences have discovered fractal patterns among the distributions of coding and non-coding genes, which is unlocking new theories about how cell nuclei may regulate gene expression⁷⁹. Similarly, various forms of chromatin molecules have been found to follow fractal models of movement, also suggesting that fractal dynamics play a role in how cells regulate signaling on a molecular level^80,81. This may be related to more general polymer physics scaling laws and criticality, which are suspected to underpin physiologically relevant protein interactions and behaviour⁸².

Cellular organization can be considered fractal by evaluating how cell-scale properties reflect underlying molecular-scale organization. Beyond the scaling of membrane-bound structures ubiquitous to cells, there are various relationships in cellular organization and resultant structure-function properties that adhere to fractal scaling laws. For instance, structural collagen content scales with resultant tissue stiffness in a characteristic power law relationship typical of fractals⁸³. Similarly, nuclear lamin content has also been found to scale in power law proportionality with collagen content and stiffness, which has implications about how cells may regulate nuclear mechanosensing and gene expression. This is especially notable because these proportionalities appear to be conserved across a range of organs in the body and from various sources of datasets^83–85. Other cell-level fractal patterns that may be considered include microvillar search by T-cells, where microvilli follow fractal scanning patterns during antigen detection and recognition, suggestive of a most efficient search process⁸⁶. It may be interesting to consider how this finding resonates with how eyes also scan the environment in a fractal search pattern⁴⁷. Another area where fractal patterns are notable is in stem cell populations. Stem cell populations can be considered as fractal networks as they divide and migrate⁸⁷. The hierarchical divisions and subsequent branching and clustering may be modeled with fractal tools and scaling⁸⁸, and could shed some light on how cells are distributed with respect to stem cell niches throughout the body⁸⁹.

Finally, as cells scale in number to form coordinated tissues and organs, higher order geometries become common, for example, in branched tissues like the lungs, vasculature, kidneys, and mammary glands, where fractal patterning provides suitable packing to provide high surface areas³. Collective cell migration and local geometric constriction are currently leading notions explaining the mechanisms of tissue scale branching^3,90,91.

Taken together, the above suggests that the precise fractal organization that scales across several orders of magnitude may be involved in governing overall collective behaviour of a biological system.

3.8. Wound repair

Collagens, polylaminins, elastins, and proteoglycans are essential components of various extracellular matrices and are involved in the cell’s establishment of its local matrix and basement membrane, in migration, and in interaction with other cells. These building-block structures thus often self-assemble in self-similar hierarchies as they grow into larger functional entities (Fig. 3C). Quantification of collagen fibers using fractal dimension has been applied to the analysis of scar formation and wound healing, for example, where collagen staining shows that scars have higher fractal dimension than unwounded skin⁹ (Fig. 2F). Similarly, fractality of the microenvironment has been applied in vitro to generate a more effective minimal matrix model of scar tissue⁹². The applicability of fractal dimension in scar quantification has also been demonstrated to be more sensitive than other methods such as x-ray diffraction, laser scattering, and Fourier transform analysis, and could present its utility in assessing collagen abnormalities more broadly⁹.

The fractality of polylaminins has also been studied in the context of axonal regeneration in models of spinal cord injury, noting that while laminin is not fractal, its polymerized forms are⁹³. This is interesting considering that polylaminins are present throughout the body in several different forms, suggesting that some of these variations may be associated with the scaling and self-assembling nature of fractals. Elastin, too, which is responsible for elasticity in several tissue types, also forms fractal fibrillar networks and aggregates, where α-elastin units form a polypeptide system capable of self-aggregating in different forms⁹⁴. Again, this could be consistent with the notion that there is a ‘healthy dose’ of fractality specifically tailored to different tissues performing different functions, and that the specificity of different forms of molecular aggregates in different locations could be derived from self-assembling mechanisms of scaling fractal growth.

Similar fractal structure and function properties have also been suggested for proteoglycan networks e.g. in the cornea^95,96. Furthermore, macromolecules in general have been proposed to have fractal properties with functional consequences, such as for molecular binding potential⁹⁷. Likely, the extent of fractal scaling and degree of fractality would be relevant in many proteins and biological molecules, for specifying their function, localization, and interactions with other structures within the body.

3.9. Bone

Bone is another example of tissue that exhibits an intertwining motif of ordered and disordered self-similar structures across several scales. From the nanoscale crystal organization of minerals and collagen, up to macroscale lamellar and trabecular bone structure, the fractal-like organization of bone was comprehensively and thoroughly mapped to at least 12 levels using three-dimensional structural characterization by Reznikov et al. (Fig. 3D), suggesting a key role of nested fractal patterning to the evolution of the optimally stiff and tough properties of bone³⁹. Thus, characterizing bone in terms of its fractal properties has been fairly common, and has been used to demonstrate successful delineation of several types of bone abnormalities and pathologies. For example, ageing, postmenopausal osteoporosis, and inflammation mediated osteopenia had reduced fractal complexity of trabecular bone microarchitecture relative to young and control trabecular bone in rat models⁹⁸. Decreases in fractal complexity were also observed with other forms of osteoporosis such as Kashin-Beck disease⁹⁹, in the mandible of patients with periodontitis¹⁰⁰, and in cancellous bone of patients who had vertebral fractures¹⁰¹. By contrast, fractal dimension was increased in mandible bone of cancer patients on bisphosphonate treatment¹⁰², and in right ventricular trabecular bone of pulmonary hypertension patients¹⁰³. Overall, fractal dimension appears to be effective in supplementing standard forms of bone tissue quantification and diagnosis, as it correlates well with most existing bone quantification practices^{101,104–106}. In some cases it performed even more sensitively, for example, than bone mineral density^107,108 and cancellous bone area¹⁰¹. Note however that results are specific to the particular region of tissue under consideration as well as the modality used to obtain images¹⁰⁶.

3.10. Vasculature

The significance of the vasculature’s fractal aspects is not trivial. Vessel morphology or spatial organization is known to change under many pathological conditions¹⁰⁹, such as atherosclerosis¹¹⁰, cancers¹¹¹, arteriovenous malformations¹¹², infections¹¹³, stroke^114,115, hypertension¹¹⁶, diabetes and obesity¹¹⁷, Alzheimer’s disease¹¹⁸, and even normal aging¹¹⁶. Thus, nuances in the fractal properties of microvasculature may be used as a prognostic factor for many illnesses. In particular, imaging of retinal microvasculature has provided a non-invasive window into the vascular properties of an individual. Fundus cameras are designed to photograph the interior surface of the eye, whereby retinal microvascular tree patterns may be obtained and studied. The retinal vascular network may serve as a representative of the entire vascular system, reflecting the pressure relationships and branching patterns of the whole body¹¹⁶. Thus, changes in retinal microvasculature reveal insight not only directly related to eye health^119,120, but about other possible systemic risks such as renal^11,121, cardiac¹²², diabetic^117,123, brain health¹¹⁸, and more. While many studies have been based on the identification of vasculature changes in normal versus pathologic cases, some studies have prognostic value. For example, reduced retinal microvascular fractal dimension has been found to predict mortality from coronary heart disease¹²². For pregnant mothers, decreased fractality of retinal microvasculature has been shown to relate to uteroplacental vasculature in delayed fetal growth and birth size¹⁰ (Fig. 2G). Retinal microvasculature also was found to correlate with chronic kidney disease, where sub-optimal (low or high quantiles) levels of retinal vascular fractality was associated with increased risk of chronic kidney disease¹¹ (Fig. 2H). Note however that these applications have yet to develop standardized procedures and subgroup classifications that would ensure consistency of study results^124–128. That retinal microvasculature can reflect the state of so many other organ systems emphasizes the interconnectedness of physiological function throughout the body as a whole.

3.11. Heart

“The heart’s supposedly regular rhythm is not precisely regular.”

- A. Moss¹²⁹

The heart reflects fractal organization in both structural and temporal aspects. On a structural level, cardiac muscle is hierarchical and reflects a fractal property based on fibres (Fig. 3E). Fractal self-similarity appears from the molecular scale microfilament up to the striated cell and tissue scales, from nm to μm and cm. Tubular actin and myosin filaments collect into myofibrils, which then collect to form myocytes, and further collect into cardiac muscle fibres. This highly structured hierarchical organization is necessary for cardiac tissue function (synchronized contraction). The presence of properly scaling fibres serves as an indicator of cell and tissue maturation and differentiation^130,131. Similarly, the His-Purkinje network of the heart is fractal^132,133, and the entire cardiovascular system follows a multifractal structure: starting from the heart, branching out from the aorta into arteries, vessels, and capillaries, and following a characteristic power law as the vasculature distributes over the entire body^134–136.

Similarly, the heart’s electrical activity is endogenously variable, from the sinoatrial node, to cardiomyocytes, and the organ as a whole^132,137. Heart rate and heart rate variability (HRV) designate two separate but related parameters, and both may be obtained from electrocardiography and photoplethysmography readings^138–140. Heart rate measures the number of times the heart contracts in one minute, and reflects the speed of pumping. Thus, changes in heart rate can be normal, for example in exercise versus resting states, as well as under other autonomous influences. The variability of time intervals between beats are designated by HRV, since the duration of successive beat-to-beat intervals varies over time. Normal HRV has been demonstrated to be a chaotic deterministic system¹⁴¹, and has been appropriately analysed with fractal and multifractal analyses^142,143. Any changes in HRV, and its fractal properties, have been distinctly recognized for relating with pathophysiology. This has been especially useful for its predictive and diagnostic value, with the emergent general rule that reduced variability is a signature for disease and enhanced risk^{129,144–153}. Arrhythmia in particular has been found to correlate with reduced HRV, and in post-myocardial infarction patients, can predict increased mortality^148,154,155. By contrast, for stroke patients, increased fractality in HRV reflects greater stroke lesion severity¹⁵⁶, and may even serve as a prognostic tool for early stroke detection¹⁵⁷. Similarly, abnormalities in fetal heart rate patterns, such as sinusoidal patterns that have reduced variability, have been found to indicate severe distress and fetal jeopardy^158–160. Once again, the healthy dose of chaos is an important consideration, where too much can be as detrimental as too little.

4. Applying chaos and fractals in medicine

In light of the overviewed work that shows how fractal complexity in natural systems may reflect its state of health or function (Fig. 2), we will next review the typical tools and approaches involved in fractal quantification, as well as some leading practical applications of this knowledge. We also highlight important limitations associated with this type of work.

4.1. Measuring fractality

The most common applications of fractality so far have been for quantifying roughness of a shape, branching networks, detecting order in a seemingly irregular system, signal characterization, and pattern description in both 2D images and 1D temporal data¹⁶¹. For example, we reviewed how various vascularized structures like retina, pial structures, gluteus muscle, and organs, may be assessed for the network fractal dimension^162–164, and then related to other health parameters such as cardiac^122,165 and renal diseases^11,121.

The fractal dimension measures how complicated a self-similar structure is. It serves as a metric of complexity. A high fractal dimension indicates a high extent of self-similar complexity across several orders of magnitude. Integer-number dimensions indicate conformity with Euclidean geometry, and those structures are not fractal. Any apparent complexity observed in such systems may be considered random, rather than chaotic. Most methods for fractal dimension estimation rely on the power law scaling property of fractals as demonstrated by the compass method, where measured values increase without bound as measurement precision increases. Non-fractals will plateau at a constant value (Fig. 1). In general, this relationship between measurement precision and measured output for a fractal follows a power law, where the fractal dimension can be derived from the exponent in the power law, as will be detailed in Section 5. The box counting method is another approach that measures fractal dimension using sequential subdivisions of an image into grids, where feature area is measured across a range of grid sizes. Box counting methods are most common and applicable in science. There are several other quantifications of fractality, including Higuchi dimension^29,156, Hausdorff dimension^2,134, packing dimension¹⁶⁶, and many others. These nomenclatures are based on the particular method used to calculate the fractality. It is important to recognize that the choice of algorithm or method of fractal analysis will depend on the purpose of the analysis, since different approaches to measuring fractality yield different results between them, and analyses should be considered relative to the method used.

A typical approach for assessing fractality involves data pre-processing followed by fractal analysis using a suitable algorithm or software. There are many types of software available to aid in fractal analysis (Table 1), where a 1D time series, 2D image, 3D volume, or high dimensional signal dataset may be loaded. To control how the software reads a file and executes analysis, preprocessing steps such as image conversion from colour to binary or greyscale, are required. This may involve some form of bitmap compression, thresholding, outlining, de-noising, etc^73,164. Similarly, different analysis parameters will need to be specified such as range of analysis, image polarization, or algorithm selection. The specific method used will depend on the nature of the feature being analyzed^167–170. Since the case-specific methodologies and resolution influence the resultant fractal output, careful considerations must be made when measuring fractality and comparing multiple sets of data.

Table 1:

Common software used for the analysis of fractals.

Software	Application	Reference
FracLac (ImageJ)	Image analysis	171
FracLab	Image and signal processing	172
Fractalyse	Image analysis	173
FDim	Image analysis on greyscale images	174
Ultra Fractal 5	Fractal generator	175
3DFD	Volumetric reconstructions, e.g. MRI brain scans	176
Gwyddion	Analysis of scanning probe microscopy files	177
MATLAB	Various plugins and functions for fractal analysis	178
Kubios	HRV analysis	179
Benoit	1D or 2D data fractal analysis	180

4.2. Diagnostics

The distinctiveness and characteristic properties of fractal dimension as pertains to describing specific physiological states has potential to impact several diagnostic applications. Tumor morphology, microvascular network structure, and HRV patterns are examples of areas where fractal analysis-based prognosis has the potential for widespread biomedical benefit. Tumour morphology assessment using fractal dimension for tumour classification, malignancy, and risk stratification is beneficial as it can be performed using routine biopsy samples, or non-invasive images, thus providing an extra layer of information that can improve accuracy and enhanced risk assessment of a given diagnosis and treatment proposal (Fig. 4A). Microvasculature is also readily quantifiable by fractal dimension and can be routinely captured and evaluated using widely-available fundus cameras in ophthalmology offices. Measuring associated changes in fractal dimension of retinal microvasculature can provide early indication of diabetic retinopathy^125,181, as well as risk of coronary heart disease mortality¹²²(Fig. 4B). Another implementation of fractality in diagnostics is based on HRV (Fig. 4C). EEG signal monitoring has similar implementations as well^34,35 (Fig. 4D). The drastic changes in HRV that occur during various abnormalities are well quantified by fractal analysis and linked to risk stratification of various pathologies and even to mortality. This information has been proposed to serve as a signature for early detection of threatening conditions such as stroke or cardiac arrest, and holds promise for applications in Holter monitoring^149,157,182. Some such technologies are already commercial, as companies provide fractal analysis as part of their biosignal analysis solutions¹⁷⁹.

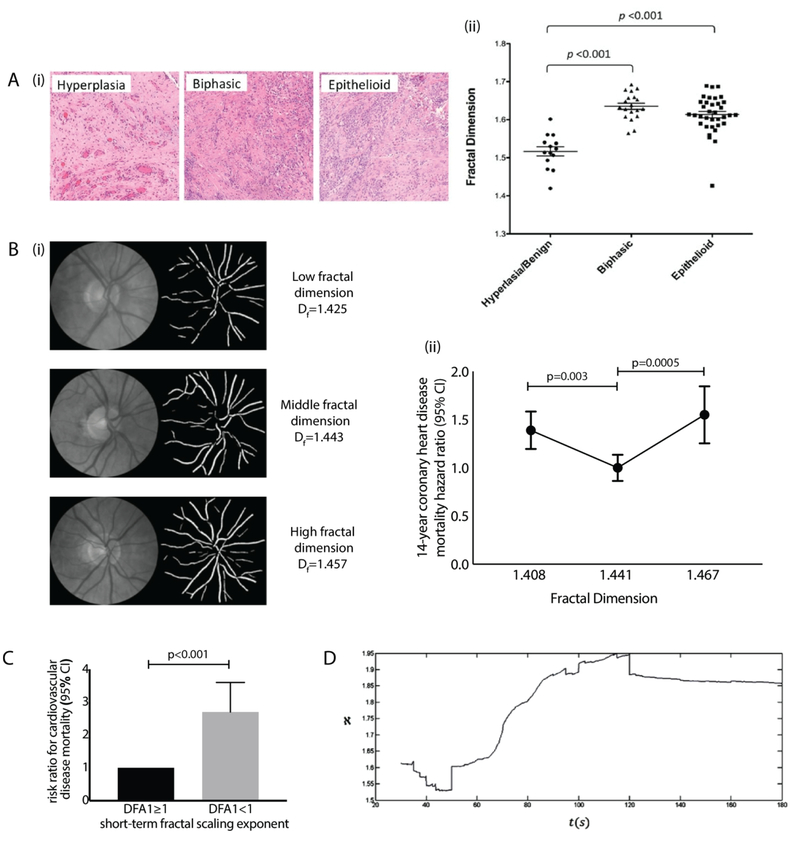
Fig. 4. Diagnostic applications of fractal variability data analysis.

(A) (i) Images of H&E-stained hyperplastic/benign, biphasic and epithelioid tumor samples, with (ii) fractal dimension analysis revealing significant differences between benign and malignant groups [reproduced with permission from⁷⁷]. (B) (i) Images of retina and skeletonized vasculature, and (ii) associated graph of fractal dimension vs hazard ratio for 14-year coronary heart disease mortality, where extreme values of fractal dimension (1st and 4th quartile ranges) were associated with elevated risk [reproduced and modified with permission from¹²²]. (C) Risk ratio for the univariate prediction of cardiovascular disease mortality based on the short-term fractal scaling exponent (DFA1). Low values of DFA1 reflect reduced correlation in heart rate variability signals, and increased risk of mortality [reproduced and modified with permission from¹⁸³]. (D) Recording of patient fractal dimension variation for EEG trace over 3 minutes, showing onset and end of epileptic seizure at 50s and 120s respectively [reproduced with permission from³⁵].

4.3. Biomedical materials

The ability to generate and design fractal structures has been useful for engineering biomimetic tools, such as tissue scaffolds, biomaterials, and microfluidic systems¹⁸⁴. Many of these designed materials are bioinspired in nature. This may be on the one hand from considering the structure-function properties of biological building blocks, such as collagen⁹, elastin⁹⁴, and polylaminin⁹³, which all exhibit fractal scaling in their polymerized structure. On the other hand, many disordered materials, such as polymers, proteins, and composites, tend to follow scaling laws and criticality patterns, for which fractal mathematics provide insight for higher-level engineering. For example, monomers that aggregate into clusters of increasing sizes; critical points in protein folding; and fragmentation sequences in martensite formation^185–187. This comes with an interest beyond simply characterizing the fractal properties of materials, to understanding the factors that influence the precise fractal scaling growth patterns with the intent of creating tunable fractality.

Current state-of-the-art of materials that are designed with fractality focus on nanostructure, micropatterns, or bulk properties. Table 2 presents a shortlist of current approaches to engineering fractality of materials, with illustrations echoed in Fig. 5.

Table 2:

Engineered materials with designed fractality.

Material	Technique	Image	Reference
Silk fibroin	Charge-controlled self-assembly	5A	Zheng, Kaplan et al. [188]
Partially ordered peptides	Mixed ordered and disordered regions	5B	Roberts, Chilkoti et al. [189]
Collagen scar tissue model	Heterogeneous embedding	5C	Dingal, Discher et al. [92]
Flexible electronics	Horseshoe design, Kirigami	5D 5E	Fan, Rogers et al. [190]; Cho, Srolovitz et al. [191]
Electrodes	Micropatterning/lithography	5F 5G	Watterson, Taylor et al. [192]; Sage, Kelley et al. [193]

Fig. 5: Fractal design approaches for novel functional materials.

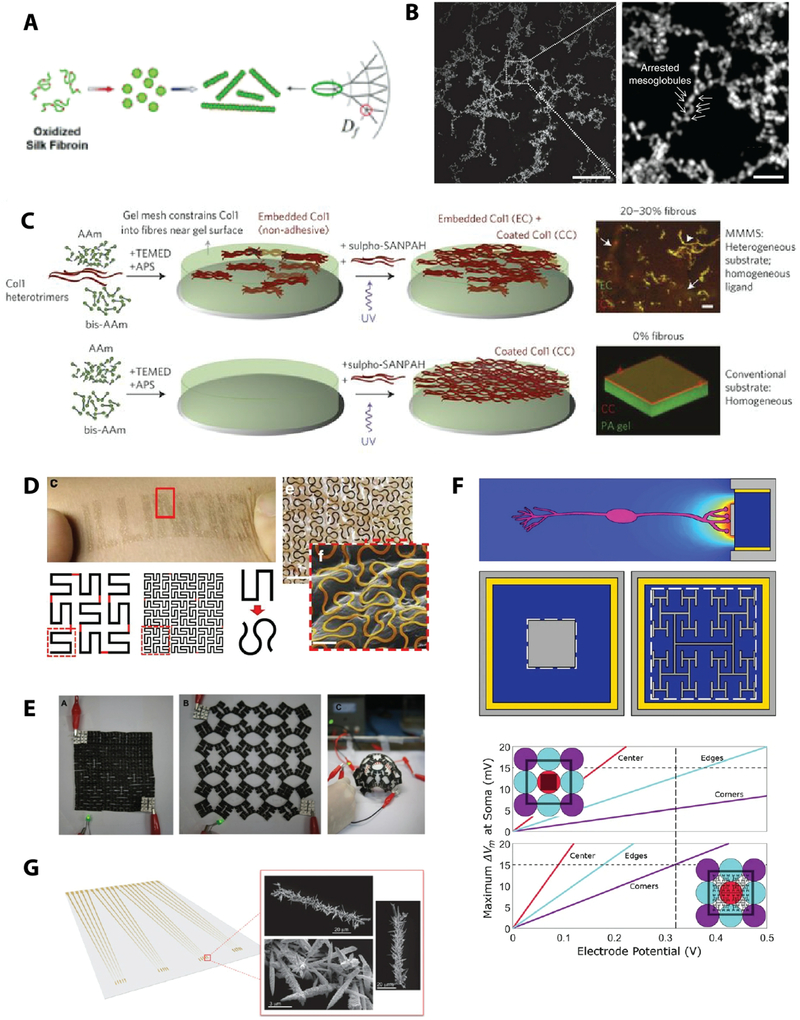
(A) Silk fibroin aggregates into defined fractal forms [reproduced with permission from¹⁸⁸]. (B) Partially-ordered-polypeptide materials form hierarchical fractal structures based on collective, scaling interactions among ordered and disordered domains, with tunable hysteresis and tissue integration properties [reproduced with permission from¹⁸⁹]. (C) Minimal matrix model of scar tissue was fabricated by heterogeneously embedding collagen into gel resulting in fractal stiffness properties [reproduced with permission from⁹²]. (D) Fractal coiling designs of wires allows conformal mounting of metal sensor devices on soft skin while providing increased stretchability and delayed elastic-to-plastic material transition properties [reproduced with permission from¹⁹⁰]. (E) Stretchable device made by kirigami-based fractal hierarchical cutting [reproduced with permission from¹⁹¹]. (F) Fractal electrodes improve excitability in simulation of neural integration for retinal therapy [reproduced with permission from¹⁹²]. (G) Fractal sensors increase surface area in a diagnostic chip to drastically reduce time-to-readout and increase signal gain by several hundred percent [reproduced with permission from¹⁹³].

On a molecular scale, fractal-inspired silk fibroin was synthesized, where the self-assembling fractality of silk fibroin networks was intentionally adjusted by modulating the negative charge on nanofibrils, which resulted in tunable mechanical properties of the materials such as hardness¹⁸⁸ (Fig. 5A). Partially-ordered peptide materials were designed with regions of order and disorder that result in fractal structures, which so far have had improved tissue integration properties, although a deeper understanding of the consequences of the biomimetic fractal structure has yet to be elucidated¹⁸⁹ (Fig. 5B). Control of the heterogeneity of structural components with a focus on fractality has also been applied to enhance bulk properties in a tissue engineering scaffold context, for example, where embedding different degrees of collagen fibers into a gel resulted in an in vitro minimal matrix model of a scar that had more physiologically relevant properties⁹² (Fig. 5C).

In the field of stretchable electronics and devices, fractal design has been used on the nano and micro scales to impart improved conductive and elastic properties. On a nanoscale, control of molecular aggregates is one approach to fractal-inspired material design. Stretchable conductors were synthesized from citrate-stabilized gold nanoparticles that maintained self-organized structural patterns across a range of strain levels, which is suspected to support continued conductance at high deformations¹⁹⁴. On a microscale, fractal patterning of metal wires has helped to impart nonlinear unraveling and deformation properties that improve flexibility and conformability, for example, with fractal “horseshoe-like” micropatterning^190,195 (Fig. 5D). A similar approach uses kirigami-based techniques to cut and fold 2D sheets to create fractal 3D structures that are highly conformable and flexible yet maintain properties of the initial material¹⁹¹ (Fig. 5E).

Micropatterned fractality has also been applied in the context of creating specific surface roughness on tissue culture scaffolds for studying stem cell behaviour¹⁹⁶. Simulation studies also suggest that fractal surface roughness and patterns in implantable electrodes are more effective at promoting interfacial contact and integrated biological function^192,197 (Fig. 5F).

Fractal designs have also been used to increase dispersion in microfluidic devices, for example, to speed up quantification of biomarkers in a diagnostic platform for high throughput analysis¹⁹³ (Fig. 5G), and to achieve greater heat dissipation in device cooling¹⁹⁸. Other constructions of fractal patterns or objects have been achieved on the molecular scale with directed self-assembly^199,200, or on larger scales with software (e.g. AutoCAD, MATLAB) followed by e.g. additive manufacturing processes or rapid laser prototyping to build 3D, 2.5D, or 2D devices or patterns^184,201,202.

It would be interesting to see the development of various synthetically designed materials that have an emphasis on incorporating fractality on all conceptual levels, as well as how the resultant properties would compare with materials that incorporate fractals on fewer conceptual levels.

4.4. Therapeutic applications

Although we have repeatedly seen how fractals may be measured for characterization in a clinical context, fractal patterning may also be applied as a stimulus in therapeutic devices. For example, there is evidence that rehabilitative devices that use more variable patterns in their stimulation programs could support more natural-like results. Functional electrical stimulators^45,46,203 (Fig. 6A), pacemakers^204–206 (Fig. 6B), and mechanical ventilators⁶⁴ (Fig. 6C) are examples of clinical devices where studies suggest that increased variability may have beneficial therapeutic function. For example, using fractal programming in the mechanical ventilator has been shown to enhance respiratory sinus arrhythmia (i.e. the extent to which heart rate variability synchronizes with respiration)⁶⁴. Similarly, fractal surfaces on electrodes, for example in pacemakers, are also suggested to have better clinical performance²⁰⁵. On a non-invasive aspect, there are also studies that suggest that viewing mid-range fractal aesthetics, such as natural scenery, elicits a more positive cognitive response than low or high fractal patterns^207–209. For example, natural scenery in the window view from hospital rooms was found to have an association with improved patient recovery²¹⁰, which could suggest a new role for non-invasive, passive approaches to therapy.

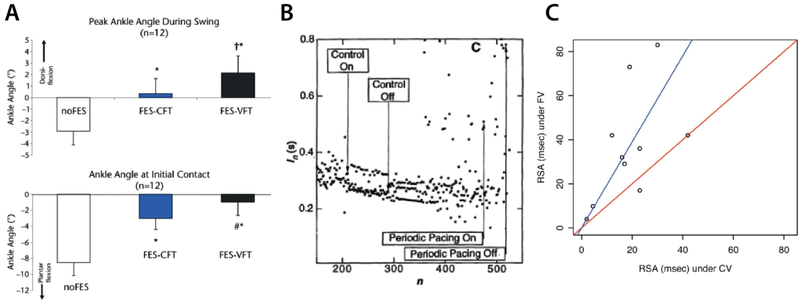
Fig. 6: Therapeutic applications enhanced with variable patterning.

A) Variable frequency trains in functional electrical stimulators (FES) can support improved gait [reproduced with permission from⁴⁶]. B) Chaotic pacing was more effective at stabilizing random arrhythmias than periodic pacing. Y-axis indicates beat-to-beat intervals and x-axis indicates beat number. Start and end positions of chaotic control and periodic control are indicated [reproduced with permission from²⁰⁶]. C) Respiratory sinus arrhythmia (RSA) is an important component of normal breathing, where heart rate increases with inspiration and decreases with expiration, and is associated with ventilation/perfusion matching. Fractal ventilation (FV) patterns in a study of mechanical ventilators was shown to increase RSA compared to conventional ventilation (CV) [reproduced with permission from⁶⁴].

4.5. Limitations and alternatives

While fractality and chaos have an unmistakable presence in natural systems and their characterization is proving useful in biomedical applications, there are several limitations and pitfalls worth addressing.

Chaos and fractality are descriptors for nonlinear dynamical systems, that often appear random and have high levels of complexity. However, although all fractals have high complexity, not all highly complex structures are fractals. Fractal dimension only reveals whether there is scaling order within a pattern. Although it often happens that high-complexity structures can contain greater extents of order than low-complexity structures, high-complexity structures can just as well have low fractality, meaning that in all the complexity, there is limited underlying organization. Thus, complexity and fractality are not necessarily related. On the other hand, the relationship of chaos and complex systems may need a clarification. In general, a complex system might be random and chaotic, and a complex system may encode system-environment interaction.

Another caution when using fractal analysis is that limitations associated with resolution and data/image quality, computing power, preprocessing steps, program and algorithm selection, and feature properties, may cause variability in results. Differences in image quality can affect the consistency or depth of scaling, as can the selection of fractal-counting algorithms. Similarly, there can be multiple features within a given structure amenable to fractal analysis, and a focus on a different set of features may yield different results. For example, there are several instances where studies on retinal vasculature have contradicting results, and could simply be an artifact of differences in methodologies, in addition to differences in the sampled population^124–128. Thus, it is important to have careful consideration of the exact methods used to measure fractality in order to justify any comparisons. Note that these factors would also account for any deviations from theoretical values, for example, the fractal characterization of an annulus. An annulus theoretically has fractal dimension 2. However, most image-based processing approaches will measure values such as 1.9, due to the limited 2D digital rendering of an annulus that is composed of thick lines.

Similarly, fractal analysis depends on the physical space and chosen metric. Although in modern data analysis it is common to consider non-Euclidean space and non-Euclidean metrics, many other areas may have tools and approaches that are based in Euclidean metrics, which can be an issue when characterizing something that is in fact outside of that scope. For example, 3D objects that are projected onto a 2D image or scan represent simplified or dimensionally reduced representations of the original structure. These limitations should be considered and accounted for when assessing fractality and chaos in reproduced images.

To support conclusions for characterizations of complex structures in micrographs and images, applying other non-fractal methods in conjunction could provide more comprehensive assessments. Structural features other than fractal scaling also have relevant degrees of prognostic value. This covers a wide range of image/texture analyses. The gray level co-occurrence method is useful for characterizing variation in sample elevation as approximated by gray levels in an image^211,212. Autocorrelation functions can be used to quantify distribution and alignment of filamentous features in an image²¹³. Scattering and diffraction patterns from x-ray and polarized light microscopy can also be assessed to measure orientation, periodicity, spacing and size of filaments^214,215. Applying Fourier or wavelet transforms to derive spectral information of an image can also be effective at quantifying spacing and orientation⁹. Colocalization studies in fluorescence microscopy can provide insight on spatial distribution and interaction of molecules, to elucidate function and signaling²¹⁶. Noise levels of certain features can also be compared by measuring e.g. fluorescence microscopy signal intensity mean and standard deviation values to get insight on feature specificity^92,217. Combined, these non-exhaustive descriptors are useful additions to fractal dimension and lacunarity analysis that could contribute to a more powerful overall understanding of results.

5. Delving deeper into biomedical chaos and fractals

The presence of fractals and chaos and its relation to health has indicative power relevant for biomedical fields. Tissue engineering and regenerative medicine are thriving fields that are working towards developing new biomedical solutions, either through the use of cell-based models to restore damaged tissues or to instruct innate reparation. The 3D tissue engineering setup has massively increased in complexity in the last decades of research, through the incorporation of more and more nuanced aspects of the native microenvironment^218–220. However, a more profound consideration of complexity itself has yet to enter into the picture. Deeper nuances of chaos theory and fractals may be important to implement in future exploration of natural systems.

5.1. Origins in nature

Although the presence of fractality in natural systems is clear, the reasons for this tendency are still generally considered as matters of hypothesis and speculation. One speculation supporting fractal variability in living things is that it stems from the non-linear dynamics of reactive and feedback-based control systems that are dominant in biological control mechanisms¹³². This setup is similarly thought to represent adaptability of a system, in the sense that it promotes easier changes in direction^132,221, and that mathematically, fractal models are more tolerant to error propagation than other scaling models²²². The self-similar nature of fractals over time is also considered to be a form of natural memory¹³². Another speculation from the perspective of energy and entropy is that self-assembling fractal structures occur in nature when energy distribution is optimized²²¹. That is, while entropy is a thermodynamic quantity that is a driving force for the behaviour of certain systems, chaos is the type of dynamical behaviour that may well describe those systems. For example: the distribution of oxygen and nutrients throughout an organism must be optimized with respect to the work required for its delivery. This would be why blood vessels branch in a fractal pattern, where each successive division serves a smaller region within an organ, thereby optimally serving the entire body¹⁶². Another hypothesis for the scaling growth of fractal networks comes from physics, where it is thought that nodes that emerge during scaling growth are driven by repulsion forces, such that each successive node orients itself in time and space as far from other nodes as possible in order to increase dispersion and robustness of the system, in an effort to “renormalize” the system^223,224. This concept alludes to how local stress and strain distributions dictate epithelial morphogenesis that gives rise to fractal-like structures in the lung alveoli^3,37,225,226, or for the progression of lumen formation²²⁷. Further experimental work on these notions could help to bridge the gap between mathematical speculation and scientific theory.

5.2. Chaotic organization

“Chaos: When the present determines the future, but the approximate present does not approximately determine the future.”

– EN Lorenz²²⁸

Understanding the causal relationships of a system is the basis for predicting its behaviour. In classical determinism, it is held that if all details of the present are known, the future should be strictly predictable. However, it is not possible to fully know the present in all its determining details: there is the uncertainty principle, instabilities in natural laws, exponential forms of error propagation, and many more dynamical factors constantly in flux around a system than we can account for, affecting the system’s trajectory in unpredictable ways. Even if we were able to determine all present parameters, it would still be challenging to understand and predict the system with all its interactions. Chaos theory aims to account for these variabilities and puts a limit to the feasible predictability window of a dynamical system. It provides an alternative framework for understanding of causality, by allowing us to recognize that any observations we strive to control are only a small selection out of an abundance of possibilities.

Chaos is difficult to grasp because it appears completely unpredictable, even though it is governed by very regular underlying order. The three tenets of chaos are: mixing (or topological transitivity), the presence of a dense set of periodic points, and sensitivity to initial conditions. Note that while sensitivity is a notable consequence of the mixing and periodic points properties²²⁹, that is, neighbor relations tend to be lost, we keep it as one of the tenets since it is well known.

i.e. If we denote a continuous map f:X→X, where X is a metric space with the metric d, that describes the evolution of the dynamical system in one time step, then a dynamical system, fⁿ, where $n\in \mathbb{N}$ and fⁿ means n iterations, is chaotic on X if topological transitivity (or chaotic mixing, topological mixing), the presence of a dense set of periodic points²²⁹, and sensitivity are satisfied.

Topological transitivity means that a system may achieve any given state when provided a long enough period to reach it.

i.e. f is called topological transitive (or chaotic mixing) if for any two open subsets U and, there exists $n\in \mathbb{N}$ so that fⁿ(U) ∩ V ≠ ∅.

This may be understood by considering that for any starting interval of conditions, as a system advances through increasing iterations of its chaotic dynamical process, it would eventually be able to fill an entire output space. This comes from the combination of chaotic error propagation with long iterations.

Periodic points appeal to those who look for patterns within a seemingly random system²³⁰, that is, for the order within chaos, since they specify the subset of chaotic space that has predictable behavior.

i.e. A point x ∈ X is called periodic if there exists $n\in \mathbb{N}$ so that fⁿ(x) = x; that is, it is a point that a dynamical system repeatedly visits.

These are certain paths that a chaotic system would be more likely to repeatedly reach over a period of iterations. A relevant notion in a chaotic system is the attractor, which is the status the system eventually will land on. Mathematically, it is an attracting set^231,232, or attracting basin with a trapping region.

i.e. We may call a pre-compact set T ⊂ X a trapping region for map f if f(T) is contained in the interior of T. A set A is called an attracting set if there exists a trapping region T such as $A={\cap }_{n=1}^{\infty }{f}^n(T)$. Note that A is invariant; that is, f(A) = A, and its attracting basin is an open set containing T. An attractor is an attracting set that contains a dense orbit.

If an attractor is fractal^231,233,234, it is termed a strange attractor. Other definitions of attractor are possible, including measure attractor²³⁵ and statistical attractor²³¹. Although a precise prediction is limited in chaotic systems, they in general share nice statistical properties, generally covered by ergodic theory²³⁶. For this reason, statistical and probability models are a good approach to analysing and predicting orbits²³⁷, with the caveat that computed approximations will still be arbitrarily far from a true orbit²³⁸.

Finally, sensitivity refers to the divergent nature of a system that results from very small differences in initial conditions.

i.e. f is sensitive to initial conditions if there exists δ > 0 such that for any open set U and for any point x ∈ U, there exists y ∈ U such that for some $n\in \mathbb{N}$, d (fⁿ(x),fⁿ(y)) > δ where δ may be called the sensitive constant.

This means that slight changes in starting parameters may result in hugely different outcomes later on. A well-known example of chaotic sensitivity is the butterfly effect – a flapping of the wings of a butterfly in Japan may lead to a tornado in New Mexico. This gives chaos its appearance of randomness, and contributes to the difficulty of predicting a chaotic system. The Lyapunov exponent is usually used to quantify the notion of sensitivity to initial conditions, and for a chaotic system, two closeby points move away from each other exponentially²³⁹. Chaotic sensitivity also reflects a type of exponential error propagation where the error signal associated with the minor difference in a starting parameter amplifies until the noise matches or exceeds the main signal. By contrast, a sensitive linear system would have signal and error values growing in harmony.

Overall, while chaotic behaviour in general may be difficult or impossible to predict, its dynamic patterns are susceptible to analysis and prediction. Note that the above definition of chaos is one among many, since for different dynamical models or real-life applications, we may encounter various properties not fully quantified by this definition that nonetheless are considered “chaotic²⁴⁰.” Current efforts looking at chaos in natural systems are focused on observing the presence of fractal patterns. Insight into the dynamics of these systems may be the next step towards achieving higher-fidelity bioengineering results.

5.3. Criticality and bifurcation

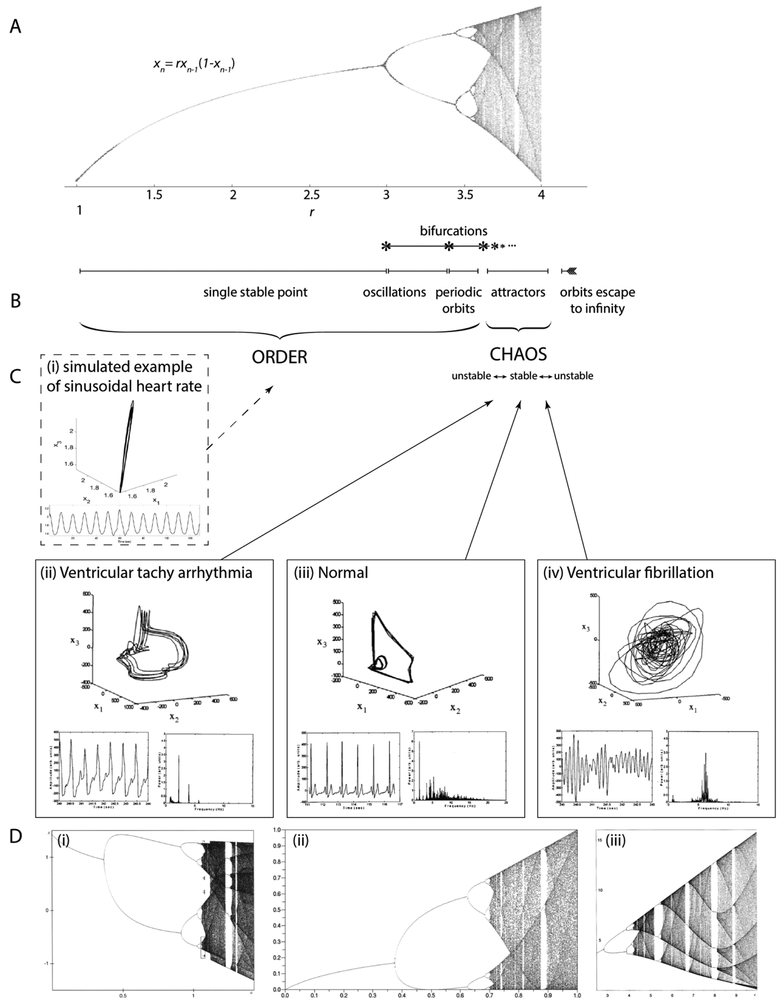
Chaos and order are two aspects of the same thing. One and the same system, governed by a set of laws, is capable of both ordered and chaotic behaviour. The prevailing state will depend on the parameters of the system, and the system can transition between the two. Natural systems often spontaneously switch states, for example, laminar and turbulent fluid flow²⁴¹, or a person transitioning from sleep to awake³¹. These transition phenomena reveal a rich framework for understanding chaos, as the two states and their transition are easily distinguishable. See the logistic model (or real quadratic family) in Figure 7 for an example of different states. In this model, r is the parameter that controls the system, and different r leads to different system behaviours.

Fig. 7. Transitions between order and chaos.

Here we draw parallels between (A) a mathematical system that transitions between order and chaos with various steady states, and (C) a physiological system that also experiences transitions between various states of health and functionality. (A) The typical bifurcation diagram for the quadratic iterator, with control parameter r on the x-axis, and stable state on the y-axis [reproduced with permission from²⁴²]. (B) Markings of the different transition regions and phenomena for the bifurcation diagram in (A). (C) Cardiac rhythms for different cardiac conditions. (i) A simulated example of a sinusoidal heart rate pattern (bottom) and generated embedding (top). Sinusoidal heart rate patterns may be observed in various severe pathologies such as severe fetal anemia, asphyxia, acidosis^158–160. (ii) Ventricular tachy arrhythmia, (iii) normal, (iv) ventricular fibrillation conditions, showing the mapped attractor (top), cardiac rhythm time series (bottom left), and corresponding frequency plot/power spectrum (bottom right) [reproduced with permission from²⁴³]. (D) Bifurcation diagrams for several other mathematical systems, showing the universality of transition properties such as bifurcations, self-similarity, and transitions between chaos and order. These universal properties may be useful to track in biological systems as well. (i) Hénon’s transformations [reproduced with permission from²]; (ii) the quadratic map x_t+1 =a(2x_t −1)² [reproduced with permission from²⁴⁴] (iii) Rössler’s system [reproduced with permission from²].

This state transition pattern involved in a dynamical system capable of chaotic dynamics is called bifurcation. Bifurcation patterns are universal and can be found in any system experiencing transition from order to chaos. It marks a crisis state where a system’s stable points begin doubling up until a transition to chaos. This ramp-up sequence is highly conserved, with bifurcation continuing through ordered period-doubling until a state of criticality right before the transition to chaos. Just like states of order and chaos, criticality carries its own set of characteristic properties useful for modeling as well²³⁷. The bifurcation diagram, which graphs the stable points or attractor of a system in the y-axis through varying parameters shown in the x-axis, visualizes how a single system can be capable of both ordered and chaotic types of behaviour and transition between them (Fig. 7A–B)

The concept of iteration is also useful in understanding chaos. Many dynamical systems are based on repetition of a process over a period of time, both on a collective scale and on a sequential scale²³⁷. When considering a system that is made up of many interacting elements, their correlations mark a collective behaviour that is important to analyze, since their accumulated outcome is what gives the resultant trajectory of the overall system^3,237. Similarly, the sequential iterations starting on the micro-level can grow into the combined macro-level state. By tracking the cascade of correlations occurring at all scales of a system, new features such as self-similarity and chaining of events can be revealed. These features are also part of the arsenal in defining and modeling chaos.

Here, we may consider that the whole is more than the sum of its parts, where as we approach the limits of a given system, new phenomena can emerge as unique entities. Features like long-range correlation, self-similarity, criticality, periodicity and bifurcation, may all be considered as entities whose properties are essential in describing both themselves and their chaotic systems as a whole. These concepts may thus be useful in our approach to analyzing biological systems that transition between healthy and unhealthy states that are marked by varying degrees of chaotic dynamics and fractality (Fig. 7C). Just as there are many different chaotic mathematical systems that share universal properties of chaos and critical transitions (Fig. 7D), many different physiological systems could have common transition properties worth exploring and unifying.

5.4. Fractals

Fractals are structures with features that remain invariant across multiple scales. If we consider that typical, Euclidean geometry and the basic view of the world is described in terms of three dimensions or scales (i.e., a line has dimension 1; a plane has dimension 2; and objects have dimension 3), then the non-integer dimensions, when scaling between 1 and 2, etc., represent fractals. Fractals take into account the complexity of structures in real-number or “fractional” dimensions. For example, a space-filling fractal curve is more than a coiled line, but less than a completely filled-in plane.

Fractals have notable properties including self-similarity, they can be approximated by feedback processes, and they have power-law scaling relationships. Self-similarity means to have the same shape regardless of size or scale of observation. In other words, it has some key features that recur regardless of the scale or position from which the structure is viewed, and if the structure were to be subdivided, its parts would resemble a reduced-size copy of the original whole. Feedback processes are a means by which self-similar fractals can be generated, using similarity transformations, such as scaling, rotation, and translation, often referred to overall as an iterated function system (IFS). By taking a given feature, modifying a portion of it with a similarity transformation, and iterating this process ad infinitum, a fractal can be created. Breaking a fractal down into its self-similar component parts and determining the originating feedback process is also possible. Note that this gives rise to certain emergent properties such as invariance. Because they are derived from the limit value of iterative processes, fractals are also considered to be geometric solutions of iterative equations. This is significant in the context of chaos, where attractors that describes the long-term behavior of their chaotic processes are fractal. Finally, power-law scaling distinguishes fractals from other commonly encountered geometric objects, as it reflects the complexity that is associated with changes in measurement precision. It provides a basis from which the fractal dimension may be measured.

To capture the above qualitative description, we may present a constructive definition of a fractal, which depends on a series of definitions. There are many approaches and definitions for constructing fractals^166,245. We will consider the iterated function system (IFS), power law, and box-counting approaches.

For the IFS approach, we may call a finite set of positive numbers (r₁,r₂,…,r_n) a contracting ratio list if r_i < 1 for all i = 1,…,n. On a complete metric space X, a map f:X→X is called a similarity, with the similarity ratio r > 0 if d(f(x),f(y)) = rd(x,y) for all x,y ∈ X. A collection of functions fi:X→X, i = 1,…,n, is called an IFS realizing the contracting ratio list (r₁,r₂,…,r_n) if f_i are similarities with ratio r_i. By the Hutchinson theorem, there exists a unique non-empty compact subset K ⊂ X such that K = f₁(K) ∪ … ∪ f_n(K). We call such K a fractal (associated with the IFS realization the contraction ratio list¹⁶⁶ (r₁,r₂,…,r_n). This IFS-based construction implies the self-similarity of a fractal structure. Moreover, an IFS may be considered as a dynamical system, if we denote W(A)≔f₁(A) ∪ … ∪ f_n(A) for a given object A. Then, A_{n + 1} =W(A_n) for n = 1,… with A₁ the initial state (initial object). Then, $\underset{n\to \infty }{\text{lim}}{A}_n=K$., where the fixed point of W is thus the fractal K.

Another notion of dimension for a fractal is related to the exponent of the power law scaling of a fractal with respect to measurement precision (Fig. 1). Recall that in the Euclidean space, the notion of dimension connects the scale and the volume. Thus, given a fractal with self-similar structure, the relationship N(s) = (1/s)^D, where N(s) is the number of pieces into which the structure can be divided, should be satisfied for some D ≥ 0. Here, D is called the self-similarity dimension. To compare the self-similarity dimension with the exponent of the power law in equation (1), y(s) = b × (1/s)d, we assume that b = 1 is achieved by a rescaling. Here, y(s) quantifies the infinite complexity that is associated with unbounded length measures as precision increases. Note the critical relationship between N(s) and y(s) with respect to compass setting; that is, y(s) ≈ N(s)s when s is small. By taking log and this relationship into account, we know D = d + 1; that is, in the Britain’s coast length example, the exponent of the power law differs from the self-similarity dimension by 1. In this way, a fractal is measured by quantifying the infinite complexity that is associated with unbounded length measures as precision increases.

The box counting dimension (also known as Minkowski dimension) is another relevant approach to quantifying fractals. The box counting dimension of a measurable set A is defined as $\underset{\delta \to 0}{\text{lim}}\frac{\text{log}\left(N_{\delta }(A)\right)}{\text{log}(1/\delta )}$, where N_δ(A) is the smallest number of sets of a diameter of at most δ that covers A. Note that this definition captures the intuitive idea that if the box-counting dimension is s, N_δ(A) ≈ δ^s when δ is small, which is related to the definition of the self-similarity dimension. The box-counting dimension is more numerically friendly than, for example, the Hausdorff dimension. For this reason, it may be among the most commonly applied approaches for measuring fractals.

Overall, applying fractal geometry to quantifying chaotic processes is common and natural. Fractal growth is intimately connected with chaos in how collective phenomena arise through interacting elements and cascading events, thus building up to self-similar properties with multi-scale correlations, and eventual progression to criticality. As we have seen, it is very effective at classifying complex structures that are seemingly indistinguishable by other metrics, such as the heart’s electrical activity. HRV in the electrocardiogram appears too chaotic to be described by regular metrics. However, with the fractal dimension, the pattern is characteristic and effective at distinguishing healthy from diseased states in physiology²⁴⁶. Moreover, both chaos and fractals are mathematically framed by iterative processes and share associated properties. Where chaos is a dynamical state, fractals are the geometric tools to quantify it.

6. Summary

It is important to be cognisant of the fractality in the systems we study so that we can adjust our perspective and use more compatible tools and mathematical principles in our research efforts. Many systems are capable of transitioning between ordered and chaotic dynamics, and we must be prepared to understand the chaotic regime more ubiquitously. When a system is deemed to be fractal or chaotic in nature, standard Euclidean geometries and linear principles become less accurate descriptors. Non-linear dynamics governed by fractal attractors cannot be well represented by the linear models that were developed for the ordered regime. Because of the chaotic nature of biological systems, they are well-suited for fractal analysis. Parameters such as volume and surface area are not well defined for a system that is infinitely complex as it scales through many orders of magnitude, thus more general mathematical tools are needed. They also discount collective effects that arise through long-range correlations, for example, molecular-scale organization that cascades up to cell- and tissue-scale organization.

We suggest that in working with bioinspired systems, such as novel materials, engineered cell culture systems, functional electrical stimulation, and tissue engineering, applying fractal frameworks could be the difference between garnering deterministic or purely random behaviour in our experiments¹³². This may be achieved by remembering to sometimes look at our problems through the lenses of iteration, self-similarity, scaling, criticality, dimensionality and collective behaviour.

Moving forward, we suggest a few specific steps in our outlook on how to incorporate fractal frameworks in future research. In cell and tissue culture, recapitulating the fractal and chaotic aspects of the microenvironment might be a necessary step for developing higher-fidelity biomedical systems, for example, as performed by Dingal et al. in matching the fractal heterogeneity of matrix stiffness in their model of scar tissue⁹².

Another suggestion is to consider bidirectional changes in fractal optimality in studies that include pathophysiological characterization. Consistent reporting on shifts from healthy to injured states that considers fractality would add to the literature of the field, and a search for optimal levels by considering the low and high extremes of fractality could serve as a compass to guide new technological developments.

Similarly, we encourage taking a step forward by applying other fractal concepts to biomedical research, such as determining system attractors and patterns of bifurcation.

Finally, we comment that the state of today’s research in the area of bioengineering fractality is largely observational in nature, and we would like to see a bigger trend towards more generative work, that derives prognostic insight and that focuses on building or innovating new biomedical tools. Currently, studies in these areas occur in relative isolation from each other. Further collaboration and incorporation of concepts from across the different fields could accelerate the understanding of chaos in biological systems, and grant us a greater degree of dexterity and power when working with them on new endeavors.

Once understood, fractal and chaotic patterns become prevalent almost everywhere. Fractal frameworks are common in fields such as finance, meteorology²³⁷, and in computer animation²⁴⁷. They are also used in art, to assess painting authenticity^248,249 and even as a measure of creative expression^250,251. Fractal frameworks may thus provide a pivotal perspective from which we may approach our most current biomedical engineering problems, especially when the nature of the systems we are working with are chaotic themselves. Knowing the patterns of chaos and being able to recognize the ruling order of the biological systems we work with may be essential for achieving a healthy dose of chaos.