Refining the Association Between Body Mass Index and Atrial Fibrillation: G‐Formula and Restricted Mean Survival Times

Abstract

Background

Previous studies assessing the association between body mass index (BMI) and atrial fibrillation (AF) did not account for time‐varying covariates, which may be affected by previous BMI. We illustrate how the g‐formula can account for time‐varying confounding.

Methods and Results

We included 4392 participants from the Framingham Heart Study who were AF free at ages 45 to 55 years, and followed them for up to 20 years. We estimated hazard ratios (HRs) comparing time‐varying nonobese versus obese with Cox models. We used the g‐formula to compare nonobese versus obese and 10% annual decrease in BMI (until normal weight is reached) versus natural course. We estimated HRs and differences in restricted mean survival times, the mean difference in time alive and AF free. We adjusted for sex, age, and time‐varying risk factors. Cox models indicated that nonobese participants had a decreased rate of AF versus obese participants (HR, 0.83; 95% CI, 0.72–0.97). G‐formula analyses comparing everyone had they been nonobese versus obese yielded stronger associations (HR, 0.73; 95% CI, 0.58–0.91). The restricted mean survival time was 19.22 years had everyone been nonobese and 19.03 years had everyone been obese (difference, 2.25 months; 95% CI, −0.66 to 5.16). When assessing a 10% annual decrease in BMI, the association was weaker (HR 0.96; 95% CI, 0.86–1.08).

Conclusions

Decreased BMI was associated with a lower rate of AF after accounting for time‐varying covariates that depend on previous exposure using the g‐formula, which Cox models cannot accommodate. Absolute measures like the restricted mean survival time difference offer context to relative measures of association.

Clinical Perspective

What Is New?

• Repeated measures in longitudinal cardiovascular studies present the challenge of time‐varying confounding, which cannot be addressed with traditional statistical methods like Cox proportional hazards models.

• We applied the g‐formula to address the issue of time‐varying confounding and found an association of body mass index and incident atrial fibrillation.

What Are the Clinical Implications?

• Decreased BMI was associated with a lower rate of atrial fibrillation, accounting for other atrial fibrillation risk factors affected by body mass index.

• Unlike traditional methods, g‐methods such as the g‐formula can account for time‐varying confounders that are also intermediate variables, which commonly exist in cardiovascular research.

Atrial fibrillation (AF) affects about 3 to 6 million Americans, a number that is expected to rise to 12 to 15 million by 2050.1 AF is associated with increased risks of myocardial infarction, heart failure, stroke, dementia, and death; thus, prevention of AF through modifiable risk factors is key.2, 3 Body mass index (BMI) is a known, modifiable risk factor of AF.4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 Most previous studies have analyzed the association between AF and BMI at cohort entry, without accounting for changes in risk factors over time. One study examined change in BMI as a time‐varying covariate.5 However, changes in BMI may also affect other vascular risk factors via cardiac remodeling. For instance, increasing BMI increases the risk of developing hypertension and heart failure,15, 16 both associated with increased risk of AF. Thus, vascular risk factors create time‐varying confounding, which depends on past BMI; they are said to be intermediate variables.

Confounders that are also intermediate variables cannot be accounted for using traditional statistical methods, such as the Cox proportional hazards model with time‐varying covariates. For example, if obesity increases future risk of heart failure, which in turn increases future AF risk, adjustment for heart failure prevents observing the full association between obesity and AF—the causal pathway between obesity and AF is considered closed or blocked (Figure 1). Unlike standard statistical methods, the g‐methods (ie, the parametric g‐formula, inverse probability weighting of marginal structural models, and g‐estimation) can account for the fact that BMI history is associated with other time‐varying confounders.17, 18, 19, 20, 21, 22 Because the Cox model cannot address this, previous results on the association between BMI and AF may be biased. The parametric g‐formula also allows estimation of the effect of “interventions” based on real‐life scenarios but applied to all individuals: for example, the difference in AF risk had everyone been nonobese versus everyone had been obese. G‐methods have not been applied in AF research.

Figure 1.

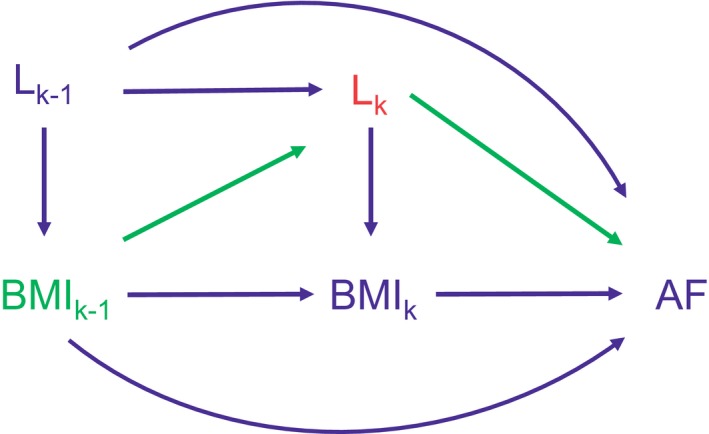
Directed acyclic graph of body mass index, other time‐varying covariates, and atrial fibrillation. The directed acyclic graph displays repeated measures at years k−1 and k. BMI _k denotes the exposure, body mass index (BMI), at year k. L_k denotes confounders at year k (eg, systolic blood pressure). AF denotes the outcome, new‐onset atrial fibrillation (AF). Arrows indicate associations (eg, the association of body mass index [BMI] and incident AF). Adjustment for intermediate variables L_k (red) in a Cox model will block the path between BMI _k−1 and AF (green), which prevents us from observing the full association. However, g‐methods can accommodate this scenario. If BMI _k−1 did not cause AF through L_k (the green arrows were not present), then L_k would not be an intermediate variable and adjustment for L_k would not block the association of BMI _k−1 and AF.

Previous applications of g‐methods on topics outside of AF research have reported relative risks, risk differences, or hazard ratios (HRs) to measure associations.18, 19, 23, 24, 25, 26 Another measure, the difference in restricted mean survival times (RMSTs), offers a clinically meaningful interpretation as the gain or loss in mean lifetime (or mean lifetime alive and free of the outcome) between exposure groups over a prespecified time horizon.27, 28, 29, 30 Reporting absolute measures of association, like the risk difference and difference in RMSTs, alongside relative measures can facilitate interpretations of associations.31

In this paper, we used the parametric g‐formula to estimate the association of hypothetical BMI interventions on the risk of AF in the FHS (Framingham Heart Study). We also show how to derive and interpret the difference in RMSTs.

Methods

We share our statistical code and an example of our analytic methods with simulated data at github.com/s-conner/afbmi-gformula. Investigators can request access to FHS data by submitting a proposal at framinghamheartstudy.org. Boston University Medical Center's institutional review board approved all FHS protocols. Participants signed informed consent forms.

Study Sample

The FHS longitudinal study began in 1948 in Framingham, MA to examine cardiovascular health. We included participants from the FHS Original and Offspring cohorts who were AF free and attended an examination at age 50 years, plus or minus 5 years. We selected the examination closest to age 50 years. For the Original cohort, the earliest examination to enter was Examination 11 (1968–1971).32, 33, 34, 35, 36 AF diagnosis, including atrial flutter, was adjudicated by 2 cardiologists using examination records, medical records, ECGs, and hospital contacts. In our analyses, follow‐up continued until the earliest of first diagnosed AF, death, last FHS examination or medical contact, or end of follow‐up (December 31, 2015, or 10 and 20 years since age 50 years, plus or minus 5 years). Our final sample consisted of 4392 AF‐free participants.

The exposure of interest was BMI over time. We adjusted analyses on sex, baseline age, and the following time‐varying covariates: smoking status (current versus former/never), systolic blood pressure, diastolic blood pressure, antihypertensive treatment, history of diabetes mellitus, heart failure, and myocardial infarction. We selected these covariates in alignment with the CHARGE‐AF (Cohorts for Heart and Aging Research in Epidemiology–Atrial Fibrillation) simple risk score, and we added sex.4, 37 We also conducted analyses stratified by sex.

Conventional Approaches

We first fit 6 conventional Cox proportional hazard models, each at 10 and 20 years of follow‐up. We estimated HRs for BMI at baseline adjusting for the aforementioned covariates at baseline, time‐varying BMI adjusting for covariates at baseline, and time‐varying BMI adjusting for time‐varying covariates. BMI associations were calculated for a 5 kg/m² decrease in BMI. Similarly, we repeated these models with BMI dichotomized as nonobese (BMI <30 kg/m²) and obese (BMI ≥30 kg/m²).

G‐Formula Method

To account for time‐varying covariates that depend on previous BMI, we estimated the associations of BMI interventions and incident AF using the parametric g‐formula method.18, 19, 20, 21, 22 This method adjusts for time‐varying covariates that depend on previous exposure by leveraging the past value of covariates. The method works in 2 steps.18, 19, 20, 21, 22 First, we estimated the joint density of time‐varying covariates given the covariate history through parametric models. Second, we conducted Monte Carlo simulation to estimate the risk of incident AF under a given BMI intervention, defined by specific BMI profiles. For example, we simulated participants maintaining BMI <30 kg/m² and maintaining BMI at least 30 kg/m² over a prespecified time period. By contrasting the counterfactual outcomes, we estimated the association for obesity and the risk of incident AF.

BMI interventions of interest

We examined BMI interventions with regard to incident AF via the following comparisons: (1) maintaining BMI between 18.5 and 29.9 kg/m² at all years (nonobese) versus maintaining BMI between 30 and 41 kg/m² at all years (obese); (2) maintaining BMI between 18.5 and 29.9 kg/m² at all years (nonobese) versus the natural course; and (3) a 10% decrease in BMI each year in participants with BMI >25.0 kg/m² at a given time versus the natural course (Table S1). These interventions and comparisons are fashioned to emulate real‐life weight management strategies, such as bariatric surgery or more gradual weight management.38, 39, 40 The interventions are maintained until the prespecified time period, AF, or death. The natural course consists of simulating the risk of incident AF under the observed empirical distribution of time‐varying BMI in the absence of loss to follow‐up.41

Causal structure and covariate history

In Figure 1, we present a directed acyclic graph to illustrate the pathways between BMI, other covariates, and AF over time. Directed acyclic graphs are a popular tool in epidemiology to visualize confounding and causal relationships. Figure 1 illustrates the causal structure between time‐varying BMI, time‐varying confounder L, and the risk of AF. Time goes from left to right, and thus BMI and L occur before AF; measures at time k−1 occur before those at time k. Arrows from one variable to another indicate that we make the assumption of a direct causal effect from the first variable to the second (not mediated by other variables in the graph). Adjustment for L_k as a time‐varying covariate in a Cox proportional hazards model would block the path between BMI_k−1 and subsequent AF, preventing one from observing the full association between BMI_k−1 and AF. However, g‐methods such as the parametric g‐formula can accommodate this causal structure.

In our analyses, we incorporated the covariate history with a lag of 3 years. At year k, the associations between BMI history (BMI_k−1) and L_k indicate how a participant's other risk factors may be affected by his or her previous BMI at years k−3, k−2, and k−1. The risk of incident AF at year k may be influenced by their current BMI (BMI_k), their BMI history (${\text{BMI}}_{\mathrm{k}-3},{\text{BMI}}_{\mathrm{k}-2},{\text{BMI}}_{\mathrm{k}-1}$), and their risk factors (${\mathrm{L}}_{\mathrm{k}-3},{\mathrm{L}}_{\mathrm{k}-2},{\mathrm{L}}_{\mathrm{k}-1},{\mathrm{L}}_{\mathrm{k}}$).

Parametric models for time‐varying covariates and AF

We fit models to predict covariates in the following sequence: smoking, BMI, systolic blood pressure, diastolic blood pressure, antihypertensive treatment, diabetes mellitus, heart failure, and myocardial infarction. We predict covariates in a given year according to the lagged values for all covariates, plus current values for the preceding variable in the sequence. We fit logistic models for dichotomous covariates and linear models for continuous covariates. Then, we fit pooled logistic models to estimate an individual's probability of AF at each year conditional on the covariate history.42, 43, 44, 45 On the basis of the individual probabilities, we estimated survival probabilities at each year.41 Additional details are provided in Data S1.

Monte Carlo simulation for association of BMI interventions

For each BMI intervention, we used the previously estimated parametric models to generate a pseudo‐population of size n=10 000 participants. Beginning with the observed covariate values, we generated covariates at each year using the estimated regression coefficients from the covariate models. Throughout the process, generated BMI values were modified to match an assigned intervention and used in generating subsequent covariate values. For example, if participants maintain a BMI <30 kg/m² over time, any simulated BMI value ≥30.0 kg/m² is updated to 29.9 kg/m². We give an example of this process in Figure S1. The risk at each time point conditional on the covariate history was also estimated using the estimated regression coefficients from the AF pooled logistic model.

Using the g‐formula, we first estimated HR and risk ratio at 10 and 20 years. We then derived the absolute risk difference and difference in RMST.

Difference in RMSTs

The RMST is the area under the survival function until a given time point, τ, given by ${\mathrm{\mu }}_{\mathrm{\tau }}={\int }_0^{\mathrm{\tau }}\mathrm{S}\left(\mathrm{t}\right)\text{dt}$.28 We considered 2 time horizons: τ=10 and τ=20 years. We used rectangular area approximation with equally spaced intervals to estimate the adjusted RMST by summing the survival probabilities at each year.

To estimate the adjusted RMST, we computed the survival probabilities with equally spaced intervals incrementing by 1 year in simulated data sets without loss to follow‐up. The difference in RMSTs is then given from the difference in RMSTs under different BMI interventions. We obtained standard errors using the nonparametric bootstrap with 500 samples. We repeated this process in 30 imputed data sets.

Multiple Imputation and Interpolation Process

FHS participants have clinic examinations every 2 to 8 years; 16% to 45% did not attend specific exams. In addition, some covariates may be missing at an attended examination. We used multiple imputation46, 47 and linear interpolation to generate data with complete covariate information available each year (Figure 2). The interpolation allows estimating the survival probabilities at each year and thus the RMSTs.

Figure 2.

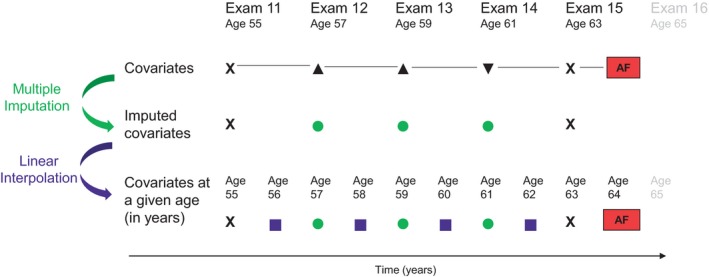
Multiple imputation and interpolation process. X completely measured, ▲ incomplete covariates, ▼ unattended examination, ● covariates multiply imputed, ■ covariates linearly interpolated. Examinations took place approximately every 2 years in the Original cohort and every 4 to 8 years in the Offspring. Covariates of interest include body mass index, smoking, systolic blood pressure, diastolic blood pressure, antihypertensive treatment, diabetes mellitus, heart failure, and myocardial infarction. [Correction added on 12 August 2019, after first online publication: The bottom panel of Figure 2 was removed.]

First, we performed sequential multiple imputation to account for temporality of covariates across successive examination cycles, while removing participants from the imputation process at death.46, 47 We used data beginning at Examination 9 in the Original cohort and Examination 1 in the Offspring cohort. We imputed missing covariate values at entry examination and both missing covariate values and nonattended examinations throughout the follow‐up period. Imputed data sets were generated within each cohort and then combined. We repeated this process for 30 imputed data sets.

Second, we updated the yearly covariate values between exams using interpolation methods. For continuous covariates, we filled in values using linear interpolation. For dichotomous covariates, we used midpoint interpolation to identify the year of the change in covariate, if any. Among participants who experienced AF or died after their last in‐clinic examination, we carried forward covariate values from the last examination (attended or imputed) until incident AF or death. We performed analyses in each of the 30 imputed data sets and combined results according to Rubin's rule.48

Sensitivity Analyses

We performed sensitivity analyses under 3 different scenarios at 20 years of follow‐up. Weight loss may be attributable to severe illness and associated with greater risk of morbidity, including AF.17, 18 Therefore, in our first sensitivity analysis, we excluded participants diagnosed with cancer at entry examination, and we censored participants upon cancer diagnosis.

In a second sensitivity analysis, we restricted to participants who attended at least 3 consecutive examinations with nonmissing covariates in the Original cohort or 2 consecutive examinations with nonmissing covariates in the Offspring cohort because of the need for lagged information (covariate history). We performed sequential multiple imputation for any missing covariate values during follow‐up, as previously described.

Third, we considered a later entry age of 55 to 65 years. Finally, following a reviewer's suggestion, we fit pooled negative binomial models for the hazard of AF instead of pooled logistic models. Additional details are provided in Data S1.

Software

All analyses were performed in SAS 9.4. We used the GFORMULA SAS macros and made modifications to accommodate multiple imputation and a pooled negative binomial model.41 To provide guidance on preparing the analytic data set and using the parametric g‐formula to estimate RMST, we share our SAS code and a working example. Our SAS program is available at github.com/s‐conner/afbmi‐gformula.

Results

Participant Characteristics

Among the 4392 AF‐free participants at ages 45 to 55 years, 53.4% were women (Table 1). The mean age at entry was 50.7 years. The mean BMI was 27.1 kg/m², and 20.4% were obese. The flow of participant selection is outlined in Figure S2. Additional participant characteristics by study cohort are available in Table S2. With a median follow‐up of 23.8 years (Q1, Q3: 16.7, 30.2), there were 847 total AF events, with 489 in men and 358 in women. At 20 years, there were 389 total AF events, with 259 in men and 130 in women. For brevity, we present results for 20 years of follow‐up. Results for 10 years of follow‐up are available in Tables 2, 3 through 4.

Table 1.

Characteristics of FHS Participants at Entry (n=4392)

	Overall (n=4392)	Men (n=2047)	Women (n=2345)
Age, y	50.7±2.2	50.7±2.2	50.8±2.2
Women	2345 (53.4)	···	···
BMI, kg/m2	27.1±5	27.9±4.2	26.3±5.6
SBP, mm Hg	125±17	128±17	123±18
DBP, mm Hg	80±10	82±10	77±10
Current smoker	1184 (29.5)	557 (29.8)	627 (29.3)
Use of hypertension medication	579 (13.2)	304 (14.9)	275 (11.7)
Diabetes mellitus	198 (5.1)	113 (6.1)	85 (4.1)
Heart failure	13 (0.3)	10 (0.5)	3 (0.1)
Myocardial infarction	95 (2.2)	81 (4)	14 (0.6)

Values are mean±SD or n (%). BMI indicates body mass index; DBP, diastolic blood pressure; FHA, Framingham Heart Study; SBP, systolic blood pressure.

Table 2.

Hazard Ratios of Associations Between BMI and Atrial Fibrillation Estimated With Conventional Cox Models

Model	Nonobese vs Obese	5 kg/m2 Decrease in BMI
10 y
All covariates at baseline	0.85 (0.72–1.00)	0.93 (0.86–1.00)
Time‐varying obesity/BMI and other covariates at baseline	0.83 (0.71–0.97)	0.90 (0.84–0.97)
All time‐varying covariates	0.82 (0.70–0.96)	0.90 (0.84–0.96)
20 y
All covariates at baseline	0.75 (0.63–0.88)	0.88 (0.81–0.95)
Time‐varying obesity/BMI and other covariates at baseline	0.82 (0.71–0.95)	0.88 (0.82–0.94)
All time‐varying covariates	0.83 (0.72–0.97)	0.88 (0.82–0.95)

Data are adjusted hazard ratios and 95% CIs. Cox models are adjusted for SBP, DBP, current smoking status, use of hypertension medication, diabetes mellitus status, history of heart failure, and history of myocardial infarction. We note that results for a 5 kg/m² decrease in BMI represent average results for a shift in BMI, and not necessarily an individual's change over time. BMI indicates body mass index; DBP, diastolic blood pressure; SBP, systolic blood pressure.

Table 3.

Relative Measures of Association Between BMI and Atrial Fibrillation Estimated With the g‐Formula

	Hazard Ratio	Risk Ratio
10 y
Nonobese vs obese	0.77 (0.49–1.21)	0.77 (0.51–1.16)
Nonobese vs natural course	0.98 (0.70–1.39)	0.98 (0.74–1.30)
10% decrease in BMI per year vs natural course	1.00 (0.81–1.25)	0.99 (0.94–1.04)
20 y
Nonobese vs obese	0.73 (0.58–0.91)	0.75 (0.63–0.89)
Nonobese vs natural course	0.92 (0.78–1.08)	0.92 (0.83–1.02)
10% decrease in BMI per year vs natural course	0.96 (0.86–1.08)	0.96 (0.92–1.00)

Numbers are estimates and 95% CIs, obtained with 500 bootstrap samples. Analyses are adjusted for SBP, DBP, current smoking status, use of hypertension medication, diabetes mellitus status, history of heart failure, and history of myocardial infarction. BMI indicates body mass index; DBP, diastolic blood pressure; SBP, systolic blood pressure.

Table 4.

Absolute Measures of Association Between BMI and Atrial Fibrillation Using Parametric g‐Formula

	Intervention	Comparator	Difference in Risk (%) or RMST (Months)
10 y
Nonobese vs obese
Risk, %	2.69 (1.35–4.03)	3.49 (1.97–5.02)	−0.81 (−2.21 to 0.59)
RMST, y	9.88 (9.79–9.96)	9.86 (9.78–9.93)	0.24 (−0.94 to 1.42)
Nonobese vs natural course
Risk, %	2.69 (1.34–4.04)	2.74 (1.65–3.83)	−0.05 (−0.92 to 0.82)
RMST, y	9.88 (9.78–9.97)	9.88 (9.83–9.93)	−0.09 (−1.00 to 0.82)
10% decrease in BMI per year vs natural course
Risk, %	2.71 (1.63–3.79)	2.75 (1.66–3.84)	−0.04 (−0.19 to 0.11)
RMST, y	9.88 (9.83–9.93)	9.88 (9.83–9.93)	0.01 (−0.06 to 0.07)
20 y
Nonobese vs obese
Risk, %	9.94 (8.48–11.40)	13.27 (11.26–15.28)	−3.33 (−5.48 to −1.18)
RMST, y	19.22 (19.01–19.43)	19.03 (18.86–19.20)	2.25 (−0.66 to 5.16)
Nonobese vs natural course
Risk, %	9.95 (8.50–11.40)	10.84 (9.73–11.96)	−0.90 (−1.97 to 0.18)
RMST, y	19.22 (19.01–19.43)	19.20 (19.10–19.29)	0.30 (−1.96 to 2.55)
10% decrease in BMI per year vs natural course
Risk, %	10.45 (9.31–11.60)	10.88 (9.75–12.00)	−0.43 (−0.86 to 0.00)
RMST, y	19.21 (19.12–19.31)	19.19 (19.10–19.29)	0.23 (−0.11 to 0.57)

Numbers are estimates and 95% CIs, obtained with 500 bootstrap samples. Analyses are adjusted for SBP, DBP, current smoking status, use of hypertension medication, diabetes mellitus status, history of heart failure, and history of myocardial infarction. BMI indicates body mass index; DBP, diastolic blood pressure; RMST, restricted mean survival time; SBP, systolic blood pressure.

Relative Measures of Associations by Conventional Approaches and the g‐Formula

At 20 years of follow‐up, Cox proportional hazards models with all covariates time varying indicated that nonobese participants had a 17% decreased hazard of AF compared with obese participants (HR, 0.83; 95% CI, 0.72–0.97; Table 2). When considering continuous BMI, on average the hazard of AF decreased by 12% per 5 kg/m² decrease in BMI (HR, 0.88–95% CI, 0.82–0.95; Table 2). We clarify that this represents a 5 kg/m² shift in BMI, and not necessarily an individual's change over time. The HRs comparing nonobese versus obese changed slightly in magnitude when adjusting for all covariates at baseline, obesity as time varying and other covariates at baseline, and both obesity and all covariates time varying. However, the analogous HRs for continuous BMI were nearly identical across models.

Using the g‐formula, the hazard of AF was 27% lower had everyone been nonobese versus obese (HR, 0.73; 95% CI, 0.58–0.91). The risk ratio (RR) was similar (RR, 0.75; 95% CI, 0.63–0.89). Comparisons of BMI interventions with the natural course showed a small but not significant benefit in favor of the BMI intervention. When comparing nonobese with the natural course, the HR and RR of AF both decreased by 8% (HR, 0.92; 95% CI, 0.78–1.08 and RR, 0.92; 95% CI, 0.83–1.02). When comparing the 10% BMI decrease per year intervention to the natural course, the HR and RR of AF both decreased by 4% (HR, 0.96; 95% CI, 0.86–1.08 and RR, 0.96; 95% CI, 0.92–1.00).

In g‐formula analyses performed in subgroups by sex, HRs and RRs comparing nonobese and obese interventions were greater in magnitude for men than women, though most 95% CIs contained the null value of 1 (Table S3). HRs and RRs for the other comparisons were similar by sex.

Absolute Measures of Associations by the g‐Formula

At 20 years of follow‐up, the absolute risk of AF was 9.94% (95% CI, 8.48%–11.40%) had everyone been nonobese and 13.27% had everyone been obese (95% CI, 11.26%–15.28%), with a difference of −3.33% (95% CI, −5.48% to −1.18%). The mean AF‐free lifetime was 19.22 years (95% CI, 19.01–19.43) had everyone been nonobese and 19.03 years (95% CI, 18.86–19.20) had everyone been obese over 20 years, with a difference in RMST of 2.25 months (95% CI, −0.66 to 5.16). The risk difference was significant, while the difference in RMSTs was not. However, the directions of associations were consistent.

When comparing nonobese and 10% decrease in BMI per year while overweight interventions to the natural course, differences favored the BMI intervention but were smaller in magnitude (Table 2). The nonobese intervention decreased risk by 0.90% points (95% CI, −1.97 to 0.18) and increased mean AF‐free lifetime by 0.30 months (95% CI, −1.96 to 2.55), while the 10% decrease in BMI per year while overweight intervention decreased risk by 0.43 percentage points (95% CI, −0.86 to 0.00) and increased AF‐free lifetime by 0.23 months (95% CI, −0.11 to 0.57). Figure 3 depicts the g‐formula Kaplan–Meier curves over 20 years for all intervention comparisons.

Figure 3.

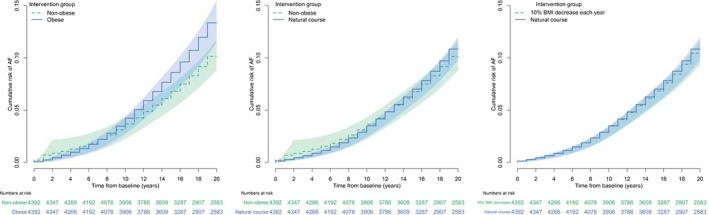
Kaplan–Meier curves of g‐formula survival probabilities comparing simulated populations under body mass index (BMI) interventions. AF indicates atrial fibrillation.

In analyses stratified by sex, the magnitude of association was again greater in men than women (Table S3). The risk difference was −3.30% (95% CI, −6.89% to 0.30%) in men and −2.69% (95% CI, −5.37 to −0.02%) in women, while the gain in mean AF‐free lifetime over 20 years between nonobese and obese was 1.89 months (95% CI, −3.67 to 7.44) in men and 1.19 months (95% CI, −2.34 to 4.71) in women. Risks and mean AF‐free lifetimes were similar between the nonobese intervention, 10% BMI decrease per year intervention, and the natural course. Though the measures of association were close to the null value, the direction of risk differences and differences in RMSTs disagreed when comparing nonobese to the natural course in both men and women. In Figure S3, we plot the Kaplan–Meier curves for men and women to illustrate how measures of association may disagree when curves cross or overlap. In this case, the difference in risks focuses on 20 years, while the difference in RMSTs reflects the entire time horizon.

Sensitivity Analyses

In additional sensitivity analyses, results were overall similar to our main findings. In cancer‐free participants (1825 men and 2045 women), both relative and absolute associations were consistent with original analyses (Table S4). For the complete‐case setting, 155 Original cohort participants and 2947 Offspring cohort participants had complete information at entry and lagged examinations. When comparing nonobese versus obese, all associations at 20 years were consistent with our main approach but slightly greater in magnitude, while comparisons of 10% decrease in BMI per year to the natural course were nearly identical (Table S5). Nonobese versus natural course associations disagreed in direction, though very small and close to the null. Our sensitivity analysis examining entry at age 60 years, plus or minus 5 years, included 3350 women and 2799 men. Both relative and absolute measures of association were similar to our main analyses but slightly smaller in magnitude (Table S6). Under all interventions, AF risks were higher while mean AF‐free lifetimes were lower (20.65% and 18.33 years under the natural course; Table S6). Finally, when fitting pooled negative binomial models instead of pooled logistic models for the hazard of AF, results were nearly identical (Table S7).

Discussion

In summary, we found that decreased BMI was associated with a lower rate of AF in men and women after accounting for time‐varying covariates, which depend on previous BMI. We demonstrated how g‐methods can account for time‐varying covariates, which are also intermediate variables, unlike conventional statistical methods.

If a variable is associated with both the exposure and outcome, the association between exposure and outcome may be biased unless confounding is addressed. In longitudinal studies, confounding is commonly addressed by adjusting for time‐varying covariates. However, if a time‐varying covariate is also an intermediate variable between exposure and outcome, it gives rise to time‐varying confounding. Adjustment for the time‐varying covariate with traditional methods will preclude observing the full association between exposure and outcome, leading to biased estimates, and statistical methods like the g‐methods are needed.

Time‐varying confounding may commonly occur in longitudinal cardiovascular studies with repeated measurements of risk factors over time. For example, when studying the association of isolated systolic hypertension and cardiovascular death, one would account for confounding by adjusting for arterial rigidity.19 However, isolated systolic hypertension may lead to arterial rigidity, which in turn leads to negative health outcomes. The association between isolated systolic hypertension and cardiovascular death may be due to increased arterial rigidity that developed in between, induced by hypertension. Therefore, standard adjustment for arterial rigidity would block the association between isolated systolic hypertension and cardiovascular death. Instead, g‐methods like the g‐formula studied here can address time‐varying confounding.

In this paper, we quantified the association both on the relative scale and on the absolute scale. Similar to prior works, we observed large associations on the relative scale when comparing nonobese and obese interventions. However, associations on the absolute scale provide important context, as the absolute risk of AF in individuals 45 to 55 years of age are relatively small at 10 and 20 years of follow‐up (2.74% and 10.84% under the natural course; Table 3).

Using the g‐formula, we observed a decrease in AF risk and a gain in mean AF‐free lifetime if participants had been nonobese compared with obese, which is consistent with the literature.12, 38 The magnitude of this difference was larger at 20 years than 10 years. However, contrasts of nonobese and 10% decrease in BMI per year to the natural course yielded weaker associations. The smaller magnitude is somewhat expected because of the different reference group between comparisons: The first comparison contrasted maximally different groups, while the second and third comparisons contrasted groups that were relatively more similar.

While conventional Cox proportional hazards models can accommodate time‐dependent covariates, they do not permit time‐dependent confounders that depend on BMI history. Therefore, the parametric g‐formula allows us to examine a different contrast of interest, that is, the difference in mean‐time free of AF had participants been obese versus nonobese over 20 years. In fact, allowing covariates to vary over time when they are actually mediated by the exposure of interest can prevent observing the association between exposure and outcome (Figure 1). Overall, HRs estimated with the g‐formula comparing nonobese versus obese were greater in magnitude than HRs estimated with the Cox model. In fact, at 20 years, the Cox HR with all covariates and obesity measured at baseline was closer in magnitude to the g‐formula estimate, while including covariates as time varying reduced the magnitude. This is likely attributable to the covariates’ role as intermediate variables between obesity and incident AF: The causal pathway between obesity and AF is blocked when adjusting for the intermediate covariates (Figure 1). However, we note that the Cox model and g‐formula HR do not measure the same thing: the Cox model compares nonobese versus obese individuals, while the g‐formula compares everyone had they been nonobese versus everyone had they been obese. Additionally, we simulated nonobese as 18.5 to 25.0 in BMI and obese as 30 to 41 in BMI to avoid BMIs out of range in our sample.

Many studies have demonstrated that obesity is an AF risk factor.4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 49 We fit conventional Cox proportional hazards models, with and without time‐varying covariates, to demonstrate that our data produce results consistent with the literature. Conventional HRs estimated with Cox models with all risk factors measured at baseline were fairly consistent with the literature. In large meta‐analyses of 51 and 25 studies, respectively, Wong et al13 and Aune et al14 demonstrated that increases in BMI were associated with increased risk of AF. Wong et al reported a 19% to 29% increase in AF odds per 5 kg/m² increase in BMI, while Aune et al reported a 28% increase in AF risk. Both of these results are greater in magnitude than the HRs we report at 20 years of follow‐up (14% increase in hazard considering all risk factors at baseline; Table 3). However, our results were similar in magnitude to Schnabel et al³⁷ findings in the Cardiovascular Health Study white subpopulation (14% increase in AF odds per 5 kg/m² increase in BMI),13, 37 which may be comparable to FHS participants.

While obesity is a known risk factor for AF, our results were sometimes small on the absolute scale. Similar findings exist in the literature. For instance, in a large randomized trial of overweight and obese individuals with type 2 diabetes mellitus, the Look AHEAD (Action for Health in Diabetes) study found that rates of AF were not affected by a lifestyle intervention that included weight loss.50 However, the weight loss of the intervention was modest (6.0% mean weight loss from baseline). Additionally, in the SOS (Swedish Obese Subjects) matched cohort study, the risk of new‐onset AF over a median follow‐up of 19 years was 12.4% among those who underwent bariatric surgery versus 16.8% among matched referents in usual care.51 However, matching was imperfect in this study.

Differences in RMSTs have an appealing interpretation and provide a magnitude of association that relative measures, such as the HR and RR, cannot provide. An advantage of a measure in the time domain is the ease in interpretation. Unlike the HR, the difference in RMSTs does not depend on the proportional hazards assumption. The median survival time is an alternative measure but cannot be estimated if the survival probability never decreases to 0.5 in the time horizon, which is common in cardiovascular outcomes. In our data, the median AF‐free survival time cannot be estimated as the probability of AF‐free survival never decreases to 0.5 over 20 years. However, the restricted mean survival time can always be estimated. To our knowledge, the difference in RMSTs using g‐formula methods has only been reported once.24 Some previous applications of the parametric g‐formula assessed examination cycles with approximately equal intervals.17, 18, 19, 52, 53, 54, 55, 56, 57, 58

There are several limitations to our findings. First, we do not know reasons for weight loss in FHS participants and major weight loss is observed infrequently. Previous trajectory analyses in FHS and the ARIC (Atherosclerosis Risk in Communities) study have identified relatively flat longitudinal patterns in weight.9, 10 Although we measure weight, variations in weight over time could be attributable to many things, including severe illness. However, a sensitivity analysis restricted to cancer‐free participants showed consistent findings. Weight loss can occur with aging, yet AF typically occurs in older ages.

Second, our statistical methods make several assumptions. As we included 7 time‐dependent confounders measured at examinations, our analytic data set was fairly high dimensional and prone to missingness, which motivated our decision to perform multiple imputation. We chose sequential multiple imputation to capture the longitudinal nature of the data and exclude participants after death.46, 48 Multiple imputation may not be appropriate if our data were missing not at random. Additionally, while time intervals should be approximately equal in a pooled logistic model, they must be equal to calculate the restricted mean survival time. However, FHS examinations are not equally spaced across participants. We chose linear interpolation to obtain covariate values at the yearly level, which assumes that covariate values change linearly between examinations.59 In addition, methods for causal inference including the parametric g‐formula assume consistency, and in consequence exchangeability (lack of confounding) and positivity (positive conditional probability of exposure), to make causal inference.22, 60 Consistency requires that interventions be well defined and does not typically hold for interventions based on BMI measurements.22, 60 This is because we do not know the underlying reasons for BMI changes in FHS participants. We also do not account for the semi‐competing risk of death, in which death may preclude incident AF.

Finally, the FHS participants are mostly of European ancestry; therefore, our results may not be generalizable to all populations.

In conclusion, decreased BMI was associated with a lower rate of new‐onset AF after accounting for time‐varying covariates that depend on previous BMI, which conventional approaches cannot do. The parametric g‐formula is a flexible method to account for time‐varying covariates that are also intermediate variables, which may commonly occur when assessing vascular risk factors. Furthermore, we illustrate how to derive and interpret absolute measures of association, including the difference in RMST. Absolute measures of association offer additional insight into the data and can improve our understanding of associations.

Directed acyclic graphs allow visualizing pathways between exposures, other covariates, and outcomes. Directed acyclic graphs can also help identifying time‐varying confounding. Unlike Cox models, g‐methods such as the parametric g‐formula, marginal structural models with inverse probability weighting, and g‐estimation, can adjust for time‐dependent confounding (if any) when analyzing data from longitudinal cardiovascular studies. Marginal structural models can be used to assess fixed interventions, while the g‐formula can also be used to assess dynamic interventions.61 SAS macros and R functions are readily available to implement these methods. Furthermore, we recommend the reporting of absolute measures of association, such as the difference in absolute risk and RMST, to give additional context to relative measures of association.

Sources of Funding

This work was supported by the National Heart, Lung, and Blood Institute's Framingham Heart Study (NIH/NHLBI 1R01HL128914; 2R01 HL092577; HHSN268201500001I; N01‐HC 25195). Ms Conner was supported by the National Institute of General Medical Sciences (NIH/NIGMS) Interdisciplinary Training Grant for Biostatisticians (T32GM74905‐14) and NHLBI (F31 HL145904‐01). Drs Lunetta, Benjamin, Anderson, Lubitz, and Trinquart were supported by the American Heart Association (Benjamin, Trinquart: 18SFRN34150007; Lunetta, Benjamin, Trinquart: 18SFRN34110082; Anderson, Lubitz: 18SFRN34250007). Dr Lubitz is also supported by NIH grant 1R01HL139731. Dr Anderson is also supported by NIH K23NS086873, R01NS103924, and a Center for Genomic Medicine Catalysis Award.

Disclosures

Dr Anderson has consulted for ApoPharma, Inc for matters unrelated to the content of this manuscript. Dr Lubitz receives sponsored research support from Bristol Myers Squibb/Pfizer, Bayer HealthCare, and Boehringer Ingelheim, and has consulted for Abbott, Quest Diagnostics, Bristol Myers Squibb/Pfizer. Dr Ellinor has consulted with Bayer AG, Novartis, and Quest Diagnostics. The remaining authors have no disclosures to report.

Supporting information

Data S1. Supplemental methods.

Table S1. Body Mass Index Interventions and Comparisons Assessed With the g‐Formula

Table S2. Characteristics of Participants by Framingham Heart Study Cohort (n=4392)

Table S3. G‐Formula Associations per Body Mass Index Intervention Group and Contrasts Between Intervention Groups by Sex at 20 Years of Follow‐Up

Table S4. G‐Formula Associations per Body Mass Index Intervention Group and Contrasts Between Intervention Groups at 20 Years of Follow‐Up in Cancer‐Free Participants (n=3870)

Table S5. G‐Formula Associations per Body Mass Index Intervention Group and Contrasts Between Intervention Groups at 20 Years of Follow‐Up, With Complete Case Data at Entry (n=3102)

Table S6. G‐Formula Associations per Body Mass Index Intervention Group and Contrasts Between Intervention Groups at 20 Years of Follow‐Up, Entry at Age 60 Plus or Minus 5 Years (n=6149)

Table S7. G‐Formula Associations per Body Mass Index Intervention Group and Contrasts Between Intervention Groups at 20 Years of Follow‐Up, Negative Binomial Model for Atrial Fibrillation (n=4392)

Figure S1. Diagram of g‐formula Monte Carlo simulation.

Figure S2. Flow diagram of study participants.

Figure S3. Kaplan–Meier curves of g‐formula survival probabilities comparing simulated populations under BMI interventions in men and women.

(J Am Heart Assoc. 2019;8:e013011 DOI: 10.1161/JAHA.119.013011.)