Abstract
Graphene has been known to possess exceptional mechanical properties, including its extremely high Young’s modulus and atomic layer thickness. Although there are several reported fiber optic pressure sensors using graphene film, a key question that is not well understood is how the suspended graphene film interacts with the backing air cavity and affects the sensor performance. Based on our previous analytical model, we will show that the sensor performance suffers due to the significantly reduced mechanical sensitivity by the backing cavity. To remedy this limitation, we will, through experimental and numerical methods, investigate two approaches to enhance the sensitivity of fiber optic acoustic pressure sensors using graphene film. First, a graphene–silver composite diaphragm is used to enhance the optical sensitivity by increasing the reflectivity. Compared with a sensor with pure graphene diaphragm, graphene–silver composite can enhance the sensitivity by threefold, while the mechanical sensitivity is largely unchanged. Second, a fiber optic sensor is developed with enlarged backing air volume through the gap between an optical fiber and a silica capillary tube. Experimental results show that the mechanical sensitivity is increased by 10× from the case where the gap side space is filled. For both approaches, signal-to-noise ratio (SNR) is improved due to the enhanced sensitivity, and COMSOL Thermoviscous acoustics simulation compares well with the experimental results. This study is expected to not only enhance the understanding of fluid–structural interaction in sensor design but also benefit various applications requiring high-performance miniature acoustic sensors.
1. Introduction
Graphene, a single atomic layer of carbon arranged in a regular hexagonal pattern, has been demonstrated to possess exceptional mechanical [1], thermal [2], electronic [3], and chemical [4] properties since its discovery in the free state [5–7]. For a monolayer graphene with a thickness of 0.34 nm, its Young’s modulus reaches 1 TPa, establishing that graphene is the strongest material ever measured [1]. It is also known that graphene can endure a large deformation of up to 20% [1]. Furthermore, graphene can survive at a temperature as high as 700 °C [8,9].
Thanks to the recent development on the fabrication of large-area graphene by mechanical exfoliation [6,10] or chemical vapor deposition (CVD) [11,12] and the techniques of transferring it to a different substrate [13–16], fruitful progress has been made to not only better understand the graphene material but also explore its use in various applications [17,18]. Examples include high-speed transistors with high carrier mobility and large saturation velocity [19,20] and biosensors having large surface areas and high electrical conductivity [21]. While most research efforts thus far have been focused on the electronic properties of graphene (e.g., the application of graphene for gas sensors [22–24]), a few endeavors have been attempted to directly take advantage of its unique mechanical properties [25–28]. In one study, a suspended graphene film was explored as the pressure transduction and electrical signal readout element, whose resistance changes with the applied pressure on the film [25]. In another study, a low finesse Fabry–Pérot (FP) interferometer was constructed using a few-layer graphene covering a fused silica capillary tube, which is spliced to the tip of an optical fiber [26]. With a diaphragm diameter of 25 µm and a cavity length of 21 µm, this graphene-based pressure sensor demonstrated a pressure sensitivity of 39.4 nm/kPa when it was calibrated using static pressure to the range of ∼10 kPa. Targeting the audible frequency range, a fiber optic acoustic sensor with a 100-nm-thick graphene film covering the end surface of a ceramic ferrule (with a typical outer diameter of 1.25 mm) was demonstrated [27]. In a following study, the same system configuration was used, but the sensor diaphragm was changed to a 13-layer graphene film [28].
In the development of dynamic pressure sensors, the graphene’s unique combination of exceptional high Young’s modulus and thickness down to atomic layers is theoretically advantageous for developing sensors with unprecedented performance despite the tradeoff between bandwidth and sensitivity. For a dynamic pressure sensor with a clamped circular diaphragm, as illustrated in Fig. 1(a), the fundamental natural frequency f1 is given by [29]:
| (1) |
where E, ν, ρ, a, and h are the Young’s modulus, Poisson’s ratio, density, radius, and thickness of the diaphragm, respectively. Here, the in-plane tension is assumed to be zero for ease of comparison. Note that the fundamental natural frequency largely determines the sensor bandwidth [30], although the damping also plays a role. On the other hand, the static mechanical sensitivity of the sensor can be calculated by the following equation [29]:
| (2) |
According to Eqs. (1) and (2), to achieve a high natural frequency f1, which usually leads to a large sensor bandwidth, it is more favorable to design a sensor with a smaller radius and a larger thickness or choose a material with a higher Young’s modulus, all of which will result in a decreased sensitivity SM0, thus the so-called tradeoff between bandwidth and sensitivity.
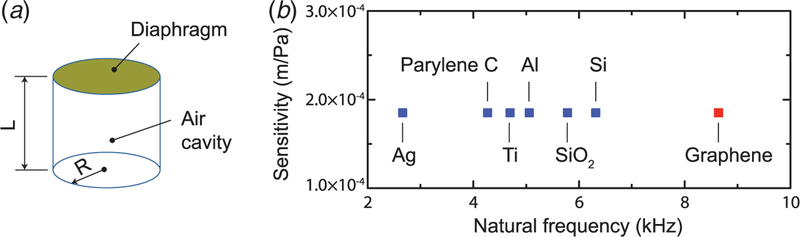
Fig. 1.
Air-backed diaphragms for acoustic pressure sensors: (a) schematic of a circular clamped diaphragm backed by a cylindrical air cavity with rigid side and bottom walls and (b) natural frequencies of using different materials to achieve the same sensitivity without considering the effect of the backing cavity (L = 67 µm, R = 40 µm)
To compare the performance of sensors made of different materials, the diameter of the circular clamped diaphragm is fixed at 80 µm and the diaphragm thickness is varied to achieve the same sensitivity. For the graphene film of 4 monolayers, the equivalent material parameters are chosen as E = 1 TPa, ν = 0.17, and ρ = 2200 kg/m3 [1,31]. As shown in Fig. 1(b) and Table 1 (columns for the “without air cavity” case), the sensor with a thin graphene diaphragm exhibits a much higher natural frequency for the same static sensitivity. This result can be understood by examining the scaling in Eqs. (1) and (2): f1 scales with hE1/2, while SM0 scales with h−3 E−1. Therefore, to achieve a higher natural frequency while maintaining the same static sensitivity, one can choose a material with a higher Young’s modulus and at the same time reduce the diaphragm thickness. For example, if a material with a Young’s modulus of eight times larger is chosen, the thickness can be reduced by half to obtain the same sensitivity, which yields a natural frequency that is more than 40% higher. This explains the advantage of graphene having an extremely high Young’s modulus and small thickness.
Table 1.
Comparison of properties and performance of different diaphragm materials for acoustic sensors
| Material properties |
Without air cavity |
With air cavity |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Material | Young’s modulus (GPa) | Poisson’s ratio | Density (103 kg/m3) | Thickness (nm) | Sensitivity (µm/Pa) | Natural frequency (kHz) | Thickness (nm) | Sensitivity (nm/Pa) | Natural frequency (kHz) |
| Silver | 83 | 0.37 | 10.5 | 3.00 | 185 | 2.66 | 5.03 | 1.42 | 14.0 |
| Parylene C | 4.5 | 0.4 | 1.29 | 7.85 | 185 | 4.70 | 9.35 | 1.42 | 14.0 |
| Titanium | 110 | 0.32 | 4.43 | 2.76 | 185 | 4.26 | 3.43 | 1.42 | 14.0 |
| Aluminum | 69 | 0.32 | 2.7 | 3.23 | 185 | 5.06 | 3.72 | 1.42 | 14.0 |
| Silicon dioxide | 90 | 0.17 | 2.2 | 3.04 | 185 | 5.78 | 3.33 | 1.42 | 14.0 |
| Silicon | 169 | 0.25 | 2.3 | 2.43 | 185 | 6.31 | 2.59 | 1.42 | 14.0 |
| Graphene | 1000 | 0.17 | 2.2 | 1.36 | 185 | 8.63 | 1.36 | 1.42 | 14.0 |
Note: The simulation results for a circular clamped diaphragm with a diameter of 80 µm. The cylindrical air cavity has the same diameter as that of the diaphragm and a length of 67 µm. The thickness in the “without air cavity” case is varied to obtain the same mechanical sensitivity for different materials. In the case of “with air cavity,” since the mechanical sensitivity is limited by the much stiffer backing air cavity, the thickness is varied to obtain the same natural frequency for different materials.
However, according to our previous theoretical study on the structural–acoustic interaction of air-backed diaphragms [32], the air cavity backing the diaphragm plays a critical role in determining the sensor performance, particularly for miniature sensors with small air cavity. To accurately predict the sensor performance, the structural–acoustic interaction between the diaphragm and the backing air cavity has to be taken into account. By using the developed continuum mechanics model, the sensitivity and fundamental natural frequency of the air-backed graphene are calculated as SM0 = 1.42 nm/Pa and f1 = 14.0 kHz, respectively. In other words, the backing air cavity reduces the mechanical static sensitivity by more than five orders of magnitude, while increasing the natural frequency by 62%. This demonstrates why it is critical to consider the effects of air cavity in small transducers. As summarized in Table 1 (columns for the “with air cavity” case), since the sensitivity is largely limited by the air cavity, the thickness for other materials can be simply varied to achieve the same sensitivity and fundamental natural frequency as the graphene.
Given the limitation on the mechanical sensitivity by the backing air cavity, the goal of this paper is to explore different ways to enhance the sensitivity of graphene-based fiber optic acoustic pressure sensors. The sensor’s ultimate sensitivity ST can be considered as the product of mechanical sensitivity SM (transduction from pressure stimulus to mechanical displacement) and optical sensitivity SO (transduction from mechanical displacement to electric voltage output), i.e., . Targeting either of these two transduction stages, one approach is to use the graphene–silver composite as the diaphragm material with the goal of enhancing the optical reflectivity to achieve higher optical sensitivity SO and the other approach is to create a larger backing cavity with the goal of increasing the mechanical sensitivity SM. These two approaches are detailed in Secs. 2 and 3, along with a discussion (Sec. 4).
2. Fiber Optic Sensors With Graphene–Silver Composite Diaphragms
2.1. Sensor Fabrication.
The schematic of the sensor is shown in the inset of Fig. 2(a). The main structure of the sensor is an ultraviolet (UV)-molded polymer cavity covered with a graphene–silver composite diaphragm, which forms an FP interferometer between the diaphragm and the fiber endface. The fabrication process of the polymer cavity is illustrated in Fig. 2(b). The first step is to construct a fiber-based mold by inserting a cleaved fiber (80 µm for the cladding diameter) into a zirconia ferrule with the fiber protruding about 67 µm and permanently fixing the fiber with a UV light-curable polymer (Dymax OP-54), following an approach detailed in Ref. [33] (step i). The polymer completely filled the gap between the ferrule and the 80-µm fiber due to the capillary force and low viscosity. The fabricated mold is then cleaned and treated with an organosilane (Gelest methacryloxypropyltrimethoxysilane, SIM6487.4) to facilitate the releasing in the molding process. The second step is to dispense a small drop of UV-curable polymer (Dymax OP-4–20632) on another cleaved optical fiber (Corning SMF-28) used as a part of the sensor by using a separate fiber placed in the middle of the mold (step ii). The sensor fiber on the left is aligned with the mold fiber on the right by coupling light through the sensor fiber and monitoring the intensity exiting the mold fiber. By adjusting the relative position of the sensor fiber to the mold, a desirable alignment can be achieved when the maximal transmitted intensity is obtained. Furthermore, the polymer is precured by using a UV light source (Hamamatsu, LC5) for 12 s at 12% intensity (step iii), followed by releasing the mold to obtain the molded cavity (diameter of 80 µm and depth of 67 µm) (step iv). Finally, the polymer cavity is postcured by using a spot UV light source (Dymax, BlueWave 50AS) for 100 s and baked on a hot plate (150 °C) for 3 h to enhance the thermal stability.
Fig. 2.
Ultraviolet-molded fiber optic sensors with graphene (or graphene–silver composite) diaphragms: (a) SEM image of the sensor with its schematic shown in the inset, (b) fabrication process of the molded cavity, and (c) schematic of transferring graphene film onto the molded cavity
The graphene film (purchased from GrapheneSuperMarket.com) is originally deposited via CVD on nickel, which is itself on top of a silicon substrate. The average thickness of graphene is four atomic layers. Silver of selected thickness (5 nm) is deposited on top of the graphene by using e-beam evaporation. To release the graphene–silver film from the substrate, a 0.5% FeCl3 solution is used to etch the nickel starting from the peripherals. When the nickel is completely removed, the released graphene film floats on top of the solution, which is then diluted by distilled water multiple times to remove the residual etchant. The released film is then transferred onto the polymer substrate by pushing down the molded cavity vertically and retreat, as illustrated in Fig. 2(c), essentially a punching process. When the top surface of the cavity is in contact with the film, the film is bonded to the polymer substrate by Van der Waals force [34] to complete the sensor fabrication. The scanning electron microscopic (SEM) image of the fabricated sensor is shown in Fig. 2(a).
2.2. Experimental Characterization.
To detect the sound pressure-induced diaphragm center displacement of the sensors, a low-coherence fiber optic interferometer (LCFOI) system [35] was used, as shown in Fig. 3(a). Compared with the conventional laser-based fiber optic interferometer, LCFOI has one particular advantage of less susceptibility to wavelength fluctuation and is thus ideal for measuring nanometer displacement or below. The light from a broadband superluminescent diode (SLD) (Thorlabs S5FC1018S, center wavelength 1310 nm, 40 BW, 30 mW) was delivered via a 1 × 2 fiber optic coupler (Gould Fiber Optics, 50:50) to the FP interferometer of the sensor head (i.e., the sensing interferometer). The reflected light was then sent to a FP tunable filter (Micron Optics FFP-TF2) (i.e., the reference interferometer) via the same 1 × 2 coupler. The output light from the tunable filter was coupled into the photodetector (New Focus, Model Velocity 2011) and converted into an electric signal, which is the voltage output of the sensor. A 1/2-in. condenser microphone (Brüel & Kjær, model 4191 with preamplifier 2690–0S2) was used as a reference sensor. A National Instruments data acquisition card (model USB-6366) was connected to a computer to output the sound stimulus through a tweeter speaker (ESS AMT, preamplified by a SONY audio receiver STR-DH100) and to acquire the signals from the reference microphone and the fiber optic acoustic sensor. The incident angle is 0 deg, i.e., the sensor front points toward the speaker.
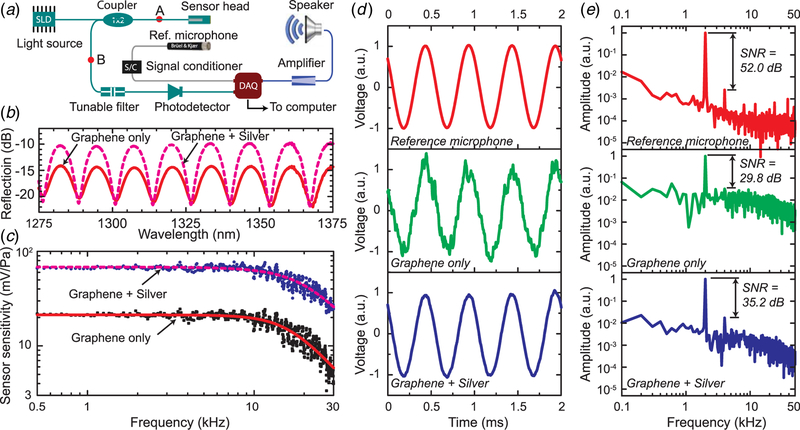
Fig. 3.
Experimental characterization of UV-molded graphene-based fiber optic sensors: (a) experimental setup with a low-coherence fiber optic interferometric system, (b) reflectivity of the Fabry–Perot interferometer of the sensor head, (c) frequency response of sensors with two different kinds of diaphragms (dots for experiments and lines for simulation), (d ) time domain signals at 2 kHz from the reference microphone (top), fiber optic sensor with graphene only as the diaphragm (middle), and sensor with graphene and silver composite diaphragm (bottom), all of which are normalized to have an amplitude of 1, and (e) Fourier transform of the signals in (d )
In order for the LCFOI system, as shown in Fig. 3(a), to work properly, the optical path differences of the sensing interferometer (i.e., the sensor head) δs and reference interferometer (i.e., the tunable filter) δr need to satisfy δs ≈ δr ≫ lc and (δs−δr) ≫ lc, where lc is the coherence length of the SLD light source [36].
Under this condition, the photodetector output I can be expressed as follows:
| (3) |
where k0 is the wave number in free space and s and are two constants determined by the mirror reflectivity in the FP interferometers and the light source intensity, respectively. Note that , where Ls and Lr are the mirror separation in each of the two FP interferometers. When the system is operated at quadrature points , where m is an integer, the LCFOI system has the maximum output in response to a dynamic change of Ls or Lr.
To quantify the enhancement of optical reflectivity of graphene–silver composite, the reflection spectrum of the sensor was measured by using an optical spectrum analyzer (OSA; Agilent 86142B) via two steps. First, disconnecting the FP sensor head, OSA is connected at point A in Fig. 3(a) to measure the input spectrum to the sensor head, where λ is the optical wavelength. Next, with the sensor head connected, OSA is inserted at point B to measure the output spectrum . Then, the reflection function of the FP sensor head can be calculated as , where the factor of two is to account for the 50:50 split ratio of the optical coupler. The measured is shown in Fig. 3(b) (dashed line) and compared with a second UV-molded sensor with a graphene-only diaphragm (solid line). With the added silver layer, is enhanced on average by a factor of 2.63 (or 4.2 dB) at the peaks and reduced by a factor of 0.84 (or 0.8 dB) at the valleys. Note that the peaks/troughs of the spectra of two sensors are well aligned, indicating that the cavity length is consistent in different samples due to the nature of the UV-molding fabrication process. In short, due to the enhanced optical reflectivity of the graphene–silver composite, the reflection spectrum of the sensor with a graphene–silver composite diaphragm exhibits a ∼3× reflectivity enhancement compared with that of the sensor with a pure graphene diaphragm.
To characterize the performance of the sensors, frequency sweep was carried out to obtain their frequency response, as shown in Fig. 3(c). Note that the sensitivity frequency response ST(f) in terms of photodetector output per unit pressure stimulus can be approximated by a lumped model as a function of excitation frequency f :
| (4) |
where ST0 is the sensitivity extrapolated to f = 0, f1 is the fundamental natural frequency, and ζ is the damping ratio. The values of ST0, f1, and ζ can be obtained through least-squares fitting, as listed in Table 2.
Table 2.
Effects of silver on graphene-based acoustic sensors
| Graphene only |
Graphene+silver |
|||
|---|---|---|---|---|
| Nominal | Uncertaintya | Nominal | Uncertaintya | |
| Sensor sensitivity, ST0 (mV/Pa) | 21.32 | 0.39 | 68.41 | 1.00 |
| Natural frequency, f1 (kHz) | 16.18 | 0.46 | 20.22 | 0.71 |
| Damping ratio, ζ | 0.73 | 0.03 | 0.79 | 0.03 |
| Mechanical sensitivity (nm/Pa) | 1.55 | 0.03 | 1.17 | 0.02 |
Expanded uncertainty using coverage factor k=2.
To obtain the mechanical sensitivity SM, an electrical sinusoidal voltage is applied to the reference interferometer (i.e., the FP tunable filter), which has a calibrated sensitivity of phase change to the voltage modulation (69.7 nm/V). Since the reference interferometer and the FP sensing interferometer are interchangeable, the phase change of the sensing interferometer due to the sound stimulus is equivalent to applying a sinusoidal modulation signal to obtain the same phase change from the tunable filter without the sound stimulus. By using this method, the mechanical sensitivity was calibrated to be 1.55 nm/Pa and 1.17 nm/Pa for the sensors without silver layer and with 5-nm-thick silver layer, respectively.
As can be seen from Fig. 3(c) and Table 2, the most prominent effect of adding the silver coating is that the optical sensitivity of the sensor is improved threefold. However, the mechanical sensitivity is largely unchanged, which confirms that the improved sensor sensitivity is mostly due to the enhanced optical reflectivity of the diaphragm. Furthermore, the natural frequency is also slightly improved (from 16.2 kHz to 20.2 kHz), but the damping ratio almost remains the same (from 0.73 to 0.79).
At a specific frequency (e.g., 2 kHz), the two fiber optic acoustic sensors are compared against the reference microphone in both time domain (Fig. 3(d)) and frequency domain (Fig. 3(e)). The waveform amplitudes are normalized to one for ease of comparison. It can be seen that the addition of silver of a few nanometers results in much cleaner signals in time domain and overall better signal-to-noise ratio (SNR) in frequency domain, an improvement of 5.4 dB (from 29.8 dB to 35.2 dB).
To compare the repeatability of the developed sensors against the reference microphone, we define the normalized error (NE) as NE(%) = (Vmax−Vmin)/Vavg × 100, where Vmax, Vmin, and Vavg are the maximum, minimum, and average amplitudes, respectively, of three measurements for frequencies between 500 Hz and 20 kHz. For the fiber optic sensor with graphene-only diaphragm, NE has a mean of 0.78% for the reference microphone and 1.77% for the fiber optic sensor and a ratio of 2.27 (= 1.77%/0.78%). With the added silver layer to enhance the optical sensitivity, this ratio is improved to 1.59 (=1.34%/0.84%).
2.3. Finite Element Simulation.
In our previous analytical model [32], the medium (air) is assumed to be lossless and only the normal velocity is compatible at the fluid–structural interface. This prevents its application for miniature fiber optic sensors where the domain size is comparable with the thermal/viscous boundary layer thickness. For example, the thermal boundary layer thickness is 49 µm at 2 kHz; the diameter and length of the cylindrical backing air cavity are 80 µm and 67 µm, respectively. To better understand the mechanical behavior of the fabricated sensors, a finite element method (FEM) model, shown in Fig. 4(a), is developed using COMSOL Thermoviscous Acoustics (TA), where the air domain is described using Navier–Stokes equations and meshed using brick second-order elements, and the diaphragm is meshed using quadrilateral second-order shell elements. At the interface, both normal and tangential velocities are assumed to be compatible and boundary layer meshes are added for each sweep frequency. In comparison, the same model can be solved using COMSOL Pressure Acoustics (PA), similar to our analytical model [32], where it is assumed to be lossless in air and the tangential compatibility constraint is relaxed.
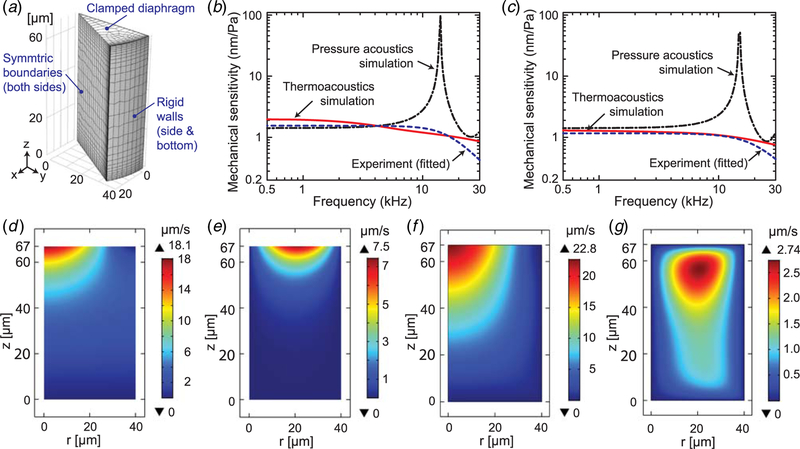
Fig. 4.
Numerical simulation to obtain the frequency response for the fabricated fiber optic sensors using COMSOL: (a) FEM model using COMSOL Multiphysics, (b) and (c) mechanical sensitivity as a function of frequency, comparing two kinds of FEM simulations with the experiment results, for the sensors with graphene-only films (b) and graphene–silver composite (c) films, (d )–(e) cross-sectional views of velocity fields (normal (d ) and tangential (e)) for the fiber optic sensor with graphene-only diaphragm at 2 kHz, obtained by using pressure acoustics simulation in COMSOL where loss is neglected, and (f) and (g) velocity fields (normal (f) and tangential (g)) for the same sensor and the same frequency as in (d )–(e) but obtained using thermoviscous acoustics simulation in COMSOL where thermal and viscous losses are considered
The material properties listed in Table 1 for graphene and silver are used in the simulation. For the graphene–silver bilayer composite diaphragm, the total thickness (6.36 nm) is the sum of graphene and silver, the density (8725 kg/m3) and Poisson’s ratio (0.33) are the weighted sum by the thickness, and the effective Young’s modulus (50.7 GPa) is calculated by using the equivalent bending stiffness [37].
As shown in Figs. 4(b) and 4(c), the TA simulation has an overall much better agreement with the experimental measurements. The difference between the lossless PA simulation and lossy TA simulation can be seen from the contour plots for the normal and tangential velocities for sound frequency 2 kHz (Figs. 4(d)–4(g)). In particular, the normal velocity field is excited deeper into the backing air domain in TA simulation (Fig. 4(f)) than in PA simulation (Fig. 4(d)). The maximum tangential velocity occurs at the interface in PA simulation (Fig. 4(e)), while it is about 10 µm from the interface in TA simulation (Fig. 4(g)). As a result, there is a significant difference in the damping characteristics of the sensor and a slight difference in the simulated sensitivity. For example, at a sound frequency of 2 kHz, the simulated mechanical sensitivity for the graphene-only sensor is 1.44 nm/Pa using PA and 1.81 nm/Pa using TA, as opposed to the measured value 1.55 nm/Pa; for the sensor with graphene–silver film, it is 1.44 nm/Pa using PA and 1.25 using TA, as opposed to the measured value of 1.16 nm/Pa. The discrepancy between the simulation and experimental results can be attributed to a number of factors, including the nonlinearity and hysteresis of the tunable filter when applying a bias to tune the cavity length, the nonideal laboratory environment for sound testing since it is not an anechoic chamber, nonnegligible tension in the diaphragm, and the inaccurate material properties used in the simulation.
3. Fiber Pptic Sensors With Graphene Diaphragm and Enlarged Backing Air Cavity
The second approach to improve the sensor sensitivity is to increase the mechanical sensitivity by enlarging the backing air cavity while not compromising the optical sensitivity. As shown in the schematic (Fig. 5(a)), the main structure of the sensor consists of an optic fiber (Corning SMF-28, 125 µm in diameter) inside a silica capillary tube (Polymicro TSP150375), which has an inside diameter of 147 µm and an outside diameter of 323 µm. Although the distance between the fiber tip and the graphene diaphragm is kept at 57 µm, the extra side gap space between the fiber and the capillary tube has a volume of 0.046 mm3. This volume divided by the inside diameter of the tube gives an equivalent cavity length of 2.7 mm, which is 47 times the distance between the fiber endface and the graphene film.
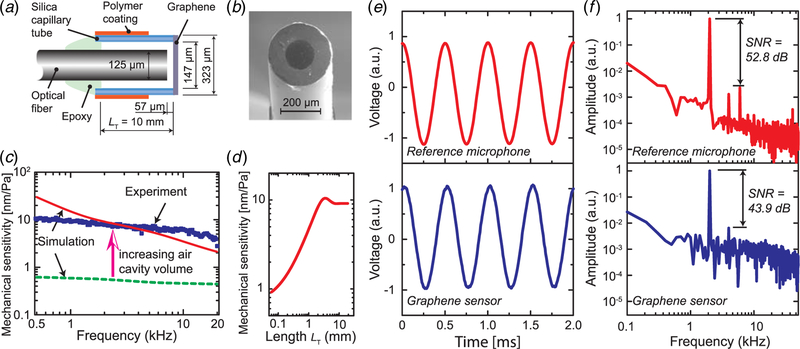
Fig. 5.
Fiber optic sensors with enlarged backing air cavity: (a) schematic of the sensor (not to scale), (b) SEM picture, (c) mechanical sensitivity spectrum: dashed line for the simulated sensitivity when there is no side gap, solid line for simulated sensitivity of the fabricated device with LT = 10 mm, and dots for the experiment data, (d ) mechanical sensitivity at 2 kHz, simulated using COMSOL thermoviscous acoustics, as a function of the length of capillary tube LT (denoted in (a)), (e) comparison of reference microphone and the graphene sensor in time domain at sound frequency 2 kHz, and (f) Fourier transform of the signals in (e)
The experimental characterization and simulation process are exactly the same as in Sec. 2, except that a different light source (Thorlabs S5FC1005S), tunable filter (Micron Optics FFP-TF), and speaker (Adam A8X) are used. The details are thus omitted for brevity.
3.1. Fabrication Process.
The first step is to cut the capillary tube to the desired length, remove the polymer coating on the one end, and polish the endface. Next, the graphene film is transferred onto the polished end of the capillary tube using the previously described punching process (see Fig. 5(b) for the SEM picture after this step). Then, a cleaved optical fiber is inserted from the back side into the capillary tube to the desired distance, which is verified by a fiber optical interrogator (Micron Optics SI155–04-ST). Finally, to enclose the opening and fix the optical fiber, a low-shrinkage UV-curable polymer (DYMAX OP-61-LS) is added and cured using a spot UV light source (DYMAX Blue Wave LED Prime UVA).
3.2. Sensor Characterization.
The measured mechanical sensitivity is shown as a function of frequency in Fig. 5(c), along with simulated results using COMSOL TA. The measured mechanical sensitivity is 6–10 nm/Pa in the frequency range of 500 Hz–10 kHz (solid line for the simulated data and dots for experimental data in Fig. 5(c)), as opposed to less than 0.6 nm/Pa for the simulated case where the side gap space is completely filled (dashed line in Fig. 5(c)). This is more than an order of magnitude of enhancement of the mechanical sensitivity. However, it does not necessarily mean that even higher mechanical sensitivity can be achieved if a longer capillary tube is used. COMSOL TA simulation shows that for the working frequency between 500 Hz and 20 kHz, increasing the capillary tube’s length beyond 2 mm–5 mm has negligible effect on the mechanical sensitivity, as shown in Fig. 5(d) for frequency at 2 kHz.
At a sound frequency of 2 kHz, the acquired signals from the reference measurement microphone and the graphene sensor are shown in Fig. 5(e) for the time domain and in Fig. 5(f) for the frequency domain. SNR of the 2 kHz signal relative to the harmonic distortion noise is 43.9 dB, which is 8.9 dB worse than the reference microphone. In comparison, the fiber optic sensor with graphene–silver diaphragm has an SNR that is 16.8 dB worse than the reference microphone as shown in Fig. 3(e). Considering that the sensor size is merely 323 µm, smaller than the 1/2 in. reference microphone by a factor of 40, this miniature fiber optic sensor compares well with the much larger reference microphone.
In terms of repeatability during the test for frequencies between 500 Hz and 20 kHz, the mean value of NE is 3.05% for the fiber optic sensor and 0.63% for the reference microphone, which yields a ratio of 4.84. Although it is larger than that for the UV-molded sensor with graphene-only diaphragm (ratio of 2.27), it is largely due to the much-enhanced mechanical sensitivity, which increases by an order of magnitude.
4. Discussion
Acoustic sensors play an important role in various applications, ranging from surveillance and security, healthcare, communication, and consumer products. As graphene has been demonstrated to possess exceptional mechanical, electronic, chemical, and thermal properties, it is very natural for researchers to explore and investigate the use of graphene in developing new acoustic sensors. As sensors for measuring airborne acoustics cannot operate without air, we have to take into account the interaction between the suspended graphene film and its backing air cavity, particularly for miniature (submillimeter) acoustic sensors to work in the audible range. Here, in this paper, we have shown that mechanical sensitivity, which relates the sound stimulus to the mechanical displacement, is severely limited by the small air cavity. This, coupled with graphene’s poor reflectivity, may make one question the appeal of graphene-based optical acoustic sensors.
To address the abovementioned limitations, we investigate two approaches of developing graphene-based fiber optic acoustic sensors, each of which targets different transduction stages, given that the sensor’s ultimate sensitivity ST is the product of mechanical sensitivity SM and optical sensitivity SO, i.e., ST = SMSO. In the first approach (type I), targeting the transduction stage from mechanical displacement to electronic output (i.e., SO), a thin layer (5 nm) of silver is added on top of the graphene film before it is transferred onto a UV-molded cavity, with the aim of enhancing the sensitivity of the optical detection system. This thin layer of reflective metal layer has been experimentally demonstrated to enhance the sensitivity by threefold. In the second approach (type II), targeting the transduction stage from the acoustic pressure stimulus to the mechanical displacement (i.e., SM), an enlarged backing air volume is created via the side gap between the optical fiber and the capillary tube. In this case, the distance between the fiber tip and the suspended diaphragm is kept around 60 µm to ensure (a) the optical sensitivity of the sensing FP interferometer is not affected and (b) the working conditions of LCFOI system are satisfied (the cavity length of the sensing FP interferometer needs to match that of the reference FP interferometer). Experimental results show an increase in mechanical sensitivity by an order of magnitude and much improved SNR.
It is expected that the combination of the aforementioned two approaches will yield high-performance fiber optic sensors with enhanced both mechanical and optical sensitivities, based on the multiplicative relationship in ST = SMSO. It could potentially rival the performance of the current state-of-art measurement microphones but with a much smaller footprint. For example, if the graphene diaphragm in the second approach is replaced by the graphene–silver diaphragm in the first approach, the sensor sensitivity is expected to be further enhanced.
It should also be pointed out that in the FEM simulation of small transducers, modeling becomes more challenging as the domain size becomes comparable to the thermal/viscous boundary layer thickness. The simplified analytical models based on lossless wave equations are useful to provide a general guideline. However, more accurate results need to be obtained from FEM simulation based on the Navier–Stokes equation, e.g., as implemented in COMSOL TA.
Acknowledgment
Certain commercial equipment, instruments, materials, or software are identified in this paper to foster understanding. Such identification does not imply recommendation or endorsement by the National Institute of Standards and Technology nor does it imply that the materials or equipment identified are necessarily the best available for the purpose.
Funding Data
• National Science Foundation (CMMI-1436347, CMMI-1663135).
• National Institute of Standards and Technology (70NANB12H211).
Footnotes
Contributed by the Technical Committee on Vibration and Sound of ASME for publication in the Journal of Vibration and Acoustics.
This work is in part a work of the U.S. Government. ASME disclaims all interest in the U.S. Government’s contributions.
Contributor Information
Qian Dong, Department of Mechanical Engineering, Temple University, Philadelphia, PA 19122.
Hyungdae Bae, Department of Mechanical Engineering, Howard University, Washington, DC 20059.
Zhijian Zhang, Department of Mechanical Engineering, University of Maryland, College Park, MD 20742.
Yongyao Chen, Department of Mechanical Engineering, University of Maryland, College Park, MD 20742.
Zhongshan Wen, Department of Mechanical Engineering, University of Maryland, College Park, MD 20742.
Douglas A. Olson, Office of Weights and Measures, National Institute of Standards and Technology, Gaithersburg, MD 20899
Miao Yu, Department of Mechanical Engineering, University of Maryland, College Park, MD 20742.
Haijun Liu, Department of Mechanical Engineering, Temple University, Philadelphia, PA 19122.
References
- [1].Lee C, Wei X, Kysar JW, and Hone J, 2008, “Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene,” Science, 321(5887), pp. 385–388. [DOI] [PubMed] [Google Scholar]
- [2].Balandin AA, Ghosh S, Bao W, Calizo I, Teweldebrhan D, Miao F, and Lau CN, 2008, “Superior Thermal Conductivity of Single-Layer Graphene,” Nano Lett, 8(3), pp. 902–907. [DOI] [PubMed] [Google Scholar]
- [3].Castro Neto AH, Guinea F, Peres NMR, Novoselov KS, and Geim AK, 2009, “The Electronic Properties of Graphene,” Rev. Mod. Phys 81(1), pp. 109–162. [Google Scholar]
- [4].Loh KP, Bao Q, Ang PK, and Yang J, 2010, “The Chemistry of Graphene,” J. Mater. Chem, 20(12), 2277–2289. [Google Scholar]
- [5].Novoselov KS, Jiang D, Schedin F, Booth TJ, Khotkevich VV, Morozov SV, and Geim AK, 2005, “Two-Dimensional Atomic Crystals,” Proc. Natl Acad. Sci. U.S.A, 102(30), pp. 10451–10453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Novoselov KS, Geim AK, Morozov SV, Jiang D, Zhang Y, Dubonos SV, Grigorieva IV, and Firsov AA, 2004, “Electric Field Effect in Atomically Thin Carbon Films,” Science, 306(5696), pp. 666–669. [DOI] [PubMed] [Google Scholar]
- [7].Novoselov KS, Geim AK, Morozov SV, Jiang D, Katsnelson MI, Grigorieva IV, Dubonos SV, and Firsov AA, 2005, “Two-Dimensional Gas of Massless Dirac Fermions in Graphene,” Nature, 438(7065), pp. 197–200. [DOI] [PubMed] [Google Scholar]
- [8].Kahng YH, Lee S, Park W, Jo G, Choe M, Lee J-H, Yu H, Lee T, and Lee K, 2012, “Thermal Stability of Multilayer Graphene Films Synthesized by Chemical Vapor Deposition and Stained by Metallic Impurities,” Nanotechnology, 23(7), 075702. [DOI] [PubMed] [Google Scholar]
- [9].Kim K, Regan W, Geng B, Alemán B, Kessler BM, Wang F, Crommie MF, and Zettl A, 2010, “High-Temperature Stability of Suspended Single- Layer Graphene,” Phys. Status Solidi (RRL) - Rapid Res. Lett, 4(11), pp. 302–304. [Google Scholar]
- [10].Hernandez Y, Nicolosi V, Lotya M, Blighe FM, Sun Z, De S, McGovern IT, Holland B, Byrne M, Gun’Ko YK, Boland JJ, Niraj P, Duesberg G, Krishnamurthy S, Goodhue R, Hutchison J, Scardaci V, Ferrari AC, and Coleman JN, 2008, “High-Yield Production of Graphene by Liquid-Phase Exfoliation of Graphite,” Nat. Nanotechnol, 3(9), pp. 563–568. [DOI] [PubMed] [Google Scholar]
- [11].Li X, Cai W, An J, Kim S, Nah J, Yang D, Piner R, Velamakanni A, Jung I, Tutuc E, Banerjee SK, Colombo L, and Ruoff RS, 2009, “Large-Area Synthesis of High-Quality and Uniform Graphene Films on Copper Foils,” Science, 324(5932), pp. 1312–1314. [DOI] [PubMed] [Google Scholar]
- [12].Reina A, Jia X, Ho J, Nezich D, Son H, Bulovic V, Dresselhaus MS, and Kong J, 2009, “Large Area, Few-Layer Graphene Films on Arbitrary Substrates by Chemical Vapor Deposition,” Nano Lett, 9(1), pp. 30–35. [DOI] [PubMed] [Google Scholar]
- [13].Chen X-D, Liu Z-B, Zheng C-Y, Xing F, Yan X-Q, Chen Y, and Tian J-G, 2013, “High-Quality and Efficient Transfer of Large-Area Graphene Films onto Different Substrates,” Carbon, 56, pp. 271–278. [Google Scholar]
- [14].Li X, Zhu Y, Cai W, Borysiak M, Han B, Chen D, Piner RD, Colombo L, and Ruoff RS, 2009, “Transfer of Large-Area Graphene Films for High-Performance Transparent Conductive Electrodes,” Nano Lett, 9(12), pp. 4359–4363. [DOI] [PubMed] [Google Scholar]
- [15].Lock EH, Baraket M, Laskoski M, Mulvaney SP, Lee WK, Sheehan PE, Hines DR, Robinson JT, Tosado J, Fuhrer MS, Hernández SC, and Walton SG, 2012, “High-Quality Uniform Dry Transfer of Graphene to Polymers,” Nano Lett, 12(1), pp. 102–107. [DOI] [PubMed] [Google Scholar]
- [16].Suk JW, Kitt A, Magnuson CW, Hao Y, Ahmed S, An J, Swan AK, Goldberg BB, and Ruoff RS, 2011, “Transfer of CVD-Grown Monolayer Graphene Onto Arbitrary Substrates,” ACS Nano, 5(9), pp. 6916–6924. [DOI] [PubMed] [Google Scholar]
- [17].Geim AK, 2009, “Graphene: Status and Prospects,” Science, 324(5934), pp. 1530–1534. [DOI] [PubMed] [Google Scholar]
- [18].Geim AK, and Novoselov KS, 2007, “The Rise of Graphene,” Nat. Mater, 6(3), pp. 183–191. [DOI] [PubMed] [Google Scholar]
- [19].Lin Y-M, Dimitrakopoulos C, Jenkins KA, Farmer DB, Chiu H-Y, Grill A, and Avouris P, 2010, “100-GHz Transistors From Wafer-Scale Epitaxial Graphene,” Science, 327(5966), p. 662. [DOI] [PubMed] [Google Scholar]
- [20].Lin Y-M, Valdes-Garcia A, Han S-J, Farmer DB, Meric I, Sun Y, Wu Y, Dimitrakopoulos C, Grill A, Avouris P, and Jenkins KA, 2011, “Wafer-Scale Graphene Integrated Circuit,” Science, 332(6035), pp. 1294–1297. [DOI] [PubMed] [Google Scholar]
- [21].Kuila T, Bose S, Khanra P, Mishra AK, Kim NH, and Lee JH, 2011, “Recent Advances in Graphene-Based Biosensors,” Biosens. Bioelectron, 26(12), pp. 4637–4648. [DOI] [PubMed] [Google Scholar]
- [22].Schedin F, Geim AK, Morozov SV, Hill EW, Blake P, Katsnelson MI, and Novoselov KS, 2007, “Detection of Individual Gas Molecules Adsorbed on Graphene,” Nat. Mater, 6(9), pp. 652–655. [DOI] [PubMed] [Google Scholar]
- [23].Hill EW, Vijayaragahvan A, and Novoselov K, 2011, “Graphene Sensors,” IEEE Sens. J, 11(12), pp. 3161–3170. [Google Scholar]
- [24].Basu S, and Bhattacharyya P, 2012, “Recent Developments on Graphene and Graphene Oxide Based Solid State Gas Sensors,” Sens. Actuators B Chem, 173, pp. 1–21. [Google Scholar]
- [25].Smith AD, Vaziri S, Niklaus F, Fischer AC, Sterner M, Delin A, Östling M, and Lemme MC, 2013, “Pressure Sensors Based on Suspended Graphene Membranes,” Solid-State Electron, 88, pp. 89–94. [Google Scholar]
- [26].Ma J, Jin W, Ho HL, and Dai JY, 2012, “High-Sensitivity Fiber-Tip Pressure Sensor With Graphene Diaphragm,” Opt. Lett, 37(13), pp. 2493–2495. [DOI] [PubMed] [Google Scholar]
- [27].Ma J, Xuan H, Ho HL, Jin W, Yang Y, and Fan S, 2013, “Fiber-Optic Fabry–Pérot Acoustic Sensor With Multilayer Graphene Diaphragm,” IEEE Photonics Technol. Lett, 25(10), pp. 932–935. [Google Scholar]
- [28].Li C, Xiao J, Guo T, Fan S, and Jin W, 2014, “Interference Characteristics in a Fabry–Perot Cavity With Graphene Membrane for Optical Fiber Pressure Sensors,” Microsyst.Technol, 21(11), pp. 2297–2306. [Google Scholar]
- [29].Ventsel E, and Krauthammer T, 2001, Thin Plates and Shells: Theory: Analysis, and Applications, CRC Press, Boca Raton. [Google Scholar]
- [30].de Silva CW, 2016, Sensor Systems: Fundamentals and Applications, CRC Press, Boca Raton, p. 227. [Google Scholar]
- [31].Poot M, and van der Zant HSJ, 2008, “Nanomechanical Properties of Few-Layer Graphene Membranes,” Appl. Phys. Lett, 92(6), 063111. [Google Scholar]
- [32].Liu H, Olson DA, and Yu M, 2014, “Modeling of an Air-Backed Diaphragm in Dynamic Pressure Sensors: Effects of the Air Cavity,” J. Sound Vib, 333(25), pp. 7051–7075. [Google Scholar]
- [33].Bae H, and Yu M, 2012, “Miniature Fabry-Perot Pressure Sensor Created by Using UV-Molding Process With an Optical Fiber Based Mold,” Opt. Express, 20(13), pp. 14573–14583. [DOI] [PubMed] [Google Scholar]
- [34].Koenig SP, Boddeti NG, Dunn ML, and Bunch JS, 2011, “Ultrastrong Adhesion of Graphene Membranes,” Nat. Nanotechnol, 6(9), pp. 543–546. [DOI] [PubMed] [Google Scholar]
- [35].Yu M, and Balachandran B, 2003, “Acoustic Measurements Using a Fiber Optic Sensor System,” J. Intell. Mater. Syst. Struct, 14(7), pp. 409–414. [Google Scholar]
- [36].Granttan KTV, and Meggitt BT, eds., 2000, Optical Fiber Sensor Technology: Fundamentals, Springer Science + Business Media, New York. [Google Scholar]
- [37].Hou MTK, and Chen R, 2004, “A New Residual Stress Measurement Method Using Ultra-Wide Micromachined Bilayer Cantilevers,” J. Micromech. Microeng, 14(4), pp. 490–496. [Google Scholar]