Automatic estimation and correction of anisotropic magnification distortion in electron microscopes

Abstract

We demonstrate a significant anisotropic magnification distortion, found on an FEI Titan Krios microscope and affecting magnifications commonly used for data acquisition on a Gatan K2 Summit detector. We describe a program (mag_distortion_estimate) to automatically estimate anisotropic magnification distortion from a set of images of a standard gold shadowed diffraction grating. We also describe a program (mag_distortion_correct) to correct for the estimated distortion in collected images. We demonstrate that the distortion present on the Titan Krios microscope limits the resolution of a set of rotavirus VP6 images to ~7 Å, which increases to ~3 Å following estimation and correction of the distortion. We also use a 70S ribosome sample to demonstrate that in addition to affecting resolution, magnification distortion can also interfere with the classification of heterogeneous data.

Introduction

Single particle electron cryo microscopy (cryo-EM) has undergone a recent surge in attainable resolutions (Bartesaghi et al., 2015; Campbell et al., 2015; Grant and Grigorieff, 2015). These gains are in large part due to the use of new direct electron detectors (Milazzo et al., 2005; Faruqi and Henderson, 2007; Li et al., 2013b), which have an improved detective quantum efficiency (DQE) (Ruskin et al., 2013; McMullan et al., 2014) and are capable of recording movies to reduce the blurring in images due to beam induced movement (Brilot et al., 2012; Campbell et al., 2012; Li et al., 2013a; Scheres, 2014; Rubinstein and Brubaker, 2014). A number of these direct detectors use relatively small physical pixel sizes, for example 5 μm (Gatan K2 summit, Gatan Inc., Pleasanton, CA) or 6.4 μm (DE-20, Direct Electron, San Diego, CA) and experience significant additional magnification due to their required positioning under the microscope column. This additional magnification means that the recorded images are taken at lower nominal magnification on the microscope than with traditional charge coupled device (CCD) cameras or the FEI Falcon detectors. It now appears that many microscopes may suffer from an anisotropic magnification distortion at these magnifications, which may have gone undetected until now, as these magnifications were not used for high-resolution work.

An anisotropic magnification distortion results in an image whose magnification varies with direction, and thus effectively leads to a directional scaling of the image. For example, a perfect circle, when imaged on a system with anisotropic magnification will appear as an ellipse. In single-particle cryo-EM, which relies on the averaging of many copies of a protein imaged with random orientations, anisotropic magnification will result in particles with different apparent dimensions that depend on their orientation in the image, and any subsequent averaging of these particles will not be fully coherent. The distortion will displace particle features from their undistorted locations and, for a centered particle, these displacements become larger with distance from the particle center. Therefore, larger particles will be affected more than small particles. For example, a 2% distortion will cause a location at the edge of a 700 Šdiameter rotavirus DLP to differ by 7 Šin the most displaced directions, or 3.5 Šfrom the average location. Locations in other directions will also be displaced from the average position, by an amount that is dependent on the direction. Averaging many images with different displacements into one 3D reconstruction will effectively apply a B-factor to the reconstruction of about 1000 Ų (Jensen, 2001), ultimately limiting its resolution. Correcting the distortion prior to averaging will reduce or remove this B-factor. In the case of a 100 Šdiameter particle, locations at the edge will be displaced by only 1 Šfrom the average position and the effect of the magnification distortion on the 3D reconstruction will be much smaller with a B-factor of about 100 Ų.

We have recently reported a 2.6 Å resolution reconstruction of the rotavirus VP6 trimer, which forms the outer shell of the rotavirus double-layer particle (DLP) (Grant and Grigorieff, 2015). The data for this reconstruction was taken on an FEI Titan Krios at a nominal magnification of 29,000x with images recorded on a K2 summit detector with a pixel size of ~1 Å per pixel. During analysis of this and other datasets, we became aware of anisotropic magnification distortion on the Titan Krios microscope that affects all magnifications typically used for data collection on a K2 summit detector. We believe the distortion arises from an issue in the projection system based on experimental observations that the distortion is magnification-dependent but not dependent on the objective lens setting. The projection system is composed of four lenses, which work in a pre-calibrated and fixed manner set by the manufacturer when changing magnification. Slight imperfections in either the calibration/alignment between the four lenses such as astigmatism in one of the lenses could lead to the observed distortion.

We set out to characterize the distortion at each of the magnifications we normally use for data collection, and developed a program to automatically estimate the distortion from a set of images of a gold covered diffraction grating. The measured values can then be used to correct images for the distortion after they are taken and prior to processing.

Method

The conversion of a circle to an ellipse and vice versa can be described by two scaling values, describing the amount of stretching or shrinking along two orthogonal axes, and an angle which describes the orientation of these axes (see Fig 1A.). Our algorithm relies on first taking a number of images (~10) of a sample containing polycrystalline gold. A cross-grating diffraction standard, which can easily be purchased and is likely to be readily available in all EM labs, works well for this purpose. Amplitude spectra of images of polycrystalline gold will exhibit diffractions spots at ~2.4 Å and ~2 Å spacings. The number and directions of these spots will depend on the number and orientation of crystals in the image; however, averaging a sufficient number of amplitude spectra from different images of randomly orientated gold crystals will result in a spectrum containing rings at the 2.4 and 2 Åspacings (e.g. Fig 1B.). In an ideal microscope, these rings would be circular; however, in a microscope with anisotropic magnification they will form an ellipse, which describes the distortion. By estimating the parameters required to make the gold diffraction rings circular, we can estimate any magnification distortion present at a given magnification.

Figure 1.

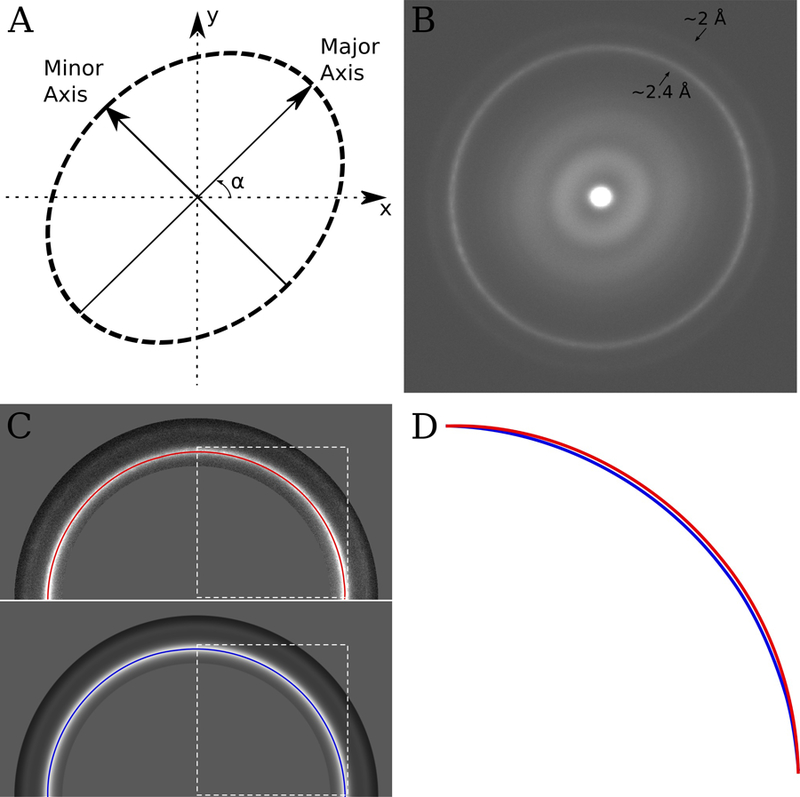
(A) An anisotropic magnification distortion can be described with 3 parameters (in this case, two scale factors which describe the scaling along the major and minor axes and α, which describes the orientation of the major axis). (B) Sum of the amplitude spectra from 10 images of a polycrystalline gold covered diffraction grating. The images were taken at a nominal magnification of 22,500 on an FEI Titan Krios. The ~2.4 Å and ~2 Å gold rings are visible in the image and are slightly elliptical suggesting anisotropic magnification. (C) Top – half of the image shown in B, with the gold rings masked out and a path tracing the ~2.4 Å gold ring. Bottom – half of the rotational average of the image shown in B, also with the gold rings masked out and a path tracing the ~2.4 Å gold ring. The dashed white box illustrates the area, which is shown zoomed and overlaid in panel D. (D) Overlay of the section of the paths traced in C surrounded by the dashed white box. The path from the original image is different compared with the rotationally averaged version, indicating anisotropic magnification. In this instance the difference is ~1%, which combined with a ~1% difference in the orthogonal direction indicates a ~2% anisotropic magnification distortion at this magnification.

To facilitate this process, we developed a program to perform this analysis automatically (mag_distortion_estimate), and another to use the estimated values to correct images for any found distortion (mag_distortion_correct). The automatic estimation takes a set of images of polycrystalline gold and an estimate of the pixel size as input and prints the estimated anisotropic magnification parameters as output. The set of input images are Fourier transformed and converted to amplitude spectra. These amplitude spectra are averaged to provide an image which should contain rings at the gold spacings (hereafter referred to as the ring image), e.g. Fig 1B. The program performs an initial coarse brute force search of three possible distortion parameters (the major axis scale factor, the minor axis scale and the distortion angle α as shown in Fig 1A). For each set of parameters, the ring image is stretched/shrunk according to the values and a cross-correlation is calculated between the stretched ring image and a rotational average of the original ring image, considering only the area encapsulating the gold rings. The parameters that maximize this correlation are considered to be the parameters that make the rings the most circular, as any rings in the rotationally averaged ring image will be a perfect circle by definition. After this initial coarse search, a number of local searches are performed around these initial parameters with increasingly fine sampling to obtain the final value. The program outputs the parameters required to correct the distortion in real space images, the output scale factors are therefore reciprocal to those found using the ring image due to the different spaces.

Once the distortion parameters are known, correction simply requires stretching (or shrinking) the image to produce an undistorted image. Stretching the image can be done in real space or Fourier space. Correction in either space will require interpolation of the pixel values which will necessarily lead to some image degradation, the exact form of which will depend on both the type of interpolation chosen and the space in which it is performed (Zhao et al., 2015). Our current correction algorithm performs a simple bilinear interpolation in real space, which will lead to some degradation of the high frequencies in the image. This degradation can be minimized by performing the distortion correction on images collected on the K2 Summit detector in super-resolution mode. Doing this, the interpolation artifacts will primarily affect frequencies near the super-resolution Nyquist frequency and should have a negligible effect at the resolution of the true Nyquist frequency and below. Since we generally resample the super-resolution images back to the physical Nyquist frequency by Fourier cropping, the resulting images are distortion corrected with minimal artifacts.

In order to assess the effectiveness of bilinear interpolation within this scheme, we calculated reconstructions of the DLP VP6 trimer using images corrected following the above scheme and using both bilinear and windowed sinc interpolations. The windowed sinc interpolation is a more computationally intensive interpolation, but should produce more accurate results. Reconstructions calculated from images corrected using the two interpolations were indistinguishable, with nearly identical FSC curves indicating that the interpolation is not limiting the resolution in this case. It should be noted that in cases where information close to the Nyquist of the corrected images is used, the use of bilinear interpolation could well be a limiting factor. In these cases, a more robust interpolation, possibly applied in Fourier space, may be required.

Our method estimates the distortion correction that both stretches the image in one direction and shrinks the image in the other direction, maintaining the average magnification and pixel size. This is because the comparison is made to a rotationally averaged version of the ring image. Shrinking the image in one of the directions leads to an edge, which may be detrimental to later image processing. Edges can be avoided by dividing both the estimated scale factors by the minor axis scale factor. The new scale factors will stretch the image in one direction and leave it unchanged in the orthogonal direction. It is important to note that while only stretching the image results in no edge, it will change the average pixel size by the amount of the distortion. In this case the new pixel size can be calculated using:

$$d_{new}=\frac{d_{old}}{S_{major}}$$ (1)

where $d_{new}$ is the new pixel size, $d_{old}$ is the old average pixel size, and $S_{major}$ is the major axis scale factor.

Anisotropic magnification will also change the apparent contrast transfer function (CTF) of the microscope affecting an image, by introducing apparent additional astigmatism that is visible in the Thon ring pattern (Thon, 1966) seen in its Fourier transform. Thus, if defocus parameter estimation is not carried out after correction for the distortion, the determined parameters will have an error. The estimated values can themselves be corrected for the distortion (Zhao et al., 2015), or more simply the defocus parameter estimation can be carried out after the distortion correction.

Results

The distortion values found for each of the magnifications we use for data collection with the K2 Summit camera are shown in Table 1. The distortion is different for each magnification, ranging from ~1.6 % to ~2.7 %. Distortion values were also estimated for data recorded at 18,000 and 29,000x magnification and taken approximately two months after the data presented in Table 1. These values were almost identical, suggesting that the distortion is constant, at least on the timescale of months. Subsequent communication with a number of different groups suggests that anisotropic magnification distortion at these levels of magnification is relatively common, affecting a number of microscopes of different types: three FEI Titan Krioses, an FEI F20 (Zhao et al., 2015) and an FEI Polara.

Table 1.

Results output from the mag_distortion_estimate program, at a number of magnification values used for data collection with a Gatan K2 Summit camera on one of the FEI Titan Krios microscopes at HHMI’s Janelia Research Campus. All of the tested magnifications demonstrated apparent anisotropic magnification, ranging in severity from 1.6% to 2.74%.

Magnification	α (degrees)	Minor axis scale factor	Major axis scale factor	% Distortion
14,000	130.7	0.988	1.013	2.53
18,000	134.0	0.986	1.013	2.74
22,500	133.5	0.989	1.011	2.22
29,000	137.3	0.989	1.011	2.16
37,000	134.1	0.991	1.007	1.60

Anisotropic magnification within images has the potential to reduce the attainable resolution, particularly at the periphery of objects, with larger objects being affected more than smaller objects. Viral capsids, as well as being large, tend to have most of their ordered density localized at the periphery, and are thus very susceptible to anisotropic magnification distortions. They are, therefore, also ideal samples to demonstrate the effect of the distortion, and the effectiveness of its subsequent correction. Fig 2A. shows the map obtained for the VP6 trimer after initial processing of a set of ~500 DLPs, using the images as collected. This reconstruction contains ~400,000 asymmetric units and is limited to ~7 Å resolution. Fig 2A also shows the reconstruction using exactly the same alignment parameters, but with images that have been corrected for magnification distortion. Here the resolution is ~3 Å, an improvement that can be attributed directly to correction of the distortion.

Figure 2.

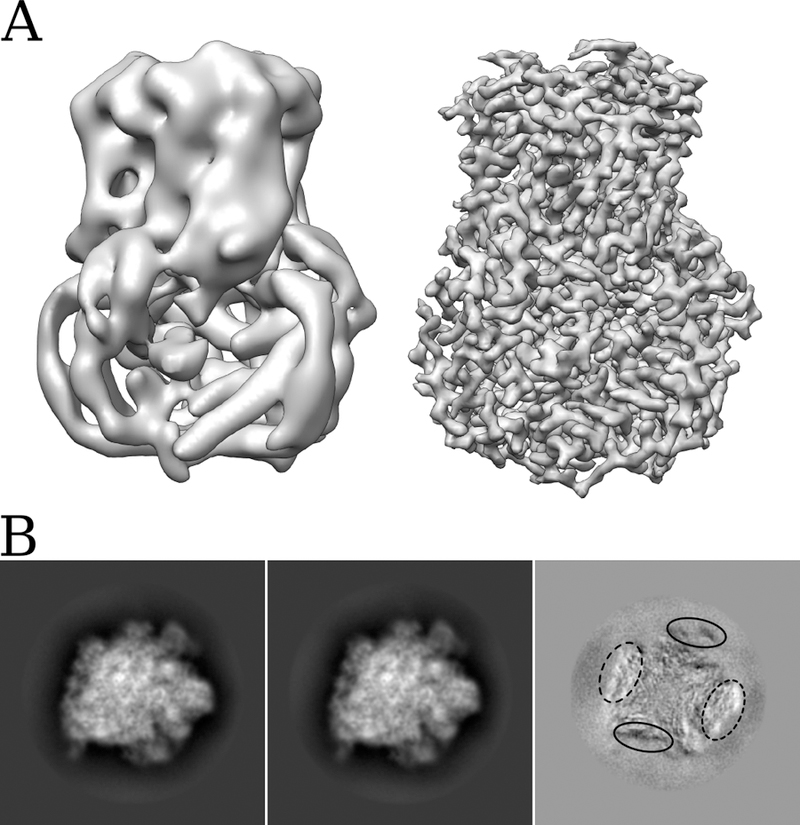
(A) Comparison of reconstructions of rotavirus VP6 obtained before estimation and correction of anisotropic magnification distortion (left), and after correction (right). The resolution improves from ~7 Å to ~3 Å. (B) Projections of two classes (first two images) obtained after 3D classification of a 70S ribosome dataset before estimation and correction of anisotropic magnification, and the result of subtracting image 2 from image 1 (third image). Superimposition of the two projections clearly demonstrates that the main difference is a stretching in one direction, coupled with a shrinking in the orthogonal direction. The difference image also demonstrates the edges of the molecule are most strongly affected by the distortion.

As well as reducing attainable resolution, anisotropic magnification distortion has the potential to cause additional problems during the processing of single particle data, such as in the classification of heterogeneous datasets, as it introduces additional apparent heterogeneity. Fig 2B shows the projections of two classes obtained by 3D classification of a dataset of 70S ribosomes using Frealign (Lyumkis et al., 2013). The two classes correspond to particles distorted along different directions depending on the particle orientations in the original images. After correcting for the magnification distortion, the classification no longer results in classes with differential stretching.

In order to explore the influence of a magnification distortion on classification further, we examined the effect on the classification of a simulated 70S ribosome dataset, which was used in previous work to characterize classification accuracy (Lyumkis et al., 2013). The model dataset had a signal-to-noise ratio of 0.05 with each dataset being composed of images from three different EMDB models (1798, 1799 and 5030). We created two versions of this dataset, one of which had an anisotropic magnification distortion imposed upon it, scaling by 1.0137 along the minor axis and 1.0411 along the major axis. This scaling results in a 2.74% distortion (the largest distortion on our Titan Krios). A second dataset was created by scaling each axis by 1.0274, resulting in images with no distortion, but similar interpolation artifacts to the distorted dataset.

Each dataset was classified into six classes using Frealign, starting from the same initial parameters and random occupancies. 30 rounds of classification with refinement of all alignment parameters were performed, and the results are shown in Table 2. For this dataset, the quality of the classification appears to be marginally worse when using images with a magnification distortion; however, the effect is minimal. It seems likely that the effect of any distortion will be dependent upon the dataset being examined. As the distortion primarily affects the periphery of the molecule, one could speculate that classification based on features at the periphery of the molecule will be affected by a magnification distortion more than classification based on features at the center.

Table 2.

Results obtained after classifying two model datasets, one without any distortion (Ori.) and one with a 2.74% anisotropic magnification distortion (Dist.). The datasets had a signal-to-noise ratio of 0.05 and were created as described in (Lyumkis et al., 2013). Each dataset was composed of images from three different EMDB models (1798, 1799 and 5030). The datasets were classified into six classes using Frealign. For each class, the percentage of images from each model is listed. The % error, defined as the percentage of images within each class that do not belong to the most represented model, is also shown for each class and both datasets.

	Class 1		Class 2		Class 3		Class 4		Class 5		Class 6
	Ori.	Dist.	Ori.	Dist.	Ori.	Dist.	Ori.	Dist.	Ori.	Dist.	Ori.	Dist.
EMDB-1798	38.5	44.3	0.1	0.2	0.0	0.0	2.5	6.8	0.0	0.1	95.0	92.9
EMDB-1799	61.3	51.5	0.1	0.6	0.0	0.0	97.5	93.2	0.1	0.0	5.0	7.1
EMDB-5030	0.3	4.2	99.8	99.2	100.0	100.0	0.0	0.0	99.9	99.9	0.0	0.0
% Error	38.7	48.5	0.2	0.8	0.0	0.0	2.5	6.8	0.1	0.1	5.0	7.1

Conclusion

Anisotropic magnification distortion affecting low magnifications commonly used to collect data on Gatan and Direct Electron direct detectors affects a number of different microscopes. If uncorrected, this distortion has the potential to reduce the attainable resolution of single particle reconstructions, particularly at the periphery of large particles. The distortion also introduces additional heterogeneity into the data, and thus has the potential to interfere with the sorting of the data into homogeneous populations. Here we have shown that significant anisotropic magnification distortion is relatively easy to measure and correct. Two programs, one to measure the amount of distortion for a particular magnification (mag_distortion_estimate) and one to correct for any estimated distortion in the raw images (mag_distortion_correct) can be downloaded at http://grigoriefflab.janelia.org/magdistortion.