Abstract
We introduce a model-based image reconstruction framework with a convolution neural network (CNN) based regularization prior. The proposed formulation provides a systematic approach for deriving deep architectures for inverse problems with the arbitrary structure. Since the forward model is explicitly accounted for, a smaller network with fewer parameters is sufficient to capture the image information compared to direct inversion approaches, thus reducing the demand for training data and training time. Since we rely on end-to-end training with weight sharing across iterations, the CNN weights are customized to the forward model, thus offering improved performance over approaches that rely on pre-trained denoisers. Our experiments show that the decoupling of the number of iterations from the network complexity offered by this approach provides benefits including lower demand for training data, reduced risk of overfitting, and implementations with significantly reduced memory footprint. We propose to enforce data-consistency by using numerical optimization blocks such as conjugate gradients algorithm within the network; this approach offers faster convergence per iteration, compared to methods that rely on proximal gradients steps to enforce data consistency. Our experiments show that the faster convergence translates to improved performance, primarily when the available GPU memory restricts the number of iterations.
Keywords: Deep learning, parallel imaging, convolutional neural network
I. Introduction
MODEL-based recovery of images from noisy and sparse multichannel measurements is now a mature area with success in several application areas such as MRI [1], CT [2], PET [3], microscopy [4]. These schemes rely on a numerical model of the measurement system, often termed as the forward model. Image recovery is then posed as an optimization problem, where the objective is to improve the consistency between the true data and the measurements obtained from the image using the forward model. Since the recovery from few measurements is an ill-posed problem, the general approach is to modify the objective function using priors that penalize solutions that fall outside the class of natural images. Carefully engineered priors including total variation [5], patch-based non-local methods, low-rank penalties [6], [7], as well as priors learned from exemplary data [8] or the measurements themselves [9] are widely used.
Recently, several researchers have proposed to exploit the power of deep convolutional neural networks (CNN) in image recovery. Some of these schemes customize existing CNN architectures (e.g., UNET [10] & ResNet [11]) to image recovery tasks [12]–[14]. These schemes rely on a single framework to invert the forward model and to exploit the extensive redundancy in the images. An alternative for this direct inversion approach is iterative algorithms that alternate between data-consistency enforcement and pre-trained CNN denoisers [15]–[17]. These schemes train the CNN denoisers to denoise Gaussian noise corrupted images; since the noise and alias terms decay with iterations, different CNNs pre-trained with different noise levels are used at different iterations [15]–[17]. End-to-end training schemes [18], [19] rely on similar architecture as pre-trained models, but the CNN parameters at different iterations are trained such that the resulting deep network recovers the images from undersampled measurements. Similar recursive neural network architectures inspired by proximal gradient algorithms [19]–[22], which alternate between CNN blocks and steepest descent steps, have also been introduced by several researchers.
The main focus of this work is to introduce a systematic approach for the development of deep architectures for arbitrary inverse problems. The proposed framework, termed as MOdel-based reconstruction using Deep Learned priors (MoDL), merges the power of model-based reconstruction schemes with deep learning. We use a variational framework involving a data-consistency term and a learned CNN to capture the image redundancy. We use an alternating recursive algorithm, which when unrolled yields a deep network. The network consists of interleaved CNN blocks, which captures the information about the image set, and data consistency blocks that encourages consistency with the measurements. The data consistency block involves a quadratic sub-problem, which has analytical solutions for simpler problems such as single channel MRI recovery [18]. When the forward model is more complex (e.g. multichannel MRI), we propose to solve the quadratic sub-problem using conjugate gradient (CG) optimization. The use of numerical optimization CG blocks within the deep network is not reported, to the best of our knowledge. In addition to accounting for the complex forward model, this approach can also facilitate hybrid strategies that incorporate other image regularization terms. For example, we have demonstrated the utility of combining patient specific STORM priors [23] along with population generalizable deep learned priors in [24]. Since the forward model and its adjoint are part of the network, a low-complexity plug-and-play CNN with a significantly lower number of parameters is sufficient to learn the image set, compared to some existing CNN methods that do not have data consistency term. We propose to train the framework assuming different forward models (e.g. sampling patterns), which enables the learning of a network that can be re-used in a variety of sampling conditions.
We now briefly describe the differences between the proposed framework and the current methods as described above. The proposed framework is very different from direct inversion schemes [12]–[14] that cannot guarantee data consistency. While the ability of these methods to learn the inverse is remarkable, they have some practical drawbacks. Since the receptive field of the CNN has to match the support of the point spread function, large networks with many parameters (e.g., UNET) are often needed in applications including tomography and Fourier recovery from undersampled measurements. Learning such a large network reliably requires extensive amounts of training time and training data, which is often scarce in the biomedical imaging setting. In addition, since the learned inverse network is tied to the specific forward model, different large trained models are often needed in a clinical setting, where different acquisition parameters (e.g. matrix size, resolution, undersampling patterns) may be used. The main difference of the proposed scheme with [15]–[17] is the use of end-to-end training, similar to [18], [19]. Since the network parameters in the end-to-end training strategy are trained for the specific task of image recovery, it provides a significant improvement in performance over the use of pre-trained denoisers. Specifically, the CNN parameters are learned to capture the alias artifacts and noise at each of the iterations, which depend on the forward model; the customization of the network to the specific task provides improved recovery compared to a generic CNN denoiser. In addition, the proposed scheme does not need a recipe for choosing the noise variance at each iteration or the regularization parameter as in [15], [16]. The regularization parameter is learned, while the network is trained to remove the alias patterns and noise at all iterations, which may differ in its statistical properties. A key difference of our approach with [18], [19] is that we use the same CNN blocks in all the iterations. Since different CNN blocks are used at each iteration in [18], [19], these schemes are not strictly equivalent to the model-based framework. In addition, the proposed scheme offers improved performance over the above schemes in a training data constrained setting. Specifically, several iterations are often needed for the convergence of the variational criterion. When the weights are not shared in [18], [19], the number of free parameters in these frameworks grows linearly with iterations. By contrast, the number of network parameters do not grow with the number of iterations in our setting. The decoupling of the convergence and the complexity of the network allows us to choose the number of parameters depending on the available training data. Our experiments show that this approach translates to improved reconstruction performance, especially when training data is limited. The main difference of the proposed framework against proximal gradients methods, which alternate between CNN blocks and a steepest descent step [19]–[22], is the use of conjugate gradients optimization algorithms within the network. Specifically, the proximal gradient algorithm is attractive in compressed sensing (CS) setting since each of the sub-steps are computationally inexpensive, even though the total number of iterations may be high. Unfortunately, the number of iterations/unfolding steps that the proximal gradient RNN can be trained with is limited, especially on GPUs with limited onboard memory. By contrast, the CG subblocks in our approach result in quite a significant reduction in data consistency error at each iteration, thus offering a faster reduction of cost per iteration. Note that replacing a steepest descent step with several CG steps is not associated with increased memory demand during training. Our experiments show that this strategy offers improved performance compared to the proximal gradients based approaches.
In summary, the main novelties of the proposed scheme over related deep-learning schemes described above are (a) the architecture involving numerical optimization blocks within the deep network, which enables the easy use of complex forward models and additional image priors [24], while offering better performance than current RNN methods that rely on proximal gradients [19]–[21]. The use of numerical optimization blocks within deep networks has not been reported before, to the best of our knowledge. (b) the variational model based formulation, and the iterative algorithm, which translates to an unrolled network architecture with shared weights. By decoupling the network complexity from convergence, the weight sharing strategy provides better performance in training data constrained settings compared to [18], [19], while the end-to-end training offers improved performance compared to pre-trained models [15]–[17]. While some of these components have been independently used by other researchers, the specific combination naturally emerges from the model-based formulation; in addition, the benefit of this specific strategy over competing methods have not been rigorously tested and validated, which is a contribution of this work.
II. Background
A. Image formation & forward model
The imaging system can be thought of as an operator that acts on a continuous domain image to yield a vector of measurements . The goal of image reconstruction is to recover a discrete approximation, denoted by the vector from b.
Model-based imaging schemes [25], [26] use a discrete approximation of , denoted by the matrix A, that maps x to b; model-based algorithms make the central assumption that
| (1) |
For example, in the single-channel Cartesian MRI acquisition setting, we have , where F is the 2-D discrete Fourier transform, while S is the fat sampling matrix that pick rows of the Fourier matrix.
The recovery of x from b is ill-posed, especially when A is a rectangular matrix. The general practice in model-based imaging is to pose the recovery as a regularized optimization scheme:
| (2) |
The regularization prior is often carefully engineered to restrict the solutions to the space of desirable images. For example, is a small scalar when x is a noise and artifact-free image, while its value is high for noisy images. Classical choices include norms of wavelet coefficients [27], total variation [28], as well as their combinations. Recently, several authors have also recently introduced structured low-rank based priors that encourage super-resolution image recovery [26], [29]–[31]. Plug-and-play approaches that also rely on off-the-shelf image denoisers have been introduced as regularizers [32].
B. Deep learned image reconstruction: the state-of-the-art
Many of the current deep learning based algorithms recover the images as
| (3) |
where is a learned CNN [33]. The operator AH(·) transforms the measurement data to the image domain, since CNNs are designed to work in the image domain. We thus have the relation
| (4) |
Thus, the CNN network is learned to invert the normal operator ; i.e., for signals living in the image set.
For many measurement operators (e.g Fourier sampling, blurring, projection imaging), AH A is a translation-invariant operator; the convolutional structure makes it possible for CNNs to solve such problems [34]. However, the receptive field of the CNN has to be comparable to the support of the point spread function corresponding to (AH A). In applications involving Fourier sampling or projection imaging, the receptive field of the CNNs has to be the same as that of the image; large networks such as UNET with several layers are required to obtain such a large receptive field. A challenge with such large network with many free parameters is the need for extensive training data to reliably train the parameters. Another challenge is that the CNN structure may not be well-suited for problems such as parallel MRI, where AH A is not translational-invariant.
An alternate approach is to unroll an iterative algorithm involving a CNN-based regularizer [16], [35], [36], which is similar to the proposed scheme; we will discuss the differences between these schemes and the proposed method in the next section.
III. Proposed Method
We formulate the reconstruction of the image the optimization problem:
| (5) |
Here, is a learned CNN estimator of noise and alias patterns, which depends on the learned parameters w. We express as
| (6) |
where is the “denoised” version of x, after the removal of alias artifacts and noise. The use of the CNN-based prior , which gives high values when x is contaminated with noise and alias patterns, results in solutions that are data-consistent and are minimally contaminated by noise and alias patterns. Here, λ is a trainable regularization parameter. Substituting from (6), in (5), we obtain
| (7) |
Since these schemes rely on forward models, the receptive field of the networks need not be the full image size. In addition, since the network only needs to capture the redundancies in the images, a network consisting of many fewer parameters is sufficient to obtain good results. Note that the above formulation is very similar to the plug-and-play prior approach in [37]; the main difference is the denoiser is a deep CNN in our setting, similar to [16]. Unlike [16], that uses networks pre-trained for denoising, we rely on end-to-end training as described in the next subsection. We set λ as a trainable parameter. If the constrained setting can yield improved reconstructions, high values of λ would be selected during the training process.
A. Unrolling the recursive network
We note that the non-linear mapping can be approximated using Taylor series around the nth iterate as
| (8) |
where Jn is the Jacobian matrix. Setting xn + ∆x = x, the penalty term can be approximated as
| (9) |
We note that the second term tends to zero for small perturbations (i.e, a small value of ). Since the above approximation is only valid in the vicinity of xn, we obtain the alternating algorithm that approximate (7):
| (10a) |
| (10b) |
The sub-problem (10a) can be solved using the normal equations :
| (11) |
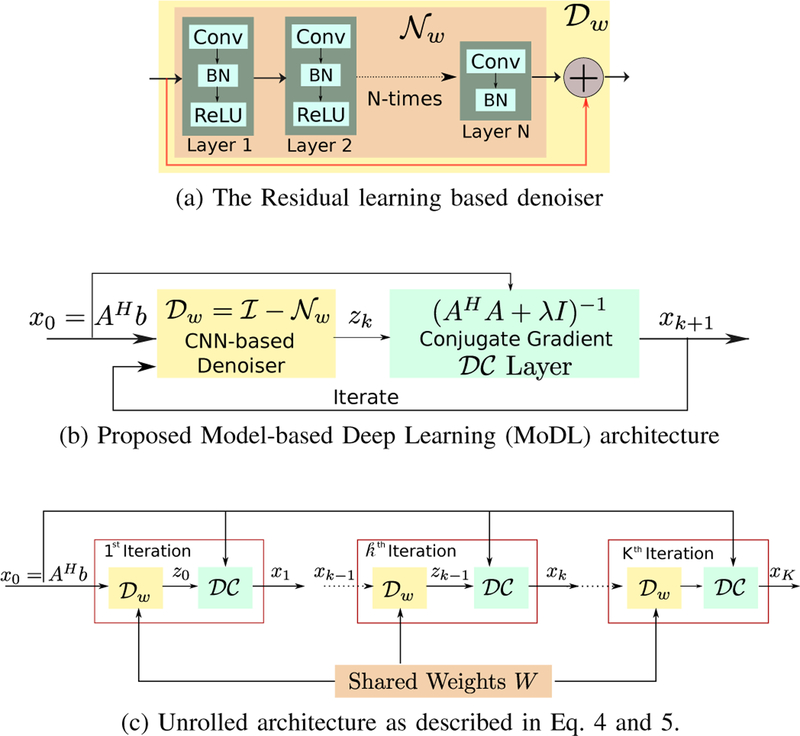
The algorithm is initialized with z0 = 0. The outline of the iterative framework is shown in Fig. 1(b). Once the number of iterations is fixed, the update rules can be viewed as an unrolled deep linear CNN, as shown in Fig. 1(c), whose weights at different iterations are shared. The proposed unrolled architecture has similarities to [16], [18], [19]. However, unlike these works, we use the same denoising operator w at each iteration. Similarly, we use the same trainable regularization parameter at each iteration for consistency with (10a) & (10b). [18] and [19], (5). The key benefit of the proposed scheme is the quite significant reduction in the number of network parameters. Specifically, the number of parameters is smaller by a factor of the number of iterations. Our experiments demonstrate the improvement in the robustness of the training procedure and the improved quality of the reconstructions.
Fig. 1.
MoDL: Proposed MOdel-based Deep Learning framework for image reconstruction. (a) shows the CNN based denoising block Dw. (b) is the recursive MoDL framework that alternates between denoiser in (10b) and the data-consistency (DC) layer in (11). (c) is the unrolled architecture for K iterations. The denoising blocks share the weights across all the K iterations.
We relied on using a penalized formulation and an alternating minimization algorithm for simplicity. An alternative is a constrained setting, where the prior is imposed as a constraint using an ADMM scheme [37]. In this setting, rigorous convergence guarantees can be derived as in [37]. Similar rigorous ADMM based architectures are also considered in [38], which can result in a slightly different architecture; these architectures can be adapted to our setting as well. We note that the weights at different layers are not shared in [38]. We note that convergence guarantees are not too relevant in our setting since it is not practical to iterate the network till convergence. Note that the constraint in our case is satisfied when λ → ∞.
B. Data consistency layer
When the forward model is simple, the solution to (11) can be analytically computed. For example, in the single channel undersampled MRI acquisition, where S is a sampling matrix, obtained by keeping only the relevant rows of an identity matrix. Specifically, the mth row is retained is the corresponding Fourier sample is sampled. F is the Fourier matrix. In this case, the Fourier transform of the image at the sampling location m can be analytically evaluated as
| (12) |
The operator is not analytically invertible for complex operators such as multichannel MRI. In this case, we propose to solve (11) using conjugate gradient optimization scheme. This implies that the unrolled deep network will have sub-blocks consisting of numerical optimization layers. The standard approach to dealing with complex for-ward models is to use proximal gradient algorithms [19]–[21], which alternates between CNN blocks and steepest descent steps. We observe that such algorithms are attractive in compressed sensing (CS) setting since each of the sub-steps are computationally inexpensive, even though the total number of iterations may be high. Unfortunately, the number of iterations/unfolding steps that the proximal gradient RNN can be trained with is limited, especially on GPUs with limited on-board memory. Specifically, the RNN need to be unrolled for training, a assuming fixed number of iterations; all of the intermediate results at each iteration and layer need to stored to perform backpropagation, which constrains the number of iterations the RNN can be unrolled during training. By contrast, the CG sub-blocks, involving several CG steps, in our approach results in the more accurate enforcement of the data-consistency constraint at each iteration, thus offering a faster reduction of cost per iteration. Note that there are no trainable parameters within the CG algorithm, and hence the intermediate results at each step of the CG algorithm need not be stored to perform backpropagation. The gradients can be backpropagated through the CG block using another CG as shown in Section III-C. This implies that a large number of CG steps can be performed at each iteration with almost no memory overhead during training. Our experiments show that this strategy offers improved performance compared to the proximal gradients based approaches. In addition to accounting for complex forward models, this approach also facilitate the easy incorporation of other image regularization terms (e.g subject specific priors [24]).
C. End-to-end training of the deep network
One strategy for incorporating the deep learned prior in Eq. (10b) is to reuse networks pre-trained for image denoising task in the reconstruction framework, with a heuristic approach to select the noise level at each iteration [16]. Decoupling the training process from the specifics of the acquisition will significantly simplify the approach. However, the statistics of the artifacts introduced by undersampling cannot be fully captured by Gaussian noise process. Our experiments show the performance of the network can be improved significantly by training the network in an end-to-end fashion.
We fix the number of iterations as K and specify the loss function as the mean square error between xK and the desired image t:
| (13) |
where t(i) is the ith target image.
The goal of training is to determine the weight parameter w, which is shared across the iterations. The gradient of the cost function with respect to the shared weights can be determined using the chain rule
| (14) |
where the Jacobian matrix Jw(z) has entries and zk is the output of the CNN at the kth iteration.
Note that the noise/alias terms in the signal at each of the iterations xk may be significantly different. In plug-and-play CNN approaches, different networks that are trained for (pre-determined) decreasing noise variances [15], [16] are used at different iteration. By contrast, we share the same network Dw and same regularization parameter λ across iterations. During training, the non-linear CNN thus learns to denoise noise/alias patterns with several different statistics. The added benefit of our end-to-end training approach is that we do not require a recipe for the choosing the noise variance at each iteration or regularization parameter.
Note that the backpropagation scheme requires the evaluation of the terms . These terms can be evaluated recursively using backpropagation as in a regular deep learning network. The main difference with the traditional CNN training is that we have numerical optimization blocks within the deep network. We now focus on how to back-propagate through these conjugate gradient (CG) blocks [39]. Note that the CG block does not have any trainable parameters. We have
| (15) |
where the Jacobian matrix Jz(x) has entries . Note from (11) that , where and . The Jacobian matrix of is given by
| (16) |
Since is symmetric, we have
| (17) |
We can evaluate the above expression using a CG algorithm, run until convergence, determined by the saturation of the data-consistency cost. Note that the above gradient calculation is only valid if we implement or equivalently let CG algorithm converge. This result thus shows that the gradients can be back-propagated through the CG block using a CG algorithm. Once the relation (17) is established, we propose to update the network parameters w of the network as well as the regularization parameter λ using the Adam optimization scheme [40]. This scheme maintains two learning rates corresponding to each parameter. These learning rates are estimated from the first and second moments of the gradients. Note that the data consistency term specified by (11), and hence its gradient can be computed analytically in the Fourier domain. This strategy allows the computation of the gradients of the weights using backpropagation; the weight gradients evaluated using the chain rule will have contributions from all the iterations. To make the learned network less sensitive to changes in acquisition scheme, we use training data with different undersampling patterns. We rely on the variable sharing strategies in TensorFlow to implement the unrolled architecture. The parameters of the networks at each iteration are initialized and updated together.
D. Implementation details
The CNN architecture used in this work is shown in Fig. 1(a). We used N layer model with 64 filters at each layer to implement the block. Each layer consists of convolution (conv) followed by batch normalization (BN) [41] and a non-linear activation function ReLU (rectified linear unit, f (x) = max(0, x)). The Nth-layer does not have ReLU to avoid truncating the negative part of the learned noise patterns. Following the residual learning strategy, the learned noise from block is added with the input of block to get the reconstructed image as the output of the block. The number of trainable parameters at each layer of the CNN network is shown in Table I. The output of block is fetched into data consistency (DC) layer as described in Fig. 1(b). The proposed recursive model, shown in Fig. 1(b), was unrolled assuming K iterations of the alternating strategy (10b) and implemented in TensorFlow. Specifically, we set the number of layers N as 5 and number of iterations K as 10. Since MR images are complex, the data consistency (DC) layer explicitly works with complex inputs and returns a complex output. The CNN part handles complex data by concatenating the real and imaginary part as channels i.e. we convert from space space.
TABLE I.
Description of the Trainable Parameters used in the deep network in case of with sharing (WS) and no sharing (NS) architectures between iterations. The weight sharing strategy provides a 10 times reduction in the number of trainable parameters, improving robustness when training data is scarce.
| BN (β + γ + μ + σ2) | Conv.filters | Total | |
|---|---|---|---|
| conv 1 | 64 + 64 + 64 + 64 | 3 × 3 × 2 × 64 | 1408 |
| conv2 | 64 + 64 + 64 + 64 | 3 × 3 × 64 × 64 | 37120 |
| conv3 | 64 + 64 + 64 + 64 | 3 × 3 × 64 × 64 | 37120 |
| conv4 | 64 + 64 + 64 + 64 | 3 × 3 × 64 × 64 | 37120 |
| conv5 | 2 + 2 + 2 + 2 | 3 × 3 × 64 × 2 | 1160 |
| λ | 1 | ||
| number of trainable parameters in WS strategy: | 113,929 | ||
| no. of parameters in NS = #WS × 10 iterations: | 1,139,290 | ||
We use a two-step approach to initialize the network for training. We first trained a model for only one iteration, initializing the parameters with random values. This training is considerably faster than training the entire network. Since we use a recursive network with the same weights across iterations, the weights of the unrolled network at each iteration in Fig. 1(c) are initialized using the weights learned from the single iteration model. We observe that this two-step training strategy is considerably faster and reliable than initializing the full network using random weights. Since we use the same weights across iterations, we may choose the number of iterations in the reconstruction algorithm to be different from the ones assumed during training. The source code for the proposed MoDL scheme can be downloaded from this link: https://github.com/hkaggarwal/modl
IV. Experiments and Results
This section describes various experiments conducted to quantitatively and qualitatively evaluate the performance of the proposed method.
A. Deep learning variants used in the validation
The implementations of many of the existing deep learning methods are not readily available and often not directly applicable in our setting. We hence propose to compare our scheme against variants that differ on optimization strategy, training approach, and network architecture as shown in Table. II. All these variants were trained with the same dataset as for MoDL and with the same number of slices (total 360). The proximal gradients algorithm uses a single steepest descent (SD) step to encourage data consistency at each iteration. By contrast, we solve the quadratic subproblem using CG at each iteration. We rely on end-to-end training (ET) of the network to learn the parameters. An alternate strategy in the literature is to use pre-trained CNN based denoiser (PD). In the PD scheme, we use different denoisers at each step, which are pre-trained to different noise levels that monotonically decrease with iteration as suggested in [15], [16]. In [15], [16], 25 different models were trained with noise levels between 5 and 25 with a step size of 2. Similarly, we had trained 10 different models between noise levels 0.02 and 0.25 with step size of 0.02 (nearly). The particular values were: 0.02, 0.04, 0.06, 0.08, 0.10, 0.13, 0.15, 0.17, 0.20, 0.25. The regularization parameter in the PD setting is tuned to obtain the best performance to be fair. The same value of λ was used in all the iterations. Based on these parameters the proposed MoDL framework can be categorized as CG-ET-WS strategy.
TABLE II.
Categorization of iterative deep-learning frameworks
| Optimization Strategy | Training Strategy | Network Architecture |
|---|---|---|
| Steepest Descent (SD) | Pre-trained Denoiser (PD) | No Sharing (NS) |
| Conjugate Gradient (CG) | End-to-End Training (ET) | With Sharing (WS) |
|
Deep learning frameworks derived based on above three parameters | ||
| Framework | Description |
|---|---|
| CG-ET-WS | Proposed MoDL framework, which uses conjugate gradient algorithm to solve the DC subproblem, with end-to-end training (ET) strategy, and with sharing (WS) of weights across iterations. |
| CG-ET-NS | The difference from MoDL is that the weights are not shared (NS) across iterations. |
| SD-ET-WS | The difference from MoDL is the change the optimization algorithm in the DC layer to steepest descent (SD) instead of CG. |
| CG-PD-NS | The difference from MoDL is the use of pre-trained denoisers (PD) within the iterations. We trained 10 different Dw blocks with descending noise variance and use them in 10 iterations during testing. Since these are different denoisers, therefore, the weights are not shared (NS). |
In the following subsections, we show the benefit of CG-ET-WS strategy by varying each of these three parameters. Specifically, we compare with SD-ET-WS approach where we utilize SD algorithm in DC step instead of CG. We also compare with CG-PD-NS approach where a different pretrained denoiser is utilized at each iteration of Eq. (10b).
Since training data are scarce in the medical imaging setting, we relied on a dataset with images of cats and dogs for the experiments that determine the impact of training data size. Please note that we did not use this data to pre-train the network in the remaining experiments involving MRI data. The CatDog dataset is available for research from the Kaggle website https://www.kaggle.com/c/dogs-vs-cats/data. This dataset consists of 25,000 images of cats and dogs. We extracted a random subset of 3,000 images for training and 100 images for testing. The images were pre-processed to crop and resize to the same spatial dimensions of 256 × 232 as that of MR dataset. We simulated the MRI acquisition on the CatDog dataset. The complex DFT of each of the images were sampled on a 4x undersampling pattern using variable-density Cartesian random sampling masks. We did not assume multichannel sampling. The goal of using this dataset is to demonstrate the reduced data demand of the proposed algorithm and not to produce state of the art results.
B. Data for training and testing the algorithm
The MRI data used for this study were acquired using a 3D T2 CUBE sequence with Cartesian readouts using a 12-channel head coil. The matrix dimensions were 256 × 232 × 208 with 1 mm isotropic resolution. Fully sampled multichannel brain images of five volunteers were collected out of which data from four subjects were used for training, while the data from the fifth subject were used for testing. Since the readout is fully sampled, we evaluated the inverse Fourier transform of each readout. We retrospectively undersampled the phase encodes to train and test the framework; we note that this approach is completely consistent with a future prospective acquisition, where a subset of phase encodes can be pre-selected and acquired. All the experiments were performed with variable-density Cartesian random sampling mask with different undersampling factors mentioned at their use.
Out of the total 208 slices for each subject, we selected 90 slices that had images of parts of the anatomy for training. The coil sensitivity maps were estimated from the central k-space regions of each slice using ESPIRiT [42] and were assumed to be known during experiments. Thus, the training data had dimensions in rows × columns × slices × coils as 256 × 232 × 360 × 12 and testing data had dimensions 256 × 232 × 164 × 12. The testing was performed on 164 slices out of 208 available for the test subject since the initial 22 and the last 22 slices did not have any brain region but noise. To reduce the sensitivity to acquisition settings, including undersampling patterns, we used different variable density Cartesian pseudo-random sampling masks for each training slice. The same sampling mask was used for the data from all 12 coils of the same slice. The undersampling factors are mentioned at their use in the experiments. The sampling masks used during the testing were different from the ones used during the training.
C. Impact of optimization strategy and number of iterations
The graph in Fig. 2 shows the effect of increasing the number of iterations of alternating strategy in Eq. (10b). We compare the proximal gradients approach (SD) with the proposed approach of using CG blocks within the network. The graph also indicates the benefit of utilizing CG instead of SD in the DC block. Since CG solves the quadratic subproblem in (11) completely as compared to SD, we get a faster reduction of data consistency cost per CG block; this translates to better performance. Note that there are no trainable parameters within the CG block, and hence no intermediate results need to be stored within this block; the memory demand of the training scheme is only proportional to the number of iterations and is independent of the number of CG steps per iteration. The faster reduction of data-consistency cost translates to improved performance than proximal gradients based schemes with the same number of iterations.
Fig. 2.
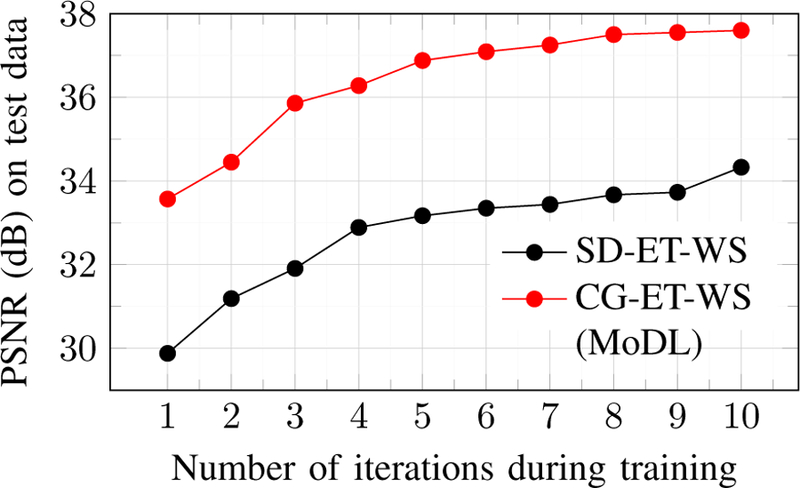
Improvement in reconstruction quality at 10x acceleration as we increase the number of iterations of the network during training. We observe that the testing performance saturates around 8–10 iterations.
It can be observed that average PSNR values on the testing data improve as we increase the number of model iterations. Therefore, it is beneficial to unroll the model for several iterations. Since the performance of MoDL saturates around 8–10 iterations, we used this setting in the rest of the experiments. We trained 10 different five-layer models corresponding to each of the 10 iterations as indicated on the x-axis in Fig. 2. The graph was plotted for average PSNR values obtained corresponding to the reconstruction at 10x acceleration on the 164 testing slices.
D. Effect of dataset size
We relied on the CatDog dataset to determine the impact of training data size on performance. Figure 3 shows the comparison of the with sharing (WS) network architecture with that of no sharing (NS) network architecture when the number of training images were increased from 50 to 2100. To conduct a fair comparison of the two network architectures WS and NS, we trained two five-iteration models with nearly the same number of trainable parameters corresponding to WS and NS architectures. In particular, a 3 layer (3L) model with NS strategy had 199K number of trainable parameters that is almost same as the number of parameters in the 7 layer WS strategy model which have 188K parameters.
Fig. 3.
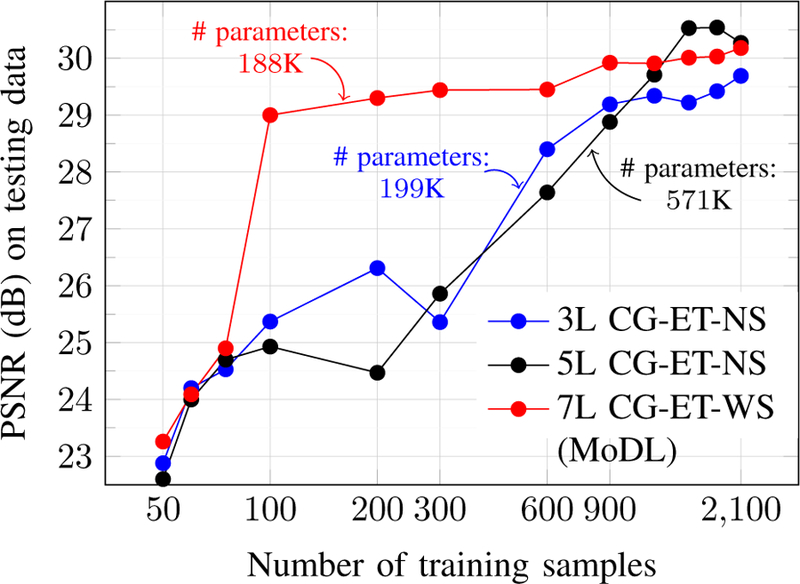
Effect of training dataset size. The x-axis is shown on the logarithmic scale. nL in the legend represents that n layer model was used. Figure shows the change in PSNR values on the testing data as we increase the training dataset size from 50 samples to 2100 samples.
We observe that our WS model is relatively insensitive to training data beyond 100 images, thanks to significantly reduced model parameters over NS strategy. Specifically, increasing the number of training samples from 100 to 2100 (21 fold increase) only resulted in 1 dB improvement in PSNR during testing. By contrast, the black curve in Fig. 3 correspond to an NS model with three times more network parameters, which requires significantly more data to achieve the same performance as the WS scheme. The blue curve corresponds to an NS strategy with the same number of parameters as the WS scheme with five unfolding iterations. The performance of this scheme is worse than the proposed scheme at all training data sizes. This comparison suggests that it is better to use a more complex CNN and share its weights across iterations when more data is available.
E. Insensitivity of the framework to acquisition settings
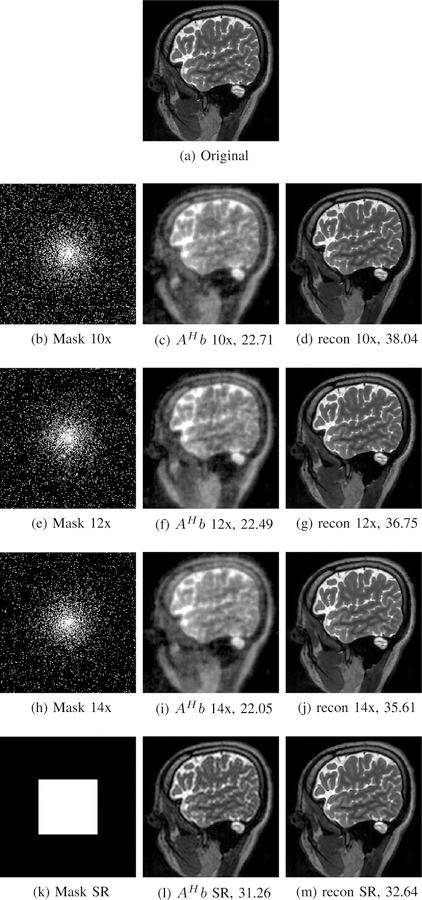
Note that we trained the network with different undersampling patterns to reduce the insensitivity to a specific sampling pattern. In this set of experiments, we show that a single model trained in a particular acceleration setting can be utilized to reconstruct the images from different acceleration settings. In particular, we utilized the trained network at 10x acceleration to reconstruct images from 10x, 12x, and 14x acceleration settings. These results in Figure 4 show that the trained network is relatively insensitive to the undersampling setting. Since we account for the forward model in the network, we expect the learned network to be relatively insensitive to acquisition settings. To improve the insensitivity, we had trained the network with different undersampling patterns with each slice but with same 10x acceleration factor. This training procedure forces the network to learn the manifold of image patches rather than the properties of the forward model; the network learns to estimate the alias patterns and noise that is not localized to the manifold.
Fig. 4.
The insensitivity of the trained network to acquisition settings. A single MoDL in a 10-fold acceleration setting was used to recover images from 10x, 12x, and 14x acceleration as well as in super-resolution (SR) settings. The numbers shows PSNR values in dB.
Further experiments were carried to check the robustness of the trained model in super-resolution (SR) settings. We took the central 100 × 100 k-space region as the sampling mask shown in Fig. 4(k). The resulting low-resolution image Fig. 4(l) was passed through the same network, that was trained for 10x acceleration, to get the high-resolution image as shown in Fig. 4(m).
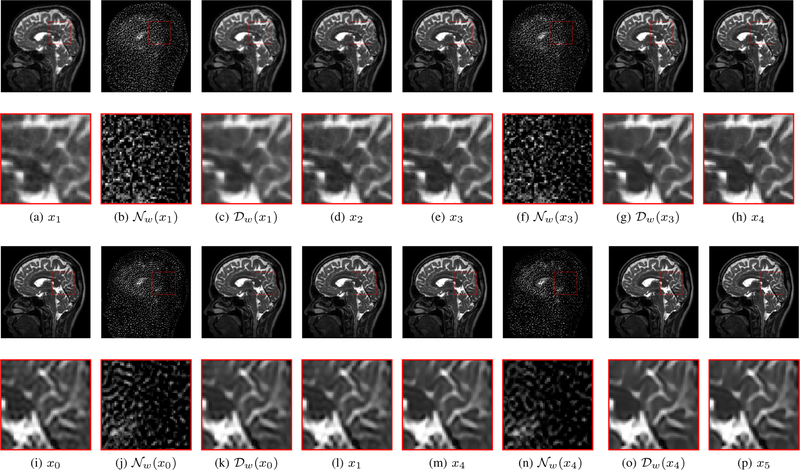
We show the intermediate steps of the reconstruction scheme at two different iterations in Fig. 5. The top row correspond to the 16-fold random undersampling setting. Please refer to Fig. 1(c) for an illustration of the unrolled network architecture. At each iteration, the input xk is fed to the plug-and-play CNN, which extracts the alias/noise components . We note that the noise/alias terms estimated at each iteration are different, with the variance within the brain regions decreasing as iterations progress. The addition of the noise components to the input yields the denoised output . The data consistency block, denoted by combines the denoised outputs with the other terms to yield xk+1. The process is repeated for ten iterations that gradually improve the reconstruction quality and decrease the noise as evident from the figure.
Fig. 5.
Intermediate results in the deep network. Figure (a)-(h) corresponds to the 16-fold acceleration setting, where (a)-(d) corresponds to iteration 2 and (e)-(h) corresponds to iteration 4. Note that the network at each iteration estimates the alias and noise signals denoted by from the signal to obtain the denoised image . Figures (i)-(p) corresponds to the super-resolution setting considered in Fig. 4. (i)-(l) corresponds to iteration 1 and (m)-(p) corresponds to iterations 5. At ith iteration, xi−1 is the input and xi is the output. Note that the nature of the noise in both cases is very different. Nevertheless, the same network trained at 10x setting is capable of effectively removing the undersampling artifacts.
The end-to-end training strategy ensures that the CNN learns the information that is complementary to the ones obtained from coil sensitivity and data consistency information. Fig. 5 also shows the reconstruction outputs extracted from intermediate layers in a super-resolution setting. It is evident from Figures 5(j) and 5(n) that network is able to predict the alias patterns and the aliasing decays as the number of iterations increase. Note that the same network was used in both the experiments, which shows the ability of the same network to remove alias patterns that are dramatically different.
F. Comparison with other deep learning frameworks
In this subsection, we compare the proposed MoDL framework (CG-ET-WS) with other three deep learning frameworks as described in Table II. We also compare the performance of the proposed MoDL framework with compressed sensing based technique that utilizes total variation regularization acronym-ed as CSTV [5]. The graph shown in Fig. 6 compares the average PSNR values of 164 slices on testing data when acceleration factor varies from 2x to 20x. For deep learning methods CG-ET-WS, CG-ET-NS, and SD-ET-WS training was performed on 10x acceleration in the presence of Gaussian noise of standard deviation σ = 0.01 with same amount of training data. The method CG-PD-NS was trained with uniformly decreasing amount of Gaussian noise from σ = 0.25 to σ = 0.02 for a total of ten different noise levels. Table III shows quantitative values for 6x and 10x acceleration for different algorithms. It can be observed that the standard deviation (std) of PSNR values from from the mean is lowest for the proposed MoDL framework.
Fig. 6.
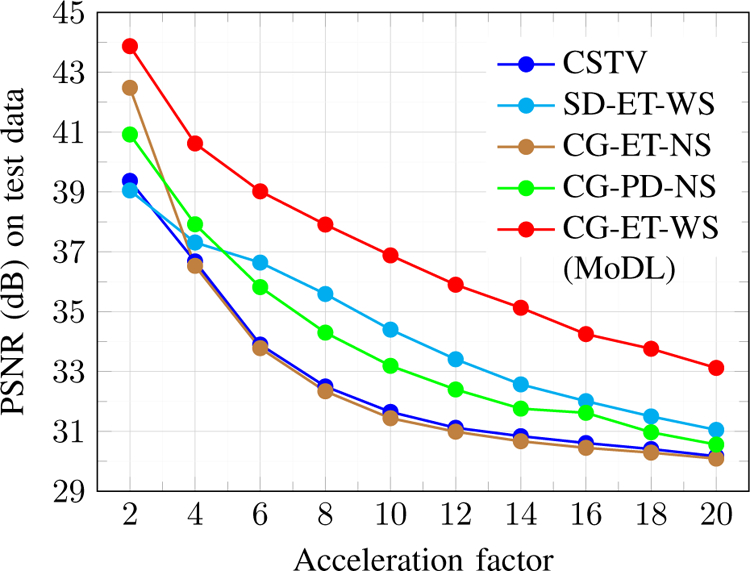
Performance comparison of various algorithms at different acceleration factors. It can be observed that the proposed MoDL performs better than other techniques for all different acceleration factors.
TABLE III.
Comparison of psnr (dB) values obtained by different methods. The values are shown for 6X and 10X acceleration factors in the format: mean ± std, min / max.
| Method | 6 fold acceleration | 10 fold acceleration |
|---|---|---|
| CSTV | 34.50±1.62, 28.42/37.39 | 31.98±1.26, 29.00/35.26 |
| SD-ET-WS | 37.30±1.42, 29.44/41.07 | 34.63±1.93, 30.06/39.51 |
| CG-ET-NS | 33.83±1.97, 23.33/38.39 | 31.53±1.65, 24.98/35.84 |
| CG-PD-NS | 36.52±1.72, 29.57/39.93 | 33.89±1.35, 30.03/38.03 |
| MoDL | 39.24±1.18, 35.27/42.38 | 37.35±1.16, 32.70/40.61 |
The consistently improved performance of proposed MoDL for different acceleration factors may be attributed to the combination of the CG in DC layer, end-to-end training of unrolled network, and a weight sharing network architecture. Further, the optimization is performed on a much lower dimensional space, which is more robust when training data is scarce. Since the Gaussian noise model does not capture the complexity of the alias-induced noise, the PSNR of the CG-PD-NS network is lower than the proposed one. These results show the benefit of performing end-to-end training, compared to pre-training strategy.
The technique CG-ET-NS performs poorest among all other methods since an NS network architecture is a 10 times large capacity model than corresponding weight sharing strategy. Therefore, it requires a large amount of training data to learn the aliasing patterns. The proposed MoDL performs better than compressed sensing based technique CSTV because the MoDL has the benefit of adaptive learning the regularization-prior from the data itself as opposed to fixed total variation prior used in CSTV. Note that CG-PD-NS provides better performance than CG-ET-NS since the denoisers at each iteration are trained independently to denoise from Gaussian corrupted images, and hence it does not suffer from training data constraint unlike the end-to-end strategy in CG-ET-NS. Significantly more training data is needed to obtain good performance with CG-ET-NS as seen from Fig. 3.
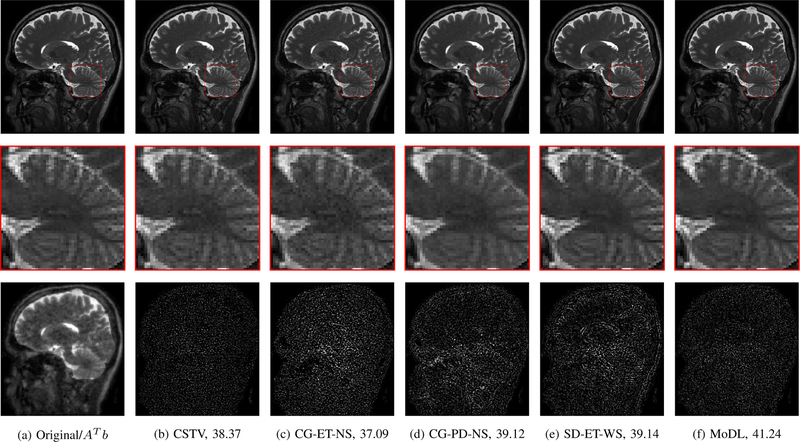
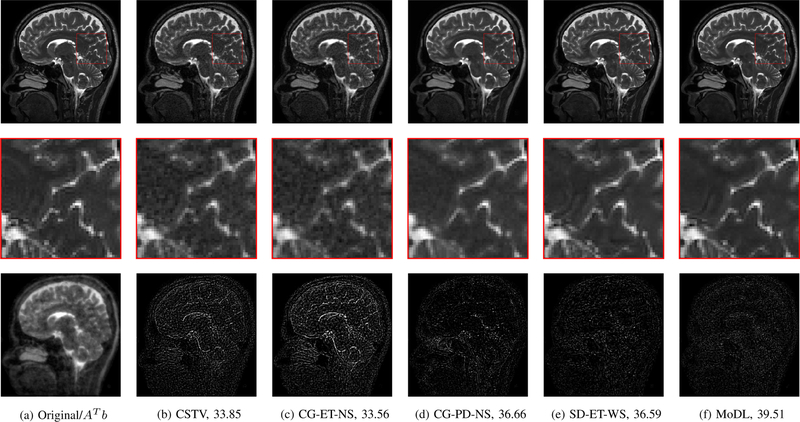
Figures 7 and 8 visually compare two different slices at 4x and 8x accelerated data acquisition in the presence of Gaussian noise of σ = 0.01. The testing slices are from a subject, whose data was not used for training. It is evident from the zoomed portions that the reconstruction quality by the proposed method is better than the techniques compared against.
Fig. 7.
Comparison of the proposed MoDL framework with state of the art parallel imaging strategies. The experiments correspond to a 4-fold accelerated case with random noise of σ = 0.01 added in k-space. The column 1 shows fully sampled image on top and AH b on the bottom. The row 2 shows zoomed portions of the reconstructed images by different methods. The row 3 shows corresponding error images. The numbers in the caption shows the PSNR values in dB. The AH b had PSNR value of 25.30 dB.
Fig. 8.
Comparison of the proposed MoDL framework with state of the art parallel imaging strategies. The experiments correspond to an 8-fold accelerated case with random noise of σ = 0.01 added in k-space. The numbers in the caption show the PSNR values in dB. The AH b had PSNR value of 24.33 dB.
Table IV shows the five-fold cross-validation results. In the cross-validation process, we did training with the data of four subjects and testing on the fifth subject. We repeated this process five times with different split of the training and testing sets. The average PSNR values obtained on each of the five testing subjects during cross-validation at 6x and 10x acceleration factors are summarized in Table IV. The average cross-validation results suggest that the proposed MoDL is robust enough to be used in practice. The average results on subject 4 are relatively less as compared to the other four subjects since this particular subject was of the significantly different physical structure. The results can be improved by adapting the data augmentation that considers different zoom factors during the training process.
TABLE IV.
Five-fold cross-validation results. The PSNR values are shown for 6X and 10X acceleration factors in the format: mean ± std, min / max. Column 1 represents the ith testing subject as Sub i.
| Testing on | 6 fold acceleration | 10 fold acceleration |
|---|---|---|
| Sub 1 | 39.57±1.55, 36.40/43.79 | 37.95±1.68, 34.30/42.48 |
| Sub 2 | 39.56±1.23, 35.13/43.85 | 37.57±1.26, 34.92/42.71 |
| Sub 3 | 39.19±0.98, 36.46/43.03 | 37.38±1.15, 33.58/41.44 |
| Sub 4 | 37.73±1.15, 34.07/41.11 | 36.27±1.13, 33.24/39.66 |
| Sub 5 | 39.35±1.27, 35.33/42.59 | 37.59±1.16, 33.77/40.73 |
| Avg. | 39.08±1.23, 35.47/42.87 | 37.35±1.27, 33.96/41.40 |
Table V reports the training and testing time for different algorithms compared against. The CSTV does not require any training and it was run on the CPU with parallel processing turned on. The deep learning techniques were run on the GPU.
TABLE V.
Training and testing times for different algorithms. The training time is mentioned in hours whereas the testing time is mentioned in seconds. The testing time is mentioned for reconstructing all the 164 slices.
| CSTV | SD-ET-WS | CG-ET-NS | CG-PD-NS | MoDL | |
|---|---|---|---|---|---|
| training | - | 3.6 | 10.8 | 7.6 | 10.6 |
| testing | 162 | 8 | 28 | 49 | 28 |
V. Discussion
The main focus of this paper is to introduce the MoDL framework for general inverse problems and demonstrate its benefits over other deep learning strategies. In our experiments, we restricted the model to ten iterations and five-layer CNN due to GPU memory limitations. The performance of this preliminary implementation may be improved using strategies such as more training data, data augmentation, regularization priors, and drop-outs. Similarly, deeper CNNs with improved performance may be learned when more training data is available; our experiments show that when more training data is available, increasing the complexity of the network and repeating it as in Fig. 1(b) is a better strategy than using different networks at different layers. However, these enhancements are beyond the scope of this work and will be dealt elsewhere.
We relied on a training strategy involving several variable density sampling patterns to reduce the sensitivity of the algorithm to the specific acquisition setting. However, this approach might have resulted in the framework relying more on the lower k-space samples, with a slight loss in high-frequency details. Improved results may be possibly obtained by fixing the sampling pattern during training, as pursued by most of the deep learning image recovery strategies [16], [18], [33], [34], [43], albeit with increased sensitivity to acquisition settings. We used a simple alternating strategy to solve (5) and hence unroll the network. Alternate approaches such as ADMM [44] or the use of momentum terms [45] may have offered faster convergence. This will be a focus of our future work.
We have not theoretically analyzed the convergence of the network in this work. Note that we use the proposed approach with a finite fixed number of iterations, where convergence issues are not too important. We will evaluate the benefit of using more iterations, as well as a detailed theoretical analysis of the framework in our future work.
VI. Conclusions
We have introduced a model-based approach for image reconstruction using a deep learned prior. The proposed MoDL framework combines the power of data-driven learning with the physics derived model-based framework. This framework provides a systematic approach for designing deep architectures for inverse problems with the arbitrary structure. The introduction of the optimization algorithm (CG) within a network layer allows extending the model to complex forward models such as multi-channel MRI, where the analytical inverse of the normal operator does not exist. Also, this strategy offers the easy inclusion of additional image priors, when available.
The sharing of the weights across iterations facilitates the decoupling of the convergence from the complexity of the network. The ability of the network to perform more iterations without increasing the degrees of freedom reduces the risk of overfitting, especially in medical imaging settings where training data is scarce. Our results show that the model provides improved results compared to state-of-the-art, despite the relatively smaller number of trainable parameters. Since we presented different sampling patterns during training, we obtained reduced sensitivity to acquisition parameters such as under-sampling ratio and amount of noise, which eliminates the need for training multiple large networks for each acquisition setting.
Acknowledgments
This work is supported by NIH 1R01EB019961-01A1 and onrn000141310202.
Contributor Information
Hemant K. Aggarwal, Email: hemantkumar-aggarwal@uiowa.edu, Department of Electrical and Computer Engineering, The University of Iowa, Iowa City, IA 52242 USA..
Merry P. Mani, Department of Radiology, The University of Iowa, Iowa City, IA 52242 USA.
Mathews Jacob, Department of Electrical and Computer Engineering, The University of Iowa, Iowa City, IA 52242 USA..
REFERENCES
- [1].Fessler JA, “Model-Based Image Reconstruction for MRI,” IEEE Signal Process. Mag, vol. 27, no. 4, pp. 81–89, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Elbakri IA and Fessler JA, “Statistical image reconstruction for polyenergetic x-ray computed tomography,” IEEE Trans. Med. Imag, vol. 21, no. 2, pp. 89–99, 2002. [DOI] [PubMed] [Google Scholar]
- [3].Verhaeghe J, Van De Ville D, Khalidov I, D’Asseler Y, Lemahieu I, and Unser M, “Dynamic PET reconstruction using wavelet regularization with adapted basis functions,” IEEE Trans. Med. Imag, vol. 27, no. 7, pp. 943–959, July 2008. [DOI] [PubMed] [Google Scholar]
- [4].Aguet F, Van De Ville D, and Unser M, “Model-based 2.5-D deconvolution for extended depth of field in brightfield microscopy,” IEEE Trans. Image Process, vol. 17, no. 7, pp. 1144–1153, July 2008. [DOI] [PubMed] [Google Scholar]
- [5].Ma S, Yin W, Zhang Y, and Chakraborty A, “An Efficient Algorithm for Compressed MR Imaging using Total Variation and Wavelets,” in Computer Vision and Pattern Recognition, 2008, pp. 1–8.
- [6].Lingala SG, Hu Y, DiBella E, and Jacob M, “Accelerated dynamic MRI exploiting sparsity and low-rank structure: kt SLR,” IEEE Trans. Med. Imag, vol. 30, no. 5, pp. 1042–1054, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Lingala SG and Jacob M, “A blind compressive sensing frame work for accelerated dynamic mri,” in IEEE Int. Symp. Bio. Imag IEEE, 2012, pp. 1060–1063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Ravishankar S and Bresler Y, “L0 Sparsifying Transform Learning With Efficient Optimal Updates and Convergence Guarantees,” IEEE Trans. Signal Process, vol. 63, no. 9, pp. 2389–2404, 2015. [Google Scholar]
- [9].Lingala SG and Jacob M, “Blind Compressive Sensing Dynamic MRI,” IEEE Trans. Med. Imag, vol. 32, no. 6, pp. 1132–1145, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Ronneberger O, Fischer P, and Brox T, “U-net: Convolutional networks for biomedical image segmentation,” in International Conference on Medical Image Computing and Computer-Assisted Intervention (MIC-CAI) Springer, 2015, pp. 234–241. [Google Scholar]
- [11].He K, Zhang X, Ren S, and Sun J, “Deep Residual Learning for Image Recognition,” in IEEE Conference on Computer Vision and Pattern Recognition, 2016, pp. 770–778.
- [12].Chen H, Zhang Y, Kalra MK, Lin F, Chen Y, Liao P, Zhou J, and Wang G, “Low-Dose CT with a Residual Encoder-Decoder Convolutional Neural Network,” IEEE Trans. Med. Imag, vol. 36, no. 12, pp. 2524–2535, 2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Wang G, “A Perspective on Deep Imaging,” IEEE Access, vol. 4, no. nn, pp. 8914–8924, 2016. [Google Scholar]
- [14].Zhang K, Zuo W, Member S, Chen Y, Meng D, and Zhang L, “Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising,” IEEE Trans. Image Process, vol. 26, no. 7, pp. 3142–3155, 2017. [DOI] [PubMed] [Google Scholar]
- [15].Zhang L and Zuo W, “Image Restoration: From Sparse and Low-Rank Priors to Deep Priors,” IEEE Signal Process. Mag, vol. 34, no. 5, pp. 172–179, 2017. [Google Scholar]
- [16].Zhang K, Zuo W, Gu S, and Zhang L, “Learning Deep CNN Denoiser Prior for Image Restoration,” in IEEE Conference on Computer Vision and Pattern Recognition, 2017, pp. 2808–2817.
- [17].Chang JHR, Li C-L, Poczos B, Kumar BVKV, and Sankaranarayanan AC, “One Network to Solve Them All — Solving Linear Inverse Problems using Deep Projection Models,” in IEEE International Conference on er Vision, 2017, pp. 1–12.
- [18].Schlemper J, Caballero J, Hajnal JV, Price A, and Rueckert D, “A Deep Cascade of Convolutional Neural Networks for MR Image Reconstruction,” in Information Processing in Medical Imaging, 2017, pp. 647–658. [DOI] [PubMed]
- [19].Hammernik K, Klatzer T, Kobler E, Recht MP, Sodickson DK, Pock T, and Knoll F, “Learning a Variational Network for Reconstruction of Accelerated MRI Data,” Magnetic resonance in Medicine, vol. 79, no. 6, pp. 3055–3071, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Mardani M, Monajemi H, Papyan V, Vasanawala S, Donoho D, and Pauly J, “Recurrent Generative Adversarial Networks for Proximal Learning and Automated Compressive Image Recovery,” in IEEE Conference on Computer Vision and Pattern Recognition, 2018, p. na.
- [21].Putzky P and Willing M, “Recurrent Inference Machines for Solving Inverse Problems,” in arXiv, 2017, pp. 1–12.
- [22].Gregor K and LeCun Y, “Learning fast approximations of sparse coding,” in International Conference on Machine Learning Omnipress, 2010, pp. 399–406. [Google Scholar]
- [23].Poddar S and Jacob M, “Dynamic mri using smoothness regularization on manifolds (storm),” IEEE Trans. Med. Imag, vol. 35, no. 4, pp. 1106–1115, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Biswas S, Aggarwal HK, Poddar S, and Jacob M, “ Model-based free-breathing cardiac MRI reconstruction using deep learned and STORM priors: MoDL-STORM,” in IEEE International Conference on Acoustics, Speech, and Signal Processing, 2018, p. NA. [DOI] [PMC free article] [PubMed]
- [25].Ongie G and Jacob M, “Super-resolution mri using finite rate of innovation curves,” in IEEE Int. Symp. Bio. Imag IEEE, 2015, pp. 1248–1251. [Google Scholar]
- [26].Ongie G, Biswas S, and Jacob M, “Convex recovery of continuous domain piecewise constant images from non-uniform Fourier samples,” IEEE Trans. Signal Process, vol. 66, no. 1, pp. 236–250, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Figueiredo MAT, Nowak RD, Member S, and Nowak RD, “An EM Algorithm for Wavelet-Based Image Restoration,” IEEE Trans. Image Process, vol. 12, no. 8, pp. 906–916, 2003. [DOI] [PubMed] [Google Scholar]
- [28].Hu Y and Jacob M, “Higher Degree Total Variation (HDTV ) Regularization for Image Recovery,” IEEE Trans. Image Process, vol. 21, no. 5, pp. 2259–2271, 2012. [DOI] [PubMed] [Google Scholar]
- [29].Ongie G and Jacob M, “Off-the-Grid Recovery of Piecewise Constant Images from Few Fourier Samples,” SIAM on Imag. Sci, vol. 9, no. 3, pp. 1004–1041, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Lee D, Jin KH, Kim EY, Park S-H, and Ye JC, “Acceleration of mr parameter mapping using annihilating filter-based low rank hankel matrix (aloha),” Magnetic resonance in medicine, vol. 76, no. 6, pp. 1848–1864, 2016. [DOI] [PubMed] [Google Scholar]
- [31].Haldar JP, “Low-Rank Modeling of Local k-Space Neighborhoods (LORAKS) for Constrained MRI,” IEEE Trans. Med. Imag, vol. 33, no. 3, pp. 668–681, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Dabov K, Foi A, Katkovnik V, and Egiazarian K, “Image denoising by sparse 3-d transform-domain collaborative filtering,” IEEE Trans. Image Process, vol. 16, no. 8, pp. 2080–2095, 2007. [DOI] [PubMed] [Google Scholar]
- [33].Mousavi A and Baraniuk RG, “Learning to Invert: Signal Recovery via Deep Convolutional Networks,” in IEEE Intel. Conf.Acou., Speech, Sig Proces, 2017, pp. 2272–2276.
- [34].Jin KH, McCann MT, Froustey E, and Unser M, “Deep Convolutional Neural Network for Inverse Problems in Imaging,” IEEE Trans. Image Process, vol. 29, pp. 4509–4522, 2017. [DOI] [PubMed] [Google Scholar]
- [35].Schlemper J, Caballero J, Hajnal JV, Price AN, and Rueckert D, “A deep cascade of convolutional neural networks for dynamic mr image reconstruction,” IEEE Trans. Med. Imag, vol. 37, no. 2, pp. 491–503, 2018. [DOI] [PubMed] [Google Scholar]
- [36].Diamond S, Sitzmann V, Heide F, and Wetzstein G, “Unrolled Optimization with Deep Priors,” in arXiv:1705.08041, 2017, pp. 1–11.
- [37].Chan SH, Wang X, and Elgendy OA, “Plug-and-Play ADMM for Image Restoration: Fixed Point Convergence and Applications,” IEEE Transactions on Computational Imaging, vol. 3, no. 1, pp. 84–98, 2017. [Google Scholar]
- [38].yang y., Sun J, Li H, and Xu Z, “Deep admm-net for compressive sensing mri,” in Advances in Neural Information Processing Systems 29, 2016, pp. 10–18. [Google Scholar]
- [39].Press WH, Teukolsky SA, Vetterling WT, and Flannery BP, “Numerical recipes in c,” Cambridge University Press, vol. 1, p. 3, 1988. [Google Scholar]
- [40].Kingma DP and Ba JL, “Adam: a Method for Stochastic Optimization,” International Conference on Learning Representations 2015, pp. 1–15, 2015.
- [41].Ioffe S and Szegedy C, “Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift,” in IEEE International Conference on Machine Learning, 2015, pp. 448–456. [Online]. Available: http://arxiv.org/abs/1502.03167
- [42].Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, and Lustig M, “ESPIRiT - An eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA,” Magnetic Resonance in Medicine, vol. 71, no. 3, pp. 990–1001, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Kang E, Min J, and Ye JC, “A deep convolutional neural network using directional wavelets for low-dose x-ray ct reconstruction,” Medical Physics, vol. 44, no. 10, pp. e360–e375, 2017. [DOI] [PubMed] [Google Scholar]
- [44].Boyd S, Parikh N, Chu E, Peleato B, and Eckstein J, “Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers,” Foundations and Trends® in Machine Learning, vol. 3, no. 1, pp. 1–122, 2010. [Google Scholar]
- [45].Beck A and Teboulle M, “A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems,” SIAM J. Imag. Sci, vol. 2, no. 1, pp. 183–202, 2009. [Google Scholar]