Changes in the Distribution of Sustained Attention Alter the Perceived Structure of Visual Space

Abstract

Visual spatial attention is a critical process that allows for the selection and enhanced processing of relevant objects and locations. While studies have shown attentional modulations of perceived location and the representation of distance information across multiple objects, there remains disagreement regarding what influence spatial attention has on the underlying structure of visual space. The present study utilized a method of magnitude estimation in which participants must judge the location of briefly presented targets within the boundaries of their individual visual fields in the absence of any other objects or boundaries. Spatial uncertainty of target locations was used to assess perceived locations across distributed and focused attention conditions without the use of external stimuli, such as visual cues. Across two experiments we tested locations along the cardinal and 45° oblique axes. We demonstrate that focusing attention within a region of space can expand the perceived size of visual space; even in cases where doing so makes performance less accurate. Moreover, the results of the present studies show that when fixation is actively maintained, focusing attention along a visual axis leads to an asymmetrical stretching of visual space that is predominantly focused across the central half of the visual field, consistent with an expansive gradient along the focus of voluntary attention. These results demonstrate that focusing sustained attention peripherally during active fixation leads to an asymmetrical expansion of visual space within the central visual field.

Introduction:

Vision is a fundamental sense with which humans assess their environments and plan actions to interact within these environments. Implicit in any theory of visual perception is the assumption of a spatial structure, whether it is a field within which both an observer and external object exists, or the internal spatial structure of a single object. The development of accurate spatial metrics regarding the direction and distance of an object is critical for allowing observers to effectively interact with their environment, whether reaching for a cup off of a kitchen counter or more complex actions such as navigating through crowded city streets.

At any given moment, however, our perception of the world is not simply a passive representation of the external environment. One factor that is known to modulate visual perception is the current attentional state of an observer. Changes in the focus of visuospatial attention alter not only the quality of object representations (Anton-Erxleben, Henrich, & Treue, 2007; Carrasco, 2011; Carrasco, Ling, & Read, 2004; Fortenbaugh, Prinzmetal, & Robertson, 2011; Kosovicheva, Fortenbaugh, & Robertson, 2010; Tsal & Shalev, 1996) but also the perceived location of those objects (Adam, Paas, Ekering, & Loon, 1995; Bocianski, Müsseler, & Erlhagen, 2010; Fortenbaugh & Robertson, 2011; Prinzmetal, 2005; Tsal & Bareket, 2005; Tsal & Shalev, 1996; Uddin, Kawabe, & Nakamizo, 2005; Yamada, Kawabe, & Miura, 2008).

While changes in attentional distribution have been shown to alter perceived object size and location, there are conflicting theories regarding what these effects imply for the underlying structure of visual space. Some studies (Tsal & Bareket, 1999, 2005) using visual cues to direct attention toward or away from a given location have found that shifts in attention can alter perceived location by shifting the perceived locations away from fixation. Other studies have shown that directing attention toward the location of a target stimulus improves location precision, reducing its spatial spread. Still other studies (Adam, Davelaar, van der Gouw, & Willems, 2008; Newby & Rock, 2001; Prinzmetal, Amiri, Allen, & Edwards, 1998) have used dual-task paradigms to test how a secondary task performed at fixation alters perceived location in the parafoveal and nearer the periphery (i.e., < 10º eccentricity). Interestingly, some of these dual-task studies (Adam et al., 2008) found evidence that being able to focus attention in a single-task relative to a dual-task condition reduces foveal biases, or underestimations of target eccentricity, while other studies (Newby & Rock, 2001; Prinzmetal, 2005; Prinzmetal et al., 1998) only found evidence for reductions in spatial spread of response locations. Given that the use of visual cues or dual-task paradigms introduce additional visual stimuli in a display, in addition to already known landmark effects that can alter localization performance (Diedrichsen, Werner, Schmidt, & Trommershäuser, 2004; Eggert, Ditterich, & Straube, 2001; Kerzel, 2002; Werner & Diedrichsen, 2002; Yamada et al., 2008), an additional paradigm that has been used to study the effects of voluntary attention on localization is to alter the distribution of sustained attention across blocks of trials by manipulating spatial uncertainty in the region where targets can appear (Fortenbaugh & Robertson, 2011). Manipulations of spatial uncertainty in these localization tasks provide a complementary approach to visual cueing paradigms by altering the spatial spread of voluntary attention, rather than shifting the focus of attention, in a manner similar to dual task paradigms but without introducing external objects into the display. Across these studies, several theories regarding the impact of attention on peripheral localization have been developed. Specifically, findings related to focusing voluntary attention have been interpreted as evidence for: (1) attention decreasing variability in perceived location without inducing spatial biases (Newby & Rock, 2001; Prinzmetal, 2005) and (2) attention expanding visual space at the focus of attention and increasing perceived target distances or the size of attended objects (Anton-Erxleben et al., 2007; Fortenbaugh et al., 2011; Fortenbaugh & Robertson, 2011).

The present study was designed to address the latter hypothesis, that distributing voluntary attention across smaller and smaller regions of space can systematically alter where objects are seen in the visual periphery. In particular, the results of the study by Fortenbaugh and Robertson (2011) showed systematic changes in judged location across three attention conditions that manipulated the distribution of attention by varying the number of attended visual axes from fixation (i.e., spatial uncertainty). Targets could appear along 1, 2 or 4 horizontal or vertical axes. The task was to judge target location relative to fixation and a 30º aperture boundary that was mounted on a computer monitor. Results showed that when participants distributed attention across all four visual axes they significantly underestimated the eccentricity of the targets (i.e. foveal bias). For example, reporting 25% when the target was at 30% eccentricity from fixation. As spatial uncertainty and thus the number of attended axes was reduced, the degree of foveal bias was also reduced, consistent with an expansion of visual space.

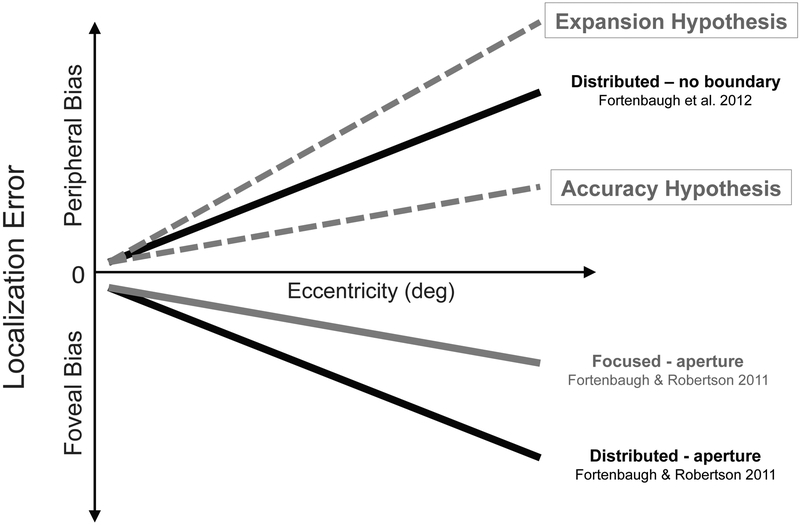
However, the observed reduction in foveal bias could be due to two potential effects of attention on perceived location: namely, an increase in location accuracy along the attended axes (the Accuracy hypothesis) or an expansion of perceived space along these axes (the Expansion hypothesis). In order to tease apart these two competing hypotheses, in the present study we utilized methods from another study looking at peripheral localization judgments with the same response method but within a Goldmann perimeter. This perimeter type is traditionally used to map visual fields in optometry exams and is a half-dome that allows peripheral localization judgments relative to perceived visual field extent without visible external object contours (Fortenbaugh, Sanghvi, Silver, & Robertson, 2012). Importantly, this study showed that when attention was distributed across the four cardinal visual axes participants showed a peripheral localization bias, overestimating the target eccentricities for similar briefly flashed, static targets (e.g., reporting 35% when the target was at 30%). This stimulus design thus provides an opportunity to disentangle the two hypotheses regarding the impact of focusing attention on perceived location (see Figure 1). Specifically, given that in the experimental context of the Goldman, participants already show a peripheral bias when attention is spread across the visual field, the accuracy hypothesis predicts that focusing attention on a subset of axes will reduce peripheral biases relative to this baseline (attending to all axes), thus reducing the absolute magnitude of errors during localization. In contrast, the expansion hypothesis predicts that focusing attention will increase the perceived distance between fixation and the target location, increasing peripheral biases and leading to less accurate performance on the task.

Figure 1. Theoretical Predictions.

The graph shows the pattern of localization errors found in previous experiments. When judging target locations within a circular aperture in Fortenbaugh & Robertson (2011), focusing attention along a visual axis reduced the degree of foveal bias (underestimation of target eccentricity). In contrast, under distributed attention conditions, participants show a peripheral bias (overestimation of target eccentricity) when judging target locations relative to their perceived visual field extent with no external object boundaries present (Fortenbaugh et al., 2012). The dotted lines show the predicted change in error patterns with focused attention and no external boundary if focusing attention serves to make perception more accurate (Accuracy Hypothesis) or expands visual space regardless of the error pattern in distributed attention conditions (Expansion Hypothesis).

Experiment 1

Method

Participants.

Fifteen naïve participants completed the experiment (8 female; 20.3 ± 2.7 years). All participants reported 20/20 visual acuity, either without any optical correction or with contact lenses. Participants were excluded if they wore eyeglasses, as these can artificially restrict visual field extent (Steel, Mackie, & Walsh, 1996). One participant did not complete all blocks. The remaining fourteen participants were included in the following analyses. All procedures were approved by the Committee for the Protection of Human Subjects at the University of California, Berkeley, and followed the tenets of the Declaration of Helsinki. All participants provided signed informed consent before the study began.

Materials and procedure.

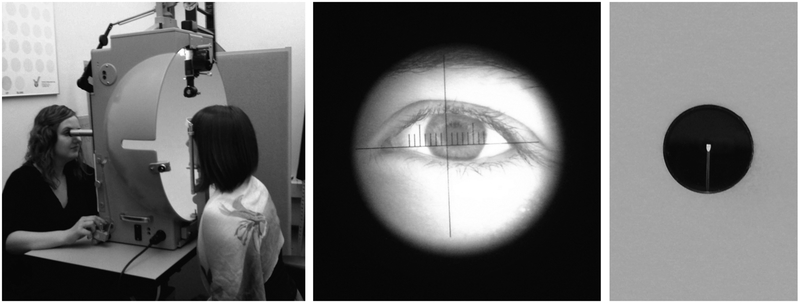
The methods followed those developed in our previous study (Fortenbaugh et al., 2012). Briefly, participants were seated in a Goldmann kinematic perimeter, a self-illuminated half-dome with a uniform white background that allows targets dots to be presented at any location within the visual field (see Figure 2). Visual field extent was first measured using standard clinical procedure. The experimenter was seated on the opposite side and viewed the participant’s right eye through a telescope and monitored participant fixation. The telescope is affixed to the center of the dome where a 1º radius hole with a glass plate (1cm diameter) is located. Within the hole, a metal pin provides a fixation point in the exact center of the dome for participants (Figure 1, right panel). For each participant, binocular visual field extent along the four cardinal axes (left and right horizontal; upper and lower vertical) was measured using the III4e test target (0.44° target dot; viewing distance = 30cm; 318cd/m² on a background luminance of 10cd/m²; Weber contrast ratio = 30.8). While the participant fixated on a point in the center of the perimeter, the experimenter first presented the target at a location outside of the visual field. The experimenter then slowly moved the target foveally along a visual meridian. When the participant first detected the target dot entering their visual field they pressed a button that made a tone and the experimenter marked the location on a chart.

Figure 2. Goldmann Perimeter.

The left image shows a participant seated on the right, facing the dome, and an experimenter seated on the left. The experimenter controls the position of the target light by moving the projector via a bar with their left hand. The bar has a marker on the experimenter’s side (not shown) that indicates the target light position on a chart in polar coordinates. The target light is presented by pressing a lever with the right hand (the experimenter is shown with her hand on the lever). Fixation is monitored through a telescope. The middle image shows a photograph of a participant’s eye taken through the telescope to illustrate the magnified view of the participant’s eye. The right image shows the hole in the center of the dome from the perspective of the participant with the metal pin used as a fixation point.

The behavioral task used the same experimental set-up as for the visual field measurements. However, here, while participants maintained fixation at the center of the perimeter, the experimenter briefly flashed the target dot. Presentation of target dots is manually controlled in the Goldmann perimeter, with average target durations of 176.8ms ±25.5ms (Fortenbaugh et al., 2012). Across trials, potential target locations were eccentricities from 10° to 90° in 10° increments (or as far as possible given each participant’s visual field extent) along the four cardinal axes. All target locations were tested four times with a pre-generated random sequence for each participant. On each trial, participants were required to provide a verbal magnitude estimate between 0-100 after target presentation, with 0 indicating that the target appeared at fixation and 100 indicating that the target appeared at the edge of their visual field, or as far out into the periphery as they could see in that direction.

Any trial where eye movements were detected or participants reported not maintaining fixation was repeated. Also if participants reported not seeing the target, the trial was repeated. The test target was supra-threshold for locations within the boundaries of the visual field. However, on rare occasions the target may have been missed due to an eye blink or the target being located at the edge of the visual field. Missed trials were not recorded. The trial was simply repeated and the response given on the second attempt recorded. For targets on the very edge of the visual field, if the target was not detected on the second attempt the trial was skipped. Across participants, this occurred on 0.18% of trials. There was no occurrence of a trial closer within the boundaries of a participant’s visual field being missed more than once.

In order to manipulate the distribution of attention, three attention conditions were tested across eight blocks of trials. In the Attend All condition, targets were presented along all four axes within a single block with the order of target locations intermixed. In the two Attend Meridian conditions, targets appeared either along the horizontal or the vertical meridian in separate blocks. In the Attend Axis condition, targets were only presented along one axis throughout each of the four blocks, allowing participants to focus their attention along one direction. Breaks were provided between each of the seven blocks of trials and another break was provided halfway through the Attend All condition block. Block order was randomized across participants. We note that for each participant the total number of target locations tested across each of the four axes was constant across the three attention conditions. The attention manipulations therefore did not vary the number of locations that were tested across all experimental blocks, but rather the probability that a given target location would be tested within a single block of trials.

Results and Discussion

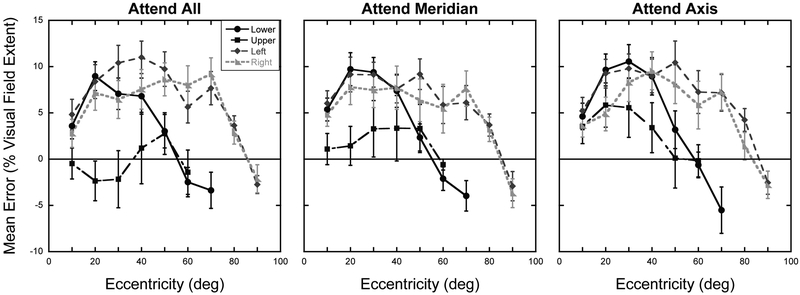
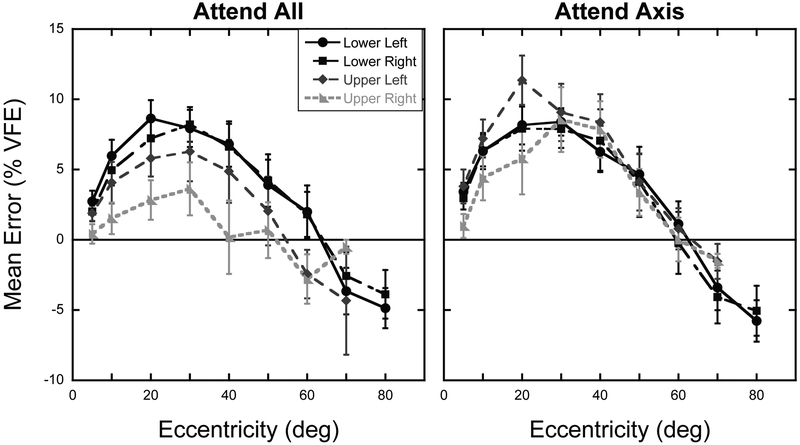
The mean measured binocular visual field extents were: left = 87.4° ± 6.1°, right = 87.4° ± 7.3°, upper = 51.5° ± 7.6°, lower = 72.0° ± 3.7°. Errors in magnitude estimates were calculated by subtracting the true magnitude of each target location from the judged magnitude for each trial. The true target magnitude in percentage of visual field extent (%VFE) was calculated by dividing the target eccentricity in degrees of visual angle by the measured visual field extent along the axis tested and multiplying by 100. Mean errors were then calculated across the four repeats for each target location, axis, and attention condition. Figure 3 shows the mean errors as a function of axis tested for the three attention conditions. A 4 Axis × 3 Eccentricity × 3 Attention condition repeated-measures ANOVA was calculated on the mean errors, including only the 10º, 20º, and 30º eccentricities as these were represented in all participants along all axes. Greenhouse-Geisser corrections were applied when the assumption of sphericity was violated. Results show a significant main effect of Axis, F(3,39) = 9.19, p < 0.001, and Eccentricity, F(1.2,15.9) = 4.67, p = 0.04, with peripheral biases increasing with eccentricity in this range. Importantly, we find a significant main effect of Attention, F(2,26) = 4.67, p = 0.02, with peripheral biases increasing as attention was focused on smaller regions of space. The attention effect is primarily seen for the upper axis as reflected in the significant Attention × Axis interaction, F(2.7,35.7) = 4.66, p = 0.009. No other interaction terms were significant.

Figure 3. Experiment 1: Localization errors.

Mean errors in percent of visual field extent as a function of target eccentricity for the four axes and three attention conditions tested. Error bars represent ±1 S.E.M. The solid horizontal line at zero represents expected performance if no distortion exists.

Given that only one participant had an upper visual field extent less than 40º, we reran the error analysis including the four eccentricities from 10º-40º with this participant excluded. The same pattern of results was observed including the main effect of Attention, F(2,24) = 6.18, p = 0.007, and the Attention × Axis interaction, F(2.3,28.1) = 3.56, p = 0.035. Testing out to 50º was not possible in this analysis as five of the participants had upper visual field extents less than 50º. To further explore the Attention × Axis interaction, additional post-hoc 4 Eccentricity × 3 Attention condition repeated-measures ANOVAs were calculated using the same eccentricities as above for each of the four axes separately (using Greenhouse-Geisser corrections when the appropriate). For the Upper Axis, results show a main effect of Attention, F(2,24) = 15.83, p < 0.0001. No main effect of Eccentricity or Attention × Eccentricity interaction was found (Eccentricity: F(1.3,16.1) = 0.26, p = 0.69; Interaction: F(6,72) = 1.43, p = 0.22). For the Lower Axis, a main effect of Eccentricity was observed, F(1.7,22.5) = 4.04, p = 0.04. No main effect of Attention or Attention × Eccentricity interaction was found (Attention: F(2,26) = 1.76, p = 0.19; Interaction: F(6,78) = 0.52, p = 0.80). The same pattern was observed for the Left Axis, with only a main effect of Eccentricity, F(1.8,23.9) = 5.09, p = 0.02, and no main effect of Attention or Attention × Eccentricity interaction (Attention: F(2,26) = 0.25, p = 0.78; Interaction: F(6,78) = 1.18, p = 0.33). Finally, for the Right Axis, results show no main effect of Attention, F(2,26) = 0.30, p = 0.74, of Eccentricity, F(1.6,21.3) = 3.49, p = 0.06. However, the Attention × Eccentricity interaction was significant, F(6,78) 2.44, p = 0.03, with the greatest peripheral biases occurring in the Attend Meridian condition in the central two eccentricities and larger peripheral biases for the Attend Axis condition for the farthest two eccentricities. Collectively, however, the results support that the Attention × Axis interaction in the full ANOVA is driven by changes in perceived location along the Upper Axis, the only one of the four axes to show an overall main effect of Attention in the separate ANOVAs.

Given the individual differences in visual field extent across participants and axes, the above analyses on mean localization errors was only able to assess changes in position within the central 40º of the visual field. In order to examine the effect of attention across the breadth of eccentricities tested in each participant and along each axis, our next analysis examined the scaling patterns of magnitude estimates as a function of eccentricity (Figure 4). In our previous study (Fortenbaugh et al., 2012), a hierarchical regression analysis run on the raw magnitude estimates for all eccentricities determined that a power function best captured the non-linear scaling pattern as a function of eccentricity, with significant differences observed in the best-fitting exponent parameter across the four axes. This power function is given in Equation 1.

Figure 4. Example Raw Magnitude Estimate Data From Single Participant.

A scatter plot showing the raw magnitude estimates as a function of the true target magnitude for a single participant in the Attend All condition for the right axis. The dotted line shows the best fitting power function while the solid line shows the expected magnitude estimates if no distortion exists. Four repeats were tested at each location for a total of 36 data points along this axis.

In the present study, we wanted to determine the change in scaling pattern across the three attention conditions as these functions capture the pattern of perceived locations across all

$$J=\lambda D^{\alpha }\text{where}:\lambda =\text{slope}(\text{global scaling});\alpha =\text{exponent}(\text{local scaling})$$ (EQ 1)

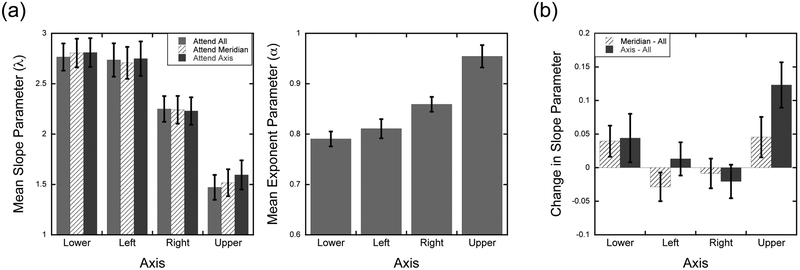
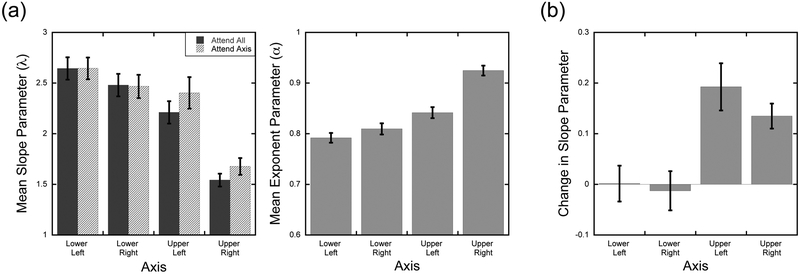
eccentricities tested. We therefore modified the model fitting as follows. For each participant, the raw magnitude estimates for each axis and attention condition was fit separately with the constraint that the estimated exponent parameter (α) be shared across the three attention conditions. The slope parameter (λ), which represents a global scaling pattern that affects all eccentricities similarly, was free to vary across the three attention conditions. Thus, any change in scaling across attention conditions is reflected in this parameter rather than potentially being spread across the two parameters. The data were well fit by the power functions (mean R² = 93.2%; range: 75.7-98.0). Figure 5a shows the mean slope and exponent factors as a function of axis. A 4 Axis × 3 Attention repeated-measures ANOVA calculated on the slope parameters showed a main effect of Axis, F(3,39) = 12.62, p < 0.001. There was no main effect of Attention, F(2,26) = 1.84, p = 0.18, but there was a significant Attention × Axis interaction, F(6,78) = 2.34, p = 0.04. Figure 5a highlights that the average slopes and exponents is consistent with those observed in previous studies using this localization task in the Goldmann perimeter (Fortenbaugh et al., 2012; Fortenbaugh, Silver, & Robertson, 2015). However, as seen in Figure 5a, the variation across Axes is much larger (> 10×) than the variation within an axis across the three Attention conditions, which is the primary focus of the present study. Therefore, in order to better highlight the pattern in slope changes across the three attention conditions, difference scores were calculated and plotted in Figure 5b. Using the Attend All condition as a baseline, the slope in the Attend All condition was subtracted from the calculated slopes in the Attend Meridian and Attend Axis conditions for each participant. As seen in Figure 5b, the Attention × Axis interaction observed in the analysis of the slopes is driven primarily by the increase in slopes along the upper vertical meridian in the Attend Meridian and Axis conditions compared to the Attend All condition. In contrast, no change in slopes is seen for the left or right axes. Further post-hoc statistical tests confirmed this pattern. Separate repeated-measures ANOVAs were calculated across the three attention conditions for each axis separately. Results show a significant main effect of Attention for the Upper Axis, F(2,26) = 4.72, p = 0.018. In contrast, no main effect of Attention was observed for any of the other three axes (p > 0.338 for all).

Figure 5. Experiment 1: Power Function parameters.

(a) Mean estimated slope and exponent parameters as a function of axis tested and attention condition. Exponent parameters were a shared parameter across the three attention conditions in the model fitting. (b) The change in the slope parameter in the Attend Meridian and Attend Axis conditions relative to the Attend All condition as a function of axis tested. Error bars represent within-subject ±1 S.E.M.

The results of the present study are more consistent with the expansion hypothesis than the accuracy hypothesis outlined in the introduction. When attention effects were found, focusing attention increased peripheral biases, effectively making performance worse on this task. While no change in scaling across attention conditions (Figure 5b) was found along the left and right axes along the horizontal meridian, it is also the case that under no condition did focusing attention reduce the degree of peripheral biases observed, the key prediction of the accuracy hypothesis. The present results give an indication of expansion with more focused attention, but results show significant expansions only along the upper visual axis. However, in our previous study (Fortenbaugh & Robertson, 2011) using the same attention manipulation and magnitude estimate response, attention effects were found along all four axes. In that study, however, a clear aperture boundary was present at 30° eccentricity for all four cardinal axes. Within the typical human visual field the brow provides the clearest boundary, framing the upper visual field. A second experiment therefore was run shifting the location of the target axes to examine if similar expansions would be seen in other non-cardinal locations across the upper and lower hemifields.

Experiment 2

In Experiment 1, the targets were presented along the four cardinal axes and attentional modulations were found predominantly along the upper vertical axis. To investigate if similar expansions of judged location occur across the upper hemifield, the four diagonal oblique axes were tested, focusing on the Attend All and Attend Axis conditions.

Method

Participants.

Fifteen naïve participants completed the experiment (9 female; 20.2 ± 1.7 years). The same inclusion criteria from Experiment 1 applied here.

Materials and procedure.

The same method from Experiment 1 was used with the following three changes. First, targets were presented along the 45° oblique axes (lower left, lower right, upper left, and upper right). Second, only the Attend All and Attend Axes conditions were tested across five blocks of trials. Finally, given the small upper vertical hemifields in multiple participants in the previous experiment (upper vertical VFE < 50°), the natural individual variability in visual field size across participants (Niederhauser & Mojon, 2002), and the fact that it is not possible to a priori select participants based on their visual field extents without measuring them, an additional target location at 5° was tested on all axes. As in Experiment 1, block order was randomized across participants. The same repeating procedure as Experiment 1 was used for trials where participants reported not seeing the target. Only 1 trial (0.02% of all trials) for a target at the edge of a participant’s visual field was skipped due to the participant not seeing the target twice in a row.

Results and Discussion

The mean measured binocular visual field extents were: lower left = 84.2° ± 4.4°, lower right = 84.3° ± 3.5°, upper left = 65.3° ± 3.5°, upper right = 64.7° ± 3.4°. Mean errors were calculated in the same manner as Experiment 1. Figure 6 shows the mean errors as a function of axis tested for the two attention conditions. The larger visual field extents along the oblique upper hemifield axes allowed an analysis with a 4 Axis × 7 Eccentricity × 2 Attention condition repeated-measures ANOVA on the mean errors, including the seven eccentricities from 5º-60º as these were represented in all participants along all axes (using Greenhouse-Geisser corrections where appropriate). The results mirror those of Experiment 1, with significant main effects of Axis, F(1.7,24.5) = 5.11, p =0.017, and Eccentricity, F(1.7,23.3) = 8.71, p = 0.002. There was also a significant main effect of Attention, F(1,14) = 8.12, p = 0.01, and a significant Attention × Axis interaction, F(3,42) = 6.99, p = 0.001, reflecting the increase in peripheral bias for target locations along the two upper hemifield axes in the Attend Axis condition compared to the Attend All condition, while little to no change in errors is seen for the lower hemifield axes. No other interaction terms were significant.

Figure 6. Experiment 2: Localization errors.

Mean errors in percent of visual field extent as a function of target eccentricity for the four axes and two attention conditions tested. Error bars represent ±1 S.E.M. The solid horizontal line at zero represents expected performance if no distortion exists.

As in Experiment 1, separate 7 Eccentricity × 2 Attention condition repeated-measures ANOVAs were calculated for each of the four axes separately to further explore the Attention × Axis interaction (using Greenhouse-Geisser corrections where appropriate). Results here show a clear dissociation between the lower and upper hemifields. For the lower left and lower right axes only a main effect of Eccentricity was observed (Lower Left: F(2.1,29.38) = 7.95, p = 0.002; Lower Right: F(1.6,22.3) = 6.95, p = 0.007). No main effects of Attention, or Attention × Eccentricity interaction, was observed along either axis (p > 0.40 for all). For the two upper hemifield axes, significant main effects of Attention were observed for both axes (Upper Left: F(1,14) = 14.93, p = 0.002; Upper Right: F(1,14) = 11.05, p = 0.005) in addition to the main effect of Eccentricity (Upper Left: F(2.1,29.7) = 7.26, p = 0.002; Upper Right: F(2.5,34.8) = 3.95, p = 0.021). No Attention × Eccentricity interaction was seen for either axis (p > 0.12 for both). These additional analyses confirm that the expansion of perceived location as attention was more focused on a single axis only occurred for axes within the upper hemifield.

As before, for each participant, power functions were fit to the raw magnitude estimates for each axis and attention condition with the constraint that the exponent parameter be shared across the two attention conditions. Again, the data were well fit by this model (mean R² = 95.3%; range = 81.8-98.6). Figure 7a shows the mean slope and exponent factors as a function of axis tested. A 4 Axis × 2 Attention repeated-measures ANOVA calculated on the slope parameters showed a main effect of Axis, F(3,42) = 13.50, p < 0.001. In contrast to Experiment 1, a main effect of Attention was found, F(1,14) = 5.75, p = 0.03, as was an Attention × Axis interaction, F(3,42) = 5.49, p = 0.003. As in Experiment 1, difference scores using the Attend All condition as a baseline were calculated across the two Attention conditions for each participant along each of the four axes in order to better highlight the pattern of slope changes across participants (Figure 7b). As seen in Figure 7b, the Attention × Axis interaction reflects the increase in slope in the Attend Axis condition for both axes in the upper hemifield. As only two attention conditions were tested in this experiment, paired-samples t-tests were calculated separately on the slopes for each of the four axes. Results show greater slopes in the Attend Axis condition for the two upper hemifield locations (Upper Left: t(14) = 2.79, p = 0.015; Upper Right: t(14) = 2.72, p = 0.017), while no change in slopes was observed for the two axes in the lower hemifield (p > 0.73 for both).

Figure 7. Experiment 2: Power Function parameters.

(a) Mean estimated slope and exponent parameters as a function of axis tested and attention condition. Exponent parameters were a shared parameter across the two attention conditions in the model fitting. (b) The change in the slope parameter in the Attend Axis condition relative to the Attend All condition as a function of axis tested. Error bars represent within-subject ±1 S.E.M.

Comparisons Across Experiments – Estimated Midpoint of Visual Axes:

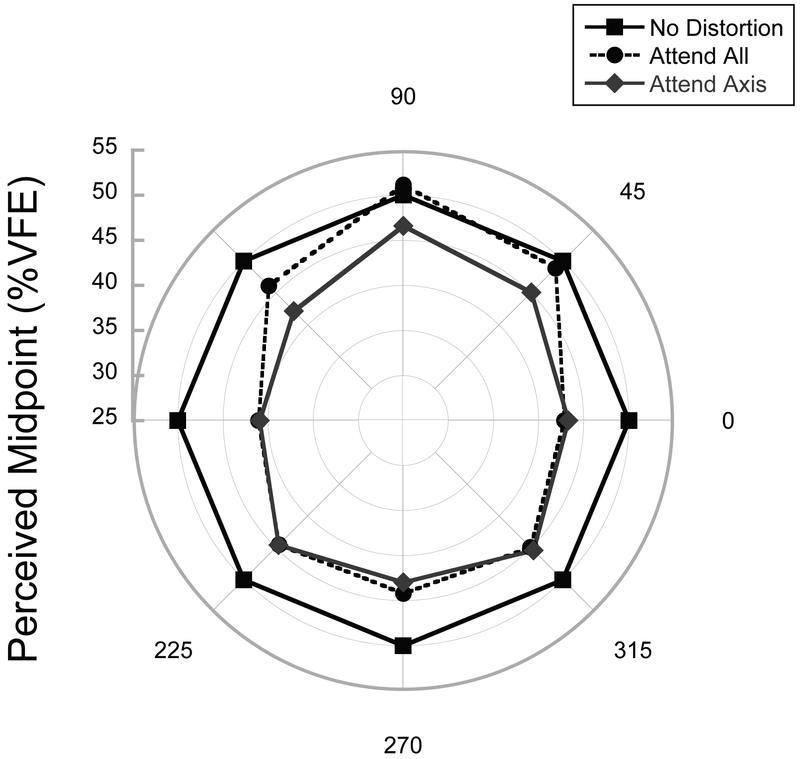
Across the two experiments attentional modulations of perceived location occurred primarily in the upper hemifield. To further illustrate this change, we calculated for each participant and axis where participants perceived the midpoint of each axis to be using the parameter fits from their raw magnitude estimates and solving for J=50, which provides the estimated midpoint in terms of %VFE. Here, values less than 50 indicate a shift of the estimated midpoint toward fixation, reflecting an expansion of visual space in the central portion of the visual axis. Figure 8 shows the %VFE corresponding to the perceived midpoint of each axis for the Attend All and Attend Axis conditions averaged over participants for the eight axes tested in Experiments 1 and 2. As seen in Figure 8, increasing foveal shifts in the estimated midpoint are observed for the three upper hemifield axes while no shift is seen along the horizontal meridian or the lower hemifield. In particular, along the horizontal meridian expansions were large and attention-independent.

Figure 8. Comparison of perceived midpoint across Experiments 1 and 2.

Estimated midpoint of each axis calculated from the individual subject power functions fit to the raw magnitude estimates for the Attend All and Attend Axis conditions. The square markers show the location of the estimated midpoint if no distortion exists. Values less than 50 correspond to a peripheral bias in the central region of the visual field, indicative of an expansion of the central visual field.

Comparisons Across Experiments – Variability in Localization Responses:

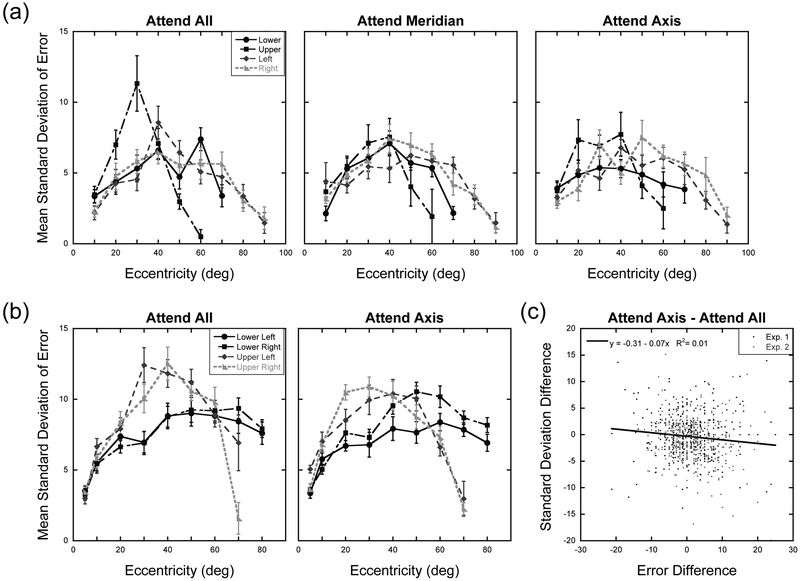
To what extent could changes in the distribution of sustained attention affect the response variability of participants and can changes in variability explain the changes in location bias? Duration thresholds for target detection have not been systematically studied across the full expanse of the visual field. However, results of at least one previous study using similar target sizes and luminance contrast, suggest that the target duration used in the present study is well above duration threshold levels within the central 60º of the visual field (Edwards & Goolkasian, 1974) which is where the shifts in perceived location across attention conditions was observed in the present experiments. However, despite the findings of Edwards and Goolkasian (1974) and the fact that trials were repeated when participants reported the target was not detected, it is possible that targets were not well detected in at least a few trials. In these cases participants would have relied on guessing the locations of the targets. If guessing played a role it is of interest to know to what extent it could explain the change in perceived position across attention conditions. Thus, for a final analysis we examined the spatial dispersion of localization errors across the conditions tested in the two experiments. Figure 9 shows the mean standard deviation of localization errors as a function of target eccentricity and axis tested for each of the attention conditions tested in Experiments 1 and 2. We assessed in a post-hoc manner whether the degree of peripheral bias observed in the localization errors could be accounted for by participants increasingly relying on “guessing” where targets were located in the Attend All condition compared to Attend Axis condition, as these attention conditions were tested in both experiments. If so a monotonic relationship between changes in localization errors and changes in the standard deviation of localization errors across the attention conditions should result. Specifically, regardless of axis or eccentricity, increasing peripheral biases in the Attend Axis condition should be accompanied by reductions in variability of localization errors. For this analysis we therefore calculated difference scores. For the localization errors, for each participant we subtracted the mean localization error in the Attend All condition from the Attend Axis condition for each eccentricity tested along each of the four axes. Thus, greater positive values indicate an increase in peripheral bias as attention is more focused on a given visual axis. Difference scores in the standard deviation of localization errors were calculated in the same manner. For Experiment 1, this provided us with 401 pairs of difference scores, while there were 483 difference score pairs for Experiment 2. Lilliefors goodness-of-fit tests showed that the distributions of scores were not normally distributed in either experiment so Spearman’s Rho correlations were calculated to assess whether monotonic trends were found. For Experiment 1, no correlation was found across the localization and standard deviation difference scores, r_s = −0.06, p = 0.21. For Experiment 2, a small but significant negative correlation was observed, r_s = −0.13, p = 0.004. Collectively, across both experiments, shifts in the response variability accounted for only 1% of the variance in localization errors (Figure 9c).

Figure 9. Standard deviations of localization responses across Experiments 1 and 2.

Mean standard deviation of localization errors in percent of visual field extent as a function of target eccentricity and axis tested for each attention condition in Experiment 1 (a) and Experiment 2 (b). Error bars represent ±1 S.E.M. (c) Scatterplot showing the relationship between differences in localization error and standard deviation of localization errors. Difference scores were calculated by subtracting the value in the Attend All condition from the Attend Axis condition. Each data point represents the value for a single participant at a given target location. Data points were concatenated across target axis, target eccentricity, and participant.

To further explore whether the changes in response variability co-varied with changes in localization bias along the axes where significant attention effects were observed, separate correlations were run for the three axes in the upper hemifield. Without correcting for multiple comparisons, results show no significant relationship between changes in localization bias and response variability for the upper vertical meridian, r_s = −0.03, p = 0.81, the upper right diagonal axis, r_s = −0.18, p = 0.06, and the upper left diagonal axis, r_s = −0.02, p = 0.83, with each analysis run on 66, 108, and 106 pairs of scores, respectively. These analyses suggest that while there may be a weak overall relationship between focusing attention, reduced response variability, and increased peripheral biases, the overall pattern of results suggests that reductions in spatial uncertainty and guessing alone cannot explain the shifts in perceived location observed in the upper hemifield across the attention conditions.

General Discussion

The present studies show that focusing sustained attention on a select axis of the visual field can lead to a perceptual expansion across that axis compared to when attention is distributed across a broader region. Additionally, this attentional distortion was limited to the upper hemifield, leading to expansive shifts in perceived position that were focused along the upper vertical meridian in Experiment 1 and the two upper oblique axes in Experiment 2. Importantly, along the horizontal meridian and the axes in the lower hemifield, participants exhibited consistent peripheral biases across all attention conditions and no shift toward a reduction in this peripheral bias was observed with attentional focus. Collectively, these results are more consistent with the expansion hypothesis, in which focusing voluntary on one region of the visual field leads to a perceived expansion of space within the attended region, and is inconsistent with greater accuracy.

Consistent with our previous findings (Fortenbaugh et al., 2012), estimates of perceived location in the distributed Attend All condition showed the least distortion along the upper vertical meridian, with the mean slope and exponent parameters close to a value of 1 and the average errors for each eccentricity close to zero. However, as seen in Figures 3, 6, and 8, focusing attention along an axis in the upper hemifield introduced more error into participants responses, expanding the perceived distance between fixation and target eccentricity, thereby effectively making participants worse at the task. As only one out of four axes were located in the upper hemifield in Experiment 1 (i.e., upper vertical meridian) while half of the axes were located in the upper hemifield in Experiment 2 (i.e., upper right and left meridians), it is likely that the greater number of upper hemifield axes lead to the significant overall main effects of Attention observed in the scaling patterns in Experiment 2 which were not found in Experiment 1. Post-hoc analyses of each axis, however, confirm significant increases in peripheral biases for target locations across the three upper hemifield axes tested, driving the Axis × Attention interactions observed in both experiments.

Why were attention effects observed only within the upper hemifield? The most likely possibility is that the intrinsic border of the brow defines the edges of the upper hemifield, and thus provides a clearer anchor point and smaller range than the other axes. In our previous study (Fortenbaugh & Robertson, 2011), a circular aperture at 30° eccentricity defined the testing region equally in all directions. It is possible that smaller regions of space and clearer borders are necessary to observe shifts in perceived location due to changes in the distribution of attention. This is supported by the baseline pattern of errors observed in the Attend All condition with the largest peripheral biases along the horizontal meridian and the least error along the upper vertical axis, the smallest visual field axis tested with a mean visual field extent of 51° across participants and a maximal value of 62° in one participant. The large horizontal meridian biases, which have now been replicated across three studies (Fortenbaugh et al., 2012; Fortenbaugh, VanVleet, Silver, & Robertson, 2015), may cause a ceiling effect, whereby any changes in perceived position due to attention are overwhelmed by the distortions that are intrinsically present when judging locations relative to visual field extent. This can be seen in Figure 8, where the baseline Attend All midpoint error along the horizontal meridian averages 8% VFE. In contrast, the average upper hemifield midpoint error goes from 1.3% to 5.4%, approaching but never reaching the baseline error along the horizontal meridian even in the Attend Axis condition. From the present data, however, it is not possible to rule out the possibility that sustained attention in unbounded conditions has a greater or differential impact for locations within the upper hemifield as upper/lower hemifield perceptual asymmetries have been reported in a variety of tasks (Fortenbaugh, Silver, et al., 2015; McCourt & Garlinghouse, 2000; Rubin, Nakayama, & Shapley, 1996).

In addition to the upper/lower hemifield asymmetry, the greatest shifts in perceived location were seen for targets presented in the central half of the visual field. As the task required participants to maintain fixation on each trial this is not surprising. Maintaining fixation is an active process, and maintaining fixation over long periods of time requires volitional control on the part of an observer. Indeed, neurophysiological evidence has shown a significant degree of overlap in the neural networks involved in covert shifts of attention versus saccadic eye-movements (Corbetta et al., 1998). To this extent, it is quite possible that the distribution of attention in the Attend Axis conditions was not constant across the entire axis but rather had a gradient, decreasing in magnitude with eccentricity. This would still alter the shape of the attentional distribution relative to the Attend All condition by altering the shape of the attentional gradient as a function of eccentricity. This hypothesis is consistent with recent models of attention on peripheral localization that have suggested voluntary attention can alter baseline activity in neural activity, increasing neural activity at attended locations and suppressing baseline firing rates at unattended locations (Bocianski et al., 2010).

Several previous studies of attention on peripheral localization have shown that focusing attention reduces spatial uncertainty in target locations compared to localization performance in divided attention conditions when dual tasks are completed at fixation (Prinzmetal et al., 1998; Tsal & Bareket, 1999, 2005). Inspection of Figure 9 shows some similarity in the present results with reductions in response variability along the upper hemifield axes in the Attend Axis condition compared to the Attend All condition. However, correlation analysis suggests that while focusing attention may well reduce spatial uncertainty in responding to where targets are located, uncertainty alone cannot explain the changes in location bias observed across the upper hemifield. It seems likely that both effects may be operating, consistent with the findings of Tsal and Bareket (1999) who found both an increased peripheral bias and precision (i.e., reduced response variability) in a computer-based localization task that manipulated attentional focus using valid and invalid visual cues that cued a given location. Importantly, however, the changes in response variability alone cannot explain the systemic shifts in perceived location that were observed in the present study.

To what extent might eye movements influence the results of the present study? The Goldmann perimeter includes a telescope that provides a magnified view of the participant’s eye. However, human observations of eye movements are not as precise as those obtained using modern eye-tracking systems. Large saccades are easily detectable in the Goldmann but to date no assessments have been made to determine what the lower bound of this range is. We therefore conducted a post-hoc test to assess the degree to which eye movements could be detected. Here, a naïve observer randomly chose across 50 trials to move their eyes to the left, right, or maintain fixation (3AFC task; chance = 33.3%), after which the experimenter reported what they saw. Two different experimenters were tested in their ability to detect 1º or 0.5º eye movements. Results show that eye movements in this range can reliably be detected (mean accuracy: 1º = 96%; 0.5º = 86%). While these results provide strong evidence that saccades can be reliably detected, eye movements of 0.5º or less, known as microsaccades, may be missed. In recent years, studies have begun to understand the neural basis of microsaccades and their impact on perception. In particular, physiological studies have shown that microsaccades have the same genesis in superior colliculus activity as larger saccades (for review see: Hafed, Chen, & Tian, 2015). Additionally, high-resolution eye tracking studies that have controlled for microsaccades show that they play an important role in perception. Specifically, the direction of these small fixational eye movements increases performance on high-resolution acuity judgments with the direction of microsaccades being systematically directed toward target locations (Poletti, Listorti, & Rucci, 2013). Other studies have shown that brief spatial distortions occur just prior to a microsaccade and can explain some previous findings in covert attention tasks (Hafed, 2013). Hafed (2013) showed that spatial distortions occur just prior to microsaccade execution producing a similar pattern to the saccadic compression seen with larger eye movements (Ross, Morrone, & Burr, 1997; Ross, Morrone, Goldberg, & Burr, 2001). Specifically, for microsaccades, a peripheral mislocalization was observed for probes up to 2.5º while a foveal mislocalization was found for more peripheral 5º eccentricity targets (Hafed, 2013). Cueing effects for a discrimination task at 5º eccentricity were also correlated with the pattern of microsaccades. When microsaccades were made in the direction of the cued side immediately before target presentation, increases in performance were observed relative to when no microsaccades were observed. These results suggest a tight coupling between eye movement preparation signals and covert shifts of attention, in line with the premotor theory of attention (Kustov & Robinson, 1996; Rizzolatti, Riggio, Dascola, & Umiltá, 1987).

Applying the results of these microsaccade studies to the present results, it is clear that microsaccade patterns alone are unlikely to explain the current findings. As noted above, in the study by Hafed (2013) targets located close to fixation were peripherally mislocalized while more peripheral targets were mislocalized in a foveal direction. If we compare the Attend All and Axis conditions in the present study, based on results from studies of microsaccades (Engbert & Kliegl, 2003; Hafed, 2013; Hafed et al., 2015; Yuval-Greenberg, Merriam, & Heeger, 2014), we would predict a greater bias to make small eye movements toward the known target axis in the Attend Axis condition relative to the Attend All condition. In Attend Axis condition we find evidence of increased peripheral biases within the central regions of the visual field along the upper hemifield but the range of eccentricities far exceeds the bias observed in studies of microsaccades. Specifically, Hafed (2013) found that by 5º eccentricity a reversal was observed with targets at this location being foveally mislocalized. Targets at 5º were the smallest eccentricity we tested in this study and we find greater peripheral biases well beyond 30º along some axes. Therefore, within the premotor framework and known distortion patterns related to saccadic and microsaccadic compression, the pattern of results would be more consistent with mislocalizations being related to saccade generation signals if the “planned” but not executed saccades were to land far out along the visual axis, close to the edge of the visual field. While traditional cueing paradigms with discrete target locations have been used to assess the relationship between microsaccades and covert shifts of attention (Engbert & Kliegl, 2003; Hafed, 2013), to our knowledge no studies to date have examined the effect of changes in attentional distribution similar to the present paradigm on the pattern of microsaccades generated by fixating observers. It therefore remains an open and interesting question for future research how microsaccade patterns may be related to changes in the distribution of attention across the visual field and how these changes might relate to changes in perception.

In conclusion, across two experiments we varied attentional demands across blocks of trials to alter the distribution of sustained attention across the visual field. In the absence of any external objects or boundaries, we assessed perceived location across a large range of eccentricities and demonstrate that purely endogenous changes in the distribution of spatial attention lead to systematic distortions, effectively expanding visual space in the attended direction.