Noninvasive Estimation of Electrical Properties from Magnetic Resonance Measurements via Global Maxwell Tomography and Match Regularization

Abstract

Objective:

In this paper, we introduce Global Maxwell Tomography (GMT), a novel, volumetric technique that estimates electric conductivity and permittivity by solving an inverse scattering problem based on magnetic resonance measurements.

Methods:

GMT relies on a fast volume integral equation solver, MARIE, for the forward path and a novel regularization method, Match Regularization, designed specifically for electrical properties estimation from noisy measurements. We performed simulations with three different tissue-mimicking numerical phantoms of different complexity, using synthetic transmit sensitivity maps with realistic noise levels as the measurements. We performed an experiment at 7T using an 8-channel coil and a uniform phantom.

Results:

We showed that GMT could estimate relative permittivity and conductivity from noisy magnetic resonance measurements with an average error as low as 0.3% and 0.2%, respectively, over the entire volume of the numerical phantom. Voxel resolution did not affect GMT performance and is currently limited only by the memory of the Graphics Processing Unit. In the experiment, GMT could estimate electrical properties within 5% of the values measured with a dielectric probe.

Conclusion:

This work demonstrated the feasibility of GMT with Match Regularization, suggesting that it could be effective for accurate in vivo electrical property estimation. GMT does not rely on any symmetry assumption for the electromagnetic field and can be generalized to estimate also the spin magnetization, at the expenses of increased computational complexity.

Significance:

GMT could provide insight into the distribution of electromagnetic fields inside the body, which represents one of the key ongoing challenges for various diagnostic and therapeutic applications.

I. Introduction

ELECTRICAL properties (EP), namely electric permittivity and conductivity, dictate the interaction between electromagnetic (EM) waves and materials [1], [2]. Accurate estimation of the EP of biological tissue could improve therapeutic applications, such as radiofrequency (RF) ablation [3], [4], tailored transcranial magnetic stimulation [5], [6], and hyperthermia treatment [7], [8], [4], among others. Magnetic resonance (MR) is a promising tool for robust EP estimation, since it can provide tomographic measurements that reflect the curvature of the EM field inside an object due to EP. Current MR–based techniques can be divided into differential and integral approaches, which can be further categorized based on whether they use direct or iterative reconstruction.

Initial work in MR–based inverse scattering focused on manipulating the differential forms of Maxwell’s Equations to reconstruct EP directly. Haacke et al. first proposed using the ratio between the curvature of the transmit field $\left(b_1^{+}\right)$, measured by its gradient, and the absolute value of $b_1^{+}$ to estimate conductivity in the one-dimensional case, using an iteration scheme to refine guesses of conductivity [9]. Katscher et al. introduced Electrical Properties Tomography (MR–EPT), a technique that extends the previous approach to three dimensions, and relies on post–processing $b_1^{+}$ maps to estimate EP [10], [11]. MR–EPT assumes that transmit and receive phases are equal (the “transceive phase assumption”) and that the z–component of the magnetic field is negligible. These conditions are fully satisfied only in the central body regions surrounded by a birdcage coil at low field strength (≤ 1.5 T) [11], [12]. Furthermore, MR–EPT’s central equation neglects gradients of EP, which is not valid at boundaries between tissues, or in electrically inhomogeneous tissues [11], [13].

More recent work has focused on addressing these simplifying assumptions of MR–EPT. Liu et al. and Zhang et al. extended MR–EPT to the case of multiple transmit coils and incorporated the effective receive fields into their algorithm [14], [15]. Huang et al. incorporated finite–element discretization in their MR–EPT implementation to improve conditioning [16], whereas Michel et al. proposed a nonlinear filter to denoise $b_1^{+}$ maps prior to MR–EPT in order to reduce reconstruction errors [17]. Wan et al., Lee at al., and Marqués et al. proposed versions of MR–EPT that use receive sensitivities $\left(b_1^{-}\right)$, which are simpler to measure and usually have higher SNR than $b_1^{+}$, to estimate EP [18], [19], [20]. Lee et al. extended these approaches by operating on the phase of the product of transmit and receive sensitivities, in the low flip–angle regime [21]. Song and Seo tried to simplify the problem by allowing EP to vary in–plane, while assuming that the EP are constant in the through–slice direction [22]. Gurler and Ider proposed a variation of the phase-based EPT technique for rapid mapping of electrical conductivity [23], which does not use the transceive assumption and accounts for EP gradients to avoid boundary artifacts [24]. Sodickson et al. proposed the first differential technique free of any assumptions, dubbed Local Maxwell Tomography, which uses both transmit and receive fields from multiple RF coils to reconstruct EP on a voxel–by– voxel basis [25]. Various multi–modal approaches have also been proposed, usually combining MR–EPT with electrical impedance tomography (EIT), which is an invasive method [26], [27], [16], [28]. While most techniques reconstruct EP directly, some recently proposed differential techniques are implemented with iterative reconstruction schemes. Ammari et al. proposed an iterative MR–EPT algorithm that does not assume dominant homogeneity of EP [29]. Borsic et al. used total–variation–like regularization along with iterative reconstructions to improve MR–EPT robustness to noise [30].

All differential approaches are inherently limited by the need to numerically approximate first– and second–order derivatives, which considerably amplifies noise present in the measurements. Furthermore, the spatial resolution of the EP maps is dictated by the size of the derivative kernel [31], which has at least three voxels in each dimension, but usually more than three in order to filter out some of the noise. On the other hand, approaches based on integral operators are much less sensitive to spurious fluctuations due to noise. Balidemaj et al. recently proposed a two–dimensional integral equation–based technique, dubbed contrast–source inversion electrical properties tomography (CSI–EPT) [32]. To deal with noise, CSI–EPT uses a multiplicative regularization scheme that seeks to adaptively set the regularization weight as the algorithm iterates. As with MR–EPT, CSI–EPT also makes use of the transceive phase assumption, which limits its applicability [32]. Schmidt and Webb recently proposed an integral equation–based technique that follows a simple iteration scheme based on the Fast Fourier Transform (FFT), but this technique is applicable only to single slices and assumes a negligible longitudinal magnetic field component b_1,z [33]. More recently, Hong et al. proposed a 3D iterative, residual– based technique that relies on volume integral equations, but it is not practical since it requires knowledge of the absolute RF phase of $b_1^{+}$, which cannot be measured directly in MR [34]. Guo et al. have proposed an iterative, integration–based method, but they use a number of simplifications, including the transceive phase assumption [35].

In this work, we present Global Maxwell Tomography (GMT), a volume–integral–equation–based method for EP estimation that is posed as an inverse problem with respect to the EP. GMT is the first truly global method for MR– based EP estimation, meaning that all EP in a volume are inferred at once, instead of in a slice–by–slice fashion as in all previous differential and integral techniques. GMT is similar to its differential counterpart, LMT [25], in the fact that it does not make any assumptions about the transceive phase. We also introduce a novel regularization strategy, dubbed “Match Regularization,” which is inspired by Total Variation and is tailored for the volumetric EP estimation problem in GMT. Preliminary simulation results of GMT have been presented at recent scientific meetings [36], [37], [38], [39]. Here, we investigate the feasibility of GMT using both simulations and experiments.

II. Theory

GMT is based on a box-constrained optimization procedure that iteratively refines guesses of EP by reducing the difference between measured and predicted quantities. The algorithm includes Match Regularization as an additive regularization term.

A. Technical Background

GMT relies on MARIE, a fast, FFT–based volume integral equation solver [40], [41], [42], to calculate the electromagnetic field. For the convenience of the reader, here we summarize the two key components of our approach and we refer to [40], [41], [43] for further details.

1). Functional Form of Volume Integral Equations:

GMT employs the second-form functional system of equations of MARIE:

$$\left(\mathcal{I}-{\mathcal{M}}_{\chi /ϵ}\mathcal{N}\right)j(\mathit{r})=c_e{\mathcal{M}}_{\chi /ϵ}{e}_i$$ (1)

The operator ${\mathcal{M}}_{\chi /ϵ}$ denotes pointwise multiplication of the Cartesian components of the volumetric currents j(r) by the ratio χ/ϵ. This is the ratio of complex relative electric susceptibility to complex relative permittivity, which is defined as $ϵ={ϵ}_{\text{R}}+\raisebox{1ex}{$\sigma $}\!\left/ \!\raisebox{-1ex}{$iw{ϵ}_0$}\right.$, where ϵ_R is the scalar relative permittivity, σ is the conductivity, $\text{i}=\sqrt{-1}$, ω is the angular frequency of the applied fields, and ϵ₀ is the permittivity of free space. The $\mathcal{N}$ operator encodes the ∇ × ∇ × operation on the Helmholtz Green’s Function integral. c_e is short-hand for iωϵ₀. The term e_i denote the incident electric field, namely the field generated by transmit sources in the absence of a scatterer.

Once the volumetric currents j(r) are calculated with the previous equation, the total electric and magnetic fields can be derived as the superposition of the incident fields and the scattered fields:

$$e_t=e_i+\frac{1}{c_{ϵ}}(\mathcal{N}-\mathcal{I})j(\mathit{r})$$ (2a)

$$h_t=h_i+\mathcal{K}j(\mathit{r})$$ (2b)

$\mathcal{K}$ is the dual integro–differential operator of $\mathcal{N}$. and encodes the ∇ × operation on the Helmholtz Green’s Function integral, while h_i is the incident magnetic field.

2). Discretized Form of Volume Integral Equations:

In GMT, the system in Eq. 1 is discretized via Galerkin projection with a piecewise linear basis. Due to the Toeplitz structure of $\mathcal{N}$ and $\mathcal{K}$, these can be embedded in three-dimensional circulant operators, so that the matrix–vector product is then achieved via FFT, dramatically reducing computational cost [40]. The piecewise linear basis is given by four basis functions for each current component at each voxel [43]:

$$f_n^1(\mathit{r})=P_n(\mathit{r})$$ (3a)

$$f_n^2(\mathit{r})=P_n(\mathit{r})\left(x-x_n\right)/{\text{Δ}}_x$$ (3b)

$$f_n^3(\mathit{r})=P_n(\mathit{r})\left(y-y_n\right)/{\text{Δ}}_y$$ (3c)

$$f_n^4(\mathit{r})=P_n(\mathit{r})\left(z-z_n\right)/{\text{Δ}}_z$$ (3d)

where r_n = (x_n, y_n, z_n) is the center of each voxel, Δ_x, Δ_y, Δ_z are the voxel spacing along each dimension and P_n(r) is a volumetric pulse that is equal to 1 inside voxel n and 0 otherwise. The resulting discretized linear system of equations to calculate the discretized currents j is

$$\left(\text{Δ}-M_{\mathit{\chi }/\mathit{ϵ}}N\right)\mathit{j}=c_e{M}_{\mathit{\chi }/\mathit{ϵ}}\text{Δ}{e}_i.$$ (4)

From j, e_i and h_i we obtain the total fields via Eqs. 2a and 2b. The discretized currents j, as well as the fields e_i and h_i are elements of ${ℂ}^{12N_s}$, where N_s is the number of voxels in the domain of the scatterer. These fields are vectorized from dimensions N_s × 3 × 4 to dimensions 12N_s ×1. The term Δ is a diagonal matrix, whose elements are equal to Δ_x·Δ_y·Δ_z for constant pulses (Eq. 3a) and Δ_x·Δ_y·Δ_z /12 for sloped pulses (Eqs. 3b, 3c, 3d).

B. Inverse Problem

The recovery of the unknown electrical properties is formulated as an optimization problem with regularization [44]. The following subsections detail our approach.

1). Optimization Algorithm:

A cost function that measures the degree of mismatch between measured and predicted quantities is minimized to estimate the underlying EP distribution. The cost function, f(ϵ), includes a regularization term, f_r(ϵ) weighted by a constant parameter α, that is proportional to EP inhomogeneity (see subsection below about Match Regularization). Box constraints on the real and imaginary parts of complex relative permittivity are applied to ensure realistic EP, namely ϵ_R ≥ 1 and σ ≥ 0.

$$\begin{gathered} \underset{\mathit{ϵ}\in {ℂ}^{N_s}}{\text{minimize\hspace{1em}}}f(\mathit{ϵ})+\alpha f_r(\mathit{ϵ}) \\ \text{s.t.\hspace{1em}}\text{Re}\left\{\mathit{ϵ}\right\}={\mathit{ϵ}}_{\text{R}}\ge 1 \\ \text{Im}\left\{\mathit{ϵ}\right\}=-\frac{\mathit{\sigma }}{\omega {\mathit{ϵ}}_0}\le 0 \end{gathered}$$ (5)

The co-gradients of the cost functions f(ϵ) and f_r(ϵ) with respect to the complex relative permittivity are provided in Appendix A. While other choices are possible without changing the GMT algorithm, in this work the cost function uses only $b_1^{+}$, which describes the transmit sensitivity of an MRI coil, because it can be measured experimentally and it is independent from the spin magnetization. In particular, the cost function operates on the weighted L₂ norm of the residual between measured and predicted $b_1^{+}$ maps. We choose to use the L₂ norm because its smoothness is amenable to our particular optimization algorithm (L–BFGS–B, see Methods).

$$f(\mathit{ϵ})=\frac{\sqrt{{\sum }_k{\sum }_n{\Vert {\mathit{w}}_k\odot {\mathit{w}}_n\odot {\mathit{\delta }}_{kn}\Vert }_2^2}}{\eta },$$ (6a)

Where

$${\mathit{\delta }}_{kn}={\widehat{\mathit{b}}}_k^{+}\odot \overline{{\widehat{\mathit{b}}}_n^{+}}-{\mathit{b}}_k^{+}\odot \overline{{\mathit{b}}_n^{+}}$$ (6b)

$$\eta =\sqrt{\sum _k\sum _n{\Vert {\mathit{w}}_k\odot {\mathit{w}}_n\odot {\widehat{\mathit{b}}}_k^{+}\odot {\widehat{\mathit{b}}}_n^{+}\Vert }_2^2}$$ (6c)

And

$${\widehat{\mathit{b}}}_k^{+}\odot \overline{{\widehat{\mathit{b}}}_n^{+}}\equiv |{\widehat{\mathit{b}}}_k^{+}|\odot |{\widehat{\mathit{b}}}_n^{+}|\odot e^{j\left({\widehat{\varphi }}_k^{+}-{\widehat{\varphi }}_n^{+}\right)}.$$ (6d)

The symbol ☉ denotes the Hadamard product. The two summations over n and k iterate over all of the unique field maps of a multiple–channel transmit array. $b_k^{+}$ and ${\widehat{b}}_k^{+}$ refer to the k^th estimated and measured $b_1^{+}$ maps, respectively. The exponential term in Eq. 6d denotes the relative phase factor between maps k and n. Note, in fact, that the absolute phase of the transmit fields cannot be measured with standard MRI experiments [25]. w_k refers to a set of weights pertaining to map k, which, depending on the specific numerical experiment, were set either to the ratio of $|b_k^{+}|$ to its peak amplitude or to the square root of such ratio (see Results section). We introduced these weights to prioritize regions with higher SNR when estimating EP.

2). Forward Path:

The forward problem involves calculating quantities that can be compared with measurements obtained in the MR setting. The first step consists of solving for equivalent volumetric distributions of currents induced by given incident fields within the scatterer (Eq. 2b), which allow us to calculate the total magnetic field (h_t). Then $b_1^{+}$ maps, which are equivalent to the right-hand circularly polarized component of the magnetic flux densities in the imaging sample (i.e., the scatterer), can be calculated as:

$${\mathit{b}}^{+}=F{\mu }_0{\mathit{h}}_t=F{\mu }_0\left({\mathit{h}}_i+K\mathit{j}\right).$$ (7)

The operator F carries out the extraction of the piecewise constant right-handed circularly polarized component. The operator K is the discretization of the operator in 2b. Given the discretized total magnetic field h_t, the operator F is defined as

$$F\equiv \left[\begin{array}{lll}1\hfill & \text{i}\hfill & 0\hfill \end{array}\right]\otimes \left[\begin{array}{llll}1\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right]\otimes I_{N_s},$$ (8)

where $I_{N_s}$ denotes the identity matrix of dimensions N_s × N_s and ⊗ denotes the Kronecker product. Note that the z– component of the total magnetic field is lost when $b_1^{+}$ is extracted. In fact, MR coils have very limited sensitivity to detect the z–component of the RF field, because it is oriented in the same direction of the much stronger static magnetic field.

3). Match Regularization:

Regularization is essential to address additive physical noise in the measurements and ill– conditioning in the optimization. Our proposed Match Regularization algorithm acts on the finite–difference approximation of EP along each Cartesian axis | Δ_τϵ| for every voxel:

$$f_{\text{M}}\left({\text{Δ}}_{\tau }ϵ\right)=f_{\text{S}}\circ f_{\text{TV}}\left({\text{Δ}}_{\tau }ϵ\right)=1-e^{\beta \left(c-\sqrt{c^2+{\left|{\text{Δ}}_{\tau }ϵ\right|}^2}\right)}$$ (9)

where τ = x, y, z. The symbol denotes the composition of the following two nonlinear operations on the magnitude of the difference in complex relative permittivity at each voxel:

$$y=f_{\text{TV}}(x)=\sqrt{c^2+|x{|}^2}-c$$ (10a)

$$f_{\text{S}}(y)=1-e^{-\beta y}$$ (10b)

The first function is a continuous relaxation of L₁–based total variation. The second function is a saturation function that causes the output to be bounded between 0 and 1. This saturation is a critical part of Match Regularization because for large jumps in EP, the saturation causes the differential dependence of the regularizer on the magnitude of the jump in EP to vanish. In other words, the regularizer leaves large transitions in EP unperturbed. This behavior is essential for GMT because the unregularized problem is ill-conditioned, which in the case of typical regularizers, results in small gradients of f(ϵ) (see Eq. 5) in the vicinity of large jumps in EP being dominated by gradients that do not decay to 0. The quantities c and β in Eqs. 9 and 10 are judiciously chosen constants. In particular, β can be used to specify the desired sensitivity to changes in EP, by defining

$$\beta =\frac{c^2}{|\Delta \mathit{ϵ}{|}_{\text{min}}^2\sqrt{c^2+|\Delta \mathit{ϵ}{|}_{\text{min}}^2}}.$$ (11)

In this expression, |Δϵ|_min is the smallest jump in EP along any direction that one expects to be resolved by GMT and Eq. 11 guarantees that the derivative $\frac{\text{d}{f}_{\text{M}}}{\text{d}x}$ attains a maximum for such value.

The behavior of the nonlinear transformation in Eq. 9 can be characterized according to the magnitude of the jump |Δ_τϵ|. For small inputs y, f_S(y) ≈ βy/2. Therefore, for sufficiently small jumps in material properties along direction τ, $f_{\text{M}}\left(\left|{\text{Δ}}_{\tau }ϵ\right|\right)\approx \frac{\beta }{2}{f}_{\text{TV}}\left(\left|{\text{Δ}}_{\tau }ϵ\right|\right).$. When |Δ_τϵ|<c, $f_{\text{TV}}\left(\left|{\text{Δ}}_{\tau }ϵ\right|\right)\approx \frac{{\left|{\text{Δ}}_{\tau }ϵ\right|}^2}{2c}$, which resembles L₂–based Tikhonov regularization. When |Δ_τϵ| > c and βf_TV (Δ_τϵ) ≪ 1, f_TV (|Δ_τϵ|) ≈ |Δ_τϵ| which resembles L₁–based TV regularization. Finally, when βf_TV (Δ_τϵ) ≪ 1 no longer holds, the saturation function starts to contribute, saturating at a value of 1 and causing the differential dependence of f_M to decay exponentially. The overall result is a nonlinear transformation that for very small arguments maps to L₂–based regularization, then, as the arguments increase, to L₁–based regularization, and finally, for large arguments, to what can be considered to be a relaxation of L₀–based regularization. For the purposes of GMT, L₂– based regularization tends to minimize the overall presence of jumps, L₁–based regularization tends to enforce sparsity in the jumps of EP, and L₀–based regularization would amount to an even more extreme version of L₁–based regularization, again enforcing sparsity in jumps in EP.

Finally, the regularization cost function, f_r(ϵ) in Eq. 5 is given by

$$f_r(\mathit{ϵ})=\frac{1}{3N_s^{\frac{2}{3}}}\sum _{\mathit{n}\in \mathit{S}}\sum _{\tau \in \{x,y,z\}}{f}_{\text{M}}\left(\left|{\text{Δ}}_{\tau }{ϵ}_n\right|\right),$$ (12)

where S denotes the set of indices of the voxels of the scatterer. This cost function is simply an average over all voxels after the nonlinear transformation in Eq. 9 is applied to each voxel and along each axis. The normalization constant $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\left(3N_s^{2/3}\right)$}\right.$ is not simply $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$(3N_s)$}\right.$ because, for a voxelized geometry, the number of jumps in EP scales as $N_s^{\frac{2}{3}}$. This normalization strategy reduces the dependence on the underlying resolution when applying regularization, which is another feature of GMT.

III. Methods

A. Numerical Phantoms

1). Four–Compartment Phantom:

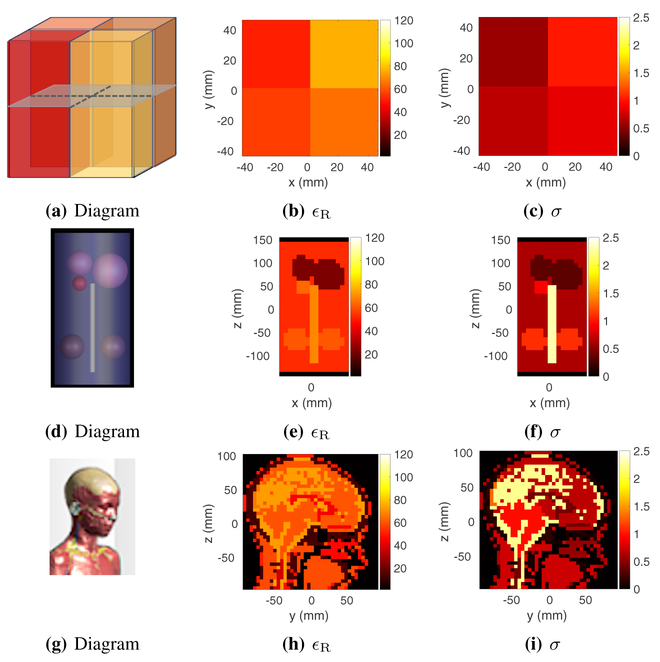
We used a numerical phantom shaped as a 10 cm × 10 cm × 10 cm rectangular parallelepiped. The unique tissue-like relative permittivities and corresponding conductivity values of the four compartments were 51, 56, 65 and 76, and $0.56\raisebox{1ex}{$\text{S}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{m}$}\right.$, $0.69\raisebox{1ex}{$\text{S}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{m}$}\right.$, $0.84\raisebox{1ex}{$\text{S}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{m}$}\right.$ and $1.02\raisebox{1ex}{$\text{S}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{m}$}\right.$, respectively. Figs. 1b and 1c show the ground truth material property distributions of the Four-Compartment Phantom. This phantom was used to test GMT at 6 mm and 3 mm isotropic resolutions to evaluate the dependence of GMT on voxel size.

Fig. 1:

Numerical phantoms and corresponding ground truth of relative permittivity (ϵ_R) and conductivity (σ). (a-c) Tissue–Mimicking Four–Compartment Phantom (transverse slice); (d-f) Torso–Mimicking Phantom (coronal slice); (g-i) Human–Head Phantom (sagittal slice).

2). Torso–Mimicking Phantom:

We also used a torso– mimicking phantom, characterized by sharp contrast and a high degree of asymmetry in the EP.

This phantom, which was previously proposed to evaluate EP mapping techniques [25], had five compartments mimicking the electrical properties of lungs, torso, kidneys, heart and spine (Fig. 1d). The associated relative permittivity and conductivity values were 22.62, 52.64, 60.95, 63.46, and 69.22; and $0.337\raisebox{1ex}{$\text{S}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{m}$}\right.$, $\text{0.6314}\raisebox{1ex}{$\text{S}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{m}$}\right.$, $\text{1.0975}\raisebox{1ex}{$\text{S}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{m}$}\right.$, $\text{0.92}\raisebox{1ex}{$\text{S}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{m}$}\right.$, and $\text{2.3}\raisebox{1ex}{$\text{S}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{m}$}\right.$; respectively. Figs. 1e and 1f depict the ground truth EP distribution of the Torso–Mimicking Phantom, which was used with an isotropic resolution of 10 mm.

3). Human–Head Phantom:

We evaluated our technique for the case of a realistic human head model. In particular, we used Billie from the Virtual Family [45], with an isotropic resolution of 5 mm. More specifically, we cropped the head from the rest of the body. The ground truth EP at 300 MHz are shown in Figs. 1h and 1i.

B. Simulations

1). Incident Field Distributions:

The performance of GMT, as that of any EP mapping technique, depends on the number of independent measurements available to solve for the unknown quantities at each voxel. For this reason, the particular transmit array design and linear combination of the associated fields (e.g., RF shims) used for the excitation can affect the accuracy of the reconstructed EP maps. In order to investigate the performance of GMT and Match Regularization independently from transmit array design and excitation strategy, we used basis functions instead of actual coils. Specifically, we generated a basis set of orthogonal Maxwell’s Equations-compliant incident fields from equivalent volumetric sources, adapting an approach previously proposed to calculate the ultimate intrinsic signal-to-noise (SNR) inside an heterogeneous head model [46], [47], and chose the first eight principal components of the basis sets as transmit elements of an hypothetical array. This truncation was motivated by the fact that 7 Tesla MR systems can typically support eight independent transmit channels. We used the transmit fields without applying any RF shimming combinations. The generation of basis fields is summarized in Appendix B.

2). Synthetic Noise Generation:

It is challenging to characterize the SNR of a $b_1^{+}$ map. One possible choice is to use the mean SNR over the entire volume; however, when a map is highly localized, the mean SNR can deviate significantly from the SNR present in excited regions of tissue. Therefore, we opted to characterize SNR by its peak value. In particular, we added noise to all of the uncorrupted $b_1^{+}$ maps by setting the standard deviation of the noise to the ratio of the peak value of $b_1^{+}$ to the prescribed peak SNR (Fig. 2). This process was separately repeated for every $b_1^{+}$ map in consideration.

Fig. 2:

Comparison of $b_1^{+}$ maps before (a, c, e) and after (b, d, f) corruption with additive Gaussian noise. $b_{1,k}^{+}$ and η_k refer to the k^th uncorrupted $b_1^{+}$ map and associated noise map, respectively. The peak SNR of the noisy $b_1^{+}$ maps was set to 50.

C. Experiment

1). Data Acquisition:

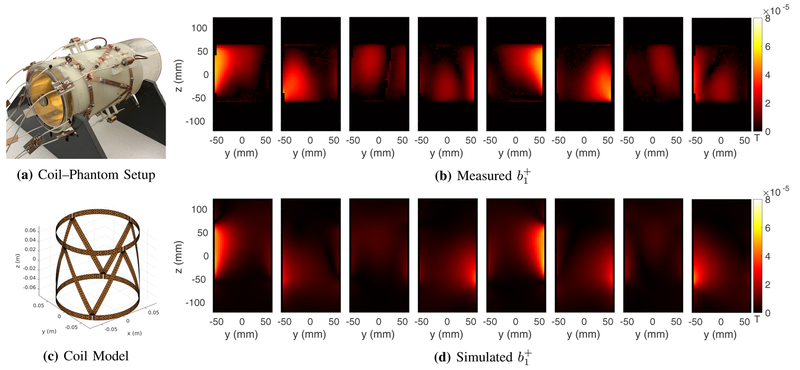
Experimental measurements were performed on a 7 T MR scanner (Magnetom, Siemens Healthineers, Erlangen, Germany), equipped with 8 transmit channels and 32 receive channels. We constructed a mono–compartment cylindrical phantom (diameter of 12 cm, length of 24 cm), and filled it with a solution of distilled water, sodium chloride and Polyvinylpyrrolidone [48]. We used a dielectric probe (Agilent, Santa Clara, CA) to measure the relative permittivity and electrical conductivity of the solution, which were 64 and $0.65\raisebox{1ex}{$\text{S}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{m}$}\right.$, respectively. We matched and tuned (297.2 MHz, the operating frequency of the 7 T scanner) an 8–element transmit/receive RF coil array prototype [49] in the presence of the constructed phantom. We used a 3D version of a previously proposed MR Fingerprinting technique [50] to reconstruct $b_1^{+}$ maps for each of the 8 transmit channels (Fig. 7) for a 64–slice transverse slab at the center of the cylindrical phantom (256 × 256 matrix size, 1.0 × 1.0 × 2.0 mm³ voxel resolution, TE/TR = 3.3/7.5 ms, $\text{BW}=600\raisebox{1ex}{$\text{Hz}$}\!\left/ \!\raisebox{-1ex}{$\text{pxl}$}\right.$.

Fig. 7:

Experimental coil-phantom setup (a) and measured $b_1^{+}$ magnitude of each transmit coil for the central coronal plane (b) are compared to the $b_1^{+}$ maps simulated with the coil model (d) using a numerical phantom with the same electrical properties and dimensions of the actual phantom. Due to the complexity of the transmit array, the incident fields could not be accurately modeled; therefore measured and simulated maps were not identical.

2). Radiofrequency Coil Modeling:

We constructed a model of the array using GMSH [51] with 2912 triangular mesh elements. Each coil in the array had three fixed (4–8 pF) and three variable capacitors for capacitive decoupling of 1st order neighbors, while 2nd order neighbors were decoupled through a pair of perfectly counter wound inductors (22 nH). Each port was matched to 50 Ω by a capacitor connected in parallel to the port.

The electromagnetic scattering phenomena of the coil were simulated with the surface electric field integral equation expanded with RWG basis functions [52], while the lumped elements and the feed ports were simulated with the delta-gap method [53]. In order to account for the effect of currents scattered from the object to the coil conductors, we performed a coupling simulation [41] based on a volume-surface IE solver.

Tuning and matching of the array were performed as follow, using a numerical phantom with the same electrical properties (based on the dielectric probe measurements) and dimensions of the actual phantom. First, we removed the tuning capacitors and treat them as feeding-ports. Second, we performed 24 coupling simulations, by considering 1 V at each feeding-port, while the other ports were short-circuited. This resulted in a 24 × 24 S parameter matrix, which was reduced to an 8 × 8 matrix, through an optimization procedure that consisted in testing different values for the tuning capacitors until each entry of the matrix was smaller than −17 dB. Third, the capacitors, with the optimized values, were re-inserted on the coil and 8 additional coupling simulations were performed to retrieve the surface equivalent currents j_coil,p on the coil, generated by each port p = 1, …, 8 independently. Finally, the incident electromagnetic fields in the absence of the scatterer were calculated as [54]

$$e_{i,\text{p}}=\mathcal{N}{j}_{coil,\text{p}}(\mathit{r})$$ (13a)

$$h_{i,\text{p}}=\mathcal{K}{j}_{coil,\text{p}}(\mathit{r}),$$ (13b)

where the operators $\mathcal{N}$ and $\mathcal{K}$ were defined in Eqs. 2a and 2b.

3). Transmit Voltage Calibration:

Due to uncertainty in the coil model, the scattering parameters obtained in simulation during tuning and matching were not accurate. Since the incident fields depends on both the prescribed transmit voltage and the scattered voltage, we performed an optimization to infer the total voltages at each coil. More precisely, we minimized the same cost function of GMT over a set of complex-valued weights (ξ), or RF shims, needed to accurately drive each coil:

$$\begin{gathered} \underset{{}_{\mathit{\xi }\in {ℂ}^{N_c\times N_{\text{tx}}}}}{\mathrm{minimize}}f(\xi ) \\ \text{ s.t. }\text{Re}\left\{\left({\xi }_{1,1}\right)\right\}\ge 0 \\ \text{Im}\left\{\left({\xi }_{1,1}\right)\right\}=0, \end{gathered}$$ (14)

where

$$f(\mathit{\xi })=\frac{\sqrt{{\sum }_k{\sum }_n{\Vert {\mathit{w}}_k\odot {\mathit{w}}_n\odot {\mathit{\delta }}_{kn}(\mathit{\xi })\Vert }_2^2}}{\eta },$$ (15)

And

$${\mathit{\delta }}_{kn}={\widehat{\mathit{b}}}_k^{+}\odot \overline{{\widehat{\mathit{b}}}_n^{+}}-\left(B_k^{+}{\xi }_k\right)\odot \overline{\left(B_n^{+}{\mathit{\xi }}_n\right)}.$$ (16)

N_c refers to the number of coils and N_tx is the number of transmit maps (8 in our case). The cost function minimizes the difference between the measured ${\widehat{\mathit{b}}}^{+}$ maps and the shimmed B⁺ maps, generated by driving each coil with 1 V, while setting the others to 0 V and using the same numerical phantom employed for tuning and matching. Since absolute transmit phases are not measurable in MR, we constrained the phase of the first coil to be zero and compute all other coil phases relative to it (Eq. 14).

D. Optimizer

Due to the sheer size of the inverse scattering problem (hundreds of thousands of unknowns at 3 mm isotropic resolution), the Hessian of the GMT cost function cannot be computed efficiently. As such, we rely on quasi–Newton algorithms that form approximations of the Hessian. Specifically, we used L– BFGS–B, or limited-memory BFGS with box constraints [55]. The box constraints are an essential part of the algorithm, as a lower limit on the real part of permittivity of 1 and a lower bound on conductivity of 0 guarantee physically compliant EP. No upper bounds on EP were imposed.

IV. Results

A. Four–Compartment Phantom

For the 6 mm resolution phantom, we set the peak SNR to 50 and ${\mathit{w}}_k=\raisebox{1ex}{$|{\mathit{b}}_k^{+}|$}\!\left/ \!\raisebox{-1ex}{${\Vert {\mathit{b}}_k^{+}\Vert }_{\infty }$}\right.$ for the cost function. As a result, the associated mean SNRs of the eight volumetric $b_1^{+}$ maps were approximately 19.1, 26.2, 22.4, 24.9, 15.1, 14.6, 21.7 and 28.6.

We selected the regularization parameters heuristically, setting c = 0.5 and |Δϵ|_min = 1.5 in Eqs 9 and 11, and α = 10⁻² in Eq. 5.

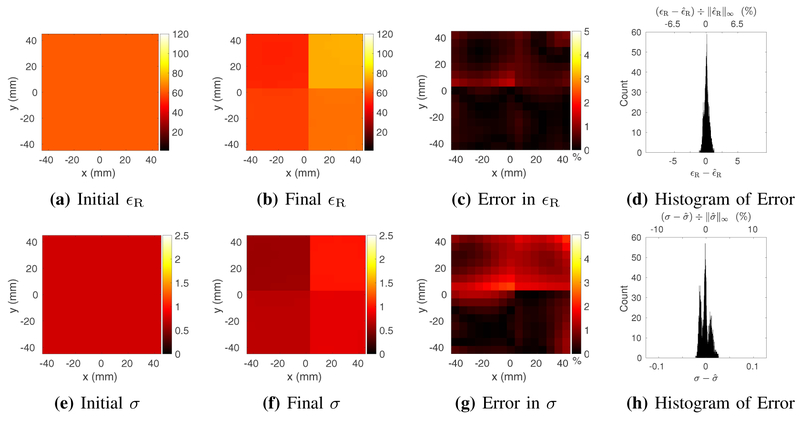
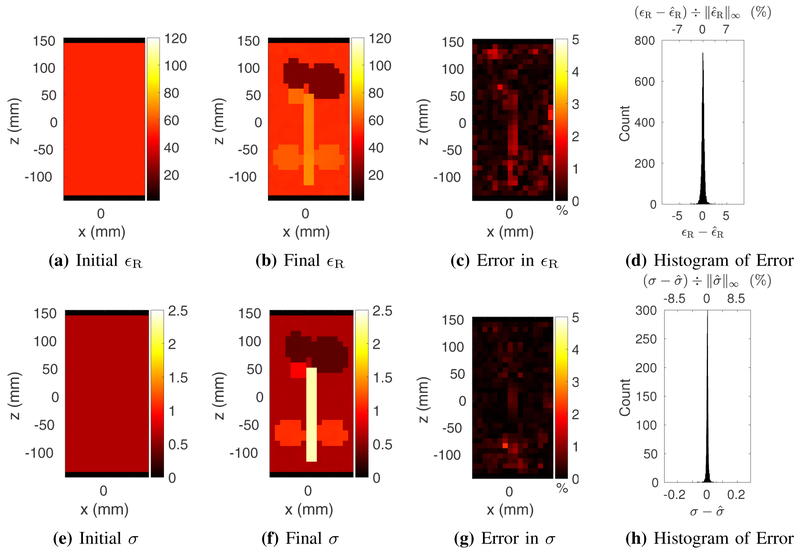
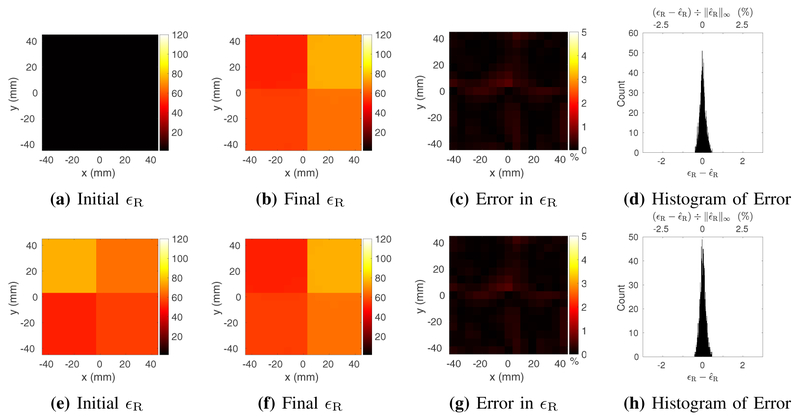
Starting from a homogeneous initial guess of EP, after 148 iterations of GMT, the peak relative errors in permittivity and conductivity were approximately 1.64% and 2.55%, respectively, while the corresponding average errors over 3,375 voxels were 0.38% and 0.77%, respectively (Fig. 3).

Fig. 3:

Estimated relative electric permittivity (top) and conductivity (bottom) for the four–compartment phantom at 6 mm isotropic resolution, reconstructed from a homogeneous initial guess (a and e) and using $b_1^{+}$ measurements with peak SNR of 50. Reconstructed EP are shown for a representative transverse slice through the center of the phantom, at the end of the GMT procedure (b and f). Figs. c and g show the peak-normalized absolute error, along the same transverse slice. Figs. d and h show the distribution of the error in the final EP over all 3,375 voxels.

For the same phantom at 3 mm resolution, we again set the peak SNR to 50 and ${\mathit{w}}_k=\raisebox{1ex}{$|{\mathit{b}}_k^{+}|$}\!\left/ \!\raisebox{-1ex}{${\Vert {\mathit{b}}_k^{+}\Vert }_{\infty }$}\right.$, to maintain consistency with the 6 mm case. The associated mean SNRs over the volume of the eight maps were approximately 17.9, 25.4, 17.2, 24.3, 13.6, 15.4, 20.5, and 29.1. We did not need to change the regularization parameters because, as explained in the Theory section, our Match Regularization approach is roughly independent of resolution.

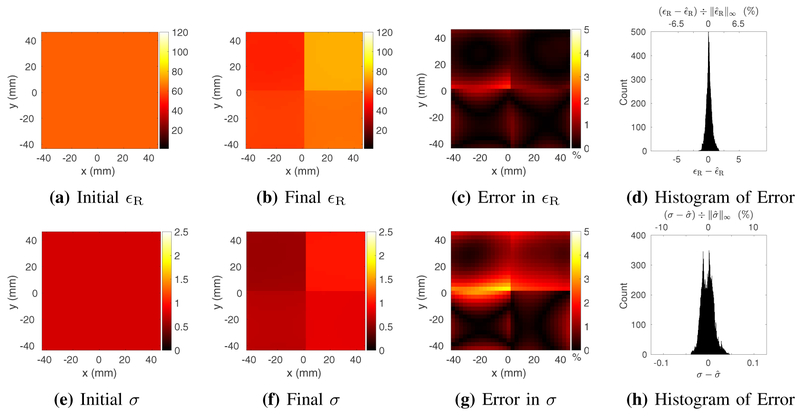
After 257 iterations, starting again from a worst–case homogeneous guess, the peak relative errors for permittivity and conductivity were 2.26% and 4.54%, respectively, whereas the corresponding average errors over 27,900 voxels were 0.44% and 1.06%, respectively (Fig. 4).

Fig. 4:

Estimated relative electric permittivity (top) and conductivity (bottom) for the four–compartment phantom at 3 mm isotropic resolution, reconstructed from a homogeneous initial guess (a and e) and using $b_1^{+}$ measurements with peak SNR of 50. Reconstructed EP are shown for a representative transverse slice through the center of the phantom, at the end of the GMT procedure (b and f). Figs. c and g show the peak-normalized absolute error, along the same transverse slice. Figs. d and h show the distribution of the error in the final EP over all 27,900 voxels.

B. Torso–Mimicking Phantom

For the torso–mimicking phantom, at an isotropic resolution of 10 mm, we set the peak SNR to 200. The associated mean SNRs of the eight maps were approximately 45.6, 84.0, 89.9, 85.5, 68.7, 79.5, 76.7, and 67.8. We found it beneficial to set ${\mathit{w}}_k=\sqrt{\raisebox{1ex}{$|{\mathit{b}}_k^{+}|$}\!\left/ \!\raisebox{-1ex}{${\Vert {\mathit{b}}_k^{+}\Vert }_{\infty }$}\right.}$. We did not exhaustively search for new regularization parameters in this case, instead opting to recycle the values for c and |Δϵ|_min and setting α to 6 10⁻⁴.

Fig. 5 show the GMT results for the torso-mimicking phantom. After 500 GMT iterations, starting from a homogeneous initial guess, the peak relative errors in permittivity and conductivity were 20.6% and 2.89%, respectively, although the average errors over 5,730 voxels were 0.32% and 0.16%, respectively.

Fig. 5:

Estimated relative electric permittivity (top) and conductivity (bottom) for the tissue–mimicking phantom at 10 mm isotropic resolution, reconstructed from a homogeneous initial guess (a) and using $b_1^{+}$ measurements with peak SNR of 200. Reconstructed EP are shown for a representative coronal slice through the center of the phantom, at the end of the GMT procedure (b and f). Figs. c and g show the peak-normalized absolute error, along the same coronal slice. Figs. (d) and (h) show the distribution of the error in the final EP over all 5,730 voxels.

C. Human–Head Phantom

For the human–head phantom, at an isotropic resolution of 5 mm, we set the peak SNR to 200. The associated mean SNRs of the eight maps were approximately 71.8, 90.3, 85.0, 78.2, 85.1, 64.7, 82.0 and 88.9. We set ${\mathit{w}}_k=\sqrt{\raisebox{1ex}{$|{\mathit{b}}_k^{+}|$}\!\left/ \!\raisebox{-1ex}{${\Vert {\mathit{b}}_k^{+}\Vert }_{\infty }$}\right.}$. We used the same c and |Δϵ|_min as for the torso–mimicking phantom, but we set α to 2 10⁻⁴.

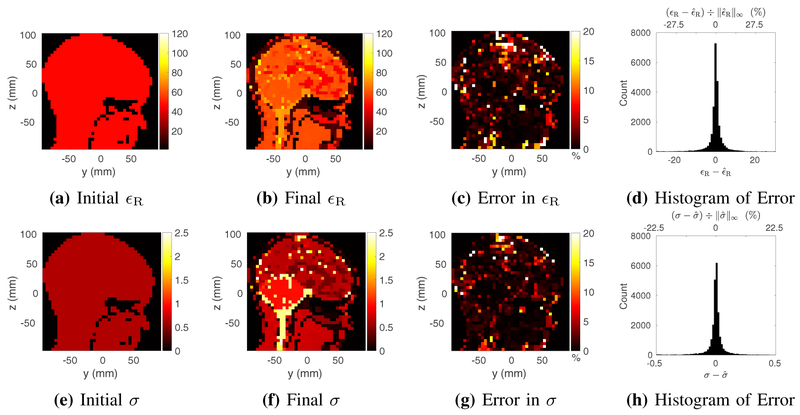
The results for the human–head phantom are shown in Fig. 6. After 1000 GMT iterations, starting from a homogeneous initial guess, the average errors in permittivity and conductivity over 24,144 voxels were 3.82% and 2.33%, respectively. The corresponding peak errors of 262% and 99% were outliers.

Fig. 6:

Estimated relative electric permittivity (top) and conductivity (bottom) for the Billie head phantom at 5 mm isotropic resolution, reconstructed from a homogeneous initial guess (a and e) and using $b_1^{+}$ measurements with peak SNR of 200. Reconstructed EP are shown for a representative sagittal slice through the center of the phantom, at the end of the GMT procedure (b and f). Figs. c and g show the peak-normalized absolute error, along the same sagittal slice. Figs. d and h show the distribution of the error in the final EP over all 24,144 voxels.

D. Experiment

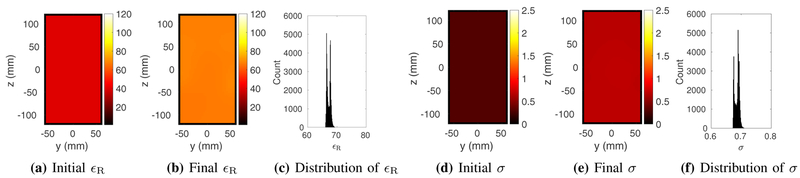
The experimental $b_1^{+}$ maps (Fig. 7) were downsampled to a 4.0 mm³ isotropic voxel resolution, due to computation time and memory limitations of the Graphics Processing Unit (GPU). We set ${\mathit{w}}_k=|{\mathit{b}}_k^{+}|\odot (r<R)\odot (|{\mathit{b}}_k^{+}|\ge \frac{{\Vert {\mathit{b}}_k^{+}\Vert }_{\infty }}{10}),$, where R represents the inner radius of the phantom (i.e., we removed voxels belonging to the plastic shell) and the normalization by 10 was heuristically chosen to avoid numerical zeros in the optimization. While $b_1^{+}$ maps were acquired only for central slab half the size of the phantom, the optimization was performed over the entire volume of the phantom, which coincided with the field of view of the array. After few trial and error iterations, we set c = 1.0, |Δϵ|_min = 3.0 and α to 4 10⁻¹. Fig. 8 summarizes the experimental results. After 421 iterations, starting from a homogeneous initial guess (ϵ_R = 40, and $\sigma =0.30\raisebox{1ex}{$\text{S}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{m}$}\right.$), the reconstructed relative permittivity and conductivity for the cylindrical phantom were 67.2 ± 0.6 and $\text{0.686}\pm \text{0.007}\raisebox{1ex}{$\text{S}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{m}$}\right.$, respectively. These values are within 5% deviation from the EP measured invasively with the dielectric probe.

Fig. 8:

Estimated relative electric permittivity (top) and conductivity (bottom), reconstructed from a homogeneous initial guess (a and d), using experimental $b_1^{+}$ measurements (see Fig. 7). Reconstructed EP are shown for a representative coronal slice through the center of a uniform cylindrical phantom, at the end of the GMT optimization (b and e). The final distribution of EP over 44,713 voxels is shown in c and f. Voxels belonging to the plastic shell surrounding the phantom were treated as vacuum.

V. Discussion

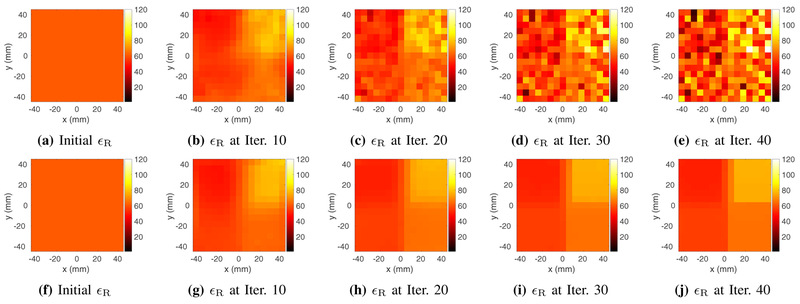
We demonstrated through three numerical experiments that GMT with Match Regularization can estimate EP with negligible errors. Using dielectric probe measurements as the gold standard, we showed that GMT could estimate EP in a phantom at 7 T with high precision and accuracy. Although a quantitative comparison with previous work is not possible, due to different numerical phantoms and SNR definitions, to our knowledge, there is no other technique capable of delivering similar results from noisy MR measurements. GMT infers conductivity and permittivity for the entire object volume at once, without making any assumptions on the distribution of either the EM field or the electrical properties. The only other assumption–free EP mapping technique, LMT [25], showed comparable experimental results on a single slice for a uniform phantom, but proved to be impractical in the presence of noise and EP boundaries, as all differential techniques intrinsically are to various extents. Integral approaches based on iterative algorithms can address noise via regularization. For example, CSI–EPT [32] uses a multiplicative regularizer to improve conditioning in the presence of noisy measurements, but that comes at the expense of blurring near regions of high contrast. In fact, all regularization strategies proposed until now for EP estimation have resulted in blurring or corruption of the reconstructed EP maps. Our proposed Match Regularization is ideally suited for piecewise homogeneous data, because it tends to enforce sparsity in the number of edges without corrupting the gradient of the cost function in the presence of large jumps in EP. Fig. 9 confirms that, without Match Regularization, after few iterations GMT would start to fit the noise and then rapidly converge to a noise map. While our results demonstrate the effectiveness of Match Regularization for GMT, the same regularization approach could be adapted in a straightforward manner to other EP mapping techniques and inverse problems, for which it is known a priori that the solution consists of piecewise constant blocks. On the other hand, Match Regularization would not be effective for applications such as image smoothing, because images are typically not piecewise constant but exhibit smooth gradients in their intensity.

Fig. 9:

Evolution of the estimated relative permittivity starting from the same homogeneous initial guess (a and f) using the unregularized cost function (b-e) vs. Match Regularization (g-j), for the four–compartment phantom at 6 mm isotropic resolution using peak SNR of 50 for the synthetic $b_1^{+}$ measurements. Without regularization, GMT starts fitting the noise after a few iterations and converges to a noisy map after 40 iterations. With Match Regularization the solution converges toward the correct values. Final results after 148 iterations are shown in Fig. 3b.

Previous EP mapping techniques derived from the original MR–EPT [10], [11] either used the transceiver phase assumption or other symmetry assumptions, which have limited their applicability. While GMT can be used without making any such assumptions, its current implementation requires modeling the transmit array in order to calculate the incident fields. For the simulations, we used basis modes as transmit elements in order to decouple the performance of the algorithm from the quality of the excitation. This also avoided the need to test GMT for various coil designs, which would have been a time–consuming endeavor beyond the scope of this work. In general, as far as a non–zero ${\text{b}}_1^{+}$ excitation can be produced at every voxel by at least one transmit coil, GMT should be able to reconstruct artifact–free EP maps. The basis modes used here may even provide physical insight to design a transmit array and/or a shimming approach that it is optimal for GMT. For the experiment, we used an existing coil array prototype available at our research center. Due to the peculiar coil design and uncertainty in some values of the lumped elements, we could not accurately model the coil, which limited the achievable accuracy of the experimental reconstruction. Even after performing a separate optimization to calibrate the transmit voltages at each port, accounting for coupling between elements, the modeled fields were not completely accurate (Fig. 7). In principle, the calibration of the incident fields could be done once on a phantom of known electrical properties and used for any other experiment. However, that is not possible with the current implementation of GMT because it does not include a volume-surface IE solver in the forward problem, therefore the currents on the coils do not account for the effect of the scattered fields, i.e., they do not depend on the EP. This feature will be incorporated in the next version of GMT. To avoid errors associated with inaccurate coil modeling, future work will include designing and constructing a tailored coil array. Directional couplers near the ports could be integrated in the design to calibrate the transmit voltages directly during the experiment for each specific object [56]. This could enable reliable experiments without needing a volume-surface IE solver in GMT, but the reconstructed EP would be sensitive to calibration errors.

While we showed that GMT performance is independent from voxel size, the highest achievable spatial resolution is currently limited by the memory of GPU. For example, using a K40 GPU (Nvidia, Santa Clara, CA) would enable in vivo experiments for small anatomies (e.g., the head) with approximately 3 mm isotropic voxels and require several days to reconstruct EP. GPUs with more memory and/or optimizing the GMT code, which is currently written in MATLAB (Math-Works, Natick, MA), would enable EP mapping at typical clinical resolutions in the future.

Increasing the speed of GMT would also be a critical factor for clinical translation. In this work we used a homogeneous initial guess and Fig. 10 shows that our results were not biased by this particular choice and, in fact, the accuracy of GMT could further improve using different initial guesses. Furthermore, starting from an EP distribution closer to the underlying object structure would reduce the required number of iterations. This could be achieved, for example, by registering morphological images, or parameter maps (e.g., T1 and T2 maps), to the entries of a pre–computed anatomical atlas with average tissue EP. GMT could be further accelerated by parallelizing its execution over several GPUs. In addition, Krylov subspace–recycling techniques could be employed to further reduce the computational cost of solving the forward and adjoint systems.

Fig. 10:

Estimated relative electric permittivity for the four–compartment phantom at 6 mm isotropic resolution, using $b_1^{+}$ measurements with peak SNR of 200. Results are shown for a homogeneous initial guess of vacuum (a) and using the true permittivity distribution rotated by 90° as the initial guess (e). In both cases the results (b and f) are accurate and comparable to the results in Fig. 3, obtained with a different initial guess.

In this work, we tuned the parameters of the regularization function manually, by trial and error. Such an approach could be time consuming for in vivo applications and lead to sub– optimal performance. A possible solution to ensure high performance of Match Regularization could be to train a machine learning algorithm to automatically tune the parameters for each specific case.

In the case of the human–head phantom, the large errors in the EP maps were outliers, mostly localized in regions, such as the skull, where it is not possible to obtain accurate ${\text{b}}_1^{+}$ measurements. However, knowledge of EP in these regions is less important than in other areas, such as the brain, where the GMT reconstruction was accurate.

VI. Conclusion

In conclusion, we introduced a new technique for EP estimation from MR measurements and a new regularization strategy, specifically tailored to the inverse scattering problem in question. We demonstrated the performance of GMT with Match Regularization in simulation using ${\text{b}}_1^{+}$ maps with realistic SNR levels as measurements. We confirmed the accuracy and precision of GMT in a 7 T experiment. In future work we will explore the use of both ${\text{b}}_1^{+}$ and MR signal measurements in the cost function, with the goal to solve for the unknown spin magnetization in addition to EP. Such an implementation would increase the computational complexity of the algorithm roughly by a factor equal to the number of receive RF coils, requiring further software optimization to be practical.

Appendix A. Gradient of the Cost Function

We used Complex–Real (CR) or Wittinger calculus to obtain the co-gradients of the cost function with respect to the complex relative permittivities [57]. The resulting gradients effectively constitute an adjoint formulation of the forward problem in terms of integro-differential operators, with a computational cost roughly equal to that of the forward problem.

The complex-valued co-gradient of the $b_1^{+}$–based cost function (Eq. 6a) can be calculated as

$${\left(\frac{\partial f}{\partial \mathit{ϵ}}\right)}^{*}=-\frac{{\mu }_0{Q}^{\text{T}}}{f(\mathit{ϵ}){\eta }^2}\left(\sum _k\overline{{\mathit{\psi }}_k}\odot {\mathit{\gamma }}_k\oslash {\overline{\mathit{ϵ}}}^2\right),$$ (17a)

where ⊘ denotes Hadamard division, η is defined in Eq. 6c. The terms γ_k and ψ_k are given by the following equations:

$$A^{*}{\mathit{\gamma }}_k=K^{*}{F}^{*}\left(\sum _n{\mathit{w}}_k\odot {\left|{\mathit{w}}_n\right|}^2\odot {\mathit{b}}_n\odot {\mathit{\delta }}_{kn}\right)$$ (17b)

and

$${\mathit{\psi }}_k=c_e\text{Δ}{e}_k^i+N{\mathit{j}}_k.$$ (17c)

where c_e is short-hand for jωϵ₀. The term A* refers to the adjoint system of equations (see Eq. 4) and K is the operator that maps from currents to magnetic field Eq. 7. The residual δ_kn is defined in Eq. 6b. Given a vectorized input, the operator Q^T is given by

$$Q^{\text{T}}=\left[\begin{array}{lll}1\hfill & 1\hfill & 1\hfill \end{array}\right]\otimes \left[\begin{array}{llll}1\hfill & 1\hfill & 1\hfill & 1\hfill \end{array}\right]\otimes I_{N_s},$$ (18)

where $I_{N_s}$ denotes the N_s × N_s identity matrix. More concisely, the operator Q^T sums the basis function coefficients at each voxel. Finally, the operator F^* is given by

$$F^{*}\equiv \left[\begin{array}{c}1\\ -\text{i}\\ 0\end{array}\right]\otimes \left[\begin{array}{l}1\hfill \\ 0\hfill \\ 0\hfill \\ 0\hfill \end{array}\right]\otimes I_{N_s}.$$ (19)

The complex-valued co-gradient of the Match Regularization cost function in Eq. 12 can be calculated as where

$${\left(\frac{\partial f_r}{\partial \mathit{ϵ}}\right)}^{*}=\frac{\beta }{6N_s^{\frac{2}{3}}}\sum _{\tau \in \{x,y,z\}}{\mathbf{\text{Δ}}}_{\tau }^{*}{\mathit{g}}_{\tau }$$ (20)

where

$${\mathit{g}}_{\tau }=\left(e^{c-\sqrt{c^2+{\left|{\text{Δ}}_{\tau }\right|}^2}}\odot {\text{Δ}}_{\tau }\mathit{ϵ}\oslash \sqrt{c^2+{\left|{\text{Δ}}_{\tau }\mathit{ϵ}\right|}^2}\right)$$

Appendix B. Basis Fields Generation

The generation of the basis set used for the incident fields is summarized as follows. A low-rank approximation of the transfer function from currents to fields was generated by first applying the Adaptive Rank Finder algorithm and then applying the full Randomized Singular Value Decomposition (rSVD) algorithm [58]. More specifically, in each voxel of the source region S_r, we embedded Cartesian electric and magnetic currents, j^′ and m^′, and calculated the fields in the target region S_t. The transfer function from sources to scaled flux densities (b^′ and d^′) is given by

$$\left[\begin{array}{l}{\mathit{d}}^{\prime }\hfill \\ {\mathit{b}}^{\prime }\hfill \end{array}\right]={\left[\begin{array}{cc}\sqrt{\text{Δ}}& 0\\ 0& \sqrt{\text{Δ}}\end{array}\right]}^{-1}\left[\begin{array}{cc}\mathbf{\text{N}}& -c_{e}K\\ c_{m}K& N\end{array}\right]\left[\begin{array}{cc}\sqrt{\text{Δ}}& 0\\ 0& \sqrt{\text{Δ}}\end{array}\right]\left[\begin{array}{c}{\mathit{j}}^{\prime }\\ {\mathit{m}}^{\prime }\end{array}\right]$$ (21)

where c_e = jωϵ₀ and c_m = j!χ₀. The input and output of this system are “semi–volumetric”, meaning that the pointwise representation of the waves is scaled by the square root of the Gramian operator. The fields are orthogonalized in semi– volumetric format so as to ensure that the näıve inner product of the coefficients of the fields is equal to the functional inner product of the fields described by the coefficients.

Once the range of the system in Eq. 21 is sufficiently approximated [58], the SVD basis is truncated according to a predefined tolerance. After truncation, the pointwise incident electric and magnetic fields can be extracted from the scaled flux densities as follows.

$$\left[\begin{array}{c}{\mathit{e}}_i\\ {\mathit{h}}_i\end{array}\right]={\left[\begin{array}{cc}\sqrt{\text{Δ}}& 0\\ 0& \sqrt{\text{Δ}}\end{array}\right]}^{-1}{\left[\begin{array}{cc}{c}_e& 0\\ 0& c_m\end{array}\right]}^{-1}\left[\begin{array}{l}{\mathit{d}}^{\prime }\hfill \\ {\mathit{b}}^{\prime }\hfill \end{array}\right]$$ (22)

Given pointwise incident and magnetic fields, $b_1^{+}$ can be calculated following Eq. 7.