FairSubset: A tool to choose representative subsets of data for use with replicates or groups of different sample sizes

Abstract

High-impact journals are promoting transparency of data. Modern scientific methods can be automated and produce disparate samples sizes. In many cases, it is desirable to retain identical or pre-defined sample sizes between replicates or groups. However, choosing which subset of originally acquired data that best matches the entirety of the data set without introducing bias is not trivial. Here, we released a free online tool, FairSubset, and its constituent Shiny App R code to subset data in an unbiased fashion. Subsets were set at the same N across samples and retained representative average and standard deviation information. The method can be used for quantitation of entire fields of view or other replicates without biasing the data pool toward large N samples. We showed examples of the tool’s use with fluorescence data and DNA-damage related Comet tail quantitation. This FairSubset tool and the method to retain distribution information at the single-datum level may be considered for standardized use in fair publishing practices.

HIGHLIGHT

FairSubset is freely available R software to address problems of bias in representation of individual data points and in replicates with different sample sizes. The core algorithm performs 1000 choices within each sample of data and compares the average (user set to mean or median) and standard deviation of these subsets to the original data. It outputs the subset which best represents the original data for each sub-group and compares this subset to what may have been inappropriately chosen by a strictly random tool (the “worst subset”). This tool can be accessed without any knowledge of R programming as a free online app at https://delaney.shinyapps.io/FairSubset/. Constituent code and R package are available on GitHub.

INTRODUCTION

Science has progressed by including more transparent and detailed statistics in publications. The first paper on dietary restriction, published in Science in 1884, is only one paragraph long [1]. It described the lack of deleterious effects of starving a single spider for a period of 204 d. Since then data size, presentation, and transparency has gradually matured. Now there is universal demand for multiple replicates per experiment, but the ways to present and manage data from such replicates are varied. It may be desirable to present smaller subsets of the data. A common example of this occurs when each group analyzed has a different quantity of data points acquired, yet it is necessary to analyze or present consistent, equal numbers from each group.

How might the groups be selected to create equal sample sizes with minimum bias? Agnostic randomization can be performed, but may unintentionally skew the data simply by random chance. A better method is to find a portion of data points to represent all acquired data within the sample. However, this method of choosing data would require a determination of which subset of cells (or other subject of the image) best represents the entire population. The number of choices possible, where k is the quantity of chosen data points and N is the number of all data points, is: possible choices = N! / (k!* (N-k)!). This number is enormous for even the relatively small N typically present in scientific images or cytometry data. It is unreasonable to expect scientists to manually perform these permutations to decide which subset most accurately maps the data within the image in an unbiased, random manner. Here, we present a point-and-click tool, FairSubset, which performs these randomizations and calculations automatically to determine a representative subset.

Target problems for FairSubset

FairSubset was designed to find representative subsets for three main situations. The first is very simple: more data was acquired than desired. Why might this ever happen? The method of acquisition may randomly acquire more or less data sample-to-sample. This could occur for images (fields of view with differing number of features), fluorometric measurements in cytometry (each volume contains stochastically different numbers of fluorescent molecules), and naturally random events (radiation measurements over a period of time), among other examples [2,3]. In these cases, the FairSubset tool is designed to choose subsets with equal number of data points across all samples (Fig. 1A). This is expected to be the main use of FairSubset, but other nuanced uses are possible and are indeed common in biological investigation.

Figure 1.

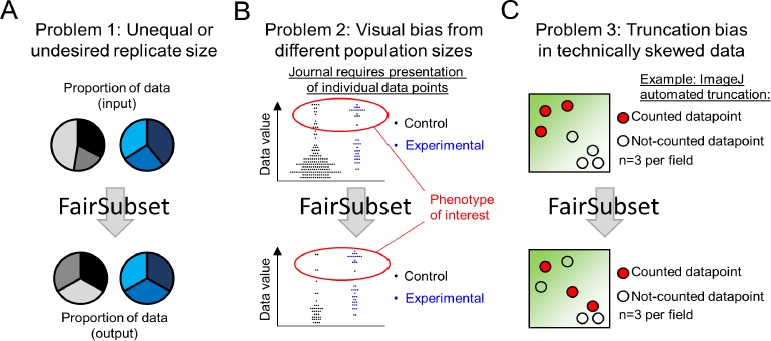
Examples of uses for FairSubset. A. A common problem of automated data acquisition methods is that they do not always allow for an equal number of outputs. Yet it is often desirable to have an equal number of data points between replicates or samples. FairSubset provides an automated method to find which equal N subsets best represent the original data in an unbiased fashion. B. One case in which equal subsets may be desired are experiments in which the control group and experimental group have substantially different N and the phenotype of interest is a rare event. Plotting raw data may produce a visual bias wherein the experimental ratio of the rare event appears less skewed than the data would suggest. In this unique scenario, FairSubset may be considered as a standard to identify subsets for rigorous visual presentation. These individual points may then be overlaid with a violin plot or a boxplot for optimal presentation value. C. Automated imaging is an example where choosing the first set of data points (automated truncation of 20 cells per image, for example) may yield bias sample-to-sample. There are often technical artifacts, sometimes invisible to the naked eye but not to quantitation software, where a portion of the field of view has increased or decreased intensity values. Depending on where the regions of interest (e.g., cells or nuclei) are found in individual images, this may skew the data for images with higher density of regions of interest. FairSubset can be used without knowledge of biased intensity regions to consistently save data from a defined N per image without such skewing of the data. For (B-C), these are proposed uses, but additional uses of fairly subsetting identical N per replicate or sample are likely to be spread throughout science.

In the second situation, there is a chance for visual bias if all original data are plotted. The choice of how to represent data visually is important for many aspects of science. Readers’ evaluation of the authors’ claims in publications or grant submissions is often limited by the choice of visualization. Bar graphs hide distribution information and over-emphasize the difference from zero [4,5]. Therefore, there is value in displaying data as individual points while also comparing averages and error bars. Some journals now require box-and-whisker plots and/or the plotting of single data points to give readers an understanding of sample size and distribution of data. While violin plots or symmetrically jittered data can relieve some visual biases from the data presentation, largely different sample sizes preclude accurate and consistent interpretation of plots containing individual datum-level presentation. An example is common in medical literature: a rare disease-causing genotype will more often yield an unusual observation of a disease phenotype relative to control genotypes (Fig. 1B). Yet, it is easier to find a large cohort of controls than rare-genotyped individuals for study. If a reader looks at the dataset with each individual’s data plotted, it may appear that the phenotype of interest is not qualitatively different in the control condition compared to the experimental condition (red marked regions of Fig. 1B). However, by plotting equal numbers of individual data points from data fairly subset by FairSubset, it becomes clearer that the experimental group is indeed different (lower panel of Fig. 1B).

For the third situation, systemic bias was considered. Fig. 1C depicts a common problem where illumination bias may cause a high signal in one corner of an acquired picture, which may vary between images. While it would be ideal to correct the technical problem, sometimes this is either impossible (e.g., the interaction of the plate with the laser), or unknown (e.g., the bias is subtle and the user is unaware, or the imaging system is automated and only rare images contain technical bias). If data is produced by scanning an image from the upper left to the lower right, then truncating the data will produce a bias toward a specific location on the image (Fig. 1C). This potential for truncation bias is a default setting with numerous acquisition and analysis tools. An example would be the widely used tool ImageJ [6], which is used to quantify images of cells and other biological subjects. ImageJ creates regions of interest from the top-left to the bottom-right. If a user decides to use a pre-defined number of cells per image for further analysis, then technical issues which may be invisible to the ImageJ user will bias the data. Using FairSubset for all images helps reduce the false positive or false negative errors in such situations (lower panel of Fig. 1C) in a systemic fashion.

Design and algorithm of FairSubset

To find the subset of data which best represents the original data, we designed a tool called FairSubset. This R Shiny App tool takes as inputs columns of data, wherein each column contains quantified data of disparate number (rows) (Fig. 2A). Columns may represent different experimental conditions or different replicates within the same condition. By default, the tool detects which column has the least individual data points and sets that number as the choice N to use as a sample size across all columns. The option is also offered to set a defined sample size N for all columns, if it is less than the smallest column of data.

Figure 2.

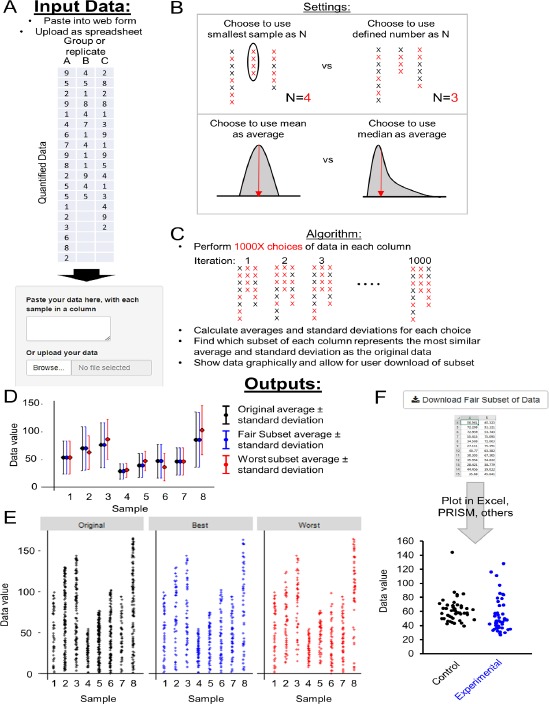
Inputs, outputs, and algorithm of FairSubset. A. Input data is pasted into the free text box or uploaded as a spreadsheet (.tsv, .csv, or .txt). Data must have each control, experimental condition, or sample replicate separated in columns. Rows must contain the quantified data. B. Adjustable settings allow for using either the lowest N sample or a defined N subset. This is useful to choose to use either the most data or a convenient and consistent sample size. The user can decide to use mean or median as the average criterion, or a more advanced Kolmogorov–Smirnov test for skewed data. C. Diagram of method underlying FairSubset calculations. 1000 random choices of subset are made for each sample (colored red). Standard deviations and averages are calculated for each random subset. Whichever subset has the most similar standard deviation and average as the original sample is then marked as the Fair Subset. These data are the most representative of the sample. Conversely, the worst subset is that in which the average and standard deviation are most different from the original sample and represents the worst-case scenario for what could have happened by randomly choosing points. D. Plot output showing the mean and standard deviation of original (black), Fair Subset (blue), or the worst subset (red) within 1000 tested subsets. E. Output graphically depicting how individual data may be plotted for original (black), Fair Subset (blue), or the worst subset (red) within 1000 tested subsets. This is a first-pass check on the subsetting method’s successful implementation. It is recommended to then export the data and plot using plotting programs such as Excel and PRISM. F. Buttons to download the Fair Subset and worst subset data for use in external plotting programs and/or statistical software.

FairSubset then uses this sample size N to randomly select N samples from each column. It performs a random subset choice 1000 times for each column. An average and standard deviation calculation is performed for each column for each randomization and saved in the tool’s memory. Users may choose either mean or median as the average criterion for most normally distributed data (Fig. 2B). Once these 1000 averages and standard deviations are calculated, the tool calculates the difference between the subset average and the original data’s average. It performs a similar calculation for standard deviation. The tool weighs both the average and standard deviation equally and then chooses which randomly chosen sample most closely resembles the original column of data (Fig. 2C). For noisier or skewed data, the user can select a Kolmogorov-Smirnov calculation [7]. In this case, medians and standard deviations are still calculated per sample per randomization, but a P-value from the Kolmogorov-Smirnov test is also determined between the random subset and the original data. FairSubset then chooses the random simulation with the highest P-value. If multiple simulations contain the highest P-value, then the median and standard deviation calculations are secondarily used.

The tool then combines these best representative subsets of data into a matrix, called the “Fair Subset”. It also saves the matrix of data which least represents the original data (the subsets in which the average and standard deviation which are most unlike the original data). It automatically plots the original average, the Fair Subset average, and the worst subset average along with the standard deviation (Fig. 2D). This enables an immediate understanding of whether or not the Fair Subset contains the desired characteristic of a similar average and distribution to the original data. It also shows, via the worst subset, what could have been erroneously used as a consistent N dataset by random choice or truncation, which can be measurably different from the original data (red data points in Fig. 2D). The presentation of the “worst subset” is intended to show the benefits of using the FairSubset tool, not to enable the use of the worst subset for further statistical analysis or plotting.

A corresponding automatically generated plot shows a preliminary depiction of what single-datum plotting may look like for the three output data sets (Fig. 2E). This can help determine if the tool is appropriate for the input data prior to generation of professional data plots. Finally, the matrix containing the Fair Subset of each column can be downloaded by clicking on an interactive button (Fig. 2F). These data can then be input into Microsoft Excel, PRISM, or other plotting software to produce the desired publication-quality plots.

FairSubset was developed with the intent to distribute an easy-to-use tool for scientists with limited or no bioinformatic background to subset a representative sample from disparate N datasets. It is available to use online for free at https://delaney.shinyapps.io/FairSubset/. Links to complementary tools may be found at http://www.delaneyapps.com/. Code is provided for free use and distribution. It is covered under General Public License 3 (GPLv3, https://www.gnu.org/licenses/gpl-3.0.en.html). Code is maintained at: https://github.com/jrdelaney/FairSubset. An R package is available to use for automated scripts: FairSubset, available for download and installation from the GitHub repository.

IMPLEMENTATION

An example of visual bias correction by FairSubset

Visual bias can arise when one set of data contains more values than another set of data. The larger sample size means that outliers may be visually more striking; since simply having more data gives rise to more outliers. In this example, a measure of DNA damage was quantified from previously published images (Fig. 5 from reference [8]). The images were run through the OpenComet plugin for ImageJ and the tail moment (% of DNA in the Comet tail) was used as the phenotypic data for the Y-axis. The “Control” set included Comets from 0–12 h and the “Experimental” set included data from the treated cells after 12 h of media rescue. With classical presentation of the data, it may appear qualitatively to some readers that the control group contains more or equivalent DNA damage compared to the experimental group (Fig. 3A). To address this problem, a scientist may readily subset the data using FairSubset into equal sample size and visualize and initial result of these subsets (Fig. 3B). The raw subset data can then be exported to generate a professional plot (Fig. 3C). After the use of FairSubset, the data plot now displays a comparable number of outliers in the high percentage of DNA range.

Figure 3.

Example of visual bias correction. A. Data comparison control Comet tail quantitation to an experimental condition. Individual data points are plotted for each group adjacent to median and standard deviation indicators. The N in the control group is 145 and the N in the experimental group is 27. With the disparate N, a reviewer of the data may be disinclined to believe the statistical significance showing an increased Comet tail distribution in the experimental group, since more outliers are present in the larger N group. B. Data are input into FairSubset and resultant subgroups are plotted in Microsoft Excel. The Fair Subset represents the subset which best matched the original data using only 27 data points, from 1000 choices of the subsets. The Worst subset represents the subset in the group of 1000 subsets which had the farthest median and standard deviation from the original data. The experimental group is identical since the program defaults to the lowest N from each group; it chose all 27 data points. C. A finalized graph which includes individual data points of the Fair Subset of control compared to the experimental group. The distribution of individual data points is more comparable between groups and the outlier visual bias is reduced. Some statistical significance is lost if represented in this fashion since N is reduced in the larger group, however some authors may choose to indicate in figure legends the original significance if the Fair Subset method is cited solely as a way to reduce visual bias. P-values represent output of a Wilcoxon rank-sum test.

An example of normalizing sample sizes across replicates without unintended bias

A common use of FairSubset would be to equalize sample sizes between different replicates for the same experimental condition. It is customary to have multiple technical or biological replicates to build a dataset. However, it is often the case that by using automated or manual data collection criteria each replicate may not have the same sample size. For example, if a cytotoxic drug is used and equal cells are initially seeded, by the end of the experiment less cells are available to analyze per field of view in the cytotoxic drug condition. Truncating the data for each replicate is a reasonable choice, but may introduce bias depending on how the data were collected. To reduce bias, FairSubset is an option to choose which subset of data within each replicate is most representative for the whole population while retaining the desired sample size.

A real-world example of where this type of correction may be useful and appropriate is provided. A common experiment contains three technical replicates for both a control and experimental group. In this example of previously published [9] microscopy data for single cell GFP fluorescence, one control image contains more cells (yellow data points, Fig. 4A). This replicate happens to have the least fluorescence of the three replicates, and shifts the mean and median to a lower value. However, it is more appropriate to consider each replicate equally, with one-third of the aggregated data each. To enable this, we used FairSubset by inputting replicates as different columns of data. While the mean ± standard deviation remains the same for each replicate after FairSubset (Fig. 4B), the proportion of data used from each replicate is equalized (Fig. 4C). This results in a shift in the average of the replicate-combined data and the subsequent statistical analysis (Fig. 4D). The results then do not achieve statistical significance, avoiding a spurious false positive from a heavily weighted single technical replicate.

Figure 4.

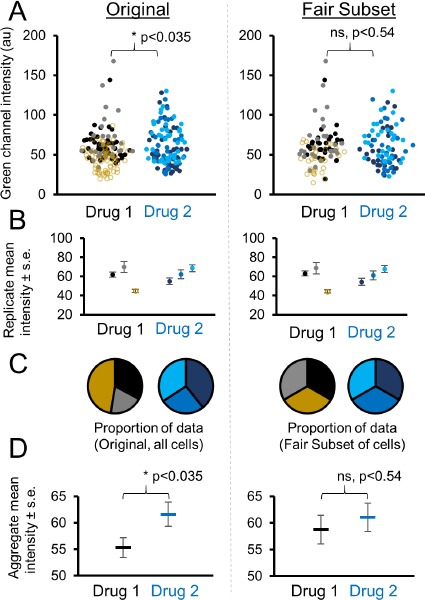
Example of normalizing replicates to avoid a spurious false positive. A. Comparison of immunofluorescence data from two drug-treated conditions and three replicates. Replicates are represented by different shades of grey or blue. One Drug 1 replicate contains substantially more data points and is highlighted in yellow. Data was input into FairSubset and the Fair Subset was downloaded for subsequent statistics and plotting in Microsoft Excel. Before subsetting, a t-test determines the samples are significantly different with a P #x003C; 0.05 cutoff. After subsetting identical N from each image, the significance is abrogated. B. The mean ± standard error of each replicate remains the same before and after subsetting, which is by design of FairSubset. C. The proportion of data contributing to the mean is shown in pie charts. Prior to subsetting, one picture dominates the data from Drug 1 with nearly half the data points (yellow slice). After subsetting using FairSubset, this high N replicate represents a fairer proportion of the overall statistics calculations with only 1/3 of the total (N). D. After using FairSubset, the group mean of the three replicates does change, even though the mean of individual replicates does not. This example illustrates a case when biasing the overall data toward a single replicate would be undesirable or unethical. P-values represent the output of a two-tailed unpaired t-test.

DISCUSSION

Replicate and visual bias can produce poor representations of hard-earned scientific data. While some computation-savvy scientists may be able to fairly represent their data by using programmatic algorithms or advanced statistical methods, the FairSubset online tool can do this for most datasets without requiring the scientist to know any programming language. We additionally provide the R Shiny App code and an R package so the FairSubset strategy can be incorporated into other software, such as automated microscopes or other high-throughput machines.

While it is expected most users will utilize FairSubset to equalize numbers between replicates, a discussion of alternate uses is warranted. As scientific journals transition to requiring or preferring presentation of single datum-level plots [10], counter-intuitive visual bias may entice some reviewers to suggest the authors did not correctly analyze the data based on what appears to be plotted. Different sample sizes may be required to achieve significance in real-world data, particularly in epidemiological studies with rare subjects (thus, the study requires small N for an experimental sample, large N for a control sample). However, plotting all such data can lead the reader to qualitatively confuse the observations of the experiment (Fig. 1B, Fig. 3A). Appropriate alternate plots would include boxplots, violin plots, or a combination of either with individual points symmetrically jittered and superimposed. In such situations when it is not possible or visually striking to use these plots, FairSubset provides a means to automatic subsetting of appropriate individual data points which have less chance of producing a visual bias.

In some situations, automated determination of subsets may reduce false-positive calls. The use of student’s t-test, Mann–Whitney U test, and other comparative methods require observations to be truly independent for the tests’ hypotheses to hold true. Otherwise, the calculated P-value does not accurately represent a statistical test of the data. The false-positive example in Figure 4 represents a case wherein the samples may not be independent; a replicate of Drug 1 was biased to have a low signal. While tests such as the Grubbs’ test may identify these biased replicates as outliers, the bias may be too subtle for such tests to properly identify them, or the user may be unaware of the need to use an outlier test. Via FairSubset, users can choose a pre-defined sample size across all replicates and reduce the chance that an unusual replicate will have an outsized, inappropriate effect on statistical calculations of significance. However, it should be noted that all users should understand the requirements and hypotheses of the statistical test to follow FairSubset data outputs. The variance between repeated measures is typically less than the variance of constituent data used to create such repeated measures [11]. In many cases, it may be more appropriate to average the data within each replicate and use these replicate averages in statistical tests (Fig. 4B), not the individual data points which are used to calculate these averages.

FairSubset is not appropriate in all situations and is not a replacement for an educated statistician. Reduced sample size will also raise P-values in most situations, and FairSubset is not an exception. If users are more concerned with false negatives than false positives, FairSubset should be used with caution. The real-world examples shown in Figure 3 and Figure 4 may better benefit from consultation with a statistician, who will be able to apply more sophisticated methods of analysis for repeated measures, such as ANOVA or linear mixed models. Like all statistical tools, the proper use of FairSubset depends, in part, on the knowledge of the user.

In summary, FairSubset provides an unbiased method to quickly and easily normalize between replicates for entire datasets. Most importantly, no programming knowledge is required to use the tool. The software has been successfully tested by scientists with no more than a bachelor’s degree, providing ease of use for all scientists at any level of their career.

TROUBLESHOOTING

Please contact Joe Delaney, delaneyj@musc.edu, for any requests and comments including bug reporting. We encourage users to contact us regarding novel uses of the tool, for which we may be able to provide added features to enable ease of use. We expect to maintain this web application for at least two years and code will remain updated in GitHub.