Principles of tRNA^Ala Selection by Alanyl–tRNA Synthetase Based on the Critical G3·U70 Base Pair

Abstract

Throughout evolution, the presence of a single G3·U70 mismatch in the acceptor stem of tRNA^Ala is the major determinant for aminoacylation with alanine by alanyl–tRNA synthetase (AlaRS). Recently reported crystal structures of the complexes AlaRS–tRNA^Ala/G3·U70 and AlaRS–tRNA^Ala/A3·U70 suggest two very different conformations, representing a reactive and a nonreactive state, respectively. On the basis of these structures, it has been proposed that the G3·U70 base pair guides the −CCA end of the tRNA acceptor stem into the active site of AlaRS, thereby enabling aminoacylation. The crystal structures open up the possibility of directly computing the energetics of tRNA specificity by AlaRS. We have carried out molecular dynamics free-energy simulations to quantitatively estimate tRNA discrimination by AlaRS, focusing on the mutations of the single critical base pair G3·U70 to uncover the energetics underlying the accuracy of tRNA selection. The calculations show that the reactive complex is highly selective in favor of the cognate tRNA^Ala/G3·U70 over its noncognate analogues (A3·U70/G3·C70/A3·C70). In contrast, the nonreactive complex is predicted to be unselective between tRNA^Ala/G3·U70 and tRNA^Ala/A3·U70. Utilizing our calculated relative binding free energies, we show how a simple three-step kinetic scheme for aminoacylation, involving both an initial nonspecific binding step and a subsequent transition to a selective reactive complex, accounts for the observed kinetics of the process.

Introduction

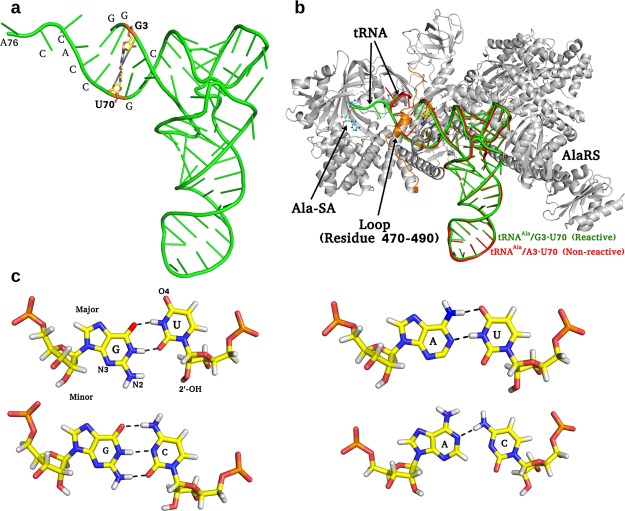
Correct amino acid attachment to its cognate tRNA followed by correct mRNA–tRNA interaction during mRNA decoding on the ribosome ensures the accuracy of genetic code translation. An aminoacyl–tRNA synthetase (aaRS) selects its cognate tRNA and ligates the correct amino acid at the 3′-CCA end with an extremely high specificity, corresponding to an error rate of 10^–4–10^–5.¹ A set of structural elements in the tRNA (identity set) is recognized by aaRS for cognate tRNA selection.²⁻⁷ For alanine tRNA (tRNA^Ala), a single wobble G3·U70 base pair in the acceptor stem away from the anticodon triplet (Figure 1a) is the major determinant of the tRNA identity⁸⁻¹⁰ and is recognized by alanyl–tRNA synthetase (AlaRS) in all kingdoms of life.¹¹ Mutation of the G3·U70 pair thus diminishes the aminoacylation with alanine by AlaRS.¹² On the other hand, transfer of the G3·U70 pair to small RNAs (acceptor stem mimics of tRNAs), tRNA^Cys and tRNA^Phe, enables alanine charging by AlaRS.^{2,8,9,13−18} Wobble G·U pairs constitute an important structural element of tRNA architecture and are related to the function of RNA in diverse biological systems.¹⁹⁻²¹

Figure 1.

tRNA^Ala, AlaRS–tRNA^Ala complex, and identity base pair and its variants (a) tRNA^Ala (green) and the identity base G3·U70 (yellow stick) at the acceptor stem. (b) Reactive (green) and nonreactive (red) conformations of tRNA^Ala in complex with AlaRS (gray); Ala-SA (ball and stick) and flexible loop (residue 470–490) shown in orange color. (c) Close-up view of G·U (major and minor grooves highlighted), A·U, G·C, and A·C base pairing.

Crystal structures of AlaRS from Arachaeoglobus fulgidus in complex with native tRNA^Ala (tRNA^Ala/G·U) and the mutated variant with A3·U70 (tRNA^Ala/A·U),²² in complex with the alanyl-adenylate analogue, 5′-O-[N-(l-alanyl)sulfamoyl]adenosine (Ala-SA),²³ have recently been reported (Figure 1). These structures suggested an explanation to the long-standing mystery of the strict specificity of AlaRS for tRNA^Ala containing the conserved G3·U70 wobble pair.²² In the AlaRS–tRNA^Ala/G·U complex, the 3′-CCA end of tRNA^Ala has reached into the active site (reactive complex: R) where aminoacylation can occur, whereas in the AlaRS–tRNA^Ala/A·U complex, the 3′-CCA end of tRNA^Ala folds back into a different route away from the active site (nonreactive complex: NR) (Figure 1b). Flexible domains allow proteins to access multiple conformational states and the highly mobile loop region of AlaRS that spans the minor groove of the acceptor stem (residues 470–490 with an average backbone B-factor ≈ 195 Ų)²² might have a prominent role in selectivity (Figure 1b). An interesting feature of the G3·U70 wobble geometry is the availability of the exocyclic −NH₂ group of G3 in the minor groove, and O4 of U70 in the major groove, for hydrogen-bonding interaction with the protein. AlaRS is thus able to establish a specific interaction network with G3·U70 both in the major and minor grooves to recognize the tRNA for alanine acylation. Other base pairs such as A3·U70, G3·C70, and A3·C70 change the shape of major/minor grooves and alter the mode of stacking and hydrogen bonding (Figure 1c).

The crystal structures show that the interaction between AlaRS and the major and minor grooves of the G3·U70 base pair is disrupted in the A3·U70 variant.²² It has also been suggested that the geometrical difference between G3·U70 and A3·U70 propagates to the 3′-CCA end of tRNA^Ala, resulting in distinctly different orientations of the acceptor stem to yield the reactive conformation for tRNA^Ala/G·U and the nonreactive one for tRNA^Ala/A·U. The proposed mechanism gives a clue to how a small difference in sequence away from the anticodon may result in tRNA^Ala specificity at the k_cat level.²² The ratio of k_cat for aminoacylation between the G3·U70 and A3·U70 variants of tRNA^Ala is approximately 100-fold.²² Interestingly, many other proteins similar to the editing domain of class II aaRSs have also been isolated, which can edit misacylated tRNAs even after they have been released from the synthetase.²⁴⁻²⁷

The difference between the R and NR complexes is mainly characterized by the alternate orientations of the 3′-CCA end of tRNA^Ala as the AlaRS structure is very similar in the two medium-resolution (∼3.4 Å) X-ray structures.²² However, several key issues regarding the tRNA^Ala specificity of AlaRS remain unclear. For example, the replacement of G3·U70 by A3·U70 could perhaps already change the conformational preference of the CCA end (NR over R) of free tRNA^Ala in water, leading to the NR complex upon AlaRS binding. Another question is how strongly the cognate tRNA^Ala G3·U70 wobble pair is preferred with respect to its variants (A3·U70, G3·C70, and A3·C70) by AlaRS in the R conformation and whether or not it is also preferred in NR. Moreover, the structures of noncognate complexes such as those containing G3·C70 or A3·C70 have not been resolved experimentally. The near-atomic resolution crystallographic complexes,²² however, now provide sufficiently good models for structure-based computational evaluation of the energetics associated with the states they are trapped in (R and NR). Here, we report molecular dynamics (MD) free-energy calculations of cognate and near-cognate AlaRS–tRNA^Ala complexes to examine how the energetics of tRNA binding is affected by different variants of the 3.70 base pair in the reactive and nonreactive conformations. The quantitative estimation of tRNA^Ala specificity by AlaRS offers a simple view of how fidelity in the aminoacylation process is achieved, thereby establishing a link among three-dimensional (3D) structures, thermodynamics, and experimentally measured kinetics.

Methods and Simulation Details

MD Procedure

The MD procedure is described in Figure S1. The structures of tRNA^Ala bound to AlaRS, in the reactive and nonreactive conformations, were taken from the Protein Data Bank (pdb codes 3WQY and 3WQZ, with crystallographic resolutions of 3.3 and 3.49 Å, respectively). Spherical systems with radius 25 Å, centered on the N9 atom of the G3/A3 nucleotide of tRNA^Ala, were cut out from the crystallographic structures and used for MD simulations. Harmonic positional restraints to experimental coordinates were then applied to all heavy atoms in the “buffer region” between 22 and 25 Å from the sphere center. The force constants of the restraints in the buffer region were increased linearly between 3.0 and 5.0 kcal/mol/Ų in the direction toward the outer boundary. The inner 22 Å radius sphere was treated as fully flexible in the production of MD simulations. This system was solvated by overlaying a cubic water box with an edge length 80 Å, where water which overlapped with AlaRS–tRNA was removed. This yielded a total of about 49 000 atoms in the simulations, which included ∼14 900 water molecules. Periodic boundary conditions (using the particle mesh Ewald method²⁸) for electrostatics with tinfoil boundary conditions^29,30 were used for running MD simulations. van der Waals interactions were truncated with a 16 Å cutoff. Temperature and pressure were kept at 310 K and 1 bar, respectively. Langevin dynamics³¹ for nonhydrogen atoms with a coupling coefficient of 5 ps^–1 were used to control the temperature. The pressure was controlled by a Langevin piston using the Nose–Hoover method.³² The CHARMM36 force field³³⁻³⁷ and TIP3P water model³⁸ were used for running MD simulations. Simulations were performed using the CHARMM^39,40 and NAMD⁴¹ programs. For each simulation model, we ran 5–10 replicas starting with different initial velocity distributions. Each replica involved 340 ps of equilibration (where the system was heated up to 310 K in the initial stages and then kept fixed throughout the simulations), followed by at least 4 ns production dynamics. Overall, 240–360 ns of production dynamics distributed over 5–10 replicas were considered for structural analysis for the AlaRS–tRNA complex and free tRNA in water. In the initial stage of equilibration, harmonic restraint was applied to the inner region (within 22 Å) with a force constant of 4.0 kcal/mol/Ų, and at the final stage of equilibration, the restraint (within 22 Å) was completely removed. The simulation models were overall neutral, which was achieved by scaling the partial charges of the phosphate backbone of tRNA. The X-ray structures of AlaRS–tRNA complexes do not contain counterions within the reduced 25 Å truncated model. Hence, instead of placing the counterions at random locations, we mimicked the backbone neutralization by scaling down the partial charges of the RNA phosphates which are away from the 3.70 pair. The charges of the RNA base pair undergoing mutation (i.e., 3.70) and its nearby base pairs (2.71, 4.69, and 5.68) were not modified. The truncated 25 Å model centered at N9 of A3/G3 was neutralized by adding a +1 charge distributed over four atoms of the phosphate group of RNA residues (Table S1) present outside 13.4 Å from the center. Bond lengths between hydrogen and heavy atoms were constrained by the ShakeH algorithm implemented in NAMD⁴¹ with an allowable bond-length deviation of 1.0 × 10^–8 Å. A 2 fs time step was used for performing MD simulations. RMSD and RMSF of heavy atoms within 22 Å of unrestrained simulation sphere were calculated with respect to the X-ray structure, and the average RMSD and RMSF were calculated over the last 5 ns of the 7 ns MD trajectory with a 1 ps interval.

Free-Energy Calculations

Relative binding free energies (ΔΔG_bind) for tRNA mutations in the AlaRS–tRNA complexes (R and NR) were calculated by alchemically transforming G3/A3/U70 into A3/G3/C70 (horizontal legs of the thermodynamic cycle in Figure 2a). The vertical legs of the thermodynamic cycle correspond to tRNA binding and the horizontal legs correspond to the alchemical transformation of tRNA (Figure 2a). It should be noted that the horizontal paths (alchemical transformation) cannot be realized experimentally. We computed the free-energy changes along the alchemical transformations (ΔG^comp and ΔG^free) and calculated the relative binding free energy as ΔΔG^bind = ΔG^comp – ΔG^free = ΔG_A3·U70^bind – ΔG_G3·U70. We used a hybrid energy function (U) which represents a mixture of two endpoint states of the horizontal leg (Figure 2a), as applied in previous studies.⁴²⁻⁴⁶ The coupling parameter λ connects the end states by modifying the electrostatics, van der Waals energy, and bonded terms. Changing λ from 1 to 0 thus transforms AlaRS–tRNA^Ala/G3·U70 into AlaRS–tRNA^Ala/A3·U70 by means of the mapping energy function: U = λU(G3) + (1 – λ)U(A3). The free-energy derivative was calculated as ∂G/∂λ = ⟨∂U/∂λ⟩_λ = ⟨U(λ = 1) – U(λ = 0)⟩_λ, where the brackets “⟨ ⟩” represent averaging over an MD trajectory for a particular value of λ. For the alchemical transformation of G3 into A3, we used 17 λ values between 1 and 0 (1.0, 0.999, 0.99, 0.95, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1, 0.05, 0.01, 0.001, and 0.0), whereas for the transformation of U70 into C70, we used 11 equally spaced λ values between 1 and 0 (1.0, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1, and 0.0). The free-energy derivative at each λ was calculated by computing the difference ⟨U(λ = 1) – U(λ = 0)⟩_λ. Each λ window simulation lasted for 1–2 ns, and the data from the last 600–1600 ps were used for averaging. Numerical integration (with the standard trapezoidal method) was used for calculating the free-energy change. The last 600–1600 ps of the trajectory at each λ was divided into two batches, and the deviation of the batch averages was reported as an uncertainty associated with the free-energy derivatives. The same is reported as the statistical error associated with the calculated ΔG^comp or ΔG^free for each run. The average result obtained from 5 to 10 trajectories is used for computing ΔΔG. The uncertainty in the averaged ΔG is reported as the standard error of the mean (from 5 to 10 replicas), and the error in the final ΔΔG in the manuscript is calculated by propagating the standard error of the mean associated with the averaged ΔG (Figure 2b). The uncertainty in the averaged ΔG (∼1.0 kcal/mol) is well within the acceptable statistical uncertainty.⁴⁵ Free energies were calculated for the forward and reverse alchemical transformations (say G3 → A3 and A3 → G3) in tRNA, either in complex with AlaRS or free in water (Table S2). The results were averaged over the forward and backward runs, except for the reactive AlaRS–tRNA^Ala/G3·U70 complex (Table S2). A relatively large hysteresis (difference between the G3 → A3 and A3 → G3 runs) was observed (Table S2a) only in the reactive complex (∼5 kcal/mol), and hence averaging was done based on the forward runs. The reverse alchemical transformation (AlaRS–tRNA^Ala/A3·U70 → AlaRS–tRNA^Ala/G3·U70) in the reactive complex could not disrupt the salt bridge Arg483–Asp450 interaction and get back the G3–Asp450 interaction (Figure S2), which causes the hysteresis. A reasonable estimate of the free energy of G → A transformation in the reactive complex is only possible to obtain from the forward runs. The reverse runs (A → G) in the reactive conformation do not end up in the X-ray structure (Figure S2), which makes it necessary to discard these for reliable free-energy estimates. To minimize the hysteresis, we have extended MD simulations at 8λ windows (which showed a significant deviation between the forward and reverse free-energy derivatives) of the reverse run by 10–20 ns each. The hysteresis was reduced from ∼5 to ∼2 kcal/mol, as a result of long MD simulations (distributed over 117 ns alchemical free-energy simulations). However, the hysteresis was not eliminated. Disruption of the salt-bridge interaction between Asp450 and Arg483 seems to be a remedy in solving the hysteresis issue. Hence, we mutated Arg483 → Ala483 in the reactive complex (model R#) and performed G3.U70 → A3.U70 (forward) and A3.U70 → G3.U70 (reverse) and found almost no hysteresis (∼0.6 kcal/mol) and ΔΔG = 3.3 kcal/mol. Thus, it can be argued that R# does not have hysteresis problem but still yields strong discrimination.

Figure 2.

Energetics of tRNA^Ala binding to AlaRS. (a) Thermodynamic cycle for AlaRS–tRNA binding. Vertical legs correspond to binding; horizontal legs correspond to the alchemical transformation of the identity base pair, either in the solvated protein (upper leg) or in solution (bottom leg). (b) Graph shows the calculated tRNA^Ala binding free-energy differences (kcal/mol) between tRNA containing the identity base pair G3·U70 and its variants (A3·U70, G3·C70, and A3·C70). Red and gray bars denote reactive and nonreactive states, respectively. Binding free energies are in kcal/mol and standard error is shown as vertical bars (black line) in parentheses.

The free-energy calculations for each system were based on 340–880 ns of MD data averaged over 5–10 replicas with different initial velocities. Overall, a total of about 2 μs of MD free-energy simulations have been done to get a good convergence and a reasonable standard error of the mean (<1 kcal/mol). To compute the binding free-energy difference between G3·U70 and A3·C70, we performed direct calculations for two different paths, G3·U70 → A3·U70 and A3·U70 → A3·C70, and the result was then obtained indirectly from the free energies obtained from these two direct paths. As an additional check, the free-energy calculations for G → A in the reactive complex (ΔG^comp of Figure 2a) were also performed with a smaller water box with a 70 Å side. The computed ΔG^comp values are virtually identical for the two different water box sizes. The robustness of the calculated energetics was examined by repeating the calculations for G3.U70 → A3.U70 and G3.U70 → G3.C70 transformations (in reactive complex, free tRNA) with different MD setups, viz. (a) spherical droplets instead of water box; (b) considering explicit Na⁺ ions for neutralization instead of scaled-down phosphate charges in a water box. The calculated energetics are found to be robust and independent of the box size, solvation protocol, and statistical methods employed in extracting free energies.

Results

Structure-Based Energetics of tRNA^Ala Selectivity in AlaRS

To compute the energetics of AlaRS binding specificity for tRNA^Ala and elucidate the roles of the different conformational states (R and NR) in tRNA selection, we carried out MD simulations of tRNA^Ala/G·U and its variants (tRNA^Ala/A·U, tRNA^Ala/G·C, and tRNA^Ala/A·C) in complex with AlaRS and free in water (Figure 2a), using both reactive and nonreactive crystallographic structures²² as starting points. These calculations involve computing the change in the binding affinity of AlaRS for tRNA^Ala upon G3·U70 → A3·U70, G3·U70 → G3·C70, and A3·U70 → A3·C70 mutations in both the reactive and nonreactive complexes (Figure 2b). The results reveal several remarkable features. First, the reactive complex strongly favors tRNA^Ala/G·U with respect to the A·U variant (ΔΔG_bind ≈ 5 kcal/mol). The nonreactive state is almost nonselective between tRNA^Ala/G·U and tRNA^Ala/A·U (ΔΔG_bind ≈ 0.1 kcal/mol). Hence, the conformational change from NR to R can boost the discrimination strength (by ΔΔG_bind ≈ 5 kcal/mol) between the cognate tRNA^Ala/G·U and near-cognate tRNA^Ala/A·U, favoring the former. Second, both the reactive and nonreactive conformations disfavor the noncognate tRNA^Ala/G·C with an equal strength of ∼5 kcal/mol compared to the cognate tRNA^Ala/G·U. Third, the reactive complex shows the highest discriminatory power for tRNA^Ala/A·C rejection. Fourth, the difference in the discrimination strength between the reactive and nonreactive complexes can thus be linked with the purine (A3/G3)–AlaRS interaction.

Consideration of the free unbound tRNA in water is essential for understanding tRNA binding to AlaRS. Local geometrical differences between G3·U70 and A3·U70 in the free tRNA^Ala might alter the conformational preference (i.e., the orientation of the 3′-CCA arm of tRNA leading to reactive or nonreactive conformation) of the free tRNA^Ala in water. To understand the energetics of the conformational change in the free tRNA^Ala, we have also compared the mutation free energies for G3·U70 → A3·U70 in the reactive and nonreactive conformations of free tRNA^Ala in solution using the appropriate thermodynamic cycle (Figure S3). The very small computed ΔΔG_free^NR→R ≈ −0.2 ± 0.9 kcal/mol suggests that the geometrical difference between G3·U70 and A3·U70 does not play any significant role in driving the conformational change (NR ⇆ R) in the free tRNA^Ala in water.

X-ray Versus MD Structures of AlaRS–tRNA^Ala Complexes

The crystal structure²² of the reactive AlaRS–tRNA^Ala/G3·U70 (Figure 3a) complex shows a double hydrogen-bonded G3·U70 wobble base pair. This wobble pair forms H-bonds with AlaRS involving its major (U70–O4 with Asn359) and minor (G3–N2 with Asp450) groove sides. The 2′-OH group of C4 forms an H-bond with the side chain of Ser451 in the minor groove and C71–N4 with the main chain carbonyl of Asn359 in the major groove. The possibility of hydrogen bonding between the 2′-OH group of C71 and the side chain of Asp450 has also been suggested.²² In the nonreactive AlaRS–tRNA^Ala/A3·U70 complex (Figure 3b), A3 shifted upward away from the minor groove and U70 shifted downward away from the major groove, disrupting the tRNA–enzyme major–minor groove interactions. In the nonreactive complex, A76 at the 3′-CCA terminal of tRNA^Ala is placed near A3 (∼9 Å), whereas in the reactive complex (Figure 3a), A76 is over 30 Å away from G3.

Figure 3.

Structural insights from the X-ray and MD simulations of the AlaRS–tRNA^Ala complex. The 3.70 base pair is represented by sticks at the center; C4, C71, and A76 are the tRNA nucleotides shown in lines. The base of C4 has not been shown for clarity, and few hydrogens are shown to clarify the H-bonds. Amino acid residues interacting with the tRNA nucleotides are shown as sticks. (a) G3·U70–AlaRS interaction proposed in the X-ray structure.²² (b) A3·U70–AlaRS interaction proposed in the X-ray structure;²² color code is the same as in Figure 1b. MD structures of the reactive (left side) and nonreactive (right side) complexes are shown in (c–f), where tRNA is shown in yellow color and AlaRS in cyan color. Water is indicated by red spheres.

The equilibrated MD structures of G3·U70 and A3·U70 in complex with AlaRS (Figure 3c,d) are very similar to their corresponding template X-ray²² structures (Figure 3a,b), with a small MD-averaged RMSD of ∼1.9 Å, with a standard deviation of less than 0.2 Å. The loop region (Figure 1b) is highly flexible and its averaged RMSF is considerably large (Figures S4 and S5).

The robust structural features observed in our MD structures (Figure 3c,d) are as follows: (i) U70–O4 always makes an H-bond with the side chain Asn359 in both the reactive G3·U70 and nonreactive A3·U70 complexes; (ii) the side chain of Asn359 forms a stable H-bond with the main chain NH group of Asp727; this interaction locks the conformation of the Asn359 side chain such that its side chain −NH₂ points toward O4 of U70; (iii) the 2′-OH group of U70 forms an H-bond with the ribose ring oxygen of C71 and/or the backbone of Asp450; and (iv) the side chain of Arg483 of the highly flexible loop region (Figure 1b) forms a direct salt-bridge interaction with the side chain of Asp450 in the nonreactive AlaRS–tRNA^Ala/A3·U70 complex (Figure 3d) but not in the reactive AlaRS–tRNA^Ala/G3·U70 case (Figure 3c). The 2′-OH groups of C71 and C4 of tRNA form water-mediated/direct interactions with Asp450 and Ser451, respectively, in the minor groove of the reactive AlaRS–tRNA^Ala/G3·U70 complex (Figure 3c). This might indicate the importance of the 2′-OH group of the nearby nucleotides in the overall structural stability leading to facile alanylation.¹⁵

MD Structures of NonCognate AlaRS–tRNA^Ala Complexes

The reactive AlaRS–tRNA^Ala/A3·U70 (Figure 3e) and nonreactive AlaRS–tRNA^Ala/G3·U70 (Figure 3f) complexes were modeled by alchemically mutating G3/A3 into A3/G3 in the experimentally resolved reactive/nonreactive complex. The alchemical transformation AlaRS–tRNA^Ala/G3·U70 → AlaRS–tRNA^Ala/A3·U70 in the reactive complex (Figure 3e) results in the disruption of the G3–Asp450 interaction and the formation of an Arg483–Asp450 salt bridge. Note that the Arg483–Asp450 interaction in the reactive AlaRS–tRNA^Ala/A3·U70 complex (Figure 3e) is the same as in the nonreactive complex (Figure 3d), suggesting that the G3 → A3 mutation in the reactive complex might reorient the Arg483 side chain, resulting in the Arg483–Asp450 salt bridge.

The nonreactive AlaRS–tRNA^Ala/G3·U70 complex (Figure 3f) shows almost the same interaction pattern as seen in the reactive complex (Figure 3d), except for the formation of a water-mediated interaction between Asp450 and Arg483. A loss of the interaction between C70 and Asn359 in the major groove is observed in the G3·C70 and A3·C70 complexes (Figure 4) because of the electrostatic repulsion. In complexes with the A3·C70 mismatch (Figure 4c,d), A3 is shifted upward toward the major groove, whereas C70 is shifted downward toward the minor groove, thereby disrupting the interactions in the major and minor grooves. It should be noted that the Asp450–Arg483 salt-bridge interaction in the nonreactive state is consistently observed in the MD trajectories (Figures 3d,f and 4b,d).

Figure 4.

MD structures of the reactive (left side: a,c) and nonreactive (right side: b,d) complexes with tRNA containing G3·C70 and A3·C70 base pairs. Representation and color coding are the same as in Figure 3c–f.

Structure-Based Energetics and Its Connection to Kinetics

A key question is how the calculated structure-based energetics of Figure 2b is related to the observed kinetics. Our calculations suggest that the reactive complex strongly prefers tRNA^Ala/G3·U70 with respect to its A3·U70 variant, whereas the nonreactive complex is nonselective or only very weakly prefers the latter. It should be noted that alanine charging by AlaRS is also possible for G3·U70 containing mini- or microhelices^13,18 with a substantially increased Michaelis constant (K_M) but an almost unaffected k_cat. This suggests that all the helices containing G3·U70 undergo aminoacylation at a comparable rate once they are bound to the enzyme. A3·U70 in mini-/microhelices completely failed to demonstrate any aminoacylation by alanine, even after prolonged incubation with substrate-level enzyme concentration.^12,13,18 Recently, an approximately 100-fold difference in k_cat was reported between wild-type tRNA^Ala/G3·U70 and tRNA^Ala/A3·U70, whereas the K_M values were relatively similar. Moreover, single turnover measurements²² revealed that both the rate of the chemical step and the binding affinity were similar for the two cases, with differences being much smaller than the 2 orders of magnitude effect on k_cat. To account for this observation, a kinetic model was proposed where the substrate can bind reversibly in both reactive and nonreactive conformations, which can also interconvert on the enzyme. After an irreversible aminoacyl transfer step occurring from the reactive state, the system ends up in the reactive-bound product state where the product can either dissociate directly or via the nonreactive conformation, all these later steps being reversible. This complex model, with no less than 13 adjustable rate parameters, was fitted to the pre-steady-state kinetic curves.²² However, although this model correctly predicts the 100-fold change in k_cat, a closer examination of the resulting rate constants reveals that the k_cat/K_M and K_M values clearly disagree with the experiments. Thus, the predicted K_M for tRNA^Ala/A3·U70 is markedly lower (0.03 μM) than that for tRNA^Ala/G3·U70 (0.9 μM) because of its strong binding to the NR state implied by the model. Moreover, the fitted forward and reverse rate constants for substrate binding in the reactive and nonreactive conformations would also imply that the nonreactive state is more selective for tRNA^Ala/A3·U70 (>3 kcal/mol) than the reactive state is for tRNA^Ala/G3·U70 (∼0.7 kcal/mol).²² This is clearly at variance with our free-energy calculations based on the experimental crystal structures, which thus are not consistent with the proposed kinetic model. Furthermore, both the cognate and noncognate thermodynamic cycles connecting the free enzyme to its substrate-bound states in the reactive and nonreactive conformations are subject to an ∼2 kcal/mol closure error, if the fitted rate constants are used.

Application of Occam’s razor to the present problem suggests that a much simpler kinetic model, based on our calculated selectivities of the reactive and nonreactive states, can better account for the observed data. Such a sequential three-step model is shown in Figure 5, where an initial unselective binding step yields a nonreactive complex (E·tRNA^NR), which can subsequently reversibly convert to the reactive complex (E·tRNA^R). Once formed, E·tRNA^R undergoes aminoacylation with the same rate, irrespective of whether the tRNA is cognate or noncognate. According to our free-energy calculations, E·tRNA^R is strongly selective for cognate tRNA^Ala/G3·U70, and it is basically the different (Boltzmann) probabilities of reaching this state that are responsible for the observed difference in k_cat. A key feature is also that the initial E·tRNA^NR state does not show any significant kinetic or thermodynamic discrimination between cognate and noncognate tRNAs. It thus essentially has the same properties as those obtained here for the crystallographic nonreactive state, which could be considered as one example of an unspecific binding state. This scheme is thus similar to that proposed for the initial selection of aminoacyl–tRNA on the mRNA-programmed ribosome.⁴⁶ Further, the conformational change from the weakly selective nonreactive complex to the highly selective reactive complex is proposed to be downhill for cognate tRNA^Ala/G3·U70. The calculated energetics then automatically places the reactive AlaRS–tRNA^Ala/A3·U70 complex uphill from its nonreactive state. This would explain why the crystal structures only trap AlaRS–tRNA^Ala/G3·U70 in the reactive state and AlaRS–tRNA^Ala/A3·U70 in the nonreactive conformation. The kinetic parameters of the proposed scheme (Figure 5) are thus

1

and

2

Here, the absolute magnitude of K_M (and k_cat/K_M) is of course dependent on the effective association rate constant k₁, but the accuracy A = (k_cat/K_M)^cognate/(k_cat/K_M)^non-cognate is independent of k₁. By inserting the values of k₃ (aminoacylation step) in the correct experimental range^22,47 and adjusting k₃ so as to get K_M also in the correct range, this model accounts well for the experimental kinetic data when we insert our calculated values for the selectivities of the NR and R states. A numerical example is shown in Table 1.

Figure 5.

Schematic free-energy diagram for tRNA^Ala selection by AlaRS (without proofreading). Illustration of how the nonselective (nonreactive complex: NR) and highly selective (reactive complex: R) states can be used to drive aminoacylation favoring cognate tRNA/G3·U70. Binding free-energy differences between the cognate tRNA/G3·U70 and the noncognate tRNA/A3·U70 are approximately 0.1 and 5 kcal/mol for NR and R complexes, respectively. The reactive complex (R) is downhill for cognate tRNA/G3·U70 and uphill for noncognate tRNA/A3·U70 (see text). Biochemically plausible activation barriers for the elementary steps are depicted as ∼14–16 kcal/mol and are assumed to be the same for both the cognate and near-cognate tRNA.

Table 1. Numerical Analysis of Aminoacylation without Proofreading^a.

rate constant (s–1)	correct (G3·U70)	incorrect (A3·U70)	correct (kcal/mol)	incorrect (kcal/mol)
k1 (μM–1 s–1)	10	10	ΔG(NR)	ΔG(NR)
k–1	30	30	0	0
k2	500	500	ΔG(R)	ΔG(R)
k–2	20	50 000	–2.1	+3.1
k3	15	15
kcat	14.0 (14.4b)	0.15 (0.14b)
KM (μM)	1.6	3.0
kcat/KM (μM–1 s–1)	8.8	0.05

^aRate constants for the nonspecific AlaRS–tRNA association (k₁), dissociation from the nonspecific complex (k_–1), the nonreactive (NR) ↔ reactive (R) conformational change (k₂ and k_–2), and for aminoacylation from the reactive complex (k₃). The calculated relative binding free-energy values at the experimental temperature of 333 K²² are given in the two rightmost columns.

^bPre-steady-state kinetic constants from ref (22).

Concluding Discussion

Kinetic and structural studies^12,22 have certainly enriched our understanding of tRNA selection by AlaRS. We are, nevertheless, lacking a detailed structure-based free-energy landscape of tRNA selection by the enzyme, as the link between the kinetics and 3D structure is still missing. However, MD simulations should in principle be able to fill this gap. Here, we have performed MD free-energy calculations and computed the relative tRNA^Ala binding free energies to AlaRS in the reactive and nonreactive complexes for various cases, G3·U70, A3·U70, G3·C70, and A3·C70. It was found that the reactive complex consistently disfavors A3·U70, G3·C70, and A3·C70 with respect to the cognate tRNA^Ala/G3·U70 by ΔΔG over 5 kcal/mol. In contrast, the nonreactive complex does not discriminate between A3·U70 and G3·U70, although the discrimination against G3·C70 and A3·C70 is clearly evident. The magnitudes of the relative binding free energies (ΔΔG) are experimentally unknown. Hence, our calculated relative binding strengths cannot, at present, be compared to the experimental data, but their magnitudes appear biochemically realistic.

MD free-energy calculations adopted here have proven to be sufficiently accurate for the quantitative prediction of base-pairing energetics related to protein synthesis on ribosomes (including mRNA decoding during initiation, elongation, termination, and the role of tRNA modification in decoding, etc).^48,49 The application of MD simulations in studying RNA and DNA has been discussed extensively in the literature.^50,51 A truncated spherical region (radii ≈ 25–40 Å) cut out of the large molecular assembly and solvated by a spherical droplet/box of explicit water is often the preferred model for performing MD simulations.⁴⁹⁻⁵¹ If the energetics is controlled by localized interactions, then the reduced truncated model is a very good choice, which reduces the computational cost and improves the convergence by not sampling the irrelevant large-scale conformational motion.^{44−46,48,52,53} Large-scale conformational change certainly requires the consideration of a much larger truncated/complete biomolecular system and exhaustive sampling.

The reactive and nonreactive complexes are distinctly different in two aspects, the orientation of the tRNA 3′-CCA arm (as described previously)²² and the RNA–protein interactions in the minor groove. The 3′-CCA arm is placed in the aminoacylation site only in the reactive complex and folded back in the nonreactive complex (Figure 1b). The MD simulations suggest that the Arg483–Asp450 interaction in the minor groove is a unique feature of the nonreactive complex, as it is evident from most of the MD runs. It should be noted that the loop region (Figure 1b) containing Arg483 was poorly resolved (with a B-factor ≈ 195 Ų) in the X-ray structure.²² A different orientation of Arg483 in the reactive and nonreactive complexes is also evident from the X-ray structures (Figure S6). The large RMSF (Figure S4) obtained from the MD trajectories further suggests a high flexibility of this loop region. On the other hand, the Arg483–Asp450 salt bridge seems to be the characteristic feature of the nonreactive AlaRS–tRNA^Ala/A3·U70 complex (Figure S5) and is stable throughout the trajectories of the nonreactive complex.

Interestingly, the interaction between the negatively charged side chain of Asp450 and the exocyclic −NH₂ of G3 is crucial for the stability of the native complex (Figure 3c) and a major reason for the mutation of G3 to A3 leading to a large discrimination in the reactive complex.

It should be noted that the forward alchemical transformation of AlaRS–tRNA^Ala/G3·U70 into AlaRS–tRNA^Ala/A3·U70 in the reactive complex (Figure 3e) spontaneously produces the Arg483–Asp450 salt bridge, which appears as a characteristic structural feature of the nonreactive complex (Figure 3d). The NR conformation need not be unique, and different conformations of the −CCA end could probably yield nonreactive states with little selectivity (ΔΔG ≈ 0 kcal/mol). Hence, the observed X-ray conformation of the NR complex could be seen as one of those possibilities, and it seems clear that it is the difference in the local environment around the 3.70 base pair that is responsible for the differential selectivity.

We have shown here how a simple three-state kinetic model (Figure 5) can explain how the single wobble pair ensures tRNA specificity by altering k_cat (favoring correct tRNA by ∼100-fold) and keeping K_M more or less similar (Table 1). The activation barriers for the forward processes are considered to be identical for the correct and incorrect tRNAs in this model. Hence, irreversible amino acid attachment will take place once the “R” state is reached, regardless of the nature of tRNA (correct or incorrect). It is rather the differential probability of reaching the highly selective “R” complex that gives different k_cat values for correct and incorrect tRNA, thereby ensuring accuracy in tRNA selection by AlaRS.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.9b01827.

• MD setup; MD structure of AlaRs–tRNA^Ala/G3·U70 at the beginning and at the end of the reverse alchemical transformation (A3·U70 → G3·U70); thermodynamic cycle for tRNA conformational change in water; RMSF; MD versus X-ray flexible loop comparison; Arg483 comparison between experimentally resolved reactive and nonreactive complexes; partial changes; and detailed free-energy changes for the alchemical transformations (PDF)

The authors declare no competing financial interest.