Dynamic heterogeneity and life history variability in the Kittiwake

Abstract

1. Understanding the evolution of life histories requires an assessment of the process that generates variation in life histories. Within-population heterogeneity of life histories can be dynamically generated by stochastic variation of reproduction and survival or be generated by individual differences that are fixed at birth.

2. We show for the Kittiwake that dynamic heterogeneity is a sufficient explanation of observed variation of life histories.

3. The total heterogeneity in life histories has a small contribution from reproductive stage dynamics and a large contribution from survival differences. We quantify the diversity in life histories by metrics computed from the generating stochastic process.

4. We show how dynamic heterogeneity can be used as a null model and also how it can lead to positive associations between reproduction and survival across the lifespan.

5. We believe our approach to identifying the nature of among-individual heterogeneity yields important insights into the forces that generate within-population variation of life history traits. It provides an alternative to claims that fixed individual differences are a major determinant of heterogeneity in life histories.

INTRODUCTION

A central undertaking in biology is to explain and predict the evolution of life-histories (Stearns, 1992). Longitudinal studies of natural populations reveal great diversity in individual life histories within populations and large amounts of phenotypic variation among individuals for traits such as survival, onset of reproduction, reproductive output and reproductive frequencies to name a few (Beauplet et al., 2006). There are many possible explanations for this diversity. Genetic differences may explain little of the overall diversity in life histories because estimates of the heritability of life history traits in wild populations are typically small (Kruuk et al., 2000; Price & Schluter, 1991, but see Pettay et al., 2005; Reale & Festa-Bianchet, 2000). Constraints on life histories, such as a trade-off between reproduction and survival (Lack, 1947; Stearns, 1992; Williams, 1957), has been difficult to detect in natural populations (Ricklefs & Cadena, 2007; Van Noordwijk & de Jong, 1986); such trade-offs could reduce the variability in life histories. Environmental variation can generate variability in life histories among species, populations, or individuals (Knops, Koenig & Carmen, 2007; Lenormand, Roze & Rousset, 2009; Tavecchia et al., 2005), but its realized role is unclear. A fundamental question is how to quantify the realized contribution of each of these potential influences on life history diversity. The widespread view that life histories are optimal subject to trade-offs may be correct but remains problematic in the absence of a proper accounting of within-population trait variation (Orzack & Sober, 1994).

No matter what influence one regards as the primary determinant of life history diversity, distinguishing between heterogeneity caused by fixed differences among individuals and heterogeneity caused by stochastic events is an important goal. Fixed differences that arise at birth (Van Noordwijk & de Jong, 1986) are often described as quality, vitality, or frailty differences that cannot be observed directly (Vaupel, Manton & Stallard, 1979). Extensive effort has been undertaken to identify such fixed differences by searching for positive correlations between reproduction and survival throughout the life of individuals in natural populations (Cam et al., 2002; van de Pol & Verhulst, 2006; Wintrebert et al., 2005). In contrast, variation in biotic and abiotic environmental conditions (e.g. density dependence or weather, see Knops, Koenig & Carmen, 2007; Tavecchia et al., 2005) may generate variation in reproduction and survival. Tuljapurkar, Steiner & Orzack (2009) showed that such “dynamic heterogeneity” is a sufficient explanation of observed distributions of reproductive success in a variety of species.

Here, our aim is to assess whether the variation among individuals within a population of the Kittiwake (Rissa tridactyla), Linnaeus, is generated by fixed and/or dynamic differences. To identify the processes that generate variation in life histories we use an analysis in which stages are defined by different levels of reproductive success (Nichols et al., 1994) and estimate the Markovian transitions between stages over the lifetime. We quantify the diversity of individual life histories and persistence in life histories, and show how dynamic heterogeneity generates variation in survivorship and in lifetime reproduction among individuals in a cohort (population). If there are fixed differences we expect early, middle and late reproduction to be positively correlated, that is, there should be high persistence of reproductive stage over the lifetime; fixed differences should also reduce the diversity in life histories compared to dynamic differences. We demonstrate that the estimated multi-stage model can serve as a “null” model that is, one that can explain observed life history patterns without appeal to latent individual traits fixed at birth. Fixed differences should increase the variance in lifetime reproductive success and survival compared to the null model; we do not observe such an increase. Our results show that the variation among individuals in their life histories can be explained solely by dynamic heterogeneity. This finding conflicts with claims that heterogeneity of life histories in this species is due to fixed differences among individuals (Cam et al., 2002; Cam, Monnat & Royle, 2004).

FIELD METHODS

Kittiwakes are colonial seabirds that lay one to three eggs per clutch. We analyzed data on known-age individually-marked Kittiwakes nesting at the nature reserve of Goulien Cap-Sizun in Brittany, France (Cam et al., 1998). Unknown-aged birds (such as immigrants) were excluded from the analysis. Chicks were banded with unique combinations of color bands and a metal leg band. Birds were monitored between 1979 and 2002. We restricted the analyses to individuals that attempted to breed at least once, which upwardly biases our estimates of life time reproductive success and age at death. In any given year, an individual is faithful to its mate and reproduction can be allocated only to the pair (Coulson & Thomas, 1983; Naves, Monnat & Cam, 2006). However, individuals can change mates over time and we analyzed the sexes separately.

In a given breeding season, individuals that had not yet attempted to breed were classified as immature (I). Those that had previously attempted reproduction but skipped breeding in a given breeding season were classified as non-breeders (NB). Those that attempted to breed but did not succeed in fledging at least one chick were classified as failed breeders (FB). Finally, those that fledged one chick were classified as F1 and those that fledged two or three chicks were classified as F2. This classification follows that of Cam and Monnat (2000a). In a few instances, the outcome could not be accurately determined; our method for dealing with such outcomes (Fujiwara & Caswell, 2002) and more details on the data set is presented in the Supporting Information.

PATTERNS IN SURVIVAL AND REPRODUCTION

An individual life history can be viewed as a sequence of breeding stages terminating with death. We first analyzed the dynamics of life histories in terms of transitions between the five breeding stages described above. We also assessed whether and how survival rates are influenced by age, cohort, and two individual covariates, cumulative reproduction and age of first breeding. We used a capture-mark recapture (CMR) analysis (Lebreton et al., 1992) because no deaths were recorded; resighting of adults was perfect, whereas immatures were assumed to be unobservable (Cam et al., 1998). We used Akaikés Information Criteria corrected for small sample size and overdispersion (QAICc) for model selection in all analyses (Burnham & Anderson, 2002). Overdispersion was estimated using the logistic regression method available in program MARK (White & Burnham, 1999). We interpreted a difference of 2 or more between QAICc values to indicate that two models differed in their support (Burnham & Anderson, 2002). Detailed methods are provided in the Supporting Information.

REPRODUCTIVE STAGES AND EFFECTS OF AGE ON SURVIVAL RATES

Female survival rate depends on reproductive age and stage; in males, the support for an age- and stage-dependent survival rate model is equal to a model without such dependencies (see Table S1 of Supporting Information). For reasons of simplicity between sexes (see Supporting Information), we chose a model in which survival and transition rates in each sex are age-dependent up to age four and subsequently have age-independent values. We used the structure of this model and an explicit likelihood computation that accounted for uncertain events in order to estimate the final model for each sex (see Supporting Information).

REPRODUCTIVE STAGE DYNAMICS AND INDIVIDUAL HETEROGENEITY

Our multi-stage model describes reproductive-stage dynamics using a first-order Markov process. The estimated transition probability matrices Ψ_m(a) for males and Ψ_f(a) for females for ages a = 1, 2, 3, 4 and ≥ 5 years old are shown in the Supporting Information and Table 1. All individuals remain in stage I during the first two years of life. In years three and four, some individuals enter the breeding cohort and by age five most individuals (>95% males, >87% females) have attempted to breed.

Table 1.

Transition matrices Ψ_m for males and Ψ_f for females. Element i, j is the estimated probability of transition from stage i to j for individuals older than age four (for younger ages, see Supporting Information). Transition probabilities for mature stages are in italic.

		I	NB	FB	F1	F2
Ψm(>4) Males	I	0.205	0	0.465	0.249	0.081
	NB	0	0.205	0.463	0.268	0.064
	FB	0	0.124	0.469	0.285	0.122
	F1	0	0.064	0.371	0.393	0.172
	F2	0	0.03	0.352	0.38	0.238
Ψf(>4) Females	I	0.332	0	0.417	0.210	0.041
	NB	0	0.321	0.404	0.225	0.05
	FB	0	0.17	0.47	0.25	0.11
	F1	0	0.059	0.38	0.397	0.164
	F2	0	0.035	0.326	0.378	0.261

The reproductive stage dynamics past age four are governed by the transition matrix shown in Table 1. This matrix implies that two or more individuals who start in the same reproductive stage at a given age will likely have distinct reproductive stage sequences (trajectories) as they become older (Tuljapurkar et al. 2009) (see below and Fig. 1 a & b). Survival rates past age four are lower for non-breeders (NB survival rate is 0.73 for males, 0.78 for females) and failed breeders (FB survival rate is 0.79 for males and 0.78 for females) than for successful breeders (F1 survival rate is 0.82 for males, 0.83 for females; F2 survival rate is 0.80 for males, 0.81 for females) (see also Supporting Information). The positive association between survival and reproduction has been reported in previous studies of this species (Cam et al., 1998; Cam et al., 2002; Cam & Monnat, 2000b) and in many other species (Ricklefs et al., 2007; Van Noordwijk et al., 1986).

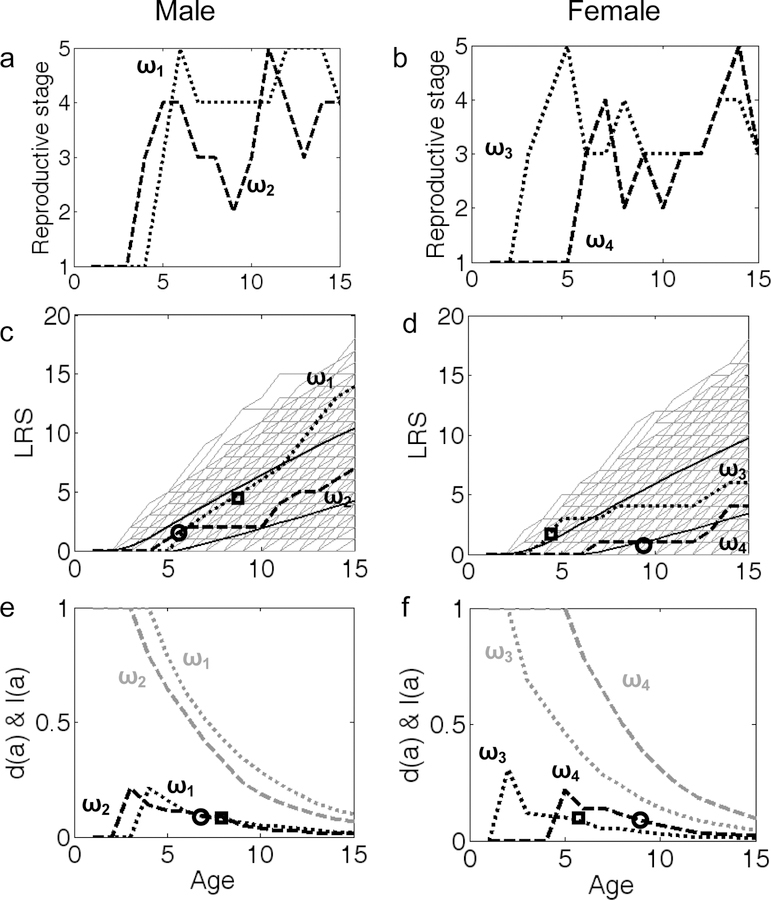
Fig 1:

Dynamic heterogeneity in fitness components generated by transitions between reproductive stages (see Table 1). (a & b) Four sample reproductive sequences (trajectories) ω₁ (dotted line) and ω₂ (hatched line) in males and ω₃ (dotted line) and ω₄ in females. (c & d) age-specific reproductive success, and (e & f) age-specific survivorship (gray lines) and death rate (black lines). (c & d) Thin gray lines show the age-specific “lifetime reproductive success”, LRS, of a large number of life history trajectories, black solid lines show 95% confidence intervals based on 3000 simulated trajectories. Open symbols mark the expected lifetime reproductive success (c & d) and expected age at death (e & f) for the example trajectories ω₁, ω₃ (squares) and ω₂, ω₄ (circles).

HOW DYNAMIC HETEROGENEITY GENERATES VARIABILITY IN LIFE HISTORIES AMONG INDVIDUALS

Our analysis describes a stochastic process that generates variation among life histories. We characterize the variation by describing the features of the underlying process, and quantify the diversity among and persistence within life histories. The variation is driven by differences among life history strategies and stochastic variation in survival of individuals following the same life history strategy. We show how our model can be used as a null model to describe variation in fitness.

Examples of reproductive stage sequences (ω_i) are shown in Fig. 1 a & b; we call these sequences “trajectories”. Each trajectory can also be seen as a life history strategy. Individuals change their reproductive stages frequently throughout life, which generates the variability among trajectories that is shown in Fig. 1 c & d. This variability is solely generated by the stochastic nature of the transitions in reproductive stages. Any reproductive trajectory ω_i has an associated probability of survival to age a, l(a), as shown in Fig. 1 e & f. The proportions of individuals of a cohort expected to die at age a, d(a), are shown in Fig. 1 e & f for the four example trajectories (black lines). We decompose the total variance among individuals as follows.

VARIABILITY GENERATED BY REPRODUCTIVE DYNAMICS

We quantify the variability generated solely by differences among life history strategies (Fig. 1 c & d). For each trajectory ω_i, we can estimate the mean lifetime reproductive success (LRS) for an individual if it follows a given trajectory ω_i (see Tuljapurkar et al. 2009 for formal calculations). For the four example trajectories shown in Fig. 1 c & d, the expected LRS (in fledglings) for males is 4.58 (ω₁) and 1.80 (ω₂) and for females it is 2.02 (ω₃) and 1.19 (ω₄). The mean LRS across all trajectories is 2.70 fledglings for males and 2.61 fledglings for females. The variance is 1.12 for males and 1.20 for females. The expected age at death for males is 8.16 (ω₁) and 6.90 (ω₂); for females, it is 5.50 (ω₃) and 8.81 (ω₄) (Fig. 1 e & f). The mean life expectancy across all trajectories is 7.71 years for males and 8.26 for females. The variance is 1.61 for males and 1.64 for females.

VARIABILITY GENERATED BY SURVIVAL

Individuals that follow the same trajectory ω_i, are expected to die at different ages; this generates within-trajectory variation in age at death and LRS (see Fig. 1 e & f). This variance in LRS for males is 35.39 (ω₁) and 4.70 (ω₂) and for females it is 5.88 (ω₃) and 3.04 (ω₄). The variance of LRS within trajectories is 8.82 for males and 8.41 for females. The variance in age at death for males is 21.76 (ω₁) and 18.59 (ω₂) and for females it is 18.16 (ω₃) and 18.37 (ω₄). The variance of age at death within all trajectories is 18.66 for males and 19.45 for females.

VARIATION GENERATED BY REPRODUCTIVE DYNAMICS AND SURVIVAL

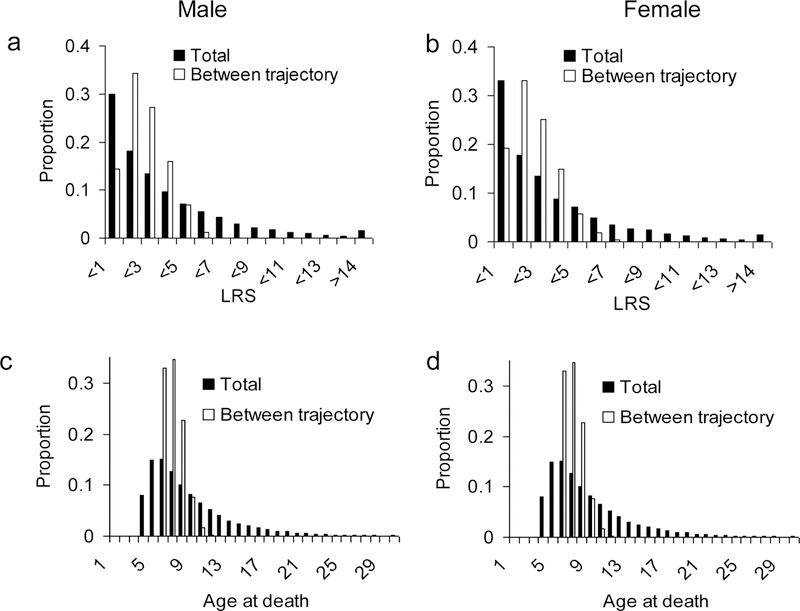
We compare the total distribution of LRS (Fig. 2 a & b) and the total distribution of age at death (Fig. 2 c & d) with the distribution generated by variation between trajectories. The variance between trajectories (LRS: 1.12 for males and 1.20 for females; age at death: 1.61 for males and 1.64 for females) is much smaller than variance within trajectories (LRS: 8.82 for males and 8.41 for females; age at death: 18.66 for males and 19.45 for females). This suggests that a substantial amount of the variation is generated by differences in survival not related to reproductive sequences (trajectories) and that fixed differences among individuals in their reproductive strategy contribute little to the overall variation.

Fig. 2:

Distributions of (a & b) lifetime reproductive success (LRS) and (c & d) age at death for male (a & c) and female (c & d) Kittiwakes. The total distribution (black bars) is generated from 10⁵ simulated individuals from the final multi stage model (see Supporting Information); the between-trajectory distribution is generated from the expected LRS and age at death of 3000 trajectories. The between-trajectory distribution is solely generated by dynamic heterogeneity and does not account for differences in age at death of individuals following the same trajectory.

QUANTIFYING DIVERSITY AND PERSISTENCE OF LIFE HISTORIES

The diversity of life histories can be estimated by the entropy of our model; we also determine correlations between early, middle, and late reproduction by estimating the persistence of an individual’s reproductive stage at any age a and its future reproductive success. Our estimate of entropy and persistence accounts for survival differences between individuals using matrix R (Matthews, 1970; see Supporting Information); previous analysis of this and other species (Tuljapurkar et al., 2009) did not account for survival differences and therefore are less accurate descriptors.

QUANTIFYING DIVERSITY

If all individuals follow one or a few trajectories that have similar survival rates for reproductive stages, the entropy, H, is close to 0. In such a case, differences between individual trajectories would be due only to fixed heterogeneity. Alternatively, if individuals experience at random the four mature stages (NB, FB, F1, F2) and survival between stages is identical, H has its maximum value [= ln(number of stages) = ln(4) = 1.39]. In this case, differences between individual trajectories are due only to dynamic heterogeneity. For the sex-specific matrices R_m and R_f (calculated from Ψ_m and Ψ_f in Table 1 and the stage survival estimates) we exclude the transient stage (I), compute the entropies of the resulting sub-matrices, and then compute the ratio entropy/maximum entropy (see Supporting Information). This scaled entropy is 0.87 in males and 0.88 in females, showing that there is substantial diversity in the trajectories. The scaled entropy estimates calculated from the transition matrices Ψ_m and Ψ_f (Table 1) (ignoring survival) differ slightly from these values in the Kittiwakes; for other species the two kinds of estimates can differ markedly (unpublished). The high estimate of scaled entropy is similar to that found for other natural populations (Tuljapurkar et al., 2009) and suggests that dynamic heterogeneity is an important source of variation between individual life histories.

PERSISTENCE OF REPRODUCTIVE SUCCESS

Persistence in reproductive success can be measured by the correlation between an individual’s reproductive stage at age a and its stage at age a + t, which is approximately exp(− t/τ), where τ = −1/log |λ₁| and λ₁ is the subdominant eigenvalue of the transition matrix R (see Supporting Information). The correlation between an individual’s breeding success two years apart is 0.05 (τ =0.739) for males and 0.09 (τ =1.139) for females.

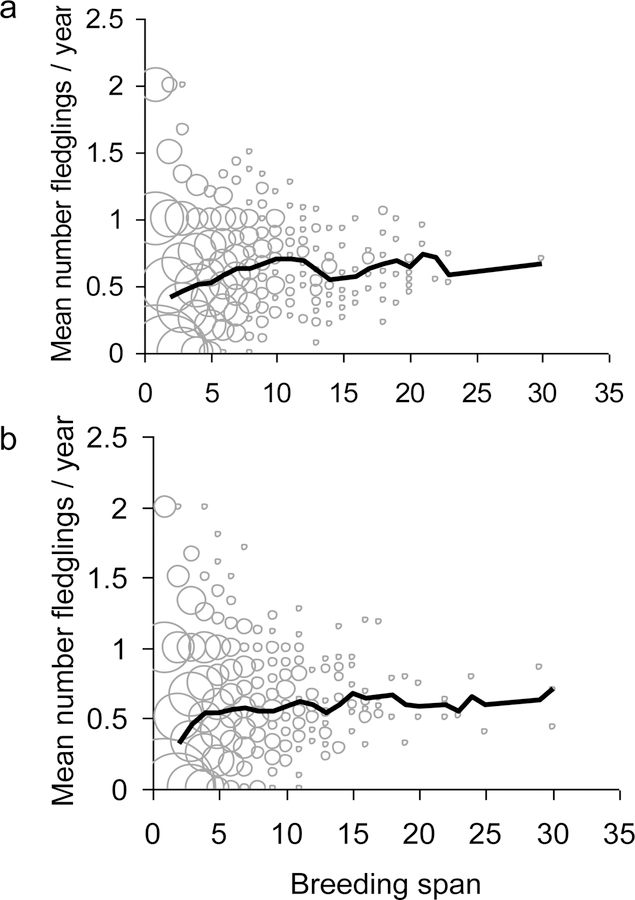
Another measure of persistence is the average time spent in a reproductive stage i before making a transition to another stage, which is 1/(1 – r_i,i), where r_i,i is the ith diagonal element of R. These averages for stages I, NB, FB, F1, and F2 are 1.35, 1.24, 1.87, 1.68, and 1.31 years for males and 1.71, 1.46, 1.85, 1.70, and 1.36 years for females. The transition from immature stage I to a breeding stage occurs at age three or four for approximately 78% of males and 61% of females; the average age of leaving stage I is 4.00 for males and 4.58 years for females. These estimates are close to the observed average ages of first breeding of 3.97 years for males and 4.36 for females. In our sample, the average time between first and last reproduction is 3.68 years for males and 3.71 years for females. These spans are much longer than the average residence times in any breeding stage, which implies that every individual is likely to change reproductive stage more than once during its reproductive life. The mean reproductive spans above are minimum estimates, because of right censoring in the data. Simulations based on a transition matrix estimated without right-censored data (see Fig. 5) yield a mean reproductive span of 4.92 years for males and 4.80 years for females.

Fig. 5:

Reproductive span versus average brood size during the reproductive span for 1000 simulated males (a) and females (b). Reproductive span is defined as the number of years between the ages of first and last reproduction. The thick black line shows the average brood size for a given reproductive span. The size of each grey circle is proportional to the number of individuals at the point.

MORTALITY PLATEAUS AND QUASI-STATIONARY STAGE DISTRIBUTIONS

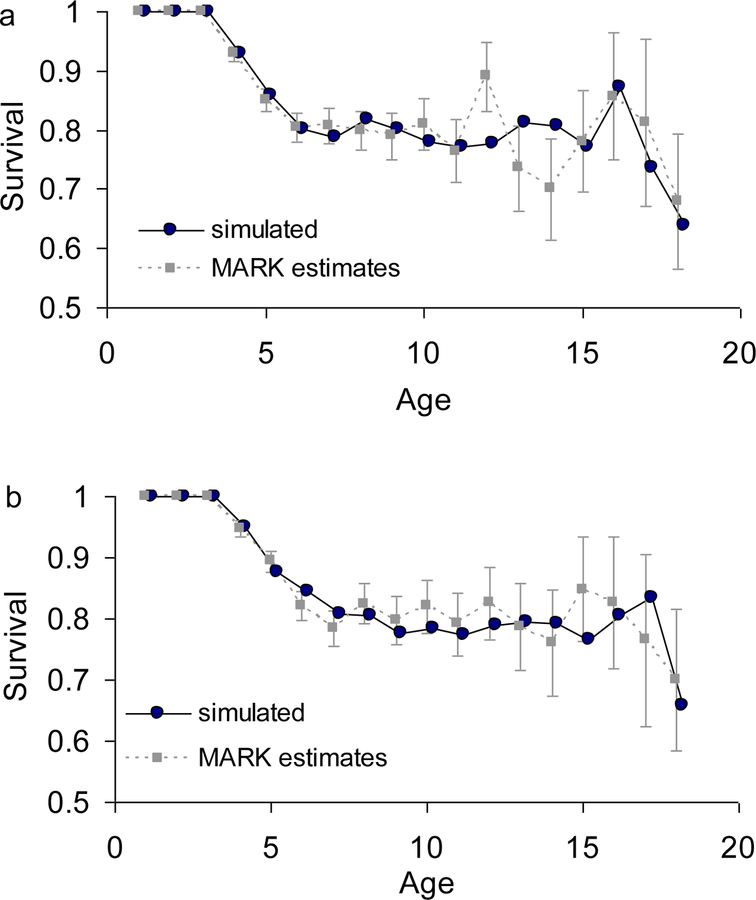
The dynamics of our multi-stage model generate a plateau in mid-life survival rates because every cohort eventually reaches a quasi-stationary stage distribution and the observed survival rates show a similar pattern (see below and Fig. 3). This plateau is not generated by intracohort selection operating on fixed heterogeneity (Horvitz & Tuljapurkar, 2008; Vaupel & Yashin, 1985).

Fig. 3:

Survival rates for (a) males and (b) females estimated in program MARK from model 1, Table 2 and averages from 1000 simulated males and females from the final multi stage model (see Supporting Information and Fig. 5). Survival rate in the first three years is fixed at 1.0.

A large fraction of adult individuals in any year are likely to be in stage FB (failed to fledge a chick) or in stage F1 (fledge one chick), because the quasi-stationary stage distribution has NB, FB, F1, and F2 fractions of 0.09, 0.41, 0.35, and 0.15, respectively, for males, and 0.13, 0.40, 0.32, and 0.15, respectively, for females. The expected time for a cohort to reach this quasi-stationary stage distribution is age (5 + 2 τ) ≈ 6.5 years for males and 7.3 years for females. Any one individual continues to switch reproductive stages over time. However, the proportions in the different stages are quasi-stationary after age seven or eight, as are the average annual reproduction and the average survival rate for a cohort.

We did not detect a decline of survival at older ages (past age seven) in either sex (Fig. 3 gray squares and dotted lines, see below and Table 2 for model selection). Cam et al. (2002) also found no senescence at the population level but suggested that this was due to intracohort selection on latent survival differences. We have shown that the observed pattern at the population level can be explained without invoking latent differences.

Table 2:

Influence of age (a), year (y), and cohort (c) on survival rates of males and females (models 1–8), and the influence of the individual covariates cumulative reproduction (CR) and age of first breeding attempt (AFB) on survival rates (models 9–12). Covariates are only included as linear and quadratic trends with underlying age-specificity in survival. In the covariate models, the influence of age is parametrically linear or quadratic.

#	Survival model	QAICc	Males ΔQAICc	Estimable parameters	QAICc	Females ΔQAICc	Estimable parameters
1	age	1589.29	0.00	15	1323.39	0.00	15
2	year	1903.67	314.38	20	1568.87	245.48	20
3	cohort	1923.39	334.10	19	1590.64	267.25	19
4	constant	1948.60	359.31	1	1595.62	272.23	1
5	age: linear trend	1677.80	88.51	2	1447.68	124.29	2
6	age: linear and quadratic trend	1637.96	48.67	3	1365.53	42.14	3
7	age x year	1721.32	132.03	157	1472.58	149.19	151
8	age + year	1604.02	14.73	35	1470.25	146.86	35
9	age: linear regressions for CR	1602.49	13.20	26	1406.28	82.89	25
10	age: linear & quadratic regressions for CR	1618.20	28.91	37	1379.10	55.71	35
11	age: linear regressions for AFB	1600.52	11.23	26	1405.01	81.62	25
12	age: linear & quadratic regressions for AFB	1613.11	23.82	34	1378.52	55.14	34

All QAICc values are corrected for overdispersion ĉ = 3.59 for males and 3.76 for females, as calculated from model 1.The overdispersion factor could not be calculated from model 7. The correction for overdispersion was applied in the covariate models (Models 9–12).

If there were a late-age decline in survival at the individual level the estimates we calculated from the original data (Fig. 3 gray squares and dotted lines) would deviate from the estimates from simulations in which survival rates above age four were assumed to be constant (Fig. 3 black circles and solid lines). The estimates match each other closely, suggesting that dynamic heterogeneity can explain the observed patterns and that intracohort selection need not be invoked.

DISTRIBUTION OF CUMULATIVE REPRODUCTION

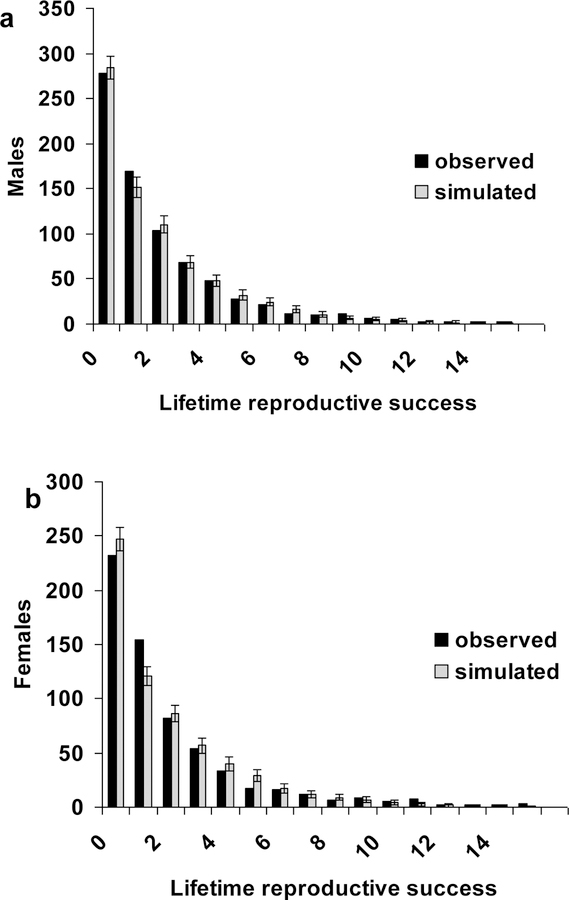
An important component of an individual’s relative fitness is lifetime reproductive success. Our multi-stage model predicts the distribution of LRS using simulated trajectories (see Supporting Information). Figure 4 shows the agreement between the simulated and observed distributions of LRS for both sexes (Two-sided Kolmogorov-Smirnov: males D = 0.1875, p-value = 0.9412; females D = 0.25, p-value = 0.6994; one-sided tests to assess whether there is a deficit or excess of low “quality” individuals are also non-significant). Our multi-stage model predicts a positive relationship between reproductive span and the average annual brood size (Fig. 5). Hence, individuals that live long also have large broods in any given year. Such individuals are simply lucky (see below).

Fig. 4:

Distribution of lifetime reproductive success (LRS) for males (a) and females (b). The simulated distribution is derived from 50 simulated populations whose reproductive and survival dynamics are governed by the final multi-stage model (Supporting Information). Note we use the term LRS, even though both the observed and simulated distributions include right censored individuals (see Supporting Information).

THE NATURE OF HETEROGENEITY

The comparison of the observed and simulated LRS distributions (Fig. 4) is more than a measure of the goodness-of-fit of our multi-stage model. The simulated LRS distributions can be used as a “null” model. Imagine that individuals with low values of a latent factor, Z, have lower survival at every reproductive stage as compared to those with high Z. Intra-cohort selection will cause low Z individuals to have lower LRS than expected with only dynamic heterogeneity; the converse would be true for individuals with high Z. The resulting distribution of LRS will have a higher variance than if it were generated solely by dynamic heterogeneity. A latent factor that affects breeding success will also do this. To this extent, the simulated distribution can be used as a “null” model in order to assess the nature of the observed distribution. In the present instance, the fit between the two distributions (Fig. 4) suggests that dynamic heterogeneity is sufficient to generate the observed heterogeneity of LRS. We acknowledge that higher-order Markov multi-stage models (see Brownie et al., 1993) are worthy of investigation; however, deriving meaningful estimates from such models requires much more data than are available in the present study.

Dynamic heterogeneity can generate a positive correlation between reproduction and survival. The increasing relationship between mean number of fledglings and breeding span (Fig. 5) is the same for the observed data set and for a simulated data set containing only dynamic heterogeneity (Slope estimates ± SE in Females: Observed = 0.0225 ± 0.0048, Simulated = 0.0241 ± 0.0048, test for difference in slopes, t = 0.269, P = 0.767, and Males: Observed = 0.0251 ± 0.0050, Simulated = 0.0242 ± 0.0050, test for difference in slopes t = −0.184, P = 0.854). The data set for the test statistics takes right censoring into account and therefore differs slightly from the one used in Fig. 5. Such a positive relationship between reproduction and survival has frequently been taken as evidence for fixed individual heterogeneity. A random-effect analysis of the simulated individuals shown in Fig. 5 would suggest that there is fixed heterogeneity influencing reproduction and/or survival. In contrast, when dynamic heterogeneity generates the positive correlation between reproduction and survival, individuals that survive and reproduce well are lucky. The point is not that fixed heterogeneity does not exist; instead, our point is that random effect models may tend to overestimate the extent of unobservable fixed effects.

AGE-DEPENDENT SURVIVAL PATTERNS

We now assess how survival rate depends on age, year, and cohort, but exclude reproductive dynamics (Models 1 to 4 in Table 2). In both sexes we found that age, rather than year or cohort, was the most important single influence on survival rate (the QAICc for model 1 is smaller than that for models 2 – 4). Models in which age-specific survival has a linear or parametric trend in age-specific survival were not better supported than the general age-specific model (QAICc for Model 1 is smaller as compared to that for Models 5 and 6). In our age-specific model (Model 1) the survival rate of individuals over five years old fluctuated between 0.68 and 0.89 for males (mean 0.79 ± 0.02 SE) and 0.70 and 0.85 (mean 0.80 ± 0.01 SE) for females (Fig. 3, grey symbols and dotted lines). There was no support for additional yearly variation of survival rate (compare the QAICc values for Models 1, 7 and 8).

INFLUENCE OF CUMULATIVE REPRODUCTION AND ONSET OF BREEDING ON SURVIVAL

Cumulative reproduction to age a and the age of the first breeding attempt did not influence survival rate at age a in either sex, as shown by reduced support for models including these covariates as compared to a model without covariates (in Table 2 compare model 1 without covariates with models 9 to 12 with covariates). This suggests that there are no substantial differences in individual quality that influence the covariates (see Cam et al., 2000a for a conflicting result with respect to onset of breeding on survival.) Cam et al. (2002) argued that latent quality differences explained most variability in breeding probabilities. In their analysis, the probability of a given future state does not depend on its present state, and any autocorrelation in a transition matrix is explained by unobserved fixed heterogeneity. A subsequent analysis found fixed heterogeneity for breeding probability after individuals dispersed (Cam et al., 2004) although there was no evidence of fixed heterogeneity for breeding success.

DISCUSSION

We have demonstrated how dynamic heterogeneity generates variability of lifetime reproductive success, and how it can be decomposed into contributions from survival differences of individuals following the same trajectory (reproductive sequence) and from reproductive and survival differences among trajectories.

Many life history studies characterize differences among a few defined reproductive sequences within a population and describe them as optimal life history strategies. Our results indicate that focusing on a few trajectories has little potential to explain the observed variability in the data, because most variability is associated with survival differences within trajectories and not among trajectories. Such a typological approach is limited, as there can be a large number of observed trajectories generated by dynamic heterogeneity (Fig. 1 c & d).

We have shown for the Kittiwake that there is a high diversity of reproductive trajectories (high entropy), and that breeding success does not persist across lifetimes. Individuals switch reproductive stages throughout their lives, and breeding success in a particular year has little correlation with breeding success in the future; specific causes behind stage transitions are likely environmental variation, cohort identity, mate choice, nest location, or colony location (Aebischer & Coulson, 1990; Cam et al., 2000a; Coulson, 1966; Coulson & Wooller, 1976; Danchin, Boulinier & Massot, 1998).

A common explanation for positive associations between reproduction and survival is fixed heterogeneity for a latent trait (Cam et al., 2002). There are several reasons why we believe that fixed differences are not a major influence, if any, on the traits we have examined in the Kittiwake. First, there is substantial diversity of life histories, as shown by high entropy; it is expected to be lower if latent traits have large effects. Second, a latent trait with large effect would generate a strong correlation of breeding success over an individual’s life, and we find a weak correlation. Third, natural selection on latent traits is expected to lead to differences in survival rates at old ages between the population and the individual level; however we did not find such differences (Fig. 3). The observed survival rate pattern is consistent with a mortality plateau generated solely by dynamic heterogeneity (Horvitz & Tuljapurkar, 2008) and differs from the pattern generated by intracohort selection operating on fixed heterogeneity (Vaupel & Yashin, 1985). Fourth, selection on fixed differences that affect survival and reproduction should generate more variance of lifetime reproductive success than is observed (Fig. 4). Previous analyses have estimated the variance in latent fixed traits using either Bayesian (Cam et al., 2002) or frailty (Wintrebert et al., 2005) methods. However, these approaches do not account for trait dynamics or for the breeding success in the previous year. Ignoring such influences can lead to spurious support for the existence of latent traits (see Fig. 5). Finally, we do not find an influence of cumulative reproduction or age of first breeding attempt on survival rates, which would be expected if there are large fixed effects.

We cannot prove that fixed differences are absent. Models that contain both dynamic and fixed heterogeneity are needed in order to estimate how much each contributes to the total variation among individual life histories. One approach is to extend the recent work of (Gimenez et al., 2007) to age-specific multi-stage models. Important work by Clark et al. (2005) showed for Taitu Hills rats (Praomys delectorum), Thomas, that adding random effects to stage dynamic models only slightly increases the variance in the estimated transition probabilities, but does not substantially change the transition probabilities. These results are consistent with our expectation that dynamic heterogeneity could be very common in natural populations (Tuljapurkar et al., 2009) and that fixed heterogeneity might be less important than commonly believed.

How might variability in fitness be maintained across generations if there is fixed heterogeneity? One possibility is that there is very low or even negative heritability in fixed traits (Coulson & Tuljapurkar, 2008). Dynamic heterogeneity generates variation anew each generation and does not alter the mean population fitness. A combination of dynamic heterogeneity and a small amount of fixed heterogeneity might plausibly be maintained over time, though we do not know the necessary theoretical conditions for such an equilibrium.

How general is our conclusion about the importance of dynamic heterogeneity as a generator of variability of life histories? Analyses similar to the one described here indicate that dynamic heterogeneity generates substantial heterogeneity of life history traits in the Mute Swan (Cygnus olor), Bechstein, and in the Northern Fulmar (Fulmarus glacialis), Linnaeus (unpublished; see also Tuljapurkar et al., 2009). The entropy of reproductive trajectories in the swan and the Fulmar is comparable to the Kittiwake. The autocorrelation is stronger in the swan than in the Kittiwake; the estimate for Fulmar is approximately equivalent to that of the Kittiwake. We did not find any fixed heterogeneity in the swan or Fulmar and simulated and observed LRS distributions for the swan and the Fulmar are in statistical agreement. Analysis of other species suggests that these results are not exceptional (Tuljapurkar et al. 2009).

Our dynamical approach can be applied to any focal trait that can be integrated in a multi-stage model. Observed patterns of fitness distributions can be compared to a “null” model solely generated by trait dynamics. The deviation between the distributions helps reveal the potential contributions of dynamical and fixed heterogeneity to life history variation. In this way, our approach leads to an improved understanding of the forces that shaped and maintain life history variation in natural populations.