Abstract
Summary
DIFFpop is an R package designed to simulate cellular differentiation hierarchies using either exponentially-expanding or fixed population sizes. The software includes functionalities to simulate clonal evolution due to the emergence of driver mutations under the infinite-allele assumption as well as options for simulation and analysis of single cell barcoding and labeling data. The software uses the Gillespie Stochastic Simulation Algorithm and a modification of expanding or fixed-size stochastic process models expanded to a large number of cell types and scenarios.
Availability and implementation
DIFFpop is available as an R-package along with vignettes on Github (https://github.com/ferlicjl/diffpop).
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Differentiation is a complex cellular process necessary for multicellular organisms to develop and maintain their tissue systems (Orkin and Zon, 2008). Cell populations throughout differentiation hierarchies have been characterized by increased clonality driven by stochasticity and selection (Akunuru and Geiger, 2016; Jaiswal et al., 2014; Steensma et al., 2015). Branching processes are a class of stochastic processes that can be used to model the growth and composition of reproducing populations based on growth parameters specified for the individuals that compose those populations (Haccou et al., 2005). Branching processes are used to investigate the dynamics of cancer evolution and questions regarding pre-existing versus newly acquired resistance using high complexity barcoding libraries, in which each single cell is tagged with a unique genetic barcode (Bhang et al., 2015). Contrasting the growing populations in a branching process, a stochastic process model known as the Moran model describes populations of strictly constant size in which cell proliferation events are balanced by cell death events (Moran, 1962). Simulation of complex processes such as cellular differentiation can be implemented using the Gillespie Stochastic Simulation Algorithm (SSA) (Gillespie, 1977).
DIFFpop uses the branching process, Moran process and Gillespie Algorithm to simulate cellular differentiation, where each barcode or cellular clone and its progeny are tracked over time. The process instantiates all populations using user-specified proliferation, death and differentiation parameters. Throughout a simulation, cellular ancestry can be tracked in each population of the hierarchy using individual barcodes. Selection is introduced to the system by choosing cells for proliferation according to their fitness. During a mitosis event, one daughter cell may harbor a new mutation with a specified probability, giving rise to a new clone. This new cell inherits the fitness of its parent plus an additional change in fitness chosen from a probability distribution specified by the user.
Our package was designed to work in tandem with experiments using cell labeling and barcoding in complex differentiation systems (Busch et al., 2015; Sun et al., 2014). Results from simulations using DIFFpop can then be compared to experimental data to eliminate sets of parameters that result in findings not compatible with available data.
2 Description
To simulate exponentially growing populations, DIFFpop uses the direct Stochastic Simulation Algorithm (Gillespie, 1977) to advance the simulation by first determining the time until the next event followed by a stochastic choice of the type of event taking place. For fixed-size populations, DIFFpop simulates a multi-type modified Moran model using tau-leaping (Gillespie, 2001) with the introduction of differentiation events, whereby events are coupled together to maintain fixed population sizes; for instance, a mitosis event generating an additional cell is followed by a differentiation or apoptosis event to eliminate a cell. In both simulation scenarios, when a mitosis event occurs, one daughter cell may mutate to produce a new clone with probability , where is the population of the parent cell. In such situations, new clones are formed according to the infinite allele assumption (Pakes, 1989), and the parameter for the change in fitness of the new clone is randomly chosen from a user-specified fitness distribution. As a default, fitness changes are drawn from a normal distribution such that the lower bound for the fitness of any clone is 0.
The flexible nature of the package allows the user to customize the process, easily change the underlying differentiation structure, parameters and distributions, and achieve updated results. The hierarchical structure, population types and attributes and event rates are specified using functions in R, allowing the user to quickly create multiple possible trees and implement simulations of each. Users may also vary the selective pressures at work in the cell populations by specifying population-level mutation rates and the distribution from which fitness changes of mutated cells are drawn. Setting the mutation probabilities to zero results in a process in which no new clones appear. Allowing for a positive mutation probability but setting the passenger probability, the probability that a mutation does not affect a clone’s fitness, to 1 simulates the infinite-allele process where mutations are recorded, but due to a lack of variability in fitness are selectively neutral (McDonald and Kimmel, 2015). After simulation initiation, no new barcodes are created, and therefore the maximum total number of barcodes is set at the initiation of the simulation, allowing for the calculation of diversity indices to compare populations with different model settings.
3 Applications
Our software package uses simulations to explore and test hypotheses in tandem with experimental barcoding or labeling data. The simulation outputs include statistics related to the population size, barcode diversity, event rates, mutation events and the fraction of labeled cells. Additionally, the user can specify how often to output a census of the entire system to longitudinally track clonal dynamics throughout the hierarchy. Users may then draw repeated samples from this population census to compare against data generated from single cell barcoding or cell labeling experiments.
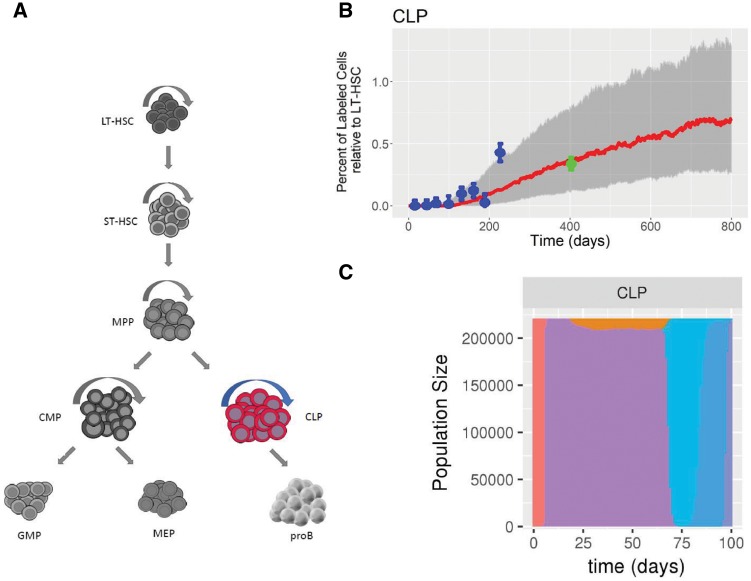
To illustrate a possible application to experimental data, DIFFpop simulations were run for a mouse model of the hematopoietic system in which a fraction of cells contain a fluorescent protein label. Parameters for the model were determined using the data and methods from a previous study (Busch et al., 2015). Using DIFFpop, we performed 1000 simulations of the model and recorded the median trajectory along with 25th and 75th quantile confidence bands for each cell population along with the experimental data from the mouse model (Fig. 1). We found that the simulated trajectories demonstrated good agreement with experimental results, including for data points from older mice that were not used in the determination of the simulation parameters. In addition to comparing model results to experimental data, other features of DIFFpop, such as simulations including barcoded cells, can be used to investigate cellular diversity in the hematopoietic system over time. A more detailed description and example code for this application can be found in the application document. This system was further explored using DIFFpop in two coding vignettes. Additional examples of experimental methods to which DIFFpop simulation results may be applied are provided in the Supplementary Material.
Fig. 1.
Visualization of DIFFpop outputs. (A) A schematic representation of the hematopoietic system. The common lymphoid progenitor (CLP) population is the initial population in the lymphoid branch of the hematopoietic system and the focus of panels B and C. Abbreviations: Long-term hematopoietic stem cell (LT), short-term hematopoietic stem cell (ST), multi-potent progenitor (MPP), common myeloid progenitor (CMP), common lymphoid progenitor (CLP), granulocyte-macrophage progenitor (GMP), megakaryocyte-erythroid progenitor (MEP), pro-B cell (proB). (B) Experimental label progression results from Busch et al. (blue points) and DIFFpop simulated trajectories (red lines, median trajectory; grey bands, 25th and 75th percentiles) for the CLP population. Experimental data points from beyond 400 days (green points) were not used during parameter estimation but are correctly predicted using simulated results. (C) Bar plot of clone sizes denoted by different colors over the first 100 days of simulation of the CLP population
4 Conclusion
DIFFpop simulates cellular differentiation including single cell barcoding and mutation acquisition under the infinite-allele assumption, tracking evolutionary dynamics and other model outputs. Estimation methods for complex differentiation systems, including multi-type branching processes and Moran models, quickly become intractable as the model complexity increases. Simulation methods such as DIFFpop provide an alternative method for investigation of these systems and can be performed quickly on a cluster.
Supplementary Material
Acknowledgements
The authors would like to thank the Michor lab for insightful discussions and for testing the code.
Funding
This work was supported by the Dana-Farber Cancer Institute Physical Science-Oncology Center; grant number NIH U54CA193461.
Conflict of Interest: none declared.
References
- Akunuru S., Geiger H. (2016) Aging, clonality, and rejuvenation of hematopoietic stem cells. Trends Mol. Med., 22, 701–712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhang H.-E. et al. (2015) Studying clonal dynamics in response to cancer therapy using high-complexity barcoding. Nat. Med., 21, 440. [DOI] [PubMed] [Google Scholar]
- Busch K. et al. (2015) Fundamental properties of unperturbed haematopoiesis from stem cells in vivo. Nature, 518, 542. [DOI] [PubMed] [Google Scholar]
- Gillespie D.T. (1977) Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem., 81, 2340–2361. [Google Scholar]
- Gillespie D.T. (2001) Approximate accelerated stochastic simulation of chemically reacting systems. J. Chem. Phys., 115, 1716–1733. [Google Scholar]
- Haccou P. et al. (2005) Branching Processes: Variation, growth, and Extinction of Populations. No. 5. Cambridge University Press. [Google Scholar]
- Jaiswal S. et al. (2014) Age-related clonal hematopoiesis associated with adverse outcomes. N. Engl. J. Med., 371, 2488–2498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDonald T.O., Kimmel M. (2015) A multitype infinite-allele branching process with applications to cancer evolution. J. Appl. Probab., 52, 864–876. [Google Scholar]
- Moran P.A.P. (1962) The Statistical Process of Evolutionary Theory. Clarendon Press. [Google Scholar]
- Orkin S.H., Zon L.I. (2008) Hematopoiesis: an evolving paradigm for stem cell biology. Cell, 132, 631–644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pakes A.G. (1989) An infinite alleles version of the Markov branching process. J. Austr. Math. Soc., 46, 146–169. [Google Scholar]
- Steensma D.P. et al. (2015) Clonal hematopoiesis of indeterminate potential and its distinction from myelodysplastic syndromes. Blood, 126, 9–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun J. et al. (2014) Clonal dynamics of native haematopoiesis. Nature, 514, 322. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.