Abstract
Motivation
Recent advances in high dimensional phenotyping bring time as an extra dimension into the phenotypes. This promotes the quantitative trait locus (QTL) studies of function-valued traits such as those related to growth and development. Existing approaches for analyzing functional traits utilize either parametric methods or semi-parametric approaches based on splines and wavelets. However, very limited choices of software tools are currently available for practical implementation of functional QTL mapping and variable selection.
Results
We propose a Bayesian Gaussian process (GP) approach for functional QTL mapping. We use GPs to model the continuously varying coefficients which describe how the effects of molecular markers on the quantitative trait are changing over time. We use an efficient gradient based algorithm to estimate the tuning parameters of GPs. Notably, the GP approach is directly applicable to the incomplete datasets having even larger than 50% missing data rate (among phenotypes). We further develop a stepwise algorithm to search through the model space in terms of genetic variants, and use a minimal increase of Bayesian posterior probability as a stopping rule to focus on only a small set of putative QTL. We also discuss the connection between GP and penalized B-splines and wavelets. On two simulated and three real datasets, our GP approach demonstrates great flexibility for modeling different types of phenotypic trajectories with low computational cost. The proposed model selection approach finds the most likely QTL reliably in tested datasets.
Availability and implementation
Software and simulated data are available as a MATLAB package ‘GPQTLmapping’, and they can be downloaded from GitHub (https://github.com/jpvanhat/GPQTLmapping). Real datasets used in case studies are publicly available at QTL Archive.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Many quantitative traits (such as growth and development) are dynamically varying in time and characterized by the underlying age-related genetic process. In collected datasets of such function-valued traits, repeated measurements are available over multiple time points. Modern high-throughput phenotyping approaches have been increasingly applicable in the field of animal and plant genetics to acquire a high resolution time course data, with hundreds of individuals and hundreds of time points. This makes it possible to combine information (‘borrow strength’) over time points and jointly model the time-dependent measurements, which may increase the statistical power to identify significant genetic variation associated with the time-dependent traits. Such a principle is currently routinely used in approaches developed for mapping quantitative trait loci (QTLs) in function-valued traits (see e.g. Li and Sillanpää, 2015; Wu and Lin, 2006).
Many different parametric and non-parametric techniques have been applied in functional QTL mapping literature to fit a smooth function or curve over time points. These include, e.g. parametric maximum likelihood approaches (Ma et al., 2002), estimation equation (Xiong et al., 2011), two-stage methods (Li et al., 2014; Liu et al., 2018), a simple regression based method (Kwak et al., 2014), a functional principal component approach (Kwak et al., 2016), random regression (Ning et al., 2017), penalized regression (Li et al., 2015) and Bayesian methods (Sillanpää et al., 2012; Yang and Xu, 2007). Li and Sillanpää (2013) used Bayesian p-splines with (non-parametric) B-spline bases to model each marker’s effect on phenotype over time. A unique property of the method was the degree of smoothness of each QTL trajectory was determined automatically. Their estimation was performed in a variational Bayes framework and they used a multiple-marker model considering marker contributions jointly and selecting model variables (QTL) in a stepwise manner. Residual dependence between time points was handled by assuming autoregressive AR(1) covariance structure. The related spline-based models for function-valued traits were previously presented in a mixed model context (Fan et al., 2012; Yang et al., 2009) and will be presented in a Gaussian process (GP, Rasmussen and Williams, 2006) model context here.
A GP is a stochastic process that can be used to set probability distribution over functions (Rasmussen and Williams, 2006). Hence, it is especially attractive for longitudinal studies where the aim is to estimate functional responses. In genomics, GP regression methods have been proposed to analyze gene expression and transcription data (Äijö et al., 2014; Honkela et al., 2011, 2015; Nguyen et al., 2016), and detect gene-to-gene interactions (Zou et al., 2010). Use of GP models for longitudinal traits have been proposed for heritability estimation (Jaffrezic and Pletcher, 2000; Pletcher and Geyer, 1999). Here, we formulate a similar model to Li and Sillanpää (2013) in a GP framework and show that it provides a competitive and flexible alternative to it. The estimation of the model hyperparameters is performed using maximum a posterior (MAP) with gradient based optimization after which the inference on functional traits is done analytically. Another notable feature of the GP approach is that it can efficiently marginalize out the missing data during the estimation procedure. This avoids an extra step of imputation of the missing data done ahead of QTL analysis (Kwak et al., 2014).
Simultaneous estimation of function-valued traits of either a vast amount of markers and/or time points is statistically and computationally challenging (Kwak et al., 2014). Variable selection can be used to keep only the most important loci in the model (e.g. loci which are most associated with the quantitative traits) and discard the irrelevant ones. This can greatly reduce the dimension of the model speeding up QTL mapping and making the results more interpretable. Similar to Li and Sillanpää (2013), we adopted a (forward) stepwise approach for variable selection. However, we propose a novel extension to their method which allows for variable selection according to approximate Bayesian posterior probabilities of alternative marker combinations. We propose a novel prior that penalizes the complexity of the model in terms of the number of time points.
The structure of the rest of the article is as follows. In the Section 2, we introduce the GP regression model for analyzing function-valued QTL data, the Bayesian forward selection approach to select the most important markers and the MAP estimate for the hyperparameters. In the Section 3, we evaluate the performance of our novel method under five public datasets, including two simulated datasets following the scheme of Li and Sillanpää (2013), an Arabidopsis dataset (Moore et al., 2013), a mouse body weight data (Gray et al., 2015) and a mouse behavior dataset (Xiong et al., 2011). In the Section 5, we summarize the strength of our GP approach, and also point out some future research directions.
2 Materials and methods
2.1 GP model for functional QTL mapping
A multivariate Gaussian linear regression model for functional QTL mapping for individuals and markers can be specified as
| (1) |
| (1) |
where yi(t) is the measurement of the phenotypic value of individual i at time t and β0(t) is the intercept term representing the non-genetic additive effect at time point t. The genotype of individual i at marker j is denoted by xij and coded as 1 for genotype AA, 0 for Aa and −1 for aa; βj(t) is the additive effect of marker j at time t and ϵi(t) is the Gaussian residual error. Here, we assumed either independent residuals or a first order continuous time autoregressive residual model [AR(1)] (Hartmann et al., 2017). For k measurement time points, the residual distribution is then . With independent errors, the covariance matrix where is a k × k identity matrix and is the residual variance. In the AR(1) model where ρϵ is the autocorrelation decay parameter. In model (1), the effects of multiple loci are included in the same equation and we assume no dominance effects.
We model the dependency between the observations at multiple time points with a GP prior for the regression coefficients representing the genetic additive effects
| (2) |
| (2) |
where denotes the covariance between additive effects at any two time points (). A GP is fully defined by its covariance and mean functions (here we fixed the mean function at zero) which determine the properties of the process, such as its smoothness and variability. This suggests that we can introduce a certain degree of smoothness via the prior on additive effects straightforwardly by selecting a covariance function.
Here we use the Mátern covariance function (Fahrmeir and Kneib, 2011).
| (3) |
| (3) |
where Kν(⋅) represents a modified Bessel function, ν is the degrees of freedom, ρ is a non-negative decay parameter which governs how fast the correlation between two function values drops and σ2 is a variance parameter governing the a priori variance of βj(t). The Bessel function is available in closed form for ν = 1/2, 3/2, 5/2,… leading to an analytical representation of the covariance. The ν parameter influences the level of smoothness in the additive effects. The smoothness of the estimated effect increases as a function of ν (Supplementary Fig S1). At the limit ν → ∞ we get the widely used Gaussian covariance function (Rasmussen and Williams, 2006). Other choices of the covariance function could also be used and interestingly, the Bayesian penalized B-spline regression introduced in Li and Sillanpää (2013) can also be considered as a special case of the GP model (see the online Supplementary Material). In our experiments ν = 5/2 performed well and it is used in all of our case studies,
| (4) |
| (4) |
We denote the covariance function parameters by θ and the residual covariance parameters by θϵ and refer to them jointly as hyperparameters. With iid residuals and with AR(1) residuals . All additive effects can have their own variance and decay parameters, in which case , or share the same parameters, in which case . We follow the principles of weakly informative priors that penalize for model complexity (Hartmann et al., 2017; Simpson et al., 2017) when setting the hyperpriors. The inverse of decay parameters, 1/ρ, was assigned with a half Student-t prior with scale 0.1 and 4 degrees of freedom, which favors smoother functions, and the variance parameter, σ2, was given a half Student-t prior with scale 1 and 4 degrees of freedom. The residual variance was given an Inverse Gamma prior Inv-Ga(α, β) with α = β = 10–4 and the residual length-scale ρϵ was given a half Student-t prior with scale 0.1 and 4 degrees of freedom, which favors short correlation times.
2.2 Variable selection
2.2.1 Variable selection using posterior probabilities of alternative models
One of the key questions in QTL mapping is variable selection; i.e. which markers should be included into the model (1). Here, we conduct the variable selection using (approximate) Bayesian posterior probabilities for alternative models. We denote by the total number of markers and by a model with a certain subset of them. A model’s posterior probability,
| (5) |
| (5) |
where is the marginal likelihood (ML) of a model and is model’s prior probability, which represents its credibility among the alternatives after conditioning to the data (O’Hagan and Forster, 2004; Piironen and Vehtari, 2017). First, we search for the model with the MAP probability. After that we use this model to map the marker specific function-valued traits as detailed in Section 2.3.
In practice, evaluating all a priori plausible models becomes infeasible when the number of markers is large. Alternatively, a (forward) stepwise approach was used here to only focus on a low dimension of the model space. Briefly, the forward search algorithm starts from a null model with only the intercept term, and at each step it adds to the model a new variable (i.e. a marker), which may improve the model by maximizing the model posterior. The model search stops when either the model posterior cannot be improved anymore, or the maximum number of iterations specified by the user has been reached.
2.2.2 Marginal likelihood
A GP prior for the additive effects implies that we can analytically marginalize over them. Moreover, the marginalization properties of a GP allow for easy treatment of data where measurements are missing from some individuals and time points. For notational simplicity we assume that all individuals are measured at the same time points and comment on missing data when needed. The conditional distribution of observations given the hyperparameters is
| (6) |
| (6) |
where collects all measured phenotypic values arranged so that first we have all measurements for individual 1, then for individual 2 and so on. The matrix is a block diagonal matrix where the j’th block contains the covariance matrix of βj. The matrix X is an such that , where Equation (6) implies also the hyperparameters’ ML and can be computed for any collection of observations. If observations for an individual are missing for some time points, we just remove the corresponding rows from y and X and the corresponding rows and columns of Σϵ. Calculating (6) as written is inefficient since it involves inversion of the nk × nk covariance matrix which is easily overwhelmingly large. We use the Woodbury–Sherman–Morrison lemma (Harville, 1997) and sparse matrix routines (Davis, 2006) for efficient implementation as described in detail in the Supplementary Material. Given (6) a model’s ML is
| (7) |
| (7) |
Calculating the likelihood requires computationally intensive numerical integration over the hyperparameters (Hartmann et al., 2017). Since the number of alternative models, , is extremely large, carrying this integration out for all compared models would render the approach impractically slow. We propose to simplify the ML calculations by fixing the covariance function parameters and integrating numerically only over the residual covariance parameters.
As the first option we fix the covariance function parameters to their MAP estimates which can be found with gradient based optimization as described in Section 2.3. This is justified since the ML surface (6) is rather insensitive to small changes in covariance function parameters near their MAP estimate (Vanhatalo et al., 2010; Zhang, 2004). To avoid time consuming optimization with very large datasets, we tested also fixing the covariance function parameters to a pre-defined constant. We set to a value that allows modeling the variation in trait values; for normalized trait values. Analogously to non-longitudinal models the variable selection with fixed values can be seen as an alternative to optimizing the variance parameters with shrinkage priors. When fixing the decay parameters ρj, we use prior understanding about the functional traits to guide the choice. If the longitudinal traits are known to vary fast (slow) we adjust the decay parameter to small (large) values so that the prior predictive draws from GP look reasonable for the modeled trait. As a general approach, we set ρ=SD of the measurement times (in practice ρ = 1 and the observation times are standardized to have mean zero and standard deviation one). This choice led to reliable variable selection in our experiments.
After fixing θ, we marginalize over using grid integration (Monahan, 2011), such that in case of the iid residuals model
| (8) |
| (8) |
where are integration points and is the width of the integration grid cell. This summation can be conducted efficiently by constructing the grid around MAP estimate of θϵ and parallelizing the summation.
2.2.3 Priors for alternative models
A prior for alternative models is equivalent to giving non-zero prior probability for an additive effect to be zero. A typical approach to construct a model prior in non-dynamic QTL models is the following. Let be a latent variable that defines whether marker j has non-zero (zj = 1) additive effect or not (zj = 0). A model, M, can then be indexed by a vector . We assume that a priori the expected number of important markers is m and each marker is equally likely to be important. Then, the prior probability for a marker to have non-zero additive effect is . Hence, the prior probability for a model M is where . This prior over the model space has been used by, e.g. Benner et al. (2016) in (non-dynamic) genome-wide association studies and is equivalent to the spike-and-slab prior for additive effects (O’Hara and Sillanpää, 2009).
In our work, additive effects are stochastic processes and, hence, each marker has an infinite number of additive effects (one for every possible point in time). To accommodate this, the latent variable zj is extended to a latent function zj(t) and instead of giving prior probability for zj = 0 we define a stochastic process for zj(t). This extension is similar to construction of spatially and spatio-temporally structured spike-and-slab priors but instead of working with a finite dimensional vector (Andersen et al., 2014, 2017), we define the spike-and-slab prior for a stochastic process (see Supplementary Material). To summarize, when constructing the prior process for we assume for all t and j and restrict the model space to consider only models where zj(t) is either one or zero for all t. When calculating a model’s posterior conditional on finite data at k measurement times, the model prior corresponds to the marginal prior probability where is a matrix of latent variables for markers at times . The resulting prior probability for a model with p non-zero markers is
| (9) |
| (9) |
which is analogous to the spike-and-slab prior in non-dynamic studies with the difference that the total number of active and non-active markers is multiplied by the number of time points in the data. Intuitively this can be understood so that the model prior has to account for the fact that the number of parameters in model (1) increases with the number of measurement time points.
By choosing the marker inclusion probability π to be small, the model prior penalizes the number of markers included in the model favoring a parsimonious model. This is in line with the oligogenic assumption for genetic architecture which suggests that there should only be a few markers that contribute significantly to (dynamic) trait variation. Hence, m should be of the order of 10 or less. To avoid explicitly determining a value of π, we could alternatively assign a Beta prior to π, and calculate the marginal probability of model M by integrating out π as , where B represents the Beta function. The hyperparameters α and β can be chosen in a way that the prior mean of the Beta prior equals m but there is significant variation around it.
2.3 Quantitative trait mapping: inference with selected markers
After selecting the markers to be included in the model, we optimize the hyperparameters to their (marginal) MAP estimate
| (10) |
| (10) |
where is the prior for the hyperparameters and is given in (6). We search for the MAP solution with a scaled conjugate-gradient algorithm.
We use the multivariate Gaussian equations (O’Hagan and Forster, 2004) to derive the (conditional) posterior predictive distribution of the additive effects at any collection of time points
| (11) |
| (11) |
Here, collects all the values of additive effects at times and . Hence, conditional on the hyperparameters we can analytically calculate the mean and variance of the additive effects. Note also that we have denoted the prediction times with in order to emphasize that the predictive distribution can be calculated for any collection of times, not only on measurement points. This allows for prediction of additive effects at missing time points. A computationally demanding alternative approach would be to approximate the marginal posterior distribution using Markov chain Monte Carlo. In this case, we would first sample from the posterior , then marginalize over θ, θϵ by sampling β from the multivariate Gaussian (11) for each joint sample of θ and θϵ.
The trait heritability or the proportion of phenotypic variation explained by molecular markers can be estimated for multiple time points analogously to the heritability estimation for a single time point (Sillanpää, 2011). For each time point tr, we first estimate the residual variance as , where m is the total number of markers included in the optimal model (see Section 2.2). The heritability at the given time point is then defined as .
3 Experiments
The GP analysis was conducted on two simulated and three real datasets as previously described. In all the examples, the variable selection was conducted first to determine an optimal subset of markers to be included in the model based on model posterior probabilities. The maximum number of iterations (i.e. markers) of the variable selection is specified as 15 in the simulation studies, and 10 in all the real datasets. Selected markers were judged as putative QTL and the quantitative trait mapping was done using these markers. We ran the experiments with both iid and AR(1) residual structures, but report the results for iid residuals only given lack of significant differences between the two residual error models. For variable selection, we tested both optimizing the hyperparameters to their MAP estimate and fixing them to the pre-defined constants. Since the putative QTL obtained with these two methods were identical, we report the results only for the latter. In the Bernoulli prior for markers, we tested π = 0.01 and π = 0.2 as two default choices of hyperparameters (a prior sensitivity analysis is illustrated in Fig. 1), as well as a third option a Beta(1, 1) prior to π and integrating it out. We compared our method to the Bayesian p-splines method of Li and Sillanpää (2013) and to the stability selection method (Alexander and Lange, 2011, see Supplementary Material for details; Meinshausen and Bühlmann, 2010) to measure the importance of the markers and judge QTL.
Fig. 1.
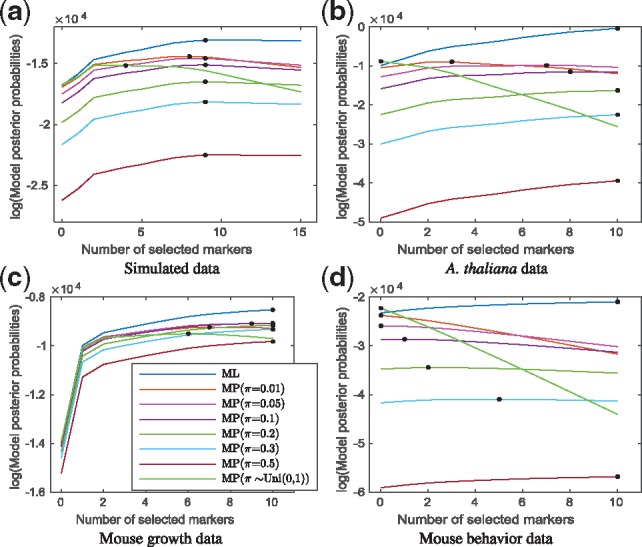
The change of ML and posterior model probabilities in (a) small simulated (b) A.thaliana (c) mouse growth and (d) mouse behavior datasets [assuming a Bernoulli prior with marker inclusion probabilities π =0.01, 0.05, 0.1, 0.2, 0.3, 0.5 as well as Beta(1, 1) prior for π and integrating it out] over the number of markers included in the model under the forward selection procedure (in solid lines). The asterisks indicate the optimal number of included markers corresponding to the maximum of the ML or posterior model probabilities. (a) Simulated data, (b) A.thaliana data, (c) Mouse growth data and (d) Mouse behavior data
3.1 Simulated analyses
The first, small simulated dataset includes 453 single nucleotide polymorphism (SNP) markers distributed over 5 chromosomes of 1 Morgan each from 2025 individuals with a population structure as in Coster et al. (2010). New phenotypic data were simulated in the same way as in Li and Sillanpää (2013). Briefly, on the basis of the genotypic data of a sub-sample of 500 individuals, we simulated new phenotypic data with 9 additive QTL (for the markers at 40, 56 and 88 cM of Chr1, 4, 31 and 88 cM of Chr2, 25 cM of Chr3, 85 cM of Chr4 and 81 cM of Chr5) and an intercept term in the simulation model. The coefficients were simulated to have various shapes at different QTL. The functional forms of the varying coefficients of the nine QTL can be found in Li and Sillanpää (2013). The simulation was replicated 50 times to measure the GP’s statistical power to detect QTL and its ability to control false positives. To evaluate the performance of the GP approach under incomplete data, we repeated simulation study generating completely at random 5, 10, 15 and 20 missing data points for each of the 500 individuals.
The second, large simulated dataset was created on the basis of a genome-wide marker dataset of a commercial outbred mouse population (Parker et al., 2016). The original genotype set comprised over 200 000 SNPs distributed over 1150 individuals. To reduce the computational complexity of the analysis, we selected 10 015 markers at every 20 kb of the physical map to be included in the study. To evaluate whether the GP approach is sensitive to the sample size, n = 100, 200, 500 and 1000 individuals were randomly selected to generate phenotypes. As in the previous simulated dataset, we simulated time-dependent additive effects based on nine QTL as well as an intercept term. The simulation was replicated 10 times to evaluate the average performance of the methods.
3.2 Mouse growth data
The intercross F2 mouse dataset was initially introduced by Gray et al. (2015) in a study on genetic regulation of extreme phenotypes in an island population. An F2 population comprising 1374 individuals was generated by crossing Gough Island mice and mainland mice (denoted as WSB). The body weights were measured from 1 week to 16 weeks age for all mice. Only 1212 mice with missing phenotypes at <4 time points were used in the QTL study. Genotyping was done using an llumina Infinium array, which resulted in 11 833 markers. Since the nearby markers in the linkage map were highly correlated with each other, they may represent the same QTL. Hence, we applied a bin approach introduced in Xu (2013) to divide the linkage map to many non-overlapping windows with roughly 10 cM length. In each bin, we calculated the mean genotypic value of the SNPs located within that bin, and used the average genotypes to replace the original SNP data. Consequently, the 11 833 markers were reduced to 116 bins. Sex was also included in the analysis as an extra covariate.
3.3 Mouse behavior data
The dataset was introduced by Xiong et al. (2011). The phenotypic data contains active state probabilities () with 222 repeated measurements of 89 backcross mice at consecutive 6-min time intervals in a 24-h period (from 1:48 pm–1: 54 pm to 11: 54 am–12: 00 am, with 7 pm–7 am as dark period and otherwise as light period). The genotypic data consist of 233 informative polymorphic SNP markers distributed over 19 chromosomes. Before the analysis, the missing genotypes at a SNP were imputed by borrowing the known genotypic information from the flanking markers (Haley and Knott, 1992). As in Li and Sillanpää (2013), a logit transformation was applied to the active state probabilities to make the phenotypes more normally distributed before the analysis.
3.4 Arabidopsis thaliana datasets
The dataset comes from a study (Moore et al., 2013) aimed at identifying QTL influencing the root gravitropism in Arabidopsis thaliana. In total 162 Arabidopsis recombinant inbred lines were generated, with 8–20 replicate genotypes in each line. For simplicity, only one replicate from each recombinant inbred line was used in the analysis. The phenotypes were measured at 241 time points, every 2 min for 8 h. There were 234 SNPs distributed over 5 chromosomes. Missing genotypes were imputed in the same way as in the mouse behavior data.
3.5 Data availability
The A.thaliana, mouse growth and mouse behavior data are available at QTL Archive http://qtlarchive.org/db/q? pg=projdetails&proj=moore_2013b, http://phenome.jax.org/db/q? rtn=projects/projdet&reqprojid=539, http://qtlarchive.org/db/q? pg=projdetails&proj=xiong_2011. The simulated data are available as Supplementary Material.
4 Results
4.1 Analysis of simulated replicates
The variable selection when setting π = 0.01 had small false positive and false negative rates correctly identifying seven out of nine true significant markers in at least half of 50 replicates (Supplementary Table S1, Fig. 2a). Applying a more liberal inclusion probability (π = 0.2) compared to the true 9/453= 0.02 QTL fraction, all the nine simulated QTL were correctly detected (Fig. 2b), but the false positive rate increased at the same time. Stability selection (conducted only on a single replicate) also correctly identified the same nine markers as significant loci (Fig. 2c). In the nine QTL model, the estimated QTL effects over time were almost identical compared to the true simulated effects (Fig. 2b), and they together explained 20–55% of the phenotypic variation over time based on the heritability estimation (Fig. 3a). In the seven QTL model (Fig. 2a), the estimated QTL effects were also quite accurate (Fig. 2b) except the effect of intercept, which was slightly upwardly biased. On the datasets with missing measurements, the GP approach still had high power to detect the true QTL. Furthermore, the additive genetic effect estimates were accurate on all the missing data scenarios even when using a dataset with 67% missingness (Supplementary Fig S2).
Fig. 2.
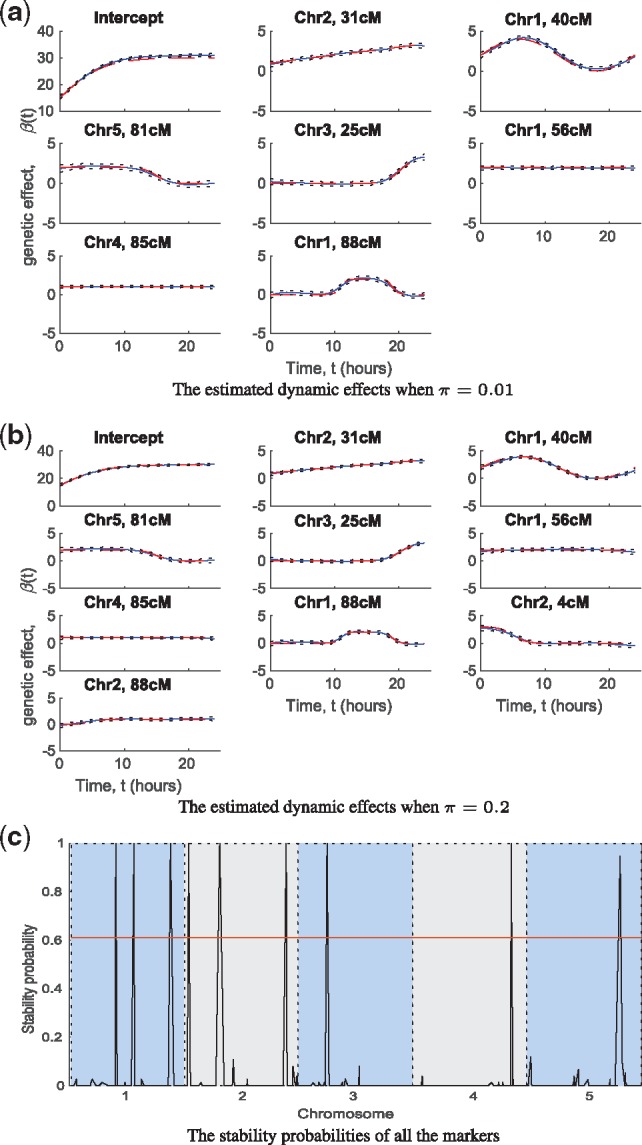
In the simulation dataset: (a) and (b) the estimated dynamic effects of model intercept and selected significant markers (solid lines), and their credible intervals (dashed lines) when the marker inclusion probability π in the model prior was 0.01 (a) and 0.2 (b). (c) The stability probabilities of all the markers estimated by the stability selection with the horizontal line representing the significance threshold obtained using a false discovery rate approach. The results are from single replicate of simulated data but results for other replicates are similar.
Fig. 3.
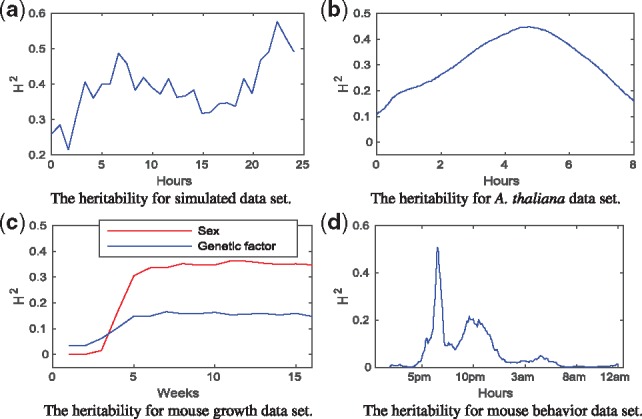
The heritabilities estimated over time for (a) simulated, (b) A.thaliana, (c) mouse growth and (d) mouse behavior datasets.
The GP approach had equally good power to identify QTL in the large dataset as in the small dataset when the number of individuals was the same (Supplementary Table S2). This indicates that the GP method was not sensitive to the total number of markers, and has potential to be applied to high dimensional genomic datasets. The performance of the variable selection depended more on the number of individuals. With a sufficiently large number of individuals (i.e. n = 500, 1000), the variable selection correctly detected QTL and controlled for false positives, regardless of different choices of hyper-prior parameters π (Supplementary Table S3). However, when the number of individuals was small (n = 100, 200), maximum likelihood estimation (π = 0.5) led to a high number of false positives while stricter model selection criteria such as π = 0.01, 0.2 led to low power to detect QTL (Supplementary Table S3).
The Bayesian B-spline approach performed similarly to the GP approach using an inclusion probability π = 0.2 for variable selection (Supplementary Tables S1–S3). However, the GP method had somewhat better ability to control false positives.
4.2 Analysis of mouse growth data
The GP variable selection (π = 0.01) reported six loci including markers on Chr6 (0–11 cM), Chr7 (42–53 cM), Chr8 (20–31 cM), Chr10 (22–33 cM), Chr10 (56–67 cM) and Chr11 (33–44 cM) and the sex as significant variables (Fig. 4a). In another search with a more liberal prior (π = 0.2) two extra markers on Chr1 (11–21 cM) and Chr9 (31–42 cM) were detected (Fig. 4b). These eight putative QTL were also reported in Gray et al. (2015) using the same simple regression approach as Kwak et al. (2014). However, the stability selection indicated only two of them (Chr6 (0–11 cM) and Chr10 (22–33 cM)) were significant loci (Fig. 4c). In general, the QTL and sex effect on the growth of body weight constantly increased over time (Fig. 4a and b). After the mice matured, the sex explained 35% of the phenotypic variation, but the QTL only jointly explained 16% of the variation (Fig. 3c).
Fig. 4.
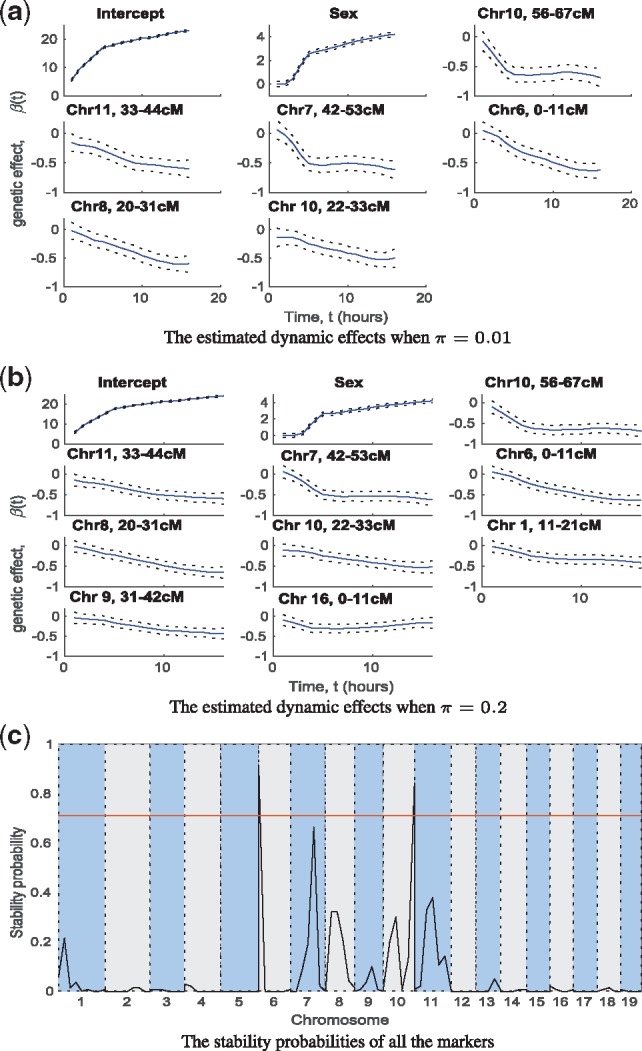
In the mouse growth dataset: (a) and (b) the estimated dynamic effects of model intercept and selected significant markers (solid lines), and their credible intervals (dashed lines) when the inclusion probability π in the model prior was 0.01 (a) and 0.2 (b). (c) The stability probabilities of all the markers estimated by the stability selection with the horizontal line representing the significance threshold.
4.3 Analysis of mouse behavior data
The variable selection with inclusion probability π = 0.01 did not identify any significant QTL (Supplementary Fig. S4a) nor did the stability selection (Supplementary Fig. S4c). Using a more liberal π = 0.2, two significant QTL on Chr1 (96 cM), and Chr9 (21 cM) were identified (Supplementary Fig. S4b). These two QTL were also found in earlier reports (Xiong et al., 2011; Li and Sillanpää, 2013). The two QTL had an effect on mouse activity probabilities during the night jointly explaining 5–50% of the phenotypic variation over 7 pm–5 am (Fig. 3d). They did not have an effect during the daytime (Supplementary Fig. S4c), indicating the underlying genes linked to the two QTL may regulate the mouse activity differentiation between day and night.
4.4 Analysis of A.thaliana dataset
Three putative QTL including loci on Chr1 (62 cM), Chr4 (45 cM) and at Chr5 (6 cM) were identified in the variable selection with a stricter criterion (π = 0.01) to be associated with the root gravitropism trait (Supplementary Fig. S3a). On the basis of the same dataset, Kwak et al. (2014) identified two QTL on Chromosome 1 (at 60 cM) and Chromosome 4 (at 43 cM) using a simple regression based method. In fact, their findings were practically identical to the results for first two QTL in this study (in terms of QTL locations). The three putative QTL showed different temporal patterns to regulate the development of root gravitropism. The QTL on Chr1 did not have an effect on the trait at the starting time points (0–1 h), but increasingly influenced the trait during 1–5 h with the effect gradually decreasing during 5–8 h. While the QTL on Chr4 and Chr5 had a large effect on the trait in the beginning (its effect slowly increased during 0–4 h) it slowly decreased during 4–8 h. Kwak et al. (2014) (e.g. Fig. 4 in their article) reported similar temporal trends for the same QTL. Compared to their estimates, our estimated QTL effect curves tended to be smoother, indicating that our GP approaches were better at reducing the noise in the data. The heritability (total percentage of variation explained by QTL) was only 0.1 at the beginning, but increased to 0.45 at the midpoint, and decreases again in the late stage (Fig. 3b).
With less stringent criterion (π = 0.2) in the variable selection, the GP approach identified six extra significant QTL on Chr4 (at 28 and 35 cM), Chr5 (at 52 and 65 cM) and Chr3 (at 3 and 76 cM) (Supplementary Fig. S3b). On the other hand, the stability selection only identified the locus on Chr1 as significant (Supplementary Fig. S3c).
5 Discussion and conclusions
We propose a novel Bayesian GP regression model for analyzing function-valued (i.e. longitudinal) quantitative traits. The method utilizes approximate Bayesian model posteriors and a stepwise variable selection procedure to efficiently search the model space and find the best subset of molecular markers to be included in the model. The method has been fully implemented in the MATLAB package ‘GPQTLmapping’ (https://github.com/jpvanhat/GPQTLmapping) with the help of ‘GPstuff’ package of Vanhatalo et al. (2013).
A major advantage of the GP framework is its generalizability. The covariance function which induces the smoothness in the curve fitting can be chosen from various options and its parameters optimized automatically. The Mátern covariance function (4) used in this work has great flexibility in fitting curves with various shapes and degree of smoothness. In our work we chose only one parameter manually when setting v = 2.5, which led to promising results in all our case studies. As a comparison, in (penalized) B-splines (Li and Sillanpää, 2013), one needs to choose not only the degree of freedom of the splines, but also the number of knots and their locations, which becomes a difficult task especially in a dataset of a vast amount of non-equidistant time points. Nevertheless, the B-splines approach can also be formulated as a GP covariance function as illustrated in the Supplementary Material, and the B-spline regression can also be executed by using the same GP computational framework and software package introduced here. In this case, the benefit of fitting B-spline model under the GP formulation is that the variable selection can be done in a fully Bayesian manner as described in Section 2.2.
An extra benefit of GP formulation is the estimation and inference. The GP model has the nice property that the hyperparameters’ ML can be evaluated analytically by integrating out the regression parameters β. This allows efficient approximation for the model likelihood (at fixed covariance function hyperparameters) by numerically integrating out the residual variance . This provides a more accurate estimate of the ML than using other fast Bayesian approximation algorithms such as the Variational Bayes approach (Blei et al., 2017; Nott et al., 2013) which is only able to give a lower bound of the ML. The missing phenotypic data can also be marginalized in the GP estimation procedure, which means we do not need to use other sophisticated statistical approaches (Guo and Nelson, 2008) to impute the phenotypic data before the QTL analysis. The simulation results imply that even with a high proportion of missing items in the data, our GP approach can still provide adequately precise estimates of the regression parameters, which are comparable to the estimates using the complete data.
Similar to Li and Sillanpää (2013) and Kwak et al. (2014), a stepwise method was used for variable selection. The stepwise variable selection with an appropriate stopping rule only explores a low dimension of the model space, and therefore greatly reduces the computational complexity. The simplest approach is to use the ML as the criterion for stopping the model search, which is equivalent to setting the model prior to be uniform with π = 0.5. However, the ML criterion was overly liberal in all data analyses. To ensure the model is parsimonious, it is advisable to use a Binomial prior for the number of markers in the model as an extra penalty, which leads to a posterior model probability. Based on the simulation studies, this effectively controls against false positives especially with small datasets. As the number of individuals increases, the false negative rate becomes negligible. An open question is how much smaller π should be than 0.5? In our simulation studies, values ≤0.2 worked well, but in general, its choice can be informed by preliminary simulation tailored for a particular application or by prior knowledge on number of putative QTL. The Beta distribution can also be used to set a weakly informative prior for π that favors values <0.5. However, a detailed study on the choice of π is beyond the scope of this paper. Interestingly, the posterior model probability as a model selection criterion has a strong connection to the frequentist model selection approaches such as Bayesian information criterion (Neath and Cavanaugh, 2012). In fact, Bayesian information criterion is a consequence of a Laplace approximation to the posterior model probabilities. As illustrated in the simulated and real data analyses, the posterior model probability has equivalent or better power than the earlier proposed FDR of stability selection (Alexander and Lange, 2011) to identify QTL.
From the perspective of computational cost, the GP method is feasible even for large datasets. For example, in sequential model search, the GP method required roughly 8 h for the large simulated dataset of 500 individuals, 10 015 markers and 30 time points compared to 15 min for the A.thaliana data with 162 individuals, 234 markers and 241 time points. This indicates that the GP approach has a computational advantage when the number of time points is large and number of markers is small, but it becomes less efficient when the number of markers is large. The computational performance of the methods can be substantially improved by computing the MLs for different models in parallel. In addition, a sure independence screening approach can also be applied to significantly reduce the dimension of the genotypic data before the GP modeling (Liu et al., 2014).
In conclusion, we have developed a novel GP-based varying coefficient model and a Bayesian variable selection method for identifying QTL associated with function-valued traits. Our method is non-parametric, includes a minimal number of tuning parameters, and can be applied efficiently to high resolution dynamic data with hundreds of time points. A potential disadvantage is that the stepwise variable selection may easily get stuck at local maxima. This problem, however, is related to the search algorithm and not to the GP model or posterior model comparison as such. Therefore, the development of a more stable stochastic variable selection approach is an important area for future research. Another possible research direction is to develop GP functional QTL models for detecting gene-to-gene and/or gene-environmental interactions. Note that GPs have also been proposed to analyze high-order gene-to-gene interactions (Zou et al., 2010). It may be possible to combine their approach with ours for epistasis analysis on functional data.
Funding
The work was funded by Academy of Finland [grant 317255].
Conflict of Interest: none declared.
Supplementary Material
References
- Alexander D.H., Lange K. (2011) Stability selection for genome-wide asssociation. Genet. Epidemiol., 35, 722–728. [DOI] [PubMed] [Google Scholar]
- Äijö T. et al. (2014) Methods for time series analysis of RNA-seq data with application to human Th17 cell differentiation. Bioinformatics, 30, 113–120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersen M.R. et al. (2014) Bayesian inference for structured spike and slab priors. In: Ghahramani,Z. et al. (eds) Advances in Neural Information Processing Systems Vol. 27 Curran Associates, Inc, pp. 1745–1753. [Google Scholar]
- Andersen M.R. et al. (2017) Bayesian inference for spatio-temporal spike-and-slab priors. J. Mach. Learn. Res., 18, 1–58. [Google Scholar]
- Benner C. et al. (2016) FINEMAP: efficient variable selection using summary data from genome-wide association studies. Bioinformatics, 32, 1493–1501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blei D.M. et al. (2017) Varitional inference: a review for statisticians. J. Am. Stat. Assoc., 112, 859–877. [Google Scholar]
- Coster A. et al. (2010) QTLMAS 2009: simulated dataset. BMC Proc., 4, S1.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis T.A. (2006) Direct Methods for Sparse Linear Systems. SIAM, Philadelphia, PA. [Google Scholar]
- Fan R. et al. (2012) Longitudinal association analysis of quantitative traits. Genet. Epidemiol., 36, 856–869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fahrmeir L., Kneib T. (2011) Bayesian Smoothing and Regression for Longitudinal, Spatial and Event History Data. Oxford Press, Oxford, New York. [Google Scholar]
- Gray M.M. et al. (2015) Genetics of rapid and extreme size evolution in island mice. Genetics, 201, 213–228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo Z., Nelson J.C. (2008) Multiple-trait quantitative trait locus mapping with incomplete phenotypic data. BMC Genetics, 9, 82.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haley C.S., Knott S.A. (1992) A simple regression method for mapping quantitative trait loci in line crosses using flanking markers. Heredity, 69, 315–324. [DOI] [PubMed] [Google Scholar]
- Hartmann M. et al. (2017) Gaussian process framework for temporal dependence and discrepancy functions in Ricker-type population growth models. Ann. Appl. Stat., 11, 1375–1402. [Google Scholar]
- Harville D.A. (1997) Matrix Algebra From a Statistician’s Perspective. Springer-Verlag, Berlin. [Google Scholar]
- Honkela A. et al. (2011) tigre: transcription factor inference through Gaussian process reconstruction of expression for bioconductor. Bioinformatics, 27, 1026–1027. [DOI] [PubMed] [Google Scholar]
- Honkela A. et al. (2015) Genome-wide modelling of transcription kinetics reveals patterns of RNA production delays. Proc. Natl. Acad. Sci. USA, 112, 13115–13120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaffrézic F., Pletcher S.D. (2000) Statistical models for estimating the genetic basis of repeated measures and other function-valued traits. Genetics, 156, 913–922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwak I.-Y. et al. (2014) A simple regression-based method to map quantitative trait loci underlying function-valued phenotypes. Genetics, 197, 1409–1416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwak I.Y. et al. (2016) Mapping quantitative trait loci underlying function-valued traits using functional principal component analysis and multi-trait mapping. G3 (Bethesda), 6, 79–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Z., Sillanpää M.J. (2013) A Bayesian nonparametric approach for mapping dynamic quantitative traits. Genetics, 194, 997–1016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Z. et al. (2014) Functional multi-locus QTL mapping of temporal trends in scots pine wood traits. G3, 4, 2365–2379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Z., Sillanpää M.J. (2015) Dynamic quantitative trait locus analysis of plant phenomic data. Trends Plant Sci., 20, 822–833. [DOI] [PubMed] [Google Scholar]
- Li J. et al. (2015) Bayesian group LASSO for nonparametric varying-coefficient models with application to functional genome-wide studies. Ann. Appl. Stat., 9, 640–664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J. et al. (2018) Two-stage identification of SNP effects on dynamic poplar growth. Plant J., 93, 286–296. [DOI] [PubMed] [Google Scholar]
- Liu J. et al. (2014) Feature selection for varying coefficient models with ultrahigh dimensional covariates. J. Am. Stat. Assoc., 109, 266–274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma C.-X. et al. (2002) Functional mapping of quantitative trait loci underlying the character process: a theoretical framework. Genetics, 161, 1751–1762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meinshausen N., Bühlmann P. (2010) Stability selection. J. R. Stat. Soc. Series B, 72, 417–473. [Google Scholar]
- Monahan J.F. (2011) Numerical Methods of Statistics. Cambridge University Press, New York. [Google Scholar]
- Moore C.R. et al. (2013) High-throughput computer vision introduces the time axis to a quantitative trait map of a plant growth response. Genetics, 195, 1077–1086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neath A.A., Cavanaugh J.E. (2012) The Bayesian information criterion: background, derivation, and applications. WIREs Comput. Stat., 4, 199–203. [Google Scholar]
- Nguyen T. et al. (2016) RNA-Seq count data modelling by grey relational analysis and nonparametric Gaussian process. PLoS One, 11, e0164766.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ning C. et al. (2017) Perfomance gains in genome-wide association studies for longitudinal traits via modeling time-varied effects. Sci. Rep., 7, 590.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nott D.J. et al. (2013) Regression density estimation with variational methods and stochastic approximation. J. Comput. Graph. Stat., 21, 797–820. [Google Scholar]
- O’Hagan A., Forster J. (2004) Kendals Advanced Theory of Statistics, Volume 2B: Bayesian Inference. 2nd edn Arnold, London. [Google Scholar]
- O’Hara R.B., Sillanpää M.J. (2009) A review of Bayesian variable selection methods: what, how and which. Bayesian Anal., 4, 85–117. [Google Scholar]
- Parker C.C. et al. (2016) Genome-wide association study of behavioral, physiological and gene expression traits in commercially available outbred CFW mice. Nat. Genet., 48, 919–926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piironen J., Vehtari A. (2017) Comparison of Bayesian predictive methods for model selection. Stat. Comput., 27, 711–735. [Google Scholar]
- Pletcher S.D., Geyer C.J. (1999) The genetic analysis of age-dependent traits: modelling the character process. Genetics, 153, 825–835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasmussen C.E., Williams C.K.I. (2006) Gaussian Processes for Machine Learning. The MIT Press, Cambridge, MA. [Google Scholar]
- Simpson D.R. et al. (2017) Penalising model component complexity: a principled, practical approach to constructing priors. Stat. Sci., 32, 1–28. [Google Scholar]
- Sillanpää M.J. (2011) On statistical methods for estimating heritability in wild populations. Mol. Ecol., 20, 1324–1332. [DOI] [PubMed] [Google Scholar]
- Sillanpää M.J. et al. (2012) Simultaneous estimation of multiple quantitative trait loci and growth curve parameters through hierarchical Bayesian modeling. Heredity, 108, 134–146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanhatalo J. et al. (2010) Approximate inference for disease mapping with sparse Gaussian processes. Stat. Med., 2010, 1580–1607. [DOI] [PubMed] [Google Scholar]
- Vanhatalo J. et al. (2013) GPstuff: Bayesian modeling with Gaussian processes. J. Mach. Learn. Res., 14, 1175–1179. [Google Scholar]
- Wu R., Lin M. (2006) Functional mapping—how to map and study the genetic architecture of dynamical complex traits. Nat. Rev. Genet., 7, 229–237. [DOI] [PubMed] [Google Scholar]
- Xiong H. et al. (2011) A flexible estimating equations approach for mapping function valued traits. Genetics, 189, 305–316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu S. (2013) Genetic mapping and genomic selection using recombination breakpoint data. Genetics, 195, 1103–1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J. et al. (2009) Nonparametric functional mapping of quantitative trait loci. Biometrics, 65, 30–39. [DOI] [PubMed] [Google Scholar]
- Yang R., Xu S. (2007) Bayesian shrinkage analysis of quantitative trait loci for dynamic traits. Genetics, 176, 1169–1185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H. (2004) Inconsistent estimation and asymptotically equal interpolations in model-Based geostatistics. J. Am. Stat. Assoc., 99, 250–261. [Google Scholar]
- Zou F. et al. (2010) Nonparametric Bayesian variable selection with applications to multiple quantitative trait loci mapping with epistasis and gene-environment interaction. Genetics, 186, 385–394. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


