Modeling “Textured” Bones in Virtual Human Phantoms

Abstract

The purpose of this study was to develop detailed and realistic models of the cortical and trabecular bones in the spine, ribs, and sternum and incorporate them into the library of virtual human phantoms (XCAT). Cortical bone was modeled by 3D morphological erosion of XCAT homogenously defined bones with an average thickness measured from the CT dataset upon which each individual XCAT phantom was based. The trabecular texture was modeled using a power law synthesis algorithm where the parameters were tuned using high-resolution anatomical images of the Human Visible Female. The synthesized bone textures were added into the XCAT phantoms. To qualitatively evaluate the improved realism of the bone modeling, CT simulations of the XCAT phantoms were acquired with and without the textured bone modeling. The 3D power spectrum of the anatomical images exhibited a power law behavior (R² = 0.84), as expected in fractal and porous textures. The proposed texture synthesis algorithm was able to synthesize textures emulating real anatomical images, with the simulated CT images with the prototyped bones were more realistic than those simulated with the original XCAT models. Incorporating intra-organ structures, the “textured” phantoms are envisioned to be used to conduct virtual clinical trials in the context of medical imaging in cases where the actual trials are infeasible due to the lack of ground truth, cost, or potential risks to the patients.

I. INTRODUCTION

COMPUTATIONAL human phantoms are widely used in medical imaging research. They serve as virtual patients and can be combined with accurate models of modern imaging devices to generate simulated data from different modalities. Phantoms provide known anatomies which can be imaged repeatedly in the virtual domain to study and optimize imaging devices and techniques. With this ability, computational phantoms have become indispensable toolsets for simulating clinical trials where the actual experiments would not be practical.

Over the past fifty years, many phantoms have been extensively developed and improved to be more realistic and representative of a population of humans [1–7]. The four-dimensional extended cardiac-torso (XCAT) phantoms are a series of computational phantoms that represent a realistic population of humans with variable ages, genders, heights, and weights [8–10]. These whole-body phantoms have been modeled based on the segmentation of several sets of patient clinical computed tomography (CT) images and have been further enhanced using the high-resolution datasets from the Human Visible Male and Female projects [11, 12]. XCAT phantoms have been widely used in medical imaging research in the estimation of organ doses in X-ray based imaging systems [13–15].

In the current XCAT models, most organs and anatomical structures are defined as homogeneous materials. This is generally not an issue in dosimetry studies. However, the simulated medical images, produced from the homogenous organs in the XCAT, are not realistic enough for image quality studies which limits the broader applicability of the phantoms. For example, previous dosimetry studies used micro CT images of bone specimens to better understand the radiation dose to radiosensitive tissues of the human skeleton system. These studies have led to correction factors applied to the Monte Carlo based dosimetry to more accurately estimate doses to bones [16–18]. Such corrections are effective for dosimetry purposes, but fail to adequately represent heterogeneous bones for image quality based studies.

Ideally, the intra-organ structures should be segmented from patient-specific volumetric imaging datasets (e.g. CT or MRI), similar to the way in which the main organs have been modeled in the phantoms. However, it is challenging to segment these small structures, considering the current spatial resolution and noise in clinical datasets. Alternatively, the intra-organ structures can be modeled mathematically with parameters informed by morphometry studies and high-resolution datasets.

We have recently developed a mathematical and anatomically informed approach to model the lung non-parenchyma (pulmonary airways and vasculature) [19] and parenchyma structures [20] to create “textured” lungs in XCAT phantoms. Building upon this prior work, the present study aimed to develop a framework to model heterogeneous bone structures of the spine, ribs, and sternum within the XCAT phantoms.

II. METHODS

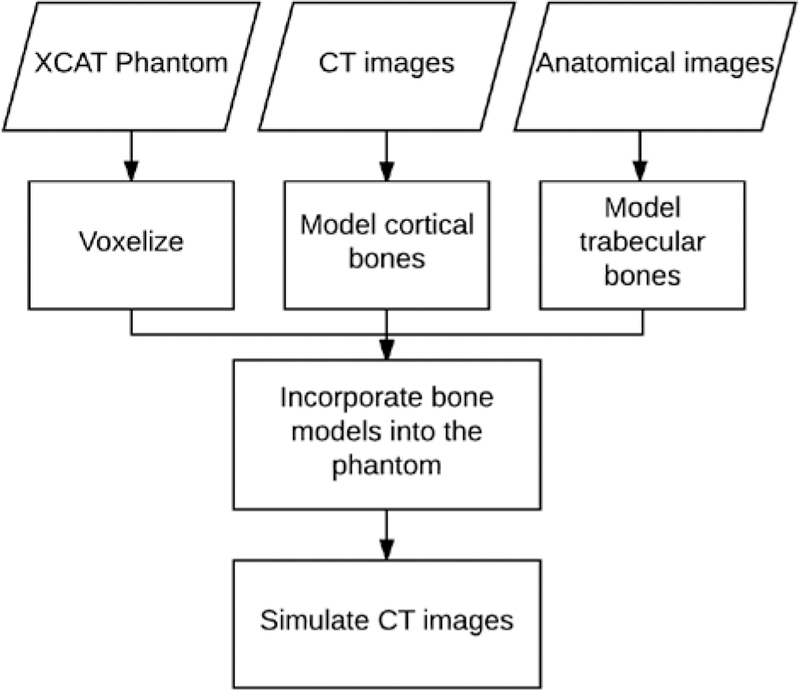
Heterogeneous models of the bones in the spine, ribs, and sternum were synthesized and incorporated into the series of XCAT phantoms. The overall framework is shown in Fig. 1. The individual steps in the process are detailed below.

Fig. 1.

Flowchart of the bone modeling. XCAT phantoms were used as the basis for each model. Cortical bones were modeled based on cortical thicknesses of corresponding CT images of each XCAT. Trabecular bones were modeled using high resolution anatomical images. Finally, each phantom’s realism was objectively evaluated by simulating its CT images.

A. Voxelizing the XCAT phantoms

The XCAT phantoms were initially modeled based on continuous non-uniform rational basis spline (NURBS) and polygon mesh surfaces. This surface-based approach does not easily lend itself to modeling heterogeneous sub-organ structures. Therefore, to model the heterogeneity, the phantoms were first transformed into a voxelized format with an isotropic resolution of 0.25 mm.

B. Modeling cortical and trabecular bones

On a macroscopic level, the main components of the spine, ribs, and sternum are cortical (compact) and trabecular (can-cellous) bones [21]. Cortical bones are the dense outer layer of the bone, whereas the trabecular bones are the inner less dense bones with a porous structure [21]. In each XCAT, the cortical and trabecular bones were modeled as follows:

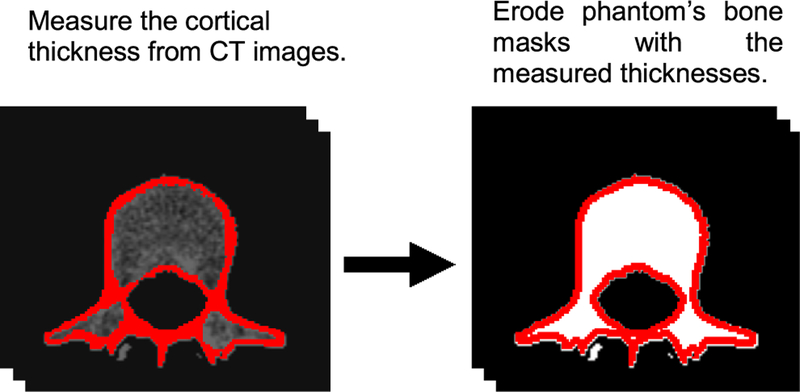
For cortical bone, the defined ribs, spines, and sternum masks in each XCAT phantom were eroded to accommodate cortical bone layers. To do so, a 3D morphological erosion function with a “cube” structuring element, was applied to the voxelized phantoms so as to obtain the desired thicknesses for the cortical layer. These thicknesses were separately measured for each XCAT phantom using its corresponding CT dataset (Fig. 2).

Fig. 2.

Procedure for modeling cortical bone in a phantom. This strategy was applied to the spine, ribs, and sternum.

For trabecular bone, while the porous “texture” of the trabecular bone is visible in CT images, this texture cannot be accurately reconstructed from CT images due to the resolution limitation and the noise in clinical images. Therefore, it is not feasible to model the trabecular bone for each XCAT phantom from its corresponding CT dataset in a patient-specific manner.

In this work, we synthesized heterogeneous structures that have “texture” similar to real trabecular bones using a 3D power law synthesis technique. This synthesis technique has been used extensively for modeling background structures in computational breast phantoms [22–25], relying on the power law behaviors of the fractal images power spectrum [26] as

$$S_x\left(f\right)=\alpha f^{-\beta },$$ (1)

where S_x is the spectral density of a spatial series x, f is the spatial frequency, and α and β are constant positive numbers. In a log-log plot, this relationship is a line with an intercept of log(α) and a slope of β.

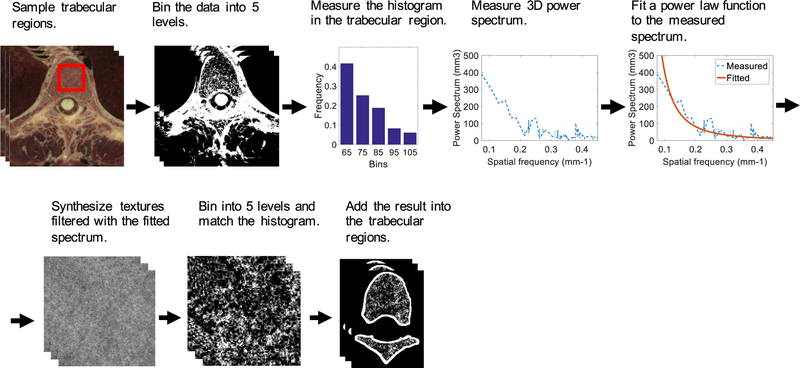
The proposed trabecular texture synthesis framework is shown in Fig. 3. A high resolution anatomical imaging dataset containing trabecular bones was used as an exemplar to inform the synthesis process. This dataset was from the Visible Female project with an isotropic resolution of 0.33 mm [11]. The Visible Female dataset was chosen over that of the Male due to its higher z-resolution (0.33 mm versus 1.0 mm for the Male).

Fig. 3.

The flowchart for synthesizing trabecular bones for the spine, ribs, and sternum, and incorporating them into the XCAT phantoms.

Trabecular regions of the Visible Female anatomical dataset were manually sampled and uniformly binned into five levels. The binning is necessary to reduce the noise from the input dataset. Less number of bins provides better noise reduction. However, a sufficient number of bins is essential to preserve the texture of the trabecular region. Heuristically, we found that binning our input dataset with five levels provides a reasonable compromise between noise reduction and texture preservation goals. After the binning, the histogram and 3D power spectrum of the sampled regions were measured [27]. Parameters α and β were calculated by fitting a power law function to the measured power spectrum.

The synthesis process was initialized with a 3D random white noise volume filtered to have the power law 3D power spectrum with the fitted α and β. Then, the filtered result was uniformly binned into five levels and transformed to match the anatomical image’s histogram. Finally, the synthesized texture was added into the trabecular regions of the XCAT phantoms.

C. Evaluation

The textured XCAT phantoms were “imaged” using a CT simulation program. The program used a voxel-based CT ray tracer [28] which was based on the geometry and physics of a commercial CT scanner (Definition Flash, Siemens Healthcare, Forcheim, Germany). The linear attenuation coefficients of all the materials in the phantom were defined using the “xraylib” library [29]. Specifically, the linear attenuation coefficients of trabecular bone with five different densities (1.00, 1.07, 1.14, 1.21, and 1.28 g.cm⁻³) were used to accommodate for the expected Hounsfield unit values of the synthesized voxels in the trabecular regions. The projection images were acquired on a helical trajectory with a pitch of one and a tube voltage of 120 kV. The projection images were reconstructed with a filtered back-projection algorithm using a commercial CT scanner reconstruction box.

The resultant images were evaluated in terms of conformance of the power spectrum with the initial design. Further, the simulated CT images of the textured bone were evaluated qualitatively in terms of their improved realism in comparison to images without the bone modeling and to real CT images. This evaluation aimed to confirm whether the created heterogeneities are realistic and representative of human anatomy.

III. RESULTS

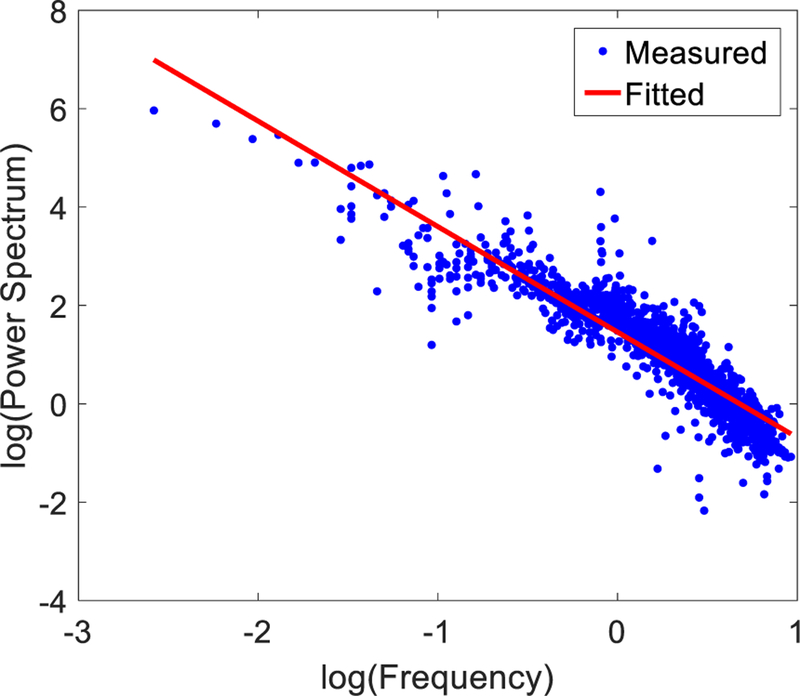
Fig. 4 shows a log-log plot of the 3D power spectrum of a 41×41×41 sampled volume of a trabecular region in the anatomical dataset. On average, the fitted power law parameters were 4.2 ± 1.1 and 2.19 ± 0.17 for α and β, respectively. The goodness of fit was 0.84 ± 0.01 affirming the power law behavior of the trabecular images’ 3D power spectrum.

Fig. 4.

An example log-log plot of the 3D power spectrum versus spatial frequency of a 41 × 41 × 41 sampled volume of a trabecular region in the anatomical dataset.

Fig. 5 shows some examples of trabecular synthesis results compared against the real texture in the high resolution anatomical images. The synthesis results produced a similar visual texture appearance to the anatomical images’ texture.

Fig. 5.

On the left: some slices of the spine region in the anatomical images of the Visible Human Female which are uniformly binned into 5 levels. On the right: some slices of the 3D texture synthesis results of the trabecular bone using the power law algorithm with α� and β� of 4.2 and 2.19, respectively.

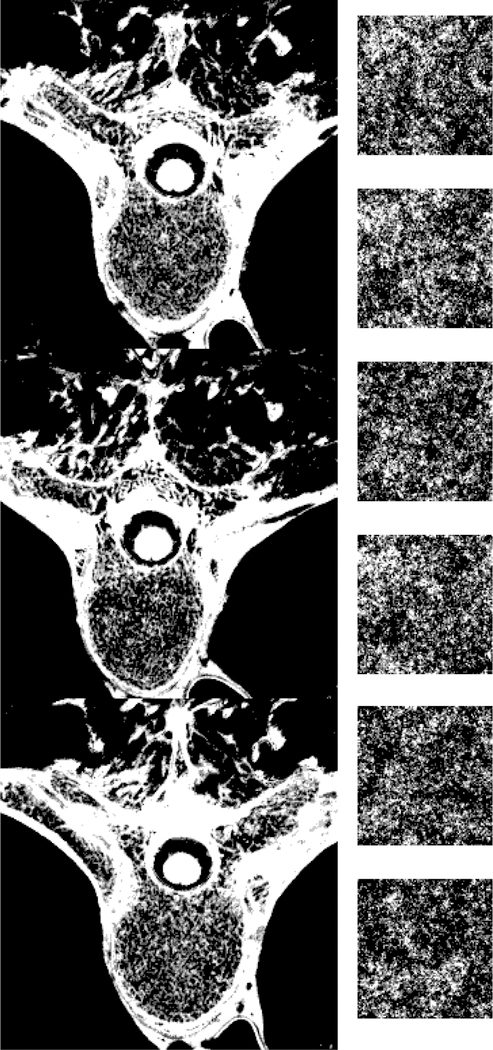
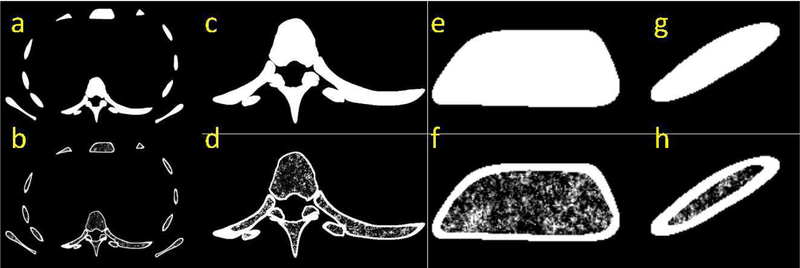
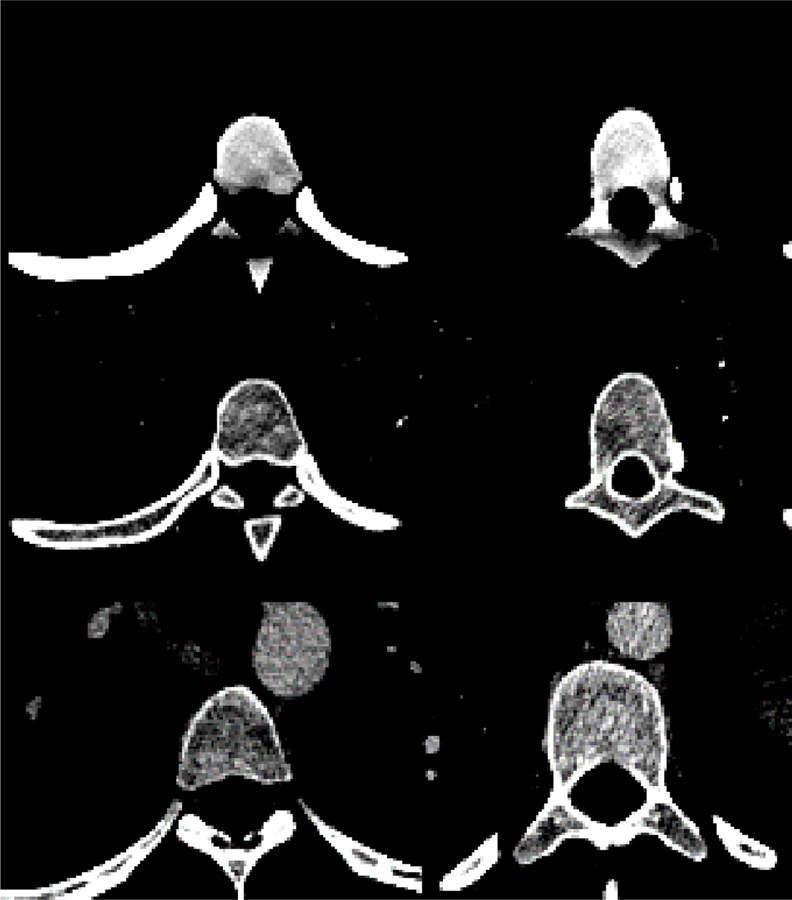
Fig. 6 illustrates some bone regions of an XCAT phantom with and without the incorporation of the cortical bone erosion and the synthesized trabecular texture. Fig. 7 shows CT simulation results of an XCAT with and without the bone modeling as well as a real CT dataset. Without the bone texture, the simulated CT images were solid in bone regions, had beam hardening artifacts, and were not realistic compared to real CT images. Qualitatively, the simulated images of the enhanced phantom were more realistic as the bone texture was more comparable to the actual patient CT scans.

Fig. 6.

An example of XCAT phantom bones without (top row) and with (bottom row) the proposed bone modeling where (a-b) are whole torso slice. Magnified images of the spine, sternum, and rib are illustrated in (c-d), (e-f), and (g-h), respectively.

Fig. 7.

Simulated CT images of a spine region in an XCAT phantom before (top row) and after (middle row) bone modeling, as we all an example of a real CT dataset (bottom row). The images were window-leveled such that the bone texture would be visible.

IV. DISCUSSION

Computational phantoms enable us to conduct clinical experiments virtually, including large-scale virtual clinical trials involving a diverse population of patients. The accuracy of these trials, however, depends on the realism of the phantoms. For the purpose of image quality based clinical trials, realistic intra-organ heterogeneity is an essential requirement for these phantoms, as the organs’ heterogeneous texture affects image quality features such as contrast, noise, and resolution.

In this study, we enhanced the XCAT phantoms by modeling cortical and trabecular bones and incorporating them into the XCAT homogenous bones. Such improvement, along with our previous enhancements in the lungs [19, 20], makes the XCAT more realistic in their representation of human anatomy and thus pave the way towards their use for image quality based virtual clinical trials, such as the improved understanding of X-ray based medical imaging systems to optimize the image quality in a task and patient specific manner, while minimizing the radiation dose to the patients. For example, our phantoms with the incorporated “textured” bone can be utilized to quantitatively assess the effects of different imaging conditions and technologies on the quality of the images in terms of resolution or noise [30]. Such studies would not be possible in the context of patient images due to the lack of ground truth, and would not be realistic in a phantom with homogenous bones. Moreover, these models of bone can be used in dosimetry studies to improve the accuracy of dose estimations in the bones by subdividing the bone into constituent materials.

Our proposed method synthesizes the trabecular texture using a power law texture synthesis algorithm, similar to the previous efforts in modeling background texture in computational breast phantoms [23–25, 31, 32]. In those studies, β ∼ 3 were found to be the optimum value to synthesize breast background structures. In trabecular bones, however, our study suggested β ∼ 2.2, by fitting the power law function to the 3D power spectrum of the high-resolution anatomical images. This trend was expected as the trabecular texture is more granular compared with the breast background texture, resulting in a smaller β.

The proposed synthesized texture has the flexibility to be incorporated into any voxelized phantom and can be combined with different medical imaging simulation packages. The flexibility of the platform enables modeling multiplicity of texture and resolution rendition of bone for virtal clinical trial, depending on the goal of the study. While we found the voxelized format more convenient in terms of modeling intraorgan heterogeneity, our synthesized texture can be converted into a surface format using nested meshes spanning the range of intensities within the textures as was done previously for the breast phantoms [33].

The isotropic voxel size used in this study was 0.25 mm. While phantoms with smaller voxel sizes offer higher spatial resolution, they would also have larger file sizes, making the simulations more computationally expensive. Our choice of a 0.25 mm voxel size is roughly half of the detector element size of a typical clinical CT scanner, the targeted modality of this study. Simulated CT images of virtual phantoms with this voxel size have shown to produce spatial resolution characteristics (in terms of modulation transfer function) comparable to real CT images [28].

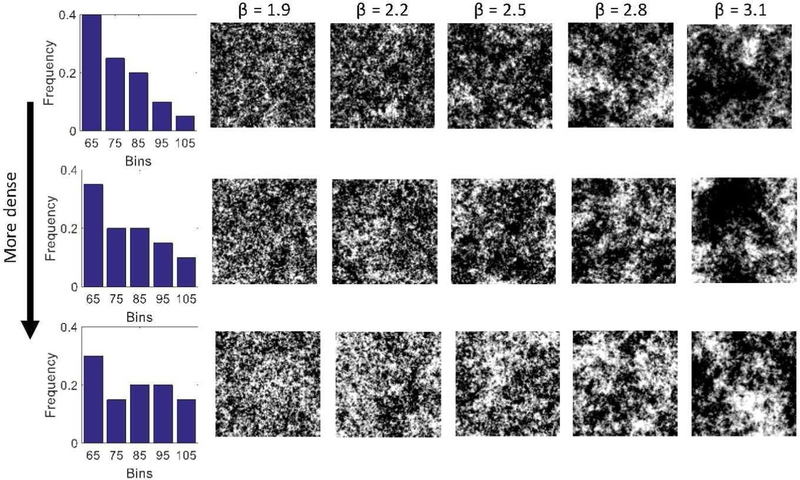
This study has several limitations. First, our approach for modeling the bone was not fully patient specific. Although we measured the average cortical layer thicknesses in each XCAT individually, we were not able to reconstruct the trabecular texture from those low-resolution datasets. Therefore, we used a single high-resolution trabecular dataset to inform our trabecular texture synthesis, which was subsequently applied to all XCAT phantoms. Nevertheless, because our proposed algorithm is parametric, its parameters can be adapted to different types of trabecular texture, which can introduce variability in trabecular texture modeling between XCAT phantoms. Furthermore, our proposed algorithm is able to generate different trabecular textures given a high-resolution dataset with histogram and fitted β. This would enable the development of textures specific to different bones or diseased processes if a high-resolution dataset were available. Fig. 8 illustrates simulations of our texture synthesis given different histograms and different βs. Results show that if an input texture exhibits a higher bone mineral density (i.e., a shift to the right in the histogram), then the synthesis algorithm would adapt itself to generate a similarly denser texture. Similarly, if an input texture exhibited a larger β, the algorithm would generate a less granular texture.

Fig. 8.

Texture synthesis results using different input histogram and β, showing the capability of the proposed method in generating variable trabecular textures in terms of bone mineral density (captured by histogram) and granularity (captured by β). This methodology, combined with high-resolution images of bone structures, can be used to generate different types of bones and introduce variability in the bone models.

Moreover, a higher resolution dataset can improve the realism of the synthesized trabecular bones. For example, high-resolution micro CT images of the bones (not available in this study) may enhance the trabecular bone modeling to the micro resolution level.

Another limitation of this study was that the simulated CT images of the phantoms were evaluated qualitatively, and no quantitative evaluation was performed on the CT simulated images. Such quantitative evaluation can be performed using either 1) observer studies, where expert imaging scientists and physicians score the level of realism of the simulated CT images, or/and 2) quantitative studies, where image quality features and metrics of the simulated images are compared to those of real CT images. Both of these evaluations are highly dependent on the accuracy of the CT simulator, and therefore, such evaluation awaits a fully confirmed CT simulator, a task currently under active development in our group.

In future work, we aim to improve the XCAT phantom library by modeling intra-organ structures in other organs. Moreover, we will expand our bone modeling strategy to model different types of bone pathologies. We also plan to investigate other data sources, such as micro CT, to improve the high-resolution detail of our bone models. These computational phantoms, along with a realistic CT simulator, can then be integrally assessed in term of their combined realism to virtual conduct imaging clinical trials to evaluate and optimize CT imaging applications in terms of image quality as well as dose.

V. CONCLUSION

Modeling intra-organ heterogeneity is an essential step towards the use of computational phantoms in virtual imaging and virtual clinical trials. Towards this goal, this work developed an algorithm to improve the realism of the bones in the XCAT phantoms. These improvements make the computational phantoms more realistic, and consequently more clinically relevant.