Mitochondrial fragmentation and network architecture in degenerative diseases

Abstract

Fragmentation of mitochondrial network has been implicated in many neurodegenerative, renal, and metabolic diseases. However, a quantitative measure of the microscopic parameters resulting in the impaired balance between fission and fusion of mitochondria and consequently the fragmented networks in a wide range of pathological conditions does not exist. Here we present a comprehensive analysis of mitochondrial networks in cells with Alzheimer’s disease (AD), Huntington’s disease (HD), amyotrophic lateral sclerosis (ALS), Parkinson’s disease (PD), optic neuropathy (OPA), diabetes/cancer, acute kidney injury, Ca²⁺ overload, and Down Syndrome (DS) pathologies that indicates significant network fragmentation in all these conditions. Furthermore, we found key differences in the way the microscopic rates of fission and fusion are affected in different conditions. The observed fragmentation in cells with AD, HD, DS, kidney injury, Ca²⁺ overload, and diabetes/cancer pathologies results from the imbalance between the fission and fusion through lateral interactions, whereas that in OPA, PD, and ALS results from impaired balance between fission and fusion arising from longitudinal interactions of mitochondria. Such microscopic difference leads to major disparities in the fine structure and topology of the network that could have significant implications for the way fragmentation affects various cell functions in different diseases.

Introduction

Mitochondrion is a ubiquitous organelle and powerhouse of the cell that exists in living cells as a large tubular assembly, extending throughout the cytoplasm and in close apposition with other key organelles such as nucleus, the endoplasmic reticulum, the Golgi network, and the cytoskeleton [1–5]. Its highly flexible and dynamic network architecture ranging from a few hundred nanometers to tens of micrometers with the ability to rapidly change from fully connected to fragmented structures makes it suitable for diverse cytosolic conditions and cell functions [6–8]. Cells continuously adjust the rate of mitochondrial fission and fusion in response to changing energy and metabolic demands to facilitate the shapes and distribution of mitochondria throughout the cell [9–11]. Similarly, stressors such as reactive oxygen species (ROS) and Ca²⁺ dysregulation interfere with various aspects of mitochondrial dynamics [12–14]. This is probably why many neuronal, metabolic, and renal diseases have been linked to primary or secondary changes in mitochondrial dynamics [9, 15–37]. Neuronal cells, due to their complex morphology and extreme energy dependent activities such as synaptic transmission, vesicle recycling, axonal transport, and ion channels and pumps activity, are particularly sensitive to changes in the topology of mitochondrial network [38–41].

The mitochondrial network organization makes a bidirectional relationship with the cell’s bioenergetics and metabolic variables [11, 42]. For example, the morphological state of mitochondria has been linked to their energy production capacity [43–46], as well as cell health and death [10, 46–49] on one hand, alterations in mitochondrial energy production caused by genetic defects in respiratory chain complexes lead to fragmentation of mitochondrial network [50, 51] on the other hand. Similarly, while ROS induces fragmentation of mitochondrial network [12–14], overproduction of ROS in hyperglycemic conditions requires dynamic changes in mitochondrial morphology and fragmentation of the network [52]. Furthermore, high cytosolic Ca²⁺ induces mitochondrial fragmentation [14], whereas fragmentation blocks the propagation of toxic intracellular Ca²⁺ signals [53, 54] and can limit the local Ca²⁺ uptake capacity of mitochondria due to their smaller sizes. Thus dynamic changes in mitochondrial morphology and fragmentation of its network can be part of the cycle that drives the progression of degenerative diseases [11–13, 18, 22, 52, 55–70].

Despite a clear association with many cell functions in physiological conditions, quantitative measures of the microscopic fission and fusion rates leading to a given topology of the mitochondrial network remain elusive. While fluorescence imagining has been instrumental in providing biologically useful insights into the structure and function of mitochondria, detailed description of the kinetics and the dynamical evolution of the complex mitochondrial networks in health and disease are still out of reach of these techniques. Although it is difficult to study such dynamics experimentally, computational techniques provide a viable alternative. Various computational studies on the identification and analysis of network parameters from experimental mitochondrial micrographs have been performed using either custom built applications [71–76] or commercially available tools [77], depending upon the particular question being asked. However, a comprehensive study quantifying the imbalance between fission and fusion responsible for the network fragmentation observed in many diseases does not exist.

In this paper, we adopt and extend the method developed in Refs. [75, 76] using a pipeline of computational tools that process and extract a range of network parameters from mitochondrial micrographs recorded through fluorescence microscopy, and simulate mitochondrial networks to determine microscopic rates of fission and fusion leading to the observed network properties. We first demonstrate our approach by application to images of mitochondrial networks in striatal cells from YAC128 Huntington’s disease (HD) transgenic mice (bearing a 111 polyglutamine repeat Q111/0 and Q111/1) and their control counterparts reported in Ref. [78]. This is followed by the application of our technique to images of mitochondria in cells with Alzheimer’s disease (AD) [79], amyotrophic lateral sclerosis (ALS) [80], Parkinson’s disease (PD) [81], optic neuropathy (OPA) [66], diabetes/cancer [65], acute kidney injury [64], Ca²⁺ overload [14], and Down syndrome (DS) [36, 82] pathologies from the literature. The images analyzed in this study were selected based on the following criteria. (1) The paper from which the images were selected reported images of mitochondrial networks both in normal and diseased cells from the same cell/animal model. (2) The images were of high enough quality so that they can be processed properly, making sure that the network extracted indeed represented the actual mitochondrial network without introducing artifacts during the processing. The cell/animal models used in these studies are listed in S1 Table in the Supplementary Information Text and detailed in the Results section below. Although we found fragmented mitochondrial networks and imbalanced fission and fusion in all these pathologies in comparison to their respective control conditions, significant differences between the microscopic properties underlying such fragmentation exist in different diseases.

Methods

Image analysis

Mitochondria in a cell can form networks of different topologies ranging from a fully disintegrated network with one mitochondrion per cluster to a well-connected network comprising of clusters with several mitochondria per cluster to a fully connected network where all clusters are connected to form a single giant cluster. These topologies can be uniquely distinguished by various network parameters such as the mean degree <k> (the average number of nearest neighbors), giant cluster N_g (the largest cluster in the network), giant cluster normalized with respect to the total number of nodes (mitochondria) or edges (connections) N_g/N, and distributions of various features such as the number of mitochondria in various linear branches, cyclic loops, and clusters comprising both branches and loops.

To extract all this information from experimental images of mitochondrial networks, we adopt and extend the procedure first reported in Ref. [75] using a pipeline of Matlab (The MathWorks, Natick, MA) tools. Often, we are required to preprocess the images for removing any legends or masking/removing areas that contain artifacts (Fig 1A). The colors representing processes other than mitochondria are removed and the resulting image is converted to grayscale image (Fig 1B). Next, we take a series of steps to extract the underlying mitochondrial network and the key information about the network.

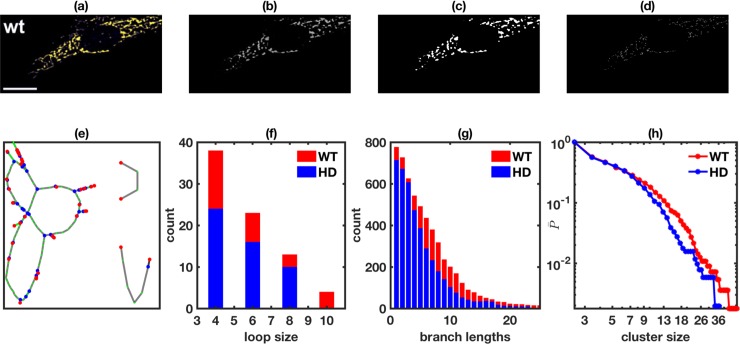
Fig 1. Steps involved in the processing of the images and retrieval of various network features.

(a) Original image, (b) the grayscale image containing mitochondrial network only, (c) binary image, and (d) skeletonized image. Panel (e) shows a graph (partially shown) representation of the skeletonized image where red, green, and blue colors represent nodes with degree 1, 2 and 3 respectively. Size distribution of cyclic loops (f) and linear branch lengths (g), and cumulative probability distribution of cluster sizes (h) in mitochondrial network in striatal cells from wildtype (NL, red) and YAC128 HD (blue) transgenic mice. The image used for the mitochondrial network extraction in panel (a) was adopted from Ref. [78] with permission.

Step 1: We use Matlab function im2bw to generate a binary image (Fig 1C) from the preprocessed gray scale image (Fig 1B) of the micrograph by applying appropriate threshold intensity using Matlab function graythresh.

Step 2: The resulting binary image is reduced to a trace of one-pixel thick lines called skeleton using Matlab function bwmorph, which represents mitochondrial network (Fig 1D).

Step 3: To extract various features of the mitochondrial network from skeletonized image, we first label different clusters using Matlab routine bwlabel. The labeled clusters are then converted to a graph (Fig 1R, only partial graph is shown for clarity) where the nodes are color-coded according to their degree. The graph is then used to extract network parameters such as <k>, N_g, and N_g/N. We also extracted size distribution of loops or cycles with no open ends (Fig 1F), size distribution of branches with at least one open end (Fig 1G), and cumulative probability distribution of individual cluster sizes (Fig 1H) in terms of number of edges, where a single cluster could have both loops and branches and is disconnected from other clusters.

All the above properties are extracted for mitochondrial networks in the cells with different pathologies and the corresponding control cells for comparison. For example, we compare the size distributions of loops, branches, and clusters in striatal cells from YAC128 Huntington’s disease (HD) transgenic mice (blue) and their control counterparts (NL, red) reported in Ref. [78] in Fig 1F–1H. A clear leftward shift in these distributions can be seen in HD, indicating a fragmented mitochondrial network as compared to NL cells. The overall number of loops and branches also decreases in HD.

Modeling and simulating mitochondrial network

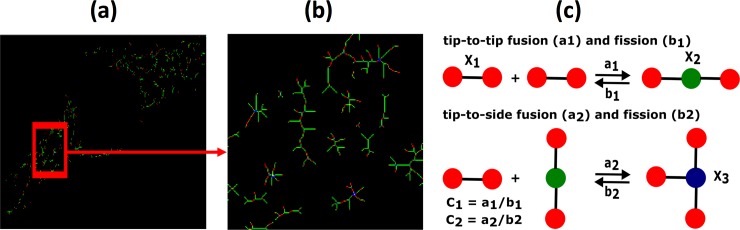
To simulate mitochondrial network, we used the model described in Sukhorukov et al. [76], where the network results from two fusion and two fission reactions (Fig 2). In the model, a dimer tip representing a single mitochondrion can fuse with other dimer tips, forming a network node. At most three tips can merge. The two possible fusion and corresponding fission reactions are termed as tip-to-tip and tip-to-side reactions. The biological equivalent of the tip-to-tip reaction would be the fusion of two mitochondria moving along the same microtubule track in the opposite directions and interacting longitudinally [83]. Similarly, tip-to-side reaction mimics the merging of two mitochondria moving laterally [83]. These two types of interactions are explained further in section “Mitochondrial interactions” of Supplementary Information text and sketched in S1 Fig. This way, the network can have nodes with degree 1 (isolated tip), degree 2 (two merged nodes), and degree 3 (three merged nodes). To each fusion process, there is an associated fission process. Thus, the four possible processes can be represented by the following two reaction equations.

Fig 2. Experimentally observed mitochondrial network and the scheme to model it.

(a) Color coded mitochondrial network retrieved from experimental image of a striatal cell from a wildtype mice and (b) its zoomed in version. (c) Model scheme representing the tip-to-tip fusion of two X1 nodes into X2 and tip-to-side fusion of one X1 node with one X2 node to make one X3 node, and their corresponding fission processes. The image used for the mitochondrial network extraction in panel (a) was adopted from Ref. [78] with permission.

$$X1+X1\begin{array}{c}\stackrel{a1}{\to }\\ \underset{b1}{\leftarrow }\end{array}X2,$$

$$X1+X2\begin{array}{c}\stackrel{a2}{\to }\\ \underset{b2}{\leftarrow }\end{array}X3.$$

Where X1 (Fig 2A, red), X2 (Fig 2A, green), and X3 (Fig 2A, blue) represent nodes with degree 1, 2, and 3 respectively. Nodes with degree 4 are not included because of their extremely low probability [75, 76]. Network edges connecting the nodes define minimal (indivisible) constituents of the organelle. Therefore, all parameters are calculated in terms of number of edges in the network.

Next, we implement the model as an agent-based model using Gillespie algorithm [75, 76, 84]. We initialize the simulation with the number of edges (N) estimated from experimental micrographs of the cell that we intend to model and all nodes initially in X1 form with their number equal to the mitochondrial components representing the cell. The number of edges in the images processed in this paper ranges from as few as 72 to as many as 19519. The network is allowed to evolve through a sequence of fusion and fission processes according to their propensities at a given time step. In all cases, we run the algorithm for 5N time steps to reach the steady state and extract various network features (<k>, N_g, branch lengths etc.) at the end of the run using various Graph and Network algorithms in Matlab. Depending on the fusion (a1 & a2) and fission (b1 & b2) rates used, networks of varying properties ranging from mostly consisting of isolated mitochondria or branched clusters to a fully connected one giant cluster can be generated [76].

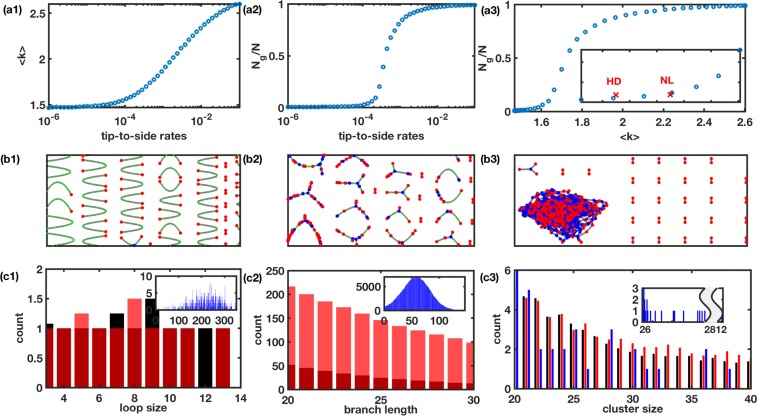
To search for a network with specific properties, we follow the procedure in [75, 76] and vary the ratio of fusion and fission processes, i.e. C1 = a1/b1 and C2 = a2/b2 by fixing b1 and b2 at 0.01 and 3b1/2 respectively, and allowing a1 and a2 to vary. For every set of (C₁, C₂) values, we repeat the simulations 100 times with different sequences of random numbers and report different parameters/features of the network averaged over all 100 runs. Results from a sample run with N = 3000 are shown in Fig 3A1–3A3, where we plot <k> (Fig 3A1) and N_g/N (Fig 3A2) as functions of C2 at fixed C1 = 0.0007. N_g/N versus <k> from the same simulation is shown in Fig 3A3. Increasing C1 shifts the curve to the right. We scan a wide range of C1 and C2 values and plot <k> and N_g/N obtained from experimental images on this two parameter phase space diagram. As an example, the red crosses in the inset in Fig 3A3 represent N_g/N versus <k> retrieved from experimental images of mitochondria in striatal cells from NL and HD transgenic mice [78]. The values from the image are mapped with the corresponding C1 and C2 values on the phase space diagram and reported as the values for that cell.

Fig 3.

Model results at different C1 and C2 values. Mean degree (a1), N_g/N (a2), and N_g/N versus <k> (a3) as functions of C2 at a fixed value of C1. Inset in (a3) shows a zoomed in version of the main plot in (a3) with superimposed N_g/N versus <k> from experimental images of mitochondria in striatal cells (red cross) from wildtype (NL) and YAC128 HD transgenic mice [78]. Mitochondrial network changes from fragmented (b1) to physiologically viable, well-connected (b2) to a fully connected network making one giant cluster (b3) as we increase C2 (or C1). Distribution of loop sizes (c1), branch lengths (c2), and cluster sizes (c3) retrieved from simulated networks at two different C2 values corresponding to mitochondrial network in striatal cells from HD transgenic mice (representative of low C2) (black bars) and striatal cells from wildtype mice in the same experiments (representative of intermediate C2) (red bars). The insets in (c1) and (c2) and the blue bars in (c3) correspond to C2 value for the normal cells in ALS experiments (representative of high C2). The inset in (c3) shows the tail of the blue distribution indicating the formation of a giant cluster at high C2. At smaller cluster sizes, the black, red, and blue bars in panel (c1) are comparable and are skipped for clarity.

Larger values of C1 and C2 mean more frequent tip-to-tip and tip-to-side fusion respectively, and vice versa. A very small value of C2 (or C1) results in a network mainly consisting of linear chains and isolated nodes (Fig 3B1) with small <k> and N_g/N (Fig 3A1 & 3A2). Medium value of C2 leads to a network having clusters with both branches and loops (Fig 3B2), whereas large C2 value results in a network having one giant cluster (Fig 3B3) with large <k> and N_g/N values. To demonstrate further that how low, intermediate, and large values of C2 (or C1) affect the fine structure of the network, we show distributions of the loop, branch, and cluster sizes from three simulations in Fig 3C1–3C3. We pick C2 values obtained for mitochondrial networks (details about C1 and C2 values for different conditions are given below) in striatal cells with HD pathology (C2 = 0.22e-4, C1 = 4.9e-4), their corresponding NL cells (C2 = 0.44e-4, C1 = 4.9e-4) [78], and NL cells from ALS experiments (C2 = 1.0e-4, C1 = 4.8e-4) reported in Ref. [80] as representatives of the three cases. We also performed simulations using C1 and C2 values representing mitochondrial networks in cells with DS pathology (C2 = 0.32e-4 value) and their corresponding NL cells (C2 = 0.88e-4 value) [36, 82] and observed a clear rightward shift in all three distributions at 0.88e-4 as compared to those at C2 = 0.32e-4 (not shown). In addition to shifting to the right, the range of all three distributions widens as we increase the value of C2, indicating that both the sizes and diversity of the network components increase.

Results

As pointed out above, we processed images of mitochondrial networks in cells with various neurological pathologies including AD [79], ALS [80], PD [81], HD [78], OPA [66], Ca²⁺ overload in astrocytes [14], and DS [36, 82] as well as other conditions such as kidney disease [64] and diabetes/cancer [65] from published literature. Details of the cell models analyzed are given in the following paragraphs and tabulated in S1 Table. Key network parameters such as <k>, N_g, N_g/N retrieved from the diseased cells and their normal counterparts are listed in Table 1. A universal signature of all pathological conditions we analyzed in this study is that mitochondrial networks in the diseased cells are fragmented as compared to normal cells. In terms of network parameters, this translates into smaller <k>, average cluster size, N_g, and N_g/N for mitochondrial networks in cells with pathological conditions as compared to control cells.

Table 1. Network parameters obtained from images of cells with different pathologies.

Column 1 lists the disease for which micrographs of normal (NL) and diseased cells were analyzed (column 2). Column 3–8 lists the total number of edges, mean degree, total number of clusters (excluding isolated nodes), average cluster size (in terms of number of edges), giant cluster size (in terms of number of edges), and the ratio of the giant cluster and network size.

Condition	Normal vs diseased	Number of edges	Mean degree <k>	Number of clusters	Avg. cluster size	Ng	Ng/N
HD	NL	2664	1.67	556	4.79	50	0.0188
	HD	2150	1.63	512	4.20	40	0.0186
AD	NL	642	1.64	144	4.46	27	0.042
	AD	1061	1.62	258	4.11	40	0.038
DS	NL	1916	1.52	623	3.08	34	0.017
	DS	1365	1.47	502	2.72	14	0.010
PD	NL	19519	1.72	3416	5.71	107	0.006
	PD	8715	1.70	1691	5.15	45	0.005
ALS	NL	103	1.75	19	5.42	38	0.369
	ALS	72	1.69	13	5.54	16	0.222
Kidney injury	NL	5038	1.66	1061	4.75	58	0.012
	Kidney injury	5386	1.64	1207	4.64	59	0.011
Diabetes/Cancer	NL	3546	1.67	715	4.96	82	0.023
	Diabetes/Cancer	3504	1.65	769	4.55	35	0.010
OPA	NL	5263	1.69	1045	5.04	49	0.0093
	OP	7772	1.67	1656	4.69	43	0.0055
Ca2+	NL	3195	1.59	903	3.54	126	0.039
	Ca2+ overload	2576	1.57	764	3.37	82	0.032

Our observations are in agreement with previous studies investigating these diseases individually. For example, it has been shown that mitochondrial dysfunction in fibroblasts from human fetuses with trisomy of Hsa21 (DS-HFF) [82], human fibroblasts from subjects with DS [36], and mouse embryonic fibroblasts derived from a DS mouse model [36] are correlated with the significant fragmentation of the underlying mitochondrial network when compared to healthy cells, in line with our results showing that <k> and N_g/N for the network in NL cells are higher than those in DS affected cells. Another study investigating mitochondrial dynamics in AD showed that neuroblastoma cells overexpressing APPswe mutant and amyloid β display more fragmented mitochondrial networks as compared to control cells [79]. Along similar lines, cells with HD pathology were shown to be accompanied by mitochondrial fragmentation and cristae alterations in several cellular models of the disease. These alterations were attributed to increased basal activity of the Ca²⁺-dependent phosphatase calcineurin that dephosphorylates the pro‐fission dynamin related protein 1 (Drp1) and mediates its translocation to mitochondria [85]. This study also showed that the upregulation of calcineurin activity results from the higher Ca²⁺ concentration in the cytoplasm in HD due to enhanced release from intracellular stores such as the endoplasmic reticulum. Parkinson’s disease is another complex multifactorial etiology, involving many genetic and environmental factors over the course of time. An in-depth analysis of the human primary skin fibroblasts obtained from sporadic late-onset PD patients with those from healthy age-matched control subjects showed that the diseased fibroblasts exhibit significantly compromised mitochondrial structure and function [81]–in line with the network parameters estimated in our study.

We also analyzed images of mitochondrial networks in mouse hippocampus-derived neuroblastoma cells, transduced with wildtype, R15L, and S59L mutations of Coiled-coil-helix-coiled-coil-helix domain-containing protein 10 (CHCHD10) that were reported in Ref. [80]. Both <k> and N_g (and N_g/N) decrease in the presence of CHCHD10 mutations as compared to wildtype CHCHD10. CHCHD10 mutations are associated with a spectrum of familial and sporadic frontotemporal dementia-ALS diseases [86, 87], Charcot–Marie–Tooth disease type 2 [88], mitochondrial myopathy and spinal muscular atrophy Jokela type [89]. Recently, Woo et al. [80] showed that CHCHD10 results in cytoplasmic accumulation of TAR DNA-binding protein 43 (TDP-43) that increases mitochondrial fission proteins Drp1 and Fis1, reduces mitochondrial fusion protein Mfn1, and promotes mitochondrial fragmentation [90, 91]. TDP-43 pathology is associated with the vast majority of ALS and frontotemporal lobar degenerations [92] and plays a major role in other neurodegenerative diseases [93, 94] and cellular toxicity in general [95, 96]. Overexpression of TDP-43 also promotes juxtanuclear aggregation of mitochondria [90, 91]. The larger average cluster size we observe in cells with CHCHD10 mutations as compared to NL cells could reflect this behavior (Table 1, column 6).

Mitochondrial damage is also believed to be a key contributor to renal diseases like acute kidney injury. By processing images of mitochondrial networks reported in Brooks et al. [64], we observe smaller <k> and N_g/N in rat proximal tubular cells and primary renal proximal tubular cells treated with azide to induced ATP depletion and model in vivo ischemia. These values confirm the conclusions in Ref. [64], where a larger number of cells exhibited fragmented mitochondrial networks in cells treated with azide and cisplatin to induce nephrotoxicity as compared to control cells. The same study also reported that both ischemic acute kidney injury and tubular apoptosis were observed to be ameliorated by Mdivi-1, a pharmacological inhibitor of Drp1.

A dimeric mitochondrial outer membrane protein, MitoNEET, is implicated in the etiology of many pathologies including obesity, insulin resistance, diabetes, and cancer. Its downregulation reduces cell proliferation and tumor growth in breast cancer adipocytes and in pancreatic cells [97–100]. Our analysis of fluorescence images of MitoNEET knockout mouse embryonic fibroblasts indicates that <k>, average cluster size, and N_g/N all decrease when compared with control mouse embryonic fibroblasts. These results are in agreement with the observations suggesting that the downregulation of MitoNEET in mouse embryonic fibroblasts and pancreatic β cells results in reduced connectivity of mitochondrial network and vice versa [99, 101].

Mitochondriopathies are also associated with many multisystemic diseases including infantile-onset developmental delay, muscle weakness, ataxia, and optic nerve atrophy caused by a homozygous mutation in the yeast mitochondrial escape 1-like 1 gene (YME1L1) [102]. YME1L1 plays a key role in mitochondrial morphology by mediating optic atrophy type 1 (OPA1) protein that is involved in mitochondrial fusion and remodeling, and is also believed to be associated with hereditary Spastic Paraplegia 7 disease, Autosomal Recessive disorder, obesity, and defective thermogenesis [73, 103–106]. We found that <k>, mean cluster size, and N_g/N all decrease in cells expressing YME1L1 missense mutation R149W and YME1L1. These results are in agreement with the observations of fragmented mitochondrial network in HeLa cells and fibroblasts from mouse and patients with proliferation defect expressing R149W or YME1L1 knockout cells [66] and SHSY5Y cells where YME1L1 is degraded in response to distinct cellular stresses that depolarize mitochondria and deplete cellular ATP [103].

Interestingly, a common feature among the pathological conditions discussed in this paper and several other degenerative diseases where mitochondrial fragmentation is observed, is that intracellular Ca²⁺ concentration in the cells affected by these pathologies is upregulated [107–120]. Therefore, we analyzed images of mitochondrial networks in cells with higher intracellular Ca²⁺ concentration. These images were reported in Ref. [14], where rat cortical astrocytes were treated with Ca²⁺ ionophore 4Br-A23187 that increases intracellular Ca²⁺ concentration in dose-dependent manner. We found that <k>, average cluster size, N_g, and N_g/N for mitochondrial network in astrocytes exposed to 4Br-A23187 are significantly lower than those observed in control cells.

Next, we perform extensive stochastic simulations (see “Modeling and simulating mitochondrial network” section) to search for the tip-to-tip and tip-to-side fusion and fission rates characterizing mitochondrial networks in cells with different pathologies and their respective control conditions. Final results from these simulations are summarized in Table 2. As is evident from columns 7 and 8, in all cases the values of C1 or/and C2 for mitochondrial network in diseased cells are smaller than those in control cells. This confirms the lower tip-to-tip or tip-to-side fusion to fission ratios in the diseased cells.

Table 2. Comparison of microscopic parameters of mitochondrial network obtained from simulations and experiments.

Column 1 lists the condition for which images of normal (NL) and diseased cells were analyzed (column 2). Columns 3 & 4 and 5 & 6 compare <k> and N_g/N respectively from experiment and theory. Columns 7 & 8 are the C1 (tip-to-tip fusion/fission) and C2 (tip-to-side fusion/fission) values obtained by fitting the model to the data and used in simulations.

Condition	Normal vs diseased	Mean degree <k> Exp            Theory		Ng/N Exp            Theory		C1	C2
HD	NL	1.67	1.67	0.0188	0.022	4.9e-4	4.40e-5
	HD	1.63	1.63	0.0186	0.0101	4.9e-4	2.20e-5
AD	NL	1.64	1.64	0.042	0.108	7.0e-4	2.30e-4
	AD	1.62	1.62	0.038	0.067	7.0e-4	1.90e-4
DS	NL	1.52	1.52	0.017	0.017	5.0e-4	0.88e-4
	DS	1.47	1.47	0.010	0.010	5.0e-4	0.32e-4
PD	NL	1.72	1.72	0.006	0.008	1.2e-3	7.00e-6
	PD	1.70	1.70	0.005	0.007	9.8e-4	7.00e-6
ALS	NL	1.75	1.75	0.369	0.359	4.8e-4	1.00e-4
	ALS	1.69	1.69	0.222	0.225	1.0e-4	1.00e-4
Kidney injury	NL	1.66	1.66	0.012	0.016	9.1e-4	4.00e-5
	Kidney injury	1.64	1.64	0.011	0.011	9.0e-4	0.25e-4
Diabetes/Cancer	NL	1.67	1.67	0.023	0.020	9.8e-4	4.50e-5
	Diabetes/Cancer	1.65	1.65	0.010	0.013	9.8e-4	2.50e-5
OPA	NL	1.69	1.69	0.0093	0.0081	9.0e-4	1.00e-5
	OPA	1.67	1.67	0.0055	0.0075	7.6e-4	1.00e-5
Ca2+	NL	1.59	1.59	0.039	0.038	7.0e-4	1.46e-4
	Ca2+ overload	1.57	1.58	0.032	0.032	7.0e-4	1.13e-4

In most cases, we identified C1 and C2 where the model gives the exact <k> and N_g/N values observed in the experiment. In some cases, the N_g/N value from simulation is slightly different than that retrieved from experimental images. However, it is possible to get C1 and C2 values that would result in the exact N_g/N values. This will require running the algorithm with smaller C1 and C2 increments, which will significantly increase computational time. On average, simulating the network with one set of C1 and C2 values and 100 repetitions to minimize the stochastic variability, takes 5 to 10 hours (depending on N). Thus, halving the increments of one or both of C1 and C2 would double or quadruple the computational time respectively.

A close look at the values of C1 and C2 reveals two main trends (Table 3). In case of HD, AD, DS, Ca²⁺ overload, kidney disease, and diabetes/cancer the fusion to fission ratio for the tip-to-tip reaction remains constant, while the fusion to fission ratio for the tip-to-side reaction decreases when compared to the control conditions. As shown by an example from HD (Fig 4A1–4A4), this results in smaller number of X3 species with a gain in X1 and X2 species in the diseased state (Fig 4A4 and Table 3). However, since the probability of cyclic loops depends on both X2 and X3, the large decrease in X3 and moderate increase in X2 lead to smaller cyclic loops and consequently smaller clusters in the diseased state (Fig 4A1 & 4A3). Larger number of X2 species with no change in X1 would translate into longer and/or larger number of linear branches. However, the simultaneous increase in the number of X1 species would result in shorter branches (Fig 4A2) and higher number of isolated mitochondria. A relatively smaller decrease in C2 leads to a smaller decrease in X3, and a smaller increase in X1 and X2, which would lead to smaller but larger number of linear chains. The larger number of linear chains could overcompensate for the small decrease in X3, resulting in a larger number of cyclic loops. Such behavior is demonstrated by an example using network statistics for diabetes (S2 Fig).

Table 3. Comparison of the fusion to fission ratio for the tip-to-tip and tip-to-side reactions in the normal and diseased states predicted by the model.

The subscripts n and d indicate normal and diseased states respectively. The C1 and C2 values estimated for different conditions are used to estimate the fractions of X1, X2, and X3 species in steady state and compare them with the diseased states.

Condition	C1n/C1d	C2n/C2d	X1n	X2n	X3n	X1n/X1d	X2n/X2d	X3n/X3d
HD	1.00	2.00	0.359	0.562	0.079	0.985	0.948	1.852
AD	1.00	1.21	0.432	0.429	0.140	0.992	0.969	1.143
DS	1.00	2.75	0.454	0.502	0.044	0.980	0.939	17.058
CA	1.00	1.29	0.441	0.459	0.100	0.990	0.969	1.238
Kidney	1.01	1.60	0.344	0.605	0.052	0.991	0.971	1.704
Diabetes/ Cancer	1.00	1.80	0.334	0.614	0.052	0.990	0.971	1.739
OPA	1.18	1.00	0.292	0.691	0.018	0.938	1.030	0.955
PD	1.22	1.00	0.260	0.728	0.012	0.922	1.032	0.954
ALS	4.80	1.00	0.341	0.468	0.191	0.875	1.129	0.976

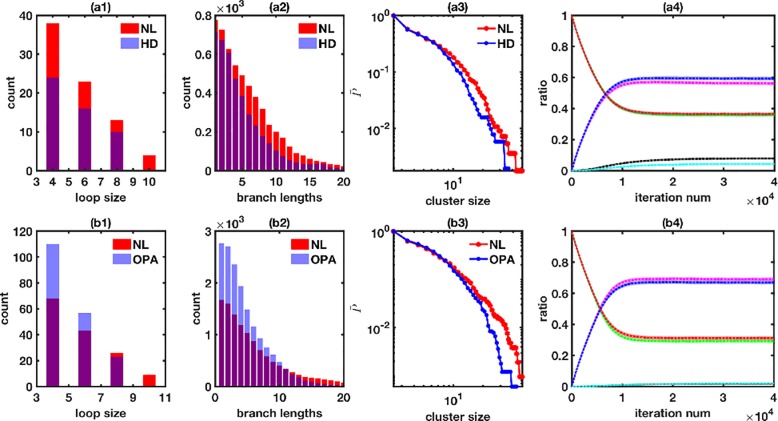
Fig 4.

Two different types of microscopic changes in the fusion to fission processes leading to mitochondrial network fragmentation demonstrated with examples from HD (striatal cells from mouse embryos bearing a 111 polyglutamine repeat Q111/0 and Q111/1) versus control [78] for the first type (top row) and OPA (mouse embryonic fibroblasts with the pathogenic mutation R149W in human YME1L1) versus control [66] for the second type (bottom row) of microscopic changes. Distributions of (a1) loop sizes, (a2) branch lengths, and (a3) cluster sizes (cumulative probability) for NL (red) and diseased cells (blue) from experimental images. (a4) Fraction of X1 (NL: green, diseased: red), X2 (NL: magenta, diseased: blue) and X3 (NL: black, diseased: cyan) species from the model as functions of the number of iterations using C1 and C2 values for HD experiments. The model results show average of 100 runs. (b1-b4) shows the same mitochondrial network features as (a1-a4) for mouse embryonic fibroblasts with OPA pathology and their normal counterparts. Note that the curves for X3 species in cells with OPA pathology and NL overlap (b4).

An opposite effect can be seen in case of OPA, PD, and ALS where C1 decreases and C2 remains constant when compared to normal cells. The lower fusion to fission ratio for the tip-to-tip reaction leads to larger and smaller number of X1 and X2 mitochondrial species respectively (Table 3). A larger decrease in C1 would lead to a larger increase in X1 and a larger decrease in X2, and consequently shorter, fewer linear chains (and larger number of isolated mitochondria) and vice versa. For example, the relatively smaller decrease in C1 in case of OPA leads to shorter linear branches (leftward shift in Fig 4B2) but the number of branches increases (taller bars) as compared to control conditions. Although the fusion to fission ratio for the tip-to-side reaction does not change, the larger number of linear chains available to make cyclic loops leads to a larger number of smaller loops (Fig 4B1). If the decrease in C1 is larger, one would see a significant decrease in the number of loops and branches (and significant increase in the number of isolated mitochondria) in addition to the leftward shift in the diseased case. Such behavior is demonstrated by an example using network statistics for PD (S3 Fig).

To see if the conclusions made above for a given disease holds when images of mitochondrial networks recorded from different cell/animal models or different experimental setup are used, we analyzed two more examples each for AD [121], PD [122], and ALS [91]. As clear from S2 Table, the results are largely consistent with our conclusions discussed above. The mean degree is higher for mitochondrial networks in NL cells as compared to their diseased counterparts. The microscopic rates (C2/C1) given by the simulations are also consistent with the above conclusions. With the exception of one example for AD and PD each, the normalized giant cluster (N_g/N) for all cases from our simulations also follows a consistent trend. For the two examples where N_g/N is slightly larger for NL cells than the diseased cells, we noticed that the overall mitochondrial network (network size in terms of the total number of edges in the cell) in the imaged area of the NL cells were significantly larger than those in the diseased cells. We suspect that this contributed to this discrepancy. Nevertheless, the mean degree in the same two examples is still consistent with our conclusions in the preceding paragraphs.

Despite the fact that the overall cumulative probability of the cluster sizes shifts to the left in all cases (see for example Fig 4A3 & 4B3), the different microscopic mechanisms for fragmentation lead to mitochondrial networks with significantly different fine structures. This is demonstrated by the fraction of X1, X2, and X3 species at steady state (Table 3, columns 4–9) obtained from simulations using C1 and C2 values for mitochondrial networks in cells with different pathologies and their respective control conditions. In the first group of conditions described above, the fraction of X3 species decreases significantly while X1 and X2 both increase moderately in the diseased state. This would lead to smaller and fewer cyclic loops. In the second group of diseases, X1 increases significantly while X2 decreases moderately. Since the propensity of X1+X2 → X3 reaction is given by a1 × X1 × X2, the relatively larger increase in X1 with the moderate decrease in X2 leads to a larger fraction of X3 species in the diseased state. A larger increase in X3 and a smaller decrease in X2 would lead to a larger number of cyclic loops (although still smaller in sizes) and vice versa.

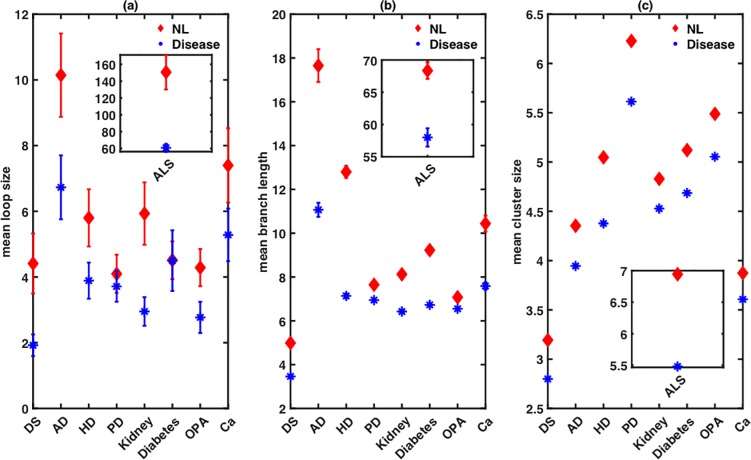
The large variability in the fine structure of the mitochondrial network resulting from the different microscopic origins of fragmentation is highlighted further in Fig 5. We simulate mitochondrial networks in different diseases and their respective control conditions using their corresponding C1 and C2 values in the model, and extract the size distributions for branch lengths, cyclic loops, and clusters. The means of these distributions are shown in Fig 5, where the relative decrease vary significantly from one disease to another. A similar variability can also be seen in the variances of these three distributions while comparing different diseases to their respective control conditions (not shown).

Fig 5. The differences in the microscopic changes leading to mitochondrial network fragmentation lead to significantly differences in the way the fine structure and topology of the network is affected in different diseases.

The mean of size distribution of (a) cyclic loops, (b) branch lengths, and (c) clusters for normal (red) and diseased (blue) cells given by the model using the estimated C1 and C2 values from the experimental micrographs of mitochondrial networks with the condition modeled. Each data point is averaged over 100 runs with error bars showing the standard error of the mean. Simulation results for ALS are plotted separately in the insets for clarity.

Discussion

A tight balance between fission and fusion of mitochondria is crucial for the normal cell function [20, 29, 123]. This is probably why many degenerative diseases have been linked to the primary or secondary changes in mitochondrial dynamics leading to fragmented mitochondrial networks [9, 15–36]. Our analysis of images of mitochondrial networks from several previously reported experimental studies indicates that in general mitochondria in normal cells form a well-connected network that can be described by larger mean degree, giant cluster, branch lengths, clusters, and loops as compared to fragmented network characterized by smaller values of all these parameters in cells with nine different types of pathologies. We exploit these differences and model mitochondrial network to gain a quantitative understanding of the changes in the fission and fusion processes due to lateral and longitudinal interactions in all these pathologies.

It is worth mentioning that the class (transient versus complete) of fusion depends on the way two mitochondria interact with each other (see for example [83] for further details). Transient fusion where two mitochondria come into close apposition, remain fused for less than 4s to 5 min with a mean duration of 45s, and re-separate, preserving their original topologies, results from oblique or lateral interaction of two mitochondria associated with separate tracks. Complete fusion on the other hand results from longitudinal merging of organelles moving along a single track.

We show that the nine conditions can be divided into two main groups. The fragmentation in cells with AD, HD, DS, Ca²⁺ overload, diabetes/cancer, and acute kidney injury pathologies mainly results from the decreased fusion in favor of fission due to lateral interaction between mitochondria. In case of OPA, PD, and ALS on the other hand, the balance between fusion and fission due to lateral interaction remains intact. However, the increased fission at the expense of fusion due to longitudinal interaction leads to fragmented mitochondrial network in these diseases.

The differences in the microscopic properties of mitochondrial fission and fusion could have key implications for the way fragmentation affects cell function depending on the morphology and the region of the cell where fragmentation occurs. For example, impaired balance between fission and fusion due to longitudinal interaction would lead to shorter linear chains of mitochondria that could significantly affect signaling along neuronal processes and synapses. Increased rate of fission at the expense of fusion due to lateral interaction on the other hand would likely have a more significant effect on the functions in regions such as cell body where a healthy mitochondrial network is key for the function of organelles such as nucleus and Golgi network.

We remark that our conclusions are based on limited data available. Consolidating these conclusions will need further future experiments and analysis of the mitochondrial networks in the different diseases using the approach discussed in this paper. Nevertheless, we believe that our framework provides a solid foundation for developing computational tools that could use these indicators for inferring the extent and types of signaling disruptions in different pathologies. While beyond the scope of this study, we believe that validating our predictions about the disruption of lateral and/or longitudinal fission/fusion in different diseases, experimental techniques similar to that used in Ref. [83] could be useful. In this technique, the exchange of matrix contents between individual mitochondria is visualized in real time as the two mitochondria fuse or detach by using mitochondrial matrix-targeted green-photoactivated, red-fluorescent Kindling fluorescent protein in combination with green or yellow fluorescence protein or the cyan-photoactivated mtPAGEP (mitochondria-targeted photoactivatable green-fluorescence protein) in combination with red fluorescence protein [83].

Supporting information

S1 Text. Description of different types of mitochondrial interactions, cell models, and diseases investigated in this study.

(DOCX)

S1 Fig. Longitudinal and lateral mitochondrial interactions (fusion/fission).

(a) End-to-end fusion of two mitochondria moving towards each other along a common microtubule (not shown), (b) Side-to-side and end-to-side fusion of two mitochondria moving on two different microtubule tracks (not shown). Arrows indicate the direction of motion.

(TIFF)

S2 Fig. A smaller decrease in C2 leads to a smaller decrease in X3, and a smaller increase in X1 and X2, which would lead to a smaller but larger number of linear chains and larger number of cyclic loops.

Here we compare mitochondrial network fragmentation in HD (striatal cells from mouse embryos bearing a 111 polyglutamine repeat Q111/0 and Q111/1) versus control [78] with C_2n/C_2d = 2.0 (top row) and diabetes (MitoNEET knockout mouse embryonic fibroblasts) versus control [65] with C_2n/C_2d = 1.8 (bottom row). Distributions of (a1) loop sizes, (a2) branch lengths, and (a3) cluster sizes (cumulative probability) for NL (red) and diseased cells (blue) from experimental images. (a4) Fraction of X1 (NL: green, diseased: red), X2 (NL: magenta, diseased: blue) and X3 (NL: black, diseased: cyan) species from the model as functions of the number of iterations using C1 and C2 values for HD experiments. The model results show average of 100 runs. (b1-b4) shows the same mitochondrial network features as (a1-a4) for MitoNEET knockout mouse embryonic fibroblasts with diabetes pathology and their normal counterparts.

(TIFF)

S3 Fig. A larger decrease in C1 leads to a significant decrease in the number of loops and branches.

Here we compare mitochondrial network fragmentation in OPA (mouse embryonic fibroblasts with the pathogenic mutation R149W in human YME1L1) versus control [66] with C_1n/C_1d = 1.18 (top row) and PD (human primary skin fibroblasts obtained from sporadic late-onset PD patients) versus those from healthy age-matched control subjects [81] with C_1n/C_1d = 1.22 (bottom row). Distributions of (a1) loop sizes, (a2) branch lengths, and (a3) cluster sizes (cumulative probability) for NL (red) and diseased cells (blue) from experimental images. (a4) Fraction of X1 (NL: green, diseased: red), X2 (NL: magenta, diseased: blue) and X3 (NL: black, diseased: cyan) species from the model as functions of the number of iterations using C1 and C2 values for OPA experiments. The model results show average of 100 runs. (b1-b4) shows the same mitochondrial network features as (a1-a4) for human primary skin fibroblasts with PD pathology and their normal counterparts. Note that the curves for X3 species in diseased and normal cells overlap (a4, b4).

(TIFF)

S1 Table. Experimental micrographs processed in this study.

Column 1 provides the disease, column 3 reports the cell/animal model, column 4 lists the condition for the experiment (normal versus diseased), and column 5 provides references where the images were originally published.

Abbreviations: WT-Wild type, KO-Knockout, NL-Normal, MEF-Mouse embryonic fibroblasts, HSF-Human skin fibroblasts, MEMN Mouse embryonic motor neurons, TM-YAC128 Transgenic mice Yeast Artificial Chromosome 128, HSF Human Skin Fibroblasts, RPTCs rat proximal tubular cells, RCA rat cortical astrocytes, CHCHD10—Coiled-coil-helix-coiled-coil-helix domain-containing protein 10, YME1L1—Yeast mitochondrial escape 1-like 1 gene.

(DOCX)

S2 Table. Comparison of microscopic parameters of mitochondrial network obtained from simulations and experiments for additional cell/animal models or experimental conditions on AD, PD, and ALS diseases.

Column 1 lists the condition for which images of normal (NL) and diseased cells were analyzed (column 2). Columns 3 & 4 and 5 & 6 compare <k> and N_g/N respectively from experiment and theory. Columns 7 & 8 are the C1 (tip-to-tip fusion/fission) and C2 (tip-to-side fusion/fission) values obtained by fitting the model to the data and used in simulations.

(DOCX)

Data Availability

All relevant data are within the manuscript and its Supporting Information files.

Funding Statement

This works was supported by National Institute of Health through grant R01 AG053988 (to GU). URL of funder website: https://www.nih.gov. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.