The Inertial Anisotropy of the Arm Is Accurately Predicted during Movement Planning

Abstract

An important theoretical concept in motor control is the idea that the CNS uses an internal model of the motor system and environment to predict the sensory consequences of motor commands. In arm movement control, a critical factor affecting the transformation from motor commands to sensory consequences is limb dynamics, including the inertial anisotropy of the arm, which refers to the fact that the inertial resistance of the arm depends on hand movement direction. Here we show that the CNS maintains an accurate internal model of the inertial anisotropy of the arm by demonstrating that the motor system can precisely predict direction-dependent variations in hand acceleration. Subjects slid an object, held beneath the index finger, across a frictionless horizontal surface to radially located targets. We recorded the normal (vertical) force exerted by the fingertip, as well as the tangential (horizontal) force proportional to hand acceleration. We found that normal force was precisely scaled in anticipation of tangential force, which, as expected, varied with direction. The peak rates of change of the normal and tangential forces, observed early in the movement, were highly correlated. Similar results were obtained regardless of whether the start position of the hand was located directly in front of the subject or rotated 45° to the right. Finally, we observed reduced force correlations under reaction time conditions. This suggests that the process of prediction, based on an internal model of the limb, is not fully completed within the reaction time interval.

The ability to predict the consequences of our own actions is essential for skilled performance. Such prediction may be achieved using internal models that mimic the behavior of the motor system and environment (Kawato et al., 1987;Johansson and Cole, 1992; Jordan and Rumelhart, 1992; Wolpert et al., 1995; Miall and Wolpert, 1996; Conditt et al., 1997; Bhushan and Shadmehr, 1999; Krakauer et al., 1999). For example, when manipulating objects, the CNS may use internal models of the arm and object, combined with a copy of the arm motor command, to predict the forces acting on the object so as to make appropriate grip adjustments (Flanagan and Wing, 1997; Blakemore et al., 1998).

Although the concept of internal models has gained considerable empirical support, many questions remain. With respect to arm movement control, an important question concerns the precision with which the CNS represents the complex dynamics of arm motion (Hollerbach and Flash, 1982). Although many researchers would agree that some representation of limb dynamics is needed for predictive control (Gribble and Ostry, 1999), it has been suggested that the motor system may use a course approximation of dynamics that allows for adequate control when coupled with intelligent reactive control processes (Atkeson, 1989).

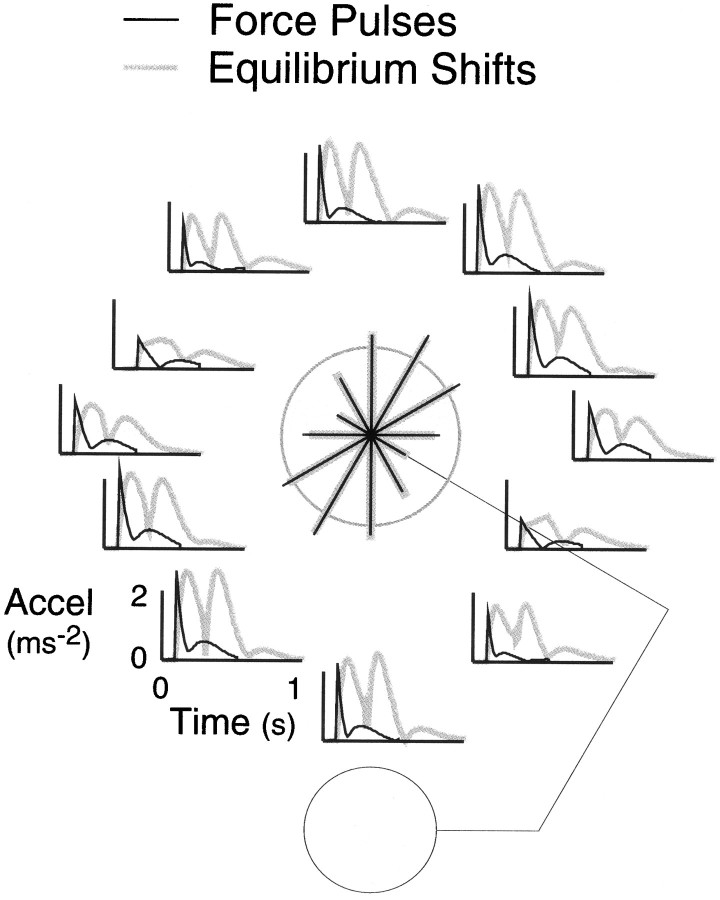
Here we ask whether the CNS maintains an accurate internal model of the inertial anisotropy of the arm, a key dynamic property that refers to the fact that the effective inertia of the arm varies with the direction of hand movement. The inertial anisotropy of the arm is illustrated in Figure 1, which shows simulated hand acceleration profiles resulting from equal force pulses applied to the hand in different directions (thin black traces) or equivalent shifts in the equilibrium position of the hand to targets in different directions (thick gray traces). Acceleration is high for low inertia movements primarily involving forearm rotation and low for high inertia movements primarily involving whole-arm rotation.

Fig. 1.

Simulated hand resultant acceleration profiles in response to force pulses (1.75 N for 0.9 sec) applied at the hand (black traces) or shifts (20 cm in 0.2 sec) in the equilibrium position of the hand (gray traces). A two-link planar arm model with single-joint and double-joint stiffness and viscosity terms was used (Flash, 1987). The initial position of the model arm, shown in the figure, matched the arm-centered condition. The polar plot in the center shows the initial peak in acceleration as a function of the direction of the applied force or equilibrium shift. The radius of the calibration circle is 2 m/sec².

Ghez and colleagues (Ghez et al., 1994; Gordon et al., 1994) found that, in horizontal pointing movements, hand acceleration varies with direction and concluded that the CNS does not alter forces to compensate for directional differences in limb inertia. Instead, they suggested that the variation in acceleration might arise as a consequence of the interaction between limb mechanics and motor commands that are not explicitly controlled to achieve constant hand acceleration.

Here we show that the CNS accurately predicts direction-dependent changes in hand acceleration. Using a horizontal reaching task in which subjects slid an inertial load held beneath the index finger, we demonstrate that the vertical normal force applied to the object (required to prevent object slip) is precisely scaled in anticipation of movement-dependent changes in horizontal load force proportional to hand–object acceleration. This prediction may be based on an internal model that captures the inertial anisotropy of the arm. We also show that the ability to predict direction-dependent load forces is independent of the position of the arm. Finally, we demonstrate weaker but still adequate prediction under reaction time conditions, suggesting that the CNS requires several hundreds of milliseconds to generate an accurate prediction based on the internal model.

MATERIALS AND METHODS

Subjects. Ten undergraduates from Queen's University between 18 and 22 years of age participated in this study after giving informed consent. A local ethics committee approved the experimental protocol. All subjects were right-handed and had normal or corrected for normal vision.

Apparatus. Participants performed arm movements in a horizontal plane over a glass table top (Fig.2A). The participant's right arm was braced at the wrist and mounted on a Plexiglas air sled that allowed for near-frictionless motion (Fig.2E). Participants moved a test object, held under the tip of their right index finger, that was also mounted on an air sled (Fig. 2D). The test object was instrumented with a three-dimensional force sensor (model F233; Novatech Measurements Ltd., St. Leonards on Sea, East Sussex, UK ) with a rectangular contact plate (2.6 × 5.0 cm) covered with medium grade sandpaper (number 220). The sensor measured the normal or vertical force applied by the fingertip (F_n), as well as the two orthogonal forces (F_x andF_y) in the horizontal plane. The centers of the contact plate, force sensor, and air sled were vertically aligned such that horizontal forces applied at the center of the contact plate would not tend to rotate the object. The mass of the test object was 0.176 kg, and the mass of each air sled was 0.173 kg. An electromagnetic position sensor (Ascension Technology Corp., Burlington, VT), attached to the middle phalanx of the right index finger, recorded the x–y position of the hand in the horizontal plane (Fig. 2E). Targets were presented on a 17 inch computer monitor positioned 60 cm directly in front of the subject at eye level. A horizontal screen mounted above the table top blocked the participant's view of their arm (Fig.2B).

Fig. 2.

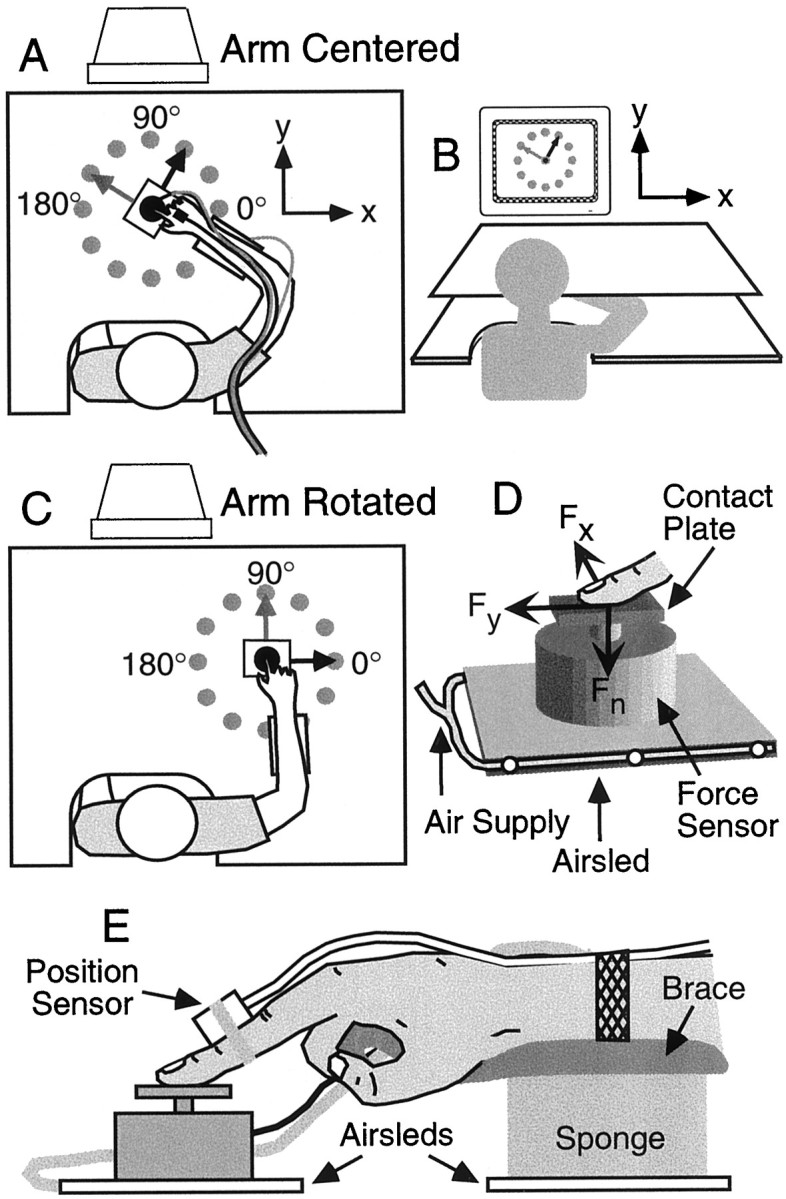
Subjects performed horizontal pointing movements to radially located targets starting with the hand in either a central (A; top view) or rotated (B) position. Target positions and the location of the hand were presented on a vertical screen in front of the subject, and vision of the arm was blocked (C). The arm was supported by a brace that prevented motion of the wrist. The brace was mounted on an air sled that gave near frictionless motion over the glass surface. Subjects held an object, instrumented with a three-dimensional force, beneath the index finger (D). The object was also mounted on an air sled and behaved as a pure inertial load. A position sensor was attached to the first phalanx of index finger.

Procedure. Participants were required to make movements to 12 targets located radially 20 cm from a start position and evenly spaced at 30° intervals (Fig. 2A). Two start positions were used. In the center position (Fig.2A), the index finger was aligned in the subject's midsagittal plane with the angle between the participant's forearm and upper arm set at 90°. In the rotated position (Fig. 2C), the arm was rotated about the shoulder 45° to the right while maintaining an elbow angle of 90°. The start position was always represented as a circle in the center of the monitor, regardless of the start position in space. Hand position was represented on the screen as a cursor. A scale factor of 9:20 related displacement on the screen to displacement in space. A movement of the hand to the right (Fig. 2A, x direction) corresponded to a rightward movement of the cursor on the screen. A movement of the hand away from the body (Fig. 2A,y direction) corresponded to an upward motion of the cursor on the screen.

All 10 participants completed three conditions. In the “arm-centered” and “arm-rotated” conditions, participants made self-initiated movements from the center and rotated start positions, respectively. Participants were asked to make fast and accurate movements, without corrective adjustments, and were told that they could start moving at any time after the target appeared. In the “reaction time” condition, in which the center start position was used, participants were instructed to make movements as quickly and accurately as possible after the appearance of the target. All participants performed the arm-centered and reaction time conditions first, in counterbalanced order, and then the arm-rotated condition. In each condition, participants completed 72 trials (six trials for each of the 12 targets) randomized across targets. Before each trial, the participant was required to place the cursor at the start position for 1 sec. The start position was represented by a circle on the screen (1 cm radius in real space). After a variable delay of 750 to 2000 msec (250 msec increments), the start circle disappeared and a target appeared at the same time. Visual feedback of the cursor was removed as soon as the target was presented. At the end of the trial, the path of the cursor was displayed on the screen. Before the first condition, participants completed 24 practice trials (two for each target).

Data analysis. Force signals were sampled at 400 Hz, and position signals were sampled at 100 Hz. The force data were digitally filtered using a low-pass, fourth-order Butterworth filter with a cutoff frequency of 20 Hz. The tangential force (F_t) applied to the contact plate (in the horizontal plane) was taken as the resultant ofF_x andF_y. The normal and tangential force rates (first time derivatives) were computed using a second-order central difference equation.

For each trial, we determined the peak normal and tangential force rates and the peak tangential force during the initial acceleratory phase of the movement. The onset of normal and tangential force was determined as the time at which the respective force rates first exceeded 2 N/sec and stayed above this threshold for at least 100 msec. Repeated-measures ANOVA and linear regression analysis were used to assess experimental effects. An α level of 0.05 was considered to be statistically significant.

Slip ratios. The normal force needed to prevent an object from slipping under a given tangential load depends on the coefficient of friction between the skin and contact surface. Häger-Ross et al. (1996) demonstrated that the friction between the fingertip and object varies with the direction of tangential force. Because the present study is concerned with adjustments in normal force for changes in tangential force in different directions relative to the fingertip, it behooves us to examine possible directional influences on friction that could affect normal force independently of tangential force. For each participant, we estimated the slip ratio, or the inverse of the coefficient of friction, for different directions of tangential force. The slip ratio was defined as the ratio of normal force to tangential force at slip. Subjects placed the tip of the index finger on the contact surface of the instrumented object that was now fixed to the table top. They were asked to press down (with a normal force exceeding 1 N) and then push outward, toward one of the targets, until slip occurred. The slip ratio at the moment of slip onset (associated with a rapid drop in tangential force) was measured. Between 25 and 45 slip events were recorded for each subject (at least two slips for each target). An elliptical model of the following form was fit to the slip ratio data for each subject:

$$\frac{x^2}{a^2}+\frac{(y+c{)}^2}{b^2}=1.$$

The model allowed for ellipses of varying eccentricity with an offset in the proximal-distal direction. The “best fit” parameters were obtained using an iterative procedure that minimized the mean square error between the predicted and actual slip ratios. Figure3B illustrates, for three subjects with quite different patterns of results, that the model provided a reasonably good fit to the data. Similarly good fits were observed for all subjects. The mean squared errors, computed for each subject, ranged from 0.003 to 0.011 with an average of 0.005. The average a, b, and c parameters were 0.73, 0.74, and 0.03, respectively. Thus, the slip ratio tended to be greater when tangential force was directed proximally as opposed to distally, a finding consistent with previous reports (Häger-Ross et al., 1996). As we will show at the end of Results, the contribution of the slip ratio to direction-dependent changes in normal force was trivial compared with the large influence of tangential forces, and we observed no important differences in regression analyses when slip ratios were factored into account.

Fig. 3.

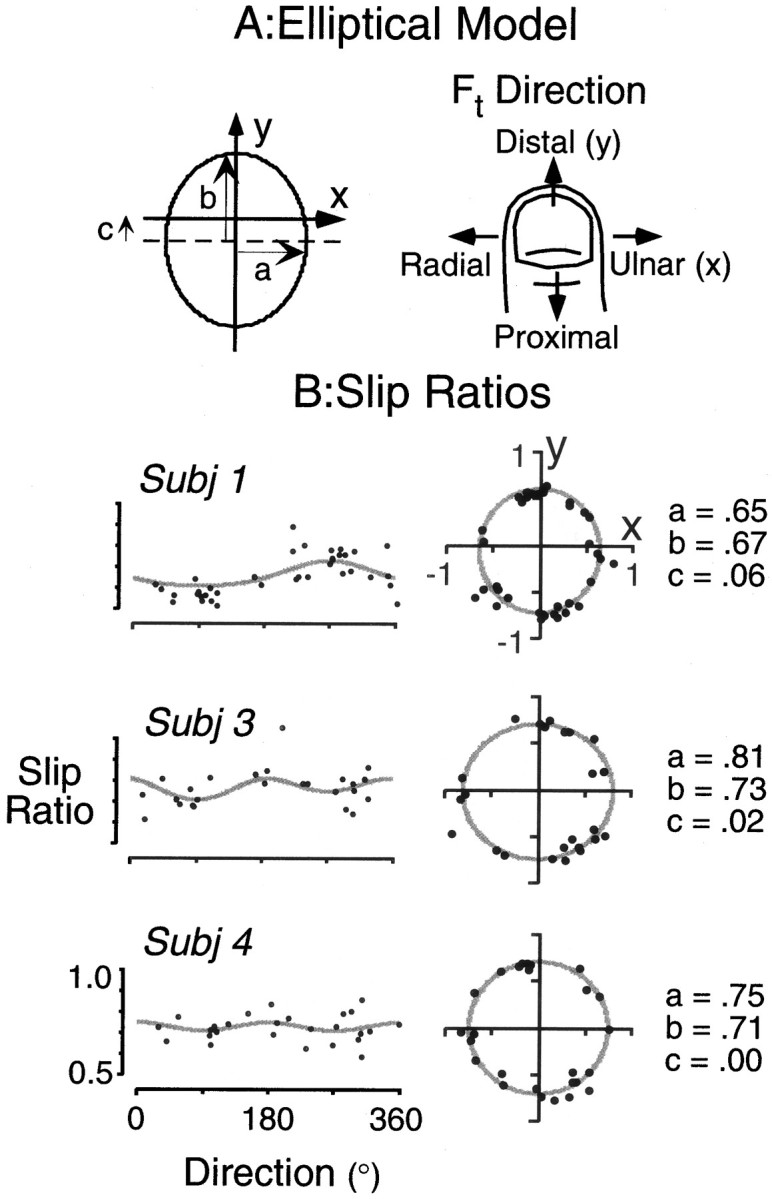
Slip ratios, estimated for load forces applied in different directions, were fit with an elliptical model (A) that allowed for different axis lengths (parameters a and b) and an offset in the distal-proximal direction (parameter c). The parameter values and the goodness of fit are illustrated for four subjects inB. The left panels show the experimentally determined and predicted slip ratios as a function of load force direction. The right panels show polar plots conveying the same information.

RESULTS

Basic coordination of normal force and tangential force

Figure 4 shows individual records from one subject for movements to two targets in the arm-centered condition (Fig. 4B). Movements to the 60° target primarily involved rotation of the forearm about the elbow and encountered low inertial resistance; movements to the 150° target primarily involved rotation of whole arm about the shoulder and encountered high inertial resistance. Hand paths for five individual movements to each target are shown in Figure 4C. Force and force rate functions for movements to the 60° (thin traces) and 150° (thick traces) targets are shown in Figure 4A. The tangential force (F_t) functions exhibited two peaks corresponding to the acceleration and subsequent deceleration of the hand and object en route to the target. Normal force (F_n) changed in phase with, and thus anticipated, fluctuations in tangential force. At the start of the movement, normal force and tangential force increased in parallel. In most trials, there were two peaks in normal force that corresponded to the two peaks in tangential force. In some trials, a local minimum in normal force was not observed between the tangential force peaks, but normal force was nevertheless elevated for both peaks. The close coupling between forces is particularly evident in the force rate functions. The initial peaks in the normal and tangential force rates coincide closely in time. These parallel changes in grip force and load force agree with previous studies in which subjects lifted and transported inertial loads (Johansson and Westling, 1984; Flanagan and Wing, 1993, 1995).

Fig. 4.

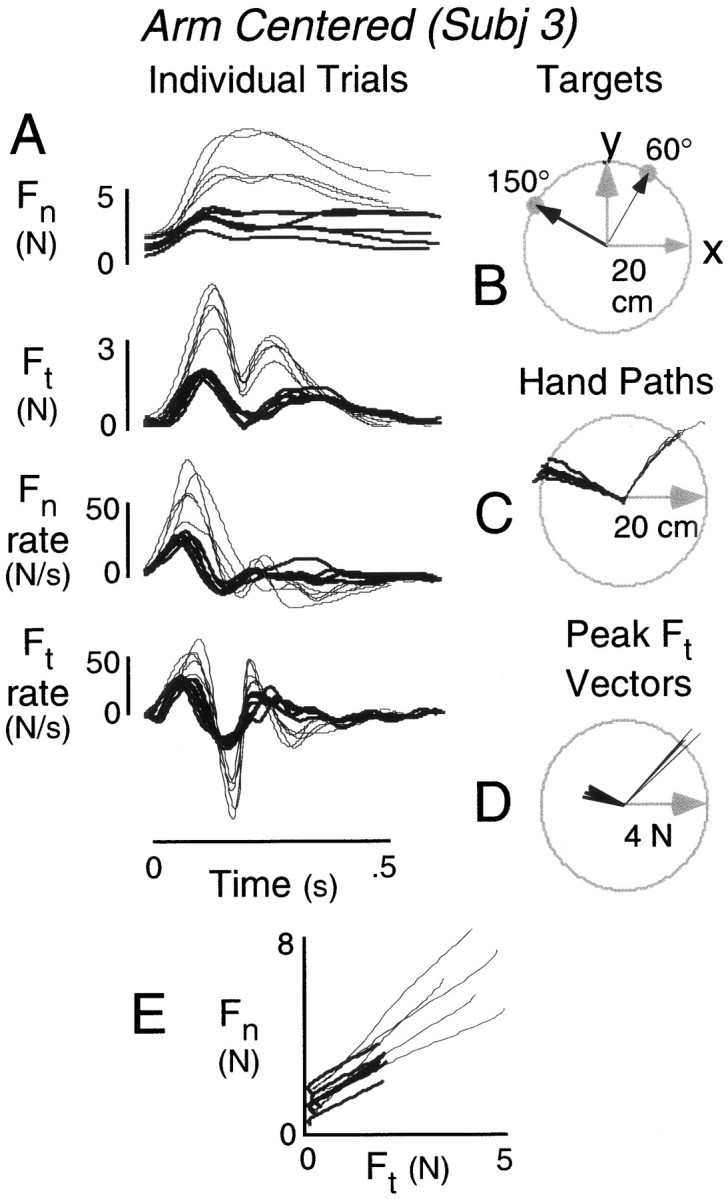
A, Normal (F_n) and tangential (F_t) force records and force rates from one subject for movements to the 150° (thick traces) and 60° (thin traces) targets (B). Five trials shown for each target. Data are from the arm-centered condition. C, Corresponding hand paths. D, Corresponding vectors representing initial peak tangential force (magnitude) plotted as a function of hand displacement (direction). Greater initial peak tangential forces were observed for movements to the 60° target. E, Normal force plotted as a function of tangential force from movement onset to the initial peak tangential force. Separate functions shown for each trial with thick and thin tracescorresponding to movements to the 150° and 60° targets, respectively.

As expected, tangential force varied with direction. The initial peaks in tangential force and tangential force rate were clearly larger for the 60° target than the 150° target. This can be appreciated by viewing the polar plot shown in Figure 4D. The length of each vector represents the magnitude of the peak tangential force, and the direction represents the direction of the hand at the end of the movement. The adjustment of normal force was clearly sensitive to this direction-dependent variation in tangential force. The initial peaks in normal force and normal force rate were alsomuch larger for the 60° target. We also observed temporal coupling between forces across target directions. For example, the initial peaks in the tangential and normal force rates both tended to occur earlier for movements to the 150° target and later for movements to the 60° target.

Importantly, the peak forces and force rates are determined by feedforward or anticipatory control mechanisms. These peaks occur early in the movement and are unlikely to be influenced by feedback control mechanisms; the time required to adjust fingertip force output in response to slip is in the order of 100 msec (Westling and Johansson, 1987; Cole and Abbs, 1988; Johansson and Westling, 1988b). Moreover, as illustrated in Figure 4, no corrective adjustments in force output are observed as would be expected if the motor system relied on reflexive control to scale normal force for direction-dependent differences in tangential force (Johansson and Westling, 1988a). Figure4E shows the relationship between normal force and tangential force for the initial phase of the movement between onset and peak tangential force. For movements to both targets, normal force increased in proportion to tangential force, and the slope of the relation was similar for both targets.

Coordination of forces under different experiments conditions

The polar plots shown on the left in Figure5 show tangential force, normal force, and the force ratio (normal/tangential), all measured at the time of peak tangential force, as a function of movement direction. Each vector represents a single trial, and all trials from one subject in the arm-centered condition are shown. A strong positive relationship between tangential and normal forces was observed and is further illustrated by the scatterplot at the bottom left of the figure. The force ratio was relatively constant across movement directions. However, to quantify the relationship between normal and tangential force, it is important to distinguish between covariation across and within hand directions. We therefore computed, for each subject and condition, the median values of the two forces (and the force ratio) for each target direction. (Median values were used to avoid any undue influence of outlying data values. However, in fact, the mean and median values were very similar in all cases.) These median values are represented as a function of the median hand movement direction on the right of Figure 5. As shown in the figure, a positive correlation between the median forces was observed, in this case more reliable than the correlation between forces from individual trials (see scatterplot at the bottom right of the figure). This latter result unambiguously demonstrates that the two forces covaried as a function of movement direction.

Fig. 5.

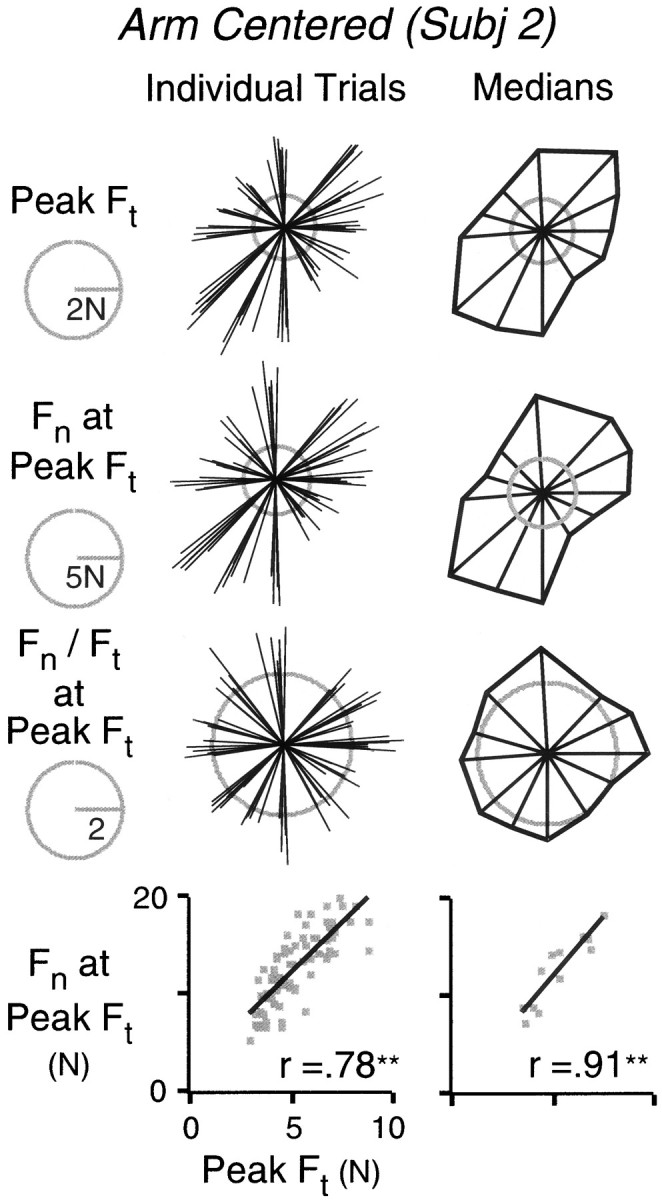
Top row, Polar plots representing initial peak tangential force (F_t) as a function of hand displacement direction. In the plot on the left, each vector represents a single movement, and all trials for a single subject are shown. In the plot on the right, each vector represents the median initial peak tangential force of the six movements directed to a given target. The direction of the each vector represents the median hand displacement of the same trials. The tips of the vectors are joined to provide an impression of the distribution. The second and third rows show corresponding plots for the normal force (F_n) and the ratio of normal force to tangential force observed at the time of initial peak tangential force. The bottom row shows the relationship between normal force, observed at initial peak tangential force, and initial peak tangential force. The relationships for individual trials and for median values are shown on the left andright, respectively.

Figure 6 shown median polar plots of tangential and normal force for two subjects and for all three experimental conditions. In all conditions, the forces were largest in directions of low inertia and smallest in directions of high inertia. In the arm-centered and reaction time conditions, the forces tended to be largest for movements aimed at 60 and 210° targets and smallest for movements aimed toward the 150 and 300° targets. (Keep in mind that the vectors are oriented in the direction of hand displacement and not the target.) In the arm-rotated condition, the forces tended to be largest for movements aimed at the 0 and 180° targets and smallest for movements aimed toward the 90 and 270° targets.

Fig. 6.

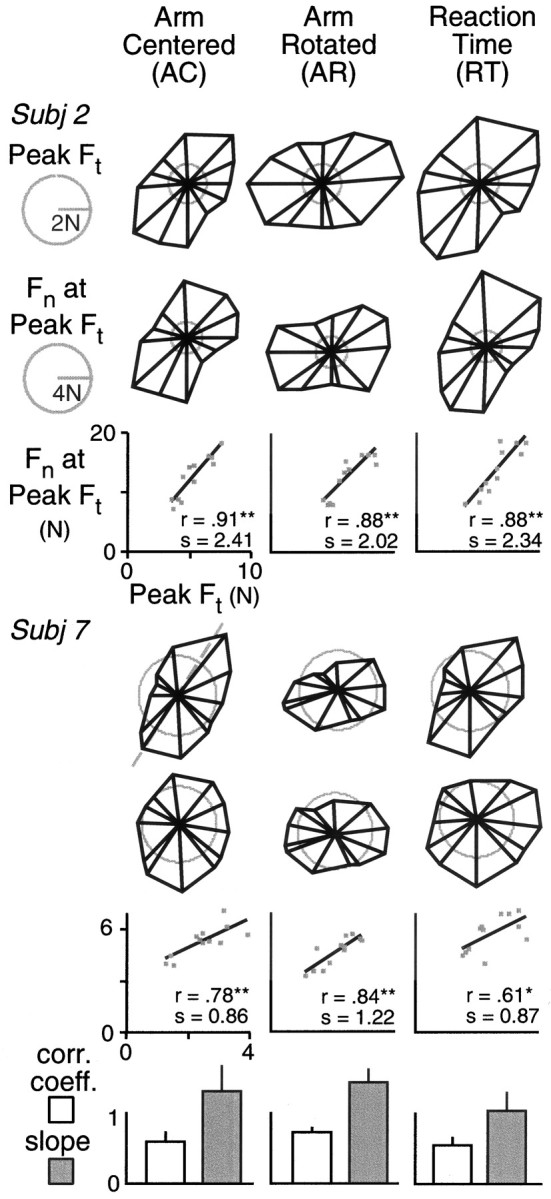
The polar plots in the top two rowsshow peak tangential force (F_t) and the normal force (F_n) at the time of peak tangential force for movements in different directions. Data shown are from one subject. Vector magnitude represents the median force for the six movements to each target, and the direction represents the median hand displacement. Separate plots are shown for each of the three experimental conditions. The third row shows normal force as a function of peak tangential force based on the median values. The correlation coefficients and slopes of the least-squares linear regression fits are indicated. The next three rows show corresponding results for a second subject. The bar graphs in the bottom row show the correlation coefficients and slopes (of the linear functions relating normal and peak tangential force) for each condition averaged across all 10 subjects. Error bars represent SEs.

In all six cases shown in Figure 6, a reliable positive relationship was observed between median normal force and median tangential force in which the individual forces were taken at the time of peak tangential force. The scatterplots show, for each case, the relationship between normal force and tangential force. We computed correlation coefficients and slopes for each subject and then computed means for each experimental condition. These means are shown in the bar charts at thebottom of the figure. The error bars represent SEs.

Planned comparisons with repeated-measures ANOVA revealed that the correlation coefficients were reliably smaller in the reaction time condition than in the other two (nonreaction time) conditions combined (F_(1,9) = 7.73; p < 0.05) but that there was no significant difference between the arm-centered and arm-rotated conditions (F_(1,9) = 2.26; p = 0.14). Planned comparisons also revealed the slope to be reliably smaller in the reaction time condition than in other conditions combined (F_(1,9) = 14.0;p < 0.01) but that there was no difference between the other two conditions (F_(1,9) = 0.23;p = 0.65).

An arguably better indication of predictive or anticipatory control is provided by the peak force rates that occur before the peak forces. Figure 7 shows polar plots of median peak tangential force and normal force rates as functions of hand direction. Plots are shown for two subjects and all three conditions. (For comparative purposes, we selected one subject whose peak force data are also shown in Figure 6.) As was the case with the forces, the peak force rates were largest in directions of low inertia and smallest in directions of high inertia, regardless of the orientation of the arm at the start point. The scatterplots show that positive correlations between the peak force rates were observed in all six cases. We computed the correlation coefficient and slope of the relationship between peak normal force rate and peak tangential force rate for each subject. The bar graphs at the bottom of the figure show, for each experimental condition, the mean coefficients and slopes. The error bars depict SEs. Planned comparisons with repeated-measures ANOVA revealed that the correlation coefficient was reliably smaller in the reaction time condition than in the other two conditions combined (F_(1,9) = 7.36; p < 0.05) but that there was no significant difference between the arm-centered and arm-rotated conditions (F_(1,9) = 0.70; p = 0.43). Planned comparisons also revealed the slope to be reliably smaller in the reaction time condition than in the other conditions combined (F_(1,9) = 12.0;p < 0.01). No reliable difference in slope was found between the arm-centered and arm-rotated conditions (F_(1,9) = 2.54; p = 0.15).

Fig. 7.

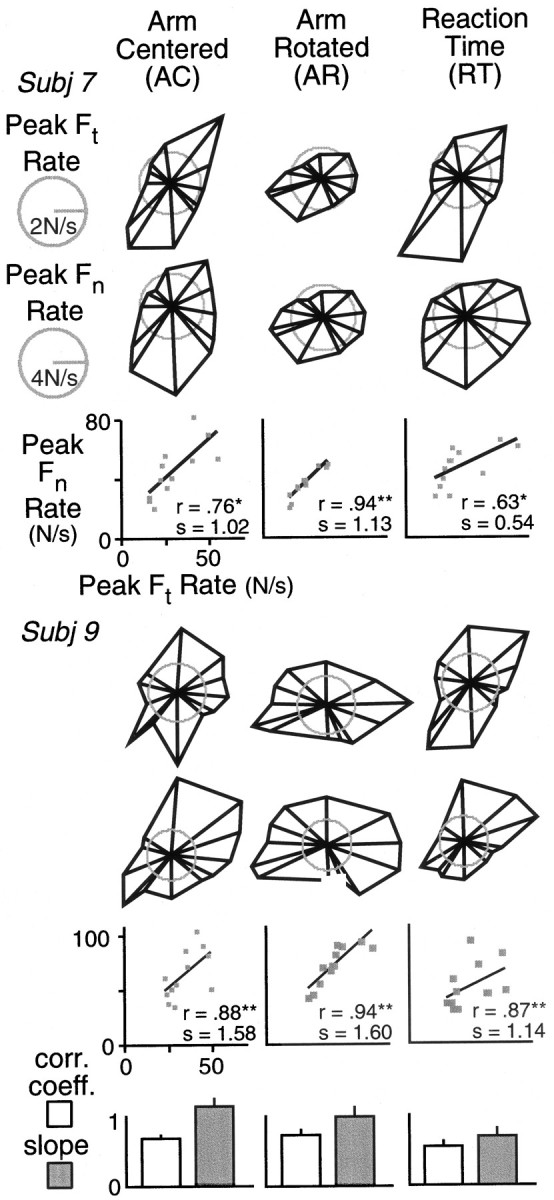
The polar plots in the top two rows show initial peak tangential force rate (F_t rate) and initial peak normal force rate (F_n rate) for movements in different directions. Data shown are from one subject. Vector magnitude represents the median peak force rates for the six movements to each target, and the direction represents the median hand displacement. Separate plots are shown for each of the three experimental conditions. The third row shows peak normal force rate as a function of peak tangential force rate based on the median values. The correlation coefficients and slopes of the least-squares linear regression fits are indicated. Corresponding results from a second subject are shown in the next three rows. The bar graphs in the bottom row show the correlation coefficients and slopes (of the linear functions relating peak normal and tangential force rates) for each condition averaged across all 10 subjects. Error bars represent SEs.

Importantly, the weaker coupling between the normal and tangential forces and between the normal and tangential force rates, observed in the reaction time condition, did not simply result from changes in the distribution of peak tangential forces or force rates across directions or from changes in the magnitudes of these peaks. To assess the shape of the distribution of tangential forces across directions, we first determined, for each subject and condition, the principal axis (through the origin) along which the maximum variance in force magnitudes was observed (Fig. 6, dashed line, Subj 7, Arm Centered). We then formed a ratio of the variance along the principal axis and the variance along the orthogonal axis. The average ratios for the arm-centered, arm-rotated, and reaction time conditions were 1.29, 1.42, and 1.31, respectively. Repeated-measures ANOVA revealed that there was a reliable effect of condition on the ratio (F_(2,18) = 4.65; p = 0.02). Pairwise comparisons (Tukey's b post hoctest) revealed that the ratio was significantly greater in the arm-rotated condition than in either of the other two conditions (p < 0.05) but that there was no difference between the arm-centered and reaction time conditions. The effect of condition on the orientation of the principal axis was also examined using repeated-measures ANOVA. Planned comparisons confirmed that there was a reliable difference (26° on average) between the arm-rotated condition and the other two conditions combined (F_(1,9) = 25.6; p < 0.001) but that there was no reliable difference between the arm-centered and reaction time conditions (F_(1,9) = 0.28; p = 0.61). These findings suggest that the weaker force coupling observed in the reaction time condition (at least compared with the arm-centered condition that shared the same start position) was not attributable to reduced variation in tangential forces or the sensitivity of these forces to hand direction.

Basic movement parameters across experimental conditions

As expected, there were clear differences in reaction time (time from target presentation until movement onset) between conditions. The average reaction time (based on subject means) in the reaction time condition was 311 ± 65 msec (mean ± SD). The average reaction times in the arm-centered and arm-rotated conditions were 617 ± 124 and 622 ± 155 msec, respectively. Apart from this difference in reaction time, the movements performed under the three experimental conditions were remarkably similar. There were no reliable differences among conditions in any of the following variables (mean values shown in parentheses): movement time (670 msec), peak velocity (1.21 m/sec), peak tangential force (2.75 N), peak normal force (5.79 N), peak tangential force rate (34.0 N/sec), and peak normal force rate (48.9 N/sec) (p > 0.05 in all cases). A small but reliable effect of condition was observed in movement displacement (F_(2,18) = 3.81; p < 0.05). Pairwise comparisons (Tukey's b post hoctest) revealed that displacement in the arm-rotated (27.3 cm) condition was significantly greater (p < 0.05) than in the arm-centered condition (25.1 cm). Displacement in the reaction time condition (26.0 cm) was not reliably different from either of the other two conditions. We also observed small differences among conditions in the time-to-peak tangential force rate (F_(2,18) = 6.0; p < 0.05) but not in the time-to-peak normal force rate. The peak tangential force rate occurred slightly earlier in the reaction time condition (95 msec) than in the arm-centered (103 msec) and arm-rotated (106 msec) conditions. Overall, the peak tangential force rate occurred 20 msec before the peak normal force rate.

Extent and direction errors

Ghez and colleagues (for review, see Ghez et al., 1994) observed that, in pointing movements to radially located targets, removal of vision of the hand results in systematic errors in extent and direction that primarily depend on the direction of hand movement and the initial position of the hand, respectively. They observed that the hand tends to overshoot targets in low inertia movements primarily involving forearm rotation and undershoot targets in high inertia movements primarily involving whole-arm rotation (Gordon et al., 1994b). They also found that, when the start position of the hand is rotated 45° clockwise from the midline, the hand is directed, on average, ∼15° clockwise from the targets (Ghilardi et al., 1995). These researchers suggested that extent errors could be attributed to the inertial anisotropy of the arm, whereas direction errors were attributed to a failure of proprioception alone to adequately encode the rotated start location of the arm (Gordon et al., 1994a).

We observed similar dependencies of extent and direction on hand movement direction and hand start position. Figure8A shows the hand paths from all trials in each of the three experimental conditions for a single subject. To summarize the hand displacements across all subjects, we first computed, for each subject and condition, the median hand displacement vectors for each target direction. For each condition, we then calculated the mean displacement vector for each target, averaging across subjects. These mean vectors are shown in Figure 8B (the gray region represents one SE, and the radius of the calibration circles in both A andB is 20 cm). Although the correspondence is not perfect, the plots show that movement extent tended to be larger for low inertia movements approximately orthogonal to the initial position of the forearm (see arm diagrams in figure) and smaller for high inertia movements parallel to the forearm. However, we observed an overall bias toward overshooting targets. To assess the overall shape of the distribution of hand displacements, we again determined the principal axis, through the origin, that accounted for the maximum variance in displacements and formed a ratio of the variance along the principal axis to the variance along the orthogonal axis. The average ratios for the arm-centered, arm-rotated, and reaction time conditions were 1.33, 1.24, and 1.36, respectively. Repeated-measures ANOVA revealed that there was not a reliable effect of condition on the ratio (F_(2,18) = 3.5; p = 0.052). Planned comparisons revealed that the orientation of the principal axis in the arm-rotated condition was significantly different (∼30°) than the average of the other two conditions (F_(1,9) = 3.11; p = 0.01) but that there was no reliable difference between the arm-centered and reaction time conditions (F_(1,9) = 0.79; p = 0.45).

Fig. 8.

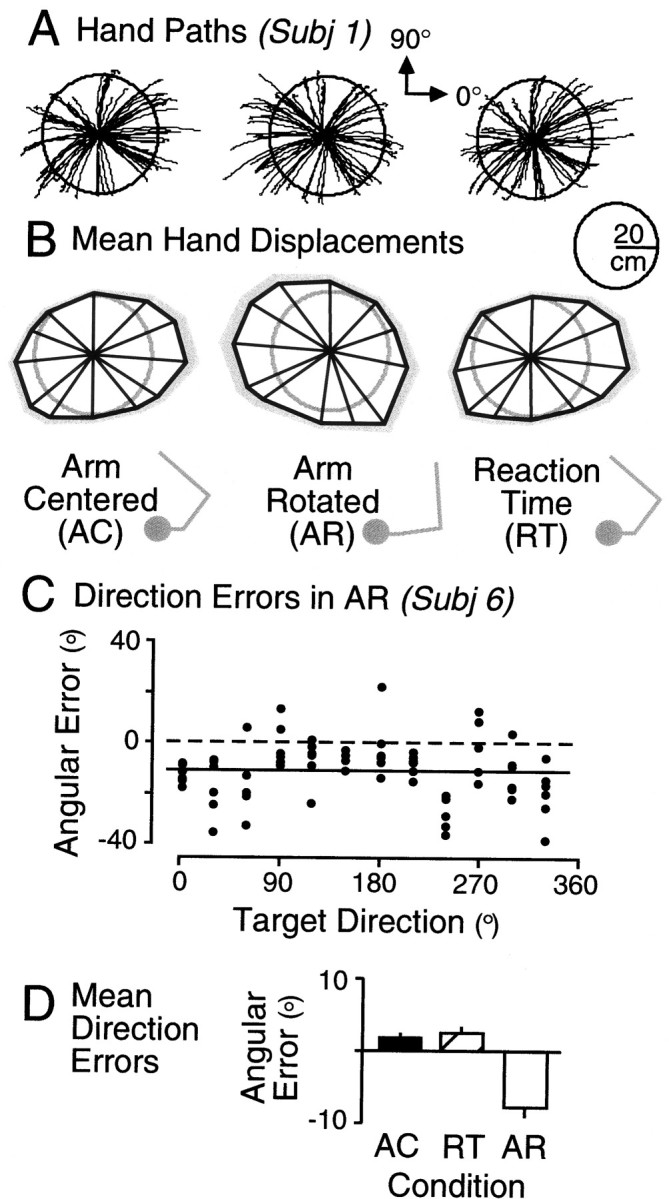
A, Hand paths from all trials from a single subject shown for each condition separately. B, Mean displacement vectors, averaged across all subjects, shown for each target. Means based on median values computed for each target and condition. The tips of the vectors are joined to provide a sense of the distribution of displacements. The gray regionsrepresent SEs. The calibration circles in A andB have a radius of 20 cm. C, Angular errors from all trials from one subject in the arm-rotated condition shown as a function of target direction. Negative errors indicate that the hand was directed clockwise from the target. Horizontal line shows the mean angular error across all trials.D, Average angular errors, based on subject means, for each condition. Error bars represent SEs.

Figure 8C shows direction errors (angular differences between the final position of the hand and the target) as a function of target direction for all trials from a single subject in the arm-rotated condition. The horizontal solid line represents the mean direction error. In line with the findings of Ghilardi et al. (1995), we observed a systematic bias in the same direction as the rotation of the hand start position (i.e., clockwise), as well as variations in directional error that depended on target direction. Figure 8D shows the mean directional errors, averaged across subjects, for the three experimental conditions. The error bars represent SEs. Planned comparisons confirmed that the difference in directional error between the arm-rotated condition and the other two conditions combined (∼10°) was reliable (F_(1,9) = 48.3; p < 0.001) and that there was no difference between the arm-centered and reaction time conditions (F_(1,9) = 1.85; p < 0.05).

Influence of slip ratios of normal force coordination

We have shown above that normal force covaries with direction-dependent (and hence inertia-dependent) changes in tangential force. However, it is important to consider whether part of the variation in normal force could be attributable to direction-dependent changes in the coefficient of friction between the fingertip and the contact surface of the object. In our task, because the wrist was braced, the index finger was closely aligned with the forearm (Fig. 2). Thus, movements perpendicular to the forearm required tangential forces at the fingertip in the ulnar-radial direction, whereas movements parallel to the forearm required tangential forces in the proximal-distal direction. The question arises whether the greater normal forces observed for (low inertia) movements perpendicular to the forearm can be explained, at least in part, by greater slip ratios in the ulnar-radial direction. Our results suggest that the answer is no. In fitting ellipses to the distribution of slip ratios across movement directions (Fig. 2), we found that, on average, the lengths of the axes in the ulnar-radial and proximal-distal directions were nearly identical (see Materials and Methods). Thus, it seems unlikely that the dependence of normal force on movement direction can be attributed to direction-dependent changes in the slip ratio. Nevertheless, we used regression analysis to assess potential contributions of the slip ratio to variations in normal forces across target directions. Specifically, we examined the contributions of peak tangential force on the normal force at the time of peak tangential force after removing the contribution of the slip ratio in the direction of the peak tangential force vector. Separate linear regressions were performed for each subject collapsing across conditions. In all 10 subjects, the contribution of peak tangential force remained significant (p < 0.05) after removing the effect of the slip ratio. On the other hand, a positive partial correlation between the slip ratio and the normal force at the time of peak tangential force (i.e., the contribution of slip force after removing the effect of peak tangential force) was observed in only two subjects (p < 0.05).

DISCUSSION

We have shown that the motor system precisely predicted variations in hand acceleration associated with direction-dependent changes in arm inertia. When sliding an object, held beneath the index finger, to targets in different directions, subjects precisely scaled normal force in anticipation of tangential forces proportional to the acceleration of the hand and object. Recently, a number of investigators have argued that such predictive control is based on the use of forward internal models that mimic the behavior of the arm and manipulated objects (Jordan and Rumelhart, 1992; Wolpert et al., 1995; Miall et al., 1996). The idea is that the CNS generates a prediction of the sensory consequences of an action by sending a copy of the motor commands (efference copy; Von Holst, 1954) to the forward model. This sensory prediction (corollary discharge; Sperry, 1950) can then be used to tailor fingertip forces in anticipation of the demands of the action (Flanagan and Wing, 1997; Blakemore et al., 1998). Within this context, our findings indicate that the forward model accurately captures the inertial anisotropy of the arm. Although the distribution of tangential forces across movement directions is necessarily influenced by the inertia anisotropy of the limb, there are presumably other factors that contribute, such as the force-generating capabilities of the muscles primarily responsible for movements in particular directions. Our results suggest that these factors are also captured by the forward model used to predict tangential forces.

Additional support for the notion that motion planning takes into account the inertial properties of the arm comes from a recent study by Sabes et al. (1998). These researchers demonstrated that, when moving the hand around an obstacle en route to a target, subjects select a trajectory ensuring that when the hand is closest to the obstacle, the arm is least sensitive to perturbations that might cause a collision. That is, subjects exploit the position-dependent inertial properties of the limb to maximize the inertial resistance of the arm to forces that would bring the hand toward the obstacle. Experiments by Pagano and colleagues suggest that inertial information related to the arm and grasped objects may also be critical in kinesthesis (Pagano and Turvey, 1995; Pagano and Donahue, 1999; Pagano, 2000).

Our finding that hand acceleration varies with direction-dependent changes in limb inertia replicates the results of Ghez and colleagues.Ghez et al. (1994) suggested that the variation in hand acceleration is not planned and, instead, arises as a consequence of the interaction between limb mechanics and motor commands that do not take inertial anisotropy into account. One candidate mechanism, suggested by Ghez et al., is equilibrium point control (Feldman, 1966; Feldman et al., 1990). It is certainly the case that, if the equilibrium position of the hand is shifted at the same constant rate to all targets, then hand acceleration will vary inversely with inertia (Fig. 1). However, our results indicate that the CNS knows about inertial anisotropy and uses this knowledge to appropriately scale normal forces for direction-dependent variations in hand acceleration (and hence the tangential load at the fingertip). One possibility is that the CNS uses equilibrium point control in conjunction with a forward model that predicts the consequences of equilibrium shifts (cf. Gomi and Kawato, 1996; Flanagan and Wing, 1997). However, it is also possible that the CNS explicitly plans for different hand accelerations to avoid excessive forces (in high inertia movements) or to satisfy some movement constraint, such as endpoint accuracy (Harris and Wolpert, 1998). If the CNS explicitly plans movement trajectories, then the motor system would need to determine the appropriate motor commands to achieve the desired trajectory. This process could involve an inverse internal model of the arm and manipulated object (Kawato et al., 1987;Shadmehr and Mussa-Ivaldi, 1994). However, other schemes based on forward models could also work. For example, Miall et al. (1993) have proposed a control model in which a forward model can be used in an iterative manner to shape motor commands before they are issued as descending signals.

We observed the same pattern of extent errors reported by Ghez and colleagues (Ghez et al., 1994; Gordon et al., 1994b) whereby low and high inertia movements overshoot and undershoot their targets, respectively. Gordon et al. (1994b) suggested that these errors result from a failure to adequately compensate for direction-dependent changes in limb inertia. However, the present results indicate that the motor system maintains an accurate representation of this inertia anisotropy. Together, the two findings suggest that the process of selecting motor commands to drive the arm is at least partly independent of the process responsible for determining the commands for normal force adjustments. One possibility is that the arm movement commands are derived from an inverse model relating target position to arm motor commands, whereas anticipatory normal force adjustments are generated using a distinct forward model. Several researchers have suggested recently that the CNS makes use of both forward and inverse models in motion planning and control. In simulating the behavior of the arm adapting to a novel force field, Bhushan and Shadmehr (1999)found that a controller combining a rapidly adapting forward model and a more slowly adapting inverse model offered the best fit. By providing an estimate of the current state of the motor system that could be used to control that arm, the forward model facilitated early adaptation to the force field at a time when the inverse model was not sufficiently adapted to account for the behavior of the arm (Flanagan and Wing, 1996). Wolpert and Kawato (Kawato and Wolpert, 1998; Wolpert and Kawato, 1998) have proposed a model of motor control based on the use of paired forward and inverse models. In this scheme, predictions from multiple forward models are used to select an appropriate inverse model. If a given forward model successfully predicts the consequences of motor commands in a given context, then its paired inverse model will be selected and used to determine subsequent motor commands.

We also observed the same bias in movement direction reported byGhilardi et al. (1995) when the start position of the arm was rotated clockwise away from the midline. Specifically, we confirmed that this manipulation results in a systematic clockwise rotation of movement direction across all targets. Ghilardi and colleagues attributed this phenomenon to incomplete coding of arm position by proprioception alone. They observed that the direction errors could be predicted on the assumption that the motor system under-represents the rotation of the arm. Thus, it appears that extent and direction errors arise from independent sources, with extent errors associated with movement dynamics (i.e., failure to fully account for inertial anisotropy) and direction errors associated with movement kinematics (i.e., erroneous proprioceptive registration of limb position) (Ghez et al., 1994). Support for the idea that kinematic and dynamic aspect of motion planning are independent comes from a recent study byKrakauer et al. (1999) demonstrating that novel kinematic and dynamic transformations can be learned independently and without interference (Flanagan et al., 1999). Our results are consistent with these ideas. We observed an equally strong coupling between normal and tangential forces in the arm-rotated condition as in the arm-centered condition. Thus, subjects were able to accurately predict tangential loads in the arm-rotated condition despite the fact that they produced systematic and rather large (10°) directional errors. Buneo and colleagues (1997) have shown that the mechanical actions of muscles acting at the shoulder vary systematically with arm posture. Thus, our finding that normal and tangential forces are equally well coordinated for movements initiated from different postures suggests that these posture-dependent changes in mechanical actions are incorporated into the internal model of the arm.

Time course of the internal model

We found that, in the reaction time condition, normal force was scaled in anticipation of direction-dependent fluctuations in tangential force but that the strength of the relationship was reliably weaker than in the other conditions. Importantly, the smaller correlation coefficients and slopes predicting normal force parameters from tangential force parameters did not appear to result from differences in movement kinematics among the conditions. Instead, the poorer force coordination in the reaction time condition may result from time limits placed on the force prediction process. Presumably, the same internal model of the inertial anisotropy of the arm is available under all conditions. Thus, the poorer prediction observed in the reaction time condition is not attributable to an inaccurate internal model per se. Rather, it would appear that, in the reaction time condition, the motor system is not able to make as good use of the internal model. More specifically, the results suggest that it takes time for the CNS to run the internal model and generate accurate predictions of tangential force that can be used to generate anticipatory changes in normal force. Under reaction time conditions, it may be the case that the prediction is only partially formed at movement onset. The difference in reaction time between the reaction time condition and the other two conditions was ∼300 msec on average. Our results suggest that, during this period, the prediction of tangential force is further refined.

Internal model acquisition and neural correlates

Studies of internal model acquisition have focused on relatively rapid adaptation to novel kinematic and dynamic environments (Shadmehr and Mussa-Ivaldi, 1994; Wolpert et al., 1995; Shadmehr and Brashers-Krug, 1997; Flanagan et al., 1999; Kawato, 1999; Krakauer et al., 1999). Such adaptation appears to involve changes in cerebellar cortex (Shadmehr and Holcomb, 1997; Imamizu et al., 2000), a finding consistent with recent models suggesting that internal models are stored in the cerebellum (Miall et al., 1993; Wolpert et al., 1998). We assume that the internal model of the arm is acquired early in life and is then updated to accommodate gradual biomechanical and neural changes that occur in development. Additional research is required to understand how the internal model of the arm is integrated with internal models of objects in the context of manipulation tasks such as tool use (Imamizu et al., 2000).