Abstract
Primary afferent depolarizations (PADs) are associated with presynaptic inhibition and antidromic discharges in both vertebrates and invertebrates. In the present study, we have elaborated a realistic compartment model of a primary afferent from the coxobasipodite chordotonal organ of the crayfish based on anatomical and electrophysiological data. The model was used to test the validity of shunting and sodium channel inactivation hypotheses to account for presynaptic inhibition. Previous studies had demonstrated that GABA activates chloride channels located on the main branch close to the first branching point. We therefore focused the analysis on the effect of GABA synapses on the propagation of action potentials in the first axonal branch. Given the large diameters of the sensory axons in the region in which PADs were likely to be produced and recorded, the model indicates that a relatively large increase in chloride conductance (up to 300 nS) is needed to significantly reduce the amplitude of sensory spikes. The role of the spatial organization of GABA synapses in the sensory arborization was analyzed, demonstrating that the most effective location for GABA synapses is in the area of transition from active to passive conduction. This transition is likely to occur on the main branch a few hundred micrometers distal to the first branching point. As a result of this spatial organization, antidromic spikes generated by large-amplitude PADs are prevented from propagating distally.
Keywords: presynaptic inhibition, primary afferent depolarization, antidromic discharge, crayfish, simulation, compartment model
The effectiveness of sensory synaptic transmission is modulated by presynaptic inhibition, which is associated with primary afferent depolarizations (PADs) in both vertebrates and invertebrates (Clarac and Cattaert, 1999; Rudomin and Schmidt, 1999). PADs are mediated by the activation of GABA receptors, which increase the conductance to chloride. During rhythmic motor activity, PADs occur in bursts during a given phase of the motor cycle and can reach sufficient large amplitude to generate action potentials that propagate antidromically (El Manira et al., 1991; Gossard et al., 1991; Cattaert et al., 1992). These action potentials do not propagate toward the axon terminals and thus do not produce any postsynaptic response (El Manira et al., 1991; Cattaert et al., 1992). Although presynaptic inhibition of sensory transmission has been extensively studied in the mammalian spinal cord, the underlying mechanisms have not been examined experimentally. Using computer simulations, several possible mechanisms have been proposed to account for PAD-associated presynaptic inhibition, including shunting of the afferent action potentials (Segev, 1990) and the inactivation of sodium and calcium channels (Graham and Redman, 1994; Walmsley et al., 1995; Lamotte d'Incamps et al., 1998).
In the crayfish, intra-axonal recording from stretch receptor afferents [coxobasipodite chordotonal organ (CBCO)] showed that these receive bursts of GABA-mediated PADs during locomotion that can generate antidromic action potentials (El Manira et al., 1991;Cattaert et al., 1992). These PADs are attributable to an increased chloride conductance and reduce the amplitude of afferent action potentials and the resulting EPSPs in postsynaptic target neurons (Cattaert et al., 1992). Using anatomical and electrophysiological techniques, we have shown recently that the GABAergic synaptic inputs mediating PADs were mainly located at the first branching point of the sensory axons (Cattaert and El Manira, 1999). Furthermore, experimental data suggest that PADs mediate their inhibitory effects mainly through shunting mechanisms and not via inactivation of voltage-gated channels (Cattaert and El Manira, 1999).
Taking advantage of the detailed data available on presynaptic mechanisms in crayfish sensory axons, we have now developed a realistic simulation model of presynaptic inhibition in crayfish primary afferents to determine the following: (1) the importance of the localization of GABAergic synapses in relation to active versus passive propagation zones; (2) the respective roles of inactivation and shunting mechanisms in the reduction of spike amplitude; and (3) how antidromic action potentials elicited by PADs are prevented from propagating distally. We find that shunting mechanisms can account for the decrease of afferent action potential amplitude. We also show that effect of the shunt is more efficient if the conductance increase is located close to the zone of transition from active to passive properties, and the same shunting phenomenon is responsible for preventing antidromic action potentials from propagating distally.
MATERIALS AND METHODS
Histology of sensory axons. An in vitropreparation of the thoracic locomotor nervous system was used as described previously (Sillar and Skorupski, 1986;Chrachri and Clarac, 1989). Sensory nerve activity was recorded with platinum en passant electrodes, connected to home-made amplifiers (gain of 10,000–100,000×). Intracellular recordings from CBCO terminals (CBTs) within the ganglion were performed with micropipettes filled with carboxyfluoresceine (5% in K acetate 0.2m), using an Axoclamp 2A amplifier (Axon Instruments, Foster City, CA). CBTs were identified on the basis of two criteria. First, injection of depolarizing current pulses elicited antidromic spikes in CBTs that were one to one correlated with extracellular spikes recorded on the CBCO sensory nerve. Second, orthodromic spikes produced by the CBCO sensory neurons were correlated with intracellular spikes at a fixed delay in CBTs. The CBTs analyzed in this study fired action potentials attributable to the existence of spontaneous activity in CBCO sensory neurons. An eight channel stimulator (A.M.P.I., Jerusalem, Israel) was used to trigger intracellular pulses in CBTs during the identification procedure. Data were displayed and printed on a four-channel digital oscilloscope (Yokogawa, Tokyo, Japan) and stored on tape (DTR 1800; Biologic, Claix, France). Anatomical data are based on recordings from five identified CBTs.
After identification of CBCO neurons, they were filled with either carboxyfluoresceine (Sigma, St. Louis, MO) or dextrane fluoresceine (Molecular Probes, Eugene, OR) by injecting negative current pulses (−8 nA, 500 msec, 1 Hz) for 45 min. The preparation was then fixed for 1 hr in a solution of 4% paraformaldehyde in 0.1 m sodium phosphate, pH 7.4, at 4°C and then rinsed eight times in PBS over approximately 2 hr. Tissues were dehydrated in graded ethanol (30, 50, 70, and 95%, absolute ethanol, 10 min each), cleared with methyl salycilate (5 min; Sigma, St. Louis, MO), mounted in Permount (Fisher Scientific, Houston, TX), and viewed with a Leica TCS 4D (Leica, Heildelberg, Germany) laser scanning confocal microscope (Fig.1A) equipped with a krypton–argon mixed gas laser. Forty to 50 optical sections 1 μm apart with a Leica 25× oil or 50× water immersion lenses were taken from single whole-mount preparations. In some experiments, the ganglion was not fixed and was observed in a confocal microscope directly after injecting the fluorescent dye. This procedure was used to avoid shrinkage.
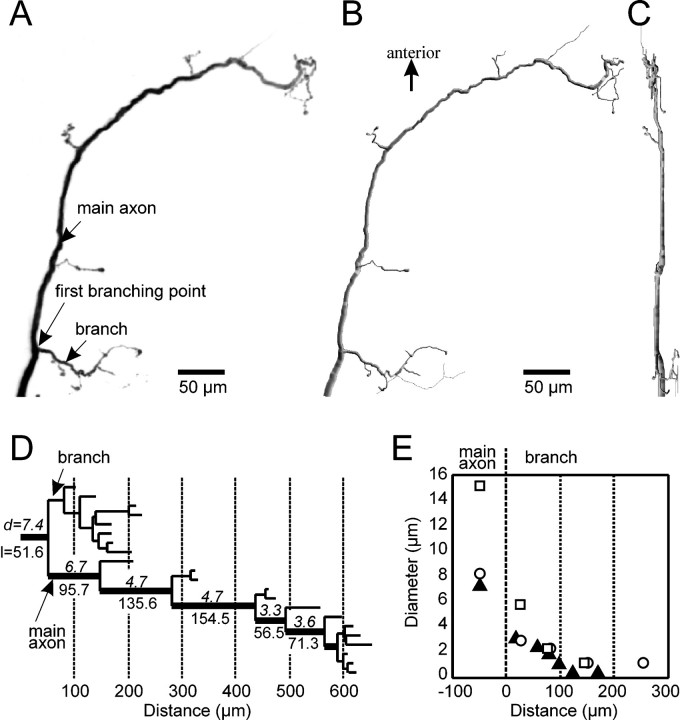
Fig. 1.
Architecture of CBCO sensory arborization in the ganglion. A, Projection file computed from a confocal image stack taken from a sensory afferent. B, Reconstructed representation of the same sensory afferent shown in A. C, Same as B but rotated 90° in the y -axis. D, Dendrogram showing the branching structure of the sensory afferent shown in A. The number on thetop of specific segments indicates the diameter, and thenumber below indicates the length of this segment. E, Histogram showing the decrease in diameter with the distance in the first branch of three representative examples of sensory afferents; all three branches are aligned to their origin on the main tree trunk of the sensory afferent, which has been arbitrarily defined as zero.
Three-dimensional reconstruction of sensory axon. The branching of sensory neurons were reconstructed (Fig. 1B,C) and analyzed in three dimensions with a commercial 3-D system (Neurolucida; MicroBrightField Inc., Colchester, VT), directly from the confocal image stack. Each reconstructed sensory afferent was represented by a set of data points consisting of the x, y, and z coordinates and the diameters of the tapered branch. Each reconstruction was approximately 500–600 digitized points. Suitable software from Neurolucida computed various morphometric parameters and generated various graphic representations of the afferent (e.g., dendrograms) (Fig. 1D).
Simulations. The propagation of action potentials into axonal terminals was simulated using a compartment model program (“SWIM”) (Ekeberg et al., 1991). The properties of each compartment can be defined independently. The simulated axons were composed of excitable compartments and passive compartments. Specific compartments received synaptic inputs. Excitable compartments were described by standard (Hodgkin and Huxley, 1952) channel kinetic equations.
In the crayfish, sensory axons are not myelinated, their diameters ranging from 7 to 15 μm in the largest area (that is, at the entry region of the ganglion, before the first branching point) (Fig. 1A–C). Generally, the diameter of the fiber remains constant (5–6 μm) for ∼150 μm after the branch and then progressively decreases to ∼3 μm at a distance of 600–800 μm from the first branching site (Fig. 1D). Because output synapses are located on axonal branches and GABA synapses seem to be located on the main axon close to the first branch (Cattaert and El Manira, 1999), we were mainly interested in simulating the propagation of events in the main branch around the first branch (100 μm on each side) and in the first branch (400 μm). The diameter of the first branch was ∼2 μm (Fig. 1E) and generally comprised between 3 (proximal part of the branch) and 1 (300 μm more distal) μm. To give the model a realistic behavior, we have included 500 μm of axon (used for spike propagation outside of the ganglion) and a distal process of 300 μm that plays a key role in the distribution of currents at the first branching point.
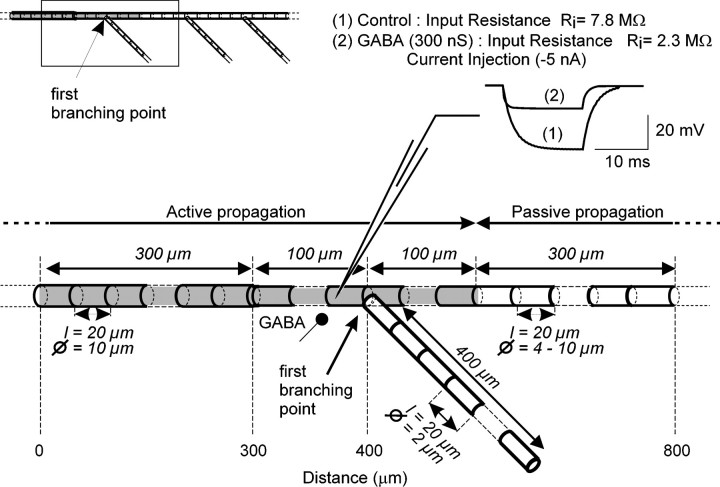
After several trials, we fixed the length of compartments to 20 μm. Longer compartments (up to 100 μm) gave similar results but did not allow to precisely localize where antidromic spikes were produced. Smaller compartments (up to 5 μm) did not significantly improve the results. The axonal model consisted of 72 compartments (Fig.2). The first 25 compartments (length of 20 μm and diameter of 10 μm) were used to simulate the sensory axons outside the ganglion. Five compartments (length of 20 μm and diameter of 4–10 μm) were used to simulate the 100 μm of axon before the first branching point, and the last 20 compartments (length of 20 μm, diameter of 4–10 μm) were used to simulate the distal processes of the sensory main axon. The first axonal branch was composed of 20 compartments (length of 20 μm and diameter of 2 μm). Two more compartments were used to mimic conduction in the remainder of the main axon and in the branch end. Terminals were modeled as sealed ends. In most of the runs, an orthodromic action potential was initiated at the proximal end of the axon, and it traveled toward the distal processes of the terminal. The temporal integration step was 100 μsec. To avoid the sealed effect produced in the first axonal compartment from interfering with the analysis, we started the observations at a distance of 400 μm from the first branching point (Fig. 2). Therefore, only 400 μm on each side of the branching point have been represented in all diagrams, corresponding to positions 0 (the more proximal axonal compartment analyzed) to 800 (the most distal compartment in the main axon and in the branch) μm.
Fig. 2.
Compartment model of a CBCO sensory arborization. In this model, we have only considered the first axonal branch of the sensory neuron (see inset). The input resistance of the model was monitored by injecting an hyperpolarizing current pulse (−5 nA, 15 msec) in the vicinity of the first branch. A decrease of input resistance from 7.8 (1) to 2.3 (2) MΩ was obtained when a 300 nS chloride conductance was used to simulated the activation of GABA synapses at the same location.
Passive properties. The intracompartmental potential, E, is described by the differential equation:
| Equation 1 |
where Ileak is the passive leakage current:
| Equation 2 |
and Eleak and Gleak are the equilibrium potential and the leak conductance, respectively. Icoreis the axial current to neighboring compartments summed over all neighbors:
| Equation 3 |
The parameter Gcore (in S) denotes the core conductance from the compartment in question to the neighboring compartment:
where diam and l are diameter and length of the compartment (in centimeters), respectively, and Ra is the specific resistance of the axoplasm (in ohm centimeter).
Ich and Isyn in Equation 1 are intrinsic and synaptic currents, respectively. Intracellular current injection can be modeled by adding current to the compartment. The parameter cm (microfarads) describes the capacitance of the compartment:
(area is the membrane surface of the compartment in square centimeters, and Cm is the specific capacitance in microfarads per square centimeter.)
All compartments had the same specific membrane resistance (Rm) as estimated from experimental data (see Results). Several values were tested (from 2000 to 8000 Ωcm2). All computations were performed assuming a specific capacitance, Cm of 1 μF/cm2 and a specific axoplasmic resistance, Ra, of 75 Ωcm (calculated from electrophysiological measurements; see Results).
Synaptic inhibition was modeled with a conductance in the postsynaptic compartment. The activation level of the postsynaptic channel, s, ranges from 0 to 1 when the synapse is “closed” or “open,” respectively. The maximum conductance Gsyn is fixed, but the value of the actual conductance, Gsyn·s, varies with s, that is, when the synapse opens and closes. The kinetics of s are controlled by two parameters: the duration and the decay time. In most of the simulations (see Figs. 3-8), the duration of GABA-mediated PADs was fixed to 2 msec and the decay time to 20 msec to fit to experimental data (Cattaert and El Manira, 1999). To analyze the contribution of sodium channels inactivation to presynaptic inhibition, long-duration PADs were produced (duration, 300 msec; decay time, 20 msec) (see Fig. 11).
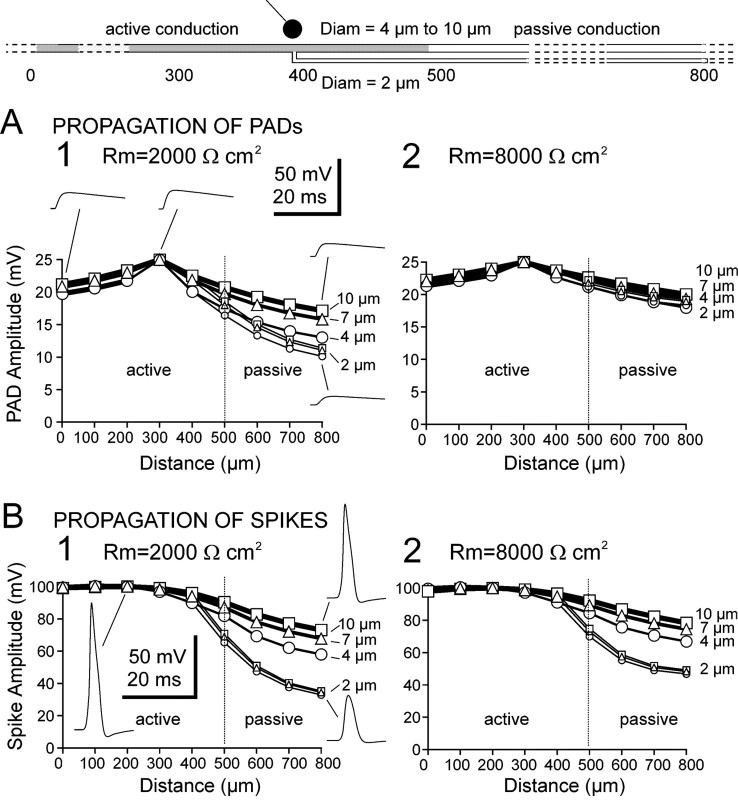
Fig. 3.
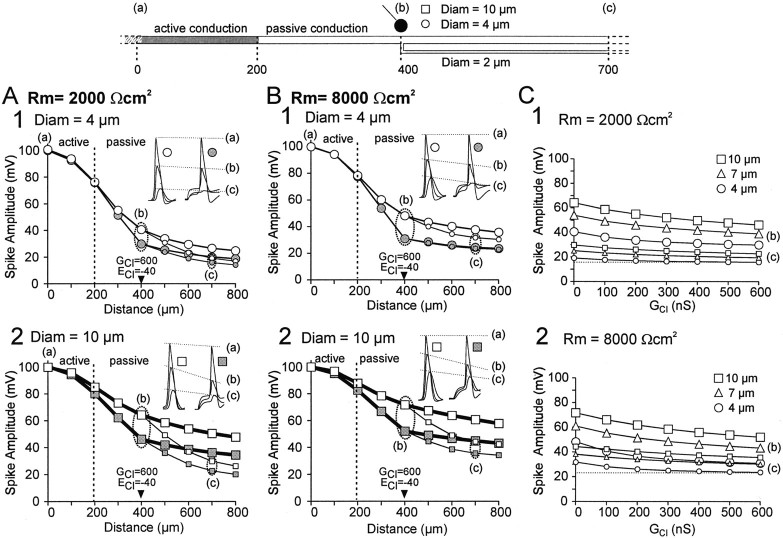
Incidence of axon diameter and specific membrane resistance (Rm) on propagation of PADs (A) and spikes (B), in the case of finite axon length. Each diagram represents the peak value of the events (PAD or spike) measured at different locations along the axon (0–300 μm, axon; 400 μm, branching; 400–900 μm, distal processes). The distal process of the axon was also simulated with three different values of diameter (4 μm, open circles; 7 μm, open triangles; 10 μm, open squares). In each case, the branch diameter was 2 μm (small symbols), and the diameter of the axon was 10 μm (in location 0–400 μm; large symbols).
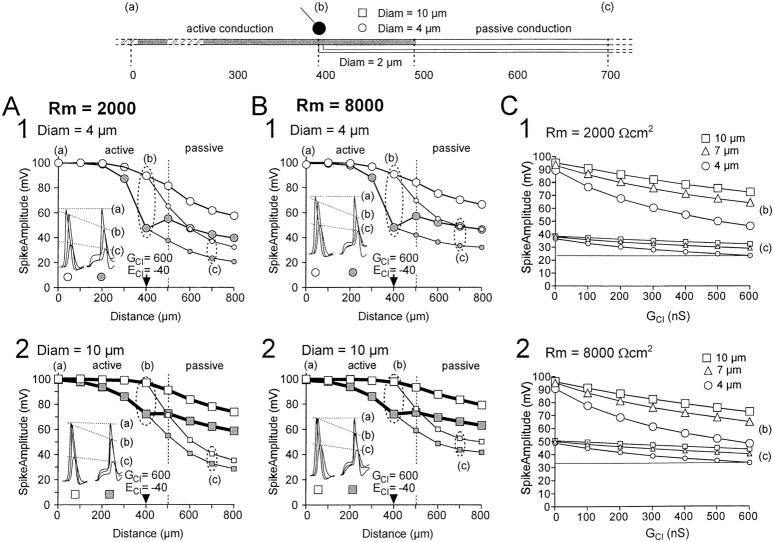
Fig. 4.
Incidence of axon diameter on the shunting effect of increased chloride conductance. The increase in chloride conductance was induced on the main axon, at the level of the branch (location 400 μm). A, Simulation of a small (4 μm) diameter main axon. B, Simulation of a large (10 μm) diameter main axon. In both cases, and in all simulations presented here, the diameter of the branch was fixed to 2 μm according to anatomical data (see Fig. 1). Each diagram represents the peak value of the spike measured at different locations along the main axon (large symbols) and the branch (small symbols). The propagation of spike in the absence of PAD is represented by open symbols; the propagation of spike in the presence of PAD is represented bygray symbols. In insets are represented the spike shapes recorded at locations indicated by a, b, and c. C, Evolution of the shunting effect produced by increasing chloride conductance from 0 to 600 nS, when specific membrane resistance was fixed to 2000 (1) and 8000 (2) Ωcm2. Both diagrams represent the peak value of the spike at location b (branching point; large symbols) and c (branch; small symbols), for three values of main axon diameter (4 μm, square; 7 μm,triangle; 10 μm, circle).
Fig. 5.
Effect of PADs on a passive conduction axon. Same disposition as in Figure 4.
Fig. 6.
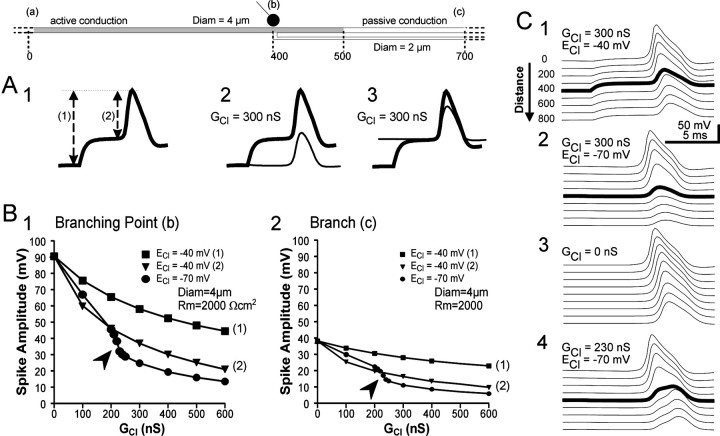
Contribution of PAD to spike propagation. PADs were applied close to the transition from active to passive conduction. Active conduction was achieved up to location 500 μm (seeschema at the top), and a 300 nS GABA synapse was simulated at the branching point at location 400 μm. A1, In these simulations, the monitoring of the spike was measured as either its peak value (1) corresponding to the sum of the PAD plus the spike, or its amplitude (2). A2, The equilibrium potential for chloride was fixed to −40 mV (thick trace) or to −70 mV (thin trace). A3, Aligning the two traces with respect to the base of the spike demonstrates that the depolarization induced by a −40 mV equilibrium potential PAD contributes to the spike propagation.B1, B2, Incidence of increasing chloride conductance on spike propagation in the case of pure shunting (ECl of −70 mV; filled circles) and when PADs are produced (ECl of −40 mV;filled triangles) at the branching point of the main axon (B1) and in the distal part of the branch (B2). For GCl > 200 nS, spike propagation is abruptly prevented (arrowhead) in the case of pure shunting, whereas this abrupt change is not observed when PADs are produced. Thefilled squares represent the peak value of spikes (that is the parameter represented in all other figures) in the case of PADs associated with a −40 mV chloride equilibrium potential. C, Spike propagation along the main axon during PAD (C1) and pure shunting (C2) and in the absence of presynaptic inhibition (C3). In the configuration represented here (4 μm main branch, Rm of 2000 Ωcm2), chloride conductance larger than 230 nS produce a failure of spike conduction (C4). For 230 nS, the failure is not complete, and the spike recovers partially in the more distal compartments that possess sodium channels.
Fig. 7.
Incidence of PAD location on presynaptic inhibition. A GABA synapse was simulated by an increase of chloride conductance (GCl of 300 nS; ECl of −40 mV) at locations 300 (A) and 400 (branching point; B) μm. In these simulations, the diameter of the main axon was fixed to 4 μm, and the intrinsic membrane resistance, Rm, was 4000 Ωcm2. Active conduction is achieved up to location 500 μm. Propagation of spikes along the main axon (large circles) and in the branch (small circles) are represented as their peak values at various locations of axonal tree, in the absence (1–5; open symbols) and presence (a–e; gray symbols) of PAD.
Fig. 8.
Production and propagation of antidromic spikes elicited by large PADs. Large PADs were elicited at location 400 μm (branching point), by increasing chloride conductance (GCl of 300 nS; ECl of −35 mV). Same disposition as in Figure 7. A, Rmof 2000 Ωcm2. B, Rm of 8000 Ωcm2. In A at location c, a nonpropagated spike is observed (asterisk) before the electrotonic image of the propagated spike (arrow). These two events are also observed at location c for the second spike in B (see Results for explanations).
Fig. 11.
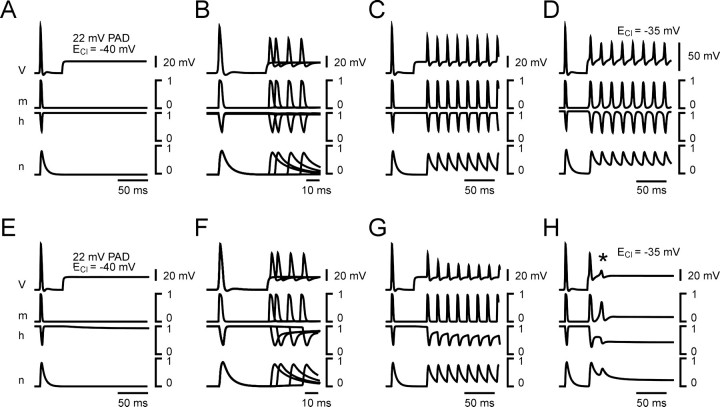
Contribution of Na+ channel inactivation to PAD-mediated presynaptic inhibition. A–D, The parameters of Na+ channel inactivation (h) were set to the following: Aαh= 0.08 mV−1 msec−1; Bαh = −45 mV; Cαh = 1 mV; and Aβh = 0.4 mV−1msec−1; Bβh = −41 mV; Cβh = 2 mV (same as in all preceding simulations; Erest of −70 mV). A control orthodromic spike is generated at t = 5 msec, and a PAD with an amplitude of 22 mV and a duration of 200 msec (ECl of −40 mV; GCl = 300 nS) is generated at location 400 μm at t = 45 msec. V, Membrane potential; m, Na+ channel activation variable; h, Na+ channel inactivation variable; and n, K+ channel activation variable. A, the PAD alone did not induce any inactivation of Na+channels. B, During the occurrence of PAD, the amplitude of orthodromic spikes was reduced because of shunting mechanisms. The inhibition of orthodromic spikes is identical whatever the delay between the onset of the PAD and that of the orthodromic spike (fourtraces are superimposed). C, During the PAD, the amount of inhibition is identical for all orthodromic spikes during a 60 Hz spike train. D, A large-amplitude PAD (ECl of −35 mV; GCl of 300 nS) generated a train of antidromic spikes without adaptation. E, F, The inactivation threshold was lowered using the following parameters of Na+ channel (h): Aαh = 0.08 mV−1msec−1; Bαh = −50 mV; Cαh = 1 mV; and Aβh = 0.4 mV−1msec−1; Bβh = −36 mV; Cβh = 2 mV. E, The resting membrane potential was set to Erest of −70 mV and during a 22 mV PAD (ECl of −40 mV; GCl of 300 nS) a very small Na+ channel inactivation occurred. F, When an orthodromic spike occurred during the PAD, Na+ channel recovery from inactivation became slower. Note that there is almost no reduction of spike amplitude when the delay between the onset of the PAD and that of the orthodromic spike increased. G, During a train of orthodromic spikes, the inactivation of Na+ channel accumulated and resulted in a decrease in the spike amplitude. H, With such parameters, only one antidromic spike could be generated by large PADs (ECl of −35 mV; GCl of 300 nS) because of the fast adaptation that results from Na+ channel inactivation. The asteriskindicates a second transient that is not propagated.
The synaptically induced current that enters the postsynaptic compartment is calculated by:
in which Esyn is the equilibrium potential for chloride ions.
Sodium and potassium channels. Sodium (Na+) current is computed as:
The activation variable m is described by:
with rate functions αm and βm:
The inactivation variable h is computed in a similar way.
with rate functions αh and βh:
In most computations, we used the following values for the Na+ channel parameters:
Activation m:
Inactivation h:
These values were adjusted from the “SWIM” model (Ekeberg et al., 1991) to produce no inactivation of Na+ channels at membrane potentials more hyperpolarized than −58 mV, as shown by the experimental data (Cattaert and El Manira, 1999). By using these parameters, the simulated PADs did not produce any inactivation of Na+ channels and thereby allowed for the analysis of the role of shunting mechanisms in presynaptic inhibition (see Fig.11A–D). Large PADs can depolarize the membrane potential above −58 mV and reach the threshold for Na+channel inactivation. To analyze the contribution of Na+ channels inactivation in PAD-mediated decrease in afferent spike amplitude, simulations were performed with the inactivation threshold shifted toward hyperpolarized membrane potential (see Fig. 11E–H) by using the following parameters: Aαh = 0.08 mV−1msec−1; Bαh = −50 mV; Cαh = 1 mV; and Aβh = 0.4 mV−1msec−1; Bβh = −36 mV; Cβh = 2 mV.
The maximum conductance density for Na+ channels in a given compartment was GNa (S) = 16.7 mS·cm−2 (unless stated otherwise). The equilibrium potential for Na+ ions was set at ENa = +50 mV.
Potassium (K+) current is computed as:
Its activation variable, n, is described by the equation:
with rate functions αn and βn:
In all computations, we used the following values for the K+ channel parameters:
The maximum conductance density for a given compartment was GK (S) = 8.3 mS·cm−2 (unless otherwise stated). The equilibrium potential for K+ ions was EK = −80 mV.
The conductance densities we used for Na+ and K+ channels (16.7 mS·cm−2 and 8.3 mS·cm−2, respectively) were smaller than in Hodgkin and Huxley (HH) model (120 mS·cm−2 and 36 mS·cm−2, respectively). They were adjusted to the minimum required to get an active conduction in the simulated sensory axon. Using HH values, we obtained qualitatively similar results, except that the spikes had a short duration and were thereby more attenuated in passive conduction compartments because of low-pass filter effect. Such characteristics partially masked the relative effects of PADs. To not minimize the effect of K+channels during trains of spikes, the Na/K ratio was set to 1:2 instead of 1:3.33 as in the HH model. However, we did not observe any noticeable difference when simulations were done with the Na/K ratio of 1:3.33 (data not shown).
RESULTS
Morphological characteristics of sensory axons
To construct a realistic model of the crayfish CBCO axons, three-dimensional confocal reconstructions were performed from sensory axons injected with carboxyfluoresceine or dextrane fluoresceine. The CBCO sensory axons have a characteristic morphology with a main axon giving rise to a small branch at the first axonal branching point (Fig.1A,B). Ninety degree rotation in the y -axis of the reconstructed CBCO axon shows that the branches project mostly laterally in the ganglion (Fig. 1C). Figure 1D shows a dendrogram of the different branches of a reconstructed CBCO sensory axon. The length of the main axon ranged between 600 and 800 μm, whereas that of the branch ranged between 100 and 200 μm. The diameter of the main axon was between 7 and 10 μm in fixed preparations (6–15 μm in fresh preparations) and decreases after the first branch to 3–4 μm in fixed preparations (Fig.1D) or 4–7 μm in fresh preparations. The diameter of the branch also decreases with distance and was approximately 2 μm within the 200 μm after the branch (in fresh and fixed preparations) (Fig.1E).
Simulation of a CBT
A model axon was built based on the morphological data (Fig. 2). The location and strength of GABA synapses mediating presynaptic inhibition used in these simulations is based on anatomical and physiological data (Cattaert and El Manira, 1999). Using conventional intracellular recordings, the input resistance (rinput) of CBTs at the first branching point was 6.5 ± 0.85 MΩ and the length constant (λ) was ∼1000 μm, for an axon diameter of 8.5 μm (Fig. 2). These parameters were used to build a model of CBCO sensory axons. Using infinite cable theory, passive parameters in the model were calculated as follows.
In an infinite cable, the input resistance (rinput) is equal to:
where λ = is the length constant, in which rm is the membrane resistance for a unit length (Ωcm), and ra is the axoplasmic resistance per unit length (Ωcm−1).
From these estimations, the specific resistance of the axoplasm (Ra),
was assumed to be 75 Ωcm, and the specific membrane resistance (Rm),
was set to be in the range of 3000–4000 Ωcm2. However, this parameter is difficult to measure precisely with sharp microelectrodes. Thus, to test how it would affect the simulations, we have tested the effect of different Rm values (2000, 4000, and 8000 Ωcm2).
The measured time constant (τm) was 3.3 msec; therefore, the specific membrane capacitance (Cm),
was assumed to be 1 μFcm−2.
Validation of the model: adjustment to real parameter values (rinput, λ, andGCl)
The compartment model was examined in the case of infinite cable configuration to ensure that the length constant (λ) obtained from simulations is similar to that obtained by theoretical calculation using infinite cable theory. The λ values obtained by simulation and theoretical calculations were similar for the different diameters and Rm values tested as shown in Table1.
Table 1.
Comparison of space constants λ for various values of diameter and specific membrane resistance Rm
| diam | Rmof 2000 Ωcm | Rm of 4000 Ωcm | Rm = 8000 Ωcm | |||
|---|---|---|---|---|---|---|
| 2 μm | 395 | 365 | 551 | 516 | 746 | 730 |
| 4 μm | 526 | 516 | 739 | 730 | 1022 | 1032 |
| 7 μm | 713 | 683 | 978 | 966 | 1367 | 1366 |
| 10 μm | 836 | 816 | 1194 | 1154 | 1659 | 1633 |
For each value of Rm, two values of λ are given: simulation (left column) and theoretical (italic bold, right column).
Estimations of the length constant (λ) were made by measuring the propagation (attenuation of amplitude Vxwith distance x) of a depolarizing current pulse (+2.5 nA, 40 msec) of initial amplitude V0.
Estimations of the length constant (λ) by theoretical calculations were made with the formula:
This validated model was used in the finite cable configuration, which corresponds to anatomical data. The calculated parameters were, therefore, adjusted to fit experimental measurements of input resistance (rinput) and the length constant (λ), both in the absence and presence of PADs simulated as an increased chloride conductance. The input resistance was measured by injecting a hyperpolarizing current pulse (−5 nA, 15 msec) (Fig. 2). The −5 nA pulse produced a 37.5 mV hyperpolarization (rinput of 7.8 MΩ). Comparable values were obtained experimentally in the in vitro preparation (El Manira and Clarac, 1991; Cattaert et al., 1992).
In in vitro experiments, when GABA receptors were activated by pressure ejection of GABA, we observed a 67% reduction of the input resistance of sensory axons (Cattaert et al., 1992). Simulations of input resistance were performed with the model presented in Figure 2, when the GABA conductance was activated. To obtain a change comparable with the results obtained experimentally, the chloride conductance associated with the GABA synapse was set to 300 nS. In the following simulations, different values of GABA synapse conductance (100, 200, 300, 400, 500, and 600 nS) were tested.
Propagation of spikes and PADs
The experimental data allowed a reasonably good estimation of most of the parameters in the area accessible to intracellular recordings. However, Rm was difficult to estimate with certainty in thin-diameter axons. Therefore, the experimental values of input resistance were likely underestimated (or overestimated). For these reasons, the passive propagation of spikes and PADs was studied using different Rm values of 2000, 4000, and 8000 Ωcm2 (only results with 2000 and 8000 Ωcm2 in the realistic model of sensory axon are presented in Fig. 3). In addition, the topological analysis of different CBCO fibers demonstrated that axon diameters ranged between 10 and 4 μm within the 200 μm after the first branching point. Therefore, simulations of spike and PAD propagation were done with axon diameters of 10 and 4 μm. The passive propagation of spikes and PADs was comparable in large-diameter axons. For example, in a 10 μm axon with Rm of 2000 Ωcm2, PAD attenuated from 25 to 17 mV (32% attenuation) between locations 300 and 800 (Fig. 3A1), and the spike attenuated from 99 to 67 mV (32% attenuation) (Fig.3B1). However, in thin branches (2 μm), PADs propagate better than spikes. PADs amplitude decreased from 23 to 11.5 mV (50% attenuation) (Fig. 3A1), whereas spike amplitude decreased from 99 to 35 mV (65% attenuation) (Fig. 3B1). The difference between the spatial attenuation of spikes and that of PADs increased in thin branches with increasing Rm; for Rm of 8000 Ωcm2 in a 2 μm diameter branch, PAD attenuated from 25 to 19.5 mV (22% attenuation) (Fig. 3A2), and spike attenuated from 99 to 47 mV (53% attenuation) (Fig.3B2).
In this configuration, the characteristics of the passive propagation of PADs in axon with different diameters (2, 4, and 10 μm) tended to become similar when Rm was increased from 2000 to 8000 Ωcm2 (Fig. 3, compare A1,A2). On the other hand, the spike spatial attenuation remained dependent on the axon diameter regardless of the Rm value used, as shown by the curves corresponding to 2, 4, and 10 μm that did not tend to converge when Rm was increased (Fig. 3, compare B1,B2). The difference in the passive propagation of spikes and PADs can be summarized as follows. PADs tended to invade all branches with reduced attenuation compared with spikes, which were more attenuated as they propagated in the fine branches.
Shunting of spikes by PADs
In these simulations, a GABA-mediated chloride conductance of 300 nS was required to produce a decrease of input resistance (67%) similar to that obtained experimentally (Cattaert et al., 1992). The chloride conductance required is directly related to the diameter of the sensory axon at the site of the GABAergic synapses and also depends on whether GABAergic synapses are in a zone with active or passive propagation. These questions are addressed in the simulations illustrated in Figures 4 and5.
Effect of axon diameter
In all the following simulations, a 100 mV spike was initiated at location 0. Figure 4A illustrates the propagation of action potentials in a 4 μm diameter axon in which active propagation of spikes occurs up to 100 μm after the first branching point (gray part of the axon). Figure 4A1shows the propagation of action potentials along the main axon and the branch in the absence (open circles) and presence (filled circles) of PAD. In inset, three superimposed profiles of spikes recorded at location 0 (a), 400 (b), and 700 (c) μm are shown. The left traces (open circle) have been obtained in the absence of PAD, and the right traces (filled circle) have been obtained in the presence of a 300 nS PAD. In the presence of PAD, the spike appears above the PAD, and the shunting mechanism is partly compensated by the amplitude of the PAD.
Three different axon diameter values (4, 7, and 10 μm) were tested in the simulations. Shunting effects were always larger at the site of the GABA synapse first branching point (location b in the drawing and graphs) than in the branch (location c) in which output synapses are likely to be located (Cattaert and El Manira, 1999). Increasing the axon diameter reduced the shunting effect of PADs on the spike amplitude. The effect of diameter on shunting efficacy in an axon with Rm of 2000 Ωcm2 was examined by comparing 4 and 10 μm axon diameters (Fig. 4A). In the absence of PAD, the spike amplitude at the first branching point (location b on the drawing and graphs) was 90.4 and 97.4 mV with an axon diameter of 4 (Fig. 4A1) and 10 (Fig. 4A2) μm, respectively. In the presence of a 600 nS chloride conductance, the spike amplitude decreased to 48.0 (Fig. 4A1) and 72.7 (Fig. 4A2) mV, which represents 53 and 74.6% of the control amplitude, respectively. The shunting thus decreased the spike amplitude by 47% in a 4 μm axon and only by 25.4% in a 10 μm axon.
When spike amplitudes were measured at location c on the branch (Fig. 4A1), the spike peak was 37.8 mV in a 4 μm axon in the absence of PAD and was reduced to 24.4 mV by a 600 nS PAD. This represents a 37.8-24.4 = 13.4 mV (35.5%) shunting effect. In a 10 μm axon (Fig. 4A2), the spike peak was 40.9 mV at location c on the branch in the absence of PAD and was reduced to 33.2 mV using a 600 nS PAD. This represents a 40.9-33.2 = 7.7 mV (18.8%) shunting effect. Thus, increasing the axon diameter by a factor of 2.5 reduced the shunting effect by ∼50% at locations b and c. These results suggest that the diameter of the axon at the site of the GABA synapse plays an important role in determining the efficacy of the shunt.
Effect of Rm
To determine the extent to which Rmaffected the shunting effect of PADs on spike amplitude, we compared the effect of PADs at two Rm values: 2000 (Fig.4A) and 8000 (Fig. 4B) Ωcm2. We present here only effects at location c because they are similar to those at location b. With an Rm value of 2000 Ωcm2 and an axon diameter of 4 μm, the amplitude of the spike at a distal location c was 37.8 mV (62.2% attenuation) in the absence of PAD and was reduced to 24.4 mV when a 600 nS increase in chloride conductance was applied at the branching point (Fig.4A1). This shows that the spike was shunted by 37.8-24.4 = 13.4 mV (35.5%). When Rm value was increased to 8000 Ωcm2, and the spike amplitude at location c was 48.9 mV (51.1% attenuation) in the absence of PAD and 33.5 mV when a 600 nS increase in chloride conductance was applied at the branching point (Fig.4B1). The spike was thus shunted by 48.9-33.5 = 15.4 mV (31.5%) because of the inhibitory synapse. Thus, a fourfold increase in Rm resulted in an increase of the shunting only by 2 mV (4%), indicating that Rmplays a minor role in determining the efficacy of shunting.
To generalize this result, we have tested different chloride conductances and different axon diameters at two different Rm values (Fig. 4C). The results show that the shunting is always more efficient in small-diameter axons (4 μm). Large Rm values improved the propagation of both unshunted and shunted spikes in small branches. Consequently, there was no dramatic increase of the shunting effect (measured in small branches), regardless of the value of the chloride conductance (100–600 nS).
Effect of active and passive propagation at the GABA synapse site
The preceding simulations were performed with the GABA synapse occurring at a site with active propagation. To determine how the shunting is affected when it occurs at a site with passive propagation, we have used the same parameters as in Figure 4 but with spikes being passively propagated (absence of Na+ and K+ channels) from location 200 μm. In a 4 μm axon with a Rm value of 2000 Ωcm2, the spike peak was 19.1 mV at location c on the branch in the absence of PAD (Fig. 5A1) and was reduced to 15.8 mV when a 600 nS chloride conductance increase applied at the branching point (location 400 μm). This shows that the spike was shunted by 19.1-15.8 = 3.3 mV. When the axon diameter was increased to 10 μm, the peak potential measured at location c was 29.8 and 22.7 mV in the absence and presence of a 600 nS PAD, respectively (Fig. 5A2). That is a 7.1 mV decrease at location c. Thus, when the GABA synapse was located at a passive site, the shunting effect was relatively more efficient in large-diameter than in small-diameter axons.
Increasing the Rm value to 8000 Ωcm2 (Fig. 5B) resulted in increasing electrotonic propagation of both not shunted and shunted spikes. In a 4 μm axon diameter, the spike peak at location c was 31.2 mV in the absence of PAD and decreased to 22.5 with a 600 nS PAD (Fig.5B1). This represents a 31.2-22.5 = 8.7 mV shunting effect. In a 10 μm axon diameter, the spike peak was 45 mV in the absence of PAD and 37.5 mV in the presence of a 600 nS PAD (Fig.5B2). The spike was then shunted by 45-37.5 = 7.5 mV. Thus, in small branches, increasing Rm increased the passive propagation of both unshunted (control) and shunted spikes. However, the effect on control spikes was larger.
The above results hold true for all chloride conductances tested (100 to 600 nS) (Fig. 5C). However, in contrast with the situation presented in Figure 4C, the inhibitory effect in the small-diameter (4 μm) axon model is less than that obtained with large-diameter (10 μm) axon model. In small-diameter axons (4 μm), spikes are rapidly attenuated as they propagate passively toward distal sites (Fig. 5A1,B1). When a 300 nS PAD was elicited, the peak potential decreased from 40.6 to 32.1 mV in location b and from 19.1 to 16.5 mV in location c (Fig.5C1, open circles). Increasing the chloride conductance to 600 nS further reduced spike peak (29.9 mV) at location b but had less effect on the spike peak (15.8 mV) measured at location c. Increasing the conductance from 400 to 600 nS did not have any further shunting effect on the spike peak at location c. This is because of PAD being better conveyed than spikes in passive axonal branches (Fig. 3); consequently, in the more distal sites (c), most of the depolarization is attributable to the PAD rather than to the spike (Fig. 5A1,B1,insets). Increasing Rm (Fig.5B,C2) only slightly improved the passive propagation of spikes but largely improved the propagation of PADs that becomes the main constituent in the measure of the peak. In all cases, GABA synapses located in passive conduction sites produced less shunting effects than those located in active sites.
Effect of PAD on active spike propagation
The respective roles of the two features, membrane depolarization and shunting, that accompany activation of GABA synapses on CBCO terminals were tested in a series of simulations (axon diameter of 4 μm; Rm of 2000 Ωcm2) (Fig. 6). In the previous figures (Figs.4, 5), the spike amplitude was measured as the sum of that PAD and spike. To estimate the relative effect of the depolarization and the shunt associated with the PAD, the spike amplitude was measured in two different ways: (1) from the resting membrane potential (−70 mV) to the peak of the spike (Fig. 6A1,1), or (2) from the top of the PAD to the peak of the spike (Fig.6A1,2). For a given increase of chloride conductance, the reversal potential for chloride ion (ECl) was either −40 mV (in this case a PAD was produced) or −70 mV, the resting membrane potential (in this case, no PAD was produced, although the shunting effect remained). This was done to isolate the effect of shunt from the effect of depolarization. An example of such simulations with ECl of −40 mV (thick trace) and −70 mV (thin trace) is shown in Figure 6, A2 andA3. The respective effects of the two chloride equilibrium potentials are compared in two ways (Fig.6A2,A3) using measure 1 and 2, respectively. Spikes were measured at two locations (as in Figs. 4, 5): at the first branching point (Fig. 6B1,b) and at a more distal location in a thin branch (Fig.6B2,c). Various values of chloride conductance from 100 to 600 nS were used.
Whatever the chloride conductance used, the peak of the spike (measure 1) was always larger with ECl of −40 mV (squares) than with ECl of −70 mV (circles) at both locations b and c. When PADs were produced by a large chloride conductance increase (600 nS), the peak value of a concomitant spike measured distally at location c is affected by the PAD (Fig.6A1; see also Fig. 4, insets). If we now consider solely the amplitude of the spike (measure 2), a pure shunting mechanism (ECl of −70 mV) resulted in an abrupt decrease of spike amplitude when chloride conductance was increased over 200 nS (see recording shown in Fig. 6A3 using a 300 nS chloride conductance). This effect, observed at both locations b and c (Fig. 6B), was unexpected if PADs inactivate sodium channels, and a 300 nS chloride conductance should have resulted in a larger decrease of spike amplitude for ECl of −40 mV than for ECl of −70 mV. However, in the present simulation, the decrease in spike amplitude was larger for ECl of −70 mV than for ECl of −40 mV. This is attributable to failure of spike propagation for ECl of −70 mV when GCl is above 230 nS. This phenomenon is illustrated in Figure 6C1–C4. Each figure represents recordings made at nine locations regularly spaced from site 0 (the most proximal; top trace) to site 800 μm (the most distal;bottom trace) on the main axon. The branching point (site 400 μm at which PADs are produced) is represented by the thick trace. When a 300 nS GCl with a −40 mV ECl is used, the spike amplitude is smaller at that site but partially recovers in the next distal (Fig.6C1; see also Fig. 4A1). When ECl is fixed at the resting membrane potential (−70 mV), the reduction of the spike amplitude is greater at the branching point (Fig. 6C2) and does not recover in the next distal site. Failure of spikes occurs with GCl above 230–240 nS (Fig.6B1, arrowhead). In the absence of PAD (GCl of 0 nS) (Fig. 6C3), distal spikes are actively propagated up to site 500 μm (traceimmediately below the thick trace) and then progressively attenuate (Fig. 4A1). The amplitude of the spike at a given location not only involves the activation of local sodium channels but also the sodium channels of neighboring sites. Any phenomenon that reduces the depolarization of preceding compartments would delay the spike in the preceding compartment and reduce the amplitude of the spike in the current compartment. These two features are illustrated in Figure 6C4. A GClof 230 nS was used, with ECl fixed at the resting potential (−70 mV). In such conditions, an incoming spike fails to generate a spike in the first branching point compartment (thick trace). In the more distal compartments, the depolarization produced by the failed spike at last reaches the threshold for spiking and a second (distal) delayed spike is produced. If the chloride conductance was above 230 nS, the depolarization was not sufficient to generate a distal spike (Fig. 6C2). Note that such failures were never observed when EClwas −40 mV.
These results demonstrate that, in the transition from an active to a passive propagating zone, PADs have conflicting effects: (1) locally, they dramatically reduce the propagating spike attributable to a shunting effect, and (2) they facilitate the propagation of the shunted spike to the more distal active compartments (up to 100 μm more distal to the first branching point). The consequence of this latter effect is that, in the absence of a depolarization accompanying the increase of GCl, an abrupt increase in the efficacy of presynaptic inhibition with increasing GCl occurs (Fig. 6B,arrowhead). From these results, it is likely that presynaptic inhibition mediated by PADs mainly involves a shunting mechanism and very little, if any, inactivation of sodium channels (see Discussion).
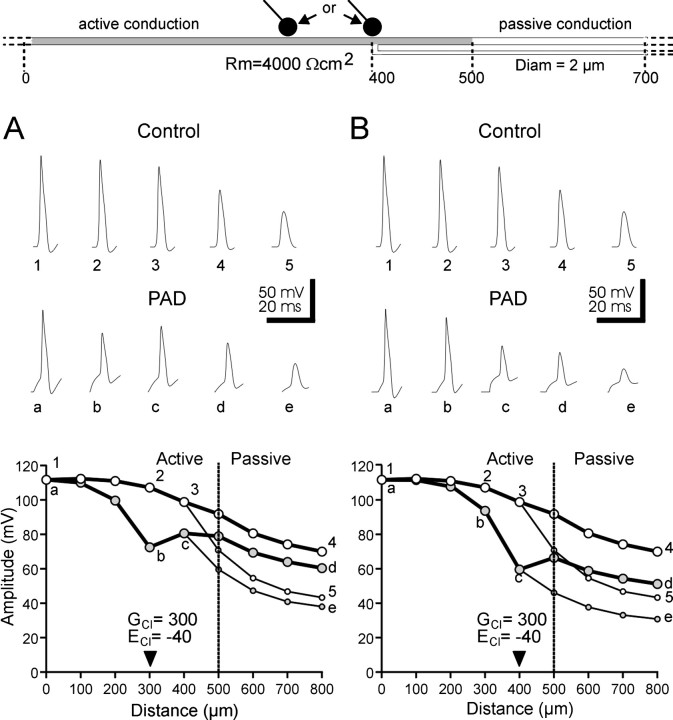
Effect of PAD position
To determine the effect of the location of the synaptic input mediating PADs along sensory axons on shunting and thereby on presynaptic inhibition, we compared the effect of PADs occurring at two different compartments. When PADs were elicited at a compartment 100 μm more proximally (300 μm) from the branching point, the spike amplitude was reduced in this compartment (Fig.7A). However, because of the existence of active conductances, the spikes regenerated between the site of PADs and the branching point (Fig. 7A). In a 4 μm axon and Rm of 4000 Ωcm2, a 300 nS increase in conductance reduced the spike amplitude from 108 (control spike; open circles) to 71 (shunted spike;filled circles) mV at the GABA synapse location (b). However, at the branching point (c), because of the presence of Na+ channels, the amplitude of the shunted spike was partially restored (80 mV). This configuration could work in an all or none manner if the GABA synapse is placed even more proximally.
In contrast, chloride conductance increase (GClof 300 nS) occurring at the branching point (Fig. 7B) markedly reduced the amplitude of spikes at the branching point. Because experimental data indicate that there is no active propagation in the branch (Cattaert and El Manira, 1999), spikes fail in the branch (Fig. 7B). However, because of the presence of active compartments up to location 500 μm in the main axon, a partial recovery of the spike occurs in the main axon. In this configuration, activation of the GABA synapses (GCl of 300 nS; ECl of −40 mV) results in a significant decrease of the spike amplitude in the branch.
Origin and propagation of antidromic spikes
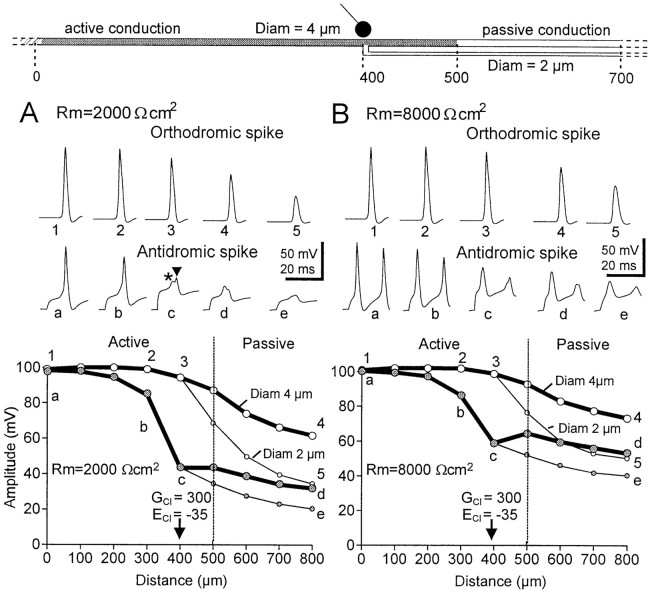
Simultaneous intracellular recordings made from a sensory terminal of a CBCO and a postsynaptic motoneuron demonstrated that large PADs were often capable of triggering antidromic spikes (El Manira et al., 1991; Cattaert et al., 1992). Such antidromic spikes were very attenuated when recorded distally (100–200 μm more distal to the first branching point) and never elicited any response in the postsynaptic motoneuron (El Manira et al., 1991; Cattaert et al., 1992). To test whether the shunting hypothesis could explain these observations, we have simulated large PADs (ECl of −35 mV) that could produce antidromic spikes.
Whatever the Rm value tested (2000, 4000, and 8000 Ωcm2), antidromic spikes were elicited when ECl was set to −35 mV (Fig.8). When Rm was low (2000 Ωcm2 in Fig. 8A), it was more difficult to elicit antidromic spikes because of the powerful shunting effect in the compartments around the GABA synapse and the fact that the depolarization is less propagated. As a result, in the compartments close to the GABA synapse, a large depolarization occurred because of the equilibrium potential for Cl−(ECl of 35 mV), but the spikes that should have been elicited by this depolarization were shunted (GCl of 300 nS), and a slight nonpropagated transient was observed (Fig. 8A,c, first smallpeak indicated by an asterisk on thetop of the PAD). However, the amplitude of this incomplete spike was large enough to depolarize more distant compartments up to spike threshold, and a full spike was generated in those compartments (Fig. 8A,b). In turn, this full spike invaded the first branching point compartment (location c), but because of the massive local shunt and the Na+ channels being inactivated, this spike was not propagated distally (Fig.8A,d,e).
With Rm high (8000 Ωcm2), antidromic spikes were elicited more easily, because the depolarization propagates better (Fig. 8, compare A1–A5 withB1–B5, see orthodromic spike propagation). When a large PAD was elicited close to the branching point, the membrane potential reached the threshold for spiking in nonshunted compartments more rapidly, so that the nonpropagated transient was not observed in the GABA synapse compartment (Fig. 8B,c). However, in such a configuration, the distal propagation of the spike generated by the PAD was greater than with Rm of 2000 Ωcm2 (Fig. 8, compare A,B). Note that with Rm of 8000 Ωcm2, two spikes were elicited by the PAD, with the second one being much more attenuated that the first one because of the inactivation of Na+ channels.
These simulations demonstrate that spikes elicited by PADs are very attenuated in the distal compartments. The attenuation of distal propagation of such spikes increases with lower Rm values. When Rm was set at 2000 Ωcm2, the distal propagation of PAD-triggered spikes was totally prevented. The result from the simulation supports the experimental observations, which demonstrates that PAD-triggered spikes do not elicit any EPSP in postsynaptic motoneuron (El Manira et al., 1991;Cattaert et al., 1992).
Validation of the simulation results
The simulation of the propagation of antidromic spikes suggests that spikes triggered by large PADs would be generated in proximal parts of the sensory axon (Fig. 8). These simulations also predicted that, at the GABA synaptic site (Fig. 8A,c), only a nonpropagated transient would be generated (asterisk). Therefore, we have performed intracellular recordings from sensory axons to test this prediction (Figs. 9,10). When antidromic spikes generated by PADs were recorded in the proximal part of the axon (400 μm before the first branching point), only full spikes were observed (Fig. 9). At this proximal site, antidromic spikes (Fig. 9B,AS) reached the same peak amplitude as orthodromic spikes (Fig. 9A,OS) (Fig. 9C, superimposedtraces). The similarity in spike amplitude between PAD-triggered and afferent spikes suggests that PAD shunting mechanism is unlikely to involve an inactivation process at such proximal sites. When intracellular recordings were made from the main axon at a location close to the first branching point (Fig. 10), PAD-triggered antidromic spikes (AS) were also observed, but their amplitude is much smaller at this site (Fig. 10A). In addition, the shape of the spike is much more complex than in more proximal sites (Fig. 9). Three components compose these spikes, corresponding to three changes in the slope of the rising phase of the spike (Fig. 10B): the PAD, a nonpropagated transient (T), and the antidromic spike (AS). The existence of the nonpropagated transient was confirmed in intracellular recordings in which they occur in the absence of antidromic spikes (Fig. 10C). The superimposition of traces (Fig.10D) of antidromically propagated spikes and nonpropagated transients occurring alone confirms that the second slope change (T) corresponds to the nonpropagated spike predicted by the simulations. The antidromic spikes being generated at some distance from the GABA synaptic site, this result also explains why no spike is generated in the distal part of the axon because of the absence of active conduction in that sites. Therefore, PAD-triggered spikes propagate antidromically but not orthodromically.
Fig. 9.
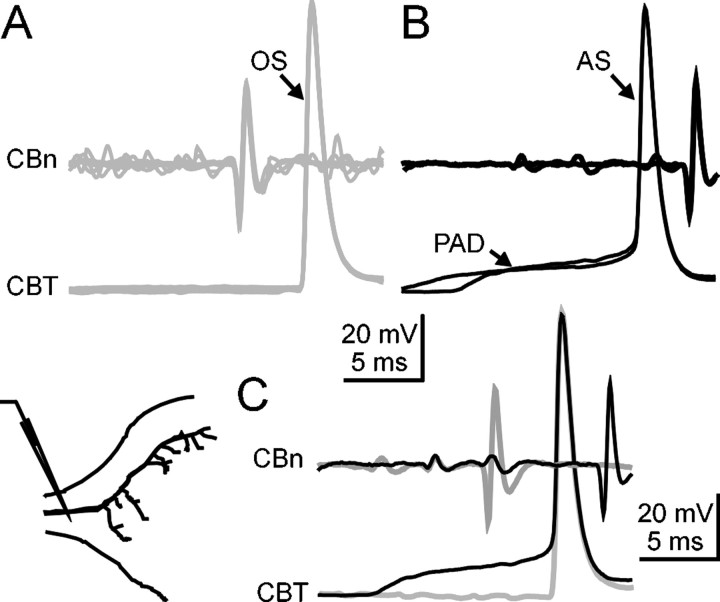
Electrophysiological evidence of antidromic spikes in CBCO sensory terminals. A, Orthodromic spike simultaneously recorded extracellularly from the CBCO nerve (CBn) and intracellularly from a CBCO terminal (CBT) at a proximal location. Orthodromic spikes (OS) conveying sensory input are recorded in the sensory nerve before intracellular recording site. B, In opposition, antidromic spikes (AS) occurring on the top of large PADs are recorded at the intracellular recording site before sensory nerve recording. C, Orthodromic spikes and PAD-triggered antidromic spikes display similar amplitude. The position of the intracellular recording electrode is shown in theinset.
Fig. 10.
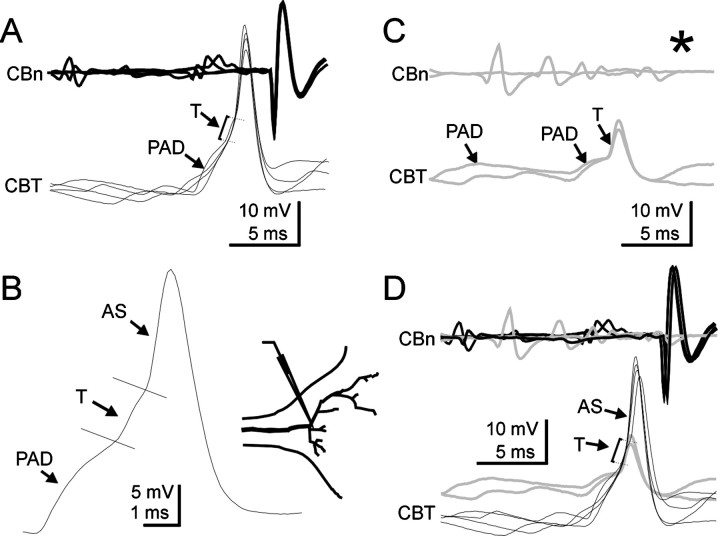
Origin of antidromic spikes in CBCO terminals. In this experiment, intracellular recordings were performed from the region of the first branching point of a CBCO terminal (seeinset). A, At this site, antidromic spikes (AS) display much smaller amplitudes and are preceded by a small nonpropagated transient (T). B, Detailed view of an antidromic spike showing the three components: PAD, nonpropagated transient (T), and the antidromically propagated spike (AS). Compare with the profile of the simulated antidromic spike recorded at location b in Figure 8A. C, In some instances, PADs fail to trigger antidromic spikes (seeasterisk) but only generate a nonpropagated transient (T) on the top of the PAD. D, Superposition of the traces in A and B shows that the change in the slope observed at the base of antidromic spikes (AS) corresponds to the nonpropagated transient (T).Schema presented in insets were drawn from Lucifer yellow staining.
Sodium channel inactivation and presynaptic inhibition
To examine the contribution of Na+ channel inactivation to the decrease of the amplitude of afferent spikes, simulations with long duration PADs (300 msec) were performed (Fig.11). Using the same parameters of inactivation as in the simulations described above (see Materials and Methods), no inactivation was induced by the PAD (Fig. 11A), and consequently, the decrease in the spike amplitude was identical regardless of the delay between the onset of the PAD and that of the spike (Fig. 11B). In these simulations, the kinetics of Na+ ion inactivation was fast and did not outlast the end of a spike, thereby, no accumulation of Na+channels inactivation was seen during a train of action potentials (Fig. 11C). The only effect observed during a spike train was that the amplitude of the first spike was slightly larger than that of following ones because of a prolonged K+ channel activation when the PAD occurred (Fig. 11B, compare the K+ channels activation, n, in spikes occurring in the absence and in the presence of a PAD). When larger PADs were produced (Fig. 11D), trains of antidromic spikes could be generated (Fig. 11D).
In a second series of simulations, the threshold for Na+ channel inactivation was lowered by using the following parameters of inactivation h:
During the occurrence of a 22 mV PAD, the threshold for Na+ channel inactivation was almost reached (Fig.11E), but when a spike occurred, the inactivation was prolonged (Fig. 11F). The increased time constant of Na+ channel inactivation (h) had a dramatic inhibitory effect on the spike amplitude during repetitive firing (Fig. 11G). The decrease of the spike amplitude in the train was more pronounced and reflects mainly an effect of Na+ channel inactivation. The parameters of h used in this series of simulations were, however, not satisfying when antidromic spikes were generated (Fig. 11H). This is because only one antidromic spike could be generated, regardless of the amplitude of the PAD, whereas trains of antidromic spikes were observed during electrophysiological recordings from sensory axons (El Manira et al., 1991; Cattaert et al., 1992).
DISCUSSION
The present results show that shunting mechanisms can account for both presynaptic inhibition and preventing antidromic spikes from propagating toward the synaptic terminals. An efficient effect of the shunt requires that the increase in conductance should be located close to the zone of transition from active to passive properties on the main axon.
Active propagation versus passive propagation: effects of PADs
In a previous study (Cattaert et al., 1992), a passive conduction zone was suspected in the distal processes of CBTs. This hypothesis was based on the observation that distally recorded spikes had a smaller amplitude than more proximal ones. The present simulation study goes one step further in the understanding of the mechanisms and demonstrates that a decrease in spike amplitude can be observed in an active zone that is not too far from a passive one (Fig.3B). This phenomenon is attributable to the fact that part of the sodium current, underlying the spike, will spread and charge the membrane at the neighboring compartment. If this compartment is passive (no sodium channels), this will result in a deficit of current in the active one (with sodium channels) and, consequently, the spike will be smaller, although it is in an active propagation zone.
The regulation of spike amplitude by PADs was greater when PADs were produced in an active zone (compare Figs. 5, 6). For axon diameters of 5–7 μm, which is the case for most of the CBTs in the region of their first branching point, the range over which spikes are reduced by PADs directly depends on whether they are produced in an active propagation zone or not (Fig. 5A1,B1). This phenomenon is even stronger for smaller axon diameters. When PADs occur in a compartment with active conductance, the chloride conductance tends to shunt the local currents associated with active propagation, and this results in a rapid reduction of spikeamplitude. When PADs occur in a compartment with a passive conduction, increased GCl acts only on passive cable properties, and because there is no competition with active depolarization, this results in a smaller reduction of the spike amplitude. These results indicate that, for an efficient shunting of action potential to occur, the synaptic inputs mediating PADs should be located in zones with active conductance but not too far from a distal passive segment.
Inactivation versus shunting mechanisms
In simulation studies, it is possible to dissociate the parameters involved in presynaptic inhibition. For example (Segev, 1990), using shunting without depolarization demonstrated that a shunting mechanism could play the major role in presynaptic inhibition. Taking into account the maximal convergence of three axo-axonic synapses onto a single bouton (Maxwell et al., 1990) and the GABAergic quantal conductance of 150–300 pS (Ropert et al., 1990; Kraszewski and Grantyn, 1992), Graham and Redman (1994) considered that 1 nS per bouton was an overestimate. For these reasons, presynaptic inhibition was proposed to primarily involve inactivation of sodium channels (Graham and Redman, 1994). In their simulation,Graham and Redman (1994) demonstrated that, with a 40 nS increase of GCl in an axon with a 1 μm diameter and 6 μm bouton diameter, the spike amplitude was decreased by 65 mV (from 110 to 45 mV) when ECl was fixed to −40 mV (i.e., when real PADs are produced), whereas the spike amplitude was only decreased by 38 mV (from 110 to 72 mV) when ECl was equal to the resting membrane potential (−80 mV). Our results are apparently in conflict with these findings. However, both situations are different because, in crayfish sensory axons, distal branches do not actively convey spikes (Cattaert et al., 1992; Cattaert and El Manira, 1999), and it is this situation that we have simulated. At the transition between active and passive compartments, the action potential threshold is higher because part of the sodium current is used to charge the membrane of passive neighboring compartments. This is the reason why spike failure is observed in our simulations. Consequently, inactivation of sodium channels was probably not seen in our simulations, because depolarization favors distal propagation of spikes (Fig. 7C1) and avoids the failure phenomenon. It is therefore likely that, in the crayfish sensory axons we have simulated, inactivation of sodium channels would not play any important role in presynaptic inhibition, which is instead achieved by a shunting mechanism. During the occurrence of large-amplitude PADs (>22 mV), there is an accumulation of sodium channel inactivation during trains of action potentials (Fig. 11G). Under these conditions, inactivation of sodium channels could also contribute to presynaptic inhibition.
Depolarization and transmitter release at the synapse
Several depolarizing events are capable of invading the CB synaptic terminals: orthodromic spikes, PADs, and antidromic spikes. Why do only orthodromic spikes elicit transmitter release? Because of the low-pass filter properties of cables, in passive conduction configuration (that occurs distally, and in branches), PADs propagate passively better than spikes in small-diameter (2–4 μm) branches (Cattaert and El Manira, 1999) (Fig. 5). Therefore, in some parameter configurations [Rm of 10000 Ωcm2, long (>400 μm) branches of small (2 μm) diameter] the PAD amplitude would be larger than the spike amplitude at releasing sites. Such events are, however, unlikely to occur in real sensory terminals because PADs would release transmitter better than spikes do. This question needs to be discussed, however, because the shape of the signal that is capable of eliciting transmitter release is up to now unknown. The shape of the depolarization constitutes a major difference between passive spikes and passive PADs at the far end of a passive terminal; spikes have always faster rise and decay time than PADs, and their time-to-peak is always 3–10 times shorter. This question is also valuable for antidromic spikes that occur on the top of large PADs; because of the presence of a PAD, their time-to-peak is larger than orthodromic spikes. This parameter is likely to be important for triggering calcium channel opening. It could also be that release of GABA activates receptors located close to the release site that inhibit calcium channels or exocytosis machinery and thereby contribute to decreasing transmitter release that could be induced by an attenuated antidromic spike.
Footnotes
This work was supported by Swedish Medical Research Council Project 11562 (A.E.), by the Sweden–France exchange program, and by Groupement d'Intérêt Scientifique (sciences de la cognition) Contract CNA 10. We thank Drs. D. Parker and Y. Manor for their comments on this manuscript, V. Fénelon for help in histological and confocal microscopy analysis, and Drs. F. Clarac and S. Grillner for valuable discussion during the course of this work.
Correspondence should be addressed to D. Cattaert, Laboratoire Neurobiologie des Réseaux, Unité Mixte de Recherche 5816, Université de Bordeaux 1, Centre National de la Recherche Scientifique, Biologie Animale, Bat B2, Avenue des Facultés, 33405 Talence Cedex, France. E-mail: d.cattaert@lnr.u-bordeaux.fr.
REFERENCES
- 1.Cattaert D, El Manira A. Shunting versus inactivation: analysis of presynaptic inhibitory mechanisms in primary afferents of the crayfish. J Neurosci. 1999;19:6079–6089. doi: 10.1523/JNEUROSCI.19-14-06079.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Cattaert D, El Manira A, Clarac F. Direct evidence for presynaptic inhibitory mechanisms in crayfish sensory afferents. J Neurophysiol. 1992;67:610–624. doi: 10.1152/jn.1992.67.3.610. [DOI] [PubMed] [Google Scholar]
- 3.Chrachri A, Clarac F. Synaptic connections between motor neurons and interneurons in the fourth thoracic ganglion of the crayfish, Procambarus clarkii. J Neurophysiol. 1989;62:1237–1250. doi: 10.1152/jn.1989.62.6.1237. [DOI] [PubMed] [Google Scholar]
- 4.Clarac F, Cattaert D. Functional multimodality of axonal tree in invertebrate neurons. J Physiol (Paris) 1999;93:319–327. doi: 10.1016/s0928-4257(00)80060-1. [DOI] [PubMed] [Google Scholar]
- 5.Ekeberg O, Wallen P, Lansner A, Traven H, Brodin L, Grillner S. A computer based model for realistic simulations of neural networks. I. The single neuron and synaptic interaction. Biol Cybern. 1991;65:81–90. doi: 10.1007/BF00202382. [DOI] [PubMed] [Google Scholar]
- 6.El Manira A, Clarac F. GABA-mediated presynaptic inhibition in crayfish primary afferents by non-A, non-B GABA receptors. Eur J Neurosci. 1991;3:1208–1218. doi: 10.1111/j.1460-9568.1991.tb00055.x. [DOI] [PubMed] [Google Scholar]
- 7.El Manira A, DiCaprio RA, Cattaert D, Clarac F. Monosynaptic interjoint reflexes and their central modulation during fictive locomotion in crayfish. Eur J Neurosci. 1991;3:1219–1231. doi: 10.1111/j.1460-9568.1991.tb00056.x. [DOI] [PubMed] [Google Scholar]
- 8.Gossard J-P, Cabelguen J-M, Rossignol S. An intracellular study of muscle primary afferents during fictive locomotion in the cat. J Neurophysiol. 1991;65:914–926. doi: 10.1152/jn.1991.65.4.914. [DOI] [PubMed] [Google Scholar]
- 9.Graham B, Redman S. A simulation of action potentials in synaptic boutons during presynaptic inhibition. J Neurophysiol. 1994;71:538–549. doi: 10.1152/jn.1994.71.2.538. [DOI] [PubMed] [Google Scholar]
- 10.Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol (Lond) 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kraszewski K, Grantyn R. Unitary, quantal and miniature GABA-activated synaptic chloride currents in cultured neurons from the rat superior colliculus. Neuroscience. 1992;47:555–570. doi: 10.1016/0306-4522(92)90165-x. [DOI] [PubMed] [Google Scholar]
- 12.Lamotte d'Incamps B, Meunier C, Monnet ML, Jami L, Zytnicki D. Reduction of presynaptic action potentials by PAD: model and experimental study. J Comput Neurosci. 1998;5:141–156. doi: 10.1023/a:1008861815083. [DOI] [PubMed] [Google Scholar]
- 13.Maxwell DJ, Christie WM, Short AD, Brown AG. Direct observations of synapses between GABA-immunoreactive boutons and muscle afferent terminals in lamina VI of the cat's spinal cord. Brain Res. 1990;530:215–222. doi: 10.1016/0006-8993(90)91285-o. [DOI] [PubMed] [Google Scholar]
- 14.Ropert N, Miles R, Korn H. Characteristics of miniature inhibitory postsynaptic currents in CA1 pyramidal neurones of rat hippocampus. J Physiol (Lond) 1990;428:707–722. doi: 10.1113/jphysiol.1990.sp018236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rudomin P, Schmidt RF. Presynaptic inhibition in the vertebrate spinal cord revisited. Exp Brain Res. 1999;129:1–37. doi: 10.1007/s002210050933. [DOI] [PubMed] [Google Scholar]
- 16.Segev I. Computer study of presynaptic inhibition controlling the spread of action potentials into axonal terminals. J Neurophysiol. 1990;63:987–998. doi: 10.1152/jn.1990.63.5.987. [DOI] [PubMed] [Google Scholar]
- 17.Sillar KT, Skorupski P. Central input to primary afferent neurons in crayfish, Pacifastacus leniusculus, is correlated with rhythmic motor output of thoracic ganglia. J Neurophysiol. 1986;55:678–688. doi: 10.1152/jn.1986.55.4.678. [DOI] [PubMed] [Google Scholar]
- 18.Walmsley B, Graham B, Nicol MJ. Serial E-M and simulation study of presynaptic inhibition along a group Ia collateral in the spinal cord. J Neurophysiol. 1995;74:616–623. doi: 10.1152/jn.1995.74.2.616. [DOI] [PubMed] [Google Scholar]