Theta-Frequency Bursting and Resonance in Cerebellar Granule Cells: Experimental Evidence and Modeling of a Slow K⁺-Dependent Mechanism

Abstract

Neurons process information in a highly nonlinear manner, generating oscillations, bursting, and resonance, enhancing responsiveness at preferential frequencies. It has been proposed that slow repolarizing currents could be responsible for both oscillation/burst termination and for high-pass filtering that causes resonance (Hutcheon and Yarom, 2000). However, different mechanisms, including electrotonic effects (Mainen and Sejinowski, 1996), the expression of resurgent currents (Raman and Bean, 1997), and network feedback, may also be important. In this study we report theta-frequency (3–12 Hz) bursting and resonance in rat cerebellar granule cells and show that these neurons express a previously unidentified slow repolarizing K⁺ current (I_K-slow). Our experimental and modeling results indicate that I_K-slow was necessary for both bursting and resonance. A persistent (and potentially a resurgent) Na⁺ current exerted complex amplifying actions on bursting and resonance, whereas electrotonic effects were excluded by the compact structure of the granule cell. Theta-frequency bursting and resonance in granule cells may play an important role in determining synchronization, rhythmicity, and learning in the cerebellum.

Neurons process information by generating action potentials organized either in regular discharges (fast repetitive firing) or in bursts (Connors and Gutnik, 1990), which can occur repetitively when they are sustained by slow membrane potential oscillations (Wang and Rinzel, 1999). Moreover, some neurons respond better to a preferential input frequency, a property called resonance (Hutcheon and Yarom, 2000). Oscillations, bursting, and resonance have been related to synchronization of neuronal activity and to the emergence of brain rhythms (Llinas, 1988).

Oscillations and bursting can arise from various mechanisms that involve slow depolarizing and repolarizing currents. Noteworthy examples are provided by the interaction of a persistent Na⁺ current (I_Na-p) with a slow K⁺ current (I_M) in hippocampal pyramidal neurons (Gutfreund et al., 1995; Pape and Driesang, 1998) or with an inward rectifier current (I_h) in entorhinal neurons (Alonso and Llinas, 1989; Dickson et al., 2000). In thalamic neurons, depolarization and delayed repolarization are determined by low-threshold Ca²⁺ current (I_T) activation and inactivation and are regulated by other currents, includingI_h (McCormick and Huguenard, 1992). In invertebrate cells, Ca²⁺-dependent bursts are terminated by a Ca²⁺-dependent K⁺ current (I_AHP) (Wang and Rinzel, 1999). In addition, bursting emerges when a membrane potential difference is established between dendrites and soma, causing rebound depolarization after a spike (Mainen and Sejinowski, 1996). Rebound depolarization may also be caused by currents activated by spike repolarization, e.g., by a resurgent Na⁺current (Raman and Bean, 1997). Despite the multitude of mechanisms that potentially generate oscillation and bursting, resonance essentially requires a slow repolarizing current that reduces neuronal excitability at low input frequency (Hutcheon et al., 1996a,b; Hutcheon and Yarom, 2000).

The most apparent discharge mode of cerebellar granule cells is fast repetitive firing (Gabbiani et al., 1994; D'Angelo et al., 1995). However, a more complex electrical behavior has been suggested by the observation of spike bursting unveiled by pharmacological manipulation (D'Angelo et al., 1998). In this study, we report that cerebellar granule cells also show theta-frequency resonance, and we suggest that both bursting and resonance are based on a slow K⁺ current. This conclusion is supported by a mathematical model that provides a realistic reconstruction of granule cell electroresponsiveness.

Theta-frequency bursting and resonance in granule cells may play an important role in determining synchronization (Maex and DeShutter, 1998), rhythmicity (Pellerin and Lamarre, 1997; Hartmann and Bower, 1998), and learning (D'Angelo et al., 1999; Armano et al., 2000) at the major input stage of the cerebellum.

MATERIALS AND METHODS

Whole-cell patch-clamp recordings. Cerebellar granule cells were recorded in acute cerebellar slices obtained from 20 ±2-d-old rats. Slice preparation and patch-clamp recordings were performed as reported previously (Rossi et al., 1994,1998; D'Angelo et al., 1995, 1997, 1998, 1999; Armano et al., 2000).

Current-clamp recordings were performed at 30°C. The extracellular solution contained (in mm): NaCl 120, KCl 2, MgSO₄ 1.2, NaHCO₃ 26, KH₂PO₄ 1.2, CaCl₂ 2, glucose 11, and bicuculline 0.01, and was equilibrated with 95% O₂ and 5% CO₂, pH 7.4. The pipette solution contained (in mm): K-gluconate 126 (or Cs₂SO₄ 78), KCl 4 (or CsCl 4), NaCl 4, MgSO₄ 1, CaCl₂0.02, BAPTA 0.1, glucose 15, ATP 3, GTP 0.1, HEPES 5; pH was adjusted to 7.2 with KOH (or CsOH).

Voltage-clamp recordings were performed at room temperature (25.5°C). The extracellular solution contained (in mm): NaCl 100, KCl 2, KH₂PO₄ 1.2, MgSO₄ 1.2, NaHCO₃ 26, glucose 11, Tetraethyl-ammonium Cl⁻ (TEA) 20, 4-amino-piridine (4-AP) 4, Ni²⁺ 2, tetrodotoxin (TTX) 0.001, and bicuculline 0.01, and was equilibrated with 95% O₂ and 5% CO₂, pH 7.4. The pipette solution contained (in mm): K-gluconate 126, NaCl 4, MgSO₄ 1, CaCl₂0.02, BAPTA 0.1, glucose 15, ATP 3, GTP 0.1, HEPES 5; pH was adjusted to 7.2 with KOH.

TEA, 4-AP, TTX, and bicuculline were obtained from Sigma (St. Louis, MO). The glutamate receptor antagonistsd-2-amino-5-phosphonovaleric acid (APV), 7-chlorokinurenic acid (7-Cl-Kyn), and 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX) were obtained from Tocris Cookson (Bristol, UK).

Data were recorded with an Axopatch 200B amplifier, digitized with a Digidata 1200 interface (500 μsec/point), and analyzed with PClamp software (Axon Instruments, Foster City, CA). In voltage-clamp recordings, leak subtraction was performed by using a P/4 protocol. All data are reported as mean ± SD.

Mathematical modeling. A mathematical model of rat cerebellar granule cell electroresponsiveness (D'Angelo et al., 1995,1998; Brickley et al., 1996) was constructed using the NEURON simulator (Hines and Carnevale, 1997). Because granule cells have a compact electrotonic structure (Silver et al., 1992;D'Angelo et al., 1993, 1995), a single-compartment model was used. The experimental value of membrane capacitance (3 pF; see refences above) was used to calculate the granule cell surface, assuming a spherical shape and a specific membrane capacitance of 1 μF/cm².

Mathematical methods. The mathematical problem in neuronal simulation is to solve the set of differential equations representing membrane voltage, intracellular Ca²⁺ concentration, and channel gating dynamics [see for example Yamada et al. (1998)]. Voltage was obtained as the time integral of the equation:

$$\text{dV}/\text{dt}=-1/C_{\text{m}}*\{\sum [g_{\text{i}}*(V-V_{\text{i}})]+{\text{i}}_{\text{inj}}\},$$ Equation 1

where V is membrane potential,C_m is membrane capacitance,g_i is ionic conductance,V_i is reversal potential (the subscript i indicates different channels), andi_inj is the injected current. Membrane conductances were represented using Hodgkin–Huxley-like models (Hodgkin and Huxley, 1952) of the type:

$$g_{\text{i}}=G_{{max}_{\text{i}}}*x_{\text{i}}^{\text{zi}}*y_{\text{i}},$$ Equation 2

where G_maxi is the maximum ionic conductance, x_i andy_i are state variables (probabilities ranging from 0 to 1) for a gating particle, andz_i is the number of such gating particles in ionic channel i. x and y (with the suffix i omitted) were related to the first-order rate constants α and β by the equations:

$$x_{\infty }={\alpha }_{\text{x}}/({\alpha }_{\text{x}}+{\beta }_{\text{x}})y_{\infty }={\alpha }_{\text{y}}/({\alpha }_{\text{y}}+{\beta }_{\text{y}}),$$ Equation 3

$${\tau }_{\text{x}}=1/({\alpha }_{\text{x}}+{\beta }_{\text{x}}){\tau }_{\text{y}}=1/({\alpha }_{\text{y}}+{\beta }_{\text{y}}),$$ Equation 4

where α and β are functions of voltage. The equations used to parameterize α and β and the state variablesx_∞, τ_x,y_∞, and τ_yfor different ionic channels are shown in Table 1. The state variable kinetics were:

$$\text{dx}/\text{dt}=(x_{\infty }-x)/{\tau }_{\text{x}},$$ Equation 5

$$\text{dy}/\text{dt}=(y_{\infty }-y)/{\tau }_{\text{y}}.$$ Equation 6

The model included a leakage current and voltage-dependent Na⁺, Ca²⁺, and K⁺conductances (see Table 1). Nernst equilibrium potentials were calculated from ionic concentrations used in current-clamp recordings. The Ca²⁺ equilibrium potential was updated after changes in the intracellular Ca²⁺concentration.

Table 1.

Voltage-dependent conductance parameters

Conductance state variables	n	Gmax(S/cm2)	Vrev (mV)	α (sec−1)	β (sec−1)
gNa-f
Activation	3	0.013	87.39	0.9(V + 19)/(1 − exp(−(V + 19)/10))	36 exp(−0.055(V + 44))
Inactivation	1			0.315 exp(−0.3(V + 44))	4.5/(1 + exp(−(V + 11)/5))
gNa-r
Activation	1	5e−4	87.39	0.00024 − 0.015(V − 4.5)/((exp(−(V − 4.5)/6.8) − 1))	0.14 + 0.047(V + 44)/(exp((V + 44)/0.11) − 1))
Inactivation	1			0.96*exp(−(V + 80)/62.5)	0.03*exp((V + 83.3)/16.1)
gNa-p
Activation	1	2e−4	87.39	0.091(V + 42)/(1 − exp(−(V + 42)/5))	−0.062(V + 42)/(1 − exp((V + 42)/5))
				x∞ = 1/(1 + exp(−(V + 42)/5))
				τ∞ = 5/(α + β)
gK-V
Activation	4	0.003	−84.69	0.13(V + 25)/(1 − exp(−(V + 25)/10))	1.69 exp(−0.0125(V + 35))
gK-A
Activation	3	0.004	−84.69	14.67/(1 + exp(−(V + 9.17)/23.32))	2.98(exp(−(V + 18.28)/19.47))
Inactivation	1			0.33/(1 + exp((V + 111.33)/12.84))	0.31/(1 + exp(−(V + 49.95)/8.9))
				x∞ = 1/(1 + exp(−(V + 46.7)/19.8))
				y∞ = 1/(1 + exp((V + 78.8)/8.4))
gK-IR
Activation	1	9e−4	−84.69	0.4 exp(−0.041(V + 83.94))	0.51 exp(0.028(V + 83.94))
gK-Ca
Activation	1	0.004	−84.69	2.5/(1 + 1.5e − 3/[Ca] exp(−0.085V))	1.5/(1 + [Ca]/(0.15e − 3 exp(−0.085V)))
gCa
Activation	2	4.6e−4	129.33	0.15 exp(0.063 (V + 29.06))	0.089 exp(−0.039(V + 18.66))
Inactivation	1		*	0.0039 exp(−0.055(V + 48))	0.0039 exp(0.012(V + 48))
gK-slow
Activation	1	3.5e−4	−84.69	0.008 exp(0.025(V + 30))	0.008 exp(−0.05(V + 30))
				x∞ = 1/(1 + exp(−(V + 30)/6))

This Table reports the equations used to calculate α_x, β_x, α_y, and β_y (see Eqs. 3 and 4) for the membrane conductances used in the model (in a few cases x_∞ andy_∞ are reported; see Eq. 9). The number of gating particles (n), maximum conductance (G_max), and ionic reversal potential (* resting value for Ca²⁺) used to calculate ionic currents are also shown.

All ionic currents used in the model have been identified in cerebellar granule cells in situ, when the excitable response has assumed its mature pattern (>P20) (D'Angelo et al., 1997). Gating kinetics were corrected using aQ₁₀ = 3 according to the relationQ₁₀^{(Tsim–Texp)/10} (Gutfreund et al., 1995) to account for differences between simulation temperature (Tsim = 30°C) and experimental temperature (T_exp). Maximum ionic conductances were corrected for ionic concentration differences between voltage- and current-clamp recordings. A further adjustment (usually <30%) of current densities allowed us to fine tune the excitable response [for further explanations see Traub and Llinas (1979); Traub et al. (1991);Vanier and Bower (1999)].

Leakage current. Mature rat cerebellar granule cells in situ have an aspecific and a GABA-A receptor-dependent leakage (Brickley et al., 1996). In the model, leakage consisted of a 5.68 × 10⁻⁵S/cm² conductance with reversal potential at −59 mV (g_L), and of a 2.17 × 10⁻⁵S/cm² Cl⁻conductance with reversal potential at −65 mV (accounting for 28% of the total input conductance) (Armano et al., 2000). No qualitative difference was observed in model responses by setting GABA-A receptor leakage to zero (data not shown).

Na⁺currents (I_Na-f,I_Na-p,I_Na-r). Mature rat cerebellar granule cells in situ express a fast and persistent Na⁺ current (I_Na-f andI_Na-p) (D'Angelo et al., 1998) and probably also a resurgent Na⁺ current (I_Na-) (E. D'Angelo and J. Magistretti, unpublished observations). TheI_Na-f model was based on Gutfreund et al. (1995), and inactivation was slowed down around threshold to reproduce spike adaptation during bursts (Mainen et al., 1995).I_Na-f density was set to reproduce repetitive firing. I_Na-p was reproduced from Gutfreund et al. (1995) and shifted by −2 mV to match spike threshold. I_Na-p density (1/65I_Na-f) was set to reproduce Na⁺-dependent plateaus (D'Angelo et al., 1998). I_Na-r was reconstructed fromRaman and Bean (1997). I_Na-r density (initially 1/26 I_Na-f) was regulated in different simulations.

Ca²⁺current (I_Ca). TheI_Ca model was derived from high-threshold Ca²⁺ currents (mostly N-type) measured in mature rat cerebellar granule cells in situ (Rossi et al., 1994). I_Cahad fast second-order activation kinetics and slow voltage-dependent inactivation. I_Ca density was halved to account for different extracellular Ca²⁺ concentrations.

K⁺currents (I_K-V,I_K-Ca,I_K-A,I_K-slow,I_K-IR). Mature rat cerebellar granule cells in situ expressI_K-V,I_K-Ca, andI_K-A (Cull-Candy et al., 1989; Bardoni and Belluzzi, 1993), I_K-IR (Rossi et al., 1998), and I_K-slow (this study). I_K-V is a voltage-dependent K⁺ current resembling other neuronal delayed rectifiers, and its model has been adapted from Gutfreund et al. (1995). I_K-V was shifted by −5 mV to match I_Na-f.I_K-Ca is a voltage- and Ca²⁺-dependent K⁺ current corresponding to “big-K” channel recordings from granule cells in culture (Fagni et al., 1991), the kinetics of which are largely determined by those of the associated Ca²⁺ channels and intracellular Ca²⁺ fluctuations. TheI_K-Ca model is the same as in Gabbiani et al. (1994), and I_K-Ca density was set close to that of I_K-V.I_A is a fast-activating, fast-inactivating voltage-dependent K⁺current, which was reproduced from data reported by Bardoni and Belluzzi (1993). I_K-slow is a slow Ca²⁺-independent TEA-insensitive K⁺ current, which was reconstructed from data shown in Figure 5. I_K-slowvoltage dependence was shifted by −10 mV (−8 mV accounting for liquid-junction potential and −2 mV required to maintain a proper matching with I_Na-p).I_K-IR is a fast inward rectifier current that was reconstructed from data reported by Rossi et al. (1998).

Fig. 5.

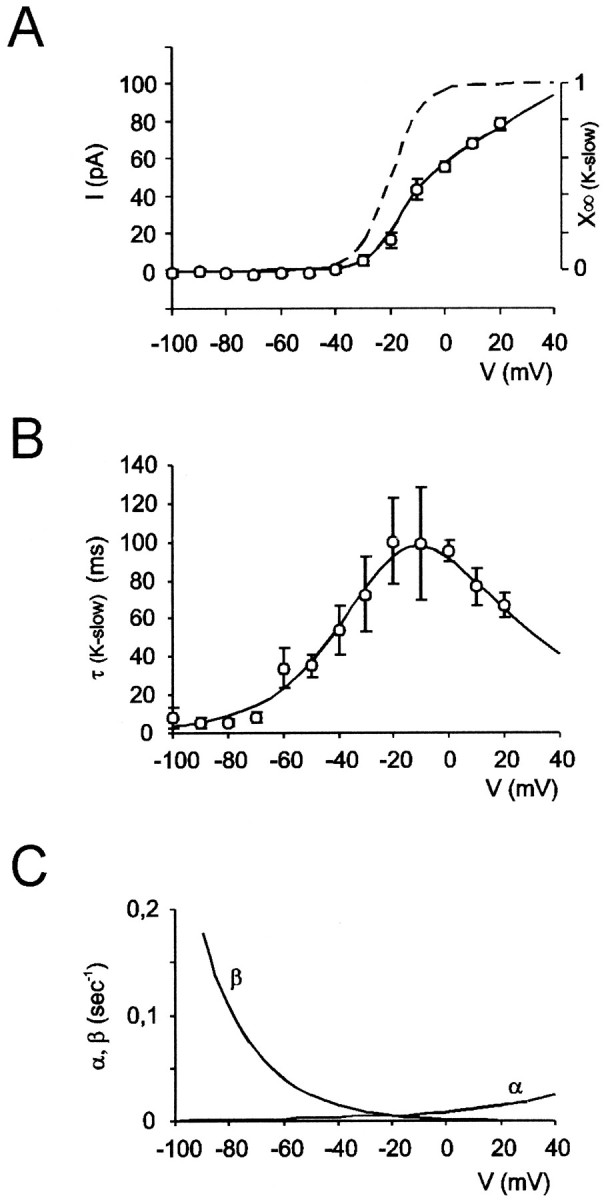
Gating properties ofI_K-slow (average data from 9 granule cells, mean ± SEM). A, AverageI–V relationship (○) fitted with Equation 8 (solid line). The broken lineis the normalized steady-state activation curve (x_∞(K-slow)) obtained with Equation 9. B, Average activation time constant (τ_(K-slow)) versus membrane potential (○). The fitting line was obtained from Equation 4 and the kinetic functions shown inC. C, Voltage dependence of the kinetic constants α and β (see Eq. 3 and Table 1).

Ca²⁺dynamics.The intracellular Ca²⁺concentration, [Ca²⁺], was calculated through the equation:

$$d[{\text{Ca}}^{2+}]/\text{dt}=-I_{\text{Ca}}/(2F*\text{Ad})-({\beta }_{\text{Ca}}([{\text{Ca}}^{2+}]-[{\text{Ca}}^{2+}{]}_0))$$ Equation 7

where d is the depth of a shell adjacent to the cell surface of area A, β_Ca determines the loss of Ca²⁺ ions from the shell approximating the effect of fluxes, ionic pumps, diffusion, and buffers (Traub and Llinas, 1979; McCormick and Huguenard, 1992; DeSchutter and Smolen, 1998), and Ca0 is resting [Ca²⁺]. OnceI_Ca andI_KCa had been set, Ca²⁺ dynamics were adapted to yield Ca²⁺ transients of ∼1 μm, similar to those reported by Gabbiani et al. (1994), and to reproduce the excitable response (Traub and Llinas, 1979; Traub et al., 1991). Parameters used in Equation 7 wered = 200 nm, β_Ca=1.5, and Ca0 = 100 nm. Ca0 was measured in rat cerebellar granule cells in culture (Irving et al., 1992; Marchetti et al., 1995) and experimentally maintained by appropriate BAPTA-Ca²⁺ buffers (see above).

Resting membrane potential. Resting membrane potential in the model settled at −80 mV, reflecting a prominent contribution of I_K-IR. Although resting membrane potential measured in rat cerebellar granule cells ranges from −60 to −85 mV (D'Angelo et al., 1995, 1998; Brickley et al., 1996; Watkins and Mathie, 1996; Rossi et al., 1998; Armano et al., 2000), at −80 mV the model was rather insensitive to manipulation of ionic conductances, which provided a useful reference potential for subsequent simulations.

RESULTS

Bursting and resonance in granule cell

Intrinsic granule cell electroresponsiveness was investigated in current-clamp recordings. During step current injection (Fig. 1A), granule cells showed inward rectification in the hyperpolarizing direction. Just-threshold depolarizing currents generated spikes, which could be clustered in doublets–triplets or longer bursts occurring at a frequency of 3–10/sec (Fig. 1A,B) [also see D'Angelo et al. (1998), their Figs. 1, 2]. Spikes were followed by a fast afterhyperpolarization (AHP), an afterdepolarization, and a slow afterhyperpolarization (Fig.1B). When stronger depolarizing currents were injected, firing became regular, and afterdepolarization and slow afterhyperpolarization were no longer observed (Fig.1A, top trace). It should be noted that recordings were performed in the presence of 10 μm bicuculline preventing granule cell rhythmic inhibition by Golgi cells (Brickley et al., 1996) and that spontaneous EPSPs were too rare (∼0.1/sec) to significantly affect spike generation (no difference was noted after application of the glutamate receptor blockers 10 μm CNQX, 100 μm APV, and 50 μm7-Cl-kyn; n = 3; data not shown). Thus, intrinsic membrane mechanisms should generate spike bursts, slow afterhyperpolarization (Alonso and Llinas, 1989; Gutfreund et al., 1995; Pape and Driesang, 1998), and spike afterdepolarization (Azouz et al., 1996; Raman and Bean, 1997).

Fig. 1.

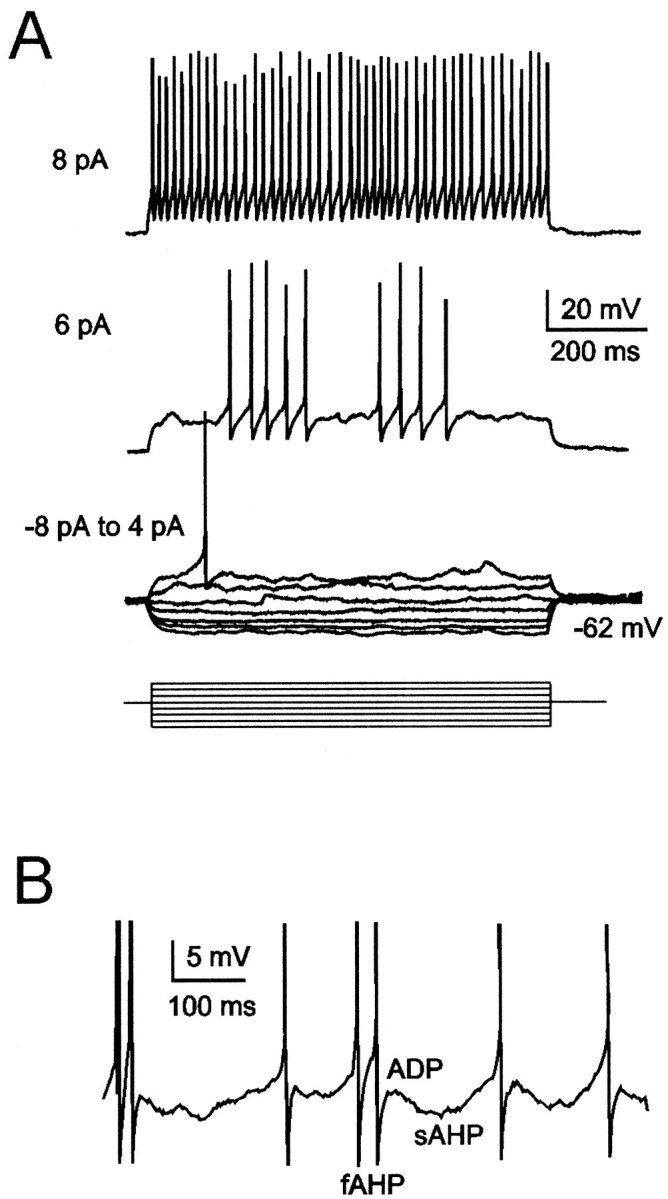
Granule cell electroresponsiveness during step current injection. A, The injection of current steps (from −8 to 6 pA, resting potential = −62 mV) causes inward rectification in the hyperpolarizing direction. Spikes are activated around −40 mV. The tracing at 4 pA shows a single spike, the tracing at 6 pA shows spikes clustered in two bursts, and the tracing at 8 pA shows regular repetitive firing. B, Just-threshold response illustrating spike fast afterhyperpolarization (fAHP), slow afterhyperpolarization (sAHP), and afterdepolarization (ADP). The neuron in B is different from that in A(spikes are truncated). Recordings in this and the following figures were performed in the presence of 10 μmbicuculline.

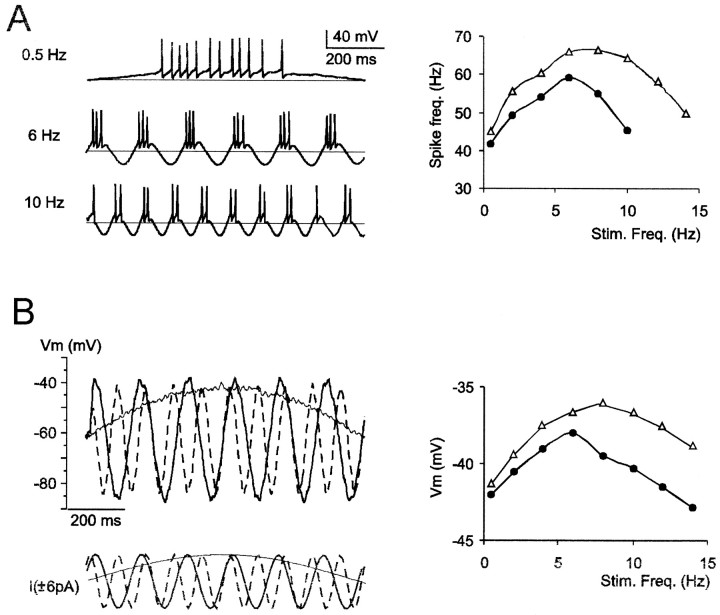
Injection of sinusoidal currents of appropriate amplitude generated spike bursts in correspondence with the positive phase of the stimulus (Fig. 2A). Spike frequency within bursts increased and then decreased with injected current frequency, therefore showing resonance. The resonance frequency was 8.9 ± 3.2 Hz (n = 8; average data are shown in Fig. 10A). Resonance was also observed in the absence of spikes (1 μm TTX in the bath) (Fig. 2B). In this case, the maximum depolarization reached during the positive phase of the sinusoidal voltage response showed a resonance frequency of 8.1 ± 2.9 Hz (n = 8; average data are shown in Fig. 10B). Regarding both spike frequency and membrane potential measurements, the resonance frequency tended to increase slightly with the intensity of the injected current (Fig. 2A,B; see Fig. 10A,B).

Fig. 2.

Resonance in a cerebellar granule cell (same cell as in Fig. 1A). A, Injection of sinusoidal currents at various frequencies (0.5–40 Hz) reveals resonance in burst spike frequency, which was measured by dividing the time period between the first and last spike in a burst by the number of interspike intervals. The plot shows that the resonance frequency was 6 Hz, with sinusoidal currents of ±6 pA (●) and 8 Hz with ±8 pA (Δ). At frequencies higher than those shown in the plot, just one or no spikes were generated, and spike frequency fell to zero. B, After 1 μm TTX perfusion, injection of sinusoidal currents at various frequencies reveals resonance in the maximum depolarization reached during the positive phase of the sinusoidal voltage response. The plot shows that the resonance frequency was 6 Hz, with sinusoidal currents of ± 6 pA (●) and 8 Hz with ±8 pA (Δ). Beyond the resonance peak, the sinusoidal voltage response decreased monotonically until 40 Hz (data not shown).

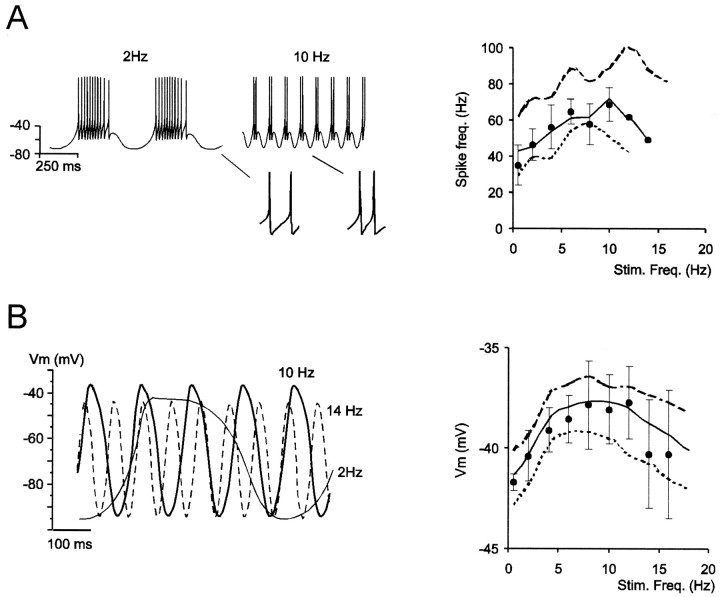
Fig. 10.

Ionic mechanisms of resonance.A, Injection of sinusoidal currents causes oscillatory bursting in the model. Tracings are generated by a ±6 pA sinusoidal current superimposed on a 12 pA current step. Insetsshow higher spike frequency in bursts generated at 10 Hz than at 2 Hz. The plot shows model resonance with three different sinusoidal current intensities (±4, ±6, or ± 8 pA superimposed on a constant 12 pA current step). The curve generated with ±6 pA is a good match with the average experimental response (●; mean ± SD; n = 5). B, Same as in A, except that maximum membrane depolarization during the positive phase of sinusoidal voltage responses is measured with I_Na-f,I_Na-p, andI_Na-r set to zero. This result is compared with experimental recordings in the presence of 1 μm TTX (●; mean ± SD; n = 5, same cells as inA). As with real granule cells, the model shows resonance ∼10 Hz.

Evidence for a K⁺-dependent mechanism in oscillation and resonance

The results shown in Figures 1 and 2 suggest that granule cells combine membrane mechanisms that generate fast repetitive firing, with others responsible for slow oscillations and resonance in the theta-frequency range. Accordingly, previous observations unveiled oscillations that sustained spike bursting by reducing K⁺ conductances with TEA and showed that they depended on a persistent TTX-sensitive Na⁺ current (D'Angelo et al., 1998). Here we investigated the ionic dependence of the slow oscillatory mechanism and of resonance during bath application of 1 mmNi²⁺, which fully blocks granule cell Ca²⁺ currents (Rossi et al., 1994; Tottene et al., 1996; D'Angelo et al., 1997, 1998), and of 4 mm 4-AP and 20 mm TEA, which block the granule cell K⁺ currentsI_K-V,I_K-Ca, andI_K-A (Cull-Candy et al., 1989;Bardoni and Belluzzi, 1993).

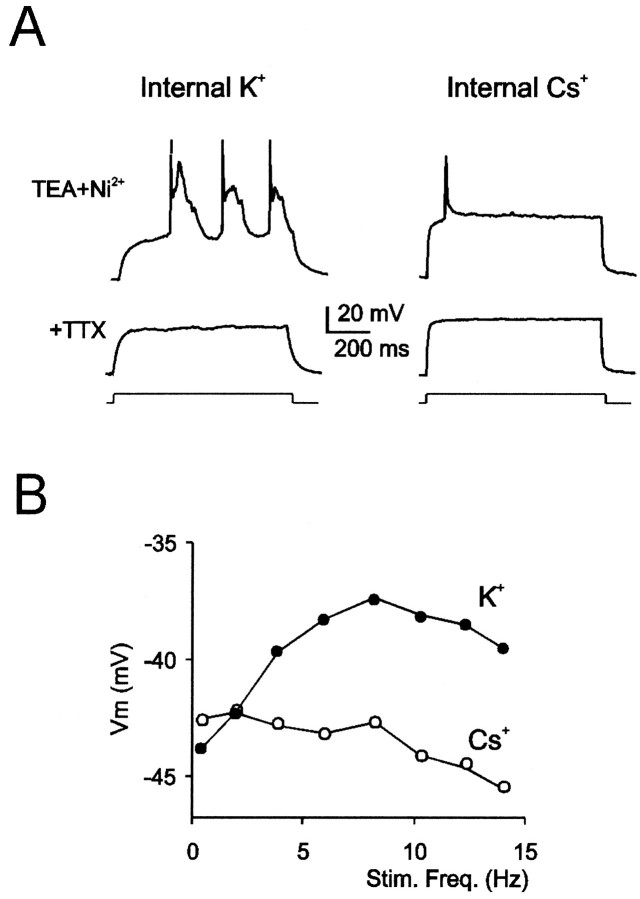
When these ionic channel blockers were used, depolarizing current steps sustained large-size oscillations surmounted by a solitary spike when the patch pipette solution contained K⁺(n = 5) but not when it contained Cs⁺ (n = 6) as the main intracellular cation (Fig.3A). In these recordings, a marked adaptation prevented repetitive spike activation and bursting. Oscillations and solitary spikes were blocked by 1 μm TTX, unveiling their Na⁺ dependence. Likewise, resonance was observed when the patch pipette contained K⁺ (n = 3) but not when it contained Cs⁺ (n = 3) (Fig. 3B). Because Cs⁺ prevents K⁺ permeation through K⁺ channels, and because Ca²⁺ channels in these recordings are blocked, oscillation and resonance are likely to involve a TEA-insensitive Ca²⁺-independent K⁺ current.

Fig. 3.

K⁺ dependence of slow oscillation and resonance. Current-clamp recordings were performed in the presence of 20 mm TEA, 4 mm 4-AP, and 1 mm Ni²⁺. A, A sustained slow oscillation is observed in granule cells recorded with K⁺-containing patch pipette during step current injection (10 pA from −80 mV). A solitary action potential is generated in a different cell recorded with a Cs⁺-containing patch pipette. In both cases, excitable responses were abolished by 1 μm TTX.B, Resonance curves in a cell recorded with K⁺ (●) and in another cell recorded with Cs⁺ (○) inside the patch pipette. Comparable voltage responses in neurons shown in A andB were obtained by properly adjusting the intensity of injected current (lower with Cs⁺- than with K⁺-containing pipettes).

Isolation of a slow K⁺ current in granule cells

A TEA-insensitive Ca²⁺-independent slow outward current (I_K-slow) was isolated by performing voltage-clamp recordings in the presence of 20 mm TEA, 4 mm 4-AP, 1 mm Ni²⁺, and 1 μm TTX (Fig. 4).I_K-slow could not be measured in cells internally perfused with Cs⁺ rather than K⁺ (data not shown), which revealed its K⁺ dependence, and was reversibly reduced by 48.7 ± 8.4% (n = 4) by extracellular perfusion of 1 mmBa²⁺ (Fig. 4A).

Fig. 4.

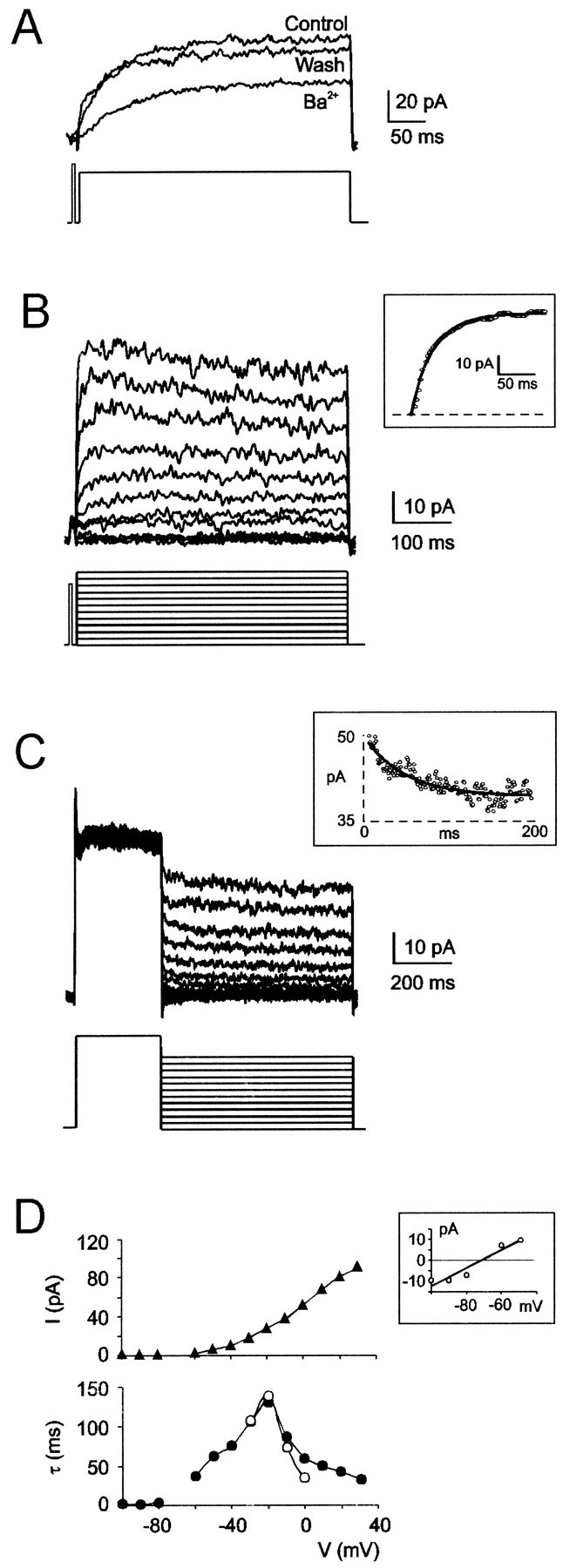
Isolation of a slow K⁺ current,I_K-slow, in the presence of 20 mm TEA, 4 mm 4-AP, 1 mmNi²⁺, and 1 μm TTX. A,I_K-slow was generated by a voltage pulse from −80 to +30 mV. I_K-slow was reversibly inhibited by application of 1 mm Ba²⁺.B, I_K-slow activation was investigated by applying 1 sec, 10 mV depolarizing voltage steps from the holding potential of −80 mV (a short pre-step was applied to inactivate I_K-A) (Bardoni and Belluzzi, 1993). The inset shows exponential fitting to the rising phase of a current recorded at 0 mV with the function I(t) =I_ss * (1 - exp(−t/τ_act)), whereI_ss = 53 pA is the steady-state current and τ _act = 33.5 msec is the activation time constant. C, I_K-slowdeactivation was investigated by using voltage jumps to different potentials after a 300 msec conditioning pulse at +30 mV (holding potential = −80 mV). The inset shows exponential fitting to a tail current recorded at −10 mV with the functionI(t) =I_ss + I₀ * exp(−t/τ_deact), where (I_o +I_ss) = 48.9 pA is the instantaneous current, I_ss = 39.2 pA is the steady-state current, and τ_deact = 46.9 msec is the deactivation time constant. D, Voltage dependence of steady-state amplitude of deactivation curves (I_ss, ▴), and of time constants obtained by exponential fitting to activation (τ_act, ○) and deactivation (τ_deact, ●) curves. The insetshows intersection of the linear regression curve to instantaneous tail current amplitude with the voltage axis at −71.4 mV. Data inB–D were obtained from the same granule cell.

During application of depolarizing voltage steps from the holding potential of −80 mV (Fig. 4B),I_K-slow activated around −40 mV, and its amplitude increased by increasing the test potential.I_K-slow rising phase was well fitted by a single exponential function (Fig. 4B,inset), indicating first-order activation kinetics. Exponential time constants ranged from 10 to >100 msec for test potentials between −40 and 0 mV, reaching values two orders of magnitude higher than those of other granule cell outward currents (Cull-Candy et al., 1989; Bardoni and Belluzzi, 1993).I_K-slow persisted for >1 sec, but in six of nine cells it showed a slight tendency to inactivate at positive test potentials (<15% after 1 sec at +30 mV).

Voltage jumps to different potentials after a 300 msec conditioning pulse at +30 mV (when I_K-slow was almost fully activated) generated tail currents that relaxed with an exponential time course (Fig. 4C). Exponential fitting (Fig.4B, inset) yielded the activation time constant, the instantaneous tail current amplitude (time = 0), and the steady-state current. According to the Nernstian equilibrium potential of K⁺ ions, the instantaneous tail current was zero at −74.8 ± 5.5 mV (n = 4) and shifted to −37.7 ± 6.1 mV (n = 4) when extracellular K⁺ was raised to 25 mm by equimolar Na⁺substitution.

Voltage dependence of the steady-state current and the activation time constant obtained from data shown in Figure 4, A andB, are shown in Figure 4D. TheI–V curve showed outward rectification, and the activation time constant showed a bell-shaped voltage dependence. It should be noted that time constants measured from activation and deactivation currents coincided, consistent with a first-order gating mechanism. However, deactivation currents were preferred to activation currents for gating reconstruction, because they covered a more extended membrane potential range and were free of potential contamination by I_K-A, which is not completely blocked even by 4 mm 4-AP in cerebellar granule cells (Bardoni and Belluzzi, 1993).

Figure 5 shows average data obtained from nine granule cell recordings. The I–V curve (Fig. 5A) was fitted with a Boltzman equation of the form [see Rossi et al. (1998)]:

$$I(V)=[G_{max}(V-V_{\text{rev}})]/[1+exp((V-V_{1/2})/k)]$$ Equation 8

where G_max = 0.8 nS is the maximum conductance, V_rev = −70.2 mV is the reversal potential, V_1/2 = −20 mV is the half-activation potential, and k = 6 mV⁻¹ is the activation voltage dependence. These parameters were used to reconstruct steady-state I_K-slowactivation (Fig. 5A) by using the equation:

$$G(V)/G_{max}=1/[1+exp((V-V_{1/2})/k)].$$ Equation 9

The relationship between activation time constant and voltage (Fig. 5B) was fitted by Equation 4 using the kinetic constants shown in Figure 5C. As in other ionic current models (Gutfreund et al., 1995; Mainen et al., 1995), independent expressions for the activation time constant and steady-state activation improved data representation. These results allowedI_K-slow reconstruction according to a first-order Hodgkin–Huxley kinetic scheme (Yamada et al., 1998) (see Materials and Methods; Table1).

Mathematical reconstruction of intrinsic excitability

To investigate the role ofI_K-slow in oscillations, bursting, and resonance, we developed a mathematical model of granule cell excitability (see Materials and Methods; Table 1). WithI_Na-f,I_Ca,I_K-V,I_K-Ca,I_K-A, andI_K-IR, the model generated inward rectification and fast repetitive firing (Gabbiani et al., 1994). The model was then endowed with a persistent Na⁺ current (I_Na-p) (D'Angelo et al., 1998) andI_K-slow, and was extended to test the potential contribution of a resurgent Na⁺ current (I_Na-r) (Raman and Bean, 1997). WithI_Na-p,I_K-slow, andI_Na-r, just-threshold step current injection generated membrane potential oscillations and spike bursts, with the spikes showing fast- and slow-afterhyper-polarization and afterdepolarization (Fig.6A,B). With stronger current injection, the model generated regular repetitive firing (Fig. 6A; see Fig. 8). Moreover, the model reproduced TEA-induced bursting (see Fig. 9) and intrinsic resonance (see Fig. 10).

Fig. 6.

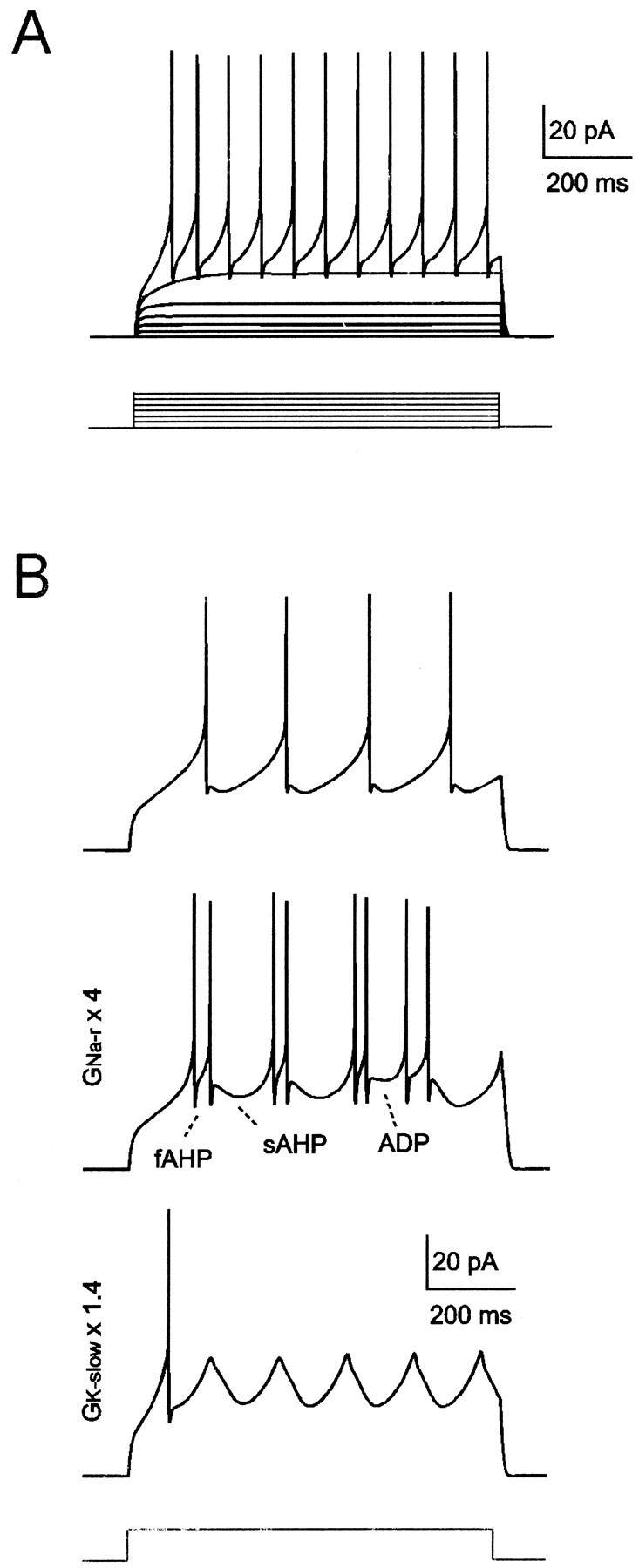
Mathematical modeling of granule cell excitability. A, Model responses to 2 pA step current injection from −80 mV. The model generates inward rectification in subthreshold responses, followed by regular repetitive firing with almost no adaptation. B, Slow oscillations, slow afterhyperpolarization, occasional uncoupling of spike prepotential from upstroke, and spike bursts can be generated by the model by using just-threshold stimulation (10.5 pA in the top andmiddle tracings, 12 pA in the bottom tracing). The shape of oscillations and bursting could be modified by changing the G_Na-r orG_K-slow intensities.

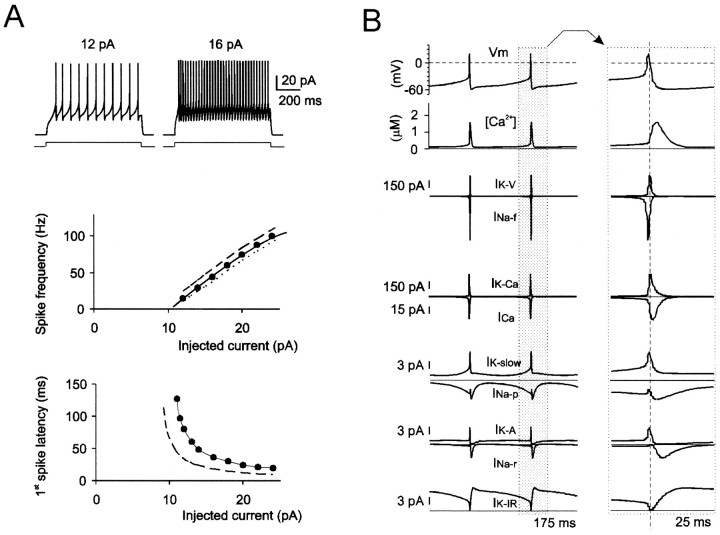
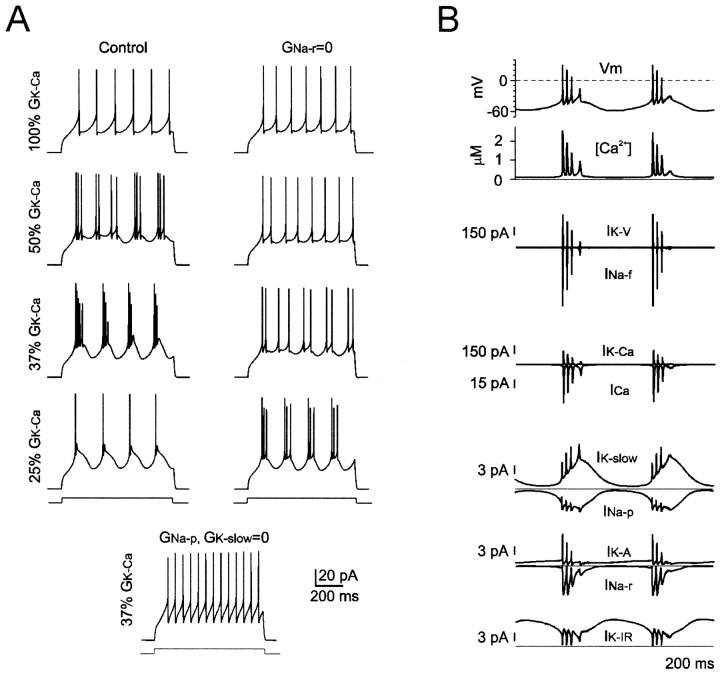
Fig. 8.

Ionic mechanisms of repetitive firing.A, Model tracings show regular firing with negligible adaptation at >100 Hz. The top plot(f–I plot) reports firing frequency in control conditions (●) and after having turned offI_K-A (broken line) orI_Na-r (dotted line). Thebottom plot shows first-spike latency in control conditions (●) and after having turned offI_K-A (broken line).B, Ionic currents and [Ca²⁺] changes during repetitive firing. The right set oftracings is an enlargement of currents associated with an action potential. Note that both I_Na-pand I_Na-r are activated after the spike.

Fig. 9.

Ionic mechanisms of bursting. A, Tracings show intensification of bursting and spike adaptation by progressively increasing G_K-Ca inhibition during injection of 11 pA current steps. StrongerG_K-Ca inhibition is needed to generate bursting when G_Na-r is set to zero. No bursting is generated when G_Na-p andG_K-slow are turned off, butG_Na-r is left active. B, Ionic currents and [Ca²⁺] changes during bursting elicited with I_K-Ca reduction to 37% of its normal value. Note that I_K-slow andI_Na-p are greatly enhanced during bursting compared with repetitive firing.

The ionic mechanism of slow oscillations

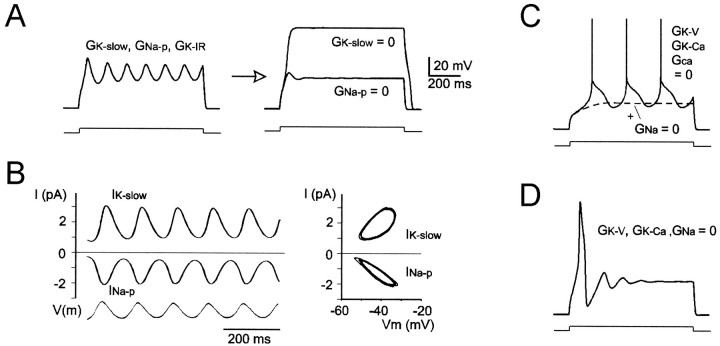
Model simulations showed thatI_Na-p andI_K-slow were sufficient to generate regular theta-frequency oscillations, which were eliminated when either of these currents was turned off (Fig.7A). During oscillations,I_Na-p andI_K-slow showed activation/deactivation cycles describing stable orbits in the phase plane (Fig.7B). The histerisis observed inI_K-slow (and to a lesser extent inI_Na-p) trajectory reflected its delayed gating during membrane potential changes.

Fig. 7.

The oscillatory mechanism in granule cells.A, Simulation of stable oscillations sustained byG_K-slow and G_Na-pduring injection of an 11 pA current step. Oscillations are eliminated by turning off either G_K-slow orG_Na-p. All other active conductances were set to zero except G_K-IR, which was used to keep input conductance close to its normal value.B, Time course and phase-plane trajectory ofI_K-slow and I_Na-pduring membrane potential oscillations (dotted line).C, Voltage responses to an 11 pA current step simulating TEA (G_K-V = 0,G_K-Ca = 0), and Ni²⁺(G_Ca = 0) application. Thebroken line simulates subsequent application of TTX (G_Na = 0). D, Voltage responses to an 11 pA current step simulating TEA (G_K-V = 0,G_K-Ca = 0) and TTX (G_Na = 0) application. Same calibration in A, C, and D.

The model generated repetitive oscillations whenG_K-V,G_K-Ca, andG_Ca were set to zero, reproducing the pharmacological application of 20 mm TEA and 1 mm Ni²⁺ (Fig.7C; compare Fig. 2). Moreover, the model generated a solitary Ca²⁺ action potential whenG_K-V,G_K-Ca, andG_Na were set to zero, reproducing the pharmacological application of 20 mm TEA and 1 μm TTX (Fig. 7D) [compare Fig. 3 inD'Angelo et al. (1998) and Fig. 10 in D'Angelo et al. (1997)]. Modeling results therefore indicated that slow oscillations in granule cells depend on the interaction ofI_Na-p andI_K-slow but are independent from Ca²⁺ currents.

Repetitive firing

Figure 8A shows repetitive firing in the model. As in experimentally recorded granule cell responses (D'Angelo et al., 1995, 1998; Brickley et al., 1996), spikes showed negligible adaptation, and first-spike latency decreased whereas spike frequency increased when the injected current intensity was raised. The frequency–intensity (f–I) plot was almost linear between 0 and 100 Hz, with a slope of 7.3 spikes per pA⁻¹ · sec⁻¹.

Spikes were generated by a suddenI_Na-f raise followed by activation ofI_K-V and theI_Ca/I_K-Casystem (Fig. 8B). The intracellular Ca²⁺ wave peaked after the spike and decayed to zero in ∼3 msec. I_Na-f,I_K-V,I_Ca, andI_K-Ca accounted for most of the active current during the spike and the fast AHP, whereas other currents were two orders of magnitude smaller. I_Na-pincreased during the spike prepotential and persisted for several milliseconds. I_Na-r increased just after the spike. I_K-A,I_K-IR, andI_K-slow were mostly active during the interspike trajectory. Thus, whereasI_Na-p andI_Na-r enhanced spike activation,I_K-A,I_K-IR, andI_K-slow delayed it. The regulatory action of I_Na-r andI_K-A on spike frequency is shown in the plots of Figure 8A.

TEA-induced bursting

Figure 9A illustrates theta-frequency bursting in the model after partialI_K-Ca blockage, simulating experimental TEA application (D'Angelo et al., 1998, their Figs. 6 and 8). A relatively modest I_K-Ca blockage caused spike doublets–triplets, whereas stronger blockage caused marked membrane potential oscillations surmounted by adapting spike bursts. Thus, I_K-Ca prevented activation of theI_Na-p/I_K-slowoscillatory mechanism. Bursting was enhanced byI_Na-r (Fig. 9A, compareleft with right column), but no bursting was generated by I_Na-r alone when theI_Na-p/I_K-slowmechanism was turned off (Fig. 9A, bottom panel).

TEA-induced bursting was characterized by a remarkable rise inI_Na-p associated with a progressiveI_K-slow activation (Fig.9B, compare Fig. 7B). During the burst,I_Na-f inactivation caused spike amplitude adaptation.

Resonance

Injecting the granule cell model with sinusoidal currents of different frequency generated resonant responses. Resonance in burst spike frequency is shown in Figure10A, and resonance in maximum membrane depolarization (with spikes blocked by settingI_Na-f,I_Na-p, andI_Na-r to zero mimicking TTX block) is shown in Figure 10B. In both cases a family of resonant curves is shown, one of which matches average experimental measurements from a set of five granule cells.

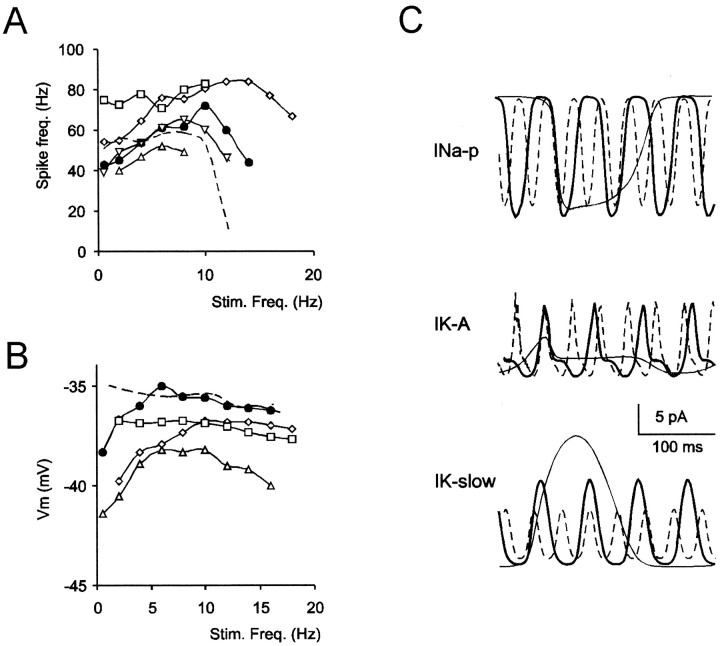
The model was used to investigate the ionic mechanisms of resonance. Resonance was eliminated by blockingI_K-slow, which determined the ascending branch of resonance curves (Fig.11A,B). The descending branch of resonance curves was determined by passive membrane filtering, as demonstrated by its persistence when the ionic channels involved in resonance were blocked. In addition,I_K-A markedly accelerated the descending branch. Enhanced activation ofI_K-slow at low frequency andI_K-A at high frequency is shown in Figure 11C. It should be noted that resonance was not eliminated by blocking I_Na-p (Fig.11A,B), which showed minor frequency-dependent changes (Fig. 11C). Finally,I_Na-r (in the case of burst spike frequency) decelerated the descending branch of resonance curves.

Fig. 11.

Resonance regulation. This Figure shows resonance being regulated by injection of a ±6 pA sinusoidal current superimposed on a 12 pA current step. A, Resonance in burst spike frequency in different conditions: ●, control; ■,I_K-slow = 0; ⋄,G_K-A = 0; Δ,G_Na-p = 0; ▿,G_Na-r = 0. No resonance could be observed in the model when I_Na-p,I_K-slow, andI_Na-r were turned off (thin dotted line). B, Resonance in maximum membrane depolarization during the positive phase of sinusoidal voltage responses in different conditions: control (Δ,I_Na-p,I_Na-f,I_Na-r = 0; TTX condition); ■, I_K-slow = 0, ⋄, I_K-A= 0; ●, I_Na-p active. No resonance could be observed in the model whenI_Na-p,I_K-slow, andI_Na-r were turned off (thin dotted line). C,I_Na-p,I_K-slow, andI_K-A at three different frequencies (thick line, 8 Hz; thin line, 2 Hz;broken line, 14 Hz). Note the different frequency-dependent activation of these currents.

DISCUSSION

This study shows that in addition to generating fast repetitive firing, cerebellar granule cells generate oscillations, bursting, and resonance in the theta-frequency range. Experimental and modeling results indicated that these aspects of intrinsic excitability require a slow K⁺ current (I_K-slow) to be generated.

I_K-slow is a Ca²⁺-independent TEA-insensitive K⁺ current activating in the spike threshold region with slow kinetics (10–100 msec). A current likeI_K-slow has not been reported previously in cerebellar granule cells, although a persistent TEA-resistant current component was noted in cell culture (Cull-Candy et al., 1989) [also see Bardoni and Belluzzi (1993), their Fig. 10B]. I_K-slowbiophysical and pharmacological properties are similar to those ofI_M of vertebrate neurons (Brown and Adams, 1980; Adams et al., 1982a,b) and are suitable to generate the delayed repolarizing feedback and high-pass filtering required for bursting and resonance. Indeed, I_M has been reported to sustain oscillations and resonance in amygdaloid neurons (Pape and Driesang, 1998) and in cortical pyramidal neurons (Gutfreund et al., 1995). Alternative mechanisms that might be invoked to explain bursting and resonance are unlikely to occur in cerebellar granule cells. (1) A slow inward rectifier current (I_h) (Dickson et al., 2000) and a slow Ca²⁺-dependent K⁺ current (I_AHP) (Wang and Rinzel, 1999) are apparently not expressed in granule cells. Granule cell inward rectification is fully explained by a fast K⁺-dependent inward rectifier (Fig.6A) (Rossi et al., 1998), and granule cell slow afterhyperpolarization is fully explained byI_K-slow (Fig. 6B). It should also be noted that the I_AHPblocker apamin did not affect the excitable response, and oscillations and bursting persisted in the presence of Ca²⁺ channel blockers (Fig. 3) (D'Angelo et al., 1998). Moreover, contrary to what would be expected fromI_AHP, granule cell slow AHP occurred with just-threshold stimulation disappearing rather than being enhanced with higher spike frequency and was not associated with any spike frequency adaptation. (2) A resurgent current,I_Na-r, facilitated but proved not sufficient to induce bursting and resonance (Fig.8A). (3) Finally, return currents from the dendrites, which might generate somatic rebound depolarization and spike bursting, are unlikely to be effective because of the granule cell compact electrotonic structure. Actually, with a 10 MΩ somatodendritic resistance (calculated assuming an axial resistance of 150 Ω/cm in a 20 μm dendrite) and a somatodendritic ratio between 1 and 2 (Silver et al., 1992; D'Angelo et al., 1993;Gabbiani et al., 1994), no bursting is expected even if active conductances are expressed in the dendrites (Mainen and Sejinowsky, 1996).

Modeling reliability was based on the extensive characterization of membrane currents and the compact electrotonic structure of cerebellar granule cells (for details, see Materials and Methods). Indeed, patch-clamp recordings from mature cerebellar granule cellsin situ have been used (1) to reconstructI_Ca (Rossi et al., 1994),I_K-IR (Rossi et al., 1998),I_K-A (Bardoni and Belluzzi, 1993), andI_K-slow (this study), (2) to identify different Na⁺ current components (including I_Na-f,I_Na-p, andI_Na-r) (D'Angelo and Magistretti, unpublished results), and (3) to characterize the pharmacological properties of excitability (D'Angelo et al., 1998). Patch-clamp recordings from granule cells in culture were used to reconstructI_K-Ca (Fagni et al., 1991; Gabbiani et al., 1994). Although further investigation is required to clarify Ca²⁺ dynamics and the biophysical properties of the Na⁺ current, mathematical modeling allowed us to investigate the role ofI_Kslow in relationship to other excitable properties of the granule cell. In addition to modeling,I_Kslow involvement in oscillations, bursting, and resonance may be investigated byI_Kslow selective pharmacological blockage or by I_Kslow electronic antagonism/expression through a dynamic-clamp circuit (Hutcheon et al., 1996a,b).

Experimental and modeling observations allow the following reconstruction of the ionic mechanisms of rat cerebellar granule cell electroresponsiveness.

(1) I_Na-f andI_K-V were the core of a fast oscillatory mechanism sustaining fast repetitive firing, as in the classical Hodgkin–Huxley model (Hodgkin and Huxley, 1952).I_K-A increased spike latency (Connor and Stevens, 1971), and theI_Ca–I_K-Casystem stabilized repetitive firing by enhancing fast AHP and Na⁺ channel deinactivation [see alsoGabbiani et al. (1994)].

(2) I_Na-p andI_K-slow were the core of a slow oscillatory mechanism sustaining theta-frequency oscillation and bursting. I_Na-p has been reported to sustain oscillations in association withI_M in neocortical pyramidal neurons (Gutfreund et al., 1995) and in association withI_h in enthorinal pyramidal neurons (Alonso and Llinas, 1989; Dickson et al., 2000).I_K-slow caused delayed repolarization, terminating the positive phase of the oscillation promoted byI_Na-p.

(3) Emergence of bursting was regulated by theI_Ca–I_K-Casystem (D'Angelo et al., 1998) through the fast AHP, which reduced the depolarizing action of I_Na-p (Azouz et al., 1996) and I_Na-r (Raman and Bean, 1997) after the spike.

(4) Resonance depended on high-pass filtering caused byI_K-slow (generating the ascending branch of the resonance curve) in association with low-pass filtering caused by passive membrane properties (generating the descending branch of the resonance curve) and was amplified byI_Na-p. Thus, resonance involved subthreshold changes in membrane excitability [corresponding to subthreshold impedance resonance reported by Hutcheon et al. (1996a,b)], consistent with the identification ofI_K-slow as a “resonator” current and I_Na-p as an “amplifier” current“ (Hutcheon and Yarom, 2000). In addition, the model suggested that I_K-A, which is inactivated at low but not high frequency, accelerated the descending branch of the resonance curve. Finally, the model predicted that resonance in burst spike frequency could be intensified by spike clustering promoted byI_Na-r. Thus, resonance and bursting may have in common their dependence onI_K-slow as well as that onI_Na-r.

Granule cells are excitatory interneurons relaying information conveyed by mossy fibers into the cerebellar cortex (Marr, 1969). Although repetitive firing implements a mechanism of linear frequency coding (Gabbiani et al., 1994), intrinsic bursting and resonance tune granule cells on theta-frequency, which is diffused in sensory-motor structures (Koch, 1999). Intrinsic bursting and resonance may favor granule cell phase-locking through the recurrent Golgi cell inhibitory circuit (Maex and DeShutter, 1998). Theta-frequency discharge has indeed been recorded from the granular layer during specific activity statesin vivo (Pellerin and Lamarre, 1997; Hartmann and Bower, 1998). Finally, as observed in the hippocampus (Holsher et al., 1997), theta-frequency bursting may regulate the induction of synaptic plasticity in the mossy fiber–granule cell pathway (D'Angelo et al., 1999; Armano et al., 2000).