Membrane Potential and Conductance Changes Underlying Length Tuning of Cells in Cat Primary Visual Cortex

Abstract

Spike responses for many cells of cat primary visual cortex are optimized for the length of a drifting grating stimulus. Stimuli that are longer or shorter than this optimal length elicit submaximal spike responses. To investigate the mechanisms responsible for this length tuning, we have recorded intracellularly from visual cortical neurons in the cat while presenting drifting grating stimuli of varying lengths. We have found that the membrane potential responses of the cells also exhibit length tuning, but that the suppression of spike responses at lengths longer than the preferred is 30–50% stronger than the corresponding suppression of the membrane potential responses. This difference may be attributed to the effects of spike threshold. Furthermore, using steady injected currents, we have measured changes in the excitatory and inhibitory components of input conductance evoked by stimuli of different lengths. We find that, compared with optimal stimuli, long stimuli evoke both an increase in inhibitory conductance and a decrease in excitatory conductance. These two mechanisms differ in their contrast sensitivity, resulting in stronger end stopping and shorter optimal lengths for high-contrast stimuli. These patterns suggest that response suppression for long stimuli is generated by a combination of active inhibition from stimuli outside the excitatory receptive field, as well as decreased excitation from other cortical cells that are themselves end-inhibited.

The nature of cortical interconnections and the computations they subserve comprise a fundamental problem in cortical physiology. In primary visual cortex, such cortical interconnectivity is presumed to be responsible for local processing and gain control for stimuli within the classical receptive field (Bauman and Bonds, 1991; DeAngelis et al., 1992; Heeger et al., 1996; Carandini et al., 1999), as well as for interactions between stimuli within the classical receptive field of a neuron and stimuli outside the classical receptive field (Maffei and Fiorentini, 1976;Nelson and Frost, 1978; Kapadia et al., 1995; Levitt and Lund, 1997;Polat et al., 1998; Somers et al., 1998).

One of the most robust examples of cortical processing in primary visual cortex is length tuning or end inhibition. Hubel and Wiesel (1965) first described complex cells in which the response to a stimulus increases with the length of the stimulus up to some optimum value, after which further increases in length decreased the response. Since that time, length tuning has emerged as a common feature of many cells in primary visual cortex, including both simple and complex cells (Dreher, 1972; Gilbert, 1977; Rose, 1977; Kato et al., 1978).

Despite the attention that length tuning has received since the phenomenon was described, basic mechanisms responsible for length tuning are not yet understood. Even fundamental questions persist, such as whether length tuning is produced by inhibition from cells with distinct receptive fields or by excitation from cells of differing properties (Skottun, 1998). Recent reports have also proposed divergent mechanisms for the contrast dependence of length tuning; as stimulus contrast increases, length tuning becomes more pronounced, and the optimal length for the cell becomes shorter. It has been suggested that contrast enhancement of length tuning could be mediated by contrast sensitivity of inhibition outside the receptive field (Jagadeesh and Ferster, 1990) or by a contrast-dependent change in the spatial summation of excitation (Sceniak et al., 1999).

We have investigated the mechanisms responsible for length tuning by recording intracellularly from neurons of cat primary visual cortex while displaying drifting grating stimuli of varying length. As do spike responses, membrane potential responses were found to exhibit length tuning but with less pronounced end inhibition. Membrane potential responses also show a clear contrast dependence of length tuning, as do spike responses. To further investigate the mechanisms underlying these phenomena, we recorded responses to stimuli of varying length while injecting steady currents into the cells. These data allowed the measurement of input conductance as a function of length. By using a simple model for synaptic conductances, we computed excitatory and inhibitory components of the measured conductance (Anderson et al., 2000) and found that two mechanisms are responsible for length tuning in cortical neurons. First, an inhibitory conductance was observed in response to long stimuli. Second, excitatory conductance decreased with stimulus length, presumably because of decreased drive from cortical cells that are themselves length-tuned. Both effects are contrast dependent, and together may account for the observed contrast enhancement of length tuning. Both excitatory and inhibitory conductances also exhibited nonlinear spatial summation with stimulus length. Often, length–response curves for inhibitory conductance were bimodal, achieving maximal values in response to short or long stimuli but achieving smaller values in response to intermediate-length stimuli. Additionally, the decrease in excitatory conductance with length directly counters what would be predicted by spatial summation of excitatory inputs.

MATERIALS AND METHODS

Experimental preparation. Details of the experimental preparation have been described previously (Ferster and Jagadeesh, 1992; Anderson et al., 2000). Young adult cats were anesthetized with intravenous thiopental sodium and placed in a stereotaxic head holder. Gallamine was given to minimize motion of the eyes, and the animals were artificially respired. Phenylephrine hydrochloride and atropine sulfate were applied to the eyes to retract the nictitating membranes, dilate the pupils, and paralyze accommodation. Contact lenses with artificial pupils (4 mm in diameter) were inserted.

Visual stimulation. Visual stimuli consisted of 2–4 sec presentations on a ViewSonic (Walnut, CA) PS 775 monitor of sinusoidal gratings drifting at 2 Hz optimized for spatial frequency under computer control. Stimuli were generated by a Macintosh computer (Apple Computers, Cupertino, CA) running Matlab (MathWorks, Inc., Natick, MA) with Psychophysics Toolbox extensions (Brainard, 1997). Stimulus contrast ranged from 8 to 16% for low-contrast stimuli and from 30 to 64% for high-contrast stimuli and were chosen from the linear region of the contrast response curve for the cell, in which response saturation was not observed. Stimuli were rectangular along the axis of orientation and varied in length from 0.5° to 12° of visual angle, with uniform width of 3° of visual angle. Receptive fields were mapped by plotting the responses to small flashed spots, and stimuli were centered on this map to within 0.3° of visual angle. For all cells in the study, the receptive field diameter obtained from such mapping was <3° of visual angle.

Intracellular recording. Whole-cell patch recordings were obtained from neurons of area 17 of the visual cortex using the technique developed for brain slices by Blanton et al. (1989). Electrodes were filled with (in mm): 115 potassium gluconate, 20 KCl, 10 HEPES, 0.5 EGTA, 4 MgCl₂, 4 MgATP, and 0.3 NaGTP. Membrane potentials, recorded with an Axoclamp (Axon Instruments, Burlingame, CA) amplifier in current-clamp (bridge) mode, were low-pass filtered and digitized at 4 kHz. The measured junction potential (Neher, 1992) of 10 mV was subtracted from all recordings.

Cells were classified as simple or complex on the basis of the presence or absence of ON and OFF subregions in the receptive field. For three simple cells, recordings were performed while a stimulating electrode was present in the lateral geniculate nucleus. In all three cases, monosynaptic input with a latency <2 msec from electrical stimulation to the lateral geniculate nucleus was observed in the simple cell. The modulation component of the responses is computed as twice the amplitude of the response component at the frequency of the drifting grating. Cells were classified as end-inhibited if responses to stimuli of long lengths (8–12°) were <90% of responses to optimal lengths.

Correction for electrode resistance. The capacitance and resistance (7–12 MΩ) of the electrodes were easily neutralized before patching a cell. When a patch was obtained, however, the electrode resistance R_e increased significantly. To correct for this increased electrode resistance, responses V(t) to current pulses administered throughout the recording were fit to a double exponential:

$$V(t)/I_{\text{inj}}=R_{\text{e}}[1-exp(-t/{\tau }_{\text{e}})]+R_{\text{m}}[1-exp(-t/{\tau }_{\text{m}})],$$ Equation 1

where R_e andτ_e are the resistance and time constant of the patched electrode, andR_m andτ_m are the resistance and time constant of the cell membrane. This method allowed for compensation of electrode resistance (including any small drifts in electrode resistance throughout the recording) by subtracting the estimated electrode contribution I_injR_e from each membrane potential response to a visual stimulus (Anderson et al., 2000). Electrode resistance was <150 MΩ in all cells for which conductance was measured.

Measurement of conductance. Input conductance was measured by recording the membrane potential responses to visual stimuli while injecting, in turn, four to five different steady currents,I_inj. Injected currents ranged from −200 to 100 pA. Negative current were used most often to minimize spiking and the effects of voltage-dependent membrane nonlinearities. Stimuli with each combination of length, contrast (for cells in which more than one contrast condition was presented), and injected current were all presented in random order for a given trial. A trial, therefore, consisted of 50 or 100 stimuli (depending on whether one or two contrasts were presented), and 3–16 trials were presented for each cell. For several cells, tuning curves are constructed from the responses to >1000 stimuli. Interspersed approximately every 30 sec throughout the recording, a series of current pulses were administered to allow off-line correction for electrode resistance.

Responses were averaged across trials, and at each point in time during the response, the relationship between the injected current and the membrane potential was fitted with a line:

$$V(t)=V_{\text{visual}}(t)+I_{\text{inj}}/g(t),$$ Equation 2

where g(t), the inverse of the slope of the line, is the input conductance at time t (Anderson et al., 2000). The intercept of the line is the mean membrane potential in the absence of current injection (I_inj = 0). We refer to the intercept asV_visual(t), a linear estimate of the membrane potential recorded without injected current. Error measurements are calculated by performing the fits of Equation 2on subsets of the data containing three levels of injected current at a time and computing the SE of the resulting estimates forg(t).

Derivation of excitatory and inhibitory conductances. We derived excitatory and inhibitory conductances from the recordings of membrane potential and input conductance by first supposing that the conductance measurements we observe can be represented as the sum of three components: an excitatory conductance, an inhibitory conductance, and a resting conductance:

$$g(t)=g_{\text{e}}(t)+g_{\text{i}}(t)+g_{\text{rest}}.$$ Equation 3

The synaptic conductances are expressed relative to their value in the absence of visual stimulation. That is, in the absence of stimulation, we take the resting conductance to be equal to the total conductance and the synaptic conductances to be zero.

Given Equation 3, the visually driven membrane potential depends on the conductances as follows:

$$V_{\text{visual}}(t)=[g_{\text{e}}(t)V_{\text{e}}+g_{\text{i}}(t)V_{\text{i}}+g_{\text{rest}}{V}_{\text{rest}}]/g(t),$$ Equation 4

where V_e andV_i are the equilibrium potentials for excitatory and inhibitory synaptic conductances (Anderson et al., 2000). We find the excitatory and inhibitory synaptic conductances,g_e(t) andg_i(t), by solving Equations3 and 4. We set V_e at 0 mV andV_i at −80 mV. The latter is intermediate between the normal equilibrium potentials of GABA_A and GABA_B inhibitory channels. The GABA_A equilibrium potential in our cells may in fact be nearer to −80 mV than normal given the low levels of Cl⁻ in our recording electrodes.

RESULTS

Data for this study are taken from whole-cell patch recordings of 52 neurons in cat primary visual cortex. Of this total, 33 cells (19 complex, 14 simple, and 22 end-inhibited) had enough spikes to construct length-tuning curves for both membrane potential and spikes; 26 cells (18 complex, 8 simple, and 17 end-inhibited) were studied with current injection to obtain length-tuning curves for input conductance; 10 cells (7 complex and 3 simple; all 10 end-inhibited) were studied with current injection at multiple levels of stimulus contrast.

The iceberg effect and length tuning

An example of length tuning of membrane potential and spike responses is illustrated in Figure 1 for a simple cell. Responses to a 2 sec, 2 Hz drifting grating are shown inA. The top trace, in response to a stimulus with a length of 2°, exhibits clear modulation at the frequency of the drifting grating, with spikes generated at the peaks of the response. The bottom trace is a response to a stimulus with a length of 12°, which exhibits modulation that is similar to that of the optimal length response but slightly smaller in amplitude (B). Significantly fewer spikes are evoked than in response to the optimal length stimulus (C).

Fig. 1.

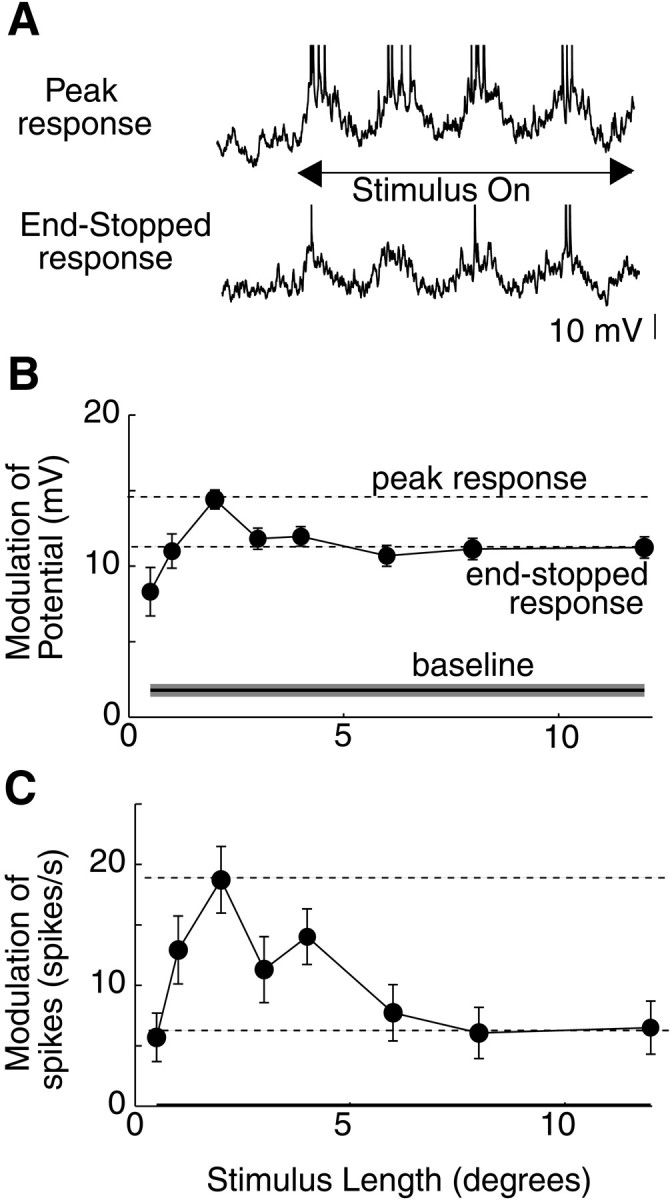
Length tuning of membrane potential and spikes in a simple cell. A, Membrane potential responses to a 2 sec drifting grating stimulus of 2° length (top) and 12 ° length (bottom). Traces show 0.5 sec before stimulus is presented. B, Peak-to-peak modulation of the membrane potential response as a function of length.Solid horizontal line shows modulation in the absence of a visual stimulus. Dashed horizontal lines show maximal (peak response) and end-stopped responses. End-stopped responses are calculated by finding the minimal response for stimuli longer than the length of the peak response. The end-stopped response is then taken as the mean of all responses of stimuli longer than or equal to the stimulus length of this minimal response. Error bars for data points and the shaded area around baseline show ±SEM across stimulus trials. C, Modulation of spikes as a function of length.

Length tuning in the cell of Figure 1, and for all other cells, was measured using an end-stopping index (ESI). This index was computed by the following formula:

$$(\text{Peak response}-\text{End stopped response})/(\text{Peak response}-\text{Baseline}).$$ Equation 5

Baseline in this formula represents the response of the cell to a blank stimulus of mean luminance. For the 33 cells in our sample in which end-stopping indices could be computed for both potential and spikes, we found that membrane potential or spike responses exhibited length tuning (ESI > 10%) in approximately half of the simple cells and most of the complex cells from which we recorded (Fig.2A). As in the cell of Figure 1, however, cells exhibited significantly greater end-stopping for spikes than for potential (Fig. 2B). Across the population of 22 cells (15 complex and 7 simple) that exhibited length tuning, ESI was 0.58 ± 0.06 for spikes and 0.37 ± 0.06 for potential (p < 0.01; two-tailed ttest), a difference of ∼50%. This difference is further shown in length-tuning curves for three complex cells in C. For all three cells, end-stopping is much more pronounced in spike responses than in membrane potential responses. This difference is striking and may be attributed to an iceberg effect, whereby spike responses are amplified for stimuli that have membrane potential responses closer to spike threshold (Carandini and Ferster, 2000; Volgushev et al., 2000).

Fig. 2.

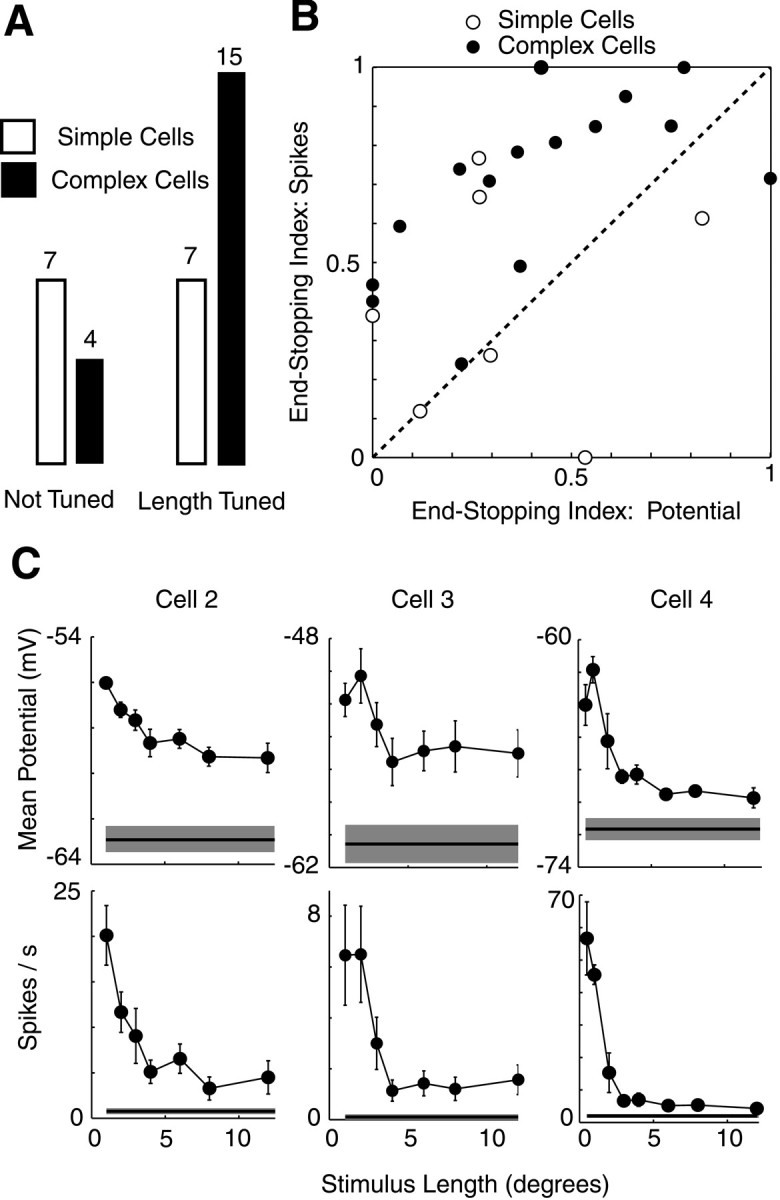
Length tuning for membrane potential and spikes in 33 cells. A, Proportion of simple and complex cells exhibiting length tuning (ESI > 0.1 for potential or spikes).B, Comparison of length tuning as measured by membrane potential and spike responses. Mean membrane potential responses are shown for complex cells and modulation of membrane potential for simple cells. C, Length-tuning curves for membrane potential and spikes for three complex cells. Error bars and shaded regions around baseline show ±SEM.

Synaptic mechanisms underlying length tuning

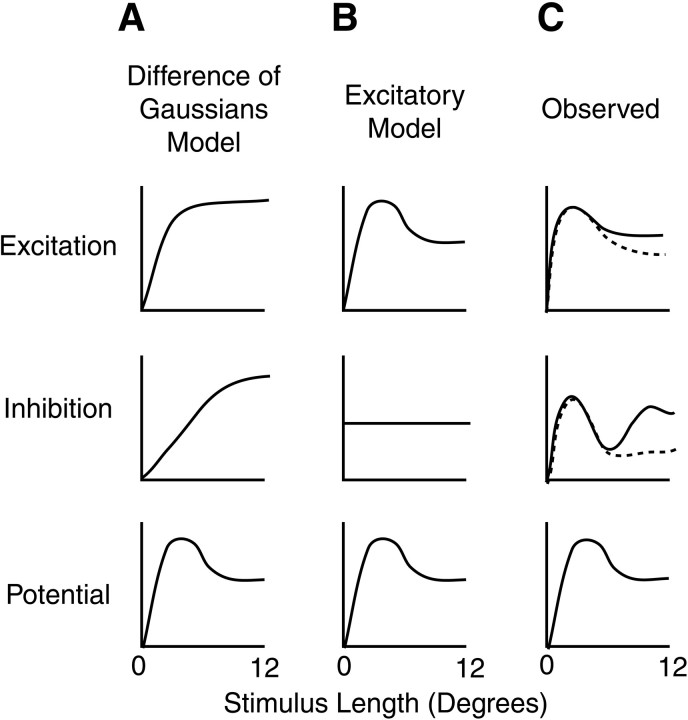
To characterize the synaptic mechanisms underlying length tuning, more information is required than length-tuning curves for membrane potential alone. Several possible mechanisms could explain length tuning of membrane potential and consequently of spikes. Figure3 outlines three such possibilities for how length tuning might be generated. One model that has been proposed to explain length tuning suggests that spatial summation of a visual response across the receptive field of a neuron may be normally distributed for both excitation and inhibition (Sceniak et al., 1999), such as is seen in retinal ganglion cells (Enroth-Cugell and Robson, 1966). In this difference-of-Gaussians model, inhibition is assumed to have a broader summation than excitation, resulting in suppression of the membrane potential response to long stimuli (A). Another model proposes that length tuning may be explained solely by excitation (Skottun, 1998). In this model, cells receive inputs from neurons with distinct orientation preferences. By combining excitatory inputs multiplicatively, the cell has a greater response to short lengths than to longer lengths, and the length tuning of the response follows the length tuning of excitatory inputs (B).

Fig. 3.

Proposed conductance models for length tuning of membrane potential. Rows show excitatory conductance, inhibitory conductance, and membrane potential responses as a function of length. A, Difference-of-Gaussians model.B, Excitatory model. C, Schematic of results obtained in the present study.

To distinguish between these possibilities, we have measured input conductance as a function of length by injecting steady currents into neurons and calculating the ratio of injected current to the change in the membrane potential response (see Materials and Methods). Additionally, by assuming that changes in conductance measurements were primarily synaptic, we have derived excitatory and inhibitory components of the changes in conductance. When we examined end-inhibited cells in this manner, we found two surprising results. First, in almost all of the cells from which we recorded, excitatory conductances show a striking suppression in response to long stimuli (Fig. 3C). Second, inhibitory conductances often show a biphasic response, in which strong inhibition for short or long stimuli is seen, with smaller inhibitory conductance for stimuli of intermediate length. This suggests that there may be two inhibitory inputs, one that acts as a gain control on high levels of excitatory conductance in response to short-length stimuli and another that inhibits stimuli in the surround of the classical receptive field.

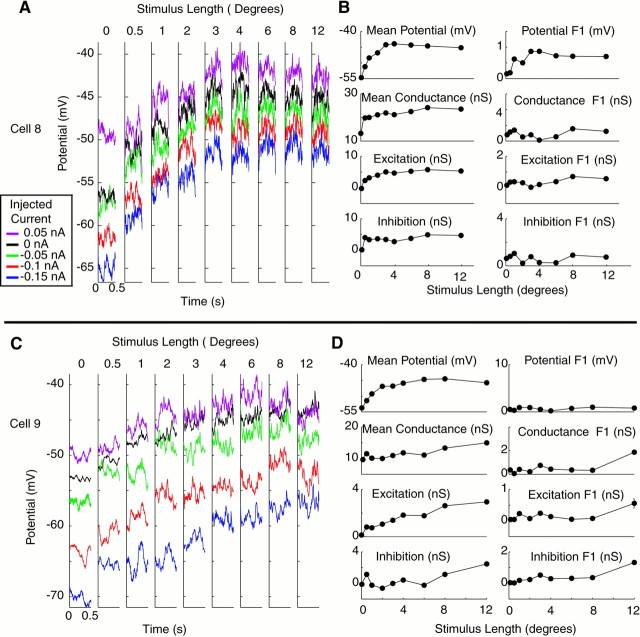
Three examples of input conductance measurements are shown in Figure4. For each cell, averaged membrane potential responses for a single cycle of the drifting grating stimulus are shown for each of four to five injected current conditions. In the first cell (A, B), length tuning is subtle, particularly in the 2 Hz modulation component of the response. InA, however, it can be seen that the traces in response to 1° or 8° stimuli are closer together than those of intermediate stimulus lengths, indicating that the input conductance is higher. When quantitative measures of conductance are obtained (B), the increase in conductance is indeed highest at 1° and 8°, in which the traces are closest together. Moreover, the effect seems predominately mediated by the responses with 0 and 0.05 nA injected current, in which membrane potential varies substantially with length, whereas responses with negative injected current show less variation with length. This would be consistent with the conductance increase being primarily an inhibitory conductance, because the responses with negative current injection are close to the inhibitory reversal potential, whereas responses with positive current injection would have a larger driving force to an inhibitory synaptic current. Derived values of excitation and inhibition bear this observation out, in that the peaks in the input conductance primarily correspond to inhibitory conductances. Bimodal length–response curves for inhibition similar to the one observed here were seen in many of our cells and may represent separate synaptic mechanisms for inhibition in response to short and long stimuli.

Fig. 4.

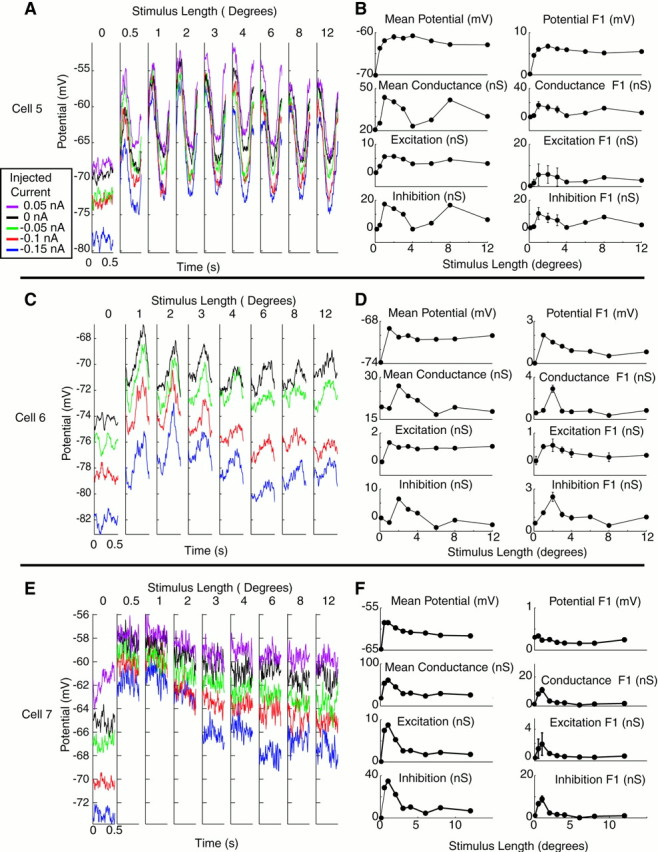
Measurement of conductance as a function of length for three end-inhibited cells. A, C,E, Average membrane potential responses with injected currents as a function of length for three cells. Eachtrace is color-coded for injected current level (seeinset legend) and represents one cycle of the drifting grating stimulus. Length of 0 indicates a blank stimulus.B, D, F, Length-tuning curves for mean and modulation of membrane potential, input conductance, and excitatory and inhibitory components of changes in input conductance. For potential, error bars show ±SEM across stimulus trials. For conductance measurements, error bars show ±SEM across conductance measurements taken from different subsets of the data (see Materials and Methods). Modulation represents peak-to-peak modulation of each parameter (2 * F1).

The second cell of Figure 4, C and D, shows a somewhat different conductance profile. As in the previous cell, the conductance is high for short stimuli. In this cell, however, a separate inhibitory conductance in response to long stimuli is not observed. This cell also differs from the one above in that modulation of the response is end-stopped more than the mean response. The third cell, a complex cell, shows again a different pattern (E,F). Here the length tuning is clearly produced by a reduction in excitatory conductance rather than an increase in inhibitory conductance in response to long stimuli.

Cells that do not exhibit length tuning show neither a decrease in excitatory conductance with stimulus length nor a bimodal length-tuning curve for inhibitory conductance. Input conductance measurements for two complex cells that were not end-inhibited are shown in Figure5. The first cell (A,B) responded to stimuli of increasing length with an increase in membrane potential, membrane conductance, and excitatory conductance responses, with a more or less constant level of inhibition. In the second cell (C, D), all four measurements increased steadily with stimulus length. These patterns were typical of cells in which length tuning was not observed.

Fig. 5.

Measurement of conductance as a function of length for two cells without end inhibition. Format is identical to Figure4.

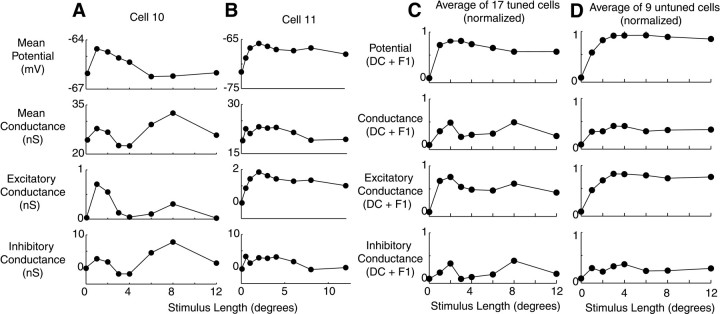
Length-tuning curves for two additional complex cells that did exhibit length tuning are shown in Figure 6. For the first cell (A), the conductance pattern is similar to the first cell of Figure 4. A strong inhibitory conductance emerges in response to long stimuli. The second cell (B) shows primarily a withdrawal of conductance with stimulus length. To evaluate trends in conductance across our population of 17 cells that showed end inhibition, we added the mean (DC) and modulation (F1) of the potential and conductance responses for each cell, normalized them, and averaged the normalized conductance values across the population as a function of length (C). The results show two average trends: excitatory conductance generally decreases with stimulus length, and inhibitory conductances show two peaks, one for short stimuli and one for long stimuli. For cells that did not exhibit length tuning (D), these trends were not observed.

Fig. 6.

Length tuning of membrane potential and input conductance in 26 cells. A, B, Mean potential, conductance, and excitatory and inhibitory components of conductance for two complex cells. Format is identical to Figure4B. Error bars for both cells are almost entirely covered by data points. C, Average potential and conductance responses in a population of 17 cells showing length tuning. In each cell, the mean and modulation responses are added for each of the four graphs and normalized to have peak 1 and baseline 0. Normalized traces for each of the four graphs were then averaged for all 17 cells. Error bars corresponding to SEM for cells are covered by data points.D, Average potential and conductance responses in a population of nine cells not showing length tuning. Error bars corresponding to SEM for cells are covered by data points.

The effects of stimulus contrast

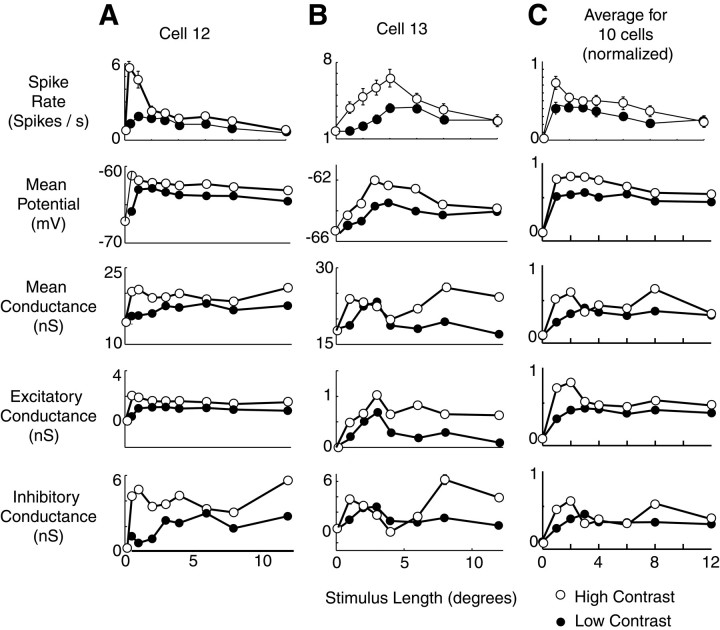
To assess the effects of stimulus contrast on conductance profiles of visual cortical neurons, we performed the measurements of Figure 6in 10 neurons for both high- and low-stimulus contrast, chosen from the linear range of the contrast response curves of the cells (see Materials and Methods). Our results are consistent with previous reports (Jagadeesh and Ferster, 1990; Sengpiel et al., 1997; Sceniak et al., 1999) that optimal length decreases and length tuning becomes more pronounced as stimulus contrast increases (Fig.7). The same two patterns of conductance shown in Figures 4 and 6 appear to underlie the contrast dependence of length tuning. In the first cell (A), a decrease in excitation and perhaps an additional inhibitory conductance at 12° correspond to the length tuning observed in the membrane potential response. In the second cell (B), a contrast-sensitive inhibitory response to long stimuli appears to be the dominant explanation behind the more pronounced length tuning seen at high contrast. When responses were averaged across the population of cells as in Figure 6, two contrast-sensitive changes in conductance are observed: an increase in excitatory conductance primarily for short stimuli and an increase in inhibition both at short stimuli (corresponding to the excitatory increase) and at long stimuli. These two effects, combined, explain the increase in length tuning observed in response to high-contrast stimuli.

Fig. 7.

Effect of stimulus contrast on length tuning of membrane potential and conductance. A, B, Mean potential, conductance, and excitatory and inhibitory components of conductance for two complex cells at high (open circles) and low (filled circles) contrast. Format is identical to Figure 4B, except that two contrast levels are shown. For both cells, high contrast was 64%, and low contrast was 16%. C, Average potential and conductance responses at high and low contrast in a population of 10 cells. Mean spike rate, membrane potential, input conductance, and excitatory and inhibitory components of conductance are shown. Traces were first normalized for each cell as in Figure 5 and then averaged across cells. High contrast among the cells ranged from 30 to 64%, and low contrast ranged from 8 to 16%.

DISCUSSION

Numerous previous studies have characterized length tuning in the visual cortex by comparing spike responses of various stimuli (Blakemore and Tobin, 1972; Dreher, 1972; Maffei and Fiorentini, 1976;Fries et al., 1977; Gilbert, 1977; Rose, 1977; Sillito, 1977; Sillito and Versiani, 1977; Kato et al., 1978; Nelson and Frost, 1978; Orban et al., 1979a,b; Albus and Fries, 1980; Yamane et al., 1985; Bolz and Gilbert, 1986; Tanaka et al., 1987; Born and Tootell, 1991; von der Heydt et al., 1992; DeAngelis et al., 1994; Sengpiel et al., 1997,1998; Sceniak et al., 1999; Dragoi and Sur, 2000). We have combined intracellular recording with current injection to measure directly the conductance and membrane potential events underlying length tuning. We found that membrane potential responses to rectangular drifting grating stimuli of varying length are tuned for stimulus length, as are spike responses in many cortical neurons. An apparent iceberg effect, however, amplifies the length tuning observed in the membrane potential responses by 30–50% to generate more dramatic length tuning in spike responses.

Measurements of input conductance and derived values for excitatory and inhibitory components of conductance further revealed that excitatory conductance is almost invariably higher for short stimuli close to the preferred length than for longer stimuli. The high excitatory conductance observed in response to short stimuli is generally accompanied by an increase in inhibitory conductance as well (Anderson et al., 2000), which may serve as a gain control mechanism. As length increases beyond the optimal length, both excitatory and inhibitory conductance responses drop. In response to even longer stimuli, an increase in inhibitory conductance is observed in some cells that also contributes to length tuning. Both the high conductance seen in response to short stimuli and the inhibitory conductance seen in response to long stimuli grow with contrast. This contrast dependence can explain the observation that optimal length decreases and magnitude of length tuning increases with stimulus contrast (Jagadeesh and Ferster, 1990; Sceniak et al., 1999).

Our results have several implications for the connectivity and local processing of cortical neurons. First, a drop in excitatory conductance with stimulus length is inconsistent with a cortical circuit that relies on spatial summation of a response over the receptive field of a neuron. Such a drop requires that synaptic inputs that are active in response to a short stimulus cease to be active as the stimulus lengthens and suggests a much more nonlinear picture of cortical processing, highly dependent on stimulus context. In particular, our results contradict a difference-of-Gaussians model for length tuning that assumes increased conductance with increased stimulus size as more synaptic inputs are recruited. It is also possible that a drop in excitatory conductance with stimulus length may reflect a precortical mechanism, such as might occur if cells in the lateral geniculate nucleus were suppressed by stimuli outside their receptive fields (Rose, 1979; Cleland et al., 1983; Murphy and Sillito, 1996). More likely, however, would be a mechanism in which cortical excitatory inputs from cells that are themselves length-tuned resulted in a decrease in excitation with stimulus length.

Second, our results also indicate two distinct stimulus conditions under which inhibition emerges. In response to small stimuli, inhibition appears to coincide closely with strong excitation, perhaps serving as a gain control mechanism. Such a role would be consistent with local disynaptic inhibitory circuits that are ubiquitous throughout the cortex (Ferster and Lindström, 1983; Martin and Whitteridge, 1984; Hirsch and Gilbert, 1991). In response to longer stimuli, secondary conductance increases were seen in some cells and were primarily inhibitory in composition. In a few cells (Figs.4B, 6A), a small increase in excitatory conductance accompanied this inhibitory increase. This effect may be attributable to either an incomplete separation of excitatory and inhibitory currents or the effects of inhibition on other excitatory inputs to the cell. Increases in inhibition in response to long stimuli support previous reports of inhibition in the receptive field surround (Orban et al., 1979a,b; DeAngelis et al., 1994) and are at odds with a mechanism for length tuning that relies solely on excitatory inputs (Skottun, 1998).

A third implication of our results on cortical connectivity relates to the function of horizontal connections in the cortex. Ultimately, a neuron that is tuned for stimulus length requires information from outside its immediate column. The putative mechanism for such interactions is horizontal connections, which can connect adjacent columns with similar orientation preferences (Gilbert, 1992; Weliky et al., 1995). Horizontal connections have been found to consist primarily of excitatory connections, but when strongly stimulated, generate a disynaptic inhibitory response that dominates the excitatory input (Hirsch and Gilbert, 1991). The inhibitory conductances in response to long stimuli in our data may reflect precisely such a mechanism of inhibition mediated by horizontal connections. This conclusion is supported by the finding that suppression of responses from contextual stimuli outside the receptive field of a neuron is contrast-dependent (Levitt and Lund, 1997) in the same manner as the inhibitory conductance generated by long stimuli in our data.

Fourth, our data suggest that inhibitory conductances produced in response to long stimuli are operative only over a limited range of stimulus lengths. For most cells in which inhibitory conductances were seen in response to long stimuli, such conductances peaked in response to stimuli of ∼8° length and decreased for longer stimuli. This effect may be explained by proposing that, as a stimulus lengthens beyond its own column, suppressive effects from adjacent columns may be realized. As stimulus length increases further, however, these suppressive effects may be mitigated as the adjacent columns in turn are suppressed by still more distant columns.

Finally, the results of the present study constrain the possible mechanisms for the contrast dependence of length tuning. Sceniak et al. (1999) first noted that the decrease in optimal length and increase in magnitude of length tuning with contrast could be explained by a difference in the spatial summation of excitation with contrast. Our data confirm this finding; excitatory conductance in most cells is highly contrast-sensitive for short stimulus lengths and increases disproportionately with contrast in response to short-length stimuli. We also see an additional effect of contrast-sensitive inhibition in response to long stimuli. Both an increase in excitatory conductance in response to short stimuli and an increase in inhibitory conductance in response to long stimuli help explain the observed changes in length tuning with contrast. Moreover, these changes in length tuning with contrast may have a computational function of allowing more precise localization of stimuli at high contrast without the sacrifice of a very low detection threshold for longer stimuli at low contrast (Sceniak et al., 1999).

Although useful in constraining possible mechanisms underlying membrane potential and spike responses, our conductance data are subject to several limitations. First, because we are presumably recording in the soma, it is possible that important computations performed in the dendrites may be invisible to our electrode. A related concern is that the space clamp in an in vivo preparation may be inadequate; injected current may not fully reach dendrites in which synaptic inputs are integrated. This may result in underestimation of input conductance. Another possible source of bias in our results lies in the use of only two synaptic conductances, one excitatory and one inhibitory, and the choice of their equilibrium potentials in our model. The excitatory equilibrium potential may, in fact, underestimate the true value at the soma because of inadequacy of the space clamp forin vivo whole-cell recordings. Raising this value would have the effect of decreasing the relative amplitude of excitatory conductance and increasing the relative amplitude of inhibitory conductance but would not substantively change the qualitative patterns for inhibitory and excitatory conductances in our data. We are encouraged by the fact that changing values of excitatory and inhibitory equilibrium potentials by 10 mV does not significantly affect the predictions of excitation and inhibition (Anderson et al., 2000). In particular, the basic conclusions of our study are unchanged when a value for V_i of −70 mV is used. Although the two-conductance model we use is very simple and does not take into account the contributions of NMDA receptors or intrinsic voltage-dependent conductances, it allows reasonable estimation of qualitative patterns of synaptic excitation and inhibition useful in deducing intracellular mechanisms (Anderson et al., 2000).

An understanding of the synaptic mechanisms underlying length tuning may yield information about a number of other cortical phenomena. Cortical gain control and contrast adaptation may be affected by the size of a stimulus (Ohzawa et al., 1985; Carandini and Heeger, 1994;Sceniak et al., 1999). Contextual modulation of stimuli, such as is postulated to occur in length tuning, has also been proposed to underlie psychophysical phenomena of feature linking (Kapadia et al., 1995; Polat et al., 1998), figure–ground separation (Zipser et al., 1996), and optical illusions such as illusory contours and perceptual fill-in (Gilbert, 1998). It is possible that these phenomena may be mediated by many of the same synaptic mechanisms operative in length tuning in primary visual cortex.