Long-Range Cortical Synchronization without Concomitant Oscillations in the Somatosensory System of Anesthetized Cats

Abstract

To determine whether neuronal oscillations are essential for long-range cortical synchronization in the somatosensory system, we characterized the incidence and response properties of gamma range oscillations (20–80 Hz) among pairs of synchronized neurons in primary (SI) and secondary (SII) somatosensory cortex. Synchronized SI and SII discharges, which occurred within a 3 msec period, were detected in 13% (80 of 621) of single-unit pairs and 25% (29 of 118) of multiunit pairs. Power spectra derived from the auto-correlation histograms (ACGs) revealed that ∼15% of the neurons forming synchronized pairs were characterized by oscillations. Although 24% of the synchronized neuron pairs (19/80) were characterized by oscillations in one or both neurons, only 1% (1/80) of these pairs displayed oscillations at the same frequency in both neurons. Similar results were observed among pairs of multiunit responses. When single-trial responses were analyzed, the vast majority of responses still did not exhibit oscillations in the gamma frequency range. These results suggest that separate populations of cortical neurons can be bound together without being constrained by the phase relationships defined by specific oscillatory frequencies.

A major issue in systems neuroscience concerns whether cortical synchronization is a mechanism for linking distributed populations of neurons that represent distinct attributes or features of a unitary stimulus (von der Malsburg, 1994;Singer and Gray, 1995; Singer et al., 1997). Although considerable controversy surrounds the view that cortical synchronization solves some of the coding problems associated with sensory perception (Ghose and Maunsell, 1999; Gray, 1999; Shadlen and Movshon, 1999; Singer, 1999), the data indicating that sensory stimulation evokes correlated activity in local regions of cortex are indisputable. In primary visual cortex, for example, adjacent groups of neurons with similar stimulus preferences exhibit correlated activity in response to an optimal stimulus that appears in their receptive fields (RFs) (Ts'o et al., 1986; Gray et al., 1989; Engel et al., 1991b; Livingstone, 1996). Furthermore, a growing body of evidence in other sensory systems demonstrates that cortical populations with similar response properties become synchronized during certain stimulus conditions (Dickson and Gerstein, 1974; Metherate and Dykes, 1985; Ahissar et al., 1992;Eggermont, 1992, 1994; deCharms and Merzenich, 1996; Swadlow et al., 1998; Roy and Alloway, 1999; Steinmetz et al., 2000).

Part of the controversy surrounding the temporal binding hypothesis concerns whether oscillations are necessary for mediating long-range cortical synchronization (Gray, 1999; Shadlen and Movshon, 1999). Support for this view comes from studies indicating that gamma frequency oscillations (20–80 Hz) are prevalent in stimulus-induced cortical responses that are synchronized across distances >2 mm (Eckhorn et al., 1988; Gray and Singer 1989; Konig et al., 1995; Murthy and Fetz, 1996a,b). Other studies, however, report that only a small fraction (<20%) of cortical spike trains contains oscillatory activity in the gamma frequency range (Tovee and Rolls, 1992; Young et al., 1992; Bair et al., 1994; Nowak et al., 1995; Gray and Viana Di Prisco, 1997). To some extent, discrepancies in the incidence of oscillatory activity may reflect the possibility that stimulus-induced oscillations are transitory and, therefore, more difficult to detect when responses are summed across several blocks of trials (Ghose and Freeman, 1992; Livingstone, 1996; Murthy and Fetz, 1996b; Gray and Viana Di Prisco, 1997). Nonetheless, the low incidence of cortical oscillations in many studies has led some to argue that long-range correlations are rare and contribute very little to perception (Shadlen and Movshon, 1999). Furthermore, it has been argued that even if cortical oscillations were prevalent, the number of independent neuronal assemblies that could be linked by oscillatory activity is limited. Synchronous activity is sometimes portrayed by paired events transpiring over intervals lasting ≥10–20 msec (Gray and Singer, 1989; Engel et al., 1991b; Murthy and Fetz, 1996b; Brecht et al., 1998), and the duration of these intervals would interfere with the possibility of simultaneously maintaining multiple phase relationships. According to this line of reasoning, the temporal binding hypothesis appears implausible unless long-range cortical synchronization can occur within extremely short time intervals lasting no more than 4 msec (Shadlen and Movshon, 1999).

To determine whether neuronal oscillations are essential for long-range cortical synchronization in the somatosensory system, we analyzed the temporal structure of stimulus-induced neuronal responses recorded simultaneously in the forepaw representations of primary (SI) and secondary (SII) somatosensory cortical areas. These regions are located in different gyri and are separated by at least 10 mm (Alloway and Burton, 1985). In contrast to studies that assessed the incidence and strength of oscillations independent of synchronization, our analysis was limited to neuronal pairs that showed significant levels of synchronization. Our results indicate that long-range cortical synchronization may occur within narrow time periods without concomitant neuronal oscillations in the gamma frequency range.

MATERIALS AND METHODS

Experiments on four adult cats followed National Institutes of Health guidelines for the use and care of laboratory animals. Most procedures are briefly described here because they have been described previously (Johnson and Alloway 1996; Roy and Alloway, 1999). Sterile techniques were used to implant a stainless steel recording chamber onto the cranium overlying SI and SII cortex. A stainless steel bolt was attached to the occipital ridge to immobilize the animal's head during recording sessions. Extracellular recordings from SI and SII were performed two times per week for 2–4 months. During recording sessions the animals were ventilated through an endotracheal tube with a 2:1 gaseous mixture of nitrous oxide and oxygen containing 0.5–0.75% isoflurane. Heart rate and end-tidal CO₂ were monitored continuously, and body temperature was maintained at 37°C by thermostatically controlled heating pads. This preparation was similar to the anesthetized preparations used to characterize neuronal oscillations in the visual system (Gray and Singer, 1989; Engel et al., 1990; Ghose and Freeman, 1992; Gray and Di Prisco, 1997).

The final experimental session was terminated by an intravenous injection of 30 mg of pentobarbital sodium. The animal was transcardially perfused with 500 ml of 0.9% saline containing 20 mg of lidocaine and 1000 USP U of heparin, followed by 500 ml of neutral formalin and then 500 ml of neutral formalin in 10% sucrose. The brain was removed and placed in fixative and 30% sucrose until it sank. The cortex was blocked, frozen, and cut into 50 μm coronal sections that were mounted onto chrom–alum-coated slides and stained with thionin.

Electrophysiology. Arrays of two to eight tungsten electrodes (2–5 MΩ; Frederick Haer) with 250–400 μm separation between adjacent electrodes were used to record multiple neurons in SI and SII cortex simultaneously. After placing one electrode array in the forelimb representation of SII cortex at a 50° angle to the parasagittal plane (Alloway and Burton, 1985), the second electrode array was advanced into the SI forelimb representation at a 25° angle (Felleman et al., 1983). In both regions, electrodes were advanced until neurons were encountered that responded to air-jet stimulation. Electrode recording depths were consistent with neurons in layers III and IV. RF boundaries of the recorded neurons were determined by stimulating the hairy skin with an air jet while each channel was monitored over an acoustic speaker. Extracellular waveforms were digitized, time stamped, and stored for off-line analysis (DataWave Technologies, Broomfield, CO). The digitized waveforms were sorted on the basis of multiple parameters (width, amplitude, time of maximum and minimum potentials, etc.) and used to construct peristimulus timed histograms (PSTHs), cross-correlation histograms (CCGs), and autocorrelation histograms (ACGs).

Cutaneous stimulation. We recorded only neurons that displayed cutaneous responses to moving the fine hairs on the distal forelimb. Neurons that responded to stimulation of the glabrous skin or the claws or to intense stimuli such as tapping, kneading, or pinching the skin were never recorded. While searching for air jet-sensitive neurons in SI and SII, we used a fine brush or a hand-held air jet to stimulate the hairy skin.

Previous work has shown that moving air jets consistently activate mechanoreceptors of the hairy skin without producing the lateral distortions caused by dragging a probe across the skin (Ray et al., 1985). We showed previously that somatosensory cortical neurons respond better to moving air jets than to stationary air jets (Roy and Alloway, 1999), and therefore we used computer-controlled moving air jets to activate cortical neurons in SI and SII. A modified Grass polygraph pen module, in which the ink pen was replaced with an air-jet tube, was used to deliver moving air jets to the hairy skin. Air flow through the tube was controlled by an electronic valve that was gated by the data acquisition system (DataWave Technologies). Air pressure during stimulation was held constant to 20 psi by a needle valve in series with a pressure gauge. The motion of the air-jet tube was controlled by a 1 Hz sine wave output from a function generator that lasted 3 sec so that the skin was stimulated three times in each direction. The trajectory of the air jet extended across the entire length of the combined RFs, typically a distance of 3–7 cm, and this corresponded to a velocity range of 6–14 cm/sec. A portion of the air-jet trajectory sometimes stimulated the glabrous skin, but in most instances the air jet was located so that its entire trajectory was over hairy skin. Air-jet stimuli were presented in blocks of 100–300 trials. Each trial consisted of a prestimulus period (2 sec), a stimulus period with the moving air jet (3 sec), and then a poststimulus period (3 sec). Intervals between trials were ∼2 sec in duration.

Cross-correlation analysis. Cross-correlation analysis was performed on neuron pairs in which both neurons discharged at least 12 times per stimulation period for an average rate of four discharges per second. Although this rate is below the gamma frequency range (20–80 Hz), a neuron discharging at least 12 times in a 3 sec period can easily display gamma range oscillations if the discharges occur at interspike intervals of 50 msec or less.

Raw CCGs were constructed to display changes in target neuron activity as a function of reference neuron discharges occurring at time 0 (Perkel et al., 1967). Stimulus coordination effects were removed by subtracting a linear shift predictor from the raw CCG to produce a neural CCG (Alloway et al., 1994; Johnson and Alloway, 1996; Roy and Alloway, 1999). The shift predictor was used to calculate 99% confidence limits, and peaks in the neural CCG that exceeded the 99% confidence limits were regarded as statistically significant (Aertsen et al., 1989; Gochin et al., 1989). Although neural CCGs were used initially to establish the statistical significance of synchronized activity, the rate and strength of neuronal synchronization were measured from the raw CCGs because these represent all of the events that are available for sensory processing.

The proportion of correlated activity among pairs of neurons can be estimated by the correlation coefficientρ(τ). The formula for calculating the cross-correlation coefficient was similar to the formula used byEggermont (1992):

$$\rho (\tau )=\frac{[CE]}{\sqrt{\{[N_T-((N_T{)}^2/T)·\mathrm{\Delta }]\ast [N_R-((N_R{)}^2/T)·\mathrm{\Delta }]\}}},$$

where Δ represents the bin size over which the coefficient is evaluated (3 msec), CE is the number of coincident events in the highest 3 msec period of the raw CCG peak, T is the time interval over which the CCG was calculated, andN_T andN_R represent the total number of discharges from the target and reference neurons during T. In contrast to studies in which CE represents the number of coincident events in the neural CCG (Eggermont, 1992), we measuredCE in the raw CCG. This modification meant that our correlation coefficients represent the portion of all activity that was correlated, not just the portion exceeding the expectation density.

The correlation coefficient indicates the proportion of activity that is correlated but does not indicate the overall rate of coincident events. Therefore, we also calculated the rate of coincident events in SI and SII to provide another measure of synchronization strength during spontaneous and stimulus-induced activity. Synchronization rate was determined by counting the number of coincident events in the tallest 3 msec period of the raw CCG peaks generated from spontaneous or stimulus-induced activity. These sums were then divided by the amount of time over which spontaneous or stimulus-induced responses were recorded (Roy and Alloway, 1999). The spontaneous rates were always based on the 2 sec prestimulus periods; the stimulus-induced rates were based on the portion of the stimulation cycle in which both neurons responded simultaneously to cutaneous stimulation.

Analysis of neuronal oscillations. Neurons displaying synchronized activity were carefully examined for the presence of gamma oscillations in their discharge sequence. As in previous reports on stimulus-induced oscillations, we estimated an empirical power spectrum by computing the fast Fourier transform (FFT) of the neuronal ACGs derived from the stimulus-induced responses (Ghose and Freeman, 1992;Gray and Viana Di Prisco, 1997). All ACGs were constructed with a time lag of 0–256 msec and a bin width resolution of 1 msec. A power spectrum derived from an ACG with these parameters has a maximum frequency of 500 Hz and a bin resolution of 3.9 Hz.

When an FFT is computed on a Gaussian white noise sequence, the resulting power spectra should be relatively flat and show random variations around a mean value. In some cases, as shown in Figure1, the power spectrum that was derived from the raw ACG contained a broad DC low-frequency component that resembled non-white noise. These low-frequency components were wider than the low-frequency signals appearing in the power spectra of earlier studies on the visual system (Ghose and Freeman, 1992; Gray and Viana Di Prisco, 1997), possibly because our cortical responses were correlated with low-frequency hair movements evoked by the air-jet stimulus. In any event, peaks in the 20–35 Hz range often appeared just above the confidence limits (see below) of the power spectrum, but it was unclear whether these peaks represented significant amounts of oscillatory power at a specific frequency or whether they simply exceeded the confidence limits because they were superimposed on a non-white low-frequency noise component. Therefore, we used well established techniques in signal processing to adjust the ACG so that we could analyze its gamma frequency components independent of effects caused by low-frequency spectral leakage (Oppenheim and Schafer, 1989). First, the impulse-like peak of the ACG near t = 0 (up to 6 msec) was removed because this narrow peak contains broad band spectral energy, including low-frequency components. Removal of time intervals representing the first 6 msec of the ACG, however, should not affect the power of gamma range signals, because these intervals represent high-frequency neuronal bursting (>165 Hz). Second, the mean bin height of the original ACG was calculated and subtracted (Oppenheim and Schafer, 1989). In addition, any linear trend in the ACG was removed by subtracting a least squares regression line (Oppenheim and Schafer, 1989). These adjustments produced a truncated ACG that was considerably flatter than the original ACG but with the same temporal rhythms that were apparent in the original pattern (Fig. 1, first panel). Power spectra estimates were computed from the resulting truncated ACG with the use of a Hamming window to further reduce spectral leakage (Oppenheim and Schafer, 1989).

Fig. 1.

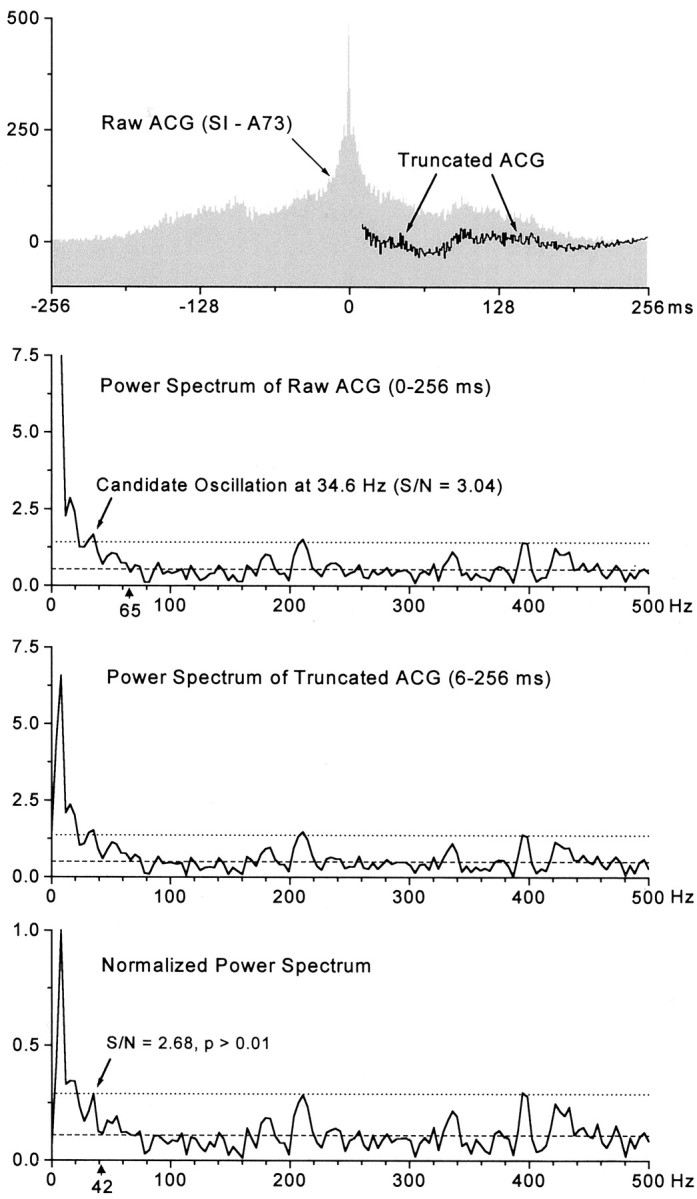
Method for detecting neuronal oscillations.Top panel, Raw and truncated ACGs for a spike train recorded in SI (A73). With the exception of the impulse peak at time 0, the same rhythmic patterns are present in both the raw and truncated ACGs. Second panel, Power spectrum of the raw ACG contains a large DC component that gradually merges into the gamma frequency range (20–80 Hz). Although power fluctuates randomly around the noise level (dashed line) at frequencies >65 Hz (arrowhead), a peak at 34.6 Hz exceeded the confidence limits (dotted line) and had a signal-to-noise ratio of 3.04. This small peak may have exceeded the confidence limits because it was superimposed on the trailing edge of an elevated low-frequency trend. Third panel, Power spectrum of the truncated ACG contained a much smaller DC component, but the low-frequency trend was still present. Bottom panel, The normalized power spectrum contained fluctuations around the noise level at frequencies as low as 42 Hz (arrowhead). After normalization, the small peak at 34.6 Hz failed to exceed the confidence limits, and its signal-to-noise ratio decreased to 2.68. Statistical analysis indicated that the distribution of values in the gamma frequency range of the normalized power spectrum was not significantly different from a Gaussian white noise distribution having the same mean value (KS test;p > 0.01).

Despite these adjustments to the ACGs, a few of the resulting power spectra still contained broad, low-frequency components that suggest the presence of colored or non-white noise (Fig. 1, third panel). Many types of noise, including Gaussian white noise, can be characterized using an ideal power law model of the following form: power = cf * Frequency^-αwhere cf determines the overall power and α determines spectral balance (Veitch and Abry, 1999). Thus, in cases where the power spectra of the truncated ACGs contained elevations in the low-frequency range, we estimated the cf and α parameters from the truncated ACGs. Most of these ACGs exhibited good fits to this power law model (χ² values >0.1) and had α values greater than zero, which suggests that their power spectra did not reflect Gaussian white noise. The presence of non-Gaussian noise in a power spectrum precludes the use of parametric measures such as variance to evaluate statistical significance. However, non-Gaussian spectra can be converted to Gaussian spectra by a standard normalization technique (Brockwell and Davis, 1991). Specifically, the non-white power spectra were divided by the theoretical power law spectra so that the resulting normalized spectra, which varied around a value of 1, resembled Gaussian white noise sequences (Brockwell and Davis, 1991). These normalized power spectra were further normalized by defining the largest peak as having a value of 1. Figure 1 shows how these adjustments affect the resulting power spectrum estimate and the classification of the neuronal spike train as oscillatory or non-oscillatory (Fig. 1, compare second,third, and bottom panels).

After power spectra that resembled white noise were obtained, those that contained peaks in the gamma frequency range (20–80 Hz) were subjected to both parametric and nonparametric statistical analysis to determine whether the peaks were likely to be significant. Previous reports assumed that the 250–500 Hz region of the power spectrum reflects Gaussian noise in the spike train (Ghose and Freeman, 1992;Gray and Viana Di Prisco 1997). As in these previous reports, we identified potential oscillations by constructing confidence limits that were equal to the mean plus 3 SDs of the values appearing in the 250–500 Hz portion of the power spectrum. These confidence limits were displayed on the power spectra of the truncated ACGs and, if necessary, on the normalized power spectra. If peaks in the 20–80 Hz range exceeded the confidence limits, then the nonparametric Kolmogorov–Smirnov (KS) test was used to evaluate the statistical significance of candidate oscillations by comparing them with a uniformly flat, ideal power spectrum having the same mean value as the “whitened” spectra (Brockwell and Davis, 1991). Peaks that were superimposed on distributions that differed significantly from the ideal power spectrum (p < 0.01; KS test) were classified as oscillatory.

We also analyzed CCGs to determine whether the relative timing of activity across SI and SII was characterized by oscillatory patterns. The procedure for analyzing oscillations in the CCGs was the same as that used to analyze the ACGs except that the CCGs were not truncated, and the analysis was conducted over all events in the CCG extending from −256 msec to +256 msec.

Simulated ACGs. To determine the sensitivity of our method for detecting neuronal oscillations within a block of 100 trials, we generated artificial ACGs to simulate spike trains, the time series of which represented either white noise or an oscillating signal (60 Hz) superimposed on a background of white noise. We treated the resulting ACGs as if they represented the neuronal response of a single trial and then combined the noise-plus-signal ACGs with the noise-alone ACGs in various proportions to represent an ACG constructed from a block of 100 trials. This resulting ACG was then examined for the presence of oscillations as described in the preceding section. This process was repeated using different proportions of the noise and the signal-plus-noise ACGs so that we could determine how many signal-plus-noise ACGs were needed in a block of 100 trials to detect an oscillating signal with the statistical criteria described in the preceding section.

For these procedures, Gaussian white noise and sinusoidal oscillations were generated using S-PLUS 2000 and S-PLUS Wavelets (MathSoft, Cambridge, MA). White noise was produced by using a wavelet-based synthesis method in which random, normally distributed discrete wavelet transform coefficients were generated at various resolution levels (Wornell, 1995). These coefficients were then summed together, and the summed coefficients were converted to a times series by an inverse wavelet transform. Thus, the white noise time series was generated by the following lines of S-PLUS 2000 code: noise.dwt <- dwt(rep(0,1024)); noise.dwt [c(“d1,” “d2,” “d3,” “d4,” “d5,” “d6”)] <- rnorm (512,256,128,64,32,16); noise <- reconstruct(noise.dwt).

The resulting noise exhibited a relatively flat, randomly fluctuating power spectrum when we analyzed it for oscillations by using the methods described in the preceding section. In addition, a pure sinusoidal signal was synthesized in S-PLUS Wavelets using the make-signal command: tone <- make.signal(“losine”,n = 1024).

The resulting sinusoidal signal was multiplied by a factor of 2, 4, or 8 to generate a total of four sinusoidal signals that had the same frequency but different amplitudes. The white noise generated earlier was then added to each sinusoidal signal to generate a simulated ACG. All of the ACGs, including the noise-alone ACG and the four signal-plus-noise ACGs, were scaled so that they all contained an equal number of discharges.

RESULTS

Air jet-sensitive responses containing at least 12 discharges per stimulus were recorded from 228 neurons in SI and 314 neurons in SII. From this sample, the number of neuron pairs recorded simultaneously in SI and SII totaled 621. Using 99% confidence limits, cross-correlation analysis revealed significant levels of stimulus-induced synchronization in 80 SI–SII neuron pairs or 13% of the total sample. Some neurons participated in several synchronized pairs, and the constituent neurons of all 80 synchronized pairs included 67 neurons in SI and 69 neurons in SII.

Pairs of neurons displayed synchronized activity only if their RFs were highly similar. The vast majority of neuron pairs that did not display synchronized responses had RFs that were nonoverlapping. In most cases of SI–SII synchronization, both neurons shared at least one-half of their RFs. Typically, the RF of the SI neuron was located on the ventral surface of one or two digits, whereas the RF of the SII neuron was larger and completely surrounded the RF of the SI neuron. The only exception to this occurred in experiments in which the SI neurons had larger RFs because they were located in the wrist representation of SI cortex (Felleman et al., 1983).

Synchronization of single-unit activity in SI and SII

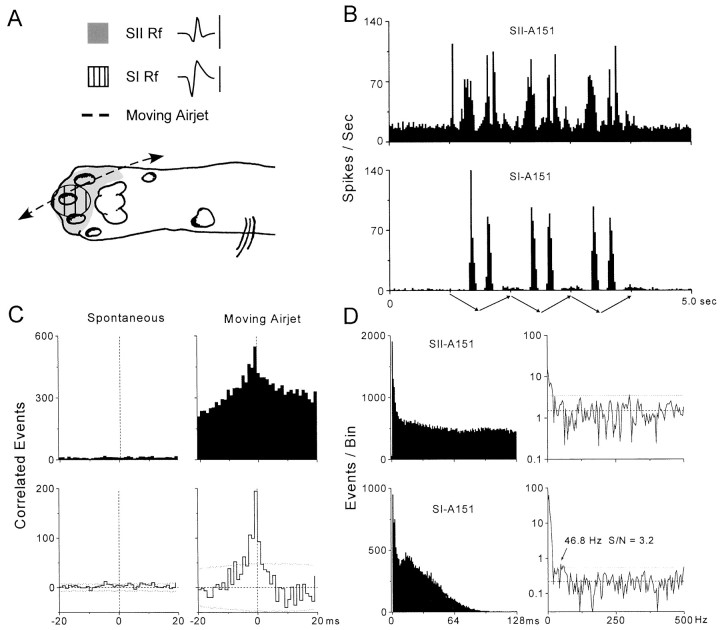
An example of long-range synchronization in SI and SII cortex is illustrated in Figure 2. As indicated by the RF drawings and PSTHs, neurons SI-A151 and SII-A151 had overlapping RFs on the distal forepaw and responded to air jets that traversed the hairy skin of their RFs. In this case, the RF for the SI neuron extended across the ventral surface of digit 3 and was completely encompassed by the RF of the SII neuron, which included the ventral surface of digits 2, 3, and 4. Consistent with this fact, comparison of the PSTHs indicates that the response of the SI neuron was restricted to a smaller portion of the stimulus cycle than the response of the SII neuron (i.e., 825 msec of the entire stimulation period). Furthermore, because we used a large, periodic air jet to stimulate relatively small RFs, both neurons displayed low-frequency components in their response pattern as indicated by prominent peaks appearing every 200–700 msec in the PSTHs. The amplitudes of the PSTH peaks show that the maximum response rate of both neurons was ∼70–90 spikes per second, and this demonstrates that much of the stimulus-induced activity occurred within the gamma frequency range (20–80 Hz).

Fig. 2.

Synchronized activity in a pair of SI and SII neurons in which one neuron contained weak oscillations in the gamma frequency range. A, Extracellular waveforms and receptive fields for a pair of simultaneously recorded neurons in experiment A151. The waveforms represent the average shape of all discharges recorded during spontaneous and stimulus-induced activity as shown in B. Trace duration: 1.5 msec; calibration: 50 μV for SII, 100 μV for SI. Drawing of the distal forepaw illustrates the trajectory of the 1 Hz moving air jet as it crosses the overlapping receptive fields of each neuron. B, PSTHs illustrating spontaneous and stimulus-induced responses across 300 trials. The arrows below the bottom PSTH illustrate the back-and-forth motion of the air jet as it repeats three consecutive 1 Hz cycles. Bin widths, 25 msec. C, Raw (top) and shift-corrected (bottom) CCGs displaying correlated discharges recorded during spontaneous and stimulus-induced activity. Dotted lines in the shift-corrected CCGs indicate 99% confidence limits. Bin widths, 1.0 msec. D, Raw ACGs (left) constructed from stimulus-induced responses during the moving air jet. Although the ACGs were constructed over lag intervals of 256 msec, only the first 128 msec are displayed to facilitate detection of oscillations occurring in the gamma frequency range (20–80 Hz). Neuron SI-A151contains a small peak at 14–24 msec that corresponds to a frequency of 41–71 Hz. Analysis of the power spectra (right) derived from the truncated ACGs revealed a significant oscillatory component at 46.8–58.6 Hz (KS test; p < 0.007) for neuronSI-A151. ACG bin widths, 1.0 msec; power spectra bin widths, 3.9 Hz. Dashed and dotted linesin the power spectra indicate mean noise and confidence limits (i.e., mean noise plus 3 SDs), respectively.

Cross-correlation analysis revealed that both neurons exhibited substantial amounts of synchronized activity during air-jet stimulation but not during prestimulus periods (Fig. 1C). Thus, the neural CCG constructed from the stimulus-induced responses contained a tall peak at time 0 that was ∼12 msec in duration at its base and 4 msec in duration at half its peak height. Based on the number of coincident events occurring within the peak of the raw CCG and the duration of simultaneous responses in both neurons, the synchronization rate was 5.4 coincident events per second. The correlation coefficient, which provides a rough estimate of the portion of stimulus-induced activity that was synchronized, was 0.12 (or 12%) for this pair of neurons. These indices of synchronization strength indicate that this pair of neurons was among the most highly synchronized pair of neurons that we recorded in our sample.

Analysis of the ACGs and corresponding power spectra indicated that one of the neurons (SI-A151) contained relatively weak oscillations in the gamma frequency range and that both neurons contained stronger oscillations in the low-frequency range (Fig. 1D). Thus, a small peak in the ACG for the SI neuron was apparent at a time lag of 14–24 msec. Computation of the power spectrum from the truncated ACG revealed a small peak (ranging from 46.8 to 58.6 Hz) with a signal-to-noise ratio (3.2) that barely exceeded the confidence limits calculated from randomly fluctuating values between 250 and 500 Hz. Because this power spectrum appeared to consist primarily of white noise (note the presence of valleys extending to the mean noise level at frequencies below 46 Hz), computation of the normalized power spectrum was not necessary. Statistical analysis of the distribution of values in the gamma frequency range confirmed that these values were significantly different from an idealized power spectrum (p < 0.0077; KS test). The ACG and power spectrum for the other neuron (SII-A151) did not contain oscillations in the gamma frequency range, but the power spectra for both neurons contained obvious peaks at 4–8 Hz. In addition to representing possible spectral leakage from the DC component, these low-frequency peaks are consistent with the fact that the PSTHs for both neurons contained rhythmic patterns that correspond to the periodicity of the air-jet stimulus.

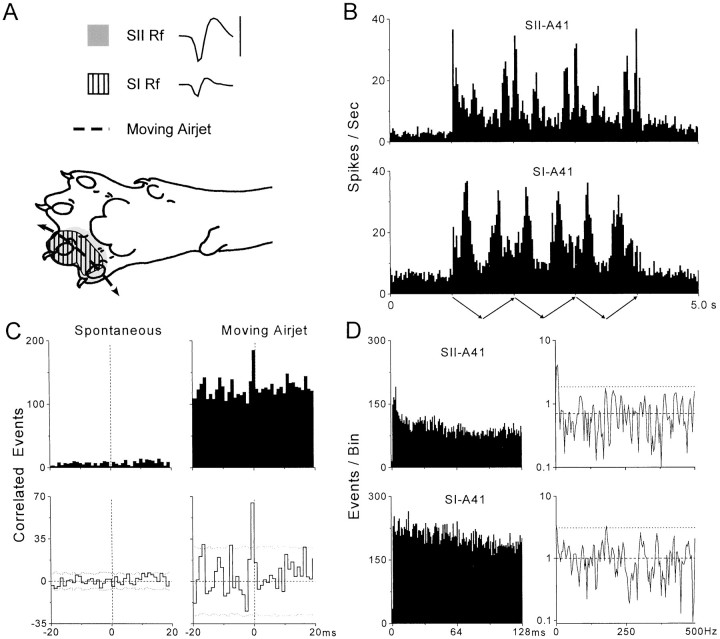
Figure 3 illustrates synchronized responses for a representative pair of SI and SII neurons (A-41) that did not oscillate in the gamma frequency range. Both of these neurons had overlapping RFs and responded vigorously as the air jet moved across their RFs in either direction. As indicated by the PSTHs, the maximum response rate of both neurons was ∼30 discharges per second, which is clearly within the gamma frequency range. Their PSTHs also displayed rhythmic patterns that correspond to the low-frequency periodicity of the cutaneous stimulus. Consistent with the fact that the RFs and response properties of these neurons were similar, the raw and neural CCGs revealed an extremely narrow peak of synchronized activity at time 0. Thus, as indicated by the neural CCG, the temporal duration of the peak half-width was only 1 msec, whereas the width of the peak at its base was only 3 msec in duration. We examined the waveforms of the neuronal discharges in SI and SII (Fig. 3A) and observed that the amplitude and shape of the waveforms were different; this effectively ruled out the possibility that the narrow peaks in the raw and neural CCGs were caused by electrical artifacts. The mean synchronization rate (0.74 coincident events per second over the entire stimulation period) and correlation coefficient (p(τ) = 0.053) for this pair of neurons placed it in the top 34% for synchronization strength when compared with all synchronized SI–SII neuron pairs.

Fig. 3.

Synchronized activity in a pair of SI and SII neurons (A-41) that did not oscillate in the gamma frequency range (20–80 Hz). Neuronal waveforms, receptive fields, and temporal patterns of spontaneous and stimulus-induced activity are illustrated as in Figure 2. In A, the waveform traces represent a duration of 1.2 msec, and the calibration bar represents 100 μV for both waveforms. The clear difference in the waveform patterns indicates that the temporal precision of synchronized activity (see C) was not caused by electrical artifacts.

Examination of the ACGs and power spectra failed to indicate the presence of gamma range oscillations in the spike trains of SI-A41 or SII-A41. The ACGs for both neurons contained substantial levels of activity at lag times (12.5–50.0 msec) that correspond to the gamma frequency range (20–80 Hz), but the fluctuations in the temporal structure of the ACGs were sporadic and did not appear to represent non-random periodicities. This belief was corroborated by the fact that the power spectra of the truncated ACGs did not contain any peaks in the 20–80 Hz range that exceeded the confidence limits. The major peak seen in both power spectra, especially for neuron SII-A41, was at a frequency of 4–8 Hz.

Synchronization of multiunit activity in SI and SII

Many studies that reported observing neuronal synchronization in the visual system were based on multiunit responses (Eckhorn et al., 1988; Gray and Singer, 1989; Engel et al., 1990; Gray et al., 1992), and this is not surprising because synchronization is easier to detect in multiunit responses than among pairs of individual neurons (deCharms and Merzenich, 1996; Bedenbaugh and Gerstein, 1997; Roy and Alloway, 1999). Therefore, we also evaluated multiunit responses in SI and SII to determine whether oscillations were more likely to be detected in the synchronized activity of small populations of neurons. Multiple isolated waveforms were recorded from a total of 99 electrodes in SI and 146 electrodes in SII; in all of these cases at least two neurons recorded by each electrode discharged at least 12 times per stimulus. Although a single electrode sometimes recorded five distinct waveforms, on average we recorded only 2.4 neurons per electrode. From this sample of multiunit responses, the number of multiunit pairs recorded simultaneously in SI and SII totaled 118. Using 99% confidence limits, cross-correlation analysis revealed significant levels of stimulus-induced synchronization in 29 pairs or 25% of the total sample. These 29 synchronized multiunit pairs were based on 24 and 28 constituent multiunit responses in SI and SII, respectively.

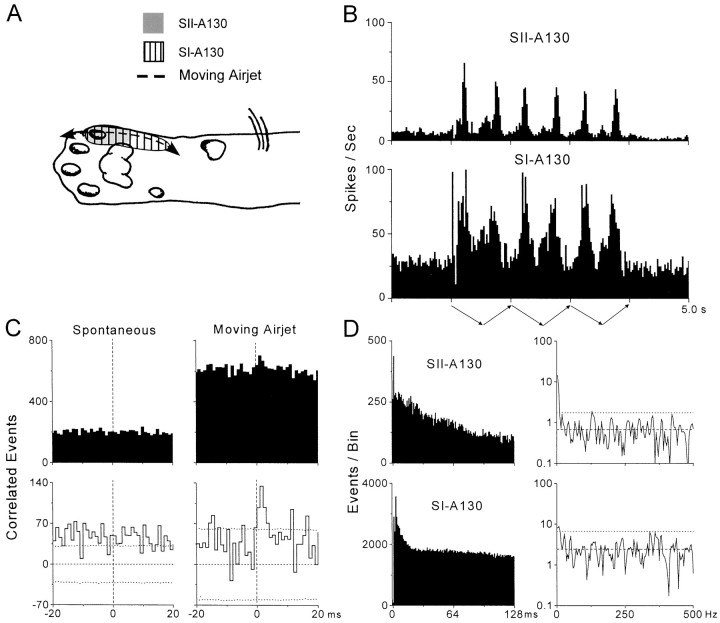
Examples of stimulus-induced multiunit responses in SI and SII are illustrated in Figure 4. Both of the SI and SII electrodes in this example recorded discharges from a pair of cortical neurons. In this particular case, the RFs of the two SI neurons (ulnar paw and wrist) completely encompassed the RFs of the SII neurons, which were restricted to digit 5. Consistent with these RF differences, the PSTHs indicate that the SII responses were restricted to a smaller portion of the stimulus cycle than the SI responses. Nonetheless, both PSTHs contained peaks at regular intervals (300–500 msec) that corresponded to the periodicity of the moving air jet. In addition, the height of these regular peaks indicates that stimulus-induced responsiveness reached a maximum rate that easily achieved the gamma frequency range for both sets of neuronal responses (up to 140 and 80 spikes per second for SI-A130 and SII-A130, respectively).

Fig. 4.

Synchronized multiunit responses in SI and SII (A-130) without concomitant oscillations. Temporal patterns of spontaneous and stimulus-induced multiunit responses are illustrated as in Figures 2 and 3. As indicated by the ACGs and power spectra in D, stimulus-induced responses in both SI and SII were devoid of oscillations in the gamma frequency range (20–80 Hz).

Cross-correlation analysis of these responses revealed substantial amounts of synchronized activity during air-jet stimulation but not during spontaneous activity (Fig. 4C). The stimulus-induced neural CCG contained a significant peak that was maximal 0–3 msec after time 0 and had a peak half-width of 4 msec. Analysis of the same 3 msec period in the corresponding peak of the raw CCG revealed a correlation coefficient of 0.25 and a mean synchronization rate of 10.9 coincident events per second over the entire stimulus period.

These stimulus-induced multiunit responses were not associated with oscillations in the gamma frequency range (Fig. 4D). Thus, the multiunit ACGs did not contain any prominent periodicities in the intervals extending up to 128 msec. Consistent with the smooth shape of the multiunit ACGs, the power spectra for the truncated ACGs did not contain any peaks between 20 and 80 Hz that exceeded the confidence limits. In fact, the only peaks in the power spectra that exceeded the confidence limits represented frequencies ∼4 Hz.

Distribution of single and multiple neuron synchronization

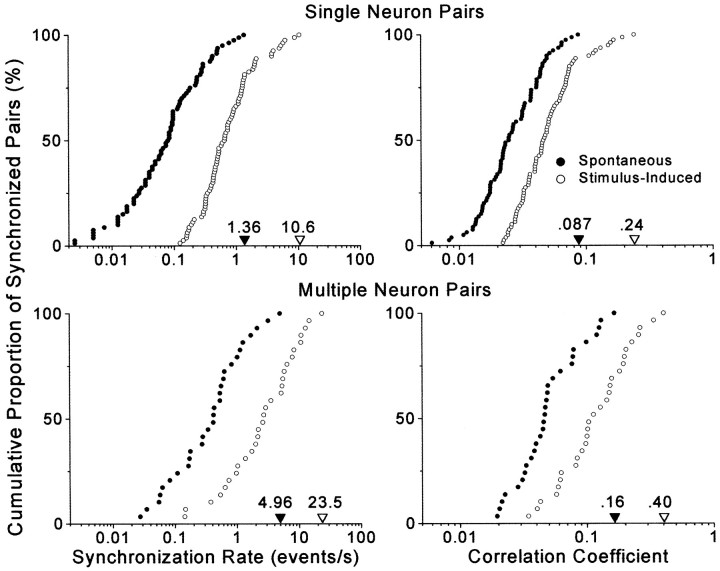
The strength of synchronized responses in SI and SII varied tremendously across pairs of recording sites. As indicated by cumulative distributions in Figure 5, both the single and multiple neuron responses displayed a hundredfold difference in the rate of coincident events when the weakest and strongest neuronal pairs were compared. Similarly, the cumulative distribution of correlation coefficients indicated that the proportion of synchronized activity varies by a factor of 10 when comparing the strongest and weakest cases of correlated activity. The margin of error for placing electrodes in corresponding parts of SI and SII is fairly small, as indicated by data showing that focal cutaneous stimulation causes synchronization among local populations of cortex that extend no more than 500 or 600 μm in diameter (Metherate and Dykes, 1985; Roy and Alloway, 1999). Thus, weakly synchronized responses seem likely to represent pairs of SI and SII neurons that are located on the perimeter of regions showing the strongest interactions. Hence, the highest values for the correlation coefficients and synchronization rates probably provide the best measure of synchronization that is typically achieved at optimal pairs of recording sites in SI and SII.

Fig. 5.

Cumulative distributions illustrating the strength of spontaneous and stimulus-induced synchronization across SI and SII. Data are based on 80 pairs of single neurons and 29 pairs of multiple neurons in which significant peaks appeared in the neural CCGs of the stimulus-induced responses. Maximum synchronization strength for each group is indicated by filled and unfilled triangles appearing along the bottom axis.

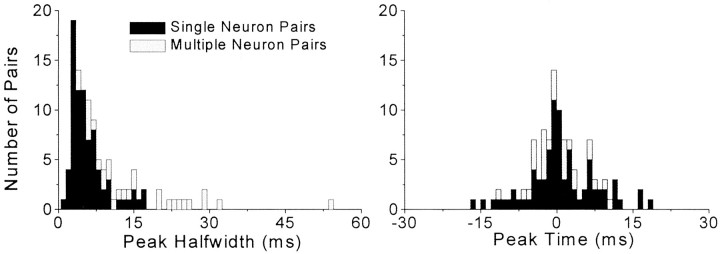
Analysis of the temporal structure of SI and SII coordination indicates that stimulus-induced synchronization was associated with a relatively high degree of temporal precision. As shown in Figure6, almost 60% of the single neuron pairs had peak half-widths that were ≤5 msec, and 90% had half-widths that were ≤10 msec. Furthermore, the peaks in the neural CCGs tended to be distributed close to time 0. Thus, for both single and multiple neuron pairs, the tallest bin of the neural CCG peaks was located within 5 msec of time 0 for 50% of the cases, and the most common time lag was only 1 or 2 msec (n = 42). These data indicate that stimulus-induced synchronization in SI and SII is composed largely of discharges that occur at approximately the same time.

Fig. 6.

Precision of temporal synchronization for single-unit and multiunit stimulus-induced responses in SI and SII.Left panel, Distribution of peak half widths for pairs of synchronized single and multiple neuron responses. A peak half width is defined as the temporal width of a peak in the neural CCG at half its height. Right panel, Distribution of neural CCG peak times with respect to time 0.

Incidence of neuronal oscillations in the ACGs

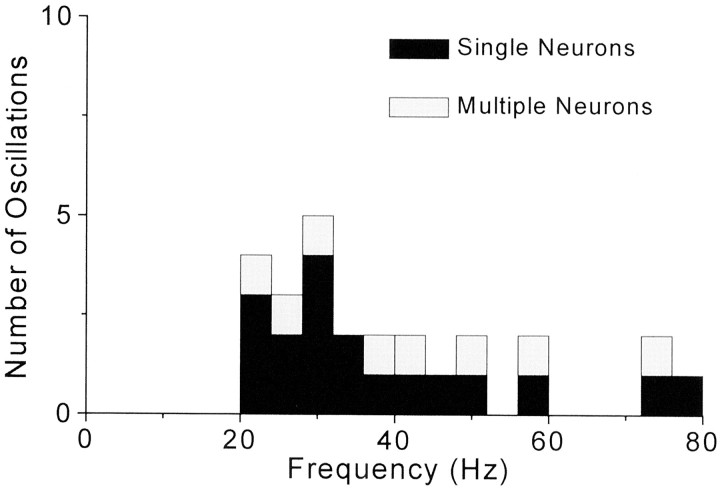
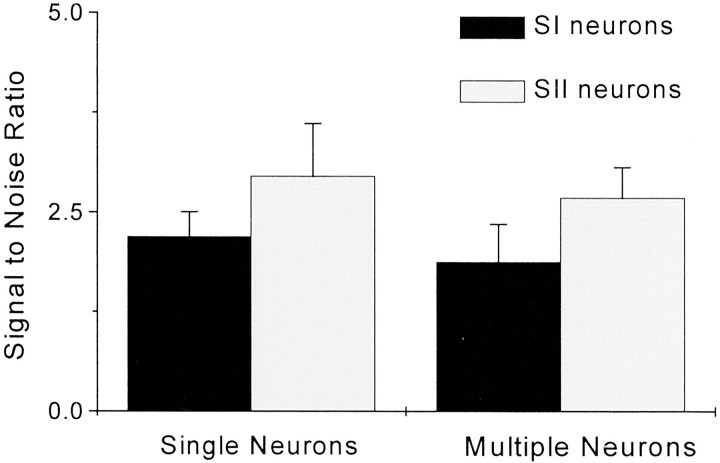
Analysis of the power spectra derived from the single and multiple neuron ACGs indicated that only a small fraction were associated with significant power levels in the gamma frequency range. Among 136 neurons in SI and SII that formed 80 synchronized pairs during air-jet stimulation, only 13% (n = 18) of these neurons contained oscillations between 20 and 80 Hz. Among the 52 multiunit responses that formed 29 synchronized pairs, only 15% (n = 8) were characterized by oscillations. Detectable oscillations spanned the entire spectrum of the gamma frequency range, but as Figure 7 indicates, the majority of these oscillations represented frequencies between 20 and 32 Hz. All of the oscillations appeared to be weak, and as shown in Figure8, the power of oscillations in the gamma frequency range was typically only two to three times greater than the mean amount of power occurring in the high-frequency (250–500 Hz) portion of the power spectrum.

Fig. 7.

Distribution of neuronal oscillations according to frequency. Stimulus-induced neuronal responses that exhibited significant levels of oscillations in the gamma frequency range are represented according to their tallest peak in the power spectrum derived from the ACG. Bin widths appear as 4 Hz increments to correspond with the frequency resolution of the power spectra.

Fig. 8.

Strength of neuronal oscillations. Eachbar represents the mean signal-to-noise ratio for significant oscillations detected in the gamma frequency range of the power spectrum. Noise was calculated as the average power level in the 250–500 Hz range. Error bars indicate SEM.

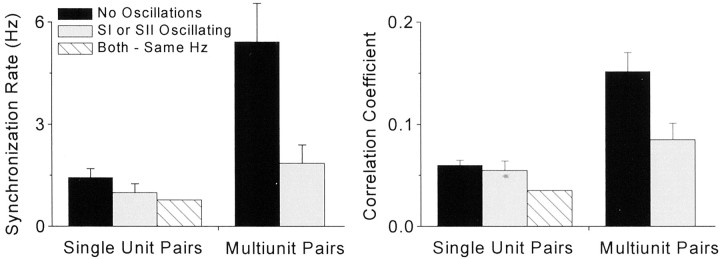
Several facts suggest that stimulus-induced synchronization in SI and SII does not depend on oscillations in the gamma frequency range. As indicated by Table 1, >76% (61/80) of the synchronized neuron pairs were devoid of oscillations, and 22% (18/80) of the neuron pairs displayed oscillations in only one neuron. The low incidence of oscillations among synchronized responses is underscored by the fact that only one pair of synchronized neurons was composed of neurons in which both cells oscillated at the same frequency. Essentially similar results were obtained among the pairs of synchronized multiunit responses (Table 1). Furthermore, and contrary to our expectations, the presence of oscillations did not increase the strength of synchronized activity in SI and SII. As summarized in Figure 9, mean synchronization rates and correlation coefficients were lower when oscillations were present in one or both of the constituent responses. Statistical analysis failed to reveal any difference in the discharge rates of oscillatory and non-oscillatory neurons (Table 2). Thus, the lower synchronization strength apparent among oscillating responses was not caused by differences in the mean rate of activity.

Table 1.

Incidence of oscillations during SI–SII synchronization

	Single unit pairs	Multiunit pairs
No oscillations	61	21
SI only	11	4
SII only	7	4
Both-different Hz	0	0
Both-same Hz	1	0
Total	80	29

Fig. 9.

Strength of synchronized activity in SI and SII as a function of the presence or absence of oscillations in the constituent neuronal responses. Left panel, Mean synchronization rate for single-unit or multiunit pairs in which oscillations were detected in neither neuronal response, in one neuronal response, or in both neuronal responses as indicated by thelegend. Right panel, Mean magnitude of correlation coefficients for the same groups shown in the left panel. Error bars indicate SEM.

Table 2.

Stimulus-induced activity of synchronized SI and SII neurons

	SI	SII
Oscillating neurons	20.8  ± 4.1	13.8  ± 5.3
Non-oscillating neurons	18.9  ± 2.3	16.9  ± 1.9

Numbers indicate discharges per second (mean ± SEM).

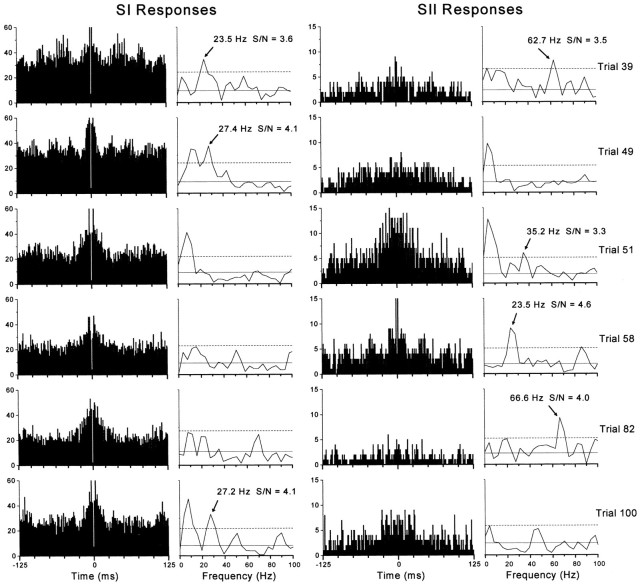
We also searched for high-frequency oscillations in individual stimulus trials because oscillations may occur momentarily and go undetected in the summed ACGs, especially if the predominant oscillatory frequency varies across trials (Ghose and Freeman, 1992; Murthy and Fetz, 1996b;Gray and Viana Di Prisco, 1997). Oscillations within a single trial cannot be detected in spike trains that contain low rates of activity, and therefore our analysis was limited to the most responsive multiunit recording experiments, such as the one depicted in Figure 4 (experimentA130). A trial-by-trial analysis revealed that the vast majority of responses in experiment A130 did not contain oscillations in the gamma frequency range. As indicated by the ACG and power spectrum obtained for each stimulus trial, responses for both SI-A130 and SII-A130 were devoid of gamma frequency oscillations in 59 of the 100 trials. Rhythmic activity between 20 and 80 Hz was detected by our statistical analysis in 41 trials, and most of these oscillations were isolated to one electrode in SI (n = 8) or SII (n = 29). Only four trials were characterized by oscillations on both electrodes, but often at different frequencies. Hence, among 200 ACGs analyzed in this experiment, only 22.5% (45/200) contained significant levels of gamma range oscillations. As shown in Figure 10, which illustrates those ACGs that contained the strongest gamma oscillations detected in experiment A130, most of the 20–80 Hz peaks in the power spectra had very low signal-to-noise ratios. In fact, visual inspection revealed clear instances of oscillations in only three ACGs (SI on trials 39 and 49, and SII on trial 58) (Fig. 10).

Fig. 10.

Trial-by-trial analysis of oscillatory responses in experiment A130. These trials illustrate the strongest oscillations (in terms of signal-to-noise ratio) that were detected among 100 trials, the summed multiunit responses of which are illustrated in Figure 4. The ACGs and power spectra represent the temporal structure of activity recorded simultaneously from SI (left) and SII (right) during specific trials as indicated.Arrows indicate peaks in the power spectra that represent significant oscillations in the gamma frequency range.Solid and dashed horizontal linesrepresent mean noise (from 250 to 500 Hz) or mean noise plus 3 SDs, respectively. Visual inspection of all 200 ACGs revealed gamma range oscillations in SI on trials 39 and 49, and in SII on trial 58.

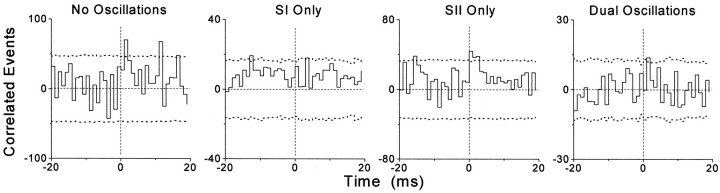
To determine the relative contribution of oscillations in synchronizing the SI and SII responses in experiment A130, we performed cross-correlation analysis separately on those trials classified as containing no oscillations, oscillations in only one cortical area, or oscillations in both SI and SII. The results of this analysis are illustrated in Figure 11. When the individual CCGs shown in Figure 11 are summed together, the resulting CCG matches the neural CCG shown in Figure 4C (bottom right). A comparison of the CCGs shown in Figure 11 indicates that each type of trial contributed some synchronized activity (events at 0–3 msec after time 0), but most of the synchronized events were produced in trials that contained no oscillations or else contained oscillations in SII alone. Given the scaling differences of these CCGs, it appears that the number of synchronized events contributed by each category was proportional to the number of trials.

Fig. 11.

Neural CCGs illustrating the degree of synchronization in experiment A130 for those trials classified as containing no oscillations (n = 59), oscillations in SI only (n = 8), oscillations in SII only (n = 29), or oscillations in both cortical areas (n = 4). Because of differences in the number of trials, the CCGs are scaled so that the 99% confidence limits span approximately the same distance in each histogram.

We also analyzed the power spectra derived from single and multiple neuron CCGs to determine whether there were periodicities in the relative timing of discharges in SI and SII. Among 80 raw CCGs based on single neuron responses, only two contained significant levels of oscillations in the 20–80 Hz range (experiment A64 at 25 Hz, experiment A101 at 33 Hz). Similarly, among 29 raw CCGs based on multiple neuron responses, only one contained a significant level of oscillatory activity (experiment A96 at 58 Hz).

Sensitivity for detecting oscillations

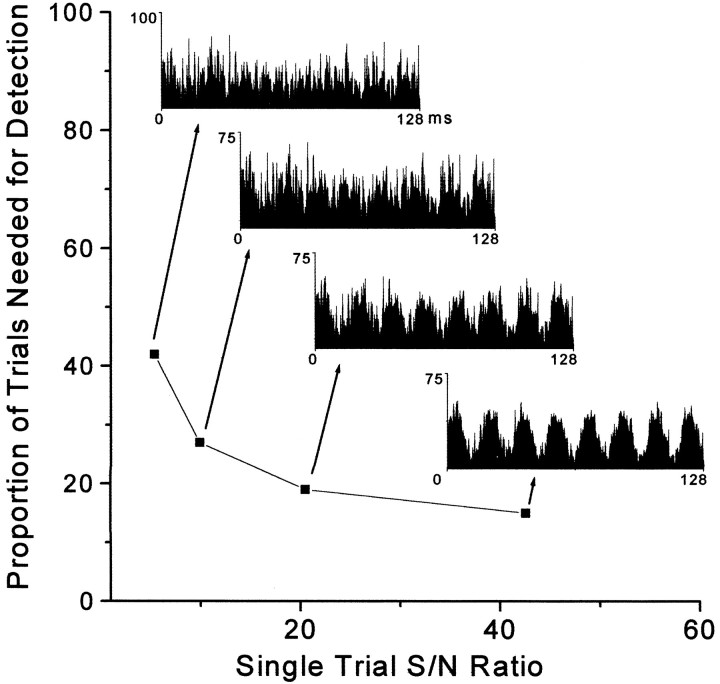
To determine the sensitivity of our methods for detecting neuronal oscillations of a specific frequency in a block of 100 trials, we constructed single-trial ACGs that contained different amplitudes of oscillating signals embedded in a background of Gaussian white noise (see Materials and Methods). As shown by Figure12, the ability to detect neuronal oscillations in a block of trials depends on the strength of the oscillation and the proportion of trial responses that contained the oscillation. For example, in cases where the power spectrum indicated that the signal-to-noise ratio of the single-trial oscillatory response was 5, this stimulus-induced response would need to be present in >40% of the trials to be detected in an analysis of the entire block of trials. In cases where single-trial oscillations had a signal-to-noise ratio of 21, only 20% of the trials would need to contain oscillations of this strength to be detected in the entire block. With further increases in the signal-to-noise ratio, however, the number of oscillatory trials that must be present to be detected in a block of trials declines only slightly (Fig. 12). This relationship is correct, however, only if the number of discharges remains constant for both oscillatory and non-oscillatory responses in individual trials. If the number of discharges increases proportionately with increases in the signal-to-noise ratio of the oscillatory response, then an increasingly smaller proportion of these trials would need to contain oscillations for them to be detected in a block of trials (data not shown).

Fig. 12.

Detectability of oscillations occurring on intermittent trials. Simulated ACGs containing oscillatory activity at varying strengths were systematically combined with Gaussian white noise ACGs to determine the number of oscillatory trials needed to detect a significant frequency in a power spectrum computed across the entire block of trials. Simulated ACGs are shown from 0–128 msec, with the mean bin height set at 25 events per bin for each trial.

DISCUSSION

This study revealed two important findings regarding the coordination of stimulus-induced activity in separate cortical areas. First, we found that tactile stimulation evokes synchronous responses in corresponding somatotopic representations of SI and SII cortex. These responses are extremely precise, usually occurring within intervals of ≤5 msec. Second, we frequently observed significant levels of long-range synchronization between SI and SII without the presence of oscillations in the constituent neurons. In instances where gamma range oscillations were detected, periodic activity was usually present in one neuron of a synchronized pair. We rarely observed simultaneous oscillations in both SI and SII at the same frequency. These findings suggest that separate populations of cortical neurons can be bound together by a sensory stimulus to form functional assemblies without being constrained by the phase relationships defined by specific oscillatory frequencies.

Variable and transient incidence of synchronized oscillations

Neuronal oscillations have received much attention as a potential mechanism for grouping distributed populations of cortical neurons, but synchronized oscillations are often transient and may not be detected if responses are summed across several blocks of trials. In the visual system, for example, experiments on both cats and monkeys have shown that stimulus-induced neuronal oscillations may occur at different frequencies on different trials (Ghose and Freeman, 1992; Livingstone, 1996; Gray and Viana Di Prisco, 1997). Furthermore, gamma range oscillations in the sensorimotor cortex of monkeys are correlated with certain manipulative behaviors, but these oscillations occur episodically throughout the behavioral task (Murthy and Fetz, 1996a,b).

These findings raise the concern that we did not detect neuronal oscillations because our ACGs were generated from spike trains acquired over multiple trials, and this approach may conceal oscillations that occur at different frequencies on different trials. Several facts, however, argue against this possibility. First, although oscillations may appear transiently, most oscillatory responses reported in the visual system were based on cumulative ACGs generated from multiple-trial spike trains. Our cumulative ACGs and their derived power spectra never displayed oscillations as prominent as those seen in visual responses that were acquired over multiple trials (Gray et al., 1989; Engel et al., 1991c; Gray and Viana Di Prisco, 1997). Second, even when we searched for periodic activity during single trials, most of the single-trial ACGs were devoid of oscillations in the gamma frequency range. In fact, only ∼2% of the single-trial ACGs contained oscillatory activity that was perceptible by visual inspection, and the remaining oscillations were barely detected by rigorous statistical analysis. Finally, oscillations in the 20–80 Hz range rarely appeared in SI and SII simultaneously but were confined almost exclusively to one cortical area or the other.

It is also conceivable that we did not observe prominent gamma-range oscillations because our preparation was anesthetized, but the evidence does not support this interpretation. The earliest studies reporting neuronal oscillations in the visual system involved anesthetized cats (Gray and Singer; 1989; Engel et al., 1990; Ghose and Freeman, 1992;Nowak et al., 1995), and this prompted the view that neuronal oscillations might reflect an artifact of anesthesia. A direct comparison of oscillating neurons in awake and anesthetized cats, however, indicated that the incidence, frequencies, and amplitudes of oscillating responses were similar in both preparations (Gray and Viana Di Prisco, 1997). Furthermore, with the use of rigorous statistical analysis, we detected gamma range oscillations in 15% of our neuronal sample, and this corresponds almost exactly with the incidence of oscillations reported in the visual cortex of anesthetized cats (Gray and Viana Di Prisco, 1997, their Table 1).

Periodic and aperiodic cortical synchronization

Although oscillations are thought to facilitate long-range cortical synchronization, our results indicate that oscillations are not always inherent among synchronized responses. Long-range synchronization may involve periodic or aperiodic neuronal activity, depending on the connectivity of the cortical network or the type of cells that are recorded (Gray and McCormick, 1996). In the visual system, some investigators observed gamma frequency oscillations in the lateral geniculate nucleus that could entrain similar oscillations in the visual cortex (Ghose and Freeman, 1992). By contrast, we reported previously that stimulus-induced responses in the ventrobasal thalamus and SI cortex are precisely coordinated, but we rarely observed any neurons that oscillated in the gamma frequency range (Johnson and Alloway, 1994, 1996).

Periodic or aperiodic synchronization across cortical areas might also depend on the context in which the cortical network is activated. Although some suggest that neuronal oscillations in visual cortex do not vary with different stimulus parameters (Ghose and Freeman, 1992), others indicate that oscillatory amplitude is altered by changes in stimulus velocity or luminance (Nowak et al., 1995; Gray and Viana Di Prisco, 1997). Similarly, significantly fewer episodic oscillations were observed in monkey sensorimotor cortex when the animals performed repetitive wrist movements than when they performed tasks that required skill and attention (Murthy and Fetz, 1996a). These findings suggest that oscillatory activity is more likely if a large part of the cortical network is involved in processing the sensory attributes of a salient stimulus.

In this context, it is plausible that we did not observe synchronized oscillations between SI and SII cortical areas because we did not use a large stimulus. Compared with the elongated, spatially extensive stimuli used to evoke synchronized oscillations in the visual system, we used a relatively focal stimulus to activate a discrete region of skin. One hypothetical function of synchronization is to link adjacent neuronal populations within a cortical area that represent co-linear stimulus attributes, such as the edge of a visual object (Singer and Gray, 1995). This function, however, would not apply to a focal stimulus that activates a focal region of cortex. Another proposed function of synchronized oscillations is to link separate cortical areas that are specialized for processing different sensory features of the same stimulus. In the visual system, for example, synchronized oscillations could link separate neuronal populations that respond primarily to the color, shape, or motion of an object. A focal stimulus like a moving air jet also has cutaneous attributes, such as texture, intensity, location, and velocity of movement, that could be differentially processed by neural circuits in SI and SII cortex. Although the differential coding functions of the SI and SII cortical areas are not understood, our data demonstrate that focal air jets evoke synchronized responses in corresponding somatotopic areas of both cortices. Whether these synchronized populations would show oscillations in response to a spatially extensive stimulus remains an empirical question. Nonetheless, our current results support the view that long-range synchronization in SI and SII is a mechanism for binding separate neural populations that represent attributes of the same stimulus.

Plausible mechanisms of SI–SII synchronization

The most likely neural circuits for mediating correlated activity in cat SI and SII involve thalamocortical and corticocortical pathways. Substantial evidence suggests that common inputs from the thalamus play a major role in coordinating these cortical areas. In cats, both SI and SII receive parallel projections from neurons in overlapping parts of the ventrobasal thalamus, and 10–15% of these thalamocortical neurons send collateral projections to both SI and SII (Hand and Morrison, 1970; Saporta and Kruger, 1979; Spreafico et al., 1981; Bentivoglio et al., 1983; Burton and Kopf, 1984). Consistent with this parallel set of projections, reversible inactivation of either SI or SII does not prevent the other cortical area from responding to cutaneous stimulation (Burton and Robinson, 1987; Turman et al., 1992; Turman et al., 1995). Cross-correlation analysis demonstrates that populations of thalamic neurons discharge synchronously during cutaneous stimulation and that stimulus-induced responses in cat SI and SII are tightly correlated with thalamic activity (Johnson and Alloway, 1994, 1996;Alloway et al., 1995; Roy and Alloway, 2001). The time delays between thalamic discharges and subsequent responses in SI or SII are in the range of 1–4 msec, and this agrees with the conduction velocity of thalamocortical impulses (Yen et al., 1985). Hence, it seems entirely plausible that synchronization of parallel thalamocortical projection neurons could synchronize functionally related responses in SI and SII cortex.

Corticocortical connections might also facilitate SI–SII synchronization. There are substantial interconnections between corresponding representations in cat SI and SII (Alloway and Burton, 1985; Manzoni et al., 1990; Schwark et al., 1992). Direct electrical stimulation of cat SI produces antidromic responses in SII with an average delay of only 4 msec (Manzoni et al., 1979). This response latency appears too short to facilitate synchronized oscillations, because an interval of 4 msec corresponds to 250 Hz. This time delay, however, is extremely similar to the time interval that characterized the majority of near-coincident events that we observed across SI and SII (Fig. 6, right panel). In support of this contention, electrical stimulation in cat SI cortex has been shown to enhance peripherally induced responses in SII cortex (Manzoni et al., 1979). Furthermore, reversible inactivation of either SI or SII alters the timing and magnitude of short-latency responses in the other cortical area (Burton and Robinson, 1987). These results suggest that interconnections between cortical areas SI and SII in cats may serve to reinforce the synchronized inputs from the thalamus.

The importance of corticocortical connections has been demonstrated in the visual system where interhemispheric connections through the corpus callosum are needed to mediate synchronization in regions that represent visual fields near the vertical meridian (Engel et al., 1991a; Munk et al., 1995). The role of callosal projections in the visual system, however, might not be comparable to the role of ipsilateral connections between SI and SII, because visual areas in different hemispheres do not receive common thalamic inputs. Thus, the contribution of corticocortical connections for synchronizing SI and SII might be subsidiary to the influence exerted by the divergent thalamocortical projections.

Hypothetical roles for synchronization in SI and SII

Synchronization among distributed populations of neurons is thought to be important for both neurotransmission and sensory perception (von der Malsburg, 1994). We hypothesize that common targets of SI and SII respond preferentially to synchronized discharges in these cortical areas, just as neurons in visual or somatosensory cortex are more likely to discharge in response to synchronous activity in the thalamus (Alonso et al., 1996; Usrey et al., 2000; Roy and Alloway, 2001). Thus, the sensorimotor portion of the neostriatum, which receives convergent inputs from corresponding representations in SI and SII (Alloway et al., 2000), may depend on synchronized activity in these cortical areas to be activated. With respect to sensory perception, local synchronization in cat SI varies with stimulus properties (Roy and Alloway, 1999), whereas local synchronization in primate SII depends on the animal's state of attention (Steinmetz et al., 2000). On the basis of these findings, we propose that the strength and spatial extent of long-range synchronization in SI and SII vary with the perceptual salience of tactile stimuli.