Abstract
Current propositions of the quantity of sound driving the central auditory system, specifically around threshold, are diverse and at variance with one another. They include sound pressure, sound power, or intensity, which are proportional to the square of pressure, and energy, i.e., the integral of sound power over time. Here we show that the relevant sound quantity and the nature of the threshold can be obtained from the timing of the first spike of auditory-nerve (AN) fibers after the onset of a stimulus. We reason that the first spike is triggered when the stimulus reaches threshold and occurs with fixed delay thereafter. By probing cat AN fibers with characteristic frequency tones of different sound pressure levels and rise times, we show that the differences in relative timing of the first spike (including latencies >100 msec of fibers with low spontaneous rates) can be well accounted for by essentially linear integration of pressure over time. The inclusion of a constant pressure loss or gain to the integrator improves the fit of the model and also accounts for most of the variation of spontaneous rates across fibers. In addition, there are tight correlations among delay, threshold, and spontaneous rate. First-spike timing cannot be explained by models based on a fixed pressure threshold, a fixed power or intensity threshold, or an energy threshold. This suggests that AN fiber thresholds are best measured in units of pressure by time. Possible mechanisms of pressure integration by the inner hair cell–AN fiber complex are discussed.
Keywords: hearing, sound, mammal, latency, spike timing, pressure, intensity, energy, modeling, inner hair cell, auditory nerve
The adequate stimuli for auditory systems of most vertebrates are rapid and small changes of pressure at the ear drum. Consequently, many basic response properties of auditory-nerve (AN) fibers and central auditory neurons are characterized and defined with respect to the sound pressure. For example, threshold is defined as the lowest sound pressure level (SPL) of a stimulus that evokes a neuronal response, usually some criterion increase in the firing rate above that measured in the absence of intentional acoustic stimulation [for AN fibers, see Tasaki (1954),Kiang et al. (1965); for review, see Evans (1975), Palmer (1987),Ruggero (1992)]. This practice implies that thresholds are sufficiently characterized by sound pressure. The assumption that neural thresholds correspond to particular values of basilar membrane displacement or velocity (Narayan et al., 1998; Ruggero et al., 2000) also follows from this practice. On the other hand, psychoacoustical measurements have shown that the sound pressure necessary for a signal to be detected depends on the signal's duration (Garner, 1947; Plomp and Bouman, 1959; Florentine et al., 1988), suggesting that time is also a critical factor. Therefore, an issue central to the understanding of the auditory system's operation is whether neural thresholds are a function of pressure only or one of pressure and time.
A second issue concerns the nature of that function. It has been observed that at low SPLs the firing rate of AN fibers appears to grow with the square of sound pressure (Müller et al., 1991; Yates, 1991), i.e., with sound intensity or sound power per unit area. Much the same applies to the DC component of the membrane potential of inner hair cells (IHCs) at higher frequencies (Goodman et al., 1982; Patuzzi and Sellick, 1983; Smith et al., 1983; Dallos, 1985). This suggests that the adequate stimulus quantity might be sound intensity or, as conjectured by Goodman et al. (1982), acoustic energy. The psychoacoustical measurements, cited above, are generally interpreted as indicating temporal integration of intensity, with threshold corresponding to a particular acoustic energy per unit area. However, this interpretation is not without pitfalls (de Boer, 1985). To our knowledge, it has not yet been critically addressed whether the central auditory system processes sound pressure, and if so how, or sound intensity or another related quantity.
Here we demonstrate, on AN fiber responses to tones, that the nature of the threshold, the type of function, i.e., the relevant stimulus quantity, and the magnitude of the threshold can be obtained from the timing of the first spike after the onsets of acoustic stimuli. We reason that the first spike after a stimulus onset, disregarding the problems of spontaneous activity for the moment, is triggered when that stimulus reaches the neuron's threshold. It was shown previously that the timing of the first spike of AN fibers varies systematically with stimulus level and with stimulus rise time but forms a relatively invariant function of the acceleration of pressure at the onset of cosine-squared rise function tones (Heil and Irvine, 1997). This demonstrates that the first spike must be determined by events at the very onset of the stimulus and not by steady-state properties. Because at stimulus onset both pressure and intensity change dynamically but differently, the differences in timing of the first spike in response to different stimuli (e.g., tones of different SPLs and rise times) can be exploited to extract the stimulus quantity that generates the first spike and to determine the nature and magnitude of the threshold.
MATERIALS AND METHODS
Surgery. Four adult cats of either sex with outer and middle ears free of infections were deeply anesthetized with pentobarbitone sodium (40 mg/kg, i.p.) and prepared for recordings from the auditory nerve, as described in detail elsewhere (Heil and Irvine, 1997). Briefly, anesthesia was maintained throughout the experiment by intravenous injections of pentobarbitone. The electrocardiogram was monitored continuously, and rectal temperature was held at 38 ± 0.3°C by a thermostatically controlled DC blanket. A round-window electrode, allowing the compound action potential to be monitored (Rajan et al., 1991), and a length of fine-bore polyethylene tubing, allowing static pressure equalization within the middle ear, were inserted through a small hole in the bulla on the recording side (left and right in two cats each). The bulla was resealed, and the external meatus was cleared of surrounding tissue and transected to leave only a short meatal stub. On the recording side, the skull was trephined caudal to the tentorium, the dura was removed, and the cerebellum over the cochlear nucleus was aspirated. The auditory nerve was exposed near its exit from the internal auditory meatus by gently pushing and holding the cochlear nucleus medially with small saline-soaked cotton swabs.
Acoustic stimulation and recording procedures. The cat was located in a sound-attenuating chamber. Stimuli were digitally produced (Tucker Davis Technology) and presented to the cat's ear via a calibrated, sealed, sound delivery system consisting of a STAX SRS-MK3 transducer in a coupler (Sokolich, 1981). Single AN fibers were recorded with micropipettes or glass-insulated tungsten microelectrodes, and spike times were stored on disc with 10 μsec resolution for off-line analysis.
For each fiber, the characteristic frequency (CF; the frequency to which a fiber is most sensitive) was determined by manually varying the stimulus frequency and amplitude. Quantitative data were obtained with CF tone bursts that were presented under computer control. All tone bursts were of 200 msec total duration (except for three fibers where the duration was 100 msec), measured from the beginning of the rise time to the end of the fall time. Tones were shaped with symmetrical cosine-squared rise and fall functions. Thus, at tone onset the pressure P(t) (in Pascal) changes with timet according to:
| Equation 1 |
where tr is the total rise time andPp the plateau pressure, i.e., the pressure reached at the end of the rise time. Throughout this paper the term pressure does not refer to the cycle-by-cycle variation of pressure but rather to the peak pressure, i.e., to the envelope or the line connecting successive peaks in the waveform (Scharf and Buus, 1986). This is reasonable, because at the higher frequencies, where all our data were collected, the response of the inner hair cells, as a result of half-wave rectification and low-pass filtering, is dominated by the DC component. This component closely follows the stimulus envelope and is not attenuated by the low-pass filters of the inner hair cell membrane, whereas the AC component, which reflects the stimulus fine structure, is negligible (Russell and Sellick, 1978; Cody and Russell, 1987; Russell and Kössl, 1991; Cheatham and Dallos, 2000).
Twenty, or in a few cases 50, repetitions of CF tones with a given rise time were presented at 2 Hz, at sound pressure levels increasing from low (usually 0 dB SPL) to high values (usually 90 dB SPL) in 10 dB steps. This was followed by recording the spikes in the same number of repetitions of 210 msec time windows, also at 2 Hz, during which no stimulus was presented. These no-stimulus windows were used to derive measures of spontaneous activity (see below). A different rise time was then selected and the recording procedure repeated. As many as seven different rise times, covering the range of 1.7–85 msec (in four fibers up to nominally 170 msec), were tested and presented in random sequence.
Data analysis. Spikes in response to the 20 or 50 presentations of a given stimulus were displayed off-line as a post-stimulus time histogram. The total number of spikes in a 210 msec window commencing with tone onset and summed over all repetitions was the measure of response for a tone of a given SPL and rise time. For each combination of SPL and rise time, the first spike on each repetition of that stimulus within the 210 msec window was used to calculate the mean latency, its SD and the SEM. Analogous analysis procedures were applied to the spikes recorded in the no-stimulus windows to obtain corresponding estimates from the spontaneous activity. Of course, mean “spontaneous” latency and its SD decrease with increasing spontaneous rate (see Figs. 2, 5, 6). Latency measures were not corrected for acoustic delays of ∼0.2 msec, brought about by the length of the sound delivery tube, unless stated otherwise. MS-Excel 7.0 was used to further analyze the data, and model functions were fitted using the Newton procedure of the Excel “Solver” module. Weights were either 1 or 0, i.e., data points were either included in the fits or excluded using criteria described in the results. We minimized the sum of the squared deviations of the logarithms of the measured mean latencies from those of the fits, rather than of the latencies themselves. There were two reasons for this approach. (1) On a linear axis, the distributions of measured latencies were strongly biased toward short values, whereas on a logarithmic axis, latencies were more evenly distributed (see Figs.1B, 2, 5, 6). These distributions are a direct consequence of the equal (nearly equal) spacing of the input variables plateau pressure (rise time) on logarithmic scales. (2) The increase of the SD of first-spike latency obtained from the 20–50 repetitions with the mean could be well described by a linear function (Heil and Irvine, 1997), so that on a logarithmic axis that increase was shallow or absent, indicating nearly constant relative errors of latency.
Fig. 2.
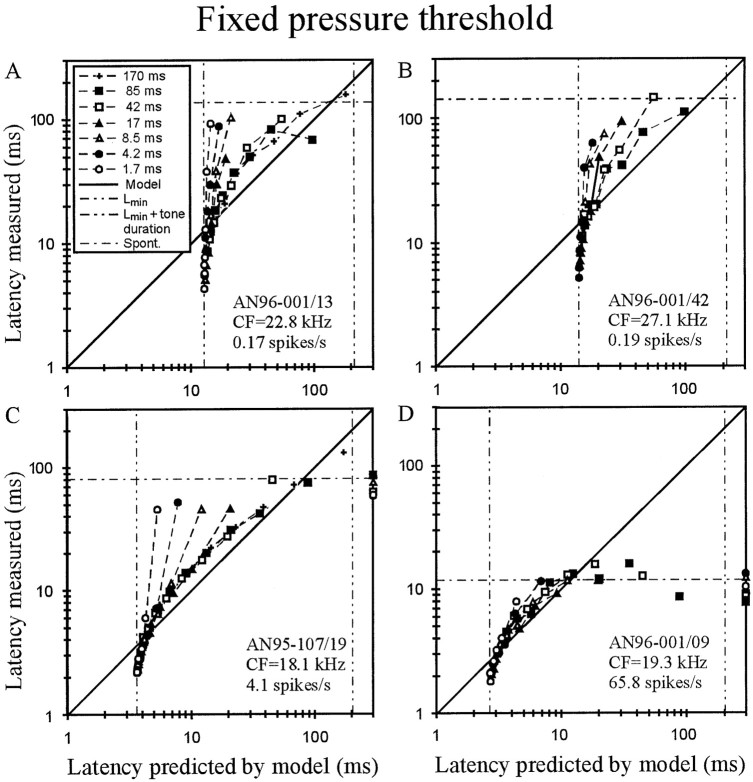
Evaluation of the fixed pressure threshold model. A–D, For four high-CF AN fibers of different spontaneous discharge rates (seeinsets), the mean first-spike latency measured is plotted against the best fit of the model, with threshold pressurePthr (in Pascal) and transmission delayLmin (in milliseconds) as the two free parameters. Data obtained with tones of different SPLs but of the same rise time (see key in A) are interconnected. Unconnected symbols represent data points that were excluded from the fits, because measured latencies were close to, or even longer than, spontaneous latency (horizontal dotted-dashed lines) and hence largely caused by spontaneous activity. Latencies unexplained by the model, i.e., when first spikes were triggered during the plateau phase of the stimulus, are plotted at the extreme right (see C, D).Left and right vertical dashed-dotted lines represent Lmin and tone duration plus Lmin, respectively. Note the systematic deviations of the data from the model.
Fig. 5.
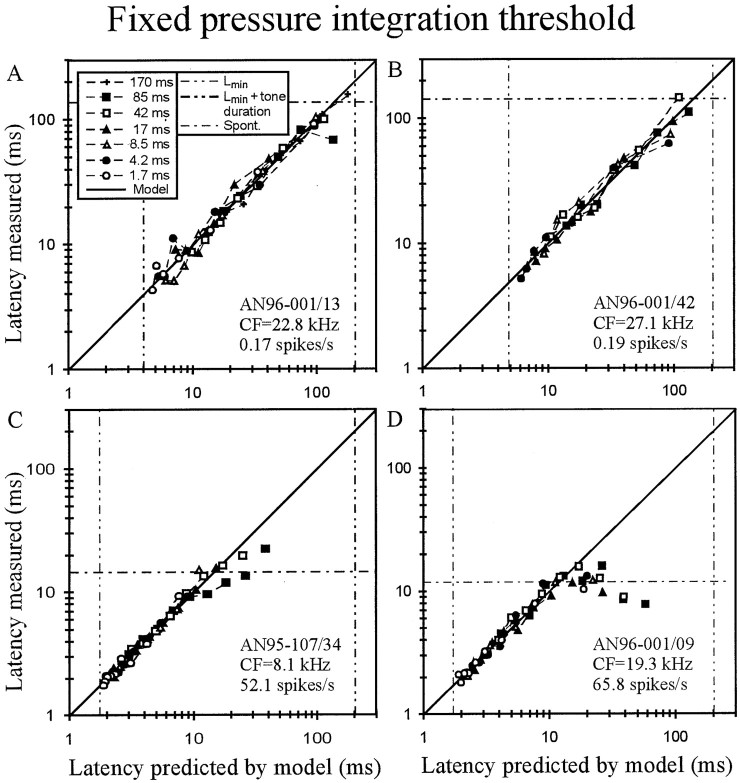
Evaluation of the fixed pressure integration threshold model. A–D, For four AN fibers of different spontaneous discharge rates (A, B, and D are identical with those of Fig. 2), the mean first-spike latency measured is plotted against the best fit of the model, with pressure integration thresholdT (in Pascal times millisecond) and transmission delayLmin (in milliseconds) as the two free parameters. Conventions as in Figure 2. Note the excellent fit of the data, up to latencies obtained from spontaneous activity.
Fig. 6.
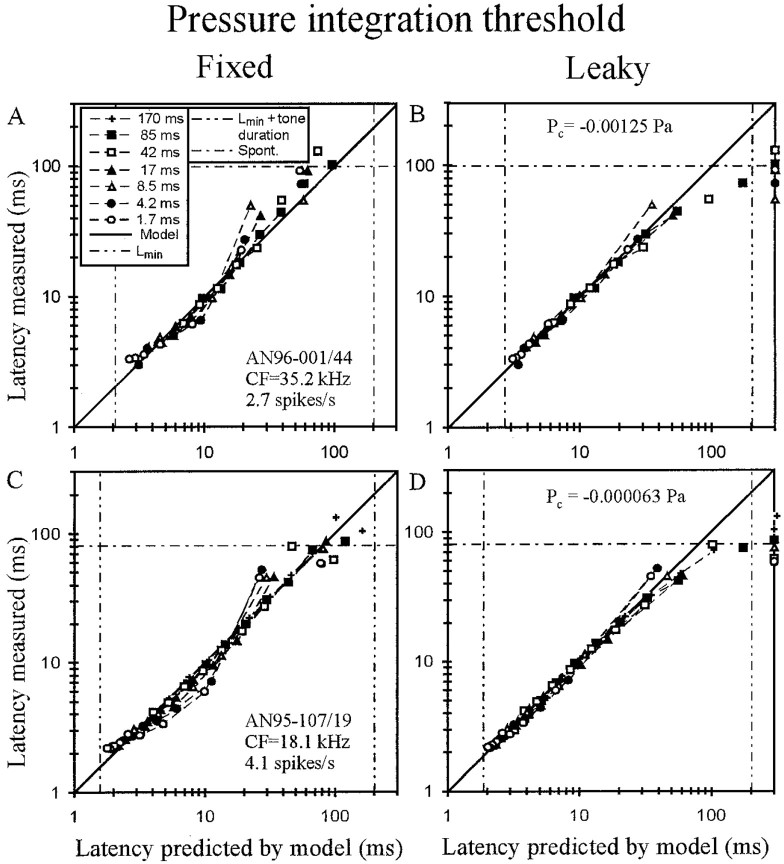
Comparison of fixed versus leaky pressure integration threshold models. A,C, As shown for two AN fibers of medium spontaneous discharge rates, the mean first-spike latencies measured can deviate systematically from a fixed pressure integration model but are described much more accurately, up to latencies obtained from spontaneous activity, by a leaky pressure integration model (B, D). Pressure losses (in Pascal) are identified. Other conventions as in Figure 2.
Fig. 1.
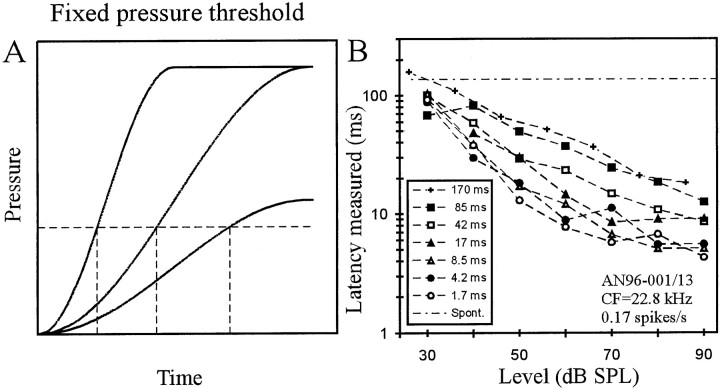
A, Scheme of a fixed pressure threshold model. Continuous lines represent the onset envelopes of three signals, all shaped with cosine-squared rise functions, but differing in plateau pressure and rise time. A fixed pressure threshold (horizontal dashed line) is reached at times (vertical dashed lines) that depend on signal level for a fixed rise time and on rise time for a fixed level.B, For one AN fiber of low spontaneous rate, first-spike latency is plotted against SPL with rise time as the parameter (seekey). Note the decrease of latency with increasing SPL and with decreasing rise time.
RESULTS
Eighty-nine AN fibers with CFs from 0.6 to 35.5 kHz and spontaneous discharge rates (SRs) between 0 and 117 spikes/sec provided data for this study. To enable better comparisons with previous studies we classified the fibers, according to the criteria of Liberman (1978), into low-SR (≤0.5 spikes/sec; n = 13; 14.6%), medium-SR (>0.5 ≤ 18 spikes/sec; n = 28; 31.5%), and high-SR fibers (>18 spikes/sec; n = 48; 53.9%), although our data do not suggest the existence of three distinct SR categories.
In the following we will test several models that might explain the timing of the first spike of AN fibers. For each model, we assume that each first spike will be triggered when the threshold is reached but will occur with some short delay thereafter. This delay is treated as constant for a given fiber and includes the acoustic delay, middle ear and cochlear delays, fixed delays of the synapse, and the axonal travel time of spikes to the recording site and will be referred to as the transmission delay Lmin (Heil and Irvine, 1996, 1997; Heil, 1997).
Fixed pressure and fixed intensity threshold models
Because AN fiber and other neuronal thresholds are routinely measured in units of sound pressure (e.g., in dB SPL), a practice that implies a fixed pressure threshold, we first tested whether such a model can account for first-spike timing. Figure1A provides a scheme of this model. The Figure shows the onset envelopes of three signals, all shaped with cosine-squared rise functions. Two have identical rise time but differ in plateau pressure, and two share the plateau pressure but differ in rise time. Figure 1A illustrates that a fixed pressure threshold (horizontal dashed line) is reached at times (vertical dashed lines) that decrease with increasing signal level for a fixed rise time and increase with increasing rise time for a fixed level. Although these dependencies are qualitatively consistent with those of first-spike latencies of AN fibers on tone level and rise time, as illustrated for one fiber in Figure 1B [see also Heil and Irvine (1997)], a detailed quantitative analysis reveals systematic mismatches, as shown below. The time needed to reach the thresholdPthr (in Pascal) is equal to the measured latency L corrected forLmin and, according to Equation 1, is given by:
| Equation 2 |
The mismatch is best demonstrated in low-SR fibers, in which the interfering effects of spontaneous activity on measures of response latencies based on first spikes are negligible or absent (Heil and Irvine 1997). Figure 2, A andB, shows data from two such fibers (the fiber of Fig.2A is identical with that of Fig.1B). The mean first-spike latency measured is plotted along the ordinate, and the best fit of the model, with threshold pressure Pthr and transmission delayLmin as the two free parameters, is plotted along the abscissa. Data obtained with tones of different SPLs but of the same rise time (see key in A) are interconnected. If the model were adequate, data points ought to lie on the diagonal (continuous line). However, for high-level tones (bottom left data points), latencies are all shorter than predicted, with many being even shorter thanLmin obtained from the fit (left vertical dashed-dotted line), and for medium- to low-level tones latencies are longer than predicted. Basically similar deviations are seen in the data from a medium-SR (Fig. 2C) and a high-SR fiber (Fig. 2D). In these latter cases several data points were excluded from the fits, namely those judged to be dominated by spontaneous activity. The judgment was based on the observations that measured latencies were close to, or even longer than, “spontaneous” latency and that total spike numbers were low, sometimes as low as those recorded without stimulation. These data points are shown in Figure 2, C and D, by symbols disconnected from the others. Note that they scatter around the spontaneous latency (Fig. 2, horizontal dotted-dashed lines). In addition, the fixed threshold pressure model is unable to explain first spikes that were triggered during the plateau phase of the stimulus. Such data points are plotted at the extreme right (at 300 msec) in Figure 2, C and D.
Qualitatively similar mismatches between data and model were observed in all 89 fibers. Hence, the fixed pressure threshold model is clearly not suited to explain first-spike timing, as suspected earlier (Heil and Irvine, 1997). Sound power and intensity are proportional to the square of the sound pressure. So, ifPthr were constant,Pthr2would be constant, but because Pthr is not constant, fixed power or fixed intensity threshold models are also not suited.
It could be suspected that the misfit of the fixed pressure threshold might be caused by accommodation, i.e., an elevation of the threshold when it is approached slowly. If this were the case, latencies for low-level and long-rise-time tones would be longer than they would be if the threshold were constant, resulting in functions that would be curved upward in the plots of Figure 2. Thus, the observed downward curvature of the functions is opposite to that expected from accommodation. Indeed, the shapes reflect the fact that as stimulus level is decreased or rise time is increased, the pressure at which the first spike is triggered decreases. This observation strongly points to an integration model in which the first spike is triggered whenever some integrated aspect of the stimulus reaches a threshold criterion, as detailed below.
Pressure integration threshold model
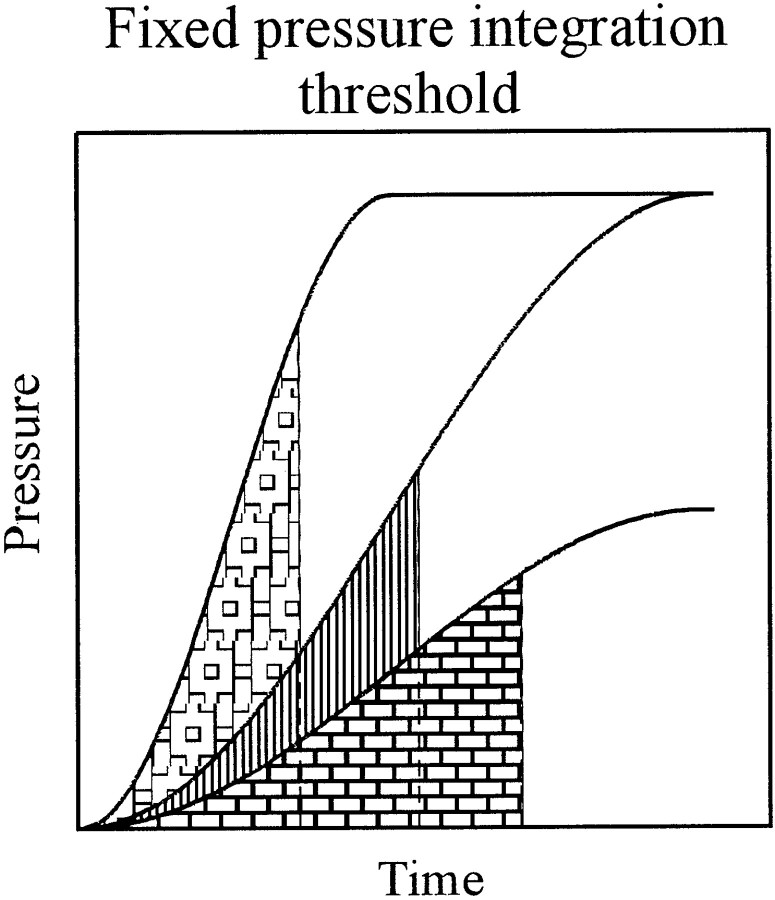
Figure 3 provides a scheme of a model with a fixed pressure integration threshold. The first spike after stimulus onset is triggered as soon as the integral of pressure over time reaches a fixed threshold, i.e., as soon as some fixed area under the stimulus is filled (Fig. 3, the shaded areas are equal in size). Note that with such a model the trigger time also depends on plateau pressure and rise time, in a manner that is qualitatively similar to but quantitatively different from that predicted by the fixed pressure threshold model (compare Fig.1A), and that the first spike is triggered at different pressures, depending on the time course of the envelope. However, it is not a priori clear which property of the acoustic wave might be integrated. At high frequencies, the DC component of the receptor potential of the IHC provides the main driving force for spike initiation in afferent AN fibers (Cheatham and Dallos, 2000). Russell and coworkers (Russell and Sellick 1978; Cody and Russell, 1987) have reported that the DC component of the inner hair cell closely follows the stimulus envelope, i.e., P(t), whereasGoodman et al. (1982), Smith et al. (1983), Patuzzi and Sellick (1983), and Dallos (1985) have provided evidence that near threshold this component grows faster than linear, possibly with the square of the pressure, i.e., withP(t)2 or stimulus intensity (see also Geisler, 1990; Müller et al., 1991; Yates, 1991). If intensity were integrated, a particular acoustic energy (per unit area) would be required for threshold.
Fig. 3.
Scheme of a fixed pressure integration threshold model. The filled areas are all equal in size and represent a pressure integration threshold. Note that threshold is reached at different pressures and at times that depend on signal level for a fixed rise time and on rise time for a fixed level, qualitatively similar to, but quantitatively different from, a fixed pressure threshold (compare with Fig. 1A).
To examine this issue we first fitted our data with a model where the threshold Tthr is equal to the integral, from onset to the latency L corrected forLmin, of the time course of the pressure P(t) raised to the power q, with Tthr,Lmin, and q as free parameters:
| Equation 3 |
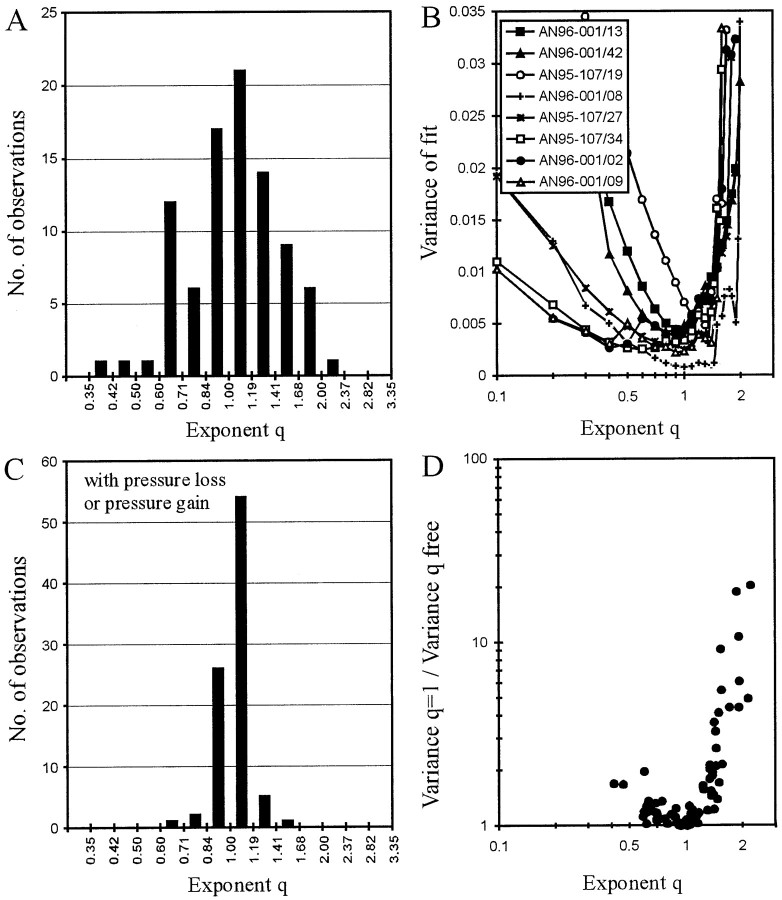
The fits should yield exponents q ≈ 1 if pressure were integrated and q ≈ 2 if intensity were integrated. Figure 4Ashows, for the 89 AN fibers, the distribution of the exponentq obtained from the fits of this free integration threshold model, which provided an excellent descriptor of the data from each AN fiber (see below). The distribution of the exponent q, along both a linear and a logarithmic axis, resembles a normal one (Kolmogoroff–Smirnoff test; p = 0.447 > 0.3 for the log axis) with a geometric mean of 1.044, i.e., very close to 1. We chose a logarithmic axis of q in Figure 4Abecause exponents of 0.5 and 2 yield functions that are mirror-images of one another around the diagonal of exponent 1. The SD in the log plot leads to an error interval from 0.74 to 1.47 on a linear axis. The nature of the distribution therefore suggests that the errors are random and stochastic. Figure 4B shows, for eight selected fibers, plots of the variance of the fit against the exponentq at fixed values between 0.1 and 2. It is clear from these functions that their minima are generally well defined. All functions are asymmetric in that the variance increases more rapidly forq greater than the optimum value. These data strongly suggest that the auditory system up to the level at which the first spike is generated acts as an integrator of pressure and not as one of intensity.
Fig. 4.
Evaluation of the integration threshold model. A, Distribution of the exponent qobtained from fits of Equation 3. Note that the 89 values are distributed around 1, and not 2, suggesting a pressure integration threshold rather than an intensity integration or energy threshold.B, Plots of the variance of the fits of Equation 3 for exponents q fixed at values between 0.1 and ∼2 (ordinate) for eight selected AN fibers. Note that the minima are generally well defined and are near 1, although additional local minima can be found below and above 1. C, Distribution of the exponent q obtained from fits of Equation 3, but including the pressure loss or gain,Pc, fixed at the value obtained from fits of Equation 4. Note that the exponent q is very narrowly distributed around 1 (compare A). Hence, a pressure integration threshold model with leakage/additional inflow can explain the first-spike timing of all AN fibers. D, Ratio of variances obtained from fits of Equation 3 withq = 1, i.e., with a fixed pressure integration threshold, and with q as a free parameter plotted against q. Note that the variance ratio increases steeply with increasing q for q > 1.
Some functions in Figure 4B have two local minima at different q values. For example, the function of AN96-001/09 (▵) has a global minimum near 0.9, but an additional local minimum near 0.4. The function for AN96-001/02 (●) is very similar in shape, but here the dip at 0.4 constitutes the global minimum and that at 0.9 a local minimum. Such functions are largely responsible for the finding that the distribution of the exponent q extends to rather low and high values (Fig. 4A). Nevertheless, some functions have an unambiguous global minimum at exponents >1 (Fig. 4B, ○, AN95-107/19). It seems unlikely that the first spike of such fibers is driven by integration of intensity or some mixture of intensity and pressure. Rather, some additional factor might be responsible for the clear deviation ofq from 1 in these cases.
To obtain a clue as to the nature of this possible additional factor, we next refitted all 89 data sets with Equation 3, but now keepingq fixed at 1, i.e., with a fixed pressure integration threshold model. The increase in variance compared with the fit withq as a free parameter could be pronounced (up to factors of ∼20) for fibers with q larger than 1, but was small (i.e., by a factor of <2) for all fibers with q close to and smaller than 1 (Fig. 4D). This asymmetry in variance increase is consistent with the asymmetric shape of the variance versusq functions (Fig. 4B). In other words, for most fibers a simple fixed pressure integration threshold model provides an excellent descriptor of the data.
Data from four AN fibers, three identical with those of Figure 2, are shown in Figure 5. Note that for the low-SR fibers in Figure, 5, A and B, the model accurately predicts first-spike latencies from the shortest up to the longest values obtained, namely 160 msec for AN96-001/13 and 147 msec for AN96-001/42, which are near the tone duration of 200 msec used in these experiments. Remarkably, for both of those fibers and for each rise time, the model also correctly predicts the absence of a response to 200 msec tones of a level 10 dB below the lowest level that did evoke a response. For such low-level tones, the pressure integration thresholds of both fibers are not reached within the duration of the tones, i.e., those fibers would likely have required longer tone durations at such low SPLs to reach threshold. For the high-SR fibers in Figure 5, C and D, the model accurately predicts first-spike latencies up to values obtained from spontaneous activity (horizontal dashed-dotted lines).
Pressure integration threshold model with leakage or additional inflow
Despite the good fit, the data from approximately one-quarter of the fibers, namely those in which q was considerably larger than 1 and the variance increased drastically by fixing q at 1 (Fig. 4D), showed small, but systematic, deviations from the fixed pressure integration threshold model. This observation suggests that an extension of the model could lead to a better description of the data. Figure 6,A and C, illustrates two clear examples, both fibers of medium SR. The curvature of the functions around the diagonal is opposite to that seen with the fixed pressure threshold model (compare Fig. 2). As discussed above, this suggests that accommodation, or leaky pressure integration, might cause the systematic deviations of the data points from the fixed pressure integration threshold model in these two fibers. We therefore extended this model by assuming, in new fits of the pressure integration threshold model, the loss (or gain, see below) of some constant pressurePc (in Pascal) to the integration process.
| Equation 4 |
In these fits, Pc leads to a linear time-dependent shift of the thresholdTthr (L −Lmin) with a slope ofPc and an intercept ofT0 =Tthr (L =Lmin). Of course, the time-dependent shift is measurable only at the instant when the first spike occurs. Because we placed no restrictions onPc, not even with respect to its sign,Pc could be positive or negative. A negative Pc can be viewed as a loss of a constant pressure to the integrator, e.g., resulting from leakage, and leads to an increase of threshold over time. Conversely, a positivePc can be viewed as a gain of a constant pressure to the integrator, e.g., resulting from additional inflow, and leads to a decrease of threshold over time. Figure 6,B and D, shows that the inclusion of the third free parameter Pc, which was −1250 μPa for fiber AN96-001/44, corresponding to a loss of 33 dB SPL, and −63 μPa for AN95-107/19, corresponding to a loss of 7 dB SPL, brings measured and fitted data points into better agreement, again with the exception of data points dominated by spontaneous activity. The same effect of a negative Pc was observed in all other fibers in which the data points deviated in the same systematic way from the fixed pressure integration threshold model. For fibers characterized by a pressure gain, i.e., by a positivePc, the simple pressure integration threshold model, without this third parameter, provided an excellent fit to the data. In other words, although for these fibers the functions relating measured to predicted latency must be curved slightly downward, this was generally not obvious to the eye (Fig.5C,D).
Comparison of models and error and reliability analyses
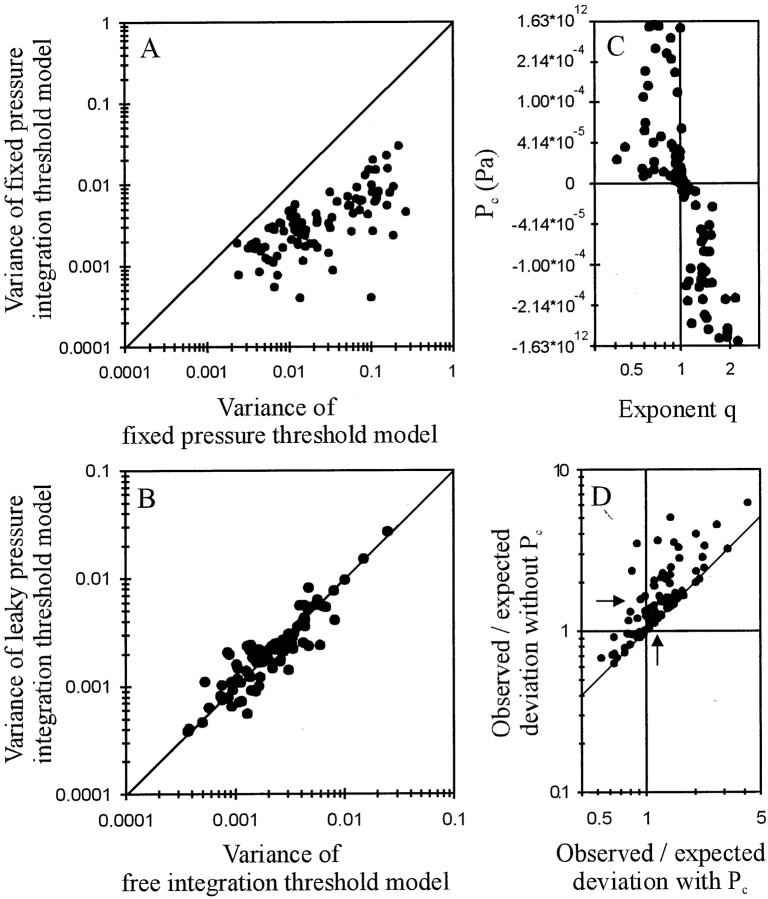
For every AN fiber, the fixed pressure integration threshold model provided a much better fit to the data than the fixed pressure threshold model (both have two free parameters), the variance of the latter being higher by factors ranging from 1.2 to 240 with a geometric mean of 7 (Fig. 7A). Overall, the fits with the pressure integration threshold model with leakage or additional inflow, i.e., with Pc as the third free parameter and q fixed at 1 (Eq. 4), were as good as the fits with the free integration threshold model, i.e., without pressure loss or gain (i.e.,Pc = 0) and q as the third free parameter (Eq. 3) (Fig. 7B) (p = 0.424 > 0.3; Wilcoxon matched-pairs signed rank test). Moreover, negative values of Pc were strictly associated with exponents q > 1, and positive values were associated with exponents q < 1 (Fig.7C). When we refitted the data with the free integration threshold model, but this time included the pressure loss or gain, Pc, fixed for each fiber at the value resulting from the above fits with Equation 4, we obtained exponent q very close to 1 (Fig. 4C). The distribution of q with pressure loss or gain was much narrower (error interval from 0.94 to 1.15) than that of qwithout pressure loss or gain, although likely not normal (Kolmogoroff–Smirnoff test, p = 0.009), but had a very similar geometric mean, namely 1.036 (Fig. 4, compare A,C). This result allows us to largely account for the deviations of the data from the two-parametric fixed pressure integration model by the addition of parameterPc. In the following we will use this pressure integration model with leakage or additional inflow, rather than the free integration threshold model, because it includes only a linear correction of the input variable P(t).
Fig. 7.
A, Scatterplot of the variance obtained with a fixed pressure integration threshold model versus that obtained with a fixed pressure threshold model. Both models have two free parameters, namely Lmin (in milliseconds) and threshold (in Pascal times millisecond and in Pascal, respectively). Solid line is the diagonal. Note that for all 89 AN fibers, the pressure integration threshold model provides a much better fit. B, Scatterplot of the variance obtained with a pressure integration threshold model with leakage/additional inflow versus the variance obtained with a free integration threshold model. Both have three free parameters and describe the data equally well. C, Scatterplot of pressure gain or loss (in Pascal), obtained from the fits with a pressure integration threshold model with leakage/additional inflow, versus the exponentq, obtained from fits with a free integration threshold model. Note that values of q greater (smaller) than 1 are associated with negative (positive) values ofPc, i.e., with pressure loss (pressure gain). Also note that the data are plotted along a nonlinearly transformed ordinate, where y = arctan(104 × x). This transformation offers high resolution near zero, where most values are located, and lower resolution of the fewer extreme values. A logarithmic axis is not useful, because Pccan be negative, and a linear axis does not allow the systematic trends around zero to be seen when all data are plotted. D, Scatterplot of the ratios between observed and expected deviations obtained with the fixed pressure integration threshold model (ordinate) against those ratios obtained with the pressure integration model with leakage or additional inflow (abscissa). For calculation of those deviations see Results. Arrows represent the geometrical means of the two distributions, and the oblique linerepresents the diagonal.
The variance of the fixed pressure integration threshold model (two free parameters) was larger than that of the model with leakage or additional inflow (three free parameters) by factors ranging from just >1 to ∼15 with a geometric mean of 1.6, indicating only relatively small improvements in the fits by inclusion ofPc in many fibers. However, across the population, only the latter model could almost fully account for the observed deviations of the data points by the deviations expected from the variability of first-spike timing, as explained in the following. To derive the expected deviation, we first divided, for each stimulus, the SEM of the first-spike latency by its corresponding mean. For each fiber, these normalized SEMs were relatively independent of the mean first-spike latency. We next extracted, for each fiber, the square root of the sum of the squares of the normalized SEMs across the different stimuli included in the fit and divided it by the square root of the number of those stimuli. This measure yields the mean expected deviation between measured and predicted (by a perfect model) mean latencies based on the statistical uncertainties attributable to the inherent variability of first-spike timing. The mean observed deviation between measured and predicted (by the model under consideration) mean latencies was calculated in an analogous way, with the normalized SEM substituted by the ratio of the absolute difference between measured and predicted mean latency and the predicted latency.
Figure 7D shows a scatterplot of the ratios between observed and expected deviations obtained with the fixed pressure integration threshold model (ordinate) against those ratios obtained with the pressure integration model with leakage or additional inflow (abscissa). For the latter model, the ratios range from ∼0.5 to 4. The geometric mean of 1.20 (vertical arrow) is remarkably close to the mean of 1 theoretically obtained if, across the sample, the observed deviations were fully accounted for by each fiber's inherent variability of first-spike timing. For the fixed pressure integration threshold model, i.e., withoutPc, the ratio of observed and expected deviations was larger for every fiber. Ratios ranged from ∼0.6 to 6 with a geometric mean of 1.55 (horizontal arrow). Thus, across the sample, the inclusion of Pcreduces the fraction of the deviations that is unexplained by the variability of first-spike timing by nearly two-thirds. This analysis also reveals that the pressure integration model with leakage/additional inflow need not really be extended further, because the effects of any additional free parameter of reducing the unexplained 20% of deviations can only be small. Finally, an ANOVA revealed that the distributions of ratios obtained with the fixed pressure integration threshold model and with the pressure integration model with leakage or additional inflow are significantly different (F(1,176) = 14.54;Fcrit = 3.89; p < 0.0002). Thus, a pressure integration model with three free parameters, namely a minimum delay Lmin (in milliseconds), a threshold T0 (in Pascal times millisecond), and a pressure loss or gainPc (in Pascal) provides an excellent descriptor of the first-spike timing of all AN fibers.
For a few representative AN fibers, namely AN96-001/13 (Fig.5A, low-SR); AN95-107/19 (Fig. 6C,D, medium-SR), and AN96-001/09 (Fig. 5D, high-SR), we also performed an analysis of the reliability of the three parameters,Lmin,T0, andPc, of this model as estimated from the fits. This was done as follows. For each fiber, we assumed that the parameters obtained from the fits with the measured latencies were perfect. We then generated 50 new sets of latencies by multiplying each measured latency with a random number drawn from a normal distribution with a mean of 1 and an SD equal to the mean observed deviation between measured and predicted mean latencies in that fiber (calculated as explained above and amounting to 16.0, 10.4, and 9.2% for fibers AN96-001/13, AN95-107/19, and AN96-001/09, respectively). Each new set of latencies was then fitted with the model in the same way the measured latencies had been fitted. The meanLmin (3.9, 1.9, and 1.6 msec for fibers AN96-001/13, AN95-107/19, and AN96-001/09, respectively), meanT0 (8.8 * 10−2, 8.1 * 10−4, and 7.4 * 10−4Pa × msec), and mean Pc (1.2 * 10−4, −6.3 * 10−5, and 4.0 * 10−5Pa) obtained from the 50 fits of simulated data were essentially identical to the corresponding parameters estimated from the actual data. Their coefficients of variation (SD/absolute mean) were 8.1, 3.2, and 4.1% for Lmin, 11.4, 10.0, and 14.9% for T0, and 107.4, 4.2, and 31.2% for Pc for fibers AN96-001/13, AN95-107/19, and AN96-001/09, respectively. Thus, it appears that, on average, the relative error of Lmin is the smallest, followed by that of T0and that of Pc.
Variation of fit parameters with spontaneous rate and characteristic frequency
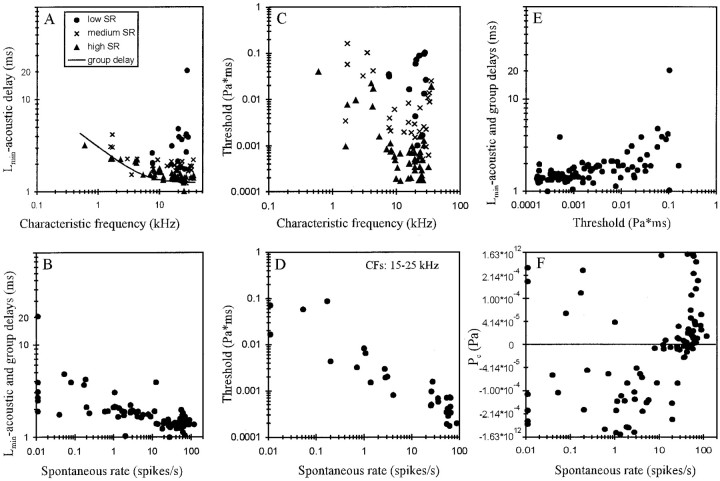
Figure 8A shows that overall the transmission delay,Lmin, here corrected for an acoustic delay of 0.2 msec, decreased with increasing CF. In those frequency ranges, where our data also contain a good sample of low-SR fibers, it is obvious that low-SR fibers tended to have the longest and high-SR fibers the shortest Lmin. Figure8A also shows that the variation ofLmin in those CF ranges is as large as, or larger than, the variation ofLmin with CF, in agreement with observations of Rhode and Smith (1985). Also, at any given CF the shortest corrected Lmin closely matches the group delay estimated by Goldstein et al. (1971) from phase-locked responses of cat AN fibers to pure tones (Fig.8A, continuous line). We therefore used their empirical equation to further correct our estimates ofLmin for differential delays related to CF and relative to 40 kHz. Such differences might arise, for example, as a consequence of different traveling wave delays and delays introduced by different axonal lengths from the IHC to the site of recording (Liberman and Oliver, 1984). Figure 8Bshows a plot of these corrected estimates ofLmin against spontaneous rate. There is a clear trend for the delays to decrease with increasing spontaneous rate from ∼2–5 msec for low-SR fibers (20 msec in one case) down to ∼1–2 msec for high-SR fibers.
Fig. 8.
A, Scatterplot of the transmission delay Lmin, corrected for the acoustic delay of 0.2 msec, against CF. Note the decrease ofLmin with increasing CF. Also note that at any given CF high-SR fibers tend to have the shortest and low-SR fibers the longest Lmin (seekey). At any given CF, the shortestLmin closely matches with the group delay estimated by Goldstein et al. (1971) and given by 1.25 × [1 + (6/CF)2]1/4 (continuous line).B, Scatterplot ofLmin, corrected for acoustic and group delays, relative to 40 kHz, against spontaneous rate. Note the decrease of Lmin with increasing spontaneous rate. C, Scatterplot of pressure integration thresholdT0 (in Pascal times millisecond) against CF. Note that threshold varies over more than three orders of magnitude. Thresholds are lowest between ∼10 and 25 kHz (symbolsas in A). At any given CF, high-SR fibers have the lowest and low-SR fibers the highest thresholds. D, Scatterplot of pressure integration thresholdT0 (in Pascal times millisecond) against spontaneous rate for fibers with CFs between 15 and 25 kHz. Note the tight correlation. E, Scatterplot ofLmin, corrected for acoustic and group delays, against pressure integration thresholdT0. Note the increase ofLmin with increasing threshold.F, Scatterplot of pressure gain/pressure loss,Pc, against spontaneous discharge rate. Same nonlinearly transformed ordinate as in Figure7C. Note that pressure losses (negative values ofPc) were obtained from low-, medium-, and high-SR fibers, but pressure gains (positive values) were obtained almost exclusively from high-SR fibers.
Thresholds, T0, varied over more than three orders of magnitude from ∼0.0001 Pa × msec (i.e., ∼10 dB SPL × msec) to ∼0.2 Pa × msec (i.e., ∼80 dB SPL × msec), with thresholds being lowest between ∼10 and 25 kHz (Fig. 8C). Also, at any given CF, thresholds can vary by up to at least 60 dB, and high-SR fibers tended to have the lowest and low-SR fibers the highest thresholds. In fact, when the analysis is restricted to narrow frequency bands, then a tight negative correlation between threshold and spontaneous rate emerges. Figure 8Dshows this relationship for fibers with CFs between 15 and 25 kHz from our sample. These findings are reminiscent of the established relationships between spontaneous rate and threshold, defined conventionally as some criterion increase in average firing rate and measured in units of pressure (Sachs and Abbas, 1974; Liberman, 1978;Kim and Molnar, 1979; Geisler et al., 1985; Rhode and Smith, 1985;Winter et al., 1990; Yates, 1991; Versnel et al., 1992; Tsuji and Liberman, 1997).
Because, at any given CF, both Lminand threshold increase with decreasing spontaneous rate,Lmin also increases with increasing threshold. Figure 8E shows the relationship between threshold and Lmin, corrected for acoustic and group delays. A similar relationship is seen whenLmin is not corrected for such delays (data not shown). As a consequence, the differences in first-spike trigger times between fibers of different thresholds in response to a given stimulus are enhanced, rather than reduced or cancelled, as the spikes travel toward the cochlear nucleus.
Figure 8F illustrates the distribution of the pressure loss or gain, Pc, over spontaneous rate. The largest pressure losses were found in low- and medium-SR fibers. Pressure gains were seen in only five low-SR fibers (including AN96-001/13 and AN96-001/42) (Fig.5A,B) and two medium-SR fibers and in the majority of high-SR fibers. For these five low-SR fibers, the inclusion of Pc as an additional free parameter reduced the variance of the fit by <3% (the population average was ∼100%); hence the effect ofPc in these five fibers is negligible. Apart from those fibers, there appears to be a systematic trend forPc to increase, i.e., there is a continuous transition from pressure losses to pressure gains, with increasing spontaneous rate (Fig. 8F). Gains and losses in excess of 25 dB SPL were obtained only from fibers of rather low (<5 kHz) and rather high CF (>33 kHz) (data not shown).
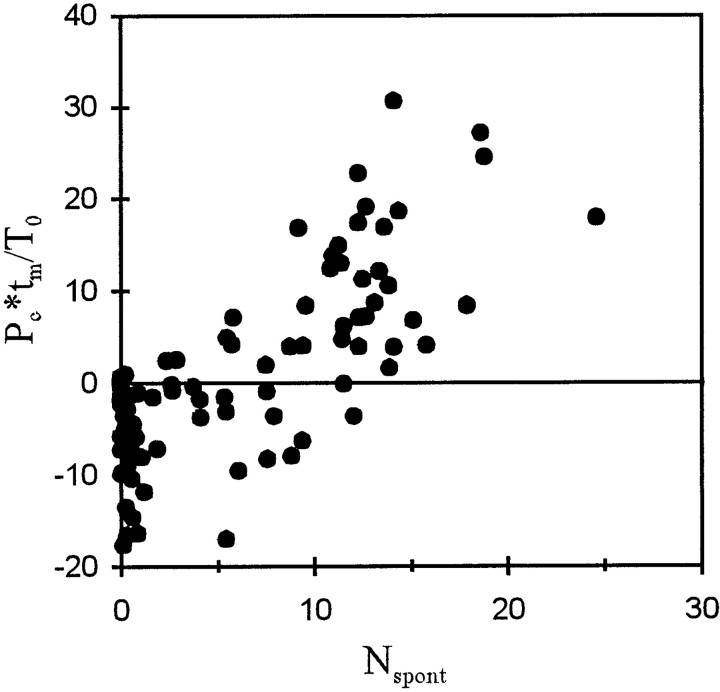
The processes that act as if there were constant pressure gains or losses, i.e., additional inflow to or leakage from the integrator, not only modify the timing of the first spike in response to acoustic stimulation, as shown above, but also appear to determine, or at least codetermine, the spontaneous activity of the fiber. To demonstrate this, we first calculated the product ofPc and the measuring timetm (in our case 210 msec), i.e., the integral of pressure gain or loss during a single observation interval in the absence of intentional acoustic stimulation. This product was next divided by T0, i.e., the pressure integration threshold, to obtain the number of times this threshold is reached (or lost) during the interval. In Figure9, this number is plotted against the average number of spontaneous spikes,Nspont, recorded within such an observation interval. Although there is considerable scatter of the data points, the number of times the threshold is reached or lost clearly increases with the number of spontaneous spikes. To a first approximation the increase is linear. A linear fit yielded an intercept of −6.4(±1.0) and a slope of 1.25(±0.12), only slightly above 1, andr2 = 0.555 (n = 89). For Pc = 0, this regression yields a Nspont of 5.1 spikes, corresponding to a spontaneous rate of ∼24 spikes/sec. This rate may therefore be viewed as a base rate, which is increased by additional inflow (positive Pc) or decreased by leakage (negative Pc).
Fig. 9.
Scatterplot of the number of times the pressure integration threshold of a fiber, T0, is reached by integration of the pressure gain/pressure loss,Pc, during a 210 msec interval,tm, (Pc ×tm/T0) against the average number of spikes,Nspont, measured in such an interval in the absence of intentional acoustic stimulation. Note the close correlation with a slope near 1 (for further explanations, see Results).
DISCUSSION
Our detailed analysis of the timing of the first spike of AN fibers in response to CF tones of different levels and rise times has revealed that the data from each fiber can be well accounted for by a simple pressure integration model. They cannot be explained by models based on a fixed pressure threshold, a fixed intensity threshold, or an intensity integration threshold, i.e., an energy threshold. Consequently, it can be concluded that up to the level at which the first spike is generated, the system acts as an approximately linear integrator of the sound pressure. In its basic form our model only requires a threshold, T0, to be measured in units of pressure by time, and a constant transmission delay, Lmin. The inclusion of a constant pressure loss or gain, Pc, to the integrator leads to further improvement, although for most fibers only minor improvement, of the fits and also accounts for much of the variation in spontaneous discharge rates across fibers (Fig. 9). To keep our model as simple as possible, we used the stimulus envelope as the model's input and, as the first step, the timing of the first spike as the model's output. To explain our results we do not need to make any assumptions about the number and properties of filters, such as order, type, or cutoffs of bandpass and lowpass filters, nor about details of the input–output functions mediating rectification, nor about the series in which filters and rectifiers may be connected, as do other models of the auditory periphery, designed to model first-spike timing (Fishbach et al., 2001; Krishna and Semple, 2001) or other properties of AN fibers (Carney, 1993).
Parameters of the model, their physiological basis, and possible implications
The transmission delay
The transmission delay is thought to include the acoustic delay, a middle ear and frequency-dependent cochlear delay, a synaptic delay, and a spike conduction delay. The transmission delay, corrected for the acoustic delay, varied with CF in a manner consistent with previous reports (Anderson et al., 1971; Goldstein et al., 1971; Palmer and Russell, 1986). When further corrected for the frequency-dependent cochlear delay (composed of traveling wave delay and filter response time) (Smolders and Klinke, 1986), the transmission delay decreased systematically with increasing spontaneous rate from ∼2–5 msec for low-SR fibers (20 msec in one such fiber) to ∼1–2 msec for high-SR fibers (Fig. 8B). The axon diameters of AN fibers, both central and peripheral to the cell bodies in the spiral ganglion, including the unmyelinated portion between the IHC and the foramen nervosum, increase with increasing spontaneous rate (Liberman, 1982;Liberman and Oliver, 1984). However, it remains to be seen whether the substantial decrease in transmission delay with spontaneous rate can be accounted for entirely by differences in conduction velocities in fibers of different spontaneous rates, or whether synaptic differences contribute.
In aiming to define the precise mechanical input to the inner hair cells, Ruggero et al. (1986, 2000) have attempted to determine the phase of AN fiber excitation relative to that of basilar membrane motion by correcting spike times for a constant (independent of frequency and of the fiber's spontaneous rate) delay of 1 msec, thought to be introduced by the synapse and the spike conduction time to the site of recording. Our data show that at a given CF, this delay can vary considerably across fibers and is correlated with spontaneous rate and threshold. It is currently unclear whether there are defined relationships between the integral of pressure driving the first spike and those driving the subsequent spikes. So, we do not know whether some of the seemingly paradoxical observations made by Ruggero et al. (1987, 2000) could be resolved by considering the actual variation of transmission delays and the temporal integration of pressure as the driving force for spike initiation.
The envelope extractor and pressure integrator
The pressure envelope could be extracted by an appropriate rectifying process that could be realized by the transducer apparatus in cooperation with synaptic processes. The integration of the pressure envelope could rely, in principle, on the integration of transducer current. However, we feel this is rather unlikely because such a process could hardly account for the up to 1000-fold difference in pressure integration thresholds seen among fibers of very similar CFs (Fig. 8C,D). Although it has not yet been possible to physiologically characterize and label fibers that innervate the same individual IHC, there is strong evidence that a given IHC is innervated by fibers of different spontaneous rates (and thresholds). This follows from the observations that each IHC is innervated by ∼20 afferent fibers (Spoendlin, 1978) and that the position of a fiber's synapse on an IHC varies systematically with spontaneous rate (Liberman, 1982; Merchan-Perez and Liberman, 1996;Tsuji and Liberman, 1997). Hence, it is unlikely that the differences in AN fiber thresholds could be accounted for by differences in the sensitivities of IHCs of very similar CFs. Also, there is no evidence that neighboring IHCs would show such large differences in thresholds.
It is feasible, however, that differences in presynaptic and postsynaptic processes could account for the differences in fiber threshold. On the postsynaptic side, one could envisage differences in the postsynaptic currents required to evoke an action potential in the afferent fiber, which in turn might require different numbers of vesicles to be released, although there is no evidence for this from recordings of EPSPs (Siegel, 1992) or EPSCs (Glowatzki and Fuchs, 2001). Threshold differences may also arise through differences in efferent control via the lateral olivocochlear system (Puel, 2001).
Presynaptic differences seem even more feasible, particularly in the light of morphological observations (Merchan-Perez and Liberman, 1996). We suggest that the pressure integrator may have its basis in presynaptic calcium currents. In response to a given membrane potential of an IHC, including its resting potential in the absence of acoustic stimulation, there might be differences at the different presynaptic sites of the cell in the magnitude of calcium currents or in mechanisms of calcium clearance, with more influx of calcium per unit time, or less efficient clearance, at presynaptic sites contacted by high-SR fibers than at sites contacted by low-SR fibers. Such a scenario could not only explain the large differences in spontaneous rate, but also those in threshold, as well as the correlation between spontaneous rate and threshold (Fig. 8C) (see also Sachs and Abbas, 1974;Liberman, 1978; Kim and Molnar, 1979; Geisler et al., 1985; Rhode and Smith, 1985; Winter et al., 1990; Yates, 1991; Versnel et al., 1992;Tsuji and Liberman, 1997), at least qualitatively. Assume that a similar amount of calcium is needed at all presynapses of a given IHC to trigger a spike in each of its afferent fibers (Beutner et al., 2001). Then, the higher the spontaneous calcium current, the higher would be the spontaneous rate and the less would be the additional stimulus-driven amount of calcium required to reach the critical amount. Consequently, for any given stimulus, threshold would be reached first by the fibers with the highest spontaneous discharge rates and vice versa, just as observed in our data. According to this view, a low threshold is a direct consequence of a high spontaneous calcium current, which in turn leads to a high spontaneous discharge rate and vice versa. If a given stimulus led to the same relative increase of the spontaneous calcium currents at all presynapses, threshold would decrease with an increasing spontaneous rate with a slope of −1 in a log–log plot. The shallower slope observed (Fig.8D) [see also Tsuji and Liberman (1997), their Fig. 3] could result, for example, if the stimulus-driven relative increase of the calcium current were smaller for higher spontaneous currents. This seems plausible given that there will be an upper limit to the maximum calcium current possible at a given presynaptic site. In that scenario, the spontaneous influx of calcium acts much like a constant pressure and may also mediate the effects summarized by the termPc in our model, which accounts for most of the variation of the spontaneous discharge rate between fibers (Fig. 9).
From the above considerations it is apparent that the integrator can be conceptualized using the metaphor of a barrel that has an inflow component that is directly proportional to P(t) and an inflow/outflow component that is constant and proportional toPc. The first spike is triggered when the amount of fluid in the barrel reaches the critical value. To achieve the observed long integration times with electrical circuit elements, e.g., RC elements, a very large resistor or capacitor, or both, would be required, which may be difficult to realize. However, fast and efficient calcium clearance systems might readily enable a calcium influx proportional to pressure and essentially unimpeded by its intracellular accumulation.
A note on the threshold
We have reasoned here that the first spike after the onset of a stimulus is triggered when that stimulus reaches an AN fiber's threshold. This analysis has shown that it is not sufficient to describe threshold as a function of pressure only. Rather, threshold is a function of pressure and time. Consequently, low-SR fibers are not less sensitive than high-SR fibers with respect to the SPL of a stimulus needed for excitation, as seems to be implied by measuring thresholds in dB SPL (Narayan et al., 1998; Köppl and Yates, 1999). In response to a given stimulus, low-SR fibers simply need to integrate over longer periods of time than do high-SR fibers to reach threshold, or viewed from the brain's perspective, the first spike reports on a shorter or longer stimulus history, depending on the fiber's threshold.
Footnotes
This study was supported in part by the Deutsche Forschungsgemeinschaft (He 1721/4-1, He 1721/5-1, and Schu 1272/1-2). We are grateful to Prof. Dexter R. F. Irvine in whose laboratory and with whose help the data were recorded. We are also grateful to Profs. Egbert de Boer, Dexter R. F. Irvine, Alan R. Palmer, and Dr. Michael Brosch for helpful comments on an earlier version of this manuscript, and to many colleagues for discussion.
Correspondence should be addressed to Dr. Peter Heil, Leibniz Institute for Neurobiology, Brenneckestrasse 6, D-39118 Magdeburg, Germany. E-mail: peter.heil@ifn-magdeburg.de.
REFERENCES
- 1.Anderson DJ, Rose JE, Hind JE, Brugge JF. Temporal position of discharges in single auditory nerve fibers within the cycle of a sine-wave stimulus: frequency and intensity effects. J Acoust Soc Am. 1971;49:1131–1139. doi: 10.1121/1.1912474. [DOI] [PubMed] [Google Scholar]
- 2.Beutner D, Voets T, Neher E, Moser T. Calcium dependence of exocytosis and endocytosis at the cochlear inner hair cell afferent synapse. Neuron. 2001;29:681–690. doi: 10.1016/s0896-6273(01)00243-4. [DOI] [PubMed] [Google Scholar]
- 3.Carney LH. A model for the responses of low-frequency auditory-nerve fibers in cat. J Acoust Soc Am. 1993;93:401–417. doi: 10.1121/1.405620. [DOI] [PubMed] [Google Scholar]
- 4.Cheatham MA, Dallos P. The dynamic range of inner hair cell and organ of Corti responses. J Acoust Soc Am. 2000;107:1508–1520. doi: 10.1121/1.428437. [DOI] [PubMed] [Google Scholar]
- 5.Cody AR, Russell IJ. The responses of hair cells in the basal turn of the guinea-pig cochlea to tones. J Physiol (Lond) 1987;383:551–569. doi: 10.1113/jphysiol.1987.sp016428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dallos P. Response characteristics of mammalian cochlear hair cells. J Neurosci. 1985;5:1591–1608. doi: 10.1523/JNEUROSCI.05-06-01591.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.de Boer E. Auditory time constants: a paradox? In: Michelsen A, editor. Time resolution in auditory systems. Springer; Berlin: 1985. pp. 141–158. [Google Scholar]
- 8.Evans EF. Cochlear nerve and cochlear nucleus. In: Keidel WD, Neff WD, editors. Handbook of sensory physiology: auditory system. Springer; Berlin: 1975. pp. 1–108. [Google Scholar]
- 9.Fishbach A, Nelken I, Yeshurun Y. Auditory edge detection: a model for physiological and psychoacoustical responses to amplitude transients. J Neurophysiol. 2001;85:2303–2323. doi: 10.1152/jn.2001.85.6.2303. [DOI] [PubMed] [Google Scholar]
- 10.Florentine M, Fastl H, Buus S. Temporal integration in normal hearing, cochlear impairment, and impairment simulated by masking. J Acoust Soc Am. 1988;84:195–203. doi: 10.1121/1.396964. [DOI] [PubMed] [Google Scholar]
- 11.Garner WR. The effect of frequency spectrum on temporal integration of energy in the ear. J Acoust Soc Am. 1947;19:808–815. [Google Scholar]
- 12.Geisler CD. Evidence for expansive power functions in the generation of the discharges of “low- and medium spontaneous” auditory-nerve fibers. Hear Res. 1990;44:1–12. doi: 10.1016/0378-5955(90)90017-j. [DOI] [PubMed] [Google Scholar]
- 13.Geisler CD, Deng L, Greenberg SR. Thresholds for primary auditory fibers using statistically defined criteria. J Acoust Soc Am. 1985;77:1102–1109. doi: 10.1121/1.392228. [DOI] [PubMed] [Google Scholar]
- 14.Glowatzki E, Fuchs PA. Excitatory postsynaptic currents in afferent terminals on inner hair cells. Abstr Assoc Res Otolaryngol. 2001;24:3859. [Google Scholar]
- 15.Goldstein JL, Baer T, Kiang NYS. A theoretical treatment of latency, group delay, and tuning characteristics for auditory-nerve responses to clicks and tones. In: Sachs MB, editor. Physiology of the auditory system. National Academy Consultants; Baltimore: 1971. pp. 133–156. [Google Scholar]
- 16.Goodman DA, Smith RL, Chamberlain SC. Intracellular and extracellular responses in the organ of Corti of the gerbil. Hear Res. 1982;7:161–179. doi: 10.1016/0378-5955(82)90012-0. [DOI] [PubMed] [Google Scholar]
- 17.Heil P. Auditory onset responses revisited: I. First-spike timing. J Neurophysiol. 1997;77:2616–2641. doi: 10.1152/jn.1997.77.5.2616. [DOI] [PubMed] [Google Scholar]
- 18.Heil P, Irvine DRF. On determinants of first-spike latency in auditory cortex. NeuroReport. 1996;7:3073–3076. doi: 10.1097/00001756-199611250-00056. [DOI] [PubMed] [Google Scholar]
- 19.Heil P, Irvine DRF. First-spike timing of auditory-nerve fibers and comparison with auditory cortex. J Neurophysiol. 1997;78:2438–2454. doi: 10.1152/jn.1997.78.5.2438. [DOI] [PubMed] [Google Scholar]
- 20.Kiang NYS, Watanabe T, Thomas EC, Clark LF. Discharge patterns of single fibers in the cat's auditory nerve. MIT Res Monograph. 1965;35:1–151. [Google Scholar]
- 21.Kim DO, Molnar CE. A population study of cochlear nerve fibres: comparison of spatial distributions of average rate and phase-locking measures of responses to single tones. J Neurophysiol. 1979;42:16–30. doi: 10.1152/jn.1979.42.1.16. [DOI] [PubMed] [Google Scholar]
- 22.Köppl C, Yates GK. Coding of sound pressure level in the barn owl's auditory nerve. J Neurosci. 1999;19:9674–9686. doi: 10.1523/JNEUROSCI.19-21-09674.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Krishna BS, Semple MN. A computational model for first-spike latency and variability in the auditory nerve. Abstr Assoc Res Otolaryngol. 2001;24:366. [Google Scholar]
- 24.Liberman MC. Auditory-nerve response from cats raised in a low-noise chamber. J Acoust Soc Am. 1978;63:442–455. doi: 10.1121/1.381736. [DOI] [PubMed] [Google Scholar]
- 25.Liberman MC. Single-neuron labeling in the cat auditory nerve. Science. 1982;216:1239–1241. doi: 10.1126/science.7079757. [DOI] [PubMed] [Google Scholar]
- 26.Liberman MC, Oliver ME. Morphometry of intracellularly labeled neurons of the auditory nerve: correlations with functional properties. J Comp Neurol. 1984;223:163–176. doi: 10.1002/cne.902230203. [DOI] [PubMed] [Google Scholar]
- 27.Merchan-Perez A, Liberman MC. Ultrastructural differences among afferent synapses on cochlear hair cells: correlations with spontaneous discharge rate. J Comp Neurol. 1996;371:208–221. doi: 10.1002/(SICI)1096-9861(19960722)371:2<208::AID-CNE2>3.0.CO;2-6. [DOI] [PubMed] [Google Scholar]
- 28.Müller M, Robertson D, Yates GK. Rate-versus-level functions of primary auditory nerve fibres: evidence for square law behaviour of all fibre categories in the guinea pig. Hear Res. 1991;55:50–56. doi: 10.1016/0378-5955(91)90091-m. [DOI] [PubMed] [Google Scholar]
- 29.Narayan SS, Temchin AN, Recio A, Ruggero MA. Frequency tuning of basilar membrane and auditory nerve fibers in the same cochleae. Science. 1998;282:1882–1884. doi: 10.1126/science.282.5395.1882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Palmer AR. Physiology of the cochlear nerve and cochlear nucleus. Br Med Bull. 1987;43:838–855. doi: 10.1093/oxfordjournals.bmb.a072221. [DOI] [PubMed] [Google Scholar]
- 31.Palmer AR, Russell IJ. Phase-locking in the cochlear nerve of the guinea-pig and its relation to the receptor potential of inner hair-cells. Hear Res. 1986;24:1–13. doi: 10.1016/0378-5955(86)90002-x. [DOI] [PubMed] [Google Scholar]
- 32.Patuzzi R, Sellick PM. A comparison between basilar membrane and inner hair cell receptor potential input-output functions in the guinea-pig cochlea. J Acoust Soc Am. 1983;74:1734–1741. doi: 10.1121/1.390282. [DOI] [PubMed] [Google Scholar]
- 33.Plomp R, Bouman MA. Relation between hearing threshold and duration for tone pulses. J Acoust Soc Am. 1959;31:749–758. [Google Scholar]
- 34.Puel JL. In vivo studies of olivocochlear efferents. Abstr Assoc Res Otolaryngol. 2001;24:492. [Google Scholar]
- 35.Rajan R, Irvine DRF, Cassell JF. Normative N1 audiogram data for the barbiturate-anesthetized domestic cat. Hear Res. 1991;53:153–158. doi: 10.1016/0378-5955(91)90222-u. [DOI] [PubMed] [Google Scholar]
- 36.Rhode WS, Smith PH. Characteristics of tone-pip response patterns in relationship to spontaneous rate in cat auditory nerve fibers. Hear Res. 1985;18:159–168. doi: 10.1016/0378-5955(85)90008-5. [DOI] [PubMed] [Google Scholar]
- 37.Ruggero MA. Physiology and coding of sound in the auditory nerve. In: Popper AN, Fay RR, editors. The mammalian auditory pathway: neurophysiology. Springer; New York: 1992. pp. 34–93. [Google Scholar]
- 38.Ruggero MA, Robles L, Rich NC. Basilar membrane mechanics at the base of the chinchilla cochlea. II. Responses to low-frequency tones and relationship to microphonics and spike initiation in the VIII nerve. J Acoust Soc Am. 1986;80:1375–1383. doi: 10.1121/1.394390. [DOI] [PubMed] [Google Scholar]
- 39.Ruggero MA, Narayan SS, Temchin AN, Recio A. Mechanical bases of frequency tuning and neural excitation at the base of the cochlea: comparison of basilar-membrane vibrations and auditory-nerve-fiber responses in chinchilla. Proc Natl Acad Sci USA. 2000;97:11744–11750. doi: 10.1073/pnas.97.22.11744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Russell IJ, Kössl M. The voltage responses of hair cells in the basal turn of the guinea-pig cochlea. J Physiol (Lond) 1991;435:493–511. doi: 10.1113/jphysiol.1991.sp018521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Russell IJ, Sellick PM. Intracellular studies of hair cells in the mammalian cochlea. J Physiol (Lond) 1978;284:261–290. doi: 10.1113/jphysiol.1978.sp012540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Sachs MB, Abbas PJ. Rate versus level functions for auditory-nerve fibers in cats: tone-burst stimuli. J Acoust Soc Am. 1974;56:1835–1847. doi: 10.1121/1.1903521. [DOI] [PubMed] [Google Scholar]
- 43.Scharf B, Buus S. Audition I, stimulus, physiology, thresholds. In: Boff KR, Kaufman L, Thomas JP, editors. Handbook of perception and human performance: sensory processes and perception. Wiley; New York: 1986. pp. 14.1–14.71. [Google Scholar]
- 44.Siegel JH. Spontaneous synaptic potentials from afferent terminals in the guinea pig cochlea. Hear Res. 1992;59:85–92. doi: 10.1016/0378-5955(92)90105-v. [DOI] [PubMed] [Google Scholar]
- 45.Smith RL, Frisina RD, Goodman DA. Intensity functions and dynamic responses from the cochlea to the cochlear nucleus. In: Klinke R, Hartmann R, editors. Hearing–physiological bases and psychophysics. Springer; Berlin: 1983. pp. 112–117. [Google Scholar]
- 46.Smolders JWT, Klinke R. Synchronized responses of primary auditory fibre populations in Caiman crocodilus (L.) to single tones and clicks. Hear Res. 1986;24:89–103. doi: 10.1016/0378-5955(86)90052-3. [DOI] [PubMed] [Google Scholar]
- 47.Sokolich WG (1981) Closed sound delivery systems. United States Patent 4251686.
- 48.Spoendlin H. The afferent innervation of the cochlea. In: Nauta RF, Fernandez C, editors. Evoked electrical activity in the auditory nervous system. Academic; New York: 1978. pp. 21–39. [Google Scholar]
- 49.Tasaki I. Nerve impulses in individual auditory nerve fibers of guinea pig. J Neurophysiol. 1954;17:97–122. doi: 10.1152/jn.1954.17.2.97. [DOI] [PubMed] [Google Scholar]
- 50.Tsuji J, Liberman MC. Intracellular labeling of auditory nerve fibers in guinea pig: central and peripheral projections. J Comp Neurol. 1997;381:188–202. [PubMed] [Google Scholar]
- 51.Versnel H, Schoonhoven R, Prijs VF. Single-fibre and whole-nerve responses to clicks as a function of sound intensity in the guinea-pig. Hear Res. 1992;15:249–260. doi: 10.1016/0378-5955(92)90111-y. [DOI] [PubMed] [Google Scholar]
- 52.Winter IM, Roberston D, Yates GK. Diversity of characteristic frequency rate-intensity functions in guinea pig auditory nerve fibres. Hear Res. 1990;45:191–202. doi: 10.1016/0378-5955(90)90120-e. [DOI] [PubMed] [Google Scholar]
- 53.Yates GK. Auditory-nerve spontaneous rates vary predictably with threshold. Hear Res. 1991;57:57–62. doi: 10.1016/0378-5955(91)90074-j. [DOI] [PubMed] [Google Scholar]